Что такое входное сопротивление линии. Как рассчитать входное сопротивление по формуле. Какие факторы влияют на входное сопротивление линии. Почему важно учитывать входное сопротивление при проектировании электрических цепей.
Что такое входное сопротивление линии и как оно определяется
Входное сопротивление линии — это комплексная величина, характеризующая отношение напряжения к току на входе линии передачи. Оно определяется по формуле:
Zвх = Uвх / Iвх
где Zвх — входное сопротивление, Uвх — напряжение на входе линии, Iвх — ток на входе линии.
Входное сопротивление зависит от параметров самой линии, а также от нагрузки, подключенной к ее выходу. При этом важно учитывать, что входное сопротивление является комплексной величиной, то есть имеет действительную и мнимую части.
Формула для расчета входного сопротивления линии
Для расчета входного сопротивления линии используется следующая формула:
Zвх = Zв * (Zн
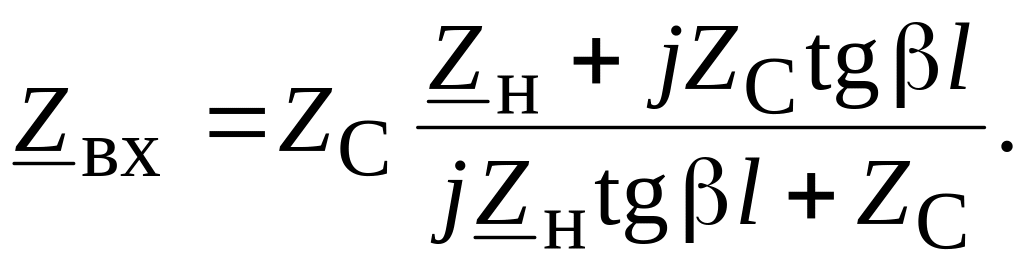
где:
Zв — волновое сопротивление линии
Zн — сопротивление нагрузки
γ — коэффициент распространения
l — длина линии
Эта формула позволяет рассчитать входное сопротивление для линии с произвольной нагрузкой. Рассмотрим несколько частных случаев.
Входное сопротивление согласованной линии
Если линия нагружена на сопротивление, равное ее волновому сопротивлению (Zн = Zв), то входное сопротивление будет равно волновому сопротивлению линии:
Zвх = Zв
Это идеальный случай, когда отсутствуют отражения волн от нагрузки. На практике к этому стремятся при проектировании линий передачи.
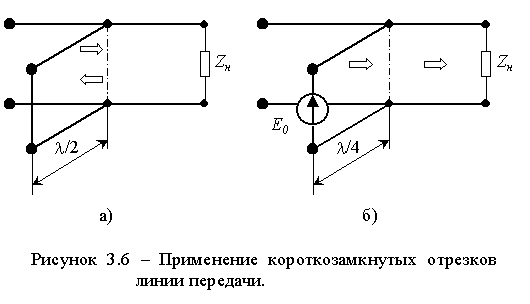
Входное сопротивление короткозамкнутой линии
Если выход линии замкнут накоротко (Zн = 0), то входное сопротивление определяется по формуле:
Zвх = jZвtg(γl)
В этом случае входное сопротивление является чисто реактивным и зависит от длины линии. При изменении длины линии входное сопротивление может быть как индуктивным, так и емкостным.
Входное сопротивление разомкнутой линии
Если выход линии разомкнут (Zн = ∞), то формула для входного сопротивления принимает вид:
Zвх = -jZвctg(γl)
Здесь также входное сопротивление является чисто реактивным, но его характер противоположен случаю короткого замыкания.
Зависимость входного сопротивления от длины линии
Входное сопротивление линии периодически изменяется при изменении ее длины. Период этих изменений равен половине длины волны в линии. Графики зависимости модуля входного сопротивления от длины для короткозамкнутой и разомкнутой линий показаны на рисунке:
[Здесь должен быть график зависимости |Zвх| от длины линии]
Как видно из графиков, входное сопротивление изменяется от нуля до бесконечности. Это свойство используется при создании согласующих устройств на основе отрезков линий.
Практическое применение расчета входного сопротивления
Знание входного сопротивления линии необходимо в следующих случаях:
- Согласование линии с источником сигнала
- Расчет коэффициента отражения и КСВ в линии
- Проектирование согласующих устройств
- Создание резонансных контуров на отрезках линий
- Расчет входных цепей антенн
Правильный учет входного сопротивления позволяет обеспечить эффективную передачу энергии от источника в нагрузку и минимизировать отражения в линии передачи.

Методы измерения входного сопротивления
На практике входное сопротивление линии можно измерить следующими способами:
- С помощью измерительного моста
- Методом стоячей волны
- Рефлектометрическим методом
- Используя векторный анализатор цепей
Каждый метод имеет свои особенности и область применения. Наиболее точные результаты дает использование современных векторных анализаторов цепей, позволяющих измерять комплексное входное сопротивление в широком диапазоне частот.
Влияние частоты на входное сопротивление линии
Входное сопротивление линии зависит от частоты сигнала. Это связано с тем, что электрическая длина линии (в длинах волн) изменяется с частотой. На низких частотах, когда длина линии много меньше длины волны, входное сопротивление близко к сопротивлению нагрузки. На высоких частотах проявляются волновые свойства линии.
График зависимости модуля входного сопротивления от частоты для линии с произвольной нагрузкой может выглядеть следующим образом:
[Здесь должен быть график зависимости |Zвх| от частоты]
Как видно из графика, на определенных частотах наблюдаются резонансы, когда входное сопротивление принимает максимальные или минимальные значения. Это свойство используется при создании узкополосных согласующих устройств.
Входное сопротивление и согласование линий
Одной из важных задач при проектировании линий передачи является их согласование. Согласование необходимо для обеспечения максимальной передачи мощности от источника в нагрузку и минимизации отражений в линии.
Условие согласования линии:
Zвх = Zг*
где Zг — внутреннее сопротивление генератора, * обозначает комплексное сопряжение.
Если это условие не выполняется, то часть энергии будет отражаться обратно к источнику, что приведет к появлению стоячих волн в линии и снижению эффективности передачи.
Для согласования линий используются различные методы:
- Четвертьволновые трансформаторы
- Шлейфы
- LC-цепи
- Ступенчатые переходы
Выбор конкретного метода зависит от требуемой полосы частот, допустимых потерь, габаритов и других факторов.

13.5. Входное сопротивление линии. 13. Цепи с распределенными параметрами. Теория электрических цепей. Курс лекций
- Главная
- Радиотехника и Электроника
- Теория электрических цепей
- 13. Цепи с распределенными параметрами
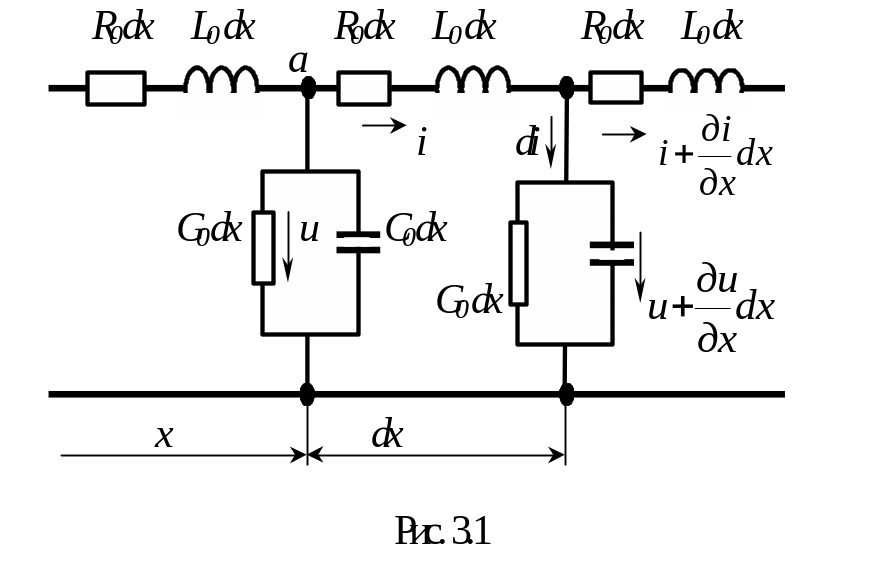
Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение для Zвх, используя уравнения передачи линии в форме (13.9 в):
Найдем выражение для Zвх, используя уравнения передачи линии в форме (13.9 в):
Рассмотрим некоторые частные режимы работы линии.
При согласованном включении линии (Zн = Zв) из (13.16) получим, что Zвх = Zв как и было установлено ранее.
Если выходные зажимы линии замкнуты накоротко (Zн = 0), формула (13.16) упрощается и принимает вид
В случае разомкнутых выходных зажимов (Zн = бесконечность)
Когда линия нагружена на произвольное сопротивление, не равное волновому (Zн <> Zв), можно пользоваться для расчетов общей формулой (13.16). Однако иногда удобно выразить Zвх через параметры XX и КЗ. Для этого разделим числитель и знаменатель (13.16) на
Данная формула позволяет по измеренным значениям сопротивлений XX и КЗ рассчитать входное сопротивление линии.
Существует еще одна форма представления входного сопротивления. Для получения ее перепишем выражение (13.16) после деления на
Для получения ее перепишем выражение (13.16) после деления на
в другом виде:
Обозначим
.
Тогда
Эта формула дает возможность по заданным параметрам Zв и Zн определить
и затем найти входное сопротивление линии.
Во всех случаях, когда нагрузка на конце линии не равна ее волновому сопротивлению, входное сопротивление определяется гиперболическим тангенсом комплексного аргумента. Чтобы дать представление о характере изменения входного сопротивления линии, на рис. 13.7, а показаны зависимости модулей сопротивлений XX и КЗ от длины линии, построенные в соответствии с формулами (13.17), а на рис. 13.7, б изображена зависимость модуля Zвх от частоты из (13.18) при несогласованной нагрузке линии.
- org/BreadcrumbList»>
- Главная
- Радиотехника и Электроника
- Теория электрических цепей
- 13. Цепи с распределенными параметрами
2.2. Входное сопротивление
Входное сопротивление ЭП определяется
как отношение малого приращения входного
напряжения к изменению входного тока.
Предположим, что в схеме на рис.2.1 в
качестве сопротивления нагрузки
выступает сопротивление R1.
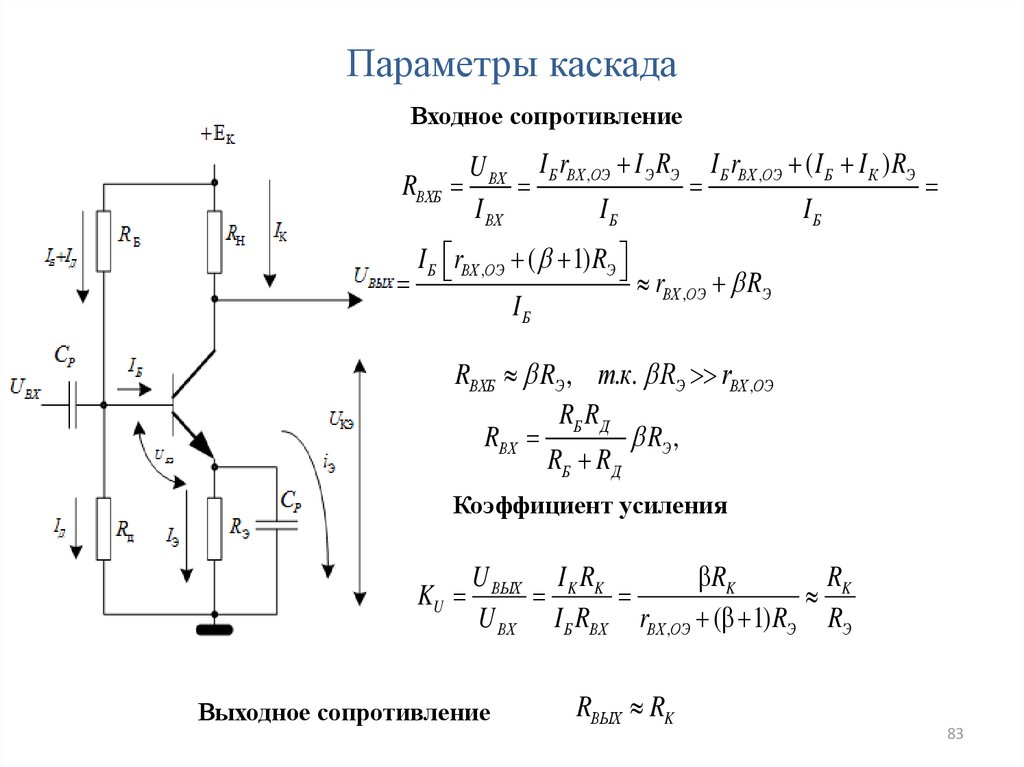
Для рассматриваемой схемы входное
напряжение — это напряжение на базе
транзистора, а входной ток — ток базы. Входное сопротивление ЭП может быть
определено по формуле
Входное сопротивление ЭП может быть
определено по формуле
rвх
= dUвх/dIвх= (dUбэ+dUвых)/dIб=dUбэ/dIб+dUвых/dIб=r
Итак входное сопротивление эмиттерного повторителя равно
rвх=rбэ+ (β+1)R1.
Пример. Найдем входное сопротивление эмиттерного повторителя при следующих исходных данных: ток коллектораIк= 1 мА,R1= 3 кОм, β = 100.
rвх=rбэ+ (β+1)R1= βuт /Iк+(β+1)R1=
=100 25,5мВ/ 1 мА + 101 3 кОм = 2,55 кОм + 303 кОм = 305,6 кОм.
Из расчета видно, что в общем входном сопротивлении доля первого слагаемого (rбэ) незначительная, поэтому часто использую более приближенную формулу для определения выходного сопротивления эмиттерного повторителя
|
rвх= βR1 |
(2. |
2.3. Выходное сопротивление
ЭП определяется, как отношение изменения выходного напряжения к изменению выходного тока rвых= —dUвых/dIвыхпри условии, что входное напряжение не изменяется, т.е.Uвх=const, аdUвх= 0.
Для определения выходного сопротивления рассмотрим схему на рис.2.3. здесь Rист– сопротивление источника входного сигнала.
|
rвых= —dUвых/dIвых= —dUвых/dIэ. |
(2.3) |
dUвх =dURист+dUбэ+dUвых.
Учитывая, что dUвх= 0, и пренебрегаяdUбэполучим
dUвых= -dURист= -dIбRист= -dIэRист
/(β+1).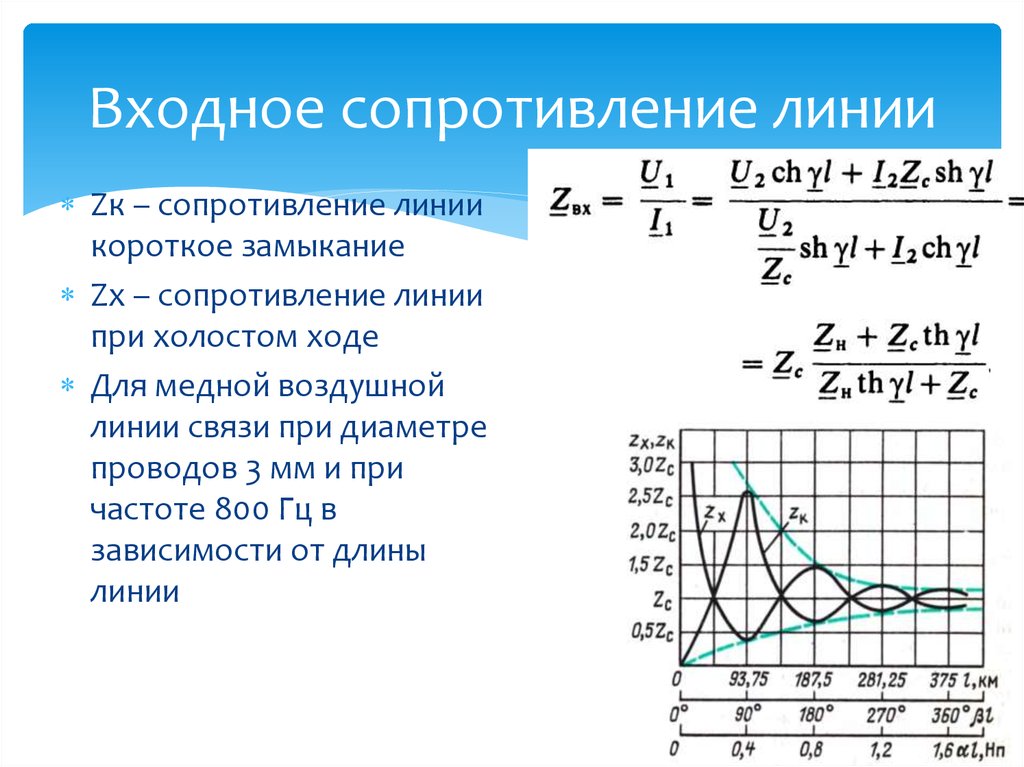
Подставим, найденное значение dUвыхв формулу (2.3) и найдем выходное сопротивление усилителя
rвых= Rист/(1+).
Из формулы видно, что выходное (внутреннее) сопротивление источника входного сигнала уменьшается в (+1) раз при подключении ЭП.
2.4. Смещение в эмиттерном повторителе
Схема на рис.2.1 пропускает на выход
сигнал, который больше, чем 0.6В (Uбэоткрытого транзистора). Для того, чтобы
схема могла усиливать разнополярные
сигналы необходимо создатьсмещение,
которое обеспечивает протекание
коллекторного тока в течение полного
периода сигнала. Смещение обеспечивается
путем подачи положительного постоянного
напряжения на базу транзистора. Переменный
входной сигнал складывается с постоянным
напряжением смещения. Величина напряжения
смещения должна быть такой величины,
чтобы при отрицательной амплитуде
входного сигнала напряжение на базе
было больше 0,6 В, т.е. транзистор был
открыт.
Смещение в усилителе можно задавать с помощью делителя напряжения R1, R2, как показано на рис.2.4. R1и R2выбраны так, чтобы на выходе формировался максимальный симметричный сигнал. Это можно обеспечить, если напряжение на эмиттере транзистора при отсутствии входного сигнала будет равно примерно половине напряжения питания Uп.При подаче на вход переменного напряжения на эмиттере сигнал будет изменяться относительно напряжения Uп / 2. Процесс выбора рабочих напряжений в схеме при отсутствии входного сигнала называетсяустановкой рабочей точки. Сопротивления R1и R2выбираются из условия, что ток протекающий через делитель (ток через сопротивление R2) должен быть намного больше ( по крайней мере в 10 раз) тока базы транзистора, чтобы изменение тока базы при изменении входного сигнала оказывало малое влияние на изменение постоянной составляющей тока делителя.
Разделительная емкость С1не
пропускает постоянное напряжение
смещения на вход источника сигнала, а
емкость С2пропускает в нагрузку
только переменный полезный сигнал.
Разделительные емкости С1и С2образуют фильтры верхних частот, нижняя граничная частота которых должна быть выбрана так, чтобы полностью пропускались нижние частоты сигнала. Величины емкости могут быть определены по формуле
С 1/ 2fRэкв, где Rэквдля вычисления С1 равно параллельному соединению сопротивлений R1,R2 и rвх. Для определения С2 предполагаем, что сопротивление нагрузки ЭП будет не меньше R3. Поэтому Rэквв этом случае выбирают равным R3.
Результаты моделирования схемы, показанной на рис.2.4 представлены на рис.2.5.
Из рисунка видно, что выходное напряжение v(5) практически полностью повторяет входное напряжение v(3). Переменное напряжение на базе v(1), по амплитуде равное входному напряжению, изменяется относительно постоянного напряжения смещения, примерно равное 7,5 В. Напряжение на эмиттере v(4) меньше напряжения на базе на Uбэ ≈ 0
Как рассчитать входное сопротивление для этой простой схемы?
\$\начало группы\$
Я хотел бы рассчитать входное сопротивление следующей цепи, предполагая, что Q1 «активен». Я знаю, что импеданс делителя напряжения равен \$\frac{R_1R_2}{R_1+R_2}\$, а импеданс эмиттерного повторителя равен \$\beta R_3\$, где \$\beta\$ — усиление , но мне непонятно, как можно рассчитать импеданс всей цепи. Я не просто ищу рецепт. Что еще более важно, я хотел бы знать, почему этот рецепт приводит к правильному ответу, зная определение импеданса, то есть \$\frac{\Delta V}{\Delta I}\$.
Я знаю, что импеданс делителя напряжения равен \$\frac{R_1R_2}{R_1+R_2}\$, а импеданс эмиттерного повторителя равен \$\beta R_3\$, где \$\beta\$ — усиление , но мне непонятно, как можно рассчитать импеданс всей цепи. Я не просто ищу рецепт. Что еще более важно, я хотел бы знать, почему этот рецепт приводит к правильному ответу, зная определение импеданса, то есть \$\frac{\Delta V}{\Delta I}\$.
имитация этой схемы – Схема создана с помощью CircuitLab
- полное сопротивление
- входное сопротивление
\$\конечная группа\$
6
\$\начало группы\$
Я не буду вдаваться в вычисления, но могу показать вам, как построить эквивалентную малосигнальную или линейную схему, из которой вы можете рассчитать входное сопротивление.
Как подчеркивают авторы комментария, нужно прибегнуть к малосигнальной модели биполярного транзистора.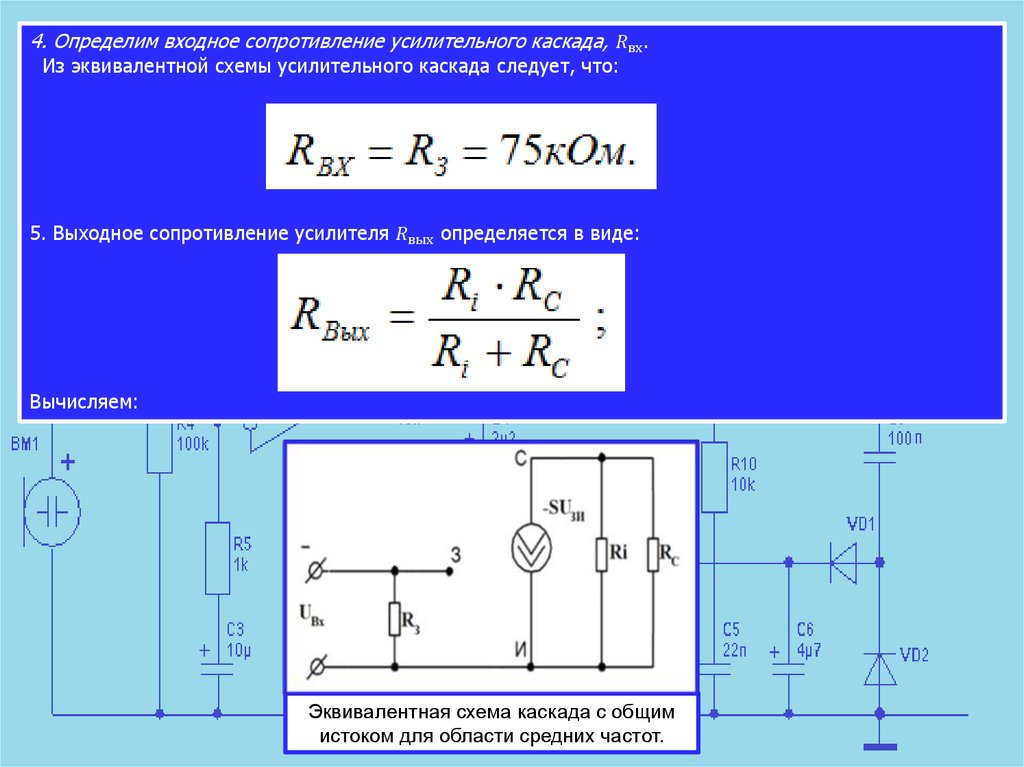 Транзистор — это очень нелинейное устройство, и вы можете линеаризовать его поведение в пределах заданной рабочей точки. Одной из простых низкочастотных версий является гибридная модель \$\pi\$, показанная ниже:
Транзистор — это очень нелинейное устройство, и вы можете линеаризовать его поведение в пределах заданной рабочей точки. Одной из простых низкочастотных версий является гибридная модель \$\pi\$, показанная ниже:
Теперь просто вставьте эту инвариантную модель в свою схему, соблюдая распиновку, и теперь у вас есть линейная схема , в которой вы может применить все классические теоремы, такие как Тевенен, суперпозиция и т. д., если это необходимо:
Вы видите, что \$V_{cc}\$ как бы прижат к земле — если мой плохой английский достаточно ясен — подразумевает заземленный коллектор и верхнее соединение \$R_2\$ также в 0 -В линия. Это так, потому что, говорим ли мы об определении сопротивления или импеданса, мы говорим о значениях слабого сигнала. Значение малого сигнала означает, что в какой-то момент имеется малоамплитудный стимул, вводящий сигнал в схему для анализа. Этот стимул будет распространяться по цепи, чтобы сформировать ответ, выходной сигнал, который вы хотите проанализировать. Некоторые провода в цепи увидят распространение этого стимула, а некоторые нет. Как правило, линия \$V_{cc}\$ хорошо развязана большим конденсатором, что означает, что, несмотря на модуляцию, примененную к цепи, вы ничего не увидите с помощью осциллографа, если будете пробовать эту линию: ее переменное напряжение равно 0 В. а источник 0 В похож на короткое замыкание в представлении переменного тока. Вот почему вы замыкаете \$V_{cc}\$ на землю при анализе переменного тока.
Некоторые провода в цепи увидят распространение этого стимула, а некоторые нет. Как правило, линия \$V_{cc}\$ хорошо развязана большим конденсатором, что означает, что, несмотря на модуляцию, примененную к цепи, вы ничего не увидите с помощью осциллографа, если будете пробовать эту линию: ее переменное напряжение равно 0 В. а источник 0 В похож на короткое замыкание в представлении переменного тока. Вот почему вы замыкаете \$V_{cc}\$ на землю при анализе переменного тока.
Чтобы определить входной импеданс (или сопротивление в вашем случае), просто установите тестовый генератор \$I_T\$ (наш стимул) и определите напряжение \$V_T\$ на источнике (наш отклик). Сопротивление, которое вам нужно, просто \$R_{in}=\frac{V_T}{I_T}\$. Это будет работать аналогичным образом, если в цепи будут элементы, накапливающие энергию, такие как катушки индуктивности или конденсаторы. но тогда он станет импедансом, определяемым как \$Z_{in}(s)=\frac{V_T(s)}{I_T(s)}\$.
В этом примере сразу видно, что \$I_T=i_b\$ и у вас есть два параллельных сопротивления, напрямую подключенных к источнику тока. Вы можете легко временно отключить их и определить промежуточное входное сопротивление без них, \$R_{int}\$. Конечным результатом будет просто \$R_{in}=R_1||R_2||R_{int}\$. Это уже часть техники быстрых аналитических схем или ФАКТОВ, которые я продолжаю проповедовать на этом дружественном сайте 🙂 Удачи в ваших упражнениях!
Вы можете легко временно отключить их и определить промежуточное входное сопротивление без них, \$R_{int}\$. Конечным результатом будет просто \$R_{in}=R_1||R_2||R_{int}\$. Это уже часть техники быстрых аналитических схем или ФАКТОВ, которые я продолжаю проповедовать на этом дружественном сайте 🙂 Удачи в ваших упражнениях!
\$\конечная группа\$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
операционный усилитель — Как рассчитать входное сопротивление и передаточную функцию
Пожалуйста, маркируйте свои компоненты в будущем. Так было бы намного проще отвечать. Вот моя версия вашей схемы для упрощения:
смоделируйте эту схему – Схема создана с помощью CircuitLab
Вот основные моменты, от которых зависит остальная часть объяснения:
-
Предполагается операционный усилитель иметь бесконечный входной импеданс, и любое его влияние на потенциал в точке X, \$v_X\$, пренебрежимо мало.
-
Предполагается, что операционный усилитель имеет нулевое выходное сопротивление. На самом деле даже неидеальный операционный усилитель с отрицательной обратной связью будет иметь выходное сопротивление, очень близкое к нулю (с некоторыми оговорками). Следовательно, на его выходной потенциал \$v_Y\$ никакая нагрузка (например, R3, R4, C2 и все, что последует) никак не повлияет.

-
Операционный усилитель сконфигурирован как повторитель напряжения со 100% отрицательной обратной связью для коэффициента усиления, равного 1. Следовательно, \$v_Y = v_X\$
-
Операционный усилитель эффективно изолирует все, что находится слева от него (входная сторона), от всего, что находится справа (выходная сторона), благодаря пунктам 1 и 2 выше.
Теперь мы можем заняться проблемой. Во-первых, убедитесь, что вы знакомы с теоремой Тевенина (вот страница в Википедии).
Делитель входного напряжения может быть уменьшен до эквивалента Тевенина, состоящего из одного источника напряжения и одного сопротивления. Источник напряжения Тевенена будет иметь половину потенциала питания:
$$ \begin{выровнено} V_{Th2} &= 5V \times \frac{R_2}{R_1+R_2} \\ \\ &= 5V \times \frac{10M\Omega}{10M\Omega+10M\Omega} \\ \\ &= 5V \times \frac{10M\Omega}{20M\Omega} \\ \\ &= 2,5В \\\\ \end{выровнено} $$
Сопротивление Тевенена \$R_{Th2}\$ будет суммарным сопротивлением R1 и R2, как если бы они были соединены параллельно:
$$ \begin{выровнено} R_{Th2} &= R_1 \параллельно R_2 \\ \\ &= \frac{R_1 \times R_2}{R_1+R_2} \\ \\ &= \frac{10M\Omega \times 10M\Omega}{10M\Omega+10M\Omega} \\ \\ &= 5М\Омега \\ \\ \end{выровнено} $$
Замените цепь, состоящую из источника питания 5 В, резисторов R1 и R2, на эквивалент Тевенина:
смоделируйте эту схему и R4 с \$R_{Th3}\$, делая вид, что источник напряжения \$v_Y\$ стал источником одной десятой \$v_Y\$ (без внутреннего импеданса) следующим образом:
$$ \begin{выровнено} v_{Th3} &= v_Y \times \frac{R_4}{R_3 + R_4} \\ \\ &= v_Y \times \frac{1k\Omega}{9к\Омега + 1к\Омега} \\ \\ &= v_Y \times \frac{1k\Omega}{10k\Omega} \\ \\ &= \frac{v_Y}{10} \\ \\ \\ R_{Th3} &= R_3 \параллельно R_4 \\ \\ &= 9к\Омега\параллельно 1к\Омега\\ \\ &= \frac{9k\Omega \times 1k\Omega}{9k\Omega + 1k\Omega} \\ \\ &= 900\Омега \end{выровнено} $$
смоделируйте эту схему
Вот вся схема с обоими эквивалентами Тевенина:
смоделируйте эту схему
Я добавил компонент с импедансом \$Z_L\$, представляющий некоторую нагрузку, подключенную к выходу.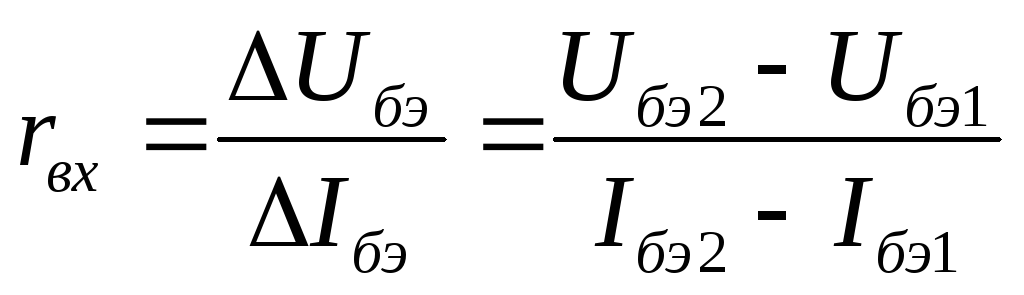 Без нагрузки конденсатор C2 не пропускает ток и не может ни с чем «соединяться по переменному току». Просто напомню, что в реальной жизни там будет нагрузкой, и это надо учитывать при расчете передаточных функций. Если нагрузка пренебрежимо мала (высокий импеданс), то можно сказать, что на C2 никогда не будет заряда, на нем не будет напряжения и \$V_{OUT} = V_Z\$.
Без нагрузки конденсатор C2 не пропускает ток и не может ни с чем «соединяться по переменному току». Просто напомню, что в реальной жизни там будет нагрузкой, и это надо учитывать при расчете передаточных функций. Если нагрузка пренебрежимо мала (высокий импеданс), то можно сказать, что на C2 никогда не будет заряда, на нем не будет напряжения и \$V_{OUT} = V_Z\$.
Из-за пунктов 1 и 4 выше, все, что подключено к IN, увидит, смотря в C1, последовательно соединенную пару C1 и \$R_{Th2}\$, за которой следует источник напряжения с нулевым импедансом. Следовательно: 9{-6})с} \\ \\ \end{выровнено} $$
Разделите схему на три независимых этапа (независимых в соответствии с пунктом 4 выше), как я сделал выше с красным (F), зеленым (G) и синим (H) прямоугольниками.
Обратите внимание, что смещение постоянного тока 2,5 В, вносимое источником \$V_{Th2}\$, можно не принимать во внимание, когда речь идет о передаточных функциях в частотной области, поскольку анализ переменного тока слабого сигнала рассматривает все узлы с фиксированным потенциалом постоянного тока, как если бы они были измельчены.

 2)
2)