Wave finite element method. Метод конечных элементов для моделирования распространения сейсмических волн: возможности и применение

Как метод конечных элементов помогает моделировать распространение сейсмических волн. Какие преимущества дает этот метод по сравнению с другими подходами. Для решения каких задач в сейсмологии и инженерной сейсмике применяется метод конечных элементов. Какие новые результаты получены с помощью этого метода.

Основы метода конечных элементов в сейсмологии

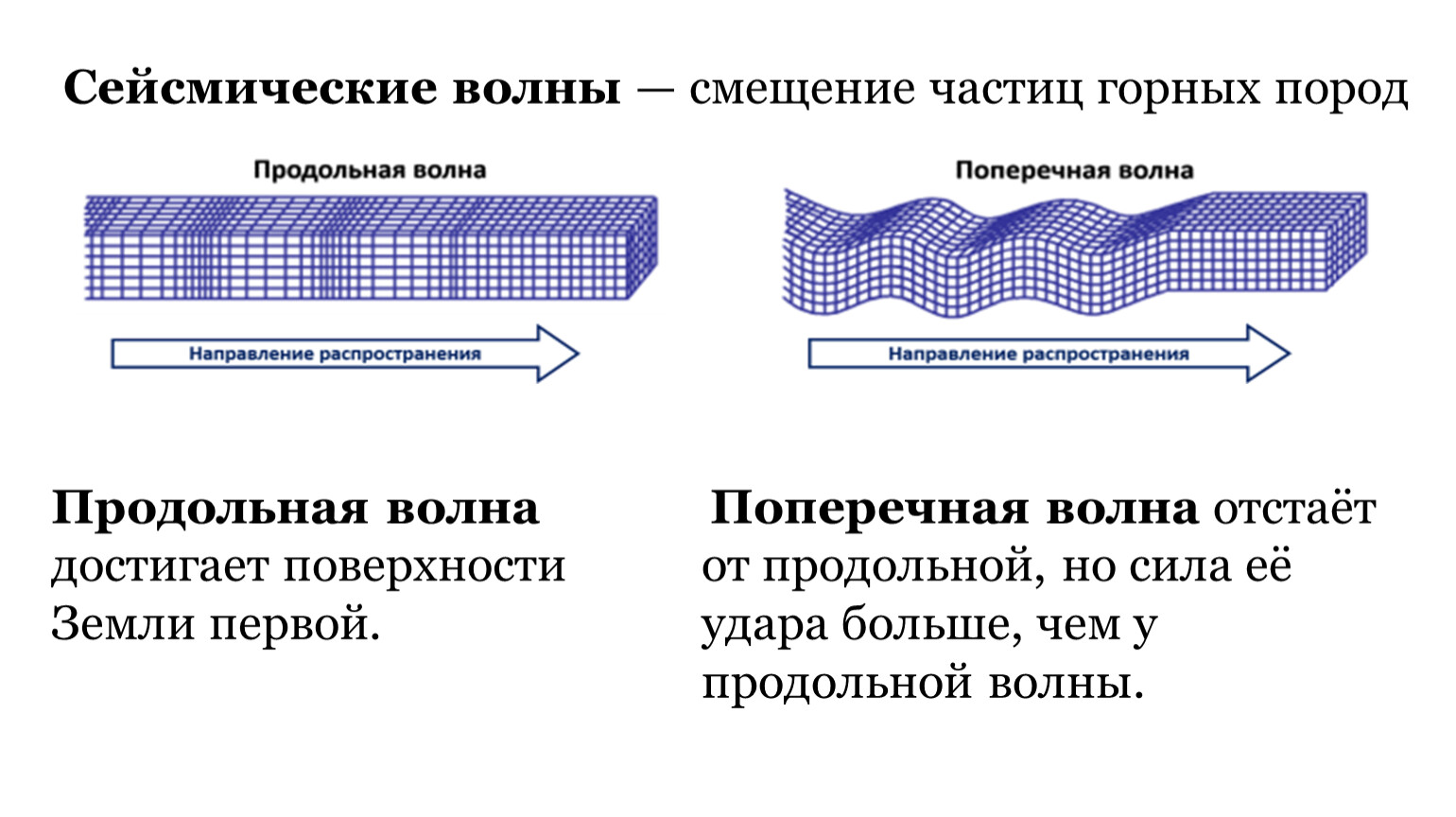
Метод конечных элементов (МКЭ) является мощным численным инструментом для моделирования распространения сейсмических волн в сложных геологических средах. Суть метода заключается в следующем:

• Исследуемая область разбивается на множество небольших элементов (обычно треугольных или четырехугольных).
• Для каждого элемента задаются физические свойства среды (плотность, модули упругости и т.д.).
• Решение волнового уравнения ищется в виде суперпозиции базисных функций на элементах.
• Составляется система линейных алгебраических уравнений относительно узловых значений искомых функций.
• Система решается численно, что позволяет получить волновое поле во всей области.

Какие преимущества дает МКЭ для задач сейсмологии? Во-первых, он позволяет учитывать сложную геометрию среды и неоднородность ее свойств. Во-вторых, метод обеспечивает высокую точность расчетов при правильном выборе параметров сетки. В-третьих, МКЭ легко адаптируется для решения различных типов задач — как прямых, так и обратных.

Применение МКЭ для моделирования топографических эффектов

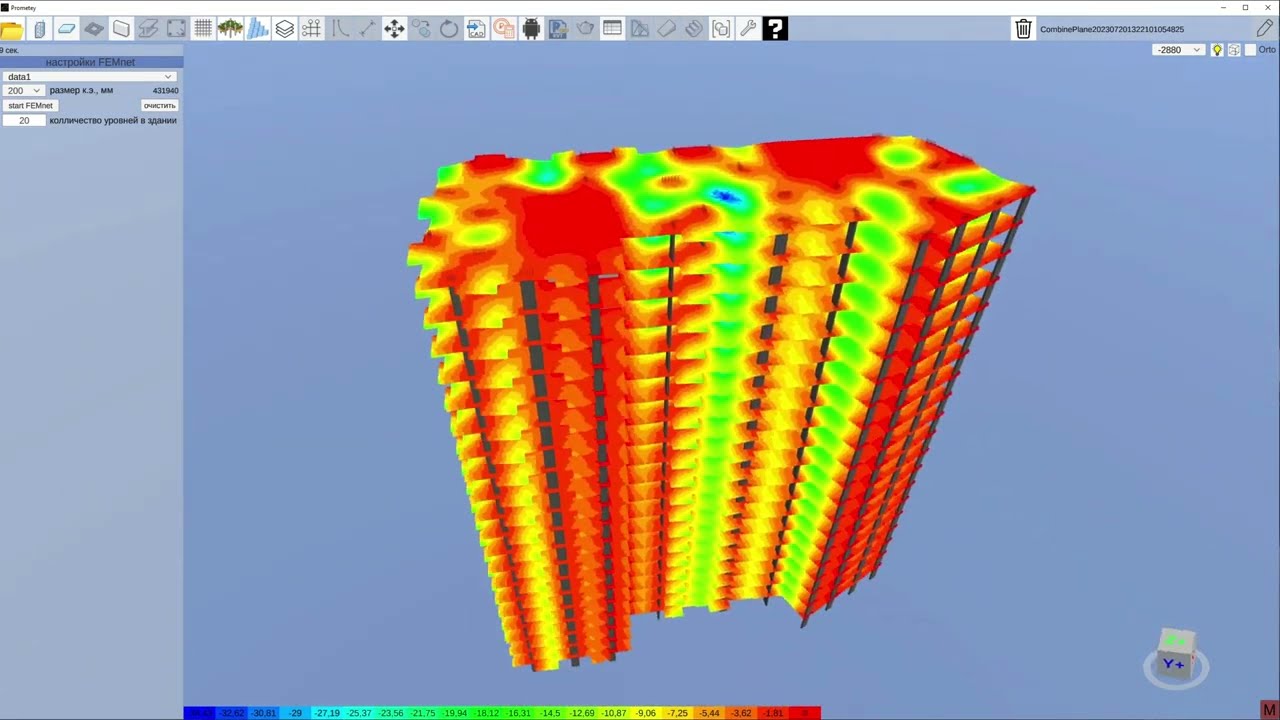
Одной из важных областей применения МКЭ в сейсмологии является изучение влияния рельефа поверхности на распространение сейсмических волн. Метод позволяет детально смоделировать взаимодействие волн со сложной топографией и оценить усиление колебаний в определенных участках.

Так, в работе Буре (Boore, 1972) методом конечных разностей было исследовано влияние простой топографии в виде горы на распространение SH-волн. Смит расширил эти результаты, применив МКЭ для моделирования прохождения P и SV волн через аналогичную топографическую структуру. Было показано, что:

• Амплитуда колебаний на вершине горы усиливается в 1.2-1.5 раза по сравнению с плоской поверхностью.
• Степень усиления зависит от частоты колебаний и угла падения волны.
• Наибольшее усиление наблюдается для SH-волн при их нормальном падении на склон.

Эти результаты хорошо согласуются с натурными наблюдениями и позволяют оценивать сейсмическую опасность в горных районах.

Моделирование распространения волн в осадочных бассейнах

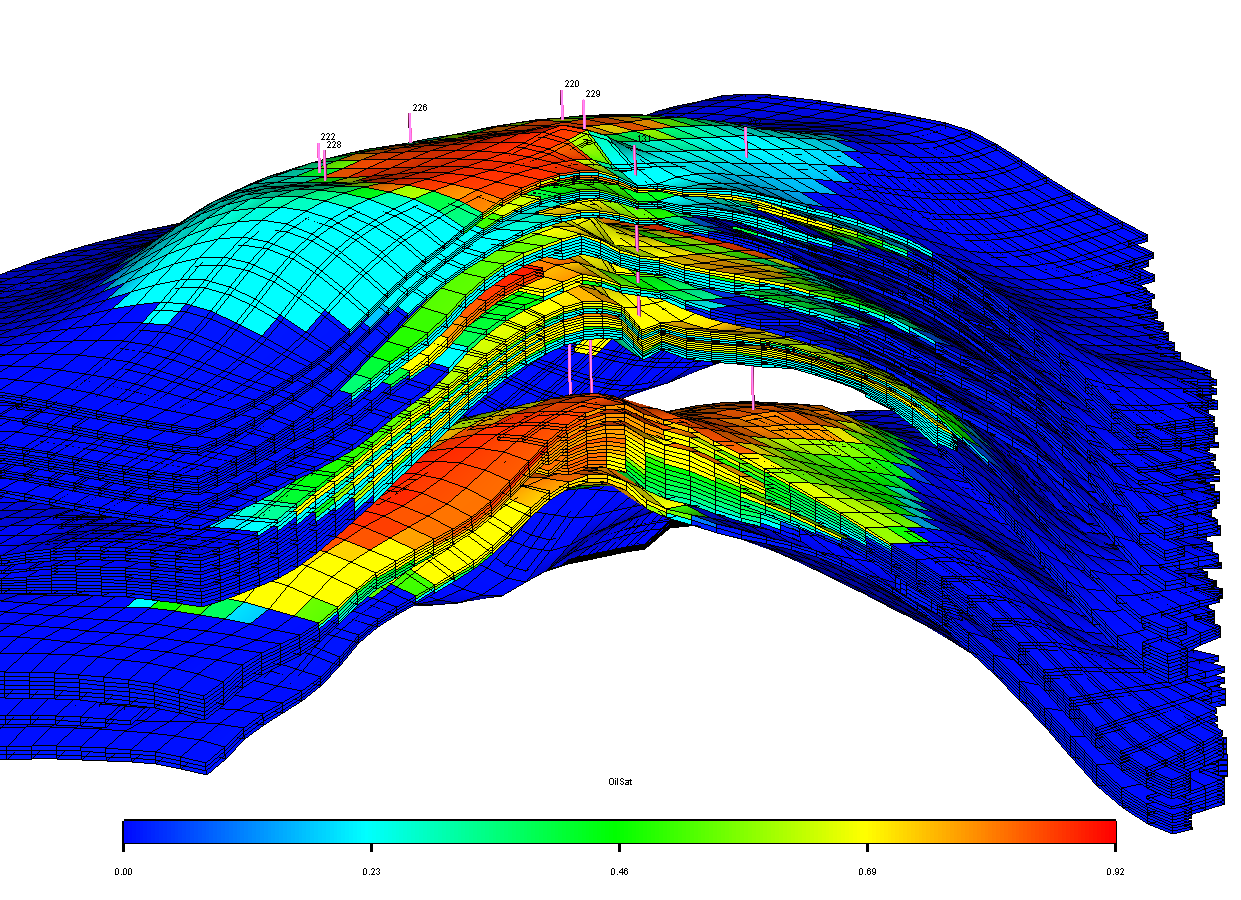
Другой важной задачей является изучение поведения сейсмических волн в осадочных бассейнах и долинах. Такие структуры могут значительно усиливать колебания из-за резонансных эффектов и образования поверхностных волн. МКЭ позволяет детально моделировать эти процессы с учетом сложной геометрии бассейнов и неоднородности их заполнения.

В частности, Трифунак (Trifunac, 1971) применил аналитический подход для расчета движения поверхности полуцилиндрической аллювиальной долины при падении плоской SH-волны. Смит воспроизвел эти результаты с помощью МКЭ и расширил их на случай P и SV волн. Основные выводы:

• В центре долины амплитуда колебаний может усиливаться до 3-4 раз по сравнению с однородным полупространством.
• На краях долины возникают сложные интерференционные картины из-за отражений от границ.
• Для P и SV волн наблюдается сильная трансформация волнового поля с образованием поверхностных волн.

Эти результаты важны для оценки сейсмической опасности в районах, расположенных на осадочных отложениях.

Моделирование глубокофокусных землетрясений

МКЭ также успешно применяется для моделирования волновых полей от глубокофокусных землетрясений. Это позволяет исследовать особенности распространения волн в верхней мантии и их взаимодействие с границами раздела.

Смит использовал двумерную модель МКЭ для реалистичного моделирования зоны глубоких землетрясений под Северным островом Новой Зеландии. Основные результаты:

• Выявлена сильная рефракция волн на границе погружающейся плиты, приводящая к изменению наблюдаемых амплитуд на поверхности.
• Обнаружены эффекты фокусировки и дефокусировки волн в зависимости от положения очага относительно структуры плиты.
• Показана возможность оценки толщины погружающейся плиты по долговременным наблюдениям местных землетрясений.

Эти результаты важны для понимания процессов в зонах субдукции и интерпретации сейсмологических данных в таких регионах.

Преимущества МКЭ перед другими численными методами

Метод конечных элементов обладает рядом преимуществ по сравнению с другими численными подходами, используемыми в сейсмологии:

1. Гибкость в описании сложной геометрии среды. МКЭ позволяет точно учитывать форму границ раздела, топографию поверхности и другие особенности строения.
2. Возможность задания произвольного распределения свойств среды. Метод легко адаптируется для моделирования сильно неоднородных и анизотропных сред.
3. Высокая точность расчетов при правильном выборе параметров сетки. МКЭ обеспечивает сходимость решения при измельчении сетки.
4. Эффективность для задач с свободной поверхностью. Метод хорошо подходит для моделирования поверхностных волн и топографических эффектов.
5. Универсальность подхода. МКЭ может применяться как для прямых задач расчета волновых полей, так и для решения обратных задач.

Эти преимущества делают МКЭ мощным инструментом для решения широкого круга задач сейсмологии и инженерной сейсмики.

Ограничения метода и пути их преодоления

Несмотря на свои преимущества, метод конечных элементов имеет ряд ограничений, которые необходимо учитывать при его применении в сейсмологии:

• Высокие требования к вычислительным ресурсам, особенно для трехмерных задач.
• Сложность построения качественной сетки для областей сложной формы.
• Проблемы с моделированием бесконечных и полубесконечных областей.
• Численная дисперсия при распространении высокочастотных волн.

Для преодоления этих ограничений разрабатываются различные подходы:

1. Использование параллельных вычислений и оптимизированных алгоритмов для ускорения расчетов.
2. Применение адаптивных сеток, автоматически измельчающихся в областях с сильными градиентами решения.
3. Разработка специальных граничных элементов для моделирования уходящих волн на искусственных границах.
4. Использование схем высокого порядка точности для уменьшения численной дисперсии.

Эти усовершенствования позволяют расширить область применения МКЭ и повысить точность получаемых результатов.

Перспективы развития и применения МКЭ в сейсмологии

Метод конечных элементов продолжает активно развиваться и находить новые применения в сейсмологии. Основные направления развития включают:

• Создание крупномасштабных трехмерных моделей для реалистичного моделирования региональных волновых полей.
• Разработку методов инверсии на основе МКЭ для уточнения скоростных моделей земной коры и верхней мантии.
• Применение МКЭ для моделирования нелинейных эффектов при сильных движениях грунта.
• Интеграцию МКЭ с другими методами (например, спектральными) для повышения эффективности расчетов.
• Использование МКЭ для оценки сейсмической опасности с учетом местных геологических условий.

Эти направления открывают новые возможности для понимания процессов генерации и распространения сейсмических волн, а также для решения практических задач сейсмостойкого строительства и сейсмического районирования.

Полноволновая модель распространения и диссипации волн во внутренней магнитосфере с использованием метода конечных элементов (конференция)

Полноволновая модель распространения и диссипации волн во внутренней магнитосфере с использованием метода конечных элементов (конференция) | ОСТИ.GOV

перейти к основному содержанию

• Полная запись
• Другое связанное исследование

Большое разнообразие плазменных волн играет важную роль в возбуждении и гибели частиц во внутренней магнитосфере. Наша способность понимать и моделировать взаимодействие волн и частиц в этом регионе требует улучшенных знаний о пространственном распределении и свойствах этих волн, а также лучшего понимания того, как волны зависят от изменений воздействия солнечного ветра и/или геомагнитной активности.

С этой целью мы разработали двумерный код конечных элементов, который решает уравнения полных волн в глобальной геометрии магнитосферы. Код описывает трехмерную волновую структуру, включая преобразование мод при запуске УНЧ, ЭМИЦ и свистовых волн в двумерной осесимметричной фоновой плазме с общей топологией магнитного поля. Мы иллюстрируем возможности кода, исследуя роль плазмосферных плюмов в распространении магнитозвуковых волн; преобразование мод на ионно-ионном и альфвеновском резонансах в результате внешних сжатий солнечного ветра; волновая структура и преобразование мод электромагнитных ионно-циклотронных волн, запускаемых в экваториальной магнитосфере и распространяющихся вдоль силовых линий магнитного поля в сторону ионосферы. Мы также обсудим преимущества метода конечных элементов для разрешения резонансных структур и способы адаптации модели для учета нелокальных кинетических эффектов.

Авторов:

Эрнест Валео, Джей Р. Джонсон, Ын-Хва и Синтия Филлипс

Дата публикации:

13. 03.2012

Исследовательская организация:

Принстонская лаборатория физики плазмы. (PPPL), Принстон, Нью-Джерси (США)

Организация-спонсор:

Департамент науки Министерства энергетики США (SC)

Идентификатор ОСТИ:

1036305

Номер(а) отчета:

ПППЛ-4743
РНН: US1201356

Номер контракта с Министерством энергетики:  

ДЕ-АСО2-09Ч32466

Тип ресурса:

Конференция

Название журнала:

Осеннее собрание AGU 2011 г. /Сан-Франциско, Калифорния, 06.12.11

Дополнительная информация журнала:

Конференция: Осеннее собрание AGU 2011/Сан-Франциско, Калифорния, 06.12.11

Страна публикации:

США

Язык:

Английский

Тема:

43 УСКОРИТЕЛИ ЧАСТИЦ; 70 ФИЗИКА ПЛАЗМЫ И ТЕХНОЛОГИЯ СТЯЖКИ; циклотроны; МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ; ГЕОМЕТРИЯ; ИОНОСФЕРА; КИНЕТИКА; МАГНИТНЫЕ ПОЛЯ; МАГНИТОАКУСТИЧЕСКИЕ ВОЛНЫ; ПРЕОБРАЗОВАНИЕ РЕЖИМОВ; ПЛАЗМА; ПЛАЗМЕННЫЕ ВОЛНЫ; ПЛЮМЫ; СОЛНЕЧНЫЙ ВЕТЕР; ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ; ТОПОЛОГИЯ; ВОЛНОВЫЕ УРАВНЕНИЯ; РАСПРОСТРАНЕНИЕ ВОЛН; ВИСТЛЕРЫ; Космическая плазменная физика, связь мод, преобразование мод

---

Форматы цитирования

• MLA
• АПА
• Чикаго
• БибТекс

Эрнест Валео, Джей Р. Джонсон, Ын-Хва и Синтия Филлипс. Полноволновая модель распространения и диссипации волн во внутренней магнитосфере с использованием метода конечных элементов . США: Н. П., 2012. Веб.

Копировать в буфер обмена

Эрнест Валео, Джей Р. Джонсон, Ын-Хва и Синтия Филлипс. Полноволновая модель распространения и диссипации волн во внутренней магнитосфере с использованием метода конечных элементов . Соединенные Штаты.

Копировать в буфер обмена

Эрнест Валео, Джей Р. Джонсон, Ын-Хва и Синтия Филлипс. 2012. «Полноволновая модель распространения и рассеяния волн во внутренней магнитосфере с использованием метода конечных элементов». Соединенные Штаты. https://www.osti.gov/servlets/purl/1036305.

Копировать в буфер обмена

@статья{osti_1036305,
title = {Полноволновая модель распространения и рассеяния волн во внутренней магнитосфере с использованием метода конечных элементов},
автор = {Эрнест Валео, Джей Р. Джонсон, Ын-Хва и Синтия Филлипс},
abstractNote = {Большое разнообразие плазменных волн играет важную роль в возбуждении и гибели частиц во внутренней магнитосфере. Наша способность понимать и моделировать взаимодействие волн и частиц в этом регионе требует улучшенных знаний о пространственном распределении и свойствах этих волн, а также лучшего понимания того, как волны зависят от изменений воздействия солнечного ветра и/или геомагнитной активности. С этой целью мы разработали двумерный код конечных элементов, который решает уравнения полных волн в глобальной геометрии магнитосферы. Код описывает трехмерную волновую структуру, включая преобразование мод при запуске УНЧ, ЭМИЦ и свистовых волн в двумерной осесимметричной фоновой плазме с общей топологией магнитного поля. Мы иллюстрируем возможности кода, исследуя роль плазмосферных плюмов в распространении магнитозвуковых волн; преобразование мод на ионно-ионном и альфвеновском резонансах в результате внешних сжатий солнечного ветра; волновая структура и преобразование мод электромагнитных ионно-циклотронных волн, запускаемых в экваториальной магнитосфере и распространяющихся вдоль силовых линий магнитного поля в сторону ионосферы. Мы также обсудим преимущества метода конечных элементов для разрешения резонансных структур и способы адаптации модели для учета нелокальных кинетических эффектов.},
дои = {},
URL-адрес = {https://www.osti.gov/biblio/1036305}, журнал = {Осенняя встреча AGU 2011/Сан-Франциско, Калифорния, 6 декабря 2011 г.},
номер = ,
объем = ,
место = {США},
год = {2012},
месяц = ​​{3}
}

Копировать в буфер обмена

---

Просмотр конференции (0,86 МБ)

Дополнительную информацию о получении полнотекстового документа см. в разделе «Доступность документа». Постоянные посетители библиотек могут искать в WorldCat библиотеки, в которых проводится эта конференция.

---

Экспорт метаданных

Сохранить в моей библиотеке

Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.

Похожие записи в сборниках ОСТИ.ГОВ:

• Аналогичные записи

Применение метода конечных элементов к задачам распространения объемных волн | Международный геофизический журнал

Журнальная статья

Уорик Д. Смит

Уорвик Д. Смит

Ищите другие работы этого автора на:

Оксфордский академический

Google Scholar

ОБЪЯВЛЕНИЯ

Примечания автора

Geophysical Journal International , том 42, выпуск 2, август 1975 г., страницы 747–768, https://doi.org/10.1111/j.1365-246X.1975.tb05890.x

Опубликовано :

01 августа 1975 г.

История статьи

Получено:

1 октября 1974 г.

Опубликовано:

01 августа 1975 г.

Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Мобильный телефон Введите поисковый запрос

Закрыть

Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Введите поисковый запрос

Advanced Search

Резюме

Показано, что метод конечных элементов является мощным инструментом для численного моделирования задач распространения объемных сейсмических волн. Приложения распространяются как на задачи в интересующем инженеров масштабе, так и на крупномасштабные сейсмологические задачи. Решения ищутся во временной области. Для этого были написаны эффективные программы. Объем численных решений был значительно расширен за счет использования ранее описанной схемы точного подавления отражений на границах модели.

Результаты конечных разностей Boore и аналитические результаты Trifunac для усиления из-за горы и аллювиальной долины соответственно сравниваются с новыми результатами конечных элементов. Новые результаты хорошо согласуются, хотя есть некоторые трудности с резонансом в задаче о аллювиальной долине. Результаты Boore SH были распространены на вертикальное падение P и SV . Зона глубокого землетрясения была реалистично смоделирована в двух измерениях, а землетрясения смоделированы на глубине. Предполагается, что изменение наблюдаемой амплитуды в верхней части зоны из-за рефракции от плиты может быть использовано для оценки толщины плиты на основе долгосрочных наблюдений местных землетрясений.

Ссылки

Абрамовиц

М.

Стегун

И. А.

,

1970

.

Справочник по математическим функциям

,

Dover Publications Inc.

, Нью-Йорк.

Альтерман

З.

Карал

Ф. К.

,

1968

.

Распространение упругих волн в слоистых средах методами конечных разностей

,

Бык. сейсм. соц. Являюсь.

,

58

,

367

–

398

.

Баразанги

М.

Исакс

Б. Л.

,

1971

.

Латеральные вариации затухания сейсмических волн в верхней мантии над зоной наклонных землетрясений островной дуги Тонга: глубинная аномалия в верхней мантии

,

J. geophys. Рез.

,

76

,

8493

–

8516

.

Boore

Д. М.

,

1972

.

Конечно-разностные методы распространения сейсмических волн в неоднородных материалах

, в

Методы вычислительной физики

, Vol.

11

, изд.

Болт

B. A.

,

Academic Press

, Нью-Йорк.

Boore

Д. М.

,

1972

.

Примечание о влиянии простой топографии на сейсмические SH волны

,

Бюлл. сейсм. соц. Являюсь.

,

62

,

275

–

284

.

Boore

Д. М.

,

1973

.

Влияние простой топографии на сейсмические волны: последствия для ускорений, зарегистрированных на плотине Пакоима, долина Сан-Фернандо, Калифорния

,

Бык. сейсм. соц. Являюсь.

,

63

,

1603

–

1609

.

Карпентер

В. К.

Гилл

П. А. Т.

,

1973

.

Автоматизированные решения нестационарных задач

,

Математика конечных элементов и приложения

,

495

, изд.

Whiteman

J. R.

,

Academic Press

, Нью-Йорк.

Клаф

Р. В.

,

1971

.

Анализ структурных колебаний и динамического отклика

.

Последние достижения в области матричных методов в структурном анализе и проектировании

, Труды американо-японского семинара, август 1969 г.

The University of Alabama Press

, Хантсвилл, Алабама.

Курант

Р.

,

1943

.

Вариационные методы решения задач о равновесии и колебаниях

,

Бюлл. Являюсь. математика. соц.

,

49

,

1

–

23

.

Дэвис

Д.

Маккензи

Д. П.

,

1969

.

Сейсмические невязки и плиты времени пробега

,

Геофиз. Дж. Р. астр. соц.

,

18

,

51

–

63

.

Дэвис

Л. Л.

Вест

Л. Р.

,

1973

.

Наблюдаемое влияние топографии на движение грунта

,

Bull. сейсм. соц. Являюсь.

,

63

,

281

–

298

.

Десаи

К. С.

Абель

Дж. Ф.

,

1972

.

Введение в метод конечных элементов

,

Van Nostrand Reinhold

, Лондон.

Дуглас

А.

,

1970

.

Конечные элементы для геологического моделирования

,

Природа

,

226

,

630

–

631

.

Дрейк

Л. А.

,

1972

.

Волны Лява и Рэлея в негоризонтально-слоистых средах

,

Бык. сейсм. соц. Являюсь.

,

62

,

1241

–

1258

.

Дрейк

Л. А.

,

1972

.

Волны Рэлея на континентальной границе методом конечных элементов

,

Бюлл. сейсм. соц. Являюсь.

,

62

,

1259

–

1268

.

Гловер

П.

МакКоуэн

Д. В.

Александр

С. С.

,

19753 9.

Расчет полей смещений и напряжений от сейсмических источников в реальных геологических структурах

,

Геофиз. Дж. Р. астр. соц.

, в печати.

Гутенберг

Б.

Рихтер

К. Ф.

,

1949

.

Сейсмичность Земли

,

Princeton University Press

, Принсто, Нью-Джерси.

Гамильтон

Р. М.

Гейл

А.

,

1968

.

Сейсмичность и структура Северного острова, Новая Зеландия

,

Ж. геофиз. Рез.

,

73

,

3859

–

3876

.

Хатертон

Т.

,

1970

.

Гравитация, сейсмичность и тектоника Северного острова, Новая Зеландия

,

N.Z.J. геол. Геофиз.

,

13

,

126

–

144

.

Джейкоб

К. Х.

,

1972

.

Глобальные тектонические последствия аномальной сейсмики P время пробега от ядерного взрыва Лонгшот

,

J. geophys. Рез.

,

77

,

2556

–

2573

.

Kuhlemeyer

R. L.

Lysmer

J.

,

1973

.

Точность конечных элементов для задач распространения волн (Техническое примечание).

J. Soil Mech. Найденный. отд., учеб. ASCE

,

99

,

SM5

,

421

–

4273 9.

Лайсмер

Дж.

Дрейк

Л. А.

,

1972

.

Метод конечных элементов для сейсмологии

. В

Методы вычислительной физики.

Том.

11

, изд.

Bolt

B. A.

,

Academic Press

, Нью-Йорк.

Lysmer

J.

Seed

H.B.

Schnabel

P.B.

,

19713 .

Влияние характеристик основной породы на реакцию грунта

,

Бык. сейсм. соц. Являюсь.

,

61

,

1213

–

1231

.

Митронов

В.

Исакс

Б. Л.

,

1971

.

Скоростные сейсмические аномалии в верхней мантии под островной дугой Тонга-Кермадек

,

J. geophys. Рез.

,

76

,

7154

–

7180

.

Муни

Х. М.

,

1970

.

Неоднородность верхней мантии под Новой Зеландией: сейсмические данные

,

J. geophys. Рез.

,

75

,

285

–

309

.

Муни

Х. М.

,

1970

.

Теоретическое и наблюдаемое время распространения глубоких землетрясений в Новой Зеландии

,

Н.З.Дж. геол. Геофиз.

,

13

,

703

–

717

.

Ньюмарк

Н. М.

,

1959

.

Метод расчета динамики конструкций.

Проц. Являюсь. соц. Гражданский Eng., J. Eng. мех. Отд.

,

85

,

EM3

,

67

–

94

.

Норри

Д. Х.

Де Врис

Г.

,

1973

.

Метод конечных элементов. Основы и приложения

,

Academic Press

, Нью-Йорк.

Оливер

Дж.

Исакс

Б. Л.

,

1967

.

Зоны глубинных землетрясений, аномальные структуры верхней мантии и литосферы

,

Ж. геофиз. Рез.

,

72

,

4259

–

4275

.

Реймер

Р. Б.

,

1973

.

Деконволюция сейсмического отклика для линейных систем

,

Кандидатская диссертация

,

Инженерный колледж Калифорнийского университета

, Беркли.

Роджерс

утра

Кац

Л. Дж.

Беннетт

Т. Дж.

,

1974

.

Топографические эффекты движения грунта при падении волн P : модельное исследование

,

Бюлл. сейсм. соц. Являюсь.

,

64

,

437

–

456

.

Шипли

С. А.

Лейстнер

Х. Г.

Джонс

Р. Э.

,

1967

.

Распространение упругих волн — сравнение предсказаний методом конечных элементов и точных решений

. Труды Международного симпозиума по распространению волн и динамическим свойствам грунтов ,

509

–

519

.

University of New Mexico Press

, Альбукерке.

Смит

В. Д.

,

1973

.

Скорости в верхней мантии, определенные по локальным наблюдениям за глубокими землетрясениями

,

Bull. сейсм. соц. Являюсь.

,

63

,

807

–

817

.

Смит

В. Д.

,

1974

.

Неотражающая плоская граница для задач распространения волн

,

J. comp. физ.

,

15

,

492

–

503

.

Трифунак

М. Д.

,

1971

.

Движение поверхности полуцилиндрической аллювиальной долины для плоскости падения SH волны

,

Бюлл. сейсм. соц. Являюсь.

,

61

,

1755

–

1770

.

Трифунак

М. Д.

,

1972

.

Опечатка к «Движение поверхности полуцилиндрической аллювиальной долины для падающих плоских волн SH »

,

Bull. сейсм. соц. Являюсь.

,

62

,

666

.

Уилсон

Э. Л.

,

1969

.

Упруго-динамическая характеристика осесимметричных конструкций

.

Исследование конструкций и материалов

, Отчет 69–2,

Инженерный колледж Калифорнийского университета

, Беркли.

Висс

М.

,

1973

. .

Зенкевич

О.К.

,

1971

.

Метод конечных элементов в технических науках

,

McGraw-Hill

, Мейденхед.

Этот контент доступен только в формате PDF.

Примечания автора

*

В отпуске от: отдела геофизики отдела научно-промышленных исследований П.О. Box 8005, Веллингтон, Новая Зеландия.

Выпуск Раздел:

Статьи

Скачать все слайды

Реклама

Цитаты

Альтметрика

Дополнительная информация о метриках

Оповещения по электронной почте

Оповещение об активности статьи

Предварительные уведомления о статьях

Оповещение о новой проблеме

Оповещение о текущей проблеме

Оповещение о теме

Получайте эксклюзивные предложения и обновления от Oxford Academic

Система астрофизических данных

Резюме объявлений

Ссылки на статьи по номеру

• Последний

• Самые читаемые

• Самые цитируемые

Оценка источника более поздних фаз цунами, связанного с извержением вулкана Хунга-Тонга в 2022 г.