Закон ома 2. Закон Ома для полной цепи: формула, применение и примеры

Что такое закон Ома для полной цепи. Как он связан с ЭДС источника тока. Формула и примеры расчетов. Применение закона в электротехнике.

Что такое закон Ома для полной цепи

Закон Ома для полной цепи устанавливает зависимость между силой тока, электродвижущей силой (ЭДС) источника и полным сопротивлением цепи. Он является обобщением закона Ома для участка цепи на случай замкнутой цепи с источником тока.

Формула закона Ома для полной цепи имеет вид:

I = E / (R + r)

где:

• I — сила тока в цепи
• E — ЭДС источника тока
• R — сопротивление внешней части цепи
• r — внутреннее сопротивление источника тока

Электродвижущая сила источника тока

Электродвижущая сила (ЭДС) — это физическая величина, характеризующая работу сторонних сил по перемещению заряда внутри источника тока. ЭДС измеряется в вольтах и численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда.

Источниками ЭДС могут быть:

• Гальванические элементы и аккумуляторы
• Электрические генераторы
• Солнечные батареи
• Термопары

Внутреннее сопротивление источника тока

Внутреннее сопротивление r — это сопротивление, которое оказывают току элементы внутри самого источника. Оно зависит от конструкции и материалов источника тока. Внутреннее сопротивление приводит к потере части напряжения внутри источника.

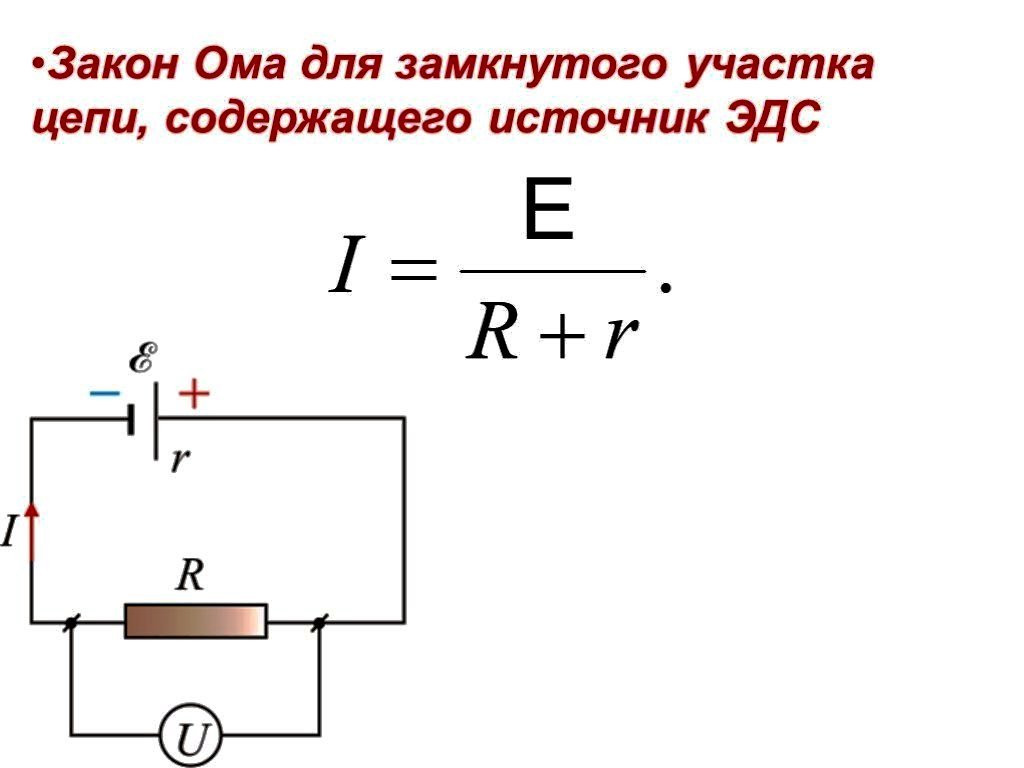
Для идеального источника тока r = 0. Для реальных источников r > 0, что приводит к уменьшению напряжения на внешней нагрузке по сравнению с ЭДС.

Применение закона Ома для полной цепи

Закон Ома для полной цепи применяется для расчета параметров электрических цепей, содержащих источники тока:

• Определение силы тока в цепи
• Расчет напряжения на участках цепи
• Подбор оптимального сопротивления нагрузки
• Определение КПД источника тока
• Расчет мощности, выделяемой в цепи

Примеры расчетов по закону Ома для полной цепи

Рассмотрим несколько примеров применения закона Ома для полной цепи:

Пример 1. Расчет силы тока

Дано: ЭДС источника E = 12 В, внешнее сопротивление R = 5 Ом, внутреннее сопротивление r = 1 Ом.

Найти: Силу тока I в цепи.

Решение:

I = E / (R + r) = 12 / (5 + 1) = 2 А

Пример 2. Расчет напряжения на нагрузке

Дано: ЭДС источника E = 9 В, сила тока I = 0,5 А, внутреннее сопротивление r = 2 Ом.

Найти: Напряжение U на внешней нагрузке.

Решение:

U = E — Ir = 9 — 0,5 * 2 = 8 В

КПД источника тока

Коэффициент полезного действия (КПД) источника тока показывает, какая часть электрической энергии источника преобразуется в полезную работу на внешней нагрузке.

КПД источника тока рассчитывается по формуле:

η = U / E = R / (R + r)

где U — напряжение на внешней нагрузке, E — ЭДС источника.

КПД всегда меньше 100% из-за потерь на внутреннем сопротивлении. Для повышения КПД нужно уменьшать внутреннее сопротивление источника.

Последовательное и параллельное соединение источников тока

При последовательном соединении нескольких одинаковых источников:

• ЭДС батареи равна сумме ЭДС отдельных элементов
• Внутреннее сопротивление батареи равно сумме внутренних сопротивлений элементов

При параллельном соединении:

• ЭДС батареи равна ЭДС одного элемента
• Внутреннее сопротивление батареи обратно пропорционально числу элементов

Режимы работы источника тока

В зависимости от соотношения внешнего и внутреннего сопротивлений различают три основных режима работы источника тока:

1. Режим короткого замыкания

Возникает при R = 0. Сила тока максимальна: I = E / r

2. Режим холостого хода

Наблюдается при R = ∞. Ток в цепи отсутствует, напряжение на выходе равно ЭДС.

3. Режим согласованной нагрузки

Достигается при R = r. В этом режиме в нагрузку передается максимальная мощность.

Частые вопросы о законе Ома для полной цепи

В чем отличие закона Ома для полной цепи от закона Ома для участка цепи?

Закон Ома для участка цепи связывает напряжение, ток и сопротивление на отдельном участке. Закон Ома для полной цепи учитывает ЭДС источника и его внутреннее сопротивление, рассматривая всю замкнутую цепь.

Всегда ли применим закон Ома для полной цепи?

Закон Ома для полной цепи применим для цепей постоянного тока с линейными элементами. Он не работает для нелинейных элементов и в цепях переменного тока.

Как измерить внутреннее сопротивление источника тока?

Внутреннее сопротивление можно определить, измерив ЭДС источника без нагрузки и напряжение при подключенной нагрузке. Зная ток через нагрузку, внутреннее сопротивление рассчитывается по формуле: r = (E — U) / I

Закон Ома и его применение

Закон Ома выражает зависимость между напряжением U, током I и сопротивлением R для участка цепи, не содержащего ЭДС:

U = I ∙ R 

где     U – напряжение, в вольтах;

I – сила тока, в амперах;

R – сопротивление, в омах.

  

Три составляющие закона Ома

 

Для участка цепи, содержащего ЭДС, закон Ома выражает зависимость между ЭДС источника тока E, сопротивлением нагрузки R_н, током I и внутренним сопротивлением r₀ источника тока:

I = E / (R_н + r₀)

 

Напряжение на зажимах источника тока U определяется по формуле:

U = E – I ∙ r₀ = I ∙ R_н

 

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления:

 

В зависимости от сопротивления нагрузки R_н существуют три режима работы:

 

режим короткого замыкания при R_н = 0

I_к.з. = I_max = E / r₀

 

режим холостого хода при R_н = ∞

U_х.х. = U_max = E

 

режим согласованной нагрузки при Rн = r₀

I = I_к.з. / 2

U = U_х.х. / 2

Р = U_х.х. ∙ I_к.з. / 4

 

         В последнем случае источник тока отдает в нагрузку максимально возможную мощность. Если сопротивление нагрузки состоит из нескольких резисторов, то справедливы следующие соотношении:

 

при последовательном соединении резисторов R1 и R2:

U₁ / U₂ = R₁ / R₂

U / U₂ = R₁ + R₂ / R₂

U₂ = U ∙ R₂ / (R₁ + R₂)

U₁ = U ∙ R₁ / (R₁ + R₂) 

где     U – подведенное напряжение;

U₁ и U₂ – падение напряжения на резисторах R₁ и R₂;

 

при параллельном соединении резисторов R₁ и R₂:

I₁ / I₂ = R₂ / R₁

 

         Подключение резисторов параллельно или последовательно измерительному прибору позволяет расширить пределы измерений. Можно показать, что расширение пределов измерения вольтметра достигается включением последовательно с ним добавочного резистора R_доб. Если верхний предел измерения вольтметра U_в, а необходимый предел измерения Uн > Uв, то включение R_доб = R_п ∙ (U_н / U_в – 1) позволяет отсчитывать максимально напряжение U_н. В приведенном выражении R_п – сопротивление прибора, равное R_п = U_в / I_в, где I_в – ток прибора при подведении к нему напряжения U_в.

         Расширение предела измерения амперметра достигается параллельным подключением к нему дополнительного резистора (шунта). Если верхний предел измерения тока амперметра I_в, а необходимый предел измерения I_н > I_в, то сопротивление шунта:

R_ш = R_п / (I_н / I_в) – 1

 

         Сопротивление вольтметра можно определить следующим способом. Измерить вольтметром напряжение на зажимах источника напряжения E и, отметив показания вольтметра, включить последовательно с ним такой добавочный резистор, при котором показание вольтметра уменьшится вдвое, т.е. при равенстве сопротивлений вольтметра и добавочного резистора.

         На этом же принципе основана и обратная задача определения величины неизвестного сопротивления с помощью вольтметра.

формула и определение, источник ЭДС

Взаимозависимость параметров системы в физике принято называть законом.

В электротехнике таковых было открыто несколько и один из главнейших — закон Ома для замкнутой цепи.

В данной статье он и все связанные с ним понятия рассматриваются подробно.

Закон Ома для замкнутой цепи

Электрическая цепь — это замкнутый контур из проводников и прочих токопроводящих элементов, по которому движутся свободные заряды, то есть протекает ток.

Какова причина их движения? Объяснить его действием электростатического поля нельзя: работа последнего при перемещении заряженной частицы по закольцованному контуру, как известно, равна нулю, а между тем в электросети в момент протекании тока явно совершается некая отличная от нуля работа — выделяется тепло, горит свет либо возникает магнитное поле.

Следовательно, должны быть какие-то иные силы, обуславливающие данное движение. Их называют сторонними (СС), а компонент электросхемы, в котором они проявляются, — источником тока (ИТ или двухполюсником). СС, преодолевая силы электростатического поля, «растаскивают» минусовые и плюсовые заряды в разные части ИТ (они называются полюсами), создавая разность потенциалов, и далее те движутся по сети под действием электростатического поля.

Аналогично подъемник «заряжает» потенциальной энергией поднимаемый груз, преодолевая силу гравитации, а циркуляционный насос — кинетической энергией частицы воды, создавая разность давлений. Электрическую сеть, включающую ИТ, называют полной или замкнутой. В противоположность ей, сеть вне двухполюсника называют внешней.

В разных ИТ сторонние силы создаются следующими способами:

1. фотонным. Разность потенциалов возникает при взаимодействии фотонов (из этих частиц состоит свет) с полупроводниковыми материалами. Действующие по такому принципу ИТ называют солнечными батареями;
2. химическим. На этом принципе основано действие гальванических элементов — батареек и аккумуляторов. К примеру, химическое разделение зарядов возникает при погружении в серную кислоту медного и цинкового электродов. Кислота изымает из каждого металла положительно заряженные ионы, но цинк отдает их легче и потому принимает относительно меди отрицательный заряд. Медный же электрод становится положительным полюсом, и если теперь соединить его с цинковым электродом проволокой, по ней потечет ток;
3. электромагнитным. СС вызываются воздействием на проводник переменного магнитного поля. Изменение его параметров, то есть его «переменность», достигается за счет движения относительно него проводника: тот совершает обороты в поле либо, наоборот, магнит вращают вокруг проводника. На этом принципе основана работа электрогенераторов (в обиходе называются динамо-машинами).

Возникновение электротока в проводнике под действием переменного электромагнитного поля, называется электромагнитной индукцией. Двигая заряды q по сети, СС совершают некую работу А. Она, очевидно, пропорциональна величине перемещаемого q, а значит, при любой величине А и Q их соотношение остается константой и может выступать характеристикой двухполюсника. Ее называют электродвижущей силой (ЭДС).

Электродвижущая сила источника тока

Математическое выражение ЭДС, обозначенной буквой Ԑ, записывается так: Ԑ = А/q. Измеряют ЭДС в тех же единицах, что и напряжение — в вольтах (В). Из последнего выражения работа СС записывается как А = Ԑ * q. С другой стороны, работа СС, согласно закону сохранения энергии, должна равняться действию электрического тока. Последняя состоит в выделении тепла (рассматривается сеть постоянного тока с активным сопротивлением).

Выделяемое тепло, в соответствии с законом Дж.-Ленца, вычисляется как произведение квадрата силы тока и электросопротивления. Последняя характеристика присуща как внешней цепи — она обозначается через R, так и ИТ (сопротивление обмоток генератора или электролита, обозначаемое через r).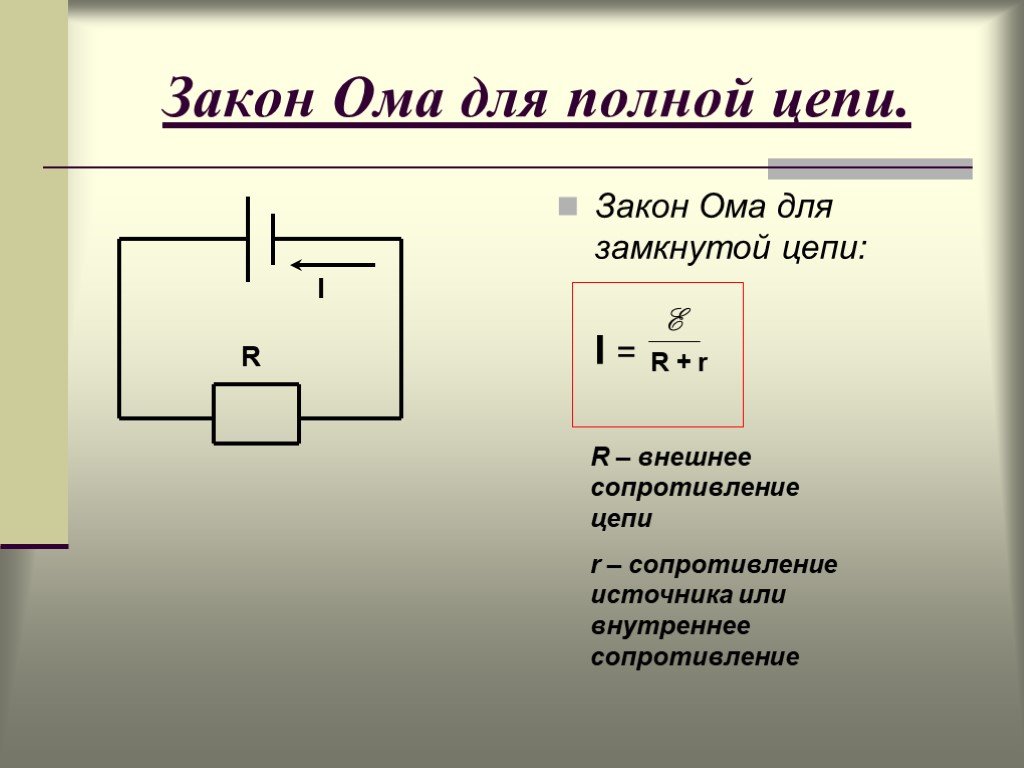

Математическая запись вышесказанного:

1. теплота, выделяющаяся во внешней сети: Q1 = I² * R * t;
2. теплота, выделяющаяся в ИТ: Q2 = I² * r * t;
3. работа СС: А = Ԑ * q = I² * R * t + I² * r * t.

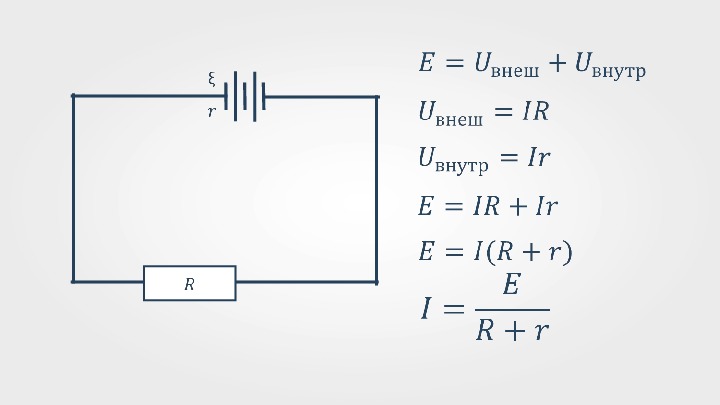
Силой тока I, как известно, называют количество заряда, пересекающее поперечное сечение проводника за единицу времени: I = q / t. Значит, q = I * t, соответственно, Ԑ * q = E * I * t. Тогда получим: А = Е * q = Ԑ * I * t = I² * R * t + I² * r * t. Сократив обе части равенства на I * t, получим: Ԑ = I * R + I * r. Откуда I = Ԑ / (R + r).

Последнее выражение представляет собой математическую запись закона Ома для замкнутой (полной) электросхемы. Сила тока в сети находится в прямой зависимости от ЭДС его источника и в обратной – от полного сопротивления. Как ясно из определения, сумму сопротивлений внешней цепи и ИТ (R + r) называют ее полным сопротивлением.

Таким образом, закон Ома для участка сети, выражаемый формулой I = U / R, является частным случаем закона для полной цепи, в котором двухполюсник во внимание не берут. Из него следует, что U = I * R. Возвращаясь к записи Ԑ = I *R + I * r, можно Заменить I * R на U, и тогда получится: Ԑ = U + I * r.

Формула закона Ома для замкнутой цепи

Поскольку через R обозначалось сопротивление всех наружных проводников, U в данном выражении определяет напряжение на ее концах, то есть на клеммах ИТ. После переноса слагаемого из одной части равенства в другую, получим: U = Ԑ – I * r.

Напряжение на клеммах двухполюсника зависит от протекающего в сети тока. Когда электросеть разомкнута и сила тока равна нулю, U = Ԑ. При коротком замыкании (КЗ), когда ток приобретает максимально возможное значение, U = 0.

Коэффициент полезного действия

Любое устройство или механизм сообщенную ему извне энергию частично расходует на всевозможные потери, а ее оставшееся количество преобразует в работу. Она именуется полезной (Апол). Отношение полезной работы к общим затратам энергии, говорит об эффективности устройства. Такую характеристику называют коэффициентом полезного действия (КПД): КПД = Апол / А.

Коэффициент полезного действия источника тока

В электротехнике «полезной» называют работу тока во внешней цепи. В самом простом случае (постоянный ток, активное сопротивление) она равна количеству тепловыделения, то есть: Апол = Qвнеш = I² * R * t. Выше было показано, что совокупная работа СС А = I² * R * t + I² * r * t, следовательно: КПД = Апол / А = I² * R * t / (I² * R * t + I² * r * t) = R / (R + r).

Приведенная формула позволяет определить КПД ИТ. В соответствии с законом сохранения энергии, он не может быть больше единицы. Принято КПД указывать в процентах. Так, при его значении, к примеру равному 0,95, говорят, что КПД составляет 95%.

Источник ЭДС

Выше было показано, что в реальном ИТ, напряжение на клеммах U зависит от силы тока в электросети. Источник ЭДС — это идеальный, теоретический ресурс напряжения (ИН) с отсутствующим внутренним сопротивлением (r = 0), то есть напряжение U на его контактах и ЭДС равны. Сила тока здесь на это равенство не влияет.

Идеальный источник напряжения

При КЗ ток становится теоретически бесконечно большим. В самом деле, если в выражении закона Ома для полной цепи: I = Ԑ / (R + r) Если полное сопротивление приравнять к нулю, сила тока I достигает бесконечности.

Поэтому источник ЭДС представляет собой теоретический бесконечный источник мощности. В реальности подобное невозможно, так как при КЗ ток в электросети ограничивается сопротивлением двухполюсника (обмоток генератора или электролита гальванического элемента).

Реальный ИН представляет собой источник конечной мощности. На схемах его обозначают как идеальный ИН с подключенным к нему последовательно элементом, соответствующим сопротивлению ИТ.

Соединение источников тока

Если одного ИТ для работы устройства недостаточно, их устанавливают несколько. Характер работы такой группы зависит от способа соединения отдельных источников.

Есть три варианта:

1. последовательное;
2. параллельное;
3. смешанное.

При последовательном подключении ИТ выстраивают в ряд, соединяя «плюсом» к «минусу». При этом заряды проходят по порядку через все источники, воспринимая энергию от каждого из них.

Следовательно, совокупные:

• ЭДС группы равна алгебраической сумме этих характеристик всех ИТ;
• сопротивления группы двухполюсников равно сумме соответствующих параметров каждого из них.

Если соединены n идентичных ИТ с ЭДС, равным Ԑ, и сопротивлением r, то эти параметры для группы окажутся, соответственно: Ԑ гр = n * E; Rгр = n * r. Тогда закон Ома для замкнутой цепи записывается в такой форме: I = (n * Ԑ) / (R + n * r).

Последовательное и параллельное соединение источников

Если направление от «минуса» к «плюсу» в источнике совпадает с движением часовой стрелки, то его ЭДС считается положительной. Электродвижущая сила, направленная в противоположную сторону, отрицательна.

Если внутреннее сопротивление источников в сравнении с R цепи пренебрежимо мало, а надо увеличить U на наружной сети, ИТ соединяют последовательно.

«Плюсы» ИТ, установленных параллельно, подсоединяются к одному концу системы проводников, а все «минусы» — к другому, при этом:

1. каждый заряд набирает энергию только в одном ИТ, потому ЭДС группы равна одноименному параметру одного двухполюсника: Ԑ гр = Ԑ;
2. через отдельно взятый ИТ протекает только доля потока, потому совокупное внутреннее сопротивление группы ниже внутреннего одного элемента в n раз: rгр = r / n. Здесь n — число ИТ в группе.

Здесь также рассматривается случай с одинаковыми ИТ. Закон Ома для полной цепи примет следующую форму: I = Ԑ / (R + (r / n)). Как видно, замена одного ИТ группой параллельно подключенных, приводит к увеличению I во внешней сети.

Соответственно, такой способ подключения применяют при необходимости повысить силу тока в электросети без увеличения напряжения, и сопротивление наружной сети соизмеримо с аналогичным параметром одного двухполюсника.

Видео по теме

Объяснение закона Ома для замкнутой цепи в видео:

Как видно, закон Ома для замкнутой электросхемы соотносит главные «электрические» параметры: силу тока, ЭДС источника напряжения и сопротивление. Потому его следует знать и понимать любому, кто стремится освоить электротехнику.

Закон Ома 2 — Действие

(0 оценок)

Нажмите здесь, чтобы оценить

Quick Look

Уровень: 10 (9-12)

Необходимое время: 3 часа

(можно разделить на несколько дней)

Расходные материалы Стоимость/группа: 10 долларов США

10 долларов США – стоимость материалов для всего класса и 9 долларов СШАстоит многоразового использования.

Размер группы: 3

Зависимость от действий: Нет

предметных областей: Физика, наука и техника

Доля:

TE Информационный бюллетень

Резюме

В этом дополнении к упражнению «Закон Ома I» учащиеся наблюдают, сколько времени требуется, чтобы израсходовать «соки» в батарее, и лучше ли использовать батареи последовательно или параллельно. Это расширение подходит для демонстрации учителю и может быть запущено до того, как учащиеся начнут работу над заданием «Закон Ома I».

Инженерное подключение

Закон Ома лежит в основе всех электрических систем. Инженеры-электрики используют это уравнение для проектирования электрических систем. Учащимся необходима прочная основа закона Ома при самостоятельном проектировании схем.

Цели обучения

Применение следующего:

• Закон Ома
• последовательные/параллельные цепи (способы их соединения и влияние на V и I)
• компоненты схемы
• мощность
• устройства, которые можно использовать для измерения напряжения и тока

Образовательные стандарты

Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.

Все более 100 000 стандартов K-12 STEM описаны в TeachEngineering собираются, поддерживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).

В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естественные науки или математика; внутри типа по подтипу, затем по классам, и т.д. .

Международная ассоциация преподавателей технологий и инженерии – технологии

ГОСТ

Предложите выравнивание, не указанное выше

Какое альтернативное выравнивание вы предлагаете для этого контента?

Подписаться

Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!

PS: Мы никому не передаем личную информацию и электронные письма.

Список материалов

Мы предлагаем покупать следующие материалы оптом и использовать ежегодно:

• 4 батареи общего назначения AAA (C-Zn)
• Лампы накаливания 2,47 В, 300 мА
• 10–12 зажимов типа «крокодил» и проволоки
• секундомер

Рекомендуется:

• 4 отдельных держателя батарей
• 2 двойных держателя батареек
• 6 патронов для ламп

Рабочие листы и вложения

Вопросы для учащихся Раздаточный материал (pdf)

Вопросы для студентов Раздаточный материал (doc)

Посетите [www.teachengineering.org/activities/view/wpi_ohm2_act_joy], чтобы распечатать или загрузить.

Больше учебных программ, подобных этому

Высший элементарный урок

Цепи: один путь для электричества

Учащиеся узнают, что движение заряда по цепи зависит от сопротивления и расположения компонентов цепи. В одном связанном практическом упражнении учащиеся строят и исследуют характеристики последовательных цепей. В другом упражнении учащиеся проектируют и строят фонарики.

Цепи: один путь к электричеству

Урок средней школы

Цепи

Студенты знакомятся с несколькими ключевыми понятиями электронных схем. Они узнают о некоторых физических принципах схем, ключевых компонентах схем и их распространенности в наших домах и повседневной жизни.

Схемы

Высший элементарный урок

Электроны в движении

Учащиеся узнают о текущем электричестве и необходимых условиях для существования электрического тока. Учащиеся строят простую электрическую цепь и гальванический элемент, чтобы понять, что такое напряжение, сила тока и сопротивление.

Электроны в движении

Высший элементарный урок

Параллельная схема и закон Ома: много путей для электричества

Студенты изучают состав и практическое применение параллельных схем по сравнению с последовательными схемами. Учащиеся проектируют и строят параллельные цепи, исследуют их характеристики и применяют закон Ома.

Параллельная схема и закон Ома: много путей для электричества

Введение/Мотивация

Вопрос:

У нас есть три лампочки, включенные в параллельную цепь. Если батареи, используемые для их питания, также расположены параллельно, будут ли они работать дольше, чем батареи, расположенные последовательно?

Объяснение:

Производитель аккумуляторов хочет знать, как долго его аккумуляторы будут служить потребителям. Напряжение очень легко измерить, однако найти ток намного сложнее. Итак, давайте поставим эксперимент, чтобы измерить время автономной работы по последовательным и параллельным схемам.

Аккумуляторы одной серии дают более яркий свет; однако они работают примерно вдвое меньше, чем батареи, подключенные параллельно.

Батареи, включенные в параллельную цепь, дают менее интенсивный свет, но служат в два раза дольше, чем батареи, соединенные последовательно.

Процедура

1. Соберите цепь из 3 ламп, соединенных параллельно, и 2 батарей, соединенных параллельно, как показано на рис. 1. Рис. 1
2. Соберите цепь из 3 ламп, соединенных параллельно, и 2 батарей, соединенных последовательно, как показано на рис. 2. Рис. 2
3. Предложите учащимся угадать, как долго продлится каждая цепь.
4. Измерьте общий ток, протекающий по каждой цепи.
5. Время, через которое лампочки перестанут светиться.

Результаты тестирования

• Время серии: ~20 минут
• Время на параллель: ~ 40 минут

Оценка

Домашнее задание или тест: Поручите учащимся ответить на семь вопросов из раздаточного материала «Вопросы для учащихся». Просмотрите их ответы, чтобы оценить глубину их понимания.

Расширения деятельности

Проведение Закона Ома 1, задание, в котором учащиеся работают над увеличением мощности электрической лампочки, проверяя батареи в последовательных и параллельных цепях.

Авторские права

© 2013 Регенты Университета Колорадо; оригинал © 2005 Вустерский политехнический институт

Авторы

Озан Баскан

Программа поддержки

K-12 Outreach Office, Вустерский политехнический институт

Благодарности

Создание этой деятельности было профинансировано Pratt & Whitney.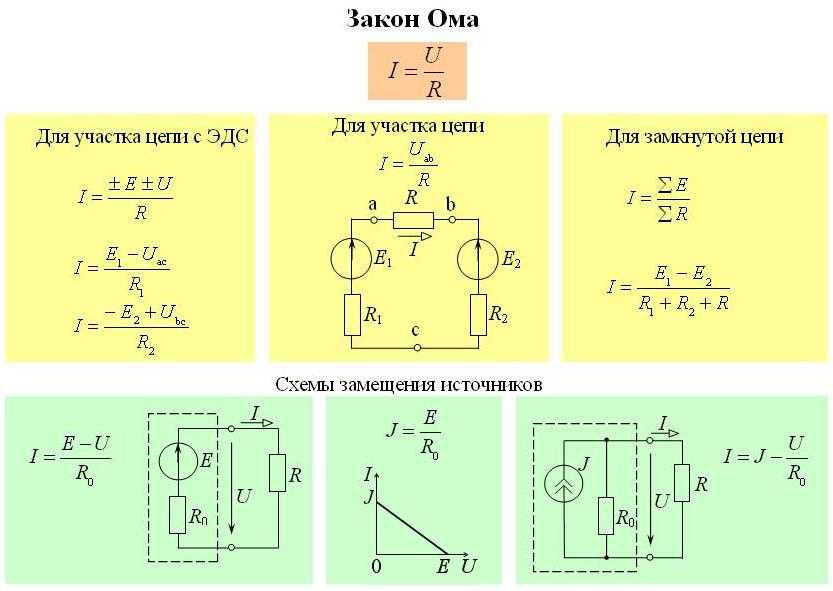

Последнее изменение: 22 августа 2018 г.

9.4 Закон Ома — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Описать закон Ома
• Распознавать, когда применяется закон Ома, а когда нет

До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление. Оказывается, многие материалы демонстрируют простую зависимость между значениями этих свойств, известную как закон Ома. Многие другие материалы не показывают этой взаимосвязи, поэтому, несмотря на то, что он называется законом Ома, он не считается законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.

Описание закона Ома

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению :

.

И∝В.И∝В.

Это важное соотношение лежит в основе закона Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, то есть экспериментально наблюдаемое явление, подобное трению. Такая линейная зависимость не всегда имеет место. Любой материал, компонент или устройство, которые подчиняются закону Ома, где ток через устройство пропорционален приложенному напряжению, известен как омический материал или омический компонент. Любой материал или компонент, который не подчиняется закону Ома, известен как неомический материал или неомический компонент.

Эксперимент Ома

В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток в различных простых электрических цепях, содержащих провода различной длины. Аналогичный эксперимент показан на рис. 9.19. Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор соединен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо поставить на резистор (параллельно резистору). Ток измеряется амперметром, который должен быть подключен к резистору (последовательно с резистором).

Рисунок 9.19 Экспериментальная установка, используемая для определения, является ли резистор омическим или неомическим устройством. (а) Когда батарея присоединена, ток течет по часовой стрелке, а показания вольтметра и амперметра положительны. б) при переключении выводов батареи ток течет против часовой стрелки, а показания вольтметра и амперметра отрицательные.

В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких разных напряжений. Когда батарея была подключена, как показано на рисунке 9. 19(а), ток протекал по часовой стрелке, а показания вольтметра и амперметра были положительными. Изменится ли поведение тока, если ток течет в противоположном направлении? Чтобы заставить ток течь в противоположном направлении, выводы батареи можно поменять местами. При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в противоположном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на рисунке 9..20.

Рисунок 9.20 Резистор включен в цепь с батареей. Приложенное напряжение варьируется от -10,00 В до +10,00 В, увеличиваясь с шагом 1,00 В. На графике показаны значения напряжения в зависимости от тока, типичные для случайного экспериментатора.

В этом эксперименте напряжение, прикладываемое к резистору, изменяется от −10,00 до +10,00 В с шагом 1,00 В. Измеряются ток через резистор и напряжение на резисторе. Строится график зависимости напряжения от тока, и результат приблизительно линейный. Наклон линии — это сопротивление или напряжение, деленное на ток. Этот результат известен как закон Ома:

В=ИК,В=ИК,

9.11

, где В — напряжение, измеренное в вольтах на рассматриваемом объекте, I — ток, измеренный через объект в амперах, а R — сопротивление в единицах Ом. Как указывалось ранее, любое устройство, демонстрирующее линейную зависимость между напряжением и током, известно как омическое устройство. Таким образом, резистор является омическим устройством.

Пример 9,8

Измерение сопротивления

Угольный резистор при комнатной температуре (20 ° C) (20 ° C) подключен к батарее 9,00 В, и ток, измеренный через резистор, составляет 3,00 мА. а) Чему равно сопротивление резистора в омах? (b) Если температура резистора повышается до 60°C60°C путем нагревания резистора, какова сила тока через резистор?

Стратегия

а) Сопротивление можно найти по закону Ома. Закон Ома гласит, что V=IRV=IR, поэтому сопротивление можно найти, используя R=V/IR=V/I.

(b) Во-первых, сопротивление зависит от температуры, поэтому новое сопротивление после нагревания резистора можно найти, используя R=R0(1+αΔT)R=R0(1+αΔT). Ток можно найти по закону Ома в виде I=V/RI=V/R.

Решение

1. Используя закон Ома и вычислив сопротивление, получим сопротивление при комнатной температуре:

   R=VI=9,00В3,00×10-3А=3,00×103Ом=3,00кОм.

2. Сопротивление при 60°C60°C можно найти, используя R=R0(1+αΔT)R=R0(1+αΔT), где температурный коэффициент для углерода равен α=−0,0005α=−0,0005. R=R0(1+αΔT)=3,00×103(1-0,0005(60°C-20°C))=2,94кОмR=R0(1+αΔT)=3,00×103(1−0,0005(60°C−20°C))=2,94 кОм.
   Ток через нагретый резистор

   I = VR = 9,00 В 2,94 × 103 Ом = 3,06 × 10–3 А = 3,06 мА. I = VR = 9,00 В 2,94 × 103 Ом = 3,06 × 10–3 А = 3,06 мА.

Значение

Изменение температуры на 40°C40°C привело к изменению тока на 2,00%. Это может показаться не очень большим изменением, но изменение электрических характеристик может оказать сильное влияние на схемы. По этой причине многие электронные устройства, такие как компьютеры, содержат вентиляторы для отвода тепла, рассеиваемого компонентами электрических цепей.

Проверьте свое понимание 9,8

Напряжение, подаваемое в ваш дом, изменяется как V(t)=Vmaxsin(2πft)V(t)=Vmaxsin(2πft). Если к этому напряжению подключить резистор, будет ли справедлив закон Ома V=IRV=IR?

Интерактивный

Посмотрите, как формула закона Ома соотносится с простой цепью, воспользовавшись приведенным ниже моделированием. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.

Неомические устройства не демонстрируют линейной зависимости между напряжением и током. Одним из таких устройств является полупроводниковый элемент схемы, известный как диод. Диод — это схемное устройство, которое позволяет току течь только в одном направлении. Схема простой цепи, состоящей из батареи, диода и резистора, показана на рис. 9.21. Хотя мы не рассматриваем теорию диода в этом разделе, диод можно проверить, чтобы увидеть, является ли он омическим или неомическим устройством.

Рисунок 9.21 Диод — это полупроводниковое устройство, пропускающее ток только в том случае, если диод смещен в прямом направлении, что означает, что анод положительный, а катод отрицательный.

График зависимости тока от напряжения показан на рис. 9.22. Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод имеет отрицательный потенциал, а катод — положительный, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет чрезвычайно большое сопротивление, и через диод и резистор протекает очень небольшой ток — практически нулевой ток. По мере увеличения напряжения, приложенного к цепи, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не начнет проводить ток, как показано на рисунке 9..22. Когда батарея и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит ток, и ток течет через диод, если напряжение больше 0,7 В. Сопротивление диода близко к нулю. (Это причина резистора в цепи; если бы его не было, ток стал бы очень большим.) Из графика на рис. 9.22 видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером неомического устройства.

Рисунок 9.22 Когда напряжение на диоде отрицательное и малое, через диод протекает очень небольшой ток. Когда напряжение достигает напряжения пробоя, диод открывается. Когда напряжение на диоде положительное и превышает 0,7 В (фактическое значение напряжения зависит от диода), диод проводит ток. По мере увеличения приложенного напряжения ток через диод увеличивается, но напряжение на диоде остается приблизительно равным 0,7 В.