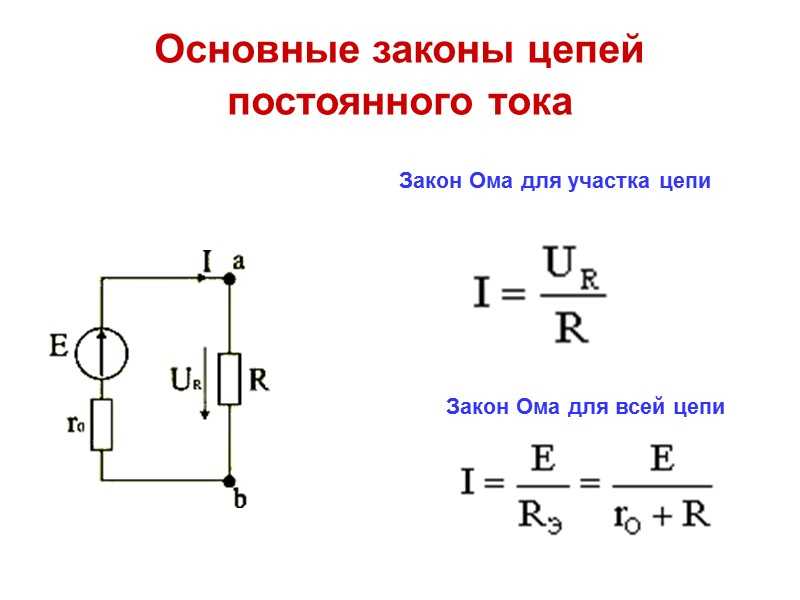
Закон ома для цепи: Закон Ома для полной цепи | Полезные статьи

Закон Ома для замкнутой цепи

Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.

Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.

Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.

Нужна помощь в продвижении в интернете? Пишите!!! [Нажмите на этот текст или кликните на картинку ниже]

Формула закона Ома для замкнутой цепи записывается в следующем виде:

где:

• I [А] – сила тока в цепи,
• ε [В] – ЭДС источника напряжения,
• R [Ом] – сопротивление всех внешних элементов цепи,
• r [Ом] – внутреннее сопротивление источника напряжения

Физический смысл закона

Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.

Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.

Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.

Примеры задач на применение закона Ома для замкнутой цепи

К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.

Дано:	Решение:
ε = 10 В r = 1 Ом R = 4 Ом I – ? U – ?	Запишем закон Ома для замкнутой цепи — I=ε/(R+r) . Падение напряжения на зажимах источника найдем по формуле U=ε-Ir=εR/(R+r). Подставим заданные значения и вычислим I=(10 В)/((4+1)Ом)=2 А, U=(10 В∙4Ом)/(4+1)Ом=8 В./li> Ответ: 2 А, 8 В.

При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.

Дано:

Решение:

R1 = 20 Ом R2 = 10 Ом I1 = 1 A I2 = 1.5 A I – ? U – ?

Запишем закон Ома для замкнутой цепи — I=ε/(R+r) . Отсюда для каждого сопротивления получим ε=I_1 R_1+I_1 r, ε=I_2 R_2+I_2 r. . Приравняем правые части уравнений и найдем внутреннее сопротивление r=(I_1 R_1-I_2 R_2)/(I_2-I_1 ). Подставим полученное значение в закон Ома ε=(I_1 I_2 (R_2-R_1))/(I_2-I_1 ). Произведем вычисления r=(1А∙20 Ом-1,5А∙10Ом)/(1,5-1)А=10 Ом, ε=(1А∙1,5А(20-10)Ом)/((1,5-1)А)=30 В. Ответ: 30 В, 10 Ом.

Нужна помощь в продвижении в интернете? Пишите!!! [Нажмите на этот текст или кликните на картинку ниже]

формула взаимосвязи между электрическими величинами, порядок расчета

Фундаментальным положением, описывающим зависимость тока, сопротивления и напряжения друг от друга является закон Ома для цепи переменного тока. Основное его отличие от одноимённого положения для участка цепи заключается в учёте полного сопротивления. Эта величина зависит от активной и реактивной составляющей линии, то есть учитывает ёмкость и индуктивность.

Поэтому и расчёт параметров для полной цепи по сравнению с участком выполнить будет сложнее.

• Основные понятия
  • Определение напряжения
  • Импеданс цепи
• Закон для переменного тока
• Использование формулы

Основные понятия

Вся наука электротехника построена на оперировании такими понятиями, как заряд и потенциал. Кроме этого, важными явлениями в цепи являются электрические и магнитные поля. Для того чтобы разобраться в сущности закона Ома, необходимо понимать, что представляют собой эти величины, и от чего зависят те или иные электромагнитные процессы.

Электричеством называется явление, обусловленное взаимодействием зарядов между собой и их движением. Это слово было введено в обиход Уильямом Гилбертом в 1600 году после открытия им способности некоторых тел наэлектризовываться. Так как свои эксперименты он проводил с кусочками янтаря, то и свойство притягивать или отталкивать ими другие вещества им было названо «янтарностью», что в переводе с греческого звучит как электричество.

В дальнейшем различными ученными, такими как Эрстед, Ампер, Джоуль, Фарадей, Вольт, Ленц и Ом был открыт ряд явлений. Благодаря их исследованиям в обиходе появились понятия: электромагнитная индукция и поле, гальванический элемент, ток и потенциал. Ими была открыта связь между электричеством и магнетизмом, что привело к появлению науки, изучающей теорию электромагнитных явлений.

В 1880 году русский инженер Лачинов теоретически указал, какие условия необходимы для передачи электричества на расстояния. А через 8 лет Генрих Рудольф Герц во время экспериментов зарегистрировал электромагнитные волны.

Таким образом было установлено, что электрические заряды способны создавать вокруг себя электрическое излучение. Условно их разделили на частицы с положительным и отрицательным знаком заряда. Было установленно, что одноимённого знака заряды притягиваются, а разноимённого — отталкиваются. Для возникновения их движения к физическому телу необходимо приложить какую-либо энергию. При их перемещении возникает магнитное поле.

Свойство материалов обеспечивать движение зарядов получило название проводимость, а величина, обратная ей, — сопротивление. Способность пропускать через себя заряды зависит от структуры кристаллической решётки вещества, её связей, дефектов и содержания примесей.

Определение напряжения

Учёными было установлено, что существует два вида перемещения зарядов — хаотичное и направленное. Первый тип не приводит ни к каким процессам, так как энергия находится в сбалансированном состоянии. Но если к телу приложить силу, заставляющую заряды следовать в одну сторону, то возникнет электрический ток. Существует два вида:

1. Постоянный — сила и направление которого остаются постоянными во времени.
2. Переменный — имеющий разную величину в определённой точке времени и изменяющий своё движение, при этом повторяющий через равные интервалы времени своё изменение (цикл). Эта переменчивость описывается по гармоническому закону синуса или косинуса.

Заряд характеризуется таким понятием, как потенциал, то есть количеством энергии, которой он обладает. Необходимая сила для перемещения заряда из одной точки тела в другую называется напряжением.

Определяется она относительно изменения потенциала заряда. Сила тока определяется отношением количества заряда, прошедшего через тело за единицу времени, к величине этого периода. Математически она описывается выражением: Im = ΔQ/ Δt, измеряется в амперах (A).

Относительно переменного сигнала вводится дополнительная величина — частота f, которая определяет цикличность прохождения сигнала f = 1/T, где T — период. За её единицу измерения принят герц (Гц). Исходя из этого синусоидальный ток выражается формулой:

I = Im * sin (w*t+ Ψ), где:

• Im — это сила тока в определённый момент времени;
• Ψ — фаза, определяемая смещением волны тока по отношению к напряжению;
• w — круговая частота, эта величина зависит от периода и равна w = 2*p*f.

Напряжение же характеризуется работой, которую совершает электрическое поле для переноса заряда из одной точки в другую. Определяется она как разность потенциалов: Um = φ1 — φ2. Затрачиваемая работа же складывается из двух сил: электрических и сторонних, называется электродвижущей (ЭДС). Зависит она от магнитной индукции. Потенциал же равен отношению энергии взаимодействия заряда окружающего поля к значению его величины.

Поэтому для гармонического изменения сигнала значение напряжения выражается как:

U = Um * sin (w*t + Ψ).

Где Um — амплитудное значение напряжения. Измеряется переменное напряжение в вольтах (В).

Импеданс цепи

Каждое физическое тело имеет своё сопротивление. Обусловлено оно внутренним строением вещества. Характеризуется эта величина свойством проводника препятствовать прохождению тока и зависит от удельного электрического параметра. Определяется по формуле: R = ρ*L/S, где ρ — удельное сопротивление, являющееся скалярной величиной, Ом*м; L — длина проводника; м; S — площадь сечения, м

2. Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.

В то же время импеданс, полное сопротивление, находится как сумма пассивной и реактивной составляющей. Первая определяется только активным сопротивлением, состоящим из резистивной нагрузки источника питания и резисторов: R = R0 + r. Вторая находится как разность между ёмкостным и индуктивным сопротивлением: X = XL-Xc.

Если в электрическую цепь поместить идеальный конденсатор (без потерь), то после того, как на него поступит переменный сигнал, он зарядится. Ток начнёт поступать далее, в соответствии с периодами его заряда и разряда. Количество электричества, протекающее в цепи, равно: q = C * U, где С — ёмкость элемента, Ф; U — напряжение источника питания или на обкладках конденсатора, В.

Так как скорости изменения тока и напряжения прямо пропорциональны частоте w, то будет справедливым следующее выражение: I = 2* p * f * C * U. Отсюда получается, что ёмкостной импеданс вычисляется по формуле:

Xc = 1/ 2* p * f * C = 1/ w * C, Ом.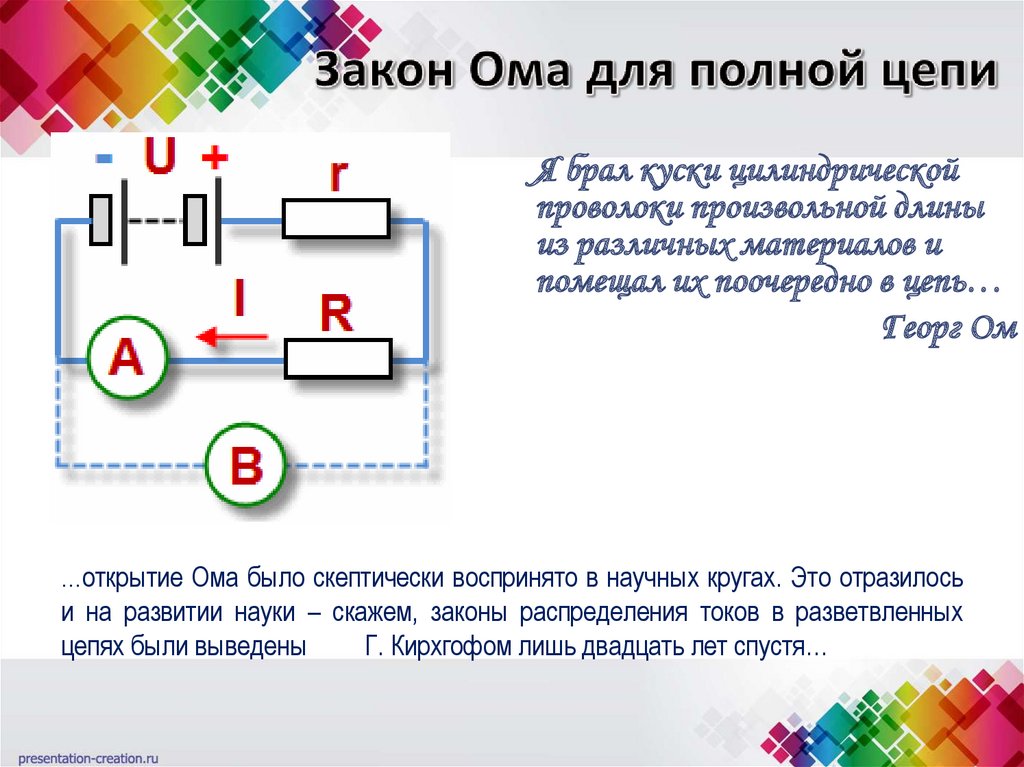

Индуктивное же сопротивление возникает вследствие появления в проводнике собственного поля, называемого ЭДС самоиндукции EL. Зависит она от индуктивности и скорости изменения тока. В свою очередь индуктивность зависит от форм и размеров проводника, магнитной проницаемости среды: L =Ф / I, измеряется в теслах (Тл). Поскольку напряжение, приложенное к индуктивности, по своей величине равно ЭДС самоиндукции, то справедливо EL = 2* p * f * L * I. При этом скорость изменения тока пропорциональна частоте w. Исходя из этого индуктивное сопротивление равно:

Xl = w * L, Ом.

Таким образом, импеданс цепи рассчитывается как: Z = (R ² +(X c-X l) ²) ^½, Ом.

То есть он зависит от частоты переменного сигнала, индуктивности и ёмкости цепи, а также активного сопротивления источника и электрической линии. При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.

Закон для переменного тока

Классический закон был открыт физиком из Германии Симоном Омом в 1862 году. Проводя эксперименты, он обнаружил связь между током и напряжением. В результате ученый сформулировал утверждение, что сила тока пропорциональна разности потенциалов и обратно пропорциональна сопротивлению. Если в электрической цепи ток уменьшится в несколько раз, то и напряжение в ней станет меньше на столько же.

Математически закон Ома был описан как:

I = U / R, А.

Это выражение справедливо как для синусоидального, так и для постоянного тока. Но такая зависимость величин соответствует идеальной ситуации, в которой не учитываются паразитные составляющие и сопротивление источника тока. В случае же гармоничного сигнала на его прохождение влияет частота, из-за присутствия ёмкостной и индуктивной составляющей в электрической линии.

Поэтому закон Ома для переменного тока описывается формулой:

I = U / Z, где:

• I — сила переменного тока, А;
• U — разность потенциалов, В;
• Z — полное сопротивление цепи, Ом.

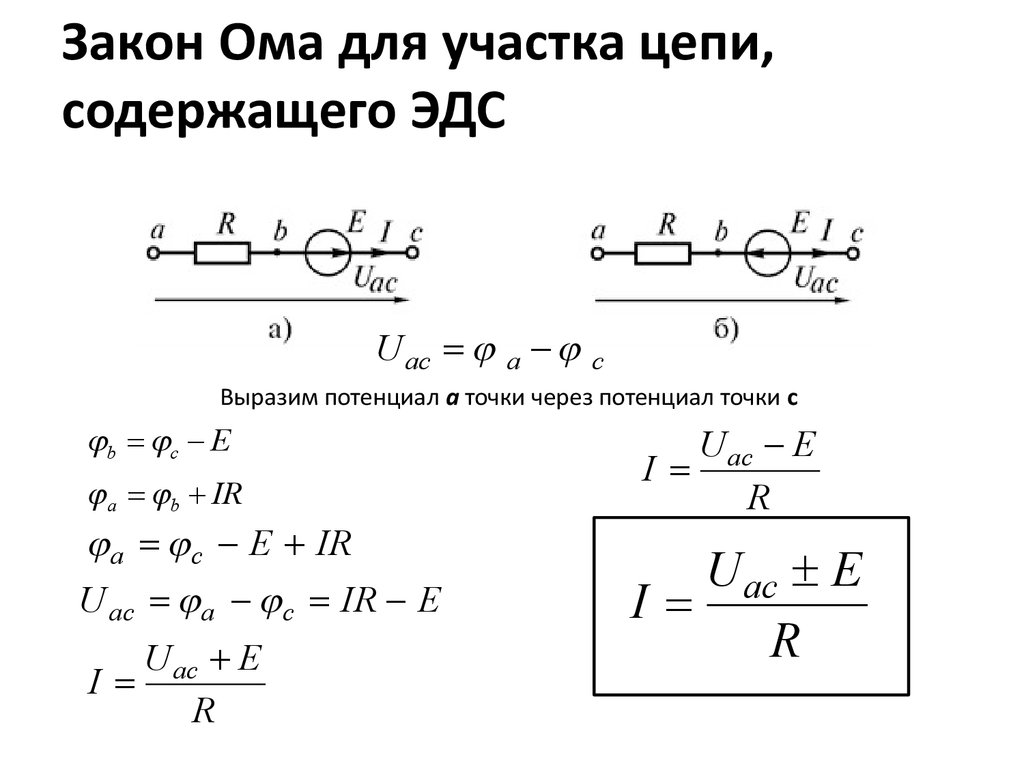
Полное сопротивление зависит от частоты гармоничного сигнала и вычисляется по следующей формуле:

Z = ((R+r)² + (w*L — 1/w*C)²)^½ = ((R+r)²+X²)^½.

При прохождении тока переменной величины электромагнитное поле совершает работу, при этом из-за сопротивления, оказываемого в цепи, выделяется тепло. То есть электрическая энергия переходит в тепловую. Мощность же пропорциональна току и напряжению. Формула, описывающая мгновенное значение, выглядит как: P = I*U.

В то же время для переменного сигнала необходимо учитывать амплитудную и частотную составляющую. Поэтому:

P = I *U*cosw*t*cos (w*t+ Ψ), где I, U — амплитудные значения, а Ψ — фазовый сдвиг.

Для анализа процессов в электрических цепях переменного тока вводится понятие комплексного числа. Связанно это со смещением фаз, появляющихся между током, и разностью потенциалов. Обозначается это число латинской буквой j и состоит из мнимой Im и вещественной Re частей.

Так как на активном сопротивлении происходит трансформирование мощности в тепло, а на реактивном она преобразуется в энергию электромагнитного поля, возможны её переходы из любой формы в любую. Можно записать: Z = U / I = z * e^j*Ψ.

Отсюда полное сопротивление цепи: Z = r + j * X, где r и x — соответственно активное и реактивное сопротивление. Если же сдвиг фаз принимается равный 90⁰, то комплексное число можно не учитывать.

Использование формулы

Использование закона Ома позволяет построить временные характеристики различных элементов. С помощью него несложно рассчитать нагрузки для электрических схем, выбрать нужное сечение проводов, правильно подобрать защитные автоматы и предохранители. Понимание закона даёт возможность применить правильный источник питания.

Использование Закона Ома можно применить на практике для решения задачи. Например, пускай есть электрическая линия, состоящая из последовательно соединённых элементов, таких как: ёмкость, индуктивность и резистор. При этом ёмкость C = 2*Ф, индуктивность L=10 мГн, а сопротивление R = 10 кОм. Требуется вычислить импеданс полной цепи и рассчитать силу тока. При этом блок питания работает на частоте равной f = 200 Гц и выдаёт сигнал с амплитудой U = 12 0 В. Внутреннее сопротивление источника питании составляет r = 1 кОм .

Вначале необходимо рассчитать реактивное сопротивление в цепи переменного тока. Так, ёмкостное сопротивление находится из выражения: Xc = 1/ (2 *p *F*C) и на частоте 200 Гц оно равно: Xc = 588 Ом.

Индуктивное сопротивление находится из выражения: XL = 2*p*F* L. На f = 200 Гц и оно оставляет: X*L = 1,25 Ом. Полное сопротивление RLC цепи будет: Z = ((10 *10 ³ +1*10 ³ ) ² + (588−1,25) ² ) ^½ = 11 кОм.

Разность потенциалов, изменяющаяся по гармоническому закону синуса, будет определяться: U (t) = U * sin (2* p *f*t) = 120*sin (3,14*t). Ток будет равен: I (t) = 10* 10 ⁻³ + sin (3,14*t+p/2).

По рассчитанным данным можно построить график тока, соответствующий частоте 100 Гц. Для этого в декартовой системе координат отображается зависимость тока от времени.

Следует отметить, закон Ома для переменного сигнала отличается от использующегося для классического расчёта лишь учётом полного сопротивления и частоты сигнала. А учитывать их важно, так как любой радиокомпонент обладает как активным, так и реактивным сопротивлением, что в итоге сказывается на работе всей схемы, особенно на высоких частотах. Поэтому при проектировании электронных конструкций, в частности импульсных устройств, для расчётов используется именно полный закон Ома.

Закон

Ома для простых электрических цепей Рона Куртуса

SfC Home > Physics > Electricity >

, автор Ron Kurtus (обновлено 7 марта 2022 г.) Он гласит, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на проводнике. Впервые он был сформулирован в 1827 году немецким физиком Георгом Омом во время экспериментов по изучению того, насколько хорошо металлы проводят электричество.

Закон Ома лучше всего проявляется в простой электрической цепи постоянного тока. Хотя это также применимо к цепям переменного тока, необходимо учитывать другие возможные переменные.

Соотношение между током, напряжением и сопротивлением в цепи позволяет вычислить одну переменную, зная значения двух других.

У вас могут возникнуть следующие вопросы:

• Что означают параметры в уравнении?
• Какая конфигурация цепи?
• Как вы применяете закон Ома?

Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц

---

---

Уравнение

Закон Ома показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи. Самая простая форма уравнения:

В = ИК

где:

• В напряжение в вольтах ( В )
• I ток в амперах или амперах ( А )
• R — сопротивление в омах ( Ом — греческая буква Омега)

Таким образом, зная ток и сопротивление, можно использовать формулу для нахождения напряжения.

Используя Алгебру, вы можете изменить порядок переменных в соответствии с вашими потребностями. Например, если вы знаете напряжение и сопротивление и хотите найти ток, вы можете использовать:

И = В/Р

Или, если вы знаете напряжение и ток и хотите найти сопротивление, вы можете использовать:

Р = В/И

Конфигурация

Простая электрическая цепь состоит из металлических проводов, идущих к источнику питания и от него, а также источника сопротивления, такого как резисторы или лампочка, соединенные последовательно с источником. Типичным источником питания является батарея постоянного тока, хотя также может применяться генератор постоянного или переменного тока.

Примечание : Если цепь переменного тока включает такие компоненты, как конденсаторы или катушки индуктивности, закон Ома не применяется.

Простая цепь постоянного тока

Использование уравнения

Важность закона Ома заключается в том, что если вы знаете значение двух переменных в уравнении, вы можете определить третью.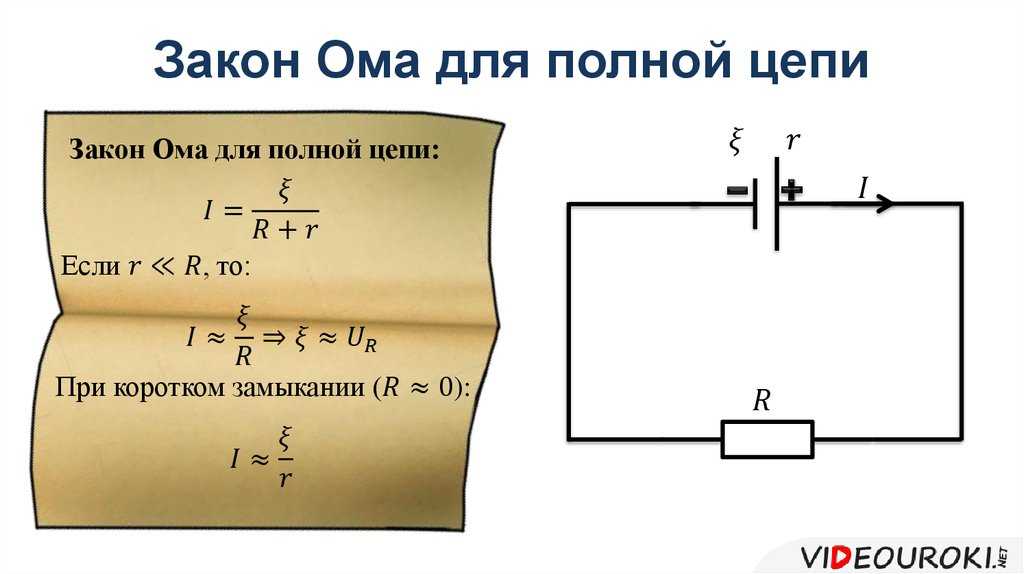 Вы можете измерить любой из параметров с помощью вольтметра. Большинство вольтметров или мультиметров измеряют напряжение, ток и сопротивление как для переменного, так и для постоянного тока.

Найти напряжение

Если известны сила тока и сопротивление, можно найти напряжение из В = I R . Например, если ток I = 0,2 А и сопротивление R = 1000 Ом , то

В = 0,2 А * 1000 Ом = 200 В

Найти ток

Если вы знаете напряжение и сопротивление, вы можете использовать алгебру, чтобы изменить уравнение на I = V / R , чтобы найти ток. Например, если В = 110 В и R = 22000 Ом , затем

I = 110 В / 22000 Ом = 0,005 А

Найдите сопротивление

Если вы знаете напряжение и ток, вы можете использовать алгебру, чтобы изменить уравнение на R = V / I , чтобы найти сопротивление. Если В = 220 В и I = 5 А , то

R = 220 В / 5 А = 44 Ом

Резюме

Закон Ома представляет собой уравнение V = I R , который показывает зависимость между напряжением, током и сопротивлением в простой электрической цепи. Он может применяться как к цепям переменного, так и постоянного тока.

---

Сделайте решение о том, чтобы сделать все возможное

---

Ресурсы и ссылки

Рон Куртус. Об Оме — Краткая история

Закон Ома — Объяснение, в том числе калькулятор закона OHM

Основные электрические законы — включает теорию цепи

Формулы электрических цепи — Уравнения высокого уровня для решения проблем

DC и AC Electricity Resources

DC и ресурсы AC

DC и AC Electrical

Книги

(Примечание: Школа чемпионов может получать комиссионные за покупку книг)

Научись электричеству и электронике Стэна Гибилиско; Макгроу-Хилл; (2001) $34,95 — Руководство для профессионалов, любителей и техников, желающих изучить схемы переменного и постоянного тока

---

Поделитесь этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.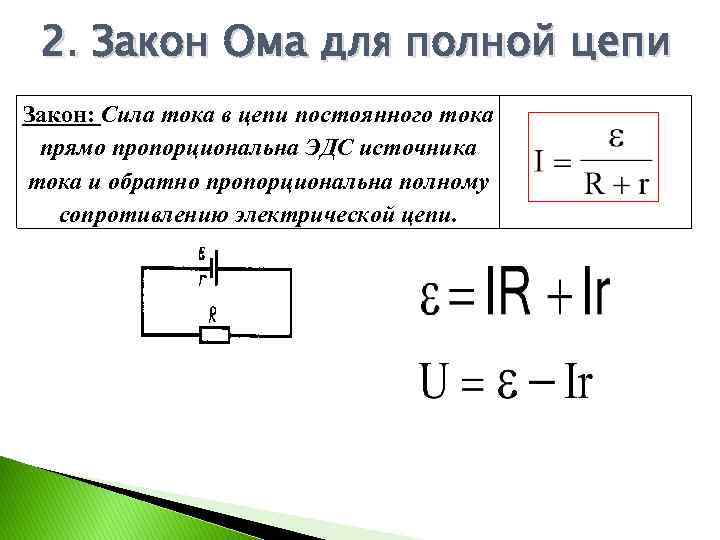 school-for-champions.com/science/
electric_ohms_law.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Copyright © Ограничения

---

Где ты сейчас?

Школа Чемпионов

Темы по физике

Закон Ома для простых электрических цепей

---

20.2: Закон Ома — сопротивление и простые схемы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2680

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснить происхождение закона Ома.
• Рассчитайте напряжения, токи или сопротивления по закону Ома.
• Объясните, что такое омический материал.
• Опишите простую схему.

Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он применяет разность потенциалов \(V\), которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.

Закон Ома

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению \(V\). Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :

\[I \propto V . \label{20. 3.1}\]

Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.

Сопротивление и простые схемы

Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (примерно похожее на трение и сопротивление воздуха), называется сопротивлением \(R\). Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или

\[I \propto \frac{1}{R} . \label{20.3.2}\]

Таким образом, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает

\[I = \frac{V}{R} . \label{20.3.3}\]

Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление \(R\), которое не зависит от напряжения \(V\) и тока \(I\). Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей измерения сопротивления является Ом и обозначается символом \(\Омега\) (греческая омега в верхнем регистре). Перестановка \(I = V/R\) дает \(R = V/I\), поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:

\[1 \Omega = 1 \frac{V} {А} . \label{20.3.4} \]

На рисунке \(\PageIndex{1}\) показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в \(R\).

Рисунок \(\PageIndex{1}\): Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. . Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Пример \(\PageIndex{1}\): Расчет сопротивления: Автомобильная фара:

Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?

Стратегия

Мы можем преобразовать закон Ома в формулу \(I = V/R\) и использовать его для нахождения сопротивления.

Решение:

Преобразование уравнения \ref{20.3.3} и подстановка известных значений дает

\[\begin{align*} R &= \frac{V}{I} \\[5pt] &= \frac{12,0 В}{2,50 А} \\[5pt] &= 4,80 \Омега . \end{align*}\]

Обсуждение:

Это относительно небольшое сопротивление, но оно больше, чем сопротивление холода фары. Как мы увидим, сопротивление металлов обычно 9{-5} \Омега\), а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление».

Дополнительное понимание достигается путем решения \(I = V/R\) для \(V\), что дает

\[V = IR . \label{20.3.5}\]

Выражение для \(V\) можно интерпретировать как падение напряжения на резисторе, вызванное низким током \(I\). Фраза \(IR\) 9Для этого напряжения часто используется падение 0298 . Например, фара в примере имеет падение \(IR\) 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как \(PE = q \Delta V\), и одно и то же \(q\) протекает через каждый . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны (рис. \(\PageIndex{2}\)).

Рисунок \(\PageIndex{2}\): Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: СОХРАНЕНИЕ ЭНЕРГИИ

В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.

Резюме

• Простая цепь — это цепь, в которой есть один источник напряжения и одно сопротивление.
• Одно из утверждений закона Ома дает отношение между током \(I\), напряжением \(V\) и сопротивлением \(R\) в простой цепи как \(I = \frac{V}{R}. \)
• Сопротивление выражается в омах (\(\Омега\)), связанных с вольтами и амперами как \(1 \Омега = 1 В/А \).
• Падение напряжения или \(IR\) на резисторе, вызванное протеканием через него тока, определяемое выражением \(V = IR\).

Глоссарий

Закон Ома

эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов V , ∝ V ; его часто записывают как I = V/R , где R — сопротивление

сопротивление

электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V/I

Ом

единица сопротивления, определяемая как 1 Ом = 1 В/А

омический

тип материала, для которого действует закон Ома

простая схема

схема с одним источником напряжения и одним резистором

---

Эта страница под названием 20.