Закон ома для напряжения. Закон Ома для переменного тока: полное объяснение и применение

Что такое закон Ома для переменного тока. Как он отличается от закона для постоянного тока. Как рассчитать силу тока и напряжение в цепи переменного тока. Какие формулы используются для расчетов. Как учитывается полное сопротивление цепи.

Что такое закон Ома для переменного тока

Закон Ома для переменного тока описывает зависимость между силой тока, напряжением и полным сопротивлением цепи переменного тока. Он является обобщением классического закона Ома для цепей переменного тока.

Основная формула закона Ома для переменного тока выглядит следующим образом:

I = U / Z

Где: I — сила переменного тока (в амперах, А) U — напряжение (в вольтах, В) Z — полное сопротивление цепи (в омах, Ом)

Главное отличие от закона Ома для постоянного тока заключается в использовании полного сопротивления Z вместо активного сопротивления R.

Полное сопротивление цепи переменного тока

Полное сопротивление Z учитывает не только активное сопротивление R, но также реактивное сопротивление цепи, которое создается индуктивностью и емкостью:

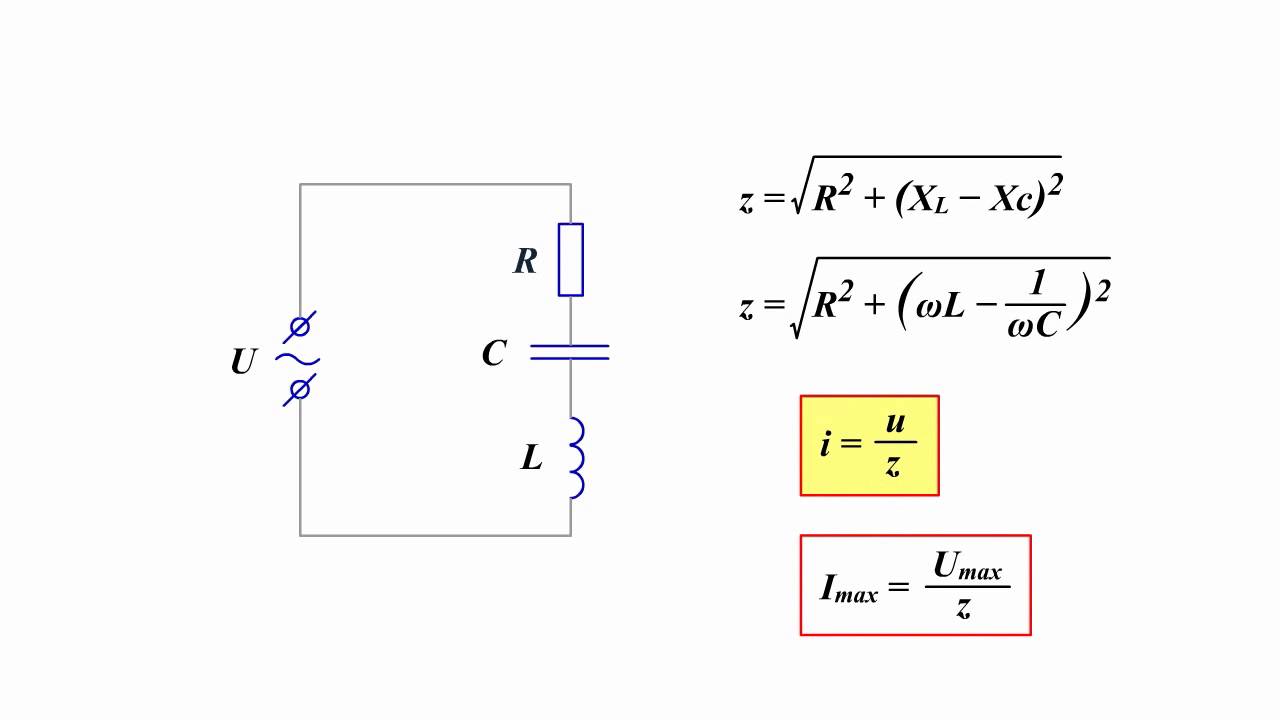
Z = √(R² + (XL — XC)²)

Где: R — активное сопротивление XL — индуктивное сопротивление XC — емкостное сопротивление

Таким образом, полное сопротивление Z зависит от частоты переменного тока, что является важным отличием от постоянного тока.

Как рассчитать силу тока и напряжение

Используя закон Ома для переменного тока, можно рассчитать: — Силу тока: I = U / Z — Напряжение: U = I * Z — Полное сопротивление: Z = U / I

При этом важно учитывать, что для переменного тока используются действующие (эффективные) значения силы тока и напряжения.

Действующие и амплитудные значения

Для переменного синусоидального тока выделяют: — Амплитудные значения — максимальные значения силы тока и напряжения — Действующие значения — эквивалентные значения постоянного тока

Связь между ними: Iд = Iа / √2 Uд = Uа / √2

Где индекс «д» — действующее значение, «а» — амплитудное.

В расчетах по закону Ома для переменного тока обычно используются действующие значения.

Особенности применения закона Ома для переменного тока

При использовании закона Ома для переменного тока важно учитывать следующие особенности:

• Полное сопротивление Z зависит от частоты переменного тока
• Необходимо учитывать сдвиг фаз между током и напряжением
• Расчеты проводятся с использованием действующих значений тока и напряжения
• Закон применим для синусоидального переменного тока

Правильное применение закона Ома позволяет рассчитывать параметры цепей переменного тока и анализировать их работу.

Примеры расчетов по закону Ома для переменного тока

Рассмотрим несколько примеров применения закона Ома для расчета параметров цепи переменного тока:

Пример 1. Расчет силы тока

Дано: Напряжение U = 220 В Активное сопротивление R = 100 Ом Индуктивное сопротивление XL = 50 Ом Емкостное сопротивление XC = 30 Ом

Решение: 1) Рассчитаем полное сопротивление: Z = √(R² + (XL — XC)²) = √(100² + (50 — 30)²) = 104.4 Ом

2) Найдем силу тока: I = U / Z = 220 / 104.4 = 2.11 А

Ответ: Сила тока в цепи составляет 2.11 А.

Пример 2. Расчет напряжения

Дано: Сила тока I = 5 А Полное сопротивление Z = 50 Ом

Решение: Используем формулу U = I * Z U = 5 * 50 = 250 В

Ответ: Напряжение в цепи равно 250 В.

Применение закона Ома для анализа цепей переменного тока

Закон Ома для переменного тока широко применяется для анализа и расчета различных электрических цепей и устройств:

• Расчет параметров трансформаторов
• Анализ работы электродвигателей переменного тока
• Проектирование систем электроснабжения
• Расчет фильтров и резонансных контуров
• Анализ линий электропередачи

Понимание закона Ома для переменного тока необходимо для грамотного проектирования и эксплуатации различных электротехнических устройств и систем.

Ограничения закона Ома для переменного тока

При применении закона Ома для переменного тока следует учитывать некоторые ограничения:

• Закон применим только для линейных цепей
• Не учитывает нелинейные эффекты в реальных устройствах
• Предполагает синусоидальную форму тока и напряжения
• Не учитывает распределенные параметры в длинных линиях

В сложных случаях может потребоваться использование более точных методов анализа цепей переменного тока.

Заключение

Закон Ома для переменного тока является фундаментальным соотношением, описывающим связь между током, напряжением и сопротивлением в цепях переменного тока. Его правильное применение позволяет анализировать работу различных электротехнических устройств и систем.

Ключевые особенности закона Ома для переменного тока:

• Учитывает полное сопротивление цепи, включая реактивные составляющие
• Применяется для расчета действующих значений тока и напряжения
• Учитывает зависимость сопротивления от частоты
• Позволяет анализировать сдвиг фаз между током и напряжением

Понимание и правильное применение закона Ома для переменного тока является важным навыком для специалистов, работающих в области электротехники и электроэнергетики.

формула взаимосвязи между электрическими величинами, порядок расчета

Фундаментальным положением, описывающим зависимость тока, сопротивления и напряжения друг от друга является закон Ома для цепи переменного тока. Основное его отличие от одноимённого положения для участка цепи заключается в учёте полного сопротивления. Эта величина зависит от активной и реактивной составляющей линии, то есть учитывает ёмкость и индуктивность. Поэтому и расчёт параметров для полной цепи по сравнению с участком выполнить будет сложнее.

Основные понятия

Вся наука электротехника построена на оперировании такими понятиями, как заряд и потенциал. Кроме этого, важными явлениями в цепи являются электрические и магнитные поля. Для того чтобы разобраться в сущности закона Ома, необходимо понимать, что представляют собой эти величины, и от чего зависят те или иные электромагнитные процессы.

Электричеством называется явление, обусловленное взаимодействием зарядов между собой и их движением. Это слово было введено в обиход Уильямом Гилбертом в 1600 году после открытия им способности некоторых тел наэлектризовываться. Так как свои эксперименты он проводил с кусочками янтаря, то и свойство притягивать или отталкивать ими другие вещества им было названо «янтарностью», что в переводе с греческого звучит как электричество.

В дальнейшем различными ученными, такими как Эрстед, Ампер, Джоуль, Фарадей, Вольт, Ленц и Ом был открыт ряд явлений. Благодаря их исследованиям в обиходе появились понятия: электромагнитная индукция и поле, гальванический элемент, ток и потенциал. Ими была открыта связь между электричеством и магнетизмом, что привело к появлению науки, изучающей теорию электромагнитных явлений.

В 1880 году русский инженер Лачинов теоретически указал, какие условия необходимы для передачи электричества на расстояния. А через 8 лет Генрих Рудольф Герц во время экспериментов зарегистрировал электромагнитные волны.

Таким образом было установлено, что электрические заряды способны создавать вокруг себя электрическое излучение. Условно их разделили на частицы с положительным и отрицательным знаком заряда. Было установленно, что одноимённого знака заряды притягиваются, а разноимённого — отталкиваются. Для возникновения их движения к физическому телу необходимо приложить какую-либо энергию. При их перемещении возникает магнитное поле.

Свойство материалов обеспечивать движение зарядов получило название проводимость, а величина, обратная ей, — сопротивление. Способность пропускать через себя заряды зависит от структуры кристаллической решётки вещества, её связей, дефектов и содержания примесей.

Определение напряжения

Учёными было установлено, что существует два вида перемещения зарядов — хаотичное и направленное. Первый тип не приводит ни к каким процессам, так как энергия находится в сбалансированном состоянии. Но если к телу приложить силу, заставляющую заряды следовать в одну сторону, то возникнет электрический ток. Существует два вида:

1. Постоянный — сила и направление которого остаются постоянными во времени.
2. Переменный — имеющий разную величину в определённой точке времени и изменяющий своё движение, при этом повторяющий через равные интервалы времени своё изменение (цикл). Эта переменчивость описывается по гармоническому закону синуса или косинуса.

Заряд характеризуется таким понятием, как потенциал, то есть количеством энергии, которой он обладает. Необходимая сила для перемещения заряда из одной точки тела в другую называется напряжением.

Определяется она относительно изменения потенциала заряда. Сила тока определяется отношением количества заряда, прошедшего через тело за единицу времени, к величине этого периода. Математически она описывается выражением: Im = ΔQ/ Δt, измеряется в амперах (A).

Относительно переменного сигнала вводится дополнительная величина — частота f, которая определяет цикличность прохождения сигнала f = 1/T, где T — период.

За её единицу измерения принят герц (Гц). Исходя из этого синусоидальный ток выражается формулой:

I = Im * sin (w*t+ Ψ), где:

• Im — это сила тока в определённый момент времени;
• Ψ — фаза, определяемая смещением волны тока по отношению к напряжению;
• w — круговая частота, эта величина зависит от периода и равна w = 2*p*f.

Напряжение же характеризуется работой, которую совершает электрическое поле для переноса заряда из одной точки в другую. Определяется она как разность потенциалов: Um = φ1 — φ2. Затрачиваемая работа же складывается из двух сил: электрических и сторонних, называется электродвижущей (ЭДС). Зависит она от магнитной индукции. Потенциал же равен отношению энергии взаимодействия заряда окружающего поля к значению его величины.

Поэтому для гармонического изменения сигнала значение напряжения выражается как:

U = Um * sin (w*t + Ψ).

Где Um — амплитудное значение напряжения.

Измеряется переменное напряжение в вольтах (В).

Импеданс цепи

Каждое физическое тело имеет своё сопротивление. Обусловлено оно внутренним строением вещества. Характеризуется эта величина свойством проводника препятствовать прохождению тока и зависит от удельного электрического параметра. Определяется по формуле: R = ρ*L/S, где ρ — удельное сопротивление, являющееся скалярной величиной, Ом*м; L — длина проводника; м; S — площадь сечения, м². Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.

В то же время импеданс, полное сопротивление, находится как сумма пассивной и реактивной составляющей. Первая определяется только активным сопротивлением, состоящим из резистивной нагрузки источника питания и резисторов: R = R0 + r. Вторая находится как разность между ёмкостным и индуктивным сопротивлением: X = XL-Xc.

Если в электрическую цепь поместить идеальный конденсатор (без потерь), то после того, как на него поступит переменный сигнал, он зарядится. Ток начнёт поступать далее, в соответствии с периодами его заряда и разряда. Количество электричества, протекающее в цепи, равно: q = C * U, где С — ёмкость элемента, Ф; U — напряжение источника питания или на обкладках конденсатора, В.

Так как скорости изменения тока и напряжения прямо пропорциональны частоте w, то будет справедливым следующее выражение: I = 2* p * f * C * U. Отсюда получается, что ёмкостной импеданс вычисляется по формуле:

Xc = 1/ 2* p * f * C = 1/ w * C, Ом.

Индуктивное же сопротивление возникает вследствие появления в проводнике собственного поля, называемого ЭДС самоиндукции EL. Зависит она от индуктивности и скорости изменения тока. В свою очередь индуктивность зависит от форм и размеров проводника, магнитной проницаемости среды: L =Ф / I, измеряется в теслах (Тл). Поскольку напряжение, приложенное к индуктивности, по своей величине равно ЭДС самоиндукции, то справедливо EL = 2* p * f * L * I. При этом скорость изменения тока пропорциональна частоте w. Исходя из этого индуктивное сопротивление равно:

Xl = w * L, Ом.

Таким образом, импеданс цепи рассчитывается как: Z = (R ² +(X c-X l) ²) ^½, Ом.

То есть он зависит от частоты переменного сигнала, индуктивности и ёмкости цепи, а также активного сопротивления источника и электрической линии. При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.

Закон для переменного тока

Классический закон был открыт физиком из Германии Симоном Омом в 1862 году. Проводя эксперименты, он обнаружил связь между током и напряжением. В результате ученый сформулировал утверждение, что сила тока пропорциональна разности потенциалов и обратно пропорциональна сопротивлению. Если в электрической цепи ток уменьшится в несколько раз, то и напряжение в ней станет меньше на столько же.

Математически закон Ома был описан как:

I = U / R, А.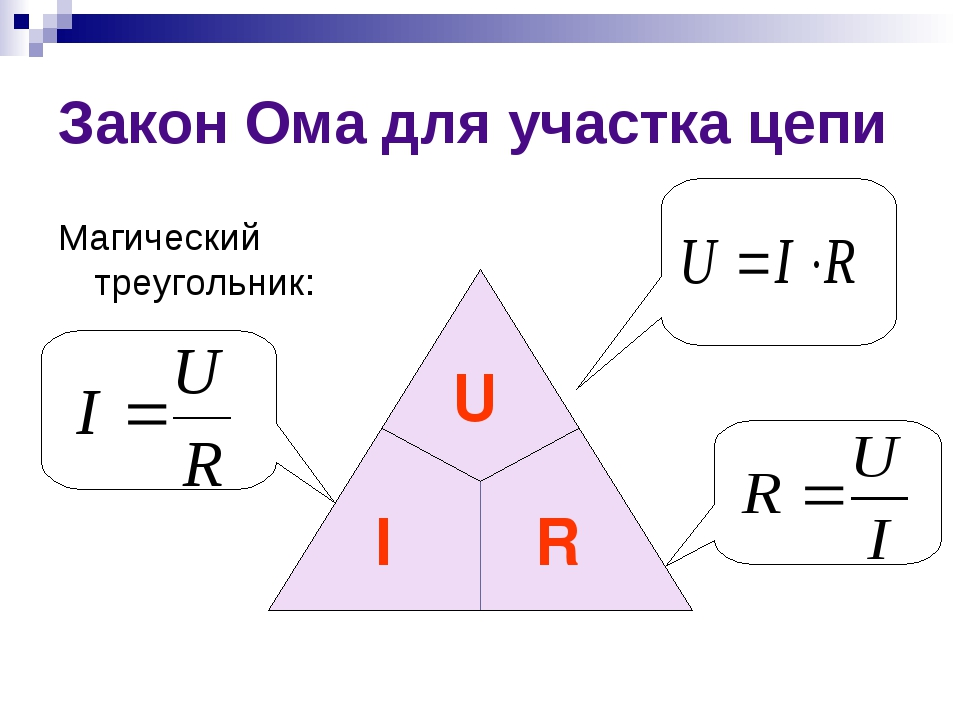

Это выражение справедливо как для синусоидального, так и для постоянного тока. Но такая зависимость величин соответствует идеальной ситуации, в которой не учитываются паразитные составляющие и сопротивление источника тока. В случае же гармоничного сигнала на его прохождение влияет частота, из-за присутствия ёмкостной и индуктивной составляющей в электрической линии.

Поэтому закон Ома для переменного тока описывается формулой:

I = U / Z, где:

• I — сила переменного тока, А;
• U — разность потенциалов, В;
• Z — полное сопротивление цепи, Ом.

Полное сопротивление зависит от частоты гармоничного сигнала и вычисляется по следующей формуле:

Z = ((R+r)² + (w*L — 1/w*C)²)^½ = ((R+r)²+X²)^½.

При прохождении тока переменной величины электромагнитное поле совершает работу, при этом из-за сопротивления, оказываемого в цепи, выделяется тепло. То есть электрическая энергия переходит в тепловую. Мощность же пропорциональна току и напряжению. Формула, описывающая мгновенное значение, выглядит как: P = I*U.

В то же время для переменного сигнала необходимо учитывать амплитудную и частотную составляющую. Поэтому:

P = I *U*cosw*t*cos (w*t+ Ψ), где I, U — амплитудные значения, а Ψ — фазовый сдвиг.

Для анализа процессов в электрических цепях переменного тока вводится понятие комплексного числа. Связанно это со смещением фаз, появляющихся между током, и разностью потенциалов. Обозначается это число латинской буквой j и состоит из мнимой Im и вещественной Re частей.

Так как на активном сопротивлении происходит трансформирование мощности в тепло, а на реактивном она преобразуется в энергию электромагнитного поля, возможны её переходы из любой формы в любую. Можно записать: Z = U / I = z * e^j*Ψ.

Отсюда полное сопротивление цепи: Z = r + j * X, где r и x — соответственно активное и реактивное сопротивление. Если же сдвиг фаз принимается равный 90⁰, то комплексное число можно не учитывать.

Использование формулы

Использование закона Ома позволяет построить временные характеристики различных элементов. С помощью него несложно рассчитать нагрузки для электрических схем, выбрать нужное сечение проводов, правильно подобрать защитные автоматы и предохранители. Понимание закона даёт возможность применить правильный источник питания.

Использование Закона Ома можно применить на практике для решения задачи. Например, пускай есть электрическая линия, состоящая из последовательно соединённых элементов, таких как: ёмкость, индуктивность и резистор. При этом ёмкость C = 2*Ф, индуктивность L=10 мГн, а сопротивление R = 10 кОм. Требуется вычислить импеданс полной цепи и рассчитать силу тока. При этом блок питания работает на частоте равной f = 200 Гц и выдаёт сигнал с амплитудой U = 12 0 В. Внутреннее сопротивление источника питании составляет r = 1 кОм .

Вначале необходимо рассчитать реактивное сопротивление в цепи переменного тока. Так, ёмкостное сопротивление находится из выражения: Xc = 1/ (2 *p *F*C) и на частоте 200 Гц оно равно: Xc = 588 Ом.

Индуктивное сопротивление находится из выражения: XL = 2*p*F* L. На f = 200 Гц и оно оставляет: X*L = 1,25 Ом. Полное сопротивление RLC цепи будет: Z = ((10 *10 ³ +1*10 ³ ) ² + (588−1,25) ² ) ^½ = 11 кОм.

Разность потенциалов, изменяющаяся по гармоническому закону синуса, будет определяться: U (t) = U * sin (2* p *f*t) = 120*sin (3,14*t). Ток будет равен: I (t) = 10* 10 ⁻³ + sin (3,14*t+p/2).

По рассчитанным данным можно построить график тока, соответствующий частоте 100 Гц. Для этого в декартовой системе координат отображается зависимость тока от времени.

Следует отметить, закон Ома для переменного сигнала отличается от использующегося для классического расчёта лишь учётом полного сопротивления и частоты сигнала. А учитывать их важно, так как любой радиокомпонент обладает как активным, так и реактивным сопротивлением, что в итоге сказывается на работе всей схемы, особенно на высоких частотах. Поэтому при проектировании электронных конструкций, в частности импульсных устройств, для расчётов используется именно полный закон Ома.

Закон Ома для действующих и амплитудных значений тока и напряжения.

⇐ ПредыдущаяСтр 7 из 10Следующая ⇒

Пусть источник тока создает переменное гармоническое напряжение (рисунок)

 

 

U(t) = U_osinωt. (1)

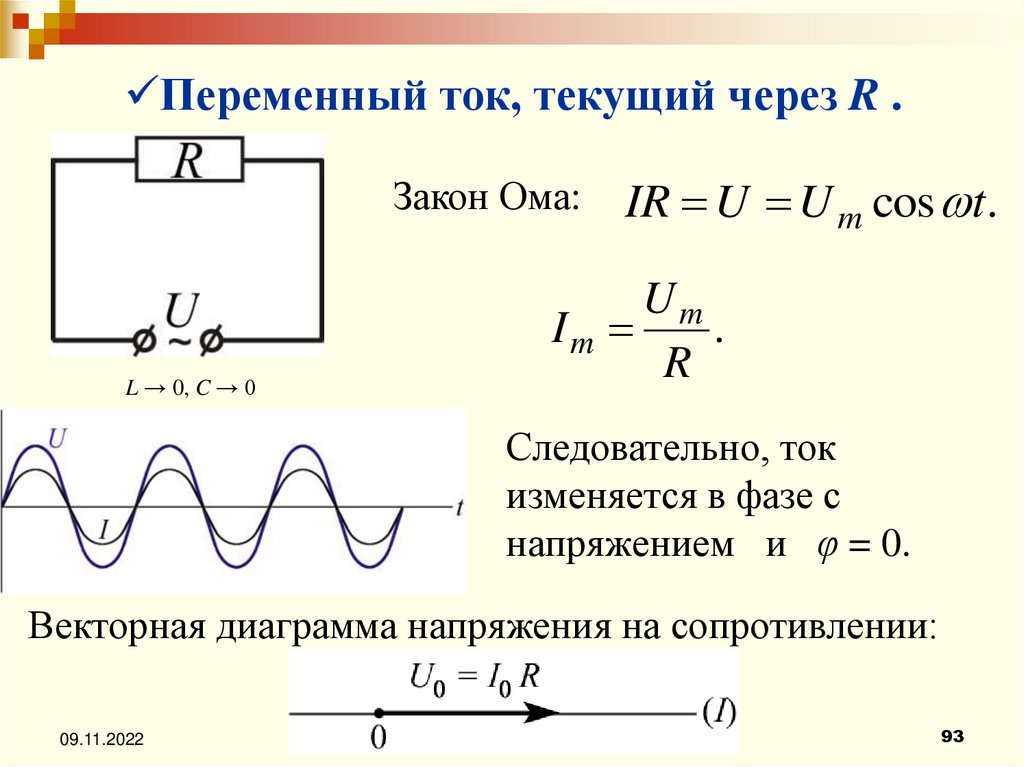
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

 

I(t) = U(t)/R = (U_o/R)sinωt = I_osinωt,

где I_o = U_o/R ? амплитудное значение силы тока в цепи.
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины U_o и I_o = U_o/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность P(t) = U(t)I(t), которая, в отличие от цепей постоянного тока, изменяется с течением времени.
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде

 

P(t) = U(t)I(t) = I²(t)R = I_o²Rsin²ωt.

Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:

 

P = UI = U_oI_osin²ωt = (1/2)U_oI_o(1 ? cos2ωt) = U_oI_o/2 ? (U_oI_o/2)cos2ωt.

Первое слагаемое не зависит от времени. Второе слагаемое ? переменная составляющая ? функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рисунок).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле

 

P_cp = U_oI_o/2 = I_o²/R.

Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока

 

P_пост =I²R,

то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока

 

I_д = I_o/?2.

Аналогично можно ввести действующее значение и для напряжения

 

U_д = U_o/?2.

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

 

P = U_дI_д = I_д²R = U_д²/R, I_д = U_д/R.

 41.1. Треугольники напряжений и сопротивлений.

Амплитуды составляющих общего напряжения:

Действующие значения:

Вектор общего напряжения:

Для того, чтобы найти значение вектора U, построим векторную диаграмму (рис. а). За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительнымнаправлением оси, от которой отсчитываются фазовые углы.

Вектор по направлению совпадает с вектором тока I, а вектор направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор общего напряжения U опережает вектор тока I на угол >0, но < , а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения вактивном и индуктивном сопротивлениях и : =Ucos

Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Ua =

Проекция вектора напряжения U на направление, перпендикулярное вектору тока называется реактивной составляющей вектора напряжения и обозначается Up. Up =

Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. б), катетами которого являются активное и индуктивное сопротивления, а гипотенузой – величина .

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.

Из треугольника сопротивлений следует:

 

41.2. Полное сопротивление.

Полное сопротивление (Z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.

— полное сопротивление цепи.

41.3. Угол сдвига фаз между напряжением и током.

Аргумент комплексного сопротивления j есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как j = arctg(X/R). Следовательно, сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи.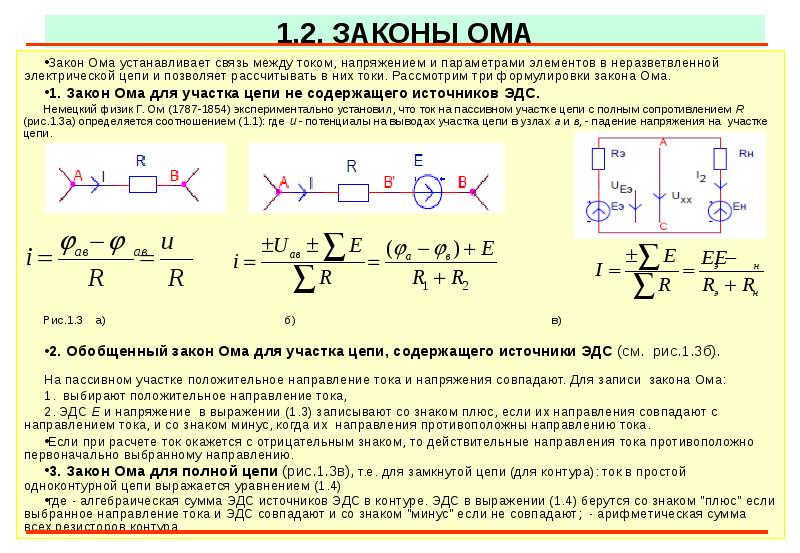 Из выражения следует, что положительные значения j соответствуют отставанию тока по фазе, а отрицательные — опережению.

 

41.4. Закон Ома для действующих и амплитудных значений тока и напряжения.

В активном элементе r происходит необратимое преобразование электрической

энергии в тепловую энергию. Мгновенные значения тока i и напряжения u связаны

законом Ома:

Если ток изменяется по синусоидальному закону тогда напряжение:

С другой стороны мгновенное значение напряжения:

Отсюда получен закон Ома для амплитудных значений: , и закон Ома для действующих значений:

 

42. Энергетический процесс. Мгновенная, активная, реактивная и полная мощности. Треугольник мощностей. Коэффициент мощности.

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:

Для единичного заряда на участке A-B:

Для всех зарядов:

Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:

Если участок цепи содержит резистор c электрическим сопротивлением R, то

Активная мощность
Измеряется в W [Вт] Ватт.
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U иI — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением

Реактивная мощность

Единица измерения — вольт-ампер реактивный (var, вар)

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Рсоотношением: .

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.

Полная мощность

Единица полной электрической мощности — вольт-ампер (V·A, В·А)

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели,распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

ТРЕУГОЛЬНИК МОЩНОСТЕЙ — графическое изображение активной, реактивной и полной мощностей в цепи переменного тока.

Треугольник мощностей получается из соотношения Р² + Q² = S².

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей.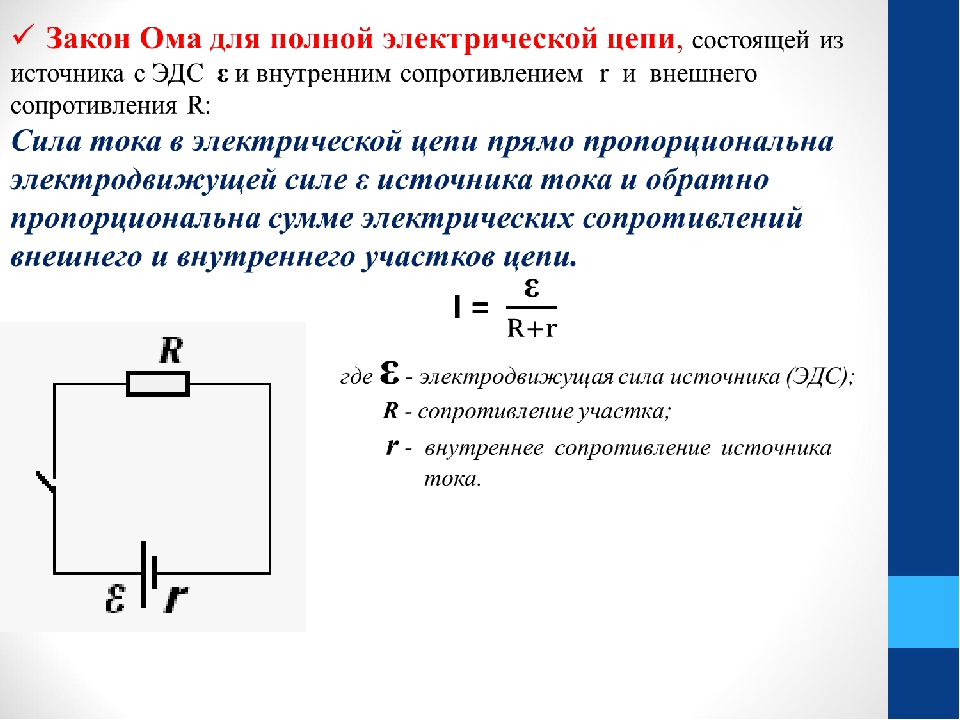 Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

 

Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы:

1.

2.

3.

4.

Здесь — активная мощность, — полная мощность, — реактивная мощность.

 

43.1. Последовательное соединение активного, индуктивного и ёмкостного сопротивлений

При последовательном соединении активного r , индуктивного xL и ёмкостного xC

сопротивлений (рис.8 а) мгновенное значение напряжения источника согласно второму закону Кирхгофа определяется алгебраической суммой мгновенных значений напряжений на

отдельных элементах:

Если все эти напряжения представить в виде векторов на векторной диаграмме,

то действующее значение напряжения источника определяется, как векторная сумма

действующих значений напряжений на отдельных элементах и может быть рассчитано по

формуле:

Учитывая, что по закону Ома

Тогда , — закон Ома ,

где: — полное сопротивление цепи при последовательном соединении элементов.

Полное сопротивление цепи Z , активное r и реактивное образуют

треугольник сопротивлений , для которого справедливы следующие соотношения:

 

43.2. II закон Кирхгофа для мгновенных значений.

 

Второй закон Кирхгофа

Рассмотрим контур, выделенный из сложной цепи переменного тока

Запишем второй закон Кирхгофа для мгновенных значений:

.

Все мгновенные значения изобразим в виде комплексов, опустим знак мнимой части, сократим на и разделим на (по аналогии с законом Ома):

.

В контуре цепи синусоидального тока алгебраическая сумма комплексов ЭДС равна алгебраической сумме комплексов падений напряжений.

 

43.3.Временная и векторная диаграммы для различного характера цепи.

1)

2)

3)

 

Рекомендуемые страницы:

Закон Ома — Традиция

Эта статья о физическом законе, относящемся к электромагнетизму. Для другого использования, см. Акустический закон Ома.

V — напряжение,
I — сила тока,
R — сопротивление. Георг Симон Ом.

Зако́н О́ма — закон, который открывает, что ток через проводник между двумя точками прямо пропорционален разности потенциалов между двумя точками. Вводя коэффициент пропорциональности, сопротивление,^[1] приходим к обычному математическому уравнению, описывающего эту связь:^[2] $$I = \frac{V}{R},$$ где:

• \(I\) — ток через проводник в амперах,
• \(V\) — разность потенциалов, измеренная через проводник в вольтах,
• \(R\) — сопротивление проводника в омах. Конкретнее, в данном случае закон Ома гласит, что R в этом отношении является величиной постоянной, независимой от тока.^[3]

Закон был назван в честь немецкого физика Георга Ома, который в трактате, опубликованном в 1827 году, описано измерения напряжения и тока с помощью простых электрических цепей, содержащих различные длины провода. Он представил несколько более сложные уравнения, чтобы объяснить его экспериментальные результаты. Приведенное выше уравнение является современной формой закона Ома.

В физике термин «закон Ома» также применяется для обозначения различных обобщений закона, первоначально сформулированного Омом. Самый простой пример это: $$\mathbf{J} = \sigma \mathbf{E},$$ где:

Эта переформулировка закона Ома принадлежит Густаву Кирхгофу.[4].

Мнемоническая диаграмма для Закона[править]

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

\(R\!= {U \over I}, \qquad(7)\)

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

\(R\!= {\varrho l \over s}, \qquad(8) \)

где:

• \(\varrho \!\) — удельное сопротивление материала, из которого сделан проводник,
• \(l\!\) — его длина
• \(s\!\) — площадь его поперечного сечения

Закон Ома и ЛЭП[править]

Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока \(P\!\) = \( {\varepsilon\! I\!} \) при минимальных потерях мощности в линии передачи \(P (r)\!\) = \( UI \) , где \(U\! = Ir \), причём \(r\!\) на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).2}. \qquad(9) \)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.3\sigma_{ij}E_j.$$

Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока[править]

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой \(\omega\), а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: $$\mathbb{U} = \mathbb{I} \cdot Z$$

где:

• U • U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z • Re^−iδ — комплексное сопротивление (электрический импеданс),
• R • √R_a² + R_r² — полное сопротивление,
• R_r • ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ • − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.{2}\cdot\tau}{m} \cdot\vec E=\sigma\cdot\vec E$$

  Здесь:

  Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

  Закон Ома может не соблюдаться:

  1. ↑ Consoliver, Earl L., and Mitchell, Grover I. (1920). Automotive ignition systems. McGraw-Hill. p. 4.
  2. ↑ Robert A. Millikan and E. S. Bishop (1917). Elements of Electricity. American Technical Society. p. 54.
  3. ↑ Oliver Heaviside (1894). Electrical papers 1. Macmillan and Co. p. 283. ISBN 0-8218-2840-1.

  Эксперимент с законом Ома [Analog Devices Wiki]

  Цель:

  В рамках этого лабораторного задания:
  Как электрический заряд соотносится с напряжением, током и сопротивлением.
  Что такое напряжение, сила тока и сопротивление.
  Что такое закон Ома и как его использовать для понимания электричества.
  Простой эксперимент для демонстрации этих концепций.

  Основы электроэнергетики:

  Приступая к изучению электричества и электротехники, полезно начать с понимания основных взаимосвязей между напряжением, током и сопротивлением.Это три основные величины, необходимые для понимания и использования электричества. Поначалу эти концепции могут быть трудными для понимания, потому что их невозможно «увидеть» физически. Мы не можем увидеть невооруженным глазом энергию, протекающую через провод, или напряжение батареи, находящейся на скамейке. Даже молния в небе, хотя и видимая, на самом деле не является обменом энергией, происходящим от облаков к земле, но это нагрев воздуха проходящей через него энергией, которая производит вспышки света.Чтобы обнаружить эту электрическую энергию, мы должны использовать измерительные инструменты, такие как мультиметры, осциллографы и анализаторы спектра, чтобы визуализировать, что происходит с электрическими сигналами в системе. Однако не бойтесь, эта лабораторная работа даст вам общее представление о напряжении, токе и сопротивлении, а также о том, как они соотносятся друг с другом.

  Электрический заряд:

  Электричество — это движение (поток) электронов. Электроны — это атомные частицы с отрицательным зарядом.Перемещение этих зарядов можно использовать для работы. Лампочка, вентилятор, радио, мобильный телефон и т. Д. — все они используют движение электронов для выполнения определенной функции. Все они работают с использованием одного и того же основного источника энергии: накопления и движения электронов.

  Три основных принципа этой активности можно объяснить с помощью электронов или, точнее, заряда, который они создают:

  1. Напряжение — это разница в заряде (больше электронов, меньше электронов) между двумя точками в пространстве.
  2. Ток — это скорость, с которой заряд (электроны) протекает между двумя точками, обычно через какой-то материал.
  3. Сопротивление — это способность материала сопротивляться прохождению заряда (электрического тока). Материалы с очень низким сопротивлением называются проводниками. Материалы с очень высоким сопротивлением называются изоляторами.

  Итак, когда мы говорим об этих значениях, мы на самом деле описываем движение заряда и, следовательно, поведение электронов. Цепь — это замкнутый контур, который позволяет заряду перемещаться из одного места в другое.Компоненты схемы позволяют нам контролировать этот заряд и использовать его для работы.

  Георг Ом был баварским ученым, изучавшим электричество. Ом начинается с описания единицы сопротивления, которая определяется током и напряжением. Итак, начнем с напряжения и продолжим.

  Напряжение

  Мы определяем напряжение как количество потенциальной энергии между двумя точками цепи. Одна точка имеет больше заряда (электронов), чем другая. Эта разница в заряде между двумя точками называется напряжением.Он измеряется в вольтах, что технически представляет собой разность потенциальной энергии между двумя точками, которая будет передавать один джоуль энергии на один кулон заряда, который проходит через нее (не паникуйте, если этот физический жаргон не имеет смысла, на самом деле это не так. важно на данный момент). Единица «вольт» названа в честь итальянского физика Алессандро Вольта, который изобрел то, что считается первой химической батареей. Напряжение представлено в уравнениях и схемах заглавной буквой «V».

  При описании электрических свойств, таких как напряжение, ток и сопротивление, общей аналогией является резервуар для воды.В этой аналогии заряд аналогичен объему воды, напряжение представлено давлением воды (глубина воды), а ток представлен потоком воды. Поэтому для этой аналогии помните:

  Вода = заряд
  Давление = напряжение
  Расход = ток

  Рассмотрим резервуар для воды на определенной высоте над землей. На дне этого бака есть шланг. Давление на конце шланга может представлять напряжение. Вода в баке представляет собой заряд.Чем больше воды в баке, тем выше заряд и тем больше давление измеряется на конце шланга.

  Мы можем представить резервуар для воды как батарею, место, где мы храним определенное количество энергии, а затем высвобождаем ее. Если мы опорожняем наш бак определенным количеством жидкости, давление, создаваемое на конце шланга, падает. Мы можем думать об этом как об уменьшении напряжения, например, когда фонарик тускнеет по мере разрядки батарей. Также уменьшается количество воды, протекающей через шланг.Меньшее давление означает, что течет меньше воды, что приводит нас к течению.

  Текущий

  Мы можем рассматривать количество воды, текущей по шлангу из бака, как ток. Чем выше давление, тем выше расход, и наоборот. С водой мы бы измерили объем воды, протекающей по шлангу за определенный период времени. С помощью электричества мы измеряем количество заряда, протекающего по цепи за определенный период времени. Сила тока измеряется в амперах (обычно просто «амперах»).Ампер определяется как 6,241 × 10 ¹⁸ электронов (1 кулон), проходящих через точку в цепи в секунду. Ампер в уравнениях обозначается заглавной буквой «I».

  Предположим теперь, что у нас есть два резервуара одинакового размера с одинаковым количеством воды в них, но шланг на одном резервуаре уже (меньший диаметр), чем шланг на другом. Мы измеряем одинаковое давление на концах обоих шлангов, потому что давление воды одинаковое, но когда вода начинает течь, расход воды в баке с более узким шлангом будет меньше, чем расход воды в бак с более широким шлангом.

  С точки зрения электричества, ток через более узкий шланг меньше, чем через более широкий шланг. Если мы хотим, чтобы поток через оба шланга был одинаковым, мы должны увеличить количество воды (заряд) и, следовательно, давление в резервуаре с помощью более узкого шланга. Это повышенное давление (напряжение) на конце более узкого шланга проталкивает больше воды через резервуар. Это аналогично увеличению напряжения, которое вызывает увеличение тока.

  Теперь мы начинаем устанавливать связь между напряжением и током.Но здесь следует учитывать третий фактор: диаметр шланга. По этой аналогии диаметр шланга определяет сопротивление потоку воды (заряду). Это означает, что нам нужно добавить еще один термин в нашу модель:

  Вода = заряд (измеряется в кулонах)
  Давление = напряжение (измеряется в вольтах)
  Расход = ток (измеряется в амперах, или «амперах» для краткости)
  Диаметр шланга = сопротивление

  Сопротивление

  Снова рассмотрим два резервуара для воды: один с трубой малого диаметра, а другой — с трубой большого диаметра.

  Само собой разумеется, что мы не можем пропустить такой же объем воды через узкую трубу, чем более широкую, при том же давлении. Это сопротивление. Узкая труба «сопротивляется» потоку воды через нее, даже если вода находится под тем же давлением, что и резервуар с более широкой трубой.

  В электрическом смысле это две цепи с одинаковым напряжением и разным сопротивлением. Схема с более высоким сопротивлением позволит протекать меньшему количеству заряда; Это означает, что в цепи с более высоким сопротивлением протекает меньший ток.

  Это возвращает нас к Георгу Ому. Ом определяет единицу сопротивления «1 Ом» как сопротивление между двумя точками в проводнике, где приложение 1 вольта вызовет 1 ампер, или 6,241 × 10 ¹⁸ электронов в секунду. Это значение обычно представлено на схемах греческой буквой «Ω», которая произносится как «омега» и очень похожа на «ом».

  Закон Ома

  Объединив элементы напряжения, тока и сопротивления, Ом разработал формулу:

  Где:
  В = напряжение в вольтах
  I = ток в амперах
  R = сопротивление в омах

  Это называется законом Ома.Например, предположим, что у нас есть цепь с потенциалом 1 вольт, током 1 ампер и сопротивлением 1 Ом. Используя закон Ома, мы можем сказать:

  Возвращаясь к аналогии с водой, предположим, что это наш резервуар с широким шлангом. Количество воды в баке определяется как 1 В, а «узость» (сопротивление потоку) шланга определяется как 1 Ом. Используя закон Ома, это дает нам ток (ток) в 1 ампер.

  Теперь рассмотрим резервуар с узким шлангом.Поскольку шланг более узкий, его сопротивление потоку выше. Для случая с более узким шлангом мы можем определить сопротивление как вдвое большее, или 2 Ом. Количество воды в баке такое же, как и в другом баке, поэтому напряжение такое же. Используя закон Ома, наше уравнение для резервуара с узким шлангом выглядит следующим образом:

  Но какой ток? Поскольку сопротивление больше, а напряжение такое же, это дает нам значение тока 0,5 ампер:

  Итак, как мы и предполагали, ток в баке с более высоким сопротивлением ниже.Теперь мы видим, что если мы знаем два значения закона Ома, мы можем решить третье.

  Продемонстрируем это на эксперименте.

  Для этого эксперимента мы хотим зажечь светодиод (Light Emitting Diode). Светодиоды несколько хрупкие, и через них должен проходить только определенный ток. Ток, превышающий максимально допустимый, может их сжечь. В техническом описании светодиода всегда будет «текущий рейтинг». Это максимальное количество тока, которое может протекать через конкретный светодиод, прежде чем он будет поврежден.

  Мы будем использовать вывод питания + 5V от ADALM1000 в качестве источника напряжения. Напоминаем, что ADALM100 имеет два фиксированных источника напряжения. Один отмечен +2,5 В, а другой + 5,0 В. Есть два общих контакта заземления, помеченных GND. Они соединены вместе на печатной плате, и можно использовать один (или оба).

  Материалы:

  Аппаратный модуль ADALM1000
  Перемычки и макетная плата
  1 светодиод, более длинный из двух выводов — анод (+), а более короткий вывод — катод (-)
  1 Резистор

  ПРИМЕЧАНИЕ. Светодиоды известны как «неомические» устройства.Это означает, что уравнение для тока, протекающего через сам светодиод, не является простой линейной зависимостью V = IR. Светодиод — это особый вид диода. Все диоды имеют то, что называется внутренним «падением напряжения». Однако в этом эксперименте мы просто пытаемся защитить светодиод от проведения слишком большого тока, поэтому на данный момент мы можем пренебречь неомическими токовыми характеристиками светодиода и выбрать номинал резистора, используя только закон Ома, чтобы гарантировать, что ток через светодиод будет безопасно меньше 20мА.

  В этом примере у нас есть выход +5 В на ADALM1000 и (красный) светодиод с номинальным током 20 миллиампер или 0,020 ампер. В целях безопасности мы бы предпочли не управлять максимальным током светодиода, а его рекомендуемым током, который указан в его техническом описании как 18 мА или 0,018 ампер. Если просто подключить светодиод непосредственно к батарее, значения закона Ома будут выглядеть так:

  Переставляем для I:

  Только с проводом и без резистора:

  Деление на ноль дает бесконечный ток! На практике не бесконечно, но ток такой, какой может обеспечить питание +5 В ADALM1000.Мы, конечно, не хотим, чтобы через светодиод протекал такой большой ток. Нам нужно будет включить резистор.

  Зеленые прямоугольники на схеме используются для обозначения подключений к контактам ADALM1000. Наши схемы подключения должны выглядеть так:

  Схема, схема для питания светодиода от источника питания +5 В

  Мы можем использовать закон Ома, чтобы определить номинал резистора, который даст нам желаемое значение тока:

  Переставляем для R:

  Подключите значения 5 Вольт и 0.018 ампер:

  Решение проблемы сопротивления:

  Итак, номинал резистора, который нам нужен для R ₁ , составляет около 277 Ом, чтобы ток через светодиод не превышал максимальный номинальный ток.

  277 Ом не является обычным значением для стандартных резисторов, поэтому для этого эксперимента используйте резистор 470 Ом (желто-пурпурно-коричневый), который является ближайшим значением, превышающим 277 в комплекте деталей ADALP2000. Ниже показано, как ваша схема должна выглядеть вместе.

  Макетная плата, схема для питания светодиода от источника питания +5 В

  Успех! Мы выбрали номинал резистора, который достаточно высок, чтобы ток через светодиод не превышал его максимального номинала, но достаточно низкий, чтобы ток был достаточным, чтобы светодиод оставался красивым и ярким. Если светодиод не загорается, обязательно дважды проверьте правильность подключения (+) и (-) концов светодиода.

  Этот пример светодиодного / токоограничивающего резистора является обычным явлением в электронике.Вам часто придется использовать закон Ома, чтобы изменить величину тока, протекающего по цепи.

  Ограничение тока до или после светодиода?

  Чтобы немного усложнить ситуацию, вы можете разместить токоограничивающий резистор по обе стороны от светодиода, и он будет работать точно так же.

  Многие читатели, впервые изучающие электронику, борются с идеей, что резистор, ограничивающий ток, может быть вставлен с любой стороны светодиода, и схема по-прежнему будет работать как обычно.Попробуйте поменять местами резистор и светодиод в вашей цепи. Светодиод по-прежнему горит с одинаковой яркостью в обоих случаях?

  Вот еще одна аналогия с водой: представьте себе водопроводную трубу, которая представляет собой непрерывный контур с насосом, который непрерывно циркулирует воду. Если бы мы поместили клапан где-нибудь в трубе, при закрытом клапане вода перестала бы течь во всей трубе, а не только в одной секции. А теперь представьте, что мы немного приоткрываем вентиль, который ограничивает поток воды. Неважно, где в петле находится частично открытый клапан, он все равно замедлит поток во всей трубе.Вода за клапаном не возвращается. Давление в участке трубы между выпускной стороной насоса и клапаном увеличивается, в то время как давление в участке трубы между клапаном и выпускной стороной насоса уменьшается. Насос аналогичен источнику напряжения, увеличивающему напряжение, а клапан аналогичен резистору, уменьшающему напряжение.

  Это чрезмерное упрощение, поскольку токоограничивающий резистор можно разместить в цепи только в двух местах; он может быть размещен по обе стороны от светодиода для выполнения своей функции.

  Чтобы получить более научный ответ, мы обратимся к закону напряжения Кирхгофа. Именно из-за этого закона резистор, ограничивающий ток, может располагаться по обе стороны светодиода и при этом иметь тот же эффект. Для получения дополнительной информации и некоторых практических задач с использованием KVL посетите этот веб-сайт.

  Измерение фактического напряжения и тока

  ADALM1000 также имеет два входных канала, которые можно использовать как вольтметр. Мы можем подключить их, как показано на следующей схеме, для измерения фактических напряжений в цепи. Вход вольтметра канала A подключен для измерения напряжения питания +5 В, , а вольтметр канала B подключен для измерения напряжения на ( +), плюс, конец диода.

  Схема, Измерьте фактическое напряжение в цепи.

  Добавьте еще две перемычки для подключения входов вольтметра, как показано.

  Макетная плата, Измерьте фактические напряжения в цепи.

  Запустите программу вольтметра ALICE M1K. Интерфейс выглядит так.

  Нажмите зеленую кнопку «Выполнить», и отобразятся напряжения в цепи. CA Volts должен отображать фактическое значение источника питания +5 V .CB Volts должен отображать фактическое напряжение на светодиодном диоде. В этом примере для красного светодиода напряжение составляло 1,81 вольт. Разница между этими двумя напряжениями, CA-CB V , будет напряжением на резисторе, которое в этом примере составляло 3,16 В.
  

  Мы можем использовать закон Ома для расчета тока в резисторе:

  Или же:

  Или же:

  6,7 мА

  Любой из двух каналов ADALM1000 также может использоваться как источник напряжения.При использовании в качестве источника напряжения можно измерить ток, подаваемый источником напряжения. Мы можем использовать эту функцию для измерения тока в диапазоне подаваемых напряжений. Снимите перемычку, подключенную к источнику питания +5 В , как показано ниже.

  Схема, Измерьте фактический ток в цепи.

  Макетная плата, Измерьте фактический ток в цепи.

  Закройте инструмент «Вольтметр» и запустите инструмент «Измеритель-источник ALICE M1K».Экран с включенным источником CA и настроенным на выход 5,0 вольт выглядит так:

  Как и в случае с простым вольтметром, CA Meter считывает +5 В источника питания. Напряжение A-B — это напряжение на резисторе, но, кроме того, теперь CA mA считывает ток, подаваемый источником на резистор. И снова, когда источник CB выключен, CB Meter измеряет напряжение на светодиодном диоде. Канал B не измеряет ток, потому что источник CB выключен.

  Попробуйте отрегулировать настройку напряжения для CA и посмотрите, как изменяются напряжение на резисторе, ток через резистор и напряжение на светодиоде. Всегда ли применим к резистору закон Ома? Меняется ли напряжение на диоде линейно с током? Другими словами, следует ли это закону Ома?

  ADALM1000 также может работать как омметр. Чтобы измерить резистор, просто подключите его между CH A и CH B, как показано здесь.

  Макетная плата, измерение сопротивления.

  Закройте инструмент «Измеритель-источник» и запустите инструмент «Измеритель сопротивления ALICE M1K». Здесь показан экран. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор на 50 Ом, который можно использовать для этого. Убедитесь, что выбран параметр Int. Уровень напряжения, который используется для измерения резистора, может быть установлен. Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите Run, и вы должны увидеть что-то подобное с резистором 470 Ом.

  Ресурсы и дальнейшее развитие

  Теперь вы должны понять концепции напряжения, тока, сопротивления и их взаимосвязь. Поздравляю! Большинство уравнений и законов для анализа цепей можно вывести непосредственно из закона Ома. Зная этот простой закон, вы понимаете концепцию, лежащую в основе анализа любой электрической цепи!

  Эти концепции — лишь верхушка айсберга. Если вы хотите продолжить изучение более сложных приложений закона Ома и проектирования электрических цепей, обязательно ознакомьтесь со следующими практическими занятиями.

  Для дальнейшего чтения:

  Вернуться к разделу «Введение в деятельность электротехнической лаборатории» Содержание

  Закон Ома для начинающих и новичков

  Закон Ома для начинающих и новичков

  Основной закон Ома
  HTML от: http://www.btinternet.com/~dtemicrosystems/beginner.htm

  ЧТО ЭТО. КАК И ГДЕ ПРИМЕНЯТЬ

  
  

  Хотя закон Ома применим не только к резисторам — как мы увидим позже — кажется, логично включить его сейчас, так как он будет хорошей точкой отсчета для резистора подробности приведены выше.

  ЧТО ТАКОЕ ЗАКОН ОМС? :
  На диаграмме слева закон Ома определяется как; «При условии, что температура остается постоянным, отношение разности потенциалов (p.d.) на концах проводника (R) к току (I), протекающему в этом проводнике, также будет постоянным ». Здесь заканчивается проповедь!

  Из этого мы заключаем, что; Ток равен напряжению, разделенному на сопротивление (I = V / R), Сопротивление равно напряжению, разделенному на ток (R = V / I), а напряжение равно току, умноженному на Сопротивление (V = IR).
  Важным фактором здесь является температура. Если расчеты по закону Ома должны давать точные результаты, это должно оставаться постоянным. В «реальном» мире это почти никогда делает, и с точки зрения новичка вам не нужно беспокоиться об этом. далее, поскольку схемы, с которыми вы, вероятно, столкнетесь в данный момент, — и около 95% все те, с которыми вы столкнетесь в будущем — будут работать нормально, даже если они горячие или холодно!
  

  ЗАКОН ОМС ПРОСТОЙ:
  На рисунке 1 слева показан наиболее распространенный треугольник закона Ома.Начиная с любого раздела треугольник, его можно читать в любом направлении — по часовой стрелке, против часовой стрелки, сверху вниз или снизу вверх — и он всегда предоставит вам расчет, который вы требуется.

  
  Если рассматривать (слегка диагональные) горизонтальные линии как знаки разделения, а короткие вертикальная линия как знак умножения, и всегда начинайте свой расчет с любого количества вы ищете, т.е. «V =», «I =» или «R =» у вас будет все возможные формулы, основанные на этом конкретном законе Ома.То есть; V = IxR, I = V / R, R = V / I. Это должно быть очевидно, что формула работает и в обратном направлении, то есть; IxR = V, RxI = V, V / I = R и V / R = I.

  Эти объяснения могут показаться немного сложными, но их легко применить на практике. Как правило, для начинающих будет более понятен полезный пример, а не эти причудливые столы, так что поехали.

  ПОЯСНЕНИЕ НА ПРИМЕРЕ:
  Допустим, друг просит вас установить красную сигнальную лампу на приборную панель его / ее автомобиля.Как энтузиаст электроники вы решили использовать красный светоизлучающий диод (LED), поскольку они излучают достаточно чистый красный свет, не выделяют чрезмерного тепла лампы накаливания, они также дешевы по сравнению и выглядят высокотехнологичными!

  С точки зрения принципиальной схемы расположение будет таким, как показано слева.
  ОГРАНИЧИТЕЛЬ ТОКА РЕЗИСТОР:
  Стандартные светодиоды не могут получать питание напрямую от 12 В без установки ограничения тока резистор включен последовательно с одним из выводов, но какое значение вы используете? Как общее правило на практике, вашему среднему светодиоду требуется около 15 мА тока для получения приемлемого света. вывод.Учитывая это, теперь у нас есть две известные величины для использования в наших расчетах: напряжение и ток. Используя треугольник закона Ома, требуемое сопротивление равно рассчитывается по формуле «R = V / I», которая дает нам 12 / 0,015 = 800 Ом (см. ниже для ‘Vf’). Не забывайте, ток измеряется в амперах.

  На первый взгляд может показаться, что это проблема, поскольку 800 Ом не является стандартным значением. доступен в диапазоне E12. Однако в этом типе схемы сопротивление не критического, и ближайшего предпочтительного значения будет вполне достаточно, а именно 820 Ом.

  НЕ ЗАБЫВАЙТЕ О ‘Vf’:
  Все электронные компоненты демонстрируют — в большей или меньшей степени — то, что известно как ‘выбывать’. Он имеет различные сокращения в зависимости от типа компонента, к которому он ссылается, но обычно они означают одно и то же. На самом деле это количество напряжения, которое используется компонентом для функционирования. Для стандартного светодиода это значение составляет около 1,5 — 3 вольт, и для наших целей мы будем считать, что это 2 В.

  Это означает, что из ваших 12 вольт от аккумулятора 2 вольта будут израсходованы светодиодом. Сама по себе, поэтому ваш расчет закона Ома должен быть основан на 10 вольт.Истинная формула действительно должно быть; (12-Vf) /0.015=666.66 Ом (повторяется для мастеров математики среди ты!). Ближайшее значение в диапазоне E12 составляет 680 Ом, поэтому в идеале это должно быть ценность для использования. В целях безопасности, когда ваши результаты заканчиваются непонятными значениями, такими как при этом всегда выбирайте ближайшее значение выше, а не следующее ниже.

  РЕЗИСТОРЫ ПОСЛЕДОВАТЕЛЬНО И ПАРАЛЛЕЛЬНО

  Возможно «изготовление» стандартных и нестандартных номиналов резисторов на соответствовать вашим потребностям, если требуемое значение отсутствует.Это достигается подключением два или более из них параллельно, последовательно или их комбинация. Однако вам нужно заранее знать, как они взаимодействуют друг с другом в этих конфигурациях.

  РЕЗИСТОРЫ СЕРИИ:
  На рисунке слева показаны три резистора, соединенные последовательно друг с другом. Это самый простой способ получить «фабричные» значения. Формула прямой для расчет окончательного значения; «R» = R1 + R2 + R3. Другими словами, независимо от от количества резисторов или их индивидуальных значений окончательное значение «R» всегда будет их суммой.Расчет по ноге изображения работает для любого количества значений, соединенных последовательно, вы просто продолжаете добавлять их в список других.
  

  ПАРАЛЛЕЛЬНЫЕ РЕЗИСТОРЫ:
  При параллельном соединении резисторов расчеты посложнее. На рисунке слева показаны три резистора, включенных параллельно. Мы будем не заботиться о трех отдельных ценностях, а сосредоточиться на том, что окончательное значение «R» будет с использованием примеров значений.Расчет у подножия изображение работает для любого количества значений, соединенных параллельно, вы просто продолжаете добавлять их в список других в скобках. Для наших целей предположим, что R1 — 47K, R2 — 150К, а R3 — 820К. Формула прямой линии для окончательного значения: «R» = 1 / ( (1 / R1) + (1 / R2) + (1 / R3)).
  В этой формуле содержится много ненужных скобок (скобок), и вот в чем причина; почти для всех расчетов электроники вам нужно использовать калькулятор, который отдает приоритет функциям умножения и деления, а также наиболее научным калькуляторы работают именно так.К сожалению, многие «простые» калькуляторы этого не делают, поэтому дополнительные скобки были показаны, чтобы компенсировать те, которые вычисляют цифры в порядок их ввода. С научным калькулятором вы можете использовать упрощенный формула прямой линии; «R» = 1 / (1 / R1 + 1 / R2 + 1 / R3).

  Важно определить значения в скобках перед применением окончательного Функция «1 /». Если вы этого не сделаете, то формула станет 1 / R1 + 1 / R2 + 1 / R3 =? если ты попробуйте это на своем калькуляторе, используя наши примеры значений, вы, вероятно, подумаете, что у вас есть неправильный ответ (0.02916 …), а у вас нет. На самом деле у вас точно есть право ответ, ему просто не хватает последней функции «1 /».

  Если в вашем калькуляторе есть «1 / X» (единица, деленная на все, что показано в display), затем нажмите эту кнопку сейчас. Если эта функция недоступна, поместите результат в памяти (убедившись, что раньше там ничего не было), очистить дисплей а затем введите «1 MR =» или другую подобную последовательность. Результат должен быть 34,29 кОм (34 290,29005 Ом), что правильно.Итак, итоговое значение всех трех резисторы, включенные параллельно — 34,29К.
  

  ДЛЯ ЧЕГО ДРУГОЙ ТРЕУГОЛЬНИК?

  На рисунке 2 слева показан второй по величине часто используемый треугольник закона Ома. К этому можно подойти точно так же, как и к выше, только на этот раз он используется для расчета мощности, напряжения и тока. В объяснения здесь таковы; Ток равен мощности, деленной на напряжение (I = P / V), мощность равна Ток, умноженный на напряжение (P = VxI), и напряжение равно мощности, деленной на ток (V = P / I).

  
  ДЕМОНСТРАЦИЯ НА ПРИМЕРЕ:
  Чтобы продемонстрировать использование этого треугольника, мы применим его к обычному электрическому / электронному компонент — трансформатор. Их характеристики обычно цитируются с точки зрения их выходное напряжение вторичной обмотки, вместе с мощностью — в ВА — это напряжение. Термин «VA» означает ватты и происходит от формулы «Вольт на Ампер» (отсюда — ВА). Это обозначается буквой «P» в треугольник закона Ома.

  КАКОЙ ТРАНСФОРМАТОР ДЕЛАТЬ НУЖНО ?
  Допустим, у вас есть цепь 9 В, которая потребляет 1.5 ампер тока. Вы хотите знать, если трансформатор с номиналом 9 В при 25 ВА будет достаточным для питания вашей цепи. Вы уже есть две величины от трансформатора — напряжение (В) и мощность (P или VA), и по ним вы хотите узнать, какой будет доступный ток (I).

  
  Используя формулу «I = P / V» из треугольника, результат: 25/9 = 2,77 усилители. Таким образом, этот трансформатор подойдет для ваших нужд на 1,5 А. В целях безопасности если цепь будет постоянно потреблять определенное количество тока, независимо от каким может быть этот ток, тогда всегда используйте трансформатор, доступный как минимум на 50% ток, чем требует ваша схема.Никогда не используйте тот, у которого «ровно столько» тока, потому что он станет слишком горячим, что приведет к изменению характеристик напряжения и текущий указан. Эти изменения сложны, и мы не будем их объяснять в этой статье. раздел для начинающих, но будьте осторожны при выборе трансформаторов.

  ohm’s law — перевод на голландский — примеры английский

  Эти примеры могут содержать грубые слова на основании вашего поиска.

  Эти примеры могут содержать разговорные слова, основанные на вашем поиске.

  Закон Ома : Напряжение и сила тока прямо пропорциональны в металлическом проводнике постоянной температуры.

  Wet van Ohm : Spanning en stroom zijn in een metalen geleider bij een constante temperatuur rechtevenredig.

  Закон Ома впервые появился в известной книге Die galvanische Kette, Mathematisch Bearbeitet (tr., Гальваническая цепь, исследованная математически) (1827), в которой он изложил свою полную теорию электричества.

  Deze Wet van Ohm verscheen in het beroemde boek Die galvanische Kette, Mathematisch Bearbeitet (De galvanische keten, wiskundig benaderd) (1827) waarin hij zijn Complete theory gaf over elektriciteit.

  Тогда ток каждой ячейки будет умножением веса и входного значения ( закон Ома ).

  De stroom in elke cel van die woordlijn stemt dan overeen met de vermenigvuldiging van de inputwaarde en de aangeleerde параметр ( wet van Ohm ).

  Закон Ома используется для расчета падения напряжения, тока короткого замыкания и других характеристик электрической цепи.

  De wet van Ohm wordt gebruikt om de spanningsval, foutstroom en andere karakteristieken van een stroomkring te berekenen.

  Это применение закона Ома .

  Это означает, что ван де Вет ван Ом .

  Закон Ома (P = I2R) описывает взаимосвязь между током, электрическим сопротивлением и генерируемой мощностью или тепловой энергией.

  De wet van Ohm (P = I2R) beschrijft de relatie tussen stroom, elektrische weerstand en het vermogen of de energie die wordt gegenereerd.

  Измерение В общем, удельное сопротивление твердого проводника может быть получено с помощью закона Ома и закона измерения сопротивления, а раствор электролита используется методом моста переменного тока.

  Meting In het algemeen kan de solide wire resistiviteit word verkregen door de wet van Ohm en de wet van weerstandsmetingen, en een elektrolytoplossing wordt gebruikt als alternatieve stroombrugmethode.

  Согласно закону Ома , напряжение = ток x сопротивление, что дает линейную зависимость между электрическим током и приложенным напряжением, как показано на графиках напряжение-ток выше.

  Uit de wet van Ohm , spanning = weerstand x stroomsterkte, volgt een lineair verband tussen de elektrische stroom en de aangelegde spanning, zoals te zien in de spanning-stroomsterkte karakteristieken.

  Закон Ома гласит, что ток …

  Нет, сэр, я люблю Закон Ома .

  Там, где другие дети читали книжки с картинками и сказки, моя мама научила меня закону Ома и теории Нортона.

  Toen andere kinderen mooie prentenboeken kregen… heeft mijn moeder me geleerd wat de wet van Ohm ru Теория Нортона такова.

  По этой причине, когда на него подается напряжение, ток высокий из-за закона Ом Ом.

  Предложите пример

  Другие результаты

  Акустический закон Ома был предложен немецким физиком Георгом Ом .

  De ohm is vernoemd naar Georg Ohm , een Duitse natuurkundige.

  Закон Ома , Закон Кирхгофа по напряжению и току ;

  Электрическое сопротивление, или сопротивление Ом против , которое важно при передаче электрической энергии.

  De elektrische weerstand, de zogenaamde weerstand van Ohm , представляет собой более красивую передачу, связанную с электричеством.

  1827 г. Джордж Саймон Ом (1789-1854), немецкий физик, сформулировал свой знаменитый закон , соединяющий напряжение, ток и сопротивление в электрической цепи (V = I.R).

  1827 Джордж Саймон Ом (1789-1854), een Duitse natuurkundige, formuleert zijn beroemde wet waarin Voltage, stroom en weerstand met elkaar in verband gebracht wordden: de wet van Ohm (V = I.

  Помимо того, что она является секретарем Лос-Ниньос, она также является председателем Фонда ОМ , советником Красного Креста отдела гуманитарных Закона о войне.

  Naast secretaris voor Los Niños is ze ook nog voorzitter van de Stichting OHM , voorlichter Rode Kruis, afdeling Humanitair

  Магический треугольник закона Ома V = I. Закон Ома определяет взаимосвязь между напряжением, током и сопротивлением.Эти основные электрические блоки относятся к прямым.

  Презентация на тему: «Магический треугольник закона Ома V = I R. Закон Ома определяет соотношение между напряжением, током и сопротивлением. Эти основные электрические единицы применимы к прямым». — Стенограмма презентации:

  1 Магический треугольник закона Ома V = I R

  2 Закон Ома определяет соотношение между напряжением, током и сопротивлением.Эти основные электрические блоки относятся к постоянному или переменному току. Закон Ома — это основа электроники и электричества. Эта формула широко используется электриками. Без полного понимания «Закона Ома» электрик не может спроектировать или устранить неисправности даже в простейших электронных или электрических цепях. Ом установил в конце 1820-х годов, что если к сопротивлению приложить напряжение, то «будет течь ток, а затем потребляться энергия».

  3 Напряжение измеряется в вольтах, обозначается буквой «V».Ток измеряется в амперах, обозначается буквой «I». Сопротивление измеряется в Ом и обозначается буквой «R».

  4

  5 Давайте посмотрим, как эти уравнения могут работать, чтобы помочь нам проанализировать простые схемы: если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой схеме, мы можем использовать закон Ома для определения третьей.

  6 вычислить количество тока (I) вычислить количество тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

  
  

  7 рассчитать величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

  8 рассчитать величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

  9 Энергопотребление по закону Ома через сопротивление Некоторыми практическими примерами этого основного правила в повседневной жизни являются: нагреватели основной платы, электрические сковороды, тостеры и электрические лампочки.Нагреватель потребляет энергию, вырабатывая тепло для тепла, сковорода потребляет энергию, производя тепло для общего приготовления пищи, тостер потребляет энергию, производя тепло для приготовления тостов, а электрическая лампочка потребляет энергию, производя тепло и, что более важно, свет.