Что такое закон Ома и как он связывает напряжение, ток и сопротивление в электрической цепи. Где применяется закон Ома и в каких случаях он не работает. Какие существуют ограничения закона Ома.
Что такое закон Ома
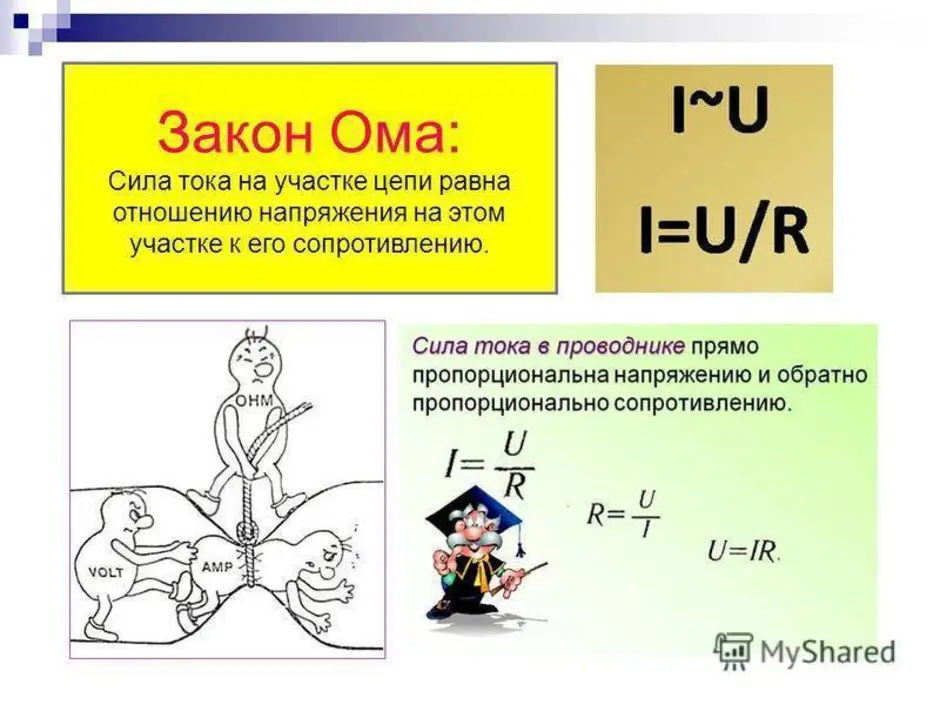
Закон Ома — это фундаментальный закон электротехники, который устанавливает связь между напряжением, током и сопротивлением в электрической цепи. Он был открыт немецким физиком Георгом Омом в 1826 году.
Согласно закону Ома, сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению:
I = U / R
где:
- I — сила тока (в амперах)
- U — напряжение (в вольтах)
- R — сопротивление (в омах)
Эта формула позволяет рассчитать любую из трех величин, зная две другие. Закон Ома справедлив для многих проводников, но имеет ограничения.
Области применения закона Ома
Закон Ома широко используется в электротехнике и электронике для расчета параметров электрических цепей. Основные области его применения:
- Расчет токов, напряжений и сопротивлений в простых и сложных электрических цепях
- Проектирование электрических схем
- Анализ работы электронных устройств
- Диагностика неисправностей в электрооборудовании
- Расчет параметров электрических сетей
Понимание закона Ома необходимо всем, кто работает с электричеством — от электриков до инженеров-электронщиков.
Ограничения закона Ома
Несмотря на широкое применение, закон Ома имеет ряд ограничений и не является универсальным законом природы. Основные ограничения:
- Справедлив только для проводников с постоянным сопротивлением
- Не работает для полупроводников и некоторых других материалов
- Неприменим к нелинейным элементам (диоды, транзисторы)
- Недействителен при очень высоких напряжениях и токах
- Не учитывает температурную зависимость сопротивления
Поэтому при расчетах нужно учитывать границы применимости закона Ома для конкретной ситуации.
Как проверить выполнение закона Ома
Чтобы экспериментально проверить выполнение закона Ома для какого-либо проводника, нужно:
- Собрать электрическую цепь с исследуемым проводником
- Изменяя напряжение, измерять соответствующие значения тока
- Построить график зависимости тока от напряжения
- Если график линейный — закон Ома выполняется
- Если график нелинейный — закон Ома не выполняется
Линейность вольт-амперной характеристики является главным признаком выполнения закона Ома для данного проводника.
Закон Ома для участка цепи
Закон Ома для участка цепи имеет вид:
U = IR
Он связывает падение напряжения U на участке цепи с силой тока I и сопротивлением участка R.
Участком цепи называют любую часть электрической цепи, содержащую последовательно соединенные элементы. Закон Ома для участка цепи позволяет рассчитывать параметры отдельных участков сложных электрических схем.
Закон Ома для полной цепи
Закон Ома для полной цепи записывается в виде:
I = E / (R + r)
где:
- E — электродвижущая сила источника тока
- R — сопротивление внешней цепи
- r — внутреннее сопротивление источника тока
Этот закон учитывает влияние внутреннего сопротивления источника тока на ток в цепи. Он позволяет рассчитывать параметры полных электрических цепей, содержащих источник тока.
Применение закона Ома в электротехнике
В электротехнике закон Ома используется для решения различных практических задач:
- Расчет токов в ветвях электрических цепей
- Определение падений напряжения на элементах схем
- Подбор сопротивлений резисторов
- Расчет мощности, выделяемой на участках цепи
- Анализ режимов работы электрических машин
- Проектирование систем электроснабжения
Знание закона Ома позволяет инженерам-электрикам и электромонтажникам грамотно проектировать и эксплуатировать электрические сети и оборудование.
Закон Ома в электронике
В электронике закон Ома применяется для расчета и анализа электронных схем. Основные области применения:
- Расчет делителей напряжения
- Определение рабочих точек транзисторов
- Анализ усилительных каскадов
- Расчет фильтров
- Проектирование источников питания
При этом нужно учитывать, что многие электронные компоненты (диоды, транзисторы) являются нелинейными элементами и не подчиняются закону Ома в чистом виде.
Нарушения закона Ома
Существует ряд случаев, когда закон Ома не выполняется:
- Для полупроводниковых приборов (диодов, транзисторов)
- В газовых разрядах
- При сверхпроводимости
- В плазме
- При очень сильных электрических полях
В этих ситуациях зависимость тока от напряжения становится нелинейной, и для расчетов требуются более сложные модели.
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме связывает плотность тока j с напряженностью электрического поля E:
j = σE
где σ — удельная электропроводность среды.
Эта форма закона Ома позволяет анализировать распределение токов в объемных проводниках и является основой для расчета электромагнитных полей.
Закон Ома для участка цепи и для полной электрической цепи — формула соотношения силы тока, напряжения и сопротивления
19 мая, 2022
1 мин
Физ 🔬
44185
0
Закон Ома для участка цепи
Закон Ома гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Открыт немецким учителем физики Георгом Омом в 1826 году.
📌 Записывается следующей формулой: I = U / R.
Формула справедлива для постоянного тока, для переменного она имеет небольшие отличия!
Закон Ома для полной электрической цепи
📍 Закон Ома для полной электрической сети звучит так: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Короткое замыкание — соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.
Мгновенное возрастание силы тока приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам.
💡 Замечание: при коротком замыкании, когда R -> 0, сила тока возрастает в R/r раз.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
45 подписчиков
+ Подписаться
Вам также будет интересно
Редакция Без Сменки
10 июня, 2022
1 мин
Био 🦠
Ароморфы млекопитающих
ОШИБКА ЛЫСОЙ ОБЕЗЬЯНЫ 🐒
Вы когда-нибудь видели полностью лысую обезьяну? Если нет, бегом на.
..
Редакция Без Сменки
10 июня, 2022
1 мин
Био 🦠
Свертывание крови
Вот представь, ты порезал палец 😱 Если бы кровь не сворачивалась, любая малюсенькая травма нас…
Редакция Без Сменки
01 июля, 2022
1 мин
Хим 🧪
Волокна
Волокно — это тонкая нить. Она может быть натуральной, искусственной или минеральной. Разберёмся,…
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
Амфибрахий
Разбираемся со стихотворным размером – Амфибрахий, ниже все самое важное, сохраняй и запоминай
Закон Ома для участка цепи – формула, определение сопротивления
4.
3
Средняя оценка: 4.3
Всего получено оценок: 304.
4.3
Средняя оценка: 4.3
Всего получено оценок: 304.
Наравне с законами Кирхгофа, закон Ома для участка цепи – один из ключевых во всей электротехники. При проектировании электросетей любой сложности закон Ома становится необходимым инструментом, так как позволяет рассчитывать требуемые для нужного результата параметры сети.
Сущность закона
Эксперименты с электрическими цепями, в которых были источник тока и элемент сопротивления, позволили Георгу Ому установить некоторые закономерности, которые легли в основу закона, названного его именем. Приведем их:
- При увеличении напряжения сила тока на участке цепи возрастала линейно.
- Сила тока уменьшалась при увеличении сопротивления участка.
Поэтому математическая формула закон Ома для участка цепи выглядит следующим образом:
$I = \frac {U}{R}$, где I – сила тока, измеряемая в амперах, U – напряжение, измеряемое в вольтах и R – сопротивление, измеряемое в омах.
Дадим словесную формулировку закона: сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Из фигурирующих в уравнении величин ключевой является сопротивление. Оно зависит от параметров проводника:
- Становится больше с увеличением длинны проводника
- Уменьшается с ростом проводимости проводника и его площади сечения.
Объяснить это очень просто: чем больше путь, проходимый электронами, тем больше вероятность столкновений с атомами в узлах решетки. Это мешает движению тока. С другой стороны, увеличение площади сечения дает больше вариантов пути электронам, уменьшается вероятность соударений. Проводимость же – исключительно свойства проводящего вещества. Например, медь оказывает меньшее сопротивление, чем железо, поскольку является более проводимым.
Закон Ома с точностью справедлив лишь для цепей, где действует идеальный источник тока. То есть такой, в котором нет внутреннего сопротивления.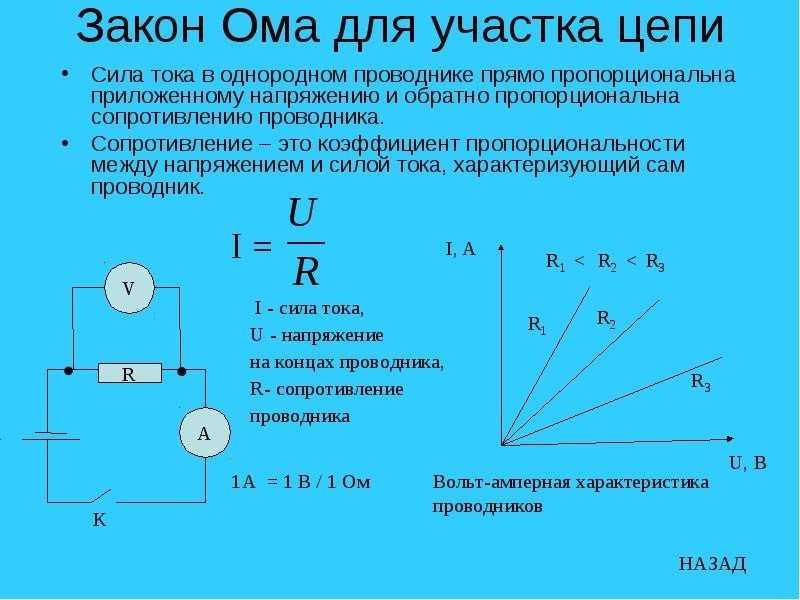
В противном случае применяется закон Ома для полной цепи.
Рассмотрим участок электрической цепи (рис. 2). В узлах 1 и 2 – потенциалы электрического поля $\phi_1$ и $\phi_2$. Между ними заключен элемент с сопротивлением R – резистор. К участку также подсоединен вольтметр.
Рис. 2. Участок цепи с резистором R и вольтметром.Тогда падением напряжения на данном участке электрической цепи будем называть величину, выраженную через закон Ома:
$U = I \cdot R$
Падение напряжения – определение, сложившееся исторически. Речь идет об изменении значения потенциала электрического поля по мере продвижения вдоль проводника.
Для запоминания закона Ома используют правило, называемое треугольником Ома.
Рис. 3. Треугольник Ома.Техника работы с ним проста. Ту величину, которую нужно найти, закрываем пальцем, а две другие дают формулу для ее нахождения. Закрыв I, получим $\frac {U}{R}$.
Задачи
- Сопротивление проводника – 2 Ом. Напряжение – 10 В. Какова сила тока? Какой будет сила тока, если увеличить длину проводника в два раза?
Решение:
Запишем закон Ома для участка цепи:
$I = \frac {U}{R}$
Подставив в него известные величины, получим:
$I = \frac {10}{2} = 5 \: А$
Теперь, зная, что сопротивление прямо пропорционально длине проводника, запишем:
$I = \frac {U}{2R} = 2,5 А$
- Амперметр показал, что сила тока на участке цепи – 0,1 А.
Аккумулятор создает напряжение в 200 В. Каково сопротивление участка цепи?
Аккумулятор создает напряжение в 200 В. Каково сопротивление участка цепи?Решение:
Запишем закон Ома для участка цепи:
$I = \frac {U}{R}$
Подставив в него известные величины и выразив R, получим:
$R = \frac {U}{I} = \frac {200}{0,1} = 2000 Ом \: А$
Что мы узнали?
В ходе урока дали математическую и словесную формулировки закона Ома для участка цепи, рассмотрели значение сопротивления для участка цепи, а также разобрались с треугольником Ома. Для закрепления материала решили задачу.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Ринат Баишев
10/10
Денис Иванов
9/10
Мария Кшевач
7/10
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 304.
А какая ваша оценка?
История закона Ома
Вы когда-нибудь задумывались, сколько из того, что мы делаем, вы могли бы понять с нуля? Сейчас завязать шнурки может показаться простым делом, но детям трудно овладеть этим навыком, а придумать его в первый раз еще сложнее.
То же самое относится и ко многим технологиям, которые мы используем каждый день. Вы бы придумали компьютерную мышь или даже компьютер, если бы их еще не было? Однако, конечно же, одно из самых простых и полезных математических уравнений, лежащих в основе электроники, — закон Ома — было бы легко понять, верно? Часто это первое, что узнаешь об электронике, но понять это в первый раз оказалось довольно сложно.
Парнем, обнаружившим связь, был Георг Ом, учитель математики и физики средней школы из Кёльна. Чего вы, возможно, не знаете, так это того, что в первый раз, когда он опубликовал это, он ошибся. Но, к счастью для нас, он понял свою ошибку и смог ее исправить.
Это не просто хорошая идея…
Закон Ома прост. Для линейного резистора ток через резистор пропорционален приложенному к нему напряжению. Константа пропорциональности обратно пропорциональна значению сопротивления в, что неудивительно, омах. Это просто причудливый математический способ сказать, что I=E/R, где E — напряжение, I — ток, а R — сопротивление.
Конечно, алгебра скажет вам, что E=IR и R=E/I.
Дважды отмерь
Куча Вольта из меди и цинка.Хотя сегодня это кажется очевидным, в 1800-х годах это было не так уж и много. Некоторые сведения об электричестве были известны еще в Древней Греции. Однако до 1800 года, когда Вольта создал «гидроэлектрическую» батарею — то есть это был мокрый элемент — не было простого способа создать постоянный ток для научных исследований.
Таким образом, с 1800 по 1820 год наука могла использовать гальваническую батарею для производства электричества. Но было большое ограничение. Не было возможности измерить силу тока в цепи. В 1781 году Генри Кавендиш экспериментировал с лейденскими банками (в основном это был высоковольтный конденсатор) и стеклянными трубками разного диаметра и длины, наполненными физиологическим раствором. Не имея возможности измерить ток, он использовал свое тело и отмечал, насколько сильным был удар. Он отметил, что ток связан с напряжением, но не упомянул об этом другим ученым, и это оставалось в значительной степени неизвестным, пока Максвелл не опубликовал результат в 1879 году.
.
Проблема измерения тока была решена в 1820 году, когда Эрстед показал, что ток создает магнитное поле. Это привело Швайггера и Поггендорфа к изобретению гальваноскопа в 1821 году. По сути, это катушка с компасом внутри. Ток в проводе отклонит стрелку компаса, а величина отклонения скажет вам, какой ток был в проводе.
Ом хотел изучить природу протекания электрического тока и построил батарею и гальваноскоп. Его эксперименты были направлены на описание силы тока, протекающего по проводу заданной длины. Он измерял ток, протекающий от батареи, используя только свой гальваноскоп, а затем вставлял отрезок провода и отмечал разницу в показаниях.
Ой…
В 1825 году Ом объявил миру свою формулу в статье, озаглавленной «Предварительное уведомление о законе, согласно которому металлы проводят контактное электричество». Не совсем кликбейтный заголовок. Однако возникла проблема: формула у него была неверная.
Имейте в виду, что были не все единицы измерения, к которым мы привыкли сегодня, поэтому формула Ома измеряла V, уменьшение отклонения стрелки, вызванное тестовой проволокой.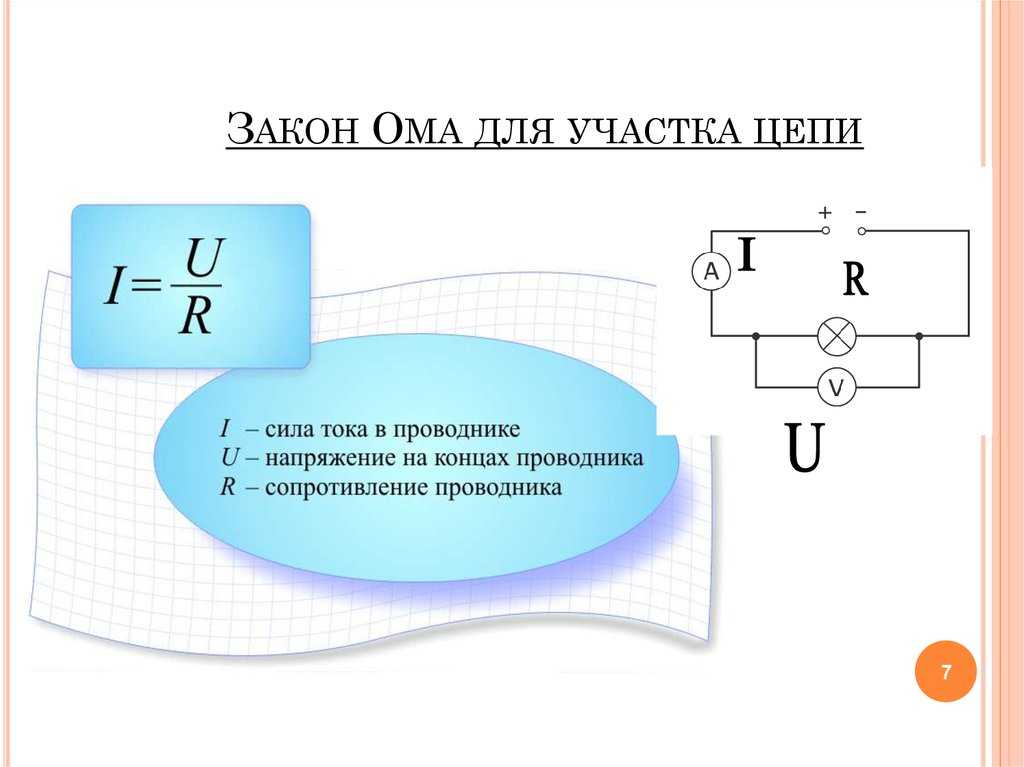
Ключевыми факторами были длина провода X и приложенное напряжение M, а также удельное сопротивление провода R. Неправильная формула была:
V=M log(1+X/R)
С тем, что мы знаем сегодня, вы можете посмотреть на это и сразу же понять, что это неверно. Однако в 1825 году это было не так очевидно. Статья была принята к публикации, но прежде чем она отправилась в печать, Ом провел новые эксперименты с другим источником питания. Он понял, что его формула неверна, но было слишком поздно.
Исправление
Проблема была в аккумуляторе. Хотя сегодня это может показаться очевидным, в 1825 году не было общего представления о том, что напряжение жидкостного элемента будет меняться под нагрузкой. Друг Ома Поггендорф предложил ему использовать термоэлектрическую батарею — то, что мы назвали бы термопарой.
В «Определении закона, по которому металлы проводят контактное электричество, вместе с изложением теории аппарата Вольта и гальваноскопа Швайггера» Ом понял правильно.
(Ему нравились длинные заголовки.) Формула не совсем походила на то, что мы думаем о законе Ома, но на самом деле это так, если учесть сопротивление источника питания. В современных обозначениях мы бы написали:
E=I*(Rb+R)
Здесь Rb — сопротивление батареи. В 1827 году Ом также опубликовал «Гальваническую батарею, трактованную математически», показывающую, что, по крайней мере, его способность писать хорошие заголовки улучшилась. Все в порядке?
Not So Fast
Казалось бы, все обрадуются закону Ома и сразу же начнут его применять. Этого не произошло. В то время наука была настроена скептически — и вы можете возразить, что это так и сейчас — и правящие круги того времени считали, что закон Ома слишком прост, чтобы ускользать от внимания сообщества в течение тридцати с лишним лет. Было также сильное мнение, что Ом поспешил с формулировкой, и отвращение к его практическим экспериментальным методам. Истеблишмент считал Ома — более или менее — позером.
Министр образования Германии заявил, что «профессор, проповедующий подобные ереси, недостоин преподавать науку».
Другие говорили, что работа была «паутиной обнаженных фантазий».
В течение шести лет мир по большей части продолжал игнорировать закон Ома. Однако в 1831 году Пуйе опубликовал статью, в которой он, сам того не зная, заново открыл формулу Ома. Вероятно, он был разочарован, когда после публикации закона Пуйе другие указали, что Ом проделал ту же работу несколькими годами ранее.
Errata
Вам может показаться странным, что Ом опубликовал неверную формулу или Пуйе повторил эксперимент, но тогда все было совсем иначе. На самом деле Барлоу пытался решить ту же проблему в 1825 году и опубликовал открытие, согласно которому сила тока в проводе обратно пропорциональна квадратному корню из длины провода.
Этот результат был неправильным, но соответствовал данным, потому что Барлоу не смог учесть внутреннее сопротивление батареи, как это сделал Ом. Даже Барлоу признал, что не уверен в правильности своего закона. С положительной стороны, Барлоу действительно изобрел колесо Барлоу, которое представляло собой умную форму двигателя, использующего металлическое колесо, магнит и ртуть.
Признание
В конце концов, работа Ома была признана, и он не только получил должное признание, но и его имя до сих пор у нас на устах каждый день.
Если вы хотите узнать больше об Оме, в Годовом отчете Совета регентов Смитсоновского института за 1891 год есть перевод обращения к Королевской Баварской академии наук, в котором эта история описана очень подробно. Вы прочтете, что после того, как его работа была признана, он начал новые эксперименты и внес вклад в акустику, хотя его акустический закон, по-видимому, не совсем верен.
Если вы действительно хотите обратиться к первоисточнику, освежите свой немецкий и просмотрите этот архив оригинальных статей Ома.
В то время как все заслуги принадлежат Ому, у Кирхгофа также есть несколько довольно важных законов.
9.5: Закон Ома — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4403
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Описывать закон Ома
- Распознать, когда применяется закон Ома, а когда нет
До сих пор в этой главе мы обсуждали три электрических свойства: ток, напряжение и сопротивление. Оказывается, многие материалы демонстрируют простую зависимость между значениями этих свойств, известную как закон Ома.
Многие другие материалы не показывают этой взаимосвязи, поэтому, несмотря на то, что он называется законом Ома, он не считается законом природы, как законы Ньютона или законы термодинамики. Но это очень полезно для расчетов с материалами, которые подчиняются закону Ома.
Описание закона Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
\[I \propto V.\]
Это важная взаимосвязь лежит в основе закона Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, то есть экспериментально наблюдаемое явление, подобное трению. Такая линейная зависимость не всегда имеет место. Любой материал, компонент или устройство, которые подчиняются закону Ома, где ток через устройство пропорционален приложенному напряжению, известен как омический материал или 9.
0110 омический компонент . Любой материал или компонент, который не подчиняется закону Ома, известен как неомический материал или неомический компонент.
Эксперимент Ома
В статье, опубликованной в 1827 году, Георг Ом описал эксперимент, в котором он измерял напряжение и ток в различных простых электрических цепях, содержащих провода различной длины. Аналогичный эксперимент показан на рисунке \(\PageIndex{1}\). Этот эксперимент используется для наблюдения за током через резистор, возникающим в результате приложенного напряжения. В этой простой схеме резистор соединен последовательно с батареей. Напряжение измеряется вольтметром, который необходимо поставить на резистор (параллельно резистору). Ток измеряется амперметром, который должен быть подключен к резистору (последовательно с резистором).
Рисунок \(\PageIndex{1}\): Экспериментальная установка, используемая для определения того, является ли резистор омическим или неомическим устройством.
(а) Когда батарея присоединена, ток течет по часовой стрелке, а показания вольтметра и амперметра положительны. б) при переключении выводов батареи ток течет против часовой стрелки, а показания вольтметра и амперметра отрицательные.В этой обновленной версии оригинального эксперимента Ома было выполнено несколько измерений тока для нескольких разных напряжений. Когда батарея была подключена, как показано на рисунке \(\PageIndex{1a}\), ток протекал по часовой стрелке, а показания вольтметра и амперметра были положительными. Изменится ли поведение тока, если ток течет в противоположном направлении? Чтобы заставить ток течь в противоположном направлении, выводы батареи можно поменять местами. При переключении выводов батареи показания вольтметра и амперметра были отрицательными, поскольку ток протекал в противоположном направлении, в данном случае против часовой стрелки. Результаты аналогичного эксперимента показаны на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{1}\): Резистор включен в цепь с батареей.
Приложенное напряжение варьируется от -10,00 В до +10,00 В, увеличиваясь с шагом 1,00 В. На графике показаны значения напряжения в зависимости от тока, типичные для случайного экспериментатора.В этом эксперименте напряжение, прикладываемое к резистору, изменяется от −10,00 до +10,00 В с шагом 1,00 В. Измеряются ток через резистор и напряжение на резисторе. Строится график зависимости напряжения от тока, и результат приблизительно линейный. Наклон линии — это сопротивление или напряжение, деленное на ток. Этот результат известен как Закон Ома. а R – сопротивление в единицах Ом. Как указывалось ранее, любое устройство, демонстрирующее линейную зависимость между напряжением и током, известно как омическое устройство. Таким образом, резистор является омическим устройством.
Пример \(\PageIndex{1}\): измерение сопротивления 9oC\) при нагревании резистора, какова сила тока через резистор?
Стратегия
(а) Сопротивление можно найти по закону Ома.
Закон Ома гласит, что \(V = IR\), поэтому сопротивление можно найти, используя \(R = V/I\).
(b) Во-первых, сопротивление зависит от температуры, поэтому новое сопротивление после нагрева резистора можно найти с помощью \(R = R_0 (1 + \alpha \Delta T)\). Ток можно найти с помощью закона Ома в виде \(I = V/R\).
9oC\) привело к изменению тока на 2,00%. Это может показаться не очень большим изменением, но изменение электрических характеристик может оказать сильное влияние на схемы. По этой причине многие электронные устройства, такие как компьютеры, содержат вентиляторы для отвода тепла, рассеиваемого компонентами электрических цепей.Упражнение \(\PageIndex{1}\)
Напряжение, подаваемое в ваш дом, изменяется как \(V(t) = V_{max} sin \, (2\pi \, ft)\). Если к этому напряжению подключить резистор, будет ли справедлив закон Ома \(V = IR\)?
- Ответить
Да, закон Ома остается в силе. В каждый момент времени ток равен \(I(t) = V(t)/R\), поэтому ток также является функцией времени, \(I(t) = \dfrac{V_{max} {R} \, sin \, (2\pi \, ft)\).
Моделирование: PhET
Посмотрите, как закон Ома (уравнение \ref{Ом}) относится к простой цепи. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Неомические устройства не демонстрируют линейной зависимости между напряжением и током. Одним из таких устройств является элемент полупроводниковой схемы, известный как диод . Диод — это схемное устройство, которое позволяет току течь только в одном направлении. Схема простой цепи, состоящей из батареи, диода и резистора, показана на рисунке \(\PageIndex{3}\). Хотя мы не рассматриваем теорию диода в этом разделе, диод можно проверить, чтобы увидеть, является ли он омическим или неомическим устройством.
Рисунок \(\PageIndex{3}\): Диод — это полупроводниковое устройство, пропускающее ток, только если диод смещен в прямом направлении, что означает, что анод положительный, а катод отрицательный.
График зависимости тока от напряжения показан на рисунке \(\PageIndex{4}\). Обратите внимание, что поведение диода показано как зависимость тока от напряжения, тогда как работа резистора показана как зависимость напряжения от тока. Диод состоит из анода и катода. Когда анод имеет отрицательный потенциал, а катод — положительный, как показано в части (а), говорят, что диод имеет обратное смещение. При обратном смещении диод имеет чрезвычайно большое сопротивление, и через диод и резистор протекает очень небольшой ток — практически нулевой ток. По мере увеличения напряжения, приложенного к цепи, ток остается практически нулевым, пока напряжение не достигнет напряжения пробоя и диод не начнет проводить ток. Когда батарея и потенциал на диоде меняются местами, что делает анод положительным, а катод отрицательным, диод проводит ток, и ток течет через диод, если напряжение больше 0,7 В. Сопротивление диода близко к нулю. (Это причина резистора в цепи; если бы его не было, ток стал бы очень большим.
) Из графика на рисунке \(\PageIndex{4}\) видно, что напряжение и ток не имеют линейной зависимости. Таким образом, диод является примером неомического устройства.
Закон Ома обычно формулируется как \(V = IR\), но первоначально он был сформулирован как микроскопическое представление, в с точки зрения плотности тока, проводимости и электрического поля. Этот микроскопический взгляд предполагает, что пропорциональность \(V \propto I\) возникает из-за дрейфовой скорости свободных электронов в металле, возникающей в результате приложенного электрического поля.
