Закон ома определение для школьников. Закон Ома: простое объяснение для начинающих

Что такое закон Ома и как он работает. Как связаны напряжение, сила тока и сопротивление. Какие формулы используются для расчетов по закону Ома. Где применяется закон Ома на практике.

Что такое закон Ома и почему он так важен

Закон Ома — это один из фундаментальных законов электротехники, который описывает взаимосвязь между напряжением, силой тока и сопротивлением в электрической цепи. Этот закон был открыт немецким физиком Георгом Омом в 1827 году и назван в его честь.

Почему же закон Ома так важен? Есть несколько причин:

• Он позволяет рассчитывать параметры электрических цепей
• На его основе проектируются электронные устройства
• С его помощью можно анализировать работу электрических схем
• Он используется при диагностике неисправностей в электрооборудовании

Без понимания закона Ома невозможно заниматься электротехникой и электроникой. Это базовые знания для любого электрика, инженера или радиолюбителя.

Формулировка закона Ома

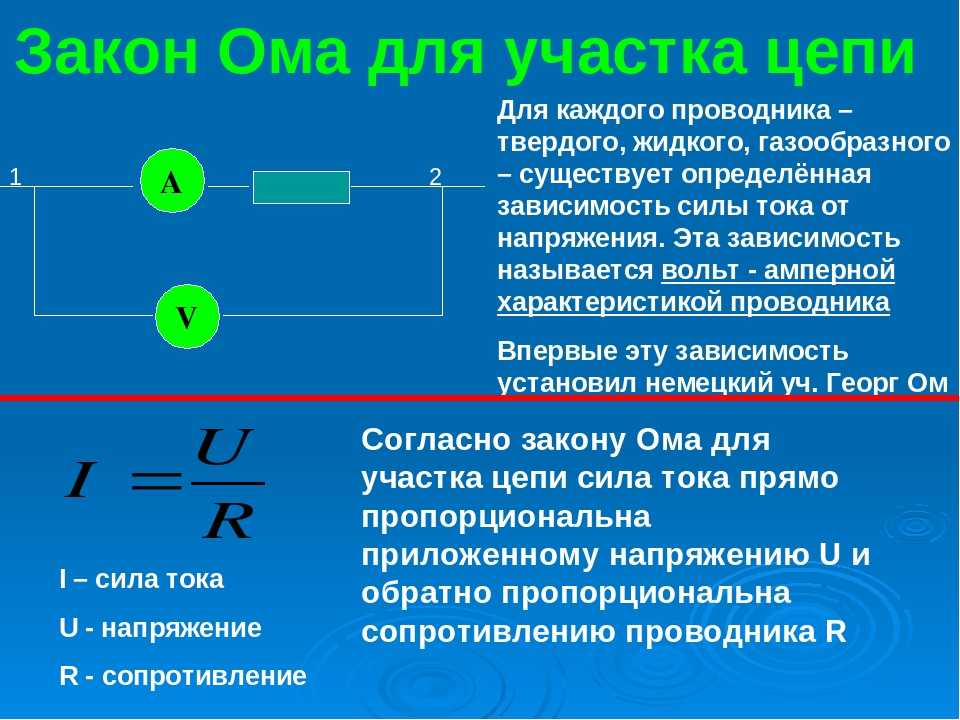
Классическая формулировка закона Ома звучит так:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

Математически это выражается формулой:

I = U / R

где:

• I — сила тока (в амперах, А)
• U — напряжение (в вольтах, В)
• R — сопротивление (в омах, Ом)

Эту формулу можно преобразовать, чтобы выразить напряжение или сопротивление:

U = I * R

R = U / I

Физический смысл закона Ома

Чтобы лучше понять физический смысл закона Ома, рассмотрим простую аналогию:

• Напряжение (U) можно сравнить с давлением воды в трубе
• Сила тока (I) аналогична потоку воды
• Сопротивление (R) схоже с сужением трубы

Чем выше давление воды (напряжение), тем сильнее поток (ток). А чем уже труба (больше сопротивление), тем слабее поток при том же давлении.

Точно так же в электрической цепи: при увеличении напряжения возрастает сила тока, а при увеличении сопротивления — уменьшается.

Применение закона Ома на практике

Закон Ома находит широкое применение в различных областях электротехники и электроники:

• Расчет параметров электрических цепей
• Проектирование источников питания
• Выбор номиналов резисторов в электронных схемах
• Расчет сечения проводов
• Настройка электрооборудования
• Диагностика неисправностей

Например, зная напряжение в сети и мощность электроприбора, можно рассчитать потребляемый им ток и подобрать соответствующий предохранитель.

Ограничения закона Ома

Хотя закон Ома очень полезен, он имеет некоторые ограничения:

• Работает только для проводников с линейной вольт-амперной характеристикой
• Не применим к полупроводниковым приборам (диодам, транзисторам)
• Не учитывает влияние температуры на сопротивление
• Не работает для сверхпроводников
• Нарушается в сильных электрических полях

Поэтому при работе со сложными электронными схемами нужно учитывать эти ограничения и при необходимости использовать более сложные модели.

Как запомнить закон Ома

Существует простой способ запомнить формулы закона Ома с помощью «треугольника Ома»:

«` «`

Чтобы найти нужную величину, достаточно закрыть ее в треугольнике. Оставшиеся величины покажут нужную формулу:

• U = I * R (напряжение равно произведению тока на сопротивление)
• I = U / R (ток равен напряжению, деленному на сопротивление)
• R = U / I (сопротивление равно напряжению, деленному на ток)

Этот простой метод помогает быстро вспомнить нужную формулу в любой ситуации.

Закон Ома для полной цепи

Помимо закона Ома для участка цепи, существует также закон Ома для полной цепи. Он учитывает внутреннее сопротивление источника тока и записывается следующим образом:

I = E / (R + r)

где:

• E — электродвижущая сила источника (в вольтах, В)
• R — сопротивление внешней цепи (в омах, Ом)
• r — внутреннее сопротивление источника (в омах, Ом)

Этот закон позволяет более точно рассчитывать параметры реальных электрических цепей, учитывая особенности источников питания.

Примеры решения задач с использованием закона Ома

Рассмотрим несколько простых примеров применения закона Ома для решения практических задач:

Задача 1: Определить силу тока в цепи, если напряжение равно 12 В, а сопротивление 4 Ом.

Решение:
Используем формулу I = U / R
I = 12 В / 4 Ом = 3 А

Задача 2: Рассчитать напряжение на резисторе сопротивлением 100 Ом, если через него протекает ток 0.5 А.

Решение:
Используем формулу U = I * R
U = 0.5 А * 100 Ом = 50 В

Задача 3: Найти сопротивление лампочки, если при напряжении 220 В она потребляет ток 0.5 А.

Решение:
Используем формулу R = U / I
R = 220 В / 0.5 А = 440 Ом

Эти примеры показывают, как с помощью закона Ома можно легко находить неизвестные параметры электрических цепей.

Заключение

Закон Ома — это фундаментальный закон электротехники, который описывает взаимосвязь между напряжением, силой тока и сопротивлением в электрической цепи. Его понимание необходимо для работы с электрическими схемами и устройствами.

Основные моменты, которые нужно запомнить:

• Формула закона Ома: I = U / R
• Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению
• Закон Ома применим к линейным цепям постоянного тока
• Существуют ограничения применения закона Ома для некоторых типов устройств и материалов
• «Треугольник Ома» помогает легко запомнить все формулы

Освоив закон Ома, вы сделаете важный шаг в понимании принципов работы электрических цепей и сможете применять эти знания на практике.

Урок 3. Три друга, один треугольник и много законов

Незнание закона не освобождает от ответственности.

Афоризм

Интересно, о каких законах пойдет речь в уроке под номером три. Неужели в электротехнике этих законов целая гора или даже куча и их все нужно запомнить? Сейчас узнаем. Здравствуйте, уважаемые! Наверное, многие из вас уже с досадой в глазах глядят на очередной урок и думают про себя: «Какая же скукотища!», а, может, даже собираются покинуть наши стройные ряды? Не спешите, всё только начинается! Начальный этап всегда скучный… С этого урока и пойдёт всё самое-самое интересное. Сегодня я расскажу, кто в электротехнике кому друг, а кому и враг, что будет, если студента-электронщика разбудить посреди ночи, и как с помощью одного пальца понять половину всей электротехники. Интересно? Тогда поехали!

С первым нашим другом мы познакомились на прошлом уроке – это сила тока. Она характеризует электричество с точки зрения скорости переноса заряда из одной точки пространства в другую под действием поля. Но, как было замечено, сила тока зависит и от свойств проводника, по которому этот ток «бежит». На силу тока прямо влияет величина удельной электропроводности материала. Теперь представим себе некий проводник (подойдёт такой, как на рисунке 3) с движущимися в нём электронами. Основным недостатком электрона я бы назвал отсутствие у него руля. Из-за этого недостатка движение электронов определяется только воздействующим на них полем и структуры материала, в котором они движутся.

Поскольку электроны «не умеют» поворачивать, некоторые из них могут столкнуться с колеблющимися под действием температуры узлами кристаллической решётки, потерять свою скорость от столкновения, и тем самым снизить скорость переноса заряда, то есть понизить силу тока. Некоторые электроны могут потерять так много энергии, что «прилипнут» к иону и превратят его в нейтральный атом. Теперь, если мы увеличим длину проводника, очевидно, что количество подобных столкновений так же увеличится, и электроны будут отдавать еще больше энергии, то есть сила тока будет снижаться.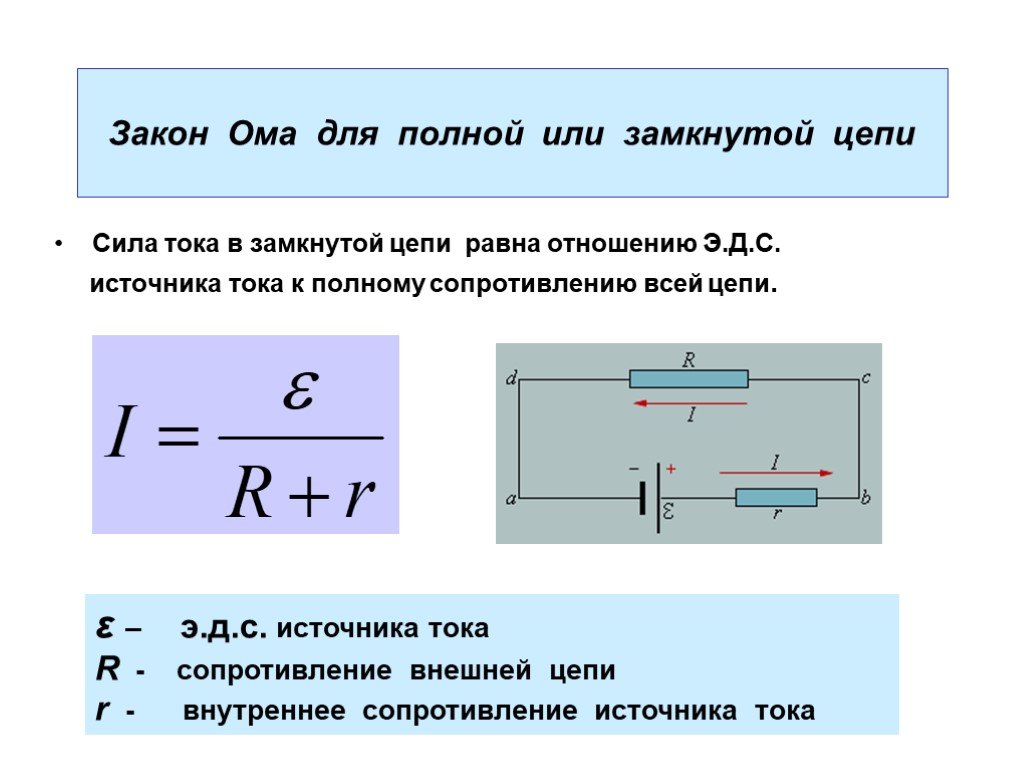

А вот при увеличении площади поперечного сечения проводника возрастает только количество свободных электронов, а количество столкновений на единицу площади практически не меняется, поэтому с ростом площади растёт и ток. Итак, мы выяснили, что электропроводность (она уже стала не удельной, так как учитывает геометрические размеры конкретного проводника) зависит сразу от трёх характеристик проводника: длины, площади сечения и материала.

Однако, чем лучше материал проводит электрический ток, тем меньше он «сопротивляется» его прохождению. Эти утверждения равнозначны. Пришло время познакомиться с нашим вторым другом – электрическим сопротивлением. Это величина, обратная величине проводимости и зависит от тех же характеристик проводника.

Рисунок 3.1 – От чего зависит сопротивление проводника

Чтобы учесть при численном расчете влияние рода вещества на его электрическое сопротивление, введена величина удельное электрическое сопротивление, характеризующая способность вещества проводить электрический ток.

Заметим, что определения электропроводности и электросопротивления идентичны, так же как и утверждения выше. Удельное сопротивление определяется как сопротивление проводника длиной 1м и площадью сечения 1м². Обозначается латинской буквой &#961 («ро») и имеет размерность Ом•м. Ом – единица измерения сопротивления, которая является обратной величине сименс. Так же для определения удельного сопротивления может использоваться размерность Ом•мм²/м, которая в миллион раз меньше основной размерности.
Таким образом, электрическое сопротивление проводника может быть описано через его геометрические и физические свойства следующим образом:

где &#961 – удельное электрическое сопротивление материала проводника;
l – длина проводника;
S – площадь поперечного сечения проводника.

Из зависимости видно, что сопротивление проводника возрастает при увеличении длины проводника и уменьшается при увеличении площади сечения, а так же напрямую зависит от величины удельного сопротивления материала.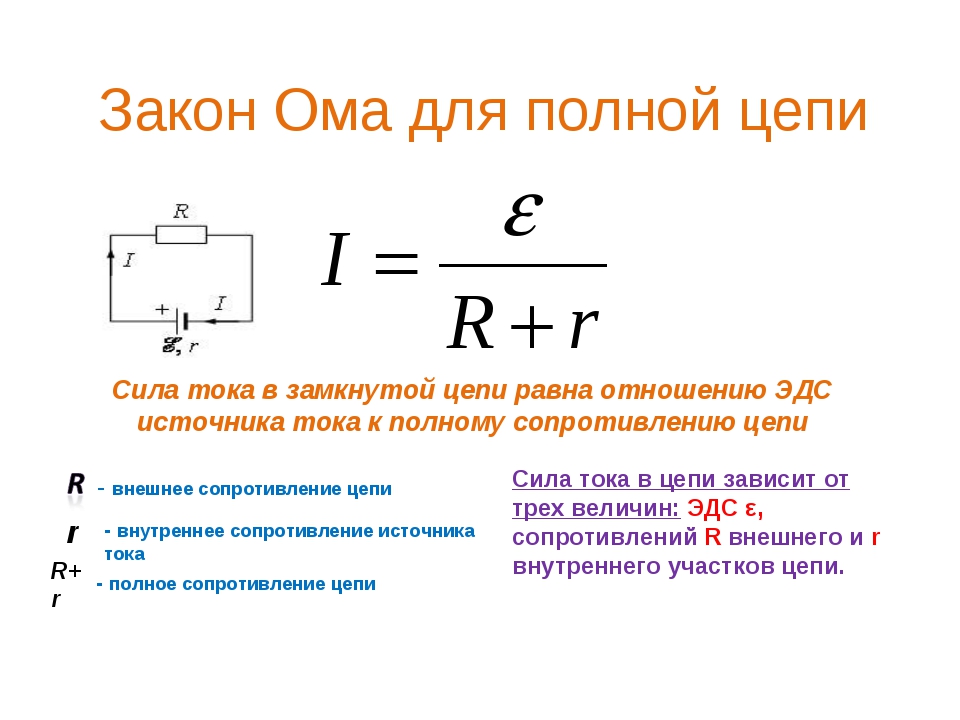

А теперь вспомним, что на величину силы тока в проводнике оказывает влияние напряженность электрического поля, под действием которого возникает электрический ток. Ох, сколько миллионов тысяч раз уже упоминалось, что электрический ток возникает под действием электрического поля! Этот факт должен всегда держаться в голове. Есть, конечно, и другие способы создать ток, но пока мы будем рассматривать только этот. Как уже говорилось выше, увеличение напряженности поля приводит к росту тока, а совсем недавно мы выяснили, что чем больше энергии сохранит электрон при движении по проводнику, тем выше значение электрического тока. Из курса механики известно, что энергия тела определяется его кинетической и потенциальной энергией. Так вот, помещённый в электрическое поле точечный заряд обладает в начальный момент времени только потенциальной энергией (поскольку его скорость равна нулю). Для характеристики этой потенциальной энергии поля, которой обладает заряд была введена величина электростатического потенциала, равная отношению потенциальной энергии к величине точечного заряда:

где W_p – потенциальная энергия,
q – величина точечного заряда.

После того, как заряд попадёт под действие электрического поля, он начнёт движение с определённой скоростью и часть его потенциальной энергии перейдёт в кинетическую. Таким образом, в двух точках поля заряд будет обладать различным значением потенциальной энергии, то есть две точки поля можно охарактеризовать различными значениями потенциала. Разность потенциалов определяется как отношение изменения потенциальной энергии (совершённой работы поля) к величине точечного заряда:

Причём работа поля не зависит от пути движения заряда и характеризует только величину изменения потенциальной энергии. Разность потенциалов так же называют электрическим напряжением. Напряжение принято обозначать английской буквой U («у»), единицей измерения напряжения является величина вольт (В), названная в честь итальянского физика и физиолога Алессандро Вольта, который изобрёл первую электрическую батарею.

Ну вот мы и познакомились с тремя неразлучными друзьями в электротехнике: ампер, вольт и ом или ток, напряжение и сопротивление. Любой компонент электрической цепи может быть однозначно охарактеризован при помощи этих трёх электрических характеристик. Первым, кто познакомился и подружился со всеми тремя сразу был Георг Ом, который обнаружил, что напряжение, ток и сопротивление связаны друг с другом определённым соотношением:

которое было впоследствии названо законом Ома.

Сила электрического тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника.

Данную формулировку необходимо знать от заглавной буквы С до точки в конце. Ходят слухи, что первая фраза любого студент-электронщик, разбуженного среди ночи, будет именно формулировкой закона Ома. Это один из основных законов электротехники. Данная формулировка носит название интегральной. Кроме неё существует так же дифференциальная формулировка, отражающая зависимость плотности тока от характеристик поля и материала проводника:

где &#963 – удельная проводимость проводника,
E – напряженность электрического поля.

Данная формулировка вытекает из формулы, приведённой во втором уроке, и отличается от интегральной тем, что не учитывает геометрические характеристики проводника, принимая во внимание только его физические характеристики. Эта формулировка интересна только с точки зрения теории и на практике не применяется.
Для быстрого запоминания и использования закона Ома можно применить диаграмму, изображённую на рисунке ниже.

Рисунок 3.2 – «Треугольный» закон Ома

Правило использования диаграммы простое: достаточно закрыть искомую величину и два других символа дадут формулу для её вычисления. Например.

Рисунок 3.3 – Как запомнить закон Ома

С треугольником мы закончили. Стоит добавить, что законом Ома называется только одна из представленных выше формул – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют. Так что не перепутайте!
Хорошей интерпретацией закона Ома является рисунок, который наиболее наглядно отражает сущность этого закона:

Рисунок 3. 4 – Закон Ома наглядно

Как мы видим, на этом рисунке изображены как раз три наших новых друга: Ом, Ампер и Вольт. Вольт пытается протолкнуть Ампер через сечение проводника(сила тока прямо пропорциональна напряжению), а Ом наоборот – мешает этому (и обратно пропорциональна сопротивлению). И чем сильнее Ом «стягивает» проводник, тем тяжелее Амперу будет пролезть. Но если Вольт посильнее пнёт…

Осталось разобраться, почему в названии урока фигурирует термин «много законов», ведь закон-то у нас один – закон Ома. Ну, во-первых, для него существует две формулировки, во-вторых, мы узнали только так называемый закон Ома для участка цепи, а ведь есть ещё закон Ома для полной цепи, который мы рассмотрим на следующем уроке, в-третьих, мы имеем, по крайней мере, два следствия из закона Ома, позволяющих находить значение сопротивления участка цепи и напряжение на этом участке. Так что закон всего один, а использовать его можно по-разному.

Напоследок расскажу ещё один интересный факт. Через 10 лет после появления «закона Ома» один французский физик (а во Франции работы Ома ещё не были известны) на основе экспериментов пришел к таким же выводам. Но ему было указано, что установленный им закон еще в 1827г. был открыт Омом. Оказывается, что французские школьники и поныне изучают закон Ома под другим именем – для них это закон Пулье. Вот так вот. На этом очередной урок закончен. До новых встреч!

• Любой участок или элемент электрической цепи можно однозначно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
• Сопротивление (R) – характеристика проводника, отражающая степень его электропроводности и зависящая от геометрических размеров проводника и рода материала, из которого он изготовлен.
• Напряжение (U) – то же самое, что и разность потенциалов; величина равная отношению работы электрического поля для перемещения точечного заряда из одной точки пространства в другую.
• Ток, напряжение и сопротивление связаны между собой отношением I=U/R, называемым законом Ома (сила электрического тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника).

А также задачки:

• Если длину проволоки вытягиванием увеличить вдвое, то как изменится её сопротивление?
• Какой проводник представляет большее сопротивление: медный сплошной стержень или медная трубка, имеющая внешний диаметр, равный диаметру стержня?
• Разность потенциалов на концах алюминиевого проводника равна 10В. Определить плотность тока, протекающего через проводник, если его длина 3м.

← Урок 2: Как пересчитать электроны | Содержание | Урок 4: Когда есть ток? →

простое объяснение для чайников с формулой и понятиями. Закон Ома для электрической цепи

Автор Andrey Ku На чтение 31 мин Опубликовано 06.10.2021

Содержание

1. Закон Ома для цепи
2. Для ЭДС
3. Для полной цепи
4. Для переменного тока
5. Для замкнутой цепи
6. Сфера применения
7. Закон Ома для замкнутой цепи
8. Закон Ома для неоднородного участка цепи
9. Закон Ома для переменного тока
10. Метода треугольника закона Ома
11. Значение Закона Ома
12. Сопротивление
13. Таблица удельных сопротивлений различных материалов
14. Резистор
15. Реостат
16. Закон Ома для участка цепи
17. Закон Ома для полной цепи
18. Что такое ЭДС и откуда она берется
19. Когда «сопротивление бесполезно»
20. Формула Закона Джоуля-Ленца
21. Преобразованные формулы Закона Ома и Джоуля-Ленца
22. Применение закона Ома на практике
23. Таблица-шпаргалка
24. Последовательное и параллельное включение элементов
25. Цепь последовательно включенных резистивных элементов
26. Цепь параллельно включенных резистивных элементов
27. Интегральная и дифференциальная формы закона
28. Параллельное и последовательное соединение
29. Последовательное соединение
30. Параллельное соединение
31. Что нам дает параллельное и последовательное соединение?
32. Интегральная и дифференциальная формы закона

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит.  Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I – ток, протекающий по участку цепи.
• R – сопротивление этого участка.
• φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

Интересно по теме: Как проверить стабилитрон.

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U1=I*R1
• U2=I*R2
• Un=I*Rn
• U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС.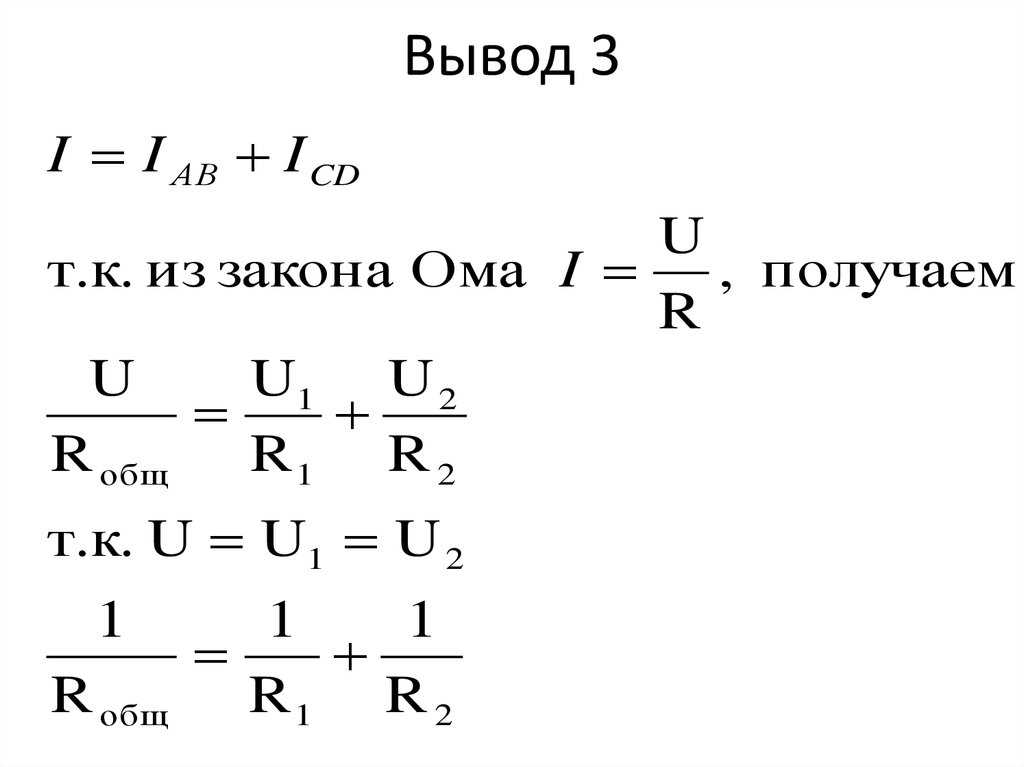 То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Следствия закона Ома.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Закон Ома для замкнутой цепи

Подобная интерпретация подразумевает наличие источника питания, а также проводника, по которому протекает ток. В этом случае, помимо сопротивления на отдельно взятом участке следует учитывать и то, которое возникает в ИП. Учитывая эти факторы, можно сказать, что сила тока будет равна отношению электродвижущей силы к сумме сопротивлений.

I = E/ Rвн+r,

где Е – ЭДС, Rвн – внешнее сопротивление, а r соответственно внутреннее.

Закон Ома для замкнутой цепи можно объяснить доступным языком. Электродвижущая сила по определению должна полноценно обеспечивать постоянную разницу потенциалов, и эта сила может иметь неприродное происхождение: химическое, если в качестве источника используется батарейка или механическая, в случае подключения к электрической цепи генератора. При подключении медной проволоки с идентичным сечением к батарейке и аккумулятору. Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.

Закон Ома для неоднородного участка цепи

Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.

Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.

Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.

На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.

Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.

Примечание: в некоторых ситуациях, некоторыми внешними факторами пренебрегают по причине того, что они очень незначительны и в числовом эквиваленте никоим образом не могут повлиять на общую картину. Это значит, что нелинейная зависимость на графике фактически совпадает с линейной.

Учитывая вышесказанное, можно установить следующую зависимость:

I = U/ R = (f1 – f2) + E/ R,

Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.

Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».

Закон Ома для переменного тока

Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:

I = U/ Z, где

I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).

Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:

• в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
• при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
• при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
• если проводник (диэлектрик) находится под высоким напряжением;
• светодиодных лампах;
• в полупроводниках и аналогичных устройствах.

На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формуми, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.

Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Сопротивление

Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.

• Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.

Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.

Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.

Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала. 2.

Знайте!СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

• Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.

Таблица удельных сопротивлений различных материалов

Удельное сопротивление ρ, Ом*мм2/м	Удельное сопротивление ρ, Ом*мм2/м
Алюминий	0,028
Бронза	0,095 – 0,1
Висмут	1,2
Вольфрам	0,05
Железо	0,1
Золото	0,023
Иридий	0,0474
Константан ( сплав Ni-Cu + Mn)	0,5
Латунь	0,025 – 0,108
Магний	0,045
Манганин (сплав меди марганца и никеля – приборный)	0,43 – 0,51
Медь	0,0175
Молибден	0,059
Нейзильбер (сплав меди цинка и никеля)	0,2
Натрий	0,047
Никелин ( сплав меди и никеля)	0,42
Никель	0,087
Нихром ( сплав никеля хрома железы и марганца)	1,05 – 1,4
Олово	0,12
Платина	0. 107
Ртуть	0,94
Свинец	0,22
Серебро	0,015
Сталь	0,103 – 0,137
Титан	0,6
Хромаль	1,3 – 1,5
Цинк	0,054
Чугун	0,5-1,0

Резистор

Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.

Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.

Вот так резистор изображается на схемах:

В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.

Вот так резистор выглядит в естественной среде обитания:

Полосочки на нем показывают его сопротивление.

На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:

Источник: сайт компании Ekits

О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.

Реостат

Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.

Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.

По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:

Сопротивление R = ρ l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм^2] ρ — удельное сопротивление [Ом*мм^2/м]

Закон Ома для участка цепи

С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.

Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».

У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.

Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

Математически его можно описать вот так:

Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом]

Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее. 2/м

Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.

Закон Ома для полной цепи

Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.

В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.

Что такое ЭДС и откуда она берется

ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.

• ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.

Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.

Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.

В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:

Закон Ома для полной цепи I = ε/(R + r) I — сила тока [A] ε — ЭДС [В] R — сопротивление [Ом] r — внутреннее сопротивление источника [Ом]

Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.

Решим задачу на полную цепь.

Задачка

Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом

Решение:

Возьмем закон Ома для полной цепи:

I = ε/(R + r)

Подставим значения:

I = 4/(3+1) = 1 A

Ответ: сила тока в цепи равна 1 А.

Когда «сопротивление бесполезно»

Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.

А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.

Ток идет по пути наименьшего сопротивления.

Теперь давайте посмотрим на закон Ома для участка цепи еще раз.

Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом]

Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.

То есть:

I = U/0 = ∞

Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.

Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.

Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.

Формула Закона Джоуля-Ленца

Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.

Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.

где P – мощность, измеряется в ваттах и обозначается Вт;U – напряжение, измеряется в вольтах и обозначается буквой В;I – сила ток, измеряется в амперах и обозначается буквой А.

Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.

Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.

Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.

Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.

Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.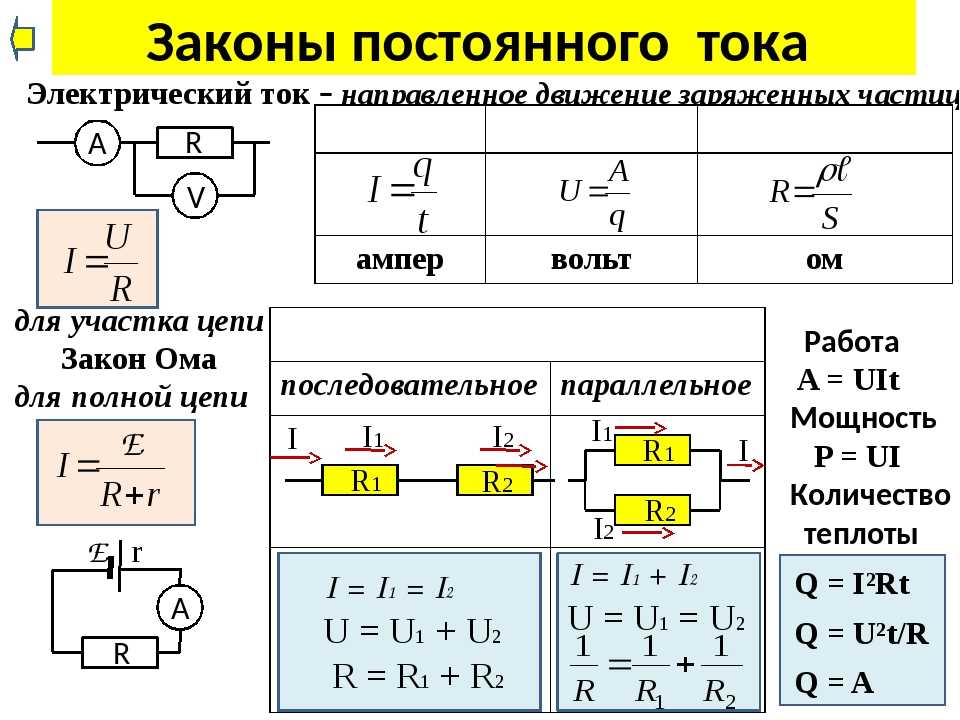

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

Применение закона Ома на практике

На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.

Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.

Таблица-шпаргалка

Используя закон Ома для участка цепи, а также формулу для мощности электрического тока: P = U*I – я подготовил для вас полезную таблицу-шпаргалку, которая позволяет соотносить между собой сопротивление (R), силу тока (I), напряжение (U) и мощность электрического тока (P). Будет точно полезно не только школьникам!

Известные величины	R (сопротивление)	I (сила тока)	U (напряжение)	P (мощность)
Ток и сопротивление			U = I × R	P = I2 × R
Напряжение и ток	R = U / I			P = U × I
Мощность и ток	R = P / I2		U = P / I
Напряжение и сопротивление		I = U / R		P = U2 / R
Мощность и сопротивление		I = P / R
Напряжение и мощность	R = U2 / R	I = P / U

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

• Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
• Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
  Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока

В общем, это наиболее распространенные варианты использования этих соединений.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Источники

• https://ElectroInfo.net/teorija/vse-o-zakone-oma-prostymi-slovami-s-primerami-dlja-chajnikov.html
• https://uelektrika.ru/osnovy-yelektrotekhniki/zakon-oma-dlya-yelektricheskoy-cepi/
• https://serp1.ru/kak-ponjat-zakon-oma-prostoe-objasnen/
• https://skysmart.ru/articles/physics/zakon-oma
• https://mnogoformul.ru/zakon-oma
• https://www.asutpp.ru/zakon-oma-dlya-uchastka-tsepi.html

Закон Ома — schip.com.ua

Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Георг Симон Ом

Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

 

Формула закона Ома записывается в следующем виде:

где

I – сила тока в проводнике, единица измерения силы тока — ампер [А];

U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].

Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.

Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Георг Симон ОМ (1787 — 1854) — биография.

Замечательный немецкий физик Георг Симон Ом, чье имя носит знаменитый закон электротехники и единица электрического сопротивления, родился 16марта 1789 г. в Эрлангене (федеральная земля Бавария). Его отец был известным в городе мастером-механиком. Мальчик Ом помогал отцу в мастерской и многому у него научился.

Отец Георга — Иоганн Вольфганг Ом, был потомственным слесарем, много времени уделявшим вопросам самообразования. Он женился на дочери эрлангенского кузнеца Марии Елизавете Беккин. Из 7 рожденных ею детей в живых осталось только трое, а сама она в 1799 умерла при родах. Иоганн Ом так и не оправился до конца жизни от потери «лучшей и нежнейшей из матерей», как он о ней говорил. Тогда его сыну Георгу было 10, Мартину -7, а дочери Барбаре — всего 5 лет. Воспитанием детей занимался отец, уделяя большое внимание их образованию.

Чтобы обеспечить семью, он ежедневно с утра до вечера занимался выполнением кузнечных и слесарных заказов, а каждую свободную минуту он посвящал детям. О том бесконечно многом, чем они обязаны отцу, впоследствии говорили оба сына слесаря Иоганна, ставшие профессорами: Георг — физиком, а Мартин — математиком. Даже на памятнике Ому в Мюнхене он изображен возле отца, крупного мужчины в рабочем фартуке, который, обняв за плечи восторженно внимающего ему сына, серьезно и нежно о чем-то рассказывает мальчику.

Учитель начальной школы подготовил Георга к поступлению в городскую гимназию В этом учебном заведении основное внимание уделялось изучению латыни и греческого языка. Что касается математики и особенно физики, то лишь занятия, которые проводил вместе с сыновьями дома Иоганн Ом, позволили им продвинуться в изучении этих наук. Из довольно ограниченных средств семьи всегда выделялись деньги для покупки книг по математике (они преобладали), но также по истории, географии, философии, педагогике, равно как и руководства по обработке металлов. Неудивительно, что у преклонявшегося перед наукой кузнеца появились знакомые (ставшие вскоре его друзьям), преподаватели университета. Они охотно занимались и с его одаренными сыновьями.

В 1805 Георг Симон Ом сам стал студентом Эрлангенского университета. При той подготовке, которая у него была, учиться в университете Георгу Ому было легко. Может быть, и по этой причине он с азартом окунулся в спорт (стал, в частности, лучшим бильярдистом и конькобежцем в университете), увлекся танцами. Отца такая перемена в сыне не могла не обеспокоить. Назревал первый и единственный раз в их жизни «конфликт отцов и детей». В результате Георг, проучившись в университете всего полтора года, покинул родительский дом, чтобы в швейцарском городке Готтштадте занять место преподавателя математики в частной школе. Так началась педагогическая деятельность Георга Ома.

Швейцария очаровала Георга. Ее природа, ее люди, в том числе его коллеги и ученики, крохотный городок, в котором самым большим зданием был старинный замок, в котором располагалась школа, наконец, хорошая зарплата — все это вызывало у него чувство восхищения, которым наполнены его письма домой. Огорчало лишь отсутствие ответных писем от отца, который был так глубоко травмирован размолвкой с сыном, что почти год не только не писал ему, но даже и отказывался читать его письма: Иоганну Ому казалось, что рухнули все надежды, которые он связывал со своим даровитым сыном. Время — лучший целитель. Постепенно переписка восстановилась, и отец, как и прежде, старался поддерживать Георга вниманием и советами.

Ом в 1911 все же вернулся в Эрланген, то уже в том же году сумел закончить университет, защитить диссертацию и получить ученую степень доктора философии. Более того, ему тут же была предложена в университете должность приват-доцента кафедры математики. Это было прекрасно, но всего через три семестра Георг Ом вынужден был по материальным соображениям искать другое место. Эти поиски были мучительными и долгое время безуспешными. Наконец пришло приглашение занять место учителя физики и математики в иезуитской коллегии Кельна. 37-летний Ом немедленно направился в Кельн.

Первым делом Георг проводит обследование всего парка приборов. Здесь обнаруживается, что многие приборы требуют ремонта, а то и замены. Но Ом не зря был прилежным учеником своего отца, который остается его первым советчиком. Тщательность работы, стремление как можно детальнее продумывать постановку экспериментов и готовить для них аппаратуру стало основой будущих успехов. Ом, который прежде уделял основное внимание математике, решительно и воодушевленно переключился на физику. Ома увлекли проблемы, связанные с протеканием электрических токов по проводникам.

Для характеристики проводников Ом в1820 г. ввел понятие «сопротивление», ему казалось, что проводник сопротивляется току. По-английски и по-французски сопротивление называется resistance, поэтому современный схемный элемент называется резистором, а первая буква R с легкой руки Ома до сих пор используется как обозначение резистора в схемах.
Школьникам наших дней, изучающим закон Ома, может показаться, что это — один из простейших законов физики: сила тока в проводнике прямо пропорциональна падению напряжения в нем и обратно пропорциональна сопротивлению. Но попробуйте мысленно перенестись в двадцатые годы 19 века!

Путь, по которому пошел Георг Ом, определялся ясным пониманием того, что первым делом нужно научиться количественно исследовать физическое явление. Для измерения тока уже раньше пытались использовать тот факт, что он вызывает нагревание проводника. Однако Г. Ом избрал для измерения тока не тепловое, а именно его магнитное действие, открытое Эрстедом. В приборе Ома ток, протекавший по проводнику, вызывал поворот магнитной стрелки, подвешенной на упругой расплющенной золотой проволочке. Экспериментатор, поворачивая микрометрический винт, к которому крепился верхний конец проволочки, добивался компенсации поворота, вызванного магнитным воздействием, и угол поворота этого винта и являлся мерилом тока.

Установка была смонтирована со всей возможной тщательностью и обеспечивала достаточную стабильность тока. Только после этого Ом устранил все первоначально имевшиеся источники неточностей и получил надежные результаты, касающиеся влияния на ток как геометрической формы проводников (их длины и сечения), так и их химического состава.

В 1826 в «Журнале физики и химии» появилась обширная статья Георга Ома «Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата мультипликатора Швейггера» (так Ом называл применявшийся им гальванометр), в которой излагались основные результаты его исследований.

Публикация результатов опытов Ома в первое время не вызвала почти никаких отзывов. Узнав о работах Ома, сам великий Майкл Фарадей заинтересовался ими и выразил сожаление, что из-за незнания немецкого языка не может изучить их обстоятельнее. Что же касается немецких коллег Ома, то, когда, наконец, был опубликован пространный отзыв одного из них, его автор счел, что исследования Ома «не внушают серьезного уважения».

Тем не менее, хлопоты Ома о предоставлении ему годичного освобождения от учебных занятий ради возможности посвятить себя полностью научным исследованиям были в 1826 удовлетворены (правда, с сохранением лишь половинного оклада).
Георг Ом переезжает в Берлин, где живет и работает его брат Мартин, и ровно через год выходит обширная, содержащая 245 страниц, монография «Теоретическое исследование электрических цепей». Противники Ома не только отрицали его заслуги, но и активно мешали ему работать. Все хлопоты о месте, где можно было бы работать, оставались тщетными. Даже выступать в печати со своими доводами Ому было не просто.

«Нет пророка в своем отечестве!» Георг Ом в полной мере испытал это. Понимая важность полученных им научных результатов, он тщетно хлопотал о предоставлении ему той должности, которой он по праву заслуживал. Хотя срок его командировки в Берлин истекал, он считал невозможным оставить этот научный центр. В конце концов, ему предложили работу в Военной школе Берлина, но почти с символической нагрузкой — 3 часа в неделю (и с соответствующей оплатой). Ом, которого поддерживал брат, принял и такое предложение. Он продолжал упорно работать. В 1829 в «Журнале физики и химии» вышла еще одна его работа. В ней фактически закладывались принципиальные основы работы электроизмерительных приборов. В частности, был предложен используемый и сегодня эталон электрического сопротивления.

Только в 1833, через 6 лет после выхода основного труда Ома, ему предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ом немедленно перебрался в Нюрнберг. Вскоре его назначили инспектором по методике преподавания и поручили заведование кафедрой математики. В 1839 к этому добавились и обязанности ректора школы. Тогда же наметился и его переход на новую научную тематику: Ома привлекла акустика. В 1843 он показал, что простейшее слуховое ощущение вызывается гармоническими колебаниями, на которое ухо разлагает сложные звуки (акустический закон Ома).

Наметилось и международное признание. В 1841 работы Ома были переведены на английский язык, в 1847 — на итальянский, в 1860 — на французский. (Хотя перевода трудов Ома на русский язык не было, но именно работавшие в России Э. Х. Ленц и Б. С. Якоби первыми привлекли внимание широкой научной общественности к трудам Ома). В 1842 произошло событие, которое явилось первым важным знаком признания научных заслуг Георга Ома: он явился вторым немецким ученым, которого Лондонское Королевское общество наградило золотой медалью и избрало своим членом.

Наконец, через 20 лет ожидания, Георг Ом получил признание и на родине. В 1845 его избрали в Баварскую Академию Наук, а через четыре года пригласили в Мюнхен на должность экстраординарного профессора. Тогда же по королевскому указу он назначается хранителем государственного собрания физико-математических приборов и референтом по телеграфному ведомству при физико-техническом отделе Министерства государственной торговли. Одновременно он продолжает читать лекции по физике и по математике. Вся жизнь Георга Ома была отдана науке и поэтому семьи он не создал.

В 1852 исполнилось давнишнее желание Ома — он получил должность ординарного профессора. Но здоровье его уже пошатнулось. В 1854 он перенес серьезный сердечный приступ. 28 июня 1854 король Максимилиан издал указ об освобождении его от обязательного чтения лекций. Но до конца жизни ему оставалось всего 12 дней. Георг Ом скончался 6 июля 1854 года в половине одиннадцатого утра. Он был похоронен на старом южном кладбище города Мюнхена.

Исследования Георга Ома вызвали к жизни новые идеи, развитие которых вывело вперед учение об электричестве. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления — 1 Ом. Этот факт — дань уважения коллег, международное признание заслуг ученого.

Закон Ома – определение, формула, применение, ограничения

Согласно закону Ома, напряжение или разность потенциалов между двумя точками пропорциональны току электричества, протекающему через сопротивление, а сопротивление цепи пропорционально току или электричество проходит через сопротивление. V=IR – это формула закона Ома. Георг Симон Ом, немецкий физик, открыл связь между током, напряжением и отношениями. Давайте подробнее рассмотрим закон Ома, сопротивление и его приложения.

Что такое закон Ома?

Напряжение, ток и сопротивление — три основных компонента электричества. Закон Ома изображает прямую связь между этими тремя переменными. Согласно закону Ома, ток, протекающий по проводнику между двумя точками, пропорционален напряжению на проводнике.

Диаграмма зависимости напряжения от силы тока

Формула закона Ома

Это одно из самых фундаментальных правил электротехники. Это помогает в расчете мощности элемента, КПД, тока, напряжения и сопротивления в электрической цепи.

В ∝ R

В = I × R

Здесь

• В — напряжение,
• I — ток,
• R 9 — сопротивление.

Единицей сопротивления в СИ является ом и обозначается Ω.

Применение закона Ома

Когда известны два других числа, закон Ома можно использовать для определения напряжения, тока, импеданса или сопротивления линейной электрической цепи.

Основные применения закона Ома:

• Это также упрощает расчет мощности.
• Чтобы сохранить желаемое падение напряжения между электрическими компонентами, используется закон Ома.
• Необходимо определить напряжение, сопротивление или ток электрической цепи.
• Закон Ома также используется для перенаправления тока в амперметрах постоянного тока и других шунтах постоянного тока.

Как установить зависимость ток-напряжение?

Отношение V ⁄ I остается постоянным для заданного сопротивления при установлении связи ток-напряжение, поэтому график разности потенциалов (V) и тока (I) должен представлять собой прямую линию.

Как узнать неизвестные значения сопротивления?

Постоянное отношение определяет неизвестные значения сопротивления. Сопротивление провода с однородным поперечным сечением зависит от длины (L) и площади поперечного сечения (А). Это также зависит от температуры проводника.

Сопротивление при данной температуре

R = ρ L ⁄ A

Здесь ρ — удельное сопротивление или удельное сопротивление, а также характеристика материала провода.

Удельное сопротивление или удельное сопротивление материала провода:

ρ = R A ⁄ L

Ограничения закона Ома

• Закон Ома не применяется к односторонним сетям. Ток может течь только в одном направлении в односторонних сетях. В таких сетях используются диоды, транзисторы и другие электронные компоненты.
• Нелинейные компоненты также не подпадают под действие закона Ома. Нелинейные компоненты имеют ток, который не пропорционален приложенному напряжению, что означает, что значение сопротивления этих элементов изменяется в зависимости от напряжения и тока. Тиристор является примером нелинейного элемента.

Резисторы

Одним из важнейших компонентов электрических цепей является резистор. Поскольку они состоят из смеси глины или углерода, они являются хорошими проводниками и хорошими изоляторами. На большинстве резисторов видны четыре цветные полосы. Первая и вторая полосы показывают первую и вторую цифры значения соответственно. Цифры значений умножаются в третьей полосе, а допуск определяется в четвертой полосе. Если нет четвертой полосы, предполагается, что допуск составляет плюс-минус 20 %.

Сопротивление в серии

Серия представляет собой группу связанных элементов, например, вдоль линии, в ряду или в определенном порядке. В электронике последовательное сопротивление означает, что резисторы соединены последовательно и что ток может проходить только через один канал.

Законы последовательных цепей

• Общее сопротивление цепи состоит из отдельных сопротивлений.
• Общее напряжение представляет собой сумму отдельных напряжений в цепи.
• Через каждую точку цепи протекает одинаковый ток.

Сопротивление в параллельном соединении

Параллельное соединение может быть организовано различными способами. Большая часть проводки в реальном мире выполняется параллельно, так что напряжение, подаваемое на любую часть сети, такое же, как напряжение, подаваемое на любой другой ее участок.

Законы параллельных цепей

• Все обратные величины сопротивлений компонентов складываются с обратными величинами общего сопротивления цепи.
• Общее потребление тока представляет собой сумму отдельных токов, потребляемых в цепи.
• Каждая точка цепи имеет одинаковое напряжение.

Примеры задач

Задача 1. Найти сопротивление электрической цепи при напряжении питания 15 В и силе тока 3 мА.

Решение:

Дано:

В = 15 В,

I = 3 мА = 0,003 А

Сопротивление электрической цепи определяется как:

R = V / I

= 15 В / 0,003 А

= 5000 Ом

= 5 кОм

Следовательно, сопротивление электрической цепи равно 5 кОм .

Задача 2: Если сопротивление электрического утюга равно 10 Ом и через сопротивление протекает ток 6 А. Найдите напряжение между двумя точками.

Решение:

Дано:

I = 6 А

R = 10 Ом

Формула для расчета напряжения:

В = I × R

В = 6 А × 10 Ом

= 60 В

Следовательно, напряжение между двумя точками равно 60 В .

Задача 3. Когда нарушается закон Ома?

Решение:

Поведение полупроводников и односторонних устройств, таких как диоды, определяется законом Ома. Если физические факторы, такие как температура и давление, не поддерживаются постоянными, закон Ома может не обеспечить ожидаемых результатов.

Проблема 4: Почему закон Ома не применим к полупроводникам?

Решение:

Полупроводниковые приборы имеют нелинейный характер, поэтому к ним не применим закон Ома. Это указывает на то, что отношение напряжения к току не остается постоянным при изменении напряжения.

Задача 5. Как применяется закон Ома?

Решение:

Статические значения компонентов схемы, таких как уровни тока, напряжения питания и падения напряжения, проверяются с помощью закона Ома.

Что такое закон Ома?

18 декабря 2020 г. от Veerendra

Что такое закон Ома?

1. Пропорциональная зависимость разности потенциалов между концами идеального проводника и протекающего по нему тока известна как закон Ома .
2. Закон Ома гласит , что ток, проходящий через идеальный проводник, прямо пропорционален разности потенциалов между его концами при условии, что температура и другие физические факторы проводника остаются постоянными.
3. Определение: В соответствии с законом Ома при постоянной температуре ток, протекающий через проводник, прямо пропорционален разности потенциалов на проводнике.
4. Таким образом, если I — ток, протекающий по проводнику, а V — разность потенциалов (или напряжение) на проводнике, то по закону Ома.
   I ∝ V (когда T постоянна)
   \(I=\frac{V}{R}\text{                    }…..\text{ (i)}\)
   , где R — константа, называемая сопротивлением проводник.
   Уравнение (i) может быть записано как
   V = I × R                          …… (ii)
5. Единица сопротивления:
   Единицей сопротивления в системе СИ (R) является ом. Ом обозначается греческой буквой омега (Ω).
   \( \text{Из закона Ома,        }R=\frac{V}{I} \)
6. Теперь, если V = 1 вольт и I = 1 ампер
   \( \text{Тогда,                           }R=\ frac{\text{1}\,\text{вольт}}{\text{1}\,\text{ампер}} \)
   Таким образом, 1 Ом определяется как сопротивление проводника, пропускающего ток силой 1 ампер протекать через него, когда на нем поддерживается разность потенциалов в 1 вольт.
7. Результаты закона Ома
   Ток, протекающий через проводник, прямо пропорционален разности потенциалов на проводнике.
   
8. Когда разность потенциалов в цепи поддерживается постоянной, ток обратно пропорционален сопротивлению проводника.
   \( I\propto \frac{1}{R} \)
9. Отношение разности потенциалов к току постоянно. Значение константы равно сопротивлению проводника (или резистора).
   \( \frac{V}{I}=R \)

Люди также спрашивают

• Как длина провода влияет на сопротивление?
• Как площадь поперечного сечения влияет на сопротивление?
• Какое определение сопротивления в физике?
• Как температура влияет на сопротивление провода?

Задачи по закону Ома с решением

1. Когда к проводнику приложена разность потенциалов 12 В, сила тока, протекающего через проводник, равна 0,2 А. Каково сопротивление проводника?
   Решение:
   \( R = \frac{V}{I} \)
   = 12/0,2
   = 60 Ом
2. Чему равна разность потенциалов на лампочке сопротивлением 5 Ом при протекании тока через это 0,5А?
   Решение:
   В = I × R
   = 0,5 × 5 = 2,5 В
3. К электрическому нагревателю приложена разность потенциалов 230 В. Через нагревательный элемент нагревателя протекает ток силой 5 А.
   (а) Каково сопротивление нагревательного элемента?
   (b) Можно ли использовать этот электронагреватель в стране, где напряжение сети составляет 110 В? Поясните свой ответ.
   Решение:
   (a) \( R = \frac{V}{I} \)
   = 230/5
   = 46 Ом
   (b) Нагреватель все еще можно использовать, но эффект нагрева будет очень сильным меньше, поскольку ток, проходящий через нагреватель, намного меньше. Ток, проходящий через нагреватель, равен:
   \( I = \frac{V}{R} \)
   = 110/46
   = 2,4 А
   Это значение меньше 5 А.
4. Электродвигатель с внутреннее сопротивление 10 Ом может работать с определенной скоростью, когда через него проходит ток 0,5 А. Скорость двигателя увеличивается, когда к нему прикладывается разность потенциалов, в два раза превышающая прежнюю. Какой новый ток проходит через двигатель?
   Решение:
   Разность потенциалов на двигателе при прохождении тока 0,5 А:
   В = IR = 0,5 x 10 = 5 В
   При удвоении разности потенциалов
   2 x 5 = I x 10
   I = 1 A

Из чего состоит сверхпроводник?

1. Большинство материалов имеют электрическое сопротивление, что приводит к потере мощности и нагреву.
2. Для многих электрических применений требуются материалы с очень низким сопротивлением — чем ниже, тем лучше.
3. Линии электропередач, электромагниты и компьютерные чипы революционизируются благодаря материалам, не обладающим сопротивлением.
4. На самом деле, в особых условиях могут быть изготовлены материалы с нулевым сопротивлением. Например, при охлаждении ртути до температуры 4,15 К ее сопротивление внезапно упало до нуля. Таким образом, ртуть становится сверхпроводником. Это явление известно как сверхпроводимость .
5. На рисунке показана сверхпроводимость. Сопротивление сверхпроводника внезапно падает до нуля, когда его температура падает ниже критической температуры T _с .
   
6. Сверхпроводник проводит электричество без потери энергии. На рисунке показан постоянный магнит, плавающий над сверхпроводником. Это эффект сверхпроводимости, возникающий из-за непрерывного протекания индуцированного тока.
   

Рубрики: Физика С тегами: Электричество, Закон Ома, Результаты закона Ома, Единица сопротивления

‎Teachers’ Voices on Apple Podcasts

26 серий

Учителя — одни из самых влиятельных силы для справедливости, доступа и качества в образовании. Они обеспечивают детей и молодых людей знаниями, навыками, отношением и инструментами, необходимыми для полного раскрытия их потенциала. «Голоса учителей» — это серия подкастов от BOLD, цифровой платформы по обучению и развитию. Присоединяйтесь к Нине Алонсо, которая делится впечатляющими историями учителей со всего мира, рассказывая их собственными словами о своем опыте, и слушайте вдохновляющие беседы с международными экспертами в области обучения и развития детей. Если вы родитель, учитель или просто заинтересованы в обучении и развитии, этот подкаст для вас. Дополнительную информацию см. на странице bold.expert 9.0003

1. Бонусный эпизод — Ресурсы для учителей 2

   Бонусный эпизод — Ресурсы для учителей 2

   В этом специальном мини-эпизоде ​​Нина отмечает Всемирный день учителя бонусным эпизодом «Голоса учителей». Слушайте вдохновляющие истории вместе с быстрыми практическими идеями и ресурсами, которыми поделились педагоги и исследователи.
   Гости
   Учителя
   Мари Карака
   Ингрид Деланж
   Моника Бхимвал
   Азмин Мистри
   Исследователи
   Сара Ричардсон и Сладана Крстич из Австралийского совета по исследованиям в области образования (ACER).
   Ресурсы и рекомендации 
   Прочтите краткое изложение исследования ACER, проведенного в сотрудничестве с Международным бакалавриатом (IB), и полный отчет.
   «Не в своем уме: научиться быть креативным», Кен Робинсон.
   День, когда мелки ушли, Дрю Дейуолт и Оливер Джефферс.
   Знание работает
   Кэт Мердок
   Летающий мальчик Джейн Де Суза
   Ресурс драмы, Дэвид Фармер
   Как сохранить любопытство детей – ответы на 5 вопросов

2. Как любопытный и творческий класс может вдохновить на обучение

   Как любознательный и творческий класс может вдохновить на обучение

   Почему любознательность и творчество так важны для любого обучения? Можно ли измерить любопытство в классе? Как исследователи и педагоги могут работать вместе для разработки стратегий обучения, которые поощряют детей к творчеству? 902:48 Нина Алонсо приветствует Сару Ричардсон и Сладану Крстич из Австралийского совета по исследованиям в области образования (ACER), которые проводят исследования в сотрудничестве с Международным бакалавриатом (IB). Они обсуждают партнерство с учителями в классе для тестирования прототипа материала с конечной целью отслеживания и поощрения творчества и любопытства среди учащихся.
   Нина также беседует с педагогами из Китая, Индии и Австралии о важности любознательности и творчества в классе. Преподаватели обсуждают свою роль в исследованиях, проводимых ACER, и разработке инструментов, которые они могут использовать для поддержки своих учащихся.
   Гости и ресурсы
   Международный бакалавриат (IB)
   IBO.org
   IB Twitter
   IB Facebook
   LinkedIn
   IB Instagram
   Австралийский совет по исследованиям в области образования (ACER)
   ACER.org/au
   ACER Twitter
   ACER Facebook
   ACER2 Linkedin Средняя школа Хантер-Вэлли (Австралия)
   Веб-страница
   Мари Карака находилась в Хантер-Вэлли во время записи и в настоящее время является сотрудником по образованию — образование для одаренных в Управлении католических школ.
   Международная школа ISA Гуанчжоу, Китай
   Linkedin
   Ингрид Деланж
   Школа Pathways, Индия
   Веб-страница
   Моника Бхимвал (директор школы Pathways)
   Бомбейская международная школа (Индия)
   Бомбейская международная школа
   Азмин Мистри
   Прочтите краткое изложение исследования ACER и полный отчет.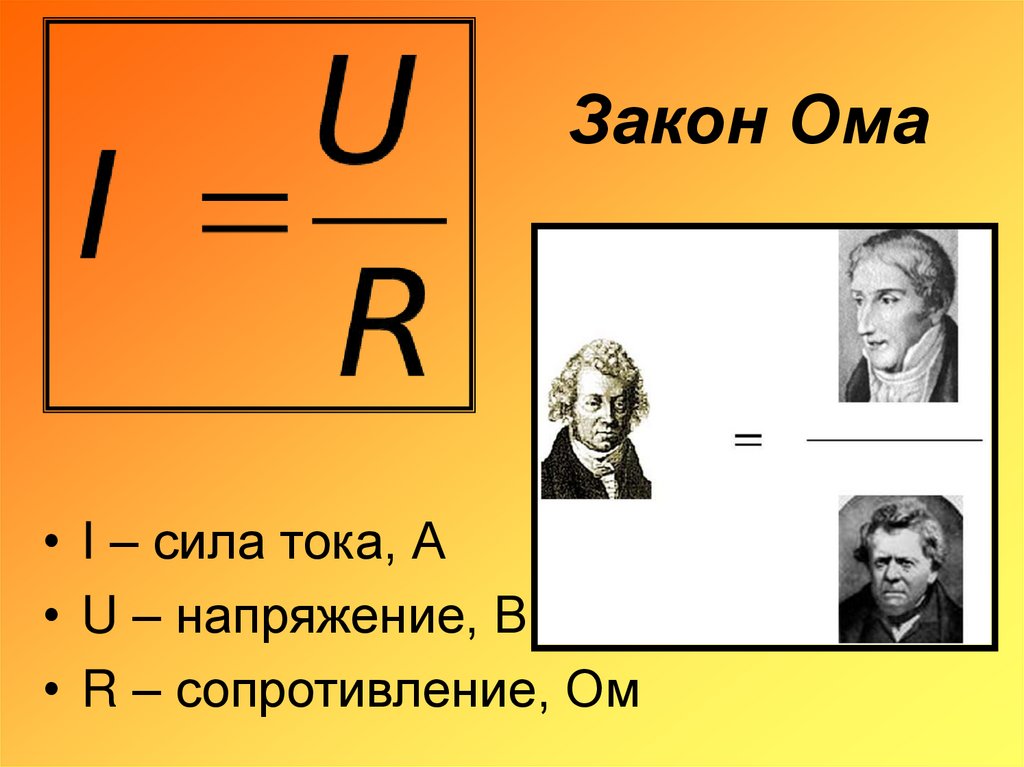
   Дополнительное исследование любознательности и креативности от имени IBO было проведено Центром оценки образования Оксфордского университета, и его можно найти здесь.
   Связаться с
   https://twitter.com/BOLD_insights
   https://twitter.com/VoicesTeachers
   Прослушать все выпуски: https://bold.expert/teachers-voices/
   Информационный бюллетень: https://bold.expert/newsletter
   https://bold.expert
   Электронная почта : [email protected]  

3. Как гендерное равенство в образовании может принести пользу всем детям

   Как гендерное равенство в образовании может принести пользу всем детям

   Как учителя могут способствовать гендерному равенству? Насколько легко начать бросать вызов стереотипам в классе? Может ли педагогика, учитывающая гендерные аспекты, помочь разрушить барьеры, сдерживающие девочек?
   В этом выпуске два педагога из Замбии и Парагвая делятся своими историями о преодолении стереотипов, а также о том, как поощрять и расширять возможности девочек в классе.
   Нина также разговаривает с Кристиной Кваук, социологом и политическим аналитиком, специализирующимся на образовании девочек. Кристина рассказывает о связи между гендерным равенством в классе и изменениями в обществе, а также о том, как гендерно-чувствительные и гендерно-преобразующие педагогические подходы могут повысить устойчивость.
   Гости и ресурсы
   Вы можете найти Кристину Кваук в Twitter и LinkedIn.
   «Дочери леса» рассказывает сильную, воодушевляющую историю о небольшой группе девочек в одном из самых отдаленных лесов, оставшихся на земле, которые посещают радикальную среднюю школу, где учатся защищать лес, которому угрожает опасность, и создавать для себя лучшее будущее.
   Инструментарий VVOB GRP4ECE: практический подход к гендерно-ориентированной педагогике для дошкольного образования.
   Дополнительные ресурсы
   ЮНИСЕФ об образовании девочек
   Фонд Малала
   Контакт
   Присоединяйтесь к нам в социальных сетях: https://twitter.com/BOLD_insights и https://twitter. com/VoicesTeachers
   Слушайте все выпуски «Голоса учителей» здесь: https://bold.expert/teachers-voices /
   Подпишитесь на информационный бюллетень BOLD: https://bold.expert/newsletter
   Будьте в курсе всех последних исследований в области развития и обучения детей: https://bold.expert
   Свяжитесь с нами: podcastteachersvoices@gmail. ком  

4. Как технологии могут стимулировать совместное обучение

   Как технологии могут способствовать совместному обучению

   Сегодняшний выпуск — это сотрудничество с Софи Бейли из подкаста Edtech. Нина и Софи исследуют тему совместного обучения с использованием образовательных технологий.
   Как исследователи сотрудничают с детьми для совместной разработки новых технологий? Какова роль учителей в работе с технологиями? Как можно использовать технологии в более сложных условиях обучения?

   Чтобы узнать больше, Нина и Софи разговаривают с Джейсоном Йипом, доцентом цифровой молодежи в Информационной школе Вашингтонского университета, и Коеном Тиммерсом, лектором, автором и основателем нескольких глобальных образовательных проектов.

   Узнайте больше о гостях, их проектах и ​​рекомендациях:

   Sophie Bailey — The Edtech Podcast
   Website
   Twitter
   Worktripp
   Professor Diana Laurillard
   The British Esports Association
   Мой секретный дневник Edtech
   Джейсон Йип
   Веб-сайт
   Твиттер
   Детская команда
   Коэн Тиммерс
   Веб-сайт
   Твиттер
   Проект Какума
   РЕЙЧЕЛ (Точка доступа для образования и обучения в отдаленных районах)

   Присоединяйтесь к нам в социальных сетях: https:// twitter.com/BOLD_insights и https://twitter.com/VoicesTeachers

   Слушайте все выпуски «Голоса учителей» здесь: https://bold.expert/teachers-voices/
   Подпишитесь на информационный бюллетень BOLD: https://bold .эксперт/информационный бюллетень
   Будьте в курсе всех последних исследований в области развития и обучения детей: https://bold.expert
   Свяжитесь с нами: [email protected]  

5. Бонусный эпизод — Ресурсы для учителей 1

   Дополнительный эпизод — Ресурсы учителей 1

   В этом специальном мини-эпизоде ​​«Голоса учителей» Нина Алонсо рассказывает о некоторых ресурсах, которыми гости поделились с ней в этом сезоне. Уделяя особое внимание учителям, работающим над тем, чтобы вовлечь своих учеников в решение экологических проблем на местном и глобальном уровнях, слушайте советы, ресурсы и источники вдохновения.
   Гостей
   Терри Годвальд зарегистрирован в Twitter и Linkedin.
   Мануэла Валентим зарегистрирована в Твиттере или на ее сайте.
   Ресурсы
   Центр глобального образования – Твиттер
   Коэн Тиммерс – педагог, автор, спикер
   Проект действий по борьбе с изменением климата
   Хашем аль-Гайли (instagram)
   Рекомендации Нины для иллюстрированных книг об окружающей среде и охране окружающей среды
   Горсть семян Моники Хьюз Принадлежность Джинни Бейкер «Вот мы: заметки о жизни на планете Земля» Оливера Джефферса «Пчелы: любовное письмо» Шабаза Ларкина «Лоракс» доктора Сьюза «Мальчик, который обуздал ветер» Уильяма Камквамбы, Брайана Милера «Мы — защитники воды» Кэрол Линдстром Giving Tree, Шел Сильверштейн, Aani and the Tree Huggers, Джанин Аткинс, рекомендация по видеоигре от Nina 9. 0248 http://neveralonegame.com/

   Путеводитель по другим иллюстрированным книгам по устойчивому развитию, подготовленным IBBY:
   ЮНЕСКО-CERLAC IBBY Каталог детских книг по устойчивому развитию

   Присоединяйтесь к нам в социальных сетях: https://twitter .com/BOLD_insights и https://twitter.com/VoicesTeachers

   Слушайте все выпуски «Голоса учителей» здесь: https://bold.expert/teachers-voices/

   Подпишитесь на информационный бюллетень BOLD: https://bold .эксперт/рассылка

   Будьте в курсе всех последних исследований в области развития и обучения детей: https://bold.expert

   Свяжитесь с нами: [email protected]   

6. Как климатическое образование может расширить возможности учащихся

   Как образование в области климата может помочь учащимся

   Изменение климата может быть непосильной задачей для молодежи. Но, возможно, его можно облегчить для понимания и отношения, продемонстрировав влияние на местном уровне и показав студентам, как молодые люди во всем мире решают схожие проблемы.
   Как молодежная активность поддерживает возможности обучения? Какие компоненты обучения лучше всего поддерживают «обучение экологически безопасным жизненным навыкам»? Как учителя уже помогают учащимся развивать эти навыки, имея совершенно другой доступ к ресурсам?
   В этом выпуске Нина разговаривает с Кристиной Кваук, междисциплинарным исследователем, специализирующимся на международном развитии, образовании и изменении климата. Она также беседует с учителями из Мадагаскара, Кении и Индонезии об их роли в повышении осведомленности учащихся, которых они обучают, и предоставлении им необходимой поддержки.
   Гостей
   Вы можете найти Кристину Кваук в Twitter и LinkedIn.
   Подробнее: Новая программа экологического обучения: подходы к качественному образованию для борьбы с изменением климата.
   Ниже приведены ресурсы Мохаммеда Райзы:
   www.