Закон ома вики. Электродвижущая сила (ЭДС): определение, формулы, применение

Что такое электродвижущая сила. Как измеряется ЭДС. Где применяется электродвижущая сила в технике и электронике. Формулы для расчета ЭДС в различных устройствах.

Что такое электродвижущая сила (ЭДС)

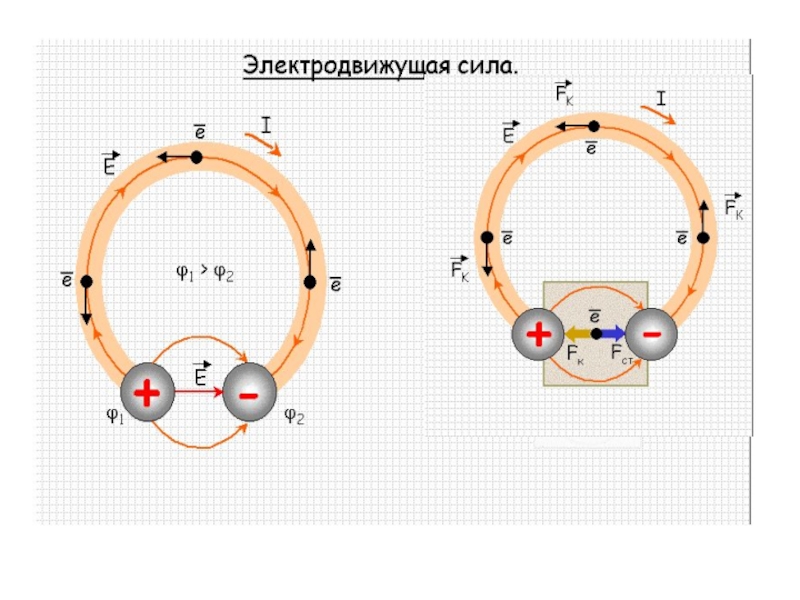
Электродвижущая сила (ЭДС) — это физическая величина, характеризующая работу сторонних (непотенциальных) сил по перемещению единичного положительного заряда. ЭДС измеряется в вольтах (В) и обозначается буквой ε (эпсилон).

Основные свойства ЭДС:

• Является причиной возникновения и поддержания электрического тока в цепи
• Создается источниками тока (батареями, генераторами и т.д.)
• Численно равна работе сторонних сил по перемещению единичного положительного заряда
• Не зависит от сопротивления цепи

Формула для расчета ЭДС

Основная формула для расчета ЭДС:

ε = A / q

где:

• ε — электродвижущая сила (В)
• A — работа сторонних сил (Дж)
• q — величина перемещаемого заряда (Кл)

Как рассчитать ЭДС по этой формуле? Для этого нужно знать работу сторонних сил и величину перемещаемого заряда. Например, если работа составляет 10 Дж, а перемещается заряд 2 Кл, то ЭДС будет равна:

ε = 10 Дж / 2 Кл = 5 В

ЭДС источника тока

ЭДС источника тока — это разность потенциалов на его полюсах при разомкнутой внешней цепи. Она определяет максимальное напряжение, которое может создать источник.

Формула для расчета ЭДС источника:

ε = IR + U

где:

• ε — ЭДС источника (В)
• I — ток в цепи (А)
• R — внутреннее сопротивление источника (Ом)
• U — напряжение на внешней нагрузке (В)

Как применять эту формулу? Допустим, мы имеем источник с внутренним сопротивлением 0.5 Ом, ток в цепи 2 А, а напряжение на нагрузке 9 В. Тогда ЭДС источника составит:

ε = 2 А * 0.5 Ом + 9 В = 10 В

ЭДС индукции

ЭДС индукции возникает в проводнике при изменении магнитного потока, пронизывающего контур. Она описывается законом электромагнитной индукции Фарадея:

ε = -dΦ/dt

где:

• ε — ЭДС индукции (В)
• Φ — магнитный поток (Вб)
• t — время (с)
• dΦ/dt — скорость изменения магнитного потока

Как использовать эту формулу? Предположим, магнитный поток через контур изменился на 0.2 Вб за 0.1 с. Тогда ЭДС индукции будет равна:

ε = -0.2 Вб / 0.1 с = -2 В

Знак минус указывает на направление индукционного тока согласно правилу Ленца.

ЭДС самоиндукции

ЭДС самоиндукции возникает в проводнике при изменении силы тока в нем. Она описывается формулой:

ε = -L * dI/dt

где:

• ε — ЭДС самоиндукции (В)
• L — индуктивность проводника (Гн)
• dI/dt — скорость изменения силы тока (А/с)

Как применять эту формулу? Допустим, в катушке с индуктивностью 0.5 Гн ток изменяется со скоростью 10 А/с. Тогда ЭДС самоиндукции составит:

ε = -0.5 Гн * 10 А/с = -5 В

Применение ЭДС в технике и электронике

ЭДС находит широкое применение в различных областях техники и электроники:

• Источники питания: ЭДС батарей, аккумуляторов и других источников тока обеспечивает работу электронных устройств
• Генераторы: ЭДС индукции используется для генерации электроэнергии на электростанциях
• Трансформаторы: ЭДС индукции позволяет изменять напряжение в электрических сетях
• Электродвигатели: ЭДС индукции создает вращающий момент в электрических двигателях
• Датчики: ЭДС индукции применяется в различных датчиках для измерения скорости, положения и других параметров

Измерение ЭДС

Для измерения ЭДС используются специальные приборы — потенциометры. Они позволяют измерять ЭДС, не нарушая режим работы источника.

Порядок измерения ЭДС потенциометром:

1. Подключить измеряемый источник к потенциометру
2. Уравновесить мост потенциометра
3. Снять показания со шкалы прибора

При измерении ЭДС важно учитывать, что вольтметр показывает напряжение на зажимах источника, которое меньше его ЭДС на величину падения напряжения внутри источника.

ЭДС и напряжение: в чем разница

ЭДС и напряжение — близкие, но не тождественные понятия. Основные отличия:

• ЭДС — характеристика источника тока, напряжение — характеристика участка цепи
• ЭДС создается сторонними силами, напряжение — электростатическим полем
• ЭДС не зависит от сопротивления цепи, напряжение зависит
• ЭДС источника всегда больше или равна напряжению на его зажимах

Важно понимать эту разницу при расчетах электрических цепей и анализе работы источников тока.

Заключение

Электродвижущая сила — фундаментальное понятие в электротехнике и электронике. Понимание природы ЭДС, методов ее расчета и измерения необходимо для анализа и проектирования электрических цепей и устройств. ЭДС играет ключевую роль в работе источников питания, генераторов, двигателей и многих других электротехнических устройств.

Закон Ома — Викизнание… Это Вам НЕ Википедия!

Закон Ома связывает величину напряжения (либо ЭДС) и силы тока в линейной электрической цепи с её сопротивлением. Открыт в 1826 году. Назван в честь Георга Ома.

Существует два варианта закона Ома в интегральной форме — для участка цепи и для всей цепи, дифференциальная форма и расширения его для случаев синусоидального переменного тока и переходных процессов.

Закон Ома для участка цепи[править]

Закон Ома для участка цепи гласит, что сила тока в участке цепи помноженная на сопротивление участка равна напряжению между его концами.

В виде формулы:

либо

где

Закон можно выразить также через величину электрической проводимости :

Обе записи закона Ома эквивалентны.

Закон Ома для всей цепи[править]

Закон ома для всей цепи гласит, что сила тока циркулирующего по неразветвлённой замкнутой цепи, помноженная на суммарное сопротивление этой цепи равна суммарной ЭДС источников в ней.

В виде формулы:

где

Закон Ома в дифференциальной форме[править]

Дифференциальная форма позволяет рассматривать не целый участок цепи, а бесконечно малый элемент проводника с током посредством связи векторов напряжённости электрического поля и плотности тока через удельное сопротивление или удельную проводимость :

, или

.

То есть дифференциальная форма закона Ома полностью аналогична интегральной с учётом замены величин, описывающих макроскопические физические тела на величины, описывающие физические поля в конкретной точке пространства. При этом однако следует учитывать, что удельные сопротивление и проводимость являются вообще говоря тензорами, и, если среда проявляет анизотропию по отношению к электрическому току, то векторы напряжённости и плотности тока могут иметь разные направления (электрический ток отклоняется от линий электрического поля).

Закон Ома для переменного тока[править]

Закон Ома применим как к постоянному току, так и к мгновенным значениям напряжения и тока:

где

• — напряжение между концами участка цепи в момент времени ,
• — сила тока, протекающего через участок цепи в момент времени .

Более того, закон Ома применим и к таким величинам, как амплитудное, действующее, среднее, минимальное, максимальное значение, размах напряжения и тока, связывая соответствующие величины между собой. Так амплитуда напряжения будет связана с амплитудой тока выражением

среднее значение напряжения и тока — выражением:

и т. д. Любая линейная функция тока и напряжения будет подчиняться закону Ома, если закону Ома подчиняется мгновенное значение.

Применимость закона Ома[править]

Закон Ома носит эмпирический характер. Он с хорошей точностью применим к подавляющему большинству материалов. К таким материалам, например, относятся металлы и сплавы, электролиты, их растворы и расплавы и многие другие вещества. Неприменим закон, или применим в очень узких пределах к полупроводникам.

Применимость закона ограничена не только материалами. Закон не учитывает различные эффекты, которые могут приводить нелинейности или непостоянству коэффициента пропорциональности. К таким эффектам можно отнести влияние саморазогрева на сопротивление, скин-эффект, электрический и термический пробой.

Протекание электрического тока через неидеальный проводник приводит к преобразованию электрической энергии в тепло, а, следовательно к повышению температуры проводника. Электрическое сопротивление материалов зависит от температуры, а значит, прохождение тока будет влиять на сопротивление, таким образом зависимость тока от напряжения будет нелинейной. Наличие обратной связи между сопротивлением и разогревом это может приводить к сложному характеру зависимости, например, к лавинообразному. Также в силу инерционности тепловых процессов он также будет иметь зависимость от времени. Эффект сильно проявляет себя в нагревательных приборах и лампах накаливания, а также используется в самовосстанавливающихся предохранителях и бареттерах.

Скин-эффект вытесняет переменный электрический ток на поверхность проводника, что приводит к возрастанию сопротивления проводника от частоты тока. Несмотря на то, что он не вносит нелинейность в зависимость тока от напряжения, возникает зависимость сопротивления от частоты. Это также приводит к искажению формы электрических сигналов с широким спектром.

Расширения закона Ома[править]

Закон Ома для реактивного сопротивления[править]

При протекании тока через такие элементы, как конденсаторы и катушки индуктивности закон Ома для мгновенных значений тока и напряжения не выполняется. Однако, если рассматривать действие на такие элементы напряжения, подчиняющемуся гармоническому закону:

в силу их линейности ток также будет гармоническим, но со сдвигом фазы :

При этом амплитудные значения напряжения и тока будут пропорциональны (при отрицательном сдвиге фаз её значение будет отрицательным), так что можно можно написать для них следующую формулу:

где коэффициент пропорциональности называется реактивным сопротивлением. Его можно вычислить по формулам:

для катушки с индуктивностью и

для конденсатора с ёмкостью ,

где — частота в герцах, — угловая частота гармонического сигнала.

Закон Ома для комплексных амплитуд[править]

метода комплексных амплитуд позволяет обобщить действие закона Ома на цепи обладающие как активным, так и реактивным сопротивлением. Для этого вводятся и — комплексные напряжение и ток, выражающие амплитуду и фазу, и комплексное сопротивление , где — активное сопротивление, — реактивное сопротивление, — мнимая единица, и сам закон принимает форму:

Ту же связь можно аналогично выразить через комплексную проводимость , где — активная проводимость и — реактивная проводимость:

laws ohm — el-pths/w Wiki

#Закон Ома

(все остальные законы)

Этот закон всех путает. Школьники бодро отвечают «напряжение равно силе тока умноженной на сопротивление». И потом спрашивают «чему равно сопротивление светодиода» или подобную ересь.

Важно понимать: в отличие от законов Кирхгоффа, этот закон не является универсальным правилом. Это экспериментальное наблюдение, а не закон. Так что он работает очень редко — фактически, только для резисторов, и то если они не нагреваются.

###Суть закона Ома

Мы помним, что напряжение — это разница «давлений» зарядов (например, электронов) между двумя точками. А ток — это количество протекающих между ними зарядов. Пусть у нас есть источник напряжения — например, розетка в стене. В нее можно включить различные приборы:

• ничего
• лампочку
• электрочайник
• кусок провода (не надо так делать!)

Во всех случаях нам интересно, какой же ток потечет через тот или иной прибор?

Георг Симон Ом путем экспериментов выяснил: для простых проводников возникающий ток пропорционален прилагаемому напряжению. То есть, чем больше напряжение — тем пропорционально больше ток.

Меру этой пропорциональности мы называем сопротивлением проводника. Величина обратная сопротивлению — проводимость.

Например, если в розетку включено «ничего», то мы понимаем что это «ничего» — а точнее воздушный промежуток — обладает огромным сопротивлением (т.е. никакой проводимостью). В то же время сопротивление чайника меньше, чем сопротивление электролампочки — поэтому через чайник течет больший ток. Сопротивление простого провода совсем мало, поэтому ток будет гигантским и сразу выбьет предохранители.

Еще раз повторим — в электронных схемах закон Ома имеет смысл только для резисторов (и изредка — некоторых участков с резистивными свойствами).

В частности если мы рассматриваем светодиод — то мы вспоминаем — напряжение на нем почти постоянно. Если задать напряжение хоть немного меньше чем надо — то ток течь не будет. Если задать немного больше — то ток будет гигантским и сожжет светодиод. Т.е. ток через светодиод не пропорционален напряжению и значит говорить о законе Ома и сопротивлении светодиода бессмысленно.

###Зачем же нам нужен закон Ома?

Дело в том что в электронных схемах нам почти везде нужно формировать некоторые конкретные, заданные напряжения и токи. И для этого мы активно используем резисторы. А раз мы используем резисторы, то мы можем считать на них связь напряжений и токов по закону Ома.

Самый типичный пример — упомянутое подключение светодиодов. Слева на картинке мы видим реальную «крутую» вольт-амперную характеристику светодиода. Посредине показана упрощенная. При увеличении напряжения на нем, ток вырастает очень резко.

Однако подключим последовательно светодиоду резистор. Теперь напряжение подключается не прямо к светодиоду — часть напряжения будет тратиться на резисторе. Чем больший ток — тем больше будет пропадать на нем. Таким образом светодиод не сможет запустить «гигантский» ток — резистор как бы «отберет» у него все напряжение. Поэтому они «договорятся». Мы расчитываем эту договоренность обычно так:

• рабочее напряжение на светодиоде примерно постоянно, пусть 1.5 Вольт

• вычтем его из напряжения питания, чтобы получить напряжение на резисторе (по 2-му закону Кирхгоффа)

• разделим на сопротивление и найдем ток (мы пользуемся тем что напряжение на светодиоде от этого тока почти не зависит)

  Iсд = Ur / R = (Uп — Uсд) / R

Глава 5. Закон Ома . Введение в электронику

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Описать три основных части цепи.

• Описать три типа конфигурации цепей.

• Описать, как можно изменять ток в цепи.

• Дать определение закона Ома, связывающего ток, напряжение и сопротивление.

• С помощью закона Ома находить ток, напряжение и сопротивление в последовательных, параллельных и последовательно-параллельных цепях.

• Описать отличия протекания полного тока в последовательных и параллельных цепях.

• Описать различия полного падения напряжения в последовательных и параллельных цепях.

• Описать различия полного сопротивления в последовательных и параллельных цепях.

Закон Ома определяет связь трех фундаментальных величин: силы тока, напряжения и сопротивления. Он утверждает, что сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

В этой главе исследуется закон Ома и его применение к электрическим цепям. Некоторые понятия были введены в предыдущих главах.

5–1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Как установлено ранее, ток течет из точки с избытком электронов в точку с дефицитом электронов. Путь, по которому следует ток, называется электрической цепью. Все электрические цепи состоят из источника тока, нагрузки и проводников. Источник тока обеспечивает разность потенциалов, которая позволяет течь току. Источником тока может быть батарея, генератор или другое устройство, описанное в главе 3. Нагрузка оказывает сопротивление протеканию тока. Это сопротивление может быть высоким или низким, в зависимости от назначения цепи. Ток в цепи течет через проводники от источника к нагрузке. Проводник должен легко отдавать электроны. В большинстве проводников используется медь.

Путь электрического тока к нагрузке может проходить через три типа цепей: последовательную цепь, параллельную или последовательно-параллельную цепи. Последовательная цепь (рис. 5–1) предоставляет току только один путь от источника к нагрузке. Параллельная цепь (рис. 5–2) предоставляет более одного пути для протекания тока. Она позволяет источнику прикладывать напряжение к более чем одной нагрузке. Она также позволяет подключить несколько источников тока к одной нагрузке. Последовательно-параллельная цепь (рис. 5–3) является комбинацией последовательной и параллельной цепей.

Рис. 5–1. Последовательная цепь предоставляет один путь для протекания тока.

Рис. 5–2. Параллельная цепь предоставляет более чем один путь для протекания тока.

Рис. 5–3. Последовательно-параллельная цепь является комбинацией последовательной и параллельной цепей.

Ток электронов в электрической цепи течет от отрицательного вывода источника тока через нагрузку к положительному выводу источника тока (рис. 5–4). Пока этот путь не нарушен, цепь замкнута и ток течет (рис. 5–5). Однако если прервать путь, цепь станет разомкнутой и ток не сможет по ней идти (рис. 5–6).

Рис. 5–4. Ток электронов течет по электрической цели от отрицательного вывода источника тока через нагрузку и возвращается в источник тока через положительный вывод.

Рис. 5–5. Замкнутая цепь обеспечивает прохождение тока.

Рис. 5–6. Разомкнутая цепь не поддерживает прохождение тока.

Силу тока в электрической цепи можно изменять, изменяя либо приложенное напряжение, либо сопротивление цепи. Ток изменяется в таких же пропорциях, что и напряжение или сопротивление. Если напряжение увеличивается, то ток также увеличивается.

Если напряжение уменьшается, то ток тоже уменьшается (рис. 5–7). С другой стороны, если сопротивление увеличивается, то ток уменьшается. Если сопротивление уменьшается, то ток увеличивается (рис. 5–8). Это соотношение между напряжением, силой тока и сопротивлением называется законом Ома.

Рис. 5–7. Силу тока в электрической цепи можно изменять путем изменения напряжения.

Рис. 5–8. Силу тока в электрической цепи также можно изменять путем изменения сопротивления цепи.

5–1. Вопросы

1. Каковы три основные части электрической цепи?

2. Дайте определения:

а. Последовательной цепи

б. Параллельной цепи

в. Последовательно-параллельной цепи

3. Нарисуйте схему цепи, показывающую, как ток будет течь по цепи. (Используйте стрелки для указания направления тока).

4. В чем отличие разомкнутой цепи от замкнутой цепи?

5. Что происходит с током в электрической цепи при увеличении напряжения? При уменьшении напряжения? При увеличении сопротивления? При уменьшении сопротивления?

5-2. ЗАКОН ОМА

Закон Ома или соотношение между силой тока, напряжением и сопротивлением был открыт Георгом Омом в 1827 году. Закон Ома утверждает, что ток в электрической цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению цепи. Это может быть выражено следующим образом:

или

I = U/R,

где I = ток в амперах,

Е = напряжение в вольтах,

R = сопротивление в омах.

Если две из этих трех величин известны, то третья всегда может быть определена.

_{ПРИМЕР. Какова сила тока в цепи, изображенной на рис. 5–9?}

_{Рис. 5–9}

_Дано:

_{ЕТ = 12 В; RT = 1000 Ом.}

_{IT =?}

_{Решение:}

_{IT = ЕТ/RT = 12/1000}

_{IT = 0,012 А или 12 мА.}

_{ПРИМЕР. Какое надо приложить напряжение к цепи на рис. 5-10, чтобы получить ток 20 миллиампер?}

_{Рис. 5-10}

_Дано:

_{IT = 20 мА = 0,02 А}

_{RT = 1,2 кОм = 1200 Ом.}

_{ЕТ =?}

_{Решение:}

_{IT = ЕТ/RT = ЕТ/1200 = 0,02}

 _{ЕТ = (0,02)(1200)}

 _{ЕТ = 24 В.}

_{ПРИМЕР. Каково должно быть значение сопротивления в цепи, изображенной на рис. 5-11, чтобы получить ток 2 А?}

_{Рис. 5-11}

_Дано:

_{IT = 2 А;  ЕТ = 120 В}

_{RT =?}

_{Решение:}

_{IT = ЕТ/RT}

_2 = 120/RT

_{120/2 = RT}

_{RT = 60 Ом}

5–2. Вопросы

1. Запишите закон Ома в виде формулы.

2. Какова величина тока в цепи сопротивлением 2400 ом, к которой приложено напряжение 12 вольт?

3. Какова должна быть величина сопротивления для того, чтобы ограничить ток 20 миллиамперами при приложенном напряжении 24 вольта?

4. Какое напряжете необходимо приложить, чтобы обеспечить силу тока 3 ампера через сопротивление 100 ом?

5-3. ПРИМЕНЕНИЕ ЗАКОНА ОМА

В последовательной цепи (рис. 5-12) через всю цепь течет один и тот же ток.

I_T = I_R1 = I_R2 = I_R3 =… = I_Rn

Рис. 5-12. В последовательной цепи сила тока одинакова во всей цепи.

Полное напряжение, приложенное к последовательной цепи, равно сумме падений напряжений на отдельных нагрузках (сопротивлениях) цепи.

E_T = E_R1 + E_R2 + E_R3 + … + E_Rn

Общее сопротивление последовательной цепи равно сумме отдельных сопротивлений цепи.

R_T = R₁ + R₂ + R₃ + … + R_n

В параллельной цепи (рис. 5-13) одинаковое напряжение прикладывается к каждой ветви цепи.

E_T = E_R1 = E_R2 = E_R3 = … = E_Rn

Рис. 5-13. В параллельной цепи токи делятся между ветвями цепи и складываются при возвращении в источник тока.

Полный ток в параллельной цепи равен сумме токов отдельных ветвей цепи.

Величина обратная полному сопротивлению равна сумме обратных величин сопротивлений отдельных ветвей.

1/R_T = 1/R₁ + 1/R₂ + 1/R₃ +… + 1/R_n

Общее сопротивление параллельной цепи всегда меньше, чем наименьшее из сопротивлений отдельных ветвей.

Закон Ома утверждает, что ток в цепи (последовательной, параллельной или последовательно-параллельной) прямо пропорционален напряжению и обратно пропорционален сопротивлению.

При определении неизвестных величин в цепи, следуйте следующим правилам:

I = E/R

1. Нарисуйте схему цепи и обозначьте все известные величины.

2. Проведите расчеты для эквивалентных цепей и перерисуйте цепь.

3. Рассчитайте неизвестные величины.

Помните: закон Ома справедлив для любого участка цепи и может применяться в любой момент. По последовательной цепи течет один и тот же ток, а к любой ветви параллельной цепи приложено одинаковое напряжение.

_{ПРИМЕР. Чему равен полный ток в цепи, изображенной на рис. 5-14?}

_{Рис. 5-14}

_Дано:

_{ET = 12 В}

_{R1 = 560 Ом; R2 = 680 Ом; R3 = 1 кОм = 1000 Ом.}

_{IT =?; RT =?}

_{Решение:} 

_{Сначала вычислим общее сопротивление цепи:}

_{RT = R1 + R2 + R3}

_{RT = 560 + 680 + 1000 = 2240 Ом.}

_{Нарисуем эквивалентную цепь. См. рис. 5-15.}

_{Рис. 5-15} 

_{Теперь вычислим полный ток:}

_{IТ = EТ/RТ = 12/2240}

_{IТ = 0,0054 А или 5,4 мА} 

_{ПРИМЕР. Каково падение напряжения на резисторе R2 в цепи, изображенной на рис. 5-16?}

_{Рис. 5-16}

_Дано:

_{EТ = 48 В}

_{R1 = 1,2 Ком = 1200 Ом; R2 = 3,9 Ком = 3900 Ом; R3 = 5,6 кОм = 5600 Ом.}

_{IT =?; RT =?}

_{Решение:}

_{Сначала вычислим общее сопротивление цепи:}

_{RT = R1 + R2 + R3}

_{RT = 1200 + 3900 + 5600 = 10700 Ом.}

_{Нарисуем эквивалентную цепь. См. рис. 5-17.}

_{Рис. 5-17}

_{Теперь вычислим полный ток:}

_{IТ = EТ/RТ = 48/10700}

_{IТ = 0,0045 А или 4,5 мА} 

_{Вспомним, что в последовательной цепи один и тот же ток течет через всю цепь. Следовательно, IR2 = IT.}

_{IR2 = ER2/R2} 

_{0,0045 = ER2/3900}

_{Е2 = (0,0045)(3900)}

_{Е2 = 17,55 В.}

_{ПРИМЕР. Чему равно значение R2 в цепи, изображенной на рис. 5-18?}

_{Рис. 5-18} 

_{Сначала найдем ток, протекающий через R1 и R2. Поскольку к каждой ветви параллельной цепи приложено одинаковое напряжение, напряжение на каждой ветви равно напряжению на источнике тока и равно 120 вольт.}

_Дано:

_{ER1 = 120 В; R1 = 1000 Ом} 

_{IR1 =?}

_{Решение:}

_{IR1 = ER1/R1 = 120/1000}

_{IR1 = 0,12 А} 

_{* * *}

_Дано:

_{ER3 = 120 В; R3 = 5600 Ом} 

_{IR3 =?}

_{Решение:}

_{IR3 = ER3/R3}

_{IR3 = 0,021 А} 

_{В параллельной цепи полный ток равен сумме токов в ветвях.}

_Дано:

_{IT = 0,200 А; IR1 = 0,120 А; IR3= 0,021 А}

_{IR2 =?}

_{Решение:}

_{IT = IR1 + IR2 + IR3}

_{0,200 = 0,12 + IR2 + 0,021}

_{0,200 = 0,141 + IR2}

_{0,200 — 0,141 = IR2}

_{0,059 A = IR2.}

_{Теперь с помощью закона Ома можно найти величину резистора R2.}

_Дано:

_{IR2 = 0,059 А; ER2 = 120 B}

_{R2 =?}

_{Решение:}

_{IR2 =  ER2/R2}

_{0,059 = 120/R2} 

_{R2 = 120/0,059}

_{R2 = 2033,9 Ом}

_{ПРИМЕР. Чему равен ток через резистор R3 в цепи, изображенной на рис. 5-19?}

_{Рис. 5-19}

_{Сначала определим эквивалентное сопротивление (RA) резисторов R1 и R2.}

_Дано:

_{R1 = 1000 Ом; R2 = 2000 Ом}

_{RА =?}

_{Решение:}

_{1/RА = 1/R1 + 1/R2}

_{1/RА = 1/1000 + 1/2000}

_{RА = 2000/3 = 666,67 Ом}

_{Теперь найдем эквивалентное сопротивление (RB) резисторов R4, R5 и R6. Сначала найдем общее сопротивление (Rs) последовательно соединенных резисторов R5 и R6.}

_Дано:

_{R5 = 1500 Ом; R6 = 3300 Ом}

_{Rs =?}

_{Решение:}

_{Rs = R5 + R6}

_{Rs = 1500 + 3300 = 4800 Ом.}

_{* * *}

_Дано:

_{R4 = 4700 Ом; Rs = 4800 Ом}

_{RB =?}

_{Решение:}

_{1/RB = 1/R4 + 1/Rs}

_{1/RB = 1/4700 + 1/4800}

_{(В этом случае общий знаменатель найти сложно. Будем использовать десятичные дроби.)}

_{1/RB = 0,000213 + 0,000208}

_{RB = 1/ 0,000421 = 2375,30 Ом}

_{Нарисуем эквивалентную цепь, подставляя RA и RB, и найдем полное сопротивление последовательной эквивалентной цепи. См. рис. 5-20.}

Рис. 5-20

_Дано:

_{RA = 666,67 Ом; R3 = 5600 Ом; RB = 2735,30 Ом}

_{RT =?}

_{Решение:}

_{RT = RA + R3 + RB}

_{RT = 666,67 + 5600 + 2375,30}

_{RT = 8641,97 Ом.}

_{Теперь с помощью закона Ома найдем общий ток в эквивалентной цепи.}

_Дано:

_{ET = 120 В; RT = 8641,97 Ом}

_{IT =?}

_{Решение:}

_{IT =  ET/RT = 120/8641,97}

_{IT = 0,0139 А или 13,9 мА.}

_{В последовательной цепи по всей цепи протекает одинаковый ток. Следовательно, ток, протекающий через R3 равен общему току в цепи.}

_{IR3 = IT = 13,9 мА}

5–3. Вопросы

1. Запишите формулы, необходимые для определения полного тока в последовательной и параллельной цепях, когда известны токи, протекающие через отдельные компоненты.

2. Запишите формулы, необходимые для определения полного напряжения в последовательной и параллельной цепях, когда известны падения напряжения на отдельных участках.

3. Запишите формулы для определения полного сопротивления последовательной и параллельной цепей, когда известны отдельные сопротивления.

4. Запишите формулы для вычисления полного тока, напряжения или сопротивления в последовательной или параллельной цепях, когда хотя бы две из трех величин (ток, напряжение и сопротивление) известны.

5. Чему равен общий ток в цепи, изображенной на рис. 5-21?

Рис. 5-21

Е_т= 12 В

R₁ = 500 Ом; R₂ = 1200 Ом; R₃ = 2200 Ом.

I_T =?

РЕЗЮМЕ

• Электрическая цепь состоит из источника тока, нагрузки и проводника.

• Путь тока в электрической цепи может быть последовательным, параллельным или последовательно-параллельным.

• Последовательная цепь предоставляет только один путь для протекания тока.

• Параллельная цепь предоставляет несколько путей для протекания тока.

• Последовательно-параллельная цепь обеспечивает комбинацию последовательных и параллельных путей для протекания тока.

• Ток электронов протекает от отрицательного вывода источника тока через нагрузку к положительному выводу источника тока.

• Протекающий в электрической цепи ток можно изменять путем изменения либо напряжения, либо сопротивления.

• Закон Ома связывает между собой силу тока, напряжение и сопротивление.

• Закон Ома утверждает, что сила тока в электрической цепи прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению цепи.

I = E/R

• Закон Ома применяется ко всем последовательным, параллельным и последовательно-параллельным цепям.

• Для определения неизвестных величин в цепи необходимо:

— Нарисовать схему цепи и обозначить все величины.

— Провести вычисления для эквивалентных цепей и перерисовать цепь.

— Вычислить все неизвестные величины.

Глава 5. САМОПРОВЕРКА

С помощью закона Ома найдите неизвестные величины в следующих примерах:

1. I =?; E = 9 В; R = 4500 Ом.

2. I = 250 мА; E =?; R = 470 Ом.

3. I = 10 A; E = 240 В; R =?

4. Найдите полный ток в изображенных цепях.

Электродвижущая сила — Вики

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил (то есть любых сил, кроме электростатических и диссипативных), действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1][2].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:

E=∮LE→ex⋅dl→{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot d{\vec {l}}},

где dl→{\displaystyle d{\vec {l}}} — элемент контура.

Несмотря на наличие слова «сила» в наименовании понятия, электродвижущая сила не является одной из сил в физике и не имеет размерности силы.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.

ЭДС и закон Ома

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид^[1]:

φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}

где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи^[1]:

E=IR,{\displaystyle {\mathcal {E}}=IR,}

где теперь R{\displaystyle R} — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:

E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}

ЭДС источника тока

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:

φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}

где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.

Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить

φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}

Из полученного соотношения следуют два вывода:

1. Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
2. В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи^[1].

ЭДС индукции

Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}

где Φ{\displaystyle \Phi } — поток магнитного поля через указанную поверхность. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.

Неэлектростатический характер ЭДС

Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектростатической природы, преодолевающей силу электрического отталкивания

Как показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу» то есть от положительного полюса источника тока к отрицательному полюсу, внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электростатической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектростатической природы (центробежная сила, сила Лоренца, силы химической природы, сила со стороны вихревого электрического поля) которая бы преодолевала силу со стороны электростатического поля. Диссипативные силы, хотя и противодействуют электростатическому полю, не могут заставить ток течь в противоположном направлении, поэтому они не входят в состав сторонних сил, работа которых используется в определении ЭДС.

Сторонние силы

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца^[3].

См. также

Примечания

Закон Ома

Зако́н О́ма — це твердження про пропорційність сили струму в провіднику прикладеній напрузі, справедливе для металів і напівпровідників при не надто великих прикладених напругах. Якщо для елемента електричного кола справедливий закон Ома, то цей елемент має лінійну вольт-амперну характеристику.

Зміст

Закон Ома справедливий для провідників, виготовлених із матеріалів, у яких є вільні носії заряду: електрони провідності, дірки або іони. Якщо до таких провідників прикласти напругу, то в провідниках виникає електричне поле, що змушуватиме носії заряду рухатися. Під час цього руху носії заряду розганяються і збільшують свою кінетичну енергію. Проте зростання енергії носіїв заряду обмежене зіткненнями між собою, зі зміщеними з положень рівноваги, внаслідок теплового руху, атомами матеріалу. Під час таких зіткнень, надлишкова кінетична енергія носіїв струму передається коливанням кристалічної ґратки, та виділяється у вигляді тепла.

В середньому, носії заряду мають швидкість, яка визначається частотою зіткнень. Математичною характеристикою таких зіткнень є час розсіяння і зв’язана із ним довжина вільного пробігу носіїв заряду. Обчислення показують, що середня швидкість носіїв заряду пропорційна прикладеному електричному полю, а отже й напрузі.

Таким чином, у матеріалах із вільними носіями заряду сила струму пропорційна напруженості електричного поля. Проходження струму крізь матеріал супроводжується виділеннями тепла. Докладніше про це — у статті закон Джоуля — Ленца.

У сильних електричних полях закон Ома часто не справджується навіть для гарних провідників, оскільки фізична картина розсіювання носіїв заряду змінюється. Розігнаний до великої швидкості носій заряду може іонізувати нейтральний атом, породжуючи нові носії заряду, які теж у свою чергу роблять внесок в електричний струм. Електричний струм різко, іноді лавиноподібно, зростає.

У деяких матеріалах за низьких температур процеси розсіювання носіїв заряду гасяться завдяки особливій взаємодії між ними та коливаннями кристалічної ґратки — фононами. В такому разі виникає явище надпровідності.

В електротехніці прийнято записувати закон Ома в інтегральному вигляді

U=I∗R{\displaystyle U=I*R}

де U — прикладена напруга, I — сила струму, R — електричний опір провідника.

При аналізі електричних схем три еквівалентні вирази закону Ома використовуються як взаємозамінні:

I=U/R{\displaystyle I=U/R} абоU=I∗R{\displaystyle U=I*R} абоR=U/I{\displaystyle R=U/I}

Проте опір є характеристикою провідника, а не матеріалу, й залежить від довжини та поперечного перерізу провідника. Тому в фізиці застосовують закон Ома у диференціальному вигляді:

j=σ⋅E{\displaystyle \mathbf {j} =\sigma \cdot \mathbf {E} }

де j — густина струму, σ — питома провідність матеріалу, E — напруженість електричного поля.

Питома провідність залежить від кількості вільних носіїв заряду в провіднику і від їхньої рухливості.

Різниця потенціалів (напруга) на кінцях провідника довжиноюl{\displaystyle l} з постійною напруженістю електричного поляE{\displaystyle E} дорівнює

U=Δφ=El{\displaystyle U=\Delta \varphi =El}

Якщо провідник має площу перерізу S, то сила струму в ньому зв’язана з густиною сили струму формулою:

I=jS{\displaystyle I=jS}.

Виходячи із закону Ома в формі

j=σE{\displaystyle j=\sigma E}

і, підставляючи значенняj=I/S{\displaystyle j=I/S} таE=U/l{\displaystyle E=U/l}, отримуємо рівняння

IS=σUl{\displaystyle {\frac {I}{S}}=\sigma {\frac {U}{l}}},

або

U=lσSI=RI{\displaystyle U={\frac {l}{\sigma S}}I=RI},

де опірR{\displaystyle R} визначається через питому провідність формулою

R=lσS=ρlS{\displaystyle R={\frac {l}{\sigma S}}=\rho {\frac {l}{S}}}.

Тутρ=1/σ{\displaystyle \rho =1/\sigma } — питомий опір.

У випадку змінного струму закон Ома можна розширити, включивши в розгляд також елементи електричного кола, які характеризуються ємністю й індуктивністю. Змінний струм проходить крізь конденсатор, та випереджає за фазою напругу. В індуктивності змінний струм відстає за фазою від напруги. Проте в обох випадках амплітуда змінного струму пропорційна амплітуді прикладеної змінної напруги. Математично це можна описати, ввівши комплексні опори (імпеданси).

Тоді можна записати

U=I⋅Z{\displaystyle U=I\cdot Z}

де U — амплітуда змінної напруги, I — амплітуда змінного струму, Z — імпеданс.

В повному колі окрім опору навантаження є ще джерело живлення, яке має власний внутрішній опір. Сила струму в ньому визначається формулою

I=ER+r{\displaystyle I={\frac {\mathcal {E}}{R+r}}}

деE{\displaystyle {\mathcal {E}}} — електрорушійна сила,R{\displaystyle R} — опір навантаження,r{\displaystyle r} — внутрішній опір джерела струму.

Георг Ом проводив дослідження протікання струму в електричному колі на початку XIX століття. На шляху до встановлення закономірності йому довелося подолати чимало перешкод. Для проведення досліджень і встановлення закономірності необхідно було мати вимірювальні прилади, джерела струму із стандартними властивостями, що не змінювалися б з часом, стандартні провідники. Усе це довелося створити або вдосконалити.

Діаграма, що допомагає запам’ятати закон Ома. Потрібно закрити шукану величину, і два інших символи дадуть формулу для її обчислення

Було добре відомо, що магнітна дія струму змінюється при зміні елементів замкнутого кола: джерела електричного струму та провідників, які з’єднують полюси джерела. Чи існує закономірність, яка пов’язує магнітну дію струму з величинами, які характеризують елементи замкнутого кола? Мабуть, таке питання виникало у багатьох дослідників.

Легко уявити обставини, в яких почалися пошуки інтуїтивно відчуваної закономірності. Поняття напруги, спаду напруги, електрорушійної сили ще не були сформульовані. Точаться суперечки щодо механізму дії гальванічних елементів, незрозуміле взаємовідношення електростатичних сил та сил, які виникають при протіканні струму; нарешті невідомо що таке рухома електрика та електрика в спокої. Ом, наприклад, називає у своїх перших працях електричний струм «контактною електрикою».

Ом керувався наступною ідеєю. Якщо над провідником, яким проходить струм, підвісити на пружній нитці магнітну стрілку, то кут повороту стрілки дасть інформацію про струм, точніше про його зміни при варіаціях елементів замкнутого кола. Ом повернувся до ідеї Кулона й сконструював крутильні терези. Магнітна стрілка виявилась точним і чуттєвим гальванометром.

В перших дослідах, результати яких Ом опублікував у 1825 році, спостерігалась «втрата сили» (зменшення кута відхилення стрілки) із збільшенням довжини провідника, підключеного до полюсів вольтового стовпа (поперечний переріз провідника був постійним). Оскільки не було одиниць вимірювання, довелося вибрати еталон — «стандартний дріт». Як залежна змінна фігурувало зменшення сили, що діяла на магнітну стрілку. Досліди виявили закономірне зменшення цієї сили при збільшенні довжини провідника. Функція отримала аналітичний вираз, але Ом не претендував на встановлення закономірності тому, що гальванічний елемент не давав постійної електрорушійної сили (е.р.с.).

Ом ще не розумів значення внутрішнього опору джерела струму. Вольтів стовп, з яким він експериментував, мав внутрішній опір, який значно перевищував зовнішній. Щоб отримати показники, достатні для оцінки відхилення магнітної стрілки «гальванометра», звичайно ж доводилося зводити до мінімуму опір зовнішньої частини кола, який визначався, по суті, коротким відрізком металевого провідника. Зрозуміло, що в такій ситуації точність встановлення залежності сили струму від опору металевих провідників була недостатньою. До того ж внутрішній опір вольтового стовпа був далеко не постійним.

Звичайно ж потрібно дивуватися тому, що закономірність для описаної ситуації була отримана вірно, хоча б у першому наближенні. Проте до встановлення закону було ще далеко.

Успіх наступних експериментів Ома вирішило відкриття термоелектрики. Німецький фізик Томас Йоганн Зеєбек брав участь у великій дискусії між прихильниками хімічної та контактної теорії. Він дотримувався думки Вольта, що е.р.с. виникає при контакті речовини незалежно від наявності хімічного реагенту, та шукав доказів. У 1822 році Зеебек виготовив спіраль з мідної смужки, всередині якої закріпив компас. Це був по-сучасному гальванометр з невеликим внутрішнім опором. Кінці спіралі приєднувались до різних металевих пластинок. Коли було взято бісмутовий диск і покладено на мідний, магнітна стрілка здригнулася. Ефекту не було, якщо диск брали не рукою, а за допомогою предмета, який мав кімнатну температуру.

Врешті-решт Зеебек з’ясував, що ефект пропорційний різниці температур двох контактів.

Одним з найважливіших чинників відкриття було те, що в руках експериментаторів з’явилося джерело, е.р.с. якого можна було плавно регулювати і підтримувати постійною.

Ом використав термопару бісмут-мідь, один спай поміщався в лід, інший — у окріп. Чутливість гальванометра довелося звичайно ж збільшити. Процес вимірів являв собою наступне: вісім експериментальних провідників почергово вмикалися в коло. В кожному випадку фіксувалося відхилення магнітної стрілки. Результат досліду Ом виразив такою формулою:

X=ab+x{\displaystyle X={\frac {a}{b+x}}}, де

• Х — сила магнітної дії провідника,
• а — стала, яка визначала е.р.с. термопари,
• х — довжина провідника.
• b — константа, яка визначала провідність всього кола.

Це був другий крок. Тут ще немає звичних нам понять сили струму, е.р.с., зовнішнього, внутрішнього опору. Вони відграняться поступово.

В наступній праці (1826 рік) Ом вводить поняття «електроскопічної сили», користується поняттям сили струму та записує закон для ділянки кола вже у формі, дуже близькій до сучасної:

X=kwal{\displaystyle X={\frac {kwa}{l}}}, де

• Х — сила струму,
• k — провідність,
• w — поперечний переріз провідника,
• а — електроскопічна сила,
• l — довжина провідника.

Незважаючи на переконливі дані експериментів та чіткі теоретичні основи, закон Ома протягом майже десяти років лишався маловідомим. Достатньо сказати, що Фарадей також не підозрював про існування закону; при описанні дослідів він був змушений вдаватися до перерахунку даних про елементи кола: кількість пластин в батареях, їхні розміри, склад електроліту, довжина, діаметр та матеріал дроту.

Омові довгий час безуспішно доводилося доводити місцевим вченим, що ним відкрито важливу істину. Ввести закон в фізику виявилося набагато складніше, ніж відкрити. І це закономірно. Фізичне мислення на той час було ще не готовим до сприйняття загальної закономірності (тим більше з рук провінційного вчителя).

Перевірка закону Ома тривала впродовж майже всього XIX століття. В 1876 році спеціальний комітет Британської асоціації провів точну перевірку, вказану Максвеллом. Справедливість закону Ома для рідких провідників було підтверджено Коном, Фітцтжеральдом та Троутоном.

• І.М. Кучерук, І.Т. Горбачук, П.П. Луцик (2006). Загальний курс фізики: Навчальний посібник у 3-х т. Т.2. Електрика і магнетизм. Київ: Техніка.
• С.Е. Фріш і А.В. Тіморєва (1953). Курс загальної фізики. Том II. Електричні і електромагнітні явища. Київ: Радянська школа.
• Сивухин Д.В. (1977). Общий курс физики. т III. Электричество. Москва: Наука.

Закон Ома для неоднородного участка цепи

На практике видно, что для поддержания стабильного тока в замкнутой цепи необходимы силы принципиально иной природы, нежели кулоновские, тогда наблюдается случай, когда на участке цепи на свободные электрические заряды одновременно действуют как силы электрического поля, так и сторонние силы (любые неконсервативные силы, действующие на заряд, за исключением сил электрического сопротивления (кулоновских сил)). Такой участок называется неоднородным участком цепи. На рисунке ниже приведен пример такого участка.

Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил:

Сформулируем закон Ома для неоднородного участка цепи — Сила тока прямо пропорциональна напряжению на этом участке и обратно пропорциональна его полному сопротивлению:

– формула закона Ома для неоднородного участка цепи.

Где

• I – сила тока,
• U12 – напряжение на участке,
• R – полное сопротивление цепи.

Работа на неоднородном участке цепи

Разность потенциалов характеризует работу силы электрического поля по переносу единичного положительного заряда (q) из точки 1 в точку 2:

— где φ1 и φ 2 – потенциалы на концах участка.

ЭДС характеризует работу сторонних сил по переносу единичного положительного заряда точки 1 в точку 2: — где ε12 – ЭДС, действующая на данном участке, численно равна работе по перемещению единичного положительного заряда вдоль контура.

Напряжение на участке цепи представляет собой суммарную работу сил ЭП и сторонних сил:

Тогда закон Ома примет вид:

ЭДС может быть как положительной, так и отрицательной. Это зависит от полярности включения ЭДС в участок. Если внутри источника тока обход совершается от отрицательного полюса к положительному, то ЭДС положительная (см. рисунок). Сторонние силы при этом совершают положительную работу. Если же обход совершается от положительного полюса к отрицательному, то ЭДС отрицательная. Проще говоря, если ЭДС способствует движению положительных зарядов, то ε>0, иначе ε

Решение задач по закону ому для неоднородного участка цепи

Определить ток, идущий по изображенному на рисунке участку АВ. ЭДС источника 20 В, внутреннее сопротивление 1 Ом, потенциалы точек А и В соответственно 15 В и 5 В, сопротивление проводов 3 Ом.

Дано:	Решение:
ε = 20 В r = 1 Ом φ1 = 15 В φ2 = 5 В R = 3 Ом	Запишем закон Ома для неоднородного участка цепи — Считая, что точка А начало участка, а точка В – конец, возьмем ЭДС со знаком «минус» и, подставив исходные данные, получим Знак «минус» говорит о том, что ток идет от точки В к точке А, от точки с меньшим потенциалом к точке с большим, что обычно для источников тока. Ответ: –2,5 А

Два элемента соединены «навстречу» друг другу, как показано на рисунке. Определить разность потенциалов между точками А и В, если ε1 = 1,4 В, r1 = 0,4 Ом, ε2 = 1,8 В, r2 = 0,6 Ом.

Дано:	Решение:
ε1 = 1,4 В r1 = 0,4 Ом ε2 = 1,8 В r2 = 0,6 Ом	Запишем закон Ома для неоднородного участка цепи — Разобьём схему на два участка: АЕ2В и ВЕ1А. Тогда получим — для первого участка цепи, — для второго участка. Ток на участках один и тот же, то есть можем приравнять правые части уравнений. Знак «минус» показывает, что потенциал точки В выше, чем потенциал точки А. Ответ: -1,56 В.

Закон Ома — що це таке, визначення та поняття — 2021

Закон Ома — це наукова формула, яка встановлює залежність між струмом, напругою та опором в електричному колі.

Електричні ланцюги завжди мають однакову роботу, струм залишає джерело живлення і проходить через всю ланцюг. Закон Ома вимірює те, як пов’язані три змінні, задіяні в цій операції.

Формула була розроблена фізиком і математиком Георгом Саймоном Омом у 19 столітті. У своїх дослідженнях він виявив електричний опір. Отже, в результаті і на його честь це вимірюється в Омах.

Компоненти формули

Три змінні, задіяні у формулі, розробленій Омом, є наступними:

• Поточний: «Це фізична величина, яка виражає кількість електрики, яка протікає через провідник за одиницю часу». Вимірюється в амперах
• Напруга: Це різниця, яка існує між електричним зарядом, який залишає джерело і з яким він нарешті досягає кінця ланцюга. Він виражається у вольтах і є фіксованою величиною.
• Витривалість. Це була змінна, виявлена ​​Омом, і це «складність, якій ланцюг протистоїть проходженню струму». Іншими словами, коли електричний заряд проходить через провідний матеріал ланцюга, він «сповільнюється», оскільки це і є опір. Вони вимірюються в Омах.

Формула закону Ома

Формула закону Ома говорить, що струм дорівнює напрузі, поділеній на опір.

Наслідки, які з цього випливають, полягають у тому, що чим вище напруга і чим менший опір, тим більша інтенсивність струму, тим більше число підсилювачів. І чим більший опір і чим менша напруга, тим менший електричний струм. Завдяки простоті формули, знаючи дві частини інформації, ми можемо знати і третю.

Таким чином, за першою формулою, знаючи струм і опір, ми можемо отримати напругу. А в правому, знаючи напругу і струм, можна отримати значення інтенсивності.

Приклад

Якщо ми маємо електричний прилад, напруга якого становить 120 В, а опір — 40 Ом. Яка інтенсивність струму?

1. I = V / R Нам потрібна формула закону Ома.
2. I = 120/40 Ми вкладаємо у формулу значення, які нам дав вислів.
3. 120/40 = 3 Ми проводимо розподіл за допомогою 3А (ампер), що є рішенням проблеми.

Процес буде однаковим, залежно від змінної, яку ми повинні очистити, значення підставляються у формулу і вона виконується.

Ви допоможете розвитку сайту, поділившись сторінкою з друзями

Резистивный электрический поток — закон Ома

Движущийся заряд чувствует сопротивление

Когда электрический заряд движется через материал, он обычно испытывает сопротивление, которое имеет тенденцию противодействовать движению, возникающее из-за их взаимодействия с другими зарядами в материале, движущемся термически.*

Исходя из нашего опыта работы с силами сопротивления, мы не можем быть уверены, зависит ли сопротивление, ощущаемое движущимся зарядом, от скорости (например, трение), пропорционально скорости (например, вязкость) или пропорционально квадрату скорости (например, сопротивление ).Во многих ситуациях кажется, что сила сопротивления, которую ощущает движущийся заряд, больше похожа на вязкость — пропорциональна скорости. Мы увидим, что предположение о том, что это то, на что похоже сопротивление, эквивалентно закону Ома — соотношению, которое очень хорошо выполняется для многих систем.{net} = qE — bv = 0$$

или

$$qE = bv.$$

Закон Ома

Теперь рассмотрим цилиндр, состоящий, скажем, из ионов и электронов, на который мы накладываем электрическое поле. Ионы будут реагировать, возможно, в 120 000 раз меньше, чем электроны (отношение массы иона меди к массе электрона), поэтому мы можем игнорировать движение ионов.

Рассмотрим цилиндр заряда площадью поперечного сечения A и длиной $L$ с носителями заряда $q$ плотностью $n$. Чтобы получить поле E по всему объему, мы наложим разность потенциалов $ΔV$.Это даст среднее поле E

.

$$E = ΔV/L.$$

Баланс наших сил дает

$$qE = bv$$

$$qΔV/л = bv$$

Теперь мы хотим избавиться от $v$ в пользу текущей, $I$ . Напомним, что ток определяется (см. страницу, определение электрического тока) количеством заряда, пересекающего площадь в секунду, или

.

$$I = \frac{\mathrm{количество\;заряда\;площадь\;пересечения\;в\;а\;время} Δt}{Δt}$$

Поскольку $I$ = (плата за один носитель)(количество перевозчиков в единице объема) x
(площадь пересечения объема во времени $Δt$), деленная на $Δt$

$$I = \frac{qn(AvΔt)}{Δt} = qnvA$$

Таким образом, мы можем найти $v$ через $I$ как

$$v = \frac{I}{qnA}$$

Включив это в наше уравнение баланса сил, мы получим

.2nA$ является свойством конкретного цилиндра, на который мы смотрим, — его материала (который определяет, что такое $q$ , $n$ , и $b$) и его формы ( что определяет $L$ и $A$).2 нА}.$$

Результатом является мощное уравнение, Закон Ома ,

$$ΔV = IR.$$

Что это значит?

В принципе, мы можем видеть из вывода, откуда берется закон Ома. Все начинается с утверждения, что толчок (исходящий из поля E) уравновешивается сопротивлением (пропорционально v), поэтому мы поддерживаем постоянную скорость (согласно второму закону Ньютона).

Поскольку мы не можем легко создавать поля E количественно, но можем легко манипулировать потенциалом, мы выражаем это через разность потенциалов на цилиндре (сопротивлении).Поскольку мы не можем легко измерить скорость наших носителей тока, но у нас есть устройства (амперметры) для непосредственного измерения тока, удобно выразить скорость через ток.

Результат интуитивно понятен: чем больше толчок, тем больше поток; большее сопротивление для того же толчка приводит к меньшему потоку.   Это стандартное уравнение потока, управляемое градиентом, в котором изменение некоторого скалярного поля в пространстве приводит к движению чего-либо. Другие примеры включают уравнение HP, тепловой поток за счет теплопроводности и закон диффузии Фика.

Чтобы понять, каковы последствия этого, нам придется рассмотреть различные модели и установить некоторые принципы использования этого закона, чтобы помочь понять, что и куда течет.

Биолог против закона Ома инженера-электрика

Поскольку электрические резисторы в основном пассивны, инженерам-электрикам очень нравится идея сопротивления — материя сопротивляется протеканию тока. Но в биологических системах система часто регулирует свое сопротивление, чтобы активно манипулировать потоком тока.2nA}{bL}$$

$$I = GΔV$$

Это одинаково действительные формы закона Ома. (Это ничем не отличается от описания движения в терминах скорости — миль/час или ее обратной величины темпа — минут/миля. Что проще использовать, зависит от того, что вы вычисляете, и формально они полностью эквивалентны.2$, а не от $1/A$.Видите ли вы из выводов, в чем источник этого различия?

Откуда берется разница в напряжении?

Поскольку мы знали, что у нас есть постоянный ток, и поскольку мы знали, что у нас есть некоторое сопротивление, Ньютон 2 сказал нам, что мы должны иметь толкающую силу, чтобы уравновесить силу сопротивления. Мы предположили, что это вызвано полем Е, связанным с разностью потенциалов. Но откуда берется эта разность потенциалов?

Давайте рассмотрим идеализированную модель, в которой у нас есть батарея (которая создает разность потенциалов и, следовательно, электрическое поле), передающая заряды по проводу.Если провод практически не имеет сопротивления (а большинство проводов имеют очень низкое сопротивление), любые заряды, которые начинают двигаться, не замедляются. Они продолжают двигаться с постоянной скоростью. Но предположим, что теперь произошло попадание в резистивную область, как показано на рисунке ниже.

Когда движущиеся заряды (синие или + на этой диаграмме) ударяют по резистору, они чувствуют сопротивление и начинают замедляться, накапливая избыточный + заряд на переднем конце резистора. Эти избыточные заряды создают поле E в резисторе, которое вытесняет положительные заряды, оставляя дефицит +, который является избытком — зарядов.

Как только это стабилизируется (примерно за наносекунду в типичной макроскопической схеме), у нас есть слой + на одной стороне резистора и слой — на другой стороне. Это похоже на конденсатор, создающий поле E между ними, которого как раз достаточно, чтобы поддерживать движение зарядов с постоянной скоростью. (В этом нет никакой магии. Если бы не было достаточно зарядов, чтобы не дать им замедлиться, то накопилось бы больше зарядов, увеличивая поле E до тех пор, пока его не стало бы достаточно. Тогда оно больше не увеличивалось бы, и устойчивое состояние было бы учредил.)

Мы можем измерить разность напряжений на концах резистора. Если бы поле E было постоянным внутри, то его величина была бы равна

$$E = \frac{\Delta V}{\Delta x} = \frac{\Delta V}{L}$$

Хотя $E$, вероятно, непостоянно, это все равно будет среднее поле E, $\langle E \rangle$.

Единицы

 

Из закона Ома ясно, что подходящей единицей измерения сопротивления является «вольт/ампер». Эту комбинацию можно распаковать —

• вольт = Джоуль/Кулон,
• Ампер = Кулон/сек,

, поэтому единица сопротивления равна

.

• Вольт/Ампер = Джоуль*сек/Кулон ² = кг-м ² /Кл ² -с.

Поскольку «b» должно быть выражено в кг/с, чтобы bv выдавало силу (кг-м/с ² ), это соответствует нашей подробной формуле для $R$.

Эта беспорядочная комбинация имеет обозначение « Ом » и пишется с греческой заглавной буквы омега (Ω). Единицей проводимости является (конечно — что еще это может быть?) «Мхо».**

*За исключением очень особых обстоятельств, таких как металлы и некоторые другие материалы при очень-очень низких температурах, когда сопротивление потоку может исчезнуть.Это называется сверхпроводимостью.

** Увы, это уже не так. Официальный термин был изменен, так что 1 инверсный Ом официально называется Сименс.

Джо Редиш 27.02.12

Упражнение: Эксперимент по закону Ома

Цель:

Рассматривается в этой лабораторной работе:
Как электрический заряд связан с напряжением, током и сопротивлением.
Что такое напряжение, ток и сопротивление.
Что такое закон Ома и как с его помощью понять электричество.
Простой эксперимент для демонстрации этих концепций.

Основы электричества:

Приступая к изучению электричества и электротехники, полезно начать с понимания основных взаимосвязей между напряжением, током и сопротивлением. Это три основные величины, необходимые для понимания и использования электричества. Поначалу эти концепции может быть трудно понять, потому что их нельзя физически «увидеть».Мы не можем увидеть невооруженным глазом энергию, текущую по проводу, или напряжение батареи, лежащей на скамейке. Даже молния в небе, хотя и видимая, на самом деле не является обменом энергией, происходящим от облаков к земле, а нагреванием воздуха проходящей через него энергией, что вызывает вспышки света. Чтобы обнаружить эту электрическую энергию, мы должны использовать измерительные инструменты, такие как мультиметры, осциллографы и анализаторы спектра, чтобы визуализировать то, что происходит с электрическими сигналами в системе.Не бойтесь, однако, эта лабораторная работа даст вам общее представление о напряжении, токе и сопротивлении и о том, как они связаны друг с другом.

Электрический заряд:

Электричество — это движение (поток) электронов. Электроны — это атомарные частицы с отрицательным зарядом. Перемещение этих зарядов можно использовать для выполнения работы. Лампочка, вентилятор, радиоприемник, мобильный телефон и т. д. используют движение электронов для выполнения какой-либо функции. Все они работают, используя один и тот же основной источник энергии: хранение и движение электронов.

Три основных принципа этой деятельности можно объяснить с помощью электронов или, точнее, создаваемого ими заряда:

1. Напряжение – это разница в заряде (больше электронов, меньше электронов) между двумя точками в пространстве.
2. Ток – это скорость, с которой заряд (электроны) течет между двумя точками, обычно через какой-либо материал.
3. Сопротивление – это способность материала сопротивляться потоку заряда (электрическому току). Материалы с очень низким сопротивлением называются проводниками.Материалы с очень высоким сопротивлением называются изоляторами.

Итак, когда мы говорим об этих значениях, мы на самом деле описываем движение заряда и, следовательно, поведение электронов. Цепь представляет собой замкнутый контур, который позволяет заряду перемещаться из одного места в другое. Компоненты в цепи позволяют нам контролировать этот заряд и использовать его для выполнения работы.

Георг Ом был баварским ученым, изучавшим электричество. Ом начинается с описания единицы сопротивления, которая определяется током и напряжением.Итак, давайте начнем с напряжения и пойдем оттуда.

Напряжение

Мы определяем напряжение как количество потенциальной энергии между двумя точками цепи. Одна точка имеет больше заряда (электронов), чем другая. Эта разница заряда между двумя точками называется напряжением. Он измеряется в вольтах, что технически представляет собой разность потенциалов между двумя точками, которые передают один джоуль энергии на кулон заряда, прошедшего через них (не паникуйте, если этот физический жаргон не имеет смысла, на самом деле это не так). важно на данный момент).Единица «вольт» названа в честь итальянского физика Алессандро Вольта, который изобрел то, что считается первой химической батареей. Напряжение обозначается в уравнениях и схемах заглавной буквой «V».

При описании электрических свойств, таких как напряжение, ток и сопротивление, часто используется аналогия с резервуаром для воды. В этой аналогии заряд аналогичен объему воды, напряжение представлено давлением воды (глубиной воды), а ток представлен потоком воды.Итак, для этой аналогии помните:

Вода = Заправка
Давление = Напряжение
Расход = Ток

Рассмотрим резервуар для воды на определенной высоте над землей. На дне этого бака есть шланг. Давление на конце шланга может представлять собой напряжение. Вода в баке представляет собой заряд. Чем больше воды в баке, тем выше заряд и тем больше давление измеряется на конце шланга.

Мы можем думать о резервуаре для воды как о батарее, месте, где мы храним определенное количество энергии, а затем высвобождаем ее.Если мы спустим наш бак на определенное количество, давление, создаваемое на конце шланга, упадет. Мы можем думать об этом как об уменьшении напряжения, например, когда фонарик тускнеет, когда батарейки садятся. Также уменьшается количество воды, протекающей через шланг. Меньшее давление означает, что течет меньше воды, что приводит нас к течению.

Текущий

Мы можем думать о количестве воды, протекающей по шлангу из резервуара, как о токе. Чем выше давление, тем выше расход, и наоборот.В случае с водой мы бы измерили объем воды, протекающей через шланг за определенный период времени. С электричеством мы измеряем количество заряда, протекающего по цепи за определенный период времени. Сила тока измеряется в амперах (обычно их просто называют «амперами»). Ампер определяется как 6,241×10 ¹⁸ электронов (1 кулон), проходящих через точку цепи в секунду. Усилители представлены в уравнениях заглавной буквой «I».

Предположим теперь, что у нас есть два бака одинакового размера с одинаковым количеством воды в них, но шланг на одном баке уже (меньшего диаметра), чем шланг на другом.Мы измеряем одинаковое давление на концах обоих шлангов, потому что давление воды одинаковое, но когда вода начнет течь, расход воды в баке с более узким шлангом будет меньше, чем расход воды в баке с более широким шлангом.

В электрических терминах ток через более узкий шланг меньше, чем ток через более широкий шланг. Если мы хотим, чтобы поток через оба шланга был одинаковым, мы должны увеличить количество воды (зарядку) и, следовательно, давление в баке с более узким шлангом.Это повышенное давление (напряжение) на конце более узкого шланга проталкивает больше воды через резервуар. Это аналогично увеличению напряжения, которое вызывает увеличение тока.

Теперь приступаем к установлению зависимости между напряжением и током. Но здесь следует учитывать третий фактор: диаметр шланга. В этой аналогии диаметр шланга определяет сопротивление потоку воды (заряду). Это означает, что нам нужно добавить еще один термин в нашу модель:

Вода = заряд (измеряется в кулонах)
Давление = напряжение (измеряется в вольтах)
Расход = ток (измеряется в амперах или сокращенно «ампер»)
Диаметр шланга = сопротивление

Сопротивление

Рассмотрим снова два резервуара для воды, один с трубой малого диаметра, а другой с трубой большого диаметра.

Само собой разумеется, что мы не можем пропустить через узкую трубу тот же объем воды, что и более широкая, при том же давлении. Это сопротивление. Узкая труба «сопротивляется» потоку воды через нее, хотя вода находится под тем же давлением, что и бак с более широкой трубой.

В электрических терминах это представлено двумя цепями с одинаковыми напряжениями и разными сопротивлениями. Цепь с более высоким сопротивлением позволит протекать меньшему заряду; это означает, что через цепь с более высоким сопротивлением протекает меньший ток.

Это возвращает нас к Георгу Ому. Ом определяет единицу сопротивления «1 Ом» как сопротивление между двумя точками в проводнике, где приложение 1 вольта вызовет течение 1 ампера, или 6,241×10 ¹⁸ электронов в секунду. Это значение обычно обозначается на схемах греческой буквой «Ω», которая произносится как «омега» и очень похожа на «ом».

Закон Ома

Объединив элементы напряжения, тока и сопротивления, Ом вывел формулу:

Где:
В = напряжение в вольтах
I = ток в амперах
R = сопротивление в омах

Это называется законом Ома.Например, скажем, что у нас есть цепь с потенциалом 1 вольт, током 1 ампер и сопротивлением 1 Ом. Используя закон Ома, мы можем сказать:

Возвращаясь к аналогии с водой, скажем, это наш резервуар с широким шлангом. Количество воды в баке определяется как 1 вольт, а «узость» (сопротивление течению) шланга определяется как 1 Ом. Используя закон Ома, это дает нам поток (ток) в 1 ампер.

Теперь рассмотрим бак с узким шлангом.Поскольку шланг уже, его сопротивление потоку выше. Для случая с более узким шлангом мы можем определить сопротивление в два раза больше или 2 Ом. Количество воды в баке такое же, как и в другом баке, поэтому напряжение такое же. Используя закон Ома, наше уравнение для бака с узким шлангом выглядит так:

Но что такое ток? Поскольку сопротивление больше, а напряжение такое же, это дает нам значение тока 0,5 ампер:

Таким образом, ток ниже в баке с более высоким сопротивлением, как мы и предсказывали.Теперь мы можем видеть, что если мы знаем два значения закона Ома, мы можем найти третье.

Давайте продемонстрируем это на эксперименте.

Для этого эксперимента мы хотим зажечь светодиод (светоизлучающий диод). Светодиоды несколько хрупкие, и через них должен протекать только определенный ток. Ток, превышающий максимально допустимый, может их сжечь. В техпаспорте на светодиод всегда будет «номинальный ток». Это максимальное количество тока, которое может протекать через конкретный светодиод до того, как он выйдет из строя.

В качестве источника напряжения мы будем использовать источник питания +5 В от ADALM2000.

Материалы:

Модуль активного обучения ADALM2000
Макетная плата без пайки и комплект перемычек
1 светодиод, более длинный из двух проводов является анодом (+), а более короткий — катодом (-)
1 Резистор

ПРИМЕЧАНИЕ. Светодиоды известны как «неомические» устройства. Это означает, что уравнение для тока, протекающего через сам светодиод, не является простой линейной зависимостью В = IR.Светодиод представляет собой особый вид диода. У всех диодов есть то, что называется внутренним «падением напряжения». Однако в этом эксперименте мы просто пытаемся защитить светодиод от слишком большого тока, поэтому мы можем пока пренебречь неомическими характеристиками тока светодиода и выбрать значение резистора, используя только закон Ома, чтобы гарантировать, что ток через светодиод будет безопасно менее 20 мА.

Для этого примера у нас есть выход В + ADALM2000, настроенный на генерацию 5 В, и (красный) светодиод с номинальным током 20 миллиампер или 0.020 ампер. Чтобы быть в безопасности, мы бы предпочли не управлять светодиодом с его максимальным током, а предпочесть рекомендуемый ток, который указан в его спецификации как 18 мА или 0,018 ампер. Если мы просто подключим светодиод напрямую к батарее, значения закона Ома будут выглядеть так:

Перестановка для I:

Только с проводом и без резистора:

Деление на ноль дает бесконечный ток! На практике не бесконечен, но такой ток, какой может обеспечить источник питания +5 В ADALM2000.Мы, конечно, не хотим, чтобы через светодиод протекал такой большой ток. Нам нужно включить резистор.

Наши соединения схемы должны выглядеть так:

Схема, схема питания светодиода от источника питания +5 В

Мы можем использовать закон Ома, чтобы определить значение резистора, которое даст нам желаемое значение тока:

Перестановка для R:

Подставляем значения 5 Вольт и 0.018 Ампер:

Решение для сопротивления:

Таким образом, номинал резистора, который нам нужен для R ₁ , составляет около 277 Ом, чтобы поддерживать ток через светодиод ниже максимального номинального тока.

277 Ом не является обычным значением для готовых резисторов, поэтому для этого эксперимента используйте резистор на 470 Ом (желто-фиолетово-коричневый), который является следующим ближайшим значением, большим, чем 277 в комплекте деталей ADALP2000. Ниже показано, как ваша схема должна выглядеть вместе.

Макет, схема питания светодиода от источника питания +5 В

Успех! Мы выбрали сопротивление резистора, достаточно высокое, чтобы ток через светодиод оставался ниже его максимального номинала, но достаточно низкое, чтобы тока было достаточно, чтобы светодиод оставался красивым и ярким. Включите положительный источник питания до 5В. Если светодиод не загорается, обязательно дважды проверьте правильность подключения контактов (+) и (-) светодиода.

Этот пример со светодиодом и токоограничивающим резистором часто встречается в электронике.Вам часто придется использовать закон Ома, чтобы изменить величину тока, протекающего через цепь.

Ограничение тока до или после светодиода?

Чтобы немного усложнить ситуацию, вы можете разместить токоограничивающий резистор с любой стороны светодиода, и он будет работать точно так же.

Многие читатели, впервые изучающие электронику, не понимают, что токоограничивающий резистор можно вставить с любой стороны светодиода, и схема будет работать как обычно.Попробуйте поменять местами резистор и светодиод в вашей схеме. Светодиод по-прежнему горит с одинаковой яркостью в обоих случаях?

Вот еще одна аналогия с водой. Представьте себе водопроводную трубу, которая представляет собой непрерывный контур с насосом, непрерывно циркулирующим воду. Если бы мы поместили вентиль где-то в трубе, то при закрытом вентиле переставала бы течь вода во всей трубе, а не только в одном ее участке. Теперь представьте, что мы немного приоткрываем вентиль, который ограничивает поток воды. Не имеет значения, в каком месте контура вставлен частично открытый клапан, он все равно замедлит поток во всей трубе.Вода не скапливается за клапаном. Давление в отрезке трубы между выпускной стороной насоса и клапаном увеличивается, а давление в отрезке трубы между клапаном и выпускной стороной насоса уменьшается. Насос аналогичен источнику напряжения, увеличивающему напряжение, а клапан аналогичен резистору, уменьшающему напряжение.

Это упрощение, так как токоограничивающий резистор можно разместить в цепи только в двух местах; его можно разместить с любой стороны светодиода для выполнения своей функции.

Для более научного ответа обратимся к закону Кирхгофа о напряжении. Именно из-за этого закона токоограничивающий резистор может располагаться с любой стороны светодиода и при этом иметь тот же эффект. Для получения дополнительной информации и решения некоторых практических задач по использованию KVL посетите этот веб-сайт.

Измерение фактического напряжения и тока

ADALM2000 также имеет два входных канала, которые можно использовать в качестве вольтметра. Мы можем соединить их, как показано на следующей схеме, для измерения фактических напряжений в цепи. Вход вольтметра канала 1 подключен для измерения источника питания +5 В , а вольтметр канала 2 подключен для измерения напряжения на ( +), плюс, конец диода.

Схема, Измерьте фактические напряжения в цепи.

Подключите входы вольтметра, как показано на рисунке.

Макетные соединения для измерения фактических напряжений в цепи.

Запустите инструмент Scopy Voltmeter. Интерфейс выглядит так.

Нажмите на зеленую кнопку Run, и отобразятся напряжения цепи. Напряжение на канале 1 должно отображать фактическое значение напряжения питания +5 В .Напряжение на канале 2 должно отображать фактическое напряжение на светодиодном диоде. В этом примере для красного светодиода напряжение составляло 1,84 вольта. Разница между этими двумя напряжениями, Канал 1-Канал 2 В , будет напряжением на резисторе, которое в этом примере составляло 3,12 вольта.

Мы можем использовать закон Ома для расчета тока в резисторе:

Или:

Или:

6,6 мА

Ресурсы и продолжение

Теперь вы должны понимать, что такое напряжение, ток, сопротивление и как они связаны между собой.Поздравляем! Большинство уравнений и законов для анализа цепей можно вывести непосредственно из закона Ома. Зная этот простой закон, вы понимаете концепцию, лежащую в основе анализа любой электрической цепи!

Эти концепции — лишь вершина айсберга. Если вы хотите продолжить изучение более сложных приложений закона Ома и проектирования электрических цепей, обязательно ознакомьтесь со следующими практическими занятиями.

Вернуться к содержанию лабораторной работы

Закон

Ом Футболка из Википедии

.

Закон Ома гласит, что ток в проводнике между двумя точками прямо пропорционален напряжению в этих двух точках. Вводя константу пропорциональности, сопротивление, приходим к обычному математическому уравнению, описывающему эту зависимость:

I = VR, {\ displaystyle I = {\ frac {V} {R}},}

, где I — ток через проводник в амперах, В — напряжение, измеренное на проводник в единицах вольт, а R сопротивление проводника в единицах ом.Точнее, закон Ома гласит, что R в этом отношении постоянна, не зависит от тока. Если сопротивление непостоянно, предыдущее уравнение нельзя назвать законом Ома , но его все же можно использовать в качестве определения статического/постоянного сопротивления. Закон Ома — это эмпирическое соотношение, которое точно описывает проводимость подавляющего большинства электропроводящих материалов при силе тока многих порядков. Однако некоторые материалы не подчиняются закону Ома; они называются неомическими.

Закон назван в честь немецкого физика Георга Ома, который в трактате, опубликованном в 1827 году, описал измерения приложенного напряжения и тока через простые электрические цепи, содержащие провода различной длины. Ом объяснил свои экспериментальные результаты немного более сложным уравнением, чем приведенная выше современная форма (см. § История ниже).

В физике термин закон Ома также используется для обозначения различных обобщений закона; например, векторная форма закона, используемого в электромагнетизме и материаловедении:

J = σE, {\ displaystyle \ mathbf {J} = \ sigma \ mathbf {E},}

, где Дж — плотность тока в данном месте в резистивном материале, E — электрическая поля в этом месте, а σ (сигма) — это зависящий от материала параметр, называемый проводимостью.Эта переформулировка закона Ома принадлежит Густаву Кирхгофу. На нем напечатано

. В Википедии более 5 миллионов статей, поэтому у нас

.

Пол Ом | Закон Джорджтауна

Пол Ом — профессор права в юридическом центре Джорджтаунского университета в Вашингтоне, округ Колумбия. В своих исследованиях, работе и преподавании профессор Ом наводит мосты между информатикой и правом, используя свою подготовку и опыт юриста, политика и программиста. и администратор сетевых систем.Его исследования посвящены конфиденциальности информации, закону о компьютерных преступлениях, слежке, технологиям и закону, а также искусственному интеллекту и закону. Профессор Ом опубликовал знаковые статьи о провале анонимизации, Четвертой поправке и новых технологиях, а также конфиденциальности широкополосного доступа. Его работа определила области научных исследований и повлияла на политиков во всем мире.

Профессор Ом, заинтересованный в превращении научных открытий в значимые изменения, является заведующим факультетом Института технологического права и политики; Центр конфиденциальности и технологий Джорджтаунского юридического факультета; и Инициатива технологий и общества Джорджтаунского университета.Он свидетельствовал перед комитетами обеих палат Конгресса и консультировал многочисленные правительственные учреждения, включая Федеральную торговую комиссию, Федеральную комиссию по связи и генеральных прокуроров нескольких штатов. Он входит в советы директоров двух самых влиятельных и инновационных некоммерческих организаций в области технологической политики: Upturn и The Markup.

Профессор Ом был признан новаторским и популярным учителем. Полагая, что юридическая практика 21 века требует глубоких знаний современных технологий, профессор Ом ведет интенсивные практические курсы, которые знакомят студентов-юристов с программированием на Python, операционной системой Linux, облачными вычислениями и многим другим.Сотни студентов юридического факультета Джорджтауна, не имевших опыта программирования, научились писать программы на Python у профессора Ома в рамках своего обучения JD. Надеясь распространить эту учебную программу на другие школы, профессор Ом поделился материалами своего курса с многочисленными коллегами из других учреждений, которые теперь предлагают аналогичные курсы. Более подробная информация о курсе Python доступна по адресу https://cp4l.org.

Опытный университетский администратор, профессор Ом работал заместителем декана по академическим вопросам как в Джорджтаунском юридическом факультете, так и в Юридической школе Университета Колорадо, где он проработал на факультете почти десять лет.Во время пандемии COVID-19 заместитель декана Ом помог руководить реагированием Джорджтаунского закона, наблюдая за переходом на онлайн-обучение и гибридное обучение. За эти усилия он был отмечен премией Стивена Голдберга за заслуги перед преподавателями. В настоящее время он является первым директором по данным Джорджтаунского права и заместителем декана в Регистрационной палате.

Твердо верящий в важность государственной службы, профессор Ом занимал множество должностей в федеральном правительстве. Он начал свою юридическую карьеру в качестве федерального прокурора в США.С. Легендарный отдел компьютерных преступлений и интеллектуальной собственности Министерства юстиции, где он работал над актуальными вопросами, связанными с Четвертой поправкой, Законом о компьютерном мошенничестве и злоупотреблениях, а также Законом о конфиденциальности электронных коммуникаций. Совсем недавно он работал старшим советником по политике конфиденциальности в Федеральной торговой комиссии и Комиссии США по разработке политики, основанной на фактических данных, в качестве назначенного Обамы Белого дома. После окончания юридического факультета он работал клерком у судьи Бетти Флетчер в девятом округе и у судьи Марианы Пфаэльцер в Центральном округе Калифорнии.

Профессор Ом получил степень юриста в Калифорнийском университете в Лос-Анджелесе и степень в области компьютерных наук и электротехники в Йельском университете. До поступления на юридический факультет он помогал администрировать и защищать компьютерные сети корпорации RAND и Йельского университета. Он пишет тысячи строк кода Python каждый год и живет своей жизнью в Emacs и организационном режиме, хотя он не держит зла ​​на тех, кто предпочитает vi.

Стипендия

Вклады в юридические обзоры и другие научные журналы

Линдси Барретт, Лаура Мой, Пол Ом и Ашкан Солтани, Иллюзорные конфликты: процедуры оформления после увольнения и технологическая экспертиза Федеральной торговой комиссии , 35 Berkeley Tech L.Дж. 793-833 (2020).

[WWW] [HEIN] [W] [L]

Пол Ом, Множество революций Карпентера , 32 Harv. JL & Tech. 357-416 (2019).

[HEIN] [W] [L]

Selected Contributions to Other Publications

Paul Ohm, Manipulation, Dark Patterns, and Evil Nudges , JOTWELL, 22 мая 2019 г. (рецензия на Daniel Susser, Beate Roessler & Helen Nissenbaum, Online Манипуляции: скрытые влияния в цифровом мире , доступно на SSRN).

[WWW] [HEIN]

Свидетельские показания Конгресса

Защита конфиденциальности, продвижение политики: формирование политики на основе фактических данных и будущее образования: слушание перед судом Х.Комм. на Образ. & the Workforce , 115th Cong., 30 января 2018 г. (заявление Пола Ома) (CIS-No.: Ожидается).

[WWW]

Главы в книгах и собрание сочинений

Пол Ом, Throttling Machine Learning , в Life and the Law in the Era of Data-Driven Agency 214-229 (Mireille Hildebrandt & Kieron O’Hara eds., Cheltenham , Великобритания: Эдвард Элгар, 2020).

[КНИГА] Загрузить всю стипендию

В новостях

31 марта 2021 г. 13 мая 2020 г. 19 марта 2020 г. 19 декабря 2019 г. Загрузить все новости

Законы Ома для постоянного и переменного тока

Поиск в Вики по сжатому воздуху

Чтобы превратить воздух в сжатый воздух, вам нужна энергия.Эта сила приходит в форме электричества: переменный ток или постоянный ток. В этой статье мы дадим краткое введение в законы Ома. Эти законы вводят сопротивление в связь между током и напряжением.

Что такое закон Ома для постоянного тока?

Закон Ома гласит, что ток в проводнике между двумя точками прямо пропорционален напряжению в этих двух точках.Вводя константу пропорциональности, сопротивление, приходим к обычному математическому уравнению, описывающему эту зависимость: U = R х I Где I — ток через проводник в единицах ампер, V — напряжение, измеренное на проводнике в единицах вольт, а R — сопротивление проводника в единицах Ом. В частности, закон Ома гласит, что R в этом отношении является постоянным и не зависит от тока.

Что такое закон Ома для переменного тока (и что такое самоиндукция)?

Переменный ток, проходящий через катушку, вызывает магнитный поток.Этот поток меняет величину и направление так же, как электрический ток. При изменении потока в катушке возникает ЭДС (электродвижущая сила) по законам индукции. Эта ЭДС противонаправлена ​​напряжению подключенного полюса. Это явление называется самоиндукцией. Самоиндукция в блоке переменного тока приводит частично к смещению фаз между током и напряжением, а частично к индуктивному падению напряжения. Сопротивление блока переменному току становится явно больше рассчитанного или измеренного при постоянном токе.Сдвиг фаз между током и напряжением представлен углом φ. Индуктивное сопротивление (называемое реактивным сопротивлением) обозначается буквой X. Сопротивление обозначается буквой R. Кажущееся сопротивление блока или проводника обозначается буквой Z.

Связанные статьи

Электрический монтаж в компрессорных системах

В этой статье мы рассмотрим электрическую систему, которая обеспечивает правильную работу компрессора.Это включает в себя двигатели, кабели, контроль напряжения и защиту от короткого замыкания.

Введение в электричество

Узнайте об основах электричества и его роли в сжатии воздуха.Некоторые основные термины и определения.

Электродвигатель

Узнайте об основах электродвигателей и о том, как они встраиваются в современные воздушные компрессоры.

Ohm’sches Gesetz (закон Ома) — wikide.wiki

Das Ohmsche Gesetz besagt, dass der Strom durch einen Leiter zwischen zwei Punkten, прямо пропорциональный zur Spannung an den beiden Punkten ist. Führt man die Proportionalitätskonstante, den Widerstand, ein, gelangt man zu der üblichen mathematischen Gleichung, die diesen Zusammenhang beschreibt: ич в р , {\ Displaystyle I {\ гидроразрыва {V} {R}},} wobei I der Strom durch den Leiter in Ampere-Einheiten ist, V die über dem Leiter gemessene Spannung in Volt-Einheiten ist und R der Widerstand des Leiters in Ohm-Einheiten ist.Genauer gesagt besagt das Ohmsche Gesetz, dass das R in dieser Beziehung unabhängig vom Strom konstant ist. Wenn der Widerstand nicht konstant ist, kann die vorherige Gleichung nicht als Ohmsches Gesetz bezeichnet werden, aber sie kann immer noch als Definition des statischen/DC-Widerstands verwendet werden. Das Ohmsche Gesetz ist eine empirische Beziehung, die die Die Leitfähigkeit der allermeisten elektrisch leitfähigen Materialien über viele Größenordnungen des Stroms genau beschreibt. Einige Materialien gehorchen jedoch nicht dem Ohmschen Gesetz; diese werden als nicht-ohmisch bezeichnet.Das Gesetz wurde nach dem deutschen Physiker Georg Ohm benannt, der in einer 1827 veröffentlichten Abhandlung Messungen der angelegten Spannung und des Stroms durch einfache elektrische Schaltkreise mit unterschiedlich langen Drähten beschrieb. Ohm erklärte seine Experimentellen Ergebnisse durch eine etwas komplexere Gleichung als die obige moderne Form (siehe § Geschichte unten). In der Physik wird der Begriff Ohmsches Gesetz auch verwendet, um sich auf verschiedene Verallgemeinerungen des Gesetzes zu beziehen; Zum Beispiel die Vektorform des in der Elektromagnetik und Materialwissenschaft verwendeten Gesetzes: Дж о Е , {\ Displaystyle \ mathbf {J} \ сигма \ mathbf {E},} wobei J die Stromdichte an einer bestimmten Stelle in einem Widerstandsmaterial ist, E das elektrische Feld an dieser Stelle ist und σ (Sigma) ein materialabhängiger Parameter ist, der als Leitfähigkeit bezeichnet wird.Diese Neuformulierung des Ohmschen Gesetzes geht auf Gustav Kirchhoff zurück. Im Januar 1781, vor der Arbeit von Georg Ohm, Experimentierte Henry Cavendish mit Leidener Gefäßen und Glasröhrchen unterschiedlichen Durchmessers und unterschiedlicher Länge, die mit Salzlösung gefüllt waren. Er maß den Strom, indem er feststellte, wie stark er einen Schock verspürte, als er den Stromkreis mit seinem Körper vollendete. Cavendish schrieb, dass die «Geschwindigkeit» (Strom) direkt als «Elektrifizierungsgrad» (Spannung) variierte.Er teilte seine Ergebnisse zu dieser Zeit anderen Wissenschaftlern nicht mit, und seine Ergebnisse waren unbekannt, bis Maxwell sie 1879 veröffentlichte. Фрэнсис Рональдс написал «Intensität» (Spannung) и «Menge» (Strom) для Trockenstapel – eine Hochspannungsquelle – 1814 mit einem Blattgold-Elektrometer. Er stellte für einen trockenen Haufen fest, dass das Verhältnis zwischen den beiden Parametern unter bestimmten meteorologischen Bedingungen nicht пропорциональная война. Ohm führte seine Arbeiten über den Widerstand in den Jahren 1825 und 1826 durch und veröffentlichte seine Ergebnisse 1827 als Buch Die galvanische Kette, mathematisch bearbeitet («Der galvanische Stromkreis mathematisch untersucht»).Er ließ sich bei der theoretischen Erklärung seiner Arbeit stark von Fouriers Arbeiten zur Wärmeleitung inspirieren. Für Experimente verwendete er zunächst Voltasäulen, später aber ein Thermoelement, da dieses eine stabilere Spannungsquelle in Bezug auf Innenwiderstand und konstante Spannung lieferte. Er verwendete ein Galvanometer, um den Strom zu messen, und wusste, dass die Spannung zwischen den Thermoelementanschlüssen, пропорциональный цур Sperrschichttemperatur war. Anschließend fügte er Testdrähte unterschiedlicher Länge, unterschiedlichen Durchmessers und unterschiedlichen Materials hinzu, um die Schaltung zu vervollständigen.Er fand heraus, dass seine Daten durch die Gleichung modelliert werden konnten Икс Эйн Б + л , {\ displaystyle x {\ frac {a} {b + l}},} wobei x der Messwert des Galvanometers war

Ограничения и применение закона Ома

Закон Ома представляет собой взаимосвязь между тремя физическими явлениями: током, напряжением и сопротивлением.Это соотношение было введено немецким физиком Джорджем Симоном Омом. Вот почему этот закон известен как закон Ома. В нем говорится, что величина постоянного тока через большое количество материалов прямо пропорциональна разности потенциалов или напряжению на материалах. Так, если напряжение V (в вольтах) между двумя концами провода, сделанного из одного из этих материалов, утроить, то и ток I (в амперах) также утроится; и отношение V/I остается постоянным. Отношение V/I для данного куска материала называется его сопротивлением R и измеряется в единицах, называемых омами.

• Ток: Ток определяется как поток положительного заряда от источника к источнику отрицательного заряда. Единицами тока являются Кл/с для количества заряда (Кл/Колумб), который проходит в единицу времени (секунду). Ампер (А) — общепринятая единица силы тока, равная 1 Кл/с, а символ тока — I. одного атома к другому в том же направлении.Его также называют разностью потенциалов. Напряжение измеряется в единицах Вольт (В).
• Сопротивление: Электрическое сопротивление объекта является мерой его сопротивления потоку электрического тока. Его обратной величиной является электрическая проводимость. Единицей сопротивления является Ом.

Для любых данных тока, напряжения и сопротивления закон Ома определяется как: через идеальный резистор прямо пропорциональна приложенному к резистору напряжению.Константа пропорциональности записывается как R, и это значение сопротивления резистора.

Основным критерием для закона Ома является поддержание постоянного сопротивления, потому что постоянной пропорциональности в соотношении является сопротивление R. Но мы знаем, что изменение температуры влияет на значение сопротивления, поэтому, чтобы поддерживать постоянное сопротивление во время экспериментов Ома по закону температура считается постоянной.

Ограничения закона Ома

1. Закон Ома неприменим к односторонним электрическим элементам, таким как диоды и транзисторы, поскольку они пропускают ток только в одном направлении.
2. Для нелинейных электрических элементов с такими параметрами, как емкость, сопротивление и т. д., напряжение и ток не будут постоянными во времени, что затрудняет использование закона Ома. Нелинейные элементы — это элементы, ток которых не точно пропорционален приложенному напряжению, что означает, что значение сопротивления этих элементов изменяется при различных значениях напряжения и тока. Примерами нелинейных элементов являются тиристор, электрическая дуга и т. д.
3. Отношение между V и I зависит от знака V (+ или -).Другими словами, если I представляет собой ток для определенного V, то изменение направления V на противоположное при неизменной его величине не приводит к возникновению тока той же величины, что и I в противоположном направлении. Это происходит, например, в случае диода.
4. Закон Ома применим только к металлическим проводникам. Так что в случае с неметаллическими проводниками это не сработает.

Применение закона Ома в повседневной жизни

Закон Ома может определять напряжение, приложенное к цепи, значение сопротивления и ток, протекающий по цепи.С помощью трех приведенных выше значений мы можем найти значение других факторов, таких как удельное сопротивление и многие другие. Некоторые ежедневные применения закона Ома:

• В предохранителях: Для защиты цепи используются предохранители и автоматические выключатели. Они соединены последовательно с электрическими приборами. Закон Ома позволяет найти значение тока, который может протекать через предохранители. Если значение тока слишком велико, то это может повредить цепь и даже привести к взрыву электронного устройства.
• Чтобы узнать потребляемую мощность: Электрические нагреватели имеют металлическую катушку с высоким сопротивлением, которая пропускает через себя определенное количество тока для обеспечения необходимого тепла. С помощью этого закона определяется мощность, которую необходимо отдать нагревателям.
• Для управления скоростью вентиляторов: Сдвинув регулятор до конца от старта, мы можем регулировать скорость вентиляторов в наших домах. Управляя сопротивлением с помощью регулятора, здесь управляется ток, протекающий через вентилятор.Мы можем измерить сопротивление, ток и, следовательно, мощность, протекающую по закону Ома, для любого конкретного значения входа.
• Для определения размера резисторов: Электроприборы, такие как электрические чайники и утюги, имеют внутри много резисторов. Чтобы обеспечить необходимое количество тепла, резисторы ограничивают величину тока, который может протекать через них. По закону Ома определяют номиналы входящих в них резисторов.

Примеры задач

Задача 1. Какова сила тока в лампочке мощностью 75 Вт, подключенной к сети 120 В?

Решение: 

Мы задали значение мощности (P = 75 Вт) и значение напряжения (V = 120 В).

Мы хотим найти ценность нынешнего I.

с использованием закона Ом,

P = IV

или

I = P / V

= 75/120

= 0.625 A.

Проблема 2: Если сопротивление электрического утюга равно 100 Ом и через сопротивление протекает ток силой 4,2 А. Найдите напряжение между двумя точками.

Решение:

Если нас попросят рассчитать значение напряжения с данными нам значением тока и сопротивления, то замкните V в треугольнике.Теперь у нас остались I и R или точнее I × R.

Таким образом, мы используем следующую формулу для расчета значения V:

V = I × R

Подставляя значения в уравнение, мы получаем

В = 4,2 А × 100  = 420 В

В = 420 В

Задача 3. Источник ЭДС 10,0 В подключен к чисто резистивному электроприбору. Через него протекает электрический ток силой 1,0 А. Считайте, что проводящие провода не имеют сопротивления.Рассчитайте сопротивление, оказываемое электроприбором.

Решение:

Когда нас просят найти значение сопротивления при данных значениях напряжения и силы тока, то мы покрываем R треугольником. Это оставляет нам только V и I, точнее V/I.

Подставляя значения в уравнение, получаем

R = V/I

R = 10 В/1 А = 10 Ом

R = 10 Ом

Задача 4. Найдите ток I через резистор сопротивлением R = 3 Ом, если напряжение на резисторе равно 9 В.

Решение:

Подставьте R на 2 и V на 6 в законе Ома V = RI.

9 = 3 I

Проблема 5. В схеме ниже резисторы R1 и R2 соединены последовательно и имеют сопротивление 5 Ом и 10 Ом соответственно. Напряжение на резисторе R ₁ равно 4 В. Найти ток, протекающий через резистор R2, и напряжение на этом же резисторе.

Решение:

Воспользуемся законом Ома V = RI, чтобы найти ток I1, проходящий через резистор R1.

4 = 5 I ₁

Найдите I ₁

I ₁ = 4 / 5 = 0,8 А

Два резистора соединены последовательно, поэтому через них проходит одинаковый ток. Следовательно, ток I ₂ через R ₂ равен 0,8 А.

Теперь воспользуемся законом Ома, чтобы найти напряжение V ₂ на резисторе R ₂ .

В ₂ = R ₂ I ₂ = 10 (0,8) = 8 В

8 Ом и 4 Ом соответственно.Ток, протекающий через R ₁ , равен 0,2 А. Найти напряжение на резисторе R ₂ и ток, протекающий через тот же резистор.

Решение:

Используйте закон Ома V = RI, чтобы найти напряжение V1 на резисторе R ₁ .

В ₁ = 8 (0,2) = 1,6 В

Напряжение на резисторе R ₁ и напряжение на резисторе R ₂ одинаковы, поскольку R ₁ и R ₂ включены параллельно.

Теперь воспользуемся законом Ома, чтобы найти ток I ₂ , проходящий через резистор R ₂ .

1.6 = 4 I ₂

Решина для I ₂

I

I ₂ = 1,6 / 4 = 0,4 A

Проблема 7: Ток, проходящий через резистор в цепи составляет 0,01 А, когда напряжение на том же резисторе 5 В.