Что такое закон Ома и как он связывает основные электрические величины. Как применять закон Ома для расчета параметров электрических цепей. Какие формулы используются на практике при работе с законом Ома.
Закон Ома: фундаментальный принцип электротехники
Закон Ома является одним из основополагающих законов электротехники, устанавливающий связь между тремя ключевыми электрическими величинами: силой тока, напряжением и сопротивлением. Этот закон был сформулирован немецким физиком Георгом Омом в 1826 году на основе экспериментальных данных.
Согласно закону Ома, сила тока в проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника. Математически это выражается формулой:
I = U / R
где:
- I — сила тока (в амперах, А)
- U — напряжение (в вольтах, В)
- R — сопротивление (в омах, Ом)
Эта простая формула позволяет рассчитать любую из трех величин, если известны две другие. Например, зная напряжение и сопротивление участка цепи, можно определить силу протекающего по нему тока.

Практическое применение закона Ома
Закон Ома широко применяется в электротехнике для расчета и проектирования электрических цепей. Вот несколько примеров его практического использования:
- Расчет параметров электропроводки в зданиях
- Определение номиналов резисторов в электронных схемах
- Выбор предохранителей и автоматических выключателей
- Расчет мощности электроприборов
- Анализ работы электрических цепей
Применяя закон Ома, инженеры-электрики могут оптимизировать работу электрических систем, обеспечивая их эффективность и безопасность.
Формы записи закона Ома
Закон Ома может быть записан в различных формах, что позволяет легко находить нужную величину:
- I = U / R (для нахождения силы тока)
- U = I * R (для нахождения напряжения)
- R = U / I (для нахождения сопротивления)
Эти формулы эквивалентны и выбираются в зависимости от того, какая величина неизвестна и требует вычисления.
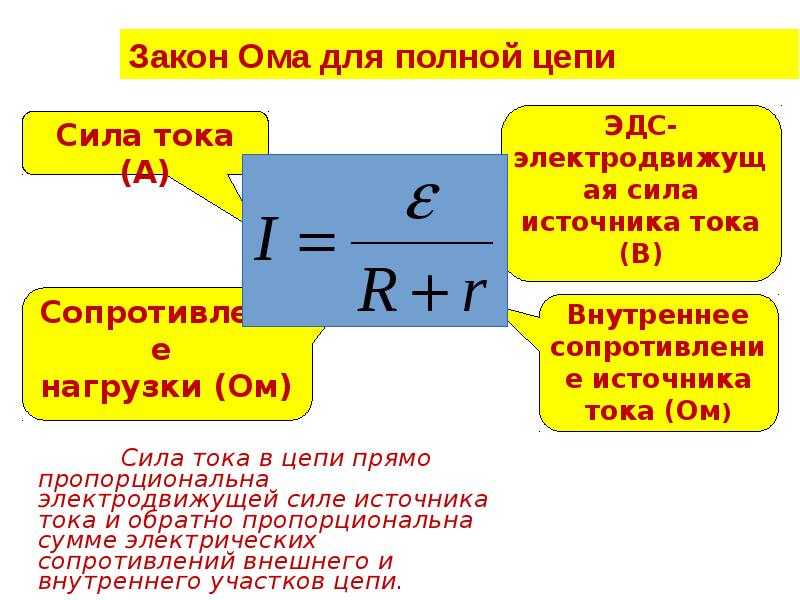
Закон Ома для участка цепи и полной цепи
Различают закон Ома для участка цепи и для полной цепи. Закон Ома для участка цепи применяется к отдельным элементам электрической схемы, в то время как закон Ома для полной цепи учитывает также внутреннее сопротивление источника тока.

Формула закона Ома для полной цепи выглядит следующим образом:
I = E / (R + r)
где:
- E — электродвижущая сила источника (в вольтах, В)
- R — сопротивление внешней цепи (в омах, Ом)
- r — внутреннее сопротивление источника (в омах, Ом)
Эта формула позволяет учесть влияние внутреннего сопротивления источника на ток в цепи, что особенно важно при работе с реальными источниками энергии.
Ограничения закона Ома
Хотя закон Ома широко применяется в электротехнике, важно помнить о его ограничениях:
- Закон справедлив только для проводников, подчиняющихся линейной зависимости между током и напряжением
- Он не применим к полупроводниковым элементам, таким как диоды и транзисторы
- При высоких температурах и сильных токах могут возникать отклонения от закона Ома
- В сверхпроводниках закон Ома не работает
Понимание этих ограничений важно для правильного применения закона Ома в различных ситуациях.
Расчет мощности с использованием закона Ома
Закон Ома тесно связан с расчетом электрической мощности. Мощность, выделяемая на участке цепи, может быть рассчитана по формуле:

P = U * I
где P — мощность (в ваттах, Вт).
Комбинируя эту формулу с законом Ома, можно получить дополнительные выражения для расчета мощности:
- P = I^2 * R
- P = U^2 / R
Эти формулы позволяют рассчитывать мощность, зная различные параметры электрической цепи.
Применение закона Ома в бытовой электротехнике
Закон Ома находит широкое применение не только в промышленной электротехнике, но и в бытовых электрических устройствах. Вот несколько примеров:
- Расчет потребляемой мощности бытовых приборов
- Выбор сечения проводов для домашней электропроводки
- Определение оптимального напряжения для светодиодных ламп
- Расчет времени зарядки аккумуляторов
- Оценка эффективности солнечных панелей
Понимание закона Ома помогает обычным пользователям более эффективно и безопасно использовать электрические приборы в повседневной жизни.
Экспериментальная проверка закона Ома
Закон Ома можно легко проверить экспериментально, используя простые электрические компоненты. Для этого потребуется:

- Источник питания с регулируемым напряжением
- Резистор с известным сопротивлением
- Амперметр для измерения тока
- Вольтметр для измерения напряжения
Изменяя напряжение источника и измеряя ток, можно построить график зависимости тока от напряжения. Если закон Ома выполняется, график будет представлять собой прямую линию, наклон которой соответствует величине, обратной сопротивлению резистора.
Закон Ома в современной электронике
Несмотря на то, что закон Ома был открыт почти 200 лет назад, он продолжает играть важную роль в современной электронике. В микроэлектронике закон Ома применяется для расчета параметров интегральных схем и проектирования микропроцессоров.
Однако в наноэлектронике и квантовых устройствах могут наблюдаться отклонения от классического закона Ома. Изучение этих отклонений и разработка новых моделей электропроводности является актуальной задачей современной физики твердого тела.
Заключение
Закон Ома остается одним из фундаментальных принципов электротехники, обеспечивая основу для понимания и расчета электрических цепей. Его простота и универсальность делают его незаменимым инструментом как для профессиональных инженеров, так и для студентов, изучающих основы электричества.

Знание закона Ома и умение применять его на практике позволяет решать широкий спектр задач в области электротехники и электроники, от проектирования бытовых электроприборов до разработки сложных электронных систем. Поэтому изучение и глубокое понимание закона Ома остается важной частью образования в области технических наук.
Закон ома и его практическое применение
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
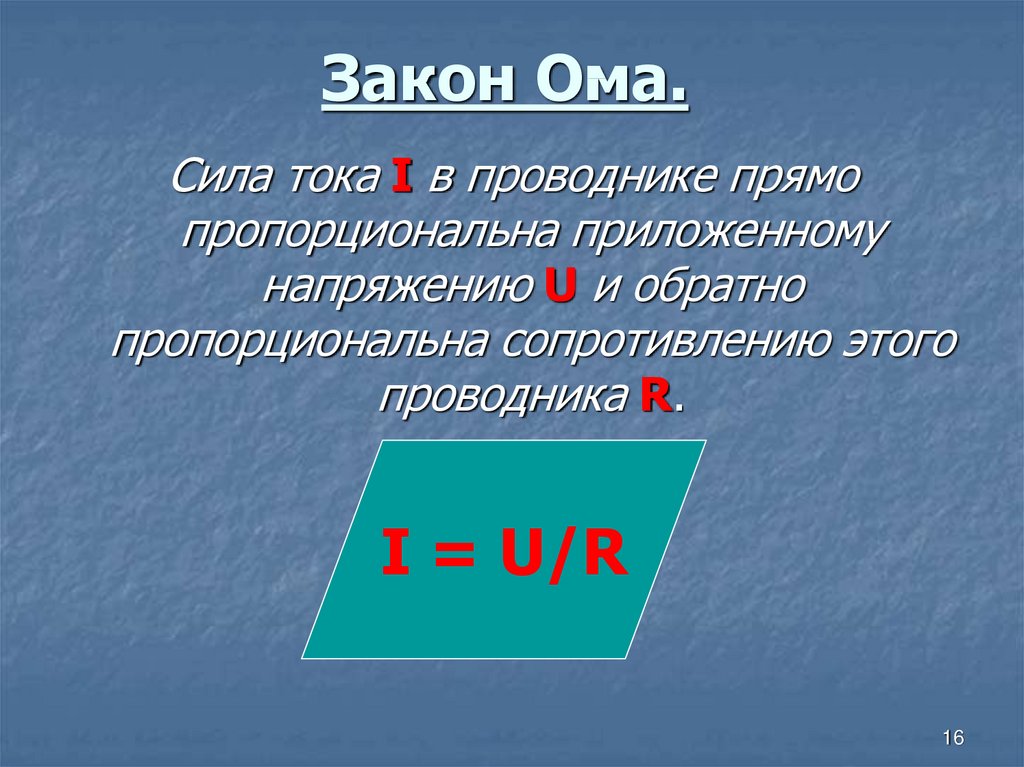
Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления.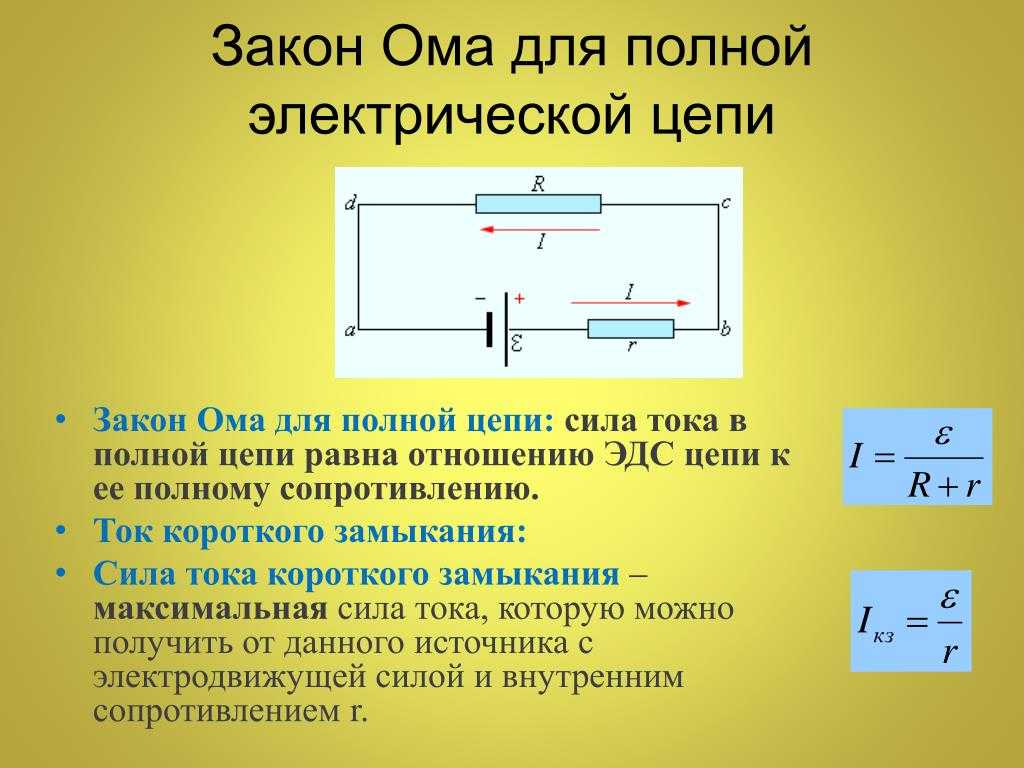 Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Принцип работы одного из основополагающих законов электротехники хочется начать объяснять с аллегории — показа небольшого карикатурного изображения 1 из трех человечков под именами «Напряжение U», «Сопротивление R» и «Ток I».
На нем видно, что «Ток» пытается пролезть через сужение в трубе, которое «Сопротивление» усердно затягивает. В то же время «Напряжение» прилагает максимально возможное усилие для прохождения, проталкивания «Тока».
Этот рисунок напоминает, что электрический ток — это упорядоченное движение заряженных частиц в определенной среде. Передвижение их возможно под действием приложенной внешней энергии, создающей разность потенциалов — напряжение. Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению.
Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению.
Рассмотрим простую схему 2, поясняющую действие закона Ома для участка электрической цепи постоянного тока.
В качестве источника напряжения U используем аккумуляторную батарею, которую подключим к сопротивлению R толстыми и одновременно короткими проводами в точках А и В. Допустим, что провода не влияют на величину прохождения тока I к резистору R.
Формула (1) выражает соотношения между сопротивлением (омы), напряжением (вольты) и током (амперы). Ее называют законом Ома для участка цепи. Кружок под формулой облегчает ее запоминание и пользование для выражения каждого из составляющих параметров U, R или I (U расположено сверху над черточкой, а R и I — снизу).
Если надо определить один из них, то мысленно закрываем его и работаем с двумя оставшимися, выполняя арифметические действия. Когда величины расположены на одной строчке, то их перемножаем. А в случае расположения их на разных уровнях выполняем деление верхнего на нижний.
А в случае расположения их на разных уровнях выполняем деление верхнего на нижний.
Эти соотношения показаны на формулах 2 и 3 рисунка 3 ниже.
В этой схеме для измерения тока используется амперметр, который соединен последовательно с нагрузкой R, а напряжения — вольтметр, подключенный параллельно точкам 1 и 2 резистора. Учитывая конструктивные особенности приборов, допустим, что амперметр не влияет на величину тока в схеме, а вольтметр — напряжения.
Определение сопротивления с помощью закона Ома
Пользуясь показаниями приборов (U=12 В, I=2,5 А) можно по формуле 1 определить величину сопротивления R=12/2,5=4,8 Ом.
На практике этот принцип заложен в работу измерительных приборов — омметров, определяющих активное сопротивление различных электрических устройств. Поскольку они могут быть настроены на замеры различных диапазонов величин, то их соответственно подразделяют на микроомметры и миллиомметры, работающие с малыми сопротивлениями и тера-, гиго- и мегаомметры — измеряющие очень большие значения.
Для конкретных условий эксплуатации их выпускают:
Принцип работы омметра
Для выполнения замеров обычно используются магнитоэлектрические приборы, хотя в последнее время широко внедряются электронные (как аналоговые, так и цифровые).
В омметре магнитоэлектрической системы используется токоограничивающий резистор R, пропускающий через себя только миллиамперы и чувствительная измерительная головка (миллиамперметр). Она реагирует на протекание малых токов через прибор за счет взаимодействия двух электромагнитных полей от постоянного магнита N-S и поля, создаваемого током, проходящим через обмотку катушки 1 с токопроводящей пружинкой 2.
В результате взаимодействия сил магнитных полей происходит отклонение стрелки прибора на определенный угол. Шкала головки для облегчения работы сразу проградуирована в омах. При этом используется выражение сопротивления через ток по формуле 3.
У омметра для обеспечения точных замеров должно поддерживаться стабилизированное значение подаваемого напряжения от батареи питания.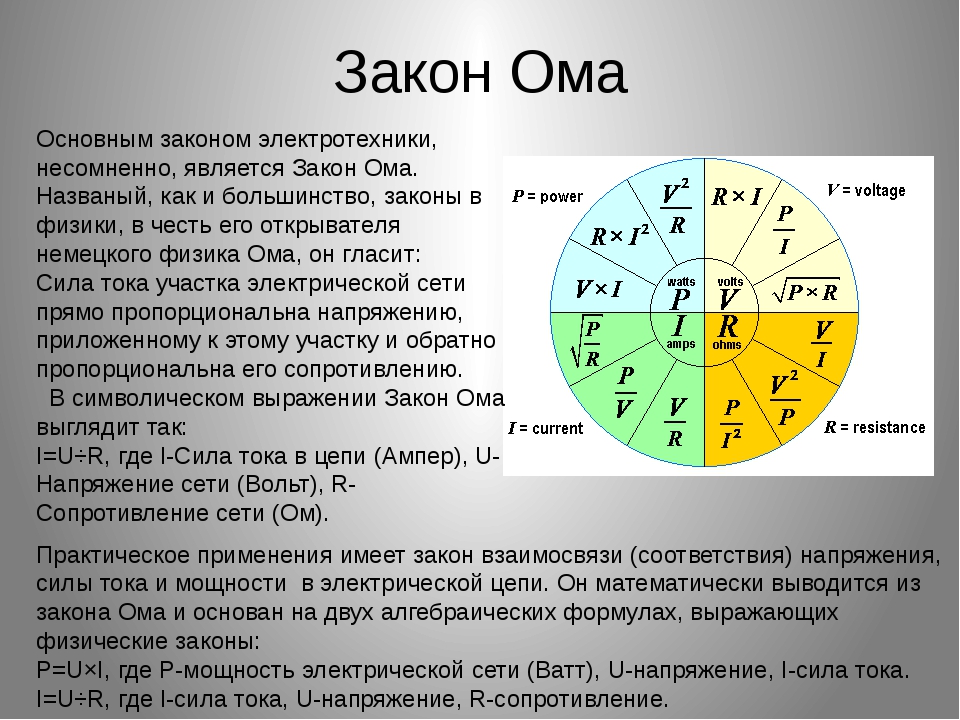 С этой целью применяется калибровка посредством использования добавочного регулировочного резистора R рег. С его помощью до начала измерения на схему ограничивается подача излишнего напряжения от источника, выставляется строго стабильная, нормируемая величина.
С этой целью применяется калибровка посредством использования добавочного регулировочного резистора R рег. С его помощью до начала измерения на схему ограничивается подача излишнего напряжения от источника, выставляется строго стабильная, нормируемая величина.
Определение напряжения с помощью закона Ома
Во время работ с электрическими схемами бывают случаи, когда необходимо узнать падение напряжения на каком-то элементе, например, резисторе, а известно его сопротивление, которое обычно маркируется на корпусе, и проходящий сквозь него ток. Для этого не обязательно подключать вольтметр, а достаточно воспользоваться расчетами по формуле 2.
В нашем случае для рисунка 3 проведем расчеты: U=2,5·4,8 =12 В.
Определение тока с помощью закона Ома
Этот случай описывает формула 3. Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.
В нашем примере расчет выглядит так: I=12/4,8=2,5 А.
Этот способ в электротехнике используют для исключения работы определенных элементов из схемы без их демонтажа. Для этого на ненужном резисторе замыкают накоротко проводником входящую и отходящую клеммы (на рисунке 1 и 2) — шунтируют.
В результате ток схемы выбирает для себя путь с меньшим сопротивлением через шунт и резко возрастает, а напряжение зашунтированного элемента падает до нуля.
Этот режим является частным случаем шунтирования и, в общем-то, показан на рисунке выше, когда закоротка устанавливается на выходные клеммы источника. При его возникновении создаются очень опасные большие токи, способные поражать людей и сжигать не защищенное электрооборудование.
Для борьбы со случайно возникающими замыканиями в электрической сети используют защиты. На них выставляют такие уставки, которые не мешают работать схеме в нормальном режиме. Они отключают питание только при аварийных случаях.
Например, если ребенок по неосторожности всунет в домашнюю розетку проволоку, то правильно настроенный автоматический выключатель вводного квартирного щита практически моментально отключит электроснабжение.
Все, что описано выше, относится к закону Ома для участка цепи постоянного тока, а не полной схемы, где процессов может быть значительно больше. Следует представлять, что это только небольшая часть применения его в электротехнике.
Закономерности, выявленные знаменитым ученым Георгом Симоном Омом между током, напряжением и сопротивлением по-разному описываются в различных средах и цепях переменного тока: однофазных и трехфазных.
Вот основные формулы, выражающие соотношения электрических параметров в металлических проводниках.
Более сложные формулы для проведения специальных расчетов закона Ома на практике.
Как видим, исследования, которые провел гениальный ученый Георг Симон Ом, имеют огромное значение даже в наше время бурного развития электротехники и автоматики.
В природе существует два основных вида материалов, проводящие ток и непроводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).
Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.
В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.
Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.
Формула Закона Ома
В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.
Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.
Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.
где I – сила тока, измеряется в амперах и обозначается буквой А; U – напряжение, измеряется в вольтах и обозначается буквой В; R – сопротивление, измеряется в омах и обозначается Oм.
Если известны напряжение питания U и сопротивление электроприбора R, то с помощью вышеприведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.
| Онлайн калькулятор для определения силы тока | |
|---|---|
| Напряжение, В: | |
| Сопротивление, Ом: | |
С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
| Онлайн калькулятор для определения величины сопротивления | |
|---|---|
| Напряжение, В: | |
| Величина тока, А: | |
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь –
Закон Джоуля-Ленца.
В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь –
Закон Джоуля-Ленца.
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается Вт; U – напряжение, измеряется в вольтах и обозначается буквой В; I – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
| Онлайн калькулятор для определения потребляемой мощности | |
|---|---|
| Напряжение, В: | |
| Сила тока, А: | |
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания.
| Онлайн калькулятор для определения силы тока в зависимости от потребляемой мощности | |
|---|---|
| Потребляемая мощность, Вт: | |
| Напряжение питания, В: | |
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Преобразованные формулы Закона Ома и Джоуля-Ленца
Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения
По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.
А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.
Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.
Три закона Ома
Недавно мы выпустили переиздание книги Фрэнка Вильчека (Frank Wilczek) «Тонкая физика. Масса, эфир и объединение всемирных сил» в мягком переплете. Автор, лауреат Нобелевской премии по физике, излагает современные взгляды на нашу невероятную Вселенную и прогнозирует новый золотой век фундаментальной физической науки. ХХ2 уже публиковали один отрывок из этой замечательной книги, теперь публикуют новый — о том, почему эквивалентные равенства могут поведать нам о разных явлениях.
Из третьей главы. Второй закон Ома
Второй закон Эйнштейна, m = E/c2, поднимает вопрос о том, может ли масса быть понята более глубоко — как энергия. Можем ли мы создать, как выразился Уилер, «массу без массы»?
Когда я ещё только собирался начать преподавать в Принстоне, мой друг и наставник Сэм Трейман позвал меня в свой кабинет. Он хотел поделиться со мной своей мудростью. Сэм вытащил из ящика стола потрёпанное руководство в мягкой обложке и сказал мне: «Во время Второй мировой войны ВМС приходилось в спешке обучать новобранцев налаживанию и использованию радиосвязи. Многие из этих новобранцев прибывали прямо с ферм, так что быстро ввести их в курс дела было очень трудно. С помощью той великолепной книги командованию военно-морского флота это удалось. Это шедевр педагогики. Особенно первая глава. Взгляни».
Сэм вытащил из ящика стола потрёпанное руководство в мягкой обложке и сказал мне: «Во время Второй мировой войны ВМС приходилось в спешке обучать новобранцев налаживанию и использованию радиосвязи. Многие из этих новобранцев прибывали прямо с ферм, так что быстро ввести их в курс дела было очень трудно. С помощью той великолепной книги командованию военно-морского флота это удалось. Это шедевр педагогики. Особенно первая глава. Взгляни».
Он вручил мне книгу, открытую на первой главе. Она называлась «Три закона Ома». Я был знаком с одним законом Ома, известным соотношением V = IR, который связывает напряжение (V), силу тока (I) и сопротивление (R) в электрической цепи.
Это оказалось первым законом Ома.
Мне было очень интересно узнать, каковы два других закона Ома. Перевернув несколько хрупких пожелтевших страниц, я обнаружил второй закон Ома: I = V/R. Я предположил, что третий закон Ома формулируется как R = I/V, и оказался прав.
Открывать новые законы легко
Тем, кто знаком с элементарной алгеброй, так очевидно, что эти три закона эквивалентны друг другу, что данная история воспринимается как шутка. Однако в ней заключён глубокий смысл. (Кроме того, в ней есть и неглубокий смысл, который, как мне кажется, Сэм хотел до меня донести. При обучении начинающих вы должны несколько раз сказать одно и то же, но по-разному. Соотношения, которые бесспорны для профессионала, могут не быть таковыми для новичка. Студенты не будут возражать против объяснения очевидного. Очень немногие люди обижаются, когда вы позволяете им почувствовать себя умными.)
Однако в ней заключён глубокий смысл. (Кроме того, в ней есть и неглубокий смысл, который, как мне кажется, Сэм хотел до меня донести. При обучении начинающих вы должны несколько раз сказать одно и то же, но по-разному. Соотношения, которые бесспорны для профессионала, могут не быть таковыми для новичка. Студенты не будут возражать против объяснения очевидного. Очень немногие люди обижаются, когда вы позволяете им почувствовать себя умными.)
Глубокий смысл содержит заявление великого физика-теоретика Поля Дирака. Когда его спросили, как он открывает новые законы природы, Дирак ответил: «Я играю с уравнениями». Суть в том, что различные способы написания одного и того же уравнения могут говорить о совершенно разных вещах, даже если они являются логически эквивалентными.
Второй закон Эйнштейна
Второй закон Эйнштейна формулируется следующим образом:
m = E/c2.
Первый закон Эйнштейна — это, разумеется, E = mc2. Здорово, что первый закон предполагает возможность получения большого количества энергии из небольшого количества массы. Он наводит на мысль о ядерных реакторах и ядерных бомбах.
Здорово, что первый закон предполагает возможность получения большого количества энергии из небольшого количества массы. Он наводит на мысль о ядерных реакторах и ядерных бомбах.
Второй закон Эйнштейна предполагает нечто совершенно иное.
Он предполагает возможность объяснения того, как масса возникает из энергии.
На самом деле этот закон неправильно называть «вторым».
В оригинальной работе Эйнштейна 1905 года вы не найдёте уравнения E = mc2. Вы встретите уравнение m = E/c2. (Поэтому, возможно, нам следует назвать его нулевым законом Эйнштейна.)
На самом деле в качестве названия этой статьи используется вопрос: «Зависит ли инерция тела от содержащейся в нем энергии?»
Другими словами, может ли некоторое количество массы тела возникать из энергии содержащегося в нем вещества? С самого начала Эйнштейн размышлял о концептуальных основах физики, а не о возможности создания бомб или реакторов.
Понятие энергии играет гораздо более важную роль в современной физике, чем понятие массы.
(Я даже не буду пытаться объяснить, что означает предыдущее утверждение, к счастью, суть заключается в самом факте утверждения.)
Таким образом, вопрос Эйнштейна бросает вызов. Если мы сможем объяснить массу в терминах энергии, мы улучшим наше описание мира. В этом случае в нашем рецепте нам потребуется меньшее количество ингредиентов. Второй закон Эйнштейна позволяет дать хороший ответ на вопрос, который мы задали ранее. Откуда берётся масса? Может быть, из энергии. На самом деле, как мы увидим далее, в основном так и есть.
Источник: https://22century.ru/popular-science-publications/tonkaya-fizika-massa-efir-i-obedinenie-vsemirnyh-sil?
Военно-техническая подготовка
1.
 2. Постоянный ток
2. Постоянный ток
1.2.1. Законы Ома.
Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника.
В своей оригинальной форме он был записан его автором в виде :
,
где X — показания гальванометра, т.е в современных обозначениях сила тока I ;
a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) ;
l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R ;
b
— параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока
r
.
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи :
,
где ε — ЭДС источника напряжения;
I — сила тока в цепи;
R — сопротивление всех внешних элементов цепи;
r — внутреннее сопротивление источника напряжения.
Из закона Ома для полной цепи вытекают следствия:
- При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
-
При
r>>R
сила тока от свойств внешней цепи (от величины нагрузки) не зависит.
 И источник может быть назван источником тока.
И источник может быть назван источником тока.
Часто выражение
,
где есть напряжение, или падение напряжения (или, что то же, разность потенциалов между началом и концом участка проводника), тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
,
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
,
применима другая формулировка:
| << |
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна
|
>> |
Выражение (5) можно переписать в виде:
,
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо, в Международной системе единиц (СИ) единицей измерения проводимости является сименс (русское обозначение: См; международное: S ), величина которого равна обратному Ому.
|
Рис 1. Схема, иллюстрирующая три составляющие закона Ома. |
Рис 2. |
1.2.2. Правила Кирхгофа.
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Законы Кирхгофа, название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного(«почти стационарного») тока.
Для формулировки правил Кирхгофа вводятся понятия
узел
,
ветвь
и
контур
электрической цепи.
Ветвью называют любой двухполюсник, входящий в цепь.
Узлом называют точку соединения трех и более ветвей.
Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
.
Первое правило Кирхгофа гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу равна сумме направленных от узла.
.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило .
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для постоянных напряжений:
для переменных напряжений:
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае.
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Особенности составления уравнений для расчёта токов и напряжений .
Если цепь содержит p узлов, то она описывается
p
— 1
уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит m ветвей, из которых содержат источники тока ветви в количестве m i , то она описывается m – m i – ( p — 1) уравнениями напряжений.
-
Правила Кирхгофа, записанные для
p
— 1
узлов или
m
– (
p
— 1)
контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.

- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
-
При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (
достаточное, но не необходимое условие
).

|
Рис 3. Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4 |
Рис 4. На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»). |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Закон ОмаГеорг Симон Ом (1787-1854) сформулировал взаимосвязь между напряжением, током и сопротивлением следующим образом:  Схема ниже демонстрирует эти взаимосвязи.
Математически закон Ома можно записать как: где I ток в амперах, E — приложенное напряжение в вольтах, а R — сопротивление в омах. Эта схема содержит амперметр, измеряющий ток в миллиамперах. Обратите внимание, что при увеличении напряжения увеличивается ток. По мере увеличения сопротивления ток уменьшается. Важно отметить, что сопротивление нельзя изменить, изменив напряжение или ток. Сопротивление в цепи является физической константой. Сопротивление в цепи можно изменить только заменой компонентов или резисторов с номиналом больше или меньше Ом. Изменение сопротивления в этой схеме имитирует физическое изменение резисторов с разными номиналами. Узнайте, как резисторы имеют цветовую маркировку, в нашем интерактивном учебном пособии по резисторам Java . ВЕРНУТЬСЯ К РУКОВОДСТВУ ПО ЭЛЕКТРИЧЕСТВУ И МАГНИТИЗМУ Вопросы или комментарии? Отправить нам письмо.© 1995-2022 автор Майкл В. Дэвидсон и Университет штата Флорида. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами.Этот веб-сайт поддерживается нашимГруппа графического и веб-программирования в сотрудничестве с Optical Microscopy в Национальной лаборатории сильного магнитного поля. Последнее изменение: среда, 7 июня 2017 г., 12:03Количество обращений с 14 апреля 1999 г. : 555167 : 555167
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что такое закон Ома? Объяснение, формула и пример решения
Что такое закон Ома? Объяснение, формула и пример решения
Закон Ома
Связь между током через проводник и напряжением на проводнике была впервые открыта немецким ученым Джорджем Саймоном Омом. Это соотношение называется законом Ома, который можно сформулировать как;
Ток «I», протекающий по проводнику, прямо пропорционален разности потенциалов, т. е. напряжению «V» на его концах, при условии, что физические условия (например, температура, деформация и т. д.) не меняются.
Другими словами;
В любой электрической цепи ток «I» прямо пропорционален приложенному напряжению «V» и обратно пропорционален общему сопротивлению цепи «R», если физическое состояние цепи остается неизменным, т. е. (температура цепи не изменяется)
Математически,
I ∝ V … или … V ÷ I => =>
Ток = Разность потенциалов ÷ Сопротивление
I = V ÷ R
Похожие сообщения:
- Закон электромагнитной индукции Ленца
- Что такое закон Фарадея? Законы электромагнитной индукции
- Что такое закон Кулона? Законы электростатики на примере
Формулы и уравнения закона Ома
Для расчета и упрощения электрических цепей (измерение тока, напряжения и сопротивления) мы можем использовать закон Ома в следующих трех формах
1.
V = I x R
VOLTAGE = CURCE X COSSAVAND
VOLT = AM AMP X OHMS (ω)
VOLT = AMP X OHMS (ω)
VOLT = AM AMP X OHMS (ω)
.
Current = Voltage ÷ Resistance
Amps = Volts ÷ Ohms (Ω)
3.
R = V ÷ I
Resistance = Voltage ÷ Current
Ohms (Ом) = Вольт ÷ Ампер
Где:
- В = напряжение в вольтах
- I = ток в амперах
- R = сопротивление в омах (Ом)
Лучшее забавное объяснение закона Ома
Щелкните изображение, чтобы увеличить его
Закон Ома: простое и забавное объяснение- Или другой забавный способ объяснить закон Ома
Нажмите на изображение, чтобы увеличить
Толкающая нагрузка на откосе аналогия для понимания закона Ома0358Как рассчитать электрические цепи с помощью закона Ома
Закон Ома можно использовать для упрощения и анализа как простых, так и сложных электрических цепей. Существует несколько версий и уравнений, используемых для нахождения значений различных величин, таких как электрический ток, напряжение и сопротивление цепи.
Существует несколько версий и уравнений, используемых для нахождения значений различных величин, таких как электрический ток, напряжение и сопротивление цепи.
Закон Ома можно применить к части или всей цепи сразу. Если применяется ко всей электрической цепи, общее напряжение делится на общее сопротивление цепи, чтобы узнать значение полного тока, протекающего в цепи. С другой стороны, если вы хотите определить и рассчитать ток в определенной части цепи, вам придется разделить напряжение этой части на соответствующее сопротивление.
Пример:
Если приложенное напряжение в цепи составляет 50 В, а в цепи последовательно подключен резистор, сопротивление которого составляет 10 Ом, то каким будет ток в этой цепи?
Решение:
Простой пример закона Ома- Похожие сообщения:
- Теорема Тевенина. Пошаговая процедура с решенным примером
- Теорема Нортона. Простая пошаговая процедура с примером (иллюстрации)
- Анализ схемы СУПЕРУЗЛА | Шаг за шагом с решенным примером
- Анализ цепей SUPERMESH | Шаг за шагом с решенным примером
- Теорема о максимальной передаче мощности для цепей переменного и постоянного тока
- Закон тока и напряжения Кирхгофа (KCL и KVL) | Решенный пример
- Теорема о компенсации – доказательство, объяснение и примеры решения
- Теорема о подстановке – пошаговое руководство с решенным примером
- Теорема Миллмана.
 Анализ цепей переменного и постоянного тока. Примеры
Анализ цепей переменного и постоянного тока. Примеры - Теорема о суперпозиции — анализ цепей с решенным примером
- Теорема Теллегена – Решенные примеры и моделирование MATLAB
- Правило делителя напряжения (VDR) — примеры решений для цепей R, L и C
- Правило делителя тока (CDR) – Решенные примеры для цепей переменного и постоянного тока
- Преобразование звезды в дельту и дельты в звезду. Преобразование Y-Δ
- Закон Эрстеда для магнитного поля прямолинейного проводника с током
- Правая рукоятка/правило большого пальца, правило штопора и правило конца/часа
Показать полную статью
Похожие статьи
Кнопка «Вернуться к началу»
L3: Закон Ома — физические вычисления
Содержание
- Закон Ома
- Связь закона Ома с нашими аналогиями с водой
- Почему \(I\), а не \(C\)?
- Обязательно используйте базовые единицы
- Общие префиксы SI
- Преобразование единиц
- Давайте проанализируем некоторые схемы!
- Пример 1: Нахождение текущего
- Шаг 1: Определение известных значений
- Шаг 2: Применение известных значений
- Шаг 3: Решение текущего значения I
- Пример 2.
 Повторное вычисление тока (но с другим сопротивлением)
Повторное вычисление тока (но с другим сопротивлением) - Пример 3. Расчет напряжения
- Пример 4. Расчет сопротивления
- Пример 1: Нахождение текущего
- Упражнение: Использование симулятора цепей
- Next Lesson
В этом уроке мы изучим Закон Ома , один из наиболее важных эмпирических законов в электрических цепях, который описывает, как ток , напряжение и сопротивление связаны друг с другом. Хотя закон Ома невероятно полезен для анализа и понимания того, как работают схемы, как и многие «законы», он не всегда соблюдается (особенно для так называемых «неомических» устройств, таких как светодиоды или другие диоды). Но мы к этому еще вернемся.
А пока закон Георга Ома!
Закон Ома
В 1827 году, после многих лет экспериментов, немецкий физик Георг Симон Ом опубликовал « Математическое исследование гальванической цепи».0433», который стал основой для закона Ома. Закон Ома гласит, что ток (\(I\) в амперах) в проводнике прямо пропорционален приложенному напряжению (\(V\) в вольтах) против сопротивления проводника (\(R\) в омах) :
\[I = \frac{V}{R}\]
Таким образом, если мы удвоим напряжение в нашей цепи, например, последовательно собрав две батареи, мы также удвоим ток.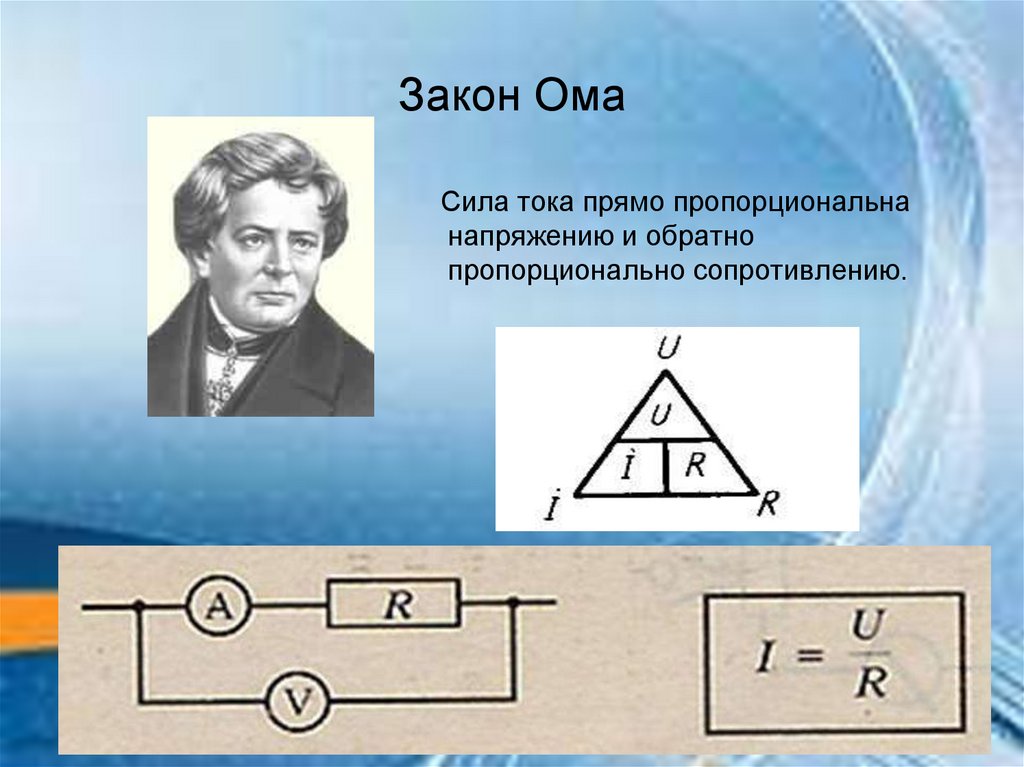 Закон Ома имеет множество последствий для того, как мы строим и используем схемы с микроконтроллерами, включая делители напряжения и резистивные датчики.
Закон Ома имеет множество последствий для того, как мы строим и используем схемы с микроконтроллерами, включая делители напряжения и резистивные датчики.
Важно отметить, что вы увидите и будете использовать закон Ома во всех трех эквивалентных воплощениях (которые можно вывести с помощью простой алгебры):
{V}{R}\)
Чтобы найти напряжение , используйте: \(V = I * R\)
Чтобы найти сопротивление , используйте: \(R = \frac{V}{I }\)
Обратите внимание, как эти уравнения соответствуют понятиям, которые мы объяснили в нашем первом уроке о напряжении, токе и сопротивлении, к которому вы, возможно, захотите вернуться. Например, \(I = \frac{V}{R}\) ясно демонстрирует, что до увеличить ток , мы можем либо увеличить напряжение , либо уменьшить сопротивление .
Связь закона Ома с нашими аналогиями с водой
Снова опираясь на наши гидравлические и электрические аналогии (которые мы широко использовали в предыдущих уроках), мы можем выделить еще одно сходство. В 1840-х годах Пуазей эмпирически показал, что расход воды через трубу равен перепаду давления в трубе, деленному на сопротивление трубы — это называется .Закон Пуазейля . И это концептуально имеет смысл: более высокая разница давлений между двумя концами трубы создает большую силу, а более низкое сопротивление обеспечивает больший поток воды.
В 1840-х годах Пуазей эмпирически показал, что расход воды через трубу равен перепаду давления в трубе, деленному на сопротивление трубы — это называется .Закон Пуазейля . И это концептуально имеет смысл: более высокая разница давлений между двумя концами трубы создает большую силу, а более низкое сопротивление обеспечивает больший поток воды.
Это уравнение звучит знакомо? Должно. Это точно закон Ома! Ток в цепи прямо пропорционален падению напряжения в цепи, деленному на ее сопротивление. См. изображение ниже.
Рис. Закон Пуазейля для плавного течения жидкости и закон Ома для электрического тока аналогичны. Изображение основано на HyperPhysics в штате Джорджия и создано в PowerPoint. Изображения Пуазейля и Ома взяты из Википедии.
ПРИМЕЧАНИЕ:
Уравнение закона Пуазейля верно только для плавного (ламинарного, а не турбулентного) потока ньютоновской жидкости, такой как вода. Но такое условие не относится к электрическому току.
Почему \(I\), а не \(C\)?
Вы можете спросить: «Если \(R\) — сопротивление r в омах (Ом), а V — напряжение v в вольтах (В), то почему \(I\) используется для представления c ток в амперах (А), а не \(С\)?» Две причины: во-первых, \(C\) уже зарезервировано для единицы СИ колумбов (C), которая используется в самом определении ампер (напомним, что \(1\A = 1\C/s\)) и таким образом, можно запутаться! Во-вторых, ампер назван в честь Андре-Мари Ампера, считающегося отцом электромагнетизма, который называл силу тока « i ntensité du courant» или « i ntensité du courant». Итак, ток равен \(I\), а не \(C\).
Обязательно используйте базовые единицы измерения
Обычная ошибка при применении закона Ома или анализе цепей в целом — это неправильная установка базовых единиц. В цифровых схемах мы часто имеем дело с 90 439 кОм (кОм) 90 440 — что составляет 1000 Ом — 90 439 миллиампер (мА) 90 440 — что равно \(\frac{1}{1000}\) (0,001) ампера — или даже микроамперы (мкА), что составляет одну миллионную (\(\frac{1}{1 000 000}\) или 0,000001) ампера, и так далее. Нам нужно преобразовать эти единицы в базовых единиц в вольтах (В), омах (Ом) и амперах (А) для выполнения нашего анализа.
Нам нужно преобразовать эти единицы в базовых единиц в вольтах (В), омах (Ом) и амперах (А) для выполнения нашего анализа.
Например, если цепь содержит резистор 2,2 кОм с батареей 9 В, для расчета тока ошибочно не пишут \(I = \frac{9V}{2,2Ω}A\), а вместо этого \(I = \фракция {9В} {2200 Ом} А\). Первый даст вам 4,1 А (большая сила тока и неправильная!), а второй даст вам правильное значение 0,0041 А, что составляет 4,1 мА.
Так что всегда проверяйте свои юниты дважды!
Общие префиксы SI 9{-12} \)
Таблица . Этот диаграмма основан на Metric Si Prefixes и Fighttit.
Преобразование единиц
Чтобы преобразовать единицу измерения с приставкой в базовую единицу, мы умножаем на коэффициент преобразования. Чтобы преобразовать базовую единицу в единицу с префиксом, мы делим на коэффициент преобразования. 9{-6}} = 37 мкА\).
9{-6}} = 37 мкА\).
Давайте проанализируем некоторые схемы!
Уф, хорошо, теперь мы готовы начать анализ некоторых цепей. Мы начнем с простой схемы и пойдем оттуда. При анализе (или даже подготовке к сборке) схем всегда полезно взять карандаш и бумагу. Пожалуйста, сделайте это сейчас.
Кроме того, полезно иметь возможность проверить нашу работу, что мы можем сделать в симуляторе схемы. Мне нравится использовать CircuitJS, но я также использовал EveryCircuit и CircuitLab — последний стоит денег.
Прежде чем мы начнем, давайте посмотрим это видео, в котором я создаю простую резистивную цепь в CircuitJS и вычисляю ее ток с учетом источника напряжения и резистора.
Видео Видео было создано с помощью симулятора CircuitJS. Прямая ссылка здесь.
Прямая ссылка здесь.
Пример 1: Найдите ток
Представьте схему с батарейным питанием и одним резистором (базовым, да, но педагогически мощным!). Если нам даны напряжение \(9V\) и сопротивление (\(100Ω\)), можем ли мы найти ток \(I\)?
Рис. Простая схема с питанием 9 В с одним резистором \(100 Ом\). Используя закон Ома, можете ли вы найти ток \(I\)? Изображения сделаны во Fritzing и PowerPoint.
Шаг 1: Идентифицируйте известные
Чтобы начать анализ, вам нужно определить все, что вы знаете об этой схеме.
Обратите внимание, что все провода, соприкасающиеся с положительной клеммой аккумулятора , имеют одинаковый электрический потенциал (\(9В\)) — который мы сейчас отметили красным — и все провода, соприкасающиеся с 0432 отрицательная клемма аккумулятора имеет одинаковый электрический потенциал (\(0V\)) — который мы отметили черным цветом. Обратите внимание, что даже несмотря на то, что медные провода имеют некоторое сопротивление, оно настолько мало (особенно для длин цифровых цепей), что мы можем смоделировать его как \(0 Ом\) (действительно, провода всегда предполагаются \(0 Ом\) в таком виде). схемотехнического анализа).
схемотехнического анализа).
И поскольку мы вычисляем ток, нам нужно использовать формулировку закона Ома: \(I = \frac{V}{R}\). Точнее, поскольку напряжение всегда относительно, электрический потенциал разность — используем \(I = \frac{V_1 — V_2}{R}\)
Рис. Все провода, соприкасающиеся с положительной клеммой аккумулятора, имеют одинаковое напряжение (9 В). Точно так же все провода, соприкасающиеся с отрицательной клеммой аккумулятора, имеют одинаковое напряжение (0 В). Изображения сделаны во Fritzing и PowerPoint.
Шаг 2: Применение известных
Установив, что все провода в верхней части цепи (те, что непосредственно подключены к положительной клемме) имеют одинаковый электрический потенциал, мы можем пометить ее как одну узел \(V_1\) . Точно так же все провода, соприкасающиеся с отрицательной клеммой аккумулятора, можно назвать узлом \(V_2\) .
Теперь мы можем заменить \(9V\) на \(V_1\) и \(0V\) на \(V_2\). И мы также знаем, что \(R=100 Ом\), что дает нам полное уравнение: \(I = \frac{9V — 0V}{100Ω}\)
И мы также знаем, что \(R=100 Ом\), что дает нам полное уравнение: \(I = \frac{9V — 0V}{100Ω}\)
Рис. Мы можем назвать все провода, соприкасающиеся с узлом положительной клеммы аккумулятора \(V_1\), и все провода, соприкасающиеся с узлом отрицательной клеммы, \(V_2\). Используя эту информацию, мы можем заменить \(9V\) для \(V_1\) и \(0V\) для \(V_2\). Изображения сделаны во Fritzing и PowerPoint.
Шаг 3: Решите для тока I
Наконец, мы готовы решить для тока \(I = \frac{9V — 0V}{100Ω} \Rightarrow 0.09A \Rightarrow 90mA\)
Мы это сделали . Мы успешно применили закон Ома для определения тока!
Пример 2: Снова вычислить ток (но с другим сопротивлением)
Попробуем снова найти ток с аналогичной схемой. На этот раз сопротивление было увеличено с \(100 Ом\) до \(4,7 кОм\).
Прежде чем делать что-либо еще: полезно подумать о концептуально что произойдет?
Ток уменьшается, верно? И делает это пропорционально.
Действительно, ток идет от \(90мА\) при \(100Ом\) до \(I = \frac{9В}{4700Ом} \Rightarrow 0,0019𝐴 \Rightarrow 1,9𝑚𝐴\), что не очень много!
Рис. Как и ожидалось, ток \(I\) падает, а сопротивление \(R\) растет.
Пример 3: Решение для напряжения
Как отмечалось выше, мы можем использовать три различные формулировки закона Ома (\(I=\frac{V}{R}\), \(V=I*R\) и \(R=\frac{V }{I}\)) чтобы помочь нам проанализировать различные неизвестные в цепи.
В этом случае давайте воспользуемся законом Ома для решения неизвестного источника напряжения . Предположим, что схема похожа на предыдущую: один источник напряжения (но неизвестного напряжения) с одним резистором размером \(100 Ом\) и током \(I=50 мА\).
Поскольку мы вычисляем напряжение, мы должны использовать формулу \(V=I*R\). Первое, что нам нужно сделать, это убедиться, что все наши измерения находятся в база шт. . Ток не указан, поэтому измените его на силу тока (а не на миллиампер): \(I=50 мА \Rightarrow 0,05A\).
Теперь мы можем легко найти \(V = 0,05 A * 100 Ом = 5 В\). Аккумулятор является источником напряжения \(5V\).
Рис. Используя \(V=I*R\) формулировку закона Ома, мы можем найти напряжение при известном токе \(I\) и известном сопротивлении \(R\). Изображения сделаны во Fritzing и PowerPoint.
Пример 4: Найти сопротивление
Держу пари, теперь ты освоишься!
Наконец, вы можете использовать \(R=\frac{V}{I}\) для определения сопротивления, если известны \(V\) и \(I\). В этом случае давайте вернемся к нашей батарее \(9 В\) и предположим, что у нас есть ток \(1,32 мА\). Каково значение резистора \(R\)?
Опять же, первое, что нужно сделать, это перевести все единицы измерения в базовые единицы. Итак, \(1,32 мА \стрелка вправо 0,00132 А\).
Теперь мы можем найти \(R = \frac{9V}{0,00132A} \Rightarrow 6818,2 Ом \Rightarrow 6,8 кОм\)
Рис. Используя \(R=\frac{V}{I}\) формулировку закона Ома, мы можем найти сопротивление \(R\) при известном напряжении \(V\) и известном токе \(I\ ). Изображения сделаны во Fritzing и PowerPoint.
Изображения сделаны во Fritzing и PowerPoint.
Упражнение: Использование симулятора цепей
Теперь, когда мы получили начальное представление о законе Ома, пришло время построить и поиграть с некоторыми схемами в симуляторе цепей.
Используя CircuitJS, создайте и проанализируйте пять различных типов резистивных цепей. Вы можете создавать любые схемы, которые хотите, соблюдая несколько требований:
- Все цепи должны иметь только один источник питания.
- Вы должны использовать только резисторы. , сделайте снимок экрана и поместите его в свой журнал прототипирования вместе с кратким описанием того, что вы наблюдали/узнали.
Вы можете сохранить свои схемы одним из двух способов: (1) загрузить их локально (Файл -> Сохранить как) или (2) экспортировать их как общую ссылку (Файл -> Экспортировать как ссылку) — используйте последний вариант. для ваших журналов прототипирования.
В свои журналы прототипирования включите скриншот каждой схемы CircuitJS вместе с кратким описанием того, что вы наблюдали, и прямой ссылкой на созданную вами схему CircuitJS.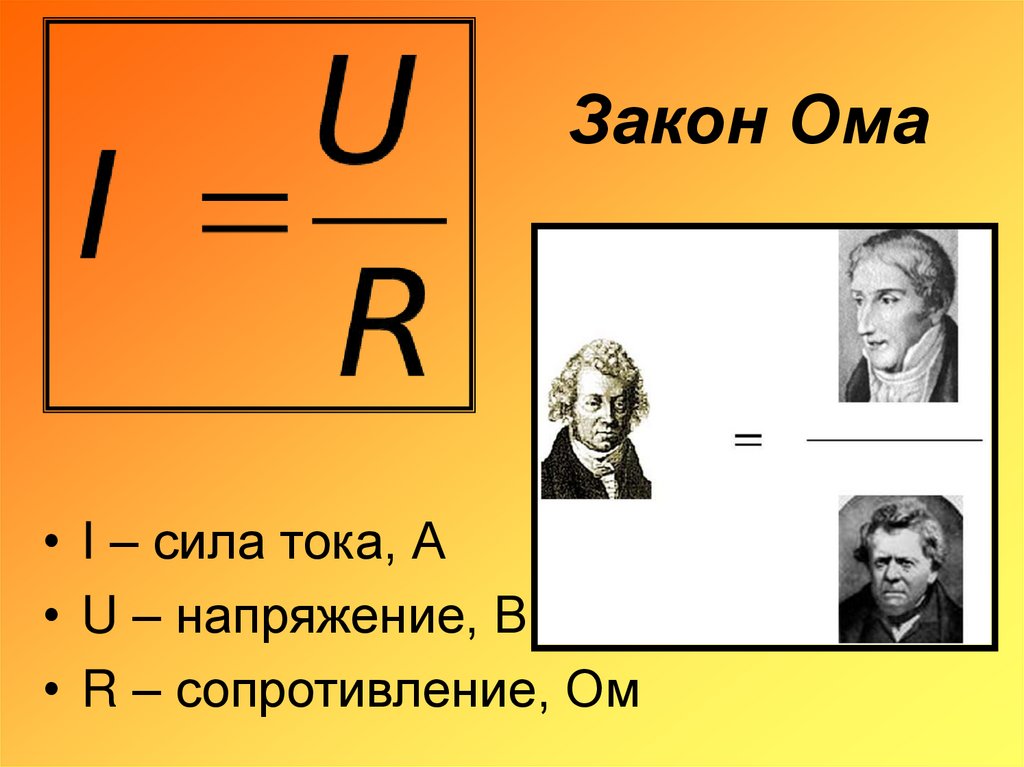


 Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

