Что такое последовательное соединение проводников. Как рассчитать общее сопротивление при последовательном соединении. Каковы особенности параллельного соединения проводников. Как определить эквивалентное сопротивление параллельной цепи. Где применяются различные типы соединений.
Основные типы соединений проводников в электрических цепях
В электротехнике выделяют два основных способа соединения проводников и элементов электрической цепи:
- Последовательное соединение
- Параллельное соединение
Каждый тип соединения имеет свои особенности и законы, определяющие распределение токов, напряжений и сопротивлений в цепи. Понимание этих законов критически важно для расчета и проектирования электрических схем.
Последовательное соединение проводников
При последовательном соединении элементы цепи подключаются один за другим, образуя неразветвленную цепь. Основные свойства такого соединения:
- Сила тока одинакова во всех элементах цепи
- Общее напряжение равно сумме напряжений на отдельных элементах
- Общее сопротивление равно сумме сопротивлений всех элементов
Закон последовательного соединения для силы тока
Сила тока I одинакова во всех последовательно соединенных элементах:

I = I1 = I2 = I3 = … = In
Это объясняется тем, что заряды не накапливаются в узлах цепи — сколько зарядов вошло в участок цепи, столько же и вышло.
Закон для напряжения при последовательном соединении
Общее напряжение U на участке цепи равно сумме напряжений U1, U2, U3 и т.д. на отдельных элементах:
U = U1 + U2 + U3 + … + Un
Расчет общего сопротивления последовательной цепи
Общее сопротивление R последовательной цепи равно сумме сопротивлений R1, R2, R3 и т.д. всех ее элементов:
R = R1 + R2 + R3 + … + Rn
Это свойство позволяет увеличивать общее сопротивление цепи, добавляя последовательно включенные резисторы.
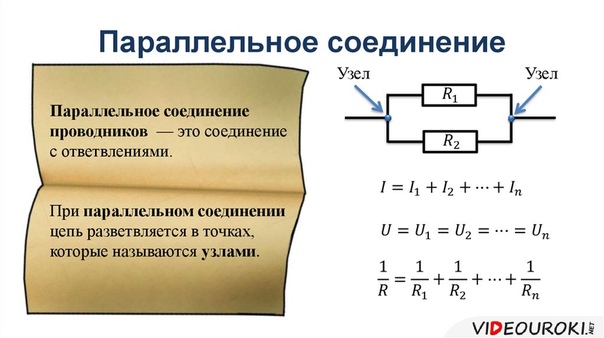
Параллельное соединение проводников
При параллельном соединении все элементы подключаются к одним и тем же двум точкам цепи. Основные свойства:
- Напряжение одинаково на всех элементах
- Общий ток равен сумме токов через отдельные элементы
- Обратная величина общего сопротивления равна сумме обратных величин сопротивлений элементов
Закон параллельного соединения для напряжения
Напряжение U одинаково на всех параллельно соединенных элементах:

U = U1 = U2 = U3 = … = Un
Закон токов для параллельного соединения
Общий ток I в неразветвленной части цепи равен сумме токов I1, I2, I3 и т.д. в отдельных ветвях:
I = I1 + I2 + I3 + … + In
Расчет эквивалентного сопротивления параллельной цепи
Для расчета общего сопротивления R параллельной цепи используется формула:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Эта формула показывает, что общее сопротивление параллельной цепи всегда меньше сопротивления любого из ее элементов.
Применение различных типов соединений
Выбор типа соединения элементов зависит от требуемых характеристик электрической цепи:
Использование последовательного соединения
- Для увеличения общего сопротивления цепи
- В делителях напряжения
- В многодиапазонных измерительных приборах
- Для защиты чувствительных элементов от перегрузки
Применение параллельного соединения
- Для уменьшения общего сопротивления цепи
- В бытовой электропроводке для независимого включения приборов
- В системах резервирования для повышения надежности
- В шунтах измерительных приборов
Понимание законов последовательного и параллельного соединения проводников позволяет грамотно проектировать электрические схемы и эффективно управлять параметрами электрических цепей.
Смешанное соединение проводников
В реальных электрических схемах часто встречается комбинация последовательного и параллельного соединения элементов. Такое соединение называется смешанным или комбинированным.
Особенности расчета смешанных цепей
При расчете смешанных цепей используют следующий алгоритм:
- Выделяют участки с чисто последовательным или параллельным соединением
- Заменяют эти участки эквивалентными сопротивлениями
- Повторяют процесс, пока вся схема не сведется к одному эквивалентному сопротивлению
Такой подход позволяет рассчитать даже сложные разветвленные электрические цепи.
Практическое применение знаний о соединениях проводников
Понимание законов соединения проводников имеет широкое практическое применение:
- Проектирование электрических схем различных устройств
- Расчет и монтаж систем электроснабжения
- Диагностика и ремонт электрооборудования
- Разработка измерительных приборов
- Оптимизация энергопотребления электрических систем
Грамотное использование различных типов соединений позволяет создавать эффективные и безопасные электрические системы в самых разных областях техники.

Урок физики в 8-м классе «Законы последовательного соединения проводников»
Цель:
- Изучить закономерности последовательного соединения потребителей тока.
- Раскрыть взаимозависимость I, U и R.
- Формировать умения рассчитывать электрические цепи с последовательным соединением проводников.
Ход урока
Изучая тему «Электрический ток», мы встречались с целым рядом физических величин. Назовите их пожалуйста ?
- Сила тока; обозначается буквой — I; единица измерения — 1А; прибор для определения – амперметр; физический смысл — характеризует электрический ток.
- Напряжение; обозначается буквой — U; единица измерения — 1В; прибор для определения – вольтметр; физический смысл – характеризует электрическое поле.
- Сопротивление; обозначается буквой — R; единица измерения – 1Ом; физический смысл – характеризует проводник.
- Физические величины: выражаются числом, их измеряют приборами, связь между ними выражается математическим соотношением.
Физические величины сила тока, напряжение и сопротивление – связаны между собой законом. Каким же?
- Закон Ома.
Как зависит сила тока от напряжения?
- Сила тока прямо пропорциональна напряжению на концах проводника, если при этом сопротивление проводника не меняется. График (рис.1).
Как зависит сила тока от сопротивления?
- Сила тока в проводнике обратно пропорциональна сопротивлению проводника, при условии, что напряжение не меняется. График (рис.2).
Так как сопротивление характеризует проводник значит оно зависит от ?
- Длинны проводника, площади сечения проводника, удельного сопротивления проводника.
Эту зависимость можно выразить формулой. Какой?
- R =
Что такое электрическая цепь?
- Различные соединения источников и потребителей электрического тока.
Простейшую электрическую цепь составляют ?
- Источник, потребитель, ключ, провода.
Потребителей много, это показывает практика; часто приходится включать не один, а несколько потребителей. Их можно включать разными способами. Какими ?
- Последовательно и параллельно.
Постройте в тетради схемы: 1 вариант – последовательного соединения потребителей, 2 вариант – параллельного соединения потребителей. Затем поменялись тетрадями взаимоконтроль.
И так тема нашего урока «Законы последовательного соединения проводников»
Соберем схему (рис.3):
Что будет, если одну вывернуть?
- Если вывернуть одну лампу, о вторая тоже погаснет, т.к. цепь разомкнется.
Вывод: особенность последовательного соединения — в ней отсутствуют разветвления: «конец» первого провода соединен с «началом» второго и т.д.
Проверим на нашей цепи и по схеме в учебнике ( рис. 78 стр. 111)
Выясним закономерности последовательного соединении:
- Начнем с силы тока. В ходе лабораторной работы № 4 мы выяснили, что при последовательном соединении сила тока в любых частях цепи одинакова:
I= I1 =I2 =I3
- А чему равно сопротивление последовательного соединённых проводников? Соединяя проводники последовательно, мы как бы увеличивали длину проводника, что же при этом можно сказать о сопротивлении цепи? Сопротивление становится больше сопротивления одного проводника, т.к.
из этого можно сделать вывод: общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников
R=R1+R2+R3.
- Осталось выяснить вопрос с напряжением. Для этого воспользуемся законом Ома (вспомним ещё раз его!).
Вывод: значит напряжение будет большим на проводнике с наибольшим сопротивлением значит
U=U1+U2+U3
Полное напряжение в цепи при последовательном соединении равно сумме напряжений на отдельных участках.
Эту формулу можно и вывести из закона Ома , т.е. доказать.
В ходе лабораторной работы № 5 «Измерение напряжения на различных участках электрической цепи». Мы выяснили, что напряжение на участке из двух спиралей было равно сумме напряжений на каждой спирали.
U = U1+ U2
Все приведенные закономерности справедливы для любого числа последовательно соединенных проводников.
Проверим экспериментально полученные соотношения. На опыте определим R и U. При последовательно соединенных проводниках.
Соберем цепь (рис.4): амперметр, вольтметр, 2 спирали , источник тока, реостат и ключ.
Амперметр – только
последовательно !!!
Вольтметр – только параллельно !!!
- Замкнем цепь.
- Определим показания амперметра (обратить внимание на цену деления!). Везде одинаково. I = I1 = I2 = 1А
- Подсоединим вольтметр (параллельно) к первой спирали. U1 = 2 В
- Вычислим сопротивление:
- Подсоединим вольтметр (параллельно) ко второй спирали.
- Подсоединим вольтметр (параллельно) к двум спиралям.
- Вычислим напряжение: U = U1 + U2= 2В + 4В = 6 В
Что и требовалось доказать! Молодцы!
Закон последовательного соединения проводников. Последовательное соединение сопротивлений. Задача на параллельное и последовательное
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R = 1/U , где R = 1 Ом
А мощность будет выделяться P = I * U , то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I = U * G &
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.
Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.
Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.
При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.
Последовательное соединение проводников
Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.
Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.
При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.
Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.
В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
Параллельное соединение проводников
В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.
При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу .
В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.
При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.
Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к . То есть все приборы подключаются независимо от подключения прочих устройств.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Смешанное соединение проводников
Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной или их группе, такое тип считается комбинированным или смешанным.
В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного. Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.
В электротехнике и электронике очень широко используются резисторы. Применяются они в основном для регулирования в схемах тока и напряжения. Основные параметры: электрическое сопротивление (R) измеряется в Омах, мощность (Вт) , стабильность и точность их параметров в процессе эксплуатации. Можно вспомнить ещё множество его параметров, — ведь это обычное промышленное изделие.
Последовательное соединение
Последовательное соединение — это такое соединение, при котором каждый последующий резистор подключается к предыдущему, образуя неразрывную цепь без разветвлений. Ток I=I1=I2 в такой цепи будет одинаковым в каждой её точке. Напротив, напряжение U1, U2 в различных её точках будет разным, причём работа по переносу заряда через всю цепь, складывается из работ по переносу заряда в каждом из резисторов, U=U1+U2. Напряжение U по закону Ома равно току, умноженному на сопротивление, и предыдущее выражение можно записать так:
где R — общее сопротивление цепи. То есть по простому идет падение напряжения в точках соединения резисторов и чем больше подключенных элементов, тем больше происходит падение напряжения
Отсюда следует, что
, общее значение такого соединения определяется суммированием сопротивлений последовательно. Наши рассуждения справедливы для любого количества последовательно соединяемых участков цепи.
Параллельное соединение
Объединим начала нескольких резисторов (точка А). В другой точке (В) мы соединим все их концы. В результате получим участок цепи, который называется параллельным соединением и состоит из некоторого количества параллельных друг другу ветвей (в нашем случае – резисторов). При этом электрический ток между точками А и B распределится по каждой из этих ветвей.
Напряжения на всех резисторах будут одинаковы: U=U1=U2=U3, их концы — это точки А и В.
Заряды, прошедшие за единицу времени через каждый резистор, в сумме образуют заряд, прошедший через весь блок. Поэтому суммарный ток через изображенную на рисунке цепь I=I1+I2+I3.
Теперь, использовав закон Ома, последнее равенство преобразуется к такому виду:
U/R=U/R1+U/R2+U/R3.
Отсюда следует, что для эквивалентного сопротивления R справедливо:
1/R=1/R1+1/R2+1/R3
или после преобразования формулы мы можем получить другую запись, такого вида:
.
Чем большее количество резисторов (или других звеньев электрической цепи, обладающих некоторым сопротивлением) соединить по параллельной схеме, тем больше путей для протекания тока образуется, и тем меньше общее сопротивление цепи.
Следует отметить, что обратная сопротивлению величина называется проводимостью. Можно сказать, что при параллельном соединении участков цепи складываются проводимости этих участков, а при последовательном соединении – их сопротивления.
Примеры использования
Понятно, что при последовательном соединении, разрыв цепи в одном месте приводит к тому, что ток перестает идти по всей цепи. Например, ёлочная гирлянда перестаёт светить, если перегорит всего одна лампочка, это плохо.
Но последовательное соединение лампочек в гирлянде даёт возможность использовать большое количество маленьких лампочек, каждая из которых рассчитана на напряжение сети (220 В), делённое на количество лампочек.
Последовательное соединение резисторов на примере 3-х лампочек и ЭДС
Зато при последовательном подключении предохранительного устройства его срабатывание (разрыв плавкой вставки) позволяет обесточить всю электрическую цепь, расположенную после него и обеспечить нужный уровень безопасности, и это хорошо. Выключатель в сеть питания электроприбора включается также последовательно.
Параллельное соединение также широко используется. Например, люстра – все лампочки соединены параллельно и находятся под одним и тем же напряжением. Если одна лампа перегорит, — не страшно, остальные не погаснут, они остаются под тем же самым напряжением.
Параллельное соединение резисторов на примере 3-х лампочек и генератора
При необходимости увеличения способности схемы рассеивать тепловую мощность, выделяющуюся при протекании тока, широко используются и последовательное, и параллельное объединение резисторов. И для последовательного, и параллельного способов соединения некоторого количества резисторов одного номинала общая мощность равна произведению количества резисторов на мощность одного резистора.
Смешанное соединение резисторовТакже часто используется смешанное соединение. Если,например необходимо получить сопротивление определенного номинала, но его нет в наличии можно воспользоваться одним из выше описанных способов или воспользоваться смешанным соединением.
Отсюда, можно вывести формулу которая и даст нам необходимое значение:
Rобщ.=(R1*R2/R1+R2)+R3
В нашу эпоху развития электроники и различных технических устройств в основе всех сложностей лежать простые законы, которые поверхностно рассматриваются на данном сайте и думаю, что вам они помогут успешно применять в своей жизни. Если например взять ёлочную гирлянду, то соединения лампочек идет друг за другом, т.е. грубо говоря это отдельно-взятое сопротивление.
Не так давно гирлянды стали соединятся смешанным способом. Вообще, в совокупности все эти примеры с резисторами взяты условно, т.е. любым элементом сопротивления может быть ток проходящий через элемент с падением напряжения и выделением тепла.
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
или
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи : 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей.
Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Законы последовательного соединения — презентация онлайн
1. Законы последовательного соединения
Сила токаIобщ = I1 = I2
Сопротивление Rобщ=R1+R2
Напряжение
Uобщ=U1+U2
2. Как соединены лампочки в гирлянде?
3. Что произойдет если одна из лампочек перегорит?
4. Что произойдет если одна из лампочек перегорит?
Освещение в квартире5. Тема урока: Параллельное соединение проводников.
4 ноябряТема урока:
Параллельное соединение
проводников.
Подготовил учитель физики
МОУ «Школа-лицей №1» г.Алушты
Успаленко Игорь Николаевич
6. Параллельное соединение проводников.
Все электроприборывключены в электрическую цепь
параллельно!
Как включается в цепь амперметр?
1 2
0
A
15 Ом
0
A
1
2
Как
подключен
потребителю?
вольтметр
Параллельно?
5
0
V
10
к
9. — Сила тока измеряется амперметром (подключается последовательно) — Напряжение измеряется вольтметром (включается параллельно)
Параллельное соединение- это соединениепри котором все входящие в него проводники
одним своим концом присоединены к одной
точке (т. А), а вторым к другой (т.В).
А
В
Если выкрутить одну из ламп, цепь не разомкнется и
вторая лампочка не перестанет светиться.
12. Законы параллельного соединения
U1=U2=Ua
b
Напряжение на каждой ветви
одинаково и равно напряжению
на неразветвленной части цепи
13. Законы параллельного соединения
I1+I2=IСила тока в неразветвленной части цепи равна сумме
сил токов в каждой ветви
14. Законы параллельного соединения
IU
Т.к.
R1
a
R2
I1
I2
то
b
Сокращаем на U, получим:
или
пусть сопротивления всех n резисторов одинаковы и равны R1,
Величина, обратная участку параллельного
тогда:
соединения, равна сумме величин , обратных
Откуда
сопротивлениям ветвей.
n слагаемых
15. Законы соединений
ПоследовательноеПараллельное
Разные
Iобщ = I1 = I2
Iобщ = I1 + I2
Uобщ = U1 + U2
Uобщ = U1 = U2
Rобщ = R1 + R2
0
1
2
Определите тип соединения
резисторов.
Комбинированное или смешанное.
A
5
0
V
1
2
3
10
17. Определите тип соединения
1.2.
3.
4.
5.
Параллельное
Неправильное
Последовательное
Перпендикулярное
Косое
Определите тип соединения
1.Параллельное
2.Вертикальное
3.Последовательное
4.Смешанное
Определите тип соединения
1.Параллельное
2.Последовательное
3.Вертикальное
4.Перпендикулярное
Определите тип соединения
1.Параллельное
2.Вертикальное
3.Последовательное
4.Смешанное
Определите тип соединения
1.Параллельное
2.Последовательное
3.Вертикальное
4.Перпендикулярное
5.Смешанное
0
A
1
2
В
установке
использованы
две
одинаковые
лампы.
Вычислите
сопротивление каждой лампы и их
общее
сопротивление.
Вычертите
принципиальную схему этой цепи.
5
0
V
10
0
1
2
В
установке
использованы
две
одинаковые
лампы.
Вычислите
сопротивление каждой лампы и их
общее
сопротивление.
Вычертите
принципиальную схему этой цепи.
A
5
0
V
10
24. ПРАВИЛЬНО!
дальшеНЕПРАВИЛЬНО!
назад
МОЛОДЕЦ!!!
Гринченко А.А.
Параллельное и последовательное соединение — презентация онлайн
Параллельное ипоследовательное
соединения проводников
Урок–закрепление в 8 классе
Учитель: Митрофанова Светлана Дмитриевна.
2. Последовательное соединение проводников
ПОСЛЕДОВАТЕЛЬНОЕСОЕДИНЕНИЕ ПРОВОДНИКОВ
При
последовательном
соединение проводников конец
одного
проводника
соединяется с началом другого
и т.д.
На рисунках изображены цепь
последовательного соединения
двух лампочек и схема такого
соединения.
Если сгорит одна из лампочек,
то цепь разомкнется и другая
лампочка погаснет.
3. Параллельное соединение проводников
При параллельном соединении проводников их начала иконцы имеют общие точки подключения к источнику тока.
ПАРАЛЛЕЛЬНОЕ
СОЕДИНЕНИЕ ПРОВОДНИКОВ
4. Законы последовательного соединения
ЗАКОНЫ ПОСЛЕДОВАТЕЛЬНОГОСОЕДИНЕНИЯ
При последовательном соединении проводников сила тока на всех
участках цепи одинакова:
I I1 I 2
По закону Ома, напряжения U1 и U2 на проводниках равны:
U1 IR1
U 2 IR2
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и
U2:
U U1 U 2 I ( R1 R2 ) IR
где R – электрическое сопротивление всей цепи. Отсюда следует:
R R1 R2
При последовательном соединении полное сопротивление цепи равно
сумме сопротивлений отдельных проводников.
5. Законы параллельного соединения проводников
ЗАКОНЫ ПАРАЛЛЕЛЬНОГОСОЕДИНЕНИЯ ПРОВОДНИКОВ
При параллельном соединении напряжения U1 и U2 на всех участках
цепи одинаковы:
U U U
1
2
Сумма токов I1 и I2, протекающих по обоим проводникам, равна току в
неразветвленной цепи:
I I1 I 2
Записывая на основании закона Ома:
I1
U
U
U
, I2
иI ,
R1
R2
R
где R – электрическое сопротивление всей цепи, получим
1 1
1
R R1 R2
При параллельном соединении проводников величина, обратная общему
сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно
включенных проводников.
6. Задача1 Два проводника соединены последовательно. Сопротивление одного проводника R = 2 Ом, другого R= 3 Ом. Показание
ЗАДАЧА1ДВА
ПРОВОДНИКА
СОЕДИНЕНЫ
ПОСЛЕДОВАТЕЛЬНО. СОПРОТИВЛЕНИЕ ОДНОГО
ПРОВОДНИКА R = 2 ОМ, ДРУГОГО R= 3 ОМ.
ПОКАЗАНИЕ АМПЕРМЕТРА, СОЕДИНЁННОГО С
ПЕРВЫМ ПРОВОДНИКОМ, I= 0,5 ОМ.
ОПРЕДЕЛИТЬ СИЛУ ТОКА, ТЕКУЩЕГО ЧЕРЕЗ
ВТОРОЙ ПРОВОДНИК, ОБЩУЮ СИЛУ ТОКА В
ЦЕПИ,
ОБЩЕЕ
НАПРЯЖЕНИЕ
ЦЕПИ.
7. Решение задачи
РЕШЕНИЕ ЗАДАЧИДано:
R1= 2 Ом
R2= 3 Ом
I1= 0,5 А
Решение:
I1= I2= Iu; I2= Iu= 0, 5 А
U1= I1R1; U1= 0.5 x 2= 1 (В)
U2= I2R2; U2= 0.5 x 3= 1, 5 (В)
Uu= U1+U2; Uu= 1+1, 5 = 2, 5 (В)
I2, Iu, Uu=?
Ответ: I2= Iu= 0, 5 А, Uu= 2, 5 В.
8. Задача 2.
ЗАДАЧА 2.Определить общее
сопротивление участка цепи
5
1
4
5
2
3
1/R = 1/5+1/5 =2/5
R = 2,5 Ом
Шаг 1.
5
4
1
2
5
3
R = 4 +2,5 = 6,5 Ом
Шаг 2.
1
4
2,5
2
3
Шаг 3.
R = 2+3 =5 Ом
6,5
1
2
3
Шаг 4.
1/R = 1/6,5 + 1/5 = 35/100
R =100/35 = 2,86 Ом
6,5
1
5
Шаг 5. R = 1 + 2,86 = 3,86 Ом
1
2,86
Ответ: 3,86 Ом
14. Задача 3.
ЗАДАЧА 3.Доктора Ватсона и Шерлока Холмса в новогоднюю ночь пригласили в гости
друзья. И, вдруг, как гласит один из законов Мерфи: «Все, что должно
сломаться, обязательно сломается, причем в самый неподходящий момент».
И, что же произошло? Когда хозяин дома стал включать елочную гирлянду
для детей, одна из лампочек рассчитанных на напряжение в 3,5 В
перегорела.
Дети расстроились, хозяин в панике, ведь под рукой нет запасной лампочки.
Надо спасать праздник, решил Холмс. И, попросив всех успокоиться, Холмс
произнес магические слова и сделал одно действие.
Ко всеобщей радости детей, гирлянда загорелась.
Позже доктор Ватсон спросил у Холмса, что же он сделал?
Что же ответил Холмс?
15. Домашнее задание:
ДОМАШНЕЕ ЗАДАНИЕ:1.
2.
3.
4.
Приведите примеры
соединений проводников у вас
дома.
Повт. § 48, 49.
https://www.youtube.com/watch?v=yLk39C_
EKhM
https://www.youtube.com/watch?v=g3ZGCI1
Fpbs
Соединения проводников — материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):
Рис. 1. Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2):
Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как и , то и , т. е. .
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3):
Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от к (по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:
откуда
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).
Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
B;
B.
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
A;
A.
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор течёт ток A.
Законы последовательного и параллельного соединения проводников
В основном элементы электрических цепей соединяют между собой параллельным либо последовательным методом. Электрику необходимо знать определения этих видов связей, иметь представление о различиях между ними и вариантах практического применения.
Последовательно соединенные проводники
Последовательное соединение
Этот способ подразумевает, что все приборы, входящие в состав электроцепи, связываются между собой проводами так, что во фрагменте цепи, где происходит включение, отсутствуют какие-либо узелки. При последовательном соединении проводников значение токовой силы в разных участках будет иметь одно и то же значение. Это связано с тем, что в безузловой цепи электронный заряд идет по одному и тому же проводнику. Чтобы вычислить общий показатель цепного напряжения, нужно сложить данные по всем фрагментам цепи:
U = U1 + U2 +…+Un.
При объединении аккумуляторных или гальванических единиц в одну батарею последовательный способ поможет увеличить рабочее напряжение.
Резисторы
Общее сопротивление цепи с последовательно связанными резисторами высчитывается по тому же правилу, что и напряжение: оно равно сумме показателей для каждого элемента.
Катушка индуктивности
Когда дроссели соединены последовательно так, чтобы магнитное поле каждой катушки не накладывалось на соседние дроссели, общая индуктивность такого соединения будет равна сложенным параметрам всех катушек:
L = L1+L2 +…+Ln.
Электрический конденсатор
Когда несколько конденсаторов соединяется между собой в цепь, соотношение их емкостей может быть описано такой формулой:
1/С = 1/С1 +1/С2 +…+ 1/Cn.
Мемристоры
Мемристивность цепи оценивается как сумма показателей всех подсоединенных компонентов:
M = M1 +M2 +… + Mn.
Выключатели
Если несколько таких устройств подсоединены в цепь последовательно, она будет замкнутой только при замыкании всех устройств. Если хоть один переключатель разомкнуть, цепь также размыкается. При выходе из строя какого-либо устройства остальные тоже перестанут функционировать. Это правило распространяется и на цепь из нескольких розеток.
Для домашней разводки проводов
Хотя данный способ потенциально мог бы принести потребителю определенные выгоды (экономия проводников, упрощение подключения заземления), на практике для подключения бытовых электроприборов он не используется. Это связано с тем, что неисправность одного из устройств приводит к прекращению функционирования остальных. Этот пример можно проиллюстрировать на елочной гирлянде: в ней используется именно рассматриваемый тип соединения, в случае перегорания какой-либо из ламп остальные затухают. Именно поэтому электроприборы в домашнюю сеть всегда подключаются параллельно.
Важно! При принятии решения соединить последовательно несколько устройств целесообразно составить таблицу их мощностей и оценить на предмет величины перепадов. Если подключить в одну электроцепь, например, нагреватель воды с большой мощностью, потребляющий много энергии, и маломощный прибор вроде старого приемника, более мощный прибор не сможет работать.
Практическое использование последовательной схемы
Для замены кабелей
Если соединить несколько кабелей в одну линию, в случае перегорания какого-либо из элементов ток будет пропадать на всей протяженности конструкции. Поэтому подключение параллельных проводников является более практичным вариантом. Его применяют в качестве замены толстого провода, подходящего для высокомощных нагрузок. Когда такого провода нет в наличии, подключают серию более тонких, в сумме они переносят ток, эквивалентный одному толстому. Нужные сечения находят расчетным путем, опираясь на данные о потерях напряжения. Такие конструкции широко применяются при обустройстве электролиний большой протяженности.
Параллельное соединение
Параллельное соединение проводников предполагает объединение связываемых сетью приборов посредством двух узловых соединений. В этом случае токовая сила на участке, не принадлежащем разветвлению, равна сумме значений этого параметра для каждого из параллельно подключенных кабелей. Значение напряжения, напротив, одинаковое для любого из элементов соединения:
U = U1 = U2 =…=Un.
Схема параллельного соединения
Резисторы
Когда эти элементы соединены параллельно, значения сопротивлений находятся в таком отношении между собой, что общая проводимость (параметр, обратно пропорциональный сопротивлению, то есть равный 1/R) равна сумме проводимостей всех резисторных элементов:
1/R = 1/R1 + 1/R2 + … + 1/Rn.
Катушка индуктивности
Общая индуктивность и показатели для каждой из подсоединенных дросселей находятся в таком соотношении:
1/L = 1/L1 + 1/L2 + … + 1/Ln.
Электрический конденсатор
Общая емкость в данном случае будет равной суммированным показателям отдельных приборов:
C = C1 +C2 +…+ Cn.
Мемристоры
При параллельном включении нескольких мемристоров в сеть соотношение их основных характеристик выражается такой формулой:
M = (M1-1 + M2-1 +…+ Mn-1)-1
Выключатели
В случае параллельного подключения нескольких таких устройств цепочка считается замкнутой, когда в этом положении находится хотя бы один переключатель.
Примеры использования
Последовательная схема применяется для соединения компонентов квартирного звонка, карманного фонаря (выключатель, лампа и батарея) и других устройств, в которых необходимо обеспечить активизацию при нажатии кнопки. На ней также построены елочные гирлянды.
Примерами параллельного соединения могут служить люстры и осветительные приборы в квартире. Если в этом случае воспользоваться последовательным вариантом, при включении любой лампы будут включаться и прочие, что совершенно не входит в цели монтажа. Кроме того, в этом случае цепь перестанет работать при неисправности одного из устройств. Подключая лампы параллельно, можно оснастить каждое разветвление собственным выключателем, тогда им можно будет управлять, не затрагивая других элементов.
Важно! В ПУЭ указывается, что силовые нагрузки можно соединять параллельно в том случае, если провод питания может выдержать суммарную нагрузку одновременно работающих устройств. Когда розетки будут установлены, от каждой из них к распредкоробке протягивают прямой провод.
Правила для различных соединений проводников
Для обоих вариантов соединения существуют правила подсчета различных параметров электрической цепи.
Законы последовательной цепи
Законы последовательного соединения имеют такой вид:
- ток на всех участках цепочки идентичен, тогда как напряжение на ее концах равно сумме значений для каждого ее участка;
- у соединенных конденсаторов электрозаряды на обкладках примут одинаковые значения;
- когда в такую цепь соединены резисторы, ток идет в начале через первый элемент, потом через второй и, последовательно проходя все устройства, доходит до последнего (общая величина спада напряжения равна суммированным потерям его для каждого из резисторов).
Законы параллельного соединения проводников
Здесь следующая картина:
- когда электроприбор перегорает, путь электротока не блокируется, а остальные приборы не выключаются;
- ток распределяется на все распараллеленные участки и принимает на них разные значения, напряжение везде остается прежним;
- при подключении конденсаторов заряд на каждом из них равен произведению напряжения (одинакового для всех) и емкости конкретного устройства, общая емкость равна суммированным показателям всех приборов.
Смешанное соедиение проводников
Смешанное соединение – сложная конфигурация из нескольких проводников, часть из которых коммуницируют параллельно, часть – последовательно. Чтобы рассчитать значения разных показателей (ток, сопротивление и т.д.) для такого соединения, его разбивают на структурные элементы и проводят вычисления для каждого из них. При подсчете данных для укрупненных единиц их можно заменять на эквивалентные.
Примеры смешанных схем
При соединении нескольких устройств в одну цепочку важно выбрать правильный способ соединения. Если он не будет соответствовать практическим задачам, устройства не будут функционировать корректно.
Видео
|
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: |
|
Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего). |
Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… |
2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). |
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: — чем больше сопротивление, тем больше напряжение. |
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. .
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: — чем больше сопротивление, тем меньше сила тока. |
Тема урока параллельное соединение проводов. Последовательное и параллельное соединение проводов. Законы последовательного соединения проводов
Текст слайда: 1. Законы соединений. 2. Задачи. Параллельное и последовательное соединение проводов
Текст слайда: Последовательное соединение проводов При последовательном соединении проводов конец одного проводника соединяется с началом другого и т. Д. На рисунках показано последовательное соединение двух лампочек и схема такого соединения.Если одна из лампочек загорится, цепь разомкнется, а другая лампочка погаснет.
Поездка в аэропорт внушает людям немного страха, и не зря! Длинные очереди, несколько контрольно-пропускных пунктов и бесконечные коридоры, которые кажутся бесконечными. Иногда можно легко перемещаться по аэропорту, а в другое время просто нужно добраться из одной точки в другую.
Дорожка в аэропорту очень похожа на схему, которая является прототипом прохождения электронов.Электрические цепи очень полезны — например, дорожки, по которым подается электричество для электроприборов, освещения и других вещей в вашем доме. Схемы бывают двух основных форм. Первый — это серия, в которой устройства соединяются последовательно. Этот тип схемы обеспечивает единый путь для движения электронов. Второй тип — это параллельная схема, соединяющая устройства разветвленными путями. Этот тип схемы обеспечивает отдельные пути электронов.
Текст слайда: Когда проводники соединены последовательно, ток во всех частях цепи одинаков: Согласно закону Ома, напряжения U1 и U2 на проводниках равны: Общее напряжение U на обоих проводников равняется сумме напряжений U1 и U2: где R — электрическое сопротивление всей цепи.Отсюда следует: При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Законы последовательного соединения
Законы последовательного соединения проводов
Мы подробно рассмотрим принципиальные схемы в другом уроке. А пока давайте сосредоточимся на том, как параллельные цепи работают с устройствами. Параллельные цепи получили свое название, потому что устройства в цепи соединены параллельно. Это похоже на наличие нескольких рентгеновских экранов в одном терминале аэропорта.Линия сначала начинается как однофайловая линия, но затем разбивается на несколько отдельных строк, когда вы проходите через выбранный вами рентгеновский аппарат.
Текст слайда: Параллельное соединение проводов При параллельном соединении проводов их начало и конец имеют общие точки подключения к источнику тока.
Текст слайда: Законы параллельного соединения проводов. При параллельном соединении напряжения U1 и U2 на всех участках цепи одинаковы: Сумма токов I1 и I2, протекающих по обоим проводникам, равна току в неразветвленной цепи: Записываем на основании закона Ома:, получаем При параллельном соединении проводов обратное от общего сопротивления цепи равно сумме значений, обратных сопротивлениям параллельно соединенных проводников.
Остальные позади вас могут выбрать другой рентгеновский аппарат, а количество строящихся линий зависит от того, сколько автомобилей открыто. Пройдя через рентгеновский аппарат, все сливаются в одну линию и продолжают свой путь к своим воротам. Так же, как каждая линия рентгеновского аппарата независима от других, устройства в параллельной цепи также независимы друг от друга. Подумайте об этом: если следующая линия движется медленнее, чем ваша, это не влияет на скорость или скорость движения ваших линий.
То же самое относится к ответвлениям параллельных цепей. И из-за этой независимости, в то время как общий ток в цепи делится между параллельными ветвями, величина тока в каждой ветви конкретно связана с величиной сопротивления в этой ветви. Сопротивление исходит от самого устройства и противоположно движению электрона через устройство. Поскольку сопротивление сопротивляется движению тока, величина тока в каждой ветви обратно пропорциональна сопротивлению этой ветви.
Текст слайда: Задача1 Два проводника соединены последовательно. Сопротивление одного проводника R = 2 Ом, другого R = 3 Ом. Показание амперметра, подключенного к первому проводнику, I = 0,5 Ом. Определите ток, протекающий по второму проводнику, общий ток в цепи, полное напряжение цепи.
Это имеет смысл, если задуматься. Возможно, очередь рядом с вами движется медленнее, потому что сотрудники службы безопасности вручную сканируют каждую ручную кладь.Это сопротивление замедляет линию, затрудняя перемещение людей вокруг точки защиты и к следующему пункту назначения. То же самое относится к ветвям, расположенным параллельно. Чем больше сопротивления в одной ветви, тем больше сопротивления течет в лицо, когда она проходит.
Но действительно интересно, что, хотя каждая ветвь независима, общее сопротивление цепи зависит от общего количества присутствующих ветвей. Фактически, с увеличением количества ветвей общее сопротивление цепи уменьшается.Вернемся в аэропорт, чтобы понять, почему это так. Если бы был только один рентгеновский аппарат, была бы открыта одна длинная очередь, и всем пришлось бы проходить через нее. В общем, это было бы очень неэффективно и обеспечило бы большее сопротивление полному перемещению людей через пост безопасности.
Текст слайда: Решение проблемы: Дано: R1 = 2 Ом R2 = 3 Ом I1 = 0,5 A Решение: I1 = I2 = Iu; I2 = Iu = 0, 5 и U1 = I1R1; U1 = 0,5 x 2 = 1 (В) U2 = I2R2; U2 = 0,5 x 3 = 1, 5 (B) Uu = U1 + U2; Uu = 1 + 1, 5 = 2, 5 (B) I2, Iu, Uu =? Ответ: I2 = Iu = 0, 5 А, Uu = 2, 5 В.
Текст слайда: Задача 2.
Но если откроется другой рентгеновский аппарат, линия может разделиться на две части, и все будут двигаться намного быстрее. Добавьте еще один рентгеновский аппарат, и «сопротивление» уменьшится еще больше, потому что у людей есть другой путь, по которому они могут двигаться.
То же самое и с параллельной схемой. Добавление филиалов похоже на открытие большего количества рентгеновских станций в цепи. Чем больше ветвей, тем больше путей для тока, что снижает общее сопротивление цепи.Мы можем построить нашу собственную простую параллельную схему из двух ветвей, каждая с лампочкой, подключенной к одним и тем же двум точкам. К этим двум точкам также подключается аккумулятор. Если каждая ветвь замкнута, что означает, что в цепи нет разрыва, ток течет от батареи по каждой ветви, через каждое устройство, а затем обратно к батарее.
Номер слайда 10
Номер слайда 11
Номер слайда 12
Слайд №13
Подобно тому, как сердце качает кровь через ваше тело, батарея вырабатывает напряжение, которое «прокачивает» ток по цепи.Следовательно, большее напряжение означает больший ток. Мы также знаем, что, как и при закупорке артерии, сопротивление сопротивляется потоку, поэтому большее сопротивление означает меньший ток.
Фактически, эта взаимосвязь между напряжением, током и сопротивлением резюмируется в законе Ома, который гласит, что ток прямо пропорционален напряжению в цепи и обратно пропорционален сопротивлению. Поскольку каждое устройство подключено к одной и той же точке, напряжение на каждом устройстве одинаковое. Независимо от того, сколько ветвей вы добавите, у всех будет одинаковое напряжение, поэтому свет не будет тусклым, когда вы добавите больше в схему! Это также означает, что, в отличие от последовательности огней елки, которые соединены последовательно, если одна лампочка в параллельной цепи включена, другие не будут затронуты и будут гореть.
Номер слайда 14
Текст слайда: Задание 3. Доктор Ватсон и Шерлок Холмс были приглашены на новогоднюю ночь друзьями. И вдруг, как гласит один из законов Мерфи: «Все, что должно сломаться, обязательно сломается, и в самый неподходящий момент». И что случилось? Когда хозяин дома стал включать еловую гирлянду для детей, перегорела одна из лампочек, рассчитанная на напряжение 3,5 В. Дети расстроились, хозяин был в панике, ведь под рукой нет запасной лампочки.«Нам нужно спасти праздник, — решил Холмс. И, попросив всех успокоиться, Холмс произнес волшебные слова и совершил одно действие. На всеобщую радость детей гирлянда загорелась. Позже доктор Ватсон спросил Холмса, что он сделал? Что сказал Холмс?
Схема — это путь, по которому могут проходить электроны. Когда электроны движутся по этим путям, это похоже на движение людей через аэропорт, проходящих по множеству коридоров и контрольно-пропускных пунктов по всему зданию. Параллельные цепи являются одним из основных типов цепей, и они соединяют устройства по разветвленным путям.В простой параллельной схеме каждая ветвь подключается к тем же двум точкам, к которым также подключена батарея. Батарея питает напряжение, которое, подобно сердцу, «прокачивает» ток по цепи.
Эти несколько путей позволяют разделить общий ток между ветвями, но это также означает, что напряжение на каждой ветви одинаково. Сила тока в каждой ветви зависит от сопротивления устройства. Ток обратно пропорционален сопротивлению, потому что сопротивление противоположно движению электрона через устройство.Подобно тому, как более тщательный досмотр каждого пассажира замедляет очередь людей, большее сопротивление устройства уменьшает текущее движение по этой ветке.
Слайд №15
Текст слайда: Достоинства и недостатки соединений. Пример последовательного подключения: гирлянда. Пример параллельного подключения: светильники в офисе. Достоинства и недостатки подключений: Параллельное — при перегорании одной лампы горят другие. Но когда вы включите лампу с минимально возможным напряжением, она перегорит.Последовательный — лампы с более низким возможным напряжением подключаются к цепи с более высоким напряжением, но при перегорании одной лампы не сгорят все.
Подобно рентгеновским аппаратам в аэропорту, каждое ответвление параллельной цепи не зависит от других. Это означает, что то, что происходит в одной ветви, не влияет на другие. Однако общее сопротивление цепи зависит от количества ветвей. Так же, как открытие большего количества рентгеновских аппаратов в аэропорту, добавление ответвлений в параллельную цепь снижает общее сопротивление самой цепи.
Рассмотрение концепций в этом уроке позволит вам видео. Обсудите структуру параллельной цепи и объясните, как в параллельной цепи течет ток.
- Запомните определение схемы.
- Поймите цель сопротивления.
- Обобщите закон Ома.
Слайд №16
Текст слайда: Домашнее задание: Приведите примеры последовательного и параллельного подключения проводов в вашем доме.Отчет § 48, 49. Исх. 22 (2), упражнение 23 (3.4).
Цель урока: 1. Ознакомить учащихся с последовательным и параллельным соединением проводов 2. Существующие в цепи закономерности при последовательном и параллельном соединении проводов. Приложение 3. Научите решать задачи по теме: Последовательное и параллельное соединение проводов 4. Усилить у студентов знания о различных соединениях проводов и сформировать умение рассчитывать параметры комбинированных цепей
В вашем автомобиле практически каждый компонент, который требует электричества, работает при постоянном напряжении 12 вольт.Ответ заключается в том, как подключены электрические цепи. Для этих и многих других электрических систем решением является параллельное соединение компонентов схемы.
Применение определения: пример
Прежде чем перейти к определению параллельной цепи, давайте быстро рассмотрим некоторые из основных принципов электрических цепей, в основном напряжение, ток, сопротивление и несколько законов. Вот те, которые нам нужны. Напряжение — это электрическая сила, отвечающая за движение электрического заряда.Сопротивление — это мера того, насколько компонент противодействует движению тока через него. Текущий закон Кирхгофа — это просто утверждение, что заряд должен быть сохранен, и поэтому сумма токов, идущих к узлу схемы, должна быть равна сумме токов, исходящих из того же узла. Закон Киршоффа по напряжению гласит, что если вы сложите напряжения вокруг любого контура в цепи, вы получите ноль. Сила тока — это мера движения электрического заряда во времени. . Сначала рассмотрим техническое определение параллельной цепи.
Преимущества и недостатки последовательного подключения Преимущества: Имея элементы, рассчитанные на низкое напряжение (например, лампочки), вы можете соединять их последовательно в необходимом количестве и подключать к источнику с высоким напряжением (так устроены елочные гирлянды. расположен) Недостаток: для одного устройства (или элемента) достаточно, чтобы цепь была разомкнута, а все другие устройства не работают
Два или более электрических компонента считаются подключенными параллельно, если общий электрический ток, протекающий в параллельной сети делится между компонентами, затем снова объединяется в один и тот же общий ток.это может показаться не самым интуитивным определением, поэтому посмотрите на последствия. Параллельная схема будет иметь следующие определяющие характеристики.
Компоненты соединены таким образом, что все они имеют одинаковые узлы на каждой стороне компонента. Ток, протекающий в параллельном соединении, совпадает с током и равен сумме отдельных токов, протекающих через каждый компонент.
- Он начинается с двух или более компонентов, соединенных вместе в цепочку.
- Каждый из компонентов должен иметь только два электрических контакта.
- Напряжение на всех подключенных параллельно компонентах одинаковое.
Преимущества и недостатки параллельного подключения. Преимущества: При выходе из строя одной из веток остальные продолжают работать. В этом случае каждую ветку можно подключать и отключать отдельно. Недостаток: возможно включение устройств, рассчитанных только на это напряжение
Применение последовательного соединения Основным недостатком последовательного соединения проводов является то, что при выходе из строя одного из соединительных элементов отключаются и другие.Например, если выйдет из строя одна из ламп на елке, все остальные погаснут. Этот недостаток может обернуться достоинством. Представьте, что некоторая цепь должна быть защищена от перегрузки: при увеличении тока цепь должна автоматически отключиться. Как это сделать? (Как это сделать? (Например, использовать предохранители) При проведении примеров последовательного подключения проводов
Использование определения — еще один пример.
При попытке определить, параллельны ли несколько элементов цепи, вы не можете просто увидеть, как схема нарисована, необходимо использовать электрические характеристики параллельной цепи.Какие компоненты образуют параллельную цепь? Только компоненты номер 1 и номер 2, так как оба они удовлетворяют следующим трем условиям.
- У них одинаковые узлы в каждой точке подключения.
- На каждом из них одинаковое напряжение.
Применение параллельного подключения В одну электрическую цепь могут быть включены самые разные потребители электроэнергии. Такая схема подключения тока применяется, например, в жилых помещениях. Вопрос к студентам: Как соединены между собой электроприборы в вашей квартире?
Можно ли использовать две одинаковые лампы, рассчитанные на 110 В, в сети с напряжением 220 В? Как? Сколько одинаковых резисторов было подключено последовательно, если каждый из них имеет сопротивление 50 Ом, а их общее сопротивление — 600 Ом? Два резистора с сопротивлением 5 Ом и 10 Ом подключены параллельно к батарее.Ток в каком больше? Как изменится сопротивление электрической цепи, если мы подключим другой резистор к любому звену цепи: а) последовательно; б) параллельно? Как подключить четыре резистора с сопротивлением 0,5 Ом, 2 Ом, 3,5 Ом и 4 Ом, чтобы их общее сопротивление составляло 1 Ом? Проверка знаний
Параллельное соединение. Последовательное и параллельное соединение проводов
Повторение
Чижова Вера Александровна
Учитель физики и информатики
МБОУ СОШ, Красный,
Ненецкий автономный округ.
- Скорость переноса заряда по проводнику
- Заряд, проходящий через проводник за 1 с
- Обозначается ()
- Единица измерения (А) ампер
- Измеряется амперметром
- Зависит от напряжения и сопротивление (закон Ома)
- Напряжение — это работа электрического поля по движению одиночного заряда (1С) по проводнику
- Обозначается буквой (U)
- Измеряется вольтметром
- Единица измерения (В) вольт
- Свойство проводника препятствовать движению заряженных частиц по проводнику под действием электрического поля
- Обозначается R
- Единица измерения (Ом)
- Зависит от физических свойств проводника
Законы последовательного соединения проводов
- Ток одинаков во всех частях цепи
- Суммарное сопротивление цепи равно сумме сопротивлений отдельных участков цепи
- Общее напряжение равно сумме напряжений в отдельных участках
- 1) Требуется сделать елочную гирлянду из лампочек.рассчитан на напряжение 6 В, чтобы его можно было подключить к сети 120 В. Сколько для этого лампочек?
- A) 4. B) 8 B) 16 D) 20 D) 30.
- 2) Определить полное сопротивление цепи, если сопротивление входящих проводов 2 Ом, включенной части реостата
- 64 Ом и лампы 294 Ом (рисунок 159).
- 1. 240 Ом; 2. 180 Ом; 3. 100 Ом; 4. 120 Ом; 5. 360 Ом.
- 3) При замере напряжения на проводе R 1 оно оказалось равным 12 В.Когда вольтметр был подключен к проводнику R 2 , , тогда он показал 45 В (рисунок 160). Рассчитайте сопротивление R 2, если R 1 = 40 Ом.
- А) 360 Ом; Б) 135 Ом; Б) 150 Ом; Г) 4 Ом; Г) 40 Ом.
- 4) В каждом из двух ТЭНов ток котла 5 А. Определить ток в питающих проводах, если элементы соединены последовательно.
- А) 25 А; Б) 5 А; Б) 10 А; Г) 2,5 А.
- 5) Проводники сопротивления 2.4 и 6 Ом включены последовательно и включены в сеть 36 В. Рассчитайте ток в проводниках.
- А) 3 А; Б) 0,33 А; Б) 432 А; Г) 0,5 А; E) 0,3 А.
- 1) Ток в проводнике R 1 составляет 4 А. Какой ток в проводнике R 2 (рисунок 161).
- А) 4 А; Б) 2 А; Б) 8 А; Г) 16 А.
- 2) Сопротивление лампы R 1 = 300 Ом, а напряжение на ней 90 В.Что покажет вольтметр, если его подключить к лампе с сопротивлением R2 = 400 Ом (рисунок 162)?
- А) 240 В; Б) 180 В; Б) 100 В; Г) 120 В; Г) 360 В.
- 3) Три одинаковые лампы соединены последовательно с напряжением 120 В (рисунок 163). Какое напряжение на каждом из них?
- А) 360 В; Б) 120 В; Б) 60 В; Г) 4 В; Г) 40 В.
- 4) На рисунке 164 показан ступенчатый реостат, в котором сопротивление R 1 = R 2 = R 3 =… = R 5 = 10 Ом. Рассчитайте сопротивление в данном положении подвижного контакта К.
- А) 20 Ом; Б) 50 Ом; Б) 40 Ом; Г) 30 Ом; Г) 3,3 Ом.
- 5) Лампа электрического сопротивления R , а амперметр был подключен к сети 200 В, как показано на рисунке 165. Вычислите сопротивление R , , если амперметр показывает силу тока 0,5 А. Сопротивление лампы 240 Ом.
- А) 120 Ом; Б) 160 Ом; Б) 260 Ом; Г) 60 Ом.
- В цепи с напряжением 12 В подключен резистор сопротивлением 2 (Ом). Какое сопротивление нужно подключить к другому резистору, чтобы сила тока была 2А
Повтор: Последовательное соединение проводов
- В цепи с напряжением 12В подключаются два резистора и лампочка. Напряжение на лампочке 5В, на первом резисторе 3В. Сопротивление второго резистора 6 (Ом). Определяем сопротивление первого резистора и лампочки .
- Сила тока в неразветвленной части цепи равна сумме токов в ветвях
- Напряжение на всех параллельных участках одинаково
- Обратная величина общего сопротивления равна сумме значений взаимного сопротивления всех параллельных участков
Задачи по параллельному подключению потребителей
Сопротивления резисторов соответственно равны 4,6,12 (Ом).Определите ток в каждом резисторе, если напряжение между точками A и B составляет 24 В. Определить ток в неразветвленном участке цепи
Ток в резисторах 2А, 1,5А, 3А соответственно. Определите сопротивление резисторов, если напряжение между точками A и B составляет 16 В.
Д / с § 48,49 упражнение 22 (1.2), упражнение 23 (3)
Цель урока: 1.Познакомить студентов с последовательным и параллельным соединением проводов. 2. Закономерности, существующие в цепи при последовательном и параллельном соединении проводов. Приложение 3. Научить решать задачи по теме: Последовательное и параллельное соединение проводов 4. Закрепить знания студентов о различных соединениях проводов и сформировать умения рассчитывать параметры комбинированных цепей
Преимущества и недостатки последовательного подключения Преимущества: Имея элементы, рассчитанные на низкое напряжение (например, лампочки), вы можете соединить их последовательно в необходимом количестве и подключить источник с высоким напряжением (как устроены елочные гирлянды).Недостаток: достаточно одному устройству (или элементу) выйти из здания, так как цепь размыкается, а все остальные устройства не работают
Преимущества и недостатки параллельного подключения Преимущества: Если одна из ветвей выходит из строя, остальные продолжают работать. В этом случае каждую ветку можно подключать и отключать отдельно. Недостаток: возможно включение устройств, рассчитанных только на это напряжение
Использование последовательного соединения Главный недостаток последовательного соединения проводов заключается в том, что при выходе из строя одного из элементов соединения отключаются остальные.Так, например, если перегорит одна из ламп на елке, все остальные погаснут. Указанный недостаток может обернуться достоинством. Представьте, что некоторая цепь должна быть защищена от перегрузки: при увеличении тока цепь должна автоматически отключиться. Как это сделать? (Как это сделать? (Например, использовать предохранители) Приведу примеры использования последовательного соединения проводов
Применение параллельного подключения В одну электрическую цепь параллельно могут быть включены самые разные потребители. Такая схема подключения потребителей тока применяется, например, в жилых помещениях.Вопрос к ученикам: Как подключены электрические приборы в вашей квартире?
Могу ли я использовать две одинаковые лампы на 110 В в сети с напряжением 220 В? Как? Сколько одинаковых резисторов было подключено последовательно, если каждый из них имеет сопротивление 50 Ом, а их общее сопротивление — 600 Ом? Два резистора, сопротивление которых составляет 5 Ом и 10 Ом, подключены параллельно к батарее. Текущая сила у кого из них больше? Как изменится сопротивление электрической цепи, если подключить еще один резистор к любому звену цепи: а) последовательно б) параллельно? Как подключить четыре резистора, сопротивление которых равно 0.5 Ом, 2 Ом, 3,5 Ом и 4 Ом, чтобы их общее сопротивление составляло 1 Ом? Проверка знаний
«Проводники в электрическом поле» — Диполь. Проводники в электрическом поле. Диэлектрики. В других проводниках электрического поля нет. Поскольку E0 = E1, то E = E0-E1 = 0 Внутри проводника отсутствует электрическое поле. Рассмотрим электрическое поле внутри металлического проводника … В электрическом поле любой диэлектрик становится полярным.
«Параллельное и последовательное соединение» — Законы последовательного соединения.Параллельное соединение проводов. А1. A2. Задача: выделить в схемах участок последовательного соединения проводов. Последовательное соединение. Применение последовательного подключения. Цель: изучить различные соединения проводников.
«Проводники в электростатическом поле» — внутреннее поле ослабит внешнее. Неполярный. +. Евнеш. Полярный. — Металлы; жидкие растворы и расплавы электролитов; плазма. Евнутр. Проводники и диэлектрики в электростатическом поле.Электростатические свойства однородных металлических проводников. К проводникам относятся: К диэлектрикам относятся воздух, стекло, эбонит, слюда, фарфор, сухое дерево.
«ВТСП» Высокотемпературная сверхпроводимость (ВТСП). Важнейшие открытия в современном естествознании. Открытие WCS. 1. Исследование природы и свойств ВТСП. 2. Влияние внешних факторов на свойства ВТСП материалов. 5. Сильноточные приложения. 4. Слаботочные приложения. В соответствии со структурой программы, основными направлениями работы являются:
«Электрическое сопротивление проводника» — Вставьте пропущенные буквы! Схема 2.Схема 3. Узнаем: А) Амперметр — параллельно. Электрический ток называется: Д) Амперметр — последовательно. Б) Вольтметр параллельный. Выберите пары. Электрическое сопротивление Обозначение: Единица измерения (СИ): В) Вольтметр — последовательно. Расчет сопротивления проводника.
«Соединительные проводники» — Когда проводники соединены последовательно: — ток, протекающий по каждому проводнику, одинаков: I1 = I2 = I3 — общее напряжение в цепи равно сумме напряжений в отдельных секциях. цепи U = U1 + U2 — полное сопротивление цепи равно сумме сопротивлений отдельных участков цепи R = R1 + R2.Подключения проводов.
Всего 6 презентаций
Текст слайда: 1. Законы соединений. 2. Задачи. Параллельное и последовательное соединение проводов
Текст слайда: Последовательное соединение проводников Когда проводники подключаются последовательно, конец одного проводника соединяется с началом другого и так далее. На схемах изображена схема последовательного соединения двух лампочек и схема такого подключения. Если одна из лампочек загорится, цепь разомкнется, а другая лампочка погаснет.
Текст слайда: Когда проводники соединены последовательно, ток на всех участках цепи одинаков: Согласно закону Ома, напряжения U1 и U2 на проводниках равны: Общее напряжение U на обоих проводниках равно равняется сумме напряжений U1 и U2: где R — электрическое сопротивление всей цепи. Отсюда следует: При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.Законы последовательного подключения
Текст слайда: Параллельное соединение проводников При параллельном подключении проводов их концы и концы имеют общие точки подключения к источнику тока.
Текст слайда: Законы параллельного соединения проводников При параллельном подключении напряжения U1 и U2 одинаковы на всех участках цепи: сумма токов I1 и I2, протекающих по обоим проводникам, равна току в неразветвленная цепь: Запишем на основе закона Ома: где R — электрическое сопротивление всей цепи, мы получаем Когда проводники соединены параллельно, обратная величина общего сопротивления цепи равна сумме обратной величины сопротивление параллельно соединенных проводов.
Текст слайда: Задача1 Два проводника соединены последовательно. Сопротивление одного проводника R = 2 Ом, другого R = 3 Ом. Показание амперметра, подключенного к первому проводнику, I = 0,5 Ом. Определите ток, протекающий по второму проводнику, общий ток в цепи, полное напряжение цепи.
Текст слайда: Решение проблемы Дано: R1 = 2 Ом R2 = 3 Ом I1 = 0,5 A Решение: I1 = I2 = Iu; I2 = Iu = 0, 5 А U1 = I1R1; U1 = 0,5 x 2 = 1 (В) U2 = I2R2; U2 = 0.5 x 3 = 1, 5 (B) Uu = U1 + U2; Uu = 1 + 1, 5 = 2, 5 (B) I2, Iu, Uu =? Ответ: I2 = Iu = 0, 5 А, Uu = 2, 5 В.
Текст слайда: Задача 2.
Слайд № 10
Слайд №11
Слайд № 12
Слайд № 13
Слайд №14
Текст слайда: Задание 3. Доктора Ватсон и Шерлок Холмс в канун Нового года пригласили друзей в гости. И, вдруг, как гласит один из законов Мерфи: «Все, что должно сломаться, обязательно сломается, причем в самый неподходящий момент.«А, что случилось? Когда хозяин дома стал включать гирлянду на елку для детей, перегорела одна из лампочек, рассчитанная на напряжение 3,5 В. Дети расстроены, хозяин в панике, потому что есть запасной лампочки под рукой нет. Надо спасти праздник, решил Холмс. И, прося всех успокоиться, Холмс произнес волшебные слова и сделал одно дело. К всеобщей радости детей, гирлянда загорелась. Позже доктор Ватсон спросил Холмса, что он сделал? Что сказал Холмс?
Слайд № 15
Текст слайда: Преимущества и недостатки соединений Пример последовательного соединения: гирлянда.Пример параллельного подключения: светильники в офисе. Достоинства и недостатки подключений: Параллельное — при перегорании одной лампы горят другие. Но когда вы включите лампу с меньшим напряжением, она перегорит. Последовательный — лампы с меньшим возможным напряжением включаются в цепь с высоким напряжением, но если одна лампа перегорела, все не сгорят.
Слайд № 16
Текст слайда: Домашнее задание: Приведите примеры последовательного и параллельного соединения проводов в вашем доме.Povt. § 48, 49. Упражнение. 22 (2), упражнение 23 (3.4).
правил Кирхгофа | Безграничная физика
Введение и важность
Законы цепи Кирхгофа — это два уравнения, которые касаются сохранения энергии и заряда в контексте электрических цепей.
Цели обучения
Опишите взаимосвязь между законами цепи Кирхгофа и энергией и зарядом в электрических цепях.
Основные выводы
Ключевые моменты
- Кирхгоф использовал работу Георга Ома в качестве основы для создания закона Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) в 1845 году.Их можно вывести из уравнений Максвелла, появившихся 16-17 лет спустя.
- Невозможно проанализировать некоторые схемы с обратной связью путем упрощения в виде суммы и / или ряда компонентов. В этих случаях можно использовать законы Кирхгофа.
- Законы Кирхгофа — частные случаи сохранения энергии и заряда.
Ключевые термины
- резистор : электрический компонент, который передает ток прямо пропорциональный напряжению на нем.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея.Она измеряется в вольтах (не в ньютонах, Н; ЭДС — это не сила).
- конденсатор : Электронный компонент, состоящий из двух проводящих пластин, разделенных пустым пространством (иногда вместо этого между пластинами помещается диэлектрический материал), и способный хранить определенное количество заряда.
Введение в законы Кирхгофа
Законы цепи Кирхгофа — это два уравнения, впервые опубликованные Густавом Кирхгофом в 1845 году. По сути, они касаются сохранения энергии и заряда в контексте электрических цепей.
Хотя законы Кирхгофа можно вывести из уравнений Джеймса Клерка Максвелла, Максвелл не публиковал свою систему дифференциальных уравнений (которые составляют основу классической электродинамики, оптики и электрических цепей) до 1861 и 1862 годов. Кирхгоф, скорее, использовал Георга. Работа Ома как основа для закона Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) .
Законы Кирхгофа чрезвычайно важны для анализа замкнутых цепей.Рассмотрим, например, схему, показанную на рисунке ниже, состоящую из пяти резисторов, соединенных последовательно и параллельно. Упрощение этой схемы до комбинации последовательного и параллельного включения невозможно. Однако, используя правила Кирхгофа, можно проанализировать схему, чтобы определить параметры этой схемы, используя значения резисторов (R 1 , R 2 , R 3 , r 1 и r 2 ) . Также в этом примере важно то, что значения E 1 и E 2 представляют источники напряжения (например.г., батарейки).
Замкнутая цепь : Чтобы определить все переменные (т. Е. Падение тока и напряжения на разных резисторах) в этой цепи, необходимо применить правила Кирхгофа.
В заключение, законы Кирхгофа зависят от определенных условий. Закон напряжения представляет собой упрощение закона индукции Фарадея и основан на предположении, что в замкнутом контуре нет нет флуктуирующего магнитного поля . Таким образом, хотя этот закон может быть применен к схемам, содержащим резисторы и конденсаторы (а также другие элементы схемы), его можно использовать только как приближение к поведению схемы при изменении тока и, следовательно, магнитного поля.
Правило перекрестка
Правило соединения Кирхгофа гласит, что в любом соединении цепи сумма токов, протекающих в этот переход и выходящих из него, равна.
Цели обучения
Сформулируйте правило пересечения Кирхгофа и опишите его ограничения
Основные выводы
Ключевые моменты
- Правило соединения Кирхгофа — это применение принципа сохранения электрического заряда: ток — это поток заряда за время, и если ток постоянный, то, что течет в точку в цепи, должно быть равно тому, что вытекает из нее.{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex], где I k — ток k, а n — общее количество проводов, входящих и выходящих из соединения. с учетом.
- Закон перехода Кирхгофа ограничен в его применимости в регионах, в которых плотность заряда может быть непостоянной. Поскольку заряд сохраняется, это возможно только при наличии потока заряда через границу области. Этот поток был бы текущим, что нарушало бы закон.
Ключевые термины
- электрический заряд : квантовое число, определяющее электромагнитные взаимодействия некоторых субатомных частиц; по соглашению, электрон имеет электрический заряд -1, а протон +1, а кварки имеют дробный заряд.
- ток : временная скорость протекания электрического заряда.
Правило соединения Кирхгофа, также известное как текущий закон Кирхгофа (KCL), первый закон Кирхгофа, правило точки Кирхгофа и узловое правило Кирхгофа, является применением принципа сохранения электрического заряда.
Правило соединений Кирхгофа гласит, что в любом соединении (узле) в электрической цепи сумма токов, протекающих в этом соединении, равна сумме токов, вытекающих из этого соединения.Другими словами, при условии, что ток будет положительным или отрицательным в зависимости от того, течет ли он к стыку или от него, алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю. Визуальное представление можно увидеть на.
Закон соединения Кирхгофа : Закон соединения Кирхгофа, проиллюстрированный как токи, текущие в соединение и выходящие из него.
Теория правил Кирхгофа петли и соединений : Мы оправдываем правила Кирхгофа, исходя из сохранения энергии.{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex]
, где n — общее количество ветвей, по которым ток идет к узлу или от него.
Этот закон основан на сохранении заряда (измеряется в кулонах), который является произведением силы тока (в амперах) и времени (в секундах).
Ограничение
Применимость закона Кирхгофа ограничена. Это справедливо для всех случаев, когда полный электрический заряд (Q) постоянен в рассматриваемой области. На практике это всегда так, если закон применяется к определенной точке.Однако в определенной области плотность заряда может быть непостоянной. Поскольку заряд сохраняется, это возможно только при наличии потока заряда через границу области. Этот поток был бы током, что нарушало бы закон Кирхгофа.
Правило цикла
Правило петли Кирхгофа гласит, что сумма значений ЭДС в любом замкнутом контуре равна сумме падений потенциала в этом контуре.
Цели обучения
Сформулируйте правило петли Кирхгофа, учитывая его допущения.
Основные выводы
Ключевые моменты
- Правило петли Кирхгофа — это правило, относящееся к схемам, основанное на принципе сохранения энергии.\ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
- Правило петли Кирхгофа является упрощением закона индукции Фарадея и выполняется при предположении, что нет флуктуирующего магнитного поля, связывающего замкнутый контур.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой. Резистор
- : Электрический компонент, который передает ток прямо пропорционально напряжению на нем.
Правило петли Кирхгофа (также известное как закон напряжения Кирхгофа (KVL), правило сетки Кирхгофа, второй закон Кирхгофа, или второе правило Кирхгофа ) — это правило, относящееся к схемам, и основано на принципе сохранения энергия.
Сохранение энергии — принцип, согласно которому энергия не создается и не разрушается — широко используется во многих исследованиях в области физики, включая электрические схемы. Применительно к схемотехнике подразумевается, что направленная сумма разностей электрических потенциалов (напряжений) вокруг любой замкнутой сети равна нулю.Другими словами, сумма значений электродвижущей силы (ЭДС) в любом замкнутом контуре равна сумме падений потенциала в этом контуре (которые могут исходить от резисторов).
Другое эквивалентное утверждение состоит в том, что алгебраическая сумма произведений сопротивлений проводников (и токов в них) в замкнутом контуре равна общей электродвижущей силе, имеющейся в этом контуре. Математически правило петли Кирхгофа можно представить как сумму напряжений в цепи, которая приравнивается к нулю:
Теория правил Кирхгофа петли и соединений : Мы оправдываем правила Кирхгофа, исходя из сохранения энергии.\ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
Здесь V k — напряжение на элементе k, а n — общее количество элементов в замкнутой цепи. Иллюстрация такой схемы показана на. В этом примере сумма v 1 , v 2 , v 3 и v 4 (и v 5 , если он включен), составляет нуль.
Правило петли Кирхгофа : Правило петли Кирхгофа гласит, что сумма всех напряжений вокруг петли равна нулю: v1 + v2 + v3 — v4 = 0.
Учитывая, что напряжение является мерой энергии на единицу заряда, правило петли Кирхгофа основано на законе сохранения энергии, который гласит: общая энергия, полученная на единицу заряда, должна равняться количеству энергии, потерянной на единицу заряда .
Пример
иллюстрирует изменения потенциала в простой петле последовательной цепи. Второе правило Кирхгофа требует, чтобы ЭДС-Ir-IR 1 -IR 2 = 0. После перестановки это ЭДС = Ir + IR 1 + IR 2 , что означает, что ЭДС равна сумме падений IR (напряжения) в контуре.ЭДС подает 18 В, которое уменьшается до нуля из-за сопротивления, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, всего 18 В.
Правило цикла : Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) В этой стандартной схеме простой последовательной цепи ЭДС подает 18 В, которое снижается до нуля из-за сопротивлений, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки для всего 18 В.(b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и понижается за счет сопротивлений. (Обратите внимание, что сценарий E означает ЭДС.)
Ограничение
Правило петли Кирхгофа является упрощением закона индукции Фарадея и выполняется при предположении, что нет флуктуирующего магнитного поля, связывающего замкнутый контур. В присутствии переменного магнитного поля могут индуцироваться электрические поля и возникать ЭДС, и в этом случае правило петли Кирхгофа нарушается.
Приложения
Правила Кирхгофа можно использовать для анализа любой схемы и модифицировать для схем с ЭДС, резисторами, конденсаторами и т. Д.
Цели обучения
Опишите условия, при которых полезно применять правила Кирхгофа.
Основные выводы
Ключевые моменты
- Правила Кирхгофа могут применяться к любой цепи, независимо от ее состава и структуры.
- Поскольку часто легко комбинировать элементы параллельно и последовательно, не всегда удобно применять правила Кирхгофа.
- Чтобы найти ток в цепи, можно применить правила петли и соединения. Как только все токи связаны правилом соединения, можно использовать правило петли, чтобы получить несколько уравнений, которые будут использоваться в качестве системы для нахождения каждого значения тока в терминах других токов. Их можно решить как систему.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
Обзор
ПравилаКирхгофа можно использовать для анализа любой схемы, изменяя их для схем с электродвижущими силами, резисторами, конденсаторами и т. Д. На практике, однако, правила полезны только для характеристики тех цепей, которые нельзя упростить, комбинируя элементы последовательно и параллельно.
Последовательные и параллельные комбинации, как правило, намного проще выполнить, чем применение любого из правил Кирхгофа, но правила Кирхгофа применимы более широко и должны использоваться для решения проблем, связанных со сложными схемами, которые нельзя упростить, комбинируя элементы схемы последовательно или параллельно.
Пример правил Кирхгофа
показывает очень сложную схему, но можно применить правила Кирхгофа для петель и соединений. Чтобы решить схему для токов I 1 , I 2 и I 3 , необходимы оба правила.
Правила Кирхгофа: пример задачи : На этом изображении показана очень сложная схема, которую можно сократить и решить с помощью правил Кирхгофа.
Применяя правило Кирхгофа в точке a, находим:
[латекс] \ text {I} _1 = \ text {I} _2 + \ text {I} _3 [/ latex]
, потому что I 1 течет в точку a, а I 2 и I3 вытекает.То же самое можно найти в точке e. Теперь мы должны решить это уравнение для каждой из трех неизвестных переменных, что потребует трех разных уравнений.
Рассматривая цикл abcdea, мы можем использовать правило цикла Кирхгофа:
[латекс] — \ text {I} _2 \ text {R} _2 + \ mathrm {\ text {emf}} _ 1- \ text {I} _2 \ text {r} _1- \ text {I} _1 \ text { R} _1 = — \ text {I} _2 (\ text {R} _2) + \ text {r} _1) + \ mathrm {\ text {emf}} _ 1- \ text {I} _1 \ text {R} _1 = 0 [/ латекс]
Подставляя значения сопротивления и ЭДС из рисунка на диаграмме и отменяя единицу измерения ампер, получаем:
[латекс] -3 \ text {I} _2 + 18-6 \ text {I} _1 = 0 [/ латекс]
Это вторая часть системы трех уравнений, которую мы можем использовать, чтобы найти все три текущих значения.Последнюю можно найти, применив правило цикла к циклу aefgha, которое дает:
[латекс] \ text {I} _1 \ text {R} _1 + \ text {I} _3 \ text {R} _3 + \ text {I} _3 \ text {r} _2- \ mathrm {\ text {emf}} _2 = \ text {I} _1 \ text {R} _1 + \ text {I} _3 (\ text {R} _3 + \ text {r} _2) — \ mathrm {\ text {emf}} _ 2 = 0 [/ латекс ]
Используя замену и упрощение, это становится:
[латекс] 6 \ text {I} _1 + 2 \ text {I} _3-45 = 0 [/ латекс]
В этом случае знаки поменялись местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении.
Теперь у нас есть три уравнения, которые можно использовать в системе. Второй будет использоваться для определения I 2 и может быть изменен на:
[латекс] \ text {I} _2 = 6-2 \ text {I} _1 [/ латекс]
Третье уравнение может использоваться для определения I 3 и может быть преобразовано в:
[латекс] \ text {I} _3 = 22,5-3 \ text {I} _1 [/ латекс]
Подставляя новые определения I 2 и I 3 (которые являются общими терминами I 1 ) в первое уравнение (I 1 = I 2 + I 3 ), получаем:
[латекс] \ text {I} _1 = (6-2 \ text {I} _1) + (22.5-3 \ text {I} _1) = 28,5-5 \ text {I} _1 [/ latex]
Упрощая, получаем, что I 1 = 4,75 A. Подставляя это значение в два других уравнения, мы находим, что I 2 = -3,50 A и I 3 = 8,25 A.
6.3 Правила Кирхгофа — Введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
По окончании раздела вы сможете:
- Государственное правило Кирхгофа
- Государственное правило петли Кирхгофа
- Анализировать сложные схемы по правилам Кирхгофа
Мы только что видели, что некоторые схемы можно проанализировать, сведя схему к одному источнику напряжения и эквивалентному сопротивлению.Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рисунке 6.3.1 известна как многоконтурная схема , которая состоит из переходов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить.Попробуйте. Резисторы и включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами и. Но что же тогда делать?
Несмотря на то, что эта схема не может быть проанализирована с помощью уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной. Правила известны как правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).
(рисунок 6.3.1)
Рисунок 6.3.1 Эта схема не может быть сведена к комбинации последовательного и параллельного соединения. Однако мы можем использовать правила Кирхгофа для его анализа.ПРАВИЛА КИРХГОФА
- Первое правило Кирхгофа — правило перехода . Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
(6.3.1)
- Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любого пути (контура) замкнутой цепи должна быть равна нулю:
(6.3.2)
Теперь мы даем объяснения этих двух правил, за которыми следуют советы по их применению и рабочий пример, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рисунок 6.3.2). Как было сказано ранее, соединение или узел — это соединение трех или более проводов. Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.
(рисунок 6.3.2)
Рисунок 6.3.2 Заряд должен сохраняться, поэтому сумма токов в переходе должна быть равна сумме токов на выходе.Несмотря на то, что это чрезмерное упрощение, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рис. 6.3.2 были заменены водопроводными трубами, а вода считалась несжимаемой, объем воды, поступающей в разветвление, должен был равняться объему воды, вытекающей из разветвления.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило петли ) применяется к разности потенциалов. Правило петли сформулировано в терминах потенциальной, а не потенциальной энергии, но они связаны между собой. В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю.Например, рассмотрим простую петлю без стыков, как на рис. 6.3.3.
(рисунок 6.3.3)
Рисунок 6.3.3 Простая петля без стыков. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки,, и служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Цепь обозначается как Цикл, и метки помогают отслеживать разницу напряжений при перемещении по цепи.Начните с точки и двигайтесь к ней. Напряжение источника напряжения добавляется к уравнению, а падение потенциала на резисторе вычитается. От точки до потенциальный перепад вычитается. От до вычитается потенциальный перепад. От пунктов до ничего не делается, потому что нет компонентов.
На рис. 6.3.4 показан график напряжения при перемещении по контуру. Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор.Падение потенциала , или изменение электрического потенциала, равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
(рисунок 6.3.4)
Рисунок 6.3.4 График напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.Тогда правило петли Кирхгофа утверждает
Уравнение контура можно использовать для определения тока в контуре:
Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах. Это могут быть токи, напряжения или сопротивления.Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.
Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.
Стратегия решения проблем: правила Кирхгофа
- Обозначьте точки на принципиальной схеме строчными буквами. Эти метки просто помогают сориентироваться.
- Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов.Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток направлен на соединение, а по крайней мере один ток выходит из соединения.
- Выбрать петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
- Примените правило соединения. Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
- Примените правило цикла.Используйте карту на рисунке 6.3.5.
(рисунок 6.3.5)
Рисунок 6.3.5 Каждый из этих резисторов и источников напряжения проходит от до. (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала. (c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала.(d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.Давайте подробнее рассмотрим некоторые этапы этой процедуры. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения. Если стрелка находится в направлении, противоположном обычному потоку тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.
Рассмотрим рисунок 6.3.6. В этой цепи есть два соединения: соединение и соединение. Точки,, и не являются соединениями, потому что соединение должно иметь три или более соединений. Уравнение для соединения есть, а уравнение для соединения есть.Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
(рисунок 6.3.6)
Рисунок 6.3.6 На первый взгляд, эта схема содержит два соединения, соединение и соединение, но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 6.3.7 показаны четыре варианта петель для решения типовой схемы; варианты (a), (b) и (c) имеют достаточное количество циклов для полного решения схемы.Вариант (d) отражает больше петель, чем необходимо для решения схемы.
(рисунок 6.3.7)
Рисунок 6.3.7 Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы. На панели (d) показаны три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.Рассмотрим схему на Рисунке 6.3.8 (a). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).
(рисунок 6.3.8)
Рисунок 6.3.8 (a) Многоконтурная схема. (b) Пометьте цепь, чтобы облегчить ориентацию.Далее определяем перекрестки. В этой схеме точки и каждая имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа, нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 6.3.9 (б). Junction показывает это, а Junction это показывает. Поскольку Junction предоставляет ту же информацию, что и Junction, ее можно не принимать во внимание. Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.
(рисунок 6.3.9)
Рисунок 6.3.9 (a) Эта схема имеет два соединения, помеченных b и e, но в анализе используется только узел b. (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.Далее нам нужно выбрать петли.На рисунке 6.3.10 контур включает источник напряжения, резисторы и. Цикл начинается с точки, затем проходит через точки, и, а затем возвращается к точке. Вторая петля, петля, начинается в точке и включает резисторы и источник напряжения.
(рисунок 6.3.10)
Рисунок 6.3.10 Выберите петли в схеме.Теперь мы можем применить правило цикла Кирхгофа, используя карту на рис. 6.3.5. Начиная с точки и двигаясь к точке, резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается.При перемещении от точки к точке резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. При перемещении от точки к точке источник напряжения пересекается от отрицательной клеммы к положительной, поэтому добавляется. Между точками и нет компонентов. Сумма разностей напряжений должна равняться нулю:
Наконец, проверяем цикл. Мы начинаем с точки и переходим к точке, пересекаясь в направлении, противоположном текущему потоку.Потенциальное падение добавлено. Затем мы пересекаем и в том же направлении, что и ток, и вычитаем падения потенциала и. Обратите внимание, что через резисторы и ток одинаковый, потому что они соединены последовательно. Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура
Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.
Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока. Сначала добавьте уравнение. (1) раз к формуле. (2). Результат обозначен как уравнение. (4):
Затем вычтите уравнение. (3) из уравнения. (2). Результат обозначен как уравнение. (5):
Мы можем решить уравнения. (4) и (5) для тока. Сложив семь раз уравнение. (4) и троекратное уравнение. (5) приводит к, или. Используя уравнение.(4) приводит к. Наконец, уравнение. (1) дает. Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
Обратите внимание, что решение для тока отрицательное. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока. Питание от второго источника напряжения есть и нет.
ПРИМЕР 6.3.1
Расчет тока по правилам Кирхгофа
Найдите токи, протекающие в цепи, показанной на рисунке 6.3.11.
(рисунок 6.3.11)
Рисунок 6.3.11 Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения. Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.Стратегия
Эта схема достаточно сложна, чтобы найти токи с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.Токи обозначены, и на рисунке, и сделаны предположения об их направлениях. Места на схеме обозначены сквозными буквами. В решении мы применяем правила перехода и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение
Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения.
Упростите уравнения, поместив неизвестные в одну сторону уравнений.
Упростите уравнения. Уравнение первого цикла можно упростить, разделив обе части на. Уравнение второго цикла можно упростить, разделив обе части на.
Результатов:
Значение
Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, подаваемой источниками напряжения:
Подаваемая мощность равна мощности, рассеиваемой резисторами.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.6
При рассмотрении следующей схемы и мощности, подаваемой и потребляемой схемой, будет ли источник напряжения всегда обеспечивать питание схемы или может ли источник напряжения потреблять энергию?
ПРИМЕР 6.3.2
Расчет тока по правилам Кирхгофа
Найдите ток, протекающий в цепи, показанной на рисунке 6.3.12.
(рисунок 6.3.12)
Рисунок 6.3.12 Эта схема состоит из трех последовательно соединенных резисторов и двух батарей. Обратите внимание, что батареи подключены с противоположной полярностью.Стратегия
Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки к точке. Рассмотрим цикл и воспользуйтесь рисунком 6.3.5, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 6.3.5, батарея будет добавлена, а батарея вычтена.
Решение
Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение:
Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.
Значение
Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее течет через батарею от положительной клеммы к отрицательной клемме и потребляет мощность.
Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.7
При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в Примере 6.3.2 направление тока было выбрано по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки к точке?
Несколько источников напряжения
Для многих устройств требуется более одной батареи. Несколько источников напряжения, таких как батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.
Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи. Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно.Две последовательно соединенные батареи показаны на рисунке 6.3.13. Использование правила петли Кирхгофа для схемы в части (b) дает результат
(рисунок 6.3.13)
Рисунок 6.3.13 (a) Две батареи, подключенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннее сопротивление.Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать, а их ЭДС можно складывать вместе, чтобы получить общие значения.Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке 6.3.13 напряжение на клеммах равно
.
Обратите внимание, что в каждой батарее присутствует одинаковый ток, поскольку они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.
Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь.Например, светодиодный фонарик может иметь две батарейки типа ААА, каждая с напряжением на клеммах, чтобы обеспечить фонарик.
Любое количество батарей можно подключить последовательно. Для аккумуляторов, включенных последовательно, напряжение на зажимах равно
.(6.3.3)
, где эквивалентное сопротивление.
Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке 6.3.14, мы можем найти ток:
Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.
(рисунок 6.3.14)
Рисунок 6.3.14 Две батареи подключаются последовательно к светодиодной лампе, как в фонарике.Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке 6.3.15 показаны две батареи с одинаковыми ЭДС, включенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, а отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам.Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.
(рисунок 6.3.15)
Рисунок 6.3.15 (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый помечен значком), соединенные параллельно, которые создают одинаковую ЭДС.Рассмотрим анализ Кирхгофа схемы на рис. 6.3.15 (b). В точке и есть две петли и узел.
Расчет тока через нагрузочный резистор дает, где. Напряжение на клеммах равно падению потенциала на нагрузочном резисторе. Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.
Параллельно можно подключить любое количество батарей. Для аккумуляторов, включенных параллельно, напряжение на зажимах равно
.(6.3.4)
, где эквивалентное сопротивление.
Например, в некоторых грузовиках с дизельным двигателем параллельно используются две батареи; они производят полную ЭДС, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.
Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления.Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки. Аккумуляторы подключаются параллельно для увеличения тока нагрузки.
Массив солнечных батарей
Другой пример, имеющий дело с несколькими источниками напряжения, — это комбинация солнечных элементов , соединенных как последовательно, так и параллельно, чтобы обеспечить желаемое напряжение и ток. Фотогальваническая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте.Фотоэлектрический эффект выходит за рамки этого учебника, но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.
Большинство солнечных элементов изготовлено из чистого кремния. Большинство отдельных ячеек имеют выходное напряжение около, в то время как выходной ток зависит от количества солнечного света, падающего на элемент (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические элементы производят ток на единицу площади примерно равной площади поверхности ячейки.
Отдельные солнечные элементы электрически соединены в модулях для удовлетворения потребностей в электроэнергии. Их можно соединить последовательно или параллельно — как батареи, о которых говорилось ранее. Матрица или модуль солнечных элементов обычно состоит из промежуточных элементов и элементов с выходной мощностью до.
Солнечные элементы, как и батареи, вырабатывают напряжение постоянного тока (dc). Ток от источника постоянного напряжения однонаправлен. Большинству бытовых приборов требуется переменное напряжение.
Кандела Цитаты
Лицензионный контент CC, особая атрибуция
- Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Сопротивление | Клуб электроники
Resistance | Клуб электроникиСопротивление | В серии | Параллельно | Проводники и изоляторы
Следующая страница: Закон Ома
См. Также: Резисторы | Импеданс
Сопротивление — это свойство компонента, которое ограничивает поток заряда .Энергия расходуется, поскольку напряжение на компоненте пропускает через него ток и эта энергия проявляется в компоненте в виде тепла.
Сопротивление измеряется в омах, символ ом — омега. .
1 довольно мала для электроники, поэтому сопротивления часто указываются в k и м.
1 к
= 1000
1 млн
= 1000000.
Резисторы, используемые в электронике, могут иметь сопротивление всего 0,1. или до 10 млн.
Rapid Electronics: резисторы
Резисторы, подключенные последовательно
При последовательном соединении резисторов их суммарное сопротивление равно отдельные сопротивления суммируются.Например, если резисторы R1 и R2 соединенные последовательно, их суммарное сопротивление R определяется по формуле:
| Два резистора в серии : | R = R1 + R2 |
Его можно расширить для большего количества резисторов:
| Резисторы серии : |
R = R1 + R2 + R3 + R4 + … |
Комбинированное сопротивление в серии всегда будет на больше, чем на , чем любое из индивидуальные сопротивления.
Параллельно подключенные резисторы
При параллельном подключении резисторов их суммарное сопротивление меньше любого из отдельных сопротивлений.
Существует специальное уравнение для суммарного сопротивления двух резисторов R1 и R2, включенных параллельно:
| Два резистора в параллельно : | R = | R1 × R2 |
| R1 + R2 |
параллельно резисторов
необходимо использовать более сложное уравнение.Это суммирует , равное («на один больше») каждого сопротивления, чтобы получить , обратное комбинированного сопротивления, R:
| Резисторы в параллельно : | 1 | = | 1 | + | 1 | + | 1 | +… |
| R | R1 | R2 | R3 |
Более простое уравнение для двух резисторов , подключенных параллельно, намного проще в использовании!
Комбинированное сопротивление , включенное параллельно , всегда будет на меньше , чем любое из индивидуальные сопротивления.
Проводники, полупроводники и изоляторы
Сопротивление объекта зависит от его формы и материала из которого он сделан.Для данного материала объекты с меньшим поперечным сечением или более длинная длина будет иметь большее сопротивление.
Материалы можно разделить на три группы:
Проводники — низкоомные
Примеры включают металлы (алюминий, медь, серебро и т. Д.) И углерод. Металлы используются для изготовления соединительных проводов, контактов переключателей и нитей ламп. Резисторы изготавливают из углерода или длинных катушек из тонкой проволоки.
Полупроводники — умеренное сопротивление
Примеры включают германий и кремний.Полупроводники используются для изготовления диодов, светодиодов, транзисторов и интегральных схем (микросхем).
Изоляторы — высокое сопротивление
Примеры включают большинство пластмасс, таких как полиэтилен и ПВХ (поливинилхлорид), бумагу, дерево, резину и стекло. ПВХ используется как внешнее покрытие для проводов, чтобы предотвратить их соприкосновение.
Рекомендуемая книга
Рекомендую Электроника для детей как хорошее введение в электричество и электронику. Напечатанный в цвете с множеством иллюстраций, он знакомит с общими компонентами простых, но интересных проектов. строить на каждом этапе.Книга начинается с предположения об отсутствии предшествующих знаний, а затем тщательно выстраивает простые объяснения. о том, как работают компоненты, а также о практических методах, включая снятие изоляции с проводов, пайку и использование мультиметра.
Основные моменты включают в себя освещение светодиода лимонами, использование реле для мигания светодиода, создание музыкального инструмента, включение сигнала восхода солнца, игра по угадыванию цвета, программа проверки секретного кода и финальный проект используют три микросхемы для создания отличной игры.
Автор, Ойвинд Нидал Даль, проделал огромную работу, предоставив четкие пошаговые инструкции с макетом (или полосой). макеты, а также принципиальные схемы для проектов.Как технический рецензент книги, я сам создавал все проекты, и я очень с радостью рекомендую его всем, кто хочет весело и познавательно познакомиться с электроникой.
Следующая страница: Закон Ома | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию. Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет используется только для ответа на ваше сообщение, оно не будет передано никому.На этом веб-сайте отображается реклама, если вы нажмете на рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден. Рекламодателям не передается никакая личная информация. Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации. Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов. (включая этот), как объяснил Google.Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста, посетите AboutCookies.org.
electronicsclub.info © Джон Хьюс 2021 г.
Последовательная связь— learn.sparkfun.com
Добавлено в избранное Любимый 93Введение
Встроенная электроника — это объединение схем (процессоров или других интегральных схем) для создания симбиотической системы.Чтобы эти отдельные каналы могли обмениваться информацией, они должны использовать общий протокол связи. Для этого обмена данными определены сотни протоколов связи, каждый из которых можно разделить на две категории: параллельный или последовательный.
Параллельный и последовательный
Параллельные интерфейсы одновременно передают несколько битов. Обычно им требуется шина, данных — передача по восьми, шестнадцати или более проводам. Данные передаются огромными, грохочущими волнами единиц и нулей.
8-битная шина данных, управляемая часами, передающая байт за каждый тактовый импульс. Используются 9 проводов.
Последовательные интерфейсы передают свои данные по одному биту за раз. Эти интерфейсы могут работать всего с одним проводом, обычно не более четырех.
Пример последовательного интерфейса, передающего один бит за каждый тактовый импульс. Требуется всего 2 провода!
Думайте о двух интерфейсах как о потоке автомобилей: параллельный интерфейс будет представлять собой мегамагистраль с 8 и более полосами движения, а последовательный интерфейс больше похож на двухполосную сельскую дорогу.За установленный промежуток времени мегамагистраль потенциально может доставить больше людей к месту назначения, но эта сельская двухполосная дорога служит своей цели и стоит небольшую часть средств, чтобы построить.
Параллельная связь, безусловно, имеет свои преимущества. Это быстро, просто и относительно легко реализовать. Но для этого требуется гораздо больше линий ввода / вывода (I / O). Если вам когда-либо приходилось переносить проект с базового Arduino Uno на Mega, вы знаете, что линии ввода-вывода на микропроцессоре могут быть драгоценными и немногочисленными.Таким образом, мы часто выбираем последовательную связь, жертвуя потенциальной скоростью ради полезности контактов.
Асинхронный последовательный
За прошедшие годы были созданы десятки последовательных протоколов для удовлетворения особых потребностей встраиваемых систем. USB (универсальная последовательная шина , ) и Ethernet — это пара наиболее известных компьютерных последовательных интерфейсов. Другие очень распространенные последовательные интерфейсы включают SPI, I 2 C и стандарт последовательного интерфейса, о котором мы здесь сегодня поговорим. Каждый из этих последовательных интерфейсов можно разделить на две группы: синхронные или асинхронные.
Синхронный последовательный интерфейс всегда связывает свою линию (линии) данных с тактовым сигналом, поэтому все устройства на синхронной последовательной шине используют общие часы. Это делает последовательную передачу более простой и часто более быстрой, но также требует как минимум одного дополнительного провода между взаимодействующими устройствами. Примеры синхронных интерфейсов включают SPI и I 2 C.
Асинхронный означает, что данные передаются без поддержки внешнего тактового сигнала .Этот метод передачи идеально подходит для минимизации необходимых проводов и контактов ввода / вывода, но это означает, что нам нужно приложить дополнительные усилия для надежной передачи и приема данных. Последовательный протокол, который мы будем обсуждать в этом руководстве, является наиболее распространенной формой асинхронной передачи. На самом деле это настолько распространено, что, когда большинство людей говорят «серийный», они имеют в виду именно этот протокол (что вы, вероятно, заметите в этом руководстве).
Последовательный протокол без тактовой частоты, который мы обсудим в этом руководстве, широко используется во встроенной электронике.Если вы хотите добавить в свой проект модуль GPS, Bluetooth, XBee, ЖК-дисплеи с последовательным интерфейсом или многие другие внешние устройства, вам, вероятно, потребуется добавить несколько последовательных интерфейсов.
Рекомендуемая литература
Это руководство основано на нескольких концепциях электроники нижнего уровня, в том числе:
двоичный
Двоичная — это система счисления в электронике и программировании … поэтому важно научиться этому. Но что такое двоичный? Как это переводится в другие системы счисления, такие как десятичные?
Логические уровни
Узнайте разницу между 3.Устройства 3V и 5V и логические уровни.
Аналоговый и цифровой
В этом руководстве рассматривается концепция аналоговых и цифровых сигналов в их отношении к электронике.
Как читать схему
Обзор обозначений схем компонентов, а также советы и рекомендации для лучшего чтения схем. Щелкните здесь и станьте схематически грамотным уже сегодня!
Шестнадцатеричный
Как интерпретировать шестнадцатеричные числа и как преобразовать их в / из десятичных и двоичных чисел.
ASCII
Краткая история того, как появился ASCII, как он полезен для компьютеров, и некоторые полезные таблицы для преобразования чисел в символы.
Если вы не очень хорошо знакомы ни с одной из этих концепций, подумайте о проверке этих ссылок.
А теперь давайте отправимся в серийное путешествие …
Правила серийного номера
Асинхронный последовательный протокол имеет ряд встроенных правил — механизмов, которые помогают обеспечить надежную и безошибочную передачу данных.Вот эти механизмы, которые мы получаем для исключения внешнего тактового сигнала:
- Биты данных,
- бит синхронизации,
- бит четности,
- и скорость передачи.
Благодаря разнообразию этих сигнальных механизмов вы обнаружите, что не существует единого способа для последовательной передачи данных. Протокол легко настраивается. Важнейшая часть — убедиться, что оба устройства на последовательной шине настроены для использования точно таких же протоколов .
Скорость передачи
Скорость передачи определяет скорость передачи данных по последовательной линии.Обычно это выражается в битах в секунду (бит / с). Если вы инвертируете скорость передачи, вы можете узнать, сколько времени требуется для передачи одного бита. Это значение определяет, как долго передатчик удерживает высокий / низкий уровень последовательной линии или в какой период принимающее устройство производит выборку своей линии.
Скорость передачи может быть практически любой в разумных пределах. Единственное требование — чтобы оба устройства работали с одинаковой скоростью. Одна из наиболее распространенных скоростей передачи, особенно для простых вещей, где скорость не критична, — 9600 бит / с .Другие «стандартные» скорости: 1200, 2400, 4800, 19200, 38400, 57600 и 115200.
Чем выше скорость передачи, тем быстрее отправляются / принимаются данные, но существуют ограничения на скорость передачи данных. Обычно вы не увидите скорости, превышающей 115200 — это быстро для большинства микроконтроллеров. Поднимитесь слишком высоко, и вы начнете видеть ошибки на принимающей стороне, поскольку часы и периоды выборки просто не успевают.
Обрамление данных
Каждый блок (обычно байт) передаваемых данных фактически отправляется в пакете или кадре бит.Кадры создаются путем добавления к нашим данным битов синхронизации и четности.
Серийный корпус. Некоторые символы в кадре имеют настраиваемый размер бит.
Давайте подробно рассмотрим каждую из этих частей рамы.
Блок данных
Настоящая суть каждого последовательного пакета — это данные, которые он несет. Мы неоднозначно называем этот блок данных чанком , потому что его размер конкретно не указан. Количество данных в каждом пакете может быть установлено от 5 до 9 бит.Конечно, стандартный размер данных — это ваш базовый 8-битный байт, но другие размеры имеют свое применение. 7-битный блок данных может быть более эффективным, чем 8-битный, особенно если вы просто передаете 7-битные символы ASCII.
После согласования длины символа оба последовательных устройства также должны согласовать порядок байтов своих данных. Отправляются ли данные из старшего разряда в младший или наоборот? Если не указано иное, обычно можно предположить, что данные передаются младший бит (LSB) сначала .
Биты синхронизации
Биты синхронизации — это два или три специальных бита, передаваемых с каждым блоком данных. Это стартовый бит и стоповый бит . Верные своему названию, эти биты отмечают начало и конец пакета. Всегда есть только один стартовый бит, но количество стоповых битов можно настроить на один или два (хотя обычно его оставляют равным одному).
Стартовый бит всегда обозначается незанятой строкой данных, переходящей от 1 к 0, в то время как стоповый бит (ы) переходит обратно в состояние ожидания, удерживая строку на 1.
Биты четности
Четность — это форма очень простой низкоуровневой проверки ошибок. Он бывает двух видов: четный и нечетный. Для создания бита четности все 5-9 битов байта данных складываются, и четность суммы определяет, установлен ли бит или нет. Например, предполагая, что четность установлена на четность и добавляется к байту данных, например 0b01011101 , который имеет нечетное число 1 (5), бит четности будет установлен на 1 . И наоборот, если режим четности был установлен как нечетный, бит четности будет 0 .
Четность — необязательный и не очень широко используется. Это может быть полезно для передачи через шумные среды, но это также немного замедлит вашу передачу данных и требует, чтобы отправитель и получатель реализовали обработку ошибок (обычно полученные данные, которые терпят неудачу, должны быть отправлены повторно).
9600 8N1 (пример)
9600 8N1 — 9600 бод, 8 бит данных, без контроля четности и 1 стоповый бит — это один из наиболее часто используемых последовательных протоколов. Итак, как будут выглядеть один или два пакета данных 9600 8N1? Приведем пример!
Устройство, передающее символы ASCII «O» и «K», должно создать два пакета данных.Значение ASCII O (это верхний регистр) — 79, что разбивается на 8-битное двоичное значение 01001111 , а двоичное значение K — 01001011 . Осталось только добавить биты синхронизации.
Это конкретно не указано, но предполагается, что данные передаются в первую очередь младшим битом. Обратите внимание, как каждый из двух байтов отправляется при чтении справа налево.
Поскольку мы передаем со скоростью 9600 бит / с, время, затрачиваемое на поддержание высокого или низкого уровня каждого из этих битов, составляет 1 / (9600 бит / с) или 104 мкс на бит.
На каждый переданный байт данных фактически отправляется 10 бит: стартовый бит, 8 бит данных и стоповый бит. Итак, при 9600 бит / с мы фактически отправляем 9600 бит в секунду или 960 (9600/10) байтов в секунду.
Теперь, когда вы знаете, как создавать последовательные пакеты, мы можем перейти к разделу оборудования. Там мы увидим, как эти единицы и нули, а также скорость передачи данных реализованы на уровне сигнала!
Электромонтаж и оборудование
Последовательная шина состоит всего из двух проводов — один для отправки данных, а другой для приема.Таким образом, последовательные устройства должны иметь два последовательных контакта: приемник, RX , и передатчик, TX .
Важно отметить, что эти ярлыки RX и TX относятся к самому устройству. Таким образом, RX от одного устройства должен переходить в TX другого, и наоборот. Это странно, если вы привыкли подключать VCC к VCC, GND к GND, MOSI к MOSI и т. Д., Но это имеет смысл, если подумать. Передатчик должен разговаривать с приемником, а не с другим передатчиком.
Последовательный интерфейс, через который оба устройства могут отправлять и получать данные, — это полнодуплексный или полудуплексный . Полнодуплексный режим означает, что оба устройства могут отправлять и получать одновременно. Полудуплексная связь означает, что последовательные устройства должны по очереди отправлять и получать.
Некоторые последовательные шины могут обходиться без единого соединения между отправляющим и принимающим устройством. Например, все ЖК-дисплеи с последовательным подключением — это уши, и на самом деле у них нет никаких данных, которые можно было бы передать обратно на управляющее устройство.Это то, что известно как симплексная последовательная связь . Все, что вам нужно, это один провод от TX ведущего устройства до RX линии слушателя.
Аппаратная реализация
Мы рассмотрели асинхронный последовательный порт с концептуальной стороны. Мы знаем, какие провода нам нужны. Но как на самом деле реализуется последовательная связь на уровне сигнала? На самом деле, разными способами. Существуют всевозможные стандарты для последовательной передачи сигналов. Давайте посмотрим на пару наиболее популярных аппаратных реализаций последовательного интерфейса: логического уровня (TTL) и RS-232.
Когда микроконтроллеры и другие низкоуровневые ИС взаимодействуют последовательно, они обычно делают это на уровне TTL (транзисторно-транзисторной логики). Последовательный TTL Сигналы существуют между диапазоном напряжения питания микроконтроллера — обычно от 0 В до 3,3 В или 5 В. Сигнал на уровне VCC (3,3 В, 5 В и т. Д.) Указывает либо на свободную линию, либо на бит со значением 1, либо на стоповый бит. Сигнал 0 В (GND) представляет либо стартовый бит, либо бит данных со значением 0.
RS-232, который можно найти на некоторых из более древних компьютеров и периферийных устройств, похож на TTL-последовательный порт, перевернутый с ног на голову.Сигналы RS-232 обычно находятся в диапазоне от -13 В до 13 В, хотя в спецификации допускается любое значение от +/- 3 В до +/- 25 В. В этих сигналах низкое напряжение (-5 В, -13 В и т. Д.) Указывает либо на свободную линию, либо на стоповый бит, либо на бит данных со значением 1. Высокий сигнал RS-232 означает либо стартовый бит, либо 0- бит данных значения. Это своего рода противоположность последовательному TTL.
Между двумя стандартами последовательных сигналов, TTL намного проще внедрить во встроенные схемы. Однако низкие уровни напряжения более подвержены потерям на длинных линиях передачи.RS-232 или более сложные стандарты, такие как RS-485, лучше подходят для последовательной передачи на большие расстояния.
Когда вы соединяете два последовательных устройства вместе, важно убедиться, что их сигнальные напряжения совпадают. Вы не можете напрямую связать последовательное устройство TTL с шиной RS-232. Вам придется изменить эти сигналы!
Продолжая, мы исследуем инструменты, которые микроконтроллеры используют для преобразования своих данных по параллельной шине в последовательный интерфейс и обратно. UART!
UART
Последняя часть этой серийной головоломки — найти что-то, что могло бы создать как последовательные пакеты, так и управлять этими физическими линиями оборудования.Введите UART.
Универсальный асинхронный приемник / передатчик (UART) — это блок схемы, отвечающий за реализацию последовательной связи. По сути, UART действует как посредник между параллельным и последовательным интерфейсами. На одном конце UART находится шина из восьми или около того линий данных (плюс несколько управляющих контактов), на другом — два последовательных провода — RX и TX.
Супер-упрощенный интерфейс UART. Параллельный на одном конце, последовательный на другом.
UART существуют как автономные ИС, но чаще встречаются внутри микроконтроллеров.Вам нужно будет проверить техническое описание вашего микроконтроллера, чтобы узнать, есть ли у него какие-либо UART. У кого-то его нет, у кого-то есть, у кого-то много. Например, Arduino Uno, основанный на «старом верном» ATmega328, имеет только один UART, а Arduino Mega, построенный на ATmega2560, имеет целых четыре UART.
Как следует из аббревиатуры R и T , UART отвечают как за отправку, так и за прием последовательных данных. На передающей стороне UART должен создать пакет данных, добавив биты синхронизации и четности, и отправить этот пакет по линии передачи с точной синхронизацией (в соответствии с установленной скоростью передачи).На стороне приема UART должен выполнить выборку линии RX со скоростью в соответствии с ожидаемой скоростью передачи, выбрать биты синхронизации и выдать данные.
Блок-схема внутреннего UART (любезно предоставлена таблицей данных Exar ST16C550)
Более продвинутые UART могут сбрасывать полученные данные в буфер , где они могут оставаться до тех пор, пока микроконтроллер не придет за ними. UART обычно выпускают свои буферизованные данные по принципу FIFO. Буферы могут иметь размер от нескольких бит до тысяч байтов.
Программные UART
Если микроконтроллер не имеет UART (или его не хватает), последовательный интерфейс может быть битом , — напрямую управляться процессором. Это подход, который используют библиотеки Arduino, такие как SoftwareSerial. Bit-banging требует много ресурсов процессора и обычно не так точен, как UART, но в крайнем случае работает!
Распространенные ловушки
Вот и все, что есть о последовательной связи. Я хотел бы оставить вам несколько распространенных ошибок, которые легко сделать инженер с любым уровнем опыта:
RX-to-TX, TX-to-RX
Выглядит достаточно просто, но я знаю, что это ошибка, которую я совершал несколько раз.Как бы вы ни хотели, чтобы их метки совпадали, всегда следите за тем, чтобы линии RX и TX пересекали линии между последовательными устройствами.
FTDI Базовое программирование Pro Mini. Обратите внимание на пересечение RX и TX!Вопреки тому, что предупреждал уважаемый доктор Эгон Спенглер, пересекает ручьи .
Несоответствие скорости передачи
Скорость передачи аналогична языкам последовательной связи. Если два устройства не разговаривают с одинаковой скоростью, данные могут быть неправильно интерпретированы или полностью пропущены.Если все принимающее устройство видит на своей линии приема мусор, убедитесь, что скорости передачи совпадают.
Данные передаются со скоростью 9600 бит / с, но принимаются со скоростью 19200 бит / с. Несоответствие бода = мусор.
Разногласия в автобусе
Последовательная связь предназначена для того, чтобы только два устройства могли обмениваться данными по одной последовательной шине. Если несколько устройств пытаются передавать по одной и той же последовательной линии, вы можете столкнуться с конфликтом на шине. Дун Дун Дун ….
Например, если вы подключаете модуль GPS к Arduino, вы можете просто подключить линию TX этого модуля к линии RX Arduino.Но этот вывод Arduino RX уже подключен к выводу TX преобразователя USB-to-serial, который используется всякий раз, когда вы программируете Arduino или используете Serial Monitor . Это создает потенциальную ситуацию, когда и модуль GPS, и чип FTDI пытаются одновременно передавать данные по одной и той же линии.
Два передатчика, отправляющие сигнал одному приемнику, создают возможность конфликта на шине.
Два устройства пытаются передавать данные одновременно по одной линии — это плохо! В «лучшем» случае ни одно из устройств не сможет отправлять свои данные.В худшем случае обе линии передачи устройства выходят из строя (хотя это редко и обычно защищено от этого).
Подключение нескольких приемных устройств к одному передающему устройству может быть безопасным. Не совсем соответствует спецификациям и, вероятно, не одобряется закаленным инженером, но это сработает. Например, если вы подключаете последовательный ЖК-дисплей к Arduino, самым простым подходом может быть подключение линии RX ЖК-модуля к линии TX Arduino. TX Arduino уже подключен к линии RX USB-программатора, но это по-прежнему оставляет только одно устройство, контролирующее линию передачи.
Такое распределение линии передачи может быть опасным с точки зрения прошивки, потому что вы не можете выбрать, какое устройство слышит какую передачу. ЖК-дисплей в конечном итоге получит данные, не предназначенные для него, что может заставить его перейти в неизвестное состояние.
В общем — одна последовательная шина, два последовательных устройства!
ресурсов и дальнейшее развитие
Благодаря этим блестящим новым знаниям о последовательной связи есть множество новых концепций, проектов и технологий для изучения.
Хотите узнать больше о других стандартах связи? Может что-то синхронное? Ознакомьтесь со следующими протоколами связи.
I2C
Введение в I2C, один из основных используемых сегодня протоколов встроенной связи.
AST-CAN485 Руководство по подключению
AST CAN485 — это миниатюрная Arduino в компактном форм-факторе ProMini.В дополнение ко всем обычным функциям он имеет встроенные порты CAN и RS485, позволяющие быстро и легко взаимодействовать с множеством промышленных устройств.
Многие технологии широко используют последовательную связь:
А может, хотите посмотреть сериал в действии?
Закон 3,2 Ома: сопротивление и простые схемы
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R.R. size 12 {R} {} Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
. 3.13 I∝1R.I∝1R. размер 12 {я подпираю {{1} над {R}} «.»} {}Таким образом, например, ток уменьшается вдвое, если сопротивление увеличивается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
3.14 I = VR.I = VR. размер 12 {I = {{V} больше {R}} «.»} {}Это соотношение также называется законом Ома.Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление RR размером 12 {R} {}, которое не зависит от напряжения VV, размера 12 {V} {} и тока I.I. размер 12 {I} {} Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико.Единицей измерения сопротивления является Ом и обозначается символом ΩΩ размер 12 {% OMEGA} {} (греческое омега в верхнем регистре). Перестановка I = V / RI = V / R размер 12 {I = ital «V / R»} {} дает R = V / IR = V / I размер 12 {R = ital «V / I»} {}, и Таким образом, единицы сопротивления равны 1 Ом = 1 вольт на ампер.
На рис. 3.8 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R.R. размер 12 {R} {}
Рис. 3.8 Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Установление соединений: Соединения в реальном мире
Закон Ома (V = IRV = IR) — это фундаментальное соотношение, которое может быть представлено линейной функцией, в которой наклон линии является сопротивлением.Сопротивление представляет собой напряжение, которое необходимо приложить к резистору для создания в цепи тока 1 А. График (на рисунке ниже) показывает это представление для двух простых схем с резисторами, которые имеют разное сопротивление и, следовательно, разные наклоны.
Рис. 3.9 На рисунке показано соотношение между током и напряжением для двух разных резисторов. Наклон графика представляет значение сопротивления, которое составляет 2 Ом и 4 Ом для двух показанных линий.
Установление соединений: Соединения в реальном мире
Материалы, которые подчиняются закону Ома, имея линейную зависимость между напряжением и током, известны как омические материалы. С другой стороны, некоторые материалы демонстрируют нелинейную зависимость напряжения от тока и, следовательно, известны как неомические материалы. На рисунке ниже показаны соотношения между текущим и напряжением для двух типов материалов.
Рисунок 3.10 Показаны отношения между напряжением и током для омических и неомических материалов.
Очевидно, что сопротивление омического материала, показанного на (а), остается постоянным и может быть вычислено путем нахождения наклона графика, но это неверно для неомического материала, показанного на (b).
Пример 3.4 Расчет сопротивления: Автомобильная фара
Каково сопротивление автомобильной фары, через которую проходит 2,50 А при напряжении 12,0 В?
Стратегия
Мы можем изменить закон Ома, как указано I = V / RI = V / R размер 12 {I = ital «V / R»} {}, и использовать его для определения сопротивления.
Решение
Перестановка I = V / RI = V / R, размер 12 {I = ital «V / R»} {} и замена известных значений дает
3,16 R = VI = 12,0 В 2,50 A = 4,80 Ом R = VI = 12,0 В 2,50 A = 4,80 Ом. размер 12 {R = {{V} больше {I}} = {{«12» «.» «0 В»} больше {2 «.» «50 A»}} = «4» «.» «80»% OMEGA «.»} {}Обсуждение
Это относительно небольшое сопротивление, но оно больше, чем хладостойкость фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток во время короткого периода прогрева.
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 1012 Ом 10 12 Ом или более. У сухого человека сопротивление руки к ноге может составлять 105 Ом, 105 Ом, в то время как сопротивление человеческого сердца составляет около 103 Ом · 103 Ом. Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10-5 Ом, 10-5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление».
Дополнительную информацию можно получить, решив I = V / RI = V / R размер 12 {I = ital «V / R»} {} для V, V, размер 12 {V} {}, что дает
3,17 В = ИК. В = ИК. размер 12 {V = ital «IR.»} {}Это выражение для VV размером 12 {V} {} можно интерпретировать как падение напряжения на резисторе, создаваемое током I.I. size 12 {I} {} Фраза IRIR size 12 {ital «IR»} {} drop часто используется для этого напряжения. Например, фара в примере 3.4 имеет уменьшение IRIR размера 12 {ital «IR»} {}, равное 12.0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывая ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию).В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = qΔVPE = qΔV размер 12 {«PE» = qΔV} {}, и такой же размер qq 12 {q} {} протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. Рисунок 3.11.)
Рисунок 3.11 Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Установление соединений: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму.Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним резистором. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
.
