Как работает фильтр нижних частот на операционном усилителе. Какие бывают схемы ФНЧ для аудиотехники. Как рассчитать параметры фильтра нижних частот. Какие преимущества у активных ФНЧ на ОУ.
Принцип работы фильтра нижних частот на операционном усилителе
Фильтр нижних частот (ФНЧ) на операционном усилителе (ОУ) представляет собой активный фильтр, который пропускает сигналы с частотой ниже частоты среза и подавляет высокочастотные сигналы. Основными компонентами такого фильтра являются:
- Операционный усилитель
- Резисторы
- Конденсаторы
Принцип работы ФНЧ на ОУ заключается в следующем:
- На низких частотах конденсаторы имеют высокое сопротивление и практически не влияют на сигнал
- На высоких частотах сопротивление конденсаторов уменьшается, и они шунтируют сигнал на землю
- ОУ усиливает разницу между входным и выходным сигналами, формируя АЧХ фильтра
Частота среза ФНЧ определяется номиналами резисторов и конденсаторов. Чем больше их значения, тем ниже частота среза.
Основные схемы ФНЧ на операционных усилителях для аудиотехники
Для применения в аудиотехнике наиболее часто используются следующие схемы активных ФНЧ на ОУ:
1. ФНЧ первого порядка
Простейший вариант с одним ОУ, резистором и конденсатором. Обеспечивает наклон АЧХ -6 дБ/октаву. Подходит для несложных задач фильтрации.
2. ФНЧ Саллена-Ки
Фильтр второго порядка с наклоном АЧХ -12 дБ/октаву. Отличается простотой расчета и хорошими характеристиками. Часто применяется в кроссоверах акустических систем.
3. Фильтр Баттерворта
Обеспечивает максимально плоскую АЧХ в полосе пропускания. Может быть реализован как фильтр высоких порядков для получения крутого спада АЧХ.
4. Фильтр Чебышева
Позволяет получить более крутой спад АЧХ по сравнению с фильтром Баттерворта, но имеет неравномерность в полосе пропускания.
Расчет параметров фильтра нижних частот на ОУ
Основные этапы расчета ФНЧ на операционном усилителе:
- Определение требуемой частоты среза фильтра
- Выбор типа и порядка фильтра
- Расчет номиналов резисторов и конденсаторов по формулам для выбранной топологии
- Подбор ближайших стандартных номиналов компонентов
- Проверка расчетов с помощью моделирования
Для ФНЧ первого порядка частота среза рассчитывается по формуле:
f = 1 / (2π * R * C)
где R — сопротивление резистора, C — емкость конденсатора.
Для фильтров высших порядков используются более сложные формулы и таблицы коэффициентов.
Преимущества активных ФНЧ на операционных усилителях
По сравнению с пассивными RC-фильтрами, активные ФНЧ на ОУ имеют ряд важных преимуществ:
- Возможность получения крутых склонов АЧХ
- Отсутствие взаимного влияния каскадов
- Низкое выходное сопротивление
- Возможность усиления сигнала
- Простота каскадирования для увеличения порядка фильтра
Это делает активные ФНЧ на ОУ оптимальным выбором для многих задач фильтрации в современной аудиотехнике.
Применение ФНЧ на ОУ в аудиосистемах
Активные фильтры нижних частот на операционных усилителях широко используются в различных аудиоустройствах:
- Кроссоверы акустических систем
- Фильтры в предварительных усилителях
- Антиалайзинговые фильтры в АЦП
- Фильтры в эквалайзерах
- Разделительные фильтры в многополосных усилителях
В кроссоверах ФНЧ применяются для выделения низкочастотной составляющей сигнала, подаваемой на низкочастотные динамики. Частота среза обычно выбирается в диапазоне 100-500 Гц в зависимости от конкретной акустической системы.
В предварительных усилителях ФНЧ могут использоваться для подавления высокочастотных помех, выходящих за пределы звукового диапазона. Типичная частота среза — 20-30 кГц.
Практические рекомендации по проектированию ФНЧ на ОУ
При разработке активных фильтров нижних частот на ОУ следует учитывать несколько важных моментов:- Выбирать операционные усилители с полосой пропускания, значительно превышающей частоту среза фильтра (минимум в 10-20 раз).
- Использовать качественные конденсаторы с малыми потерями (например, пленочные) в цепях фильтрации.
- Обеспечивать хорошую развязку по питанию ОУ, применяя локальные конденсаторы.
- При каскадировании секций фильтра использовать буферные каскады для развязки.
- Учитывать возможное влияние паразитных емкостей и индуктивностей на работу фильтра на высоких частотах.
Соблюдение этих рекомендаций позволит спроектировать надежно работающий фильтр с характеристиками, близкими к расчетным.
Сравнение активных и пассивных ФНЧ для аудиоприменений
При выборе между активными ФНЧ на ОУ и пассивными RC-фильтрами для аудиоприменений следует учитывать следующие факторы:
| Параметр | Активные ФНЧ на ОУ | Пассивные RC-фильтры |
|---|---|---|
| Крутизна спада АЧХ | Высокая (до -24 дБ/окт и выше) | Низкая (-6 дБ/окт) |
| Возможность усиления | Есть | Нет |
| Выходное сопротивление | Низкое | Высокое |
| Потребление энергии | Есть | Нет |
| Стоимость | Выше | Ниже |
Активные ФНЧ на ОУ предпочтительны в большинстве современных аудиоустройств благодаря лучшим характеристикам и гибкости применения. Пассивные фильтры могут использоваться в простых некритичных приложениях или при необходимости минимального энергопотребления.
Схемы активных фильтров на ОУ для применения в аудиотехнике
В аудиотехнике широко применяются фильтры для разделения всего спектрапоступающего на вход усилителя аудиосигнала на несколько полос.
Это нужно, если в системе предусмотрена многоканальная, многополосная схема обработки аудиосигнала, например, чтобы выделить общий низкочастотный монофонический сигнал для так называемого «сабвуфера», выделить высокочастотные сигналы для их усиления и подачи на отдельные ВЧ-акустические системы, разделить спектр на полосы для схемы цвето-музыкальной установки или графического эквалайзера, либо просто ограничить сигнал по частоте сверху или снизу чтобы «вырезать» помеху или фон. Для этих целей очень удобны активные ФНЧ и ФВЧ на основе операционных усилителей.
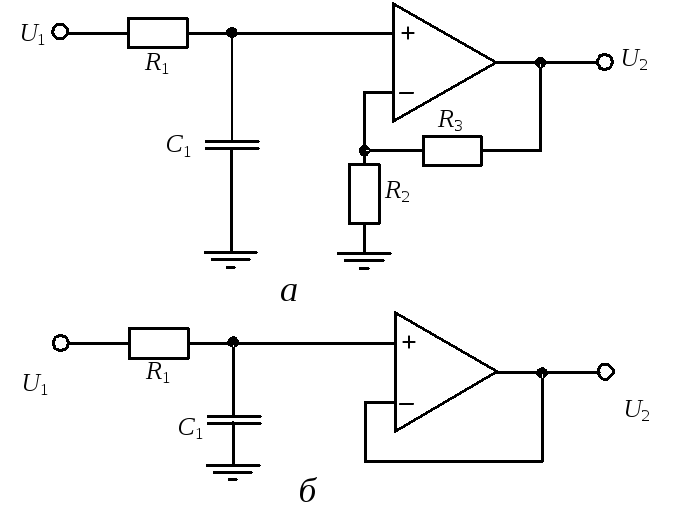
Рис. 1. Принципиальные схемы фильтров высокой и низких частот на ОУ.
Таблица 1.
| R | C | 2R | Частота раздела |
| (кОм) | (nF) | (кОм) | (Hz) |
| 15 | 47 | 30 | 160 |
| 15 | 39 | 30 | 192 |
| 12 | 47 | 24 | 200 |
| 11 | 47 | 22 | 218 |
| 15 | 33 | 30 | 227 |
| 10 | 47 | 20 | 239 |
| 12 | 39 | 24 | 240 |
| 11 | 39 | 22 | 262 |
| 15 | 27 | 30 | 278 |
| 12 | 33 | 24 | 284 |
| 10 | 39 | 20 | 289 |
| 11 | 33 | 22 | 310 |
| 7,5 | 47 | 15 | 319 |
| 15 | 22 | 30 | 341 |
| 10 | 33 | 20 | 341 |
| 12 | 27 | 24 | 347 |
| 11 | 27 | 22 | 379 |
| 7,5 | 39 | 15 | 385 |
| 10 | 27 | 20 | 417 |
| 12 | 22 | 24 | 426 |
| 7,5 | 33 | 15 | 455 |
| 1 1 | 22 | 22 | 465 |
| 10 | 22 | 20 | 512 |
| 7,5 | 27 | 15 | 556 |
| 7,5 | 22 | 15 | 682 |
| 15 | 4,7 | 30 | 1596 |
| 15 | 3,9 | 30 | 1924 |
| 12 | 4,7 | 24 | 1995 |
| 11 | 4,7 | 22 | 2177 |
| 15 | 3,3 | 30 | 2274 |
| 10 | 4,7 | 20 | 2394 |
| 12 | 3,9 | 24 | 2405 |
| 11 | 3,9 | 22 | 2623 |
| 15 | 2,7 | 30 | 2779 |
| 12 | 3,3 | 24 | 2842 |
| 10 | 3,9 | 20 | 2886 |
| 11 | 3,3 | 22 | 3100 |
| 7,5 | 4,7 | 15 | 3193 |
| 15 | 2,2 | 30 | 3410 |
| 10 | 3,3 | 20 | 3410 |
| 12 | 2,7 | 24 | 3473 |
| 11 | 2,7 | 22 | 3789 |
| 7,5 | 3,9 | 15 | 3848 |
| 10 | 2,7 | 20 | 4168 |
| 1 2 | 2,2 | 24 | 4263 |
| 7,5 | 3,3 | 15 | 4547 |
| 11 | 2,2 | 22 | 4650 |
| 10 | 2,2 | 20 | 5115 |
| 7,5 | 2,7 | 15 | 5558 |
Типовые схемы звеньев активных фильтров на основе операционных усилителей, выделяющих частоты выше частоты раздела (ФВЧ) и частоты ниже частоты раздела (ФНЧ) показаны на схеме в тексте.
Каравкин В. РК-2015-07.
Операционные усилители (на основе простейших примеров): часть 3 / Хабр
Краткое введение
Продолжаю
писать на тему операционных усилителей. В этой статье постараюсь дать обзор одной из важнейших тем, связанной с ОУ. Итак, добро пожаловать, активные фильтры.
Обзор темы
Возможно, Вы уже сталкивались с моделями RC-, LC- и RLC-фильтров. Они вполне подходят для большинства задач. Но для некоторых целей очень важно иметь фильтры с более плоскими характеристиками в полосе пропускания и более крутыми склонами. Вот тут нам и нужны активные фильтры.
Для освежения в памяти, напомню, какие бывают фильтры:
(ФНЧ) — пропускает сигнал, который ниже определенной частоты (ее еще именуют частотой среза).
Википедия
(ФВЧ) — пропускает сигнал выше частоты среза. Википедия
Полосовой Фильтр— пропускает только определенный диапазон частот. Википедия
Режекторный Фильтр — задерживает только определенный диапазон частот. Википедия
Ну еще немного лирики. Посмотрите на амплитудно-частотную характеристику (АЧХ) ФВЧ. На этом графике ничего интересного пока не ищите, а просто обратите внимание на участки и их названия:
Самые банальные примеры активных фильтров можно подсмотреть здесь в разделе «Интеграторы и дифференциаторы». Но в данной статье эти схемы трогать не будем, т.к. они не очень эффективны.
Выбираем фильтр
Предположим, что Вы уже определились с частотой, которую хотите фильтровать. Теперь нужно определиться с типом фильтра. Точнее нужно выбрать его характеристику.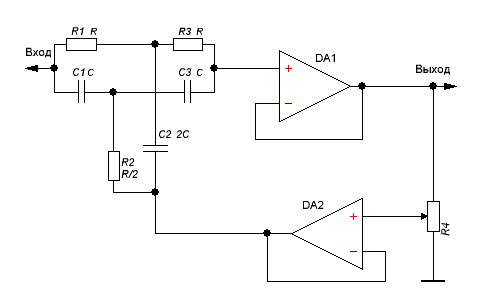
Иными словами, как фильтр будет себя «вести».
Основными характеристиками являются:
Фильтр Баттерворда — обладает самой плоской характеристикой в полосе пропускания, но имеет плавный спад.
Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
Фильтр Бесселя — имеет хорошую фазочастотную характеристику и вполне «приличный» спад. Считается лучшим выбором, если нет специфического задания.
Еще немного информации
Предположим, и с этим заданием вы справились. И теперь можно смело приступить к расчетам.
Есть несколько методов расчета. Не будем усложнять и воспользуемся самым простым. А самый простой — это «табличный» метод. Таблицы можно найти в соответствующей литературе. Чтобы Вы долго не искали, приведу из Хоровица и Хилла «Искусство Схемотехники».
Для ФНЧ:
Скажем так, это все Вы могли бы найти и прочитать и в литературе.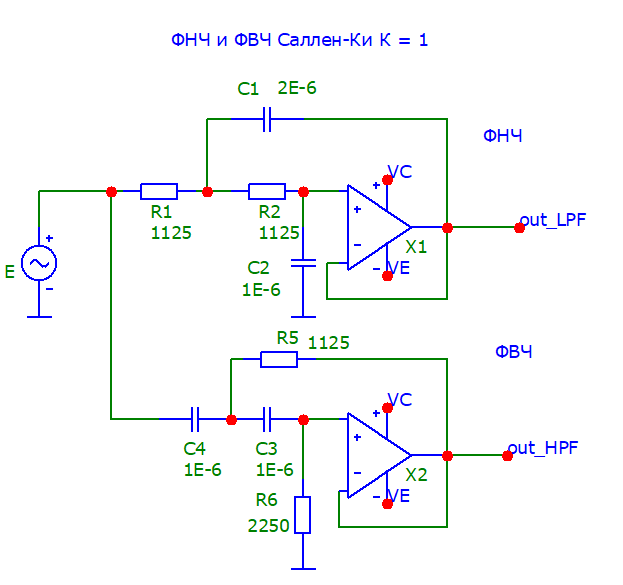
Перейдем конкретно к проектированию фильтров.
Расчет
В данном разделе попытаюсь кратко «пробежаться» по всем типам фильтров.
Итак, задание # 1. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда.
Приступим. Если мы имеем фильтр n-ного четного порядка, это означает, что в нем будет n/2 операционников. В данном задании — один.
Схема ФНЧ:
Для данного типа расчета берется во внимание, что R1 = R2, C1 = C2.
Смотрим в табличку. Видим, что К = 1.586. Это нам пригодится чуть позже.
Для фильтра низких частот справедливо:
, где, разумеется,
— это частота среза.
Сделав подсчет, получаем . Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора.
Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение R берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления R = 10 кОм, а верхний 5.8 кОм.
Соберем и промоделируем АЧХ.
Задание # 2. Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя.
Решаем. Раз фильтр четвертого порядка, то в схеме будет два операционника. Тут все совсем не сложно. Мы просто каскадно включаем 2 схемы ФВЧ.
Сам фильтр выглядит так:
Фильтр же четвертого порядка выглядит:
Теперь расчет. Как видим, для фильтра четвертого порядка у нас аж 2 значения К. Логично, что первое предназначается для первого каскада, второе — для второго. Значения К равны 1.
432 и 1.606 соответсвенно. Таблица была для фильтров низких частот (!). Для расчета ФВЧ надо кое-что изменить. Коэффициенты К остаются такими же в любом случае. Для характеристик Бесселя и Чебышева изменяется параметр
— нормирующая частота. Она будет равна теперь:
Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула:
Учтите, что для каждого отдельного каскада придется считать отдельно.
Для первого каскада:
Пусть С = 0.01 мкФ, тогда R = 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом.
Для второго каскада:
Емкость конденсатора оставим неизменной. Раз С = 0.01 мкФ, то R = 32 кОм.
Строим АЧХ.
Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик.
Для полосовых и режекторных фильтров также можно использовать «табличный метод», но тут немного другие характеристики.
Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка.
a1 и b1 — расчетные коэффициенты. Q — добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад. Δf — диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент α — еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете.
Ну ладно, хватит. Теперь рабочее задание.
Задание # 3. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1.
Поехали. Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчтными элементами.
Для первого фильтра центральная частота определяется как:
Для второго фильтра:
Конкретно в нашем случае, опять же из таблицы, определяем, что добротность Q = 10.
Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна.
Поправка усиления для области центральной частоты:
Финальная стадия — расчет компонентов.
Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра:
В том же порядке, что и (1) находим R22 = R5 = 43.5 кОм, R12 = R4 = 15.4 кОм, R32 = R6 = 54.2 Ом. Только учтите, что для второго фильтра используем
Ну и на последок, АЧХ.
Следующая остановка — полосно-заграждающие фильтры или режекторные.
Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка.
Наше последнее задание.
Задание # 4. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью Q = 2 и коэффициентом усиления в полосе пропускания равным 1.
Прежде всего, произвольно выбираем емкость конденсатора.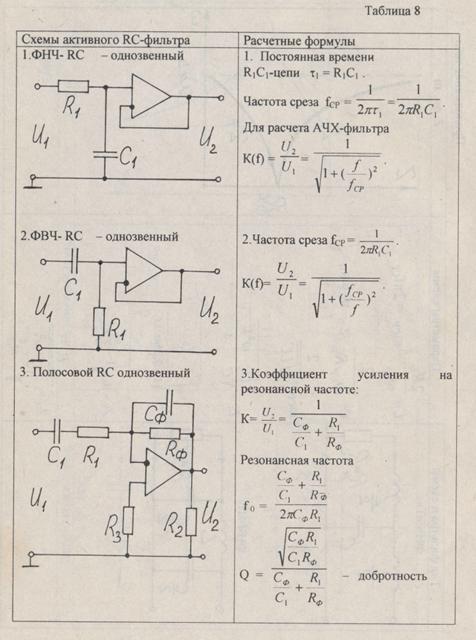
Допустим, С = 100 нФ.
Определим значение R6 = R7 = R:
Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра.
Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность.
Выберем произвольно резистор R2. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм.
Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания.
И на последок, необходимо произвольно выбрать R5 = 2R1. У меня в схеме эти резисторы имеют значение 40 кОм и 20 кОм соответственно.
Собственно, АЧХ:
Практически конец
Кому интересно узнать немного больше, могу посоветовать почитать Хоровица и Хилла «Искусство схемотехники».
Также, D. Johnson «A handbook of active filters».
Википедия
Также, кому не очень нужны расчеты, а нужны именно сами фильтры, могу посоветовать полезный софт
P.
S. Добавлю очень полезную ссылку и ее зеркало. За линк спасибо spiritus_sancti
Что такое фильтр нижних частот?
Фильтр нижних частот
По определению, фильтр нижних частот представляет собой схему, обеспечивающую легкое прохождение низкочастотных сигналов и затрудненное прохождение высокочастотных сигналов.
Существует два основных типа схем, способных выполнить эту задачу, и множество вариантов каждой из них:
- Индуктивный фильтр нижних частот и
- Емкостный фильтр нижних частот.
Индуктивный фильтр нижних частот
Сопротивление индуктора увеличивается с увеличением частоты. Этот высокий импеданс при последовательном включении блокирует попадание высокочастотных сигналов на нагрузку.
Это можно продемонстрировать с помощью SPICE-анализа: (рисунок ниже)
индуктивный фильтр нижних частот v1 1 0 ac 1 грех л1 1 2 3 rload 2 0 1k .ac лин 20 1 200 .участок переменного тока (2) .конец
Отклик индуктивного фильтра нижних частот падает с увеличением частоты.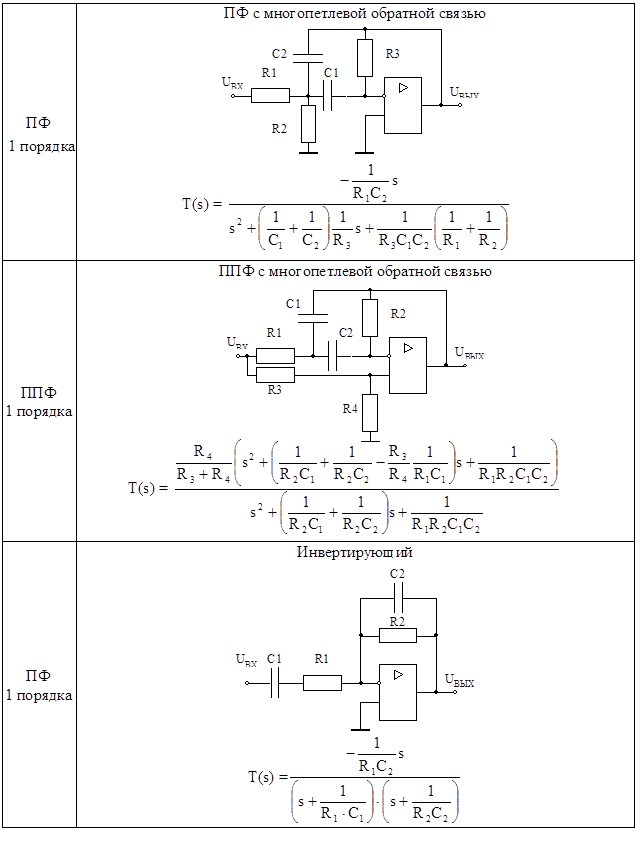
Емкостный фильтр нижних частот
Полное сопротивление конденсатора уменьшается с увеличением частоты. Этот низкий импеданс в сочетании с сопротивлением нагрузки приводит к короткому замыканию высокочастотных сигналов, что приводит к падению большей части напряжения на последовательно включенном резисторе R 1 . (Рис. ниже)
Приборы и датчики — SIS …
Пожалуйста, включите JavaScript0005
емкостный ФНЧ v1 1 0 ac 1 грех р1 1 2 500 с1 2 0 7у rload 2 0 1k .ac лин 20 30 150 .участок переменного тока (2) .конец
Отклик емкостного ФНЧ падает с увеличением частоты.
Индуктивный фильтр нижних частот — это вершина простоты, поскольку фильтр состоит только из одного компонента. Емкостная версия этого фильтра не намного сложнее, для работы необходимы только резистор и конденсатор. Однако, несмотря на их повышенную сложность, конструкции емкостных фильтров обычно предпочтительнее индуктивных, поскольку конденсаторы, как правило, являются «более чистыми» реактивными компонентами, чем катушки индуктивности, и поэтому их поведение более предсказуемо.
Под «чистым» я подразумеваю, что конденсаторы проявляют меньше резистивных эффектов, чем катушки индуктивности, что делает их реактивными почти на 100%. Катушки индуктивности, с другой стороны, обычно проявляют значительные диссипативные (резисторные) эффекты как из-за большой длины провода, используемого для их изготовления, так и из-за магнитных потерь материала сердечника.
Конденсаторы также, как правило, меньше участвуют в эффектах «связи» с другими компонентами (генерируют и/или принимают помехи от других компонентов через взаимные электрические или магнитные поля), чем катушки индуктивности, и они дешевле.
Тем не менее, индуктивный фильтр нижних частот часто предпочтительнее в источниках питания AC-DC для фильтрации «пульсаций» переменного тока, возникающих при преобразовании (выпрямлении) переменного тока в постоянный, пропуская только чистую составляющую постоянного тока. Основной причиной этого является требование низкого сопротивления фильтра на выходе такого источника питания.
Емкостный фильтр нижних частот требует дополнительного сопротивления последовательно с источником, тогда как индуктивный фильтр нижних частот этого не требует.
При проектировании сильноточной цепи, такой как источник питания постоянного тока, где дополнительное последовательное сопротивление нежелательно, индуктивный фильтр нижних частот является лучшим выбором. С другой стороны, если малый вес и компактные размеры являются более важными приоритетами в конструкции источника питания, чем низкое внутреннее сопротивление источника питания, емкостный фильтр нижних частот может иметь больше смысла.
Частота среза
Все фильтры нижних частот рассчитаны на определенную частоту среза . То есть частота, выше которой выходное напряжение падает ниже 70,7% входного напряжения. Этот процент отсечки 70,7 на самом деле не является произвольным, хотя на первый взгляд может показаться таковым.
В простом емкостно-резистивном фильтре нижних частот это частота, при которой емкостное реактивное сопротивление в омах равно сопротивлению в омах.
В простом емкостном фильтре нижних частот (один резистор, один конденсатор) частота среза определяется как:
Подставляя значения R и C из последней симуляции SPICE в эту формулу, мы получаем частоту среза 45,473 Гц. Однако, когда мы смотрим на график, созданный с помощью моделирования SPICE, мы видим, что напряжение нагрузки значительно ниже 70,7% напряжения источника (1 вольт) даже при частоте всего 30 Гц, что ниже расчетной точки отсечки.
Что не так? Проблема здесь в том, что сопротивление нагрузки в 1 кОм влияет на частотную характеристику фильтра, искажая ее по сравнению с той, которая должна быть по формуле. Без этого сопротивления нагрузки SPICE создает график Боде, числа которого имеют больше смысла: (рисунок ниже)
емкостный ФНЧ v1 1 0 ac 1 грех р1 1 2 500 с1 2 0 7у * примечание: без нагрузочного резистора! .ac лин 20 40 50 .участок переменного тока (2) .конец
Для емкостного фильтра нижних частот с сопротивлением R = 500 Ом и C = 7 мкФ Выход должен составлять 70,7 % при частоте 45,473 Гц.
f отсечка = 1/(2πRC) = 1/(2π(500 Ом)(7 мкФ)) = 45,473 Гц
При работе со схемами фильтров всегда важно помнить, что отклик фильтра зависит от значений компонентов фильтра и импеданс нагрузки. Если уравнение частоты среза не учитывает импеданс нагрузки, оно предполагает отсутствие нагрузки и не дает точных результатов для реального фильтра, передающего мощность на нагрузку.
Применение фильтра нижних частот
Одним из частых применений принципа емкостного фильтра нижних частот является проектирование цепей с компонентами или секциями, чувствительными к электрическому «шуму».
Как упоминалось в начале последней главы, иногда сигналы переменного тока могут «передаваться» от одной цепи к другой через емкость (C блуждающий ) и/или взаимная индуктивность (M блуждающий ) между двумя наборами проводников.
Ярким примером этого являются нежелательные сигналы переменного тока («шум»), которые попадают в линии питания постоянного тока, питающие чувствительные цепи: (рис.
ниже)
Шум связан паразитной емкостью и взаимной индуктивностью с «чистым» питанием постоянного тока. .
Осциллограф-метр слева показывает «чистую» мощность от источника постоянного напряжения. Однако после соединения с источником шума переменного тока через паразитную взаимную индуктивность и паразитную емкость напряжение, измеренное на клеммах нагрузки, теперь представляет собой смесь переменного и постоянного тока, при этом переменный ток нежелателен.
Обычно можно ожидать, что E нагрузка будет точно идентична E источник , потому что непрерывные проводники, соединяющие их, должны делать два набора точек электрически общими. Однако импеданс силового проводника позволяет различать два напряжения, что означает, что величина шума может варьироваться в разных точках системы постоянного тока.
Если мы хотим предотвратить попадание такого «шума» на нагрузку постоянного тока, все, что нам нужно сделать, это подключить фильтр нижних частот рядом с нагрузкой, чтобы блокировать любые связанные сигналы.
В своей простейшей форме это не что иное, как конденсатор, подключенный непосредственно к клеммам питания нагрузки, конденсатор ведет себя как очень низкоимпедансный по отношению к любому шуму переменного тока и замыкает его накоротко. Такой конденсатор называется развязывающий конденсатор : (рисунок ниже)
Развязывающий конденсатор, применяемый к нагрузке, фильтрует помехи от источника питания постоянного тока.
Беглый взгляд на переполненную печатную плату (PCB), как правило, обнаруживает разбросанные повсюду развязывающие конденсаторы, обычно расположенные как можно ближе к чувствительным нагрузкам постоянного тока. Размер конденсатора обычно составляет 0,1 мкФ или более, минимальная емкость, необходимая для создания достаточно низкого импеданса, чтобы закоротить любой шум.
Большая емкость будет лучше фильтровать шум, но размер и экономичность ограничивают использование развязывающих конденсаторов мизерными значениями.
ОБЗОР:
- Фильтр нижних частот обеспечивает легкое прохождение низкочастотных сигналов от источника к нагрузке и затрудненное прохождение высокочастотных сигналов.
- Индуктивные фильтры нижних частот включают катушку индуктивности последовательно с нагрузкой; Емкостные фильтры нижних частот включают резистор последовательно и конденсатор параллельно нагрузке. Первая конструкция фильтра пытается «заблокировать» нежелательный частотный сигнал, а вторая пытается его закоротить.
- Частота среза фильтра нижних частот — это частота, при которой выходное (нагрузочное) напряжение составляет 70,7% от входного (источника) напряжения. Выше частоты среза выходное напряжение ниже 70,7% от входного, и наоборот.
Будьте первыми, кто получит эксклюзивный контент прямо на вашу электронную почту.
Обещаем не спамить. Вы можете отписаться в любое время.
Неверный адрес электронной почты
операционный усилитель — фильтр нижних частот не работает должным образом
Краткий обзор
Давайте быстро суммируем то, что, как я думаю, я понял. Похоже, у вас есть следующие характеристики:
- \$A_v=10\$
- \$f_{_\text{L}}=20\:\text{Гц}\$
- \$f_{_\text{H}}=500\:\text{Гц}\$
- Цепи равнозначных компонентов Саллена-Ки (1-полюсные, 2-го порядка)
(У меня нет доступных шин напряжения.
Но мы можем игнорировать это. И нам пока не нужно беспокоиться об операционном усилителе.)
Сначала нужно вычислить несколько деталей, чтобы понять, устроить бандпасс. Предстоит сделать серьезный выбор, который будет совершенно разным в зависимости от результатов. Эту часть, я думаю, вы уже знаете. Но стоит сказать прямо. Итак, вот:
- \$f_{_\text{0}}=\sqrt{20\:\text{Гц}\cdot 500\:\text{Гц}}=100\:\text{Гц}\$
- дробная пропускная способность \$=\frac{f_{_\text{H}}\:-\: f_{_\text{L}}}{f_{_\text{0}}}=\frac{500\ :\text{Гц}\:-\: 20\:\text{Гц}}{100\:\text{Гц}}=4,8\$
Из этого последнего пункта я делаю вывод, что ваш подход с использованием комбинации фильтра нижних и верхних частот является правильным. Если бы относительная полоса пропускания была намного меньше, скажем, ниже 1 или еще лучше ниже 0,8, тогда вместо этого может быть аргумент в пользу объединения двух секций полосы пропускания. Но это не так. Так что вы правы, разбивая вещи так, как вы это сделали.
Пока все хорошо.
Нет входной спецификации — предполагается, что используется только генератор сигналов
Вы не указали, что управляет системой. Нет, я не имею в виду генератор сигналов, который вы использовали. Я имею в виду реальную вещь, которая будет управлять им, когда вы действительно начнете его использовать.
Иногда необходимо подключить фильтр по переменному току. Если это так и если первая секция является секцией нижних частот, вам необходимо обеспечить путь постоянного тока к земле для входа (+). Я не вижу блокирующего конденсатора постоянного тока в вашем случае. И, очевидно, он вам не нужен для симуляции. Но я понятия не имею, если вы делаете в реальной цепи. Если то, что управляет этой схемой, имеет смещение постоянного тока, вы вполне можете требует блокировки постоянного тока . Просто к вашему сведению.
Кроме того, вы не указали допустимую нагрузку, которую первый раздел представляет для фактического источника.
Ни сам импеданс источника. Так что это означает, что я в неведении об этих деталях.
Но давайте пока предположим, что это всего лишь доказательство того, что вы можете сделать дизайн и что вы будете использовать выход \$50\:\Omega\$ генератора сигналов; единственной целью всего этого является проверка возможностей конструкции.
Порядок секций и другие предположения
Я просто предполагаю, что вы знаете, что делаете, и вам нравится фильтр нижних частот в качестве первой секции и нужен фильтр высоких частот в качестве второй секции. Есть соображения, такие как шум типичных операционных усилителей, связанный с их 1/f и полосой пропускания, и так далее. Но я просто предполагаю, что вы уже сделали эти оценки, и я просто пойду дальше.
Я также предполагаю, что вы ищете максимально плоский (баттервортский) дизайн. Это важно, потому что конструкции компонентов с одинаковой стоимостью по Саллену-Ки имеют исправлено соотношение между коэффициентом усиления по напряжению и демпфированием (\$\zeta\$ или альтернативно \$Q\$.
) Вы не можете выбрать коэффициент усиления по напряжению, если ищете Баттерворта. Если вы решите выбрать усиление, вы не сможете выбрать демпфирование.
Вообще говоря, вы должны выбрать коэффициент усиления по напряжению менее 3 при всех возможных обстоятельствах. Альтернативы этому нет. Поскольку \$\sqrt{10}\gt 3\$, вы не можете получить \$A_v=10\$ с двумя из этих секций. Просто не может случиться. Добавление некоторого усиления в конце — это нормально. Но вам понадобится третья секция. От этого никуда не деться.
Конструкция нижних частот
Фильтр нижних частот имеет порог среза \$f_{_\text{C}}=500\:\text{Гц}\$.
Поскольку конденсаторы обычно не встречаются в шагах E24, вы обычно сначала выбираете номиналы конденсаторов. Идут широкими шагами. В этом случае я мог бы выбрать \$47\:\text{nF}\$. В этом случае значение ближайшего резистора будет \$6,8\:\text{k}\Omega\$. С этой комбинацией \$f_{_\text{C}}\приблизительно 498\:\text{Гц}\$. Что достаточно близко.
Усиление каскада уже установлено требуемым демпфированием для соответствия фильтру Баттерворта: \$A_v=3-\sqrt{2}\примерно 1,586\$. Это определено. Вы не можете выбрать его. Извини.
(То же самое относится и к фильтру верхних частот. Таким образом, мы уже можем сказать, что вам понадобится последняя, третья секция с \$A_v\приблизительно 4\$, чтобы достичь конечной цели \$A_v= 10\$.)
Отсюда секция нижних частот будет:
имитация этой схемы – Схема создана с помощью CircuitLab
(фактическое вычисленное значение равно \$R_4=22.845\:\text{ k}\Omega\$. Но я округлил в меньшую сторону. Цена, которую я заплатил за это, — это немного меньший коэффициент усиления по напряжению \$A_v\приблизительно 1,564\$ и небольшое изменение в демпфировании. Ну что ж. Приемлемо.)
Конструкция фильтра верхних частот
Фильтр верхних частот имеет порог среза \$f_{_\text{C}}=20\:\text{Гц}\$.
В этом случае я мог бы выбрать \$220\:\text{nF}\$.
