Как обозначается сопротивление на схеме: Резистор. Сопротивление резистора. Маркировка резисторов.

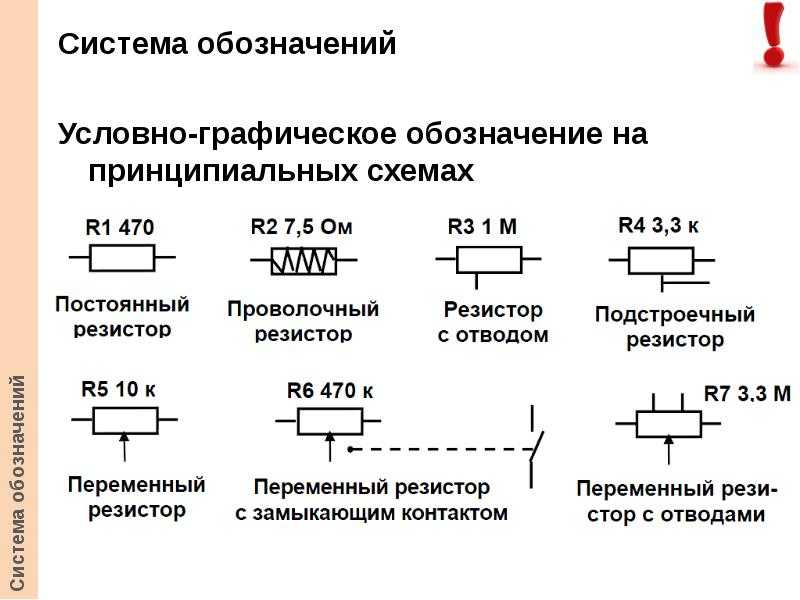
Обозначения на схемах электрических принципиальных:

На принципиальных схемах резисторы изображаються в виде прямоугольника с указанием величины сопротивления, мощности и порядкового номера.

Величина мощности указывается наклонными, продольными или поперечными линиями внутри прямоугольника: а) 0,125 Вт; б) 0.25 Вт; в) 0,5 Вт; г) 11 Вт; д) 2 Вт. Изображение переменных резисторов показано на рис. 2.9, е, а подстроечных — на рис. 2.9,ж

1. «R» — резистор — RK — терморезистор;

RP — потенциометр;

RS — шунт измерительный;

RU — варистор;

2. «R» одного номинала, соединенных:

— параллельно (рис. 8) — последовательно (рис. 9)

3. Обозначения единиц измерения около условных графических обозначений (рис. 10).

4. Обозначения: Ом — без обозначений;

кОм — «К»;

МОм — «М»;

ГОм — «Г».

5. Обозначения в перечне элементов (рис. 11).

6. Обозначения в спецификациях (рис. 12).

На рисунке 1.1 приведена схема замещения резистора, анализ которой позволяет охарактеризовать частотные свойства резисторов.

Рисунок 1.1 Схема замещения резистора.

Такая схема может использоваться всегда, если только резистор не используется на СВЧ.

Св1 и Св2— емкость выводов;

Сr – эквивалентная емкость «паразитная» зависящая от его размеров и конструкции выводов. Для малогабаритных резисторов она не велика и достигает десятки долей пикофарад.

Lr – индуктивность резистора, зависящая от его размеров и размеров выводов.

Она не велика для пленочных резисторов и увеличивается с повышением номинального сопротивления. Допустимое значение «паразитной» индуктивности не должно превышать значения 3*10^-9 Гн/Ом.

Пленочные резисторы обладают меньшими собственными индуктивностью и емкостью по сравнению с проволочными, что обеспечивает их лучшее применение на высоких частотах.

Rиз – сопротивление изоляции, определяемое началом диэлектрика, используемого для основания и обволакивания резистора(имеет значение для высокоомных резисторов).

Rr – сопротивление резистивного элемента.

Rк – эквивалентное сопротивление контактов, имеет существенное значение для низкоомных резисторов. Зависит от следующих факторов, увеличивающих его:

• перегрев;

• некачественный контакт;

• повышенная влажность;

• наличие интерметаллических контактов.

Общее сопротивление резистора состоит из активной и реактивной составляющей.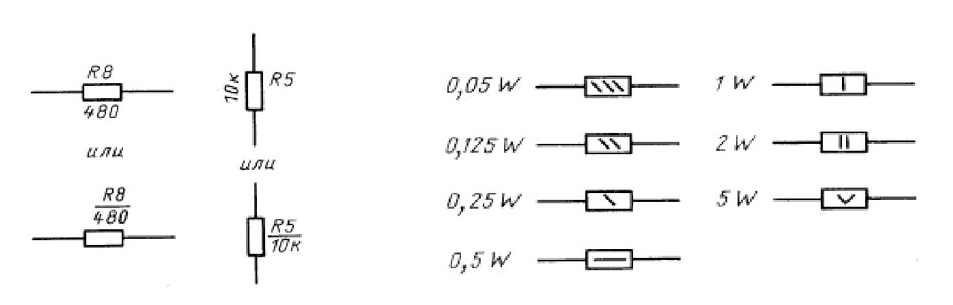 Активная включает Rr, Rк, Rиз, а реактивная – емкостную и индуктивную составляющие.

Сопротивление резистора определяется отношением:

Резисторы, используемые в условиях высокой частоты, колебательных контурах должны обладать только активной составляющей, т.е. быть безреактивными по возможности и сохранять свой параметр по всему требуемому диапазону частот.

Эквивалентные схемы используются для выбора сопротивления в схемах, работающих на высоких частотах.

Для таких схем вводится понятие критической частоты, ограничивающей использование резисторов на высоких частотах.

Для низкоомных (R<300 Ом), схема замещения приведена на рисунки 1.2., критическая частота рассчитывается :

при этом L<10^-9 Гн/Ом.

Рис.1.2 – Эквивалентная схема замещения низкоомных резисторов.

Для высокоомных резисторов (схема замещения на рис.1.3.), у которых R>3000 Ом:

причем паразитная емкость не должна превышать 1пФ.

Рисунок 1.3. –Схема замещения высокоомных резисторов.

При работе резисторов в импульсном режиме, когда через резистор проходят периодически повторяющие импульсы тока, необходимо учитывать то, что паразитные емкость и индуктивность изменяют форму импульса и уменьшают максимальное значение сигнала; электрическая энергия, рассеиваемая в резисторе, расходуется на его нагрев, её значение ограничивается допустимой температурой резистивного элемента.

Для сохранения формы импульса необходимо, чтобы

f_{max0,35 /} τ_ф, где

f_max – высокочастотная граница пропускания резистора;

τ_ф — длительность фронта импульса.

Резистор

16 декабря 2022 — Admin

Главная / Теория

Резистор — один из самых простых электронных компонентов. Вместе с тем, без резисторов не обходится практически ни одна схема. Казалось бы, что важного он делает — только сопротивляется току, и больше ничего? Но не всё так просто. В этой статье собраны все базовые знания о резисторах, необходимые электронщику.

Содержание статьи:

• Общие сведения о резисторах
• Закон Ома
• Как измерить сопротивление
• Параллельное и последовательное соединение резисторов
• Применение: делители напряжения и тока
• Рассеиваемая мощность
• Устройство резистора
• Паразитные характеристики
• Переменные и подстроечные резисторы
• Другие типы резисторов

Общие сведения

Резистор, или сопротивление, относятся к пассивным компонентам электрических цепей. Пассивный — значит, не привносящий в цепь дополнительную энергию. В отличие от, например, транзистора — который способен усиливать слабый сигнал, добавляя к нему энергию от более мощного источника питания.

Резистор оказывает сопротивление идущему через него току. В качестве механической аналогии можно представить трубу с водой. Резистор — сужение на этой трубе, замедляющее поток. Из-за сужения по трубе будет проходить меньше воды в единицу времени.

Сужение в трубе, замедляющее поток

Резистор обозначается на схеме вытянутым прямоугольником, с двумя выводами. Обычно каждому резистору присваивается буква R с порядковым номером. Иногда в зарубежной литературе можно встретить обозначение ломаной линией.

Два варианта обозначения резистора на схемах

Резистор и закон Ома

Главная характеристика резистора — его сопротивление. Оно измеряется в Омах. А ток, проходящий через резистор, зависит от приложенного напряжения. Перечисленные величины  связаны законом Ома. При этом в случае идеального резистора ток линейно зависит от напряжения, то есть резистор обладает линейной вольт-амперной характеристикой:

Вольт-амперные характеристики двух резисторов и закон Ома

Как измерить сопротивление резистора

В лаборатории радиолюбителя для измерения сопротивлений должен быть омметр. Обычно, эта функция входит в состав комбинированных приборов, мультиметров. Между тем, принцип измерения сопротивления основан всё на том же законе Ома: омметр прикладывает к тестируемому резистору небольшое напряжение и замеряет ток, после чего вычисляет сопротивление.

Измерение сопротивления с помощью мультиметра. В данном примере взят резистор 20 кОм.

Кстати, об этом нужно помнить, тыкая омметром в схемы: на схему попадает небольшое напряжение, которое для чувствительных деталей может оказаться фатальным.

Параллельное и последовательное соединение резисторов

Резисторы нужны в схеме, чтобы упрявлять токами и напряжениями. Но сначала нужно разобраться, как они взаимодействуют между собой и с другими элементами схемы.

Если соединить несколько резисторов последовательно, через каждый из них будет течь одинаковый ток. Это логично: сколько зарядов вошло в цепь, столько же должно выйти на другом конце, закон сохранения заряда. А вот напряжение (потенциал) распределяется по-разному. Чем выше сопротивление резистора, тем больше на нём падение напряжения — нужно большее усилие, чтобы протолкнуть через большое сопротивление заряды.

При этом, если просуммировать потенциал на всех резисторах, сумма будет равна напряжению, приложенному к концам цепи. Отсюда выводится формула суммарного сопротивления цепочки из последовательных резисторов: оно равно сумме сопротивлений всех резисторов.

Последовательное соединение резисторов

При параллельном соединении резисторов картина иная. Здесь фиксировано напряжение — оно одинаковое на каждом резисторе. А вот ток будет разный — он потечёт туда, где ему легче пройти. Опять же, применяя несложные рассуждения и используя закон Ома, выводится формула общего сопротивления параллельно соединённых резисторов.

Параллельное соединение резисторов

Более сложные, смешанные соединения резисторов разбиваются на небольшие блоки, и так последовательно, от меньших к большим блокам считается общее сопротивление:

Сложное соединение резисторов. Сначала считаем блок R1,R2 (параллельные), потом к этому блоку добавляем последовательно R3, наконец, считаем параллельно R1,R2,R3 и R4. Если каждое сопротивление по 10 Ом, общее сопротивление получается 6 Ом.

Нужно добавить, что иногда разбить на блоки невозможно. В этом случаи применяются более сложный метод расчёта — правила Кирхгофа.

Применение резисторов в схемах

Итак, как же с помощью резисторов управляют напряжениями и токами? Допустим, стоит задача ограничить напряжение на нагрузке. Под «нагрузкой» здесь может пониматься любой элемент или узел схемы, на котором мы хотим получить заданное напряжение или заданный ток.  Это могут быть и лампочка, и светодиод, и следующий каскад усилителя и т. д.

Самое простое — поставить последовательно с нагрузкой гасящий резистор. Как мы обсуждали выше, в этом случае напряжение распределится между элементами в соответствии с сопротивлением каждого. То есть, получается делитель напряжения.

Схема делителя напряжения, когда нагрузка является элементом делителя.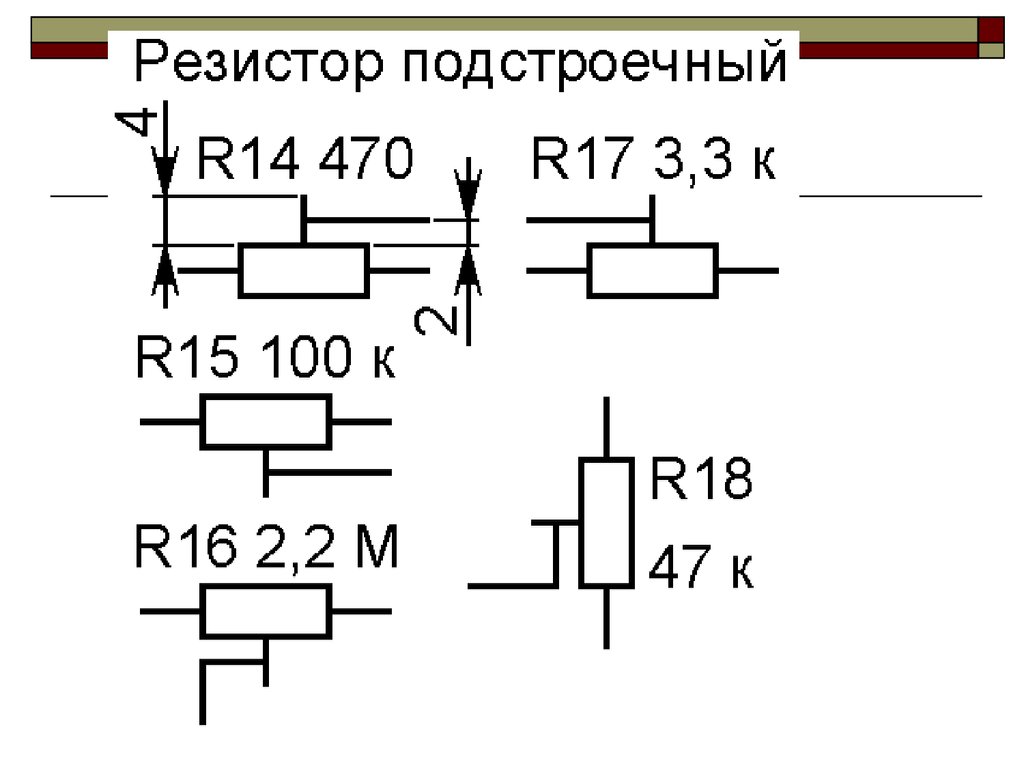

А что делать, если сопротивление нагрузки очень велико или не постоянно? В этом случае ставят два последовательных резистора, образующих плечи делителя. А нагрузка снимает напряжение с одного из них. Подчеркну, что всегда нужно помнить про сопротивление нагрузки. Оно должно быть достаточно большим, чтобы им можно было пренебречь при расчёте делителя.

Схема делителя напряжения, когда нагрузка подключена параллельно нижнему плечу делителя

Если последовательное соединение резисторов является делителем напряжения, нетрудно догадаться, что паралелльное соединение — делитель тока. На рисунке приведён способ ограничить ток через нагрузку — поставить параллельно ей резистор, так называемый шунт. Который будет отвевлять на себя часть тока, обратно пропорциональную его сопротивлению.

Схема делителя тока

Мощность резистора

Резистор сопротивляется проходящему току. Значит, он отбирает у тока часть энергии. И куда она девается? Переходит в тепло. Мощность, рассеиваемая на резисторе, считается по формуле P = U*I. Поскольку U, I и R связаны законом Ома, можно записать несколько вариантов этой формулы, выражая мощность через U и R, или через R и I. Кстати, на сайте есть онлайн-калькулятор мощности и закона Ома.

Так вот, если ток через резистор слишком велик, из-за большой рассеиваемой мощности резистор перегреется и выйдет из строя, в буквальном смысле, сгорит. В этом случае нужно взять резистор такого же номинала, но рассчитанный на бОльшую мощность рассеивания. Более мощные резисторы и физически большего размера, чтобы увеличить площадь рассеивания тепловой энергии.

Там, где это важно (где ожидаются сравнительно большие токи), на схемах указывают, на какую мощность должен быть рассчитан резистор, с помощью следующих обозначений:

Допустимая мощность рассеивания резистора

Устройство резисторов

Из школьного курса физики мы знаем, что сопротивление проводника определяется его удельным сопротивлением, длинной и сечением.

Формула сопротивления проводника

В начале статьи приводилась механическая аналогия резистора, как сужения трубы. Это работает и в элекрике: если уменьшить сечение проводника, его сопротивление увеличится.

Поэтому, резисторы делают из тонкой проволоки, из тонких плёнок разных металлов и сплавов, из композитных материалов. При этом, чтобы увеличить эффективную длину, в резистивном слое нарезают различного вида спирали и канавки:

Очень условно показано устройство резистора. Слева: на поверхности цилиндрической основы резистора слой токопроводящего материала, в котором нарезаны канавки для увеличения сопротивления. Справа: плёночный вариант.

Паразитные характеристики

Но, такой подход, кроме плюсов, даёт ещё и некоторые минусы. Дело в том, что реальный резистор, в отличие от идеального, обладает не только сопротивлением, но и некоторой индуктивностью и ёмкостью. То есть схема реального резистора выглядит примерно так:

Схема замещения резистора

Ёмкость и индуктивность — паразитные характеристики резистора, они искажают его функции в схеме. И само по себе устройство резистора может являться причиной этих паразитных свойств. Спиральные канавки в резистивном слое — чем не витки катушки индуктивности? А между близко расположенными участками проводящего слоя возникает ёмкость.

Хотя эти индуктивность и ёмкость небольшие по величине, но в некоторых ситуациях (например, на высоких частотах) способны вносить заметные искажения.

Поэтому, при изготовлении резисторов применяют различные ухищрения, чтобы снизить паразитные характеристики. Например, нарезают канавки хитрым рисунком. Впрочем, эта тема уже выходит за рамки данной статьи.

Переменные и подстроечные резисторы

Иногда в схеме необходимы резисторы с переменным сопротивлением. Они являются элементами настройки и управления.

Различают переменные резисторы (обычно их ручку выводят на панель управления) и подстроечные (которые регулируются отвёрткой на плате и к которым нет доступа, пока не разобрать корпус устройства). Вот как они выглядят:

Переменные и подстроечные резисторы

У них три вывода. Между двумя крайними постоянное сопротивление. А средний «скользит» между ними. Таким образом, получается готовый делитель напряжения, с регулируемым сопротивлением плечей.

Если средний вывод соединить с одним из крайних — получится реостат, резистор с переменным сопротивлением.

Другие типы резисторов

В заключение остаётся упомянуть некоторые специфичные типы резисторов. Например, теримистор. Его сопротивление зависит от температуры, и этот тип резисторов широко используется в электронных термометрах и схемах контроля температуры.

Или, фоторезистор. Его сопротивление зависит от освещённости.

Варисторы — уменьшают своё сопротивление при росте приложенного напряжения. Могут использоваться в схемах защиты и стабилизаторах.

Поделиться в соцсетях:

Три резистора соединены, как показано на схеме. Через резистор 5 Ом протекает ток силой 1 ампер. (i) Чему равен ток через два других резистора? (ii) Какова разность потенциалов между AB и AC.

?(iii) Каково общее сопротивление?

Последняя обновленная дата: 09 -й января 2023

•

Общее представление: 188,2K

•

Просмотры сегодня: 1,87K

Ответ

Проверено

188,2K+ Просмот Проблема, нам нужно найти разность потенциалов между B и C, тогда мы можем получить ток. Затем мы должны применить правила для последовательного и параллельного соединения, чтобы получить эквивалентное сопротивление.
Используемая формула – V=IR, полное последовательное сопротивление = сумма всех последовательных сопротивлений.

Полное пошаговое решение:
Ток от A до B и от B до C составляет 1 ампер.
Резисторы 10 и 15 Ом включены параллельно, тогда разность потенциалов на обоих резисторах будет одинакова.
Сопротивление между B и C будет $\dfrac{{10{\text{x15}}}}{{10\, + \,15}} = \dfrac{{150}}{{25}} = 6 \Омега $.
Тогда напряжение между резистором 6 Ом и током 1 ампер равно V=IR.
V=1(6)=6V
Следовательно, разность потенциалов составляет 6 вольт на резисторах 10 и 15 Ом.
(i)Тогда ток между резисторами 10 и 15 Ом равен
${I_{10}} = \dfrac{{{V_{10}}}}{{10}} = \dfrac{6}{{10 }} = 0,6A$
И ${I_{15}} = \dfrac{{{V_{15}}}}{{15}} = \dfrac{6}{{15}} = 0,4A$
( ii) Разность потенциалов между AB составляет
${V_{AB}} = {I_{AB}}{R_{AB}} = 1{\text{ x 5 = 5V}}$
${V_{BC}} = {I_{BC}}{R_{BC}} = 1{\text{ x 6 = 6V}}$
Итак, ${V_{AC}} = {V_{AB}} + {V_{BC}} = 5 + 6 = 11$
Следовательно, разность потенциалов составляет 11 вольт между переменным током и 5 вольт между AB.
(iii) Эквивалентное сопротивление между A и C можно рассчитать как:
Поскольку сопротивление между B и C составляет 6 Ом, как рассчитано выше.
И сопротивление между A и B составляет 5 Ом, мы можем ясно видеть, что они оба соединены последовательно, так как ток, проходящий через них, составляет 1 ампер.
Таким образом, когда сопротивления соединены последовательно, их сумма дает общее эффективное сопротивление. Итак, ${R_{AC}} = 6 + 5 = 11\Omega $.

Примечание. Для решения подобных задач нам необходимо знать закон Ома, согласно которому разность потенциалов прямо пропорциональна сопротивлению V=IR, а также нам необходимо знать, что при последовательном соединении сопротивление складывается, чтобы получить эффективное сопротивление, равное больше, чем наибольшее сопротивление. Также одинаковы напряжения на параллельных сопротивлениях или любых других элементах, соединенных параллельно. Знание этого решит вашу проблему.

Недавно обновленные страницы

Если расстояние bfs, пройденное частицей за время t, класс 11 физики JEE_Main

Пружина с жесткостью 5 rm, умноженная на rm 103 Нм 1is, класс 11 физики JEE_Main

Каковы эффекты движения Земли, класс 11 физики JEE_Main

Одноатомный газ массой 40 мю хранится в изолированном контейнере физики класса 11 JEE_Main

Уменьшение в потенциальной энергии шара массы 11 класс физики JEE_Main

Что из следующего верно0004

Пружина с жесткостью 5 rm, умноженная на rm 103 Нм 1is, класс 11 физики JEE_Main

Каковы эффекты движения Земли, класс 11 физики JEE_Main

Одноатомный газ массой 40 мю хранится в изолированном контейнере физики класса 11 JEE_Main

Уменьшение в потенциальной энергии шара массы 11 класс физики JEE_Main

Что из следующего верно 1 nлевый S чашка T правый класс 10 математика JEE_Main

Актуальные сомнения

Решение OpenStax College Physics для курсов AP®, глава 21, задача 8 (подготовка к экзамену для курсов AP®)

Chapter 21 question:

1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE35PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE49PE50PE51PE52PE53PE54PE55PE56PE57PE58PE59PE60PE61PE62PE63PE64PE65PE66PE67PE68PE69PE70PE71PE72PE73PE74PE75PE76PE77PE1AP2AP3AP4AP5AP6AP7AP8AP9AP10AP11AP12AP13AP

Изменить главу

Расширенный поиск

Вопрос

Был поставлен эксперимент с принципиальной схемой, показанной на рис. 21.61. Предположим, что $R_1 = 10 \textrm{ }\Omega$, $R_2 = R_3 = 5 \textrm{ }\Omega$, $r = 0 \textrm{ }\Omega$ и $E = 6\textrm{ V}$ .

1. Одним из шагов проверки установки является проверка точек с одинаковым потенциалом. Какие из следующих пунктов можно проверить?
   1. Точки b, c и d.
   2. Точки d, e и f.
   3. точек f, h и j.
   4. Точки a, h и i.
2. В каких трех точках следует измерить токи, чтобы можно было напрямую подтвердить правило соединения Кирхгофа?
   1. Точки b, c и d.
   2. Точки d, e и f.
   3. точек f, h и j.
   4. Точки a, h и i.
3. Если ток в ветви с источником напряжения восходящий, а токи в двух других ветвях нисходящий, т. е. Ia = Ii + Ic, определите, что из следующего может быть правдой? Выберите два ответа.
   1. ли = Ij — Если
   2. Тэ = Ih — Ii
   3. Ic = Ij — Ia
   4. Ид = Ih — Ij
4. Измерения показывают, что ток через R1 составляет 0,5 А, а через R3 — 0,6 А. Основываясь на ваших знаниях законов Кирхгофа, подтвердите, какие из следующих утверждений верны.
   1. Измеренный ток для R1 правильный, но для R3 неправильный.
   2. Измеренный ток для R3 правильный, но для R1 неверный.
   3. Оба измеренных тока правильные.
   4. Оба измеренных тока неверны.
5. График, показанный на следующем рисунке 21.62, представляет собой зависимость энергии, рассеиваемой на резисторе R1, от времени. На каком из рисунков 21.63 и 21.65 показан график зависимости энергии, рассеиваемой на R2, от времени?

Изображение вопроса

Рисунок 21.61 Рисунок 21.62 Рисунок 21.63 Рисунок 21.65

Вопрос от OpenStax под лицензией СС BY 4.0.

Окончательный ответ

1. (с)
2. (с)
3. (б) и (г)
4. (б)
5. (с)

Видеорешение

Зарегистрируйтесь для просмотра видеорешения!

Начать бесплатную неделю

Trustpilot

Рейтинг

ПлохоНе так уж плохоСреднеХорошоОчень хорошо

0 голосов со средним рейтингом .

Стенограмма видео

Это ответы по физике в колледже с Шоном Дычко. Имеем схему с эдс здесь 6 вольт соединенных с двумя ветвями, которые находятся параллельно; эта ветвь имеет резистор R 1 с сопротивлением 10 Ом, а эта другая ветвь имеет резисторы R 2 и R 3 равные 5 Ом каждый … это внутреннее сопротивление равно нулю, так что оно может и не быть написано здесь, мы можем просто заменить его проводом. Хорошо! Итак, часть (а) требует, чтобы одним из шагов для проверки этой схемы было тестирование точек с одинаковым потенциалом, поэтому какая из следующих точек будет иметь одинаковый потенциал? Очки f , h и j будут, потому что точки f , h и j просто соединены проводами, которые, как мы предполагаем на принципиальной схеме, имеют нулевое сопротивление, и поэтому они все одинаковы. потенциал, потому что между этими точками нет сопротивления. Вы можете просмотреть все эти другие варианты и обнаружите, что между некоторыми точками в этих других вариантах есть резисторы, которые неверны. Так что рассмотрим вариант (а) б , c и d … у нас b здесь, c здесь они на одном потенциале но тогда d с другой стороны находится с другой стороны этого резистора и так будет имеют разный потенциал, потому что на этом резисторе будет падение потенциала, поэтому b , c и d не все имеют одинаковый потенциал, и то же самое можно сказать для (b) и (d) варианты здесь. Хорошо! Вопрос (b): в каких трех точках следует измерить токи, чтобы можно было непосредственно подтвердить правило соединения Кирхгофа? Таким образом, чтобы подтвердить правило соединения, нам нужно иметь возможность измерять токи во всех частях, выходящих из одной точки, и поэтому у нас есть эти положения в f , h и j будут использоваться для подтверждения правила соединения, потому что они измеряют токи, которые все проходят через соединение g . Итак, ток будет проходить через g через j , поэтому ток I j пойдет в эту точку g , а затем отсюда. .. ну, у нас также будет ток, идущий в г из точки ф и тогда эти два вместе пойдут на h , поэтому здесь у нас будет текущий h . Итак, когда мы сравниваем, знаете ли, I j плюс I f , эта сумма должна равняться I h , чтобы подтвердить правило соединения — общий ток, входящий в соединение, равен общему выходному току, другими словами. Хорошо! Просто для исключения варианта (а) предположим, что он будет рассматривать точки b , c и d … b , c и d здесь… c и d находятся на одной ветке, а не … Я имею в виду, что ток через c и d определенно будет одинаковым, потому что они находятся на одной ветке, и они не будут равны текущему в соединение b , потому что ток разделится в этой точке через R 1 , а затем через эту ветвь через R 2 и R 3 , поэтому это нельзя будет использовать для подтверждения правила соединения, что вы обнаружите, что токи c и d равны, и они будут меньше текущего в позиции b , но это не способ подтвердить правило соединения. Хорошо! Если ток в ветви с источником напряжения направлен вверх, а токи в двух других ветвях направлены вниз, определите, что из следующего может быть верным, и нам нужно выбрать два ответа. Так что ток здесь восходящий, а ток в этих двух ветвях нисходящий. Вариант (b) будет правильным, поэтому I e будет I h минус I i поэтому ток в e будет текущим в ч минус ток в i , потому что ток в ч будет суммой i и e (давайте удалим некоторые другие вещи, которые сейчас мешают) у нас здесь будут текущие и — это также текущие и , но они находятся в одной ветке, поэтому они равны. Итак, ток i входит в соединение g , ток e также входит в соединение g , а ток i плюс ток e должен быть равен току, выходящему из соединения g , который будет током I h , и затем они решили напишите что немного по другому так I e это с одной стороны и так I e это I h минус I i и вот что они тут написали. Хорошо, и тогда вариант (d) также правильный, поэтому текущий на d равно току в ч минус ток в дж . Итак, давайте удалим здесь кое-что постороннее… то, что мы сейчас снова видим, это d равно h минус j . Хорошо! Таким образом, у нас есть ток d , равный току h минус ток j , что примерно то же самое, что и раньше. Итак, у нас есть это общее количество I h , отнимите от этого ток через j , и у вас останется ток через d и это вариант (d) здесь. Затем измерения показывают, что ток через R 1 составляет 0,5 А, а через R 3 — 0,6 А. Итак, вот R 3 , и нам говорят, что ток через R 3 составляет 0,6 А, а ток через R 1 предположительно составляет 0,5 ампера, хотя мы увидим, что с этим выводом что-то не так. Итак, какие из следующих утверждений верны? Что ж, мы можем рассчитать ток, потому что нам дано достаточно информации, и мы знаем, что напряжение на R 1 составляет 6 вольт, потому что его внутреннее сопротивление равно нулю, и поэтому этот R 1 подключен к аккумулятору, поэтому здесь напряжение 6 вольт, а сопротивление 10 Ом, и поэтому мы можем рассчитать ток через R 1 , то это 6 вольт разделить на 10 Ом, что равно 0,6 ампера. Теперь это также будет ток через эту ветвь, поскольку общее сопротивление этих двух сопротивлений, соединенных последовательно, также равно 10 Ом, и поэтому их ток будет одинаковым, и ток будет одинаковым в обоих этих резисторах, поскольку они последовательно, и это тоже будет 0,6 ампера. Так I 1 должно быть 0,6, а I 3 равно 0,6, поэтому ток через R 3 правильный, но 0,5, предположительно измеренный для R 1 , неверен, поэтому ответ (b). Этот график показывает, что энергия, рассеиваемая в R 1 , является функцией времени, и вопрос заключается в том, какой из следующих графиков показывает энергию, рассеиваемую в R 2 , как функцию времени. Что ж, ток через R 1 такой же, как ток через R 2 , потому что каждая из этих параллельных ветвей имеет одинаковое сопротивление, и поэтому через них будет проходить одинаковый ток, поскольку на них одинаковое напряжение и энергия — это рассеиваемая мощность, умноженная на время, и мощность можно заменить на Я возвел в квадрат раз сопротивление умножить на время.