Каковы основные характеристики микросхемы КР142ЕН12А. Как правильно подключить КР142ЕН12А. Для чего применяется стабилизатор напряжения КР142ЕН12А. Какие существуют аналоги КР142ЕН12А.
Общая характеристика микросхемы КР142ЕН12А
Микросхема КР142ЕН12А представляет собой регулируемый стабилизатор положительного напряжения, выполненный в пластмассовом корпусе TO-220 (КТ-28-2). Она широко применяется в источниках питания различной электронной аппаратуры.
Основные характеристики КР142ЕН12А:
- Выходное напряжение: 1,2-37 В
- Максимальный выходной ток: 1,5 А
- Минимальное падение напряжения: 3,5 В
- Нестабильность по напряжению: ≤0,01%/В
- Нестабильность по току: ≤0,2%/А
- Температурный коэффициент напряжения: ≤0,02%/°C
- Рабочая температура: -60…+85°C
Особенности конструкции и функционал КР142ЕН12А
Микросхема КР142ЕН12А имеет следующие конструктивные и функциональные особенности:
- Трехвыводной корпус TO-220
- Встроенная защита от перегрузки по току
- Встроенная защита от перегрева
- Регулируемое выходное напряжение
- Малое количество внешних компонентов
Благодаря этим особенностям, КР142ЕН12А является универсальным и надежным стабилизатором напряжения для различных применений.
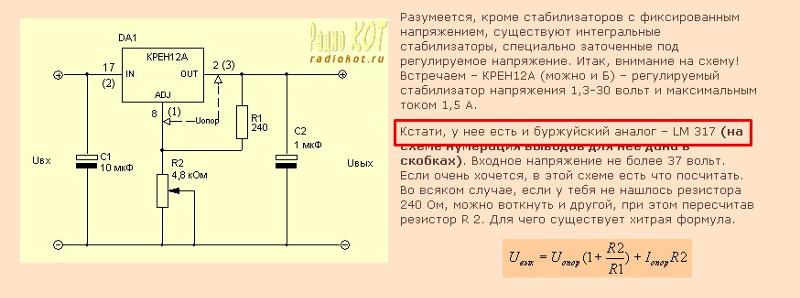
Схема включения и расположение выводов КР142ЕН12А
Для корректной работы микросхемы КР142ЕН12А необходимо соблюдать рекомендованную схему включения:
«` «`Расположение выводов КР142ЕН12А:
- Регулировка (ADJ)
- Выход (OUT)
- Вход (IN)
Для стабильной работы необходимо использовать входной и выходной конденсаторы. Величина выходного напряжения определяется соотношением резисторов R1 и R2 по формуле:
Uвых = 1,25 * (1 + R2/R1) + 50мкА * R2
Применение КР142ЕН12А в различных устройствах
Микросхема КР142ЕН12А находит широкое применение в следующих устройствах:
- Регулируемые источники питания
- Зарядные устройства
- Лабораторные блоки питания
- Стабилизаторы напряжения в различной электронной аппаратуре
- Системы автоматики и управления
Благодаря своей универсальности и надежности, КР142ЕН12А часто используется как в промышленной, так и в любительской электронике.

Аналоги и заменители КР142ЕН12А
Существует ряд микросхем, которые могут служить функциональными аналогами КР142ЕН12А:
- LM317 — популярный зарубежный аналог
- КР142ЕН12Б — отличается меньшим максимальным током (1 А)
- L7805CV — фиксированный стабилизатор на 5В, может заменить КР142ЕН12А в некоторых применениях
- LM338 — аналог с большим выходным током (до 5 А)
При замене КР142ЕН12А на аналоги необходимо учитывать различия в характеристиках и корректировать схему включения при необходимости.
Рекомендации по монтажу и эксплуатации КР142ЕН12А
При работе с микросхемой КР142ЕН12А следует учитывать следующие рекомендации:
- Использовать радиатор при токах нагрузки более 0,5 А
- Обеспечить надежный теплоотвод от корпуса микросхемы
- Соблюдать полярность подключения
- Не превышать максимально допустимые параметры
- Использовать качественные фильтрующие конденсаторы
Соблюдение этих рекомендаций позволит обеспечить долгую и надежную работу стабилизатора на основе КР142ЕН12А.
Преимущества и недостатки использования КР142ЕН12А
Как и любое техническое решение, применение КР142ЕН12А имеет свои плюсы и минусы:
Преимущества:
- Простота использования
- Широкий диапазон выходных напряжений
- Встроенные защиты
- Доступность и низкая стоимость
- Хорошая стабильность выходного напряжения
Недостатки:
- Относительно низкий КПД при большой разнице входного и выходного напряжений
- Необходимость использования радиатора при больших токах
- Ограниченный максимальный ток по сравнению с некоторыми аналогами
Несмотря на некоторые ограничения, КР142ЕН12А остается популярным выбором для многих разработчиков электронных устройств благодаря своей надежности и универсальности.
Часто задаваемые вопросы о КР142ЕН12А
Рассмотрим несколько типичных вопросов, возникающих при работе с КР142ЕН12А:
Как рассчитать резисторы для получения нужного напряжения?
Для расчета резисторов R1 и R2 можно использовать следующие формулы:
R1 = 240 Ом (фиксированное значение)
R2 = R1 * ((Uвых / 1,25) — 1)
Где Uвых — желаемое выходное напряжение.
Почему греется микросхема КР142ЕН12А?
Нагрев микросхемы — нормальное явление, особенно при больших токах нагрузки или значительной разнице между входным и выходным напряжением. Для уменьшения нагрева рекомендуется использовать радиатор и минимизировать разницу между входным и выходным напряжением.
Можно ли использовать КР142ЕН12А для зарядки аккумуляторов?
Да, КР142ЕН12А может использоваться в простых зарядных устройствах. Однако для более сложных и безопасных схем зарядки рекомендуется использовать специализированные микросхемы.
КРЕН12А характеристики микросхемы: схема подключения, распиновка КР142ЕН12А
В статье рассмотрены характеристики КРЕН12A (полная маркировка КР142ЕН12А) и схема её подключения. Данное полупроводниковое устройство представляет собой регулируемый стабилизатор положительного напряжения питания для электроприборов работающих от 1,25-37 В с током потребления до 1,5 А. Она оснащена необходимой внутренней защитой транзистора на выходе, перегрузок по току и перегрева. Для получения необходимых выходных параметров необходима дополнительная электронная обвязка, состоящая всего из двух резисторов.
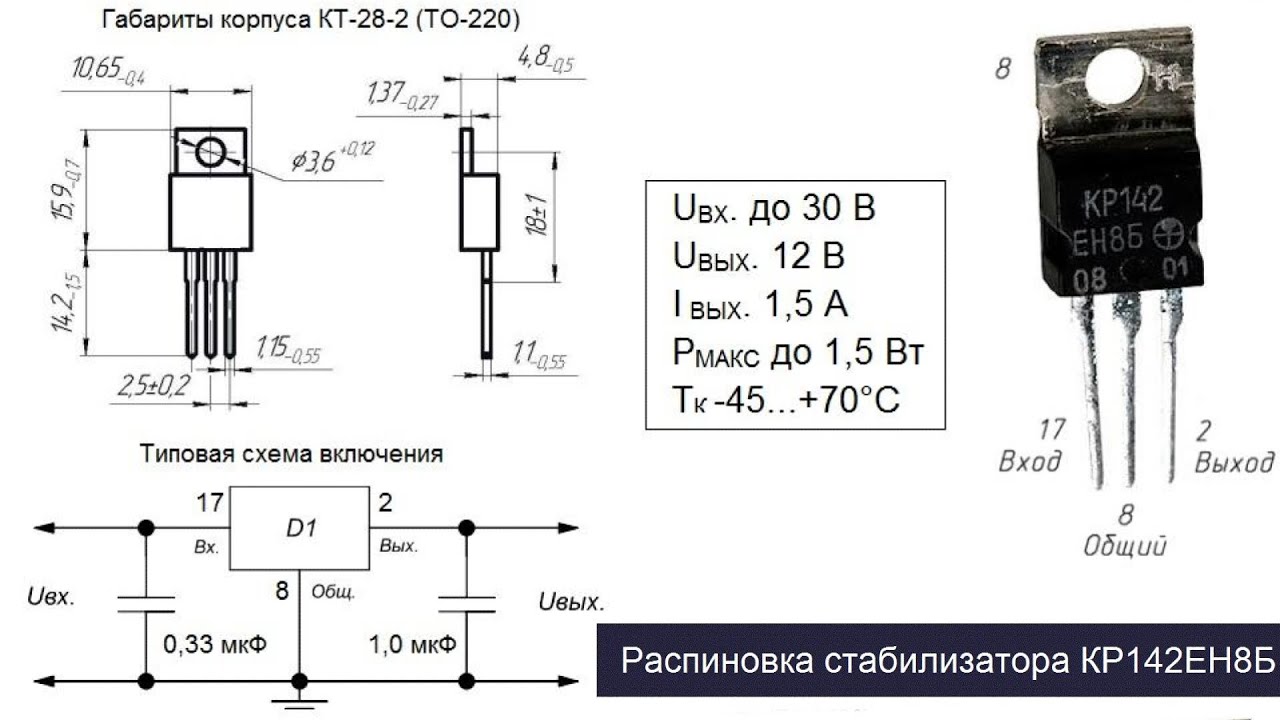
Цоколевка
Металлополимерный корпус микросхемы (КТ-28-2 или ТО-220) имеет всего три вывода и внешне очень напоминает транзистор. Внутри пластиковой упаковки размещено 276 интегральных элемента. Металлическая подложка физически соединена с контактом №2– «выход». Полная распиновка и типовое включение представлены на рисунке.
Основные параметры
Характеристики КРЕН12A, приведённые в технических описаниях (datasheet), стоит рассматривать с учётом максимальной рассеиваемой мощности устройства. В любых режимах работы не допускается её превышение, а для стабильной работы необходимо предусмотреть соответствующее охлаждение. Без использования радиатора предельная мощность ограничивается параметрами корпуса — обычно не превышает 1 Вт. Напряжение на входе микросхемы должно быть всегда больше, чем на выходе на 2-3 В.
В любых режимах работы не допускается её превышение, а для стабильной работы необходимо предусмотреть соответствующее охлаждение. Без использования радиатора предельная мощность ограничивается параметрами корпуса — обычно не превышает 1 Вт. Напряжение на входе микросхемы должно быть всегда больше, чем на выходе на 2-3 В.
Максимальные параметры
Приведём максимальные значения параметров для КРЕН12A:
- напряжение: на входе до 40 В; на выходе от 1.25 до 37 В;
- выходной ток 1.5 А;
- рассеиваемая мощность до 20 Вт;
- диапазон рабочих температур от 0 до +125 oC.
Не допускается превышать указанные значения.
Аналоги
У КРЕН12А есть отличные функциональные аналоги КР142ЕН12Б (до 1 А) и LM317T. Импортный по некоторым параметрам считается лучше отечественного. Возможно в связи с этим белорусский «Интеграл» в последнее время выпускает подобные устройства и с маркировкой «LM». Это обусловлено большой популярностью линейных стабилизаторов напряжения в мире, поэтому зарубежные производители все время совершенствуют их.
Регулировка напряжения
Вместо одного из двух резисторов можно использовать потенциометр к КР142ЕН12А и получить схему включения с регулировкой. C его помощью на выходе микросхемы добиваются необходимого напряжения. Таким образом, в домашних условиях, можно сделать простейший регулируемый стабилизатор постоянного электропитания.
На рисунке ниже представлена упрощённая схема включения крен12а для стабилизации 12V. При таком подключении ток в нагрузке ограничен максимальными параметрами микросхемы и не превышает 1 А. Рассеиваемая мощность определяется площадью радиатора — чем она больше, тем лучше.
В данной схеме для понижения выходного напряжения сопротивление R2 уменьшают. И наоборот, для повышения – увеличивают R2. Минимальное возможное значение R2 составляет 1 Ом (1.25 В), а максимальное теоретически — до 6.2 кОм (35 В).
Конечно, для полноценного регулируемого блока питания (БП) указанных компонентов будет недостаточно. Например, для подключения от сети 220 В необходимы еще трансформатор, выпрямительный диодный мост и сглаживающие конденсаторы. Упрощенную схему БП можно скачать по следующей ссылке или тут — более продвинутая конструкция БП с возможностью получения фиксированных напряжений.
Для повышения тока в нагрузке на выходе микросхемы устанавливают мощные транзисторы, однако есть еще возможность параллельного включения.
Параллельное включение
КР142ЕН12А допускает еще и параллельное включение. Таким образом тоже можно добиться увеличения значений выходных параметров. С таким подключением на выходах общей схемы, в зависимости от количества используемых КРЕНок, можно добиваться многократного роста тока в нагрузке. Наглядные примеры тестирования такого рода конструкций смотрите в видеоролике.
Производители
Скачать даташит на кр142ен12а в pdf-формате можно по здесь или кликнув по ссылке с наименованием изготовителя. Российским производителем этого изделия является брянский завод электроприборов АО «Группа Кремний ЭЛ», а ближнем зарубежье — белорусский «Интеграл».
КР142ЕН12(А,Б) — DataSheet
|
Типовая схема включения ИМС КР142ЕН12 |
|
Описание
Микросхемы представляют собой мощные высоковольтные стабилизаторы напряжения ’’взвешенного” типа с регулируемым выходным напряжением положительной полярности от 1,2 до 37 В и токами нагрузки 1 и 1,5 А. Устойчивы к импульсным перегрузкам мощности, имеют защиту от перегрузок по току. Содержат 276 интегральных элементов. Корпус пластмассовый типа КТ-28-2, масса не более 2 г. Выводы корпуса покрыты олововисмутом. Назначение выводов: 1 — регулировка; 2 — вход; 3 — выход, компенсация.
Общие рекомендации по применению
Крепление ИМС осуществляется непосредственно к печатной плате или через
переходные элементы методом распайки выводов корпуса на печатную плату. При этом радиатор закрепляется винтами: к металлической теплоотводящей шине на печатной плате — в случае использования дополнительного теплоотвода; непосредственно к печатной плате — при отсутствии дополнительного теплоотвода. Корпус ИМС электрически соединен с выводом 3 ” Uвых”. При монтаже ИМС необходимо обеспечивать изоляцию корпуса от заземленных элементов и токопроводящих элементов аппаратуры, имеющих потенциал, отличный от Uвых. Рекомендуется проводить монтаж ИМС 2 раза, демонтаж 1 раз. При всех условиях эксплуатации емкость выходных конденсаторов должна быть не менее 1 мкФ. При наличии сглаживающего фильтра входного напряжения (при отсутствии коммутирующих устройств между выходным конденсатором фильтра источника питания и ИМС, приводящих к нарастанию входного напряжения, и длине соединительных проводников не свыше 70 мм) входной емкостью может служить выходная емкость фильтра, если ее значение не менее 1 мкФ для керамических конденсаторов и не менее 10 мкФ для алюминиевых конденсаторов. В остальных
конденсатора до ИМС не более 70 мм. Для максимальной реализации выходных
параметров ИМС необходимо осуществлять контактирование резисторного делителе обратной связи и выходного конденсатора как можно ближе к выходу ИМС, а саму ИМС рекомендуется устанавливать в непосредственной близости к нагрузке. При использовании дополнительного радиатора рассеиваемая мощность не должна превышать 10 Вт. При этом температура кристалла должна быть не более 130 °С. Для снижения уровня шума и увеличения коэффициента сглаживания пульсаций при U
Uвых = Uвых,min (1 + R2/R1) + R2Iрег
где Iрег = 55 мкА — ток регулировки.
При выходных напряжениях, превышающих 25 В, если возможны короткие
замыкания на входе ИМС, и при наличии конденсатора С2 рекомендуется применять кремниевые диоды VD1 и VD2, а при отсутствии С2 — диод VD1, если емкость конденсатора С3 ≥ 25 мкФ.
Если возможны короткие замыкания только на выходе ИМС, то при наличии
конденсатора С2 достаточно подключать диод VD2.
| Электрические параметры | ||||
| Параметры | Условия | КР142ЕН12А | КР142ЕН12Б | Ед. изм. |
| Минимальное выходное напряжение | при Uвх = 5 В, Iвых = 5 мА | 1,2…1,3 | 1,2…1,3 | В |
| Минимальное падение напряжения | при Uвх = 18,5 В, Uвых = 15 В | ≤3,5 | ≤3,5 | В |
| Нестабильность по напряжению | при Uвх = 20 В, Uвых = 15 В, Iвых = 5 мА | ≤0,01 | ≤0,03 | %/В |
| Нестабильность по току | при Uвх = 20 В, Uвых = 15 В, Iвых = 5 мА | ≤0,2 | ≤0,2 | %/А |
| Температурный коэффициент напряжения | при Uвх = 5 В, Uвых = 1,18…1,33 В, Iвых = 5 мА | ≤0,02 | ≤0,02 | %/°С |
| Дрейф выходного напряжения | при Uвх = 45 В, Uвых = 15 В, Iвых = 23 мА | ≤1 | ≤1 | |
| Температура окружающей среды | — | -10…+70 | -10…+70 | °С |
| Предельно допустимые режимы эксплуатации | ||||
| Параметры | Условия | КР142ЕН12А | КР142ЕН12Б | Ед.изм. |
| Входное напряжение | — | 5…45 | 5…45 | В |
| Выходное напряжение | — | 1,2…37 | 1,2…37 | В |
| Выходной ток | — | 0,005…1,5 | 0,005…1 | А |
| Рассеиваемая мощность | T = -10…+40 °С | ≤1 | ≤1 | Вт |
| T = +70 °С | ≤0,7 | ≤0,7 | ||
| Температура окружающей среды | — | -60…+85 | -60…+85 | °С |
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Стабилизатор КРЕН12А (кр142ен12а): характеристики и схемы подключения | ShemaTok.ru
В статье рассмотрены характеристики КРЕН12A (полная маркировка КР142ЕН12А) и схема её подключения. Данное полупроводниковое устройство представляет собой регулируемый стабилизатор положительного напряжения питания для электроприборов работающих от 1,25-37 В с током потребления до 1,5 А. Она оснащена необходимой внутренней защитой транзистора на выходе, перегрузок по току и перегрева. Для получения необходимых выходных параметров необходима дополнительная электронная обвязка, состоящая всего из двух резисторов.
Цоколевка
Металлополимерный корпус микросхемы (КТ-28-2 или ТО-220) имеет всего три вывода и внешне очень напоминает транзистор. Внутри пластиковой упаковки размещено 276 интегральных элемента. Металлическая подложка физически соединена с контактом №2– «выход». Полная распиновка и типовое включение представлены на рисунке.
Параметры КР142ен12аПараметры КР142ен12а
Основные параметры
Характеристики КРЕН12A, приведённые в технических описаниях (datasheet), стоит рассматривать с учётом максимальной рассеиваемой мощности устройства. В любых режимах работы не допускается её превышение, а для стабильной работы необходимо предусмотреть соответствующее охлаждение. Без использования радиатора предельная мощность ограничивается параметрами корпуса — обычно не превышает 1 Вт. Напряжение на входе микросхемы должно быть всегда больше, чем на выходе на 2-3 В.
Максимальные параметры
Приведём максимальные значения параметров для КРЕН12A:
- напряжение: на входе до 40 В; на выходе от 1.25 до 37 В;
- выходной ток 1.5 А;
- рассеиваемая мощность до 20 Вт;
- диапазон рабочих температур от 0 до +125 oC.
Не допускается превышать указанные значения.
Аналоги
У КРЕН12А есть отличные функциональные аналоги КР142ЕН12Б (до 1 А) и LM317T. Импортный по некоторым параметрам считается лучше отечественного. Возможно в связи с этим белорусский «Интеграл» в последнее время выпускает подобные устройства и с маркировкой «LM». Это обусловлено большой популярностью линейных стабилизаторов напряжения в мире, поэтому зарубежные производители все время совершенствуют их.
Регулировка напряжения
Вместо одного из двух резисторов можно использовать потенциометр к КР142ЕН12А и получить схему включения с регулировкой. C его помощью на выходе микросхемы добиваются необходимого напряжения. Таким образом, в домашних условиях, можно сделать простейший регулируемый стабилизатор постоянного электропитания.
На рисунке ниже представлена упрощённая схема включения крен12а для стабилизации 12V. При таком подключении ток в нагрузке ограничен максимальными параметрами микросхемы и не превышает 1 А. Рассеиваемая мощность определяется площадью радиатора — чем она больше, тем лучше.
схема включения крен12асхема включения крен12а
В данной схеме для понижения выходного напряжения сопротивление R2 уменьшают. И наоборот, для повышения – увеличивают R2. Минимальное возможное значение R2 составляет 1 Ом (1.25 В), а максимальное теоретически — до 6.2 кОм (35 В).
Конечно, для полноценного регулируемого блока питания (БП) указанных компонентов будет недостаточно. Например, для подключения от сети 220 В необходимы ещё трансформатор, выпрямительный диодный мост и сглаживающие конденсаторы.
Для повышения тока в нагрузке на выходе микросхемы устанавливают мощные транзисторы, однако есть ещё возможность параллельного включения.
Параллельное включение
КР142ЕН12А допускает ещё и параллельное включение. Таким образом тоже можно добиться увеличения значений выходных параметров. С таким подключением на выходах общей схемы, в зависимости от количества используемых КРЕНок, можно добиваться многократного роста тока в нагрузке.
Производители
Российским производителем этого изделия является брянский завод электроприборов АО «Группа Кремний ЭЛ», а ближнем зарубежье — белорусский «Интеграл».
Источник https://shematok.ru/stabilizatory/kren12a
| Электрические параметры: Минимальное выходное напряжение при Uвх=5 В, Iвых=5 мА . . . . . . . . . 1,2…1,3 В Минимальное падение напряжения при Uвх=18,5 В, Uвых= 15 В . . . . . . . ≤ 3,5 В Нестабильность по напряжению при Uвх=20 В, Uвых=15 В, Iвых=5 мА: КР142ЕН12А . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .≤ 0,01 %/В КР142ЕН12Б . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .≤ 0,03 %/В Нестабильность по току при Uвх=20 В, Uвх=15 В, Iвых=5 мА . . . . . . . . . . ≤ 0,2 %/А Температурный коэффициент напряжения при Uвх=5 В, Uвых=1,18…1,33В, Iвых=5 мА . . . . . . . . . . . . . . . . . . . . . . . . . . ≤ 0,02 %/ºC Дрейф выходного напряжения при Uвх=45 В, Uвых=15 В, Iвых=23 мА . . . ≤ 1% Температура окружающей среды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . -10…+70 ºCПредельно допустимые режимы эксплуатации: Входное напряжение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5…45 В Выходное напряжение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1,2…37 В Выходной ток: КР142ЕН12А . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,005…1,5 А КР142ЕН12Б . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,005…1 А Рассеиваемая мощность: T=-10…+40 ºC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ≤ 1 Вт T=+70 ºC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ≤ 0,7 Вт Температура окружающей среды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .-60…+85 °C Примечание: изменение Pрас в диапазоне температур +40…+70 °C происходит по линейному закону. Общие рекомендации по применению: Корпус ИС электрически соединен с выводом 3 «Uвых«. При монтаже ИС необходимо обеспечивать изоляцию корпуса от заземленных элементов и токопроводящих элементов аппаратуры, имеющих потенциал, отличный от Uвых. Рекомендуется проводить монтаж ИС 2 раза, демонтаж 1 раз. При всех условиях эксплуатации емкость выходных конденсаторов должна быть не менее 1 мкФ. При наличии сглаживающего фильтра входного напряжения (при отсутствии коммутирующих устройств между выходным конденсатором фильтра источника питания и ИС, приводящих к нарастанию входного напряжения, длине соединительных проводников не свыше 70 мм) входной емкостью может служить выходная емкость фильтра, если ее значение не менее 1 мкФ для керамических и не менее 10 мкФ для алюминиевых конденсаторов. В остальных случаях входная емкость должна быть не менее 0,1 мкФ. Расстояние от входного конденсатора до ИС не более 70 мм. Для максимальной реализации выходных параметров ИС необходимо осуществлять контактирование резисторного делителя обратной связи и выходного конденсатора как можно ближе к выходу ИС, а саму ИС рекомендуется устанавливать в непосредственной близости к нагрузке. При использовании дополнительного радиатора рассеиваемая мощность не должна превышать 10 Вт. При этом температура кристалла должна быть не более 130 °С. Для снижения уровня шума и увеличения коэффициента сглаживания пульсаций при Uвых≥Uвых,min рекомендуется подключать конденсатор С2 ≤ 10 мкФ. Выходное напряжение определяется из выражения: где Iрег = 55 мкА — ток регулировки. При выходных напряжениях, превышающих 25 В, если возможны короткие замыкания на входе ИС, и при наличии конденсатора С2 рекомендуется применять кремневые диоды VD1 и VD2, а при отсутствии С2 — диод VD1, если емкость конденсатора С3 ≥ 25 мкФ. Если возможны короткие замыкания только на выходе ИС, то при наличии конденсатора C2 достаточно подключать диод VD2. |
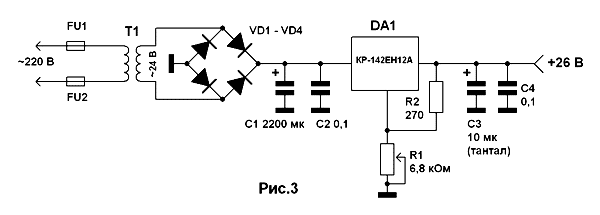
Фотореле на микросхеме КР142ЕН12 » S-Led.Ru
Микросхемы КР142ЕН12А и КР142ЕН12Б выполнены в пластмассовом корпусе Т0-220 (КТ-28-2) и представляют собой регулируемые стабилизаторы напряжения компенсационного типа. Максимальный ток нагрузки может достигать 1 А, при этом, рассеиваемая микросхемой мощность не должна превышать 1 Вт без теплоотвода и 10 Вт с теплоотводом.
Величина выходного напряжения зависит от напряжения на управляющем выводе (вывод 17). Ток управляющего вывода не превышает 120… 150 мкА, это означает, что коэффициент усиления микросхемы по току превышает 5000.
На рис. 1 приводится схема простого фотореле, в качестве нагрузки которого установлена миниатюрная лампа накаливания EL1. Фотодатчик выполнен на чувствительном импортном фототранзисторе, допускающем максимальное напряжение коллектор — эмиттер до 30 В и максимальную рассеиваемую мощность до 100 мВт. Если фототранзистор освещен, то его сопротивление минимально, напряжение на выводе его коллектора относительно общего провода не превышает 0,4 В, выходное напряжение микросхемы DA1 будет около 1,5 В, лампа EL1 светит слабым накалом.
Рис. 2
Если линзу фототранзистора прикрыть подходящим по размеру светонепроницаемым колпачком, то ток через него резко уменьшится, напряжение на управляющем выводе микросхемы возрастёт, напряжение на выходе будет зависеть от сопротивлений резисторов R1, R2, например, увеличится до 6,3 В. При необходимости увеличения чувствительности фотореле, можно пропорционально увеличить сопротивления резисторов R1, R2. Так следует поступить и в том случае, если светоуправляемый стабилизатор будет настроен на более высокое выходное напряжение.
На рис. 2 приводится другой вариант фотореле. Здесь лапа накаливания EL1 будет зажигаться на полную яркость в том случае, если фототранзистор будет освещён. Конденсатор С5 предназначен для сглаживания пульсаций на выходе стабилизатора, например, в случае, если фототранзистор будет освещаться лампами дневного цвета, которые мерцают с частотой сети или с рабочей частотой высоковольтного преобразователя напряжения, от которого они получают питание. Таким же конденсатором можно зашунтировать и фототранзистор фотореле, собранном по схеме на рис. 1.
Устройство, собранное по схеме на рис. 3, представляет собой мигалку. Особенностью этого генератора является то, что лампа накаливания в паузах между вспышками не погасает полностью, что значительно увеличивает её срок службы. В качестве генератора импульсов здесь применён мигающий светодиод Kingbright. В момент, когда светодиод вспыхивает, яркость свечения лампы накаливания понижается.
Рис. 3
Если для выполнения поставленных вами задач мощности микросхемы окажется недостаточно, то её можно усилить p-n-p транзистором, как это показано на рис. 4. В этом случае следует учитывать, что встроенная в микросхему функция ограничения максимального тока нагрузки, например, при коротком замыкании выхода, работать не будет. В описанных узлах не ограничивается использование в качестве нагрузки только ламп накаливания. Нагрузкой, например, может быть и мощное электромагнитное реле, некоторые типы электродвигателей постоянного тока, миниатюрный электропаяльник, детские игрушки. Если вместо фототранзистора использовать датчик на терморезисторе, то любой из узлов можно превратить в термореле. Интересно будет применение на месте датчика и магнитоуправляемой микросхемы, например, из серии К1116.
Рис. 4
Импортный аналог отечественной микросхемы — LM317T. Фототранзистор можно заменить на L51P3, L32P3C. Вместо транзистора КТ818Б при токе нагрузки до 3 А можно использовать любой из серий КТ818, КТ816, КТ835, КТ837. Транзистор КТ503А можно заменить на любой из серий КТ603, КТ608, КТ630, КТ503, SS8050. Мигающий светодиод — любого цвета свечения из серий L56B, L36B, L796B, L816B.
Крен 142 12 характеристики схема подключения
142ЕН1 142ЕН2 142ЕН3 142ЕН4
А. Щербина, С. Балтий, В. Иванов
В последние годы широкое распространение получили интегральные стабилизаторы напряжения. Источники питания на их основе отличаются малым числом дополнительных деталей, невысокой стоимостью и хорошими техническими характеристиками. Появилась возможность снабдить каждую плату сложного устройства собственным стабилизатором напряжения (СН), а значит, использовать для его питания общий нестабилизированный источник. Это значительно повысило надежность таких устройств (выход из строя одного СН приводит к отказу только того блока, который к нему подключен), во многом сняло проблему борьбы с наводками на длинные провода питания и импульсными помехами, порожденными переходными процессами в этих цепях. В настоящее время промышленность выпускает широкий ассортимент микросхем серий 142, К142 и КР142. В их состав входят стабилизаторы с регулирующим транзистором, включенным в плюсовой провод выходной цепи, и регулируемым выходным напряжением (142ЕН1—142ЕН4, КР142ЕН1 — КР142ЕН4), то же, но с фиксированным выходным напряжением (142EHS, 142ЕН8, 142ЕН9, К142ЕН8, К142ЕН9, КР142ЕН5, КР142ЕН8, КР142ЕН9; далее в тексте — 142ЕН5, 142ЕН8, 142ЕН9), двуполярные с фиксированным выходным напряжением (142ЕН6, К142ЕН6; далее — 142ЕН6), стабилизаторы с регулирующим элементом в минусовом проводе и регулируемым выходным напряжением (142ЕН10, 142ЕН11) и устройство управления ключевым СН (142ЕП1). Предлагаемая статья знакомит с особенностями использования приборов этой серии.
Микросхема представляет из себя трехвыводной регулируемый стабилизатор положительного напряжения от 1.2 до 37 В. Стабилизатор допускает работу с током нагрузки до 1,5 А. Микросхема КР142ЕН12А (КРЕН12А) комплементарна регулируемому стабилизатору отрицательного напряжения 142ЕН18. Микросхема выполнена в пластмассовом корпусе типа КТ-28-2 (ТО-220).
Трехвыводные стабилизаторы напряжения бывают фиксированные или регулируемые. Первые разработаны на конкретное выходное напряжение (в нашем случае 5 В). Вторые – регулируемые стабильники, которые позволяют установить необходимое напряжение в заявленных пределах.
Если вам не нужно ограничивать выходные параметры или настраивать сигнал на нестандартные параметры, то обратите внимание на стабилизатор с фиксированным напряжением КРЕН 142, который позволит использовать меньше деталей и поэтому станет лучшим выбором.
Схема КРЕН 142
Как выбрать стабилизатор по току? Устройство должно быть выбрано с номиналом, довольно близким к значению максимально возможного тока в цепи. Если стабилизатор будет слегка загружен, то со стабильностью часто бывает не всё в порядке. Однако схема должна быть подобрана оптимально и полезно во всех смыслах. То есть номинальный ток с большим запасом тоже ни к чему, поскольку ток короткого замыкания будет также слишком большим для того, чтобы защитить цепь.
Типовая схема включения КР142ен5а
Стабилизатор серии КР142ен5а с постоянным положительным напряжением на выходе в 5 В имеет широкое применение в самых различных электронных приборах. Сфера его использования – в качестве источника питания для логических систем, аппаратов высокоточного воспроизведения и других радиоэлектронных приборов. Электрическая схема КР142ЕН5А показана на рисунке ниже.
Емкости С1, С2 играют корректирующую роль. С2 предназначена для сглаживания пульсации, а С1 – для защиты от вероятного высокочастотного возбуждения микросхемы. Ток нагрузки стабилизатора рассчитан до 2 А.
Если добавить в схему вспомогательные детали можно преобразовать её в источник с регулированием напряжения. При удалённом расположении КРЕН 142 (с длиной соединительных проводов один метр и более) от фильтрующих конденсаторов выпрямителя, к его входу следует присоединить конденсатор. Для регулирования напряжения на выходе используется внешний делитель. Для правильной работы устройства потребуется применение дополнительного радиатора. Эти модели являются аналогами импортных регуляторов серии 78xx.
Цоколевка и схема включения
Микросхема КР142ен5а рассчитана на максимальный ток 5 А, и она может его обеспечить. Но превышение тока грозит выходом устройства из строя. Ниже приводится вариант включения микросхемы. Разрешается производить монтаж микросхемы два раза, демонтаж один раз.
Крепёж схемы к печатной плате выполняется методом распайки выводов корпуса, см. цоколевку микросхемы на рисунке.
Характеристики стабилизатора
Микросхема кр142ен5а представляет собой стабилизатор компенсационного типа с регулируемым выходным напряжением положительной полярности.
- защита от перегрева;
- ограничение по току КЗ;
- масса не более 1,4 г;
- габариты 14,48х15,75 мм.
Предельные значения параметров режима эксплуатации и условий окружающей среды:
- Температура хранения -55 … +150 С;
- Температур кристалла в рабочем режиме -45 … +125 С.
Все своими руками Простой стабилизатор напряжения
Опубликовал admin | Дата 30 сентября, 2011Здравствуйте дорогой читатель. После того, как появились трехвыводные стабилизаторы напряжения, жизнь для разработчиков линейных блоков питания стала лучше, жизнь стала веселее. И я тоже к ним пристрастился — удобная штука. И каких только схем на них не встретишь.
Здесь приводится типовая схема включения регулируемого трехвыводного стабилизатора напряжения на микросхеме LM117, наш полный аналог — КР142ЕН12А.
Максимальное входное напряжение КР142ЕН12А равно сорок пять вольт, минимальное входное — пять вольт. Особенно хорош верхний порог входного напряжения этой микросхемы, есть шансы, что она останется жива при аномальном перенапряжении первичной сети.
Диапазон выходных напряжений от 1,25 до 37 вольт — достойный диапазон. Максимальный выходной ток микросхемы с соответствующим радиатором составляет полтора ампера. Так как я воспитывался в оборонной промышленности, то и все элементы схем стараюсь использовать на 30 максимум на 50% от их предельно-допустимых параметров. Так стабилизатор, собранный по этой схеме с выходным напряжением 13,6 вольт и током нагрузки 400ма работает уже одиннадцать лет. Рассчитать радиатор самому очень сложно, поэтому я их подбираю. Оставляю такой радиатор, при котором температура самой микросхемы не превышала 40-50 градусов при максимальной нагрузке. Во всем должен быть запас. Конденсатор С1 на схеме необходим, если длина провода от конденсаторов фильтра до микросхемы больше восьми сантиметров. R1 может принимать значения от 220 до 270ом и устанавливать его лучше прямо на выводы микросхемы, при этом время пайки должно быть не более трех секунд. Резистор R2 можно оставить подстроечным, Но если вы делаете блок питания под конкретное напряжение, его следует заменить постоянным, сами понимаете — контакт, да еще и скользящий — опасная штука. R2 можно рассчитать по формуле — R2=R1x (Uвых/1,25 — 1). Собираясь делать радиоаппаратуру, не забывайте о том, где она у вас будет работать, или под одеялом дома, или в поле зимой на ветру. От климатических условий зависит и выбор радиокомпонентов по диапазону рабочих температур.
До свидания К.В.Ю.
Обсудить эту статью на — форуме «Радиоэлектроника, вопросы и ответы».
Просмотров:127 722
Вычислительные свойства визуальной микросхемы
% PDF-1.4 % 1 0 объект >>> эндобдж 284 0 объект > поток application / pdf
Стохастические вычисления в моделях кортикальных микросхем
Состояния сети и распределения состояний сети
Марковских констат.
Марковское состояние (или, точнее,) сети во времени определяется здесь как недавняя история времен всплесков всех нейронов в сети за период. Термин «марковский» относится к тому факту, что в мягких условиях и для достаточно длинного окна сетевая динамика нейронной цепи со временем становится независимой от сетевой активности временами, учитывая марковское состояние и внешний вход.Следовательно, динамика сети обладает марковским свойством по отношению к этому определению состояния.
Для каждого нейрона в нейронной цепи история длины импульсов определяется как список времен всплесков, испускаемых нейроном в пределах окна. Время всплесков отсчитывается относительно начала окна в. Если — количество импульсов внутри нейрона, то список принимает вид, (3) где.
Мы обозначаем пространство всех возможных сетевых состояний длины через или, если однозначно, просто через.Обратите внимание, что это определение эквивалентно определению состояния в [18], к которому заинтересованный читатель может обратиться за дальнейшими формальными деталями (например, ассоциированная -алгебра пространства состояний).
Объем теоретических результатов: Требуемые свойства сетевых и нейронных моделей шума.
Мы изучаем общие теоретические свойства моделей схем стохастических пиков, управляемых некоторым внешним, возможно векторным, входным сигналом, который может представлять, например, входные скорости в наборе входных нейронов или вводимые входные токи.Формально входная последовательность может принимать значения из любого пространства состояний; конкретным примером является векторнозначный ввод с, где — количество входных измерений.
В этой статье мы рассматриваем две разные модели шума для нейрона: В модели шума I генерация спайков непосредственно моделируется как стохастический процесс. Вся динамика сети, включая задержки аксонов, синаптическую передачу, краткосрочную синаптическую динамику, дендритные взаимодействия, интеграцию входных данных в соме и т. Д., Может быть смоделирована функцией, которая отображает состояние Маркова (которое включает недавнюю историю спайков нейрона. сам) на мгновенную вероятность всплеска.Эта модель очень гибкая и может учитывать различные типы нейронного шума. В более конкретной модели шума II механизм возбуждения нейрона считается детерминированным, и шум входит в его динамику через стохастическое высвобождение пузырьков на афферентных синаптических входах. Также для наших теоретических результатов можно предположить комбинации моделей шума I и II в одном нейроне и цепи, например нейроны с общим механизмом стохастических всплесков, которые дополнительно обладают стохастическими синапсами, или смеси нейронов из моделей I и II в одной и той же среде. схема.
В модели шума I мгновенная вероятность всплеска нейрона в определенный момент времени определяется выражением: (4) Предполагается, что эта мгновенная частота импульсов во времени ограничена и полностью определяется текущим марковским состоянием сети для некоторых достаточно больших. Точнее, для модели шума I сделаны следующие четыре допущения:
A 1 Пики — это отдельные события: Мы предполагаем, что, (5), например, выполняется, если каждый нейрон имеет некоторый независимый источник стохастичности.
A 2 Ограниченная скорость: Мгновенная скорость стрельбы ограничена сверху:
для некоторых. Последующая верхняя граница общей скорости активации сети обозначается как, т.е. Предполагается, что мгновенные ставки ограничены в любое время и при наличии любого входа.
A 3 Ограниченная память: Частота активации во времени зависит от прошлой активности сети только на основе истории недавних всплесков в конечном окне длины.Следовательно, прямой эффект всплеска во времени на будущую частоту активации всех нейронов ограничен ограниченным «периодом памяти»,. Этот ограниченный период памяти можно понимать как нижнюю границу для последующих доказательств сходимости (поскольку меньший период нарушил бы марковское свойство). В дополнение к этой зависимости ограниченной памяти от сетевых всплесков может зависеть от текущего входа любым способом, совместимым с.
A 4 Однородность по времени: Функциональное сопоставление недавних всплесков и / или входных сигналов с мгновенными скоростями воспламенения не меняется со временем.В частности, в этой работе мы не рассматриваем долговременную пластичность синаптических весов и / или возбудимости.
Допущения можно резюмировать следующим образом: Пусть и будут траекториями входных и сетевых состояний, как определено выше. Тогда существует постоянная памяти и границы скорости, такие, что для каждого нейрона существует функция, где для всех. Функция не зависит от времени, но в остальном не ограничена, и может улавливать сложные динамические эффекты, такие как нелинейные дендритные взаимодействия между синаптическими входами или кратковременная пластичность синапсов.
Входной сигнал может формально представлять любую переменную, которая оказывает произвольное влияние на мгновенную динамику сети (функции возбуждения нейронов). В простейшем случае это может быть вектор скоростей возбуждения, контролирующий пиковое поведение набора входных нейронов, например, в этих нейронах. В этом случае (на котором мы сосредоточились в основном тексте) входные нейроны формально считаются частью схемы. Обратите внимание, что в принципе он также может представлять силу токов, которые вводятся в подмножество нейронов в сети, или недавнюю историю всплесков набора внешних входных нейронов («входные марковские состояния»).Если входные данные содержат скорости или токи, они могут быть либо фиксированными (например, фиксированными входными скоростями воспламенения) или динамически изменяющимися (в частности, скоростями, которые либо подвержены стохастической эргодической динамике, либо периодически меняются скоростями). Ниже будут представлены доказательства сходимости как для фиксированных, так и для динамических входных условий. Если вход определяется в терминах входных марковских состояний, динамический входной анализ применим в условиях, описанных ниже.
В модели шума II основным случайным событием является высвобождение синаптических пузырьков (в модели шума I это спайк).Соответственно, марковское состояние сети в модели шума II определяется как список времен высвобождения везикул для каждого синаптического сайта высвобождения в сети (вместо времени спайков для каждого нейрона). Мы предполагаем, что каждый синаптический сайт высвобождения в конкретный момент высвобождает не более одного пузырька, заполненного нейротрансмиттерами. Но синаптическая связь между двумя нейронами может состоять из множества сайтов синаптического высвобождения (см. Обзоры [102], [103] и [3]). Вместо выражения сетевой динамики через функцию вероятности мгновенного срабатывания для каждого нейрона (модель шума I), для модели шума II динамика сети выражается в терминах вероятностей мгновенного срабатывания для каждого синапса:.Подобно модели шума I, предполагается, что существует длина окна, так что динамика высвобождения везикул во времени полностью определяется временем предыдущих высвобождений везикул в пределах, и, следовательно, может быть выражена в терминах соответствующего изменения определение марковского состояния. Применяется та же структура предположений, что и в модели шума I: выбросы пузырьков являются отдельными событиями, и предполагается, что функции ограничены сверху константами скорости.
Также возможны комбинации моделей шума I и II.В этом случае состояние Маркова может содержать как время всплеска, так и время высвобождения везикул. Предположения модели шума I / II, описанные выше, применимы к соответствующим стохастическим нейронам и высвобождениям везикул соответственно. В целом отметим, что все три типа сетей (основанные на модели I, II и их смесях) основаны на общей структуре определений и предположений: во всех случаях динамика описывается в терминах стохастических компонентов (нейронов, синапсов). которые генерируют точечные события (всплески / выбросы пузырьков) в соответствии с мгновенными вероятностями, которые зависят от истории недавних событий в сети.
Сходимость распределений состояний.
Ниже приведены доказательства существования и единственности стационарных распределений состояний сети для рассматриваемых сетевых моделей. Кроме того, приведены границы скорости сходимости к этому стационарному распределению. Чтобы получить полную картину, сходимость изучается при трех различных входных условиях: постоянный, стохастический и периодический вход. Все доказательства подробно описаны для модели шума I. Результаты напрямую переносятся на модель шума II и смеси этих двух моделей, поскольку одни и те же рамки допущений применимы ко всем случаям.
Сетевая динамика как марковский процесс.
Мы рассматриваем моделирование модели кортикальной микросхемы при заданных входных условиях и начиная с заданного начального состояния сети как случайный эксперимент. Формально мы обозначаем набор всех возможных исходов в этом случайном эксперименте с помощью, набор всех рассмотренных событий с помощью (то есть -алгебру), а показатель вероятности, который присваивает вероятность каждому событию с помощью. Результат — это результат одного запуска сети.Результат связан с присвоением определенных значений всем определенным случайным величинам. Событие — это набор результатов, например набор всех результатов, в которых нейрон вспыхивает в течение первых миллисекунд эксперимента. Предположим, что это случайная величина с некоторым пространством состояний, т.е. принимает значения в, и представляет собой набор событий в пространстве. Формально такая случайная величина определяется как карта, которая присваивает значение каждому возможному результату. Чтобы обозначить вероятность того, что случайная величина принимает какое-то значение в наборе, мы определяем сокращение.Кроме того, если это еще одна случайная величина, мы используем обозначение условных вероятностей и пишем еще короче, если это однозначно,. Предполагается, что базовое вероятностное пространство достаточно богато, чтобы существовали все случайные величины, которые необходимы в дальнейшем.
Мы определяем набор индексов времени и случайный процесс как описание стохастической эволюции марковских состояний сети для. Каждый раз мы определяем случайную величину (также записанную), представляющую марковское состояние сети в данный момент.принимает значения в пространстве состояний всех возможных марковских состояний некоторой фиксированной длительности. Обозначим через -алгебру, ассоциированную с. Предположения относительно сети, описанные в предыдущем разделе, подразумевают, что процесс обладает марковским свойством для марковских состояний любой длины, поскольку будущее развитие процесса в этом случае полностью не зависит от прошлого, учитывая текущее марковское состояние. Поэтому для последующих доказательств мы предполагаем некоторые из них. Мы также определяем случайную величину из полных траекторий выборки в измеряемом пространстве, т.е.е. карта . Реализации являются выборочными путями (или траекториями), то есть функциями, принимающими значения в. Поскольку реализации являются функциями, их можно рассматривать как случайную функцию.
Для последующих доказательств важно следующее определение ядра вероятности перехода : Ядро вероятности перехода на измеримом пространстве состояний — это функция, которая присваивает вероятность переходу от любой точки к любому множеству. Точнее, если фиксируется конкретное «начальное состояние», то в его целевом аргументе является вероятностная мера, соответствующая результату применения ядра перехода к (кроме того, для каждого события в целевом пространстве можно измерить исходный аргумент).Матрицы стохастических переходов цепей Маркова являются, например, ядрами вероятностей перехода.
Здесь мы записываем ядро вероятности перехода, соответствующее прогрессированию состояния сети от времени к, то есть (6) Далее мы определяем сокращение для прогрессии продолжительности, начиная с начального времени. Ядра переходов также могут применяться к вероятностным мерам начальных состояний (в отличие от одиночных начальных состояний). Мы будем писать для обозначения результата применения ядра к исходной вероятностной мере.Результатом снова является вероятностная мера, присваивающая вероятность любому событию в пространстве состояний в соответствии с: (7) Поскольку это снова вероятностная мера в пространстве состояний, ядра переходов могут применяться последовательно. Обратите внимание, что в силу марковского свойства для.
Стохастическая сетевая динамика сокращается.
Перед изучением конкретных входных условий разрабатываются несколько основных ключевых свойств сетевой динамики. Позвольте быть ядром вероятности перехода, соответствующим прогрессированию сети от времени до.Для приведенных ниже доказательств переходы в состояние покоя , будут иметь особое значение. Состояние покоя определяется как «пустое» марковское состояние, в котором не было всплесков в течение последних единиц времени. Первым ключевым наблюдением является следующее предложение:
Утверждение 1 Рассмотрим вероятность , что процесс будет в состоянии покоя в момент времени , начиная с некоторого начального состояния в момент времени .Эта «вероятность возврата» в состояние покоя ограничена снизу, (8) , где . Это сохраняется независимо от входной траектории , , управляющей сетью.
Утверждение следует непосредственно из того факта, что ограничивает сумму всех мгновенных скоростей стрельбы в сети. Следовательно, по крайней мере с вероятностью ни один нейрон не сработает в единицу времени (см. [18]). С технической точки зрения это означает, что стохастическое ядро, соответствующее длительности длины, удовлетворяет условию Дёблина [104] — свойство, которое очень полезно для доказательства сходимости и эргодичности результатов.
Утверждение 1 влечет за собой центральное свойство сжатия стохастических сетей нейронов с импульсами, которое сохраняется при любой входной траектории и формирует основу для нескольких последующих доказательств. Следующие определения важны: Ниже мы будем измерять разницу между любыми двумя распределениями вероятностей и с точки зрения общей вариации подписанной меры. Любая такая мера со знаком может быть выражена в терминах ее неотрицательных и неположительных компонентов, где и являются неотрицательными мерами (но, как правило, не являются вероятностными мерами).Полная вариация меры со знаком на измеряемом пространстве определяется как общая масса ее положительного и отрицательного компонентов. Согласно этому определению,.
Лемма 1 (лемма о сжатии) Следующее свойство строгого сжатия выполняется для марковского процесса , для любого и для любых начальных вероятностных мер и в любое время : (9) На словах: применение динамики сети для единиц времени гарантирует сокращение расстояния между любыми двумя начальными распределениями и состояний сети в раз.
Проба: Определите вспомогательную меру как ноль везде снаружи, и. Перепишем в терминах неотрицательных мер и, таких, что (10), и отметим, что это означает, что. Тогда (11) (12) (13) (14) (15) (16) (17) Равенство в (11) следует из линейности ядер переходной вероятности. Переход к (13) является применением неравенства треугольника. При переходе к (14) используется тот факт, что оба и неотрицательны: это следует из предложения 1, которое гарантирует, что мера имеет по крайней мере массу в состоянии покоя и, следовательно, для любой (неотрицательной) меры ( 18) Наконец, отметим, что (15) использует общее свойство ядер переходной вероятности, которое обеспечивает это для любой неотрицательной меры.
Обратите внимание, что приведенная выше лемма о сжатии, которая выполняется для нейронных сетей с пиками, имеет некоторое сходство с леммой 1 из [105], в которой анализировались искусственные аналоговые нейронные сети в дискретном времени.
Доказательство теоремы 1 для фиксированной скорости ввода.
Мы разделили точную формулировку теоремы 1 на две леммы: Лемма 2 является точной формулировкой для случая, когда входы фиксированы (например, фиксированные входные ставки). Лемма 3 в следующем разделе соответствует случаю, когда скорость ввода контролируется марковским процессом.Точные предположения о сетевой модели, необходимые для обеих лемм, описаны выше (см. «Объем теоретических результатов»).
Здесь мы предполагаем, что вектор входных данных, подаваемых в сеть, остается фиксированным во время испытания. Конкретно, это, например, случай, если есть набор входных нейронов с фиксированной скоростью. В данном случае — это вектор входных скоростей, который остается постоянным во времени. В этом случае входные нейроны формально считаются частью сети. В качестве альтернативы, константа может соответствовать постоянным токам, которые вводятся в подмножество нейронов.
При постоянных входных условиях, динамика процесса однородна по времени: ядра вероятности перехода инвариантны к временным сдвигам, т.е. (19)
Лемма 2 Пусть . Тогда марковский процесс имеет уникальное стационарное распределение , к которому он сходится экспоненциально быстро, (20) от любого начального марковского состояния .
Доказательство: явно невзрывоопасно, апериодично и стохастически непрерывно (см.[18]). Таким образом, для доказательства экспоненциальной эргодичности достаточно показать, что некоторая скелетная цепь геометрически эргодична (см., Например, теорему 18.1 в [106]). Каркасная цепочка с ядром вероятности перехода апериодична и неприводима и, следовательно, имеет уникальное стационарное распределение. Затем, рекурсивно применяя лемму 1 с, (21) (22) доказывая геометрическую эргодичность скелетной цепи и, следовательно, экспоненциальную эргодичность. Количественная граница сходимости следует из (22) путем выбора синглтона в качестве начального распределения и использования общего факта, что для любого ядра вероятности перехода и распределений и, (23), таким образом, гарантируется, что полное расстояние вариации не (временно) не увеличивается между и .
Лемма 2 дает общий результат об эргодичности для рассматриваемого класса стохастических пиковых сетей при наличии фиксированных входных скоростей. Доказательство опирается на два ключевых свойства стохастических сетей с пиками: апериодичность и неприводимость. Эти свойства можно интуитивно понять в контексте рисунка 1H. Если, например, внутренняя динамика сети не была апериодической, то можно было бы наблюдать колебания частот паттернов с течением времени (как на рисунке 4C). Лемма 2 доказывает, что этого не может произойти в сетях со стохастическими пиками, пока скорость ввода фиксирована.Частоты колебательного паттерна действительно могут возникать только тогда, когда входные скорости сами периодически меняются (см. Теорему 2 и рисунок 4). С другой стороны, если динамика сети не была неснижаемой, то есть если были состояния сети, которые недостижимы из некоторых других состояний сети, то потенциально можно было бы наблюдать, как частоты паттернов сходятся к разным фиксированным точкам для разных начальных состояний (например, две линии в Рисунок 1H, устанавливающийся при различных значениях). Этого не может произойти в сетях стохастических пиков из-за предложения 1, которое гарантирует, что пространство состояний связано через состояние покоя.
Отметим, что, хотя апериодичность и неприводимость являются хорошо известными необходимыми и достаточными условиями эргодичности марковских цепей с дискретным временем на пространствах конечных состояний, их недостаточно для экспоненциальной эргодичности марковских процессов с непрерывным временем на пространствах общего состояния (точные сведения см. В [107]). определения -неприводимости и апериодичности таких процессов). Дополнительные условия в этом более сложном случае, обеспечивающие экспоненциальную эргодичность, такие как невзрывоопасность, стохастическая непрерывность и геометрическая эргодичность скелетной цепи, также были учтены при доказательстве леммы 2 (т.е. сети стохастических пиков также соответствуют этим дополнительным критериям).
Лемма 2 представляет собой доказательство теоремы 1 для фиксированной скорости ввода. В основном тексте мы называем стационарное распределение схемы при фиксированном входе как. Приведенное выше доказательство гарантирует стационарное распределение как для марковских, так и для простых состояний. В основном тексте относится к простому состоянию сети, если не указано иное.
Доказательство теоремы 1 для скорости ввода, управляемой марковским процессом.
Допущения о фиксированном вводе часто могут выполняться для внешнего ввода, управляя стохастическими вычислениями в нейронной системе, только приблизительно.Во входных данных могут присутствовать стохастические флуктуации в различных пространственных и временных масштабах. Кроме того, входные данные могут иметь свою собственную краткосрочную стохастическую динамику: представьте, например, визуальную сцену из беспорядочно движущихся точек. Несмотря на наличие таких краткосрочных динамических характеристик на входе, во многих случаях все еще можно подозревать, что распределения состояний сети сходятся. В самом деле, ниже мы обобщаем результаты сходимости для случая констант на довольно большой класс стохастических (и стохастически изменяющихся) входных данных, которые порождаются равномерно эргодическим марковским процессом.Равномерная эргодичность определяется как экспоненциальная эргодичность (экспоненциально быстрая сходимость к единственному стационарному распределению) с константами сходимости, которые применяются равномерно ко всем начальным состояниям [107] (это верно, например, для констант сходимости в лемме 2).
Пусть будет однородным по времени входным марковским процессом в том смысле, что входная траектория, предоставленная сети, сама генерируется случайным образом из марковского процесса. Позвольте быть (измеримым) пространством состояний.Затем определите совместный вход / сетевой марковский процесс в пространстве состояний, где обозначает -алгебру, порожденную. Дальнейшие определения для аналогичны введенным для.
Лемма 3 Если входной процесс равномерно эргодичен, то совместный марковский процесс , имеет уникальное стационарное распределение , в совместном пространстве состояний входа / сети, сходимость к которому происходит экспоненциально быстро, т. Е. Существуют константы , так что (24) для любого начального состояния совместного марковского процесса .
Доказательство: Если бы и были полностью независимыми процессами (если не влияли), то совместный процесс автоматически был бы экспоненциально эргодичным, если бы оба и были. Хотя в данном случае не является независимым, применяется более слабая версия независимости: вероятность возврата в состояние покоя во время составляет не менее независимо от входной траектории в течение этого времени. Это свойство можно использовать, чтобы показать, что распределение времени попадания в совместное состояние покоя имеет экспоненциальную границу.Отсюда следует, что совместный процесс экспоненциально эргодичен. Подробное доказательство приведено в следующем разделе.
Вторая часть теоремы 1 (экспоненциально быстрая сходимость для случая внешнего входа, порожденного эргодическим марковским процессом) следует из леммы 3. Отметим, что в основном тексте мы слегка злоупотребляем обозначениями для динамического случая, чтобы указать стационарное распределение по состояния сети, где обозначает конкретный марковский процесс, управляющий входами.
Подробное доказательство леммы 3.
Мы разбили доказательство леммы 3 на доказательства четырех вспомогательных утверждений (предложения 2–5). Рассмотрим следующие варианты предложения 1, которые справедливы для марковского процесса, описывающего совместную динамику входных состояний и состояний сети. Обозначим через конкретную входную последовательность, определенную для (реализации входного процесса), и начальное состояние Маркова сети (с) в момент времени. Тогда (25) (26)
Легко показать, что эти свойства вместе с тем фактом, что он равномерно эргодичен, обеспечивают его неприводимость и апериодичность.Следовательно, для доказательства ее экспоненциальной эргодичности достаточно показать, что некоторая скелетная цепь геометрически эргодична [107]. С этой целью мы рассмотрим скелетную цепочку и докажем геометрическую эргодичность, показав, что распределение времени попадания в небольшой набор в совместном пространстве состояний входных и сетевых состояний допускает экспоненциальную границу.
Время срабатывания для некоторого набора во входном пространстве состояний определяется как (27) Для удобства обозначений мы сокращаем ниже.Из-за равномерной эргодичности (что подразумевает рекуррентность Харриса [107]) существует некоторое множество, для которого время попадания конечно () из любого начального состояния с вероятностью единица [108]. Кроме того, согласно [107] существует небольшой набор , и константы и, такие, что (28) Это означает, что существует небольшой набор во входном пространстве состояний, который может быть достигнут не только за конечное время из любого начального входного состояния. , но для которого распределение времени попадания в также имеет конечное среднее значение и дисперсию (и конечные моменты высшего порядка).По крайней мере одна пара констант и, которая удовлетворяет (28), гарантированно существует, но на самом деле следующее предложение показывает, что можно указать конкретную желаемую границу в правой части (по причинам, которые станут ясны позже), и найти соответствие слева.
Предложение 2 Существует , такое что (29)
Проба: Определить. Позвольте и быть любой допустимой парой констант, которая удовлетворяет (28). Тривиальный случай есть.В оставшейся части доказательства предполагается, что он «слишком велик», так что. По определению экспоненты для любого, (30) (31) По теореме Тонелли, поскольку все слагаемые неотрицательны, порядок двойной суммы можно поменять местами: (32) (33) Обратите внимание, что это моменты распространение . По равномерной эргодичности, все моменты должны существовать, а кроме того существует такой, что. Несложно увидеть, что тогда ряд сходится для всех, что является непрерывным на. Наконец, поскольку и, по теореме о промежуточном значении существует такое, что.
Обозначьте временем, когда скелетная цепь посещает малый набор в -й раз: (34) Кроме того, обозначьте временем между -м и -м посещением: (35) (36)
Согласно этому определению, можно выразить время достижения степени как. Следующее предложение расширяет экспоненциальную границу времени первого попадания до времени попадания более высоких степеней.
Предложение 3 Существует , такое что, (37)
Проба: (38) (39) (40)
Позвольте быть время попадания в малый набор на совместном пространстве состояний входных и сетевых состояний, (41)
Кроме того, пусть будет количество посещений небольшой группы до времени включительно, (42)
Предложение 4 Для любой входной траектории и любого начального состояния сети , (43)
Это следует из (25) и (26), которые гарантируют, что всякий раз, когда входной процесс посещает небольшой набор, также существует небольшая вероятность того, что сеть находится в состоянии покоя.
Утверждение 5 Существует и константа , такие что, (44)
Проба: Лет. Выберите те, которые удовлетворяют предложению 3. (45) (46) (47) (48) (49) (50) (51)
По предложению 5 экспоненциально эргодично [107]. Это завершает доказательство леммы 3.
Доказательство теоремы 2
Если входная последовательность периодична с периодом, то есть для всех, то марковский процесс будет периодическим по времени в том смысле, что ядра перехода инвариантны к сдвигам, кратным периоду: (52)
Отсюда следует следующий результат, который является более точной версией теоремы 2:
Лемма 4 При периодическом вводе, т.е.е. для всех с некоторыми , периодический по времени марковский процесс с периодом имеет периодически стационарное распределение , сходимость к которому происходит экспоненциально быстро из любого начального состояния. В частности, для каждых существует уникальное стационарное распределение , такое что (53) из любого начального марковского состояния .
Доказательство: Для каждого существует скелетная цепочка с ядром вероятности перехода, которое является однородным по времени, неприводимым и апериодическим и, таким образом, имеет уникальное стационарное распределение.Применение, которое соответствует полному периоду, уменьшает общее расстояние вариации как минимум на: (54) (55) (56) Первое неравенство следует из того факта, что применение оставшегося может только дополнительно уменьшить общее расстояние вариации между два распределения согласно (23). Второе неравенство связано с леммой 1.
Тогда лемма 4 следует из рекурсивного применения (54) — (56) для нескольких периодов и выбора одноэлементного распределения в качестве начального распределения.
В основном тексте мы используем обозначение для фазового стационарного распределения, где обозначает конкретную периодическую входную последовательность.
Оценка необходимого времени вычислений
Одномерный и многомерный анализ Гельмана-Рубина.
Различные методы были разработаны для измерения скорости сходимости к стационарному распределению в контексте выборки методом Монте-Карло цепи Маркова [56], [119], [120]. Диагностика Гельмана-Рубина, которую мы использовали в этой статье, является одним из наиболее широко используемых методов [55], [57], [58], [119], помимо других популярных методов, таких как диагностика Рафтери и Льюиса [121]. ] и Гевеке [122].Заметим, что в литературе существует единое мнение о том, что ни один метод в целом не идеален. Некоторыми привлекательными свойствами метода Гельмана Рубина являются общая применимость к любой системе MCMC (некоторые другие методы работают только, например, в контексте выборки Гиббса), простота использования, простота реализации, вычислительная эффективность и тот факт, что результаты количественная (в отличие от графической диагностики) [56], [119].
Диагностика сходимости Гельмана-Рубина [55] берет в качестве входных выборок из разных прогонов (испытаний / цепочек / последовательностей), произведенных одной и той же системой, запущенных из разных начальных состояний.Первоначально метод был разработан для систем с дискретным временем в контексте дискретизации цепи Маркова Монте-Карло. В наших симуляциях используется временной шаг, поэтому мы просто рассматриваем каждый шаг симуляции как один дискретный временной шаг в цепи Маркова. Метод Гельмана-Рубина дает на выходе потенциальный коэффициент уменьшения масштаба как функцию времени. Коэффициент уменьшения масштаба является индикатором того, сходимся ли система во времени или нет. Высокие значения указывают на то, что до сходимости требуется больше времени, в то время как близкие значения предполагают, что схождение (почти) произошло.
Для вычисления коэффициента масштабного уменьшения во времени учитываются выборки из периода из каждого прогона сети. В одномерном случае фокусируется на конкретной единственной переменной (такой как крайнее простое состояние одиночного нейрона или простое состояние нейрона со «случайным считыванием», как показано сплошными линиями на Рисунке 2G). Позвольте быть количеством выборок, полученных за период от каждого из симуляций. Затем определяется (62), где и находятся между и внутри последовательности дисперсий, соответственно, которые могут быть вычислены, как описано в [55], на основе выборок, взятых за период времени.В редком случае, например, если нейрон никогда не срабатывает и, следовательно, его состояние постоянно во всех прогонах, мы устанавливаем 1.
К сожалению, источником путаницы является тот факт, что Гельман и Рубин [55] первоначально ввели в его «дисперсионную» форму, эквивалентную уравнению (62), но позже в [57], [60] изменили это определение и определили как квадратный корень из (62). Этот вопрос особенно важен при рассмотрении пороговых значений для: пороговое значение было предложено в контексте исходного определения [59].Позже был предложен типичный порог, но этот нижний порог применялся к модифицированному определению [57], [60]. Возведение этого явно более низкого порога в квадрат снова дает типичный порог приблизительно.
В многомерном случае (например, при анализе сходимости векторнозначного простого состояния небольшого подмножества нейронов, как показано пунктирными линиями на рисунке 2G) берется векторнозначная (-мерная) выборка и вычисляется многомерное уменьшение потенциального масштаба. коэффициент согласно: (63) где — наибольшее собственное значение, и и обозначают внутри и между оценками матрицы ковариации последовательностей (подробности см. в [123]).
Анализ сходимости моделей кортикальных микросхем.
Значения Гельмана-Рубина были рассчитаны на основе прогонов, где продолжительность каждого прогона была биологическим временем. Мы также пробовали более длительные симуляции, но не заметили никаких признаков неконвергентного поведения. Случайное начальное состояние устанавливалось в каждом прогоне путем отображения случайных входных данных перед началом фактического моделирования. Этот начальный случайный ввод подавался в сеть через два обычных входных потока (по 40 нейронов в каждом), путем присвоения каждому входному нейрону случайной скорости, равномерно взятой из диапазона.Анализ сходимости маргиналов был выполнен путем применения одномерного анализа к отдельным компонентам простого состояния с. Из индивидуальных значений предельной сходимости были получены среднее и худшее предельное сходимость (как на рис. 2E, F) путем взятия во времени среднего / максимального значения по всем индивидуальным значениям в данный момент. Для парных совпадений спайков (см. Рис. 2D) мы проанализировали образцы продукта простых состояний двух нейронов (произведение равно только в том случае, если оба нейрона имели спайк в пределах последнего).
Случайное считывание для рисунка 2G было реализовано путем добавления в сеть дополнительного возбуждающего нейрона-наблюдателя, который получает синаптические входы от случайного подмножества из 500 сетевых нейронов (мы сохранили это число 500 фиксированным для моделирования с разными размерами сети, чтобы обеспечить справедливое сравнение).Количество случайно выбранных нейронов из каждого пула приведено в таблице 1.
Синапсы на считывающий нейрон создавались аналогично соединениям в модели кортикального столба: параметры краткосрочной пластичности устанавливались в зависимости от типа соединения (EE или IE) согласно [30]. Веса для соединений EE и IE были случайно выбраны из гамма-распределения со средним и масштабным параметром, а также средним и масштабным параметром, соответственно. Затем вычислялась сходимость отсчетов по Гельману-Рубину, как для предельного случая.
Анализ сходимости векторных простых состояний подмножеств нейронов (см. Рис. 2G) был выполнен путем применения многомерного анализа к случайно выбранным подсетям коркового столбца. В частности, мы случайным образом отобрали по 5 нейронов из каждого из 6 пулов, получив подсеть из 30 нейронов, и рассчитали.
Решение проблем удовлетворения ограничений в сетях импульсных нейронов
Формулировка судоку как проблемы удовлетворения ограничений.
Задача удовлетворения ограничений состоит из набора переменных, определенных в некоторой области, и набора ограничений, которые ограничивают пространство допустимых присвоений переменных.Решение проблемы состоит из присвоения каждой переменной таким образом, чтобы были соблюдены все ограничения. Чтобы сформулировать судоку как проблему удовлетворения ограничений, мы определяем для каждого из 81 поля (из стандартной сетки 9 × 9), которое должно быть заполнено цифрой от 1 до 9, набор из 9 двоичных переменных (принимающих значения в ) [124]. Каждая из этих двоичных переменных голосует ровно за одну цифру в поле. Правила игры Судоку накладывают ограничения на группы этих переменных, которые можно разделить на следующие три типа.
Заданные ограничения числа: Заданные числа головоломки фиксированы. Следовательно, двоичные переменные для данных полей ограничены фиксированными значениями, например, данное значение соответствует фиксированным двоичным значениям.
Уникальные ограничения поля: В правильном решении должна быть активна только одна цифра в каждом поле. Следовательно, в каждом поле должна быть ровно одна из 9 связанных двоичных переменных, а все остальные должны быть (эквивалентно заявлению, что сумма по этим двоичным переменным должна быть равна 1).
Уникальные ограничения группы: Есть три типа групп: строки, столбцы и подсетки 3 × 3. Есть 9 групп строк, 9 групп столбцов и 9 групп подсеток. В любой из этих групп каждая цифра должна появляться только один раз. Следовательно, в каждой группе все двоичные переменные, голосующие за одну и ту же цифру, должны суммироваться до.
Сетевая архитектура для решения судоку.
Судоку можно реализовать в нейронной сети с пиковыми сигналами, создав для каждой из 9 двоичных переменных в каждом поле судоку локальную группу пирамидных ячеек.Каждый раз, когда срабатывает одна из этих пирамидальных ячеек, соответствующая двоичная переменная устанавливается на короткий период времени. Бинарная переменная определяется только в том случае, если ни один нейрон в связанной с ней группе не сработал в последней. Это отображение позволяет считывать текущее (предварительное) решение, представленное сетью, в любое время. Предварительное решение является правильным только при соблюдении всех ограничений. Для всех моделей, которые мы использовали, в результате получилась общая пирамидальная ячейка. Ограничения среди переменных судоку могут быть реализованы посредством дисинаптического ингибирования между группами пирамидных клеток, как подробно описано ниже.
Заданные числовые ограничения реализуются путем предоставления сильных положительных входных токов выборочно тем нейронам, которые кодируют данные числа, и отрицательных токов к нейронам, кодирующим неправильные цифры в данном поле. Ограничения уникального поля реализуются путем формирования схемы «победитель получает все» (WTA) среди всех нейронов, связанных с одним и тем же полем судоку. Цепь WTA моделируется одним тормозящим нейроном, который взаимно связан со всеми пирамидными клетками.Чтобы уменьшить вероятность того, что никакая пирамидальная ячейка не сработает (что нарушит уникальное ограничение поля), пороговые значения пирамидальных ячеек устанавливаются на низкие значения (подробности см. В следующем разделе). Ограничения уникальной группы реализуются схемой WTA, в которой участвуют все нейроны в группе, имеющей код для одной и той же цифры. Таким образом, существует 81 уникальное ограничение поля и уникальное групповое ограничение (в каждой группе есть ограничение для каждой цифры), что дает общее количество цепей WTA.Эти схемы WTA частично перекрываются в том смысле, что каждая пирамидальная ячейка участвует в 4 из этих схем WTA (одна для ограничения уникального значения в своем поле и три для ограничений уникальной группы в своей строке / столбце / подсетке).
Генерация стохастических всплесков как в возбуждающих, так и в тормозных нейронах реализована в соответствии с теоретической моделью шума I (подробности см. В следующем разделе). Таким образом, сеть удовлетворяет всем теоретическим условиям теоремы 1 и гарантирует уникальное стационарное распределение состояний сети, к которому она сходится экспоненциально быстро.Этот ландшафт будет автоматически иметь пики в тех состояниях сети, которые удовлетворяют большинству ограничений игры, поскольку каждая из цепей WTA гарантирует, что недопустимые конфигурации в отношении этого ограничения маловероятны. Любая конкретная задача судоку может быть решена путем предоставления входных данных в сеть в виде сильных токов к тем нейронам, которые соответствуют заданным значениям. Это автоматически изменяет ландшафт стационарного распределения таким образом, что генерируются только (или преимущественно) решения, согласующиеся с данными.Наконец, из-за нейронного шума сеть может быстро исследовать различные пики ландшафта (разные многообещающие варианты решения) и одинаково быстро преодолевать их. Важно отметить, что этот процесс может происходить одновременно в разных местах головоломки судоку. Следовательно, можно интерпретировать динамику сети также как высокопараллельный алгоритм стохастического поиска.
Детали реализации и моделирование для рисунка 5.
Моделирование для рисунка 5 было выполнено в NEVESIM, симуляторе на основе событий для сетей пиковых нейронов, разработанном на C ++ с интерфейсом Python [125].Головоломка на рис. 5A была создана и оценена «сложно» в компании «Sudoku Solutions» [126]. Генерация спайков моделируется согласно уравнению (60) с параметрами,. Стохастический порог был установлен для возбуждающих и тормозных нейронов, соответственно. Для пирамидных клеток выбран абсолютный рефрактерный период. Чтобы максимально ускорить моделирование на основе событий, PSP моделировались упрощенным способом как прямоугольные импульсы длины на основе тока (в отличие от более сложной интеграции синаптических входов на основе проводимости, используемой для моделей кортикальных микросхем).
контуров WTA были сформированы путем реципрокного соединения одного ингибирующего нейрона со всеми участвующими пирамидными клетками. Одиночный тормозящий нейрон был смоделирован таким образом, чтобы имитировать реакцию популяции тормозящих нейронов (т. Е. Сильное торможение в течение длительного периода времени), с использованием абсолютного рефрактерного периода и сильных двунаправленных связей от и к возбуждающим нейронам (синаптические веса и, соответственно, ).
Чтобы задать конкретную головоломку, данные числа были зафиксированы путем подачи сильных входных токов в соответствующие пирамидальные ячейки.В частности, нейроны, кодирующие данные числа в поле судоку, получали постоянный положительный входной ток (постоянный вход на мембранный потенциал). Нейроны, кодирующие конфликтующие цифры в данных полях судоку, получали постоянный отрицательный входной ток силы.
Последнее практическое замечание касается количества нейронов, кодирующих каждую двоичную переменную,. Мы обнаружили, что сети с имеют ряд привлекательных свойств по сравнению с сетями с кодированием одного нейрона. В частности, частота возбуждения отдельных нейронов может быть ниже (пирамидная клетка должна постоянно взрываться, чтобы указывать на устойчивое активное состояние).Кроме того, синаптическая эффективность нейронов может быть ослаблена, и общие паттерны спайк-ответа кажутся более биологически правдоподобными. Принимая во внимание потенциальную реализацию в аналоговом нейроморфном оборудовании, присвоения переменных с популяционным кодированием также менее подвержены сбоям отдельных единиц или несоответствию устройств.
Функциональная микросхема для зрительной коры головного мозга кошки
1. Мы изучили in vivo внутриклеточные реакции нейронов зрительной коры головного мозга кошек на электрическую импульсную стимуляцию корковых афферентов и разработали микросхему, которая имитирует большую часть экспериментальных данных.2. Торможение и возбуждение — неотделимые события, потому что отдельные нейроны встроены в микросхемы, которые вносят значительный вклад в популяцию. Синхронная электрическая активация коры неизбежно приводит в движение последовательность возбуждения и торможения в каждом зарегистрированном нами нейроне. Временная форма этого ответа зависит от коркового слоя, в котором расположен нейрон. Поверхностный слой (слои 2 + 3) пирамидных нейронов демонстрирует более выраженную полисинаптическую фазу возбуждения, чем пирамиды глубоких слоев (слои 5 + 6).3. Возбуждающие эффекты на пирамидные нейроны, особенно пирамиды поверхностного слоя, в основном возникают не из-за моносинаптического входа от таламуса, а из-за полисинаптического входа из кортикальных пирамид. Поскольку таламический вход является временным, он не обеспечивает основного устойчивого возбуждения, поступающего ни в один корковый нейрон. Вместо этого внутрикортикальные возбуждающие связи обеспечивают основной компонент возбуждения. 4. Полисинаптический возбуждающий ответ сохранялся бы и после стимула, если бы не подавляющий эффект внутрикортикального торможения, вызванный импульсной стимуляцией.5. Внутриклеточная регистрация в сочетании с ионофорезом агонистов и антагонистов гамма-аминомасляной кислоты (ГАМК) показала, что внутрикортикальное ингибирование опосредуется рецепторами ГАМК и ГАМК. Компонент GABAA возникает в ранней фазе импульсной реакции. Это отражается в сильной гиперполяризации, которая следует за возбуждающей реакцией и длится около 50 мс. Компонент GABAB возникает в поздней фазе ответа и отражается в устойчивой гиперполяризации, которая длится примерно 200–300 мс.Оба компонента присутствуют во всех пирамидных нейронах коры. Однако компонент GABAA оказывается более мощным в пирамидах глубокого слоя, чем пирамидных слоях поверхностного слоя. 6. Микросхема с хорошей точностью моделирует вышеупомянутые данные экспериментов in vivo и обеспечивает новую эксплантацию для очевидного отсутствия значительного ингибирования во время визуальной стимуляции. Базовая схема может быть общей для всех исследуемых областей коры и, таким образом, микросхема может быть «канонической» микросхемой для неокортекса.
Канонические микросхемы для прогнозирующего кодирования
В этом разделе рассматриваются ламинарно-специфические соединения, лежащие в основе понятия канонической микросхемы (Douglas et al., 1989; Douglas and Martin, 1991, 2004). Сначала мы сосредоточимся на зрительной коре головного мозга млекопитающих, а затем рассмотрим, можно ли обобщить визуальную микросхему до канонической схемы для всей коры. Как функциональные, так и анатомические методы были применены для изучения внутренних (внутрикортикальных) и внешних связей.Мы подчеркнем выводы недавних исследований, в которых сочетаются оба метода.
Внутренние связи и каноническая микросхема
Основополагающая работа Дугласа и Мартина (1991), посвященная зрительной системе кошки, позволила создать модель того, как информация течет через корковый столбец. Дуглас и Мартин записали внутриклеточные потенциалы клеток первичной зрительной коры во время электростимуляции ее таламических афферентов. Они отметили стереотипный паттерн быстрого возбуждения, за которым следует более медленное и продолжительное торможение.Латентность последующей гиперполяризации позволила выделить ответы в надгранулярном и инфрагранулярном слоях. Используя модели на основе проводимости, они показали, что простая модель может воспроизвести эти реакции. Их модель содержала поверхностные и глубокие пирамидные клетки с общим пулом тормозных клеток. Все три популяции нейронов получили таламический драйв и были полностью взаимосвязаны. Глубокие пирамидные клетки получали относительно слабое таламическое движение, но сильное торможение (). Эти взаимосвязи позволили схеме усилить временные таламические входы для создания устойчивой активности в коре, сохраняя при этом баланс между возбуждением и торможением, две задачи, которые должны быть решены любой корковой цепью.Их схема, хотя и основана на записях зрительной коры головного мозга кошки, также была предложена в качестве основной темы, которая могла бы присутствовать и воспроизводиться, с небольшими вариациями, по всему кортикальному листу (Douglas et al., 1989).
Это схема классической микросхемы, адаптированная из работы Дугласа и Мартина (1991). Эта минимальная схема включает поверхностные (слои 2 и 3) и глубокие (слои 5 и 6) пирамидные клетки и популяцию гладких тормозных клеток. Входящие сигналы с прямой связью — от таламуса — нацелены на все клеточные популяции, но с акцентом на тормозящие интернейроны, а также на поверхностные и гранулярные слои.Обратите внимание на симметричное развертывание внутренних тормозящих и возбуждающих связей, которые поддерживают баланс возбуждения и торможения.
Последующие исследования использовали внутриклеточные записи и гистологию для измерения спайков (и деполяризации) в пре- и постсинаптических клетках, чья клеточная морфология может быть определена. Этот подход позволяет количественно оценить как вероятность соединения, определяемую как количество наблюдаемых соединений, деленное на общее количество записанных пар, так и силу соединения, определяемую в терминах постсинаптических ответов.Томсон и др. (2002) использовали эти методы для изучения слоев 2–5 (от L2 до L5) зрительных систем кошек и крыс. Наиболее часто соединяющиеся клетки были расположены в одном кортикальном слое, где самые большие межслойные выступы были «прямыми» связями от L4 к L3 и от L3 к L5. Возбуждающие реципрокные связи «обратной связи» не наблюдались (от L3 до L4) или наблюдались реже (от L5 до L3), что позволяет предположить, что возбуждение распространяется внутри столбца с прямой связью. Связи обратной связи обычно наблюдаются, когда пирамидные клетки в одном слое нацелены на ингибирующие клетки в другом (см. Обзор Thomson and Bannister, 2003).
В то время как многие исследования были сосредоточены на возбуждающих связях, некоторые исследовали тормозные связи. Их труднее изучать, потому что тормозные клетки менее распространены, чем возбуждающие, и потому что существует по крайней мере семь различных морфологических классов (Salin and Bullier, 1995). Однако недавние достижения в оптогенетике сделали возможным более легкое нацеливание на ингибирующие клетки: Kätzel и его коллеги объединили оптогенетику и регистрацию целых клеток, чтобы исследовать внутреннюю связность тормозных клеток в областях коры головного мозга мышей M1, S1 и V1 (Kätzel et al., 2010). Они трансгенно экспрессировали каналродопсин в тормозных нейронах и активировали их при записи из пирамидных клеток. Это позволило им оценить эффект торможения как функцию ламинарного положения относительно зарегистрированного нейрона.
Из этого подхода можно сделать несколько выводов (Kätzel et al., 2010): во-первых, L4 ингибирующие связи более ограничены в их латеральной протяженности по сравнению с другими слоями. Это подтверждает мнение о том, что в ответах L4 преобладают таламические входы, тогда как остальные пластинки интегрируют афференты от более широкого кортикального пятна.Во-вторых, первичный источник ингибирования исходит из клеток в том же слое, что отражает преобладание ингибирующих интраламинарных связей. В-третьих, несколько интерламинарных мотивов оказались общими — по крайней мере, в зернистой коре: главным образом, сильная тормозящая связь от L4 к супрагранулярному L2 / 3 и от инфрагранулярных слоев к L4. Для получения дополнительной информации о специфичности ингибирующих соединений клеточного типа см. Yoshimura and Callaway, (2005). дает сводку ключевых возбуждающих и тормозных интраламинарных связей.
Это упрощенная схема ключевых внутренних связей между возбуждающими (E) и тормозными (I) популяциями в гранулярном (L4), надгранулярном (L1 / 2/3) и инфрагранулярном (L5 / 6) слоях. Возбуждающие межслойные связи в основном основаны на Гилберте и Визеле (1983). Прямые связи обозначают прямые внешние кортикокортикальные или таламокортикальные афференты, которые реципрокны обратными или обратными связями. Анатомические и функциональные данные предполагают, что афферентный вход поступает в первую очередь в L4 и передается в поверхностные слои L2 / 3, богатые пирамидными клетками, которые выступают вперед в следующую корковую область, образуя дисинаптический путь между таламусом и вторичными кортикальными областями (Callaway, 1998).Информация из L2 / 3 затем отправляется в L5 и L6, которые отправляют (внутренние) проекции обратной связи обратно в L4 (Usrey and Fitzpatrick, 1996). Клетки L5 образуют обратную связь с более ранними областями коры, а также с легковыми, верхними бугорками и стволом головного мозга. Таким образом, прямой ввод разделяется внутренними связями на поверхностный прямой поток и глубокий обратный поток. На этой схеме мы сопоставили плотно взаимосвязанные возбуждающие и тормозящие популяции внутри каждого слоя.
Микросхемы в сенсомоторной коре
Распространяются ли особенности зрительных микросхем на другие области коры? Недавно в двух исследованиях была выявлена внутренняя взаимосвязь сенсорной и моторной коры мышей: Лефорт и его коллеги (2009) использовали множественные записи целых клеток в коре ствола мышей, чтобы определить вероятность моносинаптических связей и соответствующую силу связи. Как и в зрительной коре, самые сильные связи были интраламинарными, а самые сильные межслойные связи — восходящими L4 к L2 и нисходящими L3 к L5.
Одна загадка канонических микросхем состоит в том, имеет ли моторная кора локальная схема, качественно похожая на сенсорную кору. Этот вопрос важен, потому что моторная кора не имеет четко определенного гранулярного L4 (свойство, за которое она получила название «агранулярная кора»). Weiler и его коллеги объединили записи целых клеток в моторной коре мышей с фотостимуляцией для извлечения глутамата из клетки (Weiler et al., 2008). Это позволило им систематически стимулировать кортикальный столбец в сетке с центром на пирамидном нейроне, с которого они регистрировались.Путем записи с пирамидных нейронов в L2-6 (L1 лишен пирамидных клеток) авторы картировали возбуждающее влияние, которое каждый слой оказывает на другие. Они обнаружили, что соединение L2 / 3 с L5A / B было самым сильным — на него приходилось треть общего синаптического тока в цепи. Вторым по силе межслойным соединением было взаимное соединение L5A с L2 / 3. Этот путь может быть гомологичен известному пути от L4 / 5A к L2 / 3 в сенсорной коре. Также, как и в сенсорной коре, были заметны рекуррентные (интраламинарные) связи, особенно в L2, L5A / B и L6.Наибольшая часть синаптического входа поступает в L5A / B, что соответствует его ключевой роли в накоплении информации от широкого диапазона афферентов — перед отправкой его выхода в кортикоспинальный тракт. Таким образом, сильная связь от входного слоя к поверхностной и от поверхностной к глубокой, вместе с сильной интраламинарной связностью, предполагает, что внутренняя схема моторной коры похожа на другие области коры.
Анатомия и физиология внешних связей
Ясно, что учет микросхем должен относиться к слоям происхождения внешних связей и их ламинарным мишеням.Хотя большинство пресинаптических входов возникает из внутренних связей, области коры также сильно взаимосвязаны, где баланс между внутренней и внешней обработкой опосредует функциональную интеграцию между специализированными областями коры (Engel et al., 2010). Только по цифрам внутренние связи, по-видимому, преобладают — 95% всех нейронов, помеченных ретроградным индикатором, находятся в пределах примерно 2 мм от места инъекции (Markov et al., 2011). Остальные 5% представляют собой клетки, дающие начало внешним связям, которые, хотя и немногочисленны, могут быть чрезвычайно эффективными в управлении своими целями.Речь идет о связи LGN с V1: хотя это только шестая по силе связь с V1, афференты LGN оказывают существенное влияние на ответы V1 (Markov et al., 2011).
Иерархии и функциональные асимметрии
Современная догма утверждает, что кора головного мозга иерархически организована. Идея корковой иерархии опирается на различие между тремя типами внешних связей: прямые связи, которые связывают более раннюю область с более высокой областью, связи обратной связи, которые связывают более высокую область с более ранней областью, и боковые связи, которые связывают области на более высоком уровне. на том же уровне (см. обзор Felleman and Van Essen, 1991).Эти связи различаются по своему ламинарному происхождению и целям. Прямые связи происходят в основном из поверхностных пирамидных клеток и мишеней L4, тогда как обратные связи происходят в основном из глубоких пирамидных клеток и заканчиваются вне L4 (Felleman and van Essen 1991). Ясно, что это описание корковых иерархий является упрощением и может иметь множество нюансов: например, по мере увеличения иерархического расстояния между двумя областями процент клеток, отправляющих прямую связь (соотв.обратная связь) проекции с более низкого (соответственно более высокого) уровня становятся все более смещенными в сторону поверхностных (соответственно глубоких) слоев (Barone et al., 2000; Vezoli, 2004).
Помимо ламинарной специфичности их происхождения и мишеней, прямые и обратные связи также различаются по своей синаптической физиологии. Традиционная точка зрения утверждает, что прямые связи являются сильными и движущими, способными вызывать пиковую активность у их целей и придавать классические свойства рецептивного поля — прототипическим примером является синаптическая связь между LGN и V1 (Sherman and Guillery, 1998).Считается, что соединения обратной связи модулируют (внеклассические) характеристики рецептивного поля в соответствии с текущим контекстом; например, визуальная окклюзия, внимание, заметность, и т. д. Прототипным примером обратной связи является соединение кортикального слоя L6 с LGN. Шерман и Гиллери определили несколько свойств, которые отличают драйверы от модуляторов . Управляющие связи имеют тенденцию проявлять сильный ионотропный компонент в их синаптическом ответе, вызывать большие ВПСП и отвечать на несколько ВПСП угнетающими синаптическими эффектами.Модуляторные связи при стимуляции вызывают метаботропные и ионотропные реакции, вызывают слабые ВПСП и демонстрируют облегчение парных импульсов (Sherman and Guillery, 1998; 2011). Эти различия были основаны на входах в LGN, где входные данные сетчатки являются движущими, а входные сигналы коры являются модулирующими. До недавнего времени было доступно мало данных, чтобы оценить, применимо ли подобное различие к кортико-кортикальным связям прямой связи и обратной связи. Однако недавние исследования показывают, что корковые обратные связи выражают не только модуляторные, но и управляющие характеристики:
Являются ли обратные связи управляющими, модуляционными или и тем, и другим?
Хотя обычно считается, что обратные связи являются слабыми и модулирующими (Crick and Koch, 1998; Sherman and Guillery, 1998), недавние данные свидетельствуют о том, что обратные связи не только модулируют ответы более низкого уровня: Шерман и его коллеги зарегистрировали клетки в области мышей. V1 / V2 и A1 / A2, стимулируя афференты прямой или обратной связи.В обоих случаях наблюдались реакции, похожие на вождение, а также на модуляторные реакции (Covic and Sherman, 2011; De Pasquale and Sherman, 2011). Это указывает на то, что — для этих иерархически близких областей — обратные связи могут управлять своими целями так же сильно, как и прямые связи. Это согласуется с более ранними исследованиями, показывающими, что обратная связь может быть движущей силой: Миньяр и Малпели (1991) изучали обратную связь между областями 18 и 17, в то время как слой А LGN был фармакологически инактивирован.Это заставило замолчать клетки L4 в области 17, но сохранило активность в поверхностных слоях. Однако при поражении области 18 поверхностные клетки заглушались. Это согласуется с движущим эффектом обратной связи из области 18 при отсутствии коленчатого входа. Таким образом, обратная связь может опосредовать модулирующие и управляющие эффекты. Это важно с точки зрения прогнозирующего кодирования, потому что нисходящие прогнозы должны вызывать обязательные ответы в своих целях (ячейки, сообщающие об ошибках прогнозирования):
При кодировании с прогнозированием соединения с прямой связью передают ошибки прогнозирования, в то время как соединения обратной связи передают прогнозы от верхние области коры, чтобы подавить ошибки предсказания в нижних областях.Таким образом, в этой схеме соединения обратной связи должны иметь возможность оказывать сильное (управляющее) влияние на более ранние области для подавления или противодействия входным управляющим сигналам с прямой связью. Однако, как мы увидим позже, эти влияния также должны вызывать нелинейные или модулирующие эффекты. Это связано с тем, что предсказания сверху вниз обязательно зависят от контекста: например, перекрытие одного визуального объекта другим. Короче говоря, для прогнозирующего кодирования требуются обратные связи для управления клетками на более низких уровнях контекстно-зависимым образом, что требует модулирующего аспекта их постсинаптических эффектов.
Являются ли обратные связи возбуждающими или тормозящими?
Важно отметить, что поскольку обратные связи передают прогнозы — которые служат для объяснения и тем самым уменьшения ошибок прогнозирования на более низких уровнях — их эффективная (полисинаптическая) связность обычно считается тормозящей. Общий ингибирующий эффект обратных связей согласуется с исследованиями in vivo и . Например, электрофизиологические исследования негативности несоответствия показывают, что нейронные реакции на девиантные стимулы, которые нарушают сенсорные предсказания, установленные регулярной последовательностью стимулов, усиливаются по сравнению с предсказанными стимулами (Garrido et al., 2009). Сходным образом нарушение ожиданий слухового повторения вызывает усиление гамма-диапазона ответов в ранней слуховой коре (Todorovic et al., 2011). Считается, что эти усиленные ответы отражают неспособность высших областей коры головного мозга предсказывать и тем самым подавлять активность популяций, кодирующих ошибку предсказания (Garrido et al., 2007; Wacongne et al., 2011). Подавление предсказуемых ответов также можно рассматривать как подавление повторения, наблюдаемое в единичных записях из нижней височной коры макак (Desimone, 1996).Более того, нейроны нижневисочной коры обезьян значительно меньше реагируют на предсказанную последовательность естественных изображений по сравнению с непредсказуемой последовательностью (Meyer and Olson, 2011).
Ингибирующий эффект обратных связей дополнительно подтверждается исследованиями нейровизуализации (Murray et al., 2002; Murray, 2005; Harrison et al., 2007; Summerfield et al., 2008, 2011; Alink et al., 2010). Эти исследования показывают, что предсказуемые стимулы вызывают меньшую реакцию в ранних корковых областях. Важно отметить, что это подавление не может быть объяснено с точки зрения местной адаптации, потому что атрибуты стимулов, которые можно предсказать, не представлены в ранней сенсорной коре (например,г., Харрисон и др. 2007). Следует отметить, что подавление ответов на предсказуемые стимулы может сосуществовать с усилением внимания (сверху вниз) обработки сигналов (Wyart et al., 2012): при прогнозирующем кодировании внимание опосредуется увеличением прироста популяций, кодирующих ошибку прогнозирования. (Спратлинг, 2008; Фельдман, Фристон, 2010). Результирующая модуляция внимания (например, Hopfinger et al., 2000) может взаимодействовать с предсказаниями сверху вниз, чтобы преодолеть их подавляющее влияние — как показано эмпирически (Kok et al., 2011). См. Buschman and Miller (2007), Saalmann et al. (2007), Anderson et al. (2011) и Armstrong et al. (2012) для дальнейшего обсуждения нисходящих связей во внимании.
Дополнительные доказательства тормозящего (подавляющего) эффекта обратных связей получены из нейропсихологии: пациенты с повреждением префронтальной коры (ПФК) демонстрируют растормаживание связанных с событиями потенциальных ответов (ERP) на повторяющиеся стимулы (Knight et al., 1989; Yamaguchi). и Knight, 1990; но см. Barceló et al., 2000). Напротив, они демонстрируют ERP P300 с уменьшенной амплитудой в ответ на новые стимулы — как если бы произошла неспособность передать нисходящие предсказания сенсорной коре головного мозга (Knight, 1984). Более того, нормальные субъекты демонстрируют быструю адаптацию к девиантным стимулам, когда они становятся предсказуемыми — эффект, не наблюдаемый у префронтальных пациентов.
Несколько инвазивных исследований дополняют эти исследования на людях, предполагая общую ингибирующую роль обратных связей. В недавнем плодотворном исследовании Olsen et al.изучили кортикоталамическую обратную связь между L6 V1 и LGN, используя трансгенную экспрессию канала родопсина в L6 клетках V1. Управляя этими клетками оптогенетически — во время регистрации единиц в V1 и LGN — авторы показали, что глубокие основные клетки L6 ингибируют свои внешние мишени в LGN и свои внутренние мишени в корковых слоях 2-5 (Olsen et al., 2012). Это подавление было мощным — в LGN зрительные реакции подавлялись на 76%. Подавление также было высоким в V1, около 80-84% (Olsen et al., 2012). Эти данные согласуются с классическими исследованиями вклада кортикогенных веществ в настройку длины в LGN, показывающими, что корковая обратная связь способствует подавлению объемного звука кошачьих LGN: без обратной связи клетки LGN растормаживаются и демонстрируют более слабое объемное подавление (Murphy and Sillito, 1987). ; Sillito et al., 1993; но см. Alitto and Usrey, 2008).
В то время как эти исследования предоставляют убедительные доказательства того, что корковая обратная связь с LGN является ингибирующей, доказательства более сложны для кортикокортикальных обратных связей (Sandell and Schiller, 1982; Johnson and Burkhalter, 1996, 1997).Хюпе и его коллеги охлаждали область V5 / MT во время записи из областей V1, V2 и V3 у обезьяны. Когда зрительные стимулы предъявлялись в классическом рецептивном поле (CRF), охлаждение области V5 / MT снижало активность единиц в более ранних областях, предполагая возбуждающий эффект внешней обратной связи (Hupé et al., 1998). Однако, когда авторы использовали стимул, охватывающий внеклассическую радиочастоту, ответы нейронов V1 были — в среднем — усилены после охлаждения области V5, что согласуется с подавляющей ролью обратных связей.Эти результаты показывают, что тормозящие эффекты обратной связи могут зависеть от (естественных) стимулов, которые требуют интеграции в поле зрения. Подобные эффекты наблюдались, когда область V2 охлаждалась, и нейроны измерялись в V1: когда стимулы подавались только на CRF, охлаждение V2 уменьшало пиковую активность V1; однако, когда стимулы присутствовали в CRF и окружающей среде, охлаждение V2 увеличивало активность V1 (Bullier et al., 1996). Наконец, другие утверждали, что ингибирующий эффект обратной связи основан на времени и пространственной степени подавления окружающего звука в обезьяне V1, заключая, что эффекты подавления дальнего окружения, скорее всего, были опосредованы обратной связью (Bair et al., 2003).
Эмпирический вывод о том, что обратная связь может как облегчить, так и подавить возбуждение в нижних иерархических областях — в зависимости от содержания классических и внеклассических рецептивных полей — согласуется с прогнозирующим кодированием: Рао и Баллард (1999) обучили сеть иерархического прогнозирующего кодирования распознавать естественные образы. Они показали, что более высокие уровни иерархии учатся предсказывать визуальные особенности, которые распространяются на многие CRF на более низких уровнях (например, стволы деревьев или горизонты).Следовательно, более высокие визуальные области предсказывают, что визуальные стимулы будут охватывать рецептивные поля клеток в более низких визуальных областях. В этой настройке стимул, который ограничен CRF, вызовет сильный сигнал ошибки предсказания (потому что он не может быть предсказан). Это дает простое объяснение выводам Hupé et al (1998) и Bullier et al (1996): когда отключаются обратные связи, нет никаких нисходящих предсказаний для объяснения ответов в нижних областях, что приводит к растормаживанию ответов в нижних областях. более ранние области, когда — и только когда — стимулы можно предсказать по множеству CRF.
Обратные связи и уровень 1
Как может быть опосредован тормозящий эффект обратных связей? Установлено мнение, что внешние кортикокортикальные связи являются исключительно возбуждающими (с использованием глутамата в качестве возбуждающего нейромедиатора), хотя недавние данные свидетельствуют о том, что ингибирующие внешние связи существуют и могут играть важную роль в синхронизации удаленных регионов (Melzer et al., 2012). Однако один важный путь, с помощью которого обратные связи могут опосредовать избирательное ингибирование, — это их прекращение в L1 (Anderson and Martin, 2006; Shipp, 2007): слой 1 иногда называют бесклеточным из-за его бледного вида при окрашивании по Нисслю (классическое метод разделения слоев, выборочно маркирующий тела клеток).Действительно, недавнее исследование пришло к выводу, что L1 содержит менее 0,5% всех клеток в кортикальном столбе (Meyer et al., 2011). Эти клетки L1 почти все являются тормозящими и прочно связаны друг с другом посредством электрических соединений и химических синапсов (Chu et al., 2003). Одновременные записи патч-зажимов целых клеток показывают, что они обеспечивают сильное моносинаптическое ингибирование пирамидных клеток L2 / 3, чьи апикальные дендриты проецируются в L1 (Chu et al., 2003; Wozny and Williams, 2011). Это означает, что клетки, ингибирующие L1, находятся в лучшем положении, чтобы опосредовать ингибирующие эффекты внешней обратной связи.Ламинарное расположение, выделенное этими исследованиями — нижняя часть L1 и верхняя часть L2 / 3 — недавно было показано, как «горячая точка» ингибирования в колонке (Meyer et al., 2011). Действительно, исследование бочки коры головного мозга крысы, которая стимулировала (и инактивировала) L1, показало, что она оказывает мощный тормозящий эффект на ответы, вызванные усами (Shlosberg et al., 2006). Эти исследования показывают, что кортикокортикальные обратные связи могут оказывать сильное ингибирование, если они задействуют ингибирующий потенциал L1.
С точки зрения возбуждающего и модулирующего эффекта обратных связей, предсказательный ввод из более высоких областей коры может иметь важное влияние через дистальные дендриты пирамидных нейронов (Larkum et al., 2009). Более того, существует определенный тип ГАМКергических нейронов, которые, по-видимому, контролируют дистальную возбудимость дендритов, по-разному управляя возбуждающими сигналами сверху вниз во время поведения (Gentet et al., 2012). резюмирует исследования, которые мы обсудили в отношении роли обратной связи.
Таблица 1
Результаты электрофизиологии и нейровизуализации, согласующиеся с прогностическим кодированием.
| Прогноз нарушен | Изученная область | Нейронная экспрессия ошибки предсказания | Исследование |
|---|---|---|---|
| Обучаемые пары визуальных объектов | Нижне-височная кора головного мозга обезьяны (ИТ) | Повышенная частота возбуждения | Мейер и Олсон, 2011 г. |
| Статистика естественного изображения | Monkey V1, V2, V3 | Повышенная скорость стрельбы | Hupé et al., 1998; Bullier et al., 1996; Bair et al., 2003 |
| Повторяющийся слуховой поток | Ранняя слуховая кора человека | Повышенные потенциалы, связанные с событиями (ERP), повышенная мощность в гамма-диапазоне | Garrido et al., 2007, 2009; Тодорович и др., 2011 |
| Связность зрительной формы и движения | Человеческий V1, V2, V3, V4, V5 / MT | Усиленный ответ BOLD | Murray et al 2002; Мюррей и др. 2005; Харрисон и др., 2007 |
| Аудиовизуальное соответствие речи | Зрительная и слуховая кора | Осцилляторная активность в гамма-диапазоне | Арнал и др., 2011 г. |
| Предсказуемость зрительных стимулов в зависимости от внимания | Human V1, V2, V3 | Усиленный ЖИРНЫЙ ответ при отсутствии присмотра, уменьшенный ЖЕЛТЫЙ при посещении | Кок и др., 2011 |
| Иерархические ожидания в слуховых последовательностях | Височная кора человека | Расширенные возможности, связанные с событиями (ERP) | Wacongne et al., 2011 г. |
| Ожидаемое повторение (или чередование) раздражителей лица | FFA в фМРТ, париетальном и центральном электродах ЭЭГ | Усиленный BOLD-ответ, уменьшенное подавление повторения ERP | Summerfield et al., 2008, 2011 |
| Видимое движение зрительного стимула | V1 | Расширенный ответ жирным шрифтом | Алинк и др., 2010 г. |
Прямые и трансталамические связи
Хотя доказательства ингибирующего эффекта обратных связей должны быть тщательно оценены, доказательства возбуждающего эффекта прямых связей однозначны.Например, у обезьяны V1 проецируется моносинаптически в V2, V3, V3a, V4 и V5 / MT (Zeki, 1978; Zeki and Shipp, 1988). Во всех случаях — когда V1 обратимо инактивируется посредством охлаждения — активность отдельных клеток в целевых областях сильно подавляется (Girard and Bullier, 1989; Girard et al., 1991a, 1991b, 1992). В случаях V2 и V3 результатом охлаждения области V1 является почти полное подавление активности отдельной единицы. Эти исследования показывают, что активность в высших областях коры зависит от входных сигналов от более ранних областей коры, которые устанавливают свойства их рецептивного поля.
Наконец, хотя многие исследования были сосредоточены на внешних связях, которые проецируются непосредственно из одной области коры в другую, появляется все больше доказательств того, что управляющие связи с прямой связью (и, возможно, обратная связь) в коре могут быть опосредованы трансталамическими путями (Sherman and Guillery, 1998, 2011). Наиболее убедительное доказательство этого утверждения исходит от соматосенсорной системы, где недавно было показано, что заднее медиальное ядро таламуса (POm) — таламическое ядро более высокого порядка, которое получает прямой вход от коры головного мозга — может передавать информацию между S1 и S2 ( Хил и др.

