Какие бывают типы микросхем малой степени интеграции. Каковы их основные характеристики и особенности. Как применяются различные микросхемы И-НЕ, ИЛИ-НЕ, И, ИЛИ и другие. Какие существуют варианты выходных каскадов микросхем.
Основные типы и характеристики микросхем малой степени интеграции
Микросхемы малой степени интеграции широко используются в электронных устройствах для реализации базовых логических функций. Они подразделяются на несколько основных типов:
- И-НЕ — выполняют логическое умножение и инверсию
- ИЛИ-НЕ — выполняют логическое сложение и инверсию
- И — выполняют только логическое умножение
- ИЛИ — выполняют только логическое сложение
- НЕ — инверторы
- И-ИЛИ-НЕ — более сложные комбинационные схемы
Ключевыми характеристиками микросхем являются:
- Нагрузочная способность — количество стандартных нагрузок, которое может обеспечить выход микросхемы
- Тип выходного каскада — стандартный, с открытым коллектором, с третьим состоянием
- Быстродействие
- Потребляемая мощность
Микросхемы И-НЕ: разновидности и применение
Микросхемы И-НЕ являются одними из самых распространенных. Они выпускаются в нескольких вариантах:

- Со стандартной нагрузочной способностью (например, К155ЛА1-ЛА4)
- С повышенной нагрузочной способностью (К155ЛА6, К155ЛА12)
- С открытым коллектором (К155ЛА7-ЛА11, К155ЛА13)
- Мощные магистральные усилители (КР531ЛА16)
- С третьим состоянием выхода (КР531ЛА17, КР531ЛА19)
Микросхемы И-НЕ применяются для построения более сложных логических функций, триггеров, счетчиков и других цифровых узлов.
Особенности микросхем ИЛИ-НЕ и их использование
Микросхемы ИЛИ-НЕ также имеют несколько модификаций:
- Со стандартной нагрузочной способностью (К155ЛЕ1-ЛЕ4)
- С повышенной нагрузочной способностью (К155ЛЕ5, К155ЛЕ6)
- Со стробируемыми входами (К155ЛЕ2, К155ЛЕ3)
Микросхемы ИЛИ-НЕ используются для реализации логических функций, мультиплексоров, дешифраторов и других комбинационных схем. Стробируемые входы позволяют управлять работой микросхемы.
Микросхемы И и ИЛИ: варианты исполнения и области применения
Микросхемы, выполняющие функции И и ИЛИ без инверсии, представлены следующими основными типами:
- И со стандартным выходом (К155ЛИ1, К155ЛИ3)
- И с открытым коллектором (К155ЛИ2, К155ЛИ4)
- ИЛИ со стандартным выходом (К155ЛЛ1)
- ИЛИ с открытым коллектором (К155ЛЛ2)
Эти микросхемы применяются для построения логических схем, где требуется прямая реализация функций И или ИЛИ без дополнительной инверсии. Варианты с открытым коллектором позволяют объединять выходы нескольких микросхем.
Инверторы: типы и основные характеристики
Инверторы (микросхемы НЕ) выпускаются в следующих вариантах:
- Со стандартным выходом (К155ЛН1)
- С открытым коллектором (К155ЛН2, К155ЛН3, К155ЛН5)
- Мощные с третьим состоянием (К155ЛН6)
- С повышенной нагрузочной способностью (КР1533ЛН8)
Инверторы широко применяются в цифровых схемах для инвертирования сигналов, построения генераторов, формирователей импульсов и других узлов. Мощные инверторы с третьим состоянием удобны для работы с шинами данных.
Микросхемы И-ИЛИ-НЕ: сложные комбинационные элементы
Микросхемы И-ИЛИ-НЕ реализуют более сложные логические функции:
- К155ЛР1, К155ЛР3, К155ЛР4 — с возможностью расширения
- К555ЛР4, КР1533ЛР4 — без расширения
- КР531ЛР10 — с открытым коллектором
Эти микросхемы позволяют реализовывать сложные комбинационные функции в одном корпусе. Возможность расширения у некоторых микросхем позволяет увеличивать число входов.
Особенности выходных каскадов микросхем малой степени интеграции
Выходные каскады микросхем могут быть выполнены в нескольких вариантах:
- Стандартный выход — обеспечивает нормированные уровни напряжения и тока
- Открытый коллектор — позволяет подключать внешнюю нагрузку к источнику питания
- Третье состояние — дает возможность отключать выход от нагрузки
Выбор типа выходного каскада зависит от требований к нагрузочной способности, возможности объединения выходов и других факторов применения микросхемы.
Применение микросхем малой степени интеграции в современной электронике
Несмотря на развитие более сложных интегральных схем, микросхемы малой степени интеграции продолжают широко применяться:
- В качестве элементов сопряжения между различными устройствами
- Для реализации простых логических функций
- В учебных целях при изучении основ цифровой электроники
- В специализированных устройствах, где требуется высокая надежность
Их простота, доступность и хорошо отработанная технология производства обеспечивают микросхемам малой степени интеграции стабильное место на рынке электронных компонентов.
Как проверить работает ли микросхема или нет
Как проверить работает ли микросхема или нет
Интегральная микросхема — электронная схема произвольной сложности (кристалл), изготовленная на полупроводниковой подложке (пластине или плёнке) и помещённая в неразборный корпус или без такового, в случае вхождения в состав микросборки.
Прежде чем проверять любую микросхему на работоспособность, необходимо знать и понимать ее устройство, хотя бы приблизительно. Это нужно для того, чтобы заранее представлять себе, какие сигналы или напряжения ожидать от исправной микросхемы на ее выводах.
Лучше всего для проверки конкретной микросхемы собрать хотя бы на макетной плате схему для ее тестирования, — это в том случае, если микросхема новая или уже выпаяна.
Вообще, если устройство микросхемы известно, то в некоторых ситуациях ее можно проверить даже не выпаивая с платы, на которой она установлена, просто измерив сигналы на ножках при помощи мультиметра или осциллографа. Тогда наличие или отсутствие сигнала либо искаженная форма импульса сразу покажут, что — к чему.
Внешний осмотр микросхемы
Допустим что микросхема все еще установлена на плате и выпаивать ее сразу нежелательно. Прежде чем подавать питание на плату, внимательно осмотрите микросхему со всех сторон. Быть может есть очевидные физические признаки ее неисправности: трещина на корпусе, обгоревший или отпавший вывод, короткое замыкание между ножками из-за попадания куска провда (и такое бывет), горелые обвесные компоненты и т. д. Если при осмотре никаких поврежднеий не выявлено, можно идти дальше.
Если к текущему моменту на плату подано питание, то можно аккуратно (с соблюдением техники безопасности!) приступать к дальнейшей проверке микросхемы.
Проверка выводов питания
Первым делом диагностируют цепи питания микросхемы. Это можно проделать при помощи вольтметра (мультиметра). Уточнить выводы питания известной микросхемы очень легко — достаточно заглянуть в документацию (datasheet) на нее. Плюс положительного питания обозначаетя в даташите как VCC+, отрицательное питание VCC-, общий провод имеет обозначение GND.
Итак, минусовой щуп мультиметра устанавливается на общий провод — упирается в минусовой вывод микросхемы, а плюсовой (красный) щуп мультиметра — на соответствующую ножку питания. Если напряжение соответствует норме для микросхемы, значит питание подается как надо, следовательно цепи питания всего устройства исправны.
Если же напряжение питания не в норме, значит необходимо далее проверить саму цепь питания, хотя бы предворительно отпаяв ее от микросхемы. Если цепи питания работают нормально без микросхемы, занчит проблема в микросхеме, и в худшем случае ее действительно придется менять. Если же проблема в цепях питания, значит скорее всего необходимо ремонтировать их (конденсатор, стабилизатор и т. д.).
Проверка источника опорного напряжения
Далее проверяют все известные выводы микросхемы. Например, можно начать с измерения напряжения на выводе встроенного в микросхему источника опорного напряжения Vref, нормальное значение которого указано в документации. На этом выводе должно быть постоянное напряжение определенного значения относительно общего провода. Если оно меньше или сильно больше, занчит внутри микросхемы или в обвесных компонентах что-то не так, и следует продолжить диагностику.
Проверка времязадающих цепей
Если на микросхеме есть какая-нибудь RC-цепь, то на ней, как правило, в рабочем режиме должны наблюдаться пилообразные колебания. На этом этапе опять же полезным будет обратиться к даташиту, чтобы понять где находится данная цепь если она предусмотрена, и на какой ножке должны быть колебания.
Проверка осуществляется осциллографом. Общий его щуп цепляется на минус питания, а измерительный — на соответствующий вывод микросхемы. Если колебания есть и их форма приемлема — все в порядке, можно идти дальше. Если колебаний нет, то скорее всего проблема в микросхеме или в обвесных времязадающих компонентах.
Проверка сигнальных выводов
Наконец, проверяют сигнальные выводы (выходы) микросхемы. Если микросхема управляет каким-то ключом или следующим блоком на схеме, то на соответствующих выходах (или хотя бы на одном выходе, если он единственный) микросхемы должны присутствовать правильные сигналы. Посмотрите в даташите, к каким выводам должны подходить управляемые цепи.
Проверьте осциллографом данные выводы тем же путем, как проверяли RC-цепь. Если сигнал нормальный и значительно не искажен по сравнению с нормальной формой, значит все в порядке. Если сигнал отсутствует или сильно искажен, скорее всего микросхема повреждена, и ее следует заменить, предварительно проверив управляемую цепь, ведь в действительности она может оказаться причиной выхода микросхемы из строя.
Ранее ЭлектроВести писали, что шотландский стартап Gravitricity разработал решение, позволяющее превратить старые, неработающие шахты в гигантские хранилища электроэнергии. Схема новации следующая: когда электростанции начинают вырабатывать больше электроэнергии, чем требуется энергосети, излишки энергии идут на то, чтобы питать лебедки, поднимающие тяжелый груз наверх. Когда накопленную энергию нужно высвободить, груз опускается вниз, попутно вырабатывая электричество.
По материалам: electrik.info.
Микросхема «Микрона» для NFC- меток получила статус продукции отечественного производства первого уровня
Министерство промышленности и торговли РФ подтвердило соответствие разработанной АО «НИИМЭ» и производимой ПАО «Микрон» микросхемы для NFC-меток MIK213ND требованиям, предъявляемым к продукции отечественного производства первого уровня.
Данная микросхема используется в радиочастотных метках для маркировки широко спектра объектов, включая древесину, металл, стекло, пластик, бумагу, преимущественно в маркетинговых целях. MIK213ND , единственный российский микрочип, соответствующий стандартам NFC Forum Type 2 Tag, является первым чипом отечественного производства с NFC-интерфейсом, он не требует специального считывателя, для считывания может быть использовано любое устройство с NFC-модулем.
«Мы начали выпускать чип MIK213ND в 2017 году для RFID-маркировки продукции «Микрона». RFID NFC этикетка содержит информацию о партии, дате производства, наименовании микросхемы. Также служит своего рода защитой товара от подделок и защитой бренда», -отмечает Алексей Маркин, начальник RFID-лаборатории ПАО «Микрон».
MIK213ND представляет собой универсальный однокристальный микропроцессор, предназначенный для использования в радиочастотных метках. Он обеспечивает бесконтактную передачу информации на расстоянии до 100 мм, в зависимости от геометрии антенны и мощности считывающего-записывающего устройства. Микрочип передает данные на частоте 13.56 МГц со скоростью 106 кбит/с.
«В эпоху цифровой экономики и активного развития интернета вещей в России потребность рынка в RFID – технологиях будет неуклонно расти, создавая новые сценарии применения для NFC- меток», — считает Дмитрий Терентьев, заместитель начальника сборочного производства. На сегодняшний день микросхема MIK213ND уже используется в электронных картах в пилотном проекте по чипированию древесины в Иркутской области, а также для внутреннего складского учета в ПАО «Микрон».
***
«Микрон» – единственный производитель микросхем первого уровня для смарт-карт, ID-документов и RFID-продукции в РФ. Статус отечественной микроэлектронной продукции первого уровня подтверждает, что при проектировании и разработке указанной интегральной микросхемы не используются готовые схемотехнические решения иностранного производства, разработка, изготовление и сборка осуществляются на территории РФ компанией-резидентом.
RFID (англ. Radio Frequency IDentification, радиочастотная идентификация) – технология автоматической идентификации объектов, в котором посредством радиосигналов считываются или записываются данные, хранящиеся в метках.
Near field communication, NFC («коммуникация ближнего поля», «ближняя бесконтактная связь») — технология беспроводной передачи данных малого радиуса действия, которая дает возможность обмена данными между устройствами, простое расширение стандарта бесконтактных карт (ISO 14443), которое объединяет интерфейс смарт-карты и считывателя в единое устройство.
NFC FORUM TYPIES– стандарты рынка NFC, определяющие, как устройство с поддержкой NFC в режиме чтения / записи обнаруживает, считывает и записывает сообщение формата NDEF на платформы типа NFC FORUM TYPE TAGS.
NFC метка — это бесконтактная RFID метка способная хранить данные в формате NDEF, которая работает в инфраструктуре ISO14443 с NFC устройствами, совместимыми с правилами NFC Forum.
NDEF — (NFC Forum Data Exchange Format), формат данных для обмена сообщениями согласно правилам NFC Forum.
Микросхема 74266
74266
Описание
Микросхема 74266 содержит четыре отдельных логических элемента ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ с двумя входами каждый. Выходы имеют открытый коллектор.
Работа схемы
Все четыре логических элемента ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ микросхемы 74266 можно использовать независимо друг от друга.
Когда сигнал высокого уровня присутствует только на одном из входов микросхемы 74266, на выходе логического элемента формируется напряжение низкого уровня. Если же на оба входа подается напряжение высокого или низкого уровня, то на выходе формируется напряжение высокого уровня.
Логический элемент микросхемы 74266 можно использовать в качестве цифрового компаратора, в котором на выходе устанавливается напряжение высокого уровня при поступлении на входы сигналов одного и того же логического уровня. Если же на входы приходят сигналы разных логических уровней, то на выходе создается напряжение низкого уровня. Логический элемент может также работать как управляемый инвертор, поскольку напряжение высокого уровня на входе позволяет всегда передавать сигнал, подаваемый на второй вход, без изменения. И наоборот, напряжение низкого уровня на одном входе позволяет передавать на выход инвертированное значение напряжения со второго входа.
Выходы с открытым коллектором микросхемы 74266 дают возможность использовать микросхему в качестве 4-разрядного компаратора.
Применение
Реализация логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ, формирование и проверка на чётность-нечётность; сумматор/вычитатель, логические компараторы. Производится следующая номенклатура микросхем: 74LS266.
| Тип микросхемы | 74LS266 |
|---|---|
| Максимальное выходное напряжение, В | 5,5 |
| Время задержки прохождения сигнала, нс | 18 |
| Ток потребления, мА | 8 |
| Входы | Выход | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Рогозин заявил, что Роскосмос не может запустить ряд спутников из-за санкций США — Газета.Ru
Роскосмос не может запустить несколько спутников на орбиту из-за санкций США на поставку в Россию микроэлектроники. Об этом заявил генеральный директор госкорпорации Дмитрий Рогозин в ходе парламентских слушаний в Государственной думе, передает РИА «Новости».
По его словам, когда Роскосмос критикуют относительно того, что Соединенные Штаты вывели в космос больше космических аппаратов, чем Россия, стоит обратить внимание на то, что российских ракет на орбите «более, чем достаточно, выводить нечего».
«Потому что стоят космические аппараты, практически собранные, но в одном-другом-третьем просто не хватает одной конкретной микросхемы, которая через санкции не дается нам никаким образом к закупке», — сказал Рогозин.
Он добавил, что на фоне этого Роскосмос разворачивает работы по производству этой микроэлектроники. Рогозин уточнил, что Роскосмос в 2,5 раза увеличили производство микроэлектроники космического назначения за последние 3 года.
В конце прошлого года США ввели санкции в отношении нескольких зарубежных компаний. В их числе оказались предприятия Роскосмоса: Ракетно-космический центра «Прогресс» и головной научный институт госкорпорации ЦНИИмаш.
После введенных ограничений генеральный директор Роскосмоса обратился к правительству США с требованием отменить эти санкции ради «общего дела».
4 июня глава Роскосмоса Дмитрий Рогозин провел телефонные переговоры с главой NASA Биллом Нельсоном. Основной темой беседы стало продолжение Российско-американского сотрудничества в области космоса, прежде всего в рамках программы международной космической станции.
Глава Роскосмоса поставил перед собеседником ряд вопросов, ранее инициированных американской стороной, которые существенно затрудняют взаимодействие. Речь в том числе шла о санкциях, введенных американской администрацией в отношении предприятий Российской космической промышленности.
SIMATIC DP, МИКРОСХЕМА ASIC LSPM2, НЕ СОДЕРЖИТ СВИНЦА, ДЛЯ PROFIBUS DP, SLAVE, МАКС. 12 МБИТ/С, 32 I/O, 6 ШТУК ДЛЯ ЛАБОРАТОРНЫХ РАЗРАБОТОК (6ES7195-0BA02-0XA0)
Код товара 8112319
Артикул 6ES7195-0BA02-0XA0
Страна Филиппины
Наименование SIMATIC DP, МИКРОСХЕМА ASIC LSPM2, НЕ СОДЕРЖИТ СВИНЦА, ДЛЯ PROFIBUS DP, SLAVE, МАКС. 12 МБИТ/С, 32 I/O, 6 ШТУК ДЛЯ ЛАБОРАТОРНЫХ РАЗРАБОТОК
Упаковки
Сертификат RU C-DE.МЛ66.B01906
Характеристики
Код товара 8112319
Артикул 6ES7195-0BA02-0XA0
Страна Филиппины
Наименование SIMATIC DP, МИКРОСХЕМА ASIC LSPM2, НЕ СОДЕРЖИТ СВИНЦА, ДЛЯ PROFIBUS DP, SLAVE, МАКС. 12 МБИТ/С, 32 I/O, 6 ШТУК ДЛЯ ЛАБОРАТОРНЫХ РАЗРАБОТОК
Упаковки
Сертификат RU C-DE.МЛ66.B01906
Всегда поможем:
Центр поддержки
и продаж
Скидки до 10% +
баллы до 10%
Доставка по городу
от 150 р.
Получение в 150
пунктах выдачи
Микросхемы комбинационного типа малой степени интеграции Справочник по микросхемам ТТЛ и КМОП Любительская Радиоэлектроника
Микросхемы комбинационного типа малой степени интеграции
Существует много типов микросхем ТТЛ малой степени интеграции, различающихся по функциональному назначению, нагрузочной способности, схеме выходного каскада. Работа логических элементов этих микросхем достаточно проста. Для элементов И выходной уровень лог. 1 формируется при подаче на все входы элемента уровней лог. 1, для элемента ИЛИ для формирования уровня лог. 1 на выходе достаточно подачи хотя бы на один вход уровня лог. 1. Элементы И-НЕ (основной элемент серий ТТЛ) и ИЛИ-НЕ дополнительно инвертируют выходной сигнал, элемент И-ИЛИ-НЕ состоит из нескольких элементов И, выходы которых подключены к входам элемента ИЛИ-НЕ.
По нагрузочной способности микросхемы можно разделить на стандартные (N=10 для серий К 155 и КР531 и N = 20 и 40 для микросхем серий К555 и КР1533 соответственно), микросхемы с повышенной нагрузочной способностью (N = 30 и более), микросхемы со специальным выходным каскадом, обеспечивающим значительно более высокую нагрузочную способность в одном из логических состояний. Некоторые типы микросхем выпускают с так называемым <открытым> коллекторным выходом.
Отдельно следует отметить специальный класс микросхем с третьим состоянием выходного каскада, называемым также еще <высокоимпедансным>, или , при котором микросхема отключается по своему выходу от нагрузки. Это, как правило, буферные элементы с относительно большой нагрузочной способностью.
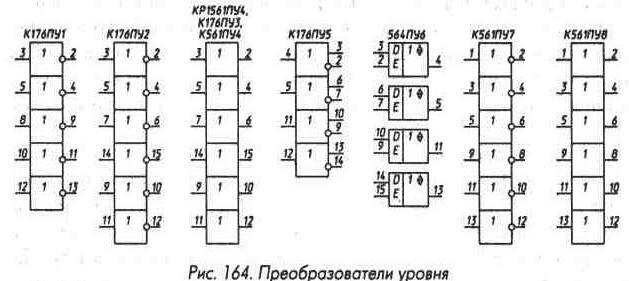
На рис. 2 приведены графические обозначения микросхем ТТЛ, выполняющих функции И-НЕ — самой многочисленной группы простых логических микросхем.
Микросхемы ЛА1 — ЛА4 имеют стандартную для своей серии нагрузочную способность, микросхемы ЛА6 и ЛА12 всех серий, КР1533ЛА21 — КР1533ЛА24 — втрое большую (здесь и далее в тексте в названии оставлена только та его часть, которая определяет тип триггера, счетчика, логического элемента и т. п., если такие же обозначения используются в микросхемах нескольких серий).
Микросхемы ЛА7 — ЛА11, ЛА13, КР1533ЛА23 выполнены с открытым коллектором, нагрузочная способность для ЛА7- ЛА11 в состоянии лог. 0 стандартная, для ЛА13 и КР1533ЛА23 — втрое большая. Максимально допустимое напряжение, которое можно подавать на выход микросхемы ЛА11, находящейся в состоянии лог. 1, — 12 В, для остальных — 5,5 В.
Микросхема КР531ЛА16 (рис. 2) — два мощных магистральных усилителя, выполняющих функцию 4И-НЕ. Нагрузочная способность каждого усилителя 60 мА в состоянии лог. 0 и 40 мА в состоянии лог. 1 при выходном напряжении 2 В, что позволяет работать на линию связи с волновым сопротивлением 50 Ом, нагруженную на конце. Кроме того, гарантируется, что при выходном напряжении 2,7 В в состоянии лог. 1 выходной ток составляет не менее 3 мА.
Микросхема КР531ЛА17 (рис. 2) — два элемента 4И-НЕ с возможностью перевода выхода в высокоимпедансное состояние при подаче на вход Е лог. 1. При подаче на вход Е лог. 0 выходы активны, допустимые выходные токи составляют 50 мА в состоянии лог. 0 и 32 мА в состоянии лог. 1 при выходном напряжении 2 В, что обеспечивает возможность работы на линию связи с волновым сопротивлением 75 Ом. Дополнительно гарантируется, что при выходном напряжении 2,7 В в состоянии лог. 1 выходной ток составляет не менее 3 мА.
Входные токи микросхем КР531ЛА12, КР531ЛА13, КР531ЛА16, КР531ЛА17 по сигнальным входам в состоянии лог. 0-4 мА, по входам Е — 2 мА.
Микросхема К155ЛА18 (рис. 2) выполнена с открытым коллектором, ее выходное напряжение в состоянии лог. 0 не более 0,5 В при выходном втекающем токе 100 мА и не более 0,8 В при токе 300 мА. Максимальное напряжение на выходе в состоянии лог. 1 _ 30 В, что позволяет коммутировать нагрузку мощностью до 9 Вт — электромагнитные реле, маломощные электродвигатели. Лампы накаливания, однако, можно использовать на номинальный ток не более 60 мА, так как сопротивление нити лампы в холодном состоянии значительно меньше номинального.
Микросхема КР531ЛА19 (рис. 2) — двенадцативходовый элемент И-НЕ с возможностью перевода выхода в высокоимпедансное состояние при подаче лог. 1 на вход Е. В состоянии лог. 1 при выходном напряжении 2,4 В микросхема допускает выходной ток до 6,5 мА, в состоянии лог. 0-20 мА.
Микросхема К155ЛП7 (рис. 2) — два стандартных логических элемента И-НЕ с двумя объединенными входами и два n-р-n транзистора с предельно допустимым коллекторным напряжением 30 В и максимальным током коллектора 300 мА. Подложка микросхемы подключена к выводу 8, что позволяет, подключив ее к источнику отрицательного напряжения, коммутировать транзистором и отрицательные сигналы, не выходящие по амплитуде за напряжение этого источника.
На рис. 3 приведены графические обозначения микросхем, выполняющих функцию ИЛИ-НЕ. На входах микросхем К155ЛЕ2, К155ЛЕЗ установлены дополнительные элементы И, позволяющие стробировать входные сигналы. Нагрузочная способность микросхем ЛЕ1 — ЛЕ4, КР531ЛЕ7 стандартная для соответствующей серии, микросхем К155ЛЕ5 и К155ЛЕ6 в состоянии лог. 0-48 мА, что соответствует N = 30, в состоянии лог. 1 — выше. Микросхема К155ЛЕ5 может обеспечить при выходном напряжении 2,4 В вытекающий ток 2,4 мА, микросхема К155ЛЕ6 — 13,2 мА.
Для микросхемы К155ЛЕ6 нормирован также ток при выходном напряжении 2 В — он составляет не менее 42,4 мА, то есть эта микросхема может обеспечивать работу на нагрузку 50 Ом, например, на коаксиальный кабель с волновым сопротивлением 50 или 75 Ом, согласованный на конце.
Микросхемы КР1533ЛЕ10 и КР1533ЛЕ11 имеют нагрузочную способность втрое большую стандартной для микросхем этой серии. Микросхема КР1533ЛЕ11 выполнена с открытым коллектором, максимальное напряжение, которое можно подать на ее выход в закрытом состоянии, — 5,5 В.
На рис. 4 приведены графические обозначения микросхем, выполняющих функцию И. Микросхемы ЛИ1, ЛИЗ, ЛИ6 имеют стандартную для своих серий нагрузочную способность, микросхемы ЛИ2
и ЛИ4 выполнены с открытым коллектором, их нагрузочная способность в состоянии лог. 0 стандартная, в состоянии лог. 1 допускается подача напряжения 5,5 В.
Микросхема К155ЛИ5 выполнена с открытым коллектором, ее нагрузочная способность такая же, как у К155ЛА18.
Микросхемы КР1533ЛИ8 и КР1533ЛИ10 имеют нагрузочную способность втрое большую стандартной для микросхем этой серии.
На рис. 5 приведены графические обозначения микросхем, выполняющих функцию ИЛИ. Микросхема ЛЛ1 имеет стандартную нагрузочную способность, микросхема К155ЛЛ2 выполнена с открытым коллектором и имеет нагрузочную способность такую же, как К155ЛА18.
Микросхема КР1533ЛЛ4 имеет нагрузочную способность втрое большую стандартной для микросхем этой серии
На рис. 6 приведены графические обозначения микросхем, выполняющих функцию НЕ (инверторы). Микросхемы ЛН1 имеют стандартную нагрузочную способность, а ЛН2, К155ЛНЗ, К155ЛН5 выполнены с открытым коллектором и имеют стандартную нагрузочную способность в состоянии лог. 0. Для К155ЛНЗ и К155ЛН5 дополнительно гарантируется, что при втекающем токе 40 мА выходное напряжение в состоянии лог. 0 не превышает 0,7 В. Допустимое напряжение на выходе микросхемы в состоянии лог. 1 составляет 5,5, 30 и 15 В для ЛН2, К155ЛНЗ и К155ЛН5 соответственно.
Микросхема К155ЛН6 (рис. 6) — шесть мощных инверторов с возможностью перевода выходов в высокоимпедансное состояние. Управление состоянием выходов производится по двум равноправным входам управления Е (1 и 15), собранным по схеме, выполняющей функцию И. При подаче на оба указанных входа лог. 0 выходы инверторов переходят в активное состояние и инвертируют входные сигналы, при подаче хотя бы на один вход лог. 1 — переходят в высокоимпедансное состояние.
Нагрузочная способность инверторов довольно велика — при лог. 0 на выходе выходной втекающий ток может достигать 32 мА, при этом выходное напряжение не более 0,4 В, при лог. 1 на выходе выходной вытекающий ток — до 5,2 мА при выходном напряжении 2,4 В.
Микросхема КР1533ЛН7 (рис. 6) — шесть инверторов с повышенной нагрузочной способностью и возможностью перевода выходов в высокоимпедансное состояние. Инверторы объединены в две группы,
у каждой из которых свой вход управления. Подача лог. 0 на вход Е1 включает инверторы с выходами 1-4, на вход Е2 — с выходами 5 и 6. Нагрузочная способность микросхемы 12 мА при 0,4 В в состоянии лог. 0 и 3 мА при 2,4 В в состоянии лог. 1.
Микросхема КР1533ЛН8 (рис. 6) — шесть инверторов с повышенной нагрузочной способностью; максимальный уровень в состоянии лог. 0 -0,4 В при втекающем токе 12 мА и 0,5 В при 24 мА, минимальный уровень в состоянии лог. 1 2,4 В при вытекающем токе 3,0 мА и 2,5 В при 0,4 мА.
Микросхема КР1533ЛН10 имеет нагрузочную способность втрое большую стандартной для микросхем этой серии. Микросхема выполнена с открытым коллектором, максимальное напряжение, которое можно подать на ее выход в закрытом состоянии — 5,5 В.
На рис. 7 приведены графические обозначения микросхем, выполняющих функцию И-ИЛИ-НЕ и расширителей И-ИЛИ. Все микросхемы И-ИЛИ-НЕ имеют стандартные выходы, кромеКР531ЛР10, которая выполнена с открытым коллектором, допустимое напряжение для нее в состоянии лог. 1 — 5,5 В. Следует отметить различие микросхем К155ЛР4 и К555ЛР4, КР1533ЛР4, а такжеК555ЛР11, КР1533ЛР11 и КР531ЛР11. Микросхемы К155ЛР1, К155ЛРЗ, К155ЛР4 имеют входы для подключения расширителей И-ИЛИ К155ЛД1 и К155ЛД2, увеличивающих число групп И в функции ИЛИ этих микросхем. Аналогичные входы для расширения числа входов по ИЛИ имеет микросхема К155ЛЕ2.
Однако более простой способ построения элементов И или ИЛИ с большим числом входов — каскадное соединение микросхем,
выполняющих функции И-НЕ и ИЛИ-НЕ. На рис. 8 (а) приведена схема элемента И на 16 входов, на рис. 8 (б) — элемента ИЛИ на 32 входа. На рис. 8 (в) приведена схема элемента совпадения, формирующего на своем выходе лог. 1 при лог. 1 на четырех верхних по схеме входах и лог. 0 на трех нижних. Такой элемент может использоваться для дешифрации определенных состояний счетчиков и других устройств.
На рис. 9 приведены графические обозначения микросхем — повторителей входного сигнала.
Микросхема ЛП8 — четыре повторителя входного сигнала с высокоимпедансным состоянием. При лог. 0 на управляющем входе Е сигналы с входа D элемента проходят на выход элемента без инверсии. При лог. 1 на входе Е выход элемента переходит в высокоимпедансное состояние. При лог. 0 на выходе микросхема К155ЛП8 обеспечивает втекающий ток 16 мА, при лог. 1 — вытекающий 5,2 мА, К555ЛП8 — 24 мА и 2,6 мА соответственно.
Микросхема К155ЛП9 (рис. 9) — шесть повторителей входного сигнала с открытым коллектором, ее выходные параметры такие же, как и у К155ЛНЗ.
Микросхема К155ЛП10 (рис. 9) — шесть мощных повторителей с возможностью перевода выходов в высокоимпедансное состояние.
Логика управления и нагрузочная способность этой микросхемы такие же, как и у К155ЛН6.
Микросхема К155ЛП11 (рис. 9) — шесть мощных повторителей, подобных повторителям микросхемы К155ЛП10, но разбитых на две группы, каждая из которых имеет свой вход управления. Подача лог. 0 на вход Е1 включает повторители с выходами 1-4, вход Е2 управляет выходами 5 и 6. Нагрузочная способность микросхемы К155ЛП11 такая же, как у К155ЛН6.
Микросхемы КР1533ЛП16 и КР1533ЛП17 имеют нагрузочную способность втрое большую стандартной для микросхем этой серии. Микросхема КР1533ЛП17 выполнена с открытым коллектором,
максимальное напряжение, которое можно подать на ее выход в закрытом состоянии — 5,5 В.
Основное назначение микросхем-повторителей входного сигнала, имеющих возможность перевода выходов в высокоимпедансное состояние, — поочередная подача на одну магистраль сигналов от различных источников. Причем благодаря большой нагрузочной способности микросхем магистраль может иметь большую емкость и большое число подключенных к ней нагрузок и источников сигналов. Эти микросхемы находят широкое применение также в качестве буферных элементов, в особенности в микропроцессорных микросхемах. Для таких же целей служат далее рассматриваемые микросхемы, графические обозначения которых приведены на рис. 10.
Микросхема КР531АП2 — четыре пары буферных неинвертирующих элементов с открытым коллектором, частично соединенных между собой. Сигналы могут передаваться со входов А1 — А4 на двунаправленные выходы С1 — С4 при лог. 0 на входе ЕА и лог 1 на входе ЕВ, с двунаправленных выводов С1 — С4 на выходы В1 — В4 при лог. 0 на входе ЕВ и лог. 1 на входе ЕА. При подаче лог. 1 на оба входа ЕА и ЕВ выходы В1 — В4 и С1 — С4 переходят в высокоимпедансное состояние. Одновременная подача лог. 0 на входе ЕА и ЕВ не допускается. Попарное соединение выводов А1 — А4 и В1 — В4 превращает микросхему в четыре двунаправленных ключа, максимальный выходной ток в состоянии лог. 0-60 мА, максимальные входное и выходное напряжения в состоянии лог. 1-10,5 В, входной ток в состоянии лог. 0 не превышает 0,15 мА.
Микросхема АПЗ (рис. 10) — восемь инвертирующих буферных элементов с повышенной нагрузочной способностью и возможностью перевода выходов в высокоимпедансное состояние. Элементы разбиты на две группы по четыре, у каждой из групп свой вход управления для включения элементов и их перевода в третье состояние (Е1 и Е2). Включение элементов каждой группы происходит при подаче на соответствующий вход (Е1 и Е2) лог. О, переход в высокоимпедансное состояние — при подаче лог. 1. Выходной втекающий ток микросхемы К555АПЗ в состоянии лог. О при напряжении на выходе 0,5 В может достигать 24 мА, вытекающий в состоянии лог. 1 при напряжении на выходе 2 В — 15 мА. Для микросхем КР1533АПЗ максимальный уровень лог. 0 0,4 В при втекающем токе 12 мА и 0,5 В при 24 мА. Минимальный уровень лог. 1 2,4 В при вытекающем токе 3 мА и 2,5 В при 0,4 мА. Нагрузочная способность микросхемы КР531АПЗ в состоянии лог. 0 64 мА, в состоянии лог. 1 3 мА при выходном
напряжении 2,4 В и 15 мА при 2 В. Входные токи по сигнальным входам D1 — D8 в состоянии лог. 0 0,4 мА.
Микросхема АП4 (рис. 10) — восемь аналогичных буферных элементов без инверсии. Отличие ее в том, что один из входов включения элементов и их перевода в третье состояние (El) — инверсный, подобно АПЗ, второй (Е2) — прямой. Нагрузочная способность этой микросхемы такая же, как у АПЗ.
Микросхема АП5 (рис. 10) — восемь неинвертирующих буферных элементов, обе группы которых имеют инверсные входы управления включением. В остальном эта микросхема аналогична АП4.
Микросхемы АПЗ — АП5 служат для буферизации и коммутации сигналов в микропроцессорных устройствах, например, сигналов адреса, сигналов управления при организации внутренних и внешних шин микро-ЭВМ. Основное их назначение — обеспечение однонаправленной передачи информации. Однако при необходимости с их помощью можно обеспечить и двунаправленную передачу. На рис. 11 в качестве примера показано соединение выводов микросхемы АП4 для получения двунаправленного буферного элемента. При подаче лог. 0 на объединенные между собой входы Е1 и Е2 происходит передача сигнала от расположенных слева по рисунку выводов микросхемы (входы А1 -А4) к правым (В1 — В4), при подаче лог. 1 — наоборот: от В1 — В4 к А1 -А4. Два треугольника в среднем поле графического обозначения микросхемы символизируют усиление и направление передачи сигнала, верхний — при подаче активного сигнала на вход Е1 (для инверсного входа — лог. 0), нижний — на вход Е2 (для прямого входа — лог. 1).
Интересно отметить, что расположение информационных входов и выходов микросхем АПЗ — АП5 сделано специально такое, как показано на рис. 11, — для удобного их соединения.
Однако для организации двунаправленной передачи информации удобнее использовать специально предназначенные для этой цели микросхемы, описываемые далее.
Микросхема АП6 (см. рис. 10) — восемь двунаправленных неинвертирующих буферных элементов. Кроме двух групп информационных выводов А1 — А8 и В1 — В8, микросхема имеет два входа управления — Е и Т. Сигнал лог. 0, подаваемый на вход Е, разрешает включение буферных элементов, лог. 1 — переводит все выводы микросхемы в Z-состояние. Сигнал на входе Т действует при лог. 0 на входе Е и определяет направление передачи сигналов — при лог. 1 на входе Т выводы А1 — А8 являются входами, В1 — В8 — выходами, при лог. 0 — наоборот; В1 — В8 — входы, А1 — А8 — выходы. Два треугольника у входа Т символизируют усиление и направление распространения сигнала, верхний — при лог. 1 на входе Т, нижний — при лог. 0.
Микросхема АП6 по своему функционированию (но, к сожалению, не по разводке выводов) соответствует микросхеме КР580ВА86, но потребляет в 1,7 раза меньшую мощность (К555АП6).
Микросхема КР1533АП14 (рис. 10) содержит восемь однонаправленных буферных элементов с возможностью перевода их выходов в высокоимпедансное состояние. При подаче на оба входа разрешения Е лог. 0 выходы микросхемы переходят в активное состояние и на них появляются без инверсии сигналы с соответствующих входов D1 — D8. При поступлении на любой из входов Е лог. 1 выходы переходят в высокоимпедансное состояние. Микросхема КР1533АП15 (рис. 10) аналогична микросхеме КР1533АП14, только она инвертирует входные сигналы.
Микросхема КР1533АП16 (рис. 10) состоит из восьми двунаправленных буферных элементов и, в основном, аналогична микросхеме КР1533АП6. Она инвертирует сигналы при передаче их с выводов А на выводы В и не инвертирует их при передаче в обратном направлении. На графическом изображении микросхемы КР1533АП16 для отражения этого свойства у вывода Т, определяющего направление передачи информации, верхний треугольник, символизирующий передачу сигналов с выводов А на выводы В при подаче на вход Т лог. 1, дополнен кружком инверсии, а нижний треугольник (на входе Т — лог. 0) показан без такого кружка.
Микросхема ИП6 (рис. 10) — четыре двунаправленных инвертирующих буферных элемента. Логика работы входов управления Е1 и Е2
следующая: при лог. 0 на обоих входах передача сигналов происходит от выводов А1 — А4 к выводам В1 — В4, при лог. 1 на обоих входах — от выводов В1 — В4 к А1 — А4. При лог. 1 на входе Е1 и лог. 0 на входе Е2 все информационные выводы микросхемы переходят в Z-состояние, подача лог. 0 на вход Е1 и лог. 1 на вход Е2 одновременно недопустима. Треугольники на графическом обозначении микросхемы и входов Е1 и Е2 символизируют усиление и направление распространения информации при подаче активных сигналов на эти входы.
Нагрузочная способность микросхемы ИП6 такая же, как у АПЗ.
Микросхема ИП7 отличается от ИП6 только тем, что не инвертирует сигналы.
На рис. 12 в качестве примера показано использование буферных микросхем для подключения внешних устройств к компьютеру <Радио-86РК>. Если из всех внешних устройств ограничиться лишь таймером КР580ВИ53, его вполне можно смонтировать на плате компьютера без буферных элементов. Если же предполагается подключение нескольких внешних устройств (таймер, часы, АЦПУ, модем и др.), из-за малой нагрузочной способности центрального процессора КР580ВМ80 необходимы буферные элементы.
На рис. 12 микросхема DD3 обеспечивает буферизацию управляющих сигналов RD, WR, RES и двух младших адресов АО и А1. Микросхема DD2 буферизирует двунаправленную шину данных. Включение этой микросхемы по входу Е должно происходить лишь при обращении к внешним устройствам, что обеспечивается микросхемой DD1 и элементами D10.4 и D10.3.
В основном варианте компьютера <Радио-86РК> адреса А000Н -BFFFH использованы для микросхемы D14. Практически используются только четыре адреса — А000Н, А001Н, А002Н, А00ЗН. Установкой дешифратора DD1 можно обеспечить при сохранении этих адресов для D14 использование следующих четырех адресов А004Н, АООЗН, А006Н, А007Н — для первого внешнего устройства, например таймера; следующих четырех А00ЗН — А00ВН — для второго; следующих четырех А00СН — A00FH — для третьего и т. д., всего можно будет подключить семь дополнительных внешних устройств, для каждого из которых будет отведено четыре адреса. Если входы 1,2,4 дешифратора DD1 подключить к другим выходам адреса микропроцессора D6, например, А10, All, A12, на каждое внешнее устройство будет отведено по 1024 адреса.
Элементы D10.4 и D10.3 необходимы для выключения DD2 при обращении микропроцессора к D14, то есть по адресам А000Н — А00ЗН. В этом случае лог. 0 с выхода О DD1 включает D10.3 и лог. 1 с его выхода выключает DD2. Направление передачи сигнала через DD2 определяется сигналом RD. При чтении из внешнего устройства сигнал RD
принимает значение лог. 0 и происходит передача сигналов через DD2 от внешнего устройства к микропроцессору, в остальных случаях — от микропроцессора к внешнему устройству.
На рис. 13 приведены микросхемы -инвертирующие триггеры Шмитта. Микросхема К155ТЛ1 — два четырехвходовых элемента И-НЕ, микросхема ТЛЗ — четыре двухвходовых, микросхема ТЛ2 — шесть инверторов.
Указанные микросхемы при плавном изменении входного сигнала обеспечивают скачкообразное переключение выходного (рис. 14). При повышении напряжения на входе элемента микросхемы от нуля выходное напряжение скачком изменяется с лог. 1 на лог. 0 при напряжении на входе около 1,65 В. При снижении напряжения на входе обратное изменение выходного напряжения происходит при напряжении на входе около 0,85 В для триггеров Шмитта серий К155 и К555ТЛ2 и около 1,2 В для КР531ТЛЗ.
Триггеры Шмитта применяют для формирования ТТЛ-сигнала из синусоидального, для приема сигналов при большом уровне помех, в формирователях и генераторах импульсов и в других случаях.
На рис. 15, а показана схема формирователя импульса сброса при включении питания, обеспечивающего крутой фронт при большой длительности импульса, на рис. 15, б — простейшего генератора импульсов.
Изучение работы более сложных микросхем удобно продолжить с микросхем последовательностного типа.
БИС 1920ВК014 — АО НТЦ «Модуль»
Микросхема 1920ВК014 представляет собой контроллер мультиплексного канала по ГОСТ Р 52070 с интегрированным ППУ. Микросхема 1920ВК014 обеспечивает сопряжение процессора с резервированной магистралью по ГОСТ Р 52070. Она позволяет существенно улучшить массогабаритные характеристики РЭА (за счет интеграции в едином кристалле микроконтроллера и приемопередатчиков) и сократить количество требуемых номиналов напряжений питания. Микросхема 1920ВК014 выполнена в радиационном исполнении с повышенной стойкостью к ВВФ.
Общие характеристики
Технология изготовления – КМОП КНИ 0,18 мкм
Корпус – планарный металлокерамический (108 выводов)
Масса микросхемы не более 4 г
Условия эксплуатации: -60°C … +85°C
Основные технические характеристики
Программно выбираемая тактовая частота FC –16 МГц (12 МГц)
Режимы контроллера шины, оконечного устройства, монитора шины по ГОСТ Р 52070
Напряжение питания UCC – от 3,0 до 3,6 В ток потребления динамический IOCC – не более 700 мА
Входное напряжение UI – не менее 0 В, не более 3,6 В
Встроенное СОЗУ 8K×16 с избыточным кодированием Хэмминга
Область применения
Микросхема предназначена для применения в бортовой радиоэлектронной аппаратуре для реализации интерфейса мультиплексного канала передачи данных по ГОСТ Р 52070-2003 с использованием управляющего вычислителя (ЦП)
Часто задаваемые вопросы
Где узнать цены на продукцию и срок поставки?
Можно позвонить по номеру +7 (499) 152-96-98 или написать на [email protected]
Как сделать заказ?
1. Выбрать типономинал интересующей микросхемы
2. Указать количество необходимых микросхем
3. Направить Заявку/договор на приобретение продукции на официальном бланке предприятия (при заказе микросхем с приёмкой «5» требуется подпись военного представителя) на имя Генерального директора АО НТЦ «Модуль» на электронный адрес отдела продаж [email protected]
Как получить заказ?
Получение заказа осуществляется самовывозом со склада по адресу г. Москва, 4-я ул 8 Марта, д.3., либо оформляется доставка курьерской службой (оплачивается отдельно).
Где можно скачать софт?
Весь поставляемый с аппаратурой софт является бесплатным, скачать его можно в разделе «Продукты — Программное обеспечение»
Как получить техническую документацию на изделие?
Если информации в разделе «Документация» на странице изделия недостаточно, необходимо написать запрос документа в свободном виде с указанием названия изделия на [email protected]
Куда обращаться, если остались вопросы?
По любым вопросам о продуктах/услугах/предоставлении информации звоните +7 (499) 152-96-98 или пишите [email protected]
ASI HF510M Неполяризованная светодиодная микросхема, используемая в HF310GR, 2 контакта, 1 микросхема и 1 прозрачная крышка, 115–230 В (упаковка из 10 шт.): Amazon.com: Инструменты и товары для дома
| Цена: | 4 доллара.27 (0,43 доллара США / клеммная колодка) |
- Убедитесь, что это подходит введя номер вашей модели.
- Аксессуар светодиодной микросхемы для клеммной колодки держателя предохранителя 5 x 20 мм HF310GR
- Указывает на перегорание предохранителя
- Имеет 2 контактных ножки, 1 неполяризованную светодиодную микросхему и прозрачную крышку.
- Для использования в цепях переменного и постоянного тока
Характеристики этого продукта
| Фирменное наименование | Взаимосвязь систем автоматизации |
|---|---|
| Ean | 0813101027339 |
| Измерительная система | Британские, Метрические |
| Номер модели | HF510M |
| Кол-во позиций | 10 |
| Номер детали | HF510M |
| Код UNSPSC | 31170000 |
| UPC | 813101027339 |
Статистический анализ свойств обработки информации пластинчатых моделей кортикальных микросхем | Кора головного мозга
Абстрактные
Основной задачей вычислительной нейробиологии является понимание вычислительной функции пластин-специфических паттернов синаптических соединений в стереотипных кортикальных микросхемах.Предыдущая работа над этой проблемой была сосредоточена на гипотезах о конкретных вычислительных ролях отдельных слоев и связях между уровнями, и эти гипотезы были проверены путем моделирования абстрактных моделей нейронных сетей. Вместо этого мы подходим к этой проблеме, изучая динамическую систему, определяемую более реалистичными моделями кортикальных микросхем в целом, и исследуя влияние, которое ее ламинарная структура оказывает на передачу и слияние информации в этой динамической системе. Модели цепей, которые мы изучаем, состоят из нейронов Ходжкина-Хаксли с динамическими синапсами, что основано на подробных данных Томсона и др. (2002), Маркрама и др. (1998) и Гупты и др. (2000).Мы исследуем, в какой степени этот шаблон кортикальной микросхемы поддерживает накопление и слияние информации, содержащейся в общих импульсных входах, в слой 4 и слои 2/3 и насколько хорошо он делает эту информацию доступной для проекционных нейронов в слоях 2/3 и 5. продемонстрировать определенные вычислительные преимущества такой модели кортикальной микросхемы на основе данных, специфичной для пластинки, путем сравнения ее производительности с различными типами управляющих моделей, которые имеют те же компоненты и одинаковую глобальную статистику нейронов и синаптических связей, но не имеют характерной для пластинки структуры реальных корковые микросхемы.Мы пришли к выводу, что компьютерное моделирование детальных пластинчатых моделей кортикальных микросхем обеспечивает новое понимание вычислительных последствий анатомических и физиологических данных.
Введение
Неокортекс состоит из нейронов в различных пластинках, которые образуют четко структурированные микросхемы. Несмотря на многочисленные различия в зависимости от возраста, области коры и вида, многие свойства этих микросхем стереотипны, что позволяет предположить, что неокортикальные микросхемы являются вариациями общего шаблона микросхем (White 1989; Douglas and others 1995; Mountcastle 1998; Nelson 2002; Silberberg и другие 2002; Дуглас и Мартин 2004; Калисман и другие 2005).Можно предположить, что такой шаблон микросхемы отличается определенными функциональными свойствами, которые позволяют ему более эффективно обслуживать огромные вычислительные и когнитивные возможности мозга, чем, например, случайно подключенная схема с тем же количеством нейронов и синапсов. . Потенциальная вычислительная функция ламинарной структуры схемы уже рассматривалась в многочисленных статьях (см., Например, Raizada and Grossberg 2003; Treves 2003; Douglas and Martin 2004; и ссылки в этих недавних публикациях).Treves (2003) и Raizada и Grossberg (2003) исследовали конкретные гипотезы относительно вычислительной роли структуры, специфичной для пластин, и подтвердили эти гипотезы с помощью компьютерного моделирования довольно абстрактных моделей нейронных цепей.
Результаты Treves (2003) показывают, что в этой более абстрактной настройке структура ламинарной схемы дает небольшое преимущество в отношении разделения двух типов информации: в каком горизонтальном положении был введен вход схемы (информация «где») и о конкретном шаблоне, который был введен туда («какая» информация).Мы дополняем этот анализ более внимательным изучением временной динамики информации в одном горизонтальном местоположении, точнее в одном столбце диаметром около 100 мкм. Мы обнаружили, что с этой точки зрения вычислительное преимущество ламинарных схем значительно больше: около 30% (в зависимости от конкретного типа задачи обработки информации), а не только 10%, как это наблюдалось в Treves (2003).
Стереотипная кортикальная микросхема — это очень повторяющаяся цепь, которая включает в себя множество наложенных друг на друга петель положительной и отрицательной обратной связи (Дуглас и Мартин 2004).Большинство методов, которые были разработаны в технических науках для проектирования и анализа таких рекуррентных схем, сосредоточены на системном поведении рекуррентной схемы в целом, поскольку оказалось невозможным понять возникающую динамику нелинейных рекуррентных схем только на основе на основе технических характеристик их компонентов. Эта системная точка зрения на стереотипные корковые микросхемы впервые была подчеркнута Дугласом и другими (1995) и привела к их определению абстрактной модели «канонической микросхемы».Дуглас и другие (1995) продемонстрировали, что подход этой системы обеспечивает новый способ понимания роли торможения в корковых микросхемах, в частности того, каким образом относительно небольшие изменения тормозной обратной связи могут вызывать большие изменения в усилении система. Однако временная динамика нейрональной и синаптической активности не принималась во внимание в этих ранних моделях. Также в то время было доступно гораздо меньше данных о стереотипных паттернах связи.Кроме того, ранее не предпринималось попыток проанализировать с помощью строгих статистических методов возникающие возможности обработки информации полученных в результате подробных моделей микросхем. Цель данной статьи — восполнить этот пробел.
Мы исследуем возможности обработки информации подробными моделями микросхем на основе данных Томсона и др. (2002) о вероятностях связей, специфичных для пластин, и силе связи между возбуждающими и тормозящими нейронами в слоях 2/3, 4, 5 и на данных. от Markram и др. (1998) и Gupta и др. (2000) относительно стереотипных динамических свойств (таких как парное подавление пульса и парное облегчение пульса) синаптических связей между возбуждающими и тормозящими кортикальными нейронами.Наш анализ основан на предположении, что стереотипные корковые микросхемы обладают некоторыми «универсальными» вычислительными возможностями и могут выполнять совершенно разные вычисления в различных областях коры. Следовательно, он концентрируется на общей способности обработки информации удерживать и объединять информацию, содержащуюся во входных цепочках импульсов Пуассона из 2 разных источников (моделирование таламического или коркового прямого ввода в слой 4 и латерального или нисходящего ввода в слои 2/3). . Кроме того, мы исследовали способность таких схемных моделей выполнять линейные и нелинейные вычисления для изменяющихся во времени скоростей срабатывания этих двух афферентных входных потоков.Чтобы избежать — обязательно весьма предвзятых — предположений о нейронном кодировании результатов таких вычислений, мы проанализировали информацию, которая доступна о результатах таких вычислений для обычных «нейронных пользователей», то есть пирамидных нейронов в слои 2/3 (которые обычно проецируются в верхние области коры) и пирамидные нейроны в слое 5 (которые обычно не только проецируются в нижние области коры или подкорковые структуры, но также проецируются, например, из V1 обратно в неспецифический таламус, т.е.е., к интраламинарным и срединным ядрам, которые не получают прямого первичного сенсорного ввода, и через это реле к более высоким кортикальным областям, см. Callaway 2004).
В отличие от модели Маасса и других (2002) (обсуждение см. В Destexhe and Marder 2004), мы не использовали простую линейную регрессию для оценки информации, доступной для таких считывающих нейронов, выход которых моделируется взвешенным сумма постсинаптических потенциалов (PSP) (с постоянной времени экспоненциального затухания 15 мс) в ответ на спайки от пресинаптических нейронов.Скорее, мы добавили сюда ограничение, согласно которому вклад возбуждающего (тормозящего) пресинаптического нейрона должен иметь положительный (отрицательный) вес в такой взвешенной сумме. Кроме того, мы приняли во внимание, что считывающий нейрон в слоях 2/3 или 5 получает синаптические входы только от довольно небольшого подмножества нейронов в микросхеме согласно данным Thomson и др. (2002) (что подразумевает, что в цепь из 560 нейронов, нейрон в слоях 2/3 имеет в среднем 84 пресинаптических нейрона, а нейрон в слое 5 имеет в среднем 109 пресинаптических нейронов, см. рис.1). Но, как и в более ранней модели, мы не изменили параметры синапсов в схеме для конкретных вычислительных задач, только веса синаптических связей с такими символьными считывающими нейронами на уровнях 2/3 и 5 (которые не были смоделированы как часть схему в том смысле, что они не проецировались обратно в схему). (Это упрощение было сделано в этой статье из прагматических соображений, поскольку первые результаты по случаю с обратной связью [Maass and others 2005] предполагают, что это требует отдельного анализа).
Рисунок 1
Шаблон кортикальной микросхемы. Цифры у стрелок обозначают силу соединения (средняя амплитуда PSP, измеренная в соме в мВ) и вероятности соединения (в скобках) согласно Thomson и др. (2002) для соединений между корковыми нейронами в 3 разных слоях, каждый из которых состоит из возбуждающего (E ) и ингибирующая (I) популяция с предполагаемым максимальным горизонтальным расстоянием до 100 мкм. Большинство данных взяты из коры головного мозга крысы, за исключением взаимосвязей в слое 4 (курсив), которые взяты из cat.(Соединения от L2 / 3-I до L5-E описаны в Thomson and others [2002], но обсуждаются только качественно. Следовательно, запись для соединений от L2 / 3-I до L5-E [отмечена знаком вопроса ] является лишь экстраполяцией. То же самое относится и к соединениям от L4-I к L2 / 3-I. Никаких данных об амплитудах тормозных PSP от L5-I к L5-I в Thomson и др. [2002] не приводится, следовательно, соответствующая запись — это всего лишь предположение.) Проценты во входных потоках обозначают вероятности соединения для входных нейронов, используемых в нашем моделировании.Кроме того, каждый нейрон получает фоновый шум, отражающий синаптические входы от большого количества более удаленных нейронов (см. Методы).
Рисунок 1
Шаблон кортикальной микросхемы. Цифры у стрелок обозначают силу соединения (средняя амплитуда PSP, измеренная в соме в мВ) и вероятности соединения (в скобках) согласно Thomson и др. (2002) для соединений между корковыми нейронами в 3 разных слоях, каждый из которых состоит из возбуждающего (E ) и ингибирующая (I) популяция с предполагаемым максимальным горизонтальным расстоянием до 100 мкм.Большинство данных взяты из коры головного мозга крысы, за исключением взаимосвязей в слое 4 (курсив), которые взяты из cat. (Соединения от L2 / 3-I до L5-E описаны в Thomson and others [2002], но обсуждаются только качественно. Следовательно, запись для соединений от L2 / 3-I до L5-E [отмечена знаком вопроса ] является лишь экстраполяцией. То же самое относится и к соединениям от L4-I к L2 / 3-I. Никаких данных об амплитудах тормозных PSP от L5-I к L5-I не приводится в Thomson et al. [2002], следовательно, соответствующая запись — это всего лишь предположение.) Проценты на входных потоках обозначают вероятности подключения для входных нейронов, используемых в нашем моделировании. Кроме того, каждый нейрон получает фоновый шум, отражающий синаптические входы от большого количества более удаленных нейронов (см. Методы).
Методы
Наиболее полный в настоящее время набор данных о вероятностях соединения и эффективности синаптических связей между 6 конкретными популяциями нейронов в корковых микросхемах (возбуждающие и тормозящие нейроны в слоях 2/3, 4 и 5) был собран в Thomson et al. (2002). ).Для сбора этих данных были сделаны внутриклеточные записи с помощью острых электродов от 998 пар идентифицированных нейронов. В общей сложности 679 парных записей были сделаны из соматосенсорных, моторных и зрительных зон взрослых крыс и 319 из зрительных зон взрослых кошек. Отбор проб производился случайным образом с латеральным разбросом 50–100 мкм (А. М. Томсон, личное сообщение). Для тех пар, где данные как от крысы, так и от кошки приведены в Thomson and others (2002), мы взяли данные от крысы (см. Рис.1). Только для пар нейронов в слое 4 данные по крысе у Thomson и др. (2002) не приводятся; следовательно, соответствующие данные на рисунке 1 взяты из cat. (Некоторые пары наблюдались редко, а соответствующие записи страдают от небольшого размера выборки [подробности см. В Thomson and others 2002]. Также очень маленькие нейроны у крысы могли быть пропущены [AM Thomson, личное сообщение]. Кроме того, возможно, что в некоторых кортикальных микросхемах существуют связи между парами нейронов, о которых не сообщалось в Thomson и др. [2002] [в случае соединений с тормозными нейронами в слоях 2/3, см., например, e.g., Dantzker and Callaway 2000]).
Известно, что краткосрочная динамика корковых синапсов (то есть их специфическая смесь парной депрессии пульса и парного облегчения пульса) зависит от типа пресинаптического и постсинаптического нейрона (см., Например, Markram and others 1998; Gupta et al. 2000; Томсон 2003). Мы смоделировали эту краткосрочную синаптическую динамику в соответствии с моделью, предложенной Markram и др. (1998), с синаптическими параметрами U, D и F . Модель предсказывает амплитуду A k PSP для k -го спайка в цепочке спайков с интервалами между спайками Δ 1 , Δ 2 ,…, Δ k −1 через рекурсивные уравнения (1) со скрытыми динамическими переменными u ∈ [0,1] и R ∈ [0,1], чьи начальные значения для 1-го всплеска равны u 1 = U и R 1 = 1 (см. Maass and Markram [2002] для обоснования этой версии уравнений, которая исправляет небольшую ошибку в Markram и др. [1998]).Детерминированная модель синапсов разработана для моделирования средней суммы постсинаптических ответов, возникающих в результате согласованного действия нескольких стохастических сайтов синаптического высвобождения. Результаты показывают, что включение краткосрочной синаптической пластичности оказывает значительное влияние на способность моделей цепей к обработке информации. (Долговременная синаптическая пластичность в моделируемой цепи не была включена в это исследование по прагматическим причинам из-за дополнительных сложных проблем, но будет рассмотрено в последующих исследованиях).Параметры U, D и F были выбраны в нашей компьютерной модели из распределений Гаусса, которые отражают данные, представленные в Markram и др. (1998) и Gupta и др. (2000) для каждого типа соединения (обратите внимание, что параметр U согласно Markram и др. [1998] в значительной степени определяется вероятностью начального высвобождения задействованных сайтов синаптического высвобождения). В зависимости от того, был ли вход возбуждающим (E) или тормозящим (I), средние значения этих трех параметров U, D, F (с D, F , выраженными в секундах) были выбраны так, чтобы иметь средние значения, которые были сообщается в этих статьях (см. Таблицу 1).Стандартное отклонение (SD) каждого параметра было выбрано равным 50% от его среднего (отрицательные значения заменены значениями, выбранными из равномерного распределения между нулем и двукратным средним).
Таблица 1Синаптические параметры, которые масштабируют краткосрочную динамику
| От / до | E | I |
| E | 0,5, 1,1, 0,05 | 0,05, 0,125, 1,2 |
| Я | 0.25, 0,7, 0,02 | 0,32, 0,144, 0,06 |
| От / до | E | I |
| E | 0,5, 1,1, 0,05 | 0,05, 0,125, 1,2 |
| I | 0,25, 0,7, 0,02 | 0,32, 0,144, 0,06 |
Синаптические параметры, масштабирующие краткосрочную динамику
| От / до | E | I |
| E | 0.5, 1,1, 0,05 | 0,05, 0,125, 1,2 |
| I | 0,25, 0,7, 0,02 | 0,32, 0,144, 0,06 |
| От / до | E | I |
| E | 0,5, 1,1, 0,05 | 0,05, 0,125, 1,2 |
| I | 0,25, 0,7, 0,02 | 0,32, 0,144, 0,06 |
Из рассмотренных нами моделей микросхем из 3 слоев, с 30%, 20% и 50% нейронов, назначенных на уровни 2/3, слой 4 и слой 5, соответственно.Каждый слой состоял из популяции возбуждающих нейронов и популяции тормозных нейронов в соотношении 4: 1. Синаптические связи между нейронами в любой паре из полученных 6 популяций генерировались случайным образом в соответствии с эмпирическими данными из таблицы 1 и рисунка 1. Большинство схем, которые были смоделированы, состояли из 560 нейронов. Среднее количество пресинаптических нейронов нейрона в такой цепи было тогда 76, что в целом давало в среднем 42 594 синапса в цепи.
В качестве моделей возбуждающих и тормозных нейронов мы выбрали основанные на проводимости однокамерные модели нейронов Ходжкина-Хаксли с пассивными и активными свойствами, смоделированные согласно Destexhe и др. (2001) и Destexhe and Pare (1999).В соответствии с экспериментальными данными о пирамидных нейронах неокортекса и гиппокампа (Стюарт, Сакманн, 1994; Маги, Джонстон, 1995; Хоффман и др., 1997; Маги и др., 1998), активные токи содержат зависящий от напряжения ток Na + (Трауб и Майлз 1991) и выпрямителя с задержкой тока К + тока (Трауб и Майлз, 1991). Для возбуждающих нейронов в модель был включен неинактивирующий ток K + (Mainen и др., 1995), ответственный за адаптацию частоты спайков.Пиковая плотность проводимости для тока Na + и тока выпрямителя с задержкой K + была выбрана равной 500 и 100 пСм / мкм 2 , соответственно, а пиковая плотность проводимости для неинактивирующего тока K + был выбран равным 5 пСм / мкм 2 . Площадь мембраны нейрона была установлена равной 34 636 мкм 2 , как у Destexhe и др. (2001). Для каждого моделирования начальные условия каждого нейрона, то есть напряжение на мембране в момент времени t = 0, выбирались случайным образом (равномерное распределение) из интервала [-70 мВ, -60 мВ].
Кортикальный нейрон получает синаптические входы не только от непосредственно соседних нейронов (которые были явно смоделированы в нашей компьютерной модели), но также меньшие фоновые входные токи от большого количества более отдаленных нейронов. Фактически, внутриклеточные записи у бодрствующих животных предполагают, что нейроны неокортекса подвергаются интенсивной бомбардировке фоновыми синаптическими входами, вызывая деполяризацию мембранного потенциала и более низкое входное сопротивление, обычно называемое «состоянием высокой проводимости» (для обзора, см. Destexhe and others 2003).Это было отражено в нашей компьютерной модели фоновыми входными токами, которые вводились в каждый нейрон (в дополнение к явно смоделированным синаптическим входам от афферентных соединений и от нейронов в цепи). Проводимость этих фоновых токов моделировалась согласно Destexhe и др. (2001) как случайный процесс с одной переменной, аналогичный процессу Орнштейна-Уленбека со средним значением g e = 0,012 мкСм и g i = 0,057 мкСм, дисперсия σ e = 0.003 мкСм и σ i = 0,0066 мкСм, а постоянные времени τ e = 2,7 мСм и τ i = 10,5 мСм, где индексы e / i относятся к входной проводимости возбуждающего и тормозящего фона соответственно. Согласно Destexhe и др. (2001), эта модель захватывает спектральные и амплитудные характеристики входных проводимостей детальной биофизической модели неокортикальной пирамидной клетки, которая была сопоставлена с внутриклеточными записями в теменной коре кошки in vivo. Кроме того, соотношение средних вкладов возбуждающей и тормозной фоновых проводимостей было выбрано равным 5 в соответствии с экспериментальными исследованиями во время сенсорных реакций (Borg-Graham and others 1998; Hirsch and others 1998; Anderson and others 2000).
Максимальные проводимости синапсов были выбраны из гауссова распределения со стандартным отклонением 70% от его среднего (с заменой отрицательных значений значениями, выбранными из равномерного распределения между нулем и двукратным средним). Средние максимальные проводимости синапсов были выбраны для воспроизведения средней амплитуды PSP, представленной на рисунке 1, при мембранном потенциале покоя (при наличии синаптической фоновой активности).
Два афферентных входных потока, каждый из которых состоит из 4 или 40 цепочек пиков (т.е., 4 или 40 входных каналов), были введены в схему. Каждый из каналов 1-го входного потока (представляющий таламический или прямой кортикальный вход) вводился не только в слой 4, то есть в 50% его тормозных нейронов и 80% его возбуждающих нейронов, но также и в 20% возбуждающих нейронов. нейроны в слоях 2/3 и 10% возбуждающих нейронов в слое 5 (все выбираются случайным образом). (Это входное распределение качественно отражает данные, приведенные в главе III White [1989], что «таламокортикальные афференты к синапсу 4 уровня не только с непирамидными нейронами 4 уровня, но и с широким спектром как пирамидных, так и непирамидных типов нейронов, чьи клеточные тела встречаются повсюду. слои 2–6.Таким образом, среднее количество входов, сходящихся к возбуждающему нейрону в слое 4, составляет 3,2 или 32. (Компьютерное моделирование предполагает, что можно выбрать меньшую вероятность подключения от внешних входных нейронов, если амплитуды результирующих PSP увеличиваются соответствующим образом. Для 40 входных каналов мы выполнили моделирование с более низким входным соединением для входного потока 1, сохранив при этом постоянное произведение амплитуды PSP и вероятности соединения. инвариантен к этим изменениям, даже если вероятности соединения для внешних входных нейронов уменьшены до 1/5 от ранее заданных значений.Это примерно находится в диапазоне, предполагаемом экспериментальными измерениями вариабельности возбуждающих постсинаптических потенциалов (ВПСП) в простых клетках зрительной коры головного мозга кошек с различными уровнями стимуляции латерального коленчатого ядра (LGN) (Ferster 1987) и экспериментами по взаимной корреляции между моносинаптическими связанные клетки LGN и зрительной коры головного мозга кошки (Tanaka 1983), что предполагает, что по крайней мере 10 клеток LGN обеспечивают вход в каждую простую клетку. Средняя проводимость входных синапсов была выбрана для генерации PSP со средней амплитудой 1.9 мВ при мембранном потенциале покоя (при наличии синаптической фоновой активности). Это значение соответствует нижней границе оценки воздействия коленчатого тела на один нейрон в слое 4 взрослых кошек, данной Chung and Ferster (1998). Это было умножено в наших симуляциях с параметром масштабирования S I1 , который отражает биологически нереалистичное количество входных нейронов в этих симуляциях (см. Обсуждение ниже). Каждый из каналов 2-го афферентного входного потока вводился в 20% возбуждающих нейронов в слоях 2/3 (также со средней амплитудой 1.9 мВ, умноженное на другой параметр масштабирования S I2 ).
Таблица 2Снижение производительности схем управления по сравнению со схемами, основанными на данных
| Задачи / схемы | Аморфные | В малых масштабах | Регулируемые по степени | Регулируемые по степени без специфичности входа или выхода | Случайно краткосрочная синаптическая динамика | Статические синапсы |
| Память | 32.6 | 41,6 | 12,0 | 35,8 | 48,3 | 65,7 |
| Нелинейный | 36,9 | 11,3 | −2,3 | 4,6 | 40,1 | 38,7 | −0,6 | 5,6 | 14,1 | 6,9 |
| Все | 25,0 | 15,4 | 1,6 | 12,0 | 30.4 | 30,6 |
| Задачи / схемы | Аморфный | Маленький мир | Управляемый градус | Управляемый градус без специфичности входа или выхода | Случайная краткосрочная синаптическая динамика | Статические синапсы |
| Память | 32,6 | 41,6 | 12,0 | 35,8 | 48,3 | 65,7 |
| Нелинейный | 36.9 | 11,3 | −2,3 | 4,6 | 40,1 | 38,7 |
| Прочие | 12,2 | 5,3 | −0,6 | 5,6 | 14,1 | 6,9 | 15,4 | 1,6 | 12,0 | 30,4 | 30,6 |
Снижение производительности цепей управления по сравнению со схемами на основе данных
| Задачи / схемы | Аморфные | 09 Small-world Управляемая по степениРегулируемая по степени без специфичности входа или выхода | Случайная краткосрочная синаптическая динамика | Статические синапсы | ||
| Память | 32.6 | 41,6 | 12,0 | 35,8 | 48,3 | 65,7 |
| Нелинейный | 36,9 | 11,3 | −2,3 | 4,6 | 40,1 | 38,7 | −0,6 | 5,6 | 14,1 | 6,9 |
| Все | 25,0 | 15,4 | 1,6 | 12,0 | 30.4 | 30,6 |
| Задачи / схемы | Аморфный | Маленький мир | Управляемый градус | Управляемый градус без специфичности входа или выхода | Случайная краткосрочная синаптическая динамика | Статические синапсы |
| Память | 32,6 | 41,6 | 12,0 | 35,8 | 48,3 | 65,7 |
| Нелинейный | 36.9 | 11,3 | −2,3 | 4,6 | 40,1 | 38,7 |
| Прочие | 12,2 | 5,3 | −0,6 | 5,6 | 14,1 | 6,9 | 15,4 | 1,6 | 12,0 | 30,4 | 30,6 |
Всего остается 3 параметра, значения которых необходимо выбрать, чтобы получить функциональные компьютерные модели кортикальных микросхем.Эти параметры S RW , S I1 , S I2 масштабируют (в виде мультипликативных множителей) амплитуды PSP для всех синаптических соединений в цепи (рекуррентные веса), амплитуды PSP из входного потока 1 и амплитуды EPSP из входного потока 2. Они должны быть выбраны таким образом, чтобы они учитывали разницу в масштабе между нашими смоделированными микросхемами и биологическими кортикальными микросхемами.Значения этих трех параметров не могут быть считаны из ранее упомянутых данных, и нужно подозревать, что адекватные значения зависят также от вида, от конкретной корковой микросхемы in vivo, которую человек хочет смоделировать, от текущего состояния различных гомеостатических процессов. , от текущего поведенческого состояния (включая внимание) организма и от интенсивности текущего афферентного воздействия.
Параметр S I1 был выбран так, чтобы афферентный входной поток 1 (состоящий из 40 последовательностей импульсов Пуассона с частотой 20 Гц) вызывал (без входного потока 2 и без повторяющихся соединений, т.е.е., S RW установлен на 0) средняя частота срабатывания 15 Гц в слое 4. Параметр S I2 был подобным образом выбран так, что афферентный входной поток 2 (сгенерированный как входной поток 1) вызвал средняя частота стрельбы 10 Гц в слоях 2/3. В любом случае был активирован только один из 2 входных потоков. С помощью этой процедуры мы получили S I1 = 14 и S I2 = 33. Для моделирования с входными потоками, состоящими из 4 последовательностей импульсов Пуассона, мы умножили эти значения на 10.Входные синапсы были выбраны статическими, то есть синаптические параметры были установлены на U = 1, D = 0 и F = 0, а их максимальные проводимости были выбраны из гауссовского распределения с SD 70% от его среднего (с заменой отрицательных значений значениями, выбранными из равномерного распределения между нулем и двукратным средним).
Параметр S RW учитывает среднюю мощность синаптических входов в нейрон от других нейронов в цепи (кроме глобально смоделированного фонового синаптического входа, см. Выше), и, следовательно, разницу в размере цепи между наши смоделированные модели микросхем и настоящая кортикальная микросхема.Оказалось, что значение 60000 / (количество нейронов в моделируемой цепи) для S RW произведено в слое 5 моделируемой схемы для стандартных значений S I1 и S I2 — это реалистичная низкая, но значительная активизация зажигания 8,5 Гц (см. Рис. 2), поэтому мы использовали это значение в качестве стандартного значения для S RW . Это значение увеличивает среднее число 76 пресинаптических нейронов в цепи из 560 нейронов до 107 раз, давая, таким образом, в среднем 8132 пресинаптических нейрона.Это число согласуется с оценками общего числа синапсов на нейроне, данными Бинцеггером и другими (2004), которые варьируются от 2981 до 13 075 для разных типов клеток зрительной коры головного мозга кошек. Некоторый дополнительный синаптический ввод моделировался фоновым синаптическим вводом (см. Выше).
Рисунок 2
( A ) Два входных потока, каждый из которых состоит из 40 последовательностей импульсов Пуассона (вход в слои 2/3 начинается здесь на 100 мс позже). ( B ) Спайковый растр модели кортикальной микросхемы на основе данных (состоящей из 560 нейронов) для 2 входных потоков, показанных в ( A ).Вертикальное измерение масштабируется в соответствии с количеством нейронов в каждом слое. Шипы тормозных нейронов показаны серым цветом. (Показатели активизации населения в разных слоях в некоторой степени, но не полностью коррелированы. Максимальный коэффициент корреляции между темпами роста населения в слоях 2/3 и 4, слоях 2/3 и уровне 5, а также в слое 4 и слое 5 [для t > 150 мс, размер интервала 1 мс и произвольная задержка] составляет 0,62, 0,65 и 0,56 соответственно.) ( C ) Распределение скоростей стрельбы в ( B ) (после начала ввода в слои 2 / 3 и слой 4), показывая автоматически возникающее экспоненциальное распределение скоростей возгорания в слое 5.Средняя частота стрельбы: 8,5 Гц. ( D ) Увеличение начального временного сегмента, показывающее распространение возбуждения от слоя 4 к поверхностным и глубоким слоям, что качественно совпадает с данными Армстронга-Джеймса и других (1992).
Рисунок 2
( A ) Два входных потока, каждый из которых состоит из 40 последовательностей пиков Пуассона (вход в слои 2/3 начинается здесь на 100 мс позже). ( B ) Спайковый растр модели кортикальной микросхемы на основе данных (состоящей из 560 нейронов) для 2 входных потоков, показанных в ( A ).Вертикальное измерение масштабируется в соответствии с количеством нейронов в каждом слое. Шипы тормозных нейронов показаны серым цветом. (Показатели активизации населения в разных слоях в некоторой степени, но не полностью коррелированы. Максимальный коэффициент корреляции между темпами роста населения в слоях 2/3 и 4, слоях 2/3 и уровне 5, а также в слое 4 и слое 5 [для t > 150 мс, размер интервала 1 мс и произвольная задержка] составляет 0,62, 0,65 и 0,56 соответственно.) ( C ) Распределение скоростей стрельбы в ( B ) (после начала ввода в слои 2 / 3 и слой 4), показывая автоматически возникающее экспоненциальное распределение скоростей возгорания в слое 5.Средняя частота стрельбы: 8,5 Гц. ( D ) Увеличение начального временного сегмента, показывающее распространение возбуждения от слоя 4 к поверхностным и глубоким слоям, что качественно совпадает с данными Армстронга-Джеймса и других (1992).
Эти стандартные значения параметров S RW , S I1 , S I2 использовались во всех наших компьютерных экспериментах, за исключением результатов, представленных на рисунках 10 и 11, где мы проанализировали влияние этих параметров на отчетные результаты.Там мы смоделировали модели схем со случайно выбранными значениями из независимых равномерных распределений в интервале [0,1 × стандартное значение, 3,1 × стандартное значение] для всех 3 параметров.
Наше компьютерное моделирование проверило, сколько информации о каждом предыдущем временном сегменте (длиной 30 мс) каждого из двух входных потоков было доступно гипотетическому проекционному нейрону в слоях 2/3 и гипотетическому проекционному нейрону в слое 5.. возбуждающие и тормозные пресинаптические нейроны для такого гипотетического считывающего нейрона были выбраны случайным образом таким же образом, как и для любого другого возбуждающего нейрона в этом слое (т.е., согласно рис. 1), но никаких синаптических связей от считывающего нейрона обратно в схему не было. Это составляло в среднем 84 пресинаптических нейрона для считывающего нейрона в слоях 2/3 и 109 пресинаптических нейронов для считывающего нейрона в слое 5. Вес синаптических связей от этих пресинаптических нейронов был оптимизирован для конкретных задач. В отличие от моделирования, описанного в Maass и др. (2002), результирующее количество входов в такой считывающий нейрон было намного меньше, чем размер схемы.Сами нейроны проекции или считывания были смоделированы как линейные нейроны, то есть их выход представлял собой взвешенную сумму спайков, отфильтрованных нижними частотами (экспоненциальный спад с постоянной времени 15 мс, моделирование постоянных времени синаптических рецепторов и мембраны считывающего устройства). нейрон). Были приняты меры для того, чтобы веса возбуждающих (тормозных) пресинаптических нейронов не могли стать отрицательными (положительными). Для этого мы использовали линейный метод наименьших квадратов с ограничениями неотрицательности (Lawson and Hanson 1974), чтобы оптимизировать веса для конкретной задачи.Это контрастирует с линейной регрессией, которая использовалась в Maass и др. (2002). Для каждого обучающего или тестового примера, который состоял из входа и целевого значения для считывающего нейрона, мы выполняли моделирование модели микросхемы. Каждый вход для считывающего нейрона был сгенерирован путем сбора отфильтрованной нижними частотами версии пресинаптических шиповых последовательностей для считывающего нейрона в момент времени t = 450 мс. Каждое соответствующее целевое значение было рассчитано для различных задач, описанных ниже (см. Результаты).Чтобы правильно применить линейный метод наименьших квадратов с ограничениями неотрицательности, последовательности импульсов тормозных (возбуждающих) нейронов были свернуты с отрицательными (положительными) экспоненциальными ядрами, а соответствующие веса считывания были умножены на -1 (+1) после обучения. Для задач классификации нейрон с линейным считыванием был обучен выводить метки классов, то есть 0 или 1, тогда как классификация была получена путем определения порога вывода на 0,5 (аналогично порогу срабатывания реального коркового нейрона).Этот алгоритм дает весовой вектор < w i ,… w n > с w i ≥ 0, если i -й пресинаптический нейрон считывания является возбуждающим. и w i ≤ 0, если i -й пресинаптический нейрон является тормозящим. В рамках этих (линейных) ограничений эта ограниченная форма линейной регрессии минимизирует ошибку считывания в обучающих примерах.(В MATLAB можно выполнить этот алгоритм оптимизации с помощью команды LSQNONNEG.) Это обычно приводило к присвоению веса 0 (соответствующего молчащему синапсу в биологической цепи) примерно 2/3 этих синапсов. Следовательно, типичный считывающий нейрон имел менее 40 ненулевых весов и, следовательно, гораздо меньшую способность извлекать информацию по сравнению с моделью, рассмотренной в Maass и др. (2002).
Для каждого компьютерного моделирования было создано не менее 10 схем.Для экспериментов, показанных на рисунках 5 и 8, мы использовали 20 схем. Мы также генерировали новые шаблоны всплесков каждый раз, когда рисовалась новая схема, чтобы избежать случайной зависимости от свойств конкретных шаблонов всплесков. Для обучения считывающих нейронов мы выполнили 1500 симуляций со случайно выбранными пуассоновскими входами в течение 450 мс, а для тестирования использовалось 300 симуляций с новыми случайно сгенерированными входами. Планки погрешностей на рисунках обозначают стандартные ошибки. Все результаты производительности в этой статье (за исключением некоторых результатов диагностики, представленных на рис.8, см. Легенду) предназначены для тестовых входов, которые не использовались для обучения считыванию, а также для недавно сгенерированных случайных начальных условий и фонового шума для всех нейронов в цепи.
Все моделирование проводилось с помощью программного обеспечения CSIM (Natschläger и др., 2003) в сочетании с MATLAB.
Результаты
Инжекция 2 входных потоков, состоящих из цугов пуассоновских спайков, в слой 4 и слои 2/3 модели микросхемы вызвала отклик (см.рис.2), чье последовательное начало в разных слоях качественно совпадает с данными о корковых микросхемах in vivo (Armstrong-James и др., 1992). Кроме того, частота воспламенения в слое 5 автоматически приобретает биологически реалистичное экспоненциальное распределение (см., Например, v. Vreeswijk and Sompolinsky 1996, 1998; Amit and Brunel 1997; Baddeley and others 1997). (Распределение скоростей воспламенения в слоях 2/3 и 4 отражает типичное распределение скоростей последовательностей импульсов Пуассона, которые были вызваны пуассоновским вводом в эти слои.Рисунок 3 дает представление о довольно большой вариабельности активности зажигания внутри схемы для одних и тех же схем ввода пиков, что является результатом дрожания на входе пиков (верхний ряд) и внутреннего шума (нижний ряд) из-за введение случайно изменяющихся фоновых входных токов ко всем нейронам для моделирования условий in vivo (см. Методы). (Кроме того, для всех рассматриваемых впоследствии вычислительных задач независимо выбранные паттерны спайков были ранее введены в качестве афферентных входов, вызывая довольно большую дисперсию начальных состояний динамических синапсов.Таким образом, смоделированные схемы качественно отражают обычно наблюдаемую большую вариабельность нервных реакций in vivo от испытания к испытанию на повторение одного и того же стимула.
Рисунок 3
Влияние временного дрожания входных пиков (гауссово распределение со средним значением 0 и SD 1 мс) и фонового шума нейронов в цепи на отклик схемы (см. Методы). Строки в середине и вверху показывают растры пиков, полученные в результате 2 испытаний с идентичным фоновым шумом и с образцами пиков на входе, которые были идентичны, за исключением их временного дрожания.В нижнем ряду показано, насколько растр пиков для испытания с новым фоновым шумом и идентичными шаблонами пиков на входе отличается от такового для испытания, показанного в средней строке. Это показывает, что смоделированные схемы (которые были подвержены обоим источникам шума) качественно отражают обычно наблюдаемую большую вариабельность нервных реакций in vivo от испытаний к испытаниям на повторение одного и того же стимула.
Рисунок 3
Влияние временного дрожания входных пиков (гауссово распределение со средним значением 0 и SD 1 мс) и фонового шума нейронов в цепи на отклик схемы (см. Методы).Строки в середине и вверху показывают растры пиков, полученные в результате 2 испытаний с идентичным фоновым шумом и с образцами пиков на входе, которые были идентичны, за исключением их временного дрожания. В нижнем ряду показано, насколько растр пиков для испытания с новым фоновым шумом и идентичными шаблонами пиков на входе отличается от такового для испытания, показанного в средней строке. Это показывает, что смоделированные схемы (которые были подвержены обоим источникам шума) качественно отражают обычно наблюдаемую большую вариабельность нервных реакций in vivo от испытаний к испытаниям на повторение одного и того же стимула.
Мы протестировали эти модели микросхем на множестве общих задач обработки информации, которые, вероятно, будут связаны с реальными вычислительными задачами нейронных микросхем в коре головного мозга: Для задач обработки информации с шаблонами спайков мы случайным образом сгенерировали шаблоны паттернов спайков, состоящие из 30 мс сегментов 40 последовательностей спайков Пуассона на частоте 20 Гц (см. рис. 4). Точнее, последовательности пиков каждого из 2 входных потоков имели длину 450 мс и состояли из 15 последовательных временных сегментов длиной 30 мс.Для каждого сегмента случайным образом были сгенерированы 2 шаблона паттернов шипов. Для фактического ввода один из 2 шаблонов каждого временного сегмента был выбран случайным образом (с равной вероятностью) и его вариация с шумом, где каждый всплеск перемещался на величину, взятую из гауссовского распределения со средним значением 0 и SD 1 мс (см. панель с правой стороны рис. 4) была введена в схему. Такой временной джиттер на входе пиков вызывает значительные изменения в отклике схемы (см. Рис. 3), и для считывающих нейронов классифицировать паттерны спайков является нетривиальной задачей, несмотря на эту довольно большую вариабельность отклика схемы от испытаний к испытаниям. .Мы также протестировали ретроактивную классификацию предыдущих паттернов спайков, которые были введены за 30 мс до этого и, следовательно, были «перезаписаны» независимо выбранными последующими паттернами спайков. Кроме того, было исследовано нелинейное вычисление исключающего ИЛИ (XOR) для шаблонов пиков в 2 одновременных входных потоках, чтобы проверить способность схемы извлекать и комбинировать информацию из обоих входных потоков нелинейным образом. Задача состоит в том, чтобы вычислить XOR (XOR выводит 1, если ровно один из двух его входных битов имеет значение 1, он выводит 0, если входные биты равны 00 или 11) двух битов, которые представляют метки двух шаблонов, из которых были сгенерированы самые последние образцы всплесков в 2 входных потоках (например,g., его целевой выход равен 1 для обоих временных сегментов для входа, показанного в правой части рис. 4). Обратите внимание, что это вычисление включает в себя операцию нелинейной привязки к шаблонам всплесков, потому что оно должно давать низкое выходное значение тогда и только тогда, когда либо шумные версии шаблонов всплесков с меткой 1 появляются как во входных потоках 1 и 2, либо если зашумленная версия шаблона шаблоны всплесков с меткой 0 появились как во входном потоке 1, так и во входном потоке 2.
-
классификация шаблонов всплесков в любом из двух афферентных входных потоков (требующая инвариантности к шуму и всплеску входного сигнала из другого входного потока)
-
временная интеграция информации, содержащейся в таких шаблонах всплесков
-
Слияние информации из шаблонов всплесков в обоих входных потоках нелинейным образом (связанное с задачами «привязки»)
-
вычислений в реальном времени для скоростей активации из обоих входных потоков.
Рисунок 4
Распределения входных данных для классификации паттернов спайков и задач XOR. Задача состоит в том, чтобы вычислить XOR двух битов, которые представляют метки 2 шаблонов, из которых были сгенерированы самые последние шаблоны всплесков в 2 входных потоках, то есть классифицировать как 1, если их метки шаблонов различны, и 0 в противном случае. . Последовательности пиков каждого из 2 входных потоков имели длину 450 мс и состояли из 15 временных сегментов длиной 30 мс. Для каждого сегмента случайным образом были сгенерированы 2 шаблона (40 последовательностей пуассоновских спайков при 20 Гц).Фактические последовательности пиков каждого входа длиной 450 мс, используемые для обучения или тестирования, были сгенерированы путем выбора для каждого сегмента одного из 2 ранее выбранных связанных шаблонов, а затем генерации версии с дрожанием путем перемещения каждого пика на величину, взятую из распределения Гаусса с среднее значение 0 и стандартное отклонение 1 мс (образец показан на панели справа).
Рисунок 4
Распределения входных данных для классификации паттернов спайков и задач XOR. Задача состоит в том, чтобы вычислить XOR двух битов, которые представляют метки 2 шаблонов, из которых были сгенерированы самые последние шаблоны всплесков в 2 входных потоках, то есть классифицировать как 1, если их метки шаблонов различны, и 0 в противном случае. .Последовательности пиков каждого из 2 входных потоков имели длину 450 мс и состояли из 15 временных сегментов длиной 30 мс. Для каждого сегмента случайным образом были сгенерированы 2 шаблона (40 последовательностей пуассоновских спайков при 20 Гц). Фактические последовательности пиков каждого входа длиной 450 мс, используемые для обучения или тестирования, были сгенерированы путем выбора для каждого сегмента одного из 2 ранее выбранных связанных шаблонов, а затем генерации версии с дрожанием путем перемещения каждого пика на величину, взятую из распределения Гаусса с среднее значение 0 и стандартное отклонение 1 мс (образец показан на панели справа).
Кроме того, мы проанализировали линейные и нелинейные вычисления для изменяющихся во времени скоростей срабатывания 2 входных потоков. Последовательности пиков каждого из 2 входных потоков имели длину 450 мс и состояли из 15 последовательных временных сегментов длиной 30 мс. Для каждого входного потока и каждого временного сегмента были сгенерированы 4 последовательности пиков Пуассона со случайно выбранной частотой от 15 до 25 Гц. Фактические скорости воспламенения, использованные для вычислений этих входных скоростей воспламенения, были рассчитаны на основе этих последовательностей импульсов со скользящим окном шириной 15 мс.Для этих тестов мы использовали входные потоки, состоящие всего из 4 последовательностей импульсов, поскольку производительность как схем на основе данных, так и схем управления была довольно низкой, если входные скорости были представлены 40 последовательностями импульсов.
Новые вычислительные свойства моделей микросхем на основе данных показаны на рисунке 5 (серые столбцы). Производительность обученных считываний для тестовых входных данных (которые генерируются из того же распределения, что и обучающие примеры, но не показаны во время обучения) была измерена для всех задач двоичной классификации с помощью коэффициента каппа, который находится в диапазоне [-1, 1], и принимает значение ≥0 тогда и только тогда, когда результирующая классификация тестовых примеров дает меньше ошибок, чем случайное предположение.(Коэффициент каппа измеряет процент соответствия между двумя классами, ожидаемыми сверх случайности, и определяется как ( P o — P c ) / (1 — P c ), где P o — наблюдаемое совпадение, а P c — случайное совпадение. Таким образом, для классификации на 2 одинаково часто встречающихся класса получается P c = 0,5.) Для задач, требующих аналогового вывода. значение, производительность обученного считывания измерялась на тестовых примерах по его коэффициенту корреляции с аналоговым целевым выходом.Точность вычислений, достигаемая обученными нейронами считывания из моделей микросхем с ламинарной структурой на основе данных, сравнивается с точностью, достигаемой обученными нейронами считывания из схем управления (черные полосы на рис. 5), чья ламинарная структура связности на основе данных была зашифрована. путем замены исходных и целевых нейронов каждого синаптического соединения в цепи на случайно выбранные нейроны того же типа, то есть возбуждающие или тормозящие нейроны, при условии, что синаптическое соединение не возникает дважды (мы обычно будем называть эти модели схем как аморфные схемы).Обратите внимание, что эта процедура не изменяет общее количество синапсов, выравнивание типа синапса относительно пре- и постсинаптического типа нейрона, глобальное распределение синаптических весов или других синаптических параметров, или наборы нейронов, которые получают афферентные входы или обеспечивают вывод на считывающие нейроны. Структура связности аморфных цепей (за исключением различных вероятностей связи между популяциями возбуждающих и тормозных нейронов и внутри них) идентична структуре графов, изучаемых в классической теории случайных графов (Bollobas 1985) (с 4 вероятностями связи для этих двух популяций). взяты из схем на основе данных).
Рисунок 5
Производительность обученных нейронов с линейным считыванием на уровнях 2/3 и уровне 5 (см. Методы) для различных задач классификации по шаблонам пиков и вычислений, выполняемых на скоростях двух входных потоков, как для моделей ламинарных микросхем на основе данных (серые полосы) и для цепей управления, в которых ламинарная структура была зашифрована (черные полосы). tcl 1/2 ( t ) обозначает ретроактивную классификацию зашумленных паттернов всплесков (входные данные были сгенерированы, как показано на рис.4) во входных потоках 1 или 2, которые были введены в течение предыдущего временного интервала [ t — 30 мс, t ] в 2 класса в соответствии с шаблоном, из которого был сгенерирован каждый образец пиков. tcl 1/2 ( t — Δ t ) относится к более сложной задаче классифицировать во время t пиковый образец перед последним, который был введен в течение временного интервала [ t — 60 мс, t — 30 мс]. Для классификации XOR задача состоит в том, чтобы вычислить в момент времени t = 450 мс XOR меток шаблона (0 или 1) обоих входных потоков, введенных в течение предыдущего временного сегмента [420 мс, 450 мс].Справа результаты вычислений в реальном времени для изменяющихся во времени скоростей срабатывания r 1 ( t ) входного потока 1 и r 2 ( t ) из входной поток 2 (оба состоят из 4 последовательностей шипов Пуассона с независимо изменяющимися скоростями воспламенения в 2 входных потоках). Белые полосы показывают результаты производительности для 2 целевых функций r 1 ( t ) / r 2 ( t ) и ( r 1 ( t ) — r 2 ( t )) 2 , а жирные столбцы — производительность нелинейных компонентов этих вычислений в реальном времени в любое время 30 мс).
Рисунок 5
Производительность обученных нейронов с линейным считыванием на уровнях 2/3 и уровне 5 (см. Методы) для различных задач классификации по шаблонам пиков и вычислений, выполняемых на скоростях двух входных потоков, как для ламинарной микросхемы на основе данных модели (серые столбцы) и для цепей управления, в которых ламинарная структура была зашифрована (черные столбцы). tcl 1/2 ( t ) обозначает ретроактивную классификацию зашумленных паттернов всплесков (входные данные были сгенерированы, как показано на рис.4) во входных потоках 1 или 2, которые были введены в течение предыдущего временного интервала [ t — 30 мс, t ] в 2 класса в соответствии с шаблоном, из которого был сгенерирован каждый образец пиков. tcl 1/2 ( t — Δ t ) относится к более сложной задаче классифицировать во время t пиковый образец перед последним, который был введен в течение временного интервала [ t — 60 мс, t — 30 мс]. Для классификации XOR задача состоит в том, чтобы вычислить в момент времени t = 450 мс XOR меток шаблона (0 или 1) обоих входных потоков, введенных в течение предыдущего временного сегмента [420 мс, 450 мс].Справа результаты вычислений в реальном времени для изменяющихся во времени скоростей срабатывания r 1 ( t ) входного потока 1 и r 2 ( t ) из входной поток 2 (оба состоят из 4 последовательностей шипов Пуассона с независимо изменяющимися скоростями воспламенения в 2 входных потоках). Белые полосы показывают результаты производительности для 2 целевых функций r 1 ( t ) / r 2 ( t ) и ( r 1 ( t ) — r 2 ( t )) 2 , а жирные столбцы — производительность нелинейных компонентов этих вычислений в реальном времени в любое время 30 мс).
Рисунок 5 показывает, что схемы на основе данных работают значительно лучше для большинства рассмотренных задач обработки информации, за исключением задач скорости для считывающего нейрона на уровне 5 и задачи tcl 2 ( t −Δ t ) для считывающего нейрона в слоях 2/3 (для которых повышение производительности не было значительным). В частности, потенциальные проекционные нейроны в слоях 2/3 и уровне 5 имеют в ламинарной схеме на основе данных лучший доступ к информации, содержащейся в текущем и предшествующем паттернах спайков из любого афферентного входного потока.Результаты показывают, что потенциальные считывающие нейроны могут классифицировать паттерны спайков от любого афферентного входного потока независимо от одновременно вводимого паттерна спайков в другом входном потоке (и независимо от довольно высокой вариабельности от испытания к испытанию, показанной на рис. 3). Одна интересная деталь может быть замечена для двух задач, связанных с расчетами скоростей стрельбы. Здесь производительность схем, основанных на данных, и схем управления примерно одинакова (см. Белые полосы на рис.5), но показания со слоев 2/3 работают для схем на основе данных значительно лучше на нелинейной составляющей этих вычислений (см. Жирные полосы перед белыми полосами на рис.5). (Эта нелинейная составляющая целевых функций r 1 / r 2 и ( r 1 — r 2 ) 2 в результате вычитания из этих функций [для рассмотренное распределение r 1 , r 2 ] оптимально подобранная линейная функция).
Фактическая производительность, достигаемая с помощью обученных считываний с моделей микросхем, зависит от размера схемы (теоретические результаты предсказывают, что она автоматически улучшится при увеличении размера схемы [Maass and others 2002]).Это показано на рисунке 6 для одной из вычислительных задач, рассмотренных на рисунке 5 (XOR меток шаблонов всплесков из 2 афферентных входных потоков), как для схем на основе данных, так и для схем управления. Рисунок 6 также показывает, что превосходные характеристики схем, основанных на данных, не зависят от размера схемы. Улучшение производительности схем, состоящих из 1000 нейронов, по сравнению со схемами, состоящими из 160 нейронов, несколько меньше для задач скорости. Например, производительность считывающего нейрона в слоях 2/3 или 5, обученных для двух задач скорости r 1 / r 2 и ( r 1 — r 2 ) 2 увеличивается в среднем только на 25% для схем на основе данных и на 20% для аморфных схем.
Рисунок 6
Производительность (см. Методы) проекционных нейронов в слоях 2/3 и 5 для различных размеров схем, с ламинарной структурой на основе данных и без нее, для вычисления задачи XOR. Эти результаты показывают, что превосходные характеристики схем, основанных на данных, не зависят от размера схемы.
Рисунок 6
Производительность (см. Методы) проекционных нейронов на уровнях 2/3 и уровне 5 для различных размеров схемы, с ламинарной структурой на основе данных и без нее, для вычисления задачи XOR.Эти результаты показывают, что превосходные характеристики схем, основанных на данных, не зависят от размера схемы.
Предыдущие результаты показывают, что микросхемы с ламинарной структурой на основе данных обладают превосходными вычислительными возможностями для большого разнообразия вычислительных задач. Возникает вопрос «почему» это так. Мы подходим к этому вопросу с двух разных точек зрения. Сначала мы исследуем, какие аспекты структуры схемы на основе данных важны для их превосходной производительности.Очевидно, что наша процедура создания аморфных схем разрушает не только слоистую структуру схем на основе данных, но и другие структурные свойства, такие как распределение степеней узлов в нижележащем графе связности и его кластерная структура. Поэтому мы вводим 3 дополнительных типа схем управления, чтобы проанализировать влияние конкретных конструктивных особенностей на производительность. Во-вторых, мы демонстрируем характерную особенность внутренней динамики этих различных типов схем, которая коррелирует с их вычислительной производительностью.
Мы сначала изучили вычислительное влияние свойств малого мира схем, основанных на данных. Сети малого мира были охарактеризованы Уоттсом и Строгатцем (1998) с помощью двух свойств. У них более высокий коэффициент кластеризации (измеряется долей непосредственных соседей узлов в графе, которые связаны ссылкой), чем у аморфных цепей, при сохранении сопоставимой средней длины кратчайшего пути. (Обратите внимание, что оба свойства относятся к структуре нижележащего «неориентированного» графа, в котором направленные ребра заменены неориентированными связями.) Основанные на данных модели кортикальных микросхем на самом деле имеют свойства маленького мира в соответствии с этим определением, потому что их коэффициент кластеризации (который имеет значение 36%) на 38% выше, чем в аморфных схемах, тогда как их средняя длина кратчайшего пути примерно такая же. (1,75 ссылки). (По данным Hilgetag и др. [2000], дальнодействующие корковые связи мозга кошек и макак имеют коэффициенты кластеризации 55% и 46% соответственно). Чтобы решить, достаточно ли этих свойств малого мира для обеспечения превосходных вычислительных свойств схем на основе данных, мы создали схемы управления, которые имеют такой же размер, коэффициент кластеризации и среднюю кратчайшую длину пути, что и схемы на основе данных по пространственному алгоритм роста, описанный в Kaiser and Hilgetag (2004) (с параметрами α = 4, β = 1.32 и 560 узлов). Впоследствии эти неориентированные графы были преобразованы в ориентированные графы путем случайной замены каждого ребра синапсом (в случайной ориентации) или взаимной синаптической связью с вероятностью, так что общее количество синаптических связей и взаимных синаптических связей идентично соответствующему количеству для схемы на основе данных. (Следует отметить, что эта процедура не воспроизводит такую же долю типов синапсов, как для схем на основе данных и аморфных схем).
Для 3-го типа схемы управления мы рассмотрели схемы, которые имеют такое же распределение входных и исходящих степеней для нейронов, что и схемы, основанные на данных. Входящая и исходящая степень нейрона определяется как общее количество входящих и исходящих синаптических соединений, соответственно.
Для этой цели мы сгенерировали схемы на основе данных и впоследствии обменивались целевыми нейронами случайно выбранных пар синапсов с пре- и постсинаптическими нейронами той же категории (возбуждающие или тормозящие), пока не исчезла ламинарно-специфическая структура связности (нет обмен был произведен, если какое-либо из двух образовавшихся новых соединений уже существовало).Этот тип схемы также имеет свойства маленького мира, но средний коэффициент кластеризации был меньше, чем для схем, основанных на данных (всего на 27% выше, чем в аморфных сетях). Мы называем этот тип цепей цепями с регулируемой степенью.
Цепи, управляемые степенями, сохраняют распределение степеней между нейронами, которые получают внешний ввод или обеспечивают ввод для считывающего нейрона. Поэтому мы добавили схемы управления, называемые схемами с управляемой степенью, без специфичности ввода или вывода, путем случайного обмена нейронами на разных уровнях схем со степенью управления.Распределение степеней нейронов для всех 5 типов цепей показано на рисунке 7.
Рисунок 7
Распределение нейронов в разных популяциях для 5 типов цепей (усредненное по 100 цепям). Все схемы имеют распределения степеней, которые могут быть лучше аппроксимированы суммами гауссианов, чем степенной закон вида P ( d ) ∝ d −γ для нейронов степени d и положительная константа γ ( я.е., схемы не свободны от масштаба). Коэффициенты корреляции для наименьших квадратов для сумм гауссианов и степенных распределений составляют> 0,96 и <0,08, соответственно. Таким образом, ни одна из этих схем не является безмасштабной, что показывает, что их различие в производительности не может быть объяснено на основе этой концепции. Вычислительный анализ (см. Таблицу 2) подразумевает, что различные местоположения пиков для разных уровней схем, основанных на данных, важны для их превосходных вычислительных характеристик.
Рисунок 7
Распределение нейронов в разных популяциях для 5 типов цепей (среднее по 100 цепям). Все схемы имеют распределения степеней, которые могут быть лучше аппроксимированы суммами гауссианов, чем степенной закон вида P ( d ) ∝ d −γ для нейронов степени d и положительная константа γ ( т.е. схемы не свободны от масштаба). Коэффициенты корреляции для наименьших квадратов для сумм гауссианов и степенных распределений> 0.96 и <0,08 соответственно. Таким образом, ни одна из этих схем не является безмасштабной, что показывает, что их различие в производительности не может быть объяснено на основе этой концепции. Вычислительный анализ (см. Таблицу 2) подразумевает, что различные местоположения пиков для разных уровней схем, основанных на данных, важны для их превосходных вычислительных характеристик.
Важной структурной особенностью всех типов цепей, рассмотренных до сих пор, является выравнивание типа синапса относительно пре- и постсинаптического типа нейрона в соответствии с таблицей 1.Чтобы проанализировать влияние выравнивания динамических синапсов на производительность, мы случайным образом обменяли триплеты синаптических параметров, то есть U, D и F , которые определяют краткосрочную пластичность между всеми синапсами. В последнем типе схемы управления мы заменили все динамические синапсы статическими синапсами (с измененными весами, чтобы средняя частота срабатывания в слое 5 оставалась неизменной).
Сводные характеристики всех 7 различных типов цепей управления показаны в таблице 2.Свойство малого мира в некоторой степени увеличивает производительность аморфных схем, но более важной структурной особенностью является распределение степеней, определяемое схемами на основе данных. Если это распределение степеней соответствует распределению степеней схем на основе данных для каждого отдельного уровня и, следовательно, соответствует также конкретной топологии ввода и вывода схем на основе данных, средняя производительность сопоставима с производительностью схем на основе данных. Таблица 2 также показывает (см. Столбец 5), что назначение типов синапсов на основе данных (в соответствии с таблицей 1) важно для хорошей вычислительной производительности.Последний столбец показывает, что схемы со статическими синапсами также имеют худшие вычислительные свойства.
Чтобы выяснить взаимосвязь между внутренними свойствами динамики схемы и вычислительной производительностью, мы более подробно изучили одну фундаментальную, но относительно простую задачу обработки информации: ретроактивную классификацию паттернов спайков на 2 класса, несмотря на шум. Точнее, задача заключалась в том, чтобы классифицировать входные последовательности пиков 2 × 4, сгенерированные из 2 шаблонов (как на рис.4) на 2 класса, несмотря на последующий период ожидания в 100 мс (в течение которого в каждом случае вводились идентичные последовательности пиков) и несмотря на сильно различающиеся начальные условия (вызванные разными предшествующими входными пиками) и относительно высокий внутренний шум, который моделирует бомбардировку несвязанным фоновым синаптическим входом в состоянии с высокой проводимостью (сравните средний и нижний ряды на рис. 3, чтобы увидеть стохастические изменения в спайковой реакции, вызванной последним). Эта задача проверяет способность схем поддерживать информацию о паттернах всплесков, которые были введены более 100 мс назад.Эта информация уменьшается из-за шума, возникающего из-за внутреннего шума в нейронах и изменения начальных условий (внутриклассовая дисперсия). Пунктирные серые линии на рисунке 8 показывают, что считывающие нейроны в слоях 2/3 и уровне 5 схем, основанных на данных, могут довольно быстро обучаться на относительно небольшом количестве обучающих примеров, чтобы угадать, какой из двух фиксированных паттернов спайков был ранее введен. Сравнение с черными линиями показывает, что их ошибка на новых примерах этой задачи (ошибка теста) значительно меньше, чем у считывающих нейронов в аморфных схемах управления.Более того, это преимущество не уменьшается, когда становится доступным больше обучающих примеров. Превосходство считывания из схем на основе данных является результатом как лучшего соответствия обучающим данным (сплошные кривые на рис. 8), так и меньшей ошибки обобщения (= расстояние между сплошной и пунктирной кривой). (Обратите внимание, что все типы схем имеют для меньшего числа обучающих примеров меньшую ошибку на обучающем наборе, но большую ошибку на тестовом наборе из-за хорошо известного эффекта переобучения, который широко изучается в статистической теории обучения [Vapnik 1998] ).
Рисунок 8
Ошибка обучения и тестирования считываний из моделей на основе данных и моделей аморфных микросхем в зависимости от размера обучающей выборки. Задача заключалась в обратной классификации 2 случайно созданных паттернов спайков длиной 100 мс (состоящих из 4 последовательностей спайков Пуассона с частотой 20 Гц) после того, как идентичный ввод длительностью 100 мс был впоследствии введен в схему, несмотря на различные начальные условия (вызванные независимыми генерируются предыдущие входные сигналы пуассоновских всплесков того же типа) и шумные фоновые входные токи, как и раньше.Верхняя панель показывает производительность потенциального считывающего нейрона в слоях 2/3 с 84 пресинаптическими нейронами, обученными линейной регрессией с ограничениями по знакам (см. Методы). На нижней панели показаны характеристики потенциального считывающего нейрона в слое 5 со 109 пресинаптическими нейронами. Оба типа считывания лучше работают для ламинарной схемы на основе данных как на обучающем наборе (с новыми случайными рисунками начальных условий и фонового шума), так и на тестовом наборе. Это справедливо для всех рассматриваемых размеров обучающей выборки.
Рисунок 8
Ошибка обучения и тестирования считываний из моделей микросхем на основе данных и аморфных микросхем в зависимости от размера обучающей выборки. Задача заключалась в обратной классификации 2 случайно созданных паттернов спайков длиной 100 мс (состоящих из 4 последовательностей спайков Пуассона с частотой 20 Гц) после того, как идентичный ввод длительностью 100 мс был впоследствии введен в схему, несмотря на различные начальные условия (вызванные независимыми генерируются предыдущие входные сигналы пуассоновских всплесков того же типа) и шумные фоновые входные токи, как и раньше.Верхняя панель показывает производительность потенциального считывающего нейрона в слоях 2/3 с 84 пресинаптическими нейронами, обученными линейной регрессией с ограничениями по знакам (см. Методы). На нижней панели показаны характеристики потенциального считывающего нейрона в слое 5 со 109 пресинаптическими нейронами. Оба типа считывания лучше работают для ламинарной схемы на основе данных как на обучающем наборе (с новыми случайными рисунками начальных условий и фонового шума), так и на тестовом наборе. Это справедливо для всех рассматриваемых размеров обучающей выборки.
Более внутреннее объяснение лучшей вычислительной производительности ламинарных схем на основе данных дает теория вычислений в динамических системах (для обзора см. Legenstein and Maass 2005). На рисунке 9 показано, что схема на основе данных работает в значительно менее хаотическом режиме, чем аморфная схема управления. Его чувствительность к незначительным различиям в начальных условиях также меньше, чем у других трех типов схем управления, которые сохраняют выбранные аспекты структуры сети на основе данных.Менее хаотическая динамика подразумевает лучшую способность обобщения новых входных данных для многих различных типов динамических систем. Это наблюдение представляет интерес, поскольку можно предположить, что количество синапсов на нейрон является важным параметром, определяющим степень хаоса в цепи. Но все схемы, результаты которых представлены на рисунке 9, имеют одинаковое количество синапсов.
Рисунок 9
Евклидовы расстояния в траекториях состояний схемы (точнее: от входных векторов до считываемых нейронов в слоях 2/3 и в слое 5) в результате перемещения одиночного входного пика (на 100 мс) на 0.5 мс. Показано среднее значение моделирования 400 случайно сгенерированных цепей с различными начальными условиями и фоновым шумом. Начальные условия и внутренний шум были выбраны идентичными в обоих испытаниях каждого моделирования, как и в стандартных тестах для оценки показателя Ляпунова (детерминированных) динамических систем, см. Legenstein and Maass (2005). Кривые показывают устойчивые различия в евклидовом расстоянии между состояниями цепей, которые примерно в два раза больше для аморфных цепей, тем самым указывая на более хаотическую динамику, чем в ламинарных цепях с тем же количеством нейронов и синапсов.
Рисунок 9
Евклидовы расстояния в траекториях состояний схемы (точнее: от входных векторов до считывающих нейронов в слоях 2/3 и в слое 5) в результате перемещения одиночного входного пика (на 100 мс) на 0,5 мс. Показано среднее значение моделирования 400 случайно сгенерированных цепей с различными начальными условиями и фоновым шумом. Начальные условия и внутренний шум были выбраны идентичными в обоих испытаниях каждого моделирования, как и в стандартных тестах для оценки показателя Ляпунова (детерминированных) динамических систем, см. Legenstein and Maass (2005).Кривые показывают устойчивые различия в евклидовом расстоянии между состояниями цепей, которые примерно в два раза больше для аморфных цепей, тем самым указывая на более хаотическую динамику, чем в ламинарных цепях с тем же количеством нейронов и синапсов.
Сплошные кривые на рисунке 8 показывают, что еще одна причина лучшей вычислительной производительности моделей цепей на основе данных заключается в том, что синаптические веса их считывающих нейронов могут лучше соответствовать обучающим данным. Этот факт можно объяснить с точки зрения «классовой дисперсии» состояний схемы большой размерности, вызванной изменением начальных условий и внутреннего шума (для повторных испытаний с одним и тем же импульсом на входе схемы).Корреляция между этой классовой дисперсией обучающих данных и ошибкой классификации обученных считываний тестовых данных для задачи, рассмотренной на рисунке 8, составляла 0,80 для показаний из слоев 2/3 и 0,72 для показаний из уровня 5 для ламинарных схем на основе данных. .
На рис. 10 показано, что для аморфных цепей управления это внутриклассовое отклонение обычно больше. Кроме того, на рисунке 10 показано, что эта функция подавления шума динамики в ламинарных схемах на основе данных не является случайным свойством фиксированной настройки трех параметров S RW , S I1 , S I2 (который масштабирует веса повторяющихся синаптических соединений, амплитуды входного потока 1 и амплитуды входного потока 2), который мы использовали для моделирования, о котором сообщалось до сих пор (см. Методы).На рисунке 10 показано, что эта функция подавления шума появляется также для всех других (случайно выбранных) настроек этих параметров, которые были протестированы.
Рисунок 10
Структура схемы на основе данных снижает влияние шума. Для каждого из 2 типов схем, то есть для схем на основе данных и аморфных схем, было сгенерировано 50 схем, и 500 идентичных входов, сгенерированных для задачи на рисунке 8, были введены в каждую из них. Разница в дисперсии откликов цепей (в среднем по 50 цепям) оценивалась с точки зрения считывающих нейронов.Точнее, мы измерили дисперсию входных данных для считывающих нейронов после 500-кратного ввода того же входа в схему и проанализировали, насколько эта дисперсия уменьшилась для структуры схемы на основе данных (выраженной в процентах изменения по сравнению с аморфной структурой). схемы управления). Меньшая дисперсия для схем, основанных на данных, показывает, что на их динамику меньше влияют внутренний шум и различные начальные условия, тем самым обеспечивая лучшие возможности обобщения обученных считываний.Этот эксперимент был повторен для 30 случайно выбранных настроек параметров масштабирования S RW , S I1 , S I2 (см. Методы), и на этом рисунке показано, сколько из этих настроек параметра a определенное снижение шума было достигнуто для цепей, основанных на данных. Среднее отклонение в классе для всех настроек параметров составило 0,58, а стандартное отклонение — 0,29 для схем на основе данных. Проценты для 5 из этих цепей не были введены в этот график, потому что их классовая дисперсия была ниже 0.01 из-за того, что они почти не ответили на ввод. Процент изменения классовой дисперсии для стандартной настройки параметров масштабирования составил -38 для показаний уровня 2/3 и -41 для показаний уровня 5. Эти результаты показывают, что способность схем на основе данных снижать уровень шума не была случайным свойством стандартной настройки параметров масштабирования.
Рисунок 10
Структура схемы на основе данных снижает влияние шума. Для каждого из 2 типов схем, то есть для схем на основе данных и аморфных схем, было сгенерировано 50 схем, и 500 идентичных входов, сгенерированных для задачи на рисунке 8, были введены в каждую из них.Разница в дисперсии откликов цепей (в среднем по 50 цепям) оценивалась с точки зрения считывающих нейронов. Точнее, мы измерили дисперсию входных данных для считывающих нейронов после 500-кратного ввода того же входа в схему и проанализировали, насколько эта дисперсия уменьшилась для структуры схемы на основе данных (выраженной в процентах изменения по сравнению с аморфной структурой). схемы управления). Меньшая дисперсия для схем, основанных на данных, показывает, что на их динамику меньше влияют внутренний шум и различные начальные условия, тем самым обеспечивая лучшие возможности обобщения обученных считываний.Этот эксперимент был повторен для 30 случайно выбранных настроек параметров масштабирования S RW , S I1 , S I2 (см. Методы), и на этом рисунке показано, сколько из этих настроек параметра a определенное снижение шума было достигнуто для цепей, основанных на данных. Среднее отклонение в классе для всех настроек параметров составило 0,58, а стандартное отклонение — 0,29 для схем на основе данных. Проценты для 5 из этих цепей не были введены в этот график, потому что их классовая дисперсия была ниже 0.01 из-за того, что они почти не ответили на ввод. Процент изменения классовой дисперсии для стандартной настройки параметров масштабирования составил -38 для показаний уровня 2/3 и -41 для показаний уровня 5. Эти результаты показывают, что способность схем на основе данных снижать уровень шума не была случайным свойством стандартной настройки параметров масштабирования.
Рисунок 11 показывает, что превосходные вычислительные характеристики моделей ламинарных микросхем на основе данных не являются случайным следствием конкретного выбора этих трех параметров, но сохраняются для большинства их потенциальных значений.Этот факт демонстрируется здесь для XOR на паттернах спайков, которые уже обсуждались ранее. (Стандартное отклонение производительности считываний от схем управления для различных настроек параметров составляло 0,15 для показаний со слоев 2/3 и 0,18 для показаний со слоя 5. Улучшение производительности для ламинарных схем на основе данных в некоторой степени коррелировало с производительностью [коэффициент корреляции 0,16 для слоев 2/3, 0,59 для показаний слоя 5]). Это говорит о том, что ламинарная схема имеет для некоторых задач превосходные вычислительные возможности для довольно большого изменения динамических режимов.Это представляет интерес, потому что разные поведенческие состояния, разные состояния гомеостатических процессов или разные входные интенсивности могут привести к множеству различных динамических режимов корковых микросхем.
Рисунок 11
Процент улучшения производительности считывания из ламинарных цепей для различных значений трех параметров масштабирования для той же задачи XOR, как показано на рисунках 4 и 5 (но только с 2 × 4 последовательностями входных пиков). Процент улучшения был измерен для 16 случайно выбранных настроек параметров масштабирования S RW , S I1 и S I2 .Две из этих настроек дали чрезвычайно низкую производительность как для схем, основанных на данных, так и для аморфных схем (ниже 0,08, следовательно, ниже SD данных производительности для всех 16 настроек параметров) и поэтому были исключены из графика. Улучшение производительности при стандартной настройке этих параметров составило 74% для показаний слоев 2/3 и 64% для показаний уровня 5. Это говорит о том, что ламинарная схема обладает превосходными вычислительными возможностями для большинства настроек параметров, следовательно, для широкого разнообразия интенсивности стимулов и регуляторных состояний нейронных систем in vivo.
Рисунок 11
Процент улучшения производительности считывания из ламинарных цепей для различных значений трех параметров масштабирования для той же задачи XOR, как показано на рисунках 4 и 5 (но только с 2 × 4 последовательностями входных пиков). Процент улучшения был измерен для 16 случайно выбранных настроек параметров масштабирования S RW , S I1 и S I2 . Две из этих настроек дали чрезвычайно низкую производительность как для схем на основе данных, так и для аморфных схем (ниже 0.08, следовательно, ниже стандартного отклонения рабочих характеристик для всех 16 значений параметров) и поэтому не были включены в график. Улучшение производительности при стандартной настройке этих параметров составило 74% для показаний слоев 2/3 и 64% для показаний уровня 5. Это говорит о том, что ламинарная схема обладает превосходными вычислительными возможностями для большинства настроек параметров, следовательно, для широкого разнообразия интенсивности стимулов и регуляторных состояний нейронных систем in vivo.
Обсуждение
Мы продемонстрировали, что структура ламинарной связи на основе данных расширяет возможности обработки информации в моделях кортикальных микросхем.В частности, мы показали, что такая модель схемы на основе данных может накапливать, удерживать и объединять информацию, содержащуюся в двух афферентных входных потоках пиков. Следует отметить, что вычисления, которые были проанализированы в наших компьютерных экспериментах, были биологически реалистичными вычислениями в реальном времени для динамически изменяющихся входных потоков, а не статическими вычислениями для пакетных входных данных, которые обычно рассматриваются в исследованиях моделирования. В отличие от схемных моделей из Buonomano и Merzenich (1995) и Maass и др. (2002), схемные модели, проанализированные в этой статье, не только имеют биологически реалистичную ламинарную структуру, но также состоят из нейронов типа Ходжкина-Хаксли (с дополнительными фоновый ввод основан на данных, которые предположительно являются репрезентативными для состояния высокой проводимости корковых цепей in vivo [Destexhe and others 2003]).Кроме того, моделирование, обсуждаемое в этой статье, учитывает существенно большую вариабельность от испытания к испытанию. Кроме того, информация извлекалась не из всех нейронов, как в Buonomano и Merzenich (1995) и Maass и др. (2002), а из гораздо меньшего подмножества нейронов, которое представляет собой типичный набор пресинаптических нейронов для проекционного нейрона в слоях 2/3 или 5. Кроме того, получение информации такими проекционными нейронами впервые было связано с ограничением, согласно которому знаки веса входящих синапсов не могут выбираться произвольно в биологической цепи, а определяются типом (возбуждающим или тормозящим) каждый пресинаптический нейрон.Хотя это означает, что не вся мощность линейной регрессии (или правила обучения персептрона) может быть использована для оптимизации таких более реалистичных показаний, мы показываем, что даже в этих биологически более реалистичных условиях значительный объем информации может быть извлечен проекционными нейронами. в слоях 2/3 или уровне 5. Кроме того, результаты на Рисунке 6 показывают, что их производительность увеличивается с увеличением размера схемы, что позволяет предположить, что почти идеальная производительность будет достигнута с помощью модели схемы, которая достаточно велика, так что количество пресинаптические нейроны приближаются к реальным значениям в несколько тысяч.
Мы продемонстрировали на рисунке 5, что модели ламинарных микросхем на основе данных работают значительно лучше, чем схемы управления (которые не имеют ламинарных структур, но в остальном идентичны в отношении своих компонентов и общей статистики соединений) для широкого спектра фундаментальной информации — задачи обработки. Это превосходство сохраняется для большинства настроек параметров, которые масштабируют глобальную силу афферентных входов и повторяющихся связей, соответствующих широкому диапазону интенсивности стимулов и регуляторных состояний нейронных систем in vivo (рис.11). Мы также проанализировали, какой аспект структуры связности ламинарных схем на основе данных отвечает за их лучшую вычислительную производительность. Мы пришли (на основе результатов, представленных в Таблице 2) к выводу, что их особое распределение степеней узлов (относительно входов схемы и проекционных нейронов) является основной причиной, в большей степени, чем свойство ограниченного мира данных — на основе схем. Мы предполагаем, что это вычислительное превосходство ламинарных схем можно понять с точки зрения свойств динамической системы, которая определяется такими моделями микросхем.Мы показали на рисунках 9 и 10, что динамика ламинарных цепей несколько меньше зависит от внутреннего шума и шума на входе, тем самым обеспечивая лучшие возможности обобщения обученных считываний и лучшее соответствие обучающим данным из-за меньшей дисперсии в ответах цепей. .
По-видимому, модели нейронных цепей, рассмотренные в этой статье, представляют собой наиболее подробные модели корковых микросхем, основанные на данных, возможности обработки информации которых были проанализированы до сих пор.Результаты этого анализа показывают, что с помощью обширного компьютерного моделирования можно продемонстрировать конкретные вычислительные последствия их ламинарной структуры, тем самым создавая связь между подробными анатомическими и нейрофизиологическими данными и их вероятными вычислительными последствиями. Мы ожидаем, что эта программа может быть продолжена для выяснения также функциональных последствий дальнейших деталей кортикальных микросхем, таких как описанные, например, у Гупта и др. (2000), Штайгера и др. (2000), Шуберта и др. (2001), Бинцеггера. и другие (2004 г.), Каллавей (2004 г.), Маркрам и другие (2004 г.) и Йошимура и другие (2005 г.).
Мы хотели бы поблагодарить Эда Каллэуэя, Родни Дугласа, Рольфа Кеттера, Генри Маркрама и Алекса Томсона за полезные обсуждения исследований, связанных с этой статьей. Работа частично поддержана австрийским научным фондом Fonds zur Förderung der Wissenschaftlichen Forschung (FWF), проект # P15386 и # S9102-N04, проект анализа паттернов, статистического моделирования и вычислительного обучения # IST2002-506778 и Fast Analog Computing with Emergent Проект «Переходные государства» № FP6-015879 Европейского Союза.
Список литературы
,.Модель глобальной спонтанной активности и локальной структурированной активности в периоды задержки в коре головного мозга
,Cereb Cortex
,1997
, vol.7
3
(стр.237
—252
),,,,.Стимульная зависимость двухуровневых колебаний мембранного потенциала зрительной коры головного мозга кошки
,Nat Neurosci
,2000
, vol.3
6
(стр.617
—621
),,.Поток возбуждения в коре головного мозга крысы при столкновении с одиночной вибриссой
,J Neurophysiol
,1992
, vol.68
4
(стр.1345
—1358
),,,,,,.Ответы нейронов первичной и нижней височной зрительной коры на естественные сцены
,Proc R Soc Lond B Biol Sci
,1997
, vol.264
1389
(стр.1775
—1783
),,.Количественная карта цепи первичной зрительной коры головного мозга кошки
,J Neurosci
,2004
, vol.24
39
(стр.8441
—8453
). ,Случайные графики
,1985
Лондон
Academic Press
,,.Визуальный ввод вызывает временное и сильное подавление шунтирования в зрительных корковых нейронах
,Nature
,1998
, vol.393
6683
(стр.369
—373
),.Временная информация, преобразованная в пространственный код нейронной сетью с реалистичными свойствами
,Science
,1995
, vol.267
(стр.1028
—1030
).Прямая связь, обратная связь и тормозные связи в зрительной коре головного мозга приматов
,Neural Netw
,2004
, vol.17
5–6
(стр.625
—632
),.Настройка силы и ориентации таламического входа к простым клеткам, выявленная электрически вызванным кортикальным подавлением
,Neuron
,1998
, vol.20
(стр.1177
—1189
),.Ламинарные источники синаптического входа в корковые тормозные интернейроны и пирамидные нейроны
,Nat Neurosci
,2000
, vol.3
7
(стр.701
—707
),.Пластичность в одиночных нейронных и схемных вычислениях
,Nature
,2004
, т.431
(стр.789
—795
),.Влияние сетевой активности на интегративные свойства пирамидных нейронов неокортекса in vivo
,J Neurophysiol
,1999
, vol.81
4
(стр.1531
—1547
),,,.Колеблющиеся синаптические проводимости воссоздают активность, подобную in vivo, в нейронах неокортекса
,Neuroscience
,2001
, vol.107
1
(стр.13
—24
),,.Состояние высокой проводимости нейронов неокортекса in vivo
,Nat Rev Neurosci
,2003
, vol.4
9
(стр.739
—751
),,,,.Рекуррентное возбуждение в контурах неокортекса
,Science
,1995
, vol.269
5226
(стр.981
—985
),.Нейронные цепи неокортекса
,Annu Rev Neurosci
,2004
, vol.27
(стр.419
—451
).Происхождение ориентационно-селективных ВПСП в простых клетках зрительной коры головного мозга кошек
,J Neurosci
,1987
, vol.7
6
(стр.1780
—1791
),,.Принципы организации разнообразных ГАМКергических интернейронов и синапсов в неокортексе
,Science
,2000
, vol.287
(стр.273
—278
),,,.Анатомическая взаимосвязь определяет организацию кластеров кортикальных областей у макак и кошек.
,Philos Trans R Soc Lond B Biol Sci
,2000
, vol.355
(стр.91
—110
),,,.Синаптическая интеграция в полосатых простых клетках коры головного мозга
,J Neurosci
,1998
, vol.18
22
(стр.9517
—9528
),,,.K + канал регуляции распространения сигнала в дендритах пирамидных нейронов гиппокампа
,Nature
,1997
, vol.387
6636
(стр.869
—875
),.Пространственный рост реальных сетей
,Phys Rev E
,2004
, vol.69
стр.036103
,,.Неокортикальная микросхема как tabula rasa
,Proc Natl Acad Sci USA
,2005
, vol.102
3
(стр.880
—885
),.Линейный метод наименьших квадратов с ограничениями линейного неравенства
,Решение задач наименьших квадратов
,1974
Энглвуд Клиффс (Нью-Джерси)
Прентис-Холл
стр.161
,. ,,,.Что делает динамическую систему вычислительно мощной?
,Новые направления в статистической обработке сигналов: от систем к мозгу
,2005
MIT Press
,,.Принципы вычислений в реальном времени с обратной связью, применяемые к моделям кортикальных микросхем
,Труды о достижениях в системах обработки нейронной информации
,2005
MIT Press
,.Синапсы как буферы динамической памяти
,Neural Netw
,2002
, vol.15
(стр.155
—161
),,.Вычисления в реальном времени без стабильных состояний: новая структура для нейронных вычислений на основе возмущений
,Neural Comput
,2002
, vol.14
11
(стр.2531
—2560
),,,.Электрическая и кальциевая передача сигналов в дендритах пирамидных нейронов гиппокампа
,Annu Rev Physiol
,1998
, vol.60
(стр.327
—346
),.Характеристика одиночных потенциалзависимых каналов Na + и Ca2 + в апикальных дендритах пирамидных нейронов CA1 крысы
,J Physiol
,1995
, vol.487
Pt 1
(стр.67
—90
),,,.Модель инициирования спайков в пирамидных нейронах неокортекса
,Neuron
,1995
, vol.15
6
(стр.1427
—1439
),,,,,.Интернейроны неокортикальной тормозной системы
,Nat Rev Neurosci
,2004
, vol.5
10
(стр.793
—807
),,.Дифференциальная передача сигналов через один и тот же аксон пирамидных нейронов неокортекса
,Proc Natl Acad Sci USA
,1998
, vol.95
(стр.5323
—5328
). ,Перцепционная нейробиология: кора головного мозга
,1998
Кембридж, Массачусетс
Harvard University Press
,,. .Компьютерные модели и средства анализа нейронных микросхем
,Базы данных нейронауки. Практическое руководство
,2003
Бостон
Kluwer Academic Publishers
(стр.123
—138
).Корковые микросхемы: разнообразны или каноничны?
,Нейрон
,2002
, т.36
1
(стр.19
—27
),.К теории ламинарной архитектуры коры головного мозга: вычислительные ключи от зрительной системы
,Cereb Cortex
,2003
, vol.13
1
(стр.100
—113
),,,,,.Слоистая внутриколоночная и трансколонарная функциональная связность пирамидных клеток слоя v в коре головного мозга крысы
,J Neurosci
,2001
, vol.21
10
(стр.3580
—3592
),,.Стереотипия в микросхемах неокортекса
,Trends Neurosci
,2002
, vol.25
5
(стр.227
—230
),,,.Ламинарные характеристики функциональной связности в коре головного мозга крысы, выявленные при стимуляции глутаматом в клетке
,Neurosci Res
,2000
, vol.37
1
(стр.49
—58
),.Активное распространение соматических потенциалов действия в дендритах пирамидных клеток неокортекса
,Nature
,1994
, vol.367
6458
(стр.69
—72
).Кросс-корреляционный анализ взаимоотношений геникулостриатных нейронов у кошек
,J Neurophysiol
,1983
, vol.49
(стр.1303
—1318
).Пресинаптическая частотно-зависимая фильтрация
,J Comput Neurosci
,2003
, vol.15
(стр.159
—202
),,,.Синаптические связи и небольшие цепи с участием возбуждающих и тормозных нейронов в слоях 2–5 неокортекса взрослых крыс и кошек: тройная внутриклеточная запись и мечение биоцитином in vitro
,Cereb Cortex
,2002
, vol.12
9
(стр.936
—953
),. ,Нейронные сети гиппокампа
,1991
Кембридж, Массачусетс
Издательство Кембриджского университета
.Вычислительные ограничения, которые могли способствовать расслоению сенсорной коры
,J Comput Neurosci
,2003
, vol.14
(стр.271
—282
). ,Статистическая теория обучения
,1998
Нью-Йорк
Джон Вили
,.Хаос в нейронных сетях со сбалансированной возбуждающей и тормозной активностью
,Science
,1996
, vol.274
(стр.1724
—1726
),.Хаотическое сбалансированное состояние в модели корковых цепей
,Neural Comput
,1998
, т.10
6
(стр.1321
—1371
),.Коллективная динамика сетей «маленького мира»
,Nature
,1998
, vol.393
(стр.440
—442
). ,Кортикальные контуры
,1989
Бостон
Birkhaeuser
,,.Возбуждающие корковые нейроны образуют мелкомасштабные функциональные сети
,Nature
,2005
, vol.433
7028
(стр.868
—873
)Заметки автора
© Автор, 2006. Опубликовано Oxford University Press. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected]
Онлайн-версия этой статьи была опубликована в рамках модели открытого доступа. Пользователи имеют право использовать, воспроизводить, распространять или демонстрировать версию этой статьи в открытом доступе в некоммерческих целях при условии, что: исходное авторство правильно и полностью указано; Журнал и Издательство Оксфордского университета указываются как место первоначальной публикации с указанием правильных сведений о цитировании; если статья впоследствии воспроизводится или распространяется не полностью, а только частично или как производное произведение, это должно быть четко указано.По вопросам коммерческого повторного использования обращайтесь по адресу [email protected].
ОТЧЕТ ПО ОБРАБОТКЕ, ХРАНЕНИЮ И КВАЛИФИКАЦИИ ПЛАСТИКОВОЙ МИКРОСХЕМЫ (PEM)
% PDF-1.6 % 3 0 obj > эндобдж 90 0 объект > поток application / pdf
Модуляция делительного усиления обеспечивает гибкое и быстрое вовлечение в неокортикальную микросхему модели
Модель неокортикальной микросхемы.
Модель, использованная в этом исследовании, является расширенной версией пространственно локализованной модели Уилсона – Коуэна (Wilson and Cowan, 1972). Эта модель неокортикальной микросхемы включает одну возбуждающую популяцию, E , и две ингибирующие субпопуляции: одну направленную на дендриты, I dend и одну межнейронную популяцию, нацеленную на сому, I сома (см.рис. 1 A ). Две ингибирующие субпопуляции различаются типом ингибирующей модуляции, которую они обеспечивают возбуждающей популяции. I dend всегда обеспечивает субтрактивное подавление, то есть субтрактивную модуляцию функции ввода-вывода своей цели: сдвиг кривой в сторону более высоких входных значений. I soma может обеспечивать комбинацию вычитающего и разделяющего ингибирования, то есть модуляции делительного усиления, на возбуждающую популяцию: уменьшая наклон и максимальный выходной сигнал функции (см. Схемы модуляции на рис. 1 A ) .
Рис.1. Модель неокортикальной микросхемы и меры увлечения. A : схематическая модель цепи неокортекса. Он включает одну возбуждающую ( E ) и две ингибирующие субпопуляции, одну нацеленную на дендриты ( I dend ) и одну межнейронную популяцию, нацеленную на сому ( I сома ), и веса ( w ). их связей. Обратите внимание, что характер подавления, передаваемого от I сома до E , определяется параметром делимости 0 ≤ q ≤ 1 (показано синим).Он варьируется от полностью вычитающей ( q = 0) до полностью разделяющей ( q = 1) модуляции. Также показаны схемы этих двух типов модуляции ввода-вывода. B : пример захвата. Первоначально схема получает постоянный входной сигнал, P ( t ) = P , и колеблется на своей собственной частоте, f ∗ [представленной активностью возбуждающего населения E ( t )]. Входной сигнал становится синусоидальной волной с амплитудой Λ и входной частотой f в .Микросхема успешно увлекается входной частотой. C : увлечение микросхемы может занять несколько циклов колебаний, как показано в этом примере. Время сходимости рассчитывается как время, необходимое для схождения активности до последнего предельного цикла. Затем рассчитывается индекс увлечения из спектра мощности сигнала E ( t ) после его схождения.
Исходная модель Уилсона – Коуэна имеет субтрактивную модуляцию, но, чтобы ввести в модель делительную модуляцию, нам нужно определить сигмоидальную функцию ввода-вывода, которая принимает три переменные: вход или привод, x ; субтрактивная модуляция,; и делительная модуляция, A:
Fe, ix, Θ, Α = αe, iαe, i + qΑ11 + exp − αe, ix − θe, i + Θ + 1 − qΑ − 11 + expαe, iθe, i, ( 1)
, где e обозначает возбуждающее, а i обозначает тормозящее.Функция определена со всеми входными данными, которые являются действительными неотрицательными значениями. Константа θ e, i — это минимальное смещение функции ввода-вывода по оси x для соответствующей совокупности, представляющее состояние по умолчанию, когда нет вычитающего запрета, который смещает функцию дальше. Константа α e, i — это максимальное усиление сигмоидальной функции для соответствующей совокупности, представляющее состояние по умолчанию, когда нет разделяющего запрета, который уменьшает усиление функции.Обратите внимание, как параметр делимости q ∈ [0, 1] управляет эффектом разделяющей модуляции A. Только тогда, когда q = 1, модуляция является чисто разделяющей. Более низкое значение приводит к комбинации вычитающей и делительной модуляции, и она становится чисто вычитающей с q = 0. Кроме того, обратите внимание, что когда A = 0, эта функция эквивалентна сигмоидальной функции, используемой в исходной модели Уилсона – Коуэна. модель (Уилсон и Коуэн, 1972). Определенная здесь функция ввода-вывода является разновидностью функции, используемой в Papasavvas et al.(2015), и мы объяснили его точный вывод в Papasavvas and Wang (2019).Используя функцию ввода-вывода F e, i , микросхема неокортекса описывается следующей системой обыкновенных дифференциальных уравнений:
τdEtdt = −Et + ke − EtFew1Et + Pt, w2Idendt, w3Isomat,
τdIdendtdt = −Idendt + ki − IdendtFiw4Et, 0,0,
τdIsomatdt = −Isomat + ki − IsomatFiw5Et, w6Idendt + w7Isomat, 0, (2)
где, аналог исходной модели Уилсона – Коуэна, limx → ∞Fe, ix, 0,0 = expαe, iθe, i1 + expαe, iθe, i.(3)Рис. 1 A показывает схему неокортикальной микросхемы с указанием возбуждающих и тормозных связей и их веса, w . Чтобы ограничить параметры этой модели, мы использовали данные, полученные в первичной зрительной коре Pfeffer et al. (2013). Во-первых, I dend подавляет I сома , но не взаимно. Во-вторых, существует самоторможение для I сома , но не для I dend .В-третьих, некоторые значения веса установлены относительно w 3 : w 7 = w 3 , w 2 = 0,54 w 3 и w 6 = 0,33 w 3 .
Параметры, используемые для функций ввода-вывода F e, i ( уравнение 1 ): θ e = 4, θ i = 3,7, α e = 1.3 и α i = 2. Это значения, использованные в исходной модели Уилсона – Коуэна (Wilson and Cowan, 1972). Постоянная времени была установлена на τ = 0,05. Это значение было выбрано на основе реакции модели неокортикальной микросхемы на мгновенный ввод (см. Дополнительный рисунок S1; см. Https://doi.org/dkwh), который имеет характерный период полураспада t 1 / 2 = 39,8 мс, что приблизительно соответствует ответу электрически стимулированных микросхем неокортекса в электрофизиологических экспериментах (Alfonsa et al.2015).
Модель микросхемы была специально разработана для исследования влияния разделяющего ингибирования, которое доставляется популяцией ингибиторов нацеливания на сому I сома , на захват микросхемы. Параметр деления q включен в модель для создания континуума между двумя крайностями: от чисто субтрактивного ингибирования до чисто разделяющего ингибирования, обеспечиваемого I сома . Изменяя параметр q от 0 до 1, мы можем количественно исследовать, используя соответствующие меры (см. Ниже), как на увлечение влияет систематическое увеличение разделяющей способности тормозной модуляции.Обратите внимание, что параметр деления управляет только модуляцией, передаваемой I сома на E , тогда как I dend всегда обеспечивает чисто субтрактивную модуляцию, и это связано с тем, что модуляция делительного усиления была связана с нацеливанием на сомы. интернейроны в неокортексе (Atallah et al. (2012); Pouille et al. (2009); Wilson et al. (2012); однако см. также Seybold et al. (2015)). Несмотря на то, что разделение обеспечивается исключительно I сома , мы по-прежнему включаем I dend в модель, чтобы можно было сравнить с предыдущими результатами моделирования.
Модели нейронной массы могут работать во многих различных режимах, даже при постоянном вводе. Систематический анализ их динамики показал, что они могут находиться в (устойчивом) стабильном состоянии, либо в устойчивой фиксированной точке, либо в стабильном предельном цикле (Grimbert and Faugeras 2006; Spiegler et al. 2010; Wilson and Cowan 1972). Они также могут находиться в предельно стабильной фиксированной точке, то есть в критической точке между поглощающим состоянием и активированным состоянием, что отражает свидетельство критичности экспериментальных данных (Cowan et al.2016). Даже хаотические режимы могут быть достигнуты в модели нейронной массы как минимум с тремя переменными (Papasavvas et al. 2015; Spiegler et al. 2011). Однако в этом исследовании, как и в предыдущей работе (Spiegler et al. 2011), мы исследуем явление увлечения только в режиме стабильного предельного цикла, то есть при существующем колебании перед любым колебательным движением. Это связано с тем, что эффект увлечения в биологическом смысле обычно рассматривается как управляемая вводом адаптация уже существующего колебания.
Выборка пространства параметров и поиск локальных оптимумов.
Чтобы исследовать влияние параметра делимости q на показатели развлечения, мы должны были установить параметры микросхемы таким образом, чтобы ее собственная колебательная активность [ответ на постоянный входной сигнал P ( t ) = P ] при q = 0 и q = 1 сопоставимо. Мы разработали стратегию выборки пространства параметров для параметров { P , w 1 , w 3 , w 4 , w 5 } и создания коллекции допустимых наборов параметров.Другие параметры подключения { w 2 , w 6 , w 7 } устанавливаются относительно w 3 (см. Выше). Чтобы набор параметров считался допустимым для исследования, он должен соответствовать следующим условиям:
-
Он следует отношениям связи, полученным из Pfeffer et al. (2013).
-
Он производит колебательное поведение как для q = 0, так и для q = 1 с постоянным входом, P ( t ) = P .
-
Разница между размахом амплитуды (см. Рис. 1) E ( t ) при q = 0 и q = 1 меньше 0,001.
-
Размах амплитуды I сома ( t ) по крайней мере такой же большой, как размах амплитуды E ( t ) как для q = 0 и q = 1.
Обратите внимание, что необходимо применить ограничение на амплитуду I сома ( t ) ( условие 4 ), поскольку существует возможность подключения параметры, уменьшающие амплитуду I сом ( t ) при сохранении колебаний в двух других популяциях.В этом случае система сводится к классической двумерной системе E — I (Wilson and Cowan 1972). Аналогичное ограничение для I dend ( t ) не является необходимым, поскольку устойчивые колебания в микросхеме невозможны при пониженной активности в I dend ( t ) при q = 1. . Чтобы создать набор таких наборов параметров, мы случайным образом выбрали гиперкуб в пространстве параметров, определяемом интервалами: P ∈ [0, 5] и w k ∈ [0, 35] для k ∈ {1, 3, 4, 5}.После того, как мы сгенерировали остальные параметры на основе условия 1 , система была смоделирована, и были сохранены только те образцы, которые соответствовали условию 2 . Эти наборы затем использовались в качестве отправных точек для задачи оптимизации. Задача оптимизации заключалась в минимизации разницы между размахом амплитуд E ( t ) при q = 0 и q = 1 ( условие 3 ) при сохранении размаха до пиковая амплитуда I сома ( t ), по крайней мере, такая же большая, как размах амплитуды E ( t ) ( условие 4 ).Во время оптимизации использовался штрафной член, чтобы гарантировать, что условие 4 выполняется и что параметры не отклоняются от гиперкуба, определенного выше. Задача оптимизации решалась с помощью решателя нелинейного программирования fminsearch в MATLAB.
Действительный набор параметров был первоначально создан с помощью этого метода и использован в качестве примера набора для результатов на рис. 2 и 3. Набор примеров: { P = 1,428, w 1 = 24,368, w 3 = 9.677, w 4 = 27,249, w 5 = 30,913}. Другие параметры подключения устанавливаются относительно w 3 , то есть w 2 = 5,225, w 6 = 3,193 и w 7 = 9,677.
С целью обобщения результатов по различным областям пространства параметров мы создали коллекцию допустимых наборов после обширной выборки. Случайная выборка из 250 000 наборов параметров сгенерировала набор из 1227 наборов параметров, которые соответствуют условиям 1 и 2 .Из этих наборов 981 считался уникальным с допуском 0,05 (с использованием уникетола в MATLAB). Эти уникальные наборы затем использовались в качестве отправных точек для задачи оптимизации. Из 981 уникальных начальных точек 359 сходились к набору параметров, который соответствовал всем четырем условиям, и 138 из них были признаны уникальными с допуском 0,05.
Сохранение торможения с помощью растормаживающей микросхемы в сетчатке
Почему блокада тормозных входов в SAC ослабляет вызванное движением торможение DSGC с шумным фоном? Мы сформулировали рабочую гипотезу, основанную на следующих двух наблюдениях, описанных в предыдущем разделе: (1) SAC у мышей Gabra2 и cKO демонстрируют повышенную активацию, вызванную мерцанием, в течение временного окна непосредственно перед их реакциями, вызванными движением, и (2) движение- вызванная деполяризация SAC не нарушается у мышей Gabra2 cKO.Наша гипотеза состоит в том, что постоянный мерцательный ответ SAC перед его деполяризацией, вызванной движением, у мышей Gabra2 cKO вызывает кратковременную синаптическую депрессию в синапсах GABAergic SAC-DSGC и тем самым ослабляет подавление DSGC, вызванное движущейся полосой. Кратковременная депрессия ГАМКергического синапса SAC-DSGC была продемонстрирована у животных P7-14 во время развития с использованием парной импульсной стимуляции (Morrie and Feller, 2015). Чтобы проверить, возникает ли эта синаптическая депрессия также в зрелой сетчатке, мы выполнили парные записи фиксации напряжения из пар SAC-DSGC у взрослых контрольных мышей.SAC деполяризовались с коротким шагом напряжения, что приводило к открытию потенциалозависимых кальциевых каналов (VGCC), показанных в виде внутреннего пика, который был синхронизирован по времени с постсинаптическим ответом DSGC и блокировался антагонистами VGCC (Lee et al. , 2010; Корен и др., 2017). IPSC DSGC показали выраженную кратковременную депрессию в протоколе парных импульсов (Рисунок 3), что указывает на то, что синапс SAC-DSGC склонен к депрессии при повторной активации SAC.
ГАМКергические синапсы SAC-DSGC у взрослых мышей обнаруживают парную депрессию пульса.
( a ) Верхний: схема парных записей фиксаторов напряжения между DSGC и SAC на нулевой стороне DSGC. Предпочтительное направление DSGC показано черной стрелкой. Нижний: командный потенциал SAC (верхний график), ток удержания SAC (средний график) и DSGC IPSC, вызванный деполяризацией SAC (нижний график). Пунктирная линия указывает начало IPSC, которое совпадает с входящим кальциевым током, активированным в SAC (Koren et al., 2017). ( b ) Пример трассировки записей SAC и DSGC с разными интервалами между импульсами (200, 400, 1600 мс). ( c ) Сводный график отношения парных импульсов (2-я / 1-я пиковые амплитуды) как функции межимпульсного интервала. Ось X в логарифмическом масштабе. N = 17 пар от трех мышей.
Затем мы спросили, может ли вызванная мерцанием деполяризация мембраны SAC в Gabra2 cKO, которая сохраняется во временном окне подавления объемного звука, может вызвать кратковременную синаптическую депрессию и уменьшить последующее высвобождение ГАМК из SAC, вызванное движущейся полосой.Чтобы решить этот вопрос, мы выполнили парные соматические записи SAC-DSGC у контрольных мышей, во время которых пресинаптический SAC был зафиксирован напряжением в соответствии с формами волны, которые имитируют паттерны активации контрольных и cKO SAC во время движущихся стержневых стимулов. Поскольку сайты высвобождения нейротрансмиттеров безаксонного SAC расположены в дистальных дендритах, мы сначала использовали компьютерное моделирование для оценки V m на дистальных дендритах SAC на основе соматических записей SAC V m во время визуальной стимуляции.Биофизическая модель SAC была построена на основе оцифрованной морфологии типичного SAC мыши, входов биполярных клеток, картированных с помощью коннектомного анализа (Ding et al., 2016), и экспериментально измеренных свойств мембраны SAC (Stincic et al., 2016; Рисунок 4a. см. Материалы и методы). Моделирование активации SAC во время движения полосы по мерцающей шахматной доске показало, что пиковые амплитуды соматического и дистального дендритных V m сопоставимы (рис. 4b). Затем мы смоделировали степень ослабления между соматическими и дистальными дендритными компартментами во время наших экспериментов с фиксацией напряжения, используя параметры, которые приблизительно соответствуют условиям фиксации напряжения в отсутствие проводимости натрия и калия.Из-за электротонической изоляции дистальных дендритов SAC от сомы (Euler et al., 2002; Koren et al., 2017; Tukker et al., 2004), мы оценили деполяризацию мембраны на концах дендритов SAC с помощью компьютерного моделирования примерно 25% соматической деполяризации в цельноклеточной конфигурации с фиксацией напряжения, использованной в нашем исследовании (рис. 4c). Поэтому мы масштабировали соматические трассы V m , полученные во время регистрации токовых клещей, в 4 раза. Масштабированные формы сигналов затем использовались в качестве командных потенциалов SAC в экспериментах по парной записи с фиксатором напряжения, так что V m на дистальной части. Дендриты SAC могут быть деполяризованы до уровня, сопоставимого с таковым при визуальной стимуляции.IPSC DSGC в каждой паре SAC-DSGC были записаны для измерения выпуска SAC GABA.
Вычислительное моделирование световых откликов SAC на концах сомы и дендритов во время стимула движущегося стержня на шумном фоне.
( a ) Оцифрованный SAC (синий) и местоположения биполярных клеточных сом (желтые точки), используемые для моделирования.( b ) Верхняя кривая: смоделированная Vm биполярной клетки во время стимула движущегося стержня на шумном фоне. Средние следы: смоделированная возбуждающая проводимость (Ge) SAC, вызванная шестью примерами входов биполярных клеток. Цветные следы — это SAC Ge, вызванные отдельными биполярными клетками. Нижние следы: моделирование соматической Vm SAC на соме и на дистальном конце дендрита. ( c ) Моделирование затухания от сомы к кончику дендрита в SAC во время записи с фиксацией напряжения. Черная кривая: масштабированная соматическая форма волны Vm (черная кривая) SAC, основанная на записи текущих фиксаторов SAC Vm во время стимула движущейся полосы на шумном фоне.Красный график: смоделированный Vm на дистальном конце дендрита SAC в конфигурации фиксации напряжения.
Для каждой пары SAC-DSGC, SAC деполяризовался в соответствии с двумя формами сигнала в случайных последовательностях. Один из них представлял собой масштабированную форму волны репрезентативной соматической V m , записанной из Gabra2 cKO SAC во время стимула движущейся полоски над случайно мерцающей шахматной доской (обозначенной «cKO pattern», Рисунок 5a, верхняя красная кривая). Другая форма волны была идентична вышеуказанному шаблону cKO, за исключением временного окна, предшествующего реакции, вызванной движением (рис. 5a, временное окно 2), чтобы включать период подавления объемного звука.В течение этого временного окна зашумленный шаблон V m для cKO SAC был заменен средним шаблоном V m SAC в контрольной группе. Вторая форма волны называется «контрольной диаграммой» (рис. 5а, верхняя черная кривая). Для каждой пары SAC-DSGC случайным образом были выбраны формы волны cKO и контрольный V m для фиксации напряжения соматического SAC V m , в то время как DSGC IPSC регистрировались одновременно (рис. 5а). Поскольку флуктуации мембран, вызванные мерцанием, в течение базового периода идентичны для cKO и контрольных паттернов, DSGC IPSC в течение этого базового периода (рис. 5a, временное окно 1) служили внутренним контролем для каждой пары для обеспечения стабильных записей и мониторинга потенциального прогона. -низка записей целых клеток.Как и ожидалось, амплитуды DSGC IPSC в течение базового периода для паттернов cKO и контроля были аналогичными (рис. 5a и b, временное окно 1). Однако DSGC IPSC, запускаемые сигналами SAC, вызванными движением (рис. 5a и b, временное окно 3), значительно различались между cKO и контрольными паттернами. Несмотря на то, что SAC был активирован той же моделью деполяризации, вызванной движением в течение временного окна 3, более активный V m непосредственно перед вызванной движением деполяризации (рис. 5a и b, временное окно 2) в форме волны cKO привел к меньшему DSGC. Пиковые амплитуды IPSC, вызванные формой волны движения (рис. 5a – d, временное окно 3).Мы сравнили IPSC в этом парном протоколе записи с таковыми во время визуальной стимуляции с шумной полосой. Пиковая амплитуда и перенос заряда IPSC в парных записях находятся в нижней части диапазона для DSGC IPSC, вызванных шумным стимулом (перенос заряда: вызванный светом: предпочтительное направление: 95,1+ / — 8,6 пА * с; нулевое направление , 198,6 + / — 22,5 пА * с, 16 клеток; парные записи: 100+ 12,1 пА * с, 22 ячейки; амплитуда: вызванная светом: предпочтительное направление: 284,2 + / — 23,2 пА; нулевое направление, 570.3 + / — 52,7 пА; парные записи: 174,5 + / — 17,9 пА), подтверждая, что измеренные токи подавления DSGC в парных записях находятся в пределах физиологического диапазона. Кроме того, синаптическое подавление, наблюдаемое в группе cKO, было устойчивым, когда мы тестировали дополнительные масштабные коэффициенты 3 и 5 для командных сигналов SAC (рис. 5d).
Паттерн активации
Gabra2 cKO SAC во время движения на шумном фоне вызывает синаптическую депрессию между SAC и DSGC у контрольных мышей.( a ) Верхние кривые: масштабированный контроль (черный) и кривые Gabra2 cKO (красный) во время шумного столбчатого стимула, используемого для ограничения напряжения SAC соматического Vm у контрольных мышей. Средние кривые: удерживающие токи SAC во время парных записей фиксации напряжения SAC-DSGC. Отклонения вниз представляют собой кальциевые токи SAC, активируемые деполяризацией мембраны. Нижние кривые: DSGC IPSC, вызванные управляющими сигналами и сигналами cKO. Схема поверх графиков указывает временные окна, соответствующие базовому периоду, вызванному полосой подавлению объемного звучания и вызванной полосой деполяризации во время экспериментов по фиксации тока на Рисунке 2.Зеленые прямоугольники с номерами 1, 2 и 3 представляют собой области в базовом, окружающем и центральном временных окнах, выбранных для последующей количественной оценки. ( b ) Попарное сравнение амплитуды DSGC IPSC, вызванной масштабированным (4x) контрольным сигналом, и сигналом cKO во временных окнах 1 и 3. Для каждой пары ячеек пиковая амплитуда IPSC, вызванная сигналом cKO, нормализуется к амплитуде сигнала cKO. форма сигнала управления для каждого временного окна. N = 17 пар от семи мышей. ( c ) То же, что и, но с другой репрезентативной формой волны cKO.( d ) То же, что и b, но с другими масштабными коэффициентами для сигналов команд SAC в c. ( e ) Пример контрольных кривых SAC Vm во время движущихся столбцов стимулов на сером фоне с различной скоростью. ( f ) Продолжительность окна гиперполяризации во время бесшумного движения стержня в зависимости от скорости стержня. 110 мкм / с: 11 клеток, 4 мыши, 440 мкм / с: 15 клеток, 4 мыши, 1320 мкм / с: 21 клетка, 6 мышей. Данные представлены как среднее значение ± стандартная ошибка среднего. ( г, ) То же, что и a, но с масштабированными формами волны cKO SAC Vm при 110 мкм / с (верхний) и 1320 мкм / с (нижний).Для сигналов управления средний мембранный потенциал сигналов управления заменяет кривые cKO во временном окне подавления объемного звука. ( h ) Краткое изложение синаптического подавления синапса SAC-DSGC, индуцированного сигналом Gabra2 cKO, относительно реакции, вызванной сигналом управления для различных скоростей движения. Экспрессия, вызванная шумом, рассчитывается как процентное уменьшение вызванной движением реакции cKO по сравнению с контролем. 110 мкм / с: 11 пар от трех мышей; 440 мкм / с: 17 пар от семи мышей; 1320 мкм / с: 11 пар от трех мышей.Данные представлены как среднее значение ± стандартная ошибка среднего. См. Также рисунок 5 — дополнение к рисунку 1.
Затем мы записали SAC Vm во время стимулов движущегося стержня с разной скоростью и исследовали продолжительность подавления объемного звука в зависимости от скорости. Мы протестировали три скорости: 4 ° (110 мкм) / с — на нижнем конце кривой настройки скорости DSGC мыши (Ding et al., 2016; Hoggarth et al., 2015), 15 ° (440 мкм) / s — около оптимальной скорости кривой настройки скорости DSGC и 44 ° (1320 мкм) / с — на верхнем конце кривой настройки.Как и ожидалось, мы наблюдали зависящую от скорости продолжительность подавления объемного звука SAC в субмиллисекундном диапазоне на этих скоростях (рис. 5e и f). В шумных условиях cKO SAC демонстрируют повышенный шумовой отклик во время окна подавления объемного звука на всех скоростях (рисунок 5 — приложение к рисунку 1). Затем мы выполнили парные записи SAC-DSGC у контрольных мышей, используя репрезентативные формы волны cKO Vm от SAC во время шумных штриховых стимулов с разной скоростью. Мы обнаружили, что для всех трех скоростей, когда случайная активация SAC, вызванная мерцанием шахматной доски, попадала во временное окно подавления объемного звука SAC, это могло привести к уменьшению вызванных движением DSGC IPSC (рис. 5g и h).Эти результаты согласуются с экспериментом с парными импульсами записей SAC-DSGC, который показывает, что кратковременная депрессия происходит в сопоставимом масштабе времени (рис. 3). Вместе эти результаты убедительно подтверждают гипотезу о том, что у мышей Gabra2 cKO вызванная мерцанием деполяризация SAC, непосредственно предшествующая вызванной движением деполяризации, вызывает кратковременную депрессию в ГАМКергическом синапсе SAC-DSGC и, таким образом, приводит к снижению ингибирования DSGC, вызываемого движущийся бар.
Учитывая обширную сеть взаимосвязанных SAC (Ding et al., 2016; Lee and Zhou, 2006), можно спросить, ослабляет ли синаптическая депрессия гиперполяризацию SAC соседними SAC в присутствии движения объекта с фоновым шумом. В соответствии с этой гипотезой, мы наблюдали ослабленную гиперполяризацию SAC с шумным фоном по сравнению с фоном без шума (Рисунок 2e по сравнению с 2 часами). Однако даже при том, что высвобождение ГАМК из SAC подавлено шумным фоном, движение объекта в поле зрения по-прежнему вызывает достаточное высвобождение ГАМК из многих соседних варикозных расширений SAC, чтобы подавить шумовые реакции в постсинаптическом SAC прямо перед движущимся объектом.
Высокопроизводительный анализ микросхем человеческого мозга с помощью мультинейронного патч-зажима нового поколения
Существенные изменения:
1) Одной из основных проблем является система очистки пипеток, адаптированная авторами. В соответствии с исходным протоколом CR Forest, необходим дополнительный этап для очистки остаточного детергента, приставшего к внешней поверхности наконечника пипетки с помощью ACSF, перед перемещением пипеток в записывающую камеру для попытки пластыря, однако Пэн и его коллеги пропустили этот шаг.Авторы заявили, что есть веская практическая причина для пропуска этого шага, но данных в поддержку этой практики предоставлено мало или они отсутствуют. Они утверждают, что не было различий в качестве записи или электрофизиологических свойствах между пипетками вначале и после очистки, но эти утверждения должны быть подтверждены данными. В частности, было бы важно сообщить, как мембранный потенциал, входное сопротивление, синаптические события и параметры потенциала действия (амплитуда, ширина и др.) Изменяются со временем после исправления и повторного сопоставления.
Благодарим вас за понимание нашего обоснования отказа от дополнительной очистки. Мы согласны с тем, что эта практика и наше заявление о неизменной физиологии нейронов должны быть подтверждены дополнительными данными. Чтобы оценить возможное влияние нашего протокола очистки на качество записи и электрофизиологические свойства, мы провели дополнительные эксперименты на острых срезах мозга из моторной коры головного мозга крыс. Мы зарегистрировали 81 нейрон в 12 срезах мозга от 2 животных (P21, P22) с помощью 28 пипеток с двумя последовательными циклами очистки и сравнили клеточную и синаптическую физиологию.Мы исключили 4 интернейрона, кроме того, были исключены 9 клеток с деполяризованным мембранным потенциалом, которые были зарегистрированы на свежих и очищенных пипетках с равной вероятностью (3/28 клеток со свежими пипетками, 2/28 клеток после первой очистки и 4/28 клеток после второй очистки. ), подробнее см. в разделе «Материалы и методы».
Мы построили график распределения клеточных и синаптических свойств свежих и очищенных пипеток на рисунке 3. Кроме того, мы рассчитали среднее относительное изменение и его доверительный интервал для всех запрошенных параметров.Мы обнаружили, что относительное изменение среднего значения этих параметров находится в пределах 10%. Мы также рассчитали доверительный интервал этих относительных средних изменений, который представляет собой границы статистически значимой эквивалентности. В целом, мы не нашли доказательств систематического воздействия нашего подхода к очистке на клеточную или синаптическую физиологию. Мы включили статистические результаты в качестве исходных данных на рис. 3 и соответствующим образом адаптировали раздел «Материалы и методы».
2) В статье слишком много внимания уделяется анализу связности и игнорируются его ограничения, например.г., ложные негативы. Вместо этого авторы могут пожелать подчеркнуть, что мультипатч-запись в настоящее время является единственным доступным методом для анализа прочности и краткосрочной пластичности моносинаптической связи.
Мы благодарим рецензента за то, что он поднял этот вопрос, и соглашаемся с тем, что существуют ограничения в отношении анализа связности с использованием мультипатч-записей. Мы включили параграф, посвященный потенциальным причинам ложноотрицательных результатов в Обсуждение.
Мы также согласны с тем, что синаптическая сила и кратковременная пластичность являются важными параметрами этих связей.Несмотря на то, что парная конфигурация записи с фиксацией фиксации представляет собой оптимальный подход к анализу этих параметров, их также можно определить, комбинируя записи с фиксацией фиксации с двухфотонным снятием каркаса глутамата или оптогенетической стимуляцией. Однако надежность пресинаптической стимуляции может быть ниже, чем при использовании метода патч-кламп. Мы подчеркнули важность этих параметров и технические преимущества мультипатч-подхода в соответствующем разделе «Обсуждение».
3) Важные отсутствующие экспериментальные детали включают указание, можно ли исправить ячейки во время записи из других ячеек, время, необходимое для проверки возможности подключения, и анализ распределения расстояний между записанными ячейками (например,g., является ли распределение ячеек по расстояниям, полученным для продления записи, таким же, как полученное изначально?).
Хотя проверка возможности подключения одновременно с установкой исправлений сэкономит время, мы воздержались от этого по нескольким практическим причинам, которые мы изложили в новом абзаце в разделе «Результаты». Мы также включили время, необходимое для проверки возможности подключения и измерения внутренних свойств ячеек (раздел «Результаты»).
Мы благодарим рецензента за то, что он поднял важный вопрос о том, что межсоматические расстояния могут влиять на вероятность соединения и что местоположения репатриированных ячеек следует контролировать, чтобы предотвратить возможное смещение.Как было предложено, мы проанализировали влияние очистки с расширением на межсоматическое расстояние в наших предыдущих экспериментах с предубикулумом крыс и обнаружили аналогичное распределение между кластерами, полученными с очисткой с расширением и без нее. Мы построили распределение расстояний на рисунке 5 — приложение к рисунку 1 и обсудили их в разделе «Результаты».
4) Авторы подчеркивают некоторые преимущества полуавтоматического подхода, но не определяют другие аспекты мультипатч-экспериментов, которые могут выиграть от автоматизации — например, сбор данных и онлайн-контроль качества, а также обнаружение соединения в реальном времени.Учитывая потенциал для сбора такого большого количества данных, следует рассмотреть формат данных (например, нейроданные без границ), совместное использование данных, автоматизацию обнаружения и анализа соединений.
Мы согласны с тем, что есть несколько аспектов экспериментов, которые можно автоматизировать в дальнейшем, и мы также убеждены, что увеличение объема данных требует стандартизации анализа и формата данных. Однако мы видим компромисс между экспериментальной гибкостью и автоматизацией сбора и анализа данных.Поскольку мы хотели максимизировать применимость для других групп и их конкретных вопросов в этом отчете, мы использовали коммерчески доступное программное обеспечение для сбора данных, в то время как автоматический анализ трассировки для обнаружения соединений, безусловно, важен и требует постоянных усилий. Хотя программное обеспечение Signal может также выполнять онлайн-анализ, мы считаем, что это необходимо только для экспериментов с замкнутым циклом. Мы включили новый абзац по этим вопросам в раздел «Обсуждение». Мы также поддерживаем усилия открытой науки и разработки стандартизированного формата данных для облегчения сотрудничества.Мы предоставили предложения по этой теме в разделе «Обсуждение».
5) Несмотря на то, что использование редких живых тканей человека и, особенно, для увеличения объема данных по каждому образцу является веским основанием для разработки систем с несколькими заплатами, возможно, еще не известно, будет ли этого достаточно, чтобы исследовать разницу между частные лица. Какие различия наблюдались при обсуждении различий между людьми? Типы ячеек, связи? Я бы посоветовал авторам смягчить это утверждение.
Мы понимаем озабоченность автора обзора относительно статистической силы наших размеров выборки для выявления значимых различий между людьми. Мы хотим подчеркнуть, что наша основная цель получения больших выборок от отдельных пациентов состоит не в том, чтобы определить эти различия между отдельными людьми, а, скорее, в том, чтобы получить возможность оценивать индивидуальную изменчивость. Мы считаем, что это очень важно, поскольку ткань получена от очень разнородной группы пациентов.Анализ данных на индивидуальном уровне может помочь нам определить инвариантные параметры, которые могут указывать на общие принципы коры головного мозга человека. С другой стороны, параметры с высокой индивидуальной вариабельностью следует анализировать с осторожностью и проводить дальнейшие исследования. Поэтому мы считаем, что получение статистически значимых наборов данных у одиноких пациентов является важным шагом для мотивации и руководства будущими исследованиями. Мы перефразировали и детализировали нашу претензию в рукописи, чтобы лучше отразить этот аспект (Аннотация; Введение; Обсуждение).
В нашем предварительном анализе мы не обнаружили существенных различий во взаимосвязи пирамидных клеток между пациентами, в то время как мы определили, что доверительный интервал различий в вероятности подключения находился в диапазоне от -5% до 9,5%. В целом, мы полагаем, что полный анализ и обсуждение потенциальных инвариантных и вариантных параметров выходят за рамки этого технического отчета, и их лучше рассмотреть в отдельной исследовательской статье. Мы добавили статистический анализ в соответствующие разделы «Результаты» и «Материалы и методы».
[Примечание редакции: до принятия были запрошены дополнительные исправления, как описано ниже.]
Рукопись была значительно улучшена, но остается одна проблема, которую необходимо решить до принятия, как указано ниже:
Относительно новых экспериментов по повторному связыванию после обработки Alconox без промывки Alconox (подраздел «Окончательная последовательность удаления не требует дополнительных лунок, содержащих aCSF»). Они убедительны и показывают, что в тканях мозга молодых крыс в целом наблюдается небольшой кумулятивный эффект процесса очистки на последующее здоровье нейронов.Здесь необходимо прояснить два момента.
1) Ожидают ли авторы, что результаты со зрелой мозговой тканью человека будут эквивалентны результатам с молодой мозговой тканью крысы? Есть ли какие-либо ограничения, о которых нам следует знать в этом валидационном эксперименте.
2) Были ли когда-либо репатриированы одни и те же нейроны после очистки? Это позволит провести прямое сравнение свойств нейронов до и после очистки патч-пипетки.
Мы провели первые ревизионные эксперименты на крысах, потому что у нас редко есть человеческие ткани и мы не получали их во время ревизии.Мы также не пытались перепатчить одни и те же нейроны. Однако нам повезло, и мы дважды получали человеческую ткань за последние две недели, и теперь мы провели дополнительные эксперименты, чтобы оценить влияние очистки на электрофизиологические свойства человеческих нейронов.
Мы сравнили свойства нейронов, покрытых свежими (n = 24) или очищенными пипетками (n = 9, рисунок 3 — приложение к рисунку 1). Мы также перепрограммировали те же нейроны той же очищенной пипеткой (n = 9, рисунок 3 — приложение к рисунку 2) или другой свежей пипеткой (n = 5, рисунок 3 — приложение к рисунку 3).Мы смогли показать, что внутренние электрофизиологические свойства человеческих нейронов были и оставались одинаковыми в разных условиях (статистические данные и тесты на рисунке 3 — исходные данные 1). Хотя мы действительно наблюдали значительное снижение входного сопротивления в клетках, повторно сопоставленных с помощью очищенной пипетки, несколько дополнительных факторов могли способствовать изменчивости в этих нейронах, например, эффект самовосстановления или прошедшее время. Эти не зависящие от очистки изменения отражаются в вариабельности, обнаруженной также в нейронах, повторно обработанных свежими пипетками (рис. 3 — приложение к рис. 3).
Поскольку мы показали, что сама пипетка не оказывает систематического влияния на внутренние свойства, мы также рассмотрели возможность того, что внеклеточный раствор, в котором пипетки были промыты, мог иметь эффект (Рисунок 3 — рисунок Приложение 4). Поэтому мы исправили кластеры нейронов (n = 19) и сравнили их свойства и синаптические связи (n = 7) до и после очистки других пипеток, чтобы смоделировать изменения во внеклеточном растворе после промывания.Опять же, мы обнаружили, что потенциал мембраны покоя и кинетика потенциала действия оставались очень стабильными (средняя относительная разница в пределах 2%), в то время как входное сопротивление и сопротивление доступа увеличивались. Мы также не наблюдали особой тенденции в постсинаптических амплитудах между этими двумя состояниями, которая показывала как небольшое увеличение, так и уменьшение (n = 7, Рисунок 3 — дополнение к рисунку 5, Рисунок 3 — исходные данные 2). Мы соответствующим образом скорректировали разделы «Результаты» и «Материалы и методы» в рукописи.
В целом, мы смогли показать, что результаты наших экспериментов по очистке нейронов человека аналогичны тем, которые мы продемонстрировали на нейронах крысы, даже когда та же самая клетка была репатриирована.Мы действительно увидели, что входное сопротивление уменьшилось в клетках, повторно обработанных с помощью очищенной пипетки, и увеличилось в клетках, зарегистрированных в ACSF после промывки. Хотя повторная синхронизация, время записи и нейронная изменчивость могут повлиять на эти параметры, мы не можем исключить эффект очистки пипетки в этом случае. Поэтому мы подчеркиваем, что эти валидационные эксперименты ограничиваются нашими настройками и вопросами исследования и что любая реализация нашей процедуры очистки другими должна быть тщательно проверена на параметры и в интересующем модельном организме.Тем более, что прилипший детергент на пипетке может зависеть от множества факторов, которые необходимо учитывать и точно настраивать для каждой экспериментальной установки (подраздел «Окончательная последовательность изгнания не обязательно требует дополнительных лунок, содержащих aCSF»).
Кроме того, поскольку каждый патч-электрод использовался более одного раза, возможно, релевантным статистическим сравнением здесь является дисперсионный анализ повторных измерений, а не статистика популяции групп, как, по-видимому, показано на рис. 3J, K и L.
Спасибо за полезный совет. Мы выполнили повторные измерения ANOVA для 14 пипеток, с помощью которых были получены три успешных записи пирамидных клеток (свежие, 1x очистка, 2x очистка). Он не показал значительной тенденции, и мы включили результаты в Рисунок 3 — исходные данные 2. Мы также соответствующим образом адаптировали разделы «Результаты» и «Материалы и методы».
https://doi.org/10.7554/eLife.48178.sa2Перепрограммирование нейронных микросхем головного мозга через выступы головки позвоночника — роль синаптоподина и внутриклеточных запасов кальция | Acta Neuropathologica Communications
Стюард О. Реорганизация нейронных связей после травмы ЦНС: принципы и экспериментальные парадигмы. J Neurotrauma. 1989. 6: 99–152.
CAS Статья PubMed Google ученый
Стюард О. Реорганизация нейронных цепей после травмы центральной нервной системы: естественные процессы и возможности терапевтического вмешательства. В: Зальцман С., Фаден А., редакторы. Нейробиология травм центральной нервной системы.Нью-Йорк: издательство Оксфордского университета; 1994. стр. 266–87.
Google ученый
Deller T, Orth CB, Del Turco D, Vlachos A, Burbach GJ, Drakew A, Chabanis S, Korte M, Schwegler H, Haas CA, Frotscher M. Роль синаптоподина и позвоночного аппарата в гиппокампе синаптическая пластичность. Анн Анат. 2007; 189: 5–16.
CAS Статья PubMed Google ученый
Бакмастер П. Прорастание мшистых волокон в зубчатом гирусе. В: Rogawski M, Delgado-Escueta A, Noebels J, Avoli M, Olsen R, редакторы. Основные механизмы эпилепсии Джаспера. 4-е изд. Bethesda (MD: Национальный центр биотехнологической информации; 2012.
). Google ученый
Деллер Т., Фротшер М. Пластичность центральных нейронов, индуцированная поражением: разрастание отдельных волокон в гиппокампе крысы после одностороннего поражения энторинальной коры.Prog Neurobiol. 1997. 53: 687–727.
CAS Статья PubMed Google ученый
McKinney RA, Debanne DG, hwiler BH, Thompson SM. Индуцированное поражением разрастание аксонов и повышенная возбудимость в гиппокампе in vitro: значение для генеза посттравматической эпилепсии. Nat Med. 1997; 3: 990–6.
CAS Статья PubMed Google ученый
Гилл Р., Чанг ПКИ, Преносил Г.А., Дин Э.С., Маккинни Р.А.Блокирование нейротрофического фактора головного мозга подавляет вызванную повреждением гипервозбудимость нейронов CA3 гиппокампа. Eur J Neurosci. 2013; 38: 3554–66.
Артикул PubMed Google ученый
Aungst S, England PM, Thompson SM. Критическая роль рецепторов trkB в реактивном разрастании аксонов и повышенной возбудимости после повреждения аксонов. J Neurophysiol. 2013; 109: 813–24.
CAS Статья PubMed PubMed Central Google ученый
Z’Graggen WJ, Fouad K, Raineteau O, Metz GAS, Schwab ME, Kartje GL. Компенсаторное прорастание и изменение направления импульса после одностороннего поражения пирамидного тракта у новорожденных крыс. J Neurosci. 2000; 20: 6561–9.
PubMed Google ученый
Келли М.С., Стюард О. Процесс реиннервации в зубчатой мозоле взрослых крыс: физиологические события во время поражения и в ранний период после поражения. Exp Neurol. 1996. 139: 73–82.
CAS Статья PubMed Google ученый
Маркус Т.М., Цай С.Ю., Болноу М.Р., Фаррер Р.Г., О’Брайен Т.Э., Киндлер-Бауманн Д.Р., Рауш М., Рудин М., Висснер С., Мир А.К. и др. Восстановление и реорганизация мозга после инсульта у взрослых и старых крыс. Энн Нейрол. 2005. 58: 950–3.
Артикул PubMed Google ученый
Fawcett JW. Пластичность и регенерация внеклеточного матрикса после повреждения ЦНС и нейродегенеративного заболевания.В: Dancause N, Nadeau S, Rossignol S, редакторы. Прогресс в исследованиях мозга. Том 218. 1-е изд. Уолтем (Массачусетс): Эльзевир; 2015. с. 213–26.
Google ученый
Брэдбери Э.Дж., Мун ЛДФ, Попат Р.Дж., Кинг В.Р., Беннетт Г.С., Патель П.Н., Фосетт Дж. В., МакМахон С.Б. Хондроитиназа ABC способствует функциональному восстановлению после травмы спинного мозга. Природа. 2002; 416: 636–40.
CAS Статья PubMed Google ученый
Эмерик AJ, Neafsey EJ, Schwab ME, Kartje GL. Функциональная реорганизация моторной коры у взрослых крыс после коркового поражения и лечения моноклональным антителом IN-1. J Neurosci. 2003; 23: 4826–30.
CAS PubMed Google ученый
Buchli AD, Schwab ME. Подавление Nogo: ключевая стратегия увеличения регенерации, пластичности и функционального восстановления пораженной центральной нервной системы. Ann Med. 2005. 37: 556–67.
CAS Статья PubMed Google ученый
Raineteau O, Schwab ME. Пластичность двигательных систем при неполной травме спинного мозга. Nat Rev Neurosci. 2001; 2: 263–73.
CAS Статья PubMed Google ученый
Fawcett JW. Восстановление после травмы спинного мозга: регенерация, пластика и реабилитация. Головной мозг. 2009; 132: 1417–8.
Артикул PubMed Google ученый
Майер IC, Ичияма Р.М., Куртин Дж., Шнелл Л., Лавров И., Эджертон В.Р., Шваб М.Э. Дифференциальные эффекты лечения антителами против Nogo-A и тренировки на беговой дорожке у крыс с неполным повреждением спинного мозга. Головной мозг. 2009; 132: 1426–40.
Артикул PubMed Google ученый
Бернинг С., Уиллиг К.И., Стеффенс Х., Дибадж П., Хелл SW. Наноскопия мозга живой мыши. Наука. 2012; 335: 551.
CAS Статья PubMed Google ученый
Fischer M, Kaech S, Wagner U, Brinkhaus H, Matus A. Рецепторы глутамата регулируют основанную на актине пластичность дендритных шипов. Nat Neurosci. 2000; 3: 887–94.
CAS Статья PubMed Google ученый
Trachtenberg JT, Chen BE, Knott GW, Feng G, Sanes JR, Welker E, Svoboda K. Долгосрочная визуализация in vivo зависимой от опыта синаптической пластичности в коре головного мозга взрослых. Природа. 2002; 420: 788–94.
CAS Статья PubMed Google ученый
Spence EF, Soderling SH. Actin Out: регуляция синаптического цитоскелета. J Biol Chem. 2015; 290: 28613–22.
CAS Статья PubMed Google ученый
Лесли AC, Ryohei Y. Пластичность дендритных шипов: субкомпартментализация передачи сигналов. Annu Rev Physiol. 2014; 76: 365–85.
Артикул Google ученый
Ричардс Д.А., Матеос Дж. М., Хюгель С., Де Паола В., Карони П., Гавилер Б. Х., МакКинни Р. А..Глутамат вызывает быстрое образование выступов головки шипа в культурах срезов гиппокампа. Proc Natl Acad Sci U S. A. 2005; 102: 6166–71.
CAS Статья PubMed PubMed Central Google ученый
Вербич Д., Преносил Г.А., Чанг ПКИ, Мурай К.К., МакКинни Р.А. Глиальный транспорт глутамата модулирует дендритные выступы головки шипа в гиппокампе. Глия. 2012; 60: 1067–77.
Артикул PubMed Google ученый
Mundel P, Heid HW, Mundel TM, Kruger M, Reiser J, Kriz W. Синаптоподин: актин-ассоциированный белок в дендритах телэнцефала и подоцитах почек. J Cell Biol. 1997. 139: 193–204.
CAS Статья PubMed PubMed Central Google ученый
Bas Orth C, Vlachos A, Del Turco D, Burbach GJ, Haas CA, Mundel P, Feng G, Frotscher M, Deller T. Специфичное для ламина распределение Synaptopodin, молекулы, связанной с актином, необходимой для позвоночный аппарат в идентифицированных основных клеточных дендритах гиппокампа мыши.J Comp Neurol. 2005; 487: 227–39.
Артикул PubMed Google ученый
Deller T, Merten T, Roth SU, Mundel P, Frotscher M. Актин-ассоциированный белок синаптоподин в формировании гиппокампа крысы: локализация в шейке позвоночника и тесная связь с позвоночным аппаратом основных нейронов. J Comp Neurol. 2000; 418: 164–81.
CAS Статья PubMed Google ученый
Vlachos A, Korkotian E, Schonfeld E, Copanaki E, Deller T, Segal M. Синаптоподин регулирует пластичность дендритных шипов в нейронах гиппокампа. J Neurosci. 2009; 29: 1017–33.
CAS Статья PubMed Google ученый
Zhang Z, Pöschel B, Faul C, Upreti C, Stanton P, Mundel P. Важная роль синаптоподина в пластичности дендритного позвоночника развивающегося гиппокампа. J Neurosci. 2013; 33: 12510–8.
CAS Статья PubMed PubMed Central Google ученый
Окубо-Судзуки Р., Окада Д., Секигучи М., Инокучи К. Синаптоподин поддерживает зависящее от нейронной активности увеличение дендритных шипов в нейронах гиппокампа. Mol Cell Neurosci. 2008. 38: 266–76.
CAS Статья PubMed Google ученый
Деллер Т., Корте М., Чабанис С., Дракью А., Швеглер Х., Стефани Г.Г., Зунига А., Шварц К., Бонхеффер Т., Целлер Р. и др. Мыши с дефицитом синаптоподина лишены позвоночника и обнаруживают дефицит синаптической пластичности.Proc Natl Acad Sci U S. A. 2003; 100: 10494–9.
CAS Статья PubMed PubMed Central Google ученый
Спейсек Дж., Харрис К.М. Трехмерная организация гладкой эндоплазматической сети в дендритах CA1 гиппокампа и дендритных шипах незрелой и зрелой крысы. J Neurosci. 1997; 17: 190–203.
CAS PubMed Google ученый
Fifková E, Markham JA, Delay RJ. Кальций в позвоночном аппарате дендритных шипов в зубчатом молекулярном слое. Brain Res. 1983; 266: 163–8.
Артикул PubMed Google ученый
Holbro N, Grunditz A, Oertner TG. Дифференциальное распределение эндоплазматического ретикулума контролирует метаботропную передачу сигналов и пластичность в синапсах гиппокампа. Proc Natl Acad Sci. 2009; 106: 15055–60.
CAS Статья PubMed PubMed Central Google ученый
Gähwiler BH, Capogna M, Debanne D, McKinney RA, Thompson SM. Органотипические культуры срезов: техника достигла совершеннолетия. Trends Neurosci. 1997; 20: 471–7.
Артикул PubMed Google ученый
Стоппини Л., Букс П.А., Мюллер Д. Простой метод для органотипических культур нервной ткани. J Neurosci Methods. 1991; 37: 173–82.
CAS Статья PubMed Google ученый
Де Паола В., Арбер С., Карони П. Рецепторы AMPA регулируют динамическое равновесие пресинаптических окончаний в зрелых сетях гиппокампа. Nat Neurosci. 2003; 6: 491–500.
CAS PubMed Google ученый
Влахос А., Икенберг Б., Ленц М., Беккер Д., Райфенберг К., Бас-Орт С., Деллер Т. Синаптоподин регулирует индуцированную денервацией гомеостатическую синаптическую пластичность. Proc Natl Acad Sci. 2013; 110: 8242–7.
CAS Статья PubMed PubMed Central Google ученый
Дин Э.С., Илие А.Е., Сиздаххани С., Дас Гупта М., Орловски Дж., МакКинни Р.А. Усиленное рекрутирование эндосомального обменника Na + / H + NHE6 в дендритные шипы пирамидных нейронов гиппокампа во время зависимой от NMDA-рецептора долгосрочной потенциации. J Neurosci. 2013; 33: 595–610.
CAS Статья PubMed Google ученый
Чанг PKY, Prenosil GA, Verbich D, Gill R, McKinney RA. Длительное воздействие ампакина обрезает дендритные шипы и увеличивает вероятность пресинаптического высвобождения для усиления долгосрочной потенциации в гиппокампе.Eur J Neurosci. 2014; 40: 2766–76.
Артикул PubMed Google ученый
Коркотян Э., Фротчер М., Сегал М. Синаптоподин регулирует пластичность позвоночника: посредничество с помощью запасов кальция. J Neurosci. 2014; 34: 11641–51.
CAS Статья PubMed Google ученый
Спейсек Дж. Трехмерный анализ дендритных шипов. II. Позвоночный аппарат и другие компоненты цитоплазмы.Анат Эмбриол. 1985; 171: 235–43.
CAS Статья PubMed Google ученый
Коркотян Э., Сегал М. Синаптоподин регулирует высвобождение кальция из запасов в дендритных шипах культивируемых нейронов гиппокампа. J Physiol. 2011; 589: 5987–95.
CAS Статья PubMed PubMed Central Google ученый
Sharp AH, McPherson PS, Dawson TM, Aoki C, Campbell KP, Snyder SH.Дифференциальная иммуногистохимическая локализация инозитол-1,4,5-трифосфат- и рианодин-чувствительных каналов высвобождения Ca 2+ в головном мозге крыс. J Neurosci. 1993; 13: 3051–63.
CAS PubMed Google ученый
Макферсон П.С., Ким И.К., Вальдивия Х., Кнудсон С.М., Такекура Х., Францини-Армстронг К., Коронадот Р., Кэмпбелл К.П. Рецептор рианодина в мозге: канал высвобождения кальция, чувствительный к кофеину. Нейрон. 1991; 7: 17–25.
CAS Статья PubMed Google ученый
Мелдолези Дж. Быстро обменивающиеся запасы Ca 2+ в нейронах: молекулярные, структурные и функциональные свойства. Prog Neurobiol. 2001; 65: 309–38.
CAS Статья PubMed Google ученый
Schwab ME, Strittmatter SM. Nogo ограничивает нервную пластичность и восстановление после травм. Curr Opin Neurobiol.2014; 27: 53–60.
CAS Статья PubMed Google ученый
Allred RP, Kim SY, Jones TA. Используйте это и / или потеряйте — почувствуйте влияние на ремоделирование мозга через некоторое время после инсульта. Front Hum Neurosci. 2014; 8.
Jedlicka P, Vlachos A, Schwarzacher SW, Deller T. Роль аппарата позвоночника в LTP и пространственном обучении. BehavBrain Res. 2008; 192: 12–9.
Google ученый
Влахос А. Синаптоподин и органелла позвоночного аппарата. Регуляторы различных форм синаптической пластичности? Анн Анат. 2012; 194: 317–20.
CAS Статья PubMed Google ученый
Jedlicka P, Schwarzacher SW, Winkels R, Kienzler F, Frotscher M, Bramham CR, Schultz C, Bas Orth C, Deller T. Нарушение долгосрочной потенциации тета-всплеска in vivo и сетевой возбудимости в зубчатая извилина синаптоподин-дефицитных мышей, лишенных позвоночного аппарата и цистернальной органеллы.Гиппокамп. 2009; 19: 130.
CAS Статья PubMed Google ученый
Grigoryan G, Segal M. Опосредованное рианодином превращение STP в LTP отсутствует у мышей с дефицитом синаптоподина. Функция структуры мозга. 2015: 1–5.
Серый EG. Электронная микроскопия синаптических контактов на дендритных шипах коры головного мозга. Природа. 1959; 183: 1592–3.
CAS Статья PubMed Google ученый
Emptage N, Bliss TVP, Fine A. Одиночные синаптические события вызывают опосредованное рецептором NMDA высвобождение кальция из внутренних запасов дендритных шипов гиппокампа. Нейрон. 1999; 22: 115–24.
CAS Статья PubMed Google ученый
Муракоши Х., Ясуда Р. Постсинаптическая передача сигналов во время пластичности дендритных шипов. Trends Neurosci. 2012; 35: 135–43.
CAS Статья PubMed PubMed Central Google ученый
Saneyoshi T, Fortin DA, Soderling TR. Регуляция образования позвоночника и синапсов с помощью зависимых от активности внутриклеточных сигнальных путей. CurrOpinNeurobiol. 2010; 20: 108–15.
CAS Google ученый
Муракоши Х., Ван Х., Ясуда Р. Локальная, стойкая активация Rho GTPases во время пластичности отдельных дендритных шипов. Природа. 2011; 472: 100–4.
CAS Статья PubMed PubMed Central Google ученый
Фишер М., Кеч С., Кнутти Д., Матус А. Быстрая актиновая пластичность дендритных шипов. Нейрон. 1998. 20: 847–54.
CAS Статья PubMed Google ученый
Asanuma K, Yanagida-Asanuma E, Faul C, Tomino Y, Kim K, Mundel P. Синаптоподин регулирует организацию актина и подвижность клеток посредством регуляции передачи сигналов RhoA. Nat Cell Biol. 2006; 8: 485–91.
CAS Статья PubMed Google ученый
Kremerskothen J, Plaas C, Kindler S, Frotscher M, Barnekow A. Синаптоподин, молекула, участвующая в формировании дендритного аппарата позвоночника, представляет собой двойной связывающий актин / α-актинин белок. J Neurochem. 2005. 92: 597–606.
CAS Статья PubMed Google ученый
Сьоблом Б., Салмазо А., Джинович-Каруго К. Структура и регуляция α-актинина. Cell Mol Life Sci. 2008; 65: 2688–701.
Артикул PubMed Google ученый
Holtmaat A, Wilbrecht L, Knott GW, Welker E, Svoboda K. Зависящий от опыта и специфичный для клеточного типа рост позвоночника в неокортексе. Природа. 2006; 441: 979–83.
CAS Статья PubMed Google ученый
Knott GW, Holtmaat A, Wilbrecht L, Welker E, Svoboda K. Рост позвоночника предшествует образованию синапсов во взрослой неокортексе in vivo. Nat Neurosci. 2006; 9: 1117–24.
CAS Статья PubMed Google ученый
McKinney RA, Capogna M, Durr R, Gahwiler BH, Thompson SM. Миниатюрные синаптические события поддерживают дендритные шипы за счет активации рецептора AMPA. Nat Neurosci. 1999; 2: 44–9.
CAS Статья PubMed Google ученый
Vuksic M, Del Turco D, Vlachos A, Schuldt G, Müller CM, Schneider G, Deller T. Односторонняя энторинальная денервация приводит к длительным дендритным изменениям гранулярных клеток гиппокампа мыши. Exp Neurol.2015; 230: 176–85.
Артикул Google ученый
Lucke-Wold BP, Nguyen L, Turner RC, Logsdon AF, Chen YW, Smith KE, Huber JD, Matsumoto R, Rosen CL, Tucker ES, Richter E. Черепно-мозговая травма и эпилепсия: ведущие механизмы захватить. Seizure Eur J Epilepsy. 2015; 33: 13–23.
Артикул Google ученый
Рао В.Р., Парко КЛ. Клинический подход к посттравматической эпилепсии.Semin Neurol. 2015; 35: 057–63.
Артикул Google ученый
Лоан DJ, Кумар А. Микроглия в головном мозге ЧМТ: хорошее, плохое и нарушение регуляции. Exp Neurol. 2016; 275 (3): 316–27.
CAS Статья PubMed Google ученый

