Что такое полосовой фильтр и как он работает. Какие бывают схемы полосовых фильтров. Как рассчитать и настроить полосовой фильтр. Где применяются полосовые фильтры в радиоэлектронике.
Что такое полосовой фильтр и принцип его работы
Полосовой фильтр — это электронная схема, которая пропускает сигналы определенного диапазона частот и подавляет сигналы за пределами этого диапазона. Полосовой фильтр сочетает в себе свойства фильтра нижних частот и фильтра верхних частот.
Принцип работы полосового фильтра основан на следующем:
- Фильтр имеет нижнюю частоту среза fн и верхнюю частоту среза fв
- Сигналы с частотой ниже fн подавляются
- Сигналы с частотой выше fв также подавляются
- Сигналы в диапазоне от fн до fв пропускаются с минимальным ослаблением
Диапазон частот между fн и fв называется полосой пропускания фильтра. Ширина полосы пропускания определяется как:
Δf = fв — fн
Центральная частота полосы пропускания вычисляется как:

f0 = √(fн * fв)
Основные типы и схемы полосовых фильтров
Существует несколько основных типов полосовых фильтров:
1. Пассивные RC-фильтры
Простейший пассивный полосовой фильтр состоит из двух RC-цепочек:
- ФВЧ на входе для подавления низких частот
- ФНЧ на выходе для подавления высоких частот
Схема такого фильтра выглядит следующим образом:
«` «`Частоты среза такого фильтра определяются формулами:
fн = 1 / (2π * R1 * C1)
fв = 1 / (2π * R2 * C2)
2. Активные фильтры на операционных усилителях
Активные полосовые фильтры строятся на основе операционных усилителей. Они имеют лучшие характеристики по сравнению с пассивными RC-фильтрами:
- Более крутые склоны АЧХ
- Возможность усиления сигнала в полосе пропускания
- Высокое входное и низкое выходное сопротивление
3. LC-фильтры
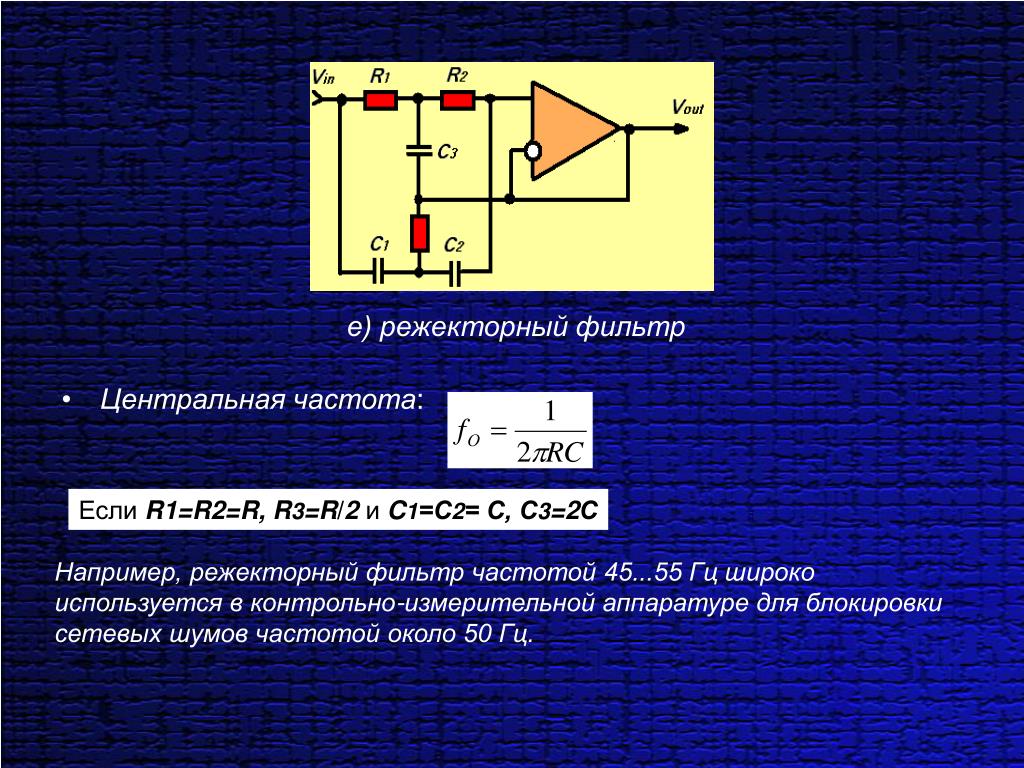
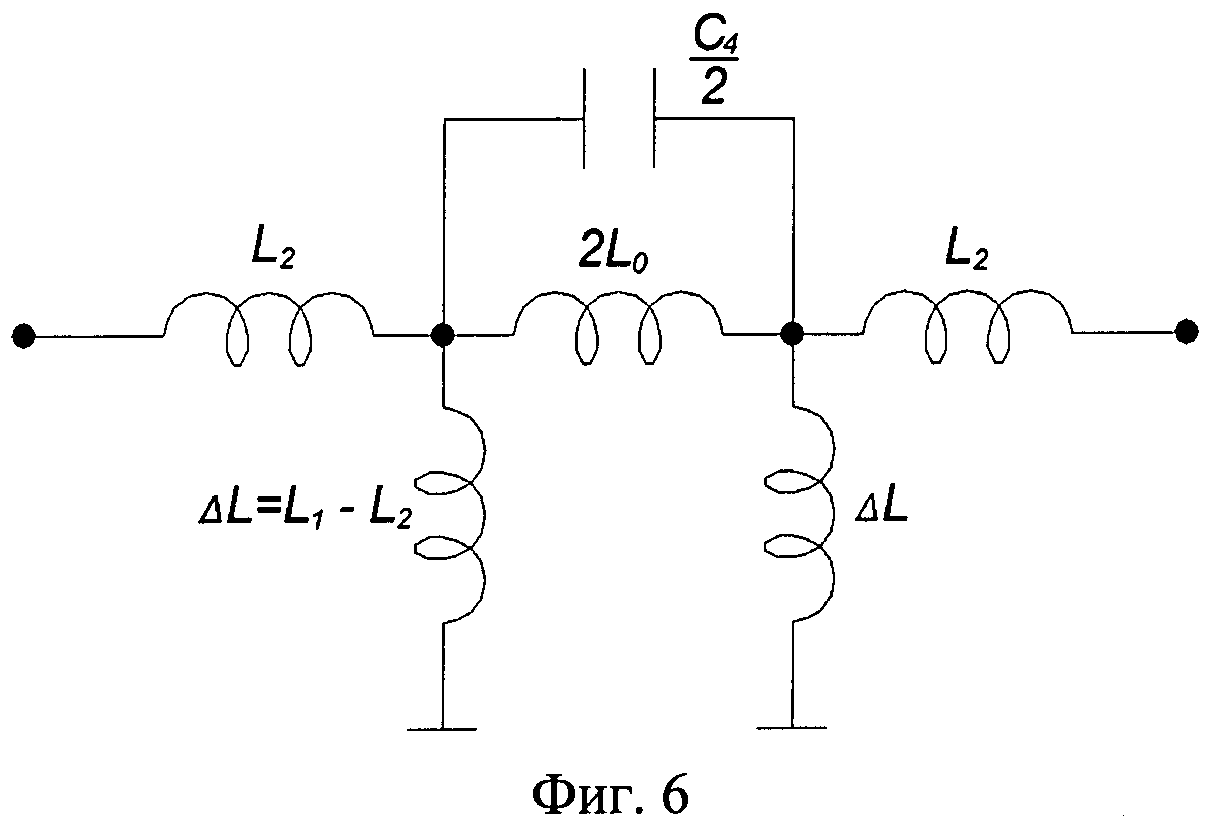
LC-фильтры строятся на основе катушек индуктивности и конденсаторов. Они применяются на высоких частотах, где RC-фильтры неэффективны. LC-фильтры обеспечивают более крутые склоны АЧХ.
Как рассчитать и настроить полосовой фильтр
Расчет полосового фильтра включает следующие этапы:
- Определение требуемой полосы пропускания (fн и fв)
- Выбор типа фильтра (пассивный/активный, порядок)
- Расчет номиналов компонентов по формулам
- Моделирование АЧХ фильтра
- Подбор ближайших стандартных номиналов
Настройка полосового фильтра выполняется следующим образом:
- Подача на вход синусоидального сигнала известной частоты
- Измерение выходного сигнала и построение АЧХ
- Корректировка номиналов компонентов для достижения требуемых параметров
Применение полосовых фильтров в радиоэлектронике
Полосовые фильтры широко применяются в различных областях радиоэлектроники:
1. Радиоприемники
В радиоприемниках полосовые фильтры используются для:
- Выделения сигнала нужной радиостанции
- Подавления помех от соседних каналов
- Фильтрации промежуточной частоты
2. Аудиотехника
В аудиотехнике полосовые фильтры применяются для:
- Разделения звукового спектра на частотные полосы
- Коррекции частотной характеристики
- Подавления внеполосных шумов
3. Измерительная техника
В измерительных приборах полосовые фильтры используются для:
- Выделения сигнала на определенной частоте
- Подавления гармоник и помех
- Формирования узкополосных сигналов
Характеристики полосовых фильтров
Основные характеристики полосовых фильтров:
- Центральная частота f0
- Полоса пропускания Δf
- Коэффициент прямоугольности АЧХ
- Неравномерность АЧХ в полосе пропускания
- Затухание в полосе заграждения
- Групповое время задержки
Эти параметры определяют качество фильтрации сигнала и выбираются исходя из требований конкретного применения.
Особенности проектирования полосовых фильтров
При разработке полосовых фильтров необходимо учитывать следующие особенности:
- Выбор оптимальной топологии схемы
- Учет паразитных параметров компонентов
- Обеспечение температурной стабильности
- Минимизация искажений сигнала
- Согласование входного и выходного сопротивлений
Правильный учет этих факторов позволяет создать фильтр с требуемыми характеристиками.
Современные тенденции в разработке полосовых фильтров
В настоящее время в области полосовых фильтров наблюдаются следующие тенденции:

- Применение цифровых фильтров на сигнальных процессорах
- Использование ПАВ-фильтров на высоких частотах
- Разработка адаптивных фильтров с перестраиваемыми параметрами
- Интеграция фильтров в специализированные микросхемы
- Оптимизация фильтров методами машинного обучения
Эти подходы позволяют создавать более совершенные фильтры для современных радиоэлектронных устройств.
Пассивный полосовой фильтр — принцип работы, характеристики, схемы, формулы — Кови
Пассивные полосовые фильтры можно изготовить, соединив вместе фильтр низких частот и фильтр высоких частот.
Полосно-пропускающие фильтры могут использоваться для изоляции или фильтрации определенных частот, которые находятся в определенной полосе или диапазоне частот. Частота среза или точка ƒc в простом пассивном RC-фильтре может точно контролироваться с помощью одного резистора, включенного последовательно с неполяризованным конденсатором, и в зависимости от того, как они подключены, мы видели, что получается либо низкочастотный, либо высокочастотный фильтр.
Одно из простых применений этих типов пассивных фильтров — использование в усилителях звука или схемах, например, в фильтрах кроссовера громкоговорителя или регуляторах тембра предварительного усилителя. Иногда необходимо пропускать только определенный диапазон частот, которые не начинаются с 0 Гц (постоянный ток) или заканчиваются в верхней высокочастотной точке, но находятся в определенном диапазоне или полосе частот, узкой или широкой.
Соединяя или «каскадируя» вместе одну цепь фильтра низких частот с цепью фильтра высоких частот, мы можем получить другой тип пассивного RC-фильтра, который пропускает выбранный диапазон или «полосу» частот, которые могут быть как узкими, так и широкими, при этом ослабляя все те, которые находятся за пределами этого диапазона. Этот новый тип пассивного фильтра создает частотно-избирательный фильтр, известный как Band Pass Filter или сокращенно BPF.
Содержание
Схема полосового фильтра
В отличие от фильтра низких частот, пропускающего только сигналы низкого диапазона частот, или фильтра высоких частот, пропускающего сигналы более высокого диапазона частот, полосовые фильтры пропускают сигналы в пределах определенной «полосы» или «разброса» частот, не искажая входной сигнал и не внося дополнительного шума. Эта полоса частот может быть любой ширины и обычно называется полосой пропускания фильтра.
Полоса пропускания обычно определяется как диапазон частот, существующий между двумя заданными точками отсечения частот ( ƒc ), которые на 3 дБ ниже максимального центра или резонансного пика, при одновременном ослаблении или затухании остальных за пределами этих двух точек.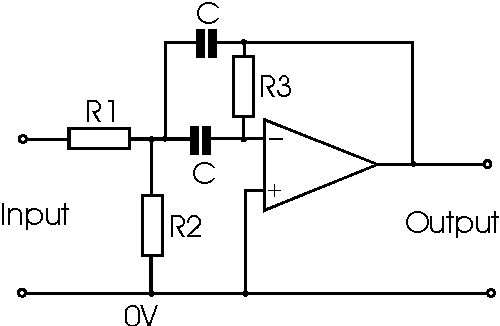
Тогда для широко разнесенных частот мы можем просто определить термин «полоса пропускания», BW, как разницу между точками нижней частоты среза ( ƒcLOWER ) и верхней частоты среза ( ƒcHIGHER ). Другими словами, BW = ƒH — ƒL. Очевидно, что для правильной работы полосового фильтра частота среза фильтра низких частот должна быть выше частоты среза фильтра высоких частот.
«Идеальный» полосовой фильтр пропускания может также использоваться для изоляции или фильтрации определенных частот, лежащих в определенной полосе частот, например, для подавления шума. Полосно-пропускающие фильтры известны как фильтры второго порядка (двухполюсные), потому что в их схеме есть «два» реактивных компонента — конденсаторы. Один конденсатор в цепи низких частот и другой конденсатор в цепи высоких частот.
Частотная характеристика полосового пропускающего фильтра 2-го порядка
Приведенный выше график Боде или кривая частотной характеристики показывает характеристики полосового фильтра. Здесь сигнал ослабляется на низких частотах, а выходное напряжение увеличивается с наклоном +20 дБ/декада (6 дБ/октава), пока частота не достигнет точки «нижней отсечки» ƒL. На этой частоте выходное напряжение снова составляет 1/√2 = 70,7% от значения входного сигнала или -3 дБ (20*log(VOUT/VIN)) от входного.
На этой частоте выходное напряжение снова составляет 1/√2 = 70,7% от значения входного сигнала или -3 дБ (20*log(VOUT/VIN)) от входного.
Выходной сигнал продолжает усиливаться до достижения точки «верхней отсечки» ƒH, где выходной сигнал уменьшается со скоростью -20 дБ/декада (6 дБ/октава), ослабляя любые высокочастотные сигналы. Точка максимального выходного усиления обычно является средним геометрическим двух значений -3 дБ между нижней и верхней точками отсечки и называется «центральной частотой» или «резонансным пиком» ƒr. Это среднее геометрическое значение рассчитывается как ƒr 2 = ƒ(UPPER) x ƒ(LOWER).
Полосовой фильтр считается фильтром второго порядка (двухполюсным), поскольку в его структуре есть «два» реактивных компонента, то фазовый угол будет в два раза больше, чем у ранее рассмотренных фильтров первого порядка, т.е. 180o. Фазовый угол выходного сигнала опережает входной на +90o до центральной или резонансной частоты, ƒr точки, где он становится «нулем» градусов (0o) или «синфазным», а затем изменяется в сторону отставания от входного на -90o по мере увеличения выходной частоты.
Верхняя и нижняя точки частоты среза для полосового фильтра могут быть найдены по той же формуле, что и для фильтров низких и высоких частот, например.
Тогда очевидно, что шириной полосы пропускания фильтра можно управлять с помощью расположения двух точек частоты среза двух фильтров.
Пример полосового фильтра No1
Необходимо построить полосовой фильтр второго порядка с использованием RC-компонентов, который будет пропускать только диапазон частот выше 1 кГц (1 000 Гц) и ниже 30 кГц (30 000 Гц). Предполагая, что оба резистора имеют значения 10kΩ, рассчитайте значения двух необходимых конденсаторов.
Этап фильтра высоких частот
Значение конденсатора C1, необходимое для получения частоты среза ƒL 1 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
Тогда значения R1 и C1, необходимые для каскада высоких частот, чтобы обеспечить частоту среза 1,0 кГц, следующие: R1 = 10kΩ и, с точностью до предпочтительного значения, C1 = 15nF.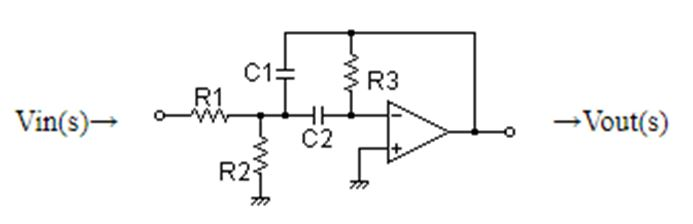
Этап фильтра низких частот
Значение конденсатора C2, необходимое для получения частоты среза ƒH 30 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
Тогда значения R2 и C2, необходимые для низкочастотного каскада, чтобы обеспечить частоту среза 30 кГц, составляют R = 10 кОм и C = 530 пФ. Однако ближайшим предпочтительным значением рассчитанного значения конденсатора 530пФ является 560пФ, поэтому вместо него используется это значение.
Учитывая, что значения сопротивлений R1 и R2 равны 10kΩ, а значения конденсаторов C1 и C2, найденные для фильтров высоких и низких частот, равны 15nF и 560pF соответственно, схема нашего простого пассивного полосового фильтра имеет вид.
Законченная схема полосового фильтра
Резонансная частота полосового фильтра
Мы также можем рассчитать «резонансную» или «центральную частоту» (ƒr) полосового фильтра, когда выходное усиление достигает максимального или пикового значения. Это пиковое значение не является средним арифметическим верхней и нижней точек отсечки -3 дБ, как можно было бы ожидать, а представляет собой «геометрическое» или среднее значение. Это среднее геометрическое значение рассчитывается, например, как ƒr 2 = ƒc(UPPER) x ƒc(LOWER):
Это среднее геометрическое значение рассчитывается, например, как ƒr 2 = ƒc(UPPER) x ƒc(LOWER):
Уравнение центральной частоты
Где, ƒr — резонансная или центральная частота
ƒL — нижняя точка частоты среза по уровню -3 дБ
ƒH — верхняя точка среза частоты -3 дБ
и в нашем простом примере выше, рассчитанные частоты среза составили ƒL = 1 060 Гц и ƒH = 28 420 Гц, используя значения фильтра.
Подставив эти значения в вышеприведенное уравнение, можно получить центральную резонансную частоту:
Краткое описание полосового фильтра
Простой пассивный полосовой фильтр может быть изготовлен путем каскадного соединения одного фильтра низких частот с фильтром высоких частот. Диапазон частот в герцах между нижней и верхней точками среза по уровню -3 дБ комбинации RC называется «полосой пропускания» фильтра.
Ширина или частотный диапазон полосы пропускания фильтра может быть очень маленькой и селективной или очень широкой и неселективной в зависимости от используемых значений R и C.
Точка центральной или резонансной частоты является средним геометрическим нижнего и верхнего срезов. На этой центральной частоте выходной сигнал максимален, а фазовый сдвиг выходного сигнала такой же, как и входного.
Амплитуда выходного сигнала полосового фильтра или любого другого пассивного RC-фильтра всегда будет меньше амплитуды входного сигнала. Другими словами, пассивный фильтр также является аттенюатором, дающим коэффициент усиления по напряжению менее 1 (Единство). Чтобы обеспечить выходной сигнал с коэффициентом усиления по напряжению больше единицы, в конструкции схемы требуется некоторая форма усиления.
Пассивный полосовой фильтр классифицируется как фильтр второго порядка, поскольку в его конструкции есть два реактивных компонента — конденсаторы. Он состоит из двух отдельных фильтрующих RC-цепей, которые сами являются фильтрами первого порядка.
При каскадном соединении нескольких фильтров результирующая схема будет называться фильтром «n-го порядка», где «n» означает количество отдельных реактивных компонентов и, следовательно, полюсов в цепи фильтра.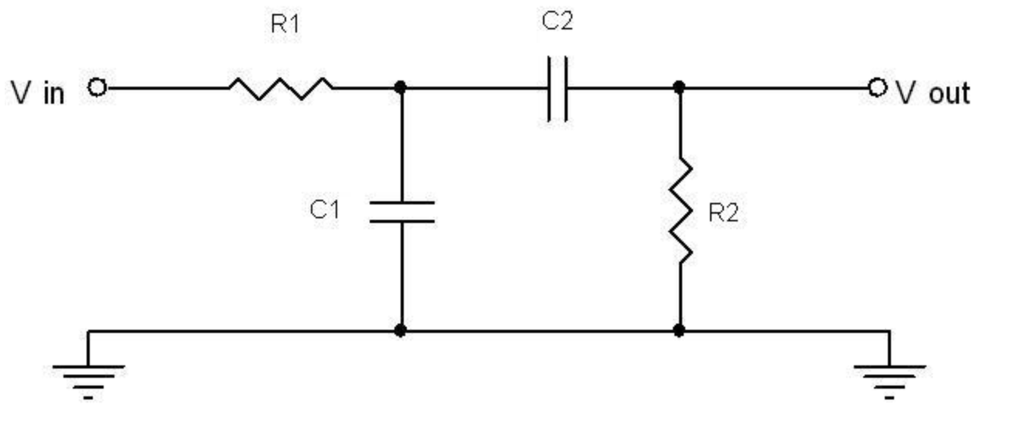 Например, фильтры могут быть 2-го порядка, 4-го порядка, 10-го порядка и т.д.
Например, фильтры могут быть 2-го порядка, 4-го порядка, 10-го порядка и т.д.
Чем выше порядок фильтра, тем круче будет наклон при n раз -20 дБ/декада. Однако один конденсатор, полученный путем объединения двух или более отдельных конденсаторов, все равно остается одним конденсатором.
Наш пример выше показывает кривую выходной частотной характеристики для «идеального» полосового фильтра с постоянным коэффициентом усиления в полосе пропускания и нулевым коэффициентом усиления в полосе останова. На практике частотная характеристика этой схемы полосового фильтра не будет такой же, поскольку входное реактивное сопротивление цепи высоких частот будет влиять на частотную характеристику цепи низких частот (компоненты подключены последовательно или параллельно) и наоборот. Один из способов преодоления этой проблемы — обеспечить электрическую развязку между двумя цепями фильтра, как показано ниже.
Буферизация отдельных ступеней фильтра
Одним из способов объединения усиления и фильтрации в одной схеме является использование операционного усилителя (Op-amp), примеры которого приведены в разделе «Операционный усилитель». В следующем уроке мы рассмотрим схемы фильтров, в которых операционный усилитель используется не только для усиления, но и для обеспечения изоляции между каскадами. Такие схемы фильтров обычно называются активными фильтрами.
В следующем уроке мы рассмотрим схемы фильтров, в которых операционный усилитель используется не только для усиления, но и для обеспечения изоляции между каскадами. Такие схемы фильтров обычно называются активными фильтрами.
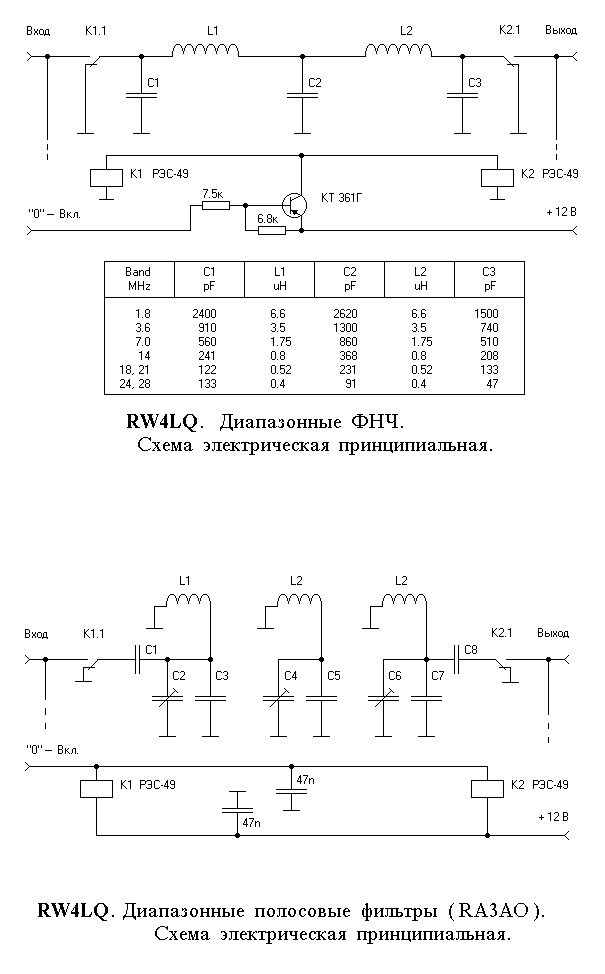
Диапазонные полосовые фильтры. Схема ДПФ для трансиверов и радиопрёмников.
|
|
Принципиальная схема полосового фильтра Теория и эксперимент
Кошмаром каждого проектировщика аналоговых устройств является шум в его схеме. Когда дело доходит до переключающих цепей, аудиоусилителей или цепей частотных сигналов, существует очень большая вероятность того, что на схему будут воздействовать шумовые сигналы. Из множества способов удаления шума из схемы наиболее часто используемый называется схема фильтра . Как следует из названия, эта схема будет отфильтровывать нежелательные сигналы (шум) от фактического сигнала. Существует много типов фильтровальных схем, но наиболее часто используемой и эффективной является схема 9.0003 Полосовой фильтр , который можно легко собрать из пары резисторов и конденсаторов. Итак, в этом уроке мы узнаем об этом полосовом фильтре, его теории и о том, как его можно использовать в практических схемах.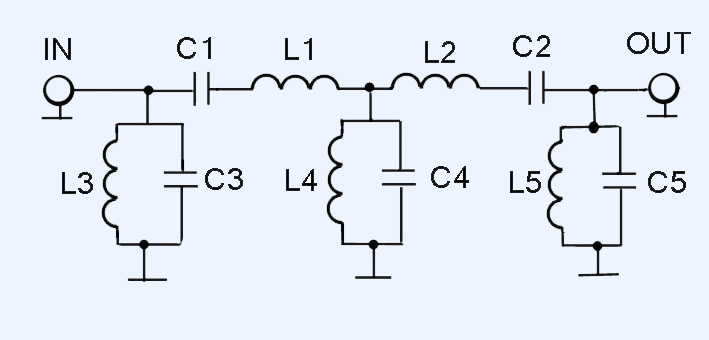
Что такое полосовой фильтр?
Схема/устройство полосового фильтра используется для того, чтобы пропускал через него только предварительно определенный набор частот. Он будет фильтровать все частоты, которые ниже установленного значения и выше установленного значения. Это комбинация фильтра верхних частот и фильтра нижних частот. Фильтр, пропускающий только те частоты, которые выше его, называется 9.0003 фильтр верхних частот и фильтр, который допускает частоты только ниже его, называется фильтром нижних частот . Полосовой фильтр можно получить путем каскадирования фильтров высоких и низких частот. Он широко применяется в схемах аудиоусилителей и беспроводных приемопередатчиках, где динамик должен воспроизводить только нужный набор частот и игнорировать остальные.
Существует два типа полосовых фильтров. Если в схеме используется какой-то внешний источник питания (активные устройства), например, транзисторы и т. д., тогда схема называется 9.0003 Активный полосовой фильтр , и если схема не включает никаких активных компонентов и состоит только из пассивных компонентов, таких как резистор, конденсатор и катушка индуктивности, тогда схема называется Пассивный полосовой фильтр . В этой статье мы более подробно обсудим пассивный полосовой фильтр. Помимо этой классификации, в этой статье будут кратко описаны другие аспекты, по которым можно классифицировать фильтр.
д., тогда схема называется 9.0003 Активный полосовой фильтр , и если схема не включает никаких активных компонентов и состоит только из пассивных компонентов, таких как резистор, конденсатор и катушка индуктивности, тогда схема называется Пассивный полосовой фильтр . В этой статье мы более подробно обсудим пассивный полосовой фильтр. Помимо этой классификации, в этой статье будут кратко описаны другие аспекты, по которым можно классифицировать фильтр.
Цепь полосового фильтра
Как уже говорилось ранее, мы обсудим пассивный полосовой фильтр , который построен с использованием резистора и конденсатора. Это комбинация фильтра верхних частот и фильтра нижних частот. Пример схемы простого пассивного полосового фильтра показан ниже.
Первая половина схемы представляет собой фильтр высоких частот , который фильтрует низкие частоты и пропускает только частоты, превышающие установленную верхнюю частоту среза (fc ВЫСОКИЙ ). Значение этой высокой частоты среза можно рассчитать по формулам
Значение этой высокой частоты среза можно рассчитать по формулам
fc HIGH = 1 / 2 π*R1*C1
Вторая половина схемы представляет собой схему фильтра нижних частот , которая фильтрует более высокие частоты и пропускает только частоты ниже установленная низкая частота среза (fc LOW ) . Значение нижней граничной частоты можно рассчитать по формулам
fc LOW = 1 / 2 π*R2*C2
Этот тип схемы фильтра называется фильтром порядка 2 и , поскольку он имеет два резистора и два конденсатора. Полосовой фильтр может быть фильтром порядка 2 и или фильтром более высокого порядка, поскольку для правильного функционирования схемы требуется как минимум два резистора и конденсатор. Теперь, когда частота входного сигнала подается на этот фильтр, он выдает частоту выше, чем fc LOW и ниже fc HIGH. Другими словами, выходная частота может быть задана как fc HIGH- fc LOW , частота, которая находится между этими диапазонами, называется полосой пропускания . Следовательно, пропускная способность фильтра может быть рассчитана как
Другими словами, выходная частота может быть задана как fc HIGH- fc LOW , частота, которая находится между этими диапазонами, называется полосой пропускания . Следовательно, пропускная способность фильтра может быть рассчитана как
. Bandwidth = fc HIGH- fc LOW
Частотная характеристика полосового фильтра
Частотная характеристика, известная как график Боде для 2Ниже показан пассивный полосовой фильтр для заказа 0081 nd .
График построен в зависимости от входной частоты по оси X и выходной частоты в децибелах по оси Y. Когда входная частота меньше нижней частоты среза (f-low), выходная частота остается меньше -3 дБ, а когда она превышает эту частоту, выходная частота достигает максимума и остается на этом уровне до тех пор, пока частота не превысит более высокую частоту среза. (f-высокий). Пик, при котором выходное усиление остается максимальным, называется резонансная частота . Это просто среднее геометрическое верхней верхней частоты среза и нижней частоты среза. Формулы для расчета того же приведены ниже
Пик, при котором выходное усиление остается максимальным, называется резонансная частота . Это просто среднее геометрическое верхней верхней частоты среза и нижней частоты среза. Формулы для расчета того же приведены ниже
Резонансная частота (Fr) = √(f – низкая * f – высокая)
Расстояние между нижней и верхней граничными частотами называется полосой пропускания. Таким образом, входной частоте будет разрешено проходить только в том случае, если она находится в пределах полосы пропускания.
Практический пример полосовых фильтров
Давайте создадим простой полосовой фильтр для фильтрации определенного набора частот и проверим, как он работает на самом деле. Экспериментальная установка, которую я использую для этого урока, показана ниже. Таким образом, более высокая частота среза для этой схемы будет равна 9-12) =7280 Гц
Из приведенных выше расчетов мы можем сделать вывод, что схема допускает частоты только в диапазоне от 1577 Гц до 7280 Гц , а все, что меньше или больше, чем это, будет отфильтровано нашим полосовым фильтром. Давайте проверим, работает ли то же самое, собрав схему на макетной плате. Моя тестовая установка выглядела примерно так:
Давайте проверим, работает ли то же самое, собрав схему на макетной плате. Моя тестовая установка выглядела примерно так:
Для тестирования схемы нам нужен функциональный генератор для генерации частоты сигнала, частотой которой можно управлять. Поскольку у меня его не было, я решил использовать свой телефон с приложением для Android, которое будет генерировать необходимые частоты через разъем для наушников 3,5 мм. Затем этот сигнал подается в качестве входной частоты в схему с помощью разъема, как показано выше.
Чтобы проверить зависимость приложения, я использовал осциллограф для измерения частоты входного сигнала и обнаружил, что частота генерации зависит. На приведенном ниже рисунке показано приложение на моем телефоне, которое генерирует около 4819 Гц входной частоты, а подключенный к нему осциллограф отображает сигнал и измеряет частоту 4,816 кГц, что является идеальным.
Теперь мы можем подключить осциллограф к выходному сигналу схемы и изменить входную частоту. Схема позволит отображать на осциллографе все частоты в диапазоне от 1500 до 7000, а остальные частоты будут отфильтрованы или зашумлены. Также имейте в виду, что эта схема предназначена только для понимания цели и, следовательно, подвергается усовершенствованиям, прежде чем применять ее в реальных условиях. Кроме того, поскольку схема построена на макетной плате, выходной сигнал может вызвать некоторый шум, поместите конденсатор как можно ближе и уменьшите длину его выводов, чтобы уменьшить проблему. Надеюсь, вы поняли о фильтрах Band Pass, если у вас есть какие-либо вопросы, оставьте их в комментариях ниже или используйте форумы.
Схема позволит отображать на осциллографе все частоты в диапазоне от 1500 до 7000, а остальные частоты будут отфильтрованы или зашумлены. Также имейте в виду, что эта схема предназначена только для понимания цели и, следовательно, подвергается усовершенствованиям, прежде чем применять ее в реальных условиях. Кроме того, поскольку схема построена на макетной плате, выходной сигнал может вызвать некоторый шум, поместите конденсатор как можно ближе и уменьшите длину его выводов, чтобы уменьшить проблему. Надеюсь, вы поняли о фильтрах Band Pass, если у вас есть какие-либо вопросы, оставьте их в комментариях ниже или используйте форумы.
Схема пассивного полосового фильтра и его применение
В предыдущих уроках мы рассмотрели фильтры нижних и верхних частот. В этом уроке мы узнаем о другой категории фильтров, известных как полосовые фильтры. В частности, мы узнаем о Passive Band Pass RC Filter, его базовой схеме, функциональных возможностях, частотной характеристике, приложениях и многом другом.
Для получения дополнительной информации о фильтрах низких и высоких частот см. руководства по пассивным фильтрам верхних частот RC , Пассивные RC-фильтры нижних частот , Активный фильтр высоких частот и Активный фильтр нижних частот .
Описание
Введение
Можно сказать, что полосовой фильтр представляет собой комбинацию фильтра нижних частот и фильтра верхних частот. Само название фильтра говорит о том, что он пропускает только определенную полосу частот и блокирует все остальные частоты.
В звуковых приложениях иногда необходимо передать только определенный диапазон частот, этот диапазон частот не начинается с 0 Гц или не заканчивается на очень высокой частоте, но эти частоты находятся в пределах определенного диапазона, широкого или узкого. Эти полосы частот обычно называют полосой пропускания.
[adsense1]
Пассивный полосовой фильтр
Полосовой фильтр получается путем каскадирования пассивных фильтров нижних частот и пассивных фильтров верхних частот. Такое расположение обеспечит избирательный фильтр, который пропускает только определенные частоты. Эта новая схема RC-фильтра может пропускать как узкий диапазон частот, так и широкий диапазон частот.
Такое расположение обеспечит избирательный фильтр, который пропускает только определенные частоты. Эта новая схема RC-фильтра может пропускать как узкий диапазон частот, так и широкий диапазон частот.
Этот диапазон частот, который может быть узким или широким, будет зависеть от того, как каскад пассивного фильтра нижних частот и фильтра верхних частот. Верхняя и нижняя частоты среза зависят от конструкции фильтра. Этот полосовой фильтр выглядит просто как частотно-селективный фильтр.
На приведенном выше рисунке показана схема полосового фильтра. На вход подается синусоидальный сигнал. Свойства комбинаций низких и высоких частот дают нам полосовой фильтр. При расположении одного набора RC-элементов последовательно и другого набора RC-элементов параллельно схема ведет себя как полосовой фильтр.
Это дает нам фильтр второго порядка, поскольку схема имеет два реактивных компонента. Один конденсатор относится к фильтру нижних частот, а другой конденсатор относится к фильтру высоких частот. Без каких-либо изменений входного сигнала этот полосовой фильтр пропускает определенный диапазон частот. Этот фильтр не создает дополнительных шумов в сигнале.
Без каких-либо изменений входного сигнала этот полосовой фильтр пропускает определенный диапазон частот. Этот фильтр не создает дополнительных шумов в сигнале.
Частота среза схемы может быть рассчитана следующим образом:
f C = 1/(2πRC)
Регулируя частоты среза фильтров верхних и нижних частот, мы можем получить соответствующую ширину полосы пропускания для полосового фильтра.
[adsense2]
Поскольку этот фильтр пропускает полосу частот, этот фильтр содержит две частоты среза: нижнюю частоту среза ‘f L ’ и верхнюю частоту среза ‘f H ’. При этом диапазон частот, пропущенных через фильтр, называется полосой пропускания фильтра. В общем случае ширина полосы канала может быть рассчитана по частотам f H и f L .
BW = f H – f L
Где , ‘f H ‘ — частота среза фильтра верхних частот, а ‘ f L ‘ — частота среза фильтр нижних частот. «BW» — это полоса пропускания фильтра. Полосовой фильтр пропускает частоты выше частоты среза фильтра верхних частот и ниже частоты среза фильтра нижних частот.
«BW» — это полоса пропускания фильтра. Полосовой фильтр пропускает частоты выше частоты среза фильтра верхних частот и ниже частоты среза фильтра нижних частот.
Это показывает, что частота среза фильтра нижних частот должна быть выше, чем частота среза фильтра высоких частот.
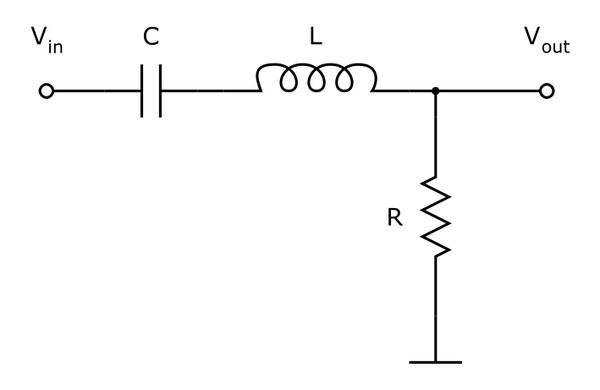
Полосовой фильтр с использованием компонентов R, L и C
Схема схемы полосового фильтра с использованием катушки индуктивности, конденсатора и резистора представлена ниже.
Центральную частоту полосового фильтра, также называемую «резонансным пиком», можно определить с помощью приведенного ниже уравнения.
f c = 1/2π√(LC)
Где L = индуктивность катушки индуктивности, единицы измерения которой выражены в Генри (Гн).
C = емкость конденсатора в фарадах (F).
Мы также можем разработать полосовой фильтр с катушками индуктивности, но мы знаем, что из-за высокого реактивного сопротивления конденсаторов конструкция полосового фильтра с RC-элементами имеет больше преимуществ, чем RL-схемы.
Частотная характеристика полосового фильтра
Частота полюса примерно равна частоте максимального усиления.
Кривая частотной характеристики полосового фильтра показана ниже: Идеальные характеристики и практические характеристики полосовых фильтров различаются из-за входного реактивного сопротивления схемы.
Усиление входного сигнала можно рассчитать, взяв 20 log (V из / V из ). Диапазон может быть довольно большим в зависимости от внутренних характеристик схемы. Сигнал ослабляется на низких частотах, выходной сигнал увеличивается с наклоном +20 дБ на декаду или 6 дБ на октаву, пока частота не достигнет нижней граничной частоты «fL».
На этой частоте усиление сигнала достигает значения 1/√2 = 70,7%.
После частоты среза f L выход будет увеличиваться с увеличением частоты со скоростью -20 дБ за декаду и достигает максимального усиления, и это усиление будет постоянным, пока не достигнет более высокой частоты среза ‘ ф_Х’.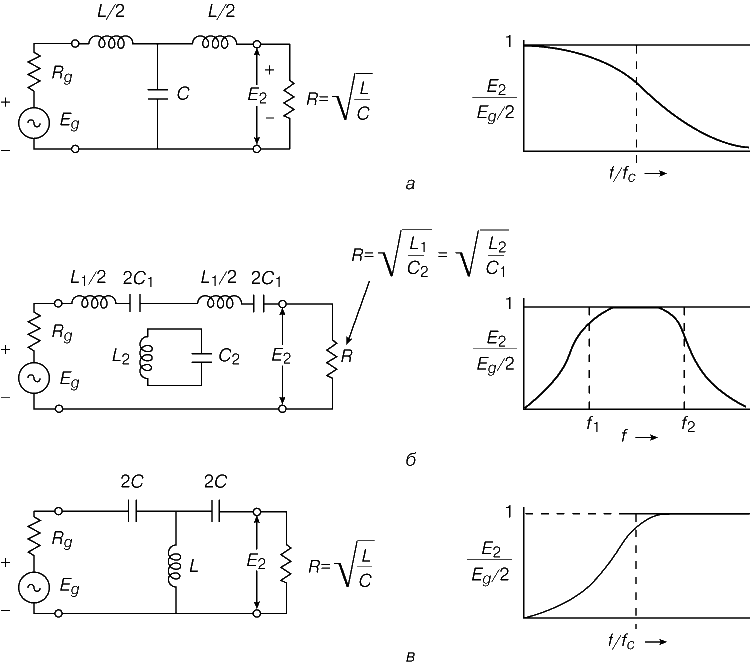 После более высокой частоты среза выходной сигнал снижается с наклоном -20 дБ/декада или -6 дБ/октава.
После более высокой частоты среза выходной сигнал снижается с наклоном -20 дБ/декада или -6 дБ/октава.
Ранее мы видели, что фазовый сдвиг фильтра первого порядка равен 90°. Мы знаем, что полосовой фильтр является фильтром второго порядка, поэтому фазовый сдвиг в два раза больше, чем у фильтра первого порядка, то есть 180°. Фазовый угол будет меняться с увеличением частоты. На центральной частоте выходные и входные сигналы синфазны друг с другом.
Ниже резонансной частоты выходной сигнал опережает входной сигнал, а выше резонансной частоты выходной сигнал отстает от входного сигнала. Амплитуда входного сигнала всегда больше выходного сигнала. Для увеличения коэффициента усиления схемы значение сопротивления R1 должно быть больше, чем сопротивление R2.
Центральная частота полосового фильтра
«Центральную частоту» или «Резонансную частоту», при которой выходное усиление максимально, можно получить, вычислив среднее геометрическое нижней и верхней частот среза.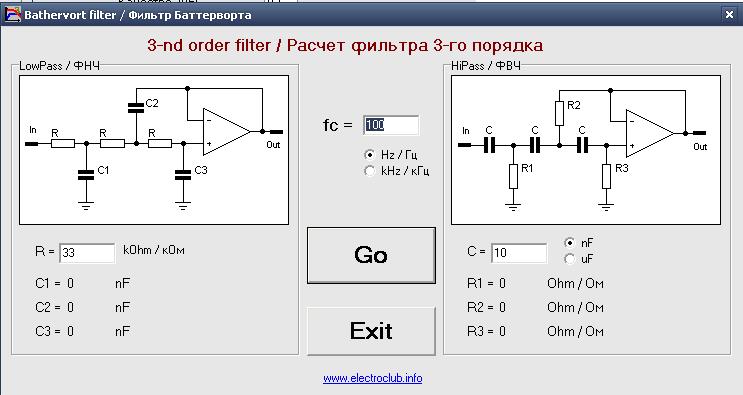
F R 2 = F H x F L
FR = √ (F H x F L )
, где FR — реконантная частота или частота центра
F 9898, где FR — реконантная частота или частота центра
F 8 8898 H, где FR — реконантная частота или частота центра 9000 2 F 8 H, где FR — резонантная частота или центр F 8
f L – нижняя частота среза -3 дБ
Полосовой фильтр Пример
Предположим, что полосовой фильтр пропускает частоты от 1 кГц до 30 кГц и содержит резистор 10 кОм. Учитывая эти значения, мы можем рассчитать емкость конденсатора.
Мы уже знаем, что значение частоты среза фильтра нижних частот должно быть выше, чем у фильтра высоких частот. Таким образом, частота среза фильтра верхних частот составляет 1 кГц, а частота среза фильтра нижних частот — 30 кГц.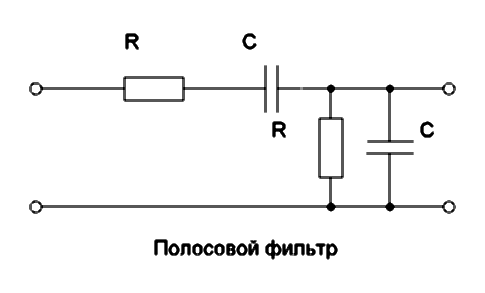
На этапе фильтра верхних частот
f L = 1 кГц и сопротивление R = 10 кОм
C = 1/(2πf L R) = 1/(2*π*1000*1000) = 15,8 нФ
На каскаде фильтра нижних частот
f H = 30 кГц и сопротивление R = 10 кОм
C = 1/(2πf H R) = 1/(00*0π* *10000) = 510 пФ
Из приведенных выше расчетов емкость конденсатора, необходимая для фильтра верхних частот, составляет 15,8 нФ, а емкость конденсатора фильтра нижних частот составляет 510 пФ.
Резюме пассивного полосового фильтра
Полосовой фильтр получается путем каскадирования фильтра нижних и верхних частот. Это фильтр второго порядка, поскольку он содержит два реактивных элемента. Порядок фильтра зависит от количества каскадных цепей, используемых в схеме.
Коэффициент усиления выходного сигнала всегда меньше входного сигнала. На центральной частоте выходной сигнал синфазен, но ниже центральной частоты выходной сигнал опережает фазу со сдвигом +90° и выше центральной частоты выходной сигнал будет отставать по фазе со сдвигом фазы на -90°.
Практические характеристики полосового фильтра немного отличаются от идеальных характеристик. Это изменение в основном связано с каскадным фильтром верхних частот с фильтром нижних частот.
Выходное усиление всегда меньше единицы. Когда мы обеспечиваем электрическую изоляцию между фильтрами верхних и нижних частот, мы можем добиться лучшей производительности фильтра.
Полосовой фильтр оптимизирует чувствительность приемника. Сначала в конструкцию добавляется фильтр верхних частот, а затем добавляется фильтр нижних частот. Даже если мы сначала добавим фильтр нижних частот, а затем фильтр верхних частот, он никогда не изменит выходной сигнал.
Коэффициент качества фильтра будет зависеть от номинала резистора R1. Если R1 низкий, то добротность низкая, а если значение R1 высокое, то добротность высокая.
Применение полосового фильтра
- Они используются в среде беспроводной связи в цепях передатчика и приемника. В секции передатчика этот фильтр пропускает только необходимые сигналы и уменьшает помехи сигналов от других станций.

.png)
 Именно поэтому, в качестве выходного и был выбран двухтактный каскад на комплементарных транзисторах.
Именно поэтому, в качестве выходного и был выбран двухтактный каскад на комплементарных транзисторах.