Построить схему на логических элементах онлайн. Построение логических схем: пошаговое руководство и онлайн-инструменты — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как построить логическую схему по заданному выражению. Какие существуют базовые логические элементы. Где найти онлайн-симуляторы для создания и тестирования логических схем. Как минимизировать и оптимизировать логические схемы.

Содержание

Что такое логические схемы и для чего они нужны

Логические схемы — это схематическое представление логических выражений и функций с помощью базовых логических элементов. Они широко используются при проектировании цифровых устройств и интегральных микросхем.

Основные области применения логических схем:

Проектирование цифровых схем компьютеров и других электронных устройств
Разработка микропроцессоров и микроконтроллеров
Создание программируемых логических интегральных схем (ПЛИС)
Моделирование и анализ работы цифровых устройств
Изучение основ цифровой электроники и схемотехники

Умение строить и анализировать логические схемы — важный навык для инженеров-электронщиков, разработчиков цифровых систем и студентов технических специальностей.

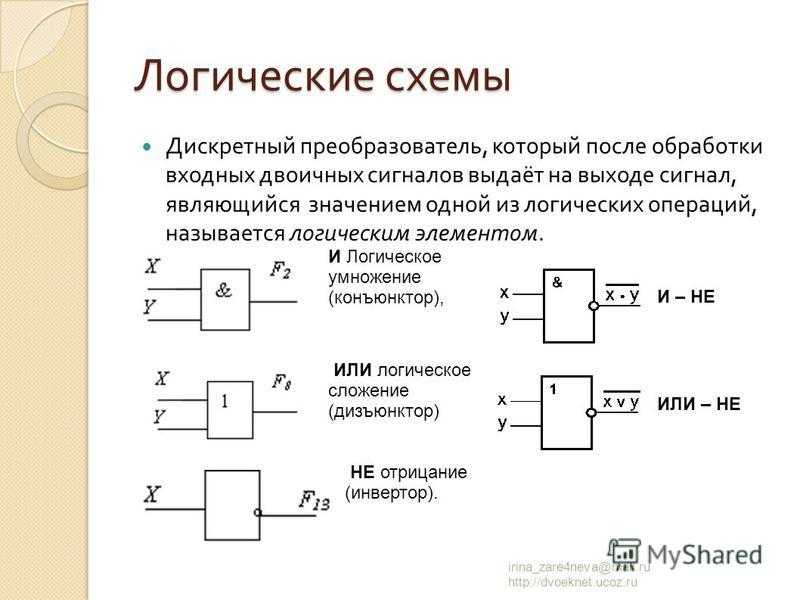
Базовые логические элементы

Логические схемы строятся на основе базовых логических элементов, реализующих элементарные логические функции. Основные логические элементы:

НЕ (инвертор) — инвертирует входной сигнал
И (конъюнктор) — реализует логическое умножение
ИЛИ (дизъюнктор) — реализует логическое сложение
И-НЕ — комбинация элементов И и НЕ
ИЛИ-НЕ — комбинация элементов ИЛИ и НЕ
Исключающее ИЛИ (XOR) — истинно когда входы различны

Каждый элемент имеет свое условное графическое обозначение и таблицу истинности, определяющую его функцию.

Алгоритм построения логической схемы

Чтобы построить логическую схему по заданному логическому выражению, следуйте такому алгоритму:

Определите количество входных переменных в выражении
Выделите базовые логические операции и их порядок выполнения

Для каждой операции подберите соответствующий логический элемент
Соедините элементы в порядке выполнения операций
Подключите входные переменные и выходы

Рассмотрим пример построения схемы для выражения F = (A + B) * !C:

Входные переменные: A, B, C
Операции: ИЛИ (+), НЕ (!), И (*)
Элементы: ИЛИ, НЕ, И
Порядок соединения: ИЛИ(A,B) — НЕ(C) — И
Подключаем входы A, B, C и выход F

Онлайн-инструменты для построения логических схем

Существует множество онлайн-сервисов, позволяющих строить и моделировать работу логических схем:

LogicLy (https://logic.ly) — простой и удобный редактор схем
CircuitVerse (https://circuitverse.org) — мощный симулятор с поддержкой сложных схем
LogiSim (http://www.cburch.com/logisim/) — классический инструмент для обучения
Logic Gate Simulator (https://academo.org/demos/logic-gate-simulator/) — простой симулятор базовых элементов

Эти инструменты позволяют быстро создавать схемы, проверять их работу и экспериментировать с различными вариантами реализации.

Минимизация логических схем

Важной задачей при проектировании логических схем является их минимизация — уменьшение количества используемых элементов. Это позволяет сократить размеры схемы, снизить энергопотребление и стоимость.

Основные методы минимизации логических схем:

Применение законов булевой алгебры для упрощения выражений
Использование карт Карно для минимизации логических функций
Метод Квайна-МакКласки для минимизации многовходовых функций
Замена комбинаций элементов на более простые эквивалентные схемы

При проектировании реальных схем важно находить баланс между минимизацией и другими параметрами — быстродействием, надежностью, технологичностью производства.

Практические советы по построению логических схем

Несколько рекомендаций, которые помогут эффективнее строить логические схемы:

Начинайте с упрощения исходного логического выражения
Используйте блочный подход, разбивая сложные схемы на модули
Применяйте стандартные комбинации элементов (полусумматоры, компараторы и т.д.)
Проверяйте работу схемы на всех возможных комбинациях входных сигналов
Оптимизируйте схему, удаляя избыточные элементы и связи
Используйте онлайн-симуляторы для отладки и тестирования

С опытом вы научитесь быстро строить оптимальные схемы для решения различных задач цифровой логики.

Заключение

Построение логических схем — важный этап проектирования цифровых устройств. Освоив базовые принципы и инструменты, вы сможете создавать сложные схемы для решения практических задач. Регулярная практика и эксперименты с онлайн-симуляторами помогут развить навыки построения эффективных логических схем.

Таблица истинности онлайн

Назначение сервиса. Онлайн-калькулятор предназначен для построения таблицы истинности для логического выражения.
Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе.
Таблица истинности содержит 2ⁿ строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные.

Решение онлайн
Видеоинструкция

Инструкция. При вводе с клавиатуры используйте следующие обозначения:

Клавиша	Оператор
!	¬	Отрицание (НЕ)
\|	\|	Штрих Шеффера (И-НЕ)
#	↓	Стрелка Пирса (ИЛИ-НЕ)
*	&	Конъюнкция (И)
+	v	Дизъюнкция (ИЛИ)
^	⊕	Исключающее ИЛИ, сумма по модулю 2 (XOR)
@	→	Импликация (ЕСЛИ-ТО)
%	←	Обратная импликация
=	≡ (~, ↔)	Эквивалентность (РАВНО)

Логическое выражение: Вывод промежуточных таблиц для таблицы истинности
Построение СКНФ
Построение СДНФ
Построение полинома Жегалкина
Построение карты Вейча-Карно
Минимизация булевой функции методом Квайна

Например, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис. y).

Максимальное количество переменных равно 10.

Проектирование и анализ логических схем ЭВМ ведётся с помощью специального раздела математики — алгебры логики. В алгебре логики можно выделить три основные логические функции: «НЕ» (отрицание), «И» (конъюнкция), «ИЛИ» (дизъюнкция).
Для создания любого логического устройства необходимо определить зависимость каждой из выходных переменных от действующих входных переменных такая зависимость называется переключательной функцией или функцией алгебры логики.
Функция алгебры логики называется полностью определённой если заданы все 2ⁿ её значения, где n – число выходных переменных.
Если определены не все значения, функция называется частично определённой.
Устройство называется логическим, если его состояние описывается с помощью функции алгебры логики.
Для представления функции алгебры логики используется следующие способы:

словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление.
описание функции алгебры логики в виде таблицы истинности.
описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
а) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
1) в таблице выбираются те строки переменных для которых функция на выходе =1.
2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
3) полученное произведение логически суммируется.
Fднф= X₁*Х₂*Х₃ ∨ Х₁x₂Х₃ ∨ Х₁Х₂x₃ ∨ Х₁Х₂Х₃
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т.е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.
б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
1) выбираем наборы переменных для которых функция на выходе =0
2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
3) логически перемножаются полученные суммы.
Fскнф=(X₁ V X₂ V X₃) ∧ (X₁ V X₂ V X₃) ∧ (X₁ V X₂ V X₃) ∧ (X₁ V X₂V X₃)
КНФ называется совершенной, если все переменные имеют одинаковый ранг.

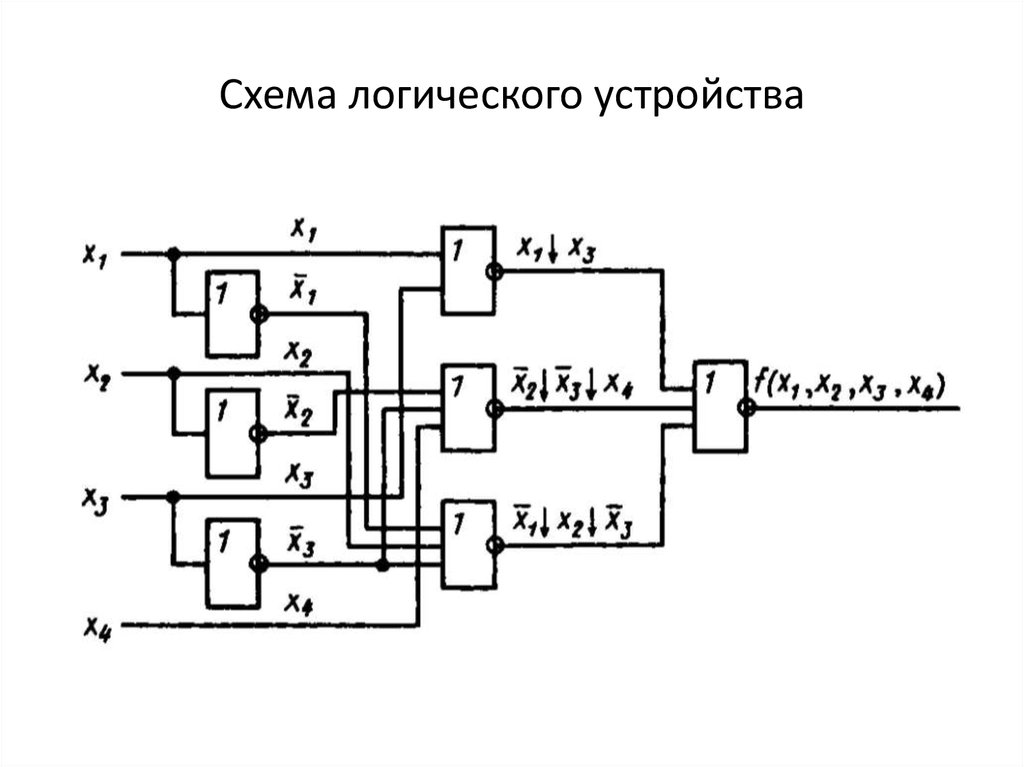
По алгебраической форме можно построить схему логического устройства, используя логические элементы.

Рисунок1- Схема логического устройства

Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2^N строк, так как существует 2^N различных комбинаций возможных значений аргументов.

Операция НЕ — логическое отрицание (инверсия)

Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:

если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.

Для операции отрицания НЕ приняты следующие условные обозначения:
не А, Ā, not A, ¬А, !A
Результат операции отрицания НЕ определяется следующей таблицей истинности:

A	не А
0	1
1	0

Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.

Операция ИЛИ — логическое сложение (дизъюнкция, объединение)

Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Применяемые обозначения: А или В, А V В, A or B, A||B.
Результат операции ИЛИ определяется следующей таблицей истинности:

A	B	А или B
0	0	0
0	1	1
1	0	1
1	1	1

Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.

Операция И — логическое умножение (конъюнкция)

Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:

A	B	А и B
0	0	0
0	1	0
1	0	0
1	1	1

Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.

Операция «ЕСЛИ-ТО» — логическое следование (импликация)

Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:

A	B	А → B
0	0	1
0	1	1
1	0	0
1	1	1

Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.

Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)

Применяемое обозначение: А ↔ В, А ~ В.

Таблица истинности:

A	B	А↔B
0	0	1
0	1	0
1	0	0
1	1	1

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

Операция «Сложение по модулю 2» (XOR,

исключающее или, строгая дизъюнкция) Применяемое обозначение: А XOR В, А ⊕ В.
Таблица истинности:

A	B	А⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Приоритет логических операций

Действия в скобках
Инверсия
Конъюнкция ( & )
Дизъюнкция ( V ), Исключающее ИЛИ (XOR), сумма по модулю 2
Импликация ( → )
Эквивалентность ( ↔ )

Совершенная дизъюнктивная нормальная форма

Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:

Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x₁,x₂,…x_n).
Все логические слагаемые формулы различны.
Ни одно логическое слагаемое не содержит переменную и её отрицание.
Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

СДНФ можно получить или с помощью таблиц истинности или с помощью равносильных преобразований.

Для каждой функции СДНФ и СКНФ определены единственным образом с точностью до перестановки.

Совершенная конъюнктивная нормальная форма

Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:

Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x₁,x₂,…x_n).
Все элементарные дизъюнкции различны.
Каждая элементарная дизъюнкция содержит переменную один раз.
Ни одна элементарная дизъюнкция не содержит переменную и её отрицание.

Построение логических схем

Цели урока:

Образовательные:

закрепить у учащихся представление об устройствах элементной базы компьютера;
закрепить навыки построения логических схем.

Развивающие:

формировать развитие алгоритмического мышления;
развить конструкторские умения;
продолжать способствовать развитию ИКТ - компетентности;

Воспитательные:

продолжить формирование познавательного интереса к предмету информатика;
воспитывать личностные качества:
активность,
самостоятельность,
аккуратность в работе;

Требования к знаниям и умениям:

Учащиеся должны знать:

основные базовые элементы логических схем;
правила составления логических схем.

Учащиеся должны уметь:

составлять логические схемы.

Тип урока: урок закрепления изученного материала

Вид урока: комбинированный

Методы организации учебной деятельности:

фронтальная;
индивидуальная;

Программно-дидактическое обеспечение:

ПК, SMART Board, карточки с индивидуальным домашним заданием.

Урок разработан с помощью программы Macromedia Flash.

Ход урока

I. Постановка целей урока.

Добрый день!

Сегодня мы продолжаем изучение темы «Построение логических схем».

Приготовьте раздаточный материал «Логические основы ЭВМ. Построение логических схем» Приложение 1

Вопрос учителя. Назовите основные логические элементы.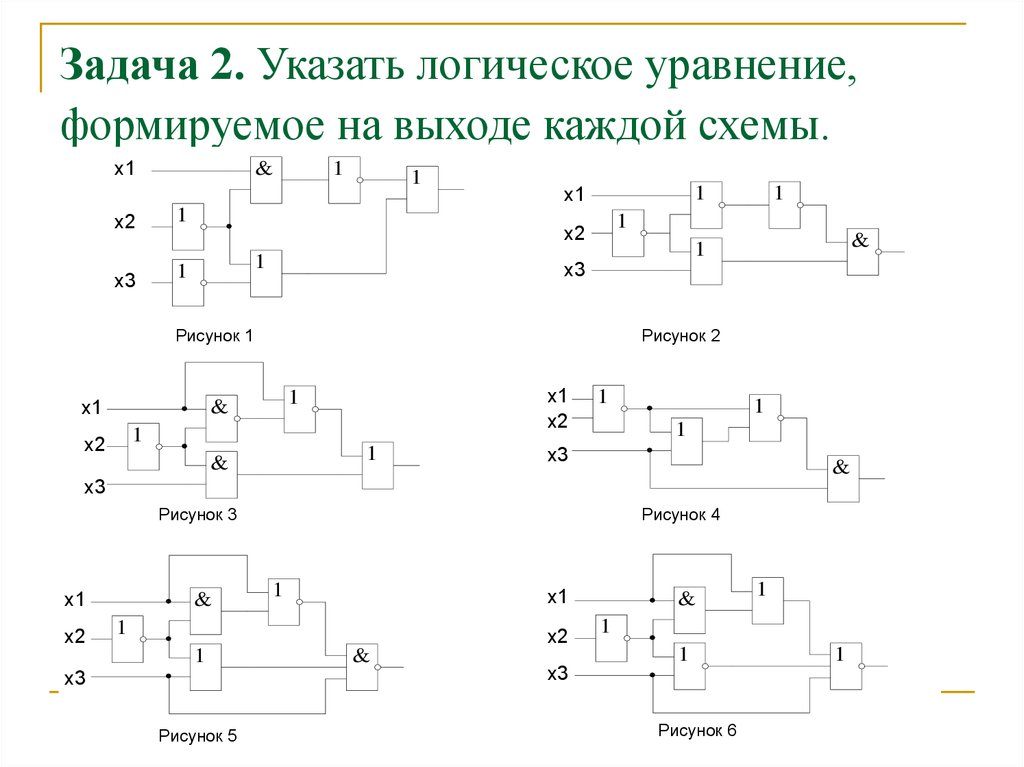 Какой логический элемент соответствует логической операции И, ИЛИ, НЕ?

Ответ учащихся. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Основные логические элементы конъюнктор (соответствует логическому умножению), дизъюнктор (соответствует логическому сложению), инвертор (соответствует логическому отрицанию).

Вопрос учителя. По каким правилам логические элементы преобразуют входные сигналы. Рассмотрим элемент И. В каком случае на выходе будет ток (сигнал равный 1).

Ответ учащихся. На первом входе есть ток (1, истина), на втором есть (1, истина), на выходе ток идет (1, истина).

Вопрос учителя. На первом входе есть ток, на втором нет, однако на выходе ток идет. На входах тока нет и на выходе нет. Какую логическую операцию реализует данный элемент?

Ответ учащихся.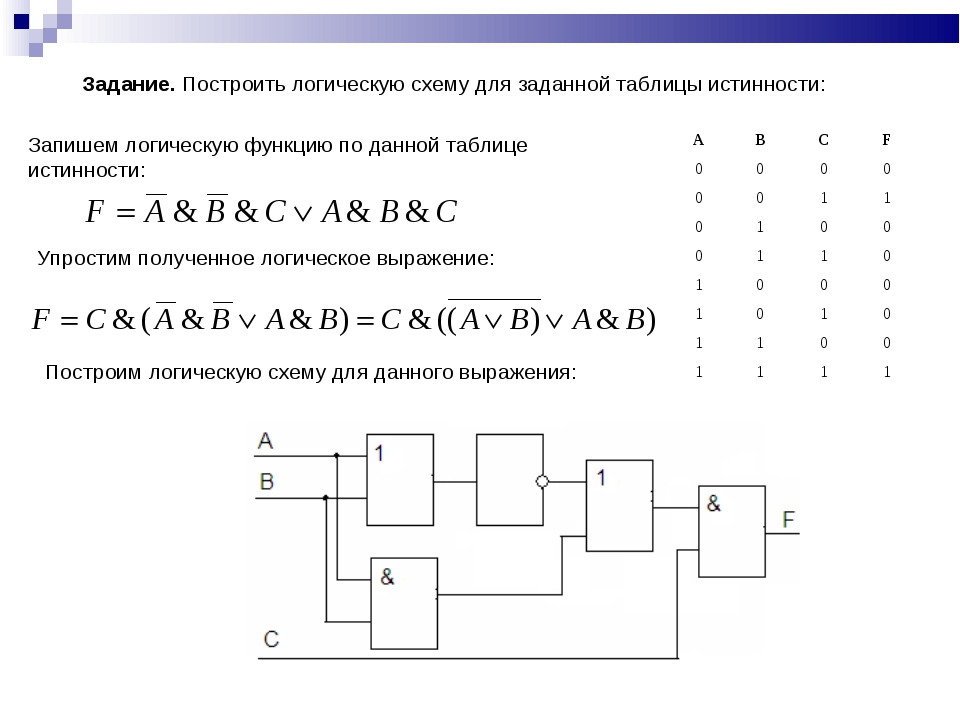 Элемент ИЛИ - дизъюнктор.

Вопрос учителя. Рассмотрим логический элемент НЕ. В каком случае на выходе не будет тока (сигнал равный 0)?

Ответ учащихся. На входе есть ток, сигнал равен 1.

Вопрос учителя. В чем отличие логической схемы от логического элемента?

Ответ учащихся. Логические схемы состоят из логических элементов, осуществляющих логические операции.

Проанализируем схему и определим сигнал на выходе.

II. Закрепление изученного материала.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Дома вам необходимо было построить логические схемы, соответствующие логическим выражениям.

Вопрос учителя. Каков алгоритм построение логических схем?

Ответ учащихся. Алгоритм построение логических схем:

Определить число логических переменных.

Определить количество базовых логических операций и их порядок.

Изобразить для каждой логической операции соответствующий ей элемент (вентиль).

Соединить вентили в порядке выполнения логических операций.

Работа со SMART Board Приложение 2

Проверка домашнего задания Приложение 1. Домашнее задание. Часть 1

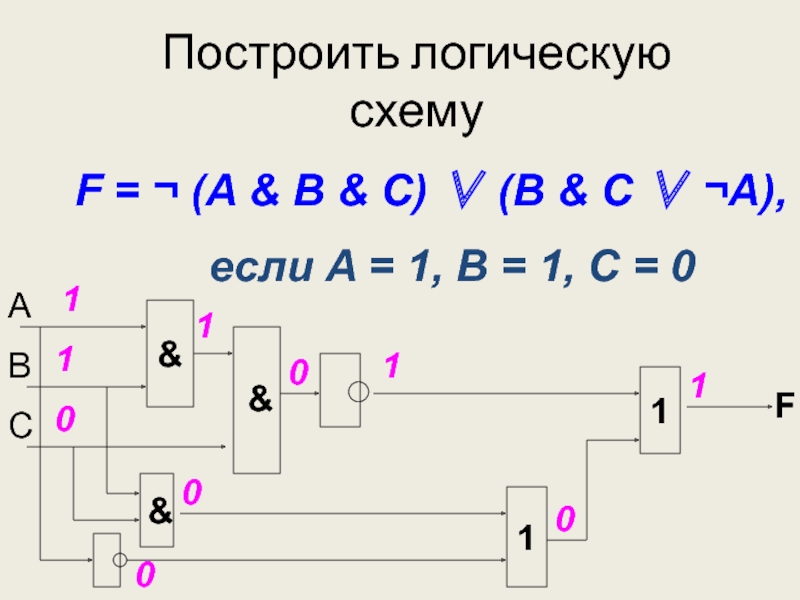
Построить логическую схему для логического выражения: .

Две переменные — А и В.
Две логические операции: &,
Строим схему.

Построить логическую схему для логического выражения:

Вычислить значение данного выражения для А=1, В=0.

Ответ F=1

III. Пропедевтика (законы логики)

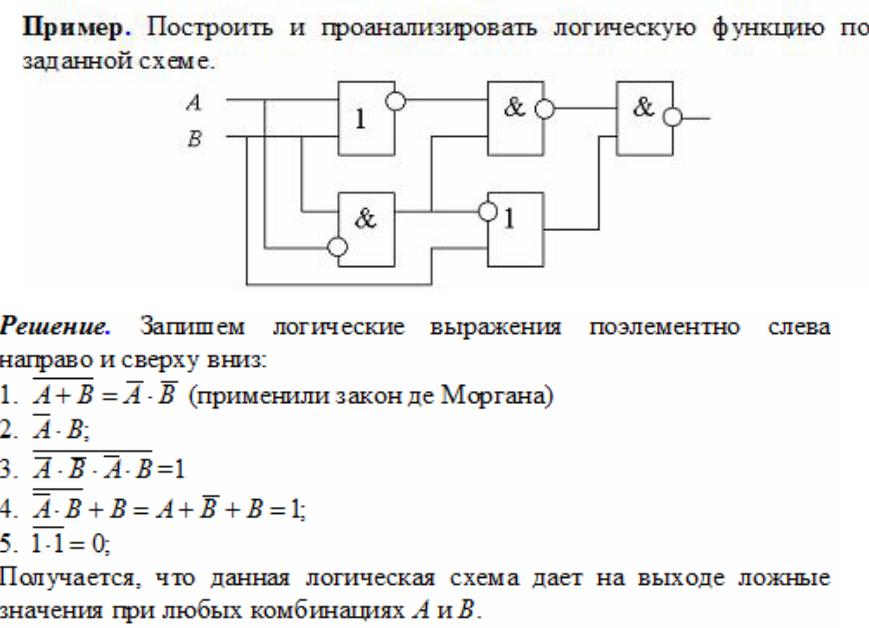
Выполним задачу обратную данной. Составим логическое выражение по заданной логической схеме:

Данное логическое выражение можно упростить.

Операция И — логическое умножение, ИЛИ - сложение. Запишем выражение, заменяя знаки & и U на * и + соответственно.

F= (A*B+B*С) Упростим F= (B*(А+С)), затем запишем и тогда логическая схема примет вид:

Вывод: Логические схемы, содержащие минимальное количество элементов, обеспечивают большую скорость работы и увеличивают надёжность устройства.

Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических схем. Проще, и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.

Таким образом, цель нашего следующего урока - изучить законы алгебры логики.

IV. Домашнее задание. Часть 2

V. Практическая работа.

Программа — тренажер «Построение логических схем»

www. Kpolyakov.narod.ru Программа «Logic»,

Спасибо за урок!

LogiJS: симулятор логической схемы

New Circuit

Используйте настольное устройство для входа в LogiJS.

Изучите основы логики

Вентили и схемы.

Новая схема

Импортируйте свои схемы как

пользовательских компонентов.

Новая схема

Сохраните и получите доступ к своим схемам

в Интернете.

Новый контур

Предыдущий Следующий

Образцы.

#1 Основные логические элементы

На этом рисунке показаны три основных логических элемента: И, ИЛИ и XOR. Он также показывает использование элементов ввода и вывода. Логические элементы являются основой любой логической схемы.

#2 Полусумматор

В этом скетче реализован половинный сумматор, который используется для сложения двух одиночных двоичных цифр. Полусумматоры можно комбинировать, чтобы сформировать полные сумматоры, используемые для сложения двоичных чисел.

#3 Полный сумматор

Этот скетч реализует полный сумматор, который используется для сложения двух одиночных двоичных цифр. Полные сумматоры состоят из двух половинных сумматоров, принимающих на вход две двоичные цифры и бит переноса. Полные сумматоры можно комбинировать для создания целочисленных сумматоров любого размера.

#4 Светофоры

Этот скетч имитирует светофоры с использованием 4-битного счетчика (см. пример №5) и диодной матрицы. Есть светофоры для дорожного движения и пешеходов. В этом примере показано использование диодов, элементов, которые соединяют провода только в одном направлении.

#5 4-битный счетчик

В этом скетче реализован простой счетчик, созданный с использованием D-затворов. Он подключен к часам, постоянно увеличивая значение двоичного выхода. Когда значение превышает максимально возможное значение (в данном случае пятнадцать), счетчик перезапускается с нуля.

Показать все

О LogiJS.

LogiJS — симулятор логических схем с открытым исходным кодом. В наши дни логические схемы используются повсюду, и поэтому их преподают в университетах по всему миру.

Наша цель — предложить программное обеспечение это не только бесплатно для всех, но и побуждает студентов проявлять творческий подход к логическим схемам и развивать глубокое понимание основных концепций.

Цель не в том, чтобы создать программное обеспечение для производственного использования или для изучения передовых методов. Вместо этого мы сосредотачиваемся на простоте, чтобы создать экспериментальную площадку, свободную от отвлекающих факторов и разочарований.

Обратите внимание, что LogiJS в настоящее время находится в активной разработке. Изменения могут произойти быстро и без предупреждения. Кроме того, мы не можем гарантировать возможную потерю данных или ущерб, причиненный в результате использования нашего программного обеспечения.

Наши планы.

Мы хотели бы иметь демонстрационный зал для схем, созданных пользователями, где вы можете просматривать схемы других пользователей и редактировать их как копии на своих собственных панелях управления. Для этого нам нужно найти способ обработки зависимостей скетча (пользовательские элементы, используемые в скетче).
VHDL и Verilog являются наиболее распространенными языками описания оборудования. Мы хотим поддерживать экспорт хотя бы в один из них. Это полезно для экспорта схем в ПЛИС и другие приложения.
Пользователи должны иметь возможность редактировать эскизы одновременно с несколькими пользователями.

Если у вас есть предложения по функциям или вы хотите сообщить о проблемах или ошибках, пожалуйста, не стесняйтесь открывать вопрос на нашем GitHub.

Симулятор логических ворот | Academo.org

Простой бесплатный онлайн-симулятор логических вентилей. Исследуйте поведение логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и исключающее ИЛИ. Выберите ворота из выпадающего списка и нажмите «добавить узел», чтобы добавить больше ворот. Перетащите от полых кругов к сплошным кругам, чтобы соединиться. Щелкните правой кнопкой мыши соединения, чтобы удалить их. Ниже приведены более подробные инструкции.

Инжиниринг Электроника логика

Приведенная выше демонстрация позволяет создавать последовательности логических элементов, чтобы увидеть, как они ведут себя при подключении к различным входам и выходам. Изначально, вам представлены простой ввод/выключение ввода и вывода. Чтобы соединить их, щелкните и перетащите из полого круга с правой стороны переключатель включения/выключения и отпустите кнопку мыши, когда вы окажетесь над сплошным кругом слева от блока «выход».

Для каждого из логических вентилей выходы — полые кружки, а входы — сплошные кружки. Наш переключатель «вкл/выкл» и «выходной блок» на самом деле не являются логическими вентилями. но они необходимы, потому что они дают нам 1 и 0, необходимые для того, чтобы увидеть, как ведут себя ворота. Нажмите кнопку включения/выключения и посмотрите, что произойдет. Становится желтым. Это наш способ различать 0 (выключено) и 1 (включено).

Чтобы добавить новый логический вентиль или дополнительный входной или выходной блок, выберите из раскрывающегося меню и затем нажмите «добавить узел». Новый узел будет помещен в верхний левый угол, и вы можете перетащить его в нужное место. Чтобы удалить узлы, щелкните маленький крестик в правом верхнем углу ограничивающего его блока. Чтобы удалить соединения, нажмите кнопку введите (сплошной круг) и перетащите и отпустите, или, в качестве альтернативы, вы можете щелкнуть правой кнопкой мыши в любом месте соединения.

Если вам нужно больше места, нажмите кнопку «Полноэкранный режим», которая увеличит размер рабочей области, чтобы заполнить размер окна. Кроме того, вы можете переименовать выход, дважды щелкнув его метку.

НЕ Ворота

Вентиль НЕ также известен как инвертор, потому что выход прямо противоположен входу. Он имеет один вход и один выход. Две возможности записаны в таблице ниже. Таблицы, в которых перечислены все подобные логические возможности, известны как 9.0103 таблицы истинности .

Input	Output
0	1
1	0

AND Gate

Логический элемент И имеет два входа и один выход. Выход равен 1, если оба входа равны 1, а во всех остальных случаях выход равен 0.

Вход 1	Вход 2	Выход
0	0	0
1	0	0
0	1	0
1	1	1

NAND Gate

Логический элемент И-НЕ ведет себя противоположно вентилю И. Вы можете думать об этом как о вентиле И, за которым сразу же следует вентиль НЕ. Его выход равен 0, когда два входа равны 1, а во всех остальных случаях его выход равен 1. Название И-НЕ происходит от соединения НЕ и И. Символ для НЕ-И такой же, как и для И, за исключением добавления маленького кружка с правой стороны.

Input 1	Input 2	Output
0	0	1
1	0	1
0	1	1
1	1	0

Ворота ИЛИ

Вентиль ИЛИ имеет два входа и один выход. Если хотя бы один из входов равен 1, то выход будет равен 1. Если ни один из входов не равен 1, выход будет равен 0.

Input 1	Input 2	Output
0	0	0
1	0	1
0	1	1
1	1	1

Ворота NOR

Точно так же, как логический элемент И-НЕ можно рассматривать как И, за которым следует НЕ, НЕ-ИЛИ можно рассматривать как ИЛИ, за которым следует НЕ.

Input 1	Input 2	Output
0	0	1
1	0	0
0	1	0
1	1	0

XOR Gate

С вентилем ИЛИ, если оба входа были 1, выход был 1. Однако с XOR (исключающее ИЛИ), если оба входа равны 1, выход равен 0. Для всех В других сценариях XOR ведет себя так же, как OR.

Input 1	Input 2	Output
0	0	0
1	0	1
0	1	1
1	1	0

Кредиты

Все логические иконки, разработанные Марко Ольджио из проекта Noun

Включите JavaScript для просмотра комментариев с помощью Disqus.