Программа для построения логических схем. Построение логических схем: пошаговое руководство с примерами

alexxlabСхем
Как построить логическую схему для логического выражения. Какие правила нужно соблюдать при построении логических схем. Какие основные логические элементы используются в схемах.

Содержание

Что такое логическая схема и для чего она нужна

Логическая схема — это графическое представление логического выражения или функции с помощью специальных символов, обозначающих логические операции. Основное назначение логических схем:

  • Наглядно отображать структуру и работу логических устройств
  • Упрощать анализ и проектирование цифровых схем
  • Служить основой для создания реальных электронных схем

Логические схемы широко применяются при разработке цифровых устройств, микропроцессоров, компьютерной техники. Умение строить и анализировать такие схемы — важный навык для специалистов в области электроники и вычислительной техники.

Основные логические элементы и их обозначения

Для построения логических схем используются следующие базовые логические элементы:


  • Элемент И (конъюнктор) — выполняет операцию логического умножения
  • Элемент ИЛИ (дизъюнктор) — выполняет операцию логического сложения
  • Элемент НЕ (инвертор) — выполняет операцию логического отрицания
  • Элемент И-НЕ — комбинация элементов И и НЕ
  • Элемент ИЛИ-НЕ — комбинация элементов ИЛИ и НЕ

Каждый логический элемент имеет стандартное условное графическое обозначение. Знание этих обозначений необходимо для правильного построения и чтения логических схем.

Правила построения логических схем

При построении логической схемы нужно придерживаться следующих основных правил:

  1. Определить число входных логических переменных
  2. Выделить базовые логические операции и определить их порядок
  3. Для каждой логической операции изобразить соответствующий ей логический элемент
  4. Соединить логические элементы в порядке выполнения логических операций
  5. Обозначить входы схемы (переменные) и выход (результат функции)

Правильное соблюдение этих правил позволяет построить корректную логическую схему для заданного выражения.


Пошаговый алгоритм построения логической схемы

Рассмотрим пошаговый алгоритм построения логической схемы на конкретном примере. Пусть дано логическое выражение:

F = (A ∧ B) ∨ (¬A ∧ C)

Шаг 1. Определяем входные переменные: A, B, C

Шаг 2. Выделяем логические операции:

  • Конъюнкция (A ∧ B)
  • Отрицание (¬A)
  • Конъюнкция (¬A ∧ C)
  • Дизъюнкция — объединяет результаты первой и третьей операций

Шаг 3. Изображаем логические элементы в порядке выполнения операций:

  • Элемент И для (A ∧ B)
  • Элемент НЕ для (¬A)
  • Элемент И для (¬A ∧ C)
  • Элемент ИЛИ для объединения результатов

Шаг 4. Соединяем элементы линиями в соответствии с логикой выражения

Шаг 5. Обозначаем входы A, B, C и выход F

В результате получаем готовую логическую схему, соответствующую заданному выражению.

Примеры построения логических схем

Рассмотрим еще несколько примеров построения логических схем для различных выражений:

Пример 1

Логическое выражение: F = A ∨ (B ∧ ¬C)

Логическая схема:

[Здесь должно быть схематичное изображение логической схемы]

Пример 2

Логическое выражение: F = (A ∧ B) ∨ (¬A ∧ ¬B)


Логическая схема:

[Здесь должно быть схематичное изображение логической схемы]

Анализ и упрощение логических схем

После построения логической схемы часто возникает необходимость ее анализа и оптимизации. Основные способы упрощения логических схем:

  • Использование законов булевой алгебры для упрощения логических выражений
  • Минимизация логических функций с помощью карт Карно
  • Замена комбинаций элементов на более простые эквивалентные схемы
  • Использование универсальных логических элементов (И-НЕ, ИЛИ-НЕ)

Грамотное применение этих методов позволяет получить более компактные и эффективные логические схемы.

Практическое применение логических схем

Логические схемы находят широкое применение в различных областях электроники и вычислительной техники:

  • Проектирование цифровых устройств и микросхем
  • Разработка узлов компьютеров (АЛУ, регистры, счетчики)
  • Системы автоматического управления
  • Программируемые логические контроллеры
  • Схемы кодирования и декодирования информации

Умение работать с логическими схемами — важный навык для специалистов в области электроники, информатики и смежных дисциплин.


Заключение

Построение логических схем — важный этап проектирования цифровых устройств. Правильное применение базовых логических элементов и соблюдение правил построения схем позволяет создавать корректные и эффективные логические устройства. Навыки работы с логическими схемами необходимы для понимания принципов работы современной цифровой техники.


Программа для построения логических схем

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнить арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.

Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Алгоритм построения логических схем :

1) Определить число логических переменных.

2) Определить количество базовых логических операций и их порядок.

3) Изобразить для каждой логической операции соответствующий ей вентиль.

4) Соединить вентили в порядке выполнения логических операций.

Составить логическую схему для логического выражения: F = ¬ X v Y & X .

1) Две переменные – X и Y .

2) Две логические операции: 1 3 2

3) Строим схему, соединяя вентили в порядке выполнения логических операций:

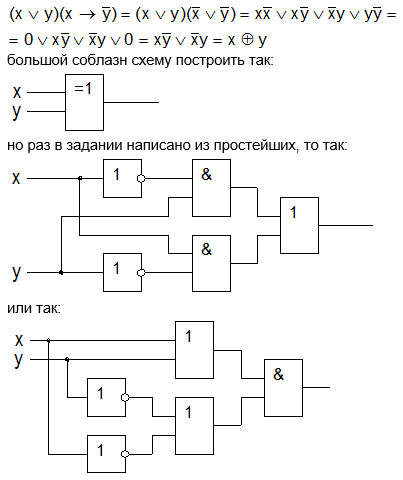
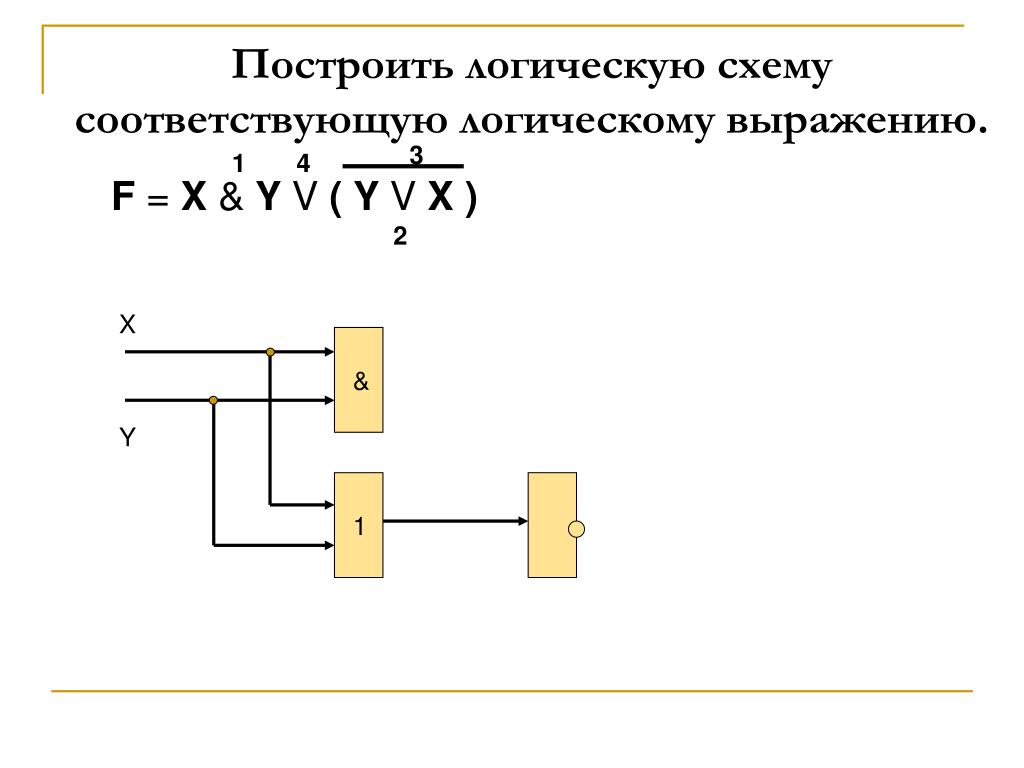
Постройте логическую схему, соответствующую логическому выражению F = X & Y v ¬ ( Y v X ).

Вычислить значения выражения для X =1, Y =0.

1) Переменных две: X и Y .

2) Логических операций четыре: конъюнкция, две дизъюнкции и отрицание. Определяем порядок выполнения операций:

3) Схему строим слева направо в соответствии с порядком выполнения логических операций:

4) Вычислим значение выражения: F =1&0 v ¬ ( 0 v 1)=0.

Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:

1) F=A v B& ¬ C, если A=1, B=1, C=1 .

2) F = ¬ (A v B&C), если A=0, B=1, C=1 .

3) F = ¬ A v B&C, если A=1, B=0, C=1 .

4) F =(A v B)&(C v B), если A=0, B=1, C=0 .

5) F = ¬ (A&B&C), если A=0, B=0, C=1 .

6) F=B& ¬ A v ¬ B&A, если A=0, B=0 .

7) F= ¬ (A&B&C) v (B&C v ¬ A), если A=1, B=1, C=0 .

Инструкция . Для добавления логического элемента выберите его тип и количество входов, нажмите на поле. Для его удаления нажмите правой кнопкой мыши над его местоположением.

  • Ввод данных
  • Решение
  • Видеоинструкция

Стандарт изображений элементов

Выберите логический элемент:

Cоединить элемент с переменной по входу Соединить

Cоединить элемент с элементом по входу Соединить

Цвет линий Цвет элементов

Для последнего элемента входы

Для послелнего элемента разделяющие линии

Операция И НЕ (штрих Шеффера)

Операция ИЛИ НЕ

Сложение по модулю2

Исключающее ИЛИ НЕ

Операция И НЕ (штрих Шеффера)

Операция ИЛИ НЕ

Сложение по модулю2

Исключающее ИЛИ НЕ

  • Каждая страница разделена на секции, каждая секция описывается названием (навигация по заголовкам).
  • Наиболее важным разделам присвоена определенная роль (навигация по ориентирам)
  • В верхней части каждой страницы вы найдете меню быстрого перехода ( ссылки внутренней навигации). Каждая ссылка привязана к определенной клавише (кнопке быстрого вызова).

Внимание: вы используете устаревший браузер! Мы советуем вам обновить программное обеспечение до новой версии или скачать альтернативный браузер: здесь вы можете загрузить последнюю версию Firefox.
Если вы работаете в операционной системе Windows на компьютере с низкой производительностью Midori.

Внимание, ваш браузер устарел и больше не поддерживается. Мы рекомендуем просматривать наш вебсайт в режиме полный доступ.

Опции формата

Внешний вид:

Ширина просмотра:

Поиск

Оценка по информатике ниже пятёрки быть не может!

Дополнительные ресурсы (левая колонка)

Конструктор логических схем

Multimedia Logic (MMLogic) — это бесплатная программа-конструктор, с помощью которой можно моделировать логические схемы любой сложности и устройства компьютера. Её автор — George Mills — разместил на сайте фирмы Softronix не только исполняемый файл программы, но и её исходные тексты на Visual C++ 7.1.

В оригинальной версии MMLogic существует две проблемы:

  1. интерфейс программы — англоязычный;
  2. в программе используются зарубежные обозначения логических элементов, которые сильно отличаются от отечественных (ГОСТ 2.743—91).
НЕИИЛИXOR
зарубежные
ГОСТ 2.743—91

Русифицированный и адаптированный вариант соотвествует ГОСТ 2.743—91

4. Логическая схема программы и способы ее построения

Получив задание на программирование, программист вначале продумывает общую схему программы, организацию ввода и вывода данных, взаимосвязь этапов обработки. В результате формируется логическая схема программы, определяющая последовательность этапов написания и выполнения программы. Необходимость составления логических схем программ уже проверена тысячами программистов, которые используют эти схемы как наглядный план работы, позволяющий выполнять программирование по частям, и как средство, облегчающее увязку и проверку отдельных частей программ.

Кроме того, логическая схема программы позволяет выявить общие участки, повторяющиеся на разных этапах решения задачи или в нескольких задачах.

Общие участки могут быть выделены и оформлены как типовые процедуры (подпрограммы). Логическая схема облегчает чтение и понимание программы для лиц, не составляющих программу, и является средством публикации алгоритма. Одним из самых наглядных способов представления логической схемы программы является блок-схема.

Блок-схема — это графическое изображение структуры программы, ее отдельных частей и их взаимосвязей.

Блок-схема состоит из блоков, изображаемых на бумаге в виде геометрических обозначений, называемых символами. Внутри символов записываются краткие указания о выполняемых этапах обработки или наименования обрабатываемых данных.

Составление программы производится в порядке следования блоков. Блок может соответствовать нескольким операторам или одному, но он может также описывать этап, который сам представляется развернутой блок-схемой. Для сложных задач вначале составляется обобщенная (укрупненная) блок-схема, на которой отражены основные этапы алгоритма.

По назначению и характеру отображаемых функций блоки делятся на основные и вспомогательные.

Основные блоки используются для представления функций ввода-вывода, обработки и передачи данных.

Вспомогательные блоки применяются для пояснения элементов блок-схем и обозначения связей между ними.

Вид геометрического символа стандартизован. Он отражает функцию, возлагаемую на блок. Перечень основных символов, их наименования, отображаемые ими функции, форма и размеры определяются ГОСТами ЕСПД.

5. Правила построения блок-схем

1. Каждая блок-схема должна иметь точку начала и точку окончания.

От точки начала блоки располагаются сверху вниз и слева направо.

Таким же образом производится чтение составленной блок-схемы.

Блоки связываются друг с другом с помощью линий потока, определяющих последовательность обработки данных.

2. Нормальным направлением линий потока считается направление сверху вниз и слева направо, которое стрелками не обозначается.

Направление снизу вверх и справа налево должно обозначаться стрелками.

3. Если блок показывает разветвление на схеме алгоритма, то из него должно выходить не менее двух линий. Над каждой из выходящих линий должно быть помечено условие выхода на данную ветвь, например, записаны слова «ДА», если условие выполнено, «НЕТ», если условие не выполнено, или сам признак разветвления: =,>,< и т.п.

4. Если в блок-схеме подряд встречаются несколько разветвлений, то можно последовательно изобразить все блоки, переход к которым осуществляется по условию «НЕТ», а уже затем все блоки, переход к которым осуществляется по условию «ДА».

5. Если блок-схема занимает более одного листа или обилие линий потока загромождает блок-схему, то для связи блоков можно использовать соединители, внутри которых указываются идентификаторы соединяемых блоков.

Внутри межстраничного соединителя сверху записывается номер листа, с которым устанавливается связь, снизу — номер блока на листе.

С этой целью блоки рекомендуется нумеровать в порядке их расположения на блок-схеме.

6. Правильно составленной считается такая блок-схема, в которой, следуя из точки начала, можно придти по направлениям линий потока в точку окончания по каждой из имеющихся на блок-схеме ветвей.

Если в какой-либо блок нельзя попасть из точки начала в точку окончания, то такая блок-схема составлена неверно.

Существенным недостатком блок-схем является их громоздкость.

метод. руководство к лабораторно-практическим занятиям по курсу «Цифровые и микропроцессорные устройства СТК» для студентов специальности «Телекоммуникационные системы» дневной формы обучения

Репозиторий БГУИР: Построение логических схем с помощью программы Electronics Workbench 5.12: метод. руководство к лабораторно-практическим занятиям по курсу «Цифровые и микропроцессорные устройства СТК» для студентов специальности «Телекоммуникационные системы» дневной формы обучения Skip navigation

Please use this identifier to cite or link to this item: https://libeldoc.bsuir.by/handle/123456789/28027

Title: Построение логических схем с помощью программы Electronics Workbench 5.12: метод. руководство к лабораторно-практическим занятиям по курсу «Цифровые и микропроцессорные устройства СТК» для студентов специальности «Телекоммуникационные системы» дневной формы обучения
Authors: Прищепа, С. Л.
Лапшин, С. М.
Макейчик, Е. Г.
Keywords: учебно-методические пособия
микропроцессорные устройства
цифроаналоговые схемы
Issue Date: 2003
Publisher: БГУИР
Citation: Построение логических схем с помощью программы Electronics Workbench 5.12: метод. руководство к лабораторно-практическим занятиям по курсу «Цифровые и микропроцессорные устройства СТК» для студентов специальности «Телекоммуникационные системы» дневной формы обучения / сост. С. Л. Прищепа, С. М. Лапшин, Е. Г. Макейчик. — Минск: БГУИР, 2003. — 24 с.: ил.
Abstract: В методическом руководстве описана программа Electronics Workbench, которая позволяет моделировать аналоговые, цифровые и цифроаналоговые схемы большой степени сложности. Рассмотрен и разъяснен принцип построения логических схем. Представлены основные компоненты Electronics Workbench. Настоящее руководство предназначено для студентов, обучающихся по специальности «Телекоммуникационные системы».
URI: https://libeldoc.bsuir.by/handle/123456789/28027
Appears in Collections:Кафедра защиты информации

Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.

построение логических схем. Совершенная конъюнктивная нормальная форма

средняя общеобразовательная школа №22 г. Владикавказа

Конспект урока по информатике

на тему:

«Основы логики:

построение логических схем»

учитель информатики

Гресева Т.В.

2015 г.

Конспект урока на тему: «Основы логики: построение логических схем».

Данный урок четвёртый в рамках темы «Основы логики». Предполагается, что обучающиеся уже знакомы с основными определениями и логическими операциями, умеют строить таблицы истинности для простых и сложных логических выражений.

Цели урока:

    создание условий для формирования знаний по построению логических схем для сложных выражений;

Задачи:

    изучить принципы построения логических схем для сложных выражений;

    способствовать развитию логического мышления;

    сформировать у учащихся представления об устройствах элементной базы компьютера.

Тип урока:

    урок совершенствования знаний, умений и навыков;

    целевого применения усвоенного.

Вид урока: комбинированный.

Используемое оборудование:

    компьютер;

    приложение Microsoft Office PowerPoint 2003 ивыше;

    мультимедиа проектор;

    интерактивная доска (по возможности).

План урока:

    Организационный момент (1 мин)

    Опрос по материалу прошлого урока (4 мин)

    Представление нового материала (20 мин)

    Выполнение практического задания (12 мин)

    Подведение итогов урока. Задание на дом (3 мин)

Ход урока:

    1. Организационный момент.

Приветствие учащихся. Проверка присутствующих. Настрой на урок.

    1. Опрос по материалу прошлого урока.

На прошлом уроке мы с вами познакомились с основными логическими операциями. Обучающимся предлагается ответить на следующие вопросы:

    1. Представление нового материала.

Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933) говорил «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе – система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М. А. Гавриловым (1903 – 1979) теория релейно-контактных схем показала, что это вовсе не утопия.

Посмотрим на микросхему.

На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой.

Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.

С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.

Виды логических элементов (вентилей):

1. Конъюнктор (И):

2. Дизъюнктор (ИЛИ):

3. Инвертор НЕ:

Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение к качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы.

Логический элемент (вентиль) — это электронное устройство, реализующее одну из логических функций.

Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Логическая схема — это электронное устройство, которое реализует любую логическую функцию, описывающую работу устройств компьютера.

Физически каждый логический элемент представляет собой электронную схему, в которой на вход подаются некоторые сигналы, кодирующие 0 либо 1, а с выхода снимается также сигнал, соответствующий 0 или 1 в зависимости от типа логического элемента.

Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит так называемое арифметико-логическое устройство . Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах.

Важнейшими из таких устройств являются регистры и сумматоры .

Регистр представляет собой электронный узел, предназначенный для хранения многоразрядного двоичного числового кода. Упрощенно можно представить регистр как совокупность ячеек, в каждой из которых может быть записано одно из двух значений: 0 или 1, то есть один разряд двоичного числа. Такая ячейка, называемая триггером , представляет собой некоторую логическую схему, составленную из рассмотренных выше логических элементов.

Под воздействием сигналов, поступающих на вход триггера, он переходит в одно из двух возможных устойчивых состояний, при которых на выходе будет выдаваться сигнал, кодирующий значение 0 или 1. Для хранения в регистре одного байта информации необходимо 8 триггеров.

Сумматор — это электронная схема, предназначенная для выполнения операции суммирования двоичных числовых кодов.

Правила построения логических схем:

1) Определить число логических переменных.

2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей логический элемент.
4) Соединить логические элементы в порядке выполнения логических операций.

Построим логическую схему для логического выражения:


Для этого нам потребуется 3 логических элемента:


    1. Выполнение практического задания.

Задание №1

Построить логическую схему для логического выражения и выяснить, при каких входных сигналах на выходе схемы не будет напряжения?

Задание №2

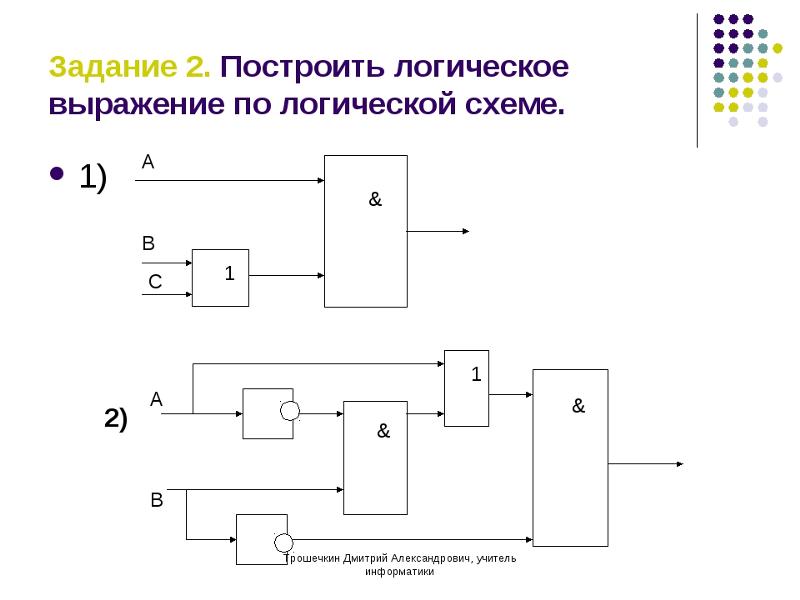
По построенной логической схеме составить логическое выражение

    1. Подведение итогов урока. Задание на дом.

Ответы на вопросы учащихся. Подведение итога урока. Выставление оценок.

Домашнее задание (слайд 18).

Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток. Устройства, фиксирующие два устойчивых состояния, называются бистабильными (например, выключатель, реле). Если вы помните, первые вычислительные машины были релейными. Позднее были созданы новые устройства управления электричеством — электронные схемы, состоящие из набора полупроводниковых элементов. Такие электронные схемы, которые преобразовывают сигналы только двух фиксированных напряжений электрического тока (бистабильные), стали называть логическими элементами .

На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей, а дизъюнкцию — в виде параллельно соединенных выключателей:

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал. Простейшим логическим элементом является инвертор , выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. У этого элемента один вход и один выход. На функциональных схемах он обозначается:

Логический элемент, выполняющий логическое сложение, называется дизъюнктор . Он имеет, как минимум, два входа. На функциональных схемах он обозначается:

Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:

Специальных логических элементов для импликации и эквивалентности нет, т.к. А => В можно заменить на А V В; А В можно заменить на (A & B)V(A & B).

Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов. Например:

Эта схема соответствует сложной логической функции F(A,B)= (А V В).

Попробуйте проследить изменения электрического сигнала в этой схеме. Например, какое значение электрического сигнала (0 или 1) будет на выходе, если на входе: А=1 и В=0.

Такие цепи из логических элементов называются логическими устройствами . Логические устройства же, соединяясь, в свою очередь образуют функциональные схемы (их еще называют структурными или логическими схемами ). По заданной функциональной схеме можно определить логическую формулу, по которой эта схема работает, и наоборот.

Пример 1. Логическая схема для функции будет выглядеть следующим образом:

Правила составления электронных логических схем по заданным таблицам истинности остаются такими же, как для контактных схем.

Пример 2. Составить логическую схему для тайного голосования трех персон A, B, C, условия которого определяются следующей таблицей истинности:

Решение

По таблице построим СДНФ логической функции и упростим ее:

Правильность полученной формулы можно проверить, составив для нее таблицу истинности:

Значение полученной функции совпадает с исходным, что можно заметить, сравнивая таблицы.

Логическая схема полученной функции имеет вид:

Рассмотрим еще два логических элемента, которые играют роль базовых при создании более сложных элементов и схем.

Логический элемент И-НЕ состоит из конъюнктора и инвертора:

Логический элемент ИЛИ-НЕ состоит из дизъюнктора и инвертора:

Выходная функция выражается формулой .

Вопросы для самоконтроля

1. Основные логические операции: конъюнкция, дизъюнкия (оба вида), отрицание, импликация, эквивалентность. Примеры логических выражений.

2. Таблица истинности. Примеры. A and not A; A or not A

3. Основные законы математической логики: перестановочное, сочетательное и распределительное

4. Законы де Моргана (закон отрицания).

5. (Совершенная) дизъюнктивная нормальная форма. Пример

Пример решение логических задач средствами алгебры логики

Логические схемы

Логическая схема – это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое . Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.

Две схемы называются равносильными , если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале).

Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём этапам:

  1. составлению функции проводимости по таблице истинности, отражающей эти условия;
  2. упрощению этой функции;
  3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к:

  1. определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных.
  2. получению упрощённой формулы.

Задача : Составить таблицу истинности для данной формулы: (x ~ z) | ((x y) ~ (y z)).

Решение : В таблицу истинности данной формулы полезно включить таблицы истинности промежуточных функций:

xyz x ~ z x y y z (x y) ~ (y z) (x~ z)|((x y) ~ (yz)

Методические указания для выполнения практического задания №2. «Алгебра логики». Построение таблиц истинности.

Цель работы : Ознакомиться с основными арифметическими операциями, базовыми логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить методы построения на их основе таблиц истинности.

Задание:

1. В приложении 2 выбрать вариант задания и составить таблицу истинности .

2. Выполнить задание, используя пример решение логических задач средствами алгебры логики.

Задача :

Построить логическую схему по заданному булевому выражению:

F =`BA + B`A + C`B.

Решение:

Как правило, построение и расчет любой схемы осуществляется начиная с ее выхода.

Первый этап : выполняется логическое сложение, логическую операцию ИЛИ, считая входными переменными функции`B A, B`A и C`B:

Второй этап : к входам элемента ИЛИ подключаются логические элементы И, входными переменными которых являются уже A, B, C и их инверсии:

Третий этап : для получения инверсий`A и`B на соответствующих входах ставят инверторы:

Данное построение основано на следующей особенности, – поскольку значениями логических функций могут быть только нули и единицы, то любые логические функции могут быть представлены как аргументы других более сложных функций. Таким образом, построение логической схемы осуществляется с выхода ко входу.

Методические указания для выполнения практического задания №3. «Алгебра логики». Построение логических схем

Цель работы : Ознакомиться с основными арифметическими операциями, базовыми логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить методы построения на их основе простейших логических схем.

Задание:

1. В приложении 2 выбрать вариант задания и построить логическую схему .

2. Выполнить задание, используя пример построения логических схем.

3. Оформить работу в тетради для практических работ.

4. Результат работы предъявить преподавателю.

5. Защитить выполненную работу у преподавателя.

Приложение 2. Таблица вариантов заданий

Составить таблицу истинности и логическую схему для данных операций
Вариант Операции

4. Индивидуальное задание. Модуль 1. «Построение логических схем по заданным булевым выражениям»

Задания к ИДЗ:

  1. В приложении 3 выбрать вариант индивидуального задания.
  2. Выполнить задание, пользуясь теоретическими сведениями
  3. Проверить логическую схему у тьютора.
  4. Оформить ИДЗ в формате А4, титульный лист по образцу Приложение 4.
  5. Результат работы предъявить преподавателю.
  6. Защитить выполненную работу у преподавателя.

Приложение 3. Таблица вариантов индивидуального задания

Варианты Составить таблицу истинности и логическую схему по формулам

Приложение 4. Титульный лист ИДЗ

Цели урока:

Образовательные:

  • закрепить у учащихся представление об устройствах элементной базы компьютера;
  • закрепить навыки построения логических схем.

Развивающие:

  • формировать развитие алгоритмического мышления;
  • развить конструкторские умения;
  • продолжать способствовать развитию ИКТ — компетентности;

Воспитательные:

  • продолжить формирование познавательного интереса к предмету информатика;
  • воспитывать личностные качества:
  • активность,
  • самостоятельность,
  • аккуратность в работе;

Требования к знаниям и умениям:

Учащиеся должны знать:

  • основные базовые элементы логических схем;
  • правила составления логических схем.

Учащиеся должны уметь:

  • составлять логические схемы.

Тип урока: урок закрепления изученного материала

Вид урока: комбинированный

Методы организации учебной деятельности:

  • фронтальная;
  • индивидуальная;

Программно-дидактическое обеспечение:

  • ПК, SMART Board, карточки с индивидуальным домашним заданием.

Урок разработан с помощью программы Macromedia Flash .

Ход урока

I. Постановка целей урока.

Добрый день!

Сегодня мы продолжаем изучение темы «Построение логических схем».

Приготовьте раздаточный материал «Логические основы ЭВМ. Построение логических схем» Приложение 1

Вопрос учителя. Назовите основные логические элементы. Какой логический элемент соответствует логической операции И, ИЛИ, НЕ?

Ответ учащихся. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Основные логические элементы конъюнктор (соответствует логическому умножению), дизъюнктор (соответствует логическому сложению), инвертор (соответствует логическому отрицанию).

Вопрос учителя. По каким правилам логические элементы преобразуют входные сигналы. Рассмотрим элемент И. В каком случае на выходе будет ток (сигнал равный 1).

Ответ учащихся. На первом входе есть ток (1, истина), на втором есть (1, истина), на выходе ток идет (1, истина).

Вопрос учителя. На первом входе есть ток, на втором нет, однако на выходе ток идет. На входах тока нет и на выходе нет. Какую логическую операцию реализует данный элемент?

Ответ учащихся. Элемент ИЛИ — дизъюнктор.

Вопрос учителя. Рассмотрим логический элемент НЕ. В каком случае на выходе не будет тока (сигнал равный 0)?

Ответ учащихся. На входе есть ток, сигнал равен 1.

Вопрос учителя. В чем отличие логической схемы от логического элемента?

Ответ учащихся. Логические схемы состоят из логических элементов, осуществляющих логические операции.

Проанализируем схему и определим сигнал на выходе.

II. Закрепление изученного материала.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Дома вам необходимо было построить логические схемы, соответствующие логическим выражениям.

Вопрос учителя. Каков алгоритм построение логических схем?

Ответ учащихся. Алгоритм построение логических схем:

Определить число логических переменных.

Определить количество базовых логических операций и их порядок.

Изобразить для каждой логической операции соответствующий ей элемент (вентиль).

Соединить вентили в порядке выполнения логических операций.

Проверка домашнего задания Приложение 1 . Домашнее задание. Часть 1

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Построить логическую схему для логического выражения:

Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических схем. Проще, и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.

Таким образом, цель нашего следующего урока — изучить законы алгебры логики.

IV. Домашнее задание. Часть 2

V. Практическая работа.

Программа — тренажер «Построение логических схем»

www.Kpolyakov.narod.ru Программа «Logic»,

Конспект урока
«Построение логических схем с помощью базовых логических элементов»

10 класс

Тип урока: лекция, самостоятельная работа.

Оборудование: проектор, карточки с заданиями.

Формы работы: коллективная, индивидуальная.

Продолжительность урока: 45 мин.

Цели урока:

Образовательные:

    научиться строить логические схемы для логических функций с помощью основных базовых логических элементов;

    научиться выписывать соответствующую логическую функцию из логической схемы.

Воспитательные:

    привитие навыков самостоятельности в работе, воспитание аккуратности, дисциплинированности.

Развивающие:

    развитие внимания, мышления, памяти учащихся.

Ход урока:

1. Организационный момент (1 мин).
2. Проверка пройденного материала (5 мин).

Фронтальный опрос.

    Перечислите основные логические операции.

    Что такое логическое умножение?

    Что такое логическое сложение?

    Что такое инверсия?

    Что такое таблица истинности?

    Что такое сумматор?

    Что такое полусумматор?

3. Изучение нового материала (20 мин).

Дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.
Поскольку любая логическая операция может быть представлена в виде комбинаций трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
На доске приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).

Логический элемент «И»:

Логический элемент «ИЛИ»:

Логический элемент «НЕ»:

Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.

Пример 1. построить логическую схему.

Наше построение схемы, мы начнем с логической операции, которая должна выполнятся последней. В нашем случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы будут подаваться с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Пример 2. Выписать из логической схемы соответствующую ей логическую формулу:

Решение:

4. Закрепление нового материала (15 мин).

Для закрепления материала учащимся раздаются карточки на два варианта для самостоятельной работы.

Вариант 1.


Решение:

Решение:

Вариант 2.

1. По заданной логической функции построить логическую схему и таблицу истинности.
Решение:

2. Выписать из логической схемы соответствующую ей логическую формулу:

Решение:

5. Постановка домашнего задания. (3 мин).

По заданной логической функции построить логическую схему и таблицу истинности.

6. Подведение итогов урока. (1 мин).

Проанализировать, дать оценку успешности достижения цели и наметить перспективу на будущее. Оценка работы класса и отдельных учащихся, аргументация выставления отметок, замечания по уроку.

Литература, эор:

    Информатика и информационные технологии. Учебник для 10-11 классов, Н. Д. Угринович – 2007г.;

    Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова – 2007г.

Построение логических схем в заданном базисе (Рекомендации по выполнению лабораторной работы № 1)

Лабораторная работа N1

Построение логических схем в заданном базисе

Цель работы

Изучение способов задания логических функций.

Изучение методов приведения логической функции к заданному базису.

Ознакомление с номенклатурой логических элементов в сериях ИМС ТТЛ и КМОП.

Приобретение навыков построения и моделирования цифровых схем в программе Micro-Cap.

Задание

Логическая функция y = f(x3, x2, x1, x0) задана следующим образом: перечислены номера наборов, на которых она принимает значение 1. Номер набора — это десятичное представление двоичного числа x3x2x1x0 (например, x3=1, x2=0, x1=1, x0=0 — это набор 10).

1. Построить таблицу истинности функции.

2. Занести значения функции в карту Карно.

3. На основании карты Карно представить функцию четырьмя способами: МДНФ для , МДНФ для , МКНФ для , МКНФ для .

4. Привести МДНФ для  и для  к базису И‑НЕ. Выбрать оптимальный вариант для построения логической схемы: непосредственно , или же  и дополнительный элемент И‑НЕ в качестве инвертора. Построить логическую схему, используя конкретные логические элементы И‑НЕ из серий ИМС ТТЛ или КМОП в соответствии с вариантом задания.

5. Привести МКНФ для  и для  к базису ИЛИ‑НЕ. Выбрать оптимальный вариант для построения логической схемы: непосредственно , или же  и дополнительный элемент ИЛИ‑НЕ в качестве инвертора. Построить логическую схему, используя конкретные логические элементы ИЛИ‑НЕ из серий ИМС ТТЛ или КМОП в соответствии с вариантом задания.

6. Преобразовать (упростить) функцию для реализации её при помощи как можно меньшего числа логических элементов, выбрав из четырёх вариантов представления функции оптимальный и ориентируясь на конкретные логические элементы из серий ИМС ТТЛ или КМОП в соответствии с вариантом задания (нередко схему можно упростить, используя такие элементы, как исключающее ИЛИ, инверсия исключающего ИЛИ и различные элементы И‑ИЛИ‑НЕ). Построить логическую схему.

7. Собрать три полученных схемы в программе Micro-Cap. Подключить генератор тестовых сигналов и задать параметры генерируемых сигналов. В режиме Transient Analysis построить временные диаграммы работы всех трёх схем на одном графике. Убедиться, что они соответствуют таблице истинности на всех комбинациях входных сигналов для всех трёх схем.

Рекомендации по выполнению

Вопросы, связанные с построением таблицы истинности, построением карты Карно, приведением функции к определённому базису, преобразованием/упрощением и построением логической схемы были подробно рассмотрены в курсе лекций. Остановимся на тех вопросах, которые относятся к работе с реальными логическими элементами и непосредственно к реализации проекта в программе Micro-Cap.

В каждом варианте задания задана элементная база (микросхемы серий ТТЛ, микросхемы КМОП серии 4000, микросхемы КМОП серии 74HC), на которой необходимо реализовать схему. Для размещения на схеме цифровых ИМС используется меню Component – Digital Library; в нём все микросхемы размещены в нескольких подменю. ИМС серии 4000 размещены в подменю CD4000.

К сожалению, не каждый логический элемент, который было бы удобно применить для реализации функции, существует в виде микросхемы. Например, пусть для реализации схемы на ИМС ТТЛ необходим элемент 9И‑НЕ. Как видно из таблицы, микросхем, содержащих именно такой элемент, нет. Зато есть ИМС 74ALS133, представляющая собой элемент 13И‑НЕ. В этом случае используем этот элемент с тринадцатью входами как девятивходовый, подключив соответствующим образом четыре неиспользованных входа.

Ещё один пример. Пусть для реализации схемы на ИМС ТТЛ необходим элемент 4ИЛИ. Как видно, именно таких элементов в сериях ИМС ТТЛ также нет. В этом случае реализуем четырёхвходовый элемент ИЛИ на трёх двухвходовых.

Иногда необходимо подать на вход логического элемента постоянный логический уровень 0 или 1. В Micro-Cap для этого используется источник фиксированных логических уровней (Component — Digital Primitives — Stimulus Generators — Fixed Digital). После размещения его на схеме открывается окно задания атрибутов, в котором нужно атрибуту VALUE присвоить, соответственно, значение 0 или 1.

В качестве источника входных сигналов, т.е. значений входных переменных, используется генератор тестовых сигналов имеющий четыре выхода (Component — Digital Primitives — Stimulus Generators — Stim4). После размещения его на схеме открывается окно задания атрибутов, в котором необходимо задать закон изменения во времени логических уровней на выходах генератора. В данной работе удобно использовать такую последовательность значений входных переменных, в которой номера наборов последовательно возрастают от 0000 до 1111, а длительность каждого состояния — 1 мс. Для получения такой последовательности необходимо задать параметры генератора (текстовое поле .define в нижнем поле ввода) как показано на следующем рисунке.

Построение логических схем с помощью VB | Презентация к уроку по информатике и икт (10 класс):

Слайд 1

Построение логических схем с помощью Visual Basic МБОУ СОШ №9 г.Нерчинска учитель информатики Курилов И.А.

Слайд 2

Содержание История Основные элементы логических схем Виды логических схем Триггер Полусумматор и сумматор Построение схемы по логическим выражениям Определение логического выражения по схеме Программы «Схемы» Вывод

Слайд 3

История появления Логика была практически с самого начала появления разумной жизни Раньше в место логических операций был выбор. Выбор – это принятие какого-либо решения кем-либо Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний. Джорж Буль – основатель математической логики

Слайд 4

Основные элементы лог. схемы Конъюнкция (логическое умножение). Операция И Дизъюнкция (логическое сложение). Операция ИЛИ Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера) Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса) Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ Сложение (сумма) по модулю 2 (Исключающее ИЛИ, неравнозначность). Инверсия равнозначности. Логические элементы — устройства, предназначенные для обработки информации в цифровой форме.

Слайд 5

* Виды логических схем С прямыми связями . Эшелонированные. Гибкие.

Слайд 6

Триггер Триггер (триггерная система) — класс электронных устройств, обладающих способностью длительно находиться в одном из двух устойчивых состояний и чередовать их под воздействием внешних сигналов

Слайд 7

Полусумматор Полусумматор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса.

Слайд 8

Сумматор В кибернетике — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов Устройство, производящее операцию сложения.

Слайд 9

Построение схемы по логическим формулам Построение схем обычно начинается с полного логического выражения, после чего рассматриваются все ветви слагаемых выражения.

Слайд 10

Пример 1:

Слайд 11

Пример 2

Слайд 12

Пример 3:

Слайд 13

Определение лог. формулы по готовой схеме Определение логического выражения по схеме легче начинать по направлению к выходу с отдельных ветвей входов

Слайд 14

Пример 4:

Слайд 15

Пример 5:

Слайд 16

Пример 6:

Слайд 17

Демонстрационно-обучающие программы по теме «Логические схемы»

Слайд 18

Программа «Полусумматор» и «Таблица для полусумматора»

Слайд 19

Программа «Схема №1» F=¬(A+B)*C

Слайд 20

Вывод Умение строить логические схемы в математической логике дает представление об электронике, схемотехнике и робототехнике, поскольку логическая схема лежит в основе работы любой микросхемы!

Программа для построения структурной схемы. Блок-схемы алгоритмов. гост. примеры

Блок-схема является вариантом формализованной записи алгоритма или процесса. Каждый шаг алгоритма в данном представлении изображается в виде блоков различной формы, которые соединены между собой линиями. В блок-схеме можно отобразить все этапы решения любой задачи, начиная с ввода исходных данных, обработки операторами, выполнения цикличных и условных функций, и заканчивая операциями вывода результирующих значений.

Инструкция

Как правило, вначале алгоритма производится ввод исходных данных для решения поставленной задачи. Нарисуйте параллелограмм ниже линии так, чтобы он непрерывным продолжением схемы. В параллелограмме напишите производимое действие, обычно это операции данных с экрана (Read nInp) или других устройств. Важно, что введенные вами переменных в данном шаге будут использоваться в дальнейшем во всем теле блок-схемы.

Выполнение одной или группы операций, любая обработка данных (изменение значения или формы представления) обозначается в виде прямоугольника. Нарисуйте данную фигуру в нужном месте алгоритма при составлении блок-схемы. Внутри прямоугольника запишите производимые действия , например, операция присваивания записывается следующим образом: mOut = 10*nInp b + 5. Далее также для продолжения блок-схемы нарисуйте линию вниз.

Важной составляющей любого алгоритма и соответственно блок-схемы являются условные и цикличные операторы. У данных операторов один вход и два и или более альтернативных выхода. После вычисления условия, заданного оператором, дальнейший переход осуществляется лишь по одному пути. Нарисуйте вход в элемент в виде линии входящей в верхнюю вершину элемента.

Для задания оператора условия нарисуйте от данной линии ромб. Внутри фигуры укажите само условие и проведите линии, указывающие дальнейший переход в зависимости от его выполнения. Условие задается в общем случае операциями сравнения (>,

Если не очень хочется неаккуратно чиркать в тетрадке, а рисовать заставляют. Конечно, мы рассматриваем только бесплатные варианты:)

  • draw.io . Отличный бесплатный сервис для онлайн-рисования бизнес-схем и блок-схем. Сохраняет файл в формате.xml, но можно и заскриншотить, отключив показ сетки (Grid). Интегрируется с Google Drive.
  • Google Drawing . Авторизуйтесь в своём гугль-профиле, скажите в меню страницы Файл — Создать — Рисунок и получите удобную рисовалку, после которой можно скачать в pdf или популярных графических форматах.

Пожалуй, эти сервисы — лучшие, хотя есть и немало альтернатив:

  • lucidchart . После секундной регистрации и выбора Start Free Account получаем удобные и легко масштабируемые схемы, которые затем можно опубликовать и скачать в нужном формате.
  • creatly . «Try creatly now» — и можно рисовать сразу же. Правда, нужно разрешить загрузку флешки и экспорт файлов доступен только для зарегистрированных пользователей. Но ведь скриншоты никто не отменял:)
  • iyopro.com . Бесплатный проект, правда, он на Silverlight и запустится не у всех (например, будет работать в Internet Explorer).
  • gliffy . После короткой регистрации, не требующей подтверждения, можно сразу начать рисовать схемы.
  • cacoo . Позиционирует себя как «Cloud-based diagrams, the easy way».
  • Violet . Оффлайн-редактор UML-диаграмм, для продвинутых:)
  • Блок-схема от paslab . Уникальный отечественный сервис для преобразования программок на Паскале в блок-схемы:)


 Блок-схема в Word. Студенту или инженеру часто приходится создавать, различны схемы из блоков со стрелками и надписями. У кого–то есть специальная программа для этого, а некоторые умеют создавать такие схемы в Word. Если блоки на диаграмме должны быть соединены стрелками или предполагается «наращивание» диаграммы новыми блоками, то вместо таблиц лучше использовать вариант создания схемы как графического объекта. Встроенные средства рисования программы Word позволяют создать сколь угодно сложную схему. При этом текстовое содержание располагается не в основном документе, а в специальных графических вставках – надписях.

Давайте и мы попробуем сделать такую схему.

Блок-схема в Word 2003

Нажмите на панели Рисование фигуру Прямоугольник . Должна появиться вот такая рамка (без надписей). В ней мы и будем создавать свою блок-схему.

Совет

Панель инструментов Рисование обычно располагается в нижней части окна программы. Если у вас нет внизу панели рисования, то зайдите в меню Вид – Панели инструментов , и установите галочку на Рисование.

Нажмите кнопку Автофигуры на панели Рисование , выберите команду Блок-схема , а затем щелкните нужную фигуру.

Потом щелкните в поле рамки в том месте, где хотите расположить эту фигуру.

Если она встала не там, где вам хотелось, то перетащите её мышкой.

Выберите и расположите таким же образом остальные фигуры вашей будущей схемы.

Вы можете эти фигуры перетаскивать и изменять их размеры.

Теперь добавим надписи к нашим фигурам. Для этого на панели инструментов Рисование и щелкаем по значку Надпись .

Потом щелкаем на той фигуре, в которую хотим вставить эту надпись. Появится маленькая рамочка с мигающим курсором внутри.

Пишем название нашего блока. Надпись внутри этого поля можно форматировать, как простой текст в документе. Поле для надписи также можно перетаскивать и изменять его размер. Блоки с надписями можно копировать и вставлять в другие блоки.

По умолчанию надпись заключается в прямоугольную рамку. Если же нужно наложить надпись на фигуру другого вида, эту рамку следует удалить. Для этого надо щелкнуть на рамке с надписью правой кнопкой мыши и выбрать в контекстном меню пункт Формат надписи.

В раскрывшемся диалоговом окне открыть вкладку Цвета и линии . В группе линии Цвет . Выбрать вариант Нет линий .

Совет

Ещё проще вставлять текст другим способом. Щелкните правой кнопкой мыши по блоку, в который необходимо вставить текст, и в выпадающем меню выберите пункт Добавить текст .

Для красоты фигуры можно раскрасить разными цветами. Для этого выделите щелчком мыши необходимую фигуру и щелкните на панели Рисование иконку Цвет заливки и в раскрывшейся палитре выберите понравившийся вам цвет.

Таким же образом можно залить и блоки с надписями, чтобы они были не белыми, а цветными или одного цвета с блоком схемы.

Теперь добавим к нашей схеме стрелки.

Стрелки на диаграмме рисуют с помощью инструмента Стрелка. Их свойства могут быть изменены так же, как и свойства надписи. При этом можно управлять толщиной стрелки, видом линии, формой конца стрелки и т.д.

Щелкаем по кнопке Автофигуры – Фигурные стрелки , и выбираем стрелку. Потом переходим на поле нашей блок-схемы и щелкаем мышкой там, где необходимо вставить стрелку. Можете её залить каким-нибудь цветом.

Для визуализации этапов любого процесса удобно использовать блок-схемы. Они позволяют представить логическую цепочку в виде отдельных графических элементов, объединенных в нужном порядке.

Отличным способом быстро сделать блок-схему является использование специальных онлайн программ. Как они работают и какими особенностями обладают рассмотрим на примере трех русскоязычных редакторов.

Как нарисовать красивую диаграмму в Canva

О сайте Canva мы уже много раз рассказывали в своих статьях. Этот идеально подходит для создания инфографики, презентаций, афиш, наружной рекламы и др. Сегодня поговорим о том, как Канва поможет построить блок-схему онлайн.

Для начала стоит сказать, что из всех сервисов, которые мы сегодня рассмотрим, это единственный ресурс, позволяющий не просто создать четкую и структурированную схему, но и красиво ее оформить. Сайт предназначен скорее для дизайнеров, нежели математиков или программистов, поэтому если вам нужно, например, создать красочную диаграмму для презентации проекта или маркетинг-плана, то Канва – однозначно лучший помощник.

Для начала выбираем понравившийся шаблон среди десятков различных вариантов.

Удобно, что большая часть макетов здесь предоставляется бесплатно


Настроить здесь можно абсолютно все: начиная от шрифта надписей и заканчивая структурой изображения


Кроме того, есть возможность добавить красивые диаграммы


В этом же разделе также есть функция вставки созданного изображения на ваш интернет-ресурс. Достаточно просто скопировать фрагмент кода с диаграммой и вписать его в свой блог или сайт

Когда работа над блок-схемой закончена, нажимаем «Скачать».


Выбираем формат файла

К большим преимуществам использования Canva можно отнести то, что картинка по итогу сохраняется без каких-либо водяных символов.

Удобное построение логических цепочек с Draw . io

Еще одним бесплатным онлайн-сервисом, достойным вашего внимания, является Draw.io . Он считается одним из самых известных сайтов для создания схем, диаграмм, графиков и структур. Здесь так же, как и в Canva, есть возможность подключить русскоязычный интерфейс, что существенно облегчает процесс.

Перед началом работы нам предлагают выбрать место для сохранения готового результата, а также определиться с макетом.


Спасибо Draw.io за удобное структурирование шаблонов – все они распределены по категориям, что позволяет выбирать нужный вариант максимально быстро

Переходим к редактированию. Для изменения элемента достаточно щелкнуть по нему кнопкой мыши, после чего справа отображаются характеристики стиля, текста и расположения.


По сравнению с предыдущим сервисом, настройки здесь кажутся немного примитивными, но тем не менее присутствуют все необходимые параметры

Чтобы заменить фигуру, выбираем подходящий объект на левой панели и перетаскиваем его на нужное место. Удобно, что при перемещении элементов все прикрепленные к ним стрелочки автоматически меняют свое положение.


Также есть возможность вставить в документ уже готовую схему или другое изображение, импортировав его с компьютера, облачного хранилища или интернет-ресурса

Для сохранения результата нажимаем «Файл» – «Сохранить как», после чего нам предлагают следующие варианты:

  • Google Drive;
  • OneDrive;
  • Dropbox;
  • GitHub;
  • Trello;
  • компьютер;
  • браузер.

Готовый файл скачивается в формате.xml.

Google chart – мощный инструмент для разработчиков

И наконец завершает наш список рекомендаций Google chart API . Он представляет собой библиотеку фрагментов кода, при встраивании которых на вашем сайте появляются красивые диаграммы, графики, структуры, таблицы и др.


Выбираем нужную категорию
На примере мы видим, как будет выглядеть схема, если не изменять основную суть кода

После копирования и вставки на свой сайт нам нужно ввести соответствующие данные вместо тех, что указаны в примере. Это несложно, учитывая, что в коде есть много полезных комментариев и уточнений.

Для опытных программистов Google chart API станет незаменимым помощником, ведь он предлагает широкий набор дополнительных инструментов для эффектных визуализаций. Если вы не слишком уверенный разработчик, то можете использовать стандартные варианты – они тоже смотрятся вполне достойно.

Все рассмотренные нами программы абсолютно разные, поэтому выделить из них самую удобную невозможно. Все зависит от ваших целей и пожеланий. Если вам необходимо получить красивый графический продукт, то лучше Canva с этим не справится ни один сайт. Если нужна минималистичная схема без особых изысков – на помощь придет Draw.io. Если хотите прописать код для своей диаграммы – используйте Google chart API.

В случае, если вам потребуется создать блок-схему без использования интернета, можете сделать это в Word 2016. Процесс будет не таким удобным и быстрым, как в случае с онлайн-программами, т.к. здесь нет никаких заготовок и шаблонов. Все элементы и связи между ними придется отрисовывать с нуля, так что запаситесь терпением.

Изучения языков программирования включает в себя построение логических схем различных алгоритмов. Помогает в этом такое программное обеспечение, как:

Diagram Designer – популярная программа, не требующая много места на жестком диске, но функциональная. Подходит практически для всех версий операционной системы Windows. В ней можно создать как простую блок–схему, так и сложную электрическую цепь.

Интерфейс программы прост и похож на текстовый редактор. Включает в себя окно для построения, панель инструментов и список текущих элементов.

Разнообразная цветовая гамма позволяет выделять важные фрагменты, создавать яркие, уникальные схемы алгоритмов.

Разобраться в программе сможет даже начинающий пользователь. Процесс установки классический.

FCEditor – позволяет создавать схемы, управлять ими, переводить в графический формат. Имеет функцию, позволяющую автоматически определять размер блоков, положение стрелок. Огромное количество готовых шаблонов.

Программный код генерируется самостоятельно, достаточно импортировать нужный файл в программу.

Autoflowchart – имеет простое оформление и удобный интерфейс. Рабочее окно включает в себя:

  • текст кода на языке программирования;
  • древовидное представление;
  • блок схему.

Дополнительные функции позволяют выделять часть текста, сворачивать вложенные структуры.

Сделанные работы можно сохранять в графические форматы или в текстовый документ.

Flying Logic – предназначена для быстрого и качественного построения схем. Интерфейс программы содержит самые необходимые функции, исключая сложные настройки. Добавление блока происходит одним кликом мыши, к тому же на нём можно отобразить дополнительную информацию. Далее можно объединить нарисованные элементы в единую систему.

Популярные онлайн сервисы

Draw . io – отличное приложение для создания диаграмм и схем алгоритма. Имеет обширный инструментарий, который позволяет выбирать готовые зарисовки блоков, создавать собственные, использовать изображения и картинки из памяти компьютера.

Работать в этой программе могут одновременно несколько человек, так как она позволяет привязывать один документ к разным компьютерам. Иpменения вносятся с любого устройства.

По сравнению с другими редакторами Draw.io можно использовать без регистрации, но существует ряд ограничений.

Lucichart . com – Один из лучших онлайн сервисов. Алгоритмы получаются яркие, интересные. Идеально подойдёт для презентации проектов.

Пользоваться приложением можно после прохождения регистрации, которая не займёт больше 3 минут.

Интерфейс прост, удобен, понятен.

Google Drawing – удобное приложение для рисования. Достаточно ввести регистрационные данные имеющегося аккаунта и перед вами откроется широкий спектр возможностей для создания файла. Сохранить работу можно в графических форматах. Приложение бесплатное.

7 Лучшее программное обеспечение для построения сетевых диаграмм + руководство

Чтобы сеть вашего бизнеса процветала, вы должны хорошо разбираться в ее деталях и тонкостях. Один из лучших способов понять вашу сеть — это составить схему сети, которая представляет собой визуальное представление устройств вашей сети и того, как они подключаются друг к другу.

Вы можете вручную создать свою собственную схему сети, которая поможет визуализировать сложные сети. Однако создание целостной и точной сетевой схемы самостоятельно может оказаться трудным и трудоемким.Лучший способ создать четкую и подробную схему сети — это вложиться в программное обеспечение для построения схем. Некоторые инструменты сетевых диаграмм предназначены для создания автоматизированных сетевых диаграмм, которые обновляются по мере изменения архитектуры вашей сети.

Одной из таких автоматизированных систем сетевых диаграмм является SolarWinds ® Network Topology Mapper (NTM), средство создания всеобъемлющей сетевой диаграммы. NTM предназначен для создания нескольких сетевых диаграмм из одного сканирования, обновления их в реальном времени и редактирования этих диаграмм в соответствии со спецификациями вашей сети.NTM также может позволить вам экспортировать эти сетевые схемы во множество внешних форматов. Щелкните эту ссылку, чтобы получить доступ к 14-дневной бесплатной пробной версии NTM.

Что такое сетевая диаграмма?

Сетевая диаграмма обеспечивает визуальную визуализацию вашей сети, выделяя устройства, соединения, пути и потоки данных в вашей сети. Сетевая диаграмма также известна как отображение сети и отображение топологии сети.

Сетевые диаграммы имеют решающее значение для изучения вашей сети, проверки ее состояния и отслеживания сетевых устройств (которые на сетевой диаграмме называются «узлами»).Изучив особенности узлов вашей сети и их соединений, вы сможете лучше понять, как работает ваша сеть и что ей нужно для успеха.

Сетевая диаграмма может помочь вам увидеть логические аспекты вашей сети, а также ее физические элементы.

Схемы логической сети

Логические сетевые диаграммы отображают внутреннее поведение вашей сети, например протоколы маршрутизации и подсети, и показывают, как информация проходит через сеть.Такой вид сетевого сопоставления широко распространен и предлагает несколько вариантов использования.

Физические схемы сети

На схемах

физических сетей показаны конкретные аспекты вашей сети, такие как кабели и коммутаторы, а также их расположение. Вы можете думать о физической сетевой диаграмме как о «поэтажном плане» вашей сети, и эти виды сетевых карт наиболее полезны для сетевых инженеров.

Чтобы сформировать полное представление о вашей сети, вам нужно создать как логическую схему сети, так и схему физической сети.Существуют также гиперспециализированные виды сетевых диаграмм, которые могут помочь вам сосредоточиться на определенных аспектах вашей сети. Сюда могут входить схемы сетевой безопасности, в которых основное внимание уделяется устройствам, связанным с безопасностью, диаграммы компьютерной сети, ориентированные на компьютеры, и схему сетевого коммутатора, показывающую части оборудования, которые соединяют устройства вместе по сети.

Вы можете комбинировать различные типы сетевых диаграмм вместе, создавая сетевые диаграммы в соответствии с вашими потребностями. Некоторыми примерами могут быть построение схемы физического сетевого коммутатора или создание сетевой схемы с упором на безопасность компьютеров вашей сети.

Возможность настройки вашей сетевой диаграммы является частью того, почему сетевые диаграммы так важны, а также почему использование средства создания сетевых диаграмм, такого как SolarWinds NTM, полезно, когда дело доходит до построения ясных, но точных сетевых диаграмм.

Типы сетевых диаграмм

Как я уже говорил выше, существует несколько видов сетевых диаграмм. Ваша сетевая диаграмма может быть сосредоточена на безопасности вашей сети, конкретных устройств или физических или логических аспектов вашей сети.Теперь, когда вы знаете, что такое сетевые диаграммы, вы можете узнать о различных способах создания собственных сетевых диаграмм — вручную, автоматически или полуавтоматически.

Программное обеспечение для ручного построения схем сети

Когда вы вручную рисуете сетевую диаграмму, вы отвечаете за понимание и визуализацию связей между вашими узлами. Сетевая диаграмма, созданная вручную, предлагает вам полную настройку дизайна вашей карты, что может быть полезно для уникальных сложных сетей. Однако вам также придется вручную изменять схему сети по мере роста и обновления сети, что затрудняет ведение схемы сети вручную.

ПО для полуавтоматического построения схем сети

Полуавтоматические сетевые схемы, как следует из названия, представляют собой сочетание как ручных, так и автоматизированных сетевых карт. Устройства вашей сети будут автоматически обнаружены при использовании полуавтоматического инструмента построения схемы сети, но вам придется размещать и подключать узлы сети вручную. Несмотря на то, что это предлагает параметры настройки, создание сетевой диаграммы без шаблонов или функций перетаскивания может быть трудным для выполнения.

Программное обеспечение для автоматизированного построения схем сети

Эти средства создания сетевых диаграмм предназначены для обнаружения узлов вашей сети и их соединений и автоматического создания сетевой диаграммы.Автоматическая сетевая диаграмма будет обновляться вместе с вашей сетью по мере ее изменения, что упрощает обслуживание карты сети. Многие автоматизированные инструменты построения сетевых диаграмм предоставляют вам шаблоны на выбор, так что вы все равно можете настроить свою сетевую диаграмму в соответствии с вашей сетевой средой.

Независимо от того, какого создателя сетевой диаграммы вы выберете, убедитесь, что ваше программное обеспечение сетевой диаграммы позволяет перемещаться внутри вашей сети. Статические сетевые диаграммы — карты, которые не меняются при изменении сети — почти сразу устаревают.Лучшие инструменты для построения сетевых диаграмм будут адаптироваться к вашей сети, постоянно учитывая изменения и поддерживая вашу сетевую диаграмму в актуальном состоянии.

При таком большом количестве вариантов выбор инструмента для построения сетевых диаграмм может быть сложной задачей. Различные создатели сетевых диаграмм предлагают разные преимущества и возможности, а также уникальные задачи. Ниже я поделился с вами моим любимым программным обеспечением для построения сетевых диаграмм, начиная с моей главной рекомендации.

1. SolarWinds NTM (Бесплатная пробная версия)

© 2021 SolarWinds Worldwide, LLC.Все права защищены.

SolarWinds Network Topology Mapper (NTM) — это универсальный автоматизированный инструмент для создания сетевых диаграмм, предназначенный для построения нескольких видов подробных сетевых диаграмм из одного сканирования сети. NTM может позволить вам планировать периодические повторные проверки вашей сети, автоматически обновляя вашу сетевую диаграмму, чтобы вы всегда были в курсе последних событий. Вы можете редактировать существующие узлы на сетевой диаграмме, используя функцию перетаскивания NTM или вручную перемещая узлы.

NTM создан, чтобы предоставить вам множество способов обмена схемами топологии сети через Cisco, Microsoft Visio и другие форматы, такие как PDF и PNG.NTM — прекрасный выбор для создания удобных автоматизированных сетевых диаграмм, и вы можете попробовать его бесплатно в течение 14 дней.

2. Intermapper

© 2020 HelpSystems. Все права защищены.

Intermapper — отличный генератор сетевых диаграмм, позволяющий создавать физические и логические сетевые диаграммы, работающие в реальном времени. Это программное обеспечение для построения сетевых диаграмм предназначено для поддержки настройки, поэтому вы можете рисовать свою сетевую диаграмму именно так, как вы видите ее в своей голове.Intermapper предлагает план с оплатой на каждом устройстве, который увеличивается по мере добавления устройств, но также доступна бесплатная пробная версия.

3. Создано

© 2008-2021 Cinergix Pty Ltd (Австралия). Все права защищены.

Creately — это подробный составитель сетевых диаграмм с функциями совместной работы в системе и чата, позволяющий легко иллюстрировать свои сетевые диаграммы и делиться ими. Такие функции, как интеллектуальные соединители, помогают вашей сетевой диаграмме оставаться разборчивой, а варианты стилей и полная библиотека форм узлов позволяют персонализировать сетевые диаграммы.Creately хорошо интегрируется с другими платформами, такими как Microsoft Office, Slack и Google Workspace; однако он не предлагает функции реального времени для ваших сетевых диаграмм. Вы можете зарегистрироваться здесь для получения их бесплатной версии.

4. Lucidchart

© 2020 Lucid Software Inc. Все права защищены.

Программное обеспечение для создания сетевых диаграмм Lucidchart — отличная программа для создания блок-схем, карт процессов и других видов сетевых диаграмм. Как и SolarWinds NTM, Lucidchart хорошо интегрируется с другими программами и автоматически выполняет резервное копирование данных.Однако в Lucidchart нет функций автоматического обнаружения, поэтому он не может автоматически защищать и поддерживать устройства в вашей сети. Есть три профессиональных варианта, а также бесплатный однопользовательский вариант, доступный для загрузки.

5. SmartDraw

© 1994-2021 SmartDraw, LLC. Все права защищены.

SmartDraw — это веб-инструмент для создания сетевых диаграмм, предназначенный для работы в любом месте со стабильным подключением к Интернету. Их цель — сделать их максимально простыми в использовании, что приводит к ограниченным возможностям настройки, но очень аккуратным, профессионально выглядящим сетевым схемам.Ограниченная настраиваемость инструмента, а также его тарифный план с оплатой по каждому пользователю делают его лучшим для небольших сетей. Вы можете подписаться на бесплатную онлайн-версию.

6. LanFlow

© 2021 Pacestar Software. Все права защищены.

LanFlow предлагает простые инструменты для построения сетевых диаграмм, но мощные возможности проектирования, включая библиотеки 2D и 3D значков. Некоторые другие полезные функции включают дополнительную сетку привязки, возможность полного увеличения и подписи фигур, которые автоматически перемещаются при редактировании.Вы также можете выбрать один из предустановленных шаблонов или полностью создать свой собственный и добавить гиперссылки и веб-сайты на свою сетевую диаграмму. LanFlow — это только инструмент для построения диаграмм — здесь нет функций автообнаружения или параметров программирования аварийных сигналов. Многие специалисты Cisco используют LanFlow для построения схем топологии сети, и вы можете загрузить 30-дневную бесплатную пробную версию.

7. Microsoft Visio

© Корпорация Майкрософт, 2020. Все права защищены.

Microsoft Visio — надежное средство создания сетевых диаграмм, предназначенное для простого взаимодействия с другим программным обеспечением и приложениями, помогая при этом обеспечивать безопасность ваших данных.Microsoft Visio предлагает частично настраиваемые шаблоны и темы, но не может включить автоматическое построение сетевых диаграмм. Доступна стандартная версия, а также более обширная и дорогая версия Pro, и вы можете попробовать ее бесплатно в течение 30 дней.

Подведение итогов сетевых диаграмм + Составление сетевых диаграмм

Сетевые диаграммы действуют как карта вашей сети, помогая вам визуализировать, как информация передается между устройствами вашей сети. Создание и использование сетевой диаграммы имеет решающее значение для поддержки вашей сети и помогает обеспечить безопасную доставку данных оттуда, где они должны быть.

Используя программное обеспечение для построения сетевых диаграмм, вы можете построить свои собственные сетевые диаграммы, наиболее подходящие для вас и членов вашей команды. Создатели автоматизированных схем сети, такие как SolarWinds Network Topology Mapper, предназначены для экономии вашего времени, энергии и ресурсов за счет автоматического обнаружения и сопоставления узлов и соединений вашей сети. NTM автоматически генерирует сетевые диаграммы, используя собранную информацию, предоставляя вам точную и ясную, но визуально яркую диаграмму топологии сети.

* По состоянию на март 2021 г.

Введение в логические блок-схемы

Введение в логические блок-схемы
При написании программы на любом языке следует много обдумывать и планировать следует продолжить собственное кодирование. Логические блок-схемы могут быть важной частью разработки логики программирования. Для простых программ, которые мы изучаем в начале этого курса логическая блок-схема очевидна. сомнительно, но для сложных программ это отличный инструмент.

При написании логической блок-схемы вы выкладываете сегмент блок-схемы для каждого абзац или модуль в программе. На блок-схеме, которая прилагается к SAMPLE1, есть сегмент блок-схемы для параграфа MAIN-PROGRAM. как и все остальные пункты программы. Я пометил абзацы с их именами COBOL, но часто имена являются практическими именами, которые передать цель модуля.

Условное обозначение Пояснение
Этот символ используется для обозначения обработки, которую необходимо выполнить: настройка линии, выполнение расчетов, открытие файлов, закрытие файлов и т. д.

Этот символ используется для обозначения того, что абзац должен быть выполнен, а затем управление вернется к следующей последовательной команде. Двойные линии указать выполнить.

Этот символ обозначает начало или конец модуля или абзаца.

Этот символ обозначает ввод / вывод, в частности, чтение записи. из файла, запись записи в файл или запись строки на печатный отчет.

Этот символ указывает на состояние — обычно ветвь вправо означает ДА а ветвь влево или вниз указывает.

Этот символ используется для перехода, когда достигнута нижняя часть страницы — он также используется как точка входа для перехода.

ГЛАВНАЯ ПРОГРАММА:


В проиллюстрированном здесь примере блок-схемы первый модуль ГЛАВНАЯ ПРОГРАММА, которая управляет программой. ОСНОВНАЯ ПРОГРАММА выполняет параграф, который обрабатывает инициализацию, параграф, который обрабатывает и абзац, который обрабатывает завершение до того, как наконец встретится перестань бежать.

A-100-ИНИЦИАЛИЗАЦИЯ:

Этот абзац или процедура просто открывает файлы. Когда при открытии файла завершено, управление возвращается в ГЛАВНУЮ ПРОГРАММУ.

B-100-ФАЙЛ-ПРОЦЕСС:

Этот абзац или процедура выполняет инициализацию READ, и если конец файла происходит изменение значения индикатора КОНЕЦ-ФАЙЛ с НЕТ на ДА. Это затем проверяет, не установлен ли индикатор КОНЕЦ ФАЙЛА на НЕТ, и если он не выполняет обработку параграфа (B-200-PROCESS-RECORD).Когда B-200-PROCESS-RECORD завершается, управление возвращается и КОНЕЦ-ФАЙЛ индикатор снова проверяется. Это повторяющийся цикл, который выполняется и снова до тех пор, пока, наконец, индикатор КОНЕЦ-ФАЙЛ не станет ДА, что означает этот конец файла достигнут. На этом абзац завершен и управление возвращается в ГЛАВНУЮ ПРОГРАММУ.

B-200-ЗАПИСЬ ПРОЦЕССА:

В этом абзаце или подпрограмме строка настраивается и записывается. Затем следующий запись в файле читается.Если обнаружен конец файла, КОНЕЦ ФАЙЛА индикатор изменится с исходного значения НЕТ на ДА. Когда параграф завершен, управление возвращается B-100-PROCESS-FILE.

C-100-ОБЗОР:

В этом абзаце или подпрограмме файлы закрываются, а затем управление возвращается в ГЛАВНУЮ ПРОГРАММУ.

ПОЛНАЯ СХЕМА:

Вся блок-схема проиллюстрирована ниже. Эта блок-схема применяется к начальная программа, обсуждаемая в классе — Sample1.

Инструмент логических диаграмм

Оставьте свои комментарии?

Пакет мощных инструментов для создания логических диаграмм

6 часов назад Программное обеспечение для логических элементов logic содержит все символы logic , необходимые для разработки любой модели logic . Независимо от того, нужен ли вам инструмент для обучения логической схеме или программное обеспечение для схем logic для инженерных целей, наш онлайн-конструктор логических схем просто отлично работает.Помимо инструмента логической схемы , мы собрали несколько шаблонов логической схемы , чтобы помочь

Веб-сайт: Online.visual-paradigm.com