Что такое генератор псевдослучайных чисел. Как работает генератор на основе регистра сдвига с обратной связью. Какие существуют виды генераторов ПСЧ на регистрах сдвига. Как выбрать параметры генератора для получения последовательности максимальной длины.
Принцип работы генератора псевдослучайных чисел на регистре сдвига
Генератор псевдослучайных чисел (ГПСЧ) на основе регистра сдвига с обратной связью является одним из наиболее распространенных и эффективных способов генерации псевдослучайных последовательностей. Рассмотрим основной принцип его работы.
Ключевые компоненты такого генератора:
- Регистр сдвига — последовательность триггеров, в которых хранятся биты
- Цепь обратной связи — комбинация выходов некоторых триггеров
- Сумматор по модулю 2 (XOR) — формирует новый бит на основе обратной связи
Принцип работы заключается в следующем:
- Регистр инициализируется начальным значением (seed)
- На каждом такте содержимое регистра сдвигается вправо на 1 бит
- Новый бит формируется схемой обратной связи и записывается слева
- Выходной бит снимается с крайнего правого разряда
Таким образом генерируется псевдослучайная последовательность битов. Ее период зависит от параметров регистра и обратной связи.

Виды генераторов ПСЧ на регистрах сдвига
Существует несколько основных разновидностей генераторов псевдослучайных чисел на регистрах сдвига:
1. Линейный конгруэнтный генератор (LFSR)
Это простейший вид ГПСЧ на регистре сдвига. Обратная связь формируется как XOR нескольких разрядов регистра. Период последовательности не превышает 2^n-1, где n — длина регистра.
2. Генератор Галуа
Вместо XOR использует более сложные нелинейные функции обратной связи. Позволяет получить более длинные и качественные последовательности.
3. Фильтрованный генератор
Применяет дополнительную функцию фильтрации к выходу LFSR для улучшения статистических свойств.
Выбор параметров для получения последовательности максимальной длины
Чтобы генератор формировал последовательность максимальной длины 2^n-1, необходимо правильно выбрать полином обратной связи. Такой полином должен быть примитивным.
Основные правила выбора:
- Степень полинома равна длине регистра n
- Полином должен быть неприводимым
- Период полинома должен равняться 2^n-1
Существуют таблицы примитивных полиномов для различных значений n. Например, для n=4 подходящий полином — x^4 + x + 1.
Применение генераторов ПСЧ на регистрах сдвига
Генераторы псевдослучайных чисел на основе регистров сдвига нашли широкое применение в различных областях:
- Криптография — для генерации ключей и шифрования
- Цифровая связь — формирование расширяющих последовательностей
- Тестирование цифровых схем
- Моделирование и статистика
- Компьютерные игры и графика
Их основные преимущества — простота реализации, высокое быстродействие и хорошие статистические свойства генерируемых последовательностей.
Анализ качества генераторов ПСЧ на регистрах сдвига
Для оценки качества генераторов псевдослучайных чисел на регистрах сдвига применяются различные статистические тесты. Основные критерии качества:
- Равномерность распределения битов
- Отсутствие корреляций между битами
- Большой период повторения
- Непредсказуемость следующего бита
Наиболее распространенные тесты включают:
- Частотный монобитный тест
- Тест на последовательность одинаковых битов
- Тест на самую длинную последовательность единиц
- Тест рангов бинарных матриц
- Спектральный тест
Хороший генератор должен успешно проходить большинство статистических тестов.

Реализация генератора ПСЧ на регистре сдвига
Рассмотрим пример реализации простого 4-битного генератора псевдослучайных чисел на регистре сдвига с обратной связью:
«`python class LFSR: def __init__(self, seed, taps): self.state = seed self.taps = taps def step(self): feedback = sum([self.state & (1 << tap) for tap in self.taps]) % 2 self.state = ((self.state << 1) & 0xf) | feedback return self.state & 1 # Инициализация генератора seed = 0b1000 # Начальное значение taps = [1, 3] # Отводы для x^4 + x + 1 lfsr = LFSR(seed, taps) # Генерация последовательности sequence = [lfsr.step() for _ in range(15)] print(sequence) ```Этот код реализует 4-битный LFSR генератор с полиномом x^4 + x + 1. Он генерирует последовательность максимальной длины 15 битов, после чего цикл повторяется.
Криптографическая стойкость генераторов на регистрах сдвига
Хотя генераторы псевдослучайных чисел на регистрах сдвига широко используются в криптографии, их криптографическая стойкость имеет ряд ограничений:
- Линейность — делает их уязвимыми к атакам на основе решения системы линейных уравнений
- Малая длина регистра — ограничивает размер ключевого пространства
- Предсказуемость — зная часть выхода, можно восстановить все состояние
Для повышения криптостойкости применяются следующие методы:
- Использование нелинейных функций обратной связи
- Комбинирование нескольких регистров сдвига
- Применение дополнительных операций перемешивания выхода
- Увеличение длины регистра
Однако даже с этими улучшениями, простые генераторы на регистрах сдвига не рекомендуется использовать в серьезных криптографических приложениях без дополнительных мер защиты.
Сравнение генераторов ПСЧ на регистрах сдвига с другими типами ГПСЧ
Генераторы псевдослучайных чисел на регистрах сдвига имеют свои преимущества и недостатки по сравнению с другими типами ГПСЧ. Рассмотрим основные отличия:
Преимущества ГПСЧ на регистрах сдвига:
- Простота реализации как в аппаратном, так и в программном виде
- Высокая скорость генерации последовательности
- Возможность получения очень длинных периодов
- Хорошие статистические свойства при правильном выборе параметров
Недостатки по сравнению с другими ГПСЧ:
- Меньшая криптостойкость, чем у современных криптографических ГПСЧ
- Более предсказуемое поведение, чем у генераторов на основе хаотических систем
- Меньшая гибкость настройки параметров, чем у программных генераторов
В целом, генераторы на регистрах сдвига остаются популярным выбором для многих приложений благодаря своей простоте и эффективности. Однако для критически важных задач, требующих высокой степени непредсказуемости, часто предпочитают более сложные типы ГПСЧ.
НОУ ИНТУИТ | Лекция | Поточные шифры и генераторы псевдослучайных чисел. Часть 2
< Лекция 8 || Лекция 9: 1234 || Лекция 10 >
Аннотация: Продолжаем знакомиться с генераторами псевдослучайных чисел, используемых для поточного шифрования информации. В частности, мы рассмотрим алгоритмы генерации псевдослучайных чисел на основе сдвиговых регистров с обратной связью и RC4. Кроме того, в этой лекции мы изучим, каким образом можно использовать режимы OFB и CTR блочных шифров для получения псевдослучайных чисел.
Ключевые слова: генератор псевдослучайных чисел, шифратор, бит, сдвиговый регистр, регистр сдвига, длина, поточный шифр, linear, feedback, shift register, LFSR, обратная связь, регистр, значение, место, операции, алгоритм, GSM, битовые операции, AES, output, блок данных, байт, OFB, шифр, параметр, поток, счетчик, CTR, выход, генератор, RC4, SSL, Windows, класс, алгоритм Прима, слово, массив, таблица, перестановка, инициализация, ключ, секретный ключ, последовательный алгоритм, потоковое шифрование, random number generator, RNG, системный таймер, получатель сообщения, надежность шифра, вероятность, безопасность, канал связи, надежность, сети передачи данных, злоумышленник, криптоанализ, distribution, center, KDC, протокол обмена ключами, центр распределения ключей, доступ, сеть, симметричное шифрование
intuit.ru/2010/edi»>Цель лекции: продолжить знакомство с генераторами псевдослучайных чисел, используемых для поточного шифрования информации, а также с некоторыми режимами блочных шифров для получения псевдослучайных чисел.Генераторы псевдослучайных чисел на основе сдвиговых регистров с обратной связью
В теории кодирования и криптографии широко применяются так называемые сдвиговые регистры с обратной связью. Они использовались в аппаратуре шифрования еще до начала массового использования ЭВМ и современных высокоскоростных программных шифраторов.
Сдвиговые регистры с обратной связью могут применяться для получения потока псевдослучайных бит. Сдвиговый регистр с обратной связью состоит из двух частей: собственно n-битного сдвигового регистра и устройства обратной связи ( рис. 8.1).
Рис.
8.
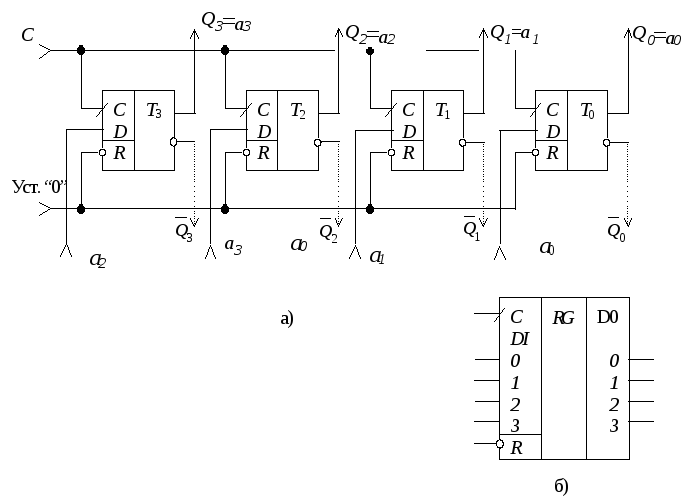
Извлекать биты из сдвигового регистра можно только по одному. Если необходимо извлечь следующий бит, все биты регистра сдвигаются вправо на 1 разряд. При этом на вход регистра слева поступает новый бит, который формируется устройством обратной связи и зависит от всех остальных битов сдвигового регистра. За счет этого биты регистра изменяются по определенному закону, который и определяет схему получения ПСЧ. Понятно, что через некоторое количество тактов работы регистра последовательность битов начнет повторяться. Длина получаемой последовательности до начала ее повторения называется периодом сдвигового регистра.
Поточные шифры с использованием сдвиговых регистров достаточно долго использовались на практике. Это связано с тем, что они очень хорошо реализуются с помощью цифровой аппаратуры.
ru/2010/edi»>Простейшим видом сдвигового регистра с обратной связью является линейный сдвиговый регистр с обратной связью (linear feedback shift register – LFSR). Обратная связь в этом устройстве реализуется просто как сумма по модулю 2 всех (или некоторых) битов регистра. Биты, которые участвуют в обратной связи, образуют отводную последовательность. Линейные сдвиговые регистры с обратной связью или их модификации часто применяется в криптографии.
Для того, чтобы стало понятнее, как работает сдвиговый регистр с обратной связью, рассмотрим 4-битовый LFSR с отводом от первого и четвертого разрядов, представленный на рис. 8.2.
Рис. 8.2.
Запишем в изображенный на рисунке регистр начальное значение 1011.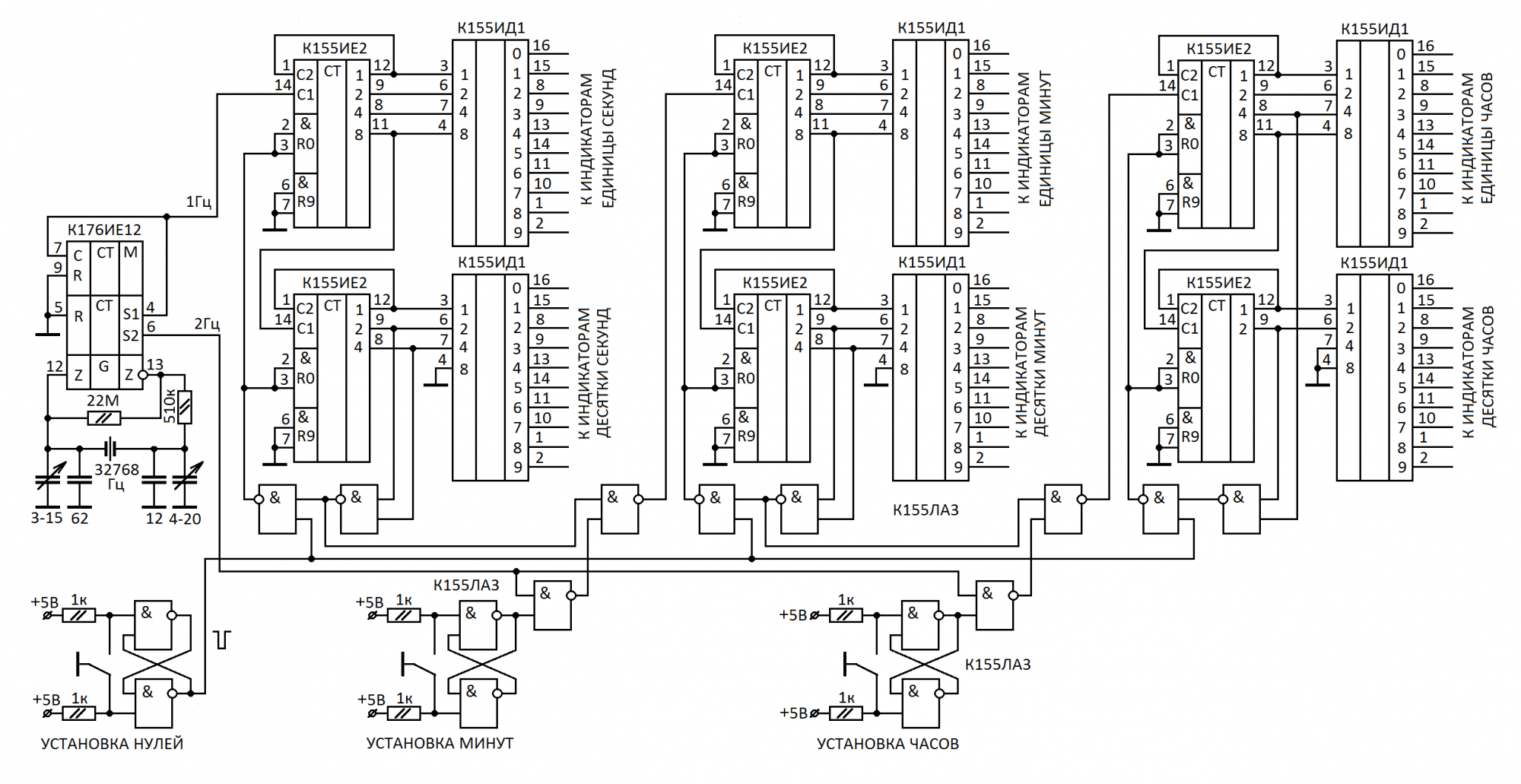 Вычислять последовательность
внутренних состояний регистра удобно с помощью таблицы, представленной на
таблица
8.1. В таблице отражены первые девять состояний регистра.
Вычислять последовательность
внутренних состояний регистра удобно с помощью таблицы, представленной на
таблица
8.1. В таблице отражены первые девять состояний регистра.
На каждом шаге все содержимое регистра сдвигается вправо на один разряд. При этом можно получить в качестве результата один бит. На освободившееся слева место поступает бит, равный результату вычисления функции обратной связи . Выходную последовательность генератора псевдослучайных бит образует последний столбец таблицы (извлекаемый бит).
| Номер состояния | Внутреннее состояние регистра b4, b3, b2, b1 | Результат вычисления функции обратной связи | Извлекаемый бит ( b1 ) |
|---|---|---|---|
| 0 | 1 0 1 1 | 0 | 1 |
| 1 | 0 1 0 1 | 1 | 1 |
| 2 | 1 0 1 0 | 1 | 0 |
| 1 1 0 1 | 0 | 1 | |
| 4 | 0 1 1 0 | 0 | 0 |
| 5 | 0 0 1 1 | 1 | 1 |
| 6 | 1 0 0 1 | 0 | 1 |
| 7 | 0 1 0 0 | 0 | 0 |
| 8 | 0 0 1 0 | 0 | 0 |
intuit.ru/2010/edi»>Линейный сдвиговый регистр размером n бит может находиться в одном из 2n-1 состояний (исключается состояние регистра из одних нулей — при появлении такого состояния далее будут порождаться лишь нули, и о псевдослучаности порождаемой последовательности говорить не приходится). Поэтому теоретически такой регистр может генерировать псевдослучайную последовательность с максимальным периодом 2n-1. Линейный сдвиговый регистр с обратной связью будет генерировать циклическую последовательность битов с максимальным периодом только при выборе в качестве отводной последовательности определенных бит. Разработана математическая теория, позволяющая выбрать подходящие номера разрядов для бит отводной последовательности.
 Такие электронные схемы предлагались и выпускались еще до второй мировой войны. Аналогичные принципы заложены и в некоторые поточные шифры, созданные в конце XX века, например, в алгоритм А5, использовавшийся в Европе для шифрования сотовых цифровых каналов связи стандарта GSM. Несмотря на то, что некоторые криптоаналитики высказывают сомнения в надежности алгоритмов поточного шифрования с использованием линейных сдвиговых регистров с обратной связью, они положены в основу функционирования различных военных и гражданских устройств связи, используемых до настоящего времени.
Такие электронные схемы предлагались и выпускались еще до второй мировой войны. Аналогичные принципы заложены и в некоторые поточные шифры, созданные в конце XX века, например, в алгоритм А5, использовавшийся в Европе для шифрования сотовых цифровых каналов связи стандарта GSM. Несмотря на то, что некоторые криптоаналитики высказывают сомнения в надежности алгоритмов поточного шифрования с использованием линейных сдвиговых регистров с обратной связью, они положены в основу функционирования различных военных и гражданских устройств связи, используемых до настоящего времени. Основным недостатком генераторов псевдослучайных чисел на базе линейных сдвиговых регистров является сложность программной реализации. Сдвиги и битовые операции легко и быстро выполняются в электронной аппаратуре, поэтому в разных странах выпускаются микросхемы и устройства для поточного шифрования на базе алгоритмов с использованием сдвиговых регистров с обратной связью.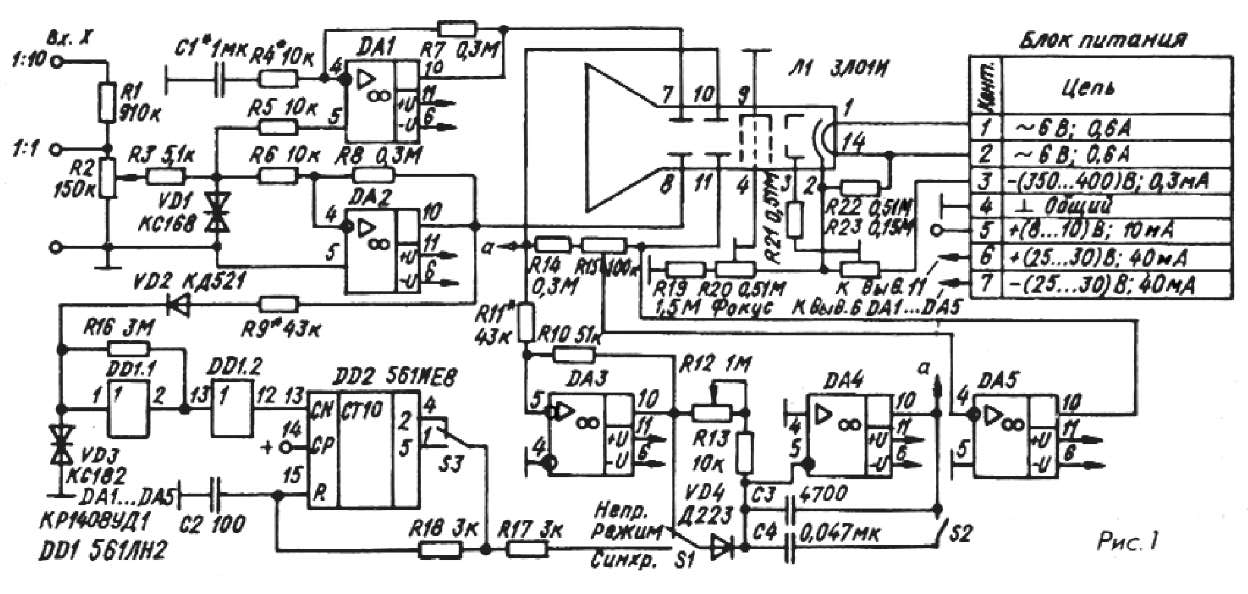
Использование режимов OFB и CTR блочных шифров для получения псевдослучайных чисел
Можно использовать любой блочный алгоритм, например AES или ГОСТ 28147-89, для поточного шифрования информации, используя режимы OFB и CTR блочных шифров.
Название режима OFB (Output FeedBack) переводится как «обратная связь по выходу».
Пусть минимальный блок данных, используемый для передачи, состоит из j бит; обычным значением является j=8 (то есть минимальной порцией передаваемых данных является 1 байт). В режиме OFB блочный шифр f на основе секретного ключа К и некоторого инициализирующего значения Y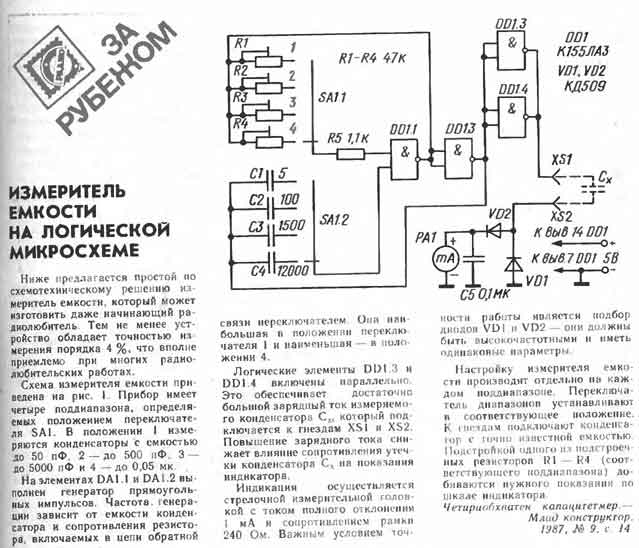 На каждом этапе шифрования из зашифрованного блока Yi выбирается j младших битов.
На каждом этапе шифрования из зашифрованного блока Yi выбирается j младших битов.
Таким образом, для получения псевдослучайной последовательности используется схема:
Yi=f(Yi-1,K), zi=j младших бит Yi, 1<=i<=k
Если размер блока шифра равен N бит, то параметр j может принимать значения от 1 до N. Значение Y0 называют также инициализирующим вектором.
Последовательность чисел zi можно использовать в качестве гаммы для шифрования потока исходных данных, состоящего из символов хi:
в результате чего получится поток зашифрованных символов yi.
Так как значения yi не зависят от открытого текста xi, то каждый раз, используя одни и те же параметры К и Y0, мы получим одну и ту же последовательность гаммы zi.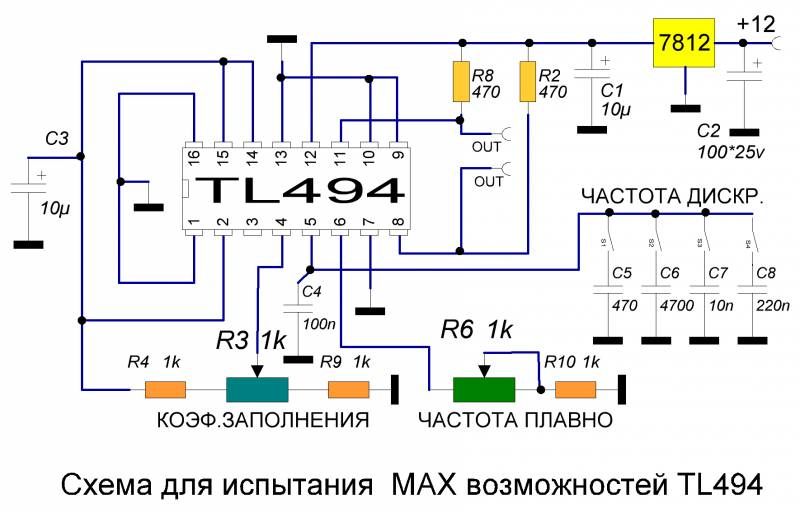 Поэтому рекомендуется менять значение ключа К для передачи каждого нового сообщения.
Поэтому рекомендуется менять значение ключа К для передачи каждого нового сообщения.
Расшифрование сообщений для описанного режима может производиться только с начала последовательности, так как невозможно получить произвольный элемент последовательности zi, не вычислив все предыдущие.
Основное достоинство режима OFB заключается в том, что последовательность z может быть сформирована заранее для того, чтобы быстро шифровать или расшифровывать поточные сообщения в момент их поступления. Это может быть актуально для систем, обрабатывающих данные в реальном масштабе времени.
Еще одно важное достоинство режима OFB состоит в том, что если при передаче данных произошла ошибка, то она не распространяется на следующие зашифрованные блоки, и тем самым сохраняется возможность расшифрования последующих блоков. Например, если в результате передачи по зашумленному каналу связи появился ошибочный бит в блоке yi, то это приведет к невозможности расшифрования только этого блока и получения одного блока исходных данных xi. Дальнейшая последовательность блоков будет расшифрована корректно.
Дальнейшая последовательность блоков будет расшифрована корректно.
Название режима CTR происходит от слова «CounTeR» — «счетчик». Этот режим является модификацией режима OFB. Единственное отличие от OFB заключается в том, что в режиме CTR шифруется не предыдущий выход шифра, а счетчик, увеличиваемый на каждом шаге на 1. Первоначальное значение счетчика определяется некоторым инициализирующим значением Y0. Общая формула выглядит следующим образом:
Yi=f(Yi-1+1,K), zi=j старших бит Yi
Преимущество режима CTR состоит в том, что любой элемент последовательности z может быть вычислен непосредственно. Этот факт связан с тем, что на каждом шаге Yi увеличивается на единицу, и, следовательно, если нам известен номер шага i, то значение Yi можно вычислить непосредственно, зная Y0 и i по формуле:
Yi=f(Y0+i,K),
intuit.ru/2010/edi»>Это дает возможность шифровать и дешифровать любые фрагменты сообщения независимо друг от друга.
Дальше >>
< Лекция 8 || Лекция 9: 1234 || Лекция 10 >
|
EWB
Цель работы: исследовать генератор псевдослучайной последовательности.
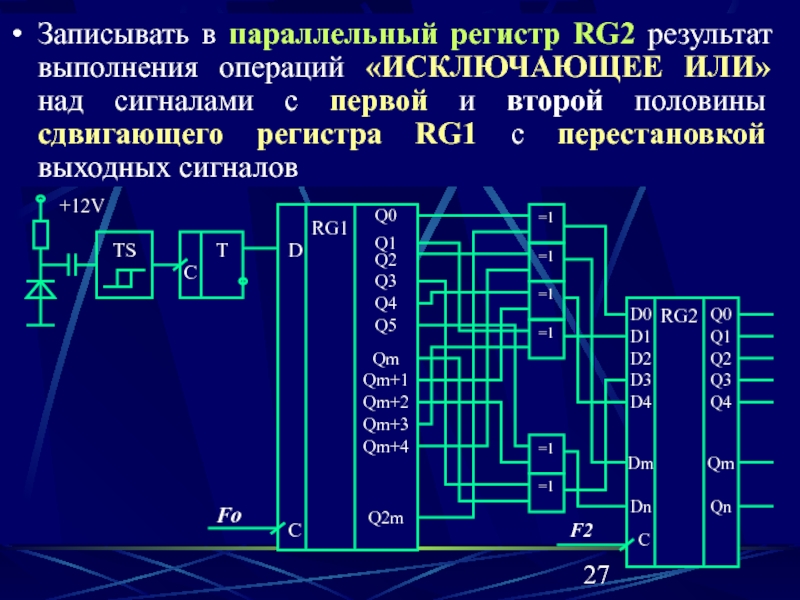
Теория Регистры сдвига (сдвигающие регистры) являются одними из основных узлов аппаратуры передачи дискретных сообщений. Любой сдвигающий регистр, состоящий из n триггеров, есть запоминающее устройство, способное принимать 2n различных состояний. Если в регистр сдвига ввести обратные связи, каждая из
которых формируется логической схемой, называемой схемой сложения по модулю два
(или «ИСКЛЮЧАЮЩЕЕ ИЛИ»), то с помощью такого устройства можно построить
генератор псевдослучайной последовательности или устройство деления одного
многочлена на другой (кодирующие и декодирующие устройства). Рассмотрим построение генератора псевдослучайной последовательности. Случайной последовательностью называется последовательность из 1 и 0, в которой каждый элемент появляется в последовательности независимо от предыдущих символов. Случайные последовательности должны удовлетворять тестам на случайность: 1) уравновешенности, когда число 1 и 0 в последовательности равно; 2) корреляции, когда при почленном сравнении случайной последовательности с любым ее циклическим сдвигом число совпадающих символов равно числу несовпадающих символов; 3) вероятность появления каждого набора из m элементов для m<n (где n – длина последовательности) равна 2—m. Случайная последовательность не имеет ни начала, ни конца.
Получить ее можно, подбрасывая монетку и рассматривая, какая сторона монетки
выпадет. Если выпал “орел”, то записывается единица, если “решка”, то
записывается ноль. Получить ПСП можно с помощью регистра сдвига с логическими
обратными связями. На простейшей схеме такого регистра на один вход сумматора
по модулю два подается сигнал с k-го разряда регистра, а на второй вход – сигнал с n-го разряда. Если в
первый разряд регистра записать единицу, а в остальные нули, то под
воздействием тактовых импульсов эта единица будет продвигаться по регистру.
Когда k-й разряд
примет состояние единицы, то на выходе сумматора появится единица, которая
поступит на вход первого разряда и запишется в него. С этого момента в регистре
сдвига будут продвигаться две единицы. Всякий раз, когда на входы сумматора по
модулю два будут подаваться различные символы, в первый разряд регистра сдвига
будет записана единица.
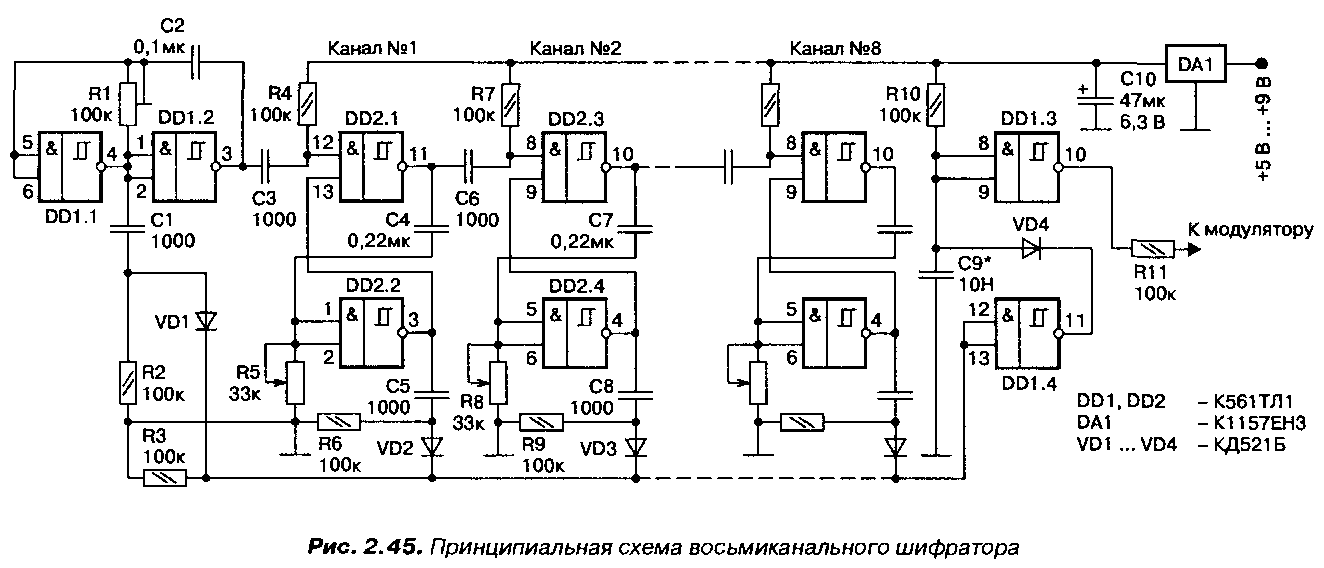
Рис. Генератор псевдослучайной последовательности
Таким образом, под воздействием каждого тактового импульса разряды регистра сдвига принимают определенные состояния, причем последовательность этих состояний зависит от способа включения обратной связи. Общее число таких различных состояний равно 2n-1, следовательно, период ПСП равен 2n-1. ПСП можно снимать с выхода любого разряда регистра, в частности с последнего. Любая выходная последовательность, имеющая такой период, называется линейной последовательностью максимальной длины. Регистр с логической обратной связью описывается характеристическим многочленом вида F(x)= xn+ An-1xn-1 +…+ A2x2 + A1x+1.
Степень многочлена равна числу разрядов регистра, а
коэффициенты Ai равны единице, если выход
данного разряда подается на вход сумматора по модулю два. В зависимости от количества и места подключения элементов обратной связи можно получить последовательность максимальной или меньшей длины. Для того чтобы последовательность имела максимальную длину, характеристический многочлен должен быть неприводимым, т.е. не разлагаться на произведение многочленов степеней, меньших n (или делиться только на единицу и на самого себя). Таким образом, чтобы построить генератор ПСП, нужно знать неприводимый многочлен степени n. Если для данного n известен неприводимый многочлен, то число элементов обратной связи (сумматоров по модулю два) равно числу ненулевых слагаемых многочлена минус два; а номера разрядов регистра, выходы которых подаются на входы сумматоров по модулю два, определяются из сопряженных многочленов. Сопряженные многочлены вычисляют следующим образом: · в характеристическом многочлене производят замену переменных x=y—1:
1/yn+An-1/yn-1+…+A2/y2+A1/y+1; · вновь полученный многочлен умножают на yn:
(yn
/yn)yn + An-1(yn /yn-1) +…+ A2(yn
/y2) + A1(yn /y) + yn= Показатели степени переменной y сопряженного многочлена, у которых коэффициенты Ai не равны нулю, соответствуют номерам разрядов регистра, выходы которых подаются на сумматор по модулю два. Для некоторых n неприводимые многочлены вычислены и сведены в таблицы. Некоторые из этих многочленов приведены далее.
Таблица. Многочлены
Рассмотрим построение генератора ПСП при n=4. Заменим переменную и найдем сопряженный многочлен: 1/y4+1/y+1, y4(1/y4+1/y+1)=1+y3+y4. Следовательно, регистр сдвига имеет четыре разряда. Число сумматоров по модулю два, включаемых в обратную связь, равно 3-2=1. Номера разрядов, выходы которых подаются на входы сумматора по модулю два, равны 3 и 4. Схема генератора ПСП приведена на рис. 44.
Рис. Генератор ПСП для n=4
Если записать в первый разряд единицу, то под воздействием тактовых импульсов содержимое регистра будет меняться. Т а б л и ц а 11
Начиная с 16-го такта последовательность состояний регистра
повторяется. В данном случае эта последовательность получена с выхода четвертого разряда регистра сдвига.
Последовательность выполнение работы Исследование генератора ПСП для n=4 1. Нарисовать схему генератора ПСП для n=4. Поместить на схему функциональный генератор (Function Generator) и осциллограф (Oscilloscope). На этой схеме логический элемент «4И-НЕ» введен для автоматической записи единицы в первый разряд регистра, если в момент включения питания все триггеры регистра сдвига установятся в состояние ноль. 2. Открыть
окно функционального генератора и установить частоту (1 кГц) и вид
генерируемого сигнала (прямоугольные импульсы).
Рис. Схема четырехразрядного генератора ПСП
3. Запустить процесс моделирования, нажав кнопку на панели инструментов, и в появившемся меню выбрать команду Run. 4. Щелкнуть по иконке осциллографа, чтобы открыть окно осциллографа, и зарисовать осциллограмму.
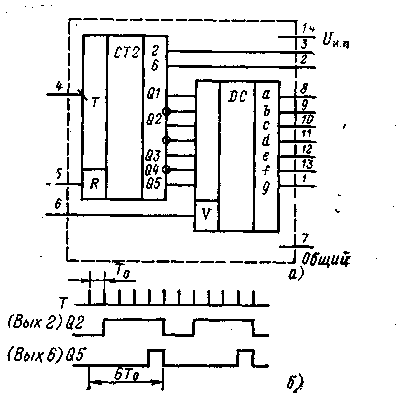
Описание осциллографа (Oscilloscope) Работа осциллографа основывается на применении
электронно-лучевой трубки (ЭЛТ), содержащей катод, излучающий поток (луч)
электронов за счет термоэмиссии, модулятор для управления интенсивностью этого
потока, систему его фокусировки, отклоняющую систему в виде двух пар пластин, и
экран из кристалликов люминофора, которые под действием падающего на них потока
электронов высвечивают траекторию движения электронного луча в пространстве,
определяемую потенциалами на пластинах отклоняющей системы. На пластины Y-канала подается исследуемый сигнал после его усиления и масштабирования вертикальным Y-усилителем. Для одновременного наблюдения n сигналов используют n усилителей, выходные сигналы которых с помощью аналоговых коммутаторов поочередно подаются на вход усилителя мощности Y-канала. На пластины X-канала подается пилообразный сигнал развертки, длительность (период) которого с помощью системы синхронизации поддерживается равным или кратным периоду исследуемого сигнала в одном из Y-каналов, что позволяет получить устойчивое, а не хаотично «бегающее» изображение контролируемого сигнала. Осциллограф имеет два канала (Channel) A и B с раздельной установкой чувствительности в диапазоне от 10
мкВ/дел (µV/Div) до 5 кВ/дел (kV/Div) и регулировкой смещения по вертикали
(Y POS).
Рис. Лицевая панель осциллографа
На панелях Channel A и Channel B с помощью кнопок выбирается режим по входу. Режим АС предназначен для наблюдения только сигналов переменного тока. В режиме «0» входной зажим замыкается на землю. В режиме DC (включен по умолчанию) можно наблюдать сигналы как постоянного, так и переменного тока. С правой стороны от кнопки DC расположен входной зажим канала. На этих панелях в окне Scale устанавливается величина развертки, а в окне Y position – величина смещения относительно оси Х. На панели Timebase с помощью кнопок
Y/T, Add, B/A, A/B выбирается режим развертки. В режиме
Y/T (обычный режим, включен по
умолчанию) устанавливается следующий режим развертки: по вертикали – напряжение
сигнала, по горизонтали – время; в режиме Add – сигналы обоих
каналов накладываются друг на друга; в режиме B/A: по вертикали – сигнал канала В, по горизонтали – сигнал канала А; в режиме А/В: по
вертикали – сигнал канала А, по
горизонтали – сигнал канала В. В режиме Y/T длительность развертки (Timebase) может быть задана в диапазоне от 0,1 нс/дел (ns/div) до 1 с/дел (s/div) с возможностью установки смещения в тех же единицах по горизонтали, т.е. по оси Х (X POS). В режиме Y/T можно установить ждущий режим в поле Trigger. В строке Edge – режим запуска по переднему (кнопка ) или по заднему (кнопка ) фронту запускающего сигнала. В окне Lever (уровень) устанавливается уровень запускающего сигнала. В этом поле с помощью кнопок Auto, А, В или Ext ждущий режим запускается от каналов А или В, от канала А, от канала В или от внешнего источника, подключаемого к находящемуся на этой панели зажиму, соответственно. С помощью кнопки Revere можно инвертировать изображение, кнопки Save можно записать данные в файл. С помощью визирных линеек (синего и красного цвета) можно
просканировать изображение. Исследование генератора ПСП для n=5 и g(x)=x5+x3+1 1. Нарисовать схему генератора ПСП для n=5 и g (x) = x5 + x3 + 1. 2. Запустить процесс моделирования, нажав кнопку на панели инструментов, и в появившемся меню выбрать команду Run. 3. Щелкнуть по иконке осциллографа, чтобы открыть окно осциллографа, и зарисовать осциллограмму. Исследование генератора ПСП для n=5 и g(x)=x5+x4+1 1. Нарисовать
схему генератора ПСП для n=5
и g (x) = x5 +
x4 + 1.
. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

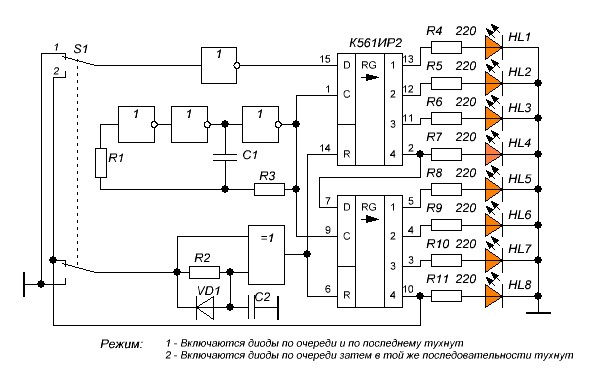
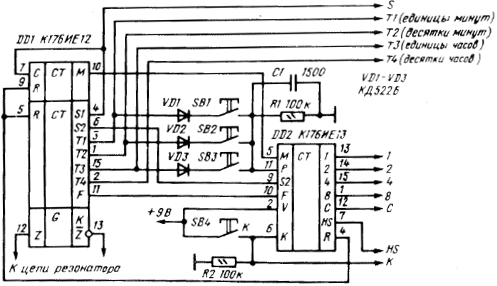 На практике такие последовательности получить нельзя. Поэтому
используют ограниченные (конечные) последовательности, которые обладали бы
некоторыми свойствами случайных последовательностей. Такие последовательности
называются псевдослучайными последовательностями (ПСП).
На практике такие последовательности получить нельзя. Поэтому
используют ограниченные (конечные) последовательности, которые обладали бы
некоторыми свойствами случайных последовательностей. Такие последовательности
называются псевдослучайными последовательностями (ПСП).

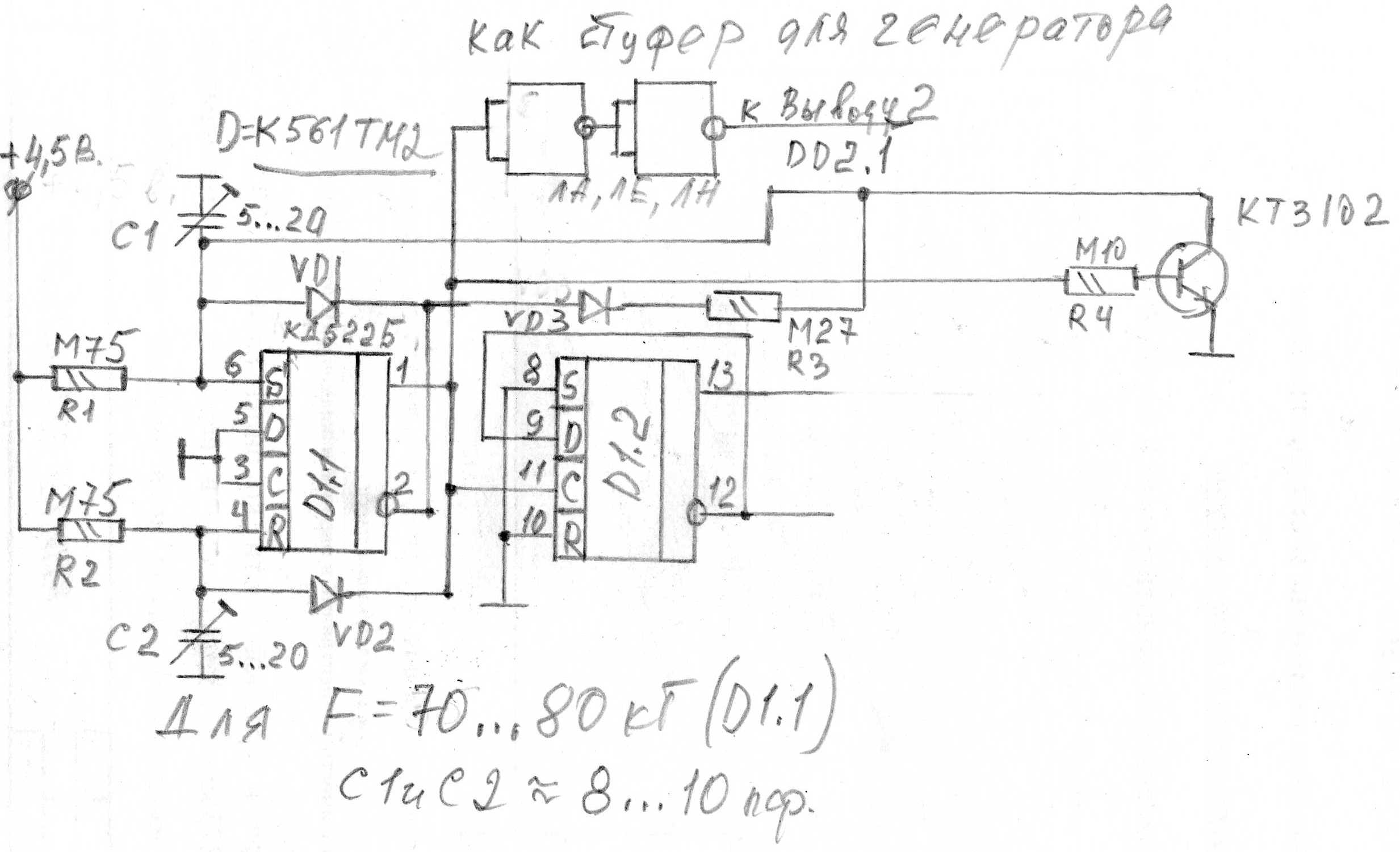
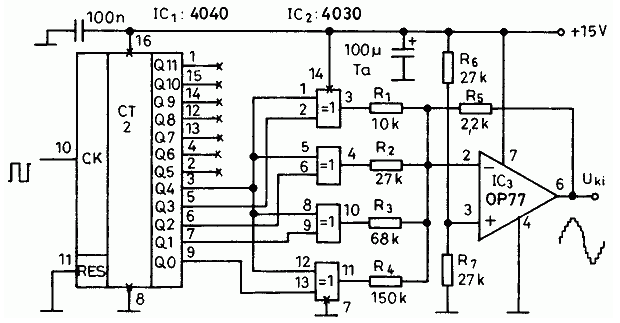 В таблице найдем
характеристический многочлен степени 4 – g(x)=x4+x+1.
В таблице найдем
характеристический многочлен степени 4 – g(x)=x4+x+1.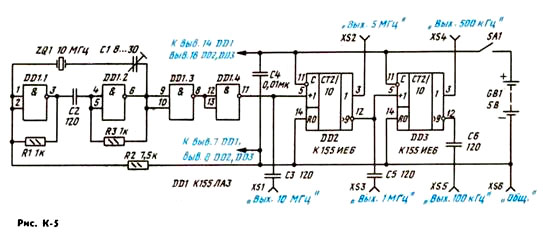 ПСП можно снимать с выхода любого разряда регистра, а также с
выхода схемы сложения по модулю два. Псевдослучайная последовательность,
генерируемая данным устройством, имеет вид 000100110101111.
ПСП можно снимать с выхода любого разряда регистра, а также с
выхода схемы сложения по модулю два. Псевдослучайная последовательность,
генерируемая данным устройством, имеет вид 000100110101111.
 Горизонтальные
пластины этой системы называются Y-каналом, вертикальные –
Горизонтальные
пластины этой системы называются Y-каналом, вертикальные –


 Результаты измерения напряжения, временных
интервалов и их приращений (между визирными линейками) отображаются в
индикаторных окошках, расположенных под экраном.
Результаты измерения напряжения, временных
интервалов и их приращений (между визирными линейками) отображаются в
индикаторных окошках, расположенных под экраном.