Что такое разновидности объектов в информатике. Как классифицируют объекты. Чем отличается естественная и искусственная классификация. Как создать схему разновидностей объектов.
Что такое разновидности объектов в информатике
Разновидности объектов в информатике — это подмножества объектов, обладающие дополнительными признаками по сравнению с родительским множеством. Например:
- Попугаи являются разновидностью птиц
- Натуральные числа — разновидность целых чисел
- Учебник — разновидность книги
Отношение между множеством и его разновидностью называется «является разновидностью». Оно отражает иерархическую связь между объектами.
Схема разновидностей объектов: как ее создать
Схема разновидностей — это графическое представление отношений «является разновидностью» между объектами. Основные правила создания такой схемы:
- Имя подмножества располагается ниже имени включающего множества
- Объекты связываются линиями, показывающими иерархию
- У объектов подмножества указываются дополнительные признаки
Схемы разновидностей широко используются в учебниках, справочниках, каталогах для наглядного представления классификации объектов.
Зачем нужна классификация объектов
Классификация объектов в информатике выполняет несколько важных функций:
- Упрощает работу с большими множествами объектов
- Позволяет выделить существенные признаки объектов
- Облегчает поиск и систематизацию информации
- Помогает выявить сходства и различия между объектами
- Способствует более глубокому пониманию предметной области
Человек способен одновременно концентрировать внимание лишь на 5-9 объектах. Классификация позволяет работать с большими множествами, разделяя их на группы.
Основные понятия классификации объектов
При классификации объектов используются следующие ключевые термины:
- Класс — подмножество объектов, имеющих общие признаки
- Основание классификации — признаки, по которым объекты разделяются на классы
- Естественная классификация — основана на существенных признаках объектов
- Искусственная классификация — основана на несущественных признаках
Правильный выбор оснований классификации очень важен для создания эффективной системы классов.
Естественная и искусственная классификация: в чем разница
Основные отличия естественной и искусственной классификации:
| Естественная | Искусственная |
|---|---|
| Основана на существенных признаках | Основана на несущественных признаках |
| Отражает закономерности предметной области | Создается для удобства использования |
| Пример: биологическая классификация живых организмов | Пример: алфавитный каталог в библиотеке |
Естественная классификация позволяет делать выводы о свойствах объектов на основе их положения в системе классов. Искусственная удобна для поиска и систематизации.
Примеры классификации объектов в информатике
В информатике широко применяется классификация различных объектов. Некоторые примеры:
- Классификация программного обеспечения (системное, прикладное, инструментальное)
- Классификация компьютерных вирусов (файловые, загрузочные, макро-вирусы и др.)
- Классификация языков программирования (по уровням, парадигмам и т.д.)
- Классификация компьютерных сетей (по масштабу, топологии и др.)
Такие классификации помогают структурировать знания в области информационных технологий.
Как создать эффективную классификацию объектов
При создании классификации объектов рекомендуется придерживаться следующих принципов:
- Выбирать существенные признаки в качестве основания
- Классы должны взаимно исключать друг друга
- Деление на классы должно быть соразмерным
- Классификация должна быть целенаправленной
- Необходимо учитывать особенности предметной области
Правильно составленная классификация позволяет эффективно систематизировать информацию об объектах.
Классификация объектов в файловой системе компьютера
Файловая система компьютера представляет собой пример классификации объектов. Основные классы объектов:
- Файлы — содержат данные
- Папки (каталоги) — содержат файлы и другие папки
- Ярлыки — ссылки на другие объекты
Файлы далее классифицируются по типам: текстовые, графические, исполняемые и т.д. Такая иерархическая структура упрощает хранение и поиск информации на компьютере.
§ 4. Разновидности объектов и их классификация
Информатика. 6 класса. Босова Л.Л. Оглавление
Отношение «является разновидностью»
Ключевые слова:
- отношение «является разновидностью»
- схема разновидностей
- классификация
Из двух множеств, связанных отношением «является разновидностью», одно является подмножеством другого. Например, множество попугаев является подмножеством множества птиц, множество натуральных чисел является подмножеством множества целых чисел.
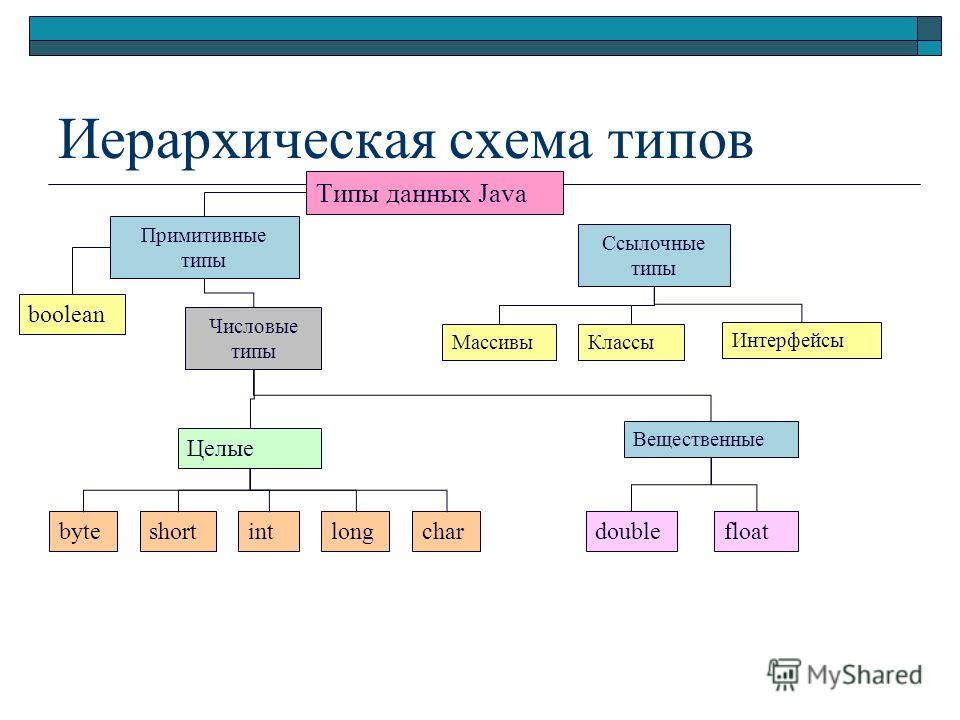
Схему отношения «является разновидностью» будем называть схемой разновидностей (рис. 12, а). Такие схемы используются в учебниках, каталогах и энциклопедиях для описания самых разных объектов, например, растений, животных, сложных предложений, транспортных средств и т. д.
На схеме разновидностей имя подмножества всегда располагается ниже имени включающего его множества.
Что изображено на рисунке 12, б?
Объекты подмножества обязательно обладают всеми признаками объектов множества (наследуют признаки множества) и кроме них имеют ещё свой, дополнительный признак (или несколько признаков).
Этим дополнительным признаком может быть свойство или действие. Например, любое домашнее животное нужно кормить, собаки, кроме того, лают и кусаются, а ездовые собаки, кроме того, ещё и бегают в упряжке.
Важно понимать, что сами по себе объекты не делятся ни на какие множества и подмножества. Например, арбузу совершенно «безразлично», относят его к семейству тыквенных растений, к подмножеству полосатых или шарообразных объектов. Подмножества объектов выделяет и обозначает человек, потому что ему так удобнее усваивать и передавать информацию. Дело в том, что человек одновременно может концентрировать свое внимание лишь на 5—9 объектах. Для упрощения работы с множеством объектов его делят на несколько частей; каждую из этих частей опять делят на части; те, в свою очередь, ещё раз и т. д. Деление большого множества на подмножества происходит не стихийно, а по некоторым признакам его объектов.
Классификация объектов
Подмножество объектов, имеющих общие признаки, называется классом.
Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются основанием классификации.
Классификация называется естественной, если в качестве её основания взяты существенные признаки объектов.
Место, занимаемое объектом в естественной классификации, позволяет судить о его признаках.
Примером естественной классификации является классификация живых существ, предложенная Карлом Линнеем (1735 г.). В настоящее время учёные разделяют множество всех живых существ на пять основных царств: растения, грибы, животные, простейшие и прокариоты. Каждое царство разделено на уровни — систематические единицы. Высший уровень называется типом. Каждый тип делится на классы, классы — на отряды, отряды — на семейства, семейства — на роды, а роды — на виды.
Ни один школьный предмет не обходится без классификаций. Так, на уроках русского языка вы пользуетесь естественной классификадией частей речи.
Графически её можно представить так (рис. 13).
Информацию о классификации систем счисления вы можете найти в электронном приложении к учебнику.
Классификация называется искусственной, если в качестве её основания взяты несущественные признаки объектов.
Пример искусственной классификации — деление множества звёзд на небе на созвездия, проводившееся по признакам, которые к самим звёздам не имели никакого отношения.
К искусственным классификациям относятся вспомогательные классификации (список фамилий, расположенных по алфавиту; алфавитно-предметные указатели, именные каталоги в библиотеках). Вспомогательная классификация не позволяет судить о признаках объектов; она служит для более лёгкого поиска объектов.
Классификация компьютерных объектовМожно предложить следующую классификацию объектов, с которыми взаимодействует пользователь при работе на компьютере (рис. 14).
Самое главное
Отношение «является разновидностью» может существовать между подмножеством некоторого множества и самим множеством.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются основанием классификации.
Классификация может производиться по существенным признакам (естественная) или по несущественным признакам (искусственная).
Вопросы и задания
1. Для каждого из указанных подмножеств назовите множество, с которым оно связано отношением «является разновидностью» (назовите общее имя, отвечающее на вопрос «Что это такое?»)
2. Среди множеств «книга», «бензин», «врач», «молоко», «строитель», «учебник», «жидкость», «справочник», «человек», найдите шесть пар, между которыми существует отношение «является разновидностью».
3. В каждом пункте перечислены объекты, сгруппированные по классам. Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам.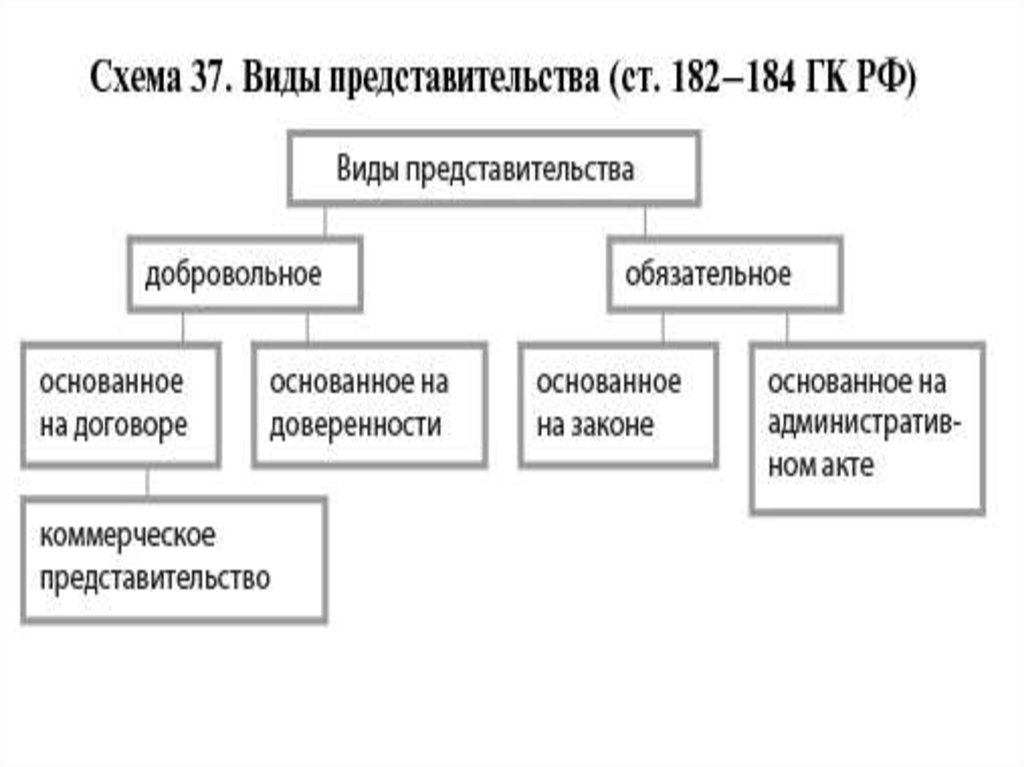
Определите основания классификаций
4. Как вы считаете, для чего нужна классификация?
5. Чем различаются естественная и искусственная классификации?
6. Приведите примеры классификаций, с которыми вы познакомились на уроках русского языка, математики, биологии и географии.
7. Предложите свою классификацию компьютерных объектов «файл» и «документ».
Компьютерный практикум
Работа 4 «Повторяем возможности текстового процессора — инструмента создания текстовых объектов»
Оглавление§ 3. Отношения объектов и их множеств§ 4. Разновидности объектов и их классификация§ 5. Системы объектов
Отношения объектов
Материалы к урокам 7 класса
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 7 классы | Планирование уроков на учебный год |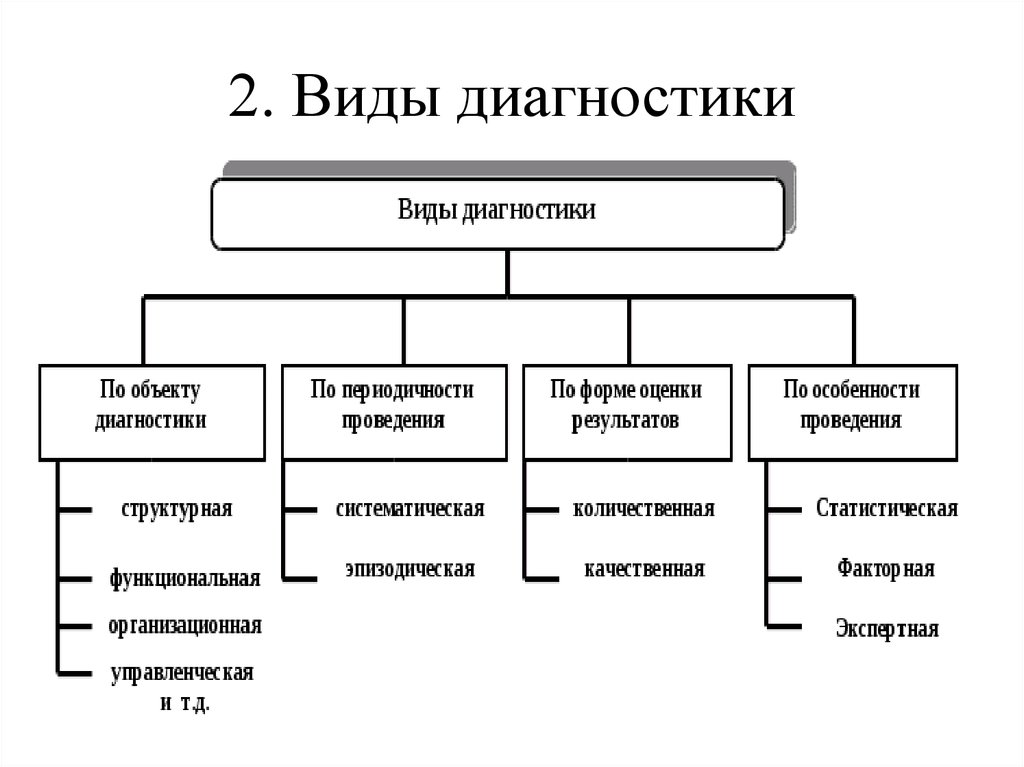
Разновидности объектов и их классификацияПрактическая работа №2
«Работаем с объектами файловой системы»
Отношения объектов
Человек может рассказать не только о свойствах объекта, но и об отношениях, в которых этот объект находится с другими объектами.
Например:
• «Иван — сын Андрея»;
• «Эверест выше Эльбруса»;
• «Винни Пух дружит с Пятачком»;
• «21 кратно 3»;
• «Кострома такой же старинный город, как и Москва»;
• «Текстовый процессор входит в состав программного обеспечения компьютера».
В каждом из приведенных предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.
Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов, например:
• «Камчатка — это полуостров (является полуостровом)».
В каждом из этих предложений описано отношение «является элементом множества».
Отношение может связывать два множества объектов, например:
• «Колеса входят в состав автомобилей»;
• «Бабочки — это насекомые (являются разновидностью насекомых)».
Попарно связаны одним и тем же отношением могут быть несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нем трудно разобраться.
Пусть про населенные пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой: населенный пункт
Для большей наглядности имеющиеся связи («соединен железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т.
д. (рис. 1.2).
Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения обозначают стрелкой на схеме отношений.
Так, на рис. 1.3 каждая стрелка направлена от отца к его сыну и поэтому отражает отношение «приходится отцом», а не «приходится сыном». Например: «Андрей приходится отцом Ивану».
Стрелки можно не использовать, если удается сформулировать и соблюсти правило взаимного расположения объектов на схеме. Например, если на рис. 1.3 имена детей всегда располагать ниже имени их отца, то можно обойтись без стрелок.
Такие отношения, как «приходится сыном», «соединен железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. А в отношениях «входит в состав» и «является разновидностью» могут находиться любые объекты.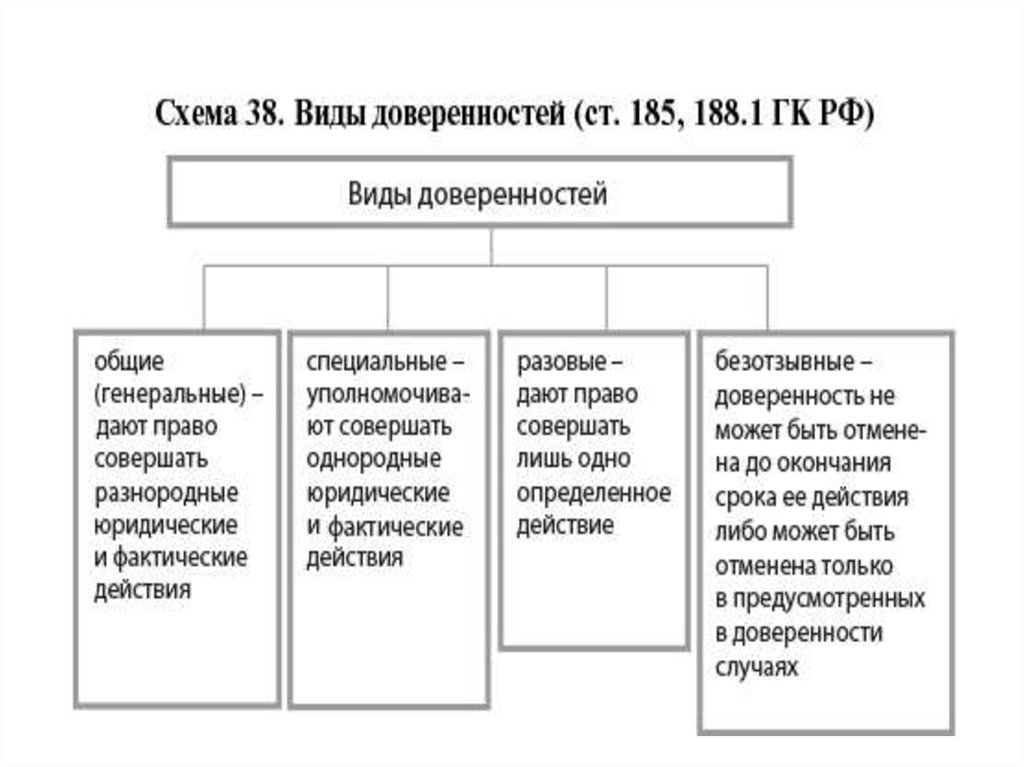
Коротко о главном
В сообщении об объекте могут быть приведены не только свойства данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.
Любые отношения между объектами можно наглядно описать с помощью схемы отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. Связи между объектами могут быть изображены линиями или стрелками.
Вопросы и задания
1. Назовите имя отношения в каждом приведенном предложении. Какое имя можно будет дать отношению, если имена объектов в предложении поменять местами? В каких парах имя отношения при этом не изменится?
а) Колобок поет песню Лисе.
б) Конек-Горбунок помогает Ивану.
в) В Москве есть Манежная площадь.
г) Пилюлькин лечит Сиропчика.
д) Страшила путешествует вместе с Элл и.
2. Для каждой пары объектов укажите соответствующее отношение.
3. Какую связь отражает каждая схема отношений на рис. 1.4-1.8? Выберите правильный ответ из следующих вариантов:
• «является разновидностью»;
• «входит в состав»;
• «является условием (причиной)»;
• «предшествует».
Разновидности объектов и их классификация
Из двух множеств, связанных отношением «является разновидностью», одно является подмножеством другого. Например, множество попугаев является подмножеством множества птиц, множество натуральных чисел является подмножеством множества целых чисел.
Схему отношения «является разновидностью» мы будем называть схемой разновидностей (рис.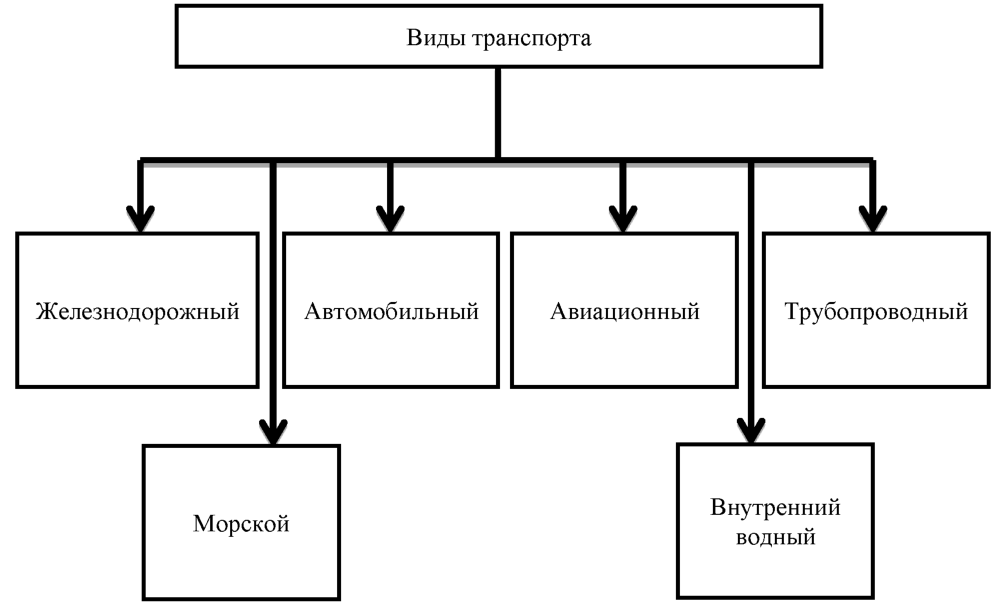
На схеме разновидностей имя подмножества всегда располагается ниже имени включающего его множества.
Объекты подмножества обязательно обладают всеми признаками объектов множества (наследуют признаки множества) и кроме них имеют еще свой, дополнительный признак (или несколько признаков). Этим дополнительным признаком может быть свойство или действие. Например, любое домашнее животное нужно кормить, собаки, кроме того, лают и кусаются, а ездовые собаки, кроме того, еще и бегают в упряжке.
Важно понимать, что сами по себе объекты не делятся ни на какие множества и подмножества. Например, арбузу совершенно «безразлично», относят его к семейству тыквенных растений, к подмножеству полосатых или шарообразных объектов.
Подмножества объектов выделяет и обозначает человек, потому что ему так удобнее усваивать и передавать информацию. Дело в том, что человек одновременно может концентрировать свое внимание лишь на 5-9 объектах. Для упрощения работы с множеством объектов его делят на несколько частей; каждую из этих частей опять делят на части; те, в свою очередь, еще раз и т. д. Деление большого множества на подмножества происходит не стихийно, а по некоторым признакам его объектов.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются основанием классификации.
Классификация называется естественной, если в качестве ее основания взяты существенные признаки объектов. Примером естественной классификации является классификация живых существ, предложенная Карлом Линнеем (1735 г.). В настоящее время ученые разделяют множество всех живых существ на пять основных царств: растения, грибы, животные, простейшие и прокариоты.
Каждое царство разделено на уровни — систематические единицы. Высший уровень называется типом. Каждый тип делится на классы, классы — на отряды, отряды — на семейства, семейства — на роды, а роды — на виды.
Классификация называется искусственной, если в качестве ее основания взяты несущественные признаки объектов. К искусственным классификациям относятся вспомогательные классификации (алфавитно-предметные указатели, именные каталоги в библиотеках). Пример искусственной классификации — деление множества звезд на небе на созвездия, проводившееся по признакам, которые к самим звездам не имели никакого отношения.
Можно предложить следующую классификацию объектов, с которыми взаимодействует пользователь в операционной системе Windows (рис. 1.10).
Коротко о главном
Схема разновидностей — это схема отношений «является разновидностью» между множествами и подмножествами объектов.
У объектов подмножества есть дополнительные признаки, кроме тех, которые есть у объектов множества, включающего данное подмножество.
Подмножество объектов, имеющих общие признаки, называется классом. Деление множества объектов на классы называется классификацией. Признаки, по которым один класс отличается от другого, называются осно¬ванием классификации.
Вопросы и задания
1. Для каждого из указанных подмножеств назовите множество, с которым оно связано отношением «является разновидностью» (назовите общее имя, отвечающее на вопрос «Что это такое?»):
а) местоимение;
б) запятая;
в) джойстик;
г) параллелограмм;
д) ратуша;
е) басня;
ж) капилляр.
2. Найдите в списке шесть пар множеств, между которыми существуют отношения «является разновидностью». Определите в каждой такой паре имя подмножества. Назовите для него хотя бы одно дополнительное свойство:
• книга;
• бензин;
• врач;
• молоко;
• строитель;
• учебник;
• жидкость;
• справочник;
• человек.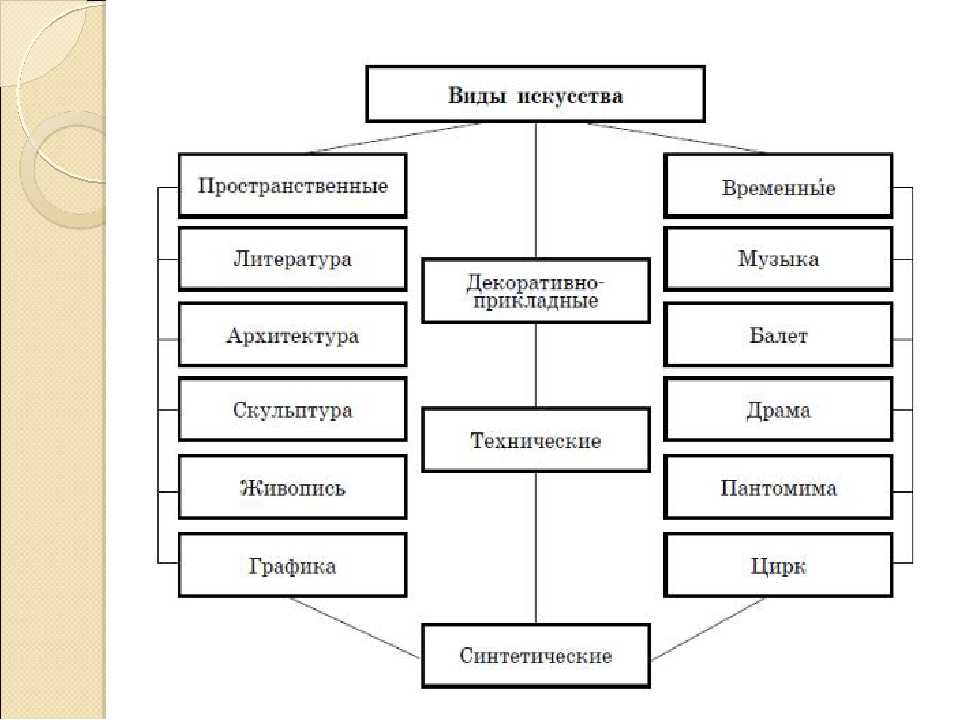
3. Выберите из списка имена девяти множеств, связанных отношениями «является разновидностью». Составьте схему разновидностей:
• яблоня;
• хвойное дерево;
• сосна;
• пихта;
• дерево;
• лиственное дерево;
• яблоко;
• ствол;
• фруктовое дерево;
• береза;
• дуб;
• лиственница;
• корень;
• желудь.
4. Используя предложенную классификацию паралле-лограммов, опишите свойства квадрата, наследующего их сразу у двух предков — прямоугольника и ромба. Какими дополнительными свойствами обладает квадрат:
а) по отношению к прямоугольнику;
б) по отношению к ромбу?
5. В каждом пункте перечислены объекты, сгруппированные по классам. Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам. Определите основания классификаций:
а) ель, сосна, кедр, пихта / береза, осина, липа, тополь;
б) картофель, лук, огурцы, помидоры / яблоки, апельсины, груши, мандарины;
в) рожь, тишь, ложь, рысь / пшеница, тишина, истина, кошка;
г) рубашка, пиджак, платье, сарафан / пальто, шуба, плащ, штормовка;
д) волк, медведь, лиса, лось / корова, собака, кошка, лошадь.
6. Предложите свою классификацию компьютерных объектов «файл» и «документ».
Практическая работа №2
«Работаем с объектами файловой системы»
1. Откройте окно Мой компьютер. Просмотрите файлы и папки, расположенные на диске С:.
2. Воспользуйтесь кнопками Вперед и Назад на панели инструментов Обычные кнопки для перемещения между ранее просмотренными объектами.
3. Выберите в меню Вид команды: Эскизы страниц, Плитка, Значки, Таблица. Проследите за изменениями в отображении папок и файлов. Найдите на панели инструментов Обычные кнопки кнопку, обеспечивающую быстрое изменение вида содержимого папок.
4. С помощью кнопки Папки отобразите в левой части окна панель Обозревателя Папки.
С ее помощью еще раз просмотрите файлы и папки, расположенные на диске С:. Проследите за изменениями, происходящими в правой части окна.
5. С помощью кнопки Поиск найдите собственную папку — папку, в которой хранятся ваши работы. Для этого в окне Помощника по поиску щелкните на ссылке Файлы и папки. В соответствующих полях укажите имя папки и область поиска.
6. Откройте собственную папку. В ней должны быть вложенные папки Документы, Заготовки_6, Заготовки_7, Презентации и Рисунки. Просмотрите содержимое этих папок.
7. Папка Заготовки_6 содержит файлы, которыми вы пользовались при выполнении работ компьютерного практикума в пошлом году. Так как эта папка вам больше не нужна, удалите ее (например, командой контекстного меню).
8. Папки Документы, Презентации и Рисунки содержат ваши прошлогодние работы. Их хотелось бы сохранить.
Создайте в собственной папке папку Архив. Для этого переведите указатель мыши в чистую область окна собственной папки и щелкните правой кнопкой мыши (вызов контекстного меню). Выполните команду [Создать-Папку].
Поочередно переместите папки Документы, Презентации и Рисунки в папку Архив. Для этого:
1) выделите папку Документы и, удерживая нажатой левую кнопку мыши, перетащите папку Документы в нанку Архив;
2) откройте контекстное меню панки Презентации, выполните команду Вырезать. Откройте папку Архив и с помощью контекстного меню вставьте в нее папку Презентации;
3) вырежьте папку Рисунки и вставьте ее в папку Архив с помощью команд строки меню.
9. С помощью контекстного меню переименуйте папку Заготовки_7 в Заготовки.
10. Убедитесь, что ваша папка имеет структуру, аналогичную приведенной ниже:
11.
Откройте файл Описание.doc из папки Заготовки.
Внесите в соответствующие ячейки таблицы информацию о свойствах трех своих файлов — текстового документа, рисунка и презентации.
12. Сохраните файл в собственной папке под именем Описание1. Вспомните как можно больше способов завершения работы с программой. Завершите работу с программой.
Теперь мы умеем
- выполнять операции с объектами файловой системы — папками и файлами; - определять свойства объектов файловой системы.
Раздел 33.3 (020C): Разновидности — проект The Stacks
В проекте Stacks мы будем использовать следующее определение разновидности.
Определение 33.3.1. Пусть $k$ — поле. Многообразие — это схема $X$ над $k$ такая, что $X$ целочисленна, а структурный морфизм $X \to \mathop{\mathrm{Spec}}(k)$ отделим и имеет конечный тип.
Это определение имеет следующий недостаток.
Предположим, что $k’/k$ является расширением полей. Предположим, что $X$ — многообразие над $k$. Тогда замена базы $X_{k’} = X \times _{\mathop{\mathrm{Spec}}(k)} \mathop{\mathrm{Spec}}(k’)$ не обязательно является многообразием над $ к’$. Это явление (в более общем виде) будет подробно рассмотрено в следующих разделах. Произведение двух разновидностей не обязательно должно быть разновидностью (это действительно одно и то же явление). Вот пример.
Пример 33.3.2. Пусть $k = \mathbf{Q}$. Пусть $X = \mathop{\mathrm{Spec}}(\mathbf{Q}(i))$ и $Y = \mathop{\mathrm{Spec}}(\mathbf{Q}(i))$. Тогда произведение $X \times _{\mathop{\mathrm{Spec}}(k)} Y$ многообразий $X$ и $Y$ не является многообразием, так как оно приводимо. (Это изоморфно несвязному объединению двух копий $X$.)
Однако если основное поле алгебраически замкнуто, то произведение многообразий является многообразием. Это следует из результатов главы об алгебре, но там мы рассматриваем гораздо более общие ситуации.
Существует также простое прямое доказательство этого, которое мы приводим здесь.
лозунг
Лемма 33.3.3. Пусть $k$ — алгебраически замкнутое поле. Пусть $X$, $Y$ — многообразия над $k$. Тогда $X \times _{\mathop{\mathrm{Spec}}(k)} Y$ является многообразием над $k$.
Доказательство. Морфизм $X \times _{\mathop{\mathrm{Spec}}(k)} Y \to \mathop{\mathrm{Spec}}(k)$ имеет конечный тип и является разделенным, поскольку он является композицией морфизмы $X \times _{\mathop{\mathrm{Spec}}(k)} Y \to Y \to \mathop{\mathrm{Spec}}(k)$, которые разделены и имеют конечный тип, см. Морфизмы, Леммы 29.15.4 и 29.15.3 и схемы, лемма 26.21.12. Для завершения доказательства достаточно показать, что $X \times _{\mathop{\mathrm{Spec}}(k)} Y$ является целым. Пусть $X = \bigcup _{i = 1, \ldots , n} U_ i$, $Y = \bigcup _{j = 1, \ldots , m} V_ j$ — конечные аффинные открытые покрытия. Если мы можем показать, что каждый $U_ i \times _{\mathop{\mathrm{Spec}}(k)} V_ j$ является целым, то это делается с помощью свойств, лемм 28.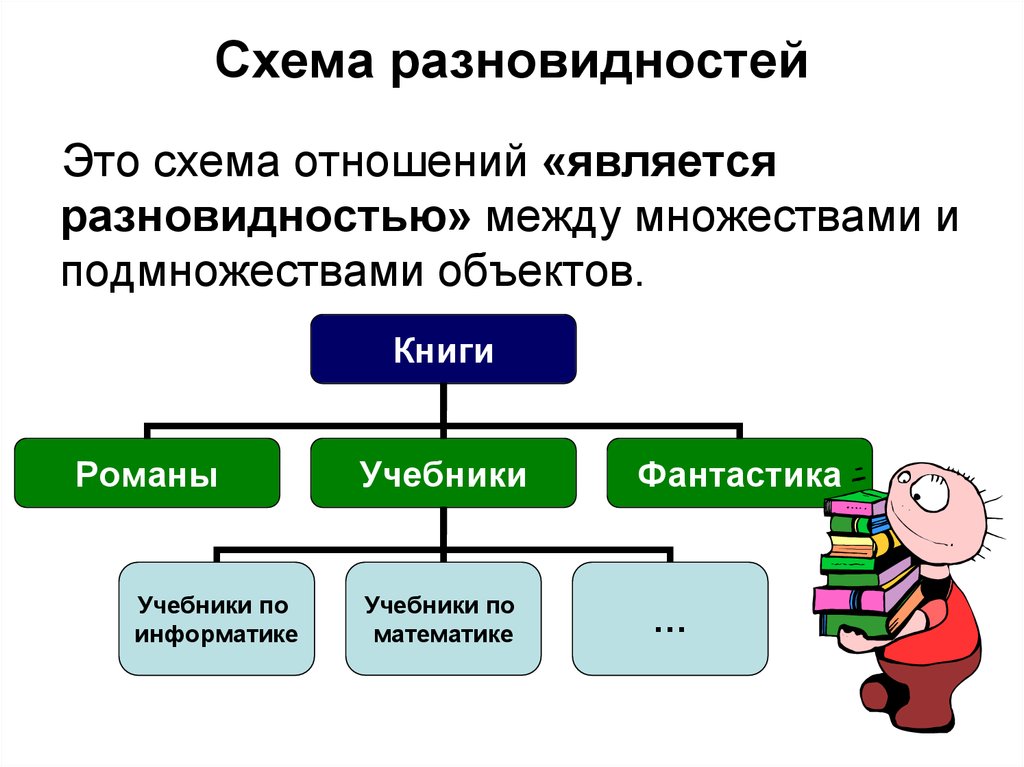
3.2, 28.3.3 и 28.3. .4. Это сводит нас к аффинному случаю.
Аффинный случай преобразуется в следующее алгебраическое утверждение: Предположим, что $A$, $B$ — области целостности и конечно порожденные $k$-алгебры. Тогда $A \otimes _ k B$ — область целостности. Чтобы получить противоречие, предположим, что
\[ (\sum \nolimits _{i = 1, \ldots , n} a_ i \otimes b_ i) (\sum \nolimits _{j = 1, \ldots , m} c_ j \otimes d_ j) = 0 \]
в $A \otimes _ k B$ с обоими множителями, отличными от нуля в $A \otimes _ k B$. Можно считать, что $b_1, \ldots , b_ n$ $k$-линейно независимы в $B$, а $d_1, \ldots , d_ m$ $k$-линейно независимы в $B$. Конечно, мы также можем предположить, что $a_1$ и $c_1$ отличны от нуля в $A$. Следовательно, $D(a_1c_1) \subset \mathop{\mathrm{Spec}}(A)$ непусто. По гильбертовскому Nullstellensatz (алгебра, теорема 10.34.1) мы можем найти максимальный идеал $\mathfrak m \subset A$, содержащийся в $D(a_1c_1)$, и $A/\mathfrak m = k$, поскольку $k$ алгебраически закрыто.
Обозначим через $\overline{a}_ i, \overline{c}_ j$ классы вычетов $a_ i, c_ j$ в $A/\mathfrak m = k$. Уравнение выше становится
\[ (\sum \nolimits _{i = 1, \ldots , n} \overline{a}_ i b_ i) (\sum \nolimits _{j = 1, \ldots , m} \overline{c }_j d_j) = 0 \]
что противоречит $\mathfrak m \in D(a_1c_1)$, линейной независимости $b_1, \ldots , b_ n$ и $d_1, \ldots , d_ m$, а также тому факту, что $B$ является домен. $\квадрат$
Алгебраическое многообразие как схема
спросил
Изменено 6 лет, 11 месяцев назад
Просмотрено 2к раз
$\begingroup$
Если взять определение многообразия как редуцированной интегральной схемы конечного типа над алгебраически замкнутым полем $k$, то многообразие, в частности, является схемой над $k$, а схема $X$ с морфизмом $X \to Spec(k)$.
Насколько я понимаю, больше внимания следует уделять морфизму, а не базовой схеме, поскольку у нас могут быть неизоморфные схемы над базой $S$, скажем, $\pi,\eta : X \to S$. Тогда даже если у нас есть конечно порожденная редуцированная $k$-алгебра $A$, можем ли мы по-прежнему иметь неизоморфные $k$-схемы $\eta, \pi : Spec (A) \to Spec (k)$? Мне кажется, что если бы это было так, то это было бы неожиданно, поскольку существует только одно разнообразие $k$, называемое Spec$(A)$, но мне не на чем основывать это, кроме того факта, что относительная точка зрения действительно никогда не применяется к разновидностям.
Это эквивалентно размещению двух неизоморфных структур $k$-алгебры на $A$, где $k$ алгебраически замкнуто, поэтому меня действительно интересует вопрос, можем ли мы иметь кольцо $A$ и два мономорфизма $i_1,i_2 :k \to A$, так что не существует автоморфизма $\varphi$ $A$ с $\varphi \circ i_2 = i_1$?
- алгебро-геометрия
- схемы
- аффинные схемы
$\endgroup$
4
$\begingroup$
Вот неаффинный пример, хотя я думаю (но не проверял), что он дает аффинный пример после удаления точки: возьмем эллиптическую кривую $E$ над $k$, $j$-инвариантная $j (E)$ перемещается некоторым автоморфизмом $g : k \to k$ из $k$.
