Схемы логических элементов. Логические элементы и схемы: основы цифровой электроники — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое логические элементы и как они работают. Какие бывают типы логических элементов. Как используются логические схемы в цифровой электронике. Как строятся сложные цифровые устройства на основе простых логических элементов.

Содержание

Основные типы логических элементов

Логические элементы — это базовые строительные блоки любой цифровой системы. Они работают с двумя логическими уровнями напряжения, обозначаемыми как 0 и 1. Основные типы логических элементов:

И (AND)
ИЛИ (OR)
НЕ (NOT)

Эти элементы позволяют реализовать любые булевы функции. Рассмотрим их подробнее.

Логический элемент И (AND)

Элемент И имеет два или более входов и выдает на выходе логическое умножение (конъюнкцию) входных сигналов. Выход равен 1 только когда все входы равны 1. В остальных случаях выход равен 0.

Таблица истинности двухвходового элемента И:

A	B	Y = A AND B
0	0	0
0	1	0
1	0	0
1	1	1

Логический элемент ИЛИ (OR)

Элемент ИЛИ имеет два или более входов и выдает на выходе логическое сложение (дизъюнкцию) входных сигналов. Выход равен 1, если хотя бы один из входов равен 1. Выход равен 0 только когда все входы равны 0.

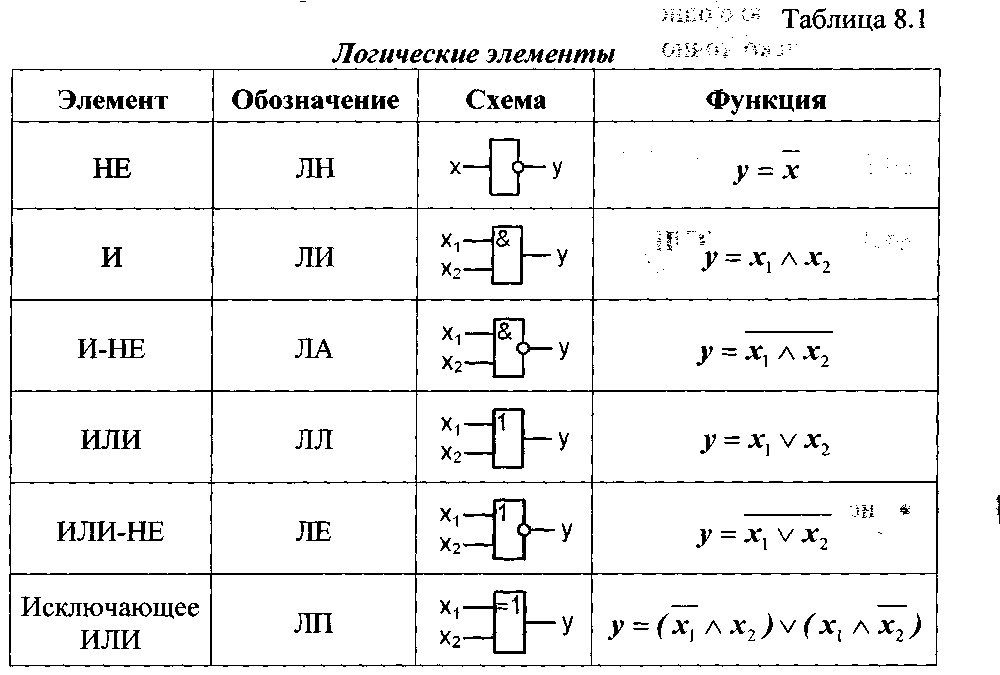
Таблица истинности двухвходового элемента ИЛИ:

A	B	Y = A OR B
0	0	0
0	1	1
1	0	1
1	1	1

Логический элемент НЕ (NOT)

Элемент НЕ имеет один вход и один выход. Он инвертирует входной сигнал — если на входе 0, то на выходе 1, и наоборот. Поэтому элемент НЕ также называют инвертором.

Таблица истинности элемента НЕ:

A	Y = NOT A
0	1
1	0

Универсальные логические элементы

К универсальным логическим элементам относятся:

И-НЕ (NAND)
ИЛИ-НЕ (NOR)

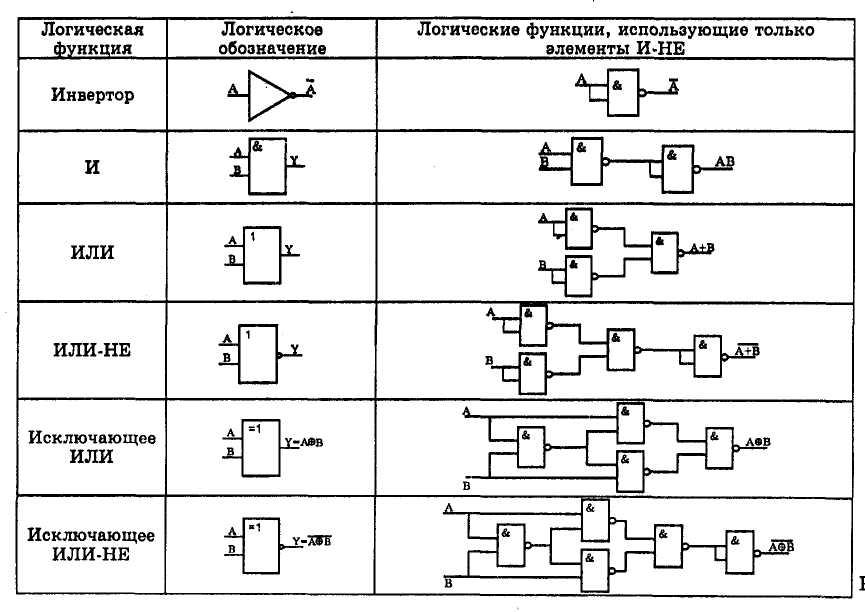
Они называются универсальными, потому что с их помощью можно реализовать любую логическую функцию. Например, используя только элементы И-НЕ можно построить схему, реализующую любую булеву функцию в виде суммы произведений.

Элемент И-НЕ (NAND)

Элемент И-НЕ реализует операцию И с последующим инвертированием результата. Его выход равен 0 только когда все входы равны 1. В остальных случаях выход равен 1.

Таблица истинности двухвходового элемента И-НЕ:

A	B	Y = NOT (A AND B)
0	0	1
0	1	1
1	0	1
1	1	0

Элемент ИЛИ-НЕ (NOR)

Элемент ИЛИ-НЕ реализует операцию ИЛИ с последующим инвертированием результата. Его выход равен 1 только когда все входы равны 0. В остальных случаях выход равен 0.

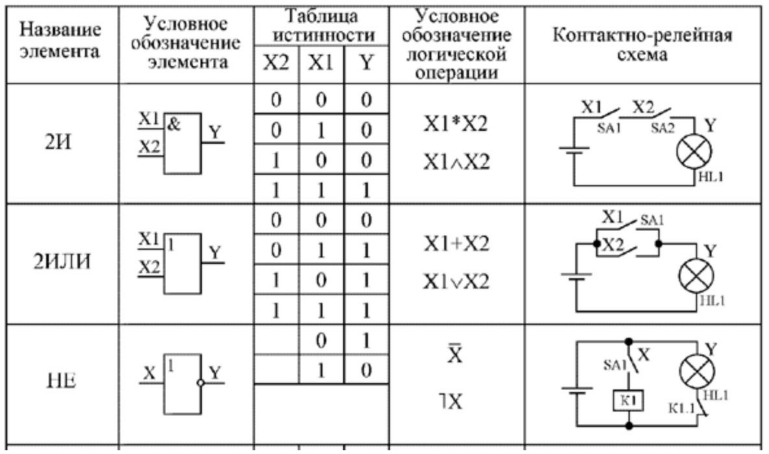
Таблица истинности двухвходового элемента ИЛИ-НЕ:

A	B	Y = NOT (A OR B)
0	0	1
0	1	0
1	0	0
1	1	0

Специальные логические элементы

К специальным логическим элементам относятся:

Исключающее ИЛИ (XOR)
Исключающее ИЛИ-НЕ (XNOR)

Эти элементы являются особыми случаями элементов ИЛИ и ИЛИ-НЕ соответственно.

Применение логических элементов в цифровых схемах

Логические элементы являются основой для построения более сложных цифровых устройств:

Шифраторов и дешифраторов
Мультиплексоров и демультиплексоров
Сумматоров
Триггеров и регистров
Счетчиков
Запоминающих устройств

Рассмотрим некоторые из этих устройств подробнее.

Триггеры — базовые элементы памяти

Триггер — это устройство с двумя устойчивыми состояниями, способное хранить 1 бит информации. Основные типы триггеров:

RS-триггер
D-триггер
JK-триггер
T-триггер

Триггеры используются для построения регистров, счетчиков и других устройств с памятью.

Регистры — устройства для хранения и сдвига данных

Регистр — это устройство для хранения нескольких бит информации. Различают:

Параллельные регистры — для одновременной записи/чтения всех бит
Последовательные регистры — для последовательной записи/чтения бит
Регистры сдвига — для сдвига хранимых данных

Регистры сдвига применяются для преобразования последовательного кода в параллельный и наоборот.

Счетчики — устройства для подсчета импульсов

Счетчик — это устройство для подсчета количества поступивших импульсов. Основные типы счетчиков:

Асинхронные (последовательные)
Синхронные (параллельные)
Реверсивные (с прямым и обратным счетом)
Кольцевые

Счетчики используются для деления частоты, формирования временных интервалов, адресации памяти и других целей.

Комбинационные логические схемы

Комбинационные схемы формируют выходные сигналы в зависимости только от комбинации входных сигналов, без учета предыдущих состояний. К ним относятся:

Дешифраторы
Шифраторы
Мультиплексоры
Демультиплексоры
Компараторы
Сумматоры

Эти схемы широко применяются для обработки и преобразования данных в цифровых устройствах.

Последовательностные логические схемы

Последовательностные схемы, в отличие от комбинационных, имеют память и формируют выходные сигналы в зависимости не только от текущих входных сигналов, но и от предыдущих состояний. К ним относятся:

Триггеры
Регистры
Счетчики
Конечные автоматы

Эти схемы позволяют реализовать более сложное поведение цифровых устройств, связанное с запоминанием и обработкой последовательностей сигналов.

Реализация логических элементов

Логические элементы могут быть реализованы различными способами:

На дискретных компонентах (транзисторах, диодах, резисторах)
В виде интегральных микросхем
На базе программируемых логических интегральных схем (ПЛИС)

Наиболее распространенные технологии изготовления интегральных логических микросхем:

ТТЛ — транзисторно-транзисторная логика
КМОП — комплементарная металл-оксид-полупроводниковая технология

КМОП-технология обеспечивает низкое энергопотребление и высокую степень интеграции, поэтому сейчас используется наиболее широко.

Логические схемы

Логические элементы, включая вентили, счетчики и запоминающие устройства, изготавливаются в виде интегральных модулей, или интегральных схем (ИС). Эти ИС разбивают на классы, называемые семействами, по числу полупроводниковых приборов, содержащихся в одной ИС. В настоящее время существуют следующие семейства.

1.	ИС низкой степени интеграции	до 10 приборов.
2.	ИС средней степени интеграции	10-100 приборов.
3.	ИС большой степени интеграции, или большие ИС (БИС)	100-1000 приборов.
4.	ИС сверхбольшой степени интеграции, или сверхбольшие ИС (СБИС)	1000-10000 приборов.
5.	Ультрабольшие ИС (УБИС)	10000-100000 приборов.

Степень интеграции определяет сложность интегральной схемы. Каждое следующее по сложности семейство характеризуется десятикратным увеличением числа элементов по сравнению с предыдущим. К ИС низкой и средней степени интеграции относятся дискретные логические элементы, такие, как вентили, счетчики и регистры. БИС иСБИС используются в качестве запоминающих устройств, микропроцессоров и законченных систем, таких, как микрокомпьютеры.

Логические состояния

Логический элемент имеет два различных состояния: состояние логического 0, представляемое низким уровнем напряжения, обычно 0 В; и состояние логической 1. представляемое высоким уровнем напряжения (положительной полярности в случае

положительной логики и отрицательной полярности в случае отрицательной логики). Уровень напряжения, который представляет логическую 1. зависит от используемого типа ИС. Для ИС, изготавливаемых по биполярной технологии, например для ПС ТТ, I (ИС на основе транзисторно-транзисторной логики), логической 1 соответствует напряжение 5 В, в то время как для ИС КМОП (ИС на комплементарных, или дополняющих, МОП-транзисторах) логическая 1 может быть представлена напряжением в диапазоне от 3 до 15 В и выше. ИС ТТЛ имеют преимущество в быстродействии, а ИС КМОП позволяют реализовать более высокую степень интеграции компонентов

(т. е. позволяют разместить большее число логических элементов в одном интегральном модуле) и не требуют использования стабилизированных источников питания.

Транзисторно-транзисторные логические элементы (ТТЛ)

ТТЛ-элементы применяются в интегральных схемах и обеспечивают высокую скорость переключения. На рис. 34.1 показана упрощенная схема логического элемента И-НЕ с многоэмиттерным транзистором T₁ на входе. Когда на обоих входах присутствует логический 0, транзистор T₁ насыщен и напряжение на его коллекторе близко к 0 В. Следовательно, транзистор T₂ находится в состоянии отсечки, и на выходе мыимеем логическую 1. Когда на оба входа подается логическая 1, транзистор T₁ закрывается и переключает транзистор T₂ в состояние насыщения. В этом случае на выходе элемента мы имеем логический 0.

Рис. 34.1. Логический элемент И-НЕ (ТТЛ-типа).

Логические элементы на полевых транзисторах

Логические схемы в настоящее время изготавливаются только в виде интегральных схем. Огромное количество логических элементов можно разместить на мельчайшем кристалле (чипе) кремния размером 1х2 мм. В силу своей простоты полевые транзисторы применяются чаще, чем биполярные транзисторы. Наиболее широко распространены логические элементы на основе так называемых КМОП-ячеек (здесь они не рассматриваются). На рис. 34.2 приведена схема логического элемента ИЛИ-НЕ на МОП-транзисторах, который работает на основе отрицательной логики. В этой схеме T

1 и T₂ — полевые МОП-транзисторы с каналом p-типа (работающие в режиме обогащения). Когда на обоих входах присутствует Уровень логического 0, транзисторы T₁ и T₂ находятся в состоянии отсечки и на выходе мы имеем логическую 1 (-V_DD= -20 В). Когда на один или на оба входа подается логическая 1 (например, -20 В), открываются один или оба транзистора и на выходе мы получаем логический 0.

Рис. 34.2. Логический элемент Рис. 34.3. Логический элемент на И-НЕ

ИЛИ-НЕ на МОП-транзисторах. МОП-транзисторах.

На рис. 34.3 показана схема логического элемента И-НЕ на основе полевых МОП-транзисторов с каналом п-типа. Поскольку используется источник питания положительной полярности, данный логический элемент работает на основе положительной логики. Транзистор T₃ постоянно смещен в активную рабочую область напряжением V_DD, подаваемым на затвор, и выполняет функцию активной нагрузки логического элемента. Когда на одном или на обоих входах присутствует логический 0, один или оба транзистора находятся в состоянии отсечки, выдавая логическую 1 на выходе. Ток через транзисторы будет протекать только в том случае, когда на оба входа будет подана логическая 1, и только в этом случае мы получим на выходе логический 0.

Булевы выражения

Функции, реализуемые отдельным логическим элементом или комбинацией логических элементов, могут быть выражены логическими формулами, называемыми булевыми выражениями. В булевой алгебре используются следующие обозначения логических функций (см. табл. 34.1):

• Функция И обозначается символом точки (·). Двухвходовый (входы А и В) логический элемент И вырабатывает на выходе сигнал, представляемый булевым выражением А · В.

• Функция ИЛИ обозначается символом (+). Двухвходовый логический элемент ИЛИ вырабатывает на выходе сигнал, представляемый булевым выражением А + В.

Таблица 34.1. Булевы выражения

Функция	Обозначение в булевой алгебре
И	А·В
или	А+В
НЕ
И-НЕ
ИЛИ-НЕ
Исключающее ИЛИ
Исключающее ИЛИ-НЕ

• Логическая функция НЕ обозначается символом черты над обозначением входного сигнала. Логическая схема НЕ с одним входом А вырабатывает на выходе сигнал, представляемый булевым выражением (читается «НЕ А»).

Через эти простые функции можно выразить более сложные:

• Функция Н-НЕ записывается как .

• Функция ИЛИ-НЕ записывается как .

• Функция Исключающее ИЛИ записывается как . Ее можно также записать, используя специальное обозначение, .

• Функция Исключающее ИЛИ-НЕ записывается как . Ее можно также записать, используя специальное обозначение, .

Комбинаторная логика

Рассмотрим логическую схему на рис. 34.4. Логическую функцию, выполняемую этой схемой, можно описать с помощью следующих булевых выражений.

Выходной сигнал логического элемента ИЛИ (i): A + В

Выходной сигнал логического элемента И-ИЕ (ii):

Выходной сигнал логического элемента ИЛИ (iii): (А + В) +

Пример 1

Обратимся к рис. 34.5.

а) Найдите булево выражение для логической функции изображенной комбинации логических элементов.

б) Составьте таблицу истинности, показывающую логические состояния во всех точках схемы, и докажите, что эту схему можно свести к одному логическому элементу.

Решение

а) Булево выражение для точки С = .

Булево выражение для точки D= .

Булево выражение для точки F = ·.

б) Таблица истинности

Входы		Точки		Выход
А	В	С	D	F
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	0	0	0

Как видно из таблицы истинности, приведенная комбинация логических элементов эквивалентна логическому элементу ИЛИ-НЕ.

Пример 2

Обратимся к рис. 34.6.

а) Найдите булево выражение для логической функции изображенной комбинации логических элементов.

Решение

а) Булево выражение для точки С = .

Булево выражение для точки D = .

Булево выражение для точки F = +.

6) Таблица истинности

Входы		Точки		Выход
А	В	С	D	F
0	0	1	1	1
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

Как видно из таблицы истинности, приведенная комбинация логических элементов эквивалентна логическому элементу И-НЕ.

Счетчики

Функцию счета в двоичном счетчике выполняет бистабильный мультивибратор, или делитель на 2, чаще называемый триггером. Цепочка из нескольких таких триггеров образует счетчик. На рис. 34.7 показан двоичный счетчик, состоящий из трех триггеров. Каждый триггер делит частоту поступающих импульсов на 2. Таким образом, два последовательных триггера обеспечивают деление на 4 (2 · 2), а три триггера – на 8 (2 · 2 · 2). Другими словами, на каждые восемь входных импульсов на выходе А появятся четыре импульса, на выходе В — два импульса и на выходе С — один импульс (рис. 34.7).

Как уже говорилось в гл. 32, бистабильный мультивибратор изменяет свое состояние только во время действия одного из фронтов входного импульса. Уровень входного импульса изменяется от 0 к 1 и обратно к 0, и так для каждого приходящего импульса. Обычно предполагается, что состояние триггера изменяется при приходе отрицательного фронта импульса (т. е. при переходе от 1 к 0).

Сигнал на выходе Q_А триггера А соответствует 2⁰, или столбцу «единиц» в табл. 34.2, сигнал на выходе Q_B— 2¹, или столбцу «двоек», и наконец, сигнал на выходе Q_C — 2², или столбцу «четверок». После поступления 6 импульсов на вход счетчика он оказывается в следующем состоянии: А (число единиц) = 0, В (число двоек) = 1. С (число четверок) = 1; это состояние соответствует десятичному числу 6 (0 + 2 + 4).

Рис. 34.7. Двоичный счетчик на трех триггерах.

Таблица 34.2

Импульс	Q_А единицы (2⁰)	Q_B двойки (2¹)	Q_C четверки (2²)
0	0	0	0
1	1	0	0
2	0	1	0
3	1	1	0
4	0	0	1
5	1	0	1
6	0	1	1
7	1	1	1
8	0	0	0

В двоичном исчислении это число записывается как 110 при порядке следования двоичных разрядов СВА. Обратите внимание, что в счетчике двоичному разряду единиц соответствует выход первого триггера, начиная от входа счетчика, а в двоичном числе разряд единиц всегда является самым правым разрядом.

Когда приходит седьмой импульс, на всех выходах счетчика устанавливается 1. Восьмой импульс сбрасывает все триггеры в 0. Еще раз отметим, что выходной сигнал каждого триггера представляет столбец в таблице двоичного кода. Сам двоичный код записывается в порядке СВА.

Обратная связь

Обратная связь вводится в двоичных счетчиках для изменения коэффициента деления частоты входного сигнала. Для примера рассмотрим действие обратной связи в счетчике на рис. 34.8(а), состоящем из трех триггеров. Процесс счета происходит обычным образом до прихода третьего импульса, когда счетчик находится в состоянии 011 (см. табл. 34.3).

Рис. 34.8. (а) Счетчик-делитель на 6 с обратной связью, охватывающей триггеры В и С.

(б) Замена петли обратной связи эквивалентным модулем деления на 3.

Таблица 34.3

Импульс	Q_А	Q_B	Q_C
0	0	0	0
1	1	0	0
2	0	1	0
3	1	1	0
Обратная связь	(0)	(0)	(1)
4	0	1	1
5	1	1	1
6	0	0	0

Четвертый импульс переключает сигнал на выходах А и В к 0 и на выходе С к 1. В отсутствие обратной связи счетчик переключился бы в состояние 100. Однако при включении обратной связи изменение сигнала на выходе С передается на вход триггера В, возвращая его выходной сигнал обратно к 1. Счетчик окажется в состоянии 110. Пятый импульс переключит все выходы к 1, и шестой импульс сбросит все триггеры в 0, т. е. получился счетчик-делитель на 6.

Вообще, можно показать, что петля обратной связи уменьшает коэффициент деления триггеров внутри петли на 1. В предыдущем примере внутри петли обратной связи находились триггеры В и С. Без обратной связи они осуществляли деление на 4. С обратной связью триггеры В и С образуют блок деления на 3 (= 4 – 1), как показано на рис. 34.8(б). С учетом триггера А вне петли обратной связи полный коэффициент деления счетчика равен 6 (= 2 · 3).

Десятичный счетчик

На рис. 34.9(а) изображена схема десятичного счетчика с двумя петлями обратной связи. Обратной связью охвачены : 1) блок 1, включающий триггеры С и D и обеспечивающий деление на 3 (= 4 – 1), и 2) блок 2, включающий блок 1 и триггер В. Из рис. 34.9(б) видно, что без обратной связи блок 2 делил бы на 6 (= 2 · 3). С обратной связью его коэффициент деления равен 5 (= 6 – 1). С учетом триггера А, не охваченного обратной связью, полный коэффициент деления счетчика равен 10 (= 2 · 5).

Регистр сдвига

Для передачи данных из одной части системы, например компьютера, в другую можно использовать два метода. Первый, более быстрый, заключается в одновременной передаче всех разрядов. При этом для передачи восьми разрядов требуется восемь отдельных линий. Для передачи информации на расстояния в несколько метров этот метод вполне пригоден, но при передаче на большие расстояния, например между городами, он становится слишком дорогим. В этом случае применяется второй, более медленный метод: данные передаются последовательно разряд за разрядом по одному проводу. Для одновременного сдвига всех двоичных разрядов влево или вправо применяется регистр сдвига. Он состоит из нескольких триггеров, способных передвигать двоичные разряды в последовательном порядке.

Рис. 34.9. Десятичный счетчик (а) и его представление в виде эквивалентных модулей (б).

Кольцевой счетчик

Кольцевой счетчик — это обычный счетчик, составленный из нескольких триггеров, в котором выходной сигнал подается обратно на вход, отсюда и происходит его название. Импульсы циркулируют по счетчику от входа к выходу и обратно на вход. В конце каждого цикла выходной сигнал кольцевого счетчика можно снять для переключения другого счетчика. Например, выходной сигнал десятичного, или декадного, счетчика можно использовать для переключения еще одного декадного счетчика, обеспечивая тем самым коэффициент пересчета, равный 100.

Фиксатор (триггер-защелка)

В гл. 32 рассматривались бистабильные мультивибраторы, или триггеры, построенные на дискретных компонентах. Триггеры — очень важные и нужные базовые элементы логических устройств. Они применяются в качестве делителей на 2, фиксаторов (одноразрядные ячейки памяти) и для других целей.

Базовый триггер, называемый RS-триггером, или триггером-защелкой, показан на рис. 34.10. Два выходных сигнала, снимаемые с выходов Q и (НЕ Q), находятся в противофазе друг к другу. Если Q = 1, то = 0, и наоборот. Таблица истинности для RS-триггера приведена на рис. 34.10(в). При подаче логической 1 на вход R (Reset — сброс) на выходе Q устанавливается уровень логического 0 (и уровень логической 1 на выходе ), при подаче логической 1 на вход S (Set — установка) на выходе Q устанавливается уровень логической 1 (и уровень логического 0 на выходе ).

S	R
0	0	Без изменений
0	1	0 1 (Сброс)
1	0	1 0 (Установка)
1	1	Неопределенное состояние

(в)

Более сложным устройством по сравнению с простым RS-триггером является тактируемый JK-триггер, в котором имеется тактовый вход и отсутствует неопределенное состояние (рис. 34.11). Тактовый вход важен для синхронных систем, в которых переключение триггеров происходит лишь тогда, когда на тактовый вход подается логическая 1. При установке логической 1 на обоих входах J и К триггера его выход переключается из уровня логического 0 в логическую 1 при поступлении каждого тактового импульса.

Тактовый вход	J	К	Q
0	X	X	Без изменений
1	0	0	Без изменений
1	0	1	1
1	1	0	0
1	1	1	Переключение

(а) (б)

Рис. 34.11. Условное обозначение (а) и таблица истинности (б) JK-триггера.

Логические элементы в виде ИС

Логические элементы изготавливаются в виде интегральных схем и выпускаются в виде модулей, содержащих большое число идентичных элементов на одном модуле (чипе). Известны два основных типа ИС: ИС ТТЛ и ИС КМОП. Примеры ИС ТТЛ приведены на рис. 34.12.

Рис. 34.12.

В этом видео рассказывается о элементах транзисторно-транзисторной логики:

Добавить комментарий

Цифровые схемы — логические элементы

Цифровые электронные схемы работают с напряжениями двух логических уровней, а именно Logic Low и Logic High. Диапазон напряжений, соответствующий низкому логическому значению, обозначен как «0». Точно так же диапазон напряжений, соответствующий логическому максимуму, обозначен цифрой «1».

Базовая цифровая электронная схема, которая имеет один или несколько входов и один выход, называется логическим вентилем . Следовательно, логические элементы являются строительными блоками любой цифровой системы. Мы можем классифицировать эти логические элементы в следующие три категории.

Основные ворота
Универсальные ворота
Специальные ворота

Теперь давайте поговорим о логических элементах, попадающих в каждую категорию по очереди.

Основные ворота

В предыдущих главах мы узнали, что булевы функции могут быть представлены либо в форме суммы произведений, либо в форме произведения сумм в зависимости от требования. Таким образом, мы можем реализовать эти булевы функции, используя базовые элементы. Основными воротами являются И, ИЛИ И НЕ ворота.

И ворота

Логический элемент И представляет собой цифровую схему, которая имеет два или более входов и производит выход, который является логическим И всех этих входов. Логическое И необязательно обозначать символом «.».

В следующей таблице показана таблица истинности 2-входного логического элемента AND.

	В	Y = AB
0	0	0
0	1	0
1	0	0
1	1	1

Здесь A, B — входы, а Y — выход двух входных И логических элементов. Если оба входа «1», то только выход, Y «1». Для оставшихся комбинаций входов выход Y равен 0.

На следующем рисунке показан символ логического элемента AND, который имеет два входа A, B и один выход Y.

Этот логический элемент И производит выход (Y), который является логическим И двух входов А, В. Аналогичным образом, если есть ‘n’ входов, то логический элемент И производит выход, который является логическим И всех этих входов. Это означает, что выход логического элемента AND будет равен «1», когда все входы равны «1».

ИЛИ ворота

Логический элемент ИЛИ — это цифровая схема, которая имеет два или более входов и создает выход, который является логическим ИЛИ всех этих входов. Это логическое ИЛИ обозначается символом «+».

В следующей таблице показана таблица истинности 2-входного ИЛИ вентиля.

	В	Y = A + B
0	0	0
0	1	1
1	0	1
1	1	1

Здесь A, B — входы, а Y — выход двух входных логических элементов ИЛИ. Если оба входа «0», то только выход, Y «0». Для остальных комбинаций входов выход Y равен «1».

На следующем рисунке показан символ логического элемента ИЛИ, который имеет два входа A, B и один выход Y.

Этот логический элемент ИЛИ выдает выход (Y), который является логическим ИЛИ двух входов A, B. Аналогично, если имеется ‘n’ входов, то вентиль ИЛИ генерирует выход, который является логическим ИЛИ всех этих входов. Это означает, что выход логического элемента ИЛИ будет равен «1», когда хотя бы один из этих входов равен «1».

НЕ ворота

Логический элемент NOT — это цифровая схема с одним входом и одним выходом. Выход NOT gate является логической инверсией ввода. Следовательно, вентиль НЕ также называется инвертором.

В следующей таблице показана таблица истинности NOT gate.

Здесь A и Y — вход и выход элемента НЕ соответственно. Если вход A равен 0, то выход Y равен 1. Точно так же, если вход A равен «1», то выход Y равен «0».

На следующем рисунке показан символ НЕ, который имеет один вход A и один выход Y.

Этот НЕ вентиль производит вывод (Y), который является дополнением ввода, A.

Универсальные ворота

Ворота NAND & NOR называются универсальными воротами . Потому что мы можем реализовать любую булеву функцию, которая находится в виде суммы продуктов, используя только вентили NAND. Точно так же мы можем реализовать любую булеву функцию, которая находится в виде суммы сумм, используя только вентили NOR.

NAND ворота

NAND gate — это цифровая схема, которая имеет два или более входов и производит выход, который является инверсией логического И всех этих входов.

В следующей таблице показана таблица истинности 2-входного вентиля NAND.

	В	Y = (AB) ‘
0	0	1
0	1	1
1	0	1
1	1	0

Здесь A, B — входы, а Y — выход двух входных вентилей NAND. Когда оба входа «1», выход Y равен «0». Если хотя бы один из входов равен нулю, тогда выход Y равен «1». Это прямо противоположно операции ввода-вывода и логического элемента.

На следующем изображении показан символ вентиля NAND, который имеет два входа A, B и один выход Y.

Работа шлюза NAND такая же, как и у шлюза AND, за которым следует инвертор. Вот почему символ ворот NAND представлен так.

NOR ворота

NOR gate — это цифровая схема, которая имеет два или более входов и производит выход, который является инверсией логического ИЛИ всех этих входов.

Следующая таблица показывает таблицу истинности 2-входного вентиля NOR

	В	Y = (A + B) ‘
0	0	1
0	1	0
1	0	0
1	1	0

Здесь A, B — входы, а Y — выход. Если оба входа равны 0, то выход Y равен 1. Если хотя бы один из входных данных равен «1», то выходным значением является «0». Это прямо противоположно операции ввода-вывода или логического элемента.

На следующем рисунке показан символ логического элемента NOR, который имеет два входа A, B и один выход Y.

Работа шлюза NOR такая же, как и у шлюза OR, за которым следует инвертор. Вот почему символ ворот NOR представлен так.

Специальные ворота

Ворота EX-OR & Ex-NOR называются специальными воротами. Потому что эти два входа — это особые случаи ворот ИЛИ ИЛИ НЕ.

Бывшие ворота

Полная форма ворот Ex-OR — это ворота Exclusive-OR . Его функция такая же, как у логического элемента ИЛИ, за исключением некоторых случаев, когда входы имеют четное число единиц.

В следующей таблице показана таблица истинности 2-входного вентиля Ex-OR.

	В	Y = A⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Здесь A, B — входы, а Y — выход двух входных шлюзов Ex-OR. Таблица истинности для шлюза Ex-OR такая же, как и для таблицы ИЛИ для первых трех строк. Единственная модификация находится в четвертом ряду. Это означает, что выход (Y) равен нулю вместо единицы, когда оба входа равны единице, поскольку входы имеют четное число единиц.

Следовательно, выход логического элемента «ИЛИ-ИЛИ» равен «1», когда только один из двух входов равен «1». И это ноль, когда оба входа одинаковы.

На следующем рисунке показан символ шлюза Ex-OR, который имеет два входа A, B и один выход Y.

Работа шлюза Ex-OR аналогична работе шлюза OR, за исключением нескольких комбинаций входов. Вот почему символ ворот Ex-OR представлен так. Выход шлюза Ex-OR равен «1», когда на входах присутствует нечетное количество единиц. Следовательно, выход шлюза Ex-OR также называется нечетной функцией .

Бывшие ворота

Полная форма ворот Ex-NOR — это ворота Exclusive-NOR . Его функция такая же, как и у шлюза NOR, за исключением некоторых случаев, когда входы имеют четное число единиц.

В следующей таблице показана таблица истинности 2-входного вентиля Ex-NOR.

	В	Y = A⊙B
0	0	1
0	1	0
1	0	0
1	1	1

Здесь A, B — входы, а Y — выход. Таблица истинности шлюза Ex-NOR такая же, как и у шлюза NOR для первых трех строк. Единственная модификация находится в четвертом ряду. Это означает, что выход равен одному вместо нуля, когда оба входа равны.

Следовательно, выход шлюза Ex-NOR равен «1», когда оба входа одинаковы. И это ноль, когда оба входа разные.

На следующем рисунке показан символ шлюза Ex-NOR, который имеет два входа A, B и один выход Y.

Работа шлюза Ex-NOR аналогична работе шлюза NOR, за исключением нескольких комбинаций входов. Вот почему символ ворот Ex-NOR представлен именно так. Выход шлюза Ex-NOR равен «1», когда на входах присутствует четное число единиц. Следовательно, выход шлюза Ex-NOR также называется четной функцией .

Из приведенных выше таблиц истинности логических элементов Ex-OR и Ex-NOR мы можем легко заметить, что операция Ex-NOR является просто логической инверсией операции Ex-OR.

Виды задач на логические элементы.

Построение логической схемы по заданной логической функции;
Запись логической функции по заданной логической схеме;
Определение сигнала на выходе логической схемы по заданным значениям сигналов на всех входах этой схемы;
Построение таблицы истинности для заданной логической схемы;

Познакомимся с ними поочередно.

Построение логической схемы по заданной логической функции.

Задача:

Дана логическая функция:

Составить логическую схему для неё.

Решение:

Расставим порядок выполнения логических операций, руководствуясь правилами:

отрицание
умножение
сложение

Не забываем про приоритет скобок.
Получаем:

Строим схему по указанному порядку. Посмотреть.

Запись логической функции по заданной логической схеме.

Задача:

Дана логическая схема:

Составить логическую функцию по ней.

Решение:

Рассматриваем схему с конца и записываем соответствующие логические операции, учитывая, что в записываемой функции три операнда А, В, С Посмотреть.

Можно сначала подписать на схеме промежуточные функции, получаемые на выходе каждого блока, а потом сцепить их логическими операциями. Посмотреть.

Определение сигнала на выходе логической схемы по заданным значениям сигналов на всех входах этой схемы.

Задача:

Дана логическая схема и значения сигналов на всех входах:

Определить значение функции F на выходе схемы.

Решение:

Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах и соответственно на входах каждого логического элемента пока не доберёмся до конца схемы. Получаем:

Ответ:

Значение функции F на выходе схемы = 1. Построение таблицы истинности для заданной логической схемы.

Задача:

Дана логическая схема:

Построить для неё таблицу истинности.

Решение:

Проверяем количество входов на схеме. Количество комбинаций сигналов на 2 входах равно 4, для 3 входов равно 8, для 4 входов равно 16 и т. д. Составляем таблицу истинности, в которой первые столбцы — это входы схемы, обозначенные буквами, следущие столбцы — функции, полученные на выходах каждого элемента схемы, а строки — отражают разные комбинации сигналов на входах. Количество строк совпадает с количеством комбинаций сигналов. Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах каждого логического элемента, т. е. по каждому столбцу пока не доберёмся до конца схемы. Получаем:

Ответ:

Конспект урока «Построение логических схем с помощью базовых логических элементов» 10 класс

Автор:
Аристамбекова Гульнара Галимбековна
учитель информатики и ИКТ
категория: вторая
МБОУ СОШ № 19 с УИОП
Республика Татарстан, г.Набережные Челны
e-mail: написать автору

Конспект урока
«Построение логических схем с помощью базовых логических элементов»

10 класс

Тип урока: лекция, самостоятельная работа.

Оборудование: проектор, карточки с заданиями.

Формы работы: коллективная, индивидуальная.

Продолжительность урока: 45 мин.

Цели урока:

Образовательные:

· научиться строить логические схемы для логических функций с помощью основных базовых логических элементов;

· научиться выписывать соответствующую логическую функцию из логической схемы.

Воспитательные:

· привитие навыков самостоятельности в работе, воспитание аккуратности, дисциплинированности.

Развивающие:

· развитие внимания, мышления, памяти учащихся.

Ход урока:

1. Организационный момент (1 мин).
2. Проверка пройденного материала (5 мин).

Фронтальный опрос.

1. Перечислите основные логические операции.

2. Что такое логическое умножение?

3. Что такое логическое сложение?

4. Что такое инверсия?

5. Что такое таблица истинности?

6. Что такое сумматор?

7. Что такое полусумматор?

3. Изучение нового материала (20 мин).

Дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.
Поскольку любая логическая операция может быть представлена в виде комбинаций трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
На доске приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).

Логический элемент «И»:

Логический элемент «ИЛИ»:

Логический элемент «НЕ»:

Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.

Пример 1. По заданной логической функции построить логическую схему.

Наше построение схемы, мы начнем с логической операции, которая должна выполнятся последней. В нашем случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы будут подаваться с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Пример 2. Выписать из логической схемы соответствующую ей логическую формулу:

А	В	F
0	0	1
0	1	0
1	0	1
1	1	1

Решение:

4. Закрепление нового материала (15 мин).

Для закрепления материала учащимся раздаются карточки на два варианта для самостоятельной работы.

Вариант 1.

1. По заданной логической функции построить логическую схему и таблицу истинности.
Решение:

2. Выписать из логической схемы соответствующую ей логическую формулу:

А	В	F
0	0	1
0	1	0
1	0	1
1	1	0

Решение:

Вариант 2.

1. По заданной логической функции построить логическую схему и таблицу истинности.
Решение:

2. Выписать из логической схемы соответствующую ей логическую формулу:

А	В	F
0	0	0
0	1	0
1	0	1
1	1	0

Решение:

5. Постановка домашнего задания. (3 мин).

По заданной логической функции построить логическую схему и таблицу истинности.

6. Подведение итогов урока. (1 мин).

Проанализировать, дать оценку успешности достижения цели и наметить перспективу на будущее. Оценка работы класса и отдельных учащихся, аргументация выставления отметок, замечания по уроку.

Литература, эор:

1. Информатика и информационные технологии. Учебник для 10-11 классов, Н. Д. Угринович – 2007г.;

2. Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова – 2007г.

Логические основы цифровых схем | Composter 2.0

В некоторых случаях функции электической схемы можно представить с помощью логических операторов Булевой алгебры. Тогда говорят, что схема цифровая, т.е. подчиняется законам, хорошо иллюстрированным логическими операциями — инверсии, логического сложения, конъюнкции, исключающего «ИЛИ» и т.п. Первым исследовал эти законы Клод Шеннон в 1938 г. на примере электрических цепей с ключами. Впрочем, каждому из нас по силам придумать пример, иллюстрирующий физические явления, подчиняющиеся законам формальной логики.

Одной из самых распространенных аналогий является управление водопроводными кранами. Рассмотрим некоторые примеры из этой области, принимая во внимание, что по электрическим схемам тоже «течет ток».

Рис 1. Вентильные схемы работы логических элементов

Во времена первых компьютеров в ходу была диодная логика, по принципу действия в чем-то схожая с работой водопроводных вентилей. Сегодня логические схемы реализуются интегральными микросхемами с высокой плотностью компоновки полупроводниковых элементов, но иногда полезно вспомнить, как формируется один логический элемент с использованием нескольких диодов.

Подключение по схеме «ИЛИ»

Практическую пользу схемы «ИЛИ» трудно переоценить: существует множество схем питания, использующих логику двух входов с диодной коммутацией. Если на одном из входов или на обеих сразу высокий логический уровень, диод (диоды) проводит ток, обеспечивая на выходе Y логическую единицу.

Рис 2. Логический элемент «ИЛИ», выполненный на двух диодах и подтягивающем резисторе

В логических элементах, основанных на диодной логике возможны состояния, при которых все диоды закрыты: для приведенной схемы «ИЛИ» это состояние, когда на входах A и B присутствует низкий уровень либо они не подключены. В этом случае, элемент «ИЛИ» должен выдавать на выход уровень логического нуля, что и обеспечивается резистором, соединяющим выход с общим проводом.

Подключение по схеме «И»

Диодный элемент «И» состоит из двух входов и выхода (Y). На вход диодной схемы может подаваться логическая единица (ей соответствует высокий уровень сигнала) или логический ноль — коммутация на общий провод («земля»). Замкнутые ключи схемы формируют ноль на выходе. Единицу можно получить только в случае, если не нажат ни один из них: высокий логический уровень на обоих входах дает высокий логический уровень на выходе.

Рис 3. Логический элемент «И», выполненный на двух диодах и подтягивающем резисторе

Для приведенной схемы диодного элемента «И» закрытое состояние обоих диодов возможно при наличии высокого уровня на обоих входах. Аналогичный результат, отсутствие тока через диоды, будет иметь место когда ключи не замкнуты

Если подтягивающие резисторы не устанавливать

Если в схеме логического «ИЛИ» все входные диоды отключены (Рис 2.а) либо в схеме логического «И» все входные диоды отключены (Рис 3.а), на выходе будет так называемое Z-состояние — состояние высокого сопротивления, несущее неопределенность. Его восприятие зависит от схемотехники входных цепей, подключенных к выходу нашего логического элемента. Не исключено, что схема сохранит работоспособность и без подтягивающего резистора, если такой резистор (в явном виде или в виде паразитных цепей утечки) имеется во входной цепи следующего каскада. Рассчитывать на такой «подарок» не следует, поэтому неопределенность устраняется подключением терминирующего резистора.

Выбор номинала для подтягивающего резистора является компромиссом: при низком сопротивлении сигнал будет «просаживаться», при высоком — внешние факторы, такие как паразитные токи утечек, окажут на работу элемента существенное влияние, и требуемый логический уровень не будет гарантирован. Чтобы избежать неопределенности, формированием логического нуля следует считать соединение входа с общим проводом, логической единицы — соединение с плюсом источника питания, а неподключенного состояния следует избегать. Для этого и нужны подтягивающие резисторы. Как видим, приведенные выше схемы на основе кнопок нарушают правила терминации, опираясь на частные случаи и рассчитывая на предсказуемую реакцию диодной логики в неподключенном состоянии (при разомкнутой кнопке).

Вентили на полевых транзисторах

Для построения сложных схем требуются элементы, способные обеспечить развязку между управляющей и ведомой цепями. В качестве таких элементов используются транзисторы. Наиболее продуктивной для логических схем оказалась CMOS-технологиях их изготовления. В качестве основы для этих транзисторов используется комплементарная структура металл-оксид-полупроводник, что и определило название всего семейства.

Рис 4. N-канальный транзистор закрыт, когда потенциал на затворе равен истоковому

В работе N-канального СMOS-транзистора используется 5-вольтовая логика: ключ на его основе окажется закрытым, если на затвор прибора подать напряжение низкого уровня и открывается при подаче +5V. Напряжение на затворе управляет проводимостью между стоком и истоком «полевика», и этот факт разработчиком схемы может использоваться для реализации заданных возможностей.

Рис 5. N-канальный транзистор откроется, если на затвор подать положительный потенциал

Стоит только изменить уровень напряжения на затворе транзистора, и он откроется, переключаясь в проводимое состояние. Если нулевой уровень запирает логическую схему, то перевести ее в противоположное (открытое) состояние можно только подав относительно истока положительное напряжение. Его уровень должен превышать определенный барьер — threshold voltage. Конструкция транзисторов СMOS-логики такова, что порог срабатывания, как правило, выше 1,5 вольта.

Примечание. Если быть предельно точным, то для надежной работы схемы переключения требуется, чтобы напряжение на затворе превышало коммутируемое напряжение. Именно поэтому в импульсных регуляторах, где ШИМ-контроллер питается от +12V и коммутируемое напряжение равно +12V применяется Boost-цепочка, формирующая напряжение в пределах 20…24V для питания затворов.

Логические элементы и их типы, микросхемы и основы цифровой электроники

Существует три основных типа логических схем:

Схема отрицания НЕ — инвертор. Схема является одновходовой, на выходе которой сигнал «Y» возникает при отсутствии сигнала «х» на входе. На принципиальных схемах элемент НЕ изображается в виде прямоугольников (рис. 20.1). Его условным символом служит цифра 1, расположенная внутри прямоугольника в левом верхнем углу, и кружок, обозначающий линию выхода. Расположенная возле изображения логического элемента таблица истинности позволяет сделать вывод, каким будет сигнал на выходе при определенной комбинации логических сигналов на входе.

Схема совпадения И представляет собой многовходовую схему, на выходе которой сигнал «Y» возникает только при наличии сигналов «Хі, х2 … хп» одновременно на всех выходах. На рис. 20.2 приведено графическое изображение логического элемента с двумя входами -2И и его таблица истинности. Характерным отличием этого элемента на схемах, является наличие внутри прямоугольника английского знака «&» (английский союз «и» — логическое умножение), в левом верхнем углу.

Схема сборки ИЛИ — многовходовая схема, сигнал «у» на выходе которой, появляется при наличии сигнала хотя бы на одном из входов. На рис. 20.3 представлено графическое изображение схемы и ее таблица истинности.

Рис. 20.1. Условное графическое обозначение логического элемента НЕ (а) и таблица истинности (б)

Рис. 20.2. Условное графическое обозначение логического элемента И (а) и таблица истинности (б)

Рис. 20.3. Условное графическое обозначение логического элемента ИЛИ (а) и таблица истинности (б)

Существуют и более сложные логические схемы, представляющие собой соединение нескольких простейших схем. Для запоминания результатов преобразований, которые выполняются логическими схемами применяют элемент памяти — триггер. Его схема имеет два выхода (единичный и нулевой) и несколько входов. Триггер может находиться в одном из возможных состояний: единичном или нулевом. Состояние триггера зависит от вида (1 или 0) дискретного сигнала, поступающего на его вход.

Микросхемы серии 155

Большой популярностью среди радиолюбителей пользуются микросхемы серии 155, которые построены на основе так называемой транзисторно-транзисторной логики (ТТЛ). Эта серия включает многовходовые элементы И-НЕ, триггеры, счетчики, дешифраторы, запоминающие устройства и т.д. Напряжение питания микросхем серии 155 составляет 5±0,25 В, которое подается на выводы 14 (+5 В) и 7 (общий провод). При изображении логических элементов на принципиальных схемах подключение к ним источника питания, как правило, не показывают. Рассмотрим практическое использование в радиоэлектронных конструкциях микросхем серии 155. Наиболее часто в конструкциях используется микросхема K155ЛA3. Условное графическое изображение K155JIA3 приведено на рис. 20.4.а. В состав микросхемы входит четыре элемента 2И-НЕ, каждый из которых выполняет операцию логического умножения сигналов по двум входам с последующей инверсией результата на выходе. Следует отметить, что логический элемент, входящий в микросхему, может работать отдельно независимо от других, в связи с этим на принципиальных схемах элементы, составляющие микросхему, изображаются отдельно один от другого. На принципиальных схемах этот факт отмечают в буквенно-цифровом обозначении, например, DD1.1, DD1.2, DD1.3 и DD1.4 (рис. 20.4.6). Принципиальная схема одного логического элемента дана на рис. 20.5.

Рис. 20.4. Условное графическое изображение интегральной микросхемы К155ЛАЗ: а — без деления на элементы, б — с выделением входящих элементов 2И-НЕ

Как видно из представленной схемы, входящие в нее транзисторы имеют непосредственную связь. В схеме транзистор VT1 имеет два эмиттера и выполняет логическое умножение, VT2 — усиление, ѴТЗ — усиление, a ѴТ4 — инверсию сигнала. Необходимый режим работы транзисторов задается резисторами R1…R4. Диоды VD1…VD3 предназначены для защиты цепей от напряжения обратной полярности. В момент поступления напряжения на один или оба входа логического элемента (выводы 1 и 2), транзистор VT1 открыт. В то время, как транзистор VT2 закрыт, на базу транзистора VT4 поступает напряжение низкого логического уровня, которое закрывает этот транзистор. В то же время, транзистор ѴТЗ открыт, так как напряжение на его базе, наоборот, соответствует уровню логической 1.

Рис. 20.5. Принципиальная схема логического элементов 2И-НЕ, входящего в интегральную микросхему К155ЛАЗ

В итоге на выходе (вывод 3) элемента оказывается напряжение высокого логического уровня и через нагрузку проходит ток. Если подать на оба входа элемента сигнал, соответствующий логической единицы, то транзистор VT1 закроется, a ѴТ2 откроется. Транзисторы ѴТЗ и ѴТ4 переключатся в противоположные состояния, на выходе появится логический 0 и через нагрузку не будет идти ток. Основными параметрами логической микросхемы, состоящей из элементов И-НЕ, являются:

Напряжение питания Un.
Потребляемая от источника питания номинальная мощность Рном.
Пороговое напряжение Unop переключения логического элемента из одного состояния в другое.
Выходное напряжение Uвых логического 0 и единицы.
Время включения tвкл и выключения tвыкл.
Коэффициент разветвления по выходу Краз показывающий, какую из микросхем можно подключить к выходу данного элемента.

Литература: В.М. Пестриков. Энциклопедия радиолюбителя.

Логические схемы РЗА | Проект РЗА

С появлением микропроцессорных терминалов и контроллеров в жизнь энергетиков прочно вошли логические схемы. Это наиболее точный способ описать принципы работы современной релейной защиты, когда на принципиальной схеме множество элементов заменены одним “черным ящиком”.

Если вы хотите работать релейщиком, то вам необходимо уметь читать логические схемы также хорошо, как и принципиальные. Скажу больше – если вы имеете дело с микропроцессорной защитой и автоматикой, то принципиальная схема не имеет никакого смысла без логической. Одна является обязательным продолжением другой.

К счастью, научиться читать логические схемы достаточно просто, особенно если вы раньше работали с “электромеханикой”. Это так потому, что логические элементы можно заменить на небольшие релейно-контактные схемы, которые может прочесть любой релейщик.

Сегодня мы поговорим как раз о том, как это сделать.

Итак, рассматриваем пять наиболее распространенных логических элементов, создаем их схемы замещения на привычных контактах и катушках реле, а после рассматриваем пример перевода большой логической схемы в электромеханическую.

Статья будет полезна как начинающим релейщикам, так и тем, кто переходит с “электромеханики” на микропроцессорную релейную защиту. Поехали!

Наличие сигнала на определенном участке логической схемы обозначается как “1”, а отсутствие – как “0”. Для релейно-контактной схемы аналогия будет следующая: “1” – наличие оперативного напряжения на участке цепи (например, на катушке реле), а “0” – отсутствие напряжения.

В обычных схемах оперативное напряжение подается на участок цепи при помощи контакта (реле, ключа, блок-контакта и т.д.) Это означает, что логические элементы можно заменить контактами, соединенными определенным образом. Сделаем это.

Самые распространенные элементы, которые вы найдете в любой логической схеме – это “ИЛИ”, “И”, “НЕ”, “ТРИГГЕР” и “ТАЙМЕР”. Пороговые элементы (сравнение с уставкой) пока трогать не будем, для упрощения.

Логическое сложение «ИЛИ»

Правило работы «ИЛИ»: если на каком-либо одном или на обоих входах есть логическая «1», то на выходе тоже появится «1».

Для пояснения приведем Табл.1, где в первом и втором столбцах указаны значения входных сигналов, а в третьем — значение выходного. Как видно, при наличии хотя бы одного входного сигнала, мы получаем сигнал на выходе.

Какой релейно-контактной схеме это соответствует? Конечно параллельному соединению контактов (см. Рис.1) При этом контакты имитируют наличие/отсутствие входного сигнала, а катушка реле — выходной сигнал.

Вместо катушки может быть подключен следующий элемент, если наш элемент «ИЛИ» не является последним.

Стоит отметить, что входных сигналов у элемента «ИЛИ» может быть 2 и более (неограниченно).

Логическое умножение «И»

Правило работы «И»: на выходе появится «1», только если на обоих входах будут логические «1», в противном случае на выходе всегда будет «0».

Таблица 2 показывает зависимость между входными и выходными сигналами.

Элемент «И» соответствует последовательному соединению контактов — см. Рис.2

Логическая инверсия «НЕ»

Правило работы «НЕ»: если на входе присутствует «1», то на выходе будет «0», и наоборот. Инверсия меняет сигнал на противоположный.

Зависимости входного и выходного сигнала указаны в Табл. 3

Построить релейно-контактную схему для элемента «НЕ» сложнее, чем для первых двух. Здесь требуется применить промежуточное реле Х, с нормальнозамкнутым контактом — см. схему на Рис. 3.

Когда контакт А замыкается, контакт Х размыкается и обесточивает катушку С. И наоборот. Таким образом, мы получили релейно-контактную схему замещения инверсии.

RS-триггер

Триггер является элементарной ячейкой памяти, т.е. этот элемент запоминает значение выходного сигнала даже при исчезновении входного.

Правила работы «RS-триггера»:

При появлении на входе S логической «1», на выходе Т появится «1», но только если на входе R будет логический «0» (нет сигнала). При исчезновении сигнала на входе S, сигнал на выходе Т останется равным «1», т.е. триггер запомнит свое состояние. Сигнал на выходе Т сбросится только тогда, когда мы подадим «1» на вход R.

Вход R обнуляет состояние триггера, т.е. когда на нем «1», то на выходе Т всегда «0», независимо от сигнала на входе S.

Можно еще сказать, что триггер «взводится» по S, а «сбрасывается» по R, причем приоритетным является именно вход R.

Таблица 4 показывает зависимости сигналов на входах и выходе триггера. Обратите внимание, на то, что если на обоих входах триггера «0», то состояние на выходе мы знать не будем. Для этого нужно провести анализ предыдущих воздействий.

Схема замещения триггера приведена на Рис. 4. Эффект запоминания достигается применением схемы самоподхвата промежуточного реле. Когда контакт А замыкается, промежуточное реле Y одним своим контактом воздействует на выходное реле С, а другим подхватывает свое срабатывание. При этом реле Y остается сработавшим даже при размыкании контакта А.

Приоритетный сброс триггера организуется при помощи размыкающего контакта В (R),который включается последовательно с катушкой реле Y.

Таймер

Таймер соответствует схеме с реле времени на Рис. 5. Думаю, здесь подробные пояснения не нужны.

Укрупненные схемы замещения

Если логическая схема состоит из нескольких элементов, то можно набирать релейно-контактную схему последовательно включая схемы замещения.

На Рис.6 показана схема замещения для последовательно включенных элементов «ИЛИ» и «НЕ»

Построение комплексной схемы замещения

Ниже приведен видеоролик, в котором показан пример построения схемы замещения относительно большой логической схемы.

Заключение

Если вы имели дело только с электромеханическими реле, а теперь переходите на микропроцессорные терминалы, то вам необходимо уметь читать схемы логики. Любую логическую схему релейной защиты и автоматики можно преобразовать в релейно-контактную принципиальную схему. Для этого нужно последовательно соединить все схемы замещения логических элементов.

После преобразования вы сможете быстро прочитать логику терминала или контроллера и разобраться в их работе. Через несколько примеров вы научитесь читать логические схемы без дополнительных преобразований, что позволит эффективно работать с современной релейной защитой.

Такой метод достаточно трудоемкий для повседневной работы, но полезен на период обучения работе с МП РЗА.

Учебное пособие по

Digital Logic Gates — Таблица истинности Logic Gates

Мы также видели, что каждый вентиль имеет противоположную или дополнительную форму самого себя в виде логического элемента И-НЕ, элемента ИЛИ-НЕ и буфера, соответственно, и что любые из этих отдельных вентилей могут быть соединены вместе для образования более сложных комбинационных логических схем. .

Мы также видели, что в цифровой электронике и вентиль И-НЕ, и вентиль ИЛИ-ИЛИ могут быть классифицированы как вентили « Universal », поскольку их можно использовать для создания вентилей любого другого типа.Фактически, любая комбинационная схема может быть построена с использованием только двух или трех входных вентилей И-НЕ или ИЛИ-ИЛИ. Мы также увидели, что вентили НЕ и буферы — это устройства с одним входом, которые также могут иметь выход Tri-state с высоким импедансом, который можно использовать для управления потоком данных по общей шине данных.

Цифровые логические вентили могут быть изготовлены из дискретных компонентов, таких как резисторы, транзисторы и диоды, для формирования схем RTL (резисторно-транзисторная логика) или DTL (диодно-транзисторная логика), но современные цифровые интегральные схемы серии 74xxx производятся с использованием TTL (транзисторно-транзисторная логика) на основе технологии биполярных транзисторов NPN или гораздо более быстрой и маломощной транзисторной логики MOSFET на основе КМОП, используемой в логических микросхемах 74Cxxx, 74HCxxx, 74ACxxx и 4000 серии.

Восемь наиболее «стандартных» отдельных цифровых логических вентилей приведены ниже вместе с соответствующими таблицами истинности.

Стандартные логические ворота

Логика и ворота

Символ	Таблица истинности
2 входа И цифровой логический вентиль	B	А	Q
	0	0	0
	0	1	0
	1	0	0
	1	1	1
Логическое выражение Q = A.В	Читается как A И B дает Q

Логические ворота ИЛИ

Символ	Таблица истинности
	B	А	Q
	0	0	0
	0	1	1
	1	0	1
	1	1	1
Логическое выражение Q = A + B	Читается как A ИЛИ B дает Q

Инвертирование логических вентилей

Логический логический элемент NAND

Символ	Таблица истинности
	B	А	Q
	0	0	1
	0	1	1
	1	0	1
	1	1	0
Логическое выражение Q = A.B	Читается как И B дает НЕ Q

Логические ворота NOR

Символ	Таблица истинности
	B	А	Q
	0	0	1
	0	1	0
	1	0	0
	1	1	0
Логическое выражение Q = A + B	Читается как A ИЛИ B дает НЕ Q

Эксклюзивные логические ворота

Логические ворота Exclusive-OR (Ex-OR)

Символ	Таблица истинности
	B	А	Q
	0	0	0
	0	1	1
	1	0	1
	1	1	0
Логическое выражение Q = A ⊕ B	Читается как A ИЛИ B, но не . ОБА дает Q (нечетное)

Ворота Logic Exclusive-NOR (Ex-NOR)

Символ	Таблица истинности
	B	А	Q
	0	0	1
	0	1	0
	1	0	0
	1	1	1
Логическое выражение Q = A ⊕ B	Прочтите, если A И B, SAME дает Q (четное)

Логические ворота с одним входом

Шестнадцатеричный буфер

Символ	Таблица истинности
	А	Q
	0	0
	1	1
Логическое выражение Q = A	Читается как A дает Q

НЕ вентиль (инвертор)

Символ	Таблица истинности
	А	Q
	0	1
	1	0
Логическое выражение Q = не A или A	Считывается как инверсия A дает Q

Работа вышеупомянутых цифровых логических вентилей и их логических выражений может быть сведена в единую таблицу истинности, как показано ниже.Эта таблица истинности показывает взаимосвязь между каждым выходом основных цифровых логических вентилей для каждой возможной комбинации входов.

Сводная таблица истинности цифрового логического шлюза

В следующей таблице истинности логических вентилей сравниваются логические функции логических вентилей с 2 входами, описанных выше.

Входы		Вывод таблицы истинности для каждого гейта
B	А	И	NAND	ИЛИ	НОР	EX-OR	EX-NOR
0	0	0	1	0	1	0	1
0	1	0	1	1	0	1	0
1	0	0	1	1	0	1	0
1	1	1	0	1	0	0	1

Вывод таблицы истинности для шлюзов с одним входом
А	НЕ	Буфер
0	1	0
1	0	1

Подтягивающий и понижающий резисторы

Последний момент, о котором следует помнить, при соединении вместе цифровых логических вентилей для создания логических схем любые «неиспользуемые» входы вентилей должны быть подключены напрямую либо к логическому уровню «1», либо к логическому уровню «0» с помощью подходящего «Подтягивающий» или «Понижающий» резистор (например, резистор 1 кОм) для создания фиксированного логического сигнала.Это предотвратит «плавание» неиспользуемого входа затвора и ложное переключение затвора и схемы.

Помимо использования подтягивающих или понижающих резисторов для предотвращения смещения неиспользуемых логических вентилей, запасные входы вентилей и защелок также могут быть соединены вместе или подключены к оставшимся или запасным вентилям в одном корпусе ИС, как показано.

логических ворот | Электроника Клуб

Логические ворота | Клуб электроники

Символы | Таблицы истинности | ИС | НЕ | И | NAND | ИЛИ | NOR | EX-OR | EX-NOR | Комбинации | Подставляя

Следующая страница: Счетные схемы

Введение

Логические вентили обрабатывают сигналы, которые представляют истинный или ложный .Обычно положительное напряжение питания + Vs соответствует истине, а 0 В — ложному. Другие термины, используемые для истинного и ложного состояний, показаны в таблице, лучше всего знать их все.

Ворота идентифицируются по их функции: НЕ, И, ИЛИ, ИЛИ, ИЛИ, EX-OR и EX-NOR. Заглавные буквы обычно используются, чтобы прояснить, что этот термин относится к логическому элементу.

Обратите внимание, что логические вентили не всегда требуются, потому что простые логические функции могут выполняться переключателями или диодами, например:

Логические состояния
True	False
1	0
High	Low
+ VS	0V
On	Выкл.

Символы логического элемента

Есть две серии символов для логических вентилей.Традиционные символы имеют отличительные формы, благодаря которым их легко узнать, они широко используются в промышленности и образовании. МЭК (Международная электротехническая комиссия) символы представляют собой прямоугольники с символом внутри, показывающим функцию ворот. Они редко используются, несмотря на их официальный статус, но вам, возможно, потребуется узнать их для экзамена.

Традиционный

МЭК

Входы и выходы

Ворота

имеют два или более входа, за исключением элемента НЕ, у которого есть только один вход.Все ворота имеют только один выход. Обычно буквы A, B, C и так далее используются для обозначения входов, а Q используется для обозначения вывода. На этой странице входы показаны слева, а выход — справа.

Обратный круг (o)

Некоторые символы ворот имеют кружок на выходе, что означает, что их функция включает инвертирует вывода. Это эквивалентно подаче выходного сигнала через вентиль НЕ. Например, символ логического элемента И-НЕ ( N или И ), показанный справа, одинаков. как символ логического элемента И, но с добавлением инвертирующего круга на выходе.

Таблицы истинности

Таблица истинности — хороший способ показать функцию логического элемента. Он показывает состояния вывода для всех возможных комбинаций состояний ввода. В таблицах истинности обычно используются символы 0 (ложь) и 1 (истина). В приведенной в качестве примера таблице истинности показаны входы и выходы логического элемента И.

Ниже приведены сводные таблицы истинности, показывающие состояния вывода для все типы ворот с 2 и 3 входами. Это может быть полезно, если вы пытаетесь выбрать подходящие ворота.

Вход A	Вход B	Выход Q
0	0	0
0	1	0
1	0	0
1	1	1

Сводные таблицы истинности

В этих сводных таблицах истинности ниже показаны состояния выходов для всех типов вентилей с 2 и 3 входами. Обратите внимание, что ворота EX-OR и EX-NOR могут иметь только 2 входа.

Сводка для всех вентилей с 2 входами
Входы		Выход каждого гейта
A	B	И	NAND	OR	NOR	EX-OR	EX-NOR
0	0	0	1	0	1	0	1
0	1	0	1	1	0	1	0
1	0	0	1	1	0	1	0
1	1	1	0	1	0	0	1

Сводка для всех вентилей с 3 входами
Входы			Выход каждого гейта
A	B	C	И	NAND	OR	NOR
0	0	0	0	1	0	1
0	0	1	0	1	1	0
0	1	0	0	1	1	0
0	1	1	0	1	1	0
1	0	0	0	1	1	0
1	0	1	0	1	1	0
1	1	0	0	1	1	0
1	1	1	1	0	1	0

Логические ИС

Логические вентили доступны на ИС (микросхемах), которые обычно содержат несколько вентилей. того же типа, например, ИС 4001 содержит четыре логических элемента ИЛИ-НЕ с 2 входами.Существует несколько семейств логических ИС, которые можно разделить на две группы: серии 4000 и серии 74

Для сравнения различных семейств см. Страницу ИС.

Семейства 4000 и 74HC лучше всего подходят для проектов с батарейным питанием, потому что они будут работать с хорошим диапазоном питающих напряжений и потреблять очень мало энергии. Однако, если вы используете их для проектирования схем и исследования логических вентилей помните, что все неиспользуемые входы ДОЛЖНЫ быть подключены к источнику питания. питания (либо + Vs, либо 0V) , это применимо, даже если эта часть IC не используется в цепи!

Дополнительная информация: ИС серии 4000 | ИС 74 серии

Rapid Electronics: 4000 серия | 74 серии

НЕ вентиль (инвертор)

Элемент НЕ может иметь только один вход, а выход является обратным входу.Вентиль НЕ также называется инвертором.

Выход Q является истинным, когда вход A НЕ истинен: Q = НЕ A

Традиционный символ

Символ МЭК

И ворота

Логический элемент И может иметь два или более входов, его выход является истиной, если все входы истинны. Выход Q является истиной, если вход A И вход B оба истинны: Q = A AND B

Вход A	Вход B	Выход Q
0	0	0
0	1	0
1	0	0
1	1	1

Традиционный символ

Символ МЭК

вентиль NAND

NAND = N от И .Это логический элемент И с инвертированным выходом, как показано буквой «o» на выходе символа. Логический элемент И-НЕ может иметь два или более входов, его выход истинен, если НЕ все входы истинны. Выход Q является истинным, если вход A И вход B НЕ оба истинны: Q = НЕ (А И В)

Вход A	Вход B	Выход Q
0	0	1
0	1	1
1	0	1
1	1	0

Традиционный символ

Символ МЭК

OR ворота

Логический элемент ИЛИ может иметь два или более входов, его выход истинен, если хотя бы один вход истинен.Выход Q является истинным, если вход A ИЛИ вход B истинен (или оба из них истинны): Q = A ИЛИ B

Вход A	Вход B	Выход Q
0	0	0
0	1	1
1	0	1
1	1	1

Традиционный символ

Символ МЭК

NOR ворота

NOR = N или OR .Это логический элемент ИЛИ с инвертированным выходом, как показано буквой «o» на выходе символа. Логический элемент ИЛИ-НЕ может иметь два или более входов, его выход является истиной, если ни один из входов не является истиной. Выход Q является истинным, если НЕ входы A ИЛИ B истинны: Q = НЕ (A ИЛИ B)

Вход A	Вход B	Выход Q
0	0	1
0	1	0
1	0	0
1	1	0

Традиционный символ

Символ МЭК

Ворота EX-OR

EX включительно- OR .Это похоже на логический элемент ИЛИ, но за исключением того, что оба входа истинны. Выход верен, если входы A и B — РАЗНЫЕ . Ворота EX-OR могут иметь только 2 входа. Выход Q является истинным, если любой вход A истинен ИЛИ вход B истинен, , но не тогда, когда они оба верны : Q = (A И НЕ B) ИЛИ (B И НЕ A)

Вход A	Вход B	Выход Q
0	0	0
0	1	1
1	0	1
1	1	0

Традиционный символ

Символ МЭК

Ворота EX-NOR

EX включительно- NOR .Это вентиль EX-OR с инвертированным выходом, как показано буквой «o» на выходе символа. Ворота EX-NOR могут иметь только 2 входа. Выход Q является истинным, если входы A и B — это ТО ЖЕ (оба истинны или оба ложны): Q = (A И B) ИЛИ (НЕ A И НЕ B)

Вход A	Вход B	Выход Q
0	0	1
0	1	0
1	0	0
1	1	1

Традиционный символ

Символ МЭК

Комбинации логических вентилей

Логические вентили можно комбинировать для выполнения более сложных функций.

Например, чтобы создать выходной сигнал Q, который является истинным только тогда, когда вход A является истинным, а вход B — ложным, мы можем объединить вентиль НЕ и вентиль И, как показано.

Q = А И НЕ B

Разработка функции калитки

Таблицы истинности могут использоваться для определения функции комбинации ворот, такой как система, показанная ниже:

Начните с создания таблицы, показывающей все возможные комбинации входных данных (A, B и C в этом примере) с достаточным количеством дополнительных столбцов для каждого промежуточного вывода (D и E в этом примере), а также окончательного вывода (Q).Затем определите все промежуточные состояния вывода, заполняя таблицу по ходу дела. Эти промежуточные выходы формируют входы для следующих ворот (или ворот), поэтому вы можете использовать их для работы. выводит следующий вывод (ы), в этом примере это конечный вывод (Q).

D = НЕ (A ИЛИ B)
E = B AND C
Q = D OR E = (НЕ (A OR B)) OR (B AND C)

Таблица истинности показывает промежуточные выходы D и E, а также окончательный результат Q.

Входы			Выходы
A	B	C	D	E	Q
0	0	0	1	0	1
0	0	1	1	0	1
0	1	0	0	0	0
0	1	1	0	1	1
1	0	0	0	0	0
1	0	1	0	0	0
1	1	0	0	0	0
1	1	1	0	1	1

Замена одного типа ворот на другой

Логические вентили доступны на ИС, которые обычно содержат несколько вентилей одного типа, например, четыре логических элемента NAND с 2 входами или три логических элемента NAND с 3 входами.Это может быть расточительным, если требуется только несколько ворот, если все они не одного типа. Чтобы не использовать слишком много IC вы можете уменьшить количество входов затвора или заменить один тип затвора другим.

Уменьшение количества входов

Количество входов в вентиль можно уменьшить, соединив два (или более) входа вместе. На схеме показан логический элемент И с тремя входами, работающий как логический элемент И с двумя входами.

Создание гейта НЕ из логического элемента И-НЕ или НЕ-НЕ

При уменьшении логического элемента НЕ-И или ИЛИ-И до одного входа создается вентиль НЕ.Схема показывает это для логического элемента И-НЕ с 2 входами.

Любые ворота могут быть построены из ворот NAND или NOR

Помимо создания ворот НЕ, ворота И-НЕ или ИЛИ-НЕ можно комбинировать для создания ворот любого типа! Это позволяет построить схему только из одного типа ворот, NAND или NOR. Например, вентиль И — это вентиль И-НЕ, а затем вентиль НЕ (для отмены инвертирующей функции). Обратите внимание, что вентили И и ИЛИ нельзя использовать для создания других вентилей, потому что в них отсутствует функция инвертирования (НЕ).

Чтобы изменить тип ворот , например изменить OR на AND, вы должны сделать три вещи:

Инвертировать (НЕ) каждый вход.
Измените тип ворот (ИЛИ на И или И на ИЛИ)
Инвертировать (НЕ) вывод.

Например, логический элемент ИЛИ может быть построен из входов NOTed, подаваемых в логический элемент И-НЕ (И + НЕ).

Эквиваленты ворот NAND

В приведенных ниже схемах показано, как использовать логические элементы И-НЕ для создания вентилей НЕ, И, ИЛИ и ИЛИ:

НЕ сделано из одного логического элемента NAND:

И состоит из двух ворот NAND:

ИЛИ из трех ворот NAND:

NOR состоит из четырех вентилей NAND:

Подстановка вентилей в примерную логическую систему

Эта система имеет 3 разных логических элемента (ИЛИ, И и ИЛИ), поэтому требуется три ИС, по одной для каждого типа ворот.

Чтобы перепроектировать эту систему с использованием логических элементов NAND, начните только с замены каждого гейт с его эквивалентом логического элемента NAND, как показано ниже:

Затем упростите систему, удалив соседние пары вентилей НЕ (отмечены X выше). Это может быть сделано, потому что вторые ворота НЕ отменяют действие первых:

Последняя система имеет пять логических элементов NAND и требует двух микросхем (по четыре логических элемента на каждой микросхеме). Это лучше, чем исходная система, для которой требовалось три микросхемы (по одной для каждого типа ворот).

Замена ворот NAND (или NOR) не всегда увеличивает количество ворот, но когда это происходит (как в этом примере), увеличение обычно составляет только одно или два входа. Настоящая выгода заключается в уменьшении количества требуемых микросхем за счет использования только одного типа затвора.

Следующая страница: Счетные схемы | Исследование

Политика конфиденциальности и файлы cookie

Этот сайт не собирает личную информацию. Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет используется только для ответа на ваше сообщение, оно не будет передано никому.На этом веб-сайте отображается реклама, если вы нажмете на рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден. Рекламодателям не передается никакая личная информация. Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации. Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов. (включая этот), как объяснил Google.Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста, посетите AboutCookies.org.

Logic Gates — Computer Science GCSE GURU

Topics / Boolean Logic / Logic Gates

Логические вентили — это строительные блоки цифровой схемы.

Каждый терминал логического элемента всегда будет в одном из двух двоичных состояний (0) или (1).

Эти двоичные состояния представляют наличие (1) или отсутствие (0) электрического напряжения.Двоичный (1) может называться положительным или ВКЛ, а двоичный (0) может называться отрицательным или ВЫКЛ.

Существует много типов логических вентилей, каждый со своими характеристиками.

На нашей странице «Логические схемы» объясняется, как эти вентили могут быть соединены вместе, чтобы сформировать схемы.

Логические ворота

Имя	Объяснение	Обозначение
НЕ	Инвертирует токовый выход, поэтому положительный (1 или ВКЛ.) Становится отрицательным (0 или ВЫКЛ. ), в то время как отрицательный (0 или OFF) станет положительным (1 или ON).	Z = НЕ A
AND	Оба входа должны быть положительными (1), прежде чем выход также станет положительным (1).	Z = A AND B
OR	По крайней мере, один вход должен быть положительным (1), чтобы дать положительный выход (1 или ВКЛ). Оба входа также могут быть положительными.	Z = A OR B
NAND	NOT AND. То же, что И, но обратный (НЕ) результат.Итак, сначала выполните И, затем примените НЕ к выходу.	Z = A NAND B
NOR	НЕ ИЛИ. То же, что ИЛИ, но обратный (НЕ) результат. Итак, сначала выполните ИЛИ, а затем примените НЕ к выходу.	Z = A NOR B
XOR	Исключительное ИЛИ. Только один вход может быть положительным (1 или ВКЛ) для получения положительного выхода (1). Если оба входа положительны (1), то результат отрицательный (0 или ВЫКЛ).	Z = A XOR B

Проверьте свои знания логических вентилей с помощью нашей быстрой викторины.

Таблицы истинности логического элемента

Таблицы истинности используются для расчета выходного сигнала логического элемента или схемы.

Каждая возможная комбинация двоичных входов содержится в таблице истинности. Отсюда мы можем ясно увидеть, каким будет результат в любом сценарии.

НЕ

НЕ таблица истинности ворот

Вход A	Выход Z
0	1
1	0

И

Таблица истинности ворот

Вход A	Вход B	Выход Z
0	0	0
0	1	0
1	0	0
1	1	1

OR

Таблица истинности ворот OR

Вход A	Вход B	Выход Z
0	0	0
0	1	1
1	0	1
1	1	1

NAND

Таблица истинности ворот NAND

Вход A	Вход B	Выход Z
0	0	1
0	1	1
1	0	1
1	1	0

NOR

Таблица истинности ворот NOR

Вход A	Вход B	Выход Z
0	0	1
0	1	0
1	0	0
1	1	0

XOR

XOR gate таблица истинности

90 035

Вход A	Вход B	Выход Z
0	0	0
0	1	1
1	0	1
1	1	0

Проверьте свои знания таблиц истинности с помощью нашей быстрой викторины.

Темы / Логическая логика / Логические вентили

Связанная теория

Логические схемы
Логические утверждения

Сопутствующие тесты

Таблицы истинности логических вентилей
Логические вентили

Цифровые сигналы и вентили | Логические ворота

Хотя двоичная система счисления представляет собой интересную математическую абстракцию, мы еще не видели ее практического применения в электронике. Эта глава посвящена именно этому: практическому применению концепции двоичных битов к схемам.

Что делает двоичное счисление таким важным для приложений цифровой электроники, так это легкость, с которой биты могут быть представлены в физических терминах. Поскольку двоичный бит может иметь только одно из двух разных значений, 0 или 1, для представления бита может использоваться любая физическая среда, способная переключаться между двумя состояниями насыщения.

Следовательно, любая физическая система, способная представлять двоичные биты, способна представлять числовые величины и потенциально имеет возможность манипулировать этими числами.Это основная концепция, лежащая в основе цифровых вычислений.

Двоичные и электронные схемы

Двоичный режим транзистора

Электронные схемы — это физические системы, которые хорошо подходят для представления двоичных чисел. Транзисторы, когда работают с предельными значениями смещения, могут находиться в одном из двух различных состояний: отключенном (отсутствие контролируемого тока) или насыщении (максимальный управляемый ток). Если схема транзистора спроектирована так, чтобы максимизировать вероятность попадания в одно из этих состояний (и не работает в линейном или активном режиме), она может служить физическим представлением двоичного бита.

Вход транзистора на «высокий»

Сигнал напряжения, измеренный на выходе такой схемы, также может служить представлением одного бита, при этом низкое напряжение представляет двоичный «0», а (относительно) высокое напряжение представляет двоичную «1». Обратите внимание на следующую схему транзистора:

В этой схеме транзистор находится в состоянии насыщения благодаря приложенному входному напряжению (5 вольт) через двухпозиционный переключатель. Из-за насыщения транзистор очень мало теряет напряжение между коллектором и эмиттером, что приводит к выходному напряжению (практически) 0 вольт.

Если бы мы использовали эту схему для представления двоичных разрядов, мы бы сказали, что входной сигнал — это двоичная «1», а выходной сигнал — двоичный «0». Любое напряжение, близкое к полному напряжению питания (разумеется, по отношению к земле), считается «1», а отсутствие напряжения считается «0».

Альтернативные термины для этих уровней напряжения: высокий (то же, что и двоичная «1») и низкий (то же, что двоичный «0»). Общий термин для представления двоичного бита напряжением цепи — это логический уровень .

Низкий уровень на входе транзистора

Перемещая переключатель в другое положение, мы прикладываем двоичный «0» к входу и получаем двоичную «1» на выходе:

Что такое логические ворота?

То, что мы создали здесь с одним транзистором, — это схема, известная как логический вентиль или просто вентиль . Затвор — это особый тип схемы усилителя, предназначенный для приема и генерации сигналов напряжения, соответствующих двоичным единицам и нулям.

Таким образом, вентили не предназначены для использования для усиления аналоговых сигналов (сигналов напряжения между 0 и полным напряжением). При совместном использовании несколько вентилей могут применяться к задаче хранения двоичных чисел (схемы памяти) или манипулирования (вычислительные схемы), причем выход каждого логического элемента представляет один бит многобитового двоичного числа.

Как это делается, — тема следующей главы. Сейчас важно сосредоточиться на работе отдельных ворот.

Инвертор или НЕ затвор

Показанный здесь затвор с одиночным транзистором известен как инвертор , или НЕ затвор, потому что он выводит цифровой сигнал, прямо противоположный входному.Для удобства схемы затвора обычно представлены своими собственными символами, а не составляющими их транзисторами и резисторами. Ниже приводится символ инвертора:

Здесь показан альтернативный символ для инвертора:

Условное обозначение ворот НЕ

Обратите внимание на треугольную форму символа затвора, очень похожую на форму операционного усилителя. Как было сказано ранее, схемы затвора на самом деле являются усилителями.

Маленький кружок или «пузырек», показанный на входной или выходной клемме, является стандартным для представления функции инверсии. Как вы могли догадаться, если бы мы удалили пузырек из символа ворот, оставив только треугольник, получившийся символ больше не означал бы инверсию, а просто прямое усиление.

Такой символ и такой вентиль действительно существуют, и они называются буфером , которому посвящен следующий раздел.

Подобно символу операционного усилителя, входные и выходные соединения показаны как одиночные провода, подразумеваемая контрольная точка для каждого сигнала напряжения — «земля».В схемах с цифровым затвором заземление почти всегда является отрицательным соединением единственного источника напряжения (источника питания).

Двойные или «разделенные» источники питания редко используются в схемах затвора. Поскольку схемы затвора являются усилителями, для работы им требуется источник питания. Как и в случае с операционными усилителями, разъемы питания для цифровых ворот часто для простоты опускаются на символе.

НЕ Ворота в цепях

Если бы мы показали все соединения, необходимые для работы этих ворот, схема выглядела бы примерно так:

Проводники источника питания редко показаны на схемах цепи затвора, даже если есть соединения источника питания на каждом затворе.Свернув линии в нашей схеме, мы получим:

«Vcc» обозначает постоянное напряжение, подаваемое на коллектор схемы биполярного переходного транзистора по отношению к земле. Все точки в цепи затвора, отмеченные меткой «Vcc», подключены к одной и той же точке, и эта точка является положительной клеммой источника постоянного напряжения, обычно 5 вольт.

Как мы увидим в других разделах этой главы, существует довольно много различных типов логических вентилей, большинство из которых имеют несколько входных клемм для приема более одного сигнала.Выход любого вентиля зависит от состояния его входа (ов) и его логической функции.

Выражение функций схемы затвора с помощью таблиц истинности

Один из распространенных способов выразить конкретную функцию схемы затвора называется таблицей истинности. Таблицы истинности показывают все комбинации входных условий в терминах состояний логического уровня («высокий» или «низкий», «1» или «0» для каждой входной клеммы логического элемента) вместе с соответствующим выходным логическим уровнем, либо «Высокий» или «низкий».«Для только что проиллюстрированной схемы инвертора, или НЕ, таблица истинности действительно очень проста:

Таблицы истинности для более сложных ворот, конечно, больше, чем таблица, показанная для ворот НЕ. Таблица истинности гейта должна иметь столько строк, сколько есть возможностей для уникальных входных комбинаций.

Для элемента с одним входом, такого как элемент НЕ, есть только две возможности, 0 и 1. Для элемента с двумя входами есть четыре возможности (00, 01, 10 и 11), и, следовательно, четыре строки для соответствующих таблица истинности.

Для вентиля с тремя входами существует восемь возможностей (000, 001, 010, 011, 100, 101, 110 и 111), и поэтому необходима таблица истинности с восемью строками. Те, кто склонен к математике, поймут, что количество строк таблицы истинности, необходимых для логического элемента, равно 2, возведенному в степень числа входных клемм.

ОБЗОР:

В цифровых схемах двоичные битовые значения 0 и 1 представлены сигналами напряжения, измеренными относительно общей точки схемы, называемой землей.Отсутствие напряжения представляет собой двоичный «0», а наличие полного напряжения питания постоянного тока представляет двоичную «1».
Логический вентиль или просто вентиль — это особая форма схемы усилителя, предназначенная для ввода и вывода напряжений логического уровня (напряжения, предназначенные для представления двоичных битов). Схемы затвора чаще всего представлены в схемах их собственными уникальными символами, а не составляющими их транзисторами и резисторами.
Так же, как и в случае с операционными усилителями, соединения источника питания с затворами часто для простоты опускаются на схематических диаграммах.
Таблица истинности — это стандартный способ представления отношений входа / выхода схемы затвора, в котором перечислены все возможные комбинации логических уровней входа с соответствующими уровнями логики выхода.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Логические ворота

— Digilent Blog

Сама основа компьютеров бинарна. В электронике все сводится к единицам и нулям. Логические вентили — это цифровые схемы, которые принимают один или несколько двоичных входов и создают двоичный выход.Вы можете проверить основы логики с помощью булевой алгебры.

Есть семь основных логических вентилей, которые мы собираемся рассмотреть сегодня.

Изображение из Википедии.

Из этого сообщения в блоге вы можете видеть, что большинство ворот принимают два входа (X и Y). НЕ — единственное исключение, принимающее 1 вход. Каждому из этих ворот соответствует таблица истинности и логический символ (мы узнаем об этом позже).

И довольно просты. Если X и Y не равны 1, будет выведен 0.

NAND является отрицанием AND. Выход всегда будет 1 , если X и Y не равны 1, когда выход будет 0.

OR — включение одного или нескольких входов создаст выход 1. С OR , X и Y могут быть 1, а выход будет 1.

NOR является отрицанием OR. Если X или Y равны 1 или X и Y равны 1, то на выходе будет 0.В NOR единственные входы для выхода 1 — это когда X и Y равны 0.

XOR — это то, что некоторые люди предполагали, OR , эксклюзивный OR . XOR выдаст результат 1 только в том случае, если между X и Y есть только 1. Два нуля или две единицы будут выводить 0.

XNOR является инверсией XOR , что означает, что только два нуля и две единицы дадут результат 1. XNOR кажется намного ближе к И , но важно помнить, что это инверсия XOR .

НЕ — простейший логический вентиль. Если передано 1, оно становится 0. Если передано 0, оно становится 1.

Эти семь логических вентилей довольно просты, но при использовании вместе друг с другом их можно использовать для создания интегральных схем!

Логические ворота

Изучив этот раздел, вы сможете:
Опишите действие логических вентилей.
• AND, OR, NAND, NOR, NOT, XOR и XNOR.
• Использование логических выражений.
• Использование таблиц истинности.
Разберитесь в использовании универсальных ворот.
• NAND.
• NOR.
Распознавать общие микросхемы серии 74, содержащие стандартные логические вентили.

Логические ворота

Семь основных логических вентилей

Фиг.2.1.1 Символы ворот ANSI и IEC

Цифровая электроника полагается на действия всего семи типов логических вентилей, называемых И, ИЛИ, И-НЕ (Не И), ИЛИ (Не ИЛИ), XOR (Исключающее ИЛИ), XNOR (Исключающее ИЛИ) и НЕ.

Рис. 2.1.1 иллюстрирует выбор основных логических вентилей, которые доступны от ряда производителей в стандартных семействах интегральных схем. Каждое семейство логики спроектировано таким образом, чтобы вентили и другие логические ИС в этом семействе (и других связанных семействах) можно было легко комбинировать и встраивать в более крупные логические схемы для выполнения сложных функций с минимумом дополнительных компонентов.

В двоичной логике разрешены только два состояния: 1 и 0 или «включено и выключено». слово НЕ в мире двоичной логики означает «противоположность». Если что-то не 1, это должно быть 0, если оно не включено, оно должно быть выключено. Таким образом, NAND (не AND) просто означает, что вентиль NAND выполняет функцию, противоположную вентилю AND.

Логический вентиль — это небольшая транзисторная схема, в основном тип усилителя, который реализован в различных формах внутри интегральной схемы. Каждый тип ворот имеет один или несколько (чаще всего два) входа и один выход.

Принцип работы состоит в том, что схема работает только на двух уровнях напряжения, называемых логическим 0 и логическим 1. Эти значения представлены двумя разными уровнями напряжения. В 5-вольтовой логике 1 идеально представлена 5В, а 0 — 0В, а в 3,3В логическая 1 идеально представлена 3,3В, а логический 0 — 0В. Когда любой из этих уровней напряжения подается на входы, выход затвора реагирует, принимая уровень 1 или 0, в зависимости от конкретной логики затвора. Логические правила для каждого типа ворот можно описать по-разному; письменным описанием действия, таблицей истинности или оператором булевой алгебры.

Логические выражения

Рис. 2.1.2 Логические символы для ворот

Действия любого из этих вентилей также можно описать с помощью логических операторов. В них используются буквы из начала алфавита, такие как A, B, C и т. Д., Для обозначения входов и буквы из второй половины алфавита, очень часто X или Y (а иногда Q или P) для обозначения выходных данных. Буквы сами по себе не имеют никакого значения, кроме обозначения различных точек в цепи. Затем буквы соединяются логическим символом, указывающим логическое действие ворот.

Символ • обозначает И, хотя во многих случаях символ • может быть опущен. (A • B может также записываться как AB или A.B)

+ обозначает ИЛИ

⊕ означает XOR (Исключающее ИЛИ)

Хотя символы • и + такие же, как и символы, используемые в нормальной алгебре для обозначения произведения (умножения) и суммы (сложения) соответственно, в двоичной логике символ + не совсем соответствует сумме. В цифровой логике 1 + (ИЛИ) 1 = 1, но двоичная сумма 1 + 1 = 10 ₂, поэтому в цифровой логике + всегда следует рассматривать как ИЛИ.

Три дополнительных типа логических вентилей дают выходной сигнал, который является инвертированной версией трех основных функций вентилей, перечисленных выше, и они обозначены полосой, нарисованной над оператором, с использованием символов И, ИЛИ или ИСКЛЮЧАЮЩЕЕ ИЛИ для обозначения И-НЕ, ИЛИ ИЛИ и XNOR.

A • B означает A AND B, но A • B означает A NAND B

Таким образом, действие любого из вентилей может быть описано с помощью его булевого уравнения.

Например, вентиль И дает выход логической 1, когда вход A И вход B находятся на логической 1, но вентиль И-НЕ дает выход логического 0 для тех же условий входа.Также, если вентиль И дает логический ноль для конкретной входной комбинации, вентиль И-НЕ даст логическую 1. Таким образом, буква «N» в имени логического элемента или полоса над логическим выражением указывает на то, что выходная логика «инвертирована». . В цифровой логике NAND — это NOT AND или противоположность AND. Точно так же NOR — это «NOT» OR, а XNOR — это «NOT» XOR.

Описание действия логических вентилей

В качестве альтернативы действие любого из 7 типов логического элемента может быть описано с использованием письменного описания его логической функции.

Выход логического элемента И находится на уровне логической 1, когда и только когда все его входы находятся на уровне логической 1, в противном случае выход находится на уровне логического 0.
Выход логического элемента ИЛИ является логической 1, когда один или несколько его входов находятся на уровне логической 1. Если все его входы имеют логическую единицу, выход имеет логический 0.
Выход логического элемента И-НЕ находится в состоянии логического 0, когда и только когда все его входы имеют логический уровень 1. В противном случае выход имеет логический 0.
Выход логического элемента ИЛИ-НЕ имеет логический 0, когда один или несколько его входов имеют логическую 1.Если все его входы имеют логический 0, выход — логический 1.
Выход элемента XOR находится на уровне логической 1, когда и только один из его входов находится на уровне логической 1. В противном случае выход имеет логический 0.
Выход логического элемента ИСКЛЮЧАЮЩЕЕ ИЛИ, когда один и только один из его входов находится в состоянии логической 1. В противном случае выход имеет логическую единицу (поэтому он аналогичен элементу ИСКЛЮЧАЮЩЕЕ ИЛИ, но его выход инвертирован).
Выход логического элемента НЕ находится на уровне логического 0, когда его единственный вход находится на уровне логической 1, и на уровне логической 1, когда его единственный вход находится на уровне логического 0.По этой причине его часто называют ИНВЕРТОРОМ.

дел>

Рис. 2.1.3 Таблицы истинности

Таблицы истинности

Еще один полезный способ описать действие цифрового шлюза (или всего цифрового cicuit) — использовать таблицу истинности. Каждая таблица состоит из двух или более столбцов, по одному столбцу для каждого ввода или вывода; количества строк в столбце будет достаточно для записи всех возможных логических состояний для этого входа или выхода. На рис. 2.1.3 показаны две типичные таблицы истинности для схем разного уровня сложности.

Верхний стол для простого двух входов и ворот. У него есть два входа, обозначенные A и B, и один столбец (X) для вывода. Сравнивая таблицу истинности с письменным описанием в разделе «Описание действия логических вентилей» (выше), можно увидеть, что таблица истинности следует письменному описанию, показывая, что выход X находится на уровне 1 только тогда, когда входы A и B находятся на уровне логики. 1, в противном случае (где три верхние строки — 00, 01 и 10) на выходе будет логический 0.

Вторая таблица на рис.2.1.3 описывает более сложную схему (из пяти вентилей NAND, имитирующих вентиль XOR). Обратите внимание, что теперь таблица истинности расширена, чтобы проиллюстрировать логические уровни на четырех дополнительных входах или выходах в дополнение к входам A и B до того, как окончательный выход X будет проиллюстрирован в правом столбце. Такие сложные таблицы могут иметь большое значение как при проектировании цифровых схем, так и при поиске неисправностей.

И Выход

NAND Gate

OR Выход

NOR Gate

Шлюз XOR

Выход XNOR

НЕ Выходной

Фиг.2.1.4 Анимация логических ворот (щелкните любой вентиль)

Анимация логических ворот

На рис. 2.1.4 вы можете проверить работу основных логических вентилей. Анимация ворот позволяет вам выбрать любой из 7 основных ворот и увидеть новую страницу с анимированным изображением действующих ворот. Используйте анимацию, чтобы познакомиться с работой каждого из ворот. Чтобы вернуться на эту страницу, просто закройте страницу с анимацией.

Чтобы легко понять более сложные цифровые схемы, важно создать хорошее мысленное представление об ожидаемом выходе каждого логического элемента для любого возможного входа.

Анимации, представленные на рис. 2.1.4, также показывают, как семь основных логических функций могут быть описаны с помощью «таблицы истинности», чтобы показать взаимосвязь между выходом (X) и всеми возможными комбинациями входов для входов A и B, показанных как четырехзначный двоичный счетчик от 00 до 11. Каждая анимированная диаграмма показывает условия ввода и вывода для одной из семи логических функций в форме двух входов. Однако некоторые типы ворот также доступны с большим количеством входов (например, от 3 до 13). Для этих ворот таблицы истинности должны быть расширены, чтобы включать все возможные входные условия.

Универсальные ворота

Поскольку вентили производятся в форме ИС, обычно содержащей от двух до шести вентилей одного и того же типа, часто неэкономично использовать полную ИС из шести вентилей для выполнения определенной логической функции. Лучшим решением может быть использование только одного типа вентилей для выполнения любых необходимых логических операций. Два типа вентилей, И-НЕ и ИЛИ-ИЛИ, часто используются для выполнения функций любых других стандартных вентилей, путем соединения нескольких из этих «универсальных» вентилей в комбинационную схему.Хотя использование нескольких универсальных вентилей для выполнения функции одного логического элемента может показаться неэффективным, если в одной или нескольких ИС И ИЛИ и ИЛИ ИС имеется несколько неиспользуемых вентилей, их можно использовать для выполнения других функций, таких как И или ИЛИ. вместо использования дополнительных микросхем для выполнения этой функции. Этот метод особенно полезен при проектировании сложных ИС, где целые схемы внутри ИС могут быть изготовлены с использованием одного типа затвора.

На рис. 2.1.5 от a до g показано, как можно использовать вентили NAND для получения любой из стандартных функций, используя только этот тип единственного логического элемента.

Рис. 2.1.5 Создание любой логической функции с использованием шлюзов И-НЕ

Функция НЕ

а. Соединение входов логического элемента И-НЕ вместе создает функцию НЕ.

г. В качестве альтернативы, функция НЕ может быть реализована путем использования только 1 входа и постоянного подключения другого входа к логической 1.

И функция

г. Добавление функции НЕ (инвертора) к выходу логического элемента И-НЕ создает функцию И.

ИЛИ Функция

г.Инвертирование входов в логический элемент И-НЕ создает функцию ИЛИ.

Функция NOR

e. Использование функции НЕ для инвертирования вывода функции ИЛИ создает функцию ИЛИ.

Функция XOR

ф. Четыре логических элемента NAND (одна микросхема), подключенные, как показано, создают функцию XOR (а микросхема Quad NAND примерно на 15% дешевле, чем микросхема Quad XOR).

Функция XNOR

г. Инвертирование вывода функции XOR создает функцию XNOR.

Аналогичные преобразования могут быть достигнуты с использованием вентилей ИЛИ-ИЛИ, но поскольку вентили И-НЕ являются, как правило, наименее дорогими ИС, преобразования, показанные на рис.2.1.5 используются чаще. Причиной таких преобразований обычно является стоимость. Это может показаться не очень полезным, поскольку ни одна из основных микросхем серии 74 не является дорогостоящей, но когда должно быть изготовлено несколько тысяч единиц конкретной схемы, небольшая экономия затрат и места на печатных платах за счет максимального использования неиспользуемых вентилей. в микросхемах с несколькими затворами может стать очень важным.

Рис. 2.1.6 Логические вентили из семейства ТТЛ IC серии 74

Логические ИС

Как правило, стандартные логические вентили доступны в 14- или 16-контактных микросхемах DIL (двойная линия).Количество вентилей на одну ИС варьируется в зависимости от количества входов на вентиль. Обычно используются вентили с двумя входами, но если требуется только один вход, например, в вентилях 7404 NOT (или инверторах), 14-контактная ИС может вмещать 6 (или шестнадцатеричных) вентилей. Наибольшее количество входов на один вентиль находится на вентиле И-НЕ 74133 с 13 входами, который размещен в 16-выводном корпусе.

Спецификации

7400 Четыре входа NAND, 2 входа

7402 Quad 2 входа NOR вентили

7404 Затворы Hex NOT (инверторы)

7408 Quad 2 входа И вентили

7432 Quad 2 входа ИЛИ вентили

7486 Четыре входа XOR, 2 входа

747266 Четыре входа XNOR, 2 входа

74133 Одиночный логический элемент И-НЕ с 13 входами

логических ворот | Блестящая вики по математике и науке

Логические вентили

построены с использованием различных комбинаций транзисторов, которые в основном представляют собой переключатели с электрическим управлением.Есть два типа транзисторов: PNP и NPN. Мы будем использовать последний в следующих примерах:

NPN-транзистор позволяет основному току течь от его входа, называемого «коллектор», к его выходу, называемому «эмиттер», когда к «базе» подается небольшой ток. Это соответствует замкнутому переключателю и логическому состоянию «1». Когда ток не подается на базу, транзистор больше не позволяет току течь от коллектора к эмиттеру.Это соответствует разомкнутому переключателю и логическому состоянию «0».

И

Когда ток подается на базу обоих транзисторов (то есть, когда a = 1a = 1a = 1 ANDANDAND b = 1b = 1b = 1), основной ток может свободно течь от верхнего коллектора транзистора ‘a’ все путь к нижнему эмиттеру транзистора «б». Если только одна из двух баз находится в состоянии «включено», основной ток будет заблокирован при достижении транзистора в состоянии «выключено» и не сможет течь.Очевидно, что если оба транзистора выключены, ток тоже не будет протекать.

ИЛИ

Когда небольшой ток подается на один из двух транзисторов или, что еще лучше, на оба из них, основной ток свободно течет сверху вниз по цепи. Только когда оба транзистора находятся в выключенном состоянии, ток не будет течь.

НЕ

Этот конкретный затвор может быть выполнен даже с одним единственным транзистором.Когда к базе передатчика не подается ток (т.е. a = 0a = 0a = 0), основной ток не сможет протекать через транзистор, и его единственный выход — пройти через провод a‾ \ overline {a} a; таким образом, a‾ = 1 \ overline {a} = 1a = 1. С другой стороны, когда на базу транзистора подается небольшой ток (a = 1) a = 1) a = 1), весь основной ток будет проходить через него, и ток не пойдет на провод a‾ \ надчеркнуть {а} а; таким образом, a‾ = 0 \ overline {a} = 0a = 0.

Примечание. Хотя показанные логические элементы И и ИЛИ довольно просты при построении реальной схемы, вентиль НЕ требует некоторых дополнительных компонентов для обеспечения надлежащих рабочих условий.Тем не менее, основная концепция остается прежней.