Схемы операционных усилителей: Операционный усилитель? Это очень просто!

Кафедра технологии бетона и строительных материалов — Технологии определяют всё

Является одним из старейших подразделений современного Брестского технического университета.

История кафедры начинается с 1967 года, когда ещё в Брестском инженерно-строительном институте (сегодня Брестский государственный  технический университет)  была основана кафедра «Строительные материалы».

Кафедру возглавляли:
Жоров Владимир Леонтьевич, к.т.н., доцент (с 1967  по 1977 год)
Зайцев Анатолий Алексеевич, к.т.н., доцент (с 1977 по 1987 год)
Волкова Флора Николаевна, к.т.н., доцент (с 1987-1988 год).

В 1988 году кафедра «Строительные материалы» была объединена с кафедрой «Технология строительного производства». Объединённая кафедра стала называться «Технология строительного производства и строительные материалы», которую возглавляли:
Бобко Фадей Александрович к.т.н., доцент (с 1988 по 1989 год)
Голубицкая Галина Андреевна, к.т.н., доцент  (с 1989 по1991 год)
Плосконосов Владимир Николаевич, к.

т.н., доцент  ( с 1991 по 1992 год).

В 1991 году в институте открывается подготовка инженеров-технологов-строителей по специальности  «Производство строительных изделий и конструкций». Организация учебного процесса по данной специальности возложена на кафедру «Технологии строительного производства и строительных материалов». Разнообразие направлений работы кафедры не позволяет эффективно управлять её деятельностью и требует совершенствования структуры управления учебным процессом. В связи с чем приказом ректора по Брестскому политехническому  институту №67 от 12 июня 1992 года в отдельное подразделение выделяется уже кафедра  «Технологии бетона и строительных материалов» которую с 1992 по1993 год возглавляет Довнар Надежда Ивановна, к.т.н., доцент.

С 1993 года кафедрой  руководит Тур Виктор Владимирович, профессор, доктор технических наук.

Кафедра технологии бетона и строительных материалов является выпускающей кафедрой по специальности 70 01 01 «Производство строительных изделий и конструкций» и готовит специалистов, имеющих квалификацию инженер-строитель-технолог, что позволяет им работать практически в любом направлении строительного, и не только, производства.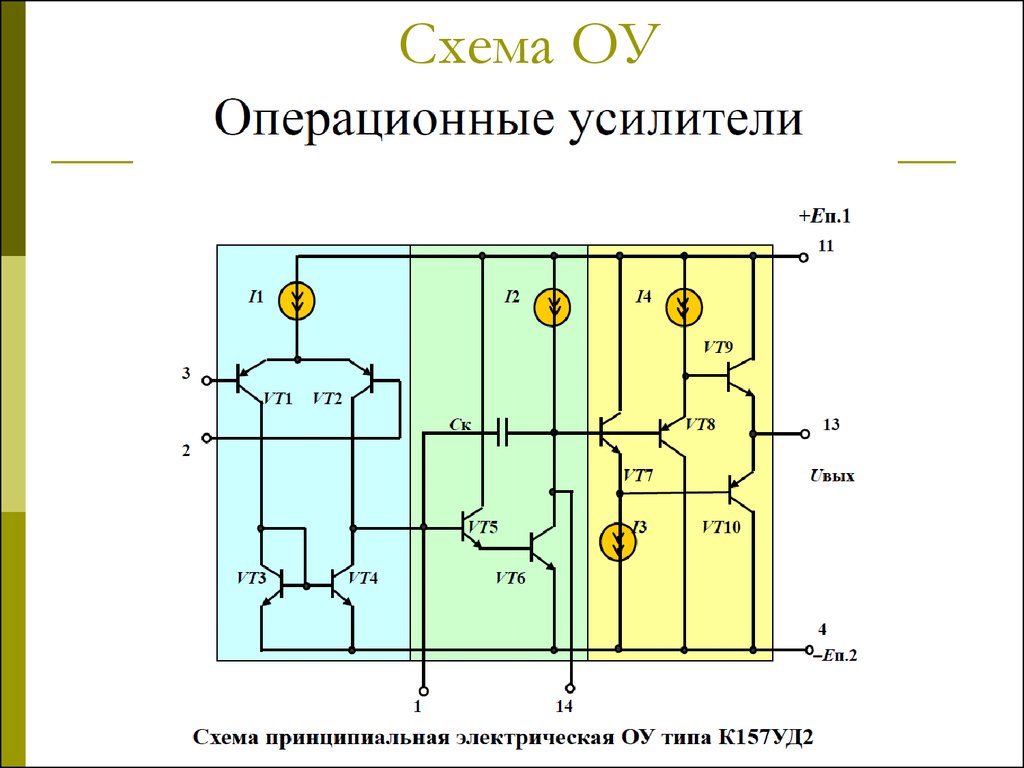

Так же на кафедре изучают специальные дисциплины строительного профиля студенты следующих специальностей очного и заочного обучения: «Промышленное и гражданское строительство» (1-70 02 01), «Автомобильные дороги» (1-70 03 01), «Экспертиза и управление недвижимостью» (1-70 02 02), «Архитектура» (1-69 01 01), «Сельское строительство и обустройство территорий» (1-74 04 0), «Автоматизация технологических процессов и производств» (1-53 01 01), «Водоснабжение, водоотведение и охрана водных ресурсов» (1-70 04 03),  «Мелиорация и водное хозяйство» (1-74 05 01), «Коммерческая деятельность» (1-25 01 10).

На кафедре проводится подготовка  аспирантов по специальности «Строительные конструкции, здания и сооружения», «Строительные материалы и изделия».

 

Схема операционного усилителя: обзор простейших примеров

Содержание

1. Основные свойства и схема операционного усилителя в современной электронике
2. Ближе к делу
3. Посмотрим на идеальную схему операционного усилителя с точки зрения Proteus
4. Реальное применение схемы операционного усилителя на примере инвертирующего и неинвертирующего усилителей
5. Пара интересных схем
6. Заключение

---

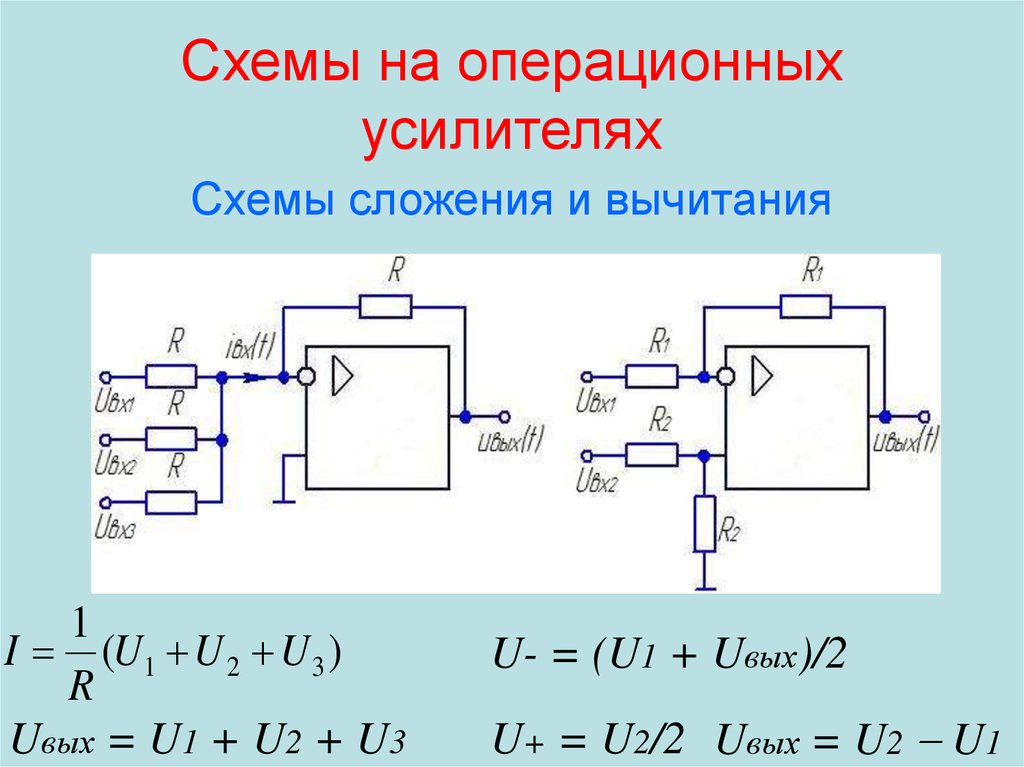
Схема операционного усилителя — это такая «штука», которая позволяет всячески оперировать аналоговыми сигналами. Самые простейшие и основные — это усиление, ослабление, сложение, вычитание и много других (например, дифференцирование или логарифмирование). Абсолютное большинство операций на операционных усилителях (далее ОУ) выполняются с помощью положительных и отрицательных обратных связей.

В данной статье будем рассматривать некий «идеал» ОУ, т.к. переходить на конкретную модель не имеет смысла. Под идеалом подразумевается cхема операционного усилителя, где входное сопротивление будет стремиться к бесконечности (следовательно, входной ток будет стремиться к нулю), а выходное сопротивление — наоборот, будет стремиться к нулю (это означает, что нагрузка не должна влиять на выходное напряжение). Также, любая идеальная схема операционного усилителя должна усиливать сигналы любых частот. Ну, и самое важное, коэффициент усиления при отсутствующей обратной связи должен также стремиться к бесконечности.

Ближе к делу

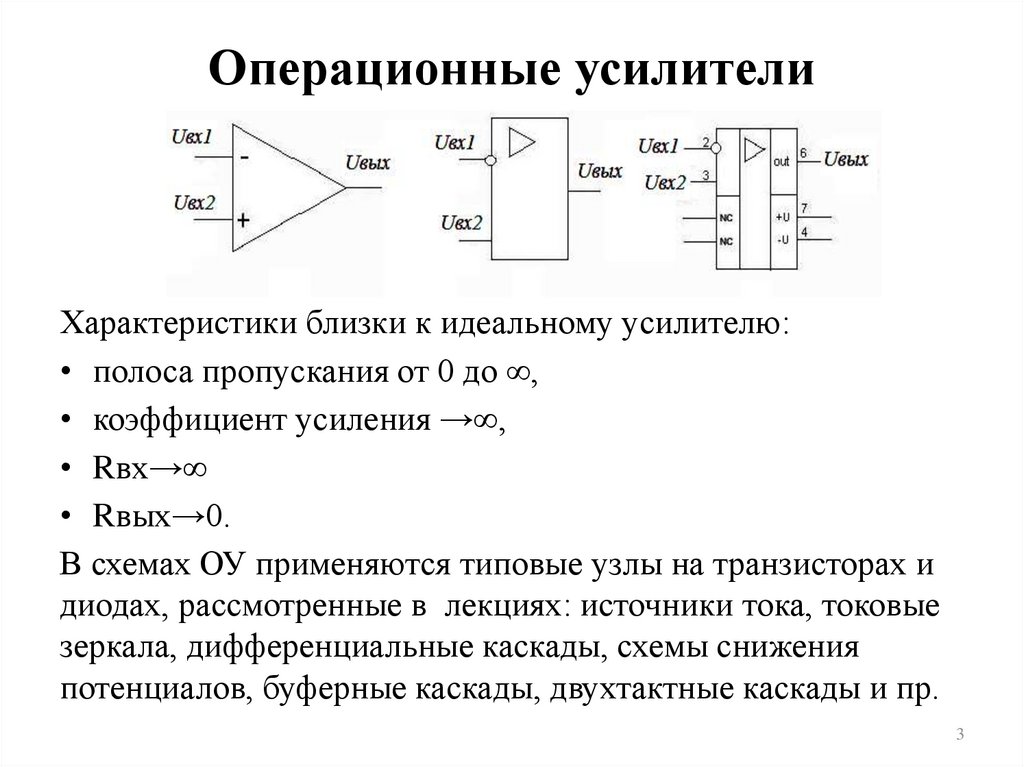
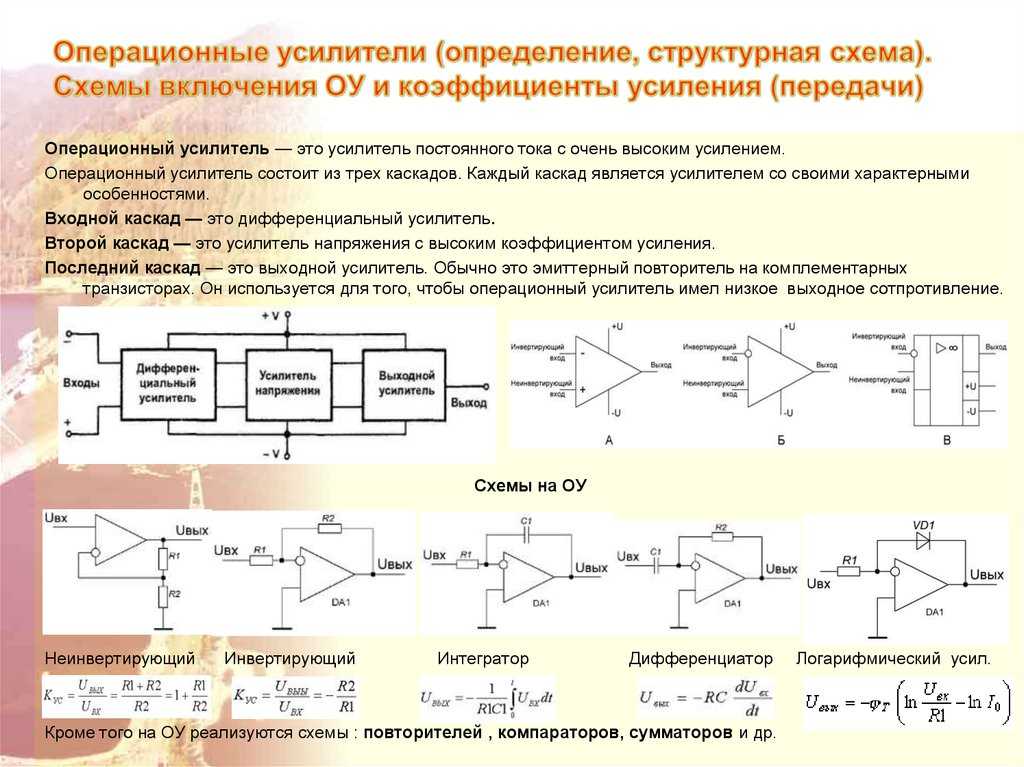
Операционный усилитель на схемах очень часто обозначается равносторонним треугольничком.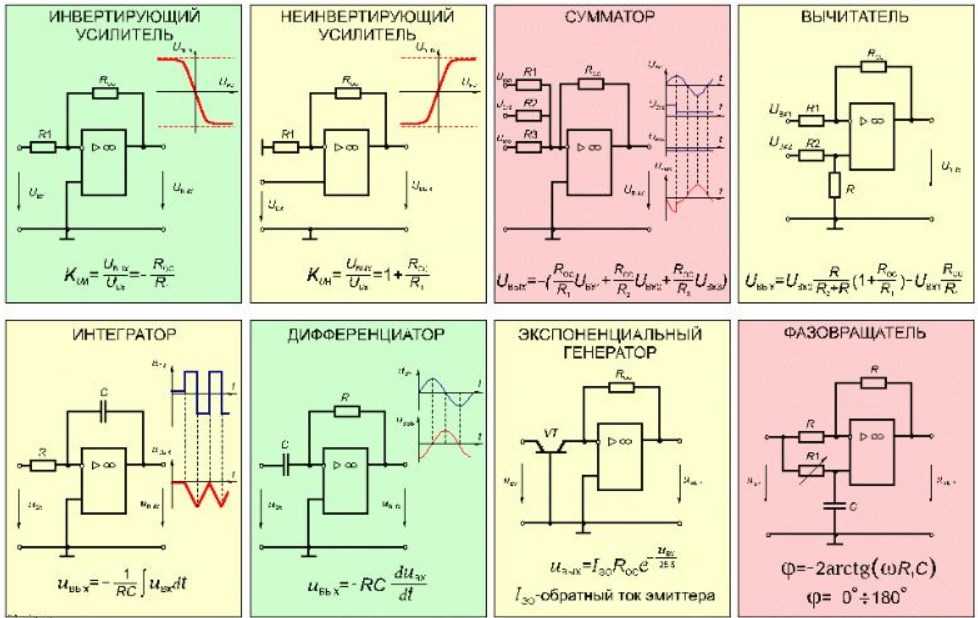 Слева расположены входы, которые обозначены «-» и «+», справа — выход. Напряжение можно подавать на любой из входов, один из которых меняет полярность напряжения (поэтому его назвали инвертирующим), другой — не меняет (логично предположить, что он называется неинвертирующий).

Питание схемы операционного усилителя, чаще всего, двуполярное. Обычно, положительное и отрицательное напряжение питания имеет одинаковое значение (но разный знак!). В простейшем случае можно подключить источники напряжения прямо ко входам ОУ. И тогда напряжение на выходе будет рассчитываться по формуле:

U_out=(U_in1-U_in2•G, где U_in1 — напряжение на неинвертирующем входе, U_in2 — напряжение на инвертирующем входе, U_out — напряжение на выходе и G — коэффициент усиления без обратной связи.

Посмотрим на идеальную схему операционного усилителя с точки зрения Proteus

Предлагаю «поиграть» с ним. На неинвертирующий вход подали напряжение в 1В. На инвертирующий 3В. Используем «идеальный» ОУ. Итак, получаем: (1V-3V)•10⁶=-2•10⁶V. Но тут у нас есть ограничитель, т.к. мы не сможем усилить сигнал выше нашего напряжения питания. Таким образом, на выходе все равно получим -15В. Итог:

Изменим коэффициент усиления (чтобы Вы мне поверили). Пусть параметр Voltage Gain станет равным двум. Та же задача наглядно решается.

Реальное применение схемы операционного усилителя на примере инвертирующего и неинвертирующего усилителей

Есть два таких основных правила:

I. Выход операционного усилителя стремится к тому, чтобы дифференциальное напряжение (разность между напряжением на инвертирующем и неинвертирующем входах) было равно нулю.

II. Входы ОУ не потребляют тока.

Первое правило реализуется за счет обратной связи. Т.е. напряжение передается с выхода на вход таким образом, что разность потенциалов становится равной нулю.

Это, так сказать, «священные каноны» в теме ОУ.

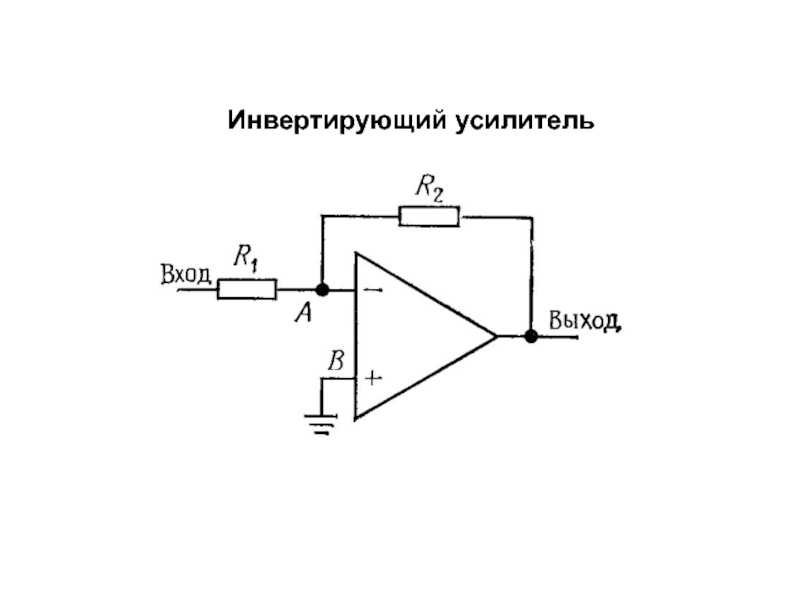
А теперь, конкретнее. Инвертирующий усилитель выглядит именно так (обращаем внимание на то, как расположены входы):

Исходя из первого «канона» получаем пропорцию:

, и немного «поколдовав» с формулой выводим значение для коэффициента усиления инвертирующего ОУ:

Приведенный выше скрин в комментариях не нуждается. Просто сами все подставьте и проверьте.

Следующий этап — неинвертирующий усилитель.

Тут все также просто. Напряжение подается непосредственно на неинвертирующий вход. На инвертирующий вход подводится обратная связь. Напряжение на инвертирующем входе будет:

, но применяя первое правило, можно утверждать, что

U=U_in

И снова «грандиозные» познания в области высшей математики позволяют перейти к формуле:

Приведу исчерпывающий скрин, который можете перепроверить, если хотите:

Пара интересных схем

Напоследок, приведу парочку интересных схем, чтобы у Вас не сложилось впечатления, что операционные усилители могут только усиливать напряжение.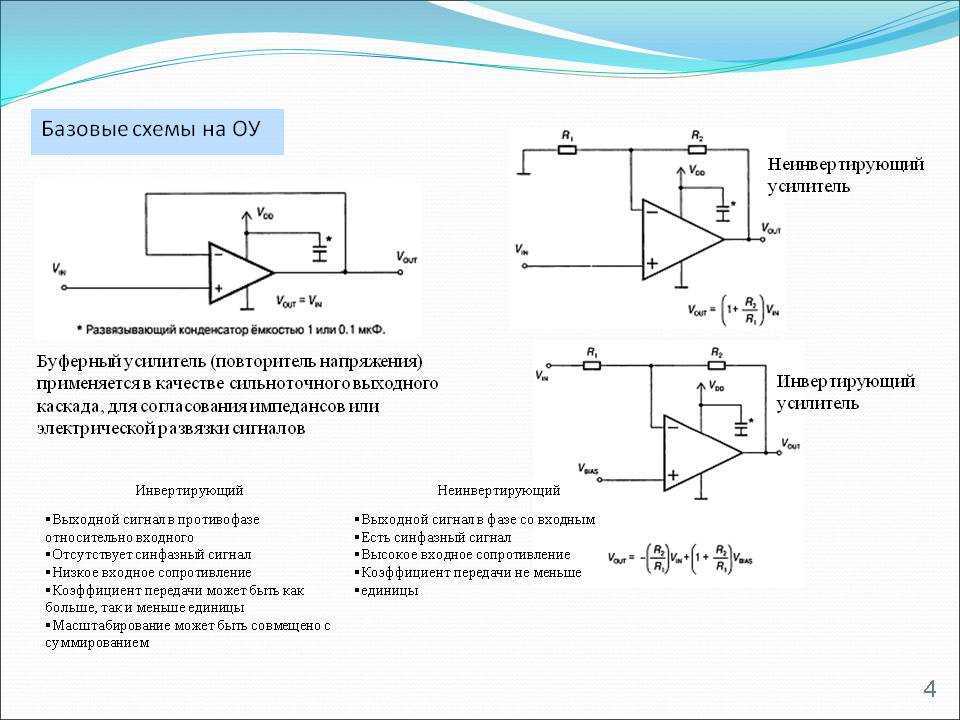

Повторитель напряжения (буферный усилитель). Принцип действия такой же, как и у транзисторного повторителя. Используется в цепях с большой нагрузкой. Также, с его помощью можно решить задачку с согласованием импедансов, если в схеме есть нежелательные делители напряжения. Схема проста до гениальности:

Суммирующий усилитель. Его можно использовать, если требуется сложить (отнять) несколько сигналов. Для наглядности — схема (снова обращаем внимание на расположение входов):

Также, обращаем внимание на то, что R1 = R2 = R3 = R4, а R5 = R6. Формула расчета в данном случае будет:

(знакомо, не так ли?)

Таким образом, видим, что значения напряжений, которые подаются на неинвертирующий вход «обретают» знак плюс. На инвертирующий — минус.

Заключение

Схемы на операционных усилителях чрезвычайно разнообразны. В более сложных случаях Вы можете встретить схемы активных фильтров, АЦП и устройств выборки хранения, усилители мощности, преобразователи тока в напряжение и многие многие другие схемы.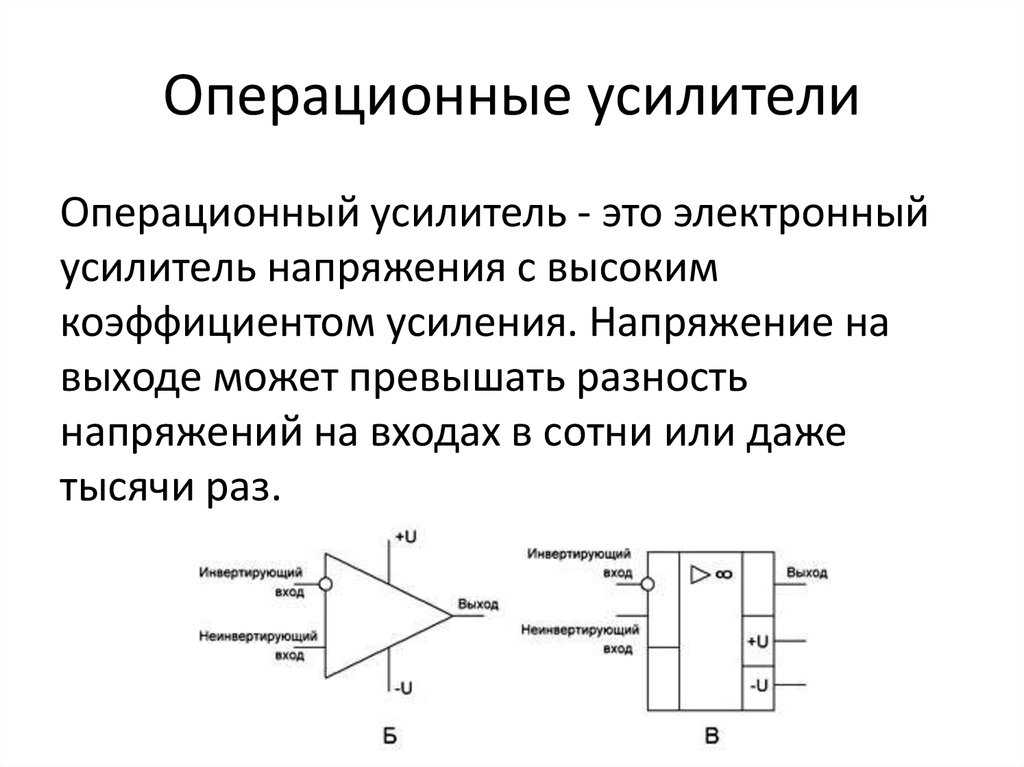

Источник: habr.com

Полное руководство по операционным усилителям. Часть 1

Это первая часть из трех частей «Полное руководство по операционным усилителям». В этой статье мы узнаем, как работают операционные усилители и как с их помощью создавать схемы. В этой серии есть еще две статьи, так что обязательно ознакомьтесь с ними после этой:

• Полное руководство по операционным усилителям. Часть 2. Линейные приложения
• Полное руководство по операционным усилителям. Часть 3. Нелинейные приложения выполнять аналоговую математику, такую ​​как интегрирование и дифференцирование. Первые операционные усилители были лампового типа. Ранними операционными усилителями на ИС были µA709.и LM101, но они быстро превратились в другие операционные усилители из-за их огромной полезности и популярности.

  Одним из самых известных из них был операционный усилитель LM741. Вы все еще видите много схем, использующих этот операционный усилитель. К счастью, производители сохранили расположение выводов неизменным для постоянно растущего и улучшающегося ассортимента операционных усилителей.

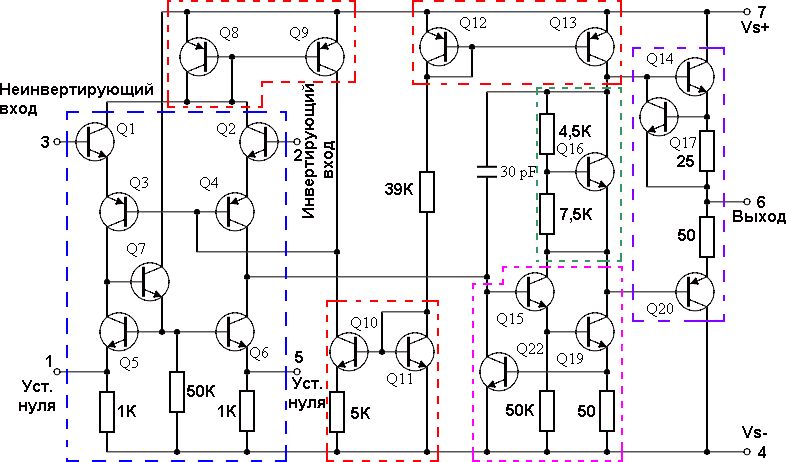
  Поскольку компоненты внешней обратной связи в значительной степени определяют поведение схем операционных усилителей, обычно их можно заменить другими операционными усилителями. Если только это не критическое приложение, такое как сверхвысокочастотная характеристика или очень низкий уровень шума или смещения.

  Выше показаны некоторые корпуса, в которых доступны операционные усилители. Одна интегральная микросхема может иметь один, два или четыре отдельных операционных усилителя.

  Как работают операционные усилители

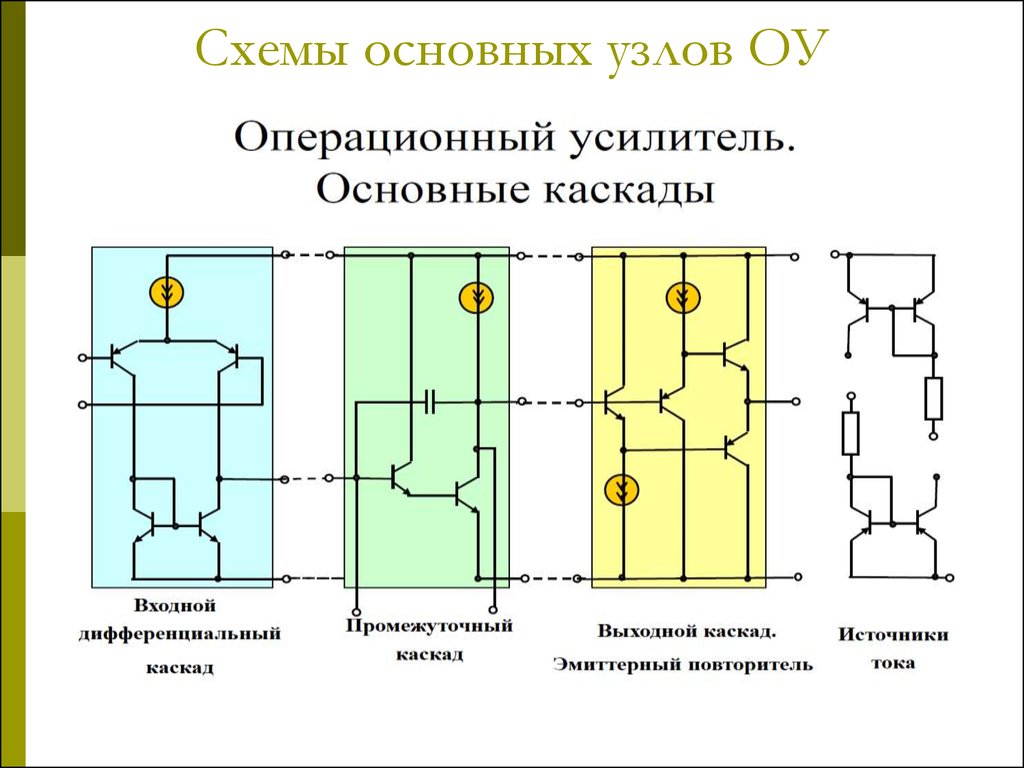
  Ниже показана внутренняя блок-схема простого операционного усилителя (без источника питания).

  Имеется два входных и один выходной контакт. Вход -ve называется инвертирующим входом , а вход +ve называется неинвертирующим входом . Входы подключены к дифференциальному усилителю, за которым следуют дополнительные каскады дифференциального усиления.

  В дифференциальном усилителе мы находим так называемую длиннохвостую пару. Транзисторы Q1 и Q2 представляют собой пару очень близко согласованных полевых транзисторов или биполярных транзисторов. Они подключены к -ve через транзистор Q3, который сконфигурирован как источник постоянного тока.

  Любая разница в напряжении между входами +ve и -ve приведет к пропорциональному колебанию коллекторов или стоков Q1 и Q2. Это называется усилением операционного усилителя без обратной связи. Любая разница в необработанных усилениях Q1 и Q2 приведет к большому нежелательному колебанию выхода. Все это можно взять под наш контроль и сделать предсказуемым, добавив несколько компонентов, обеспечивающих отрицательную обратную связь между входом и выходом.

  После дифференциального усиления каскад со сдвигом уровня центрирует колебания выходного напряжения около 0 В, поскольку все каскады связаны по постоянному току. Наконец, выходной усилитель с низким импедансом управляет нагрузкой и предотвращает влияние любых изменений на выходе на входы.

  Пример проекта

  Ниже показана схема инвертирующего усилителя с коэффициентом усиления 100, использующая операционный усилитель LM741. В инвертирующем усилителе сигнал на выходе не совпадает по фазе с входным на 180 градусов.

  Источник питания показан как +15 В и -15 В, но операционный усилитель будет работать с очень малыми источниками питания, например, +/- 9 В, ограничивая размах выходного сигнала.

  Если бы мы удалили резистор R2 в приведенной выше схеме, у нас не было бы обратной связи. Это называется разомкнутой петлей, и усиление теперь будет функцией максимального усиления операционного усилителя, которое составляет 100 дБ. Но усиление начинает быстро падать при увеличении частоты входа:

  При 10 Гц усиление начинает быстро падать на 20 дБ за декаду.

  Заменив R2, мы получили отрицательную обратную связь. К сожалению, это снижает усиление:

  Обратите внимание, где сейчас начинается спад — около 37 кГц. Это было бы нормально для звуковых целей. Если бы мы хотели продвинуть его немного дальше, нам пришлось бы увеличить обратную связь и уменьшить усиление. Если усиление становится слишком низким, нам, возможно, придется добавить вторую ступень усиления.

  Важные характеристики операционных усилителей

  Суммарные гармонические искажения (THD): Шум, создаваемый самим операционным усилителем. Обычно выражается в дБ.

  Напряжение смещения: Напряжение постоянного тока, которое при подаче на входные контакты приводит к нулевому выходному напряжению постоянного тока. Если бы оба входа были заземлены, выходное напряжение операционного усилителя не было бы равно нулю.

  Скорость нарастания: Время, необходимое для изменения выхода для данного входа. Задается как В/мс.

  Эквивалентное входное шумовое напряжение: Шумовые характеристики операционного усилителя. Идеальный источник напряжения помещается последовательно с входными контактами, которые представляют внутренний шум.

  Коэффициент подавления синфазного сигнала: Способность операционного усилителя подавлять сигналы, поступающие на оба входа одновременно. Особенно важно для применения в дифференциальных усилителях.

  Надеюсь, эта статья помогла вам понять, как работают операционные усилители, как их выбрать и как построить схему с операционным усилителем. В следующей статье мы рассмотрим практические примеры применения некоторых линейных схем. Вот следующая статья из серии: Полное руководство по операционным усилителям. Часть 2. Линейные приложения.

  
  

  Руководство по узловому анализу схем операционных усилителей

  Скачать PDF

  Abstract

  Создание операционного усилителя представило новый фундаментальный компонент и ознаменовало собой изменение мышления разработчиков аналоговых устройств. Поскольку он так широко используется, почти любая схема операционного усилителя, которую инженер должен внедрить, уже спроектирована, и инженер может просто адаптировать номиналы компонентов. Этот подход, хотя и быстрый, не всегда означает, что разработчик имеет фундаментальное понимание теории работы схемы. В этих указаниях по применению объясняется, как можно получить передаточную функцию большинства схем операционных усилителей с помощью простого процесса узлового анализа.

  Основы

  Ни один электронный компонент не идеален, и операционный усилитель не является исключением. Как обычно, мы предполагаем идеальный операционный усилитель с пониманием того, что в какой-то момент может потребоваться рассмотрение реальных ограничений.

  В частности, мы предполагаем бесконечный входной импеданс и нулевой выходной импеданс. Передний конец схемы никоим образом не нагружается операционным усилителем, и его выход может генерировать или потреблять столько тока, сколько необходимо для точного отклика на вход. С этими предположениями и конфигурациями операционных усилителей с отрицательной обратной связью напряжение на двух входах идентично, а выход настраивается на напряжение, чтобы поддерживать это состояние.

  Также предполагается, что полоса пропускания операционного усилителя достаточна для удовлетворения потребностей схемы, а коэффициент усиления разомкнутого контура усилителя бесконечен.

  Производительность современных компонентов такова, что в большинстве случаев приведенные выше допущения вполне приемлемы, и при удалении от идеала происходит очень незначительное ухудшение производительности.

  Узловой анализ

  Задолго до изобретения операционного усилителя закон Кирхгофа гласил, что ток, втекающий в любой узел электрической цепи, равен току, вытекающему из него. (Есть условия закона Кирхгофа, которые здесь не имеют значения.) Схема операционного усилителя может быть разбита на ряд узлов, каждый из которых имеет узловое уравнение. Уравнения могут быть объединены для формирования передаточной функции.

  Рассмотрим схему на входе операционного усилителя. Ток, протекающий к входному контакту, равен току, утекающему от контакта (поскольку ток не течет на контакт из-за его бесконечного входного импеданса).

  То же самое нельзя сказать о выходе, поскольку операционный усилитель может подавать или потреблять ток.

  Преобразователь тока в напряжение

  Простой преобразователь тока в напряжение показан на рис. 1. Его поведение можно легко понять, используя ранее объясненный узловой анализ. Входной ток (I _IN ), поступающий на инвертирующий вход, равен току, вытекающему из него через резистор обратной связи (R). Этот ток создает падение потенциала на R, определяемое как:

  V = I _IN × R.

  Как объяснялось ранее, напряжение на инвертирующем входе равно напряжению на неинвертирующем входе, потому что схема имеет отрицательную обратную связь; то есть инвертирующий вход фиксируется на V _REF . Эта «виртуальная земля» на инвертирующем входе означает, что операционный усилитель постоянно регулирует свое выходное напряжение (V

  OUT ) для поддержания тока I _IN , протекающего через R. V _OUT соответствует V _REF с нулевым входным током, и он уменьшается пропорционально увеличению I _IN . Результаты следующего уравнения:

  V _OUT = V _REF — (I _IN × R)

  Рисунок 1.

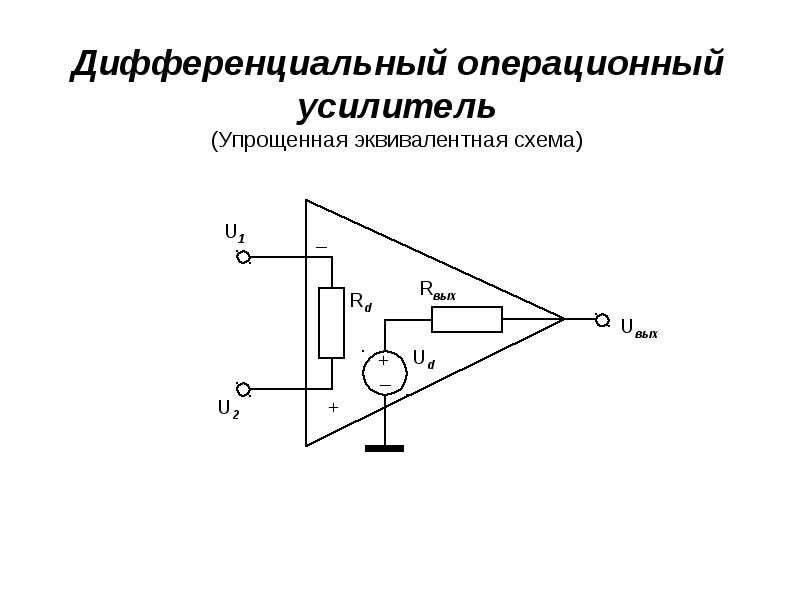
  Дифференциальный усилитель

  Развивая это понятие еще дальше, на рис. 2 показан дифференциальный усилитель. Его передаточную функцию можно рассчитать, снова учитывая токи, втекающие в узлы и выходящие из них.

  Рисунок 2.

  Рассмотрим ток, текущий к неинвертирующему контакту. Это может быть представленным:

  Точно так же ток, текущий от этого узла, может быть представлен как

  .
  Объединение уравнения 1 с уравнением 2 дает
  .

  Теперь жизнь станет проще, если мы будем использовать проводимости вместо сопротивлений. (это сводит дроби к минимуму). Таким образом,

  где

  так

  следовательно, напряжение V+ равно

  .

  Узловые уравнения для инвертирующего узла такие же простые

  Чтобы найти передаточную функцию, мы знаем

  Объединение уравнения 3 и уравнения 5 в уравнение 4 дает

  .

  так

  Другими словами, выходной сигнал зависит от дифференциального напряжения на входах и резисторах, задающих коэффициент усиления, как и следовало ожидать.

  Генератор венского моста

  Технику узлового анализа можно использовать для анализа цепей с реактивными компонентами. Точно так же, как мы рассматривали проводимости резисторов, с реактивными компонентами уравнения упрощаются за счет учета их проводимостей. Конденсатор имеет проводимость sC. Обратите внимание, что используется номенклатура Лапласа, так как опять же, это делает уравнения более простыми, и психологические последствия этого значительны. Точно так же мы могли бы использовать jw вместо s, если бы хотели получить представление о фазовых эффектах цепи, и это будет сделано позже.

  Смело продолжая вышеизложенное предположение, теперь можно проанализировать мостовой осциллятор Вина. На рис. 3 показана общая конфигурация этой схемы. Опять же, чтобы упростить уравнения, большинство инженеров используют одинаковые значения резисторов и конденсаторов. В этой схеме у нас есть как параллельные, так и последовательные сети, поэтому для простоты математики не имеет значения, используются ли проводимости или реактивные сопротивления. Следующий анализ продолжит предыдущий текст и использует допуски.

  Рисунок 3.

  Во-первых, из уравнения 3 напряжение на инвертирующем выводе равно

  .

  Стоит отметить, что если два сопротивления соединены последовательно, то общее сопротивление обратно обратно сумме их обратных величин (используется та же формула, что и для двух параллельных резисторов). Точно так же, если два адмиттанса расположены параллельно, общий адмиттанс равен сумме адмиттансов. Следовательно, проводимость от выхода операционного усилителя до неинвертирующего входа равна

  Аналогично, входное сопротивление от неинвертирующего терминала к земле составляет

  .

  Используя описанную ранее методологию, можно показать, что (в конечном итоге)

  Полагая s = jw и R = 1/G, мы получаем

  .

  Поэтому, используя принципы узлового анализа, была получена передаточная функция для генератора моста Вина. Из этого уравнения можно сделать два вывода, оба из которых являются хорошо известными условиями колебаний мостового осциллятора Вина.

  Во-первых, для возникновения колебаний должен быть нулевой фазовый сдвиг от входа к выходу. Это происходит только на одной частоте (когда w = 1/CR). На этой частоте действительные члены числителя сокращаются, а фазовый сдвиг, представленный мнимыми членами как в числителе, так и в знаменателе, аннулируется (по сути, если у вас нет j членов ни в числителе, ни в знаменателе, сдвиг фазы отсутствует). Во-вторых, на этой частоте отношение V _OUT к V ₊ (отсюда V _— ) должно быть 3. Если меньше 3, колебание затухнет. Все, что больше 3, и выход будет насыщаться. Это диктует отношение G _f к G _i для поддержания колебаний: R _f должно быть равно точно удвоенному значению R _i .