Преобразователь двоичного кода в двоично десятичный. Преобразователь двоичного кода в двоично-десятичный: особенности и применение

Как работает преобразователь двоичного кода в двоично-десятичный. Для чего используется такое преобразование. Какие существуют методы и алгоритмы преобразования. Где применяются преобразователи двоичного кода в двоично-десятичный.

Принцип работы преобразователя двоичного кода в двоично-десятичный

Преобразователь двоичного кода в двоично-десятичный (Binary-Coded Decimal, BCD) — это устройство или алгоритм, выполняющий преобразование чисел из двоичной системы счисления в двоично-десятичную. Основная задача такого преобразователя заключается в представлении двоичных чисел в формате, более удобном для восприятия человеком.

Принцип работы преобразователя основан на следующих шагах:

1. На вход подается двоичное число
2. Число разбивается на группы по 4 бита
3. Каждая группа преобразуется в десятичную цифру от 0 до 9
4. Полученные десятичные цифры формируют двоично-десятичное представление исходного числа

Например, двоичное число 1010 1100 будет преобразовано в двоично-десятичное 10100110, что соответствует десятичному числу 172.

Методы преобразования двоичного кода в двоично-десятичный

Существует несколько основных методов преобразования двоичного кода в двоично-десятичный:

Метод последовательного вычитания

Этот метод основан на последовательном вычитании степеней 10 из двоичного числа, начиная с наибольшей. На каждом шаге подсчитывается количество вычитаний, формируя соответствующую десятичную цифру.

Метод двоичных сдвигов

При этом методе выполняется поразрядный сдвиг двоичного числа влево. После каждого сдвига проверяется, не превышает ли значение тетрады 9. Если превышает, к тетраде прибавляется 6.

Табличный метод

Использует заранее подготовленную таблицу соответствия двоичных и двоично-десятичных кодов. Обеспечивает высокое быстродействие, но требует больших объемов памяти для хранения таблицы.

Области применения преобразователей двоичного кода в двоично-десятичный

Преобразователи двоичного кода в двоично-десятичный широко используются в различных электронных устройствах и системах:

• Цифровые измерительные приборы
• Системы отображения информации
• Калькуляторы
• Кассовые аппараты
• Системы автоматизированного учета

Основная цель применения таких преобразователей — представление числовой информации в формате, удобном для восприятия человеком.

Преимущества использования двоично-десятичного кода

Двоично-десятичный код имеет ряд преимуществ по сравнению с чистым двоичным представлением:

• Простота перевода в десятичную систему счисления
• Удобство выполнения арифметических операций
• Точное представление десятичных дробей
• Отсутствие ошибок округления при финансовых расчетах

Эти преимущества делают двоично-десятичный код востребованным в системах, где требуется высокая точность вычислений с десятичными числами.

Реализация преобразователя двоичного кода в двоично-десятичный

Преобразователь двоичного кода в двоично-десятичный может быть реализован как аппаратно, так и программно. Рассмотрим пример программной реализации на языке Python:

«`python def binary_to_bcd(binary): decimal = int(binary, 2) bcd = 0 multiplier = 1 while decimal > 0: bcd += (decimal % 10) * multiplier decimal //= 10 multiplier *= 16 return bcd # Пример использования binary_num = «10101100» bcd_num = binary_to_bcd(binary_num) print(f»Двоичное число: {binary_num}») print(f»Двоично-десятичный код: {bcd_num:08X}») «`

Этот код демонстрирует базовую реализацию преобразователя двоичного кода в двоично-десятичный на языке Python. Функция binary_to_bcd принимает двоичное число в виде строки и возвращает его двоично-десятичное представление.

Ограничения преобразователей двоичного кода в двоично-десятичный

При использовании преобразователей двоичного кода в двоично-десятичный следует учитывать некоторые ограничения:

• Увеличение разрядности представления чисел
• Снижение эффективности использования памяти
• Усложнение арифметических операций
• Ограниченный диапазон представления чисел

Эти ограничения необходимо принимать во внимание при проектировании систем, использующих двоично-десятичное представление чисел.

Перспективы развития преобразователей двоичного кода в двоично-десятичный

Развитие технологий преобразования двоичного кода в двоично-десятичный идет в нескольких направлениях:

• Повышение быстродействия преобразователей
• Уменьшение энергопотребления
• Разработка более эффективных алгоритмов преобразования
• Интеграция преобразователей в современные микропроцессоры

Эти направления развития позволят расширить области применения двоично-десятичного кода и повысить эффективность систем, использующих такое представление чисел.

Заключение

Преобразователи двоичного кода в двоично-десятичный играют важную роль в современной цифровой электронике, обеспечивая удобное представление числовой информации для человека. Несмотря на некоторые ограничения, двоично-десятичный код остается востребованным в различных областях, особенно там, где требуется высокая точность вычислений с десятичными числами.

Развитие технологий преобразования позволит расширить сферу применения двоично-десятичного кода и повысить эффективность систем, использующих такое представление чисел. Понимание принципов работы и особенностей применения преобразователей двоичного кода в двоично-десятичный является важным аспектом для специалистов в области цифровой электроники и вычислительной техники.

Двоично-десятичный конвертер | Инструмент двоичного и десятичного преобразования

Miniwebtool

Automatic Mode

произвольное базовое преобразованиеBCD в двоичныйBCD в десятичнойBCD в шестнадцатеричныйдвоичный код к другим базамДвоичный код в BCDдвоичный в десятичныйдвоичный код в код Греядвоичный в шестнадцатеричныйдвоичный в восьмеричныйДесятичный в BCDдесятичный в двоичныйДесятичный в шестнадцатеричныйДесятичный в восьмеричныйКод Грея в двоичный кодШестнадцатеричный код в другой шестнадцатеричныйШестнадцатеричный код в BCDшестнадцатеричный в двоичныйшестнадцатеричный в десятичныйшестнадцатеричный в восьмеричныйВосьмеричная к другим базамВосьмеричный в двоичныйВосьмеричный в десятичныйВосьмеричный в шестнадцатеричный

Двоично-десятичный конвертер используется для преобразования двоичных (Base-2) чисел в десятичные (Base-10).

Другие сопутствующие инструменты:

• двоично-восьмеричный преобразователь

• Конвертер BCD в десятичные числа

• преобразователь обычного времени в десятичное время

• Конвертер восьмеричных чисел в десятичные

• дробь в десятичный калькулятор

• Двоичный в шестнадцатеричный конвертер

• Конвертер двоичного кода в BCD

• двоичный преобразователь

• двоичный калькулятор

• шестнадцатеричный преобразователь в десятичный

Общие инструменты

• Калькулятор среднего балла (GPA)

• Калькулятор комплексных чисел

• минималистичный калькулятор дробей

• футы дюймы в сантиметры

• калькулятор ИМТ

• счетчик символов

• калькулятор времени удвоения

• конвертер фунтов в кг

• калькулятор десятичной дроби

• Калькулятор суммы кубов

• Калькулятор кинематики

• Калькулятор электроэнергии

• калькулятор даты

• калькулятор площади параллелограмма

• первый день зимы

• конвертер футов в метры

• логарифмический калькулятор

• конвертер сантиметров в дюймы

• конвертер см в футы и дюймы

• калькулятор скидок

• калькулятор объема куба (Высокая точность)

• процентный калькулятор

• конвертер дюймов в сантиметры

• Калькулятор площади поверхности цилиндра (Высокая точность)

• Калькулятор площади равностороннего треугольника

• калькулятор возраста

• Акры в Квадратные ярды Конвертер

• калькулятор квадратичных формул

• калькулятор объема конуса (Высокая точность)

• Калькулятор инфляции в США

• между двумя датами

• калькулятор площади сектора

• калькулятор овуляции

• калькулятор площади круга

• Калькулятор WACC

• Калькулятор пропорций

• конвертер кг в фунты

• калькулятор жима лежа

• Калькулятор объема сферы (Высокая точность)

• квадратный калькулятор

• Кельвин в градусы Фаренгейта Конвертер температуры

• строчные/прописные буквы

• конвертер кельвинов в градусы цельсия

• Калькулятор функции ошибки

Преобразователь — двоично-десятичный код — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

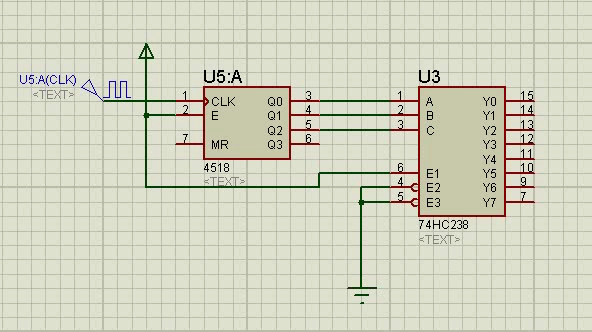
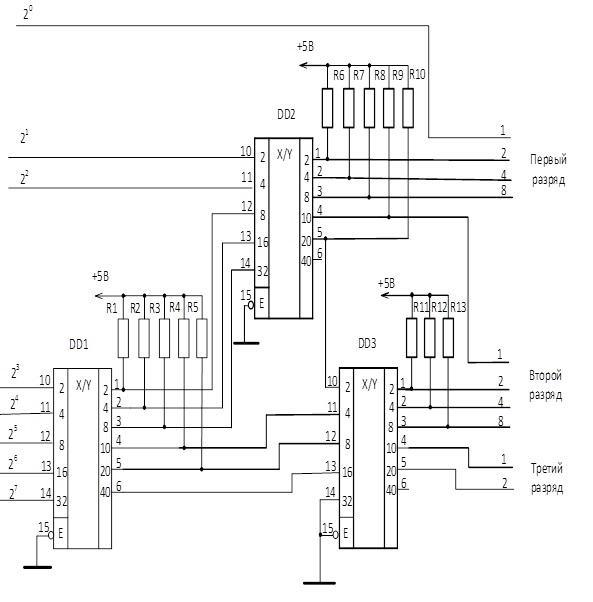
Преобразователь двоично-десятичного кода на сочетание 2 из 5 отличается от предыдущих регистром и схемой дешифратора.  [1]

Схема цифровой индикации с использованием микросхемы К155ИД1.| Логическая структура дешифратора-мультиплексора КМ155ИД4.  [2]

Преобразователь двоично-десятичного кода в десятичный для управления высоковольтным индикатором К155ИД1 ( см. рис. 1 — 64, а) содержит в себе дешифратор из двоично-десятичного кода в десятичный с выходными высоковольтными ключами. На рис. 1 — 76 приведен пример использования микросхемы К155ИД1 для работы на высоковольтный индикатор.  [3]

Логическая структура микросхемы контроля четности и нечетности КМ155ИП2.  [4]

Преобразователь двоично-десятичного кода в двоичный К155ПР6 ( см. рис. 1 — 67, о) представляет собой ЗУ, предназначенное для длительного хранения постоянной информации объемом 256 бит с организацией 32 слов по 8 разрядов. ЗУ работает только в режиме хранения и считывания.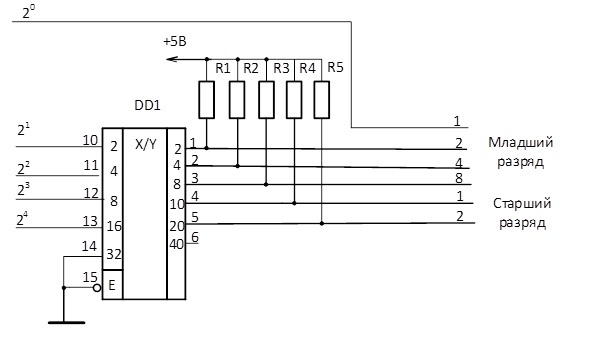

Микросхема состоит из матрицы 32X8 запоминающих ячеек и схем управления, включающих в себя адресные формирователи, входной дешифратор, схему разрешения выборки и выходные усилители считывания.  [5]

Схема элементарного преобразователя двоично-десятичного кода в двоичный код, выполненная на четырехразрядном сумматоре.  [6]

Преимуществом комбинационных преобразователей двоично-десятичного кода в двоичный является малое время преобразования, которое определяется только суммарной задержкой в максимальном числе последовательно включенных преобразователей кодов. В преобразователях же двоично-десятичного кода в двоичный, выполненный на регистрах сдвига, время преобразования равно 4 — тТн, где пг — число тетрад, Тн — период тактовых сигналов. Минимальное значение Тн определяется быстродействием элементов памяти ( ЭП), на которых выполнен сдвигающий регистр.  [7]

Для построения преобразователя двоично-десятичного кода в двоичный код необходимо спроектировать некоторый элементарный преобразователь кодов и установить правила соединения таких преобразователей для получения схемы, позволяющей преобразовывать многоразрядные двоично-десятичные числа в двоичные числа.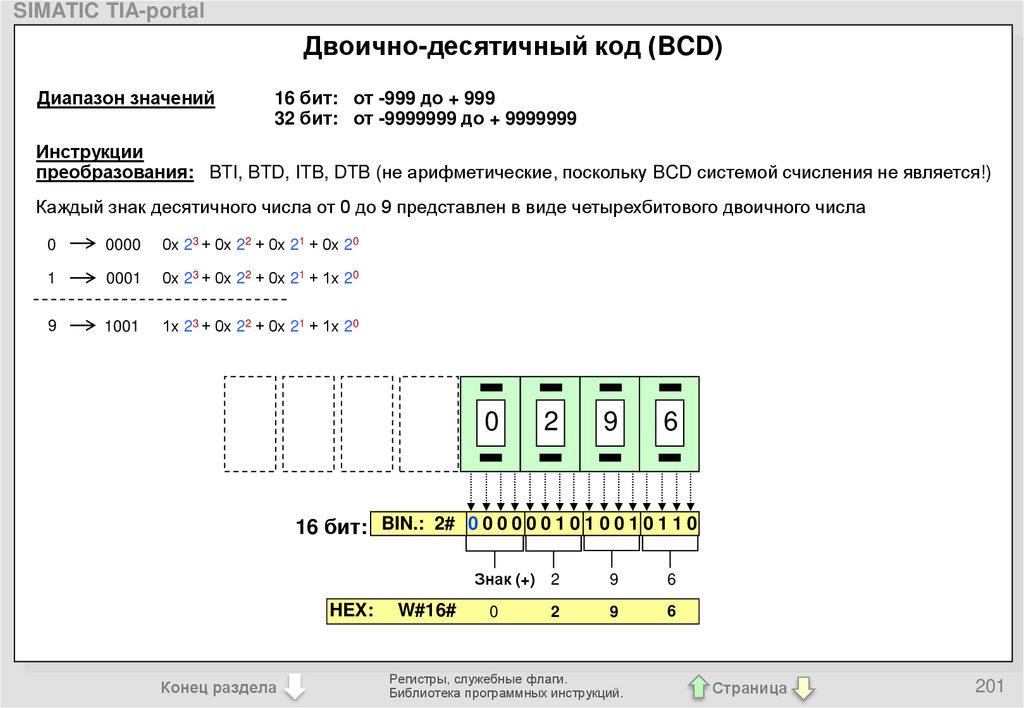 Известно [33], что преобразование двоично-десятичного кода в двоичный легко выполняется с помощью операции сдвига числа в сторону младших разрядов и коррекции числа, получаемого после сдвига. При сдвиге двоично-десятичного числа на один разряд вправо получаемое число не равно исходному, деленному на два. В табл. 1.4 использованы обозначения: ДЧ-десятичное число, ДДЧ — двоично-десятичное число, С — сдвиг, К — коррекция, МР — младший разряд. Если в старший разряд тетрады, имеющей множитель 1 ( У, поступает единица, то она приобретает вес 8 — 1 ( У.  [8]

Микросхемы представляют собой преобразователь двоично-десятичного кода в двоичный.  [9]

Более экономичную схему преобразователя двоично-десятичного кода в двоичный можно получить на основе преобразователей кодов, имеющих по пять входных и выходных сигналов, которые выполняют преобразование не одного, а двух двоично-десятичных разрядов в двоичные.  [10]

Условное обозначение элементарного преобразователя двоично-десятичного кода в двоичный код.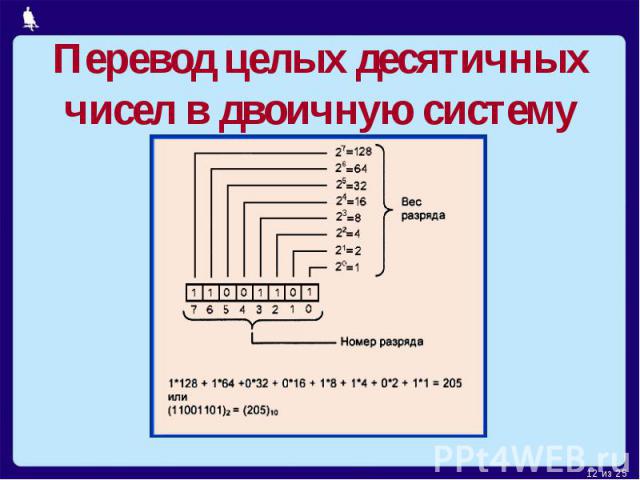 | Схема преобразователя четырехразрядного двоично-десятичного кода в двоичный код, выполненная на микросхемах 155ПР6.  [11]

Правила составления схемы преобразователя двоично-десятичного кода в двоичный с использованием данных преобразователей идентичны описанным ранее. На рис. 1.29 показана схема преобразователя четырехразрядного десятичного числа, представленного в двоично-десятичном коде, в двоичный код, составленная на основании этих правил. На схеме цифрами 0 и 1 пояснено преобразование десятичного числа 9999 в двоичное число.  [12]

Условное изображение микросхемы 564ИД1.  [13]

Микросхема 564ИД1 служит преобразователем двоично-десятичного кода в десятичный или двоичного в восьмеричный.  [14]

В интегральном исполнении на уровне СИС реализованы преобразователи кодов, обладающие типовыми функциями: преобразователи двоично-десятичного кода в двоичный и обратно, преобразователи двоичного кода в код Грея, знакогенераторы для различных типов индикаторов.  [15]

Страницы:      1    2

Десятичное число в двоичное — Преобразование

Десятичное число в двоичное Преобразование выполняется различными способами. Один из способов преобразования десятичного числа в двоичное — это рекурсивное деление заданного десятичного числа на 2. Затем остатки записываются до тех пор, пока мы не получим 0 в качестве окончательного частного. После этого шага эти остатки записываются в обратном порядке, чтобы получить двоичное значение данного десятичного числа. Система счисления — это математический способ представления чисел с помощью набора цифр или символов. Существуют различные системы счисления, такие как десятичная система счисления, двоичная система счисления, восьмеричная и шестнадцатеричная система счисления. Они идентифицируются с помощью базы, которая у них есть. Числа можно легко преобразовать из одной базы в другую, используя определенные правила.

1.	Преобразование десятичного числа в двоичное
2.	Как преобразовать десятичную систему в двоичную?
3.	Десятичная таблица в двоичную
4.	Часто задаваемые вопросы о преобразовании десятичных чисел в двоичные

Преобразование десятичного числа в двоичное

Преобразование десятичной системы счисления в двоичную означает преобразование числа из десятичной системы счисления в двоичную систему счисления. Все системы счисления имеют основу, которая определяется общим количеством цифр, используемых в системе счисления. Например, двоичная система счисления имеет основание 2, поскольку для представления числа используются только две цифры. Точно так же десятичная система счисления имеет основание 10, потому что она имеет 10 цифр для представления числа. Давайте разберемся с десятичной системой счисления и двоичной системой счисления, а затем перейдем к преобразованию десятичной системы счисления в двоичную.

Определение десятичной системы счисления

Десятичная система счисления — это система счисления, которая представляет число с основанием 10 и использует 10 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. , Она также известна как индийско-арабская система счисления, в которой каждая цифра имеет позицию и в десять раз более значима, чем предыдущая цифра. Он также использует десятичную точку для представления десятичных дробей. Например, если мы возьмем 36 в качестве десятичного числа, здесь 3 в десять раз больше, чем 6. Десятичные числа записываются как 45 ₁₀ , 118 ₁₀ и так далее. Это наиболее известная система счисления, в которой числа можно легко идентифицировать, даже если основание не записано. Другими словами, если основание числа не написано, оно считается десятичным числом.

Двоичная система счисления. Определение

Двоичная система счисления — это система счисления с основанием 2, в которой числа представлены только двумя цифрами, 0 и 1. Наименьшая единица данных в компьютере называется битом, сокращенно форма «двоичной цифры». Бит имеет единственное двоичное значение, равное 1 или 0. Двоичные числа записываются как 110 ₂ , 10 ₂ и в основном используются в компьютерах для программирования или кодирования, поскольку компьютер понимает язык только двоичных цифр, то есть 0 и 1. Следует отметить, что в двоичном числе бит крайний левый бит называется самым значащим битом (MSB), а крайний правый бит называется наименее значащим битом (LSB). Оставшаяся часть показывает величину числа.

Как преобразовать десятичную систему в двоичную?

Чтобы преобразовать числа из десятичных в двоичные, данное десятичное число несколько раз делится на 2, а остатки записываются до тех пор, пока мы не получим 0 в качестве конечного частного. Следующие шаги рассматриваются как десятичная формула в двоичную, которая показывает процедуру преобразования.

• Шаг 1: Разделите данное десятичное число на 2 и запишите остаток.
• Шаг 2 : Теперь разделите полученное частное на 2 и снова запишите остаток.
• Шаг 3: Повторяйте вышеуказанные шаги, пока не получите 0 в качестве частного.
• Шаг 4: Теперь запишите остатки таким образом, чтобы последний остаток был записан первым, а затем остальные в обратном порядке.
• Шаг 5: Это можно понимать и по-другому, согласно которому младший значащий бит (LSB) двоичного числа находится вверху, а старший значащий бит (MSB) — внизу. Это число является двоичным значением данного десятичного числа.

Разберем это на примере.

Пример: Преобразование десятичного числа 13 ₁₀ в двоичное.

Решение: Начнем многократно делить заданное число (13) на 2, пока не получим частное равное 0. Запишем остатки по порядку.

Деление на 2	Частное	Остаток
13 ÷ 2	6	1 (младший разряд)
6 ÷ 2	3	0
3 ÷ 2	1	1
1 ÷ 2	0	1 (старший бит)

Записав остатки, мы запишем их таким образом, чтобы старший бит (MSB) двоичного числа был записан первым, а затем остальные. Следовательно, двоичный эквивалент данного десятичного числа 13 ₁₀ это 1101 ₂ . Это означает, что 13 ₁₀ = 1101 ₂ .

Десятичная таблица в двоичную

Существуют различные методы преобразования десятичных чисел в двоичные. Когда мы переводим числа из десятичных в двоичные, основание числа меняется с 10 на 2. Следует отметить, что все десятичные числа имеют эквивалентные им двоичные числа. В следующей таблице показана десятичная и двоичная диаграмма первых 20 целых чисел.

Десятичные числа	Двоичные числа
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111
16	10000
17	10001
18	10010
19	10011
20	10100

☛ Похожие статьи

• Двоичная система счисления
• Преобразование десятичной дроби в двоичную формулу
• Двоичный код в десятичный
• Системы счисления

Часто задаваемые вопросы о преобразовании десятичных чисел в двоичные

Каковы правила преобразования десятичных чисел в двоичные?

Ниже приведены правила преобразования десятичных чисел в двоичные:

• Запишите число.
• Разделите его на 2 и запишите остаток.
• Разделите полученное частное на 2 и запишите остаток.
• Повторяйте тот же процесс, пока мы не получим 0 в качестве частного.
• Запишите значения всех остатков, начиная снизу вверх. Это будет требуемый ответ.

Какова цель преобразования десятичных чисел в двоичные?

Двоичные числа используются для программирования и кодирования в компьютерах. Поскольку компьютер понимает язык двоичных цифр, 0 и 1, числа преобразуются из десятичных в двоичные. Когда мы выполняем преобразование десятичных чисел в двоичные, основание десятичных чисел меняется с 10 на 2.

Что показывает таблица преобразования десятичной системы в двоичную?

Таблица преобразования десятичных чисел в двоичные представляет собой таблицу преобразования, в которой показаны все десятичные числа вместе с эквивалентными им двоичными числами. Например, он показывает, что двоичное значение 0 равно 0, двоичное значение 1 равно 1, двоичное значение 2 равно 10, двоичное значение 3 равно 11 и так далее.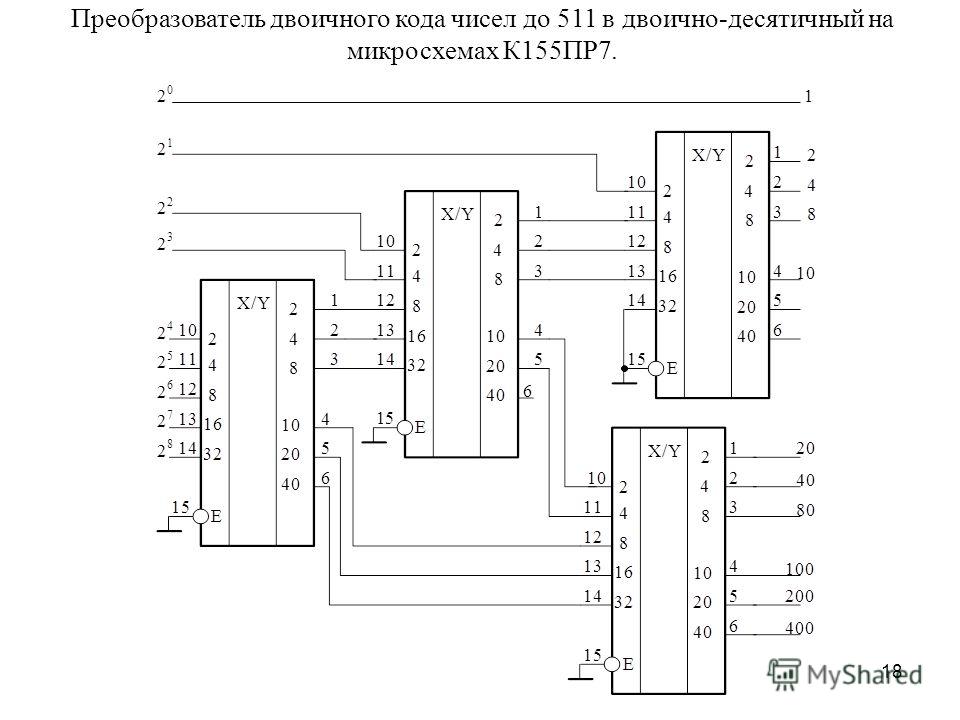

Как выполняется преобразование десятичной системы в двоичную?

Самый простой способ преобразовать десятичное число в двоичное — это многократно делить заданное число на 2, пока в частном не получится 0. Затем мы записываем остатки в обратном порядке, чтобы получить двоичное значение данного десятичного числа.

Что такое десятичное число 254 в двоичном формате?

Десятичное число 254 равно 11111110 в двоичном виде, то есть 254 ₁₀ = 11111110 ₂ .

Список десятичных и двоичных значений первых десяти десятичных чисел.

В следующем списке показаны первые десять десятичных чисел вместе с соответствующими двоичными эквивалентами.

• 0 — 0
• 1 — 1
• 2 — 10
• 3 — 11
• 4 — 100
• 5 — 101
• 6 — 110
• 7 — 111
• 8 — 1000
• 9 — 1001
• 10 — 1010

Что такое двоичный эквивалент десятичного значения 97?

Двоичный эквивалент числа 97 равен 1100001. Это можно записать как 97 ₁₀ = 1100001 ₂ , что показывает, что 97 с основанием 10 преобразуется в 1100001 с основанием 2.

Что такое десятичная формула в двоичную?

Преобразование десятичного числа в двоичное используется путем рекурсивного деления заданного десятичного числа на 2 и записи остатков до тех пор, пока в конечном частном не будет 0 или 1. Шаги, которые используются для преобразования чисел из десятичного числа в двоичное, показаны ниже.

• Шаг 1: Разделите данное десятичное число на 2 и запишите остаток.
• Шаг 2: Теперь разделите частное, полученное на предыдущем шаге, на 2 и запишите остаток.
• Шаг 3: Повторяйте описанные выше шаги, пока мы не получим 0 или 1 в качестве частного.
• Шаг 4: Запишите значения всех остатков снизу вверх. Это дает двоичное преобразование данного десятичного числа.

Преобразователь двоичных дробей

Автор Davide Borchia

Отзыв от Anna Szczepanek, PhD и Rijk de Wet

Последнее обновление: 03 ноября 2022 г.

Содержание:

• Двоичное представление
• Что такое двоичная дробь?
• Как преобразовать дроби в двоичные
• Преобразование двоичных дробей в десятичные
• Ограничения двоичных дробей
• Как использовать наш конвертер двоичных дробей?
• За пределами 0 и 1
• Часто задаваемые вопросы

Преобразовать целые числа в двоичные легко; как насчет преобразования десятичной части? Узнайте, как это сделать, с помощью нашего конвертера двоичных дробей.

Узнайте больше о своем компьютере вместе с нами. Здесь мы научим вас:

• Что такое двоичная дробь .
• Где мы используем двоичные дроби.
• Ограничения компьютера и влияние на округление.
• Как преобразовать десятичную дробь в двоичную дробь и наоборот.
• Как пользоваться нашим конвертером двоичных дробей — это просто, поверьте нам!

Двоичное представление

Компьютеры мыслят единицами и нулями — это двоичный код, и он повсюду.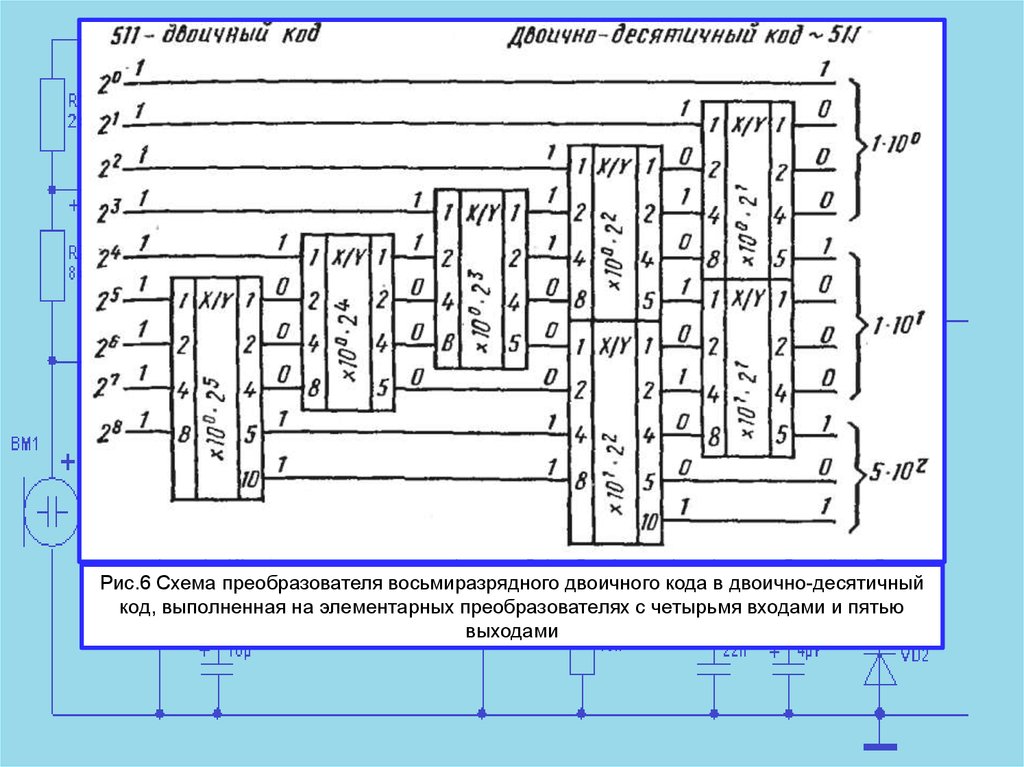 Загляните за этот преобразователь, и вы увидите много таких чисел!

Преобразование целых чисел с основанием 10 (десятичное) в основание 2 (двоичное) выполняется легко и не приводит к ошибкам. То же самое верно, когда вы рассматриваете число, записанное в позиционной нотации (когда вы указываете позицию цифры в числе). Мы не можем сказать о десятичных числах то же самое, что вы написали бы на листе бумаги, например, 0,420,420,42 и 0,33333333…0,33333333…0,33333333….

💡 Если вы хотите узнать, как преобразовать целые числа с основанием 101010 в основание 222, воспользуйтесь нашим десятичным калькулятором в двоичный! Вы просите другие базы? Мы вас поняли: попробуйте конвертер из двоичного кода в шестнадцатеричный или из двоичного в восьмеричный. Омни есть все!

Что такое двоичная дробь?

Взять десятичную часть нецелого числа. Это правильная дробь — ее значение меньше единицы. Когда знаменатель представляет собой степень числа десять (101010, 100100100, 100010001000,. ..), мы говорим о десятичные дроби .

1371000=0,137\frac{137}{1000}=0,1371000137​=0,137

Представление таких значений в базе 2 дает нам двоичных дробей !

Как преобразовать дробь в двоичную

Преобразование десятичной дроби в двоичную не так сложно. Возьмем любую десятичную дробь: мы выбрали 0,29120,29120,2912. Убедитесь, что целая часть равна 000.

Теперь умножьте на два и посмотрите, что получится.

0,2912×2=0,58240,2912\умножить на 2 = 0,58240,2912×2=0,5824

Целая часть осталась 000: это первый элемент двоичной дроби, 0,0…0,0…0,0…. Повторить шаг; на этот раз мы увидим нечто иное.

0,5824×2=1,16480,5824\times 2 =1,16480,5824×2=1,1648

Целая часть теперь равна 111: второй элемент нашей двоичной дроби будет 111: 0,01…0,01…0,01. …

Удалить целую часть (вычесть 111) и повторить шаги снова и снова; ваша бинарная фракция будет расти!

0,1684 × 2 = 0,3368 → 0,0100,3368 × 2 = 0,6736 → 0,01000,6736 × 2 = 1,3472 → 0,01001–10,3472 × 2 = 0,6944 → 0,0100100,69444472 × 2 = 0,6944 → 0,0100100,6944 × 2 = 1,3888888844 → 0,0100100,6944 × 2 = 1,38888888844 → 0,0100100,6944 × 2 = 1,388888844 → 0,0100100,6944 × 2 = 0,6944 → 0,0100100,6944 × \textcolor{красный}{0,010}\\ \footnotesize 0,3368\times 2=0,6736 \rightarrow \textcolor{red}{0,0100}\\ \footnotesize 0,6736\times 2=1,3472 \rightarrow \textcolor{red}{0,01001} \\ \textcolor{синий}{-1}\\ \footnotesize 0,3472\times 2 = 0,6944 \rightarrow \textcolor{red}{0,010010} \\ \footnotesize 0,6944\times 2 = 1,3888 \rightarrow \textcolor{red}{0,0100101} \\0,1684×2=0,3368→0,0100,3368×2=0,6736→0,01000,6736×2=1,3472→0,01001−10,3472×2=0,6944→0,0100100,6944×2=1,3888→0,0100101

Подожди!

0,3888 × 2 = 0,7776 → 0,010010100,7776 × 2 = 1,5552 → 0,010010101110,5552 × 2 = 1,1104 → 0,010010111111104 × 2 = 0,2208 → 0,0100101011011011111104 × 2 = 0,2208 → 0,01001010101101111111110, }\\ \footnotesize 0,7776\times 2=1,5552 \rightarrow \textcolor{red}{0,010010101}\\ \textcolor{синий}{-1}\\ \footnotesize 0,5552\times 2=1,1104 \rightarrow \textcolor{red}{0,0100101011} \\ \textcolor{синий}{-1}\\ \footnotesize 0. 1104\times 2 = 0.2208 \rightarrow \textcolor{red}{0.01001010110} \\0.3888×2=0.7776→0.010010100.7776×2=1.5552→0.010010101−10.5552×2=1.1104→0.0100101011−10.1104×2=0.2208→ 0,01001010110

Это не остановить! Почему бинарная дробь все еще растет? Давайте рассмотрим причину в следующем разделе.

Преобразование двоичной дроби в десятичную

Теперь, когда вы знаете, как преобразовать десятичную дробь в двоичную, давайте научимся наоборот. Возьмите двоичную дробь, любую двоичную дробь! Вы думали о 0.01101010.01101010.0110101? Отлично — мы тоже. 😆

Правило этого преобразования состоит в том, что позиция каждой цифры соответствует отрицательной степени двойки 95}=\tfrac{1}{32}1→20=11​0,1→2−1=211​=21​0,01→2−2=221​=41​0,001→2−3=231​=81​ 0,0001→2−4=241​=161​0,00001→2−5=251​=321​

🙋 Мы включили 0-ю степень двойки, которая равна 111, только для лучшего понимания этого позиционного преобразования. Не забудьте ограничить свои преобразования числами меньше 111!

Возьмите свою двоичную дробь и перепишите ее, умножив каждую цифру на соответствующую степень числа 2.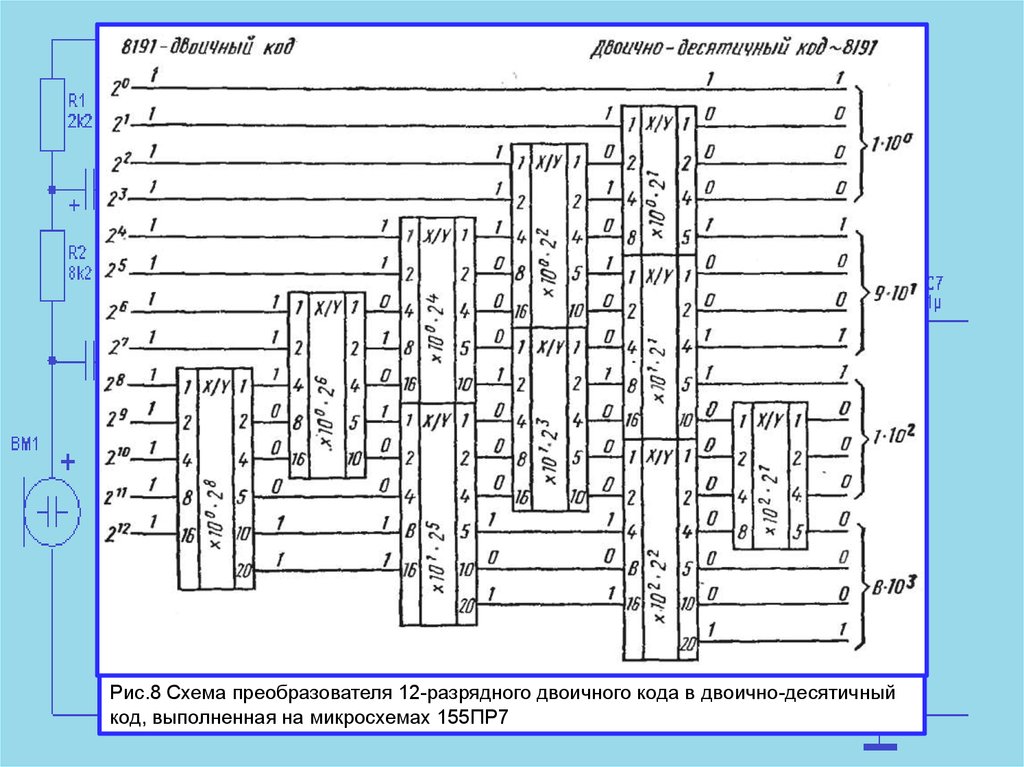 7} \end{align*}0.0110101→0×201​+0×211​++ 0×241​+1×251​+​1×221​+1×231​0×261​+1×271​​

Преобразование дробей в их десятичные эквиваленты:

0×1+0×0,5+1×0,25++1×0,125+0×0,0625++1×0,03125+0×0,015625++1×0,0078125=0,4140625\footnotesize 0\!\раз\! 1+0\!\раз\! 0,5+1\!\раз\! 0,25+\\ \размер сноски +1\!\раз\! 0,125+0\!\раз\! 0,0625+\\ \размер сноски +1\!\раз\! 0,03125+0\!\раз\! 0,015625+\\ \размер сноски +1\!\раз\! 0,0078125 = 0,41406250×1+0×0,5+1×0,25++1×0,125+0×0,0625++1×0,03125+0×0,015625++1×0,0078125=0,4140625

Вот и все — мы преобразовали десятичную дробь дробь в двоичную дробь!

0,01101012=0,4140625100,0110101_{2}=0,4140625_{10}0,01101012​=0,414062510​

Ограничения двоичных дробей

Двоичные дроби не могут точно представлять каждое десятичное число. Для десятичных дробей с конечным числом десятичных цифр ( рациональных ) вполне возможно иметь бесконечно длинное двоичное представление. Такое преобразование приводит к ошибке с величиной ошибки в зависимости от количества цифр представления 9n}=1n=1∑∞​2n1​=1

Это геометрический ряд, который сходится к 111. Удаляя элементы ad hoc , вы можете получить каждое число от 000 до 111; однако реальная проблема здесь заключается в том, чтобы решить, какие вклады мы должны стереть.

Поскольку компьютеры имеют ограниченный объем памяти — они могут вычислять только определенное количество цифр — некоторые элементы, позволяющие точное представление десятичной дроби, могут быть опущены.

Рассмотрим дробь 15\frac{1}{5}51​ в представлении из 888 цифр.

(15)10=0,2010\left(\tfrac{1}{5}\right)_{10}=0,20_{10}(51​)10​=0,2010​

Это конечная дробь: ошибка в 8-значном представлении равна нулю.

Найдите его бинарное представление , вы знаете как это сделать, но на этот раз мы вам поможем!

0,2000×2=0,4000→00,4000×2=0,8000→00,8000×2=1,6000→1−10,6000×2=1,2000→1−10,2000×2=0,4000→00,2000\times 2=0,4000{red}{rightarrow \textcolor\rightarrow 0}\\ 0,4000\умножить на 2=0,8000\стрелка вправо \textcolor{красный}{0}\\ 0,8000\умножить на 2=1,6000\стрелка вправо \textcolor{красный}{1}\\ \textcolor{синий}{-1}\\ 0,6000\умножить на 2=1,2000\стрелка вправо \textcolor{красный}{1}\\ \textcolor{синий}{-1}\\ 0,2000\times 2 = 0,4000\rightarrow \textcolor{red}{0}0,2000×2=0,4000→00,4000×2=0,8000→00,8000×2=1,6000→1−10,6000×2=1,2000→1−10,2000×2=0,4000→ 0

Последний шаг такой же, как и первый, поэтому, если мы продолжим, мы получим повторяющуюся последовательность 001100110011s:

0,210=0,001100110011… 20,2_{10}=0,001100110011\ldots_{\ 2} 0,210 = 0,00110011111111111111111111111111 . .. 2

Давайте усекаем его на восьмой цифре:

0,210≃0,0011111120.2_ {10} \ simeq0.00110011_ {2} 0,210 ≃0.0011112

. Этот бинарный фронт .20.2, хотя мы начали с этого:

0,001100112=0,19921875100,00110011_{2}=0,19{-8}7,15⋅10−8: очень мало, но все же присутствует.

Двоичное представление десятичной дроби является точным только , если 222 является единственным простым делителем знаменателя: 1/21/21/2, 3/83/83/8 и 1013/10241013/10241013/ 1024 все имеют точные представления, с другой стороны, 1/51/51/5 или 1/101/101/10 всегда имеют ошибку.

Как пользоваться нашим конвертером двоичных дробей?

Вы можете использовать наши конвертеры двоичных дробей для преобразования десятичной дроби в двоичную и из двоичной дроби в десятичную. Не забудьте выбрать правильный!

Выберите необходимое количество цифр в вашем представлении. Вы не сможете вставить больше этого числа. В результате получится усеченное и не округленное!

Вот пример: выберите из двоичного в десятичное , выберите 4 цифры и введите 0. 10100.10100.1010. Результат 0,6250,6250,625 или 5/85/85/8.

Вы заметили, что его знаменатель имеет единственный простой делитель, 222? Вводя такое число, мы неявно предполагали, что это 9.0003 конечная двоичная дробь!

🙋 Если вам нужно количество цифр, отличное от того, которое предусмотрено нашими настройками по умолчанию, перейдите в расширенный режим и вставьте нужное значение. Не забудьте обновить калькулятор, если хотите снова использовать значения по умолчанию! 😀

Помимо 0 и 1

Мы надеемся, что наш преобразователь двоичных дробей помог вам в изучении этой не очень простой темы. 🤞

У нас есть много других двоичных калькуляторов: попробуйте наш двоичный арифметический калькулятор или специальные инструменты:

• Калькулятор двоичного умножения;
• Калькулятор двоичного сложения.

Часто задаваемые вопросы

Можно ли преобразовать все дроби в двоичные?

Не все дроби могут быть ровно преобразованы в двоичные: только если знаменатель является степенью 2 , двоичная дробь будет конечной. Во всех остальных случаях будет ошибка в представлении. Величина ошибки зависит от количества цифр, используемых для ее представления.

Как преобразовать дроби в двоичные?

Возьмите десятичную дробь и начните умножать на два десятичную часть. Каждый раз, когда результат на меньше, чем 1 , добавляйте 0 к двоичному представлению. Если результат больше или равен 1 , добавьте 1 к двоичному представлению и вычтите 1 из результата умножения. Продолжайте умножать, пока результат не будет 0 или вы не достигнете желаемого количества цифр.

Узнайте больше о том, как представлять дроби в двоичном формате, на omnicalculator.com.

Как вы представляете 0,5 в двоичном формате?

Умножить 0,5 на 2 : 0,5 × 2 = 1,0 . Так как результат равен 1 , добавьте 1 к двоичной дроби: 0,1 .