Параллельное соединение трех резисторов. Параллельное соединение резисторов: принципы работы, расчеты и применение

Как работает параллельное соединение резисторов. Какие формулы используются для расчета эквивалентного сопротивления. Какие преимущества дает параллельное подключение резисторов в электрических цепях. Где применяется параллельное соединение на практике.

Принцип параллельного соединения резисторов

Параллельное соединение резисторов — это способ подключения, при котором все резисторы присоединяются к одним и тем же двум точкам электрической цепи. При таком соединении через каждый резистор проходит только часть общего тока, а напряжение на всех резисторах одинаково и равно напряжению источника.

Основные свойства параллельного соединения:

• Напряжение на всех резисторах одинаково
• Общий ток равен сумме токов через отдельные резисторы
• Эквивалентное сопротивление всегда меньше сопротивления наименьшего из резисторов

Расчет эквивалентного сопротивления при параллельном соединении

Для расчета эквивалентного сопротивления при параллельном соединении используется следующая формула:

1/R = 1/R1 + 1/R2 + 1/R3 + …

Где R — эквивалентное сопротивление, а R1, R2, R3 и т.д. — сопротивления отдельных резисторов.

Для двух параллельно соединенных резисторов формула упрощается:

R = (R1 * R2) / (R1 + R2)

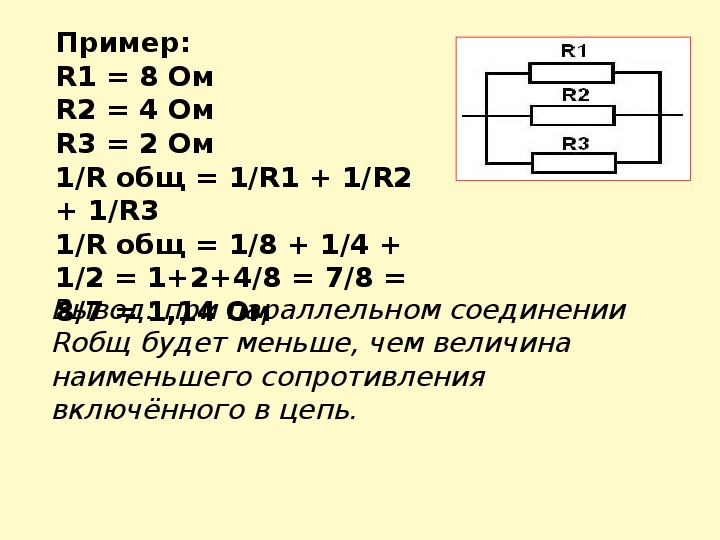
Пример расчета

Рассчитаем эквивалентное сопротивление для трех параллельно соединенных резисторов 10 Ом, 20 Ом и 30 Ом:

1/R = 1/10 + 1/20 + 1/30 = 0.1 + 0.05 + 0.033 = 0.183

R = 1 / 0.183 = 5.46 Ом

Как видим, эквивалентное сопротивление получилось меньше сопротивления наименьшего из резисторов (10 Ом).

Преимущества параллельного соединения резисторов

Параллельное соединение резисторов имеет ряд важных преимуществ по сравнению с последовательным:

• Уменьшение общего сопротивления цепи
• Увеличение общего тока в цепи
• Независимость работы параллельных ветвей друг от друга
• Возможность подключения и отключения отдельных ветвей без влияния на остальные
• Более равномерное распределение нагрузки между резисторами

Применение параллельного соединения на практике

Параллельное соединение резисторов широко используется в различных электрических и электронных устройствах:

• В системах освещения для подключения нескольких ламп
• В блоках питания для распределения нагрузки между резисторами
• В измерительных приборах для расширения пределов измерения
• В схемах делителей напряжения
• В цепях защиты от перегрузки

Пример применения в системе освещения

Рассмотрим схему подключения трех ламп параллельно к источнику питания 220В:

• Каждая лампа рассчитана на 220В
• При выходе из строя одной лампы остальные продолжают работать
• Общий ток равен сумме токов через каждую лампу
• Яркость ламп не зависит от количества включенных ламп

Особенности параллельного соединения трех и более резисторов

При параллельном соединении трех и более резисторов проявляются следующие особенности:

• Эквивалентное сопротивление всегда меньше сопротивления наименьшего из резисторов
• Чем больше параллельно соединенных резисторов, тем меньше эквивалентное сопротивление
• Ток распределяется обратно пропорционально сопротивлениям резисторов
• Мощность, выделяемая на резисторах, суммируется

Распределение тока между резисторами

При параллельном соединении ток распределяется между резисторами обратно пропорционально их сопротивлениям. Это означает, что через резистор с меньшим сопротивлением будет протекать больший ток.

Формула для расчета тока через отдельный резистор:

I(Rn) = U / Rn

Где U — напряжение источника, Rn — сопротивление конкретного резистора.

Сравнение параллельного и последовательного соединения резисторов

Параллельное и последовательное соединение резисторов имеют существенные различия:

Параметр	Параллельное соединение	Последовательное соединение
Напряжение	Одинаковое на всех резисторах	Сумма напряжений на резисторах
Ток	Сумма токов через резисторы	Одинаковый через все резисторы
Эквивалентное сопротивление	Меньше наименьшего из резисторов	Сумма сопротивлений резисторов
Влияние отключения резистора	Не влияет на работу остальных	Размыкает всю цепь

Расчет мощности в параллельных цепях

При параллельном соединении резисторов важно правильно рассчитывать мощность, выделяемую на каждом элементе и общую мощность цепи.

Формулы для расчета мощности:

• Мощность на отдельном резисторе: P = U^2 / R
• Общая мощность: P(общ) = U^2 / R(экв)

Где U — напряжение источника, R — сопротивление резистора, R(экв) — эквивалентное сопротивление параллельной цепи.

Пример расчета мощности

Рассчитаем мощность для трех параллельно соединенных резисторов 10 Ом, 20 Ом и 30 Ом при напряжении 12 В:

1. Эквивалентное сопротивление: R(экв) = 5.46 Ом (рассчитано ранее)
2. Общая мощность: P(общ) = 12^2 / 5.46 = 26.4 Вт
3. Мощность на резисторе 10 Ом: P1 = 12^2 / 10 = 14.4 Вт
4. Мощность на резисторе 20 Ом: P2 = 12^2 / 20 = 7.2 Вт
5. Мощность на резисторе 30 Ом: P3 = 12^2 / 30 = 4.8 Вт

Сумма мощностей на отдельных резисторах равна общей мощности: 14.4 + 7.2 + 4.8 = 26.4 Вт

Практические советы по использованию параллельного соединения

При работе с параллельным соединением резисторов следует учитывать несколько важных моментов:

• Убедитесь, что все резисторы рассчитаны на рабочее напряжение схемы
• Учитывайте допустимую мощность резисторов при расчете схемы
• Используйте резисторы с близкими номиналами для равномерного распределения нагрузки
• При большом количестве параллельных резисторов учитывайте возможность превышения тока источника питания
• Помните, что реальные резисторы имеют допуски, которые могут влиять на точность расчетов

Соблюдение этих рекомендаций поможет создавать надежные и эффективные схемы с параллельным соединением резисторов.

Последовательное и параллельное соединение резисторов

Широкое распространение в радиоэлектронных и электрических цепях получили резисторы, представляющие собой элементы с переменным или постоянным сопротивлением. С их помощью осуществляются различные действия, связанные с преобразованиями силы тока и напряжения, влияющих на работу всей схемы. Поэтому в большинстве случаев резисторы выполняют регулировочные функции. В большинстве цепей применяется последовательное и параллельное соединение резисторов. При необходимости они используются в комбинированном виде.

Каждый вид того или иного соединения дает различные показатели сопротивления, в связи с чем для каждого из них разработана собственная методика расчетов. Благодаря стабильным и точным параметрам резисторов, обеспечивается устойчивая и надежная эксплуатация схем с различными типами соединений.

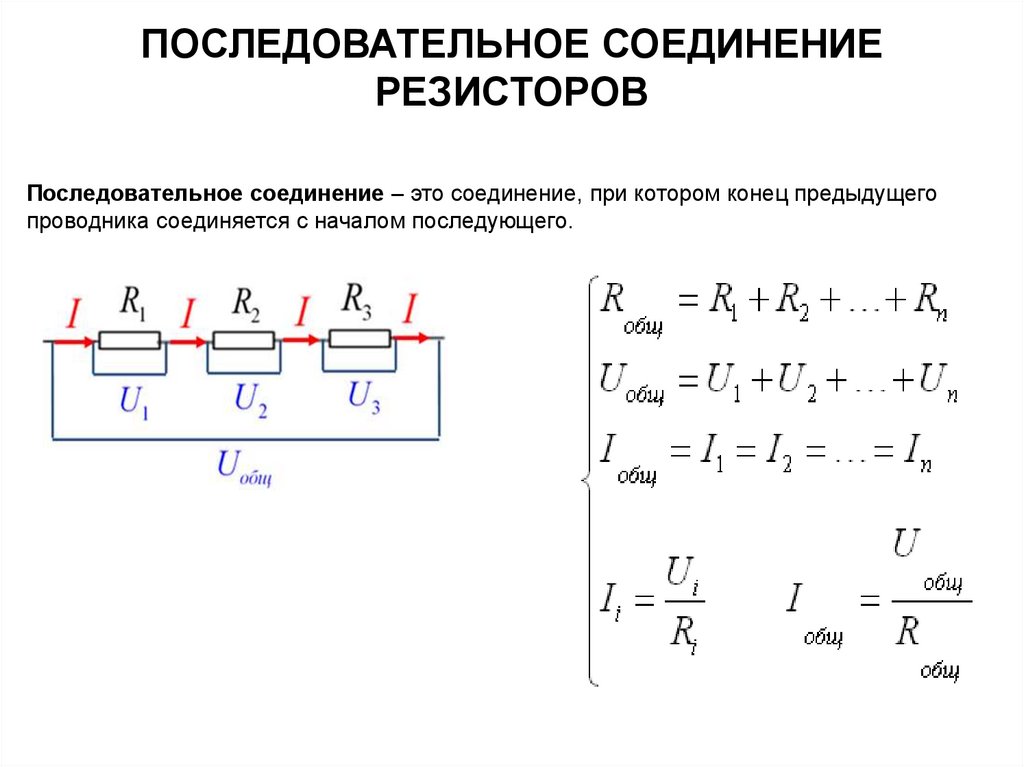
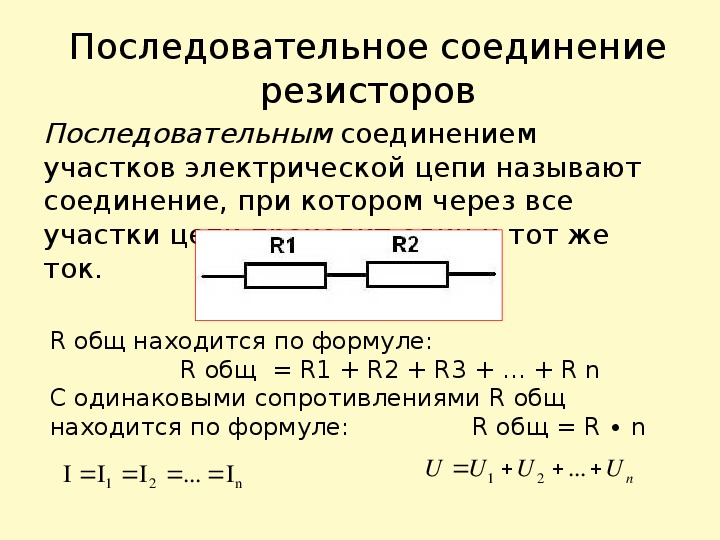
Последовательное соединение

Последовательным называется соединение двух и более резисторов, при котором конец первого элемента соединяется с началом второго и так далее. В результате получается последовательная цепочка, где по всем ее составляющим проходит одинаковый ток. В качестве примера можно взять последовательную цепь, состоящую из трех резисторов R1, R2 и R3. Сопротивление в источнике тока принимается с нулевым значением. В соответствии со вторым законом Кирхгофа получается следующая формула: E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк.

В этой формуле значение эквивалентного сопротивления последовательной цепи составит сумму сопротивлений всех резисторов, имеющихся в данной цепи: Rэк = R1 + R2 + R3. По закону Ома напряжение при последовательном соединении на отдельных участках будет иметь следующее значение, поскольку E = U: U1=IR1, U2 = IR2, U3 = IRз, то есть U = U1 + U2 +U3. Данные формулы показывают, что в резисторах, последовательно соединенных между собой, напряжения распределяются пропорционально их сопротивлениям. То есть, чем выше сопротивление любого из резисторов, тем больше напряжение, приложенное к нему. В виде формулы &mdash, это утверждение будет выглядеть следующим образом: U1 : U2 : U3 = R1 : R2 : R3.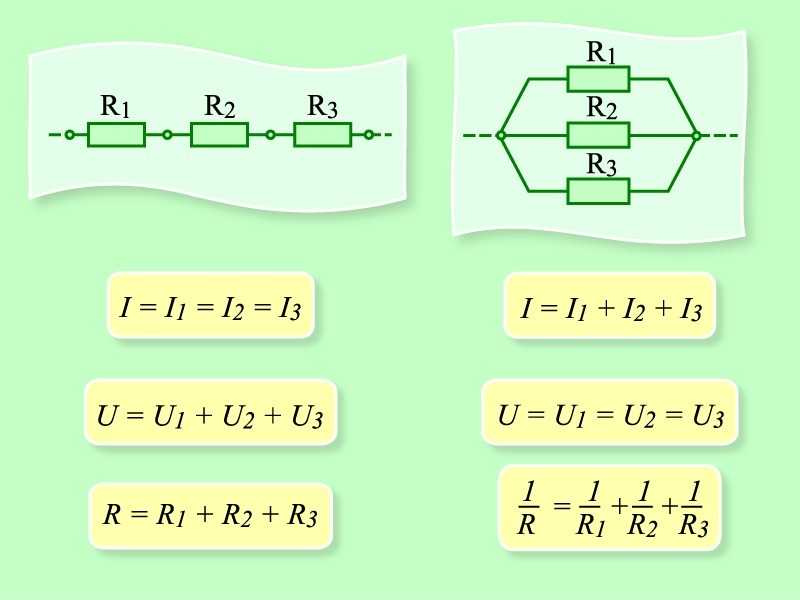

При последовательном соединении сопротивление R1 нескольких резисторов в количестве n, будет одинаковым. Следовательно, значение эквивалентного сопротивления цепи будет в n раз превышать сопротивление каждого из них: Rэк = nR1. Следовательно напряжение на каждом отдельном резисторе будет в n раз меньше, чем общее напряжение цепи: U1 = U/n.

Таким образом, изменение сопротивления любого из резисторов при последовательном соединении, приводит к изменению напряжения на других резисторах, находящихся с ним в одной цепи. Поэтому, если электрическая цепь обрывается или выключается в одной из нагрузок, в других нагрузках также прекращается течение тока. Из-за этого последовательное соединение в электрических схемах используется довольно редко.

Параллельное соединение

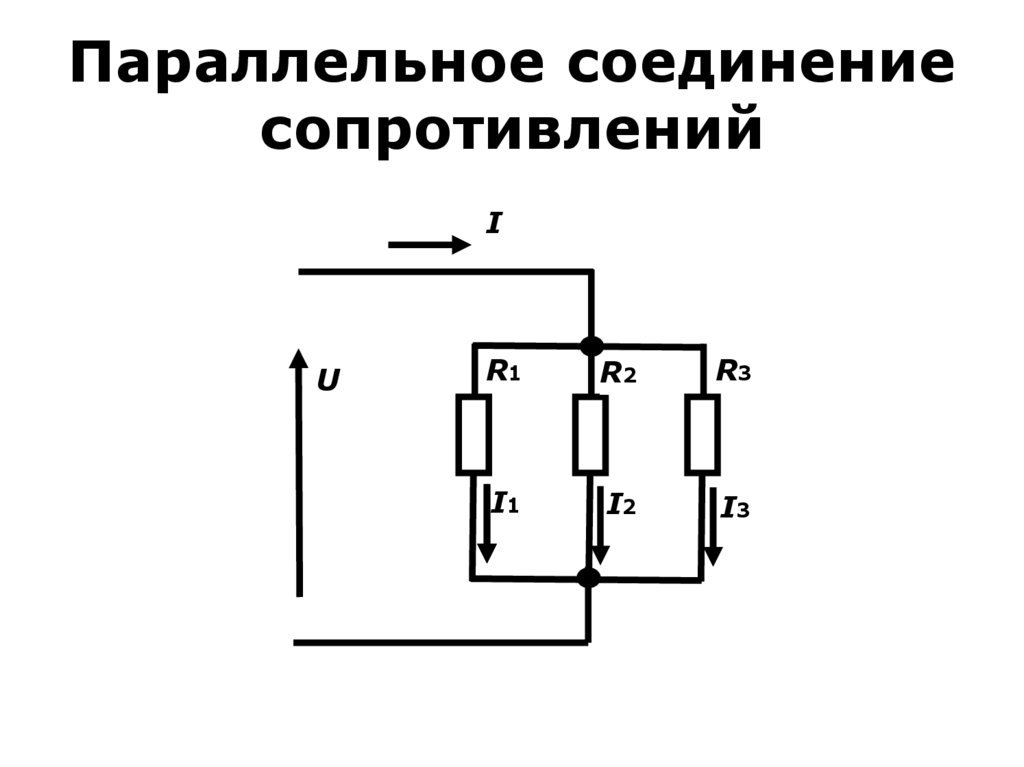
Гораздо чаще в электрических цепях применяется параллельное соединение резисторов, отличающихся наличием общих точек, где соединяются начала и концы каждого элемента. Данный вид соединения характеризуется собственными физическими свойствами.

Основными из них являются следующие:

• Каждый из подключенных резисторов, обладает одинаковым напряжением: U = U1 = U2 = U3. То есть, напряжение в параллельном соединении на каждом участке будет одно и то же.
• Общая проводимость резисторов, соединенных параллельно, включает в себя сумму проводимостей каждого отдельного сопротивления, выраженную соотношением: 1/R = 1/R1 + 1/R2 + 1/R3 = R1R2 + R1R3 + R2R3/R1R2R3. Здесь R является эквивалентным или равнодействующим сопротивлением всех трех резисторов. Оно может полностью заменить их, без изменения величины силы тока в цепи. Значение эквивалентного сопротивления можно вычислить путем сложения проводимостей каждого участка. В результате, получится общая проводимость. Обратная ей величина и будет фактически общим сопротивлением.
• Существуют и особенности эквивалентной проводимости, когда используется параллельное соединение. Она составляет сумму проводимостей всех отдельно взятых ветвей. В этом случае при параллельном соединении сопротивление эквивалентное будет всегда ниже самого маленького сопротивления, включенного параллельно.
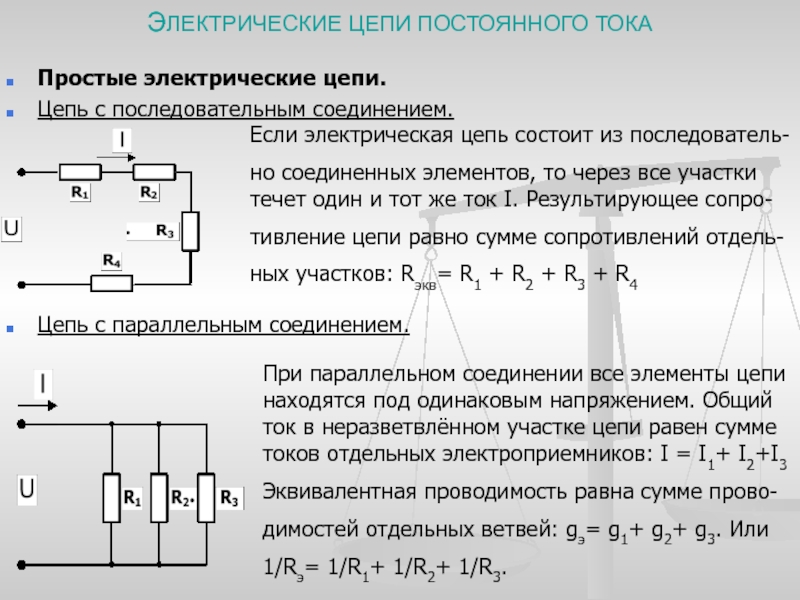
• соотношения касаются не только трех резисторов, соединенных параллельно, но и любого количества сопротивлений, соединенных этим способом. Этот способ широко используется в схемах радиотехнической аппаратуры. Параллельное включение двух и более резисторов используется при наличии слишком большой силы тока в цепи. В этом случае единственный резистор может перегреться и выйти из строя. Ярким примером служат электрические лампы освещения, включенные параллельно. Выключение ходя бы одной из них никак не повлияет на работу остальных ламп.

Калькулятор вычисления параллельного соединения резисторов
Искомая величина	R1R2Rp
Сопротивление R1	m&Omega,&Omega,K&Omega,M&Omega,
Сопротивление R2	m&Omega,&Omega,k&Omega,M&Omega,
Сопротивление Rp	m&Omega,&Omega,K&Omega,M&Omega,

Смешанное соединение

В радиоэлектронных и электрических схемах широко применяется последовательное, параллельное и смешанное соединение резисторов, наиболее подходящее на том или ином конкретном участке. Первые два соединения были рассмотрены выше, осталось лишь отметить характерные особенности комбинированного варианта.

В смешанных схемах нашли отражение свойства, присущие последовательному и параллельному соединениям. Частично выполняется последовательное подключение резисторов, а другая группа элементов подключается параллельно. Резисторы R1 и R2, изображенные на схеме, включаются последовательно, а резисторы R1, R2 и R3 соединены параллельно.

Существуют определенные трудности при расчетах сопротивления для таких цепей. Для получения правильных результатов используется специальная методика, основой которой является преобразование сложных цепей в более простые в течение нескольких этапов. Например, для одной группы резисторов применяется формула последовательного соединения, позволяющая получить предварительный результат. Точно также для другой группы элементов используется формула параллельного соединения. Постепенно складывая полученные данные можно получить точное общее значение сопротивления смешанной цепи.

(а) Три резистора соединены параллельно, а комбинация подключена к батарее, амперметру, вольтметру и ключу. Нарисуйте подходящую схему d

• #Наука
• #Школа
• #Электричество
• #CBSE 10 Класс

(a) Три резистора соединены параллельно, и комбинация подключена к батарее, амперметру, вольтметру и ключу. Нарисуйте подходящую электрическую схему и получите выражение для эквивалентного сопротивления комбинации резисторов.

(b) Рассчитайте эквивалентное сопротивление следующей сети:

40013

.

Предположим, что это эквивалентное сопротивление

Суммарный ток , I =

О применении закона Ома для каждого резистора

(b)

Эквивалентное сопротивление сети = 

Посмотреть полный ответ

Похожие вопросы

2

для функции, почему мы пишем f(x)?
• Кого вы меняете сахарный тростник, когда черный цвет превращается в белый
• Кто они изменит цвет сахарного тростника черный на белый

Экзамены CBSE 2023: класс 10, 12 образцов работ, программа доступна на cbseacademic.nic.in; Примите карту скоро

NCERT разрабатывает новый модуль для трансгендерных детей, предлагает гендерно-нейтральную униформу

CBSE 2023: практические экзамены со 2 января; Правление направляет письмо директорам школ, учителям, учащимся

Последний вопрос

• Случайная величина X имеет следующее распределение вероятностей:
• Пусть будет n-й член Г. П. положительных терминов. Если

Уже заданные вопросы

Создать учетную запись

Номер мобильного телефона (+91)

Я согласен с Политикой конфиденциальности и Условиями использования Careers360

• я уже член

Ваш ответ

Создать учетную запись

Номер мобильного телефона (+91)

Я согласен с Политикой конфиденциальности и Условиями использования Careers360

• я уже член

Три резистора соединены проводами пренебрежимо малого сопротивления.

Каково приблизительное сопротивление между двумя точками P и Q?\n \n \n \n \n

Дата последнего обновления: 21 января 2023 г.

•

Всего просмотров: 167,7 тыс.

•

Просмотров сегодня: 3.63k

Ответ

Проверено

167.7k+ просмотров

Подсказка: Эквивалентное сопротивление между двумя точками можно оценить после упрощения схемы до простых последовательно-параллельных комбинаций резисторов и последующего применения соответствующей формулы. Когда резисторы соединены последовательно, их эквивалент равен ${R_s} = {R_1} + {R_2}…….. + {R_n}$ . Когда резисторы соединены параллельно, эквивалентное сопротивление определяется как $\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2 }}} + ……… + \dfrac{1}{{{R_n}}}$.

Полный пошаговый ответ:
Последовательное соединение определяется как соединение, в котором резисторы соединены цепочкой, тогда как при параллельном соединении резисторы имеют одинаковые начальную и конечную точки в цепи.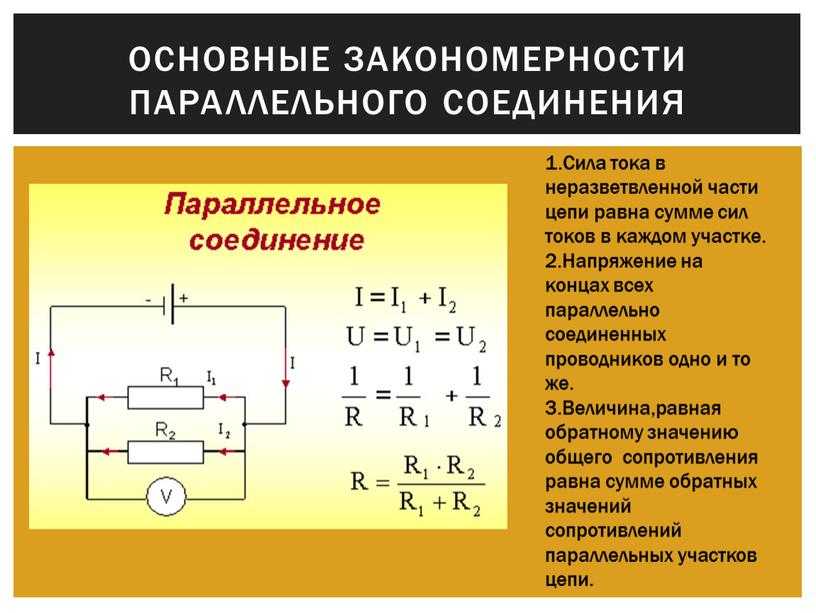 В простом проводнике, когда нет сопротивления, нет падения потенциала и, следовательно, разность потенциалов остается равной нулю. Это означает, что вдоль прямого проводника потенциал остается одним и тем же. Схема, данная нам,


При осмотре схема уменьшается до

Мы можем ясно видеть, что три резистора включены параллельно друг другу.


Пусть эквивалентное сопротивление между точками P и Q равно ${R_{eq}}$ .
Используя формулу для параллельного соединения резисторов,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}} } + ……… + \dfrac{1}{{{R_n}}}$
Здесь у нас есть три резистора, поэтому эта формула сводится к $\dfrac{1}{{{R_{eq}} }} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$ .
Пусть ${R_1} = 1,0\,\Omega $ , ${R_2} = 2,0\,\Omega $ и ${R_3} = 3,0\,\Omega $ .
Подставляя эти значения в формулу,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{1} + \dfrac{1}{2} + \dfrac{1}{ 3}$
Далее решая уравнение, получаем,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{{6 + 3 + 2}}{6}$
$ \Rightarrow \ dfrac{1}{{{R_{eq}}}} = \dfrac{{11}}{6}$
Следовательно, ${R_{eq}} = \dfrac{{11}}{6}\,\ Омега$.