Что такое преобразователи кодов и для чего они используются. Какие виды преобразователей кодов существуют. Как работают основные типы преобразователей кодов. Где применяются преобразователи кодов в цифровых устройствах.
Что такое преобразователи кодов и их назначение
Преобразователи кодов — это комбинационные логические устройства, предназначенные для преобразования информации из одной формы представления в другую. Они выполняют важную функцию в цифровых системах, позволяя согласовывать различные способы кодирования данных.
Основные задачи преобразователей кодов:
- Преобразование между различными системами счисления (например, двоичной и десятичной)
- Перевод из одного формата представления чисел в другой (например, из двоично-десятичного кода в код Грея)
- Изменение разрядности кодов
- Преобразование кодов для отображения информации на индикаторах
Использование преобразователей кодов позволяет эффективно обрабатывать и передавать информацию в цифровых устройствах.
Основные виды преобразователей кодов
В цифровой схемотехнике используются различные типы преобразователей кодов, среди которых можно выделить следующие основные виды:
1. Преобразователи двоичных кодов в двоично-десятичные
Эти устройства преобразуют двоичные числа в двоично-десятичный формат, где каждая десятичная цифра представлена 4-разрядным двоичным кодом. Они позволяют согласовать двоичную арифметику процессоров с десятичным представлением чисел для человека.
2. Преобразователи двоично-десятичных кодов в двоичные
Выполняют обратное преобразование двоично-десятичных чисел в обычный двоичный формат. Это необходимо, например, при вводе десятичных чисел в цифровые системы.
3. Преобразователи двоичных кодов в код Грея
Переводят обычные двоичные коды в код Грея, в котором соседние кодовые комбинации отличаются только в одном разряде. Код Грея применяется для повышения помехоустойчивости при передаче и преобразовании данных.
4. Дешифраторы
Преобразуют n-разрядный двоичный код в унитарный код, активируя один из 2^n выходов. Используются для адресации памяти, управления индикацией и других задач.

5. Шифраторы
Выполняют обратное преобразование — из унитарного кода в двоичный. Применяются в устройствах ввода, системах прерываний и др.
Выбор конкретного типа преобразователя зависит от решаемой задачи и особенностей цифровой системы.
Принцип работы преобразователей кодов
Рассмотрим принцип работы преобразователей кодов на примере преобразователя двоичного кода в двоично-десятичный:
- На вход поступает n-разрядный двоичный код
- Устройство анализирует входную комбинацию
- В соответствии с логикой преобразования формируется выходной двоично-десятичный код
- Каждая десятичная цифра представляется 4-разрядным двоичным числом
Для реализации преобразования используются комбинационные логические схемы на основе вентилей И, ИЛИ, НЕ. Логика работы задается с помощью карт Карно или других методов минимизации логических функций.
Применение преобразователей кодов
Преобразователи кодов находят широкое применение в различных цифровых устройствах и системах:
- Системы отображения информации (преобразование двоичных кодов для семисегментных индикаторов)
- Аналого-цифровые и цифро-аналоговые преобразователи
- Устройства ввода-вывода компьютеров и микропроцессорных систем
- Системы передачи данных (преобразование в помехоустойчивые коды)
- Цифровые измерительные приборы
- Системы управления производственными процессами
Использование преобразователей кодов позволяет эффективно согласовывать различные цифровые устройства и обеспечивать корректную обработку информации.

Реализация преобразователей кодов
Преобразователи кодов могут быть реализованы различными способами:
1. На дискретных логических элементах
Строятся из базовых логических вентилей в соответствии с разработанной логической схемой. Позволяет создавать заказные преобразователи, но занимает много места на плате.
2. На основе ПЗУ
Входной код используется как адрес ячейки памяти, а выходной код записывается в эту ячейку. Простой способ реализации сложных преобразований.
3. На программируемых логических матрицах
Логика преобразования задается путем программирования матрицы соединений. Обеспечивает гибкость при разработке.
4. На специализированных микросхемах
Выпускаются готовые микросхемы для наиболее распространенных видов преобразования кодов. Позволяют быстро создавать типовые устройства.
Выбор способа реализации зависит от сложности преобразования, требуемого быстродействия, стоимости и других факторов.
Проектирование преобразователей кодов
При разработке преобразователей кодов обычно выполняются следующие этапы:
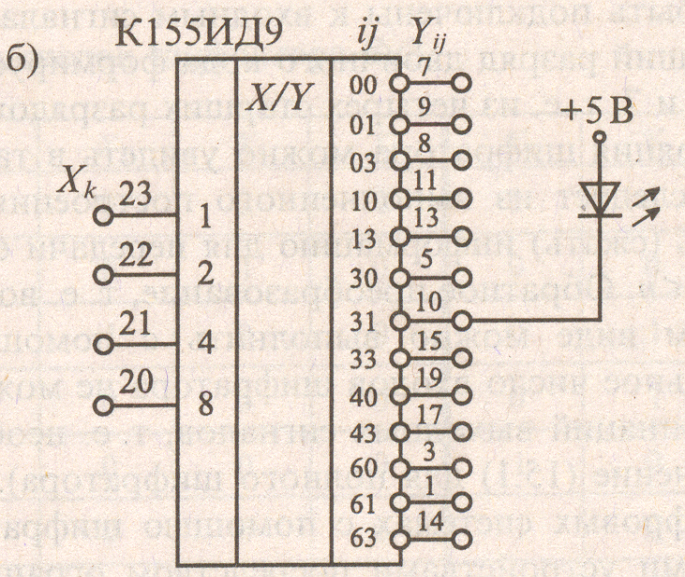
- Составление таблицы истинности, задающей соответствие между входными и выходными кодами
- Получение логических выражений для каждого выходного разряда
- Минимизация логических функций с помощью карт Карно или других методов
- Построение логической схемы на основе полученных выражений
- Выбор элементной базы для реализации схемы
- Моделирование работы преобразователя
- Изготовление и отладка устройства
Важно обеспечить корректную работу преобразователя для всех возможных входных комбинаций и минимизировать задержку преобразования.
Характеристики преобразователей кодов
Основные параметры, характеризующие работу преобразователей кодов:
- Разрядность входных и выходных кодов
- Быстродействие (максимальная частота смены входных кодов)
- Задержка преобразования
- Потребляемая мощность
- Помехоустойчивость
- Нагрузочная способность выходов
При выборе или разработке преобразователя кода необходимо учитывать эти характеристики в соответствии с требованиями конкретного применения.
Заключение
Преобразователи кодов играют важную роль в современных цифровых устройствах, обеспечивая согласование различных способов представления информации. Понимание принципов их работы необходимо для эффективного проектирования цифровых систем.

Развитие элементной базы и методов проектирования позволяет создавать все более совершенные преобразователи кодов, расширяя возможности цифровой обработки данных в различных областях техники.
Справочник по цифровой схемотехнике
Справочник по цифровой схемотехнике
ОглавлениеПРЕДИСЛОВИЕГлава 1. ЧИСЛА И КОДЫ 1.1. СИСТЕМЫ СЧИСЛЕНИЯ 1.3. МАШИННОЕ СЛОВО 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ 1.6. КОД ГРЕЯ 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ Глава 2. АЛГЕБРА ЛОГИКИ 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА 2.4. БУЛЕВА АЛГЕБРА 2.5. СТАНДАРТНЫЕ ФОРМЫ 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ 2.9. КАРТЫ КАРНО Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ 3.1. ЛОГИЧЕСКИЕ СХЕМЫ 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ 3.3. ФАКТОРИЗАЦИЯ 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ Электронные ключи на биполярных транзисторах.  Ключ на биполярном транзисторе с нелинейной обратной связью. Электронные ключи на полезых транзисторах. 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ 6 1. ТРИГГЕРЫ 6.2. РЕГИСТРЫ 6.3. СЧЕТЧИКИ Синхронные счетчики. Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ Генераторы импульсов на полевых транзисторах. 
Генераторы импульсов на логических ИМС Генераторы импульсов на основе триггеров. Генераторы импульсов на основе операционных усилителей. Формирователи и генераторы линейно изменяющегося напряжения (ЛИН). 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП 9.3. ЭЛЕМЕНТЫ АЦП 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580 Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813 СПИСОК ЛИТЕРАТУРЫ |
НОУ ИНТУИТ | Лекция | Комбинационные микросхемы.
 Часть 2
Часть 2 Аннотация: В лекции рассказывается о комбинационных микросхемах: сумматорах, преобразователях кодов, одновибраторах и генераторах, об их алгоритмах работы, параметрах, типовых схемах включения, а также о реализации на их основе некоторых часто встречающихся функций.
Ключевые слова: сумматор, adder, входной, SM, функция, единица, таблица истинности, разность, выход, быстродействие, Z-резистор, одновибраторы, monostable multivibrator, логический уровень, память, информация, инверсный выход, логический, прямой, вывод, запуск, интервал, погрешность, генератор, диапазон, значение
Сумматоры
Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных
двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов. Например, если один входной
код — 7 (0111), а второй — 5 (0101), то суммарный код на выходе будет 12 (1100).
На схемах сумматоры обозначаются буквами SM. В отечественных сериях код, обозначающий микросхему сумматора, — ИМ.
Сумматоры бывают одноразрядные (для суммирования двух одноразрядных чисел), 2-х разрядные (суммируют 2-х разрядные числа) и 4-х разрядные (суммируют 4-х разрядные числа). Чаще всего применяют именно 4-разрядные сумматоры. На рис. 6.1 показаны для примера 2-разрядный и 4-разрядный сумматоры. Микросхема ИМ6 отличается от ИМ3 только повышенным быстродействием и номерами используемых выводов микросхемы, функция же выполняется та же самая.
Рис. 6.1.
Примеры микросхем сумматоров
6.1.
Примеры микросхем сумматоров
Помимо выходных разрядов суммы и выхода переноса, сумматоры имеют вход расширения (другое название — вход переноса) С для объединения нескольких сумматоров с целью увеличения разрядности. Если на этот вход приходит единица, то выходная сумма увеличивается на единицу, если же приходит нуль, то выходная сумма не увеличивается. Если используется одна микросхема сумматора, то на ее вход расширения С необходимо подать нуль.
Для примера в табл. 6.1 приведена полная таблица истинности 2-разрядного сумматора ИМ2. Как видно из таблицы,
выходной 3-разрядный код (Р, S1, S0) равен сумме входных 2-разрядных кодов (А1, А0) и (В1, В0), а также сигнала С.
Нулевые разряды — младшие, первые разряды — старшие. Полная таблица истинности 4-разрядного сумматора будет
чрезмерно большой, поэтому она не приводится. Но суть работы остается точно такой же, как и в случае 2-разрядного
сумматора.
Сумматоры могут использоваться также для суммирования чисел в отрицательной логике (когда логической единице соответствует электрический нуль, и наоборот, логическому нулю соответствует электрическая единица). Но в этом случае входной сигнал переноса С также становится инверсным, поэтому при использовании одной микросхемы сумматора на вход С надо подать электрическую единицу (высокий уровень напряжения). Инверсным становится и выходной сигнал переноса Р, низкий уровень напряжения на нем (электрический нуль) соответствует наличию переноса. То есть получается, что сумматор абсолютно одинаково работает как с положительной, так и с отрицательной логикой.
| Входы | Выходы | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C=0 | C=1 | ||||||||
| A1 | A0 | B1 | B0 | P | S1 | S0 | P | S1 | S0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
intuit.ru/2010/edi»>Рассмотрим пример. Пусть нам надо сложить два числа 5 и 7 в отрицательной логике. Числу 5 в положительной логике соответствует двоичный код 0101, а в отрицательной — код 1010. Числу 7 в положительной логике соответствует двоичный код 0111, а в отрицательной — код 1000. При подаче на вход сумматора кодов 1010 (десятичное число 10 в положительной логике) и 1000 (десятичное число 8 в положительной логике) получаем сумму 10 + 8 = 18, то есть код 10010 в положительной логике. С учетом входного сигнала переноса С=1 (отсутствие входного переноса в отрицательной логике) выходной код сумматора получится на единицу больше: 18 + 1 = 19, то есть 10011. При отрицательной логике это будет соответствовать числу 01100, то есть 12 при отсутствии выходного переноса. В результате получили 5+7=12.
Сумматор может вычислять не только сумму, но и разность входных кодов, то есть работать вычитателем. Для
этого вычитаемое число надо просто поразрядно проинвертировать, а на вход переноса С подать единичный сигнал
(рис. 6.2).
6.2).
Рис. 6.2. 4-х разрядный вычитатель на сумматоре ИМ6 и инверторах ЛН1
Например, пусть нам надо вычислить разность между числом 11 (1011) и числом 5 (0101). Инвертируем поразрядно число 5 и получаем 1010, то есть десятичное 10. Сумматор при суммировании 11 и 10 даст 21, то есть двоичное число 10101. Если сигнал С равен 1, то результат будет 10110. Отбрасываем старший разряд (выходной сигнал Р) и получаем разность 0110, то есть 6.
Еще пример. Пусть надо вычислить разность между числом 12 (1100) и числом 9 (1001). Инвертируем поразрядно 9, получаем 0110, то есть десятичное 6. Находим сумму 12 и 6, получаем 18, а с учетом С = 1 получаем 19, то есть двоичное 10011. В четырех младших разрядах имеем 0011, то есть десятичное 3.
Каскадировать сумматоры для увеличения разрядности очень просто. Надо сигнал с выхода переноса сумматора,
обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды
(рис. 6.3).
При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд
(выход переноса Р).
Надо сигнал с выхода переноса сумматора,
обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды
(рис. 6.3).
При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд
(выход переноса Р).
Рис. 6.3. Каскадирование сумматоров ИМ6 для увеличения разрядности
Неопределенные состояния на выходах сумматора могут возникать при любом изменении любого из входных кодов
(рис. 6.4). Выходной код суммы может принимать в течение короткого времени значения, никак не связанные с
входными кодами, а на выходе переноса могут появляться короткие паразитные импульсы. Это связано прежде всего
с неодновременным изменением разрядов входных кодов. Чтобы избежать влияния этих неопределенных состояний на
дальнейшую схему, необходимо предусматривать синхронизацию или стробирование выходных сигналов. Но для этого
надо располагать информацией о моментах изменения входных кодов, которая имеется далеко не всегда.
Но для этого
надо располагать информацией о моментах изменения входных кодов, которая имеется далеко не всегда.
Рис. 6.4. Неопределенные состояния на выходах сумматора при изменении входных кодов
Задержки сумматора ИМ6 от входов до выходов суммы примерно вдвое превышает задержку логического элемента, а от входов до выхода переноса — примерно в полтора раза. Задержки сумматора ИМ3 больше задержек ИМ6 почти вдвое. Поэтому в схемах, где важно быстродействие, лучше использовать ИМ6. Особенно это существенно при каскадировании для увеличения разрядности, так как там задержки отдельных микросхем суммируются. Точные величины задержек надо смотреть в справочниках.
Дальше >>
< Дополнительный материал || Лекция 6: 1234
Преобразователи кодов — двоичные в/из кода Грея
Предпосылка – Система счисления и преобразование оснований
Система кода Грея представляет собой двоичную систему счисления, в которой каждая последующая пара чисел отличается только одним битом. Он используется в приложениях, в которых обычная последовательность двоичных чисел, сгенерированная аппаратным обеспечением, может привести к ошибке или неоднозначности при переходе от одного числа к другому.
Он используется в приложениях, в которых обычная последовательность двоичных чисел, сгенерированная аппаратным обеспечением, может привести к ошибке или неоднозначности при переходе от одного числа к другому.
Например, состояния системы могут измениться с 3(011) на 4(100) как 011 — 001 — 101 — 100. Поэтому высока вероятность чтения неправильного состояния при изменении системы с начального состояния до конечного состояния.
Это может иметь серьезные последствия для машины, использующей информацию. Код Грея устраняет эту проблему, поскольку только один бит изменяет свое значение при любом переходе между двумя числами.
Преобразование двоичного кода в код Грея –
Позвольте быть битами, представляющими двоичные числа, где LSB и MSB, и
Пусть быть битами, представляющими код Грея двоичных чисел, где LSB и является МСБ.
Таблица истинности преобразования:
Чтобы найти соответствующую цифровую схему, мы будем использовать метод K-Map для каждого бита кода Грея в качестве вывода со всеми двоичными битами в качестве входа.
К-карта для –
К-карта для –
К-карта для –
К-карта для –
Соответствующие минимизированные логические выражения для битов кода Грея –
Соответствующая цифровая схема –
Логическое выражение для преобразования двоичного кода в код Грея для n-бит:
g N = B N
G N-1 = B N XOR B N-1 ::
G 1 = B 2 XOR B 1 = B 2 XOR B 1
65 1 659 1 1 9 1,9000 1 = B 2 7765 1 = B 2 XOR B 1 59 1 = B 2 7.Преобразование кода Грея в двоичный –
Преобразование кода Грея обратно в двоичный можно выполнить аналогичным образом.
Позвольте быть битами, представляющими двоичные числа, где LSB и MSB, и
Пусть будут биты, представляющие код Грея двоичных чисел, где LSB и MSB.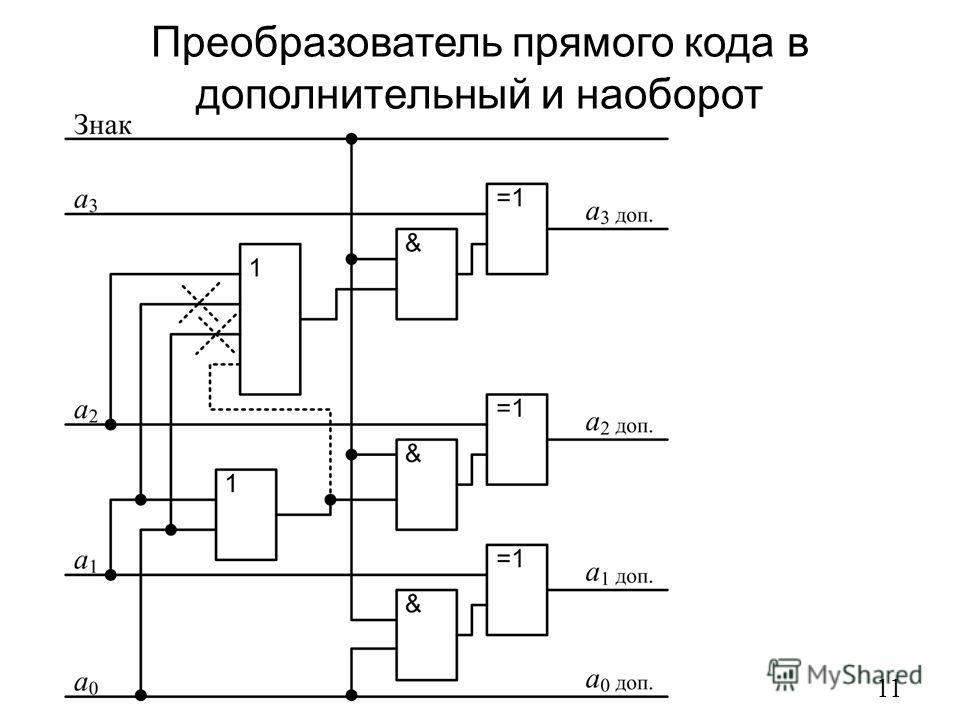
Таблица истинности-
Использование К-карты для возврата двоичных битов из кода Грея –
К-карта для –
К-карта для –
К-карта для –
К-карта для –
Соответствующие логические выражения –
Соответствующая цифровая схема –
Обобщенное логическое выражение для преобразования кода Грея в двоичный код –
Логическое выражение для преобразования кода Грея в двоичный код для n-бит : 6 n 0037 = G N B N-1 = B N XOR G N-1 = G N XOR G N-1 :: B 1 = B 2: XOR G 1 = G n XOR ………… XOR G 1 Эта статья предоставлена Chirag Manwani . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу review-team@geeksforgeeks. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше. Преобразователь кода используется для преобразования одного типа двоичного кода в другой. Существуют различные типы двоичных кодов, такие как двоично-десятичный код, код Грея, код избытка 3 и т. д. Различные коды используются для различных типов цифровых приложений. Чтобы получить требуемый код из любого одного типа кода, выполняется простой процесс преобразования кода с помощью комбинационных схем. В этом разделе обсуждаются три типа преобразования. В двоично-десятичном коде числа от 0 до 9 представляют эквивалентные двоичные числа. Для чисел выше 10 младший бит десятичного числа представлен его эквивалентным двоичным числом, а старший бит десятичного числа также представлен их эквивалентными двоичными числами. Например, двоично-десятичный код 12 представлен как В следующей таблице истинности показано преобразование между входным двоичным кодом и выходным двоично-десятичным кодом. Как видно из таблицы, 4-битное двоичное число преобразуется в 5-битный двоично-десятичный код. Десятичный код добавлен в таблицу, чтобы понять эквивалентность двоичного и двоично-десятичного кода. Преобразователь имеет 5 выходов D 0 , D 1 , D 2 , D 3 и D 4 . Из таблицы истинности можно получить minterms для каждого выхода. D 4 = ∑m(10, 11, 12, 13, 14, 15), D 3 = ∑m(8, 9), D 2 = ∑m(4, 5, 6, 7, 14, 15), D 1 = ∑m(2, 3, 6, 7, 12, 13), D 0 = ∑m(1, 3, 5, 7, 9, 11, 13, 15) Минтермы наносятся на карту Карно и получаются упрощенные булевы выражения. Узнайте, как минимизировать логическую функцию с помощью K-map? Цифровая логическая схема для преобразователя двоичного кода в двоично-десятичный разработана на основе упрощенных выходных выражений, полученных из карты Карно. Для этого процесса преобразования 4-битный код BCD считается входным, который преобразуется в 4-битный код Excess-3. Так как для двоично-десятичного кода используется 4-битный код, вывод производится только для входных значений от 0 до 9. Таблица истинности, показанная ниже, содержит только допустимые 4-битные двоично-десятичные коды. Для оставшихся входных комбинаций выход не может быть предсказан. Так что им все равно. Из таблицы истинности получаются минтермы для каждого выхода (E 3 , E 2 , E 1 , E 0 ). E 3 = ∑m(5, 6, 7, 8, 9), E 2 = ∑m(1, 2, 3, 4, 9), E 1 = ∑m(0, 3, 4, 7, 8), E 0 = ∑m(0, 2, 4, 6, 8,) Минтермы каждого выхода нанесены на k-карту, и получено упрощенное выражение. Из полученных логических выражений построена комбинационная логическая схема преобразования кода BCD в код Excess-3. Ниже показана таблица истинности с преобразованием двоично-десятичных кодов в коды Грея. Поскольку двоично-десятичный код имеет только 4 бита, всего было рассмотрено 9 двоично-десятичных цифр. Выход непредсказуем для других входных комбинаций. Из минтермов каждого выхода G 3 , G 2 , G 1 , G 0 для упрощения функции реализована карта Карно. Схема преобразователя кода из двоично-десятичного кода в код Грея нарисована, как показано ниже, из полученного выражения. Для этого преобразования 4-битный код Грея рассматривается как вход, который создает 4-битный код избытка-3 в качестве выхода. Поскольку 4-битный код считается избыточным-3, максимально возможный вывод будет «1111». Следовательно, для этого преобразования учитываются до 12 номеров. Таблица истинности для этого преобразования показана ниже. org. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
org. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
Преобразователь кодов | Типы | Таблица истинности и логические схемы
Преобразователь двоичного кода в двоично-десятичный
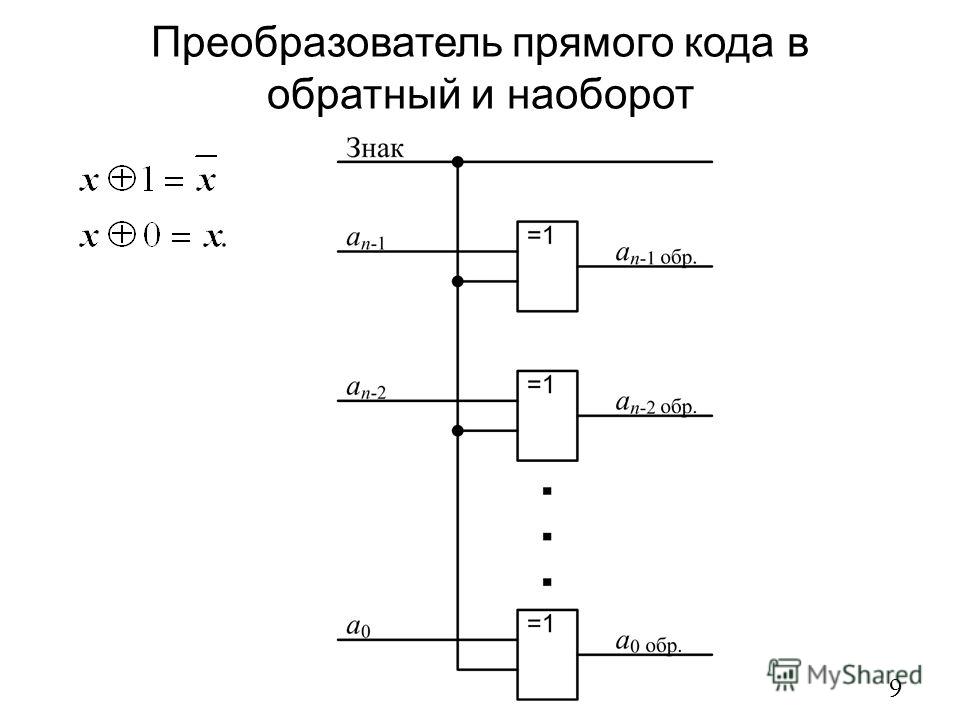
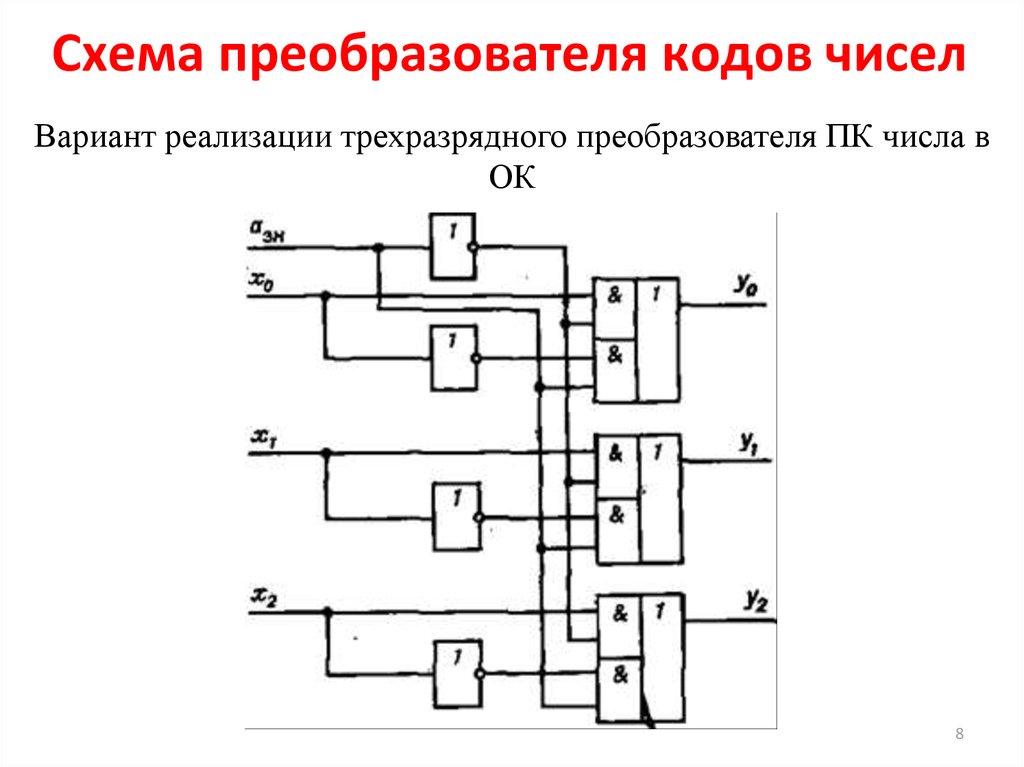
Преобразователь кода BCD в код Excess-3
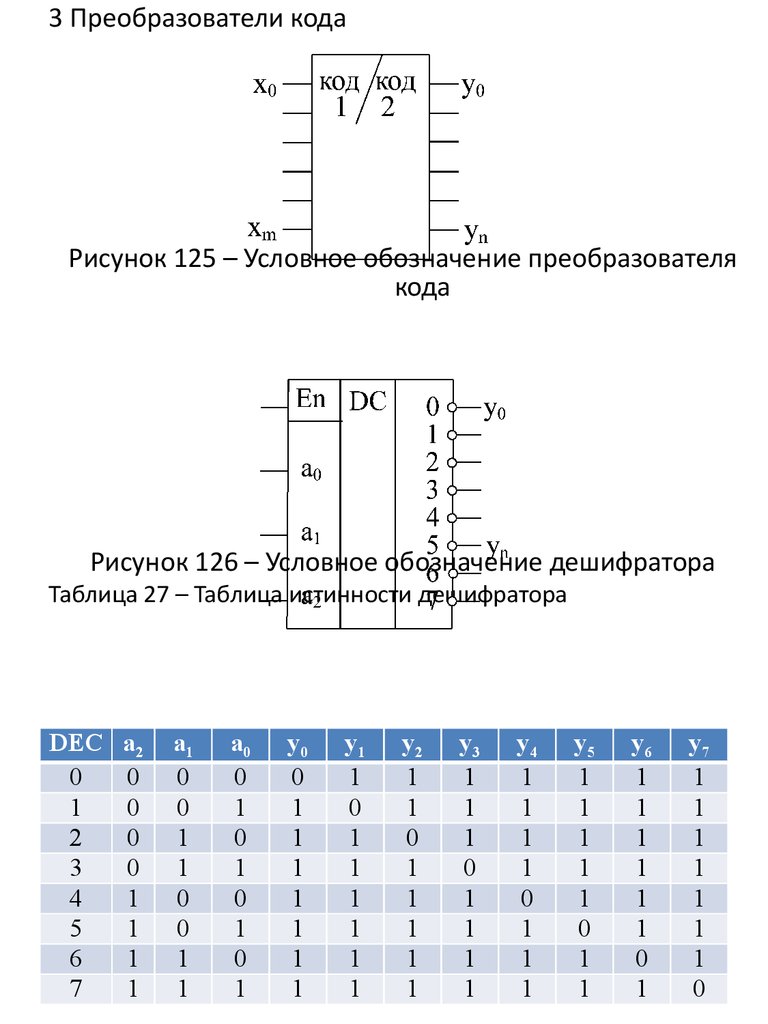
Преобразователь двоично-десятичных кодов в коды Грея
Преобразователь кода Грея в код избытка-3



