2 и не таблица истинности. Логические элементы и таблицы истинности: основы цифровой логики — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое логические элементы и как они работают. Как построить таблицу истинности для сложной логической функции. Какие бывают основные логические операции и элементы. Как применяются таблицы истинности в цифровой электронике.

Содержание

Основные логические элементы и операции

Логические элементы являются базовыми «кирпичиками» цифровых схем и выполняют элементарные логические операции над двоичными сигналами. Основными логическими элементами являются:

НЕ (инвертор) — выполняет операцию отрицания
И (конъюнктор) — реализует операцию логического умножения
ИЛИ (дизъюнктор) — выполняет операцию логического сложения
И-НЕ — комбинация элементов И и НЕ
ИЛИ-НЕ — комбинация элементов ИЛИ и НЕ

Каждый логический элемент имеет один или несколько входов и один выход. Сигналы на входах и выходах могут принимать только два значения — логический 0 или логическая 1.

Таблицы истинности логических элементов

Работа логических элементов описывается с помощью таблиц истинности. Таблица истинности показывает, какое значение будет на выходе элемента при всех возможных комбинациях входных сигналов.

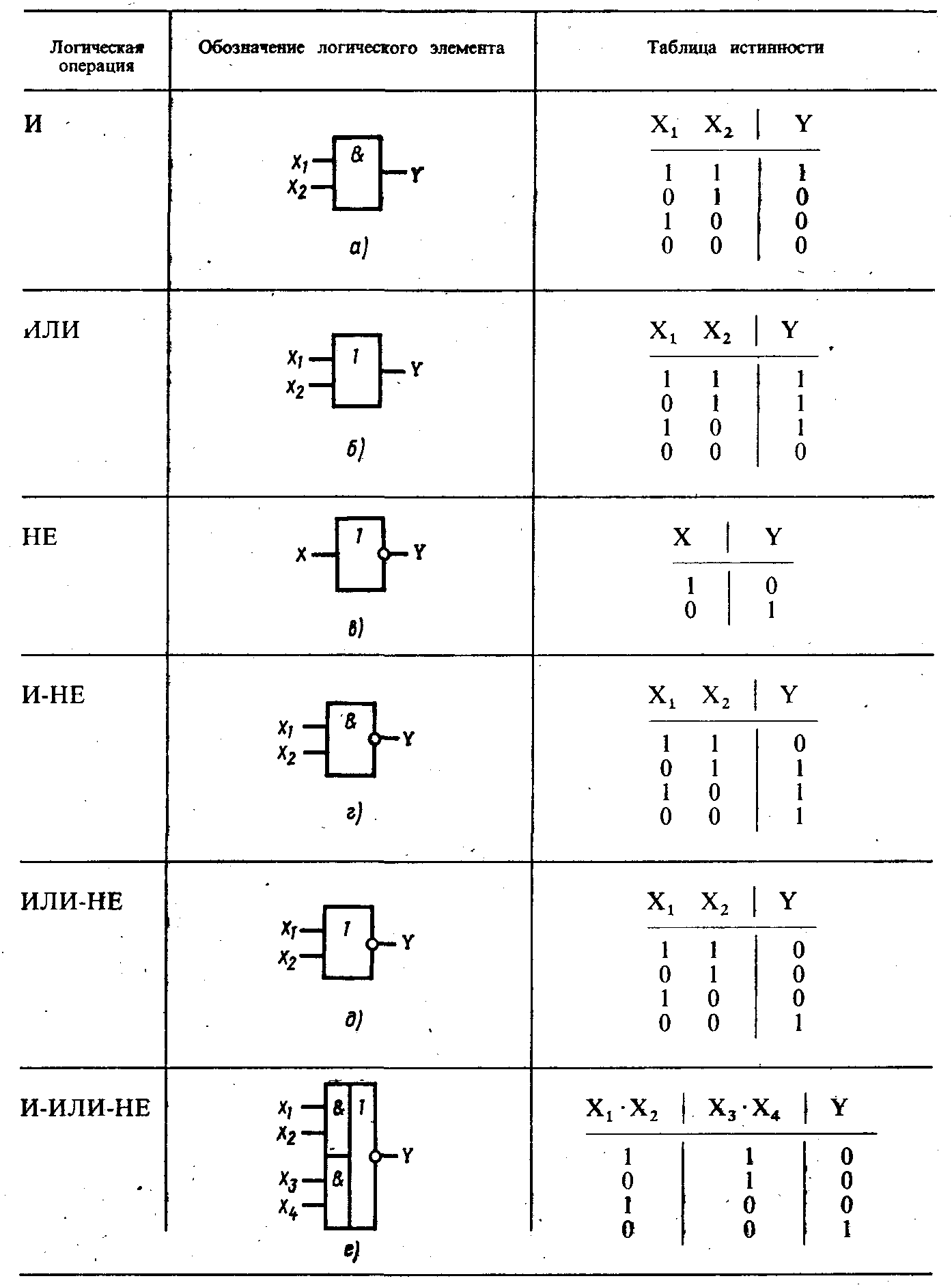
Рассмотрим таблицы истинности для основных логических элементов:

Инвертор (НЕ)

Вход	Выход
0	1
1	0

Элемент И (конъюнкция)

Вход A	Вход B	Выход
0	0	0
0	1	0
1	0	0
1	1	1

Элемент ИЛИ (дизъюнкция)

Вход A	Вход B	Выход
0	0	0
0	1	1
1	0	1
1	1	1

Таблицы истинности позволяют однозначно определить поведение логического элемента при любых входных сигналах.

Построение таблицы истинности сложной функции

Для сложных логических функций, состоящих из нескольких элементов, таблица истинности строится поэтапно. Рассмотрим процесс на примере.

Допустим, нужно построить таблицу истинности для функции:

F = (A AND B) OR (NOT C)

Алгоритм построения:

Определяем количество входных переменных (A, B, C) — их 3.
Составляем таблицу со всеми возможными комбинациями входов (2^3 = 8 строк).
Добавляем столбцы для промежуточных результатов (A AND B) и (NOT C).
Вычисляем значения для промежуточных столбцов.
Вычисляем итоговый результат F.

Получившаяся таблица истинности:

A	B	C	A AND B	NOT C	F
0	0	0	0	1	1
0	0	1	0	0	0
0	1	0	0	1	1
0	1	1	0	0	0
1	0	0	0	1	1
1	0	1	0	0	0
1	1	0	1	1	1
1	1	1	1	0	1

Такая таблица полностью описывает поведение логической функции при всех возможных комбинациях входных сигналов.

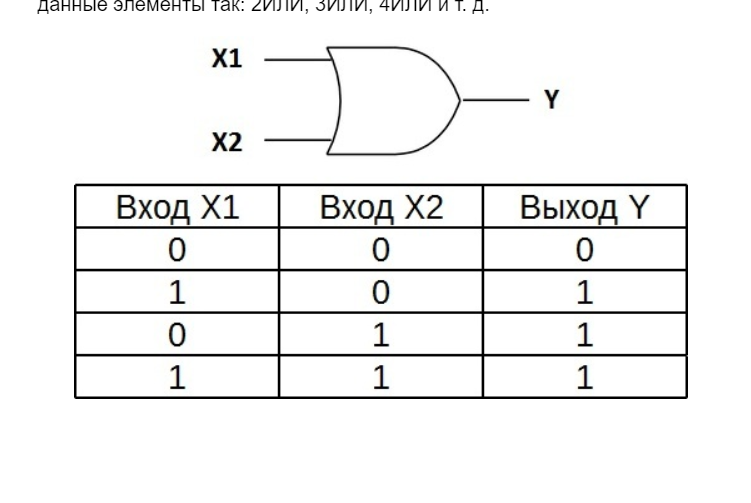
Применение таблиц истинности

Таблицы истинности широко используются в цифровой электронике и информатике для следующих целей:

Описание работы логических элементов и микросхем
Проектирование цифровых устройств
Минимизация логических функций
Анализ и отладка цифровых схем
Построение карт Карно

Понимание принципов построения и анализа таблиц истинности является важным навыком для специалистов в области цифровой электроники и программирования.

Логические элементы в интегральных микросхемах

Современные интегральные микросхемы содержат миллионы логических элементов на одном кристалле. Наиболее распространенными семействами логических микросхем являются:

TTL (транзисторно-транзисторная логика)
CMOS (комплементарная металл-оксид-полупроводниковая технология)
ECL (эмиттерно-связанная логика)

Каждая технология имеет свои особенности по быстродействию, энергопотреблению, помехоустойчивости и другим параметрам. Выбор конкретной технологии зависит от требований к разрабатываемому устройству.

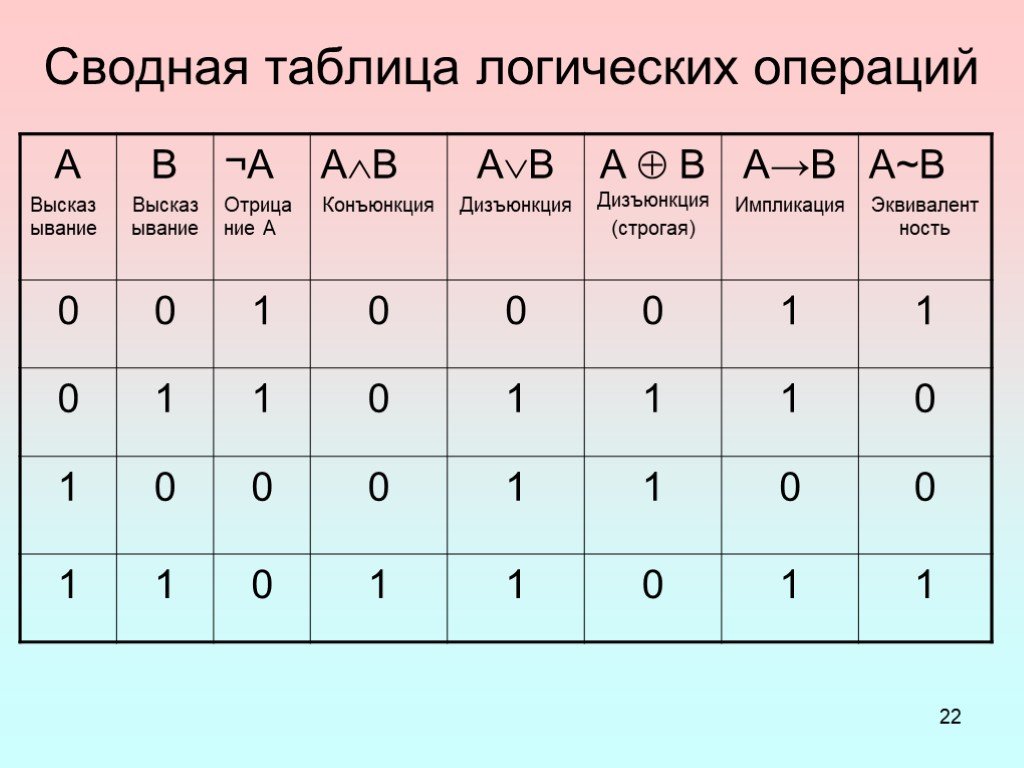
Законы алгебры логики

При работе с логическими функциями и таблицами истинности полезно знать основные законы алгебры логики:

Закон коммутативности: A AND B = B AND A, A OR B = B OR A
Закон ассоциативности: (A AND B) AND C = A AND (B AND C)
Закон дистрибутивности: A AND (B OR C) = (A AND B) OR (A AND C)
Законы де Моргана: NOT(A AND B) = (NOT A) OR (NOT B)

Эти законы позволяют преобразовывать и упрощать логические выражения, что важно при проектировании цифровых схем.

Минимизация логических функций

Одной из важных задач при проектировании цифровых устройств является минимизация логических функций. Цель минимизации — получить наиболее простую реализацию заданной функции, используя минимальное количество логических элементов.

Основные методы минимизации:

Алгебраические преобразования с использованием законов булевой алгебры
Метод карт Карно
Метод Квайна-Мак-Класки

Правильно минимизированная функция позволяет создать более эффективное устройство с меньшим энергопотреблением и стоимостью.

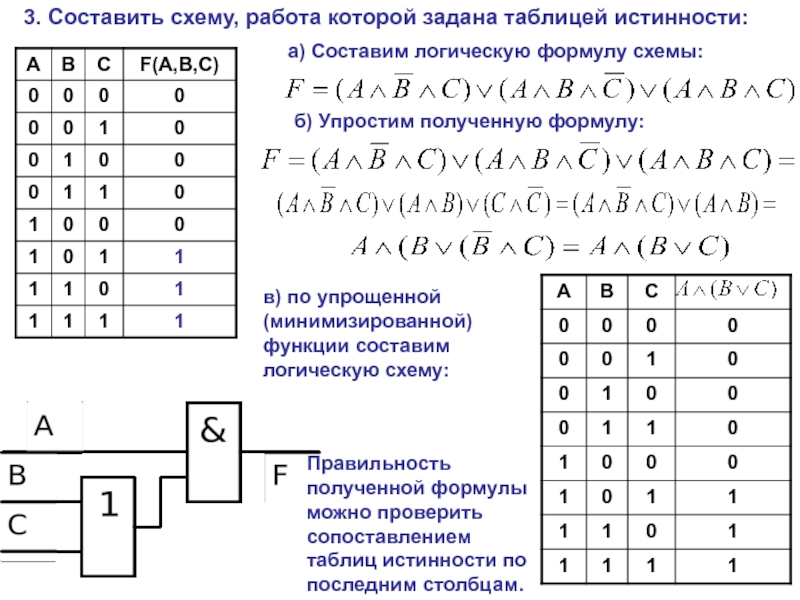
Заключение

Логические элементы и таблицы истинности являются фундаментальными концепциями цифровой электроники. Понимание принципов их работы необходимо для проектирования и анализа цифровых устройств любой сложности — от простых логических схем до современных микропроцессоров. Умение строить и анализировать таблицы истинности, а также минимизировать логические функции — важные навыки для специалистов в области цифровой техники.

2.Логические элементы и, или, не. Таблицы истинности, принципиальные схемы.

Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.1, а таблица истинности в таблице 1.

Таблица 1

х	у	*х у**
0	0	0
0	1	0
1	0	0
1	1	1

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

Связь между выходом z этой схемы и входами х и у описывается отношением z = х * у (читается как «х и у»).

Операция конъюнкции на функциональных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.

Схема ИЛИ реализует дизъюнкцию двух или более логических значений.

Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.

Условное обозначение схемы ИЛИ знак «1». Связь между выходом z этой схемы и входами х и у описывается соотношением z = х + у (читается как «х или у»). Рис.2 и таблица 2.

Таблица 2

х	у	х + у
0	0	0
0	1	1
1	0	1
1	1	1

Схема НЕ (инвертор) реализует операцию отрицания.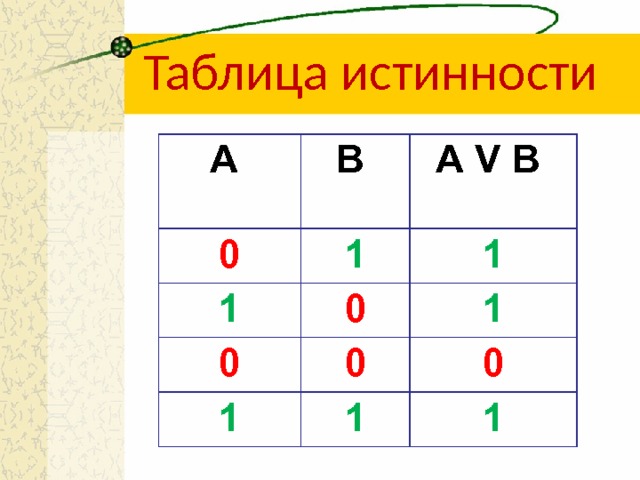

Связь между входом х этой схемы и выходом z можно записать соотношением z = , где читается как «не х» или «инверсия х».

Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора — на рис.3, а таблица истинности – в таблице 3

Таблица 3

x
0	1
1	0

3.Логические элементы и — не, или — не. Таблицы истинности. Графическое представление элементов. Графики работы.

Связь между выходом z и входами х и у схемы записывают следующим образом:

z = , где читается как «инверсия х и у».

рис. 4

Таблица 4

х	у
0	0	1
0	1	1
1	0	1
1	1	0

Условное обозначение схемы И-НЕ представлено на рис.

4, а таблица истинности схемы И-НЕ – в таблице 4.

Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.

Связь между выходом z и входами х и у схемы записывают следующим образом:

z = , где читается как «инверсия х или у».

Таблица 5

х	у
0	0	1
0	1	0
1	0	0
1	1	0

Условное обозначение схемы ИЛИ-НЕ представлено на рис.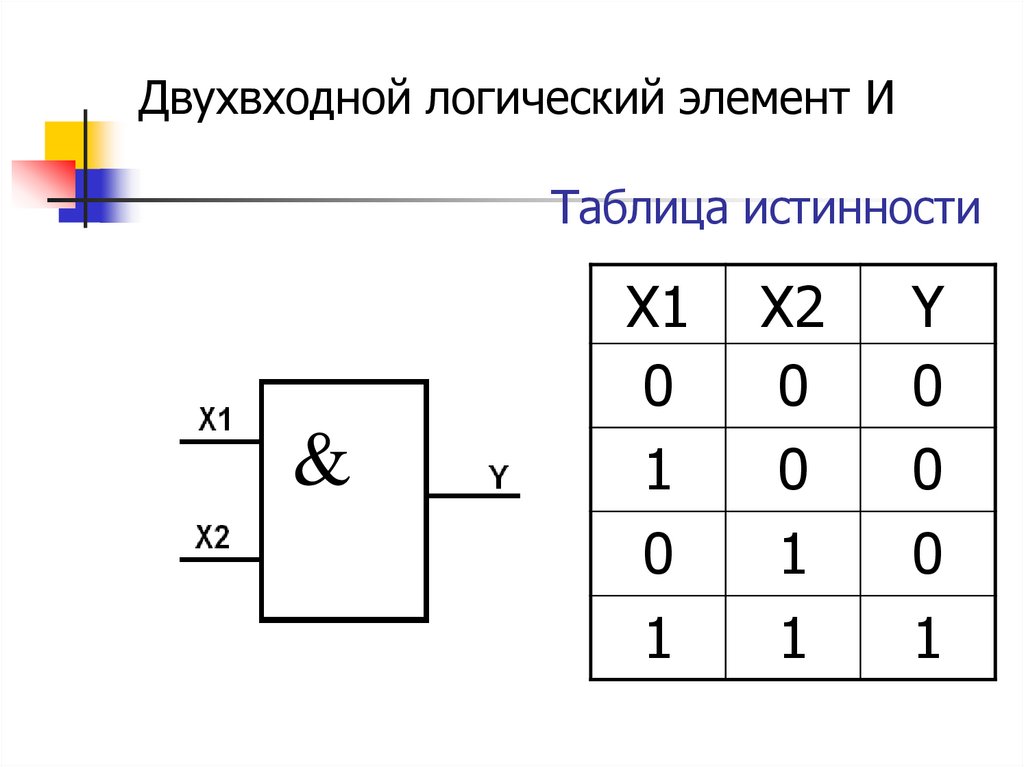 5, а таблица истинности схемы ИЛИ-НЕ – в таблице 5

4.Исключающие или, исключающие или — не. Таблицы истинности. Графическое представление элементов.

лементы Исключающее ИЛИ (по-английски — Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.

Таблица 4.1. Таблица истинности двухвходовых элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ

Вход 1	Вход 2	Выход
0	0	0
0	1	1
1	0	1
1	1	0

Рис.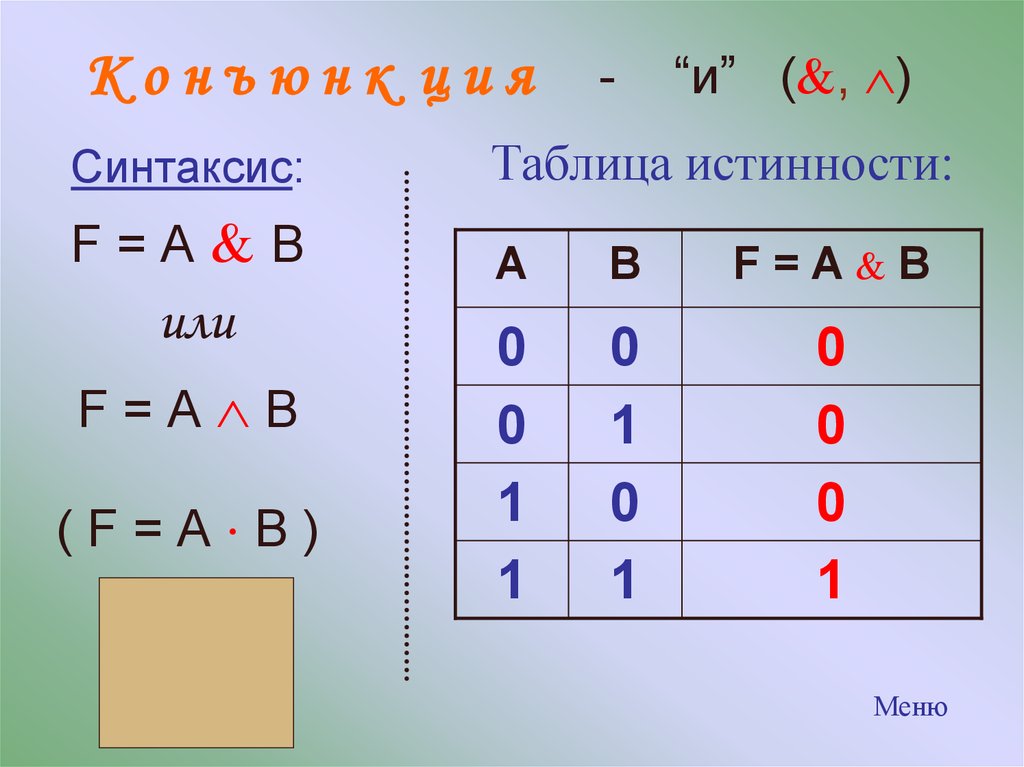 4.1. Обозначения элементов Исключающее ИЛИ: зарубежные (слева) и отечественные (справа)

Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ “=1″ как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.

Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком уж специфическая функция реализуется этими элементами.

С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию так называемого суммирования по модулю 4. Поэтому эти элементы также называются сумматорами по модулю два. Как уже отмечалось в предыдущей лекции, обозначается суммирование по модулю 2 знаком плюса, заключенного в кружок.

Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности, состоит в сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают), на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы компараторов кодов, которые будут рассмотрены в следующей лекции.

В качестве сумматора по модулю 2 элемент Исключающее ИЛИ используется также в параллельных и последовательных делителях по модулю 2, служащих для вычисления циклических контрольных сумм. Но подробно эти схемы будут рассмотрены в лекциях 14,15.

Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2). В этом случае один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает информационный сигнал. Если на управляющем входе единица, то входной сигнал инвертируется, если же нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.

Рис. 4.2. Элемент Исключающее ИЛИ как управляемый инвертор

В случае, когда имеется два сигнала одинаковой полярности (положительные или отрицательные), и при этом их одновременный приход исключается, элемент Исключающее ИЛИ может быть использован для смешивания этих сигналов (рис. 4.3). При любой полярности входных сигналов выходные сигналы элемента будут положительными.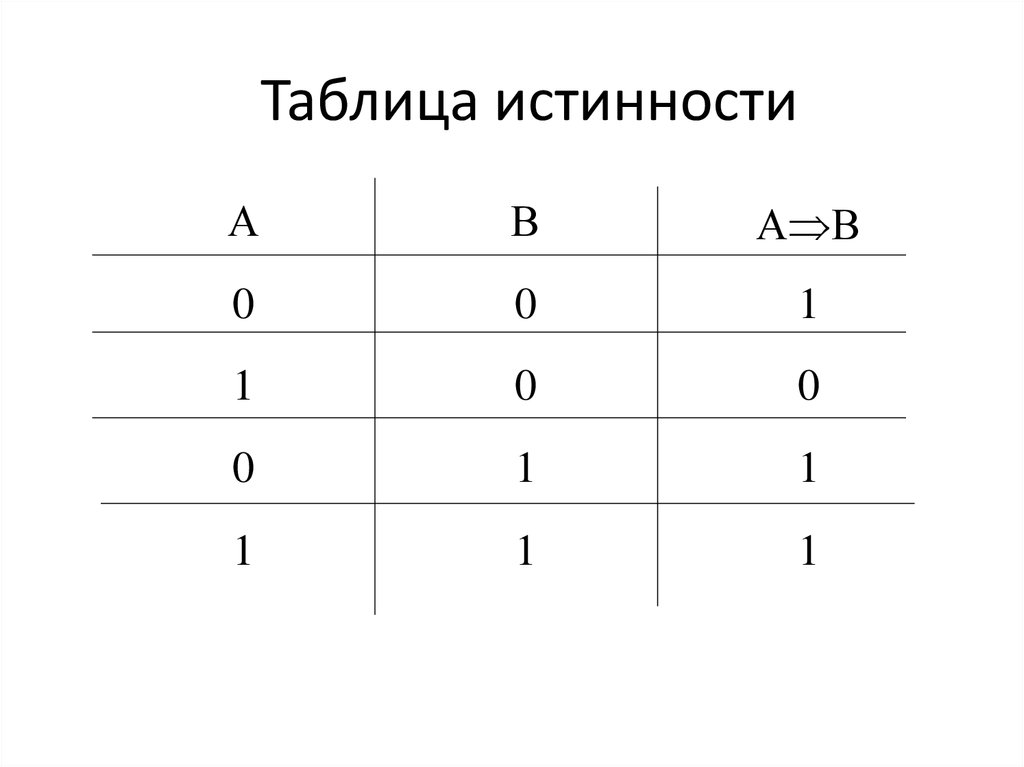 При положительных входных сигналах элемент Исключающее ИЛИ будет работать как элемент 2ИЛИ, а при отрицательных он будет заменять элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда в схеме остаются неиспользованными некоторые элементы Исключающее ИЛИ. Правда, при этом надо учитывать, что задержка распространения сигнала в элементе Исключающее ИЛИ обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.

Рис. 4.3. Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов

Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ

Еще одно важнейшее применение элемента Исключающее ИЛИ — формирование коротких импульсов по любому фронту входного сигнала (рис. 4.4). В данном случае не важно, положительный фронт входного сигнала или отрицательный, на выходе все равно формируется положительный импульс. Входной сигнал задерживается с помощью конденсатора или цепочки элементов, а затем исходный сигнал и его задержанная копия поступают на входы элемента Исключающее ИЛИ. В обеих схемах в качестве элементов задержки используются также двувходовые элементы Исключающее ИЛИ в неинвертирующем включении (на неиспользуемый вход подается нуль). В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.

Данную особенность элементов Исключающее ИЛИ надо учитывать в том случае, когда на оба входа элемента поступают изменяющиеся одновременно сигналы. При этом на выходе элемента возможно появление коротких паразитных импульсов по любому из фронтов входных сигналов. Исключить их влияние на дальнейшую схему можно, например, с помощью синхронизации, подобной рассмотренной в предыдущем разделе.

Логические элементы

Любые цифровые микросхемы строятся на основе простейших логических элементов «НЕ», «ИЛИ», «И». В настоящее время используется несколько технологий построения логических элементов:

транзисторно-транзисторная логика (ТТЛ, TTL)
логика на основе комплементарных МОП транзисторов (КМОП, CMOS)
логика на основе сочетания комплементарных МОП и биполярных транзисторов (BiCMOS)

Простейшим логическим элементом является инвертор, который работает в соответствии со следующей таблицей:

	Рис 1 Таблица истинности логического инвертора
	Рис 2 Изображение логического инвертора на принципиальных схемах.

Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:

	Рис 3 Таблица истинности схемы, выполняющей логическую функцию «И-НЕ».
	Рис 4 Изображение схемы, выполняющей логическую функцию «И-НЕ».

Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:

	Рис 5 Таблица истинности схемы, выполняющей логическую функцию «ИЛИ-НЕ».
	Рис 6 Изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ».

Построение произвольной таблицы истинности.

Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем «И» «ИЛИ» «НЕ».

При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно. Для реализации таблицы истинности при помощи логических элементов «И» достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую «1», реализуется схемой логического «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности. Входные сигналы, описанные в таблице истинности логической «1» подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим «0» подаются на вход через иверторы. Объединение сигналов с выходов схем, реализующих отдельные строки таблицы истинности, производится при помощи схемы логического ИЛИ. Количество входов в этой схеме определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая «1».

Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 7:

Рисунок 7 Произвольная таблица истинности.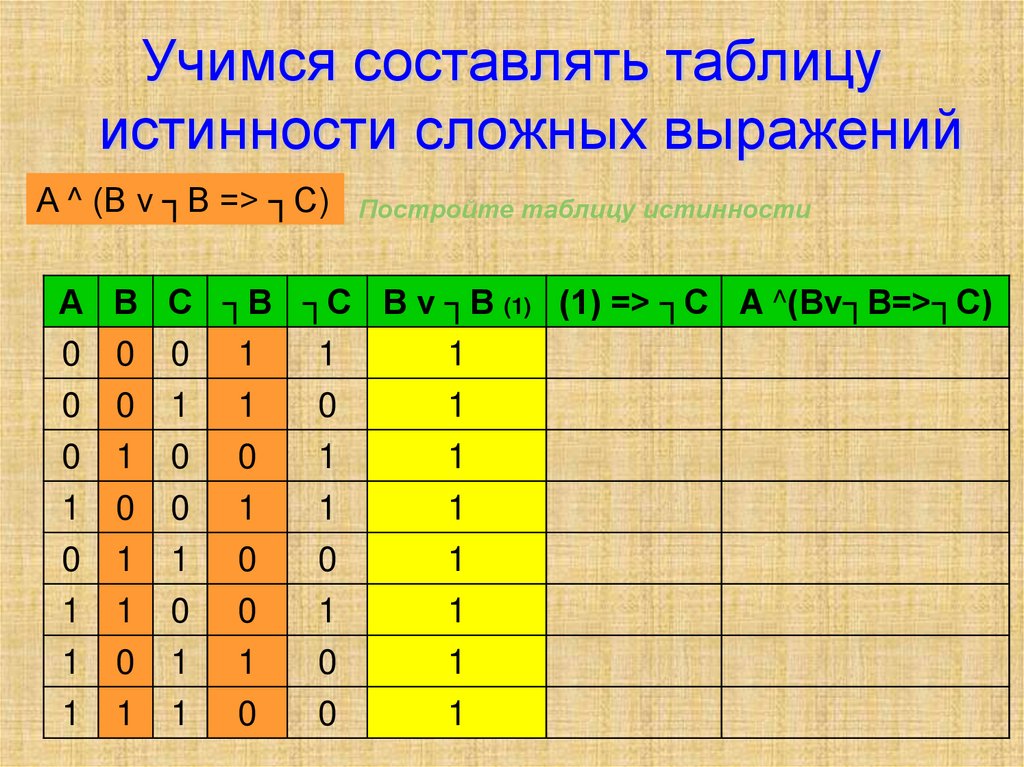

Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом. Эти строки реализуются микросхемой D2 на рисунке 8. Каждая строка реализуется своей схемой «И», затем выходы этих схем объединяются Для построения схемы, реализующей сигнал Out2, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3.

Рисунок 8. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 7.

[Содержание] [Вперёд]

таблиц истинности, тавтологии и логические эквивалентности

таблицы истинности, тавтологии и логические эквивалентности

Математики обычно используют двузначное число . логика : Каждое утверждение либо Истина , либо Ложь . Это называется Закон исключенного третьего .

Утверждение в сентенциальной логике строится из простых утверждений с использованием логические связки , , , и . Правда или ложь утверждения, построенного с помощью этих связок, зависит от истинности или ложность его составляющих.

Например, составной оператор строится с использованием логических связок , и . Правда или ложность зависит от истины или ложность P, Q и R.

Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.

Вот таблица отрицания:

Эту таблицу легко понять. Если P равно true , его отрицание ложь . Если P равно false , то true .

должно быть true , когда оба P и Q true и false иначе:

истинно , если либо P равно истинно , либо Q равно true (или оба — помните, что мы используем «или» во включающем смысле). всего ложь , если оба P и Q ложь .

Вот таблица логических следствий:

Чтобы понять, почему эта таблица именно такая, рассмотрим следующее. пример:

«Если ты получишь пятерку, я дам тебе доллар».

Утверждение будет верным , если я сдержу свое обещание и ложь если нет.

Предположим, что верно , что вы получаете пятерку, а это 9.0003 правда что я даю вам доллар. Поскольку я сдержал свое обещание, правда . Это соответствует первой строке таблицы.

Предположим, что верно , что вы получаете пятерку, но ложно что я даю вам доллар. Поскольку я не сдержал своего обещания, подразумевается false . Это соответствует второму строку в таблице.

Что, если это ложь, что вы получили пятерку? Независимо от того, дам ли я вам долларов, я не нарушил своего обещания. Таким образом, вывод не может быть ложно, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот объясняет последние две строки таблицы.

означает, что P и Q равны эквивалент . Таким образом, двойная импликация верна , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.

Вы должны помнить — или уметь составлять — таблицы истинности для логических связок. Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Легче продемонстрировать что делать, чем описать это словами, так вы увидите порядок выработано на примерах.

Примечание. (а) Когда вы строите правду таблице, вы должны рассмотреть все возможные назначения True (T) и False (F) для операторов компонентов. Например, предположим, составные операторы — это P, Q и R. Каждый из этих операторов может быть либо правда, либо ложь, так что есть возможности.

Когда вы перечисляете возможности, вы должны присвоить значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографический порядок . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого способ:

(б) Существуют различные способы составления таблиц истинности. Вы можете, для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно дорастающие до столбец для «основной» связки.

Я буду записывать вещи длинным путем, создавая столбцы для каждого «кусочек» составного высказывания и постепенно наращивая к составному утверждению. Любой стиль хорош, пока вы показываете достаточно работы, чтобы оправдать ваши результаты.

Пример. Построить таблицу истинности для формула .

Во-первых, я перечисляю все альтернативы для P и Q.

Затем в третьем столбце я перечисляю значения на основе значений P. Я использую таблицу истинности для отрицание: когда P истинно, ложно, а когда P ложно, правда.

В четвертом столбце я перечисляю значения для . Проверьте сами, что это только ложь («F»), если P истинно («T»), а Q ложно («Ф»).

В пятом столбце приведены значения моего составного выражения. Это «и» из (третий столбец) и (четвертый столбец). «И» верно только в том случае, если обе части «и» верны; в противном случае оно ложно. Поэтому я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятой колонке, иначе ставлю F.

Тавтология есть формула, которая «всегда истинно» — то есть истинно для всякого присвоения истины значения его простых компонентов. Вы можете рассматривать тавтологию как правило логики .

Противоположностью тавтологии является число . противоречие , формула, которая «всегда ложна». В Другими словами, противоречие ложно для любого присвоения истины значения его простых компонентов.

Пример. Покажите, что это тавтология.

Я строю таблицу истинности и показываю, что формула всегда верна.

Последний столбец содержит только Т. Следовательно, формула представляет собой тавтология.

Пример. Построить таблицу истинности для .

Вы можете видеть, что построение таблиц истинности для утверждений с большим количеством связок или большого количества простых утверждений довольно утомительно и подвержен ошибкам. Хотя могут быть некоторые приложения этого (например, для цифровые схемы), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это наверняка было сделано).

Суть здесь в том, чтобы понять, как значение истинности сложного утверждение зависит от истинностных значений его простых утверждений и его логические связи. В большинстве работ математики обычно не операторы использования, которые очень сложны с логической точки зрения. вид.

Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинной стоимость не может быть определена.

б) Предположим, что это неверно. Рассказывать является ли Q истинным, ложным или его истинностное значение не может быть определено.

а) Поскольку истинно, то либо Р истинно, либо истинно. Поскольку P ложно, оно должно быть истинным. Следовательно, Q должно быть ложным.

(b) Утверждение «если-то» ложно, когда часть «если» истина, а часть «тогда» ложна. Поскольку ложно, верно. Утверждение «и» истинно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.

Пример. Предположим

» » правда.

» » неверно.

«У Кельвина Баттербола фиолетовые носки» — это правда.

Определить истинность утверждения

Для простоты пусть

П = «».

Q = «».

R = «У Кэлвина Баттербола фиолетовые носки».

Я хочу определить истинное значение . Поскольку мне были даны конкретные значения истинности для P, Q, и R, я составил таблицу истинности с одной строкой, используя данные значения для P, Q и R:

Следовательно, утверждение верно .

Пример. Определить истинное значение заявление

Утверждение » » неверно. Вы не можете сказать действительно ли утверждение «Икабод Ксеркс ест шоколад кексы» истинны или ложны — но это не имеет значения. Если «если» часть утверждения «если-то» ложна, то утверждение «если-то» истинно. (Проверьте правду таблица для тех, кто не уверен в этом!) Так что данное утверждение должно быть истинным.

Два утверждения X и Y равны логически. эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простых операторы , составляющие X и Y, операторы X и Y имеют одинаковые значения истинности.

С практической точки зрения вы можете заменить оператор в доказательство любым логически эквивалентным утверждением.

Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтологией — что есть ли «все Т в столбце». Однако проще настроить таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и для Y.

Пример. Покажите, что и логически эквивалентны.

Поскольку столбцы для и идентичны, два оператора логически эквивалент. Эта тавтология называется Условное Разъединение . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.

Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.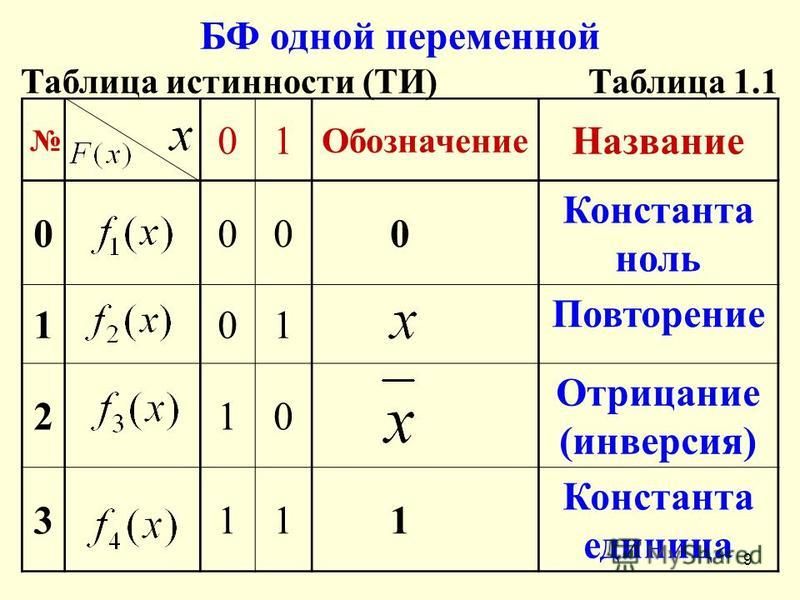

Когда тавтология имеет форму бикондиционала, два утверждения которые составляют бикондиционал, логически эквивалентны. Следовательно, вы можно заменить одну сторону другой без изменения логического значение.

Вам часто придется отрицать математическое утверждение. К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символические заявления.

Пример. Запишите отрицание следующие операторы, упрощая так, чтобы только простые операторы отрицается.

(а)

(б)

(a) Я отрицаю данное утверждение, затем упрощаю, используя логические эквивалентности. Я дал имена логических эквивалентностей на правильно, чтобы вы могли видеть, какие из них я использовал.

(б)

Я показал это и есть логически эквивалентны в предыдущем примере.

В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать в математике. идея состоит в том, чтобы преобразовать слово-выражение в символическое высказывание, затем используйте логические эквивалентности, как в предыдущем примере.

Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:

«Кэлвина нет дома или Бонзо в кино».

Пусть С будет утверждением «Кальвин дома», а В будет заявление «Бонзо в движении». Данное утверждение является . Я должен отрицать утверждение, затем упростите:

Результат: «Кальвин дома, а Бонзо нет на кино».

«Если Фиби покупает пиццу, то Кэлвин покупает попкорн».

Пусть P будет утверждением «Фиби покупает пиццу», а C будет заявление «Кэлвин покупает попкорн». Данное утверждение является . Чтобы упростить отрицание, я буду использовать тавтологию условной дизъюнкции , которая гласит:

То есть я могу заменить на (или наоборот).

Вот вам и отрицание и упрощение:

Результат: «Фиби покупает пиццу, а Кэлвин не покупает». попкорн».

Далее мы применим нашу работу с таблицами истинности и отрицающими утверждениями к задачи на построение обратной, обратной и противопоставляется утверждению «если-то».

Пример. Замените следующий оператор на его противоположность:

«Если x и y рациональны, то рационально».

По контрапозитивной эквивалентности это утверждение совпадает с «Если не рационально, то это не так что и х, и у рациональны».

Этот ответ правильный в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей позитивное утверждение легче понять, чем отрицательное утверждение.

По определению, действительное число равно 9.0003 иррациональный если это не рационально. Поэтому я мог бы заменить часть «если» противопоставляется слову «иррационально».

Часть противопоставления «тогда» есть отрицание утверждение «и». Вы могли бы переформулировать это так: «Это не случае, когда и x рационально, и y рационально». (Слово «оба» гарантируют, что отрицание применяется ко всему утверждение «и», а не только «х рационально».)

По закону Де Моргана это эквивалентно следующему: «x не является рациональным или y нерационально». В качестве альтернативы я мог бы сказать: «x есть иррационально или у иррационально».

Собрав все вместе, я мог бы выразить противоположное как: «Если иррационально, то либо х иррационально или у иррационально».

(Как обычно, я добавил слово «либо», чтобы было понятно, что часть «тогда» — это целое утверждение «или».)

Пример.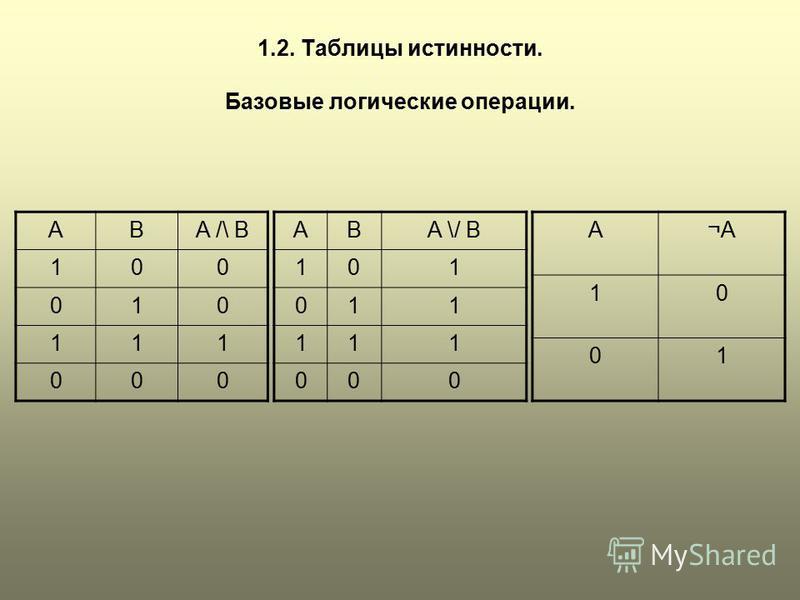 Покажите, что обратное и обратные условные логически эквивалентны.

Пусть условно. Обратное есть. Обратное.

Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для . Вместо этого я буду использовать некоторые известные тавтологии.

Начните с:

Помните, что я могу заменить утверждение логическим эквивалент. Например, на последнем шаге я заменил на Q, потому что два утверждения эквивалентны Двойное отрицание.

Пример. Предположим, что x — действительное число. Учитывать заявление

«Если , то ».

Постройте обратное, обратное и контрапозитивное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и контрапозитивное — используя свои знания по алгебре.

Обратное: «Если , то».

Противоположное: «Если , то».

Исходное утверждение неверно: , но . Поскольку исходное утверждение эквивалентно контрапозитив, то контрапозитив также должен быть ложным.

Обратное верно. Обратное логически эквивалентно обратное, значит верно и обратное.

\новая страница

\centerline{\bigssbold Список тавтологий}

Контактная информация

Домашняя страница Брюса Икенаги

Таблицы истинности – отрицание, союз, дизъюнкция («не», «и», «или»)

Таблицы истинности – это способ анализа того, как правильность утверждений (называемых высказываниями) ведет себя при использовании логического «или», или логическое «и», чтобы объединить их. Предложения либо полностью истинны, либо полностью ложны, поэтому любая таблица истинности захочет показать обе эти возможности для всех сделанных утверждений.

Во всех этих примерах мы будем считать p и q предложениями. Это могут быть такие утверждения, как «мне 25 лет» или «сейчас теплее 70°».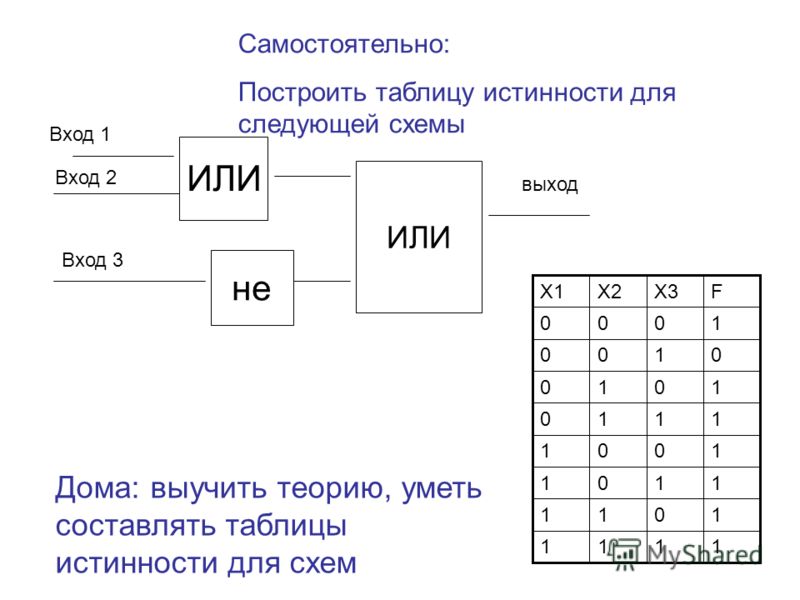 Любые утверждения, которые являются либо истинными, либо ложными.

[adsenseWide]

Отрицание — «not p»

Отрицание — это утверждение «not p», обозначаемое \(\neg p\), и поэтому оно будет иметь истинностное значение, противоположное p. Если p истинно, то \(\neg p\), если ложно. Если p ложно, то \(\neg p\) истинно. Обратите внимание, что таблица истинности показывает все эти возможности.

Союз – «и»

Рассмотрим высказывание «p и q», обозначаемое \(p \клин q\). Чтобы проанализировать это, мы сначала должны подумать обо всех комбинациях значений истинности для обоих утверждений, а затем решить, как эти комбинации влияют на утверждение «и». Прописью:

Строка 1 : оба утверждения могут быть истинными.
В этом случае имело бы смысл, что «p и q» также являются истинным утверждением.
Строка 2 : p может быть ложным, в то время как q истинно.
Чтобы «p и q» были истинными, нам нужно, чтобы ОБА утверждения были истинными. Поскольку одно ложно, «p и q» ложны.
Строка 3 : p может быть истинным, а q ложным.
Если это так, то по тому же аргументу в строке 2 «p и q» ложно.
Строка 4 : оба утверждения могут быть ложными.
Если оба утверждения ложны, то «p и q» ложны.

Порядок строк не имеет значения — если мы будем систематизированы таким образом, чтобы не пропустить ни одной возможной комбинации значений истинности для двух исходных утверждений p, q.

Дизъюнкция – «или»

Вы можете этого не осознавать, но есть два типа «или». Есть включительно или , где мы допускаем тот факт, что оба утверждения могут быть истинными, и есть исключающее или , где мы строго придерживаемся того, что только одно утверждение или другое является истинным. В математике «или», с которым мы работаем, — это включающее или, обозначаемое \(p \vee q\). Когда мы хотим работать с исключающим ИЛИ, мы конкретны и используем разные обозначения (вы можете прочитать об этом здесь: исключающее ИЛИ).