Чем отличается непрерывный аналоговый сигнал от дискретного. Как происходит преобразование аналогового сигнала в дискретный. Какие основные характеристики имеют непрерывные и дискретные сигналы. Где применяются аналоговые и дискретные сигналы в технике и быту.
Основные отличия непрерывного и дискретного сигнала
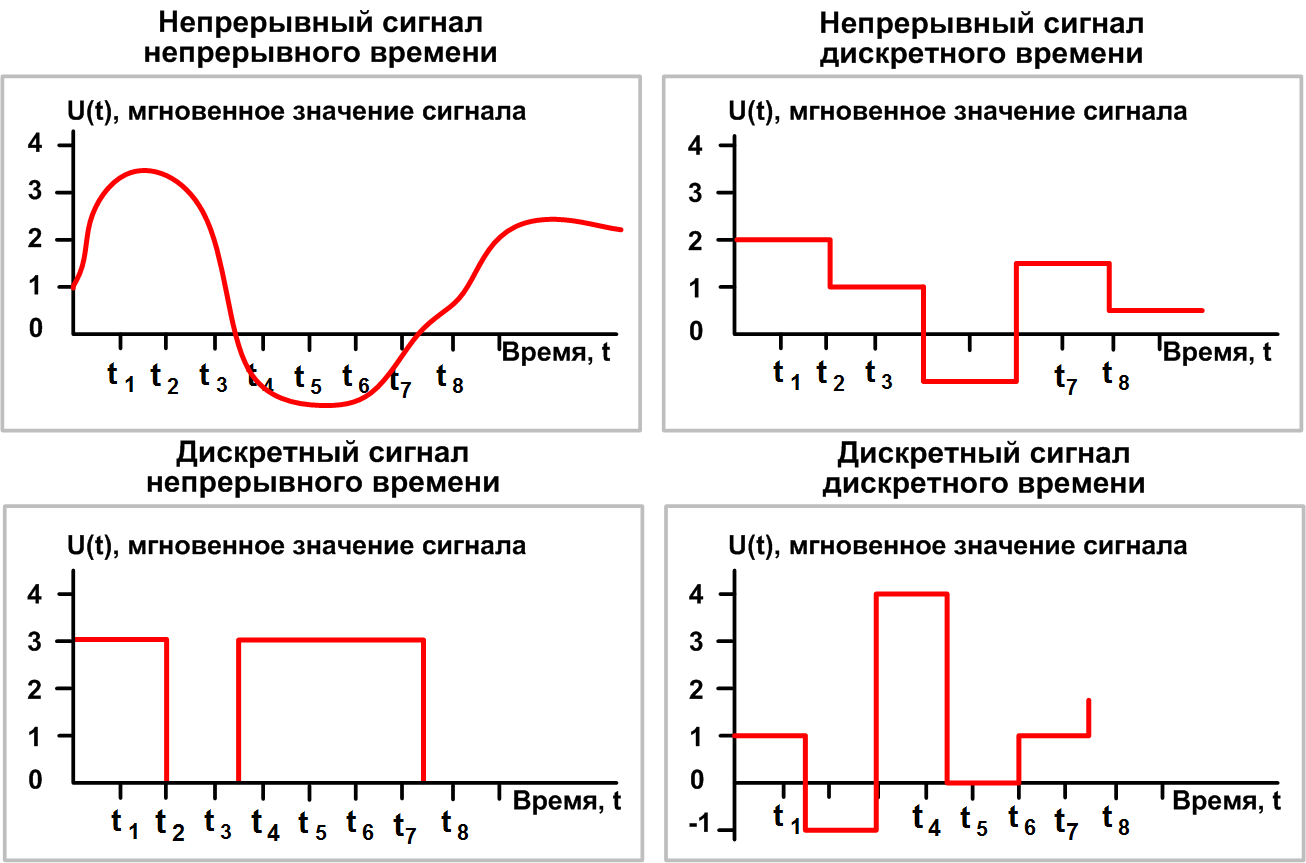
Непрерывный (аналоговый) и дискретный сигналы имеют ряд принципиальных отличий:
- Непрерывный сигнал описывается непрерывной функцией времени, а дискретный — последовательностью отсчетов в определенные моменты времени.
- Аналоговый сигнал может принимать любые значения в заданном диапазоне, а дискретный — только фиксированные уровни.
- Аналоговый сигнал содержит информацию в любой момент времени, дискретный — только в моменты отсчетов.
- Непрерывный сигнал бесконечномерный, а дискретный имеет конечное число значений.
- Аналоговый сигнал более подвержен влиянию помех и искажений при передаче.
Характеристики непрерывных сигналов
Основными характеристиками непрерывных сигналов являются:
- Амплитуда — максимальное отклонение сигнала
- Частота — число колебаний в единицу времени
- Фаза — смещение сигнала относительно начала отсчета
- Спектр — совокупность гармонических составляющих сигнала
- Длительность — время существования сигнала
Характеристики дискретных сигналов
Ключевые характеристики дискретных сигналов:
- Частота дискретизации — число отсчетов в единицу времени
- Разрядность — количество уровней квантования
- Период дискретизации — интервал между отсчетами
- Динамический диапазон — отношение максимального и минимального уровня
- Шаг квантования — расстояние между соседними уровнями
Преобразование аналогового сигнала в дискретный
Для преобразования непрерывного сигнала в дискретный выполняются следующие операции:
- Дискретизация — взятие отсчетов сигнала через равные промежутки времени
- Квантование — округление значений отсчетов до ближайших уровней
- Кодирование — представление уровней двоичным кодом
При этом важно выбрать достаточную частоту дискретизации и число уровней квантования, чтобы минимизировать потери информации.
Примеры непрерывных и дискретных сигналов
Примеры непрерывных сигналов:
- Звуковые колебания в воздухе
- Электрическое напряжение в сети
- Температура окружающей среды
- Яркость света
Примеры дискретных сигналов:
- Цифровой аудио- или видеосигнал
- Импульсы тактовой частоты в микропроцессорах
- Последовательность битов в компьютерных сетях
- Показания цифровых измерительных приборов
Применение аналоговых и дискретных сигналов
Аналоговые сигналы применяются в следующих областях:
- Аналоговое телевидение и радиовещание
- Аналоговые измерительные приборы
- Аналоговые системы управления
Дискретные сигналы используются в:
- Цифровых системах связи
- Компьютерной технике
- Цифровой обработке сигналов
- Цифровых системах записи и воспроизведения
Преимущества и недостатки непрерывных и дискретных сигналов
Преимущества непрерывных сигналов:
- Высокая точность представления информации
- Простота генерации и обработки
- Низкие требования к полосе пропускания
Недостатки непрерывных сигналов:
- Подверженность шумам и помехам
- Сложность хранения и передачи на большие расстояния
- Невозможность идеального восстановления после искажений
Преимущества дискретных сигналов:
- Высокая помехозащищенность
- Возможность идеального восстановления сигнала
- Простота хранения, передачи и обработки
Недостатки дискретных сигналов:
- Необходимость высокой частоты дискретизации
- Ограниченная точность квантования
- Высокие требования к полосе пропускания
Выбор между аналоговыми и дискретными сигналами
При выборе между аналоговыми и дискретными сигналами следует учитывать следующие факторы:
- Требуемая точность представления информации
- Допустимый уровень искажений и помех
- Необходимость дальнейшей обработки сигнала
- Ограничения по полосе пропускания канала
- Стоимость и сложность реализации системы
В современных системах чаще используются дискретные сигналы из-за их преимуществ в обработке и передаче информации. Однако в некоторых приложениях аналоговые сигналы по-прежнему остаются оптимальным выбором.

Методы анализа непрерывных и дискретных сигналов
Для анализа непрерывных сигналов применяются следующие методы:
- Преобразование Фурье
- Интегральные преобразования (Лапласа, Меллина и др.)
- Корреляционный анализ
- Спектральный анализ
Методы анализа дискретных сигналов включают:
- Дискретное преобразование Фурье (ДПФ)
- Z-преобразование
- Дискретную корреляцию
- Цифровую фильтрацию
Заключение
Непрерывные и дискретные сигналы имеют свои особенности и области применения. Понимание их различий и характеристик позволяет эффективно проектировать и использовать системы обработки информации. С развитием цифровых технологий все большее распространение получают дискретные сигналы, однако знание основ аналоговой обработки сигналов остается важным для инженеров и разработчиков.
Теорема Котельникова, АЦП и ЦАП, Шум как случайный процесс
Рассмотрены 3 темы по основам цифровой обработки сигналов: Теорема Котельникова, АЦП и ЦАП, Шум как случайный процесс.
В данном посте освещены 3 темы по основам цифровой обработки сигналов:
- Теорема Котельникова,
- АЦП и ЦАП,
- Шум как случайный процесс.
Теорема Котельникова
В этой публикации мы поговорим об основном ограничении при дискретизации аналогового сигнала, описываемого теоремой Котельникова. Это ограничение тесно связано с понятием частоты периодического дискретного сигнала. Мы помним то, что чистота – это величина обратная периоду, и она может измеряться либо в секундах либо в отсчётах в зависимости от того, говорим о непрерывном сигнале или о дискретном сигнале. Частота может измеряться в радианах в единицу времени или циклах в единицу времени.
Важно отметить то, что цикл для непрерывного сигнала может быть равен 2・π радиан, а цикл для дискретного сигнала может быть равен 2・π・m радиан, где m – это целое число. Это приводит нас к понятию неоднозначности определения частоты дискретного сигнала. Не будем углубляться в формулы, давайте посмотрим на конкретном примере.
Это приводит нас к понятию неоднозначности определения частоты дискретного сигнала. Не будем углубляться в формулы, давайте посмотрим на конкретном примере.
Мы говорим о том, что для непрерывных сигналов 2 синусоиды с разными частотами не равны друг другу, но случай двух дискретных синусоид, если частота одной отличается от другой на m・2・π мы не сможем их различить. Я поясню это на простом примере. Представьте себе обыкновенные часы. Мы явно видим минутную стрелку и часовую стрелку, потому что это непрерывно изменяющиеся величины. Но, если мы будем фотографировать эти часы в моменты времени, когда минутная стрелка накладывается на часовую стрелку, мы не увидим часовой стрелки. Фактически происходит наложение одного дискретного сигнала на другой дискретный сигнал. Тоже самое происходит при дискретизации 2 аналоговых сигналов.
Рассмотрим пример 2 синусоид. Одна синусоид изменяется медленно, другая синусоида изменяется быстро. Мы берём дискретные отсчеты этих синусоид в моменты времени 1, 2, 3, 4 и так далее, и мы можем наблюдать то, что форма 2 дискретных сигналов абсолютно одинакова.
Произошел эффект алиасинга или наложение двух сигналов при дискретизации. Слово “алиасинг” происходит от английского слова alias или псевдоним. В данном случае фактически один сигнал маскируется другим сигналом. Запомним то, что алиасинг – это эффект неразличимости сигналов при их дискретизации, и, конечно же, нам его надо избегать.
Как вы уже поняли из представленных графиков, выбранной частоты дискретизации хватает для того, чтобы описать в дискретном виде медленно изменяющуюся синусоиду, но явно не хватает, чтобы описать быстро изменяющуюся. Мы приходим к определению основного ограничения при дискретизации сигналов.
Теорема Котельникова гласит о том, что непрерывный сигнал с ограниченным спектром можно точно восстановить по его дискретным отсчётам, если они были взяты с частотой дискретизации, превышающего максимальную частоту сигнала минимум в два раза. В виде формулы это можно описать так:
В том случае, если это условие не выполняется, мы берём дискретные отсчеты слишком редко, мы не знаем, как меняется сигнал в промежутках между дискретами и конечно же теряем информацию. В том случае, если условие выполняется, между отдельными дискретными отсчётами сигнал меняется относительно медленно, и поэтому восстановление исходной формы аналогового сигнала возможно.
В том случае, если условие выполняется, между отдельными дискретными отсчётами сигнал меняется относительно медленно, и поэтому восстановление исходной формы аналогового сигнала возможно.
Давайте посмотрим на эффект алиасинга или наложения при невыполнении условий теоремы Котельникова в MATLAB. Создадим три синусоиды с частотами 250, 500 и 750 Гц. Частота дискретизации 2000 Гц.
В данном случае условия теоремы Котельникова выполняется для всех трёх синусоид. Давайте попробуем послушать, как они звучат. Мы услышали три нарастающих тона, и на графике также наблюдаем тремя цветами три различных сигнала.
Ну что будет, если мы поменяем частоту дискретизации на значение 1000 Гц. Для первого сигнала 250 Гц оно выполняется, для второго сигнала оно выполняется вплотную, и для третьего сигнала оно не выполняется. Давайте теперь послушаем и посмотрим на эти сигналы.
Мы услышали третий сигнал как будто его частота также 250 Гц, и на графике мы наблюдаем только два сигнала. В данном случае наш третий сигнал 750 Гц из-за несоблюдения условий теоремы Котельникова наложился на первый сигнал.
В данном случае наш третий сигнал 750 Гц из-за несоблюдения условий теоремы Котельникова наложился на первый сигнал.
Для того, чтобы теорема Котельникова соблюдалась всегда, достаточно постоянно брать очень большое значение частоты дискретизации. Насколько это удачное решение? На самом деле не очень, потому что мы работаем с системами передачи данных, системами хранения данных, и, если мы медленно изменяющийся сигнал будем оцифровывать с огромной частотой дискретизации, то объемы данных, которые мы должны пропускать, обрабатывать и хранить будут сильно превышать требуемые, что конечно же будет требовать больших вычислительных ресурсов и памяти для хранения. Впрочем, принцип работы некоторых устройств как раз основан на выборе завышенных значений частоты дискретизации. Одно из них это сигма-дельта АЦП, аналого-цифровой преобразователь. О аналого-цифровых, цифро-аналоговых преобразователях наша следующая публикация.
Наверх
АЦП (аналого-цифровые преобразователи) и ЦАП (цифро-аналоговые преобразователи)
В этой публикации мы кратко поговорим об аналого-цифровых и цифро-аналоговых преобразователях.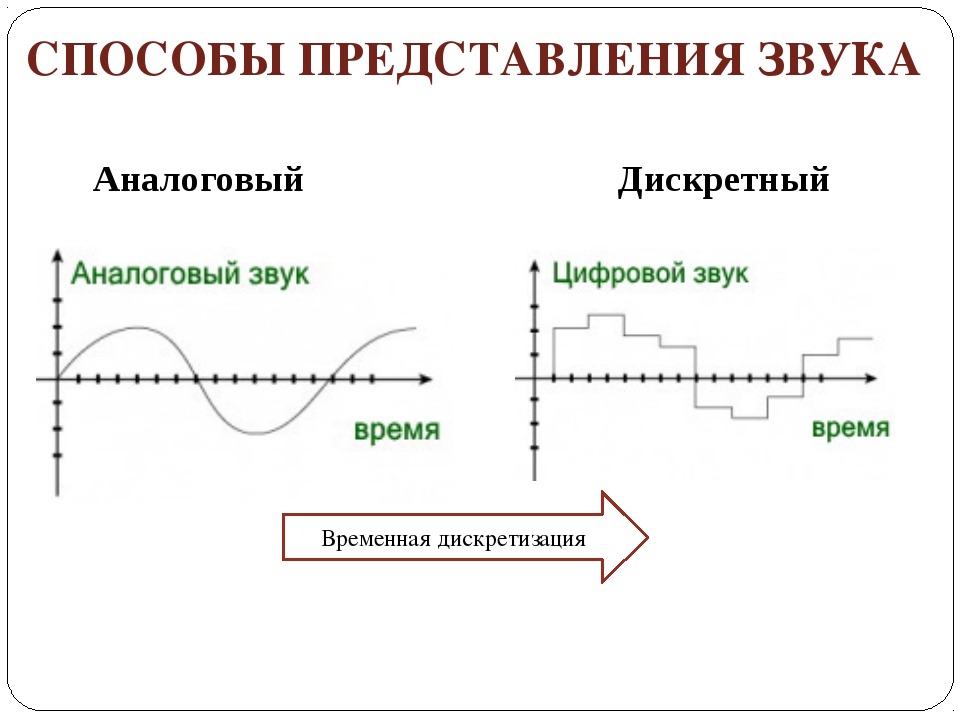
Аналого-цифровой преобразователь или АЦП – это устройство, преобразующее входной аналоговый сигнал в дискретный цифровой код. Как вы уже поняли, АЦП осуществляет операции дискретизации и квантования. Напомним, при дискретизации отсчёты непрерывного сигнала берутся только в определённые моменты или дискреты времени, а при квантовании – значение сигнала в эти моменты времени округляется до одного из фиксированных уровней.
Квантованные уровни затем представляются в двоичном виде. Таким образом мы получаем цифровой сигнал из аналогового.
Но как же устроен АЦП. Боюсь, что у нас не хватит времени подробно говорить об устройстве аналого-цифровых преобразователей с точки зрения схемотехники, но ключевые узлы и базовые принципы постараемся очертить. В большинстве АЦП есть устройство выборки и хранения, которые фиксируют и сохраняют значение напряжения на своём ходе в моменты замыкания ключа. Моменты замыкания ключа определяется задающим генератором.
Как же АЦП понимает с каким уровнем квантования проассоциировать значение сигнала. Рассмотрим простейший одноразрядный АЦП компаратор. Он принимает на свой ход два значения напряжения. В том случае, если напряжение на первом входе больше, чем на втором, он выдаёт логическую единицу, в противном случае – ноль. Допустим, мы зафиксировали значение на втором входе, это наш пороговый уровень, и, когда изменяющийся во времени сигнал на вервом входе больше этого уровня, устройство показывает единицу, когда меньше – ноль. Теперь представим, что компараторов несколько. Когда входной сигнал превышает определенный уровень, срабатывает соответствующий компарато. Выходы всех компараторов затем преобразуются схемой приоритетного кодера в двоичное представление, АЦП в которых в каждом из уровней квантования соответствует компаратор, называется АЦП прямого преобразования или флеш АЦП.
Давайте лучше поговорим об основных характеристиках АЦП.
- АЦП отличается по частоте дискретизации. Она, как я уже упоминал, определяется задающим генератором. В зависимости от назначения частота дискретизации может измеряться в кГц, МГц и даже ГГц.
- Далее идет разрядность, те количество бит в коде, который мы представляем отсчеты сигнала. От количества бит зависит количество уровней квантования, оно определяется как 2 в степени кол-во бит. Если у нас 3 бита, то это 8 возможных уровней квантования, если у нас 8 бит – это 256 уровней.
- Диапазон входного сигнала – это минимальное и максимальное значение напряжения на входе АЦП, при которых устройство работает корректно. Слишком маленькие сигналы АЦП может не различить и принять за нулевой уровень, слишком большие могут вызвать искажения, которые приведут к потере информации.
 Обычно АЦП оперируют единицами Вольт.
Обычно АЦП оперируют единицами Вольт. - Отношение сигнал/шум SNR (об этом параметре мы подробнее поговорим в дальнейших публикациях).
- Передаточная характеристика – это по определению зависимость числового эквивалента выходного кода от величины входного аналогового сигнала. Она имеет вид ступенчатой функции. Посмотрим на рисунок.
Окрестность значения входного напряжения 0,5 Вольт будет приравнена к четвертому уровню квантования. То есть значение к примеру 0,52 или 0,47 также будут представлены кодом 100.
Если мы рассматриваем АЦП с равномерным квантованием, то длина всех ступеней будет одинаковой, в некоторых АЦП специально используется неравномерное квантование, но их мы пока не рассматриваем.
Неравномерность ступенек в АЦП с равномерным квантованием – это одна из характеристик неидеальности. Мы называем её нелинейностью. Нелинейность АЦП – это отличие реальной передаточной характеристике от линейной.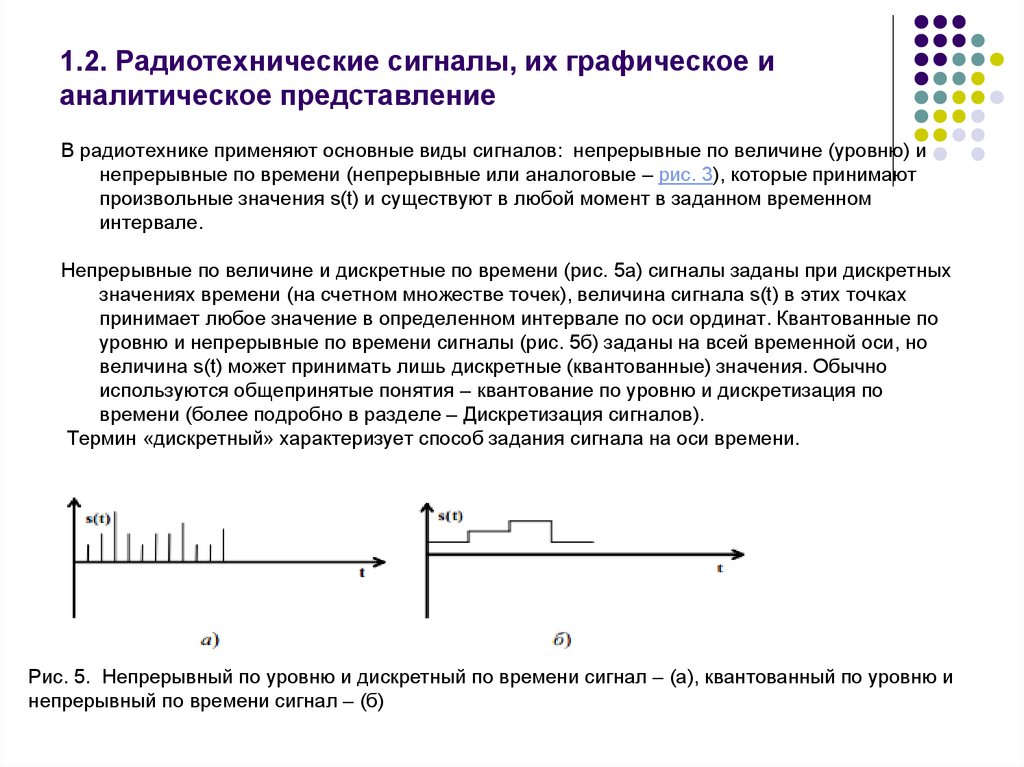
Давайте вспомним, чем линейные системы отличаются от нелинейных. Линейная система передаёт входной сигнал на выход без изменения его формы, возможно усиление или аттенюация. Нелинейная система искажает формы выходного сигнала. В том случае, когда характеристика отличается от прямой линии, формы пиков сигнала изменяется, это называется нелинейным искажением, крайне нежелательные явления. Я говорил в предыдущих публикациях, что при искажениях мы безвозвратно теряем информацию.
Для АЦП желательно, чтобы в рабочем диапазоне входных сигналов, формы передаточной характеристики аппроксимировалась прямой, но на практике небольшие отклонения всё же присутствуют. Поэтому для всех АЦП производители указывают параметры интегральной и дифференциальной нелинейности.
Шум квантования. В АЦП происходит округление реального значения аналогового сигнала. Точность представления, то, насколько близко уровень квантования к реальным значениям зависит от разрядности АЦП (количество бит). Сигнал ошибки или разницы мы называем шумом кантования. Хотя шумом его можно считать только в рамках математической модели, так как он зависит от сигнала.
Сигнал ошибки или разницы мы называем шумом кантования. Хотя шумом его можно считать только в рамках математической модели, так как он зависит от сигнала.
О математической модели шума мы поговорим подробнее в следующей публикации. Если мы квантуем непрерывный сигнал, то и шум квантования будет непрерывным. Если мы говорим о квантовании дискретного сигнала, то и сигнал ошибки также будет дискретным. Понятно, что для того, чтобы уменьшить шум квантования, надо повышать разрядность АЦП, но из-за этого увеличивается стоимость, энергопотребление, могут снизиться другие характеристики. Существует техника уменьшения влияния шума квантования без увеличения разрядности и с ними вы можете ознакомиться самостоятельно при желании.
Джиттер – это фазовый шум, вызванный нестабильностью задающего генератора. Когда мы рассматриваем идеальный процесс дискретизации непрерывного сигнала, шаг временной сетки или период дискретизации неизменен, но в реальности импульс задающего генератора могут идти не через равные промежутки времени.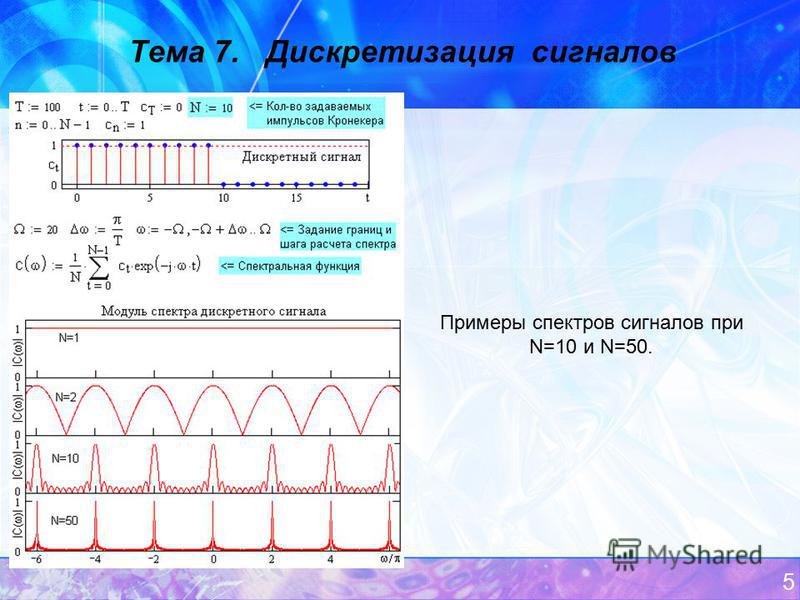 Это приводит к тому, что мы передаём устройство выборки и хранения не совсем то значение, которое должны были передать в случае идеально ровной временной сетки. Эти отклонения от так называемых реальных значений также можно представить в виде дискретного шума.
Это приводит к тому, что мы передаём устройство выборки и хранения не совсем то значение, которое должны были передать в случае идеально ровной временной сетки. Эти отклонения от так называемых реальных значений также можно представить в виде дискретного шума.
Нестабильность генераторов обычно измеряется в пико- и фемто-секундах, поэтому на медленный АЦП она особо не влияет. Шум квантования вносит гораздо больший вклад. Но если сам сигнал изменяется очень быстро, если мы говорим о частотах дискретизации 100 МГц и 1 ГГц, то в этом случае уже джиттер может стать главной проблемой.
В завершении давайте кратко поговорим о цифро-аналоговых преобразователях. Цифро-аналоговые преобразователи, как вы догадались, – это устройство преобразующее входной цифровой сигнал в аналоговый. Подробно устройства ЦАП мы не будем рассматривать, но основной принцип очертим.
На вход устройства поступает дискретные отсчеты в виде цифрового кода, который затем преобразуется в напряжение.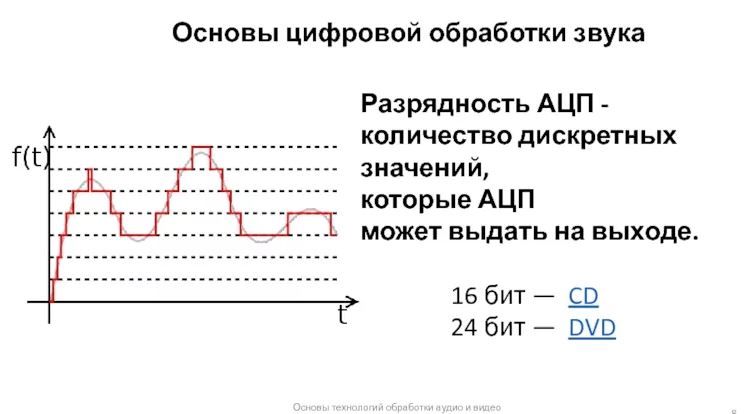 Напряжение это соответствует набору уровней, как и случае с АЦП, многие ЦАП используют равномерные уровни при преобразовании. Уровень напряжение остается неизменным до момента прихода следующего отсчёта на вход. Таким образом формируется ступенчатый непрерывный сигнал, который в дальнейшем может быть сглажен фильтром нижних частот. Один из простейших видов ФАП – широтно-импульсный модулятор. Он часто используется для управления скоростью электромоторов. С особенностями широтно-импульсной модуляции также рекомендуется самостоятельно ознакомиться. На этом с темой ЦАП и ЦАП мы заканчиваем. Следующая публикация у нас будет посвящена случайным процессам.
Напряжение это соответствует набору уровней, как и случае с АЦП, многие ЦАП используют равномерные уровни при преобразовании. Уровень напряжение остается неизменным до момента прихода следующего отсчёта на вход. Таким образом формируется ступенчатый непрерывный сигнал, который в дальнейшем может быть сглажен фильтром нижних частот. Один из простейших видов ФАП – широтно-импульсный модулятор. Он часто используется для управления скоростью электромоторов. С особенностями широтно-импульсной модуляции также рекомендуется самостоятельно ознакомиться. На этом с темой ЦАП и ЦАП мы заканчиваем. Следующая публикация у нас будет посвящена случайным процессам.
Наверх
Шум как случайный процесс
В этой публикации мы поговорим о шуме и его описании в виде случайного процесса. Для начала давайте напомним себе, что же такое шум.
Шумом мы зачастую называем нежелательные явления, мешающие нам получать информацию из полезного сигнала. Шум присутствует повсюду, он случаен по своей природе, источником его может быть как физика самого процесса, который мы пытаемся зафиксировать, так и неидеальности приёмной аппаратуры или оцифровщиков. Мы различаем понятия шума и полезного сигнала в том числе и с точки зрения их математического описания. Давайте для начала посмотрим, как мы можем описать полезный сигнал.
Мы различаем понятия шума и полезного сигнала в том числе и с точки зрения их математического описания. Давайте для начала посмотрим, как мы можем описать полезный сигнал.
Здесь в качестве математической модели мы используем детерминированный сигнал, заданный аналитической функцией. Значения сигнала можно определить в любой момент, подставив все необходимые аргументы в описывающую его аналитическую функцию. На примере представленной синусоиды: если мы зафиксируем параметры амплитуды, частоты и фазы, и будем передавать в формулу меняющееся значение времени – мы будем получать точное значение сигнала в эти моменты времени.
Детерминированный сигнал, описываемый аналитической функцией, как модель, очень удобен. Но сигналы реального мира подвержены воздействию множества физических факторов, их значения могут колебаться от наблюдения к наблюдению. Да и сами средства наблюдения также могут вносить погрешность измерений. Проще говоря, реальный сигнал будет отличаться от его аналитического описания на случайную величину ошибки.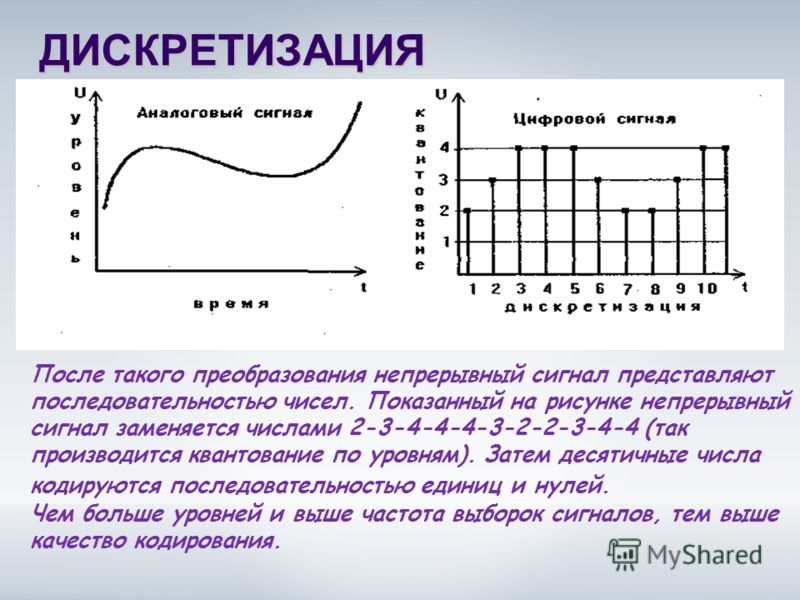
Рассмотрим очередной бытовой пример: нагрев воды в чайнике на газовой горелке. Температура воды с течением времени монотонно нарастает, но мы наблюдаем некоторые флуктуации или отклонения. Это может быть обусловлено неравномерной подачей газа в горелке, ветром, термодинамикой, неидеальностью средства измерения, наконец.
Так или иначе, полученные отсчёты мы можем приблизить прямой линией. Прямая линия – это детерминированный сигнал, описываемый функцией. Мы можем узнать его значения между соседними отсчётами, то есть интерполировать данные эксперимента, или даже подсчитать величину сигнала за пределами периода наблюдения, то есть использовать его для прогнозирования значений температуры. Но реальные значения немного отличаются от линейной зависимости в большую или меньшую сторону. Записанный сигнал мы можем рассматривать как математическую модель типа «дет сигнал + случ. Процесс»!
Если с детерминированным описанием сигнала всё более-менее понятно, то с моделью случайного процесса нам только предстоит познакомиться.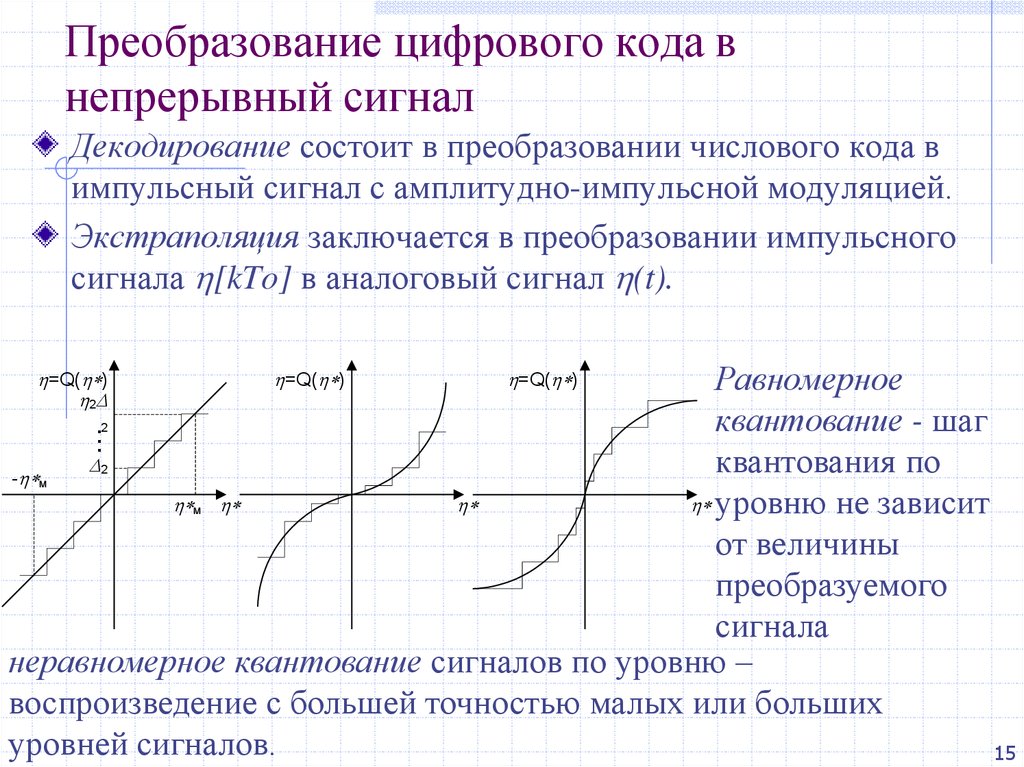
Понятие случайного процесса связано с определением случайной функции.
Случайная функция – это функция, вид которой в результате проведения эксперимента мы не можем предугадать.
Случайный процесс – есть случайная функция времени.
Конкретный вид, результат протекания случайного процесса, называется реализацией.
Справа показан ансамбль реализаций одного случайного процесса. В отличие от сигналов, описываемых аналитической функцией, реализации случайного процесса практически всегда отличаются друг от друга. Но общие характеристики у них есть. Как же нам описать случайный процесс без необходимости хранения бесконечного числа его реализаций? Для описания мы используем теорию вероятностей и математическую статистику.
Поговорим о распределении случайной величины.
Простой пример дискретной случайной величины – число, выпадающее при броске игральных костей. Может выпасть значение от 1 до 6. Величина может принимать одно из шести дискретных значений, но совершенно случайно. Нетрудно подсчитать вероятность выпадения какого-либо числа – она равна одной шестой, или 16.67% для каждого из дискретных значений.
Нетрудно подсчитать вероятность выпадения какого-либо числа – она равна одной шестой, или 16.67% для каждого из дискретных значений.
Теперь давайте рассмотрим пример непрерывной случайной величины. Рост человека. Он не изменяется дискретно, а может принимать любое значение в разумных пределах. Представим себе, что мы измеряем рост каждого посетителя, кто заходит в магазин. Измерив достаточное кол-во людей, мы можем построить вот такой график: по оси икс отложен рост в сантиметрах, по оси игрик – количество людей с таким ростом. На графике мы видим дискретные полоски, но эти полоски обозначают кол-во людей, чей рост попадает в определённые пределы, например, в пределы от 182 до 183 см. Взглянув на этот график, мы понимаем, что чаще всего в магазин заходили люди среднего роста, а посетителей ростом выше двух метров видели редко.
То, что было представлено на графике очень близко к понятию плотности распределения слуйчайной величины. Значение плотности распределения показывает вероятность того, что случайная величина примет определённое значение, а частичная площадь под графиком – вероятность того, что значение попадёт в выбранный предел. Как вы понимаете, площадь под графиком на всем диапазоне значений равна единице, или ста процентам.
Как вы понимаете, площадь под графиком на всем диапазоне значений равна единице, или ста процентам.
В случае с игральными костями мы рассматривали равномерное распределение, то есть одинаковую вероятность того, что слуйчайная величина примет то или иное значение.
В случае с ростом человека мы наблюдали нормальное распределение, так же именуемое распределением Гаусса. Нормальное распределение широко распространено в природе и используется как удобная модель случайного процесса. Популярность эта вытекает из центральной предельной теоремы. Она гласит, что сумма большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному.
На отклонение величины от среднего влияет множество факторов, подобно тому, как множество факторов влияет на рост человека, поэтому сумму их влияния можно описать СП с Гауссовским или нормальным распределением. Убедимся в этом в MATLAB.
Создадим пять векторов со случайными значениями. Функция rand позволяет нам генерировать вектора и матрицы со случайными значениями отсчётов, лежащих в пределах от нуля до единицы с равномерным распределением.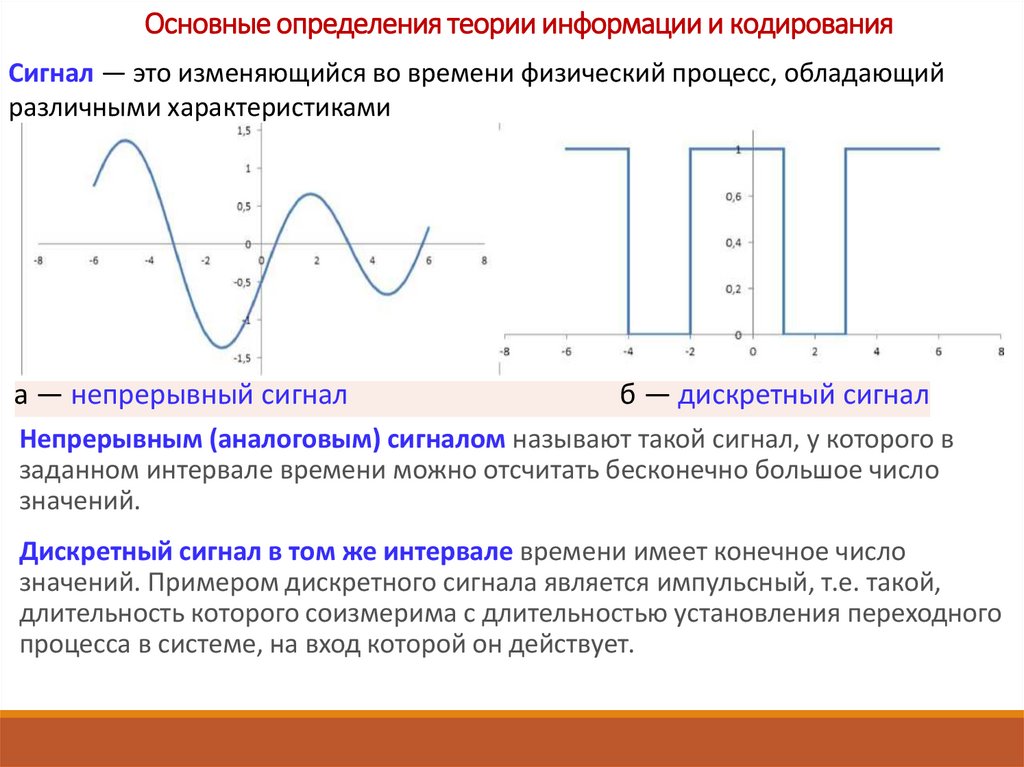 В нашем случае мы создаём пять векторов по 10 тысяч точек. Построим их на графиках и убедимся, что во временной области они выглядят как реализации случайного процесса.
В нашем случае мы создаём пять векторов по 10 тысяч точек. Построим их на графиках и убедимся, что во временной области они выглядят как реализации случайного процесса.
Далее построим гистрограммы всех векторов. Гистрограммы – это по сути графики распределения.
И мы наблюдаем, что у всех векторов распределение близко к равномерному. Мы этого и ожидали при использовании функции ранд.
А затем мы начинаем последовательно складывать вектора между собой и находить среднее арифметическое командой миан. Отразим на гистограмме распределение одного вектора, суммы двух, трёх, четырёх и пяти слагаемых.
Мы наблюдаем, что чем больше случайных величин мы берём в расчёт, тем ближе распределение суммы к нормальному, что подтверждает центральную предельную теорему.
Плотность распределения – это лишь одна из характеристик, которыми мы описываем случайные процессы. О других хар-ках, а также о видах шумов, и соотношении сигнал/шум мы расскажем в следующей публикации.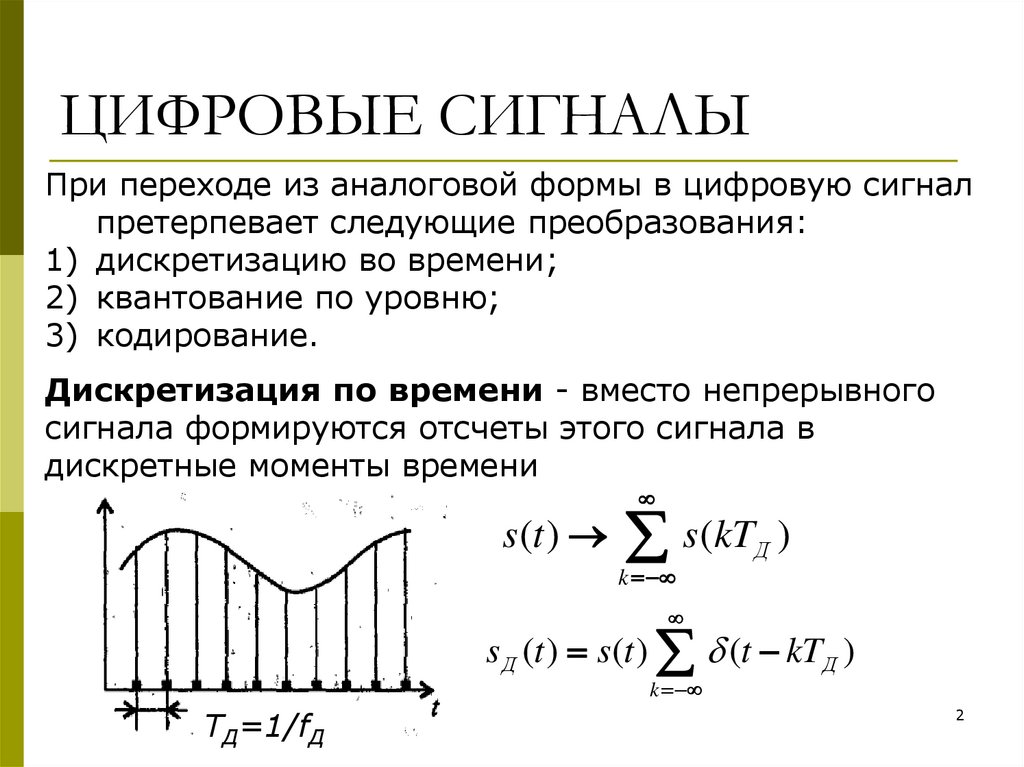
Что такое аналоговый сигнал и дискретный
При некоторых условиях, пространство L однозначно отображается в пространство l например, первые две теоремы дискретизации Котельникова. Аналоговые сигналы описываются непрерывными функциями времени , поэтому аналоговый сигнал иногда называют континуальным сигналом. Аналоговым сигналам противопоставляются дискретные квантованные , цифровые. Примеры непрерывных пространств и соответствующих физических величин:.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- 1.5.8 Восстановление сигнала по дискретным отсчетам: пример
- Чем отличается дискретный сигнал от непрерывного
- ПЛК: дискретные входы/ выходы
- Дискретный сигнал
- Входные/выходные дискретные сигналы в электроэнергетике: принципы, модули и микросхемы
- Аналоговые, дискретные и цифровые сигналы
- Дискретный выход, формирователи сигналов для соленоидов клапанов, светодиодов, клаксонов
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Программирование ПЛК.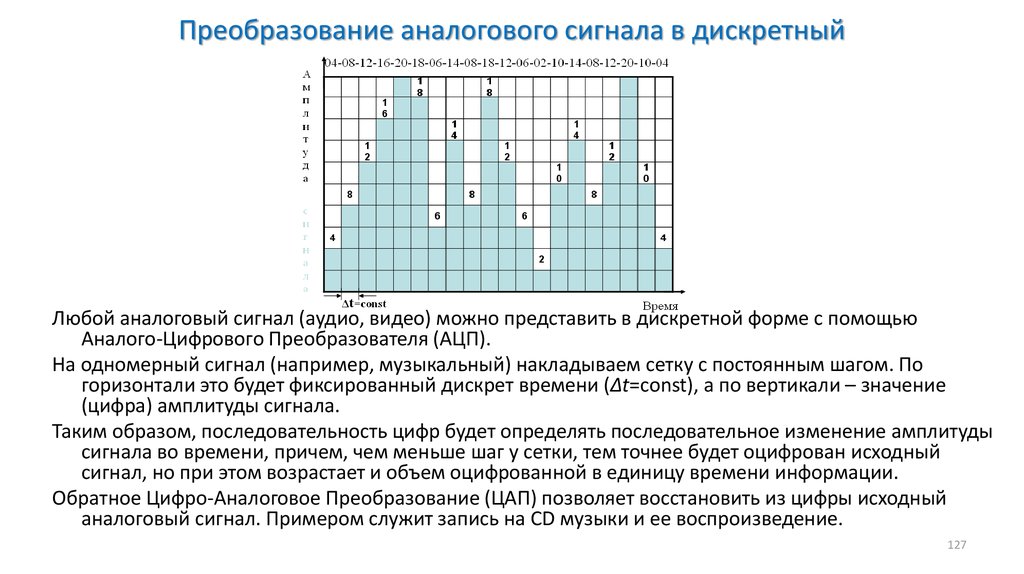 all-audio.proые и аналоговые сигналы.
all-audio.proые и аналоговые сигналы.
1.5.8 Восстановление сигнала по дискретным отсчетам: пример
Вопрос Где располагаются полюсы передаточной функции устойчивой дискретной цепи? Как пересчитать требования к дискретному цифровому фильтру в требования к аналоговому прототипу? Как рассчитываются дискретные фильтры верхних частот, полосовые и режекторные? Этот материал является базовым для понимания процессов цифровой фильтрации и обработки сигналов во многих современных информационных системах. По своей природе многие сигналы являются непрерывными.
Это объясняется тем, что источники сообщений выдают информацию непрерывно, в любые моменты времени. К таким источникам относятся, например, микрофоны телефонных аппаратов, считывающие устройства факсимильных аппаратов, передающие телевизионные камеры. Дискретные сигналы естественно возникают в тех случаях, когда источник сообщений выдает информацию в фиксированные моменты времени.
Например, устройство измерения температуры, связанное с городским световым табло, посылает сигнал на это табло в определенные промежутки времени. В других промежутках на табло высвечиваются давление, время или другие параметры. Здесь ярко проявляется характер дискретного сигнала: в паузах нет никаких сведений об изменении температуры.
Таким образом, мы имеем дело не с непрерывным изменением температуры, а лишь с ее значениями, отсчитанными через определенные промежутки времени. Подобный процесс называется дискретизацией непрерывного сигнала. Свойство дискретного сигнала — существовать лишь в определенные промежутки времени — позволяет организовать передачу по одной и той же линии радиоканалу, паре проводов, оптическому волокну сообщений от нескольких различных источников. Примером этого служит упомянутая выше передача на городское световое табло сведений от датчиков температуры, давления и т.
Говорят, что при этом происходит разделение каналов во времени. Особой разновидностью дискретных сигналов являются цифровые сигналы. Цифровой сигнал — это последовательность импульсов. Если принять условно факт наличия импульса за 1, а факт его отсутствия за 0, то импульсную последовательность можно представить как чередование двух цифр: 0 и 1.
Цифровой сигнал — это последовательность импульсов. Если принять условно факт наличия импульса за 1, а факт его отсутствия за 0, то импульсную последовательность можно представить как чередование двух цифр: 0 и 1.
Очевидно, что любое значение дискретного сигнала легко перевести в двоичное число. Поэтому цифровой сигнал можно рассматривать как закодированный двоичным кодом дискретный сигнал. В последнее время системы с цифровыми сигналами активно вторгаются в нашу жизнь. Во всем мире сейчас пользуются цифровыми телефонами; в наши дома приходит цифровое телевидение; на прилавках магазинов мы видим аппаратуру цифровой звуко- и видеозаписи.
Цифровые сигналы в телефонии, телевидении, звуко- и видеозаписи ничем не отличаются от цифровых сигналов в компьютерных сетях. Появляется возможность применять для обработки текста, звука, изображения быстродействующие компьютерные системы.
Для передачи телекоммуникационных сигналов теперь могут использоваться компьютерные сети, а для передачи компьютерных сигналов — обычная телефонная сеть. Сигнал — это физический процесс например, изменяющиеся во времени токи и напряжения , содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией. Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения — уровни квантования, которые затем кодируются двоичными числами.
Сигнал — это физический процесс например, изменяющиеся во времени токи и напряжения , содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией. Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения — уровни квантования, которые затем кодируются двоичными числами.
Если в цепь микрофона рис. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал. В отличие от непрерывного сигнала дискретный сигнал можно обозначить. Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT , следующими строго через интервал T. Используются и более краткие обозначения: и. Причем, во всех этих записях n — целое число, принимающее как положительные, так и отрицательные значения.
Используются и более краткие обозначения: и. Причем, во всех этих записях n — целое число, принимающее как положительные, так и отрицательные значения.
Так, на рис. Дискретные сигналы можно задавать графиками, как это показано на рис. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов. Пример 1. Единичный ступенчатый аналоговый сигнал приведен на рис.
Соответствующий ему дискретный сигнал называется ступенчатой последовательностью. Он определяется следующим образом:. Импульс Дирака или d-функция в аналоговой области приведена на рис. Последовательность , приведенная на рис. Этот сигнал можно сдвинуть на k интервалов:. Этот сигнал можно получить из аналогового рис.
Изобразите графики дискретных d-функций и. Интервал времени T , через который отсчитываются значения непрерывного сигнала , называется интервалом дискретизации. Отсчеты непрерывного сигнала следует брать с такой частотой или через такой интервал времени , чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного рис.
Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного рис.
Если обратиться к схеме рис. Для сигналов с ограниченным спектром, то есть для тех сигналов, у которых спектральная плотность локализована в определенной полосе частот, существуют более конкретные рекомендации по выбору интервала дискретизации Т или, что то же, частоты дискретизации.
Эти рекомендации будут даны позже. Уменьшите в два раза интервал дискретизации T исходного аналогового сигнала рис. Получение, передача и обработка непрерывных сигналов например, речевые сигналы в телефонии и радиовещании, телевизионные сигналы может осуществляться в аналоговой форме. На рис. Если задано напряжение на входе цепи и нужно найти напряжение на ее выходе , мы можем сделать это, воспользовавшись интегралом свертки:.
При передаче аналоговых сигналов необходимо учитывать влияние помех и нестабильность параметров цепи, то есть их зависимость от времени, температуры, влажности и т. Особенно сильно это влияние сказывается на очень низких частотах меньше 1 Гц и на частотах выше 20 кГц. В диапазоне сигналов звуковых частот характеристики аналоговых и дискретных цепей и сигналов сопоставимы, и выбор типа сигнала определяется прогрессом в технологии изготовления и применения современных средств микроэлектроники, а они, в свою очередь, ориентированы на цифровые устройства.
Особенно сильно это влияние сказывается на очень низких частотах меньше 1 Гц и на частотах выше 20 кГц. В диапазоне сигналов звуковых частот характеристики аналоговых и дискретных цепей и сигналов сопоставимы, и выбор типа сигнала определяется прогрессом в технологии изготовления и применения современных средств микроэлектроники, а они, в свою очередь, ориентированы на цифровые устройства.
Заменим непрерывные сигналы в схеме рис. Чтобы не вносить путаницы, время t заменим дискретными значениями nT , а время t — дискретными значениями mT. Тогда интеграл придется заменить суммой и выражение 1 запишется в виде:.
Поскольку любой отсчет сигнала — это число, то формулу 2 можно запрограммировать на ЭВМ. Останется лишь ввести в ЭВМ числа, соответствующие всем дискретным отсчетам и , и она вычислит отсчеты выходного напряжения.
Выражение 2 на языке вычислительной техники называется алгоритмом вычисления выходного сигнала. Рассчитаем отсчеты выходного напряжения в цепи, приведенной на рис. Для расчета воспользуемся формулой 2 , подставляя в нее соответствующие дискретные отсчеты входного сигнала и дискретные отсчеты импульсной характеристики , графики которых приведены на рис. График последовательности приведен на рис. Таким образом, дискретные сигналы удобны тем, что их можно обрабатывать с помощью ЭВМ.
Для расчета воспользуемся формулой 2 , подставляя в нее соответствующие дискретные отсчеты входного сигнала и дискретные отсчеты импульсной характеристики , графики которых приведены на рис. График последовательности приведен на рис. Таким образом, дискретные сигналы удобны тем, что их можно обрабатывать с помощью ЭВМ.
Однако, не следует думать, что дискретные сигналы вносятся в ЭВМ лишь с клавиатуры. Их можно вводить в ЭВМ и выводить из нее непосредственно. Непрерывный сигнал подается на ключ, на выходе которого образуются дискретные отсчеты.
Но их еще нельзя ввести в машину. Сначала нужно перевести амплитуды отсчетов в двоичный код — ведь только такой код понимает ЭВМ. Выполняет эту операцию кодер. Закодированные в двоичном коде отсчеты на рисунке обозначены. Вычислительные средства ВС могут представлять собой универсальную большую ЭВМ, специализированную микро-ЭВМ, микропроцессорное устройство или что-нибудь в этом роде.
Главное состоит в том, что в памяти ЭВМ записана программа вычисления, например, выражение 2 , и отсчеты импульсной реакции, скажем, RC -цепи. Следовательно, в результате работы программы, ЭВМ будет выдавать закодированные в двоичном коде отсчеты. Декодер преобразует код в амплитуду, и на его выходе появляются дискретные отсчеты выходного напряжения. Интерполятор Инт восстанавливает функцию между отсчетами. В итоге на выходе системы мы имеем аналоговый сигнал.
Следовательно, в результате работы программы, ЭВМ будет выдавать закодированные в двоичном коде отсчеты. Декодер преобразует код в амплитуду, и на его выходе появляются дискретные отсчеты выходного напряжения. Интерполятор Инт восстанавливает функцию между отсчетами. В итоге на выходе системы мы имеем аналоговый сигнал.
Устройство, состоящее из ключа и кодера и преобразующее непрерывный аналоговый сигнал в двоичный код или, что то же,в цифровой сигнал , называют аналого-цифровым преобразователем АЦП.
Обратное преобразование выполняет цифро-аналоговый преобразователь ЦАП , содержащий декодер и интерполятор. Как видим, ЭВМ может сыграть роль реальной цепи. И хотя самой физической цепи может и не быть в наличии, а задана она будет лишь в виде отсчетов импульсной реакции и программы вычислений, мы будем наблюдать на выходе описанной системы такое же выходное напряжение , как и на выходе реальной цепи.
Рассчитайте первые два отсчета напряжения на выходе дискретной цепи, имеющей импульсную характеристику. Комплексная спектральная плотность непрерывного сигнала в дальнейшем для краткости будем говорить: спектр сигнала вычисляется по формуле прямого преобразования Фурье.
Комплексная спектральная плотность непрерывного сигнала в дальнейшем для краткости будем говорить: спектр сигнала вычисляется по формуле прямого преобразования Фурье.
Сигнал может быть восстановлен по спектру с помощью обратного преобразования Фурье, или интеграла Фурье. В соответствии с принципом неопределенности сигнал, имеющий ограниченную протяженность во времени, обладает неограниченным по полосе спектром рис.
И наоборот, сигнал с ограниченным спектром имеет бесконечную протяженность во времени рис. Как следует из этих рисунков, непрерывный сигнал, и ограниченной и бесконечной протяженности во времени, имеет сплошной спектр. Если сигнал является периодическим, то спектр его — дискретный, то есть теперь вместо используют отсчеты. Эта ситуация показана на рис. Период сигнала равен длительности сигнала. Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае.
Чем отличается дискретный сигнал от непрерывного
Аналоговые и дискретные сигналы.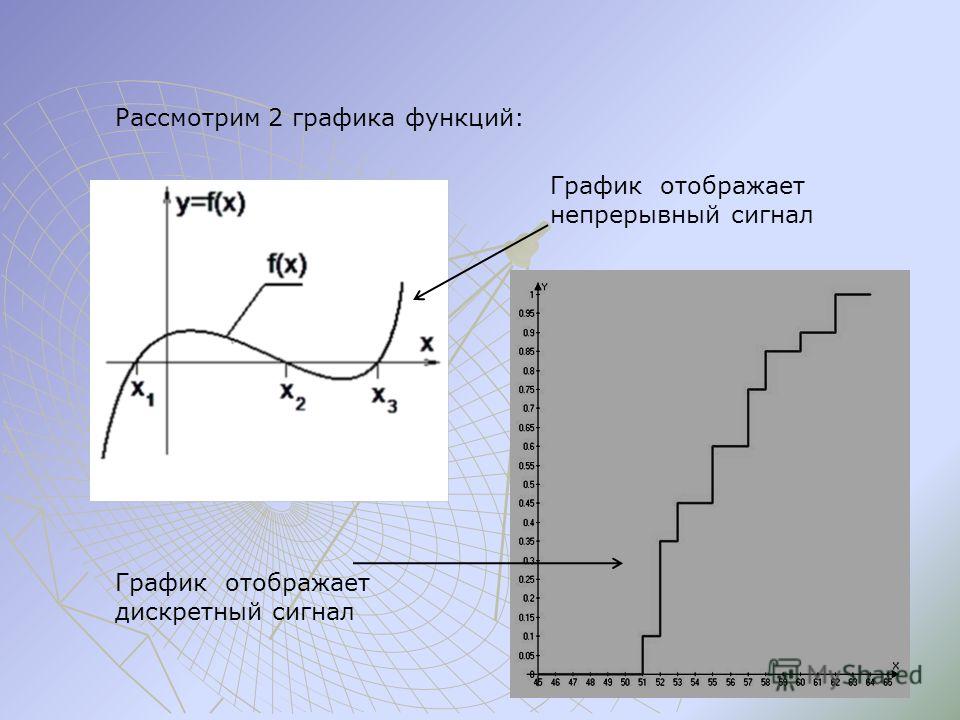 Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения — уровни квантования, которые затем кодируются двоичными числами. Если в цепь микрофона рис.
Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения — уровни квантования, которые затем кодируются двоичными числами. Если в цепь микрофона рис.
Дискретный от латинского discretus, что означает что дискретный повторяет амплитуду аналогового.
ПЛК: дискретные входы/ выходы
Для связи и передачи сообщений используют сигналы, которые отличаются друг от друга. Существуют непрерывные НС и дискретные сигналы ДС. Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом. Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции.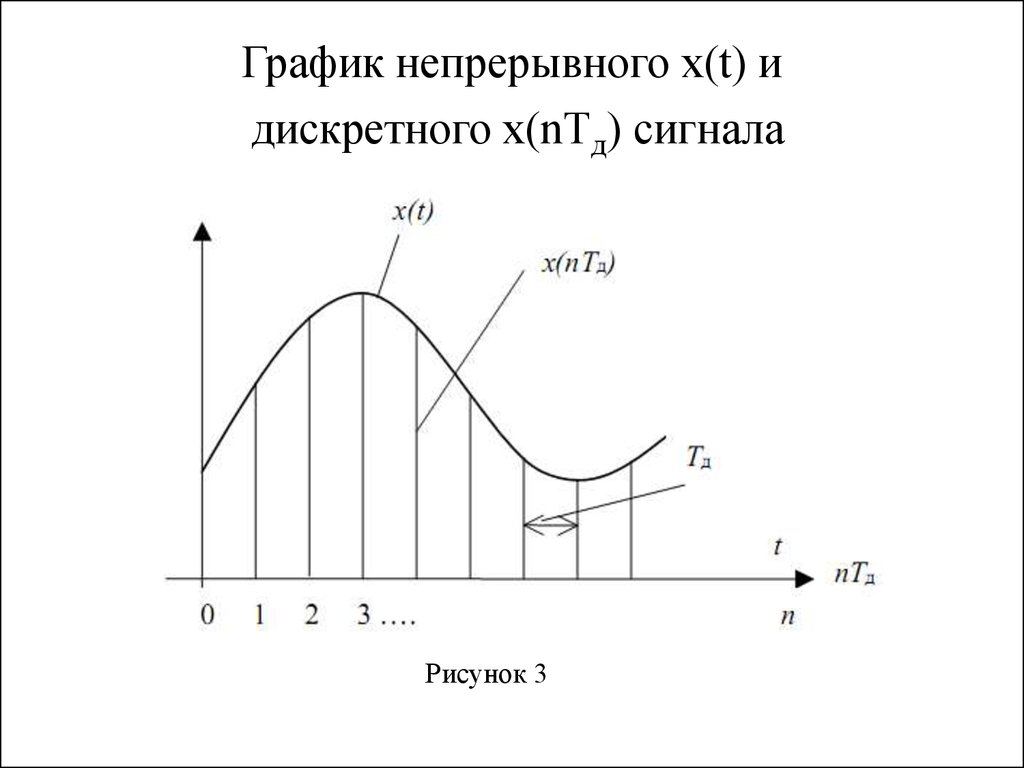 Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре. Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:. Дискретность применяется в вычислительной технике для пакетной передачи данных. Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.
Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре. Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:. Дискретность применяется в вычислительной технике для пакетной передачи данных. Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений. К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.
Дискретный сигнал
Применение ПЛК значительно упрощает процесс разработки проектов и решений, а также дает возможность значительно увеличивать жизненный цикл базовых производств и технологий, основываясь на международном стандарте IEC Во второй статье цикла рассматриваем решения Texas Instruments для организации дискретных входов и выходов ПЛК. Под ПЛК — программируемым логическим контроллером Programmable logic controllers, PLC , — как правило, понимается блочно-модульная система универсального назначения, построенная на основе микропроцессора. Данная система применяется для создания автоматизированной среды и управления последовательными процессами в разных областях промышленности, техники и других сферах инженерной деятельности. Программируемый логический контроллер доступен пользователю в виде единого модуля, включающего в себя центральный процессор, преобразователь напряжения, периферию, задающую возможность работы с коммуникационными и беспроводными интерфейсами, а также входы и выходы для взаимодействия с внешними устройствами.
Данная система применяется для создания автоматизированной среды и управления последовательными процессами в разных областях промышленности, техники и других сферах инженерной деятельности. Программируемый логический контроллер доступен пользователю в виде единого модуля, включающего в себя центральный процессор, преобразователь напряжения, периферию, задающую возможность работы с коммуникационными и беспроводными интерфейсами, а также входы и выходы для взаимодействия с внешними устройствами.
Вопрос
Входные/выходные дискретные сигналы в электроэнергетике: принципы, модули и микросхемы
Поиск по товарам с уценкой. Драйвер с цифровым выходом для управления соленоидами, 1 канала для управления нормально включенными нагрузками NE , питание через контур, мониторинг линии и клапана, выбираемый выход, SIL 3 L. Драйвер с цифровым выходом для управления соленоидами, 1 канал для управления нормальной включенными NE нагрузками, питание через контур, мониторинг состояния линии и клапана, выбираемый выход, SIL 3 L. Драйвер с цифровым выходом для управления соленоидами, цифровой выход, 1 канал для управления нормально включёнными нагрузками NE , питание через шину. Мотиторинг линии и клапана, выбираемый выход, SIL 3 2 yr. Драйвер с цифровым выходом для управления соленоидами, 1 канал для передачи сигналов управления на нормально включенную нагрузку NE во взрывоопасной зоне, питание через шину, мониторинг линии и клапана, выбираемый выход, SIL 3 2 yr.
Драйвер с цифровым выходом для управления соленоидами, цифровой выход, 1 канал для управления нормально включёнными нагрузками NE , питание через шину. Мотиторинг линии и клапана, выбираемый выход, SIL 3 2 yr. Драйвер с цифровым выходом для управления соленоидами, 1 канал для передачи сигналов управления на нормально включенную нагрузку NE во взрывоопасной зоне, питание через шину, мониторинг линии и клапана, выбираемый выход, SIL 3 2 yr.
Аналоговые, дискретные и цифровые сигналы
Операция дискретизации [1. Связь между спектром аналогового сигнала и спектром X см. Согласно теореме Котельникова аналоговый сигнал с ограниченным спектром может быть точно без потери информации преобразован в дискретный сигнал и затем точно восстановлен по отсчетам этого дискретного сигнала. Практически любой аналоговый сигнал имеет ограниченный спектр и поэтому может быть заменен при правильно выбранной частоте дискретизации соответствующим дискретным сигналом. Связь между аналоговыми и дискретными сигналами 1.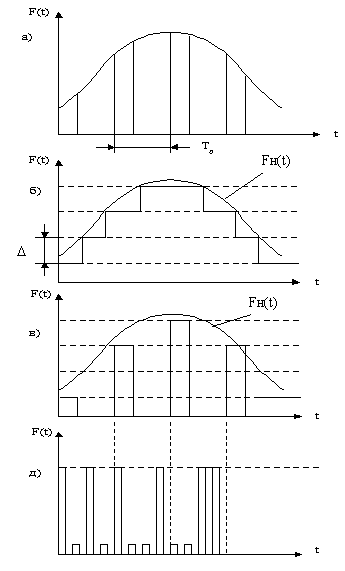
Аналоговые сигналы делятся на два типа: сигналы по току (4 20 мА) и Дискретные выходы ПЛК необходимы для управления.
Дискретный выход, формирователи сигналов для соленоидов клапанов, светодиодов, клаксонов
Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты времени, называют аналоговыми. Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом и не может полностью соответствовать аналоговому сигналу.
Цифровое телевидение охватило уже практически территорию всей страны. Качественный цифровой сигнал новые телевизоры принимают самостоятельно, старые — с помощью специальной приставки. В чем разница между старым аналоговым и новым цифровым сигналом? Многим это непонятно и требует разъяснения. Сигнал это изменение физической величины во времени и пространстве. По сути это коды для обмена данными в информационной и управленческой средах.
Распространяется под лицензией LGPL v3. Страница проекта на GitHub.
Страница проекта на GitHub.
Список возможных значений может быть непрерывным или квантованным. Существует путаница между понятиями дискретного и цифрового сигналов. Часто цифровой сигнал называют дискретным, потому что он состоит из дискретных отдельных частей samples , несмотря на то, что цифровой сигнал не является прерывистым сигналом. В английском языке используют понятия: discrete time дискретное время , для рассмотрения значений переменных в отдельные моменты времени; continuous time непрерывное время , для рассмотрения значений переменных в любой момент времени, причем между любыми двумя моментами времени существует бесконечное количество других моментов времени. Материал из Википедии — свободной энциклопедии.
Робот BotEyes. Промышленные контроллеры RealLab! Структурная схема модуля ввода дискретных сигналов NLDI подробнее см.
ПЛК: дискретные входы/выходы
28 января 2019
телекоммуникациисистемы безопасностимедицинаавтоматизацияответственные применениялабораторные приборыTexas Instrumentsстатьяинтегральные микросхемысредства разработки и материалы
Программируемые логические контроллеры – основа для создания автоматизированной среды управления технологическими процессами. Применение ПЛК значительно упрощает процесс разработки проектов и решений, а также дает возможность значительно увеличивать жизненный цикл базовых производств и технологий, основываясь на международном стандарте IEC 61131. Во второй статье цикла рассматриваем решения Texas Instruments для организации дискретных входов и выходов ПЛК.
Применение ПЛК значительно упрощает процесс разработки проектов и решений, а также дает возможность значительно увеличивать жизненный цикл базовых производств и технологий, основываясь на международном стандарте IEC 61131. Во второй статье цикла рассматриваем решения Texas Instruments для организации дискретных входов и выходов ПЛК.
Подписаться на получение уведомлений о публикации новых статей на тему ПЛК.
Под ПЛК – программируемым логическим контроллером (Programmable logic controllers, PLC), – как правило, понимается блочно-модульная система универсального назначения, построенная на основе микропроцессора. Данная система применяется для создания автоматизированной среды и управления последовательными процессами в разных областях промышленности, техники и других сферах инженерной деятельности.
Программируемый логический контроллер доступен пользователю в виде единого модуля, включающего в себя центральный процессор, преобразователь напряжения, периферию, задающую возможность работы с коммуникационными и беспроводными интерфейсами, а также входы и выходы для взаимодействия с внешними устройствами. Обобщенная структурная схема ПЛК показана на рисунке 1.
Обобщенная структурная схема ПЛК показана на рисунке 1.
Рис. 1. Обобщенная структурная схема ПЛК
Количество входов ПЛК колеблется от 6 (контроллеры нижнего уровня) до 128 и более (контроллеры верхнего уровня). Все имеющиеся на борту контроллера входы и выходы можно разделить на три класса:
- аналоговые;
- дискретные;
- специальные.
Аналоговые входы необходимы для ввода непрерывного сигнала с датчиков и других внешних устройств. Аналоговые сигналы делятся на два типа: сигналы по току (4…20 мА) и сигналы по напряжению (0…10 В). К примеру, в случае подключения к аналоговому входу внешнего датчика температуры с диапазоном измерения 0…85°С на выходе датчика величина тока в 4 мА будет соответствовать 0°С, а 20 мА – 85°С.
Аналоговые выходы ПЛК служат для плавного управления устройствами. Разделение у аналоговых выходов такое же, как и у входов (по току и по напряжению). В качестве примера использования можно привести регулировку угла поворота вентиля, подключенного к выходу (0…180°). Ток величиной в 4 мА, поданный на выход ПЛК, повернет вентиль в положение 0°, ток в 20 мА, соответственно, в положение 180°.
Ток величиной в 4 мА, поданный на выход ПЛК, повернет вентиль в положение 0°, ток в 20 мА, соответственно, в положение 180°.
Дискретные входы программируемого логического контроллера служат для получения сигналов от дискретных датчиков, таких как датчики давления, термостаты, датчики обнаружения, концевые датчики и так далее. Величина напряжения сигнала для этих датчиков составляет 24 В, что на программном уровне соответствует логической единице.
Дискретные выходы ПЛК необходимы для управления подключенными устройствами, например, разного рода магнитными пускателями, лампочками, клапанами и прочим, посредством коммутации высокого или низкого сигналов. Дискретный выход представляет собой контакт, способный выдавать сигнал, являющийся с точки зрения программы логическим нулем или единицей. Такой сигнал способен замкнуть или разомкнуть управляющую или питающую цепь подключенного устройства, тем самым выполнив необходимый алгоритм работы.
Специализированные входы/выходы – отдельный класс входов/выходов, который используется для взаимодействия с датчиками и устройствами, обладающими нестандартными параметрами — нестандартным уровнем сигнала, специфическими параметрами питания и программной обработкой.
Наибольшее распространение в промышленном оборудовании получили функциональные звенья на основе дискретных (цифровых) входов/выходов (рисунок 2). В некоторых случаях для сложных типов станков число дискретных каналов может достигать десятков и сотен.
Рис. 2. Применение дискретных входов и выходов ПЛК
Дискретные входы
Дискретные (цифровые) входы программируемого логического контроллера применяются для выполнения самых разных задач автоматизации технологического процесса, начиная от мониторинга состояния различных датчиков, таких как всевозможные кнопки, тумблеры, концевые выключатели, термостаты и прочее, до использования их при создании промышленных панелей управления – ПСП-панелей, клавиатур, аварийных выключателей, а также при приеме информации от исполнительных механизмов – актуаторов, катушек мощных контакторов и реле. По сути, к дискретному входу ПЛК можно подключить любое устройство с выходом типа «реле» или «открытый коллектор».
Дискретный вход программируемого логического контроллера может работать только с низким или высоким уровнем сигнала. Однако некоторые устройства и приборы имеют более двух состояний, соответствующих логическим нулю и единице. Для подключения таких устройств используют сразу несколько дискретных входов. Например, автоматические электронные весы, которые могут контролировать пороги допуска, имеют 2 выхода, соответствующих значениям «меньше нормы» и «больше нормы». Вес объекта таким образом определяется двумя битами информации: 01 – «меньше», 00 – «норма», 10 –«больше», 11 – «неисправность прибора».
Однако некоторые устройства и приборы имеют более двух состояний, соответствующих логическим нулю и единице. Для подключения таких устройств используют сразу несколько дискретных входов. Например, автоматические электронные весы, которые могут контролировать пороги допуска, имеют 2 выхода, соответствующих значениям «меньше нормы» и «больше нормы». Вес объекта таким образом определяется двумя битами информации: 01 – «меньше», 00 – «норма», 10 –«больше», 11 – «неисправность прибора».
Дискретный вход ПЛК, как правило, включает в себя индикатор состояния (светодиод), гальваническую развязку и защиту от неверного подключения. У некоторых контроллеров диоды индикации расположены до гальванической развязки, что дает возможность пользователю проводить диагностику работы внешних цепей до включения контроллера. Помимо этого, каждый дискретный вход оснащен аналоговым фильтром, подавляющим высокочастотные помехи и верхние гармоники спектра входного сигнала. Частота среза фильтра согласована с программным быстродействием, определяющимся типовым временем рабочего цикла ПЛК. Длительность импульса, который можно надежно зафиксировать дискретным входом общего назначения, составляет 2…3 мс. Обобщенная структурная схема дискретного входа ПЛК приведена на рисунке 3.
Длительность импульса, который можно надежно зафиксировать дискретным входом общего назначения, составляет 2…3 мс. Обобщенная структурная схема дискретного входа ПЛК приведена на рисунке 3.
Рис. 3. Обобщенная структурная схема дискретного входа ПЛК
Несмотря на то что функционал и алгоритм работы дискретного входа достаточно просты, его схемотехническая реализация оказывается не столь тривиальной задачей, особенно если учесть, что в современных решениях одновременно требуются компактные размеры, приемлемая цена, высокая надежность, а также минимальные значения потребления.
Реализация дискретных входов
Сигналы, поступающие на дискретные входы ПЛК, могут существенно отличаться друг от друга по различным параметрам, таким как продолжительность фронта и среза, наличие/отсутствие дребезга, сопротивление источника питания, амплитуда и так далее. К примеру, сигнал, который был сформирован замыкающимися контактами реле, обладает типовой величиной продолжительности фронта в 4 мс и продолжительностью среза в 2 мс, при этом допустимо возникновение дребезга. В то же время быстродействующие сигналы от полупроводниковых ключей могут иметь частоту в десятки и сотни кГц, причем дребезг у них отсутствует как таковой. В то же время, если рассмотреть этот вопрос с точки зрения схемотехники, более существенным оказывается правильный подбор характеристик тока и напряжения. Итогом является то, что все дискретные входы ПЛК можно разделить по двум параметрам: типу опрашиваемых датчиков и интервалу напряжений и токов для заданных логических состояний нуля и единицы.
В то же время быстродействующие сигналы от полупроводниковых ключей могут иметь частоту в десятки и сотни кГц, причем дребезг у них отсутствует как таковой. В то же время, если рассмотреть этот вопрос с точки зрения схемотехники, более существенным оказывается правильный подбор характеристик тока и напряжения. Итогом является то, что все дискретные входы ПЛК можно разделить по двум параметрам: типу опрашиваемых датчиков и интервалу напряжений и токов для заданных логических состояний нуля и единицы.
В соответствии с ГОСТ IEC 61131–2-2012, дискретные (цифровые) входы делятся на три типа:
- Цифровой вход типа 1 (type 1 digital input) – устройство для измерительных сигналов, получаемых от механических контактов устройств переключения, например, реле, кнопок, выключателей и тому подобного. Преобразует фактический сигнал с двумя состояниями в однобитовое двоичное число.
- Цифровой вход типа 2 (type 2 digital input) – устройство для измерительных сигналов от полупроводниковых устройств переключения, например, двухпроводных бесконтактных переключателей.
 Преобразует фактический сигнал с двумя состояниями в однобитовое двоичное число. Данный класс цифрового входа может использоваться вместо классов 1 и 3.
Преобразует фактический сигнал с двумя состояниями в однобитовое двоичное число. Данный класс цифрового входа может использоваться вместо классов 1 и 3. - Цифровой вход типа 3 (type 3 digital input) по определению аналогичен входам типа 2, но отличается величиной входных токов. Он также используется для приема сигналов, получаемых от полупроводниковых устройств переключения, например, двухпроводных бесконтактных переключателей. Данный класс цифрового входа может использоваться вместо класса 1. Цифровые входы типа 3 имеют более низкие электрические характеристики по сравнению с цифровыми входами типа 2. Благодаря меньшей допустимой токовой нагрузке удается на одном модуле разместить большее число входов типа 3. Отличие типа 3 от типа 2 заключается в том, что первый совместим с устройствами, которые, согласно IEC 60947-5-2, в состоянии «выключено» работают на низком токе.
В соответствии с ГОСТ, рабочий диапазон входа состоит из области «ВКЛ», области перехода и области «ВЫКЛ». Для входа в область «ВКЛ» необходимо, чтобы были одновременно превышены минимальные значения тока и напряжения. Для постоянного напряжения питания 24 В вход типа 1 должен переходить в состояние «ВКЛ» при напряжениях 15…30 В при токе 2…15 мА. Для входа типа 2 напряжение включения составляет 11…30 В при токе 6…30 мА. Для входа типа 3 диапазон напряжений включения составляет 11…30 В при токе 2…15 мА. Значения токов и напряжений определяют мощность, рассеиваемую на входе, которая является еще одним важным параметром, так как способна в конечном итоге оказывать влияние на габариты создаваемого решения.
Для входа в область «ВКЛ» необходимо, чтобы были одновременно превышены минимальные значения тока и напряжения. Для постоянного напряжения питания 24 В вход типа 1 должен переходить в состояние «ВКЛ» при напряжениях 15…30 В при токе 2…15 мА. Для входа типа 2 напряжение включения составляет 11…30 В при токе 6…30 мА. Для входа типа 3 диапазон напряжений включения составляет 11…30 В при токе 2…15 мА. Значения токов и напряжений определяют мощность, рассеиваемую на входе, которая является еще одним важным параметром, так как способна в конечном итоге оказывать влияние на габариты создаваемого решения.
Одной из основных проблем построения дискретных входов является изоляция цепей датчика и контроллера. Изоляция цепей датчика строится на основе гальванической развязки. Сама по себе гальваническая развязка цепей может осуществляться на основе различных принципов:
- электромагнитная – на основе принципа взаимной индуктивности, например, трансформаторы;
- оптическая – оптроны, оптореле;
- емкостная – цифровые емкостные барьеры;
- электромеханическая – электромеханические реле.

Гальваническая развязка на основе оптронов является традиционным решением, применяемым при построении дискретных входов ПЛК (рисунки 4 и 5). Скорости работы данного типа развязки достаточно для передачи цифровых сигналов, однако с развитием полупроводниковой промышленности стали доступны микросхемы, позволяющие создать изоляционный барьер за счет других, более современных технологий, позволивших уменьшить тем самым габариты и стоимость конечного решения, а также получить ряд других преимуществ.
Рис. 4. Реализация дискретного входа на основе оптрона с ограничением тока резистивным делителем
Одним из вариантов замены оптической развязки являются микросхемы, где изоляционный барьер реализуется на емкостях. Применение емкостей дает возможность исключить связь по постоянному току между приемником и передатчиком, что в сигнальных цепях, по своей сути, является гальванической развязкой.
Рис. 5. Реализация дискретного входа на основе оптрона с ограничением тока резистивным делителем и стабилизатором тока
Преимущества развязки, организованной при помощи конденсаторов, заключаются в достаточно высокой энергетической эффективности, малых габаритах и устойчивости к внешним магнитным полям. Все это дает возможность производить недорогие интегральные изоляторы с высокими показателями надежности. На данный момент такие типы изоляторов находятся в производстве у компаний: Texas Instruments, Silicon Labs и Maxim Integrated.
Все это дает возможность производить недорогие интегральные изоляторы с высокими показателями надежности. На данный момент такие типы изоляторов находятся в производстве у компаний: Texas Instruments, Silicon Labs и Maxim Integrated.
Эти компании применяют разные подходы при создании канала, тем не менее, все три компании используют диоксид кремния (SiO2) в качестве диэлектрика. Данный материал обладает высокой электрической прочностью и уже несколько десятилетий применяется в производстве микросхем. Диоксид кремния легко интегрируется в кристалл, причем для того чтобы обеспечить напряжение изоляции величиной в несколько киловольт, достаточно слоя диэлектрика толщиной всего в несколько микрометров (рисунок 6).
Рис. 6. Интеграция диоксида кремния в кристалл
По технологии, которую использует Texas Instruments, на кристалле, расположенном в корпусе микросхемы, располагаются площадки-конденсаторы, кристаллы соединяются через эти площадки, тем самым позволяя информационному сигналу проходить от приемника к передатчику через изоляционный барьер (рисунок 7). Устройства, построенные по данному принципу, получили название цифровых изоляторов. Такие изоляторы содержат в себе несколько изолированных каналов, каждый из которых превосходит традиционный оптрон по быстродействию и точности передачи сигнала, по уровню устойчивости к помехам и, как правило, по стоимости в пересчете на канал.
Устройства, построенные по данному принципу, получили название цифровых изоляторов. Такие изоляторы содержат в себе несколько изолированных каналов, каждый из которых превосходит традиционный оптрон по быстродействию и точности передачи сигнала, по уровню устойчивости к помехам и, как правило, по стоимости в пересчете на канал.
Рис. 7. Внешний вид внутренних соединений между двумя подложками цифрового изолятора Texas Instruments
Компания Texas Instruments выпустила несколько серий цифровых изоляторов, среди которых серии микросхем ISO71xx, ISO72xx, самыми передовыми из которых являются семейства ISO77xx и ISOW78xx, а также микросхемы ISO1211/12. Последние заслуживают отдельного внимания, так как именно они наиболее часто применяются при реализации дискретных входов.
Микросхемы ISO1211/12
ISO1211/12 – специализированная интегральная схема для реализации дискретных входов с индивидуальной гальванической развязкой. Посредством микросхем семейства ISO121x можно построить дискретные входы, соответствующие стандарту IEC 61131-2 и типам 1, 2 и 3, описанным ранее. К таким входам возможно подключение внешних датчиков с максимальным рабочим напряжением до 24 B (рисунок 8).
К таким входам возможно подключение внешних датчиков с максимальным рабочим напряжением до 24 B (рисунок 8).
Рис. 8. Реализация дискретного входа на основе цифрового изолятора ISO1211
Изоляторы ISO121x представляют собой простое решение с малым энергопотреблением и точным ограничением тока. Эти изоляторы не требуют источника питания с первичной стороны и работают в широком диапазоне напряжений питания 2,25…5,5 В. ISO121x имеют в своем составе входы, толерантные к напряжению ±60 В и имеющие защиту от обратной полярности, что немаловажно при отказах со значительными обратными напряжениями и токами. Цифровые изоляторы этого семейства поддерживают скорости обмена данными до 4 Мбит/с с гарантией пропускания импульса длительностью 150 нс. ISO1211 подходят для разделения каналов в многоканальных системах, а ISO1212 – в решениях с ограниченным пространством размещения. Структурная схема одного канала показана на рисунке 9.
Рис. 9. Структурная схема канала ISO1211/12
Изоляторы принимают на вход дискретные сигналы уровня 24 В и обеспечивают изолированный дискретный выход. Внешний резистор Rизм задает значение ограничения втекающего тока. Порог напряжения, при котором происходит переключение между уровнями, задается резистором Rпор. Для передачи дискретных сигналов через изоляционный барьер микросхемы семейства ISO121x используют амплитудную манипуляцию ON-OFF keying (OOK). Для оценки возможностей цифровых изоляторов доступны оценочный комплект ISO1211EVM (рисунок 10) и плата 8-канального изолированного дискретного входа ISO1212EVM (рисунок 11) производства компании Texas Instruments.
Внешний резистор Rизм задает значение ограничения втекающего тока. Порог напряжения, при котором происходит переключение между уровнями, задается резистором Rпор. Для передачи дискретных сигналов через изоляционный барьер микросхемы семейства ISO121x используют амплитудную манипуляцию ON-OFF keying (OOK). Для оценки возможностей цифровых изоляторов доступны оценочный комплект ISO1211EVM (рисунок 10) и плата 8-канального изолированного дискретного входа ISO1212EVM (рисунок 11) производства компании Texas Instruments.
Рис.10. Оценочный комплект ISO1211EVM
Рис. 11. Оценочный модуль 8-канального приемника цифровых сигналов ISO1212EVM
Основные параметры цифровых изоляторов ISO1211 и ISO1212 приведены в таблице 1.
Таблица 1. Параметры цифровых изоляторов ISO1211/12
| Наименование | ISO1211 | ISO1212 |
|---|---|---|
| Диапазон токов ограничения, мА | 2,2…7,3 | |
| Встроенный изолирующий преобразователь питания | Нет | |
| Количество каналов | 1 | 2 |
| Количество прямых/обратных каналов | 1/0 | 2/0 |
| Напряжение изоляции, В | 2500 | |
| Пиковое напряжение изоляции в течение 1 с, В | 3600 | |
| Максимальное импульсное напряжение изоляции при импульсе формы 1,2/50 мкс, В | 4000 | |
| Скорость передачи данных, Мбит/с | 4 | |
Задержка прохождения сигнала, тип. , нс , нс |
140 | |
| Максимальная частота работы, МГц | 2 | |
| Состояние по умолчанию | Нет | |
| Диапазон питающих напряжений, В | 2,25…5,5 | |
| Рабочий температурный диапазон, °С | -40…125 | |
| Корпус | 8SOIC | 16SSOP |
Цифровые изоляторы семейства ISO121x обладают более высокой скоростью работы и меньшим временем отклика по сравнению с традиционными решениями на оптронах (стандартные оптроны имеют время срабатывания в десятки микросекунд), а также обладают меньшими габаритными размерами и малыми потерями мощности (рисунок 12). Кроме того, при реализации дискретных выходов на основе ISO121x нет необходимости в дополнительном буфере с триггером Шмитта, что упрощает проектирование системы. В конечном итоге можно сказать, что микросхемы ISO1211/12 являются более предпочтительным решением для реализации развязки в дискретных входах, чем традиционные оптроны.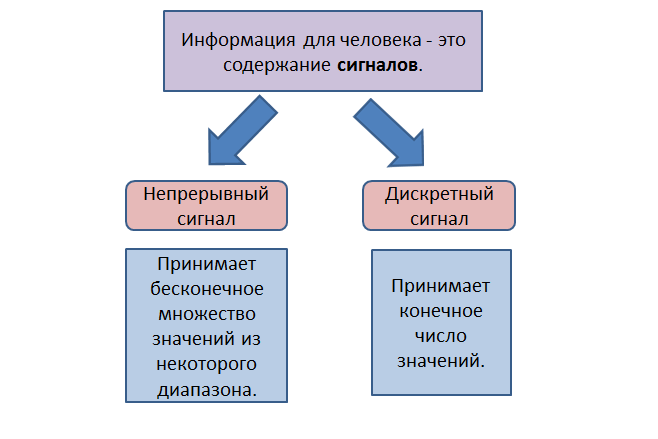
Рис. 12. Сравнение рабочих температур: традиционное решение +84,1, ISO1212 +44,9
Дискретные входы с определением обрыва
Компания Texas Instruments создала на базе микросхем семейства ISO121x решение, позволяющее определять обрыв на том или ином дискретном входе. Решение получило название TIDA-01509 (рисунок 13). Оно представляет собой компактную реализацию гальванической развязки для 16 дискретных входов. Входы TIDA-01509 поддерживают работу с сигналами с частотой до 100 кГц на канал и разделены на две группы, по 8 в каждой. Каждая группа состоит из трех двухканальных ISO1212 и двух одноканальных ISO 1211. Для работы ISO1211 и ISO1212 не требуется использовать гальванически развязанный DC/DC-преобразователь, что дает преимущество перед традиционными решениями дискретных входов.
Рис. 13. Внешний вид TIDA-01509
Обнаружение обрыва на входе выполнено при помощи только одного дополнительного оптического переключателя для каждого канала или двух оптических переключателей и одного дополнительного конденсатора для каждой группы.
Особенности TIDA-01509:
- 16 цифровых входов с допуском входного напряжения до ±60 В;
- обнаружение обрыва для одного канала с одним дополнительным компонентом;
- время, необходимое для обнаружения обрыва одного канала – 3 мс;
- обнаружение обрыва для масштабируемой конфигурации групповых каналов с тремя дополнительными компонентами;
- время, необходимое для обнаружения обрыва группы (8 каналов) – 24 мс;
- отсутствие необходимости использования дополнительного изолированного источника питания;
- наличие совместимых отладочных плат для быстрой и легкой оценки возможностей решения.
Решение состоит из микросхем ISO121x, 8-битного сдвигового регистра SN74LV165A, одиночного инвертора SN74LVC1GU04 и интегрального однонаправленного супрессора TVS3300 (рисунок 14).
Рис. 14. Структурная схема TIDA-01509
Работа решения основана на том, что оптический переключатель отключает землю от ISO121x на короткий промежуток времени и соединяет ее потом снова, в результате чего импульс на выходе ISO121x показывает, существует ли обрыв на входе.
Если рассматривать алгоритм более подробно, в качестве примера взяв обрыв провода для однотактной конфигурации, когда используется только один канал устройства ISO121x, то есть необходим только один дополнительный оптический переключатель, то алгоритм срабатывания будет выглядеть следующим образом:
- в нормальном режиме работы контакт FGND присоединен к фактической земле через оптический ключ: оптический ключ открыт, на линии контроля низкий сигнал;
- для закрытия оптического ключа подается высокий сигнал на линию контроля;
- считывается выходное состояние канала ISO121x. Если обрыва нет, то выходное состояние канала будет равно единице. Однако если в цепи присутствует обрыв — положение выхода соответствующего канала будет равно нулю.
Для оценки способностей решения TIDA-01509 возможно его подключение к отладочной плате MSP430FR5969 (рисунок 15) или любой другой плате производства Texas Instruments с таким же подключением SPI. Питание TIDA-01509, составляющее 3,3 В, в данном случае будет происходить непосредственно от отладочной платы.
Рис. 15. Внешний вид отладочной платы MSP430FR5969
Дискретные выходы
Простейший дискретный выход программируемого логического контроллера представляет собой контакты реле и способен выдавать сигнал, принимающий значения логических нуля или единицы. Такой выход относительно прост в реализации и применении, но имеет характерные для реле недостатки: ограниченный ресурс работы, достаточно невысокое быстродействие и так далее. Решением, которое могло бы заменить такой подход, является использование электронного силового элемента, который выполняется по бесконтактной схеме (транзистор – для нагрузки постоянного тока, симистор – для нагрузки переменного тока).
Согласно ГОСТ IEC 61131-2-2012, к которому мы уже обращались ранее, «цифровой выход (digital output) – это устройство, которое преобразует однобитовое двоичное число в сигнал с двумя состояниями».
Основными характеристиками цифровых выходов являются:
- номинальная токовая нагрузка 0,1/0,25/0,5/1/2 А, при этом максимальный ток составляет 0,12/0,3/0,6/1,2/2,4 А;
- тип выхода – незащищенный или устойчивый к состоянию короткого замыкания.

Стандартная схема реализации дискретного выхода показана на рисунке 16.
Рис. 16. Стандартная схема реализации дискретного выхода
Датчики тока, последовательно соединенные с нагрузкой, непрерывно контролируют ток, поступающий на нагрузку, и сообщают о наличии избыточных токов контроллеру.
Величина протекающего в цепи тока является одним из ключевых параметров безопасности. Дискретные выходы сконструированы с использованием NPN-транзисторов со встроенными диодами для защиты от перенапряжения. Система гарантирует, что при включении цифровых выходов ПЛК ток от источника питания всегда находится в пределах заданного рабочего диапазона контроллера. Токочувствительный усилитель может защитить цифровые выходы от перегрузки по току, обеспечить диагностику, чтобы устранить неисправные условия нагрузки и предупредить о сбое системы.
Однако цифровые выходы ПЛК могут быть напрямую привязаны к устройствам, работающим с большими токами, превышающими допустимый ток выхода ПЛК, такими как стартеры, лампы и прочее. В таком случае необходимо использование дополнительного полевого транзистора для управления потоком тока от источника 24 В до нагрузки. На рисунке 17 показано подключение дискретного выхода ПЛК ко внешнему низковольтному полевому транзистору.
В таком случае необходимо использование дополнительного полевого транзистора для управления потоком тока от источника 24 В до нагрузки. На рисунке 17 показано подключение дискретного выхода ПЛК ко внешнему низковольтному полевому транзистору.
Рис. 17. Схема реализации дискретного выхода с применением дополнительного полевого транзистора
Одним из недостатков такого подхода является использование внешнего дискретного компонента (полевого транзистора), что увеличивает габариты конечного решения и его стоимость. Исключением полевого транзистора из схемы может послужить применение токочувствительного усилителя INA240, разработанного компанией Texas Instruments.
INA240 – это высокоточный двунаправленный усилитель тока с малым входным смещением и дрейфом усиления по температурному диапазону, что делает его идеальным устройством для измерения токов на дискретных цифровых выходах ПЛК. Микросхема INA240 способна работать с сигналами до 400 кГц, имеет ток потребления 2,6 мА, напряжение питания 2,7…5,5 В и способна работать при температуре -40…125°C. Кроме того, INA240 обладает лучшим в отрасли сочетанием малого смещения (5 мкВ), дрейфа смещения (50 нВ/°C), ошибки и дрейфа усиления (0,05% и 0,5 ppm/°C соответственно). Также данное решение обеспечивает подавление синфазных сигналов переменного тока – 93 дБ на частоте 50 кГц.
Кроме того, INA240 обладает лучшим в отрасли сочетанием малого смещения (5 мкВ), дрейфа смещения (50 нВ/°C), ошибки и дрейфа усиления (0,05% и 0,5 ppm/°C соответственно). Также данное решение обеспечивает подавление синфазных сигналов переменного тока – 93 дБ на частоте 50 кГц.
INA240 выпускается в 8-выводных корпусах TSSOP и SO, а для оценки ее возможностей доступны модули TIDA-00909 и TIDA-00913 (рисунок 18).
Рис. 18. Внешний вид модуля TIDA-00909/00913
Другие решения Texas Instruments, используемые для реализации дискретных входов и выходов
Компания Texas Instruments не ограничивается выпуском модулей гальванической развязки и токочувствительных усилителей и предоставляет полный перечень компонентов, необходимых для реализации дискретного входа и выхода (таблица 2).
Таблица 2. Решения от Texas Instruments для реализации дискретных входов и выходов
| Наименование | Описание |
|---|---|
| TIDA-00017 | 8-канальный модуль дискретных входов для программируемого логического контроллера. Разработан в соответствии со стандартом IEC61000-4 EMC и включает в себя 8 цифровых входов до 34 В каждый, подключаемых к ПЛК через последовательный интерфейс. Модуль обладает защитой от превышения значений по току, имеет изолированный блок питания. Разработан в соответствии со стандартом IEC61000-4 EMC и включает в себя 8 цифровых входов до 34 В каждый, подключаемых к ПЛК через последовательный интерфейс. Модуль обладает защитой от превышения значений по току, имеет изолированный блок питания.
|
| TIDA-00179 | Универсальный цифровой интерфейс для подключения к энкодерам абсолютного положения, таким как EnDat 2.2, BiSS, SSI или HIPERFACE DSL. Решение способно работать со входными сигналами широкого диапазона напряжения 15…60 В. Разъем I/O логических сигналов с напряжением 3,3 В служит для организации прямой связи с головным процессором, например, Sitara AM437x или Delfino F28379. |
| TIDEP0049 | Решение для системы связи по интегрированному промышленному протоколу Ethernet. Модуль базируется на процессоре семейства Sitara и отвечает требованиям промышленного Ethernet по скорости запуска после включения питания устройства. |
| PMP9409 | Изолированный понижающий источник питания с 4 выходами для ПЛК-систем. Источник поддерживает номинальное входное напряжение 24 В и генерирует 4 изолированных напряжения смещения +15 В. Каждая из шин напряжения имеет ток нагрузки 30 мА. Источник поддерживает номинальное входное напряжение 24 В и генерирует 4 изолированных напряжения смещения +15 В. Каждая из шин напряжения имеет ток нагрузки 30 мА. |
| TIDA-00129 | Компактный источник на 1 Вт с двумя изолированными выходами для программируемых логических контроллеров. TIDA-00129 создавался специально для питания модулей, работающих с ПЛК, и автоматизации производства. Имеет изолированные выходы 24 и 3,3 В. Данный проект соответствует требованиям IEC 61010-1. |
| TIDEP0079 | Проект EtherCAT на базе Sitara AM57x и PRU-ICSS с передачей в определенных временных интервалах. Решение может быть использовано в системах ПЛК, построенных на базе EtherCAT, или в системах управления движением. |
| TIDM-HAHSCPTO | Проект высокоскоростного счетчика (HSC) и выхода с прямоугольными импульсами имеет высокую степень эксплуатационной готовности. В данном проекте TI приводится базовое решение (программное обеспечение и тестовая платформа) для двух разных индустриальных IO-функций, которые относятся к управлению движением: высокоскоростного счетчика (HSC) и выхода с прямоугольными импульсами (PTO).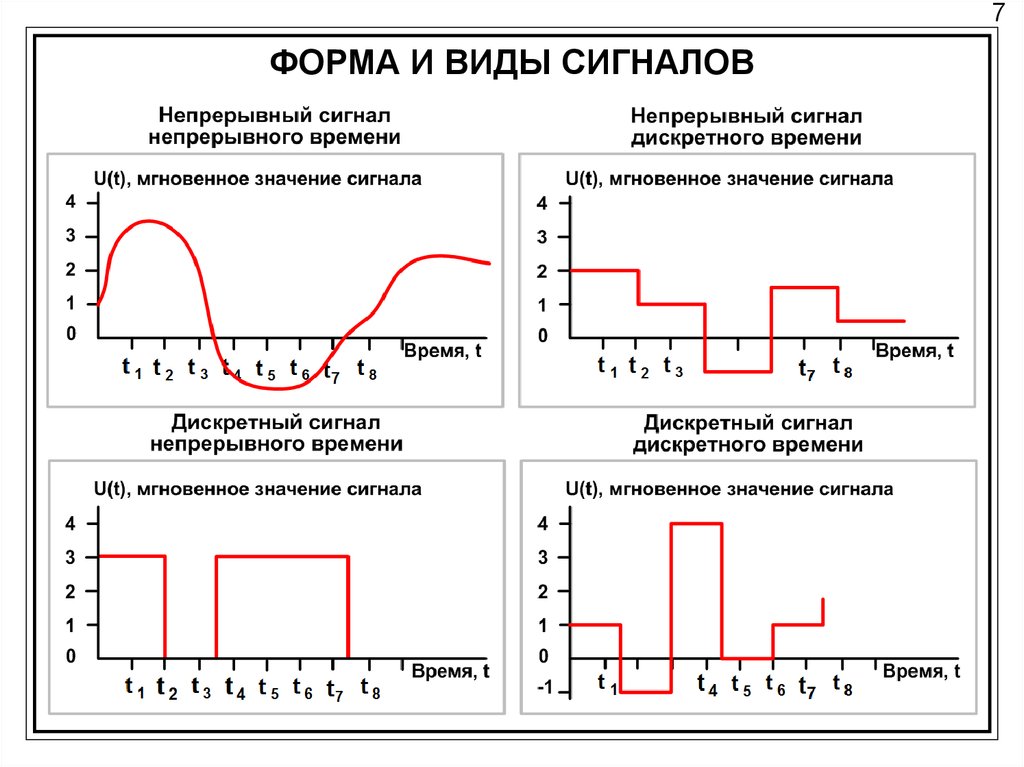 Данный проект базируется на платформе с микроконтроллером, которая подходит для использования в промышленных приложениях, где высокая степень эксплуатационной готовности и/или функциональная безопасность являются важными характеристиками. Данный проект базируется на платформе с микроконтроллером, которая подходит для использования в промышленных приложениях, где высокая степень эксплуатационной готовности и/или функциональная безопасность являются важными характеристиками. |
| TIDEP0057 | Многопротокольный цифровой интерфейс ведущего устройства для датчика углового положения с использованием AM437xс PRU-ICSS. Решение построено на базе процессора Sitara с подсистемой программируемого модуля реального времени и промышленных коммуникаций (PRU-ICSS). |
| TIDEP0003 | Платформа для создания и разработки ETHERNET/IP-коммуникаций. Дает возможность пользователям реализовывать стандарты связи Ethernet и IP для широкого диапазона устройств, используемых в промышленной автоматизации. |
| TIDA-00012 | Изолированный интерфейс CAN-Profibus. Разработан для применения в промышленных системах, требующих подачи изолированного питания на приемопередатчики CAN и/или Profibus. |
| TIDA-00230 | Интерфейс для настройки и логирования NFC (два порта FRAM: NFC ⇔ FRAM ⇔ Serial) |
| TIDA-00560 | Проект 16-канального статусного LED-драйвера PLC-модулей для индикации статуса нескольких аналоговых и цифровых входных и выходных каналов. |
| TIDA-00320 | Восьмиканальный модуль цифрового выхода для программируемых логических контроллеров. Предоставляет 0,5 А на всех 8 каналах при относительно небольших габаритах. |
| TIDA-00319 | Высокоскоростной цифровой модуль вывода для программируемых логических контроллеров (ПЛК). |
| TIDA-00766 | Дифференциальный высокоскоростной цифровой модуль вывода, оснащенный интерфейсом RS-485. Основная ниша применения — управление шаговыми двигателями. |
Заключение
В создании автоматизированных систем на базе ПЛК правильное построение дискретных входов и выходов является одной из главных задач: от разработчика требуется следование ГОСТ IEC 61131-2-2012, точное выполнение приведенных спецификаций токов и напряжений, а также обеспечение необходимого уровня защиты с соблюдением стоимостных и габаритных характеристик конечного продукта.
Решение задачи построения дискретных входов ПЛК можно значительно упростить, если строить схемы входов и выходов не на дискретных компонентах, а с привлечением интегральных систем. Цифровые изоляторы и высокоточные двунаправленные усилители производства компании Texas Instruments позволяют при минимальных затратах времени получить надежное и защищенное решение, не только отвечающее всем необходимым требованиям, но и превосходящее стандартные решения для данного класса устройств.
Цифровые изоляторы и высокоточные двунаправленные усилители производства компании Texas Instruments позволяют при минимальных затратах времени получить надежное и защищенное решение, не только отвечающее всем необходимым требованиям, но и превосходящее стандартные решения для данного класса устройств.
Литература
- ГОСТ IEC 61131–2-2012 «Контроллеры Программируемые. Часть 2. Требования к оборудованию и испытания»;
- How To Improve Speed and Reliability of Isolated Digital Inputs in Motor Drives;
- Broken Wire Detection Using an Optical Switch Reference Design;
- Safety and Protection for Discrete Digital Outputs in a PLC System Using Current Sense Amplifiers;
- ISO121x Isolated 24-V to 60-V Digital Input Receivers for Digital Input Modules. Texas Instruments, 2018;
- А. Трушников. Обновление линейки гальванических изоляторов компании Texas Instruments: повышение уровня интеграции. Компоненты и технологии №10/2017.
•••
Аналоговый и цифровой сигнал – разница между ними
Ключевые различия между аналоговым и цифровым сигналом
- Аналоговый сигнал представляет собой непрерывный сигнал, тогда как цифровые сигналы представляют собой сигналы, разделенные во времени.

- Аналоговый сигнал обозначается синусоидой, а цифровой сигнал обозначается прямоугольной волной.
- Аналоговый сигнал использует непрерывный диапазон значений, которые помогают вам представлять информацию; с другой стороны, цифровой сигнал использует дискретные 0 и 1 для представления информации.
- Сравнение цифровых и аналоговых сигналов. Полоса пропускания аналогового сигнала мала, а полоса пропускания цифрового сигнала велика.
- Аналоговые приборы дают значительные ошибки наблюдений, в то время как цифровые приборы никогда не приводят к каким-либо ошибкам наблюдений.
- Аналоговое оборудование никогда не обеспечивает гибкости реализации, но цифровое оборудование обеспечивает гибкость реализации.
- Сравнение аналоговых и цифровых сигналов. Аналоговые сигналы подходят для передачи аудио и видео, а цифровые сигналы подходят для вычислений и цифровой электроники.
Разница между аналоговыми и цифровыми сигналами
Что такое сигнал?
Сигнал — это электромагнитный или электрический ток, который используется для передачи данных из одной системы или сети в другую. Сигнал – это функция, передающая информацию о явлении.
Сигнал – это функция, передающая информацию о явлении.
В электронике и телекоммуникациях это относится к любому изменяющемуся во времени напряжению, которое представляет собой электромагнитную волну, несущую информацию. Сигнал также можно определить как наблюдаемое изменение качества, например количества. Существует два основных типа сигналов: аналоговый сигнал и цифровой сигнал.
Что такое аналоговый сигнал?
Аналоговый сигнал — это непрерывный сигнал, в котором одна изменяющаяся во времени величина представляет другую зависящую от времени переменную. Этот тип сигналов работает с физическими величинами и природными явлениями, такими как землетрясение, частота, извержение вулкана, скорость ветра, вес, освещение и т. д.
Что такое цифровой сигнал?
Цифровой сигнал — это сигнал, который используется для представления данных в виде последовательности отдельных значений в любой момент времени. Он может принимать только одно из фиксированного числа значений. Этот тип сигнала представляет собой действительное число в пределах постоянного диапазона значений. Теперь давайте узнаем некоторые ключевые различия между цифровыми и аналоговыми сигналами.
Он может принимать только одно из фиксированного числа значений. Этот тип сигнала представляет собой действительное число в пределах постоянного диапазона значений. Теперь давайте узнаем некоторые ключевые различия между цифровыми и аналоговыми сигналами.
Характеристики аналогового сигнала
Основные характеристики аналогового сигнала
- Электронные сигналы этого типа изменяются во времени
- Минимальное и максимальное значение, положительное или отрицательное.
- Может быть как периодическим, так и непериодическим.
- Аналоговый сигнал работает с непрерывными данными.
- Точность аналогового сигнала невысока по сравнению с цифровым сигналом.
- Помогает измерять натуральные или физические величины.
- Форма выходного аналогового сигнала похожа на кривую, линию или график, поэтому она может не иметь смысла для всех.
Характеристики цифровых сигналов
Здесь представлены основные характеристики цифровых сигналов.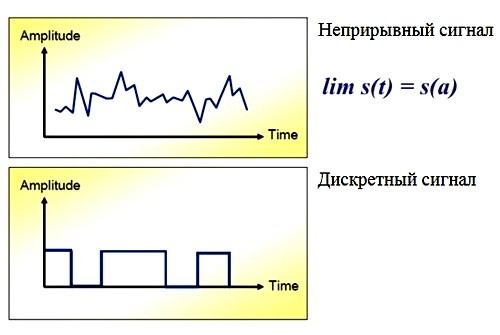
- Цифровые сигналы представляют собой сигналы, разделенные по времени.
- Электронные сигналы этого типа лучше обрабатываются и передаются по сравнению с аналоговыми сигналами.
- Цифровые сигналы универсальны, поэтому широко используются.
- Точность цифрового сигнала лучше, чем у аналогового сигнала.
Различия между аналоговым и цифровым сигналом
Вот важные различия между аналоговой и цифровой передачей:
| Аналоговый | Цифровой |
|---|---|
| Аналоговый сигнал представляет собой непрерывный сигнал, представляющий физические измерения. | Цифровые сигналы — это разделенные во времени сигналы, генерируемые с использованием цифровой модуляции. |
| Обозначается синусоидами | Обозначается прямоугольными волнами |
| Он использует непрерывный диапазон значений, которые помогают вам представлять информацию. | Цифровой сигнал использует дискретные 0 и 1 для представления информации.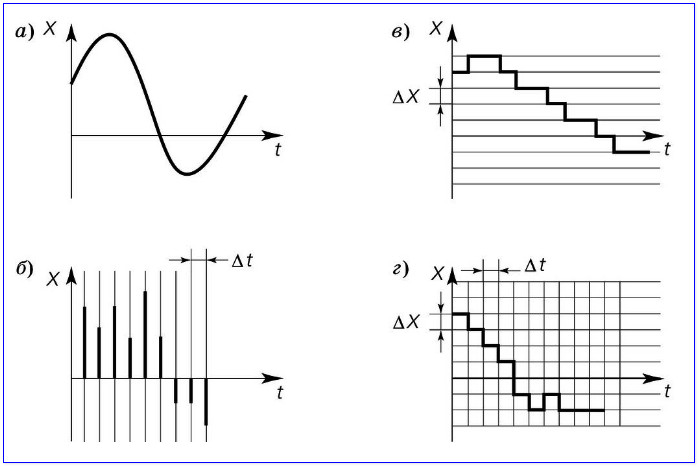 |
| Датчики температуры, FM-радиосигналы, фотоэлементы, датчик освещенности, резистивный сенсорный экран являются примерами аналоговых сигналов. | Компьютеры, компакт-диски, DVD-диски — вот некоторые примеры цифрового сигнала. |
| Низкая полоса пропускания аналогового сигнала | Широкая полоса пропускания цифрового сигнала. |
| Аналоговые сигналы ухудшаются из-за шума во время передачи, а также цикла записи/чтения. | Относительно помехоустойчивая система без ухудшений в процессе передачи и цикле записи/чтения. |
| Аналоговое оборудование никогда не обеспечивает гибкости реализации. | Цифровое оборудование обеспечивает гибкость в реализации. |
| Подходит для передачи аудио и видео. | Подходит для вычислительной техники и цифровой электроники. |
Обработка может выполняться в режиме реального времени и потребляет меньшую полосу пропускания по сравнению с цифровым сигналом.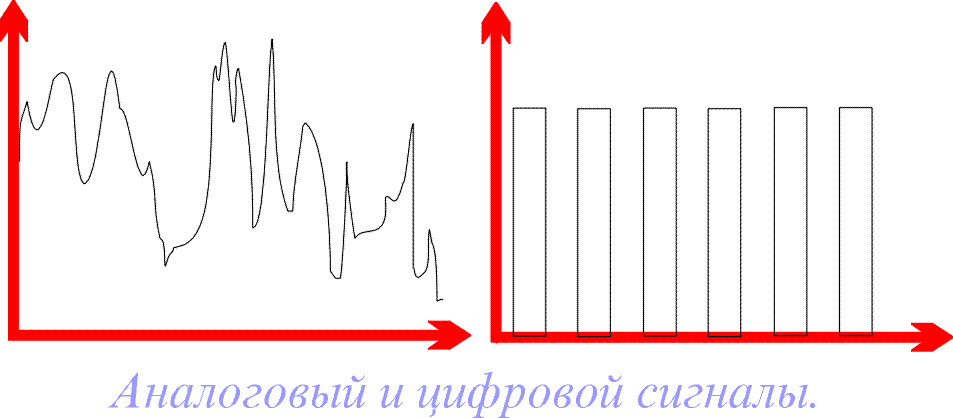 |
Никогда не гарантируется, что цифровая обработка сигнала может выполняться в режиме реального времени. |
| Аналоговые приборы обычно имеют шкалу s, которая сужена в нижней части и дает значительные ошибки наблюдения. | Цифровые приборы никогда не вызывают ошибок наблюдения. |
| Аналоговый сигнал не имеет фиксированного диапазона. | Цифровой сигнал имеет конечное число, т. е. 0 и 1. |
Преимущества аналоговых сигналов
Вот преимущества и преимущества аналоговых сигналов
- Проще в обработке
- Лучше всего подходит для передачи аудио и видео.
- Недорогой и портативный.
- Он имеет гораздо более высокую плотность, поэтому может представлять более точную информацию.
- Нет необходимости покупать новую видеокарту.
- Использует меньшую пропускную способность, чем цифровые звуки
- Обеспечивает более точное представление звука
- Это естественная форма звука.

Преимущества цифровых сигналов
Вот плюсы/преимущества цифровых сигналов:
- Цифровые данные легко сжимаются.
- Любая информация в цифровом виде может быть зашифрована.
- Оборудование, использующее цифровые сигналы, более распространено и дешевле.
- Цифровой сигнал избавляет работающие приборы от ошибок наблюдения, таких как ошибки параллакса и аппроксимации.
- Доступно множество инструментов редактирования
- Вы можете редактировать звук, не изменяя исходную копию
- Простота передачи данных по сети
Недостатки аналоговых сигналов
Минусы/недостатки аналоговых сигналов:
- Аналоговый сигнал имеет более низкое качество, чем цифровой.
- Кабели чувствительны к внешним воздействиям.
- Стоимость аналогового провода высока и неудобна для переноски.
- Низкая доступность моделей с цифровыми интерфейсами.
- Запись аналогового звука на ленту довольно дорогая, если лента повреждена
- Предлагает ограничения на редактирование
- Ленту становится трудно найти
- Довольно сложно синхронизировать аналоговый звук
- Качество легко теряется
- Данные могут быть повреждены
- Множество записывающих устройств и форматов, которые могут запутать при сохранении цифрового сигнала
- Цифровые звуки могут обрезать аналоговую звуковую волну, что означает, что вы не можете получить идеальное воспроизведение звука
- Предлагает плохие многопользовательские интерфейсы
Недостатки цифровых сигналов
- Выборка может привести к потере информации.

- Для аналого-цифрового и цифро-аналогового преобразования требуется оборудование для работы со смешанными сигналами
- Скорость процессора ограничена
- Развитие ошибок квантования и округления
- Требуется большая пропускная способность
- Системы и обработка более сложны.
1.1: Классификация и свойства сигналов
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22837
- Richard Baraniuk et al.
- Университет Райса
Введение
В этом модуле мы начнем изучение сигналов и систем с изложения некоторых основ классификации сигналов. По сути, это введение в важные определения и свойства, лежащие в основе обсуждения сигналов и систем, с кратким обсуждением каждого из них.
Классификации сигналов
Непрерывное время и дискретное время
Как следует из названий, эта классификация определяется тем, является ли ось времени 9 или нет.0293, дискретное (счетное) или непрерывное (рисунок \(\PageIndex{1}\)). Сигнал непрерывного времени будет содержать значение для всех действительных чисел по оси времени. В отличие от этого, сигнал с дискретным временем, часто создаваемый путем дискретизации непрерывного сигнала, будет иметь значения только через равные промежутки времени по оси времени.
Рисунок \(\PageIndex{1}\)
Аналоговый и цифровой
Разница между аналоговым и цифровым аналогична разнице между непрерывным и дискретным временем. Однако в этом случае разница касается значений функции. Аналоговый соответствует непрерывному набору возможных значений функции, а цифровой соответствует дискретному набору возможных значений функции. Типичным примером цифрового сигнала является двоичная последовательность, где значения функции могут быть только единицей или нулем.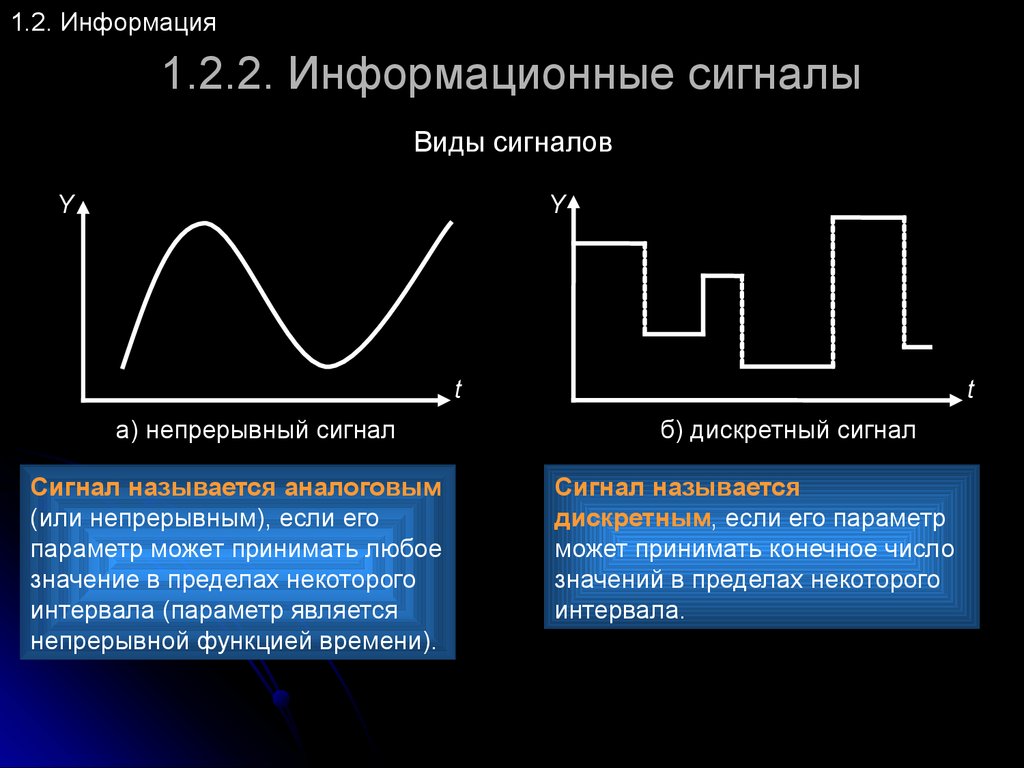
Рисунок \(\PageIndex{2}\)
Периодические и апериодические
Периодические сигналы повторяются с некоторым периодом \(T\), а апериодические или непериодические сигналы — нет (рисунок \(\PageIndex{3}\)). Мы можем определить периодическую функцию с помощью следующего математического выражения, где \(t\) может быть любым числом, а \(T\) — положительной константой:
\[f(t)=f(t+T) \label {1.1} \]
фундаментальный период нашей функции, \(f(t)\), является наименьшим значением \(T\), которое все еще позволяет уравнению \ref{1.1} быть верным.
(а) (б) Рисунок \(\PageIndex{3}\): (a) Периодический сигнал с периодом \(T_0\) (b) Апериодический сигналКонечная и бесконечная длина
Другой способ классификации сигнала — его длина вдоль временной оси. Определен ли сигнал для всех возможных значений времени или только для определенных значений времени? Математически говоря, \(f(t)\) является сигналом конечной длины , если он определен только на конечном интервале
\[ t_{1} где \(t_1 < t_2\). Каузальные сигналы — это сигналы, равные нулю в течение всего отрицательного времени, тогда как антикаузальные — это сигналы, равные нулю в течение всего положительного времени. Непричинные сигналы — это сигналы, которые имеют ненулевые значения как в положительном, так и в отрицательном времени (рис. \(\PageIndex{4}\)). Четный сигнал — это любой сигнал \(f\), такой что \(f(t) = f(-t)\). Даже сигналы можно легко обнаружить, поскольку они симметричны вокруг вертикальной оси. Нечетный сигнал , с другой стороны, является сигналом \(f\) таким, что \(f(t)=-f(-t)\) (рис. \(\PageIndex{5}\)). Используя определения четных и нечетных сигналов, мы можем показать, что любой сигнал может быть записан как комбинация четного и нечетного сигналов. \[ f(t)=\frac{1}{2}(f(t)+f(-t))+\frac{1}{2}(f(t)-f(-t)) \label{1.2} \] Умножая и добавляя это выражение, можно показать, что оно истинно. Кроме того, можно показать, что \(f(t)+f(-t)\) удовлетворяет требованию четной функции, а \(f(t)-f(-t)\) удовлетворяет требованию нечетной функции. (рис. \(\PageIndex{6}\)). Детерминистический сигнал — это сигнал, в котором каждое значение сигнала является фиксированным, определяемым математическим выражением, правилом или таблицей. С другой стороны, значения случайного сигнала строго не определены, а подвержены некоторой изменчивости. Рассмотрим сигнал, определенный для всех действительных \(t\), описанных как \[f(t)=\left\{\begin{array}{cc} Этот сигнал является непрерывным во времени, аналоговым, апериодическим, бесконечной длины, причинным, ни четным, ни нечетным, и, по определению, детерминированным. В этом модуле описываются лишь некоторые из многих способов классификации сигналов. Они могут быть непрерывными или дискретными, аналоговыми или цифровыми, периодическими или апериодическими, конечными или бесконечными, детерминированными или случайными. Мы также можем разделить их на основе их свойств причинности и симметрии. Аналого-цифровые преобразователи (АЦП) с дискретным временем, реализованные с использованием схем с переключаемыми конденсаторами, были выбором разработчиков в течение последних нескольких десятилетий. Эти АЦП обеспечивают высокую точность и точность, что делает их хорошим выбором для таких приложений, как весы, измерение температуры и измерение биопотенциала. Однако в последнее время дельта-сигма АЦП с непрерывным временем работы приобрели популярность в технических журналах и в отрасли. Они использовались в микросхемах связи, где очень полезно встроенное сглаживание, обеспечиваемое архитектурой непрерывного времени. Дельта-сигма АЦП с дискретным временем Дельта-сигма АЦП представляют собой АЦП с передискретизацией, которые дискретизируют сигнал с гораздо более высокой частотой, чем частота Найквиста. Для сигнала с максимальной пропускной способностью f B теорема Найквиста утверждает, что входные данные должны дискретизироваться с частотой > 2f Б . В дельта-сигма АЦП с дискретным временем выборка входного сигнала x(t) происходит перед петлевым фильтром (рис. 1) . Контурный фильтр H(z) представляет собой дискретное время, реализованное с использованием интеграторов с переключаемыми конденсаторами. Квантизатор вообще низкого разрешения, где-то от 1 до 5 бит. Контурный фильтр преобразует шум квантования из основной полосы частот в более высокие частоты. Цифро-аналоговый преобразователь (ЦАП) с обратной связью также реализуется в дискретном времени с помощью переключаемых конденсаторов. Контурный фильтр не формирует ошибки в ЦАП обратной связи, поэтому ЦАП должен быть не хуже общего АЦП. Выход квантователя подвергается низкочастотной фильтрации прореживающим фильтром, который выводит данные со скоростью F DR . На рис. 2 показана спектральная плотность мощности (PSD) выходного сигнала y[n] типичного дельта-сигма АЦП. Наклон формирования шума зависит от порядка петлевого фильтра H(z) и составляет 20*ndB/декада, где n — порядок петлевого фильтра. Дельта-сигма АЦП обеспечивает высокое разрешение в диапазоне f b комбинацией формирования шума и передискретизации. Более высокое разрешение можно получить, увеличив порядок петлевого фильтра или увеличив коэффициент передискретизации. 1 Дельта-сигма АЦП с непрерывным временем В дельта-сигма АЦП с непрерывным временем принцип формирования шума и передискретизации остается таким же, как и в дискретном аналоге (рис. 3) . Ключевое отличие заключается в том, где происходит операция выборки. В схеме с непрерывным временем входная выборка происходит непосредственно перед квантователем. Это отличается от интеграторов с переключаемыми конденсаторами, используемых для АЦП с дискретным временем. ЦАП с обратной связью может быть реализован либо в дискретном времени с использованием схем с переключаемыми конденсаторами, либо в непрерывном времени с помощью ЦАП с управлением по току. Выбор архитектуры ЦАП имеет решающее значение и влияет на производительность АЦП непрерывного времени. Существуют ключевые различия между ЦАП с дискретным временем, использующим схемы с переключаемыми конденсаторами, и ЦАП с непрерывным временем, управляющим током. ЦАП с управлением током более чувствителен к джиттеру тактовых импульсов, чем ЦАП с переключаемыми конденсаторами. В ЦАП с переключаемым конденсатором основная часть заряда передается интегратору в начале фазы интегрирования, а очень небольшая часть заряда передается ближе к концу фазы интегрирования 9. Для схемы непрерывного действия с обратной связью от источника тока постоянный заряд передается интегрирующему конденсатору в течение всей фазы интегрирования. Это приводит к значительному шуму, если тактовый сигнал обратной связи имеет связанный с ним джиттер. Джиттер тактового сигнала напрямую модулирует сигнал обратной связи и может вызвать свертывание шума в пределах желаемой полосы пропускания сигнала. Кроме того, требования к пропускной способности первого интегрирующего операционного усилителя (операционного усилителя) снижаются за счет использования ЦАП с регулированием тока. АЦП с непрерывным временем обычно используют ЦАП с непрерывным временем в своей обратной связи для снижения энергопотребления и обеспечения высокой скорости работы. Однако использование ЦАП с переключаемыми конденсаторами в архитектуре АЦП с непрерывным временем может значительно снизить требования к джиттеру тактовых импульсов. Преимущества дельта-сигма АЦП с непрерывным временем Входной сигнал x(t) на рисунке 1 дискретизируется с частотой F S . Глядя на рис. 3, мы видим, что входной сигнал сначала проходит через петлевой фильтр перед дискретизацией. Этот петлевой фильтр теперь действует как фильтр сглаживания, снижая требования к любому внешнему фильтру сглаживания. Кроме того, поскольку на вход квантователя вводятся сигналы с наложением спектров, петлевой фильтр ослабляет их так же, как и шум квантования. Порядок достигнутого сглаживания зависит от архитектуры контурного фильтра. Sinc-фильтр второго порядка является примером передаточной функции сигнала (STF) АЦП непрерывного времени с петлевым фильтром второго порядка со всеми полюсами (рис. 5) . Для контурного фильтра порядка n -го порядка со всеми функциями передачи полюсов получается сглаживание порядка n--го порядка . Кроме того, дельта-сигма АЦП с дискретным временем предъявляет строгие требования ко времени установления входного драйвера. Такт дискретизации F S обычно делится на две непересекающиеся фазы: φ 1 и φ 2 (рис. 6) . Во время фазы φ 1 конденсатор выборки C S подключается к формирователю входа. Действие переключения конденсатора выборки вызывает скачок на выходе драйвера, в результате чего выходной сигнал драйвера отклоняется от идеального значения. Драйвер должен иметь достаточную пропускную способность, чтобы вернуться к желаемой точности в пределах φ 1 фаза. Это приводит к повышенному энергопотреблению входного драйвера. Поскольку конструкция с непрерывным временем отодвигает выборку от входа, АЦП с непрерывным временем не представляет коммутационной нагрузки для драйвера ввода. Это ослабляет характеристики пропускной способности драйвера. Кроме того, дельта-сигма АЦП с непрерывным временем обычно потребляют меньше энергии, чем АЦП с дискретным временем, при сравнимых шумовых характеристиках. В АЦП с дискретным временем операция дискретизации со связанным с ней шумоподавлением накладывает фундаментальное ограничение на максимально достижимый динамический диапазон для данного значения конденсатора дискретизации и коэффициента передискретизации. Схема дискретизации на Рисунке 6 дискретизирует мощность шума, равную kT/C S в фазе дискретизации. Точно так же в фазе φ 2 интегратор, а также шум переключения складываются, чтобы получить еще один член αkT/C. Точное значение α зависит от реализации интегратора. В АЦП с непрерывным временем шум операционного усилителя в интеграторе не складывается, что потенциально может снизить энергопотребление операционного усилителя. Другим фактором, помогающим снизить энергопотребление, является то, что интеграторы в конструкции с непрерывным временем не переключаются. В результате к ним не предъявляются строгие требования по стабилизации и вращению, что приводит к снижению энергопотребления. 4 Обратите внимание, что требования к полосе пропускания операционного усилителя на первом интеграторе смягчаются только в том случае, если ЦАП обратной связи реализован как непрерывное время. Если ЦАП с обратной связью реализован в виде коммутируемого конденсатора, требования к установке операционного усилителя такие же, как и для схемы АЦП с дискретным временем. В конструкции с дискретным временем контурный фильтр состоит из интеграторов с дискретным временем, которые тактируются с частотой дискретизации F S . Время установления операционного усилителя, используемое в этих интеграторах, устанавливает верхний предел максимальной тактовой частоты для данного технологического узла. В схеме с непрерывным временем, использующей ЦАП с управлением по току, тактируется только квантователь. Поскольку квантователи обычно состоят только из компараторов без обратной связи, они могут синхронизироваться на более высокой тактовой частоте, чем интеграторы переключающих конденсаторов. В конструкции с дискретным временем джиттер тактовой частоты дискретизации на входе ограничивает максимально возможное отношение сигнал/шум (SNR), достигаемое АЦП. Для АЦП скорости Найквиста, предполагая, что шум джиттера белый со среднеквадратичным значением ε, отношение сигнал-шум ограничено: 5 SNR = –20LOG 10 (2π*ε*F в ) Для ADC Oversampled, SNR ограничен: SNR = –20LOG 10 (2π*ε*r. Для АЦП с непрерывным временем выборка выполняется после контурного фильтра, что снижает требования к джиттеру тактовой частоты выборки. Контурный фильтр формирует ошибку, вносимую дрожанием дискретизации. АЦП непрерывного времени с ЦАП с обратной связью на переключаемых конденсаторах имеет ослабленные требования к джиттеру как тактовой частоты дискретизации, так и обратной связи ЦАП. Недостатки дельта-сигма АЦП с непрерывным временем Дельта-сигма АЦП с непрерывным временем могут работать только на фиксированной тактовой частоте, F S . Расположение полюсов интеграторов не зависит от частоты, как в схеме с дискретным временем. Это ограничивает использование дельта-сигма АЦП с непрерывным временем в качестве элемента каталога, когда заказчики ожидают использовать в системе широкий диапазон тактовых частот. В результате АЦП с непрерывным временем в основном успешны как часть больших систем на кристалле (SoC), где тактовая частота четко определена и не может быть легко изменена. Кроме того, STF не является плоской для АЦП непрерывного времени (снова рис. 5) . Для АЦП с дискретным временем STF для аналоговой части, как правило, плоская, и в ней доминирует амплитудная характеристика прореживающего фильтра. Дельта-сигма АЦП с непрерывным временем работы также демонстрируют внеполосные пики в STF для архитектур с прямой связью. 3 Это особенно вредно, поскольку ограничивает полезный диапазон входного сигнала для АЦП. В коммуникационных приложениях с большими внеполосными помехами это может привести к нестабильности АЦП. Для этих приложений может потребоваться отфильтровать помехи или пожертвовать частью динамического диапазона АЦП, если используется архитектура с прямой связью. Обычно АЦП непрерывного действия также имеют ограниченный коэффициент подавления синфазного сигнала (CMRR) из-за несоответствия входных резисторов или входной крутизны. Уровень синфазного сигнала на первых входах интегратора напрямую зависит и от уровня синфазного сигнала внешнего входа. Напротив, синфазный уровень постоянного тока для интегратора в АЦП с дискретным временем может быть легко отделен от входного синфазного уровня с помощью конденсатора выборки. Кроме того, правильные методы дискретизации в АЦП с дискретным временем могут обеспечить очень большой КОСС. Путь ЦАП обратной связи и дрожание тактового сигнала зависят от архитектуры ЦАП, используемой в АЦП непрерывного времени, как обсуждалось ранее. Наиболее распространенные реализации АЦП с непрерывным временем работы используют ЦАП с непрерывным временем управления током для снижения энергопотребления интеграторов. Эти ЦАП более чувствительны к джиттеру тактовых импульсов, чем ЦАП с переключаемыми конденсаторами. АЦП с дискретным временем всегда использует ЦАП с переключаемыми конденсаторами и не предъявляет строгих требований к джиттеру тактового сигнала ЦАП с обратной связью. Резюме Конструкция дельта-сигма АЦП с непрерывным временем работы расширяет полосу пропускания, достижимую с помощью дельта-сигма-технологии. АЦП непрерывного времени продолжает набирать популярность по сравнению с конвейерными АЦП в коммуникационных приложениях из-за встроенной функции сглаживания. Схемы с непрерывным временем еще не использовались широко для прецизионных приложений постоянного тока, где все еще доминируют схемы дельта-сигма с дискретным временем. Невозможность изменить тактовую частоту дискретизации АЦП в соответствии с требованиями системы является самым большим недостатком, ограничивающим использование АЦП непрерывного времени в приложениях постоянного тока. № по каталогу 1. 2. James A. Cherry and W. Martin Snelgrove, Дельта-сигма модуляторы с непрерывным временем работы для Теории высокоскоростного аналогово-цифрового преобразования, Практики и основных пределов производительности , Springer, 1999 3. Люсьен Бремс и Йохан Хёйсинг , Непрерывная временная сигма-дельта-модуляция для аналого-цифрового преобразования в радиоприемниках, Springer, 2001 4. Шули Ян, Сигма-дельта аналогово-цифровое преобразование основной полосы частот с непрерывным временем для приложений ADSL, докторская диссертация, Техасский университет A&M, 2002 5. Бехзад Разави, Принципы проектирования системы преобразования данных , Wiley IEEE Press, 1994 6. Загрузите эти спецификации: ADS1610, ADC12EU050 Амит Кумар Гупта — архитектор аналоговых систем в Texas Instruments, где он определяет продукты следующего поколения для АЦП Delta-Sigma. Точно так же сигнал бесконечной длины , \(f(t)\), определен для всех значений:
Точно так же сигнал бесконечной длины , \(f(t)\), определен для всех значений: Четный против нечетного
 То есть каждый сигнал имеет нечетно-четное разложение. Чтобы продемонстрировать это, мы не должны смотреть дальше одного уравнения.
То есть каждый сигнал имеет нечетно-четное разложение. Чтобы продемонстрировать это, мы не должны смотреть дальше одного уравнения. Детерминированный и случайный

\sin (2 \pi t) / t & t \ geq 1 \\
0 & t<1
\end{массив}\right. \nonumber \] Краткий обзор классификаций сигналов
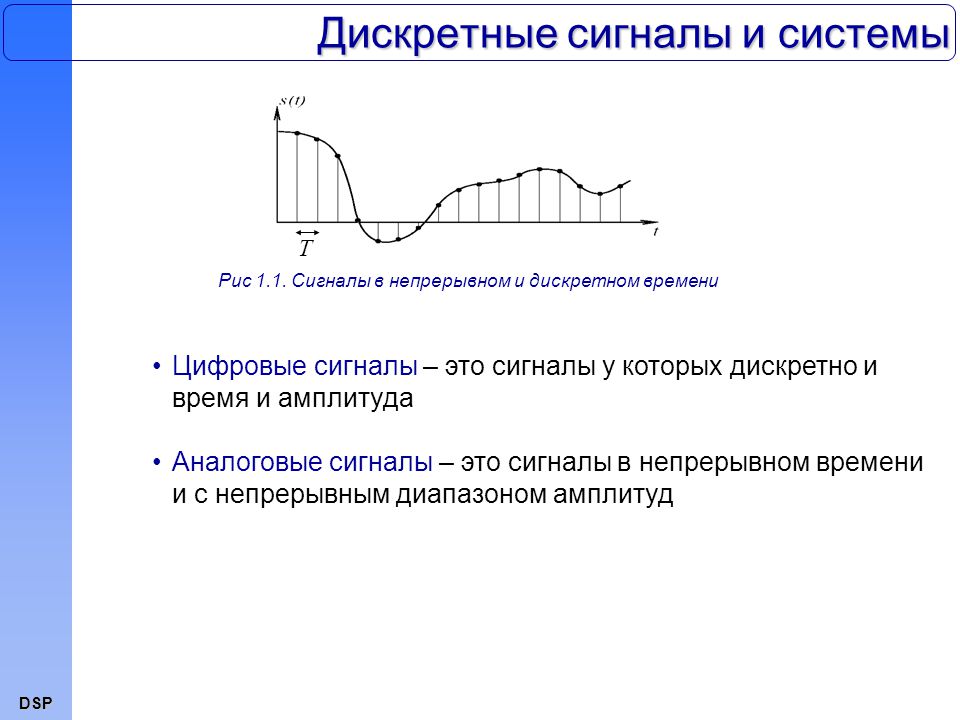
В чем разница между дельта-сигма АЦП с непрерывным и дискретным временем?
Скачать эту статью в формате .
 PDF
PDF
Этот тип файла включает в себя графику и схемы высокого разрешения, если это применимо. 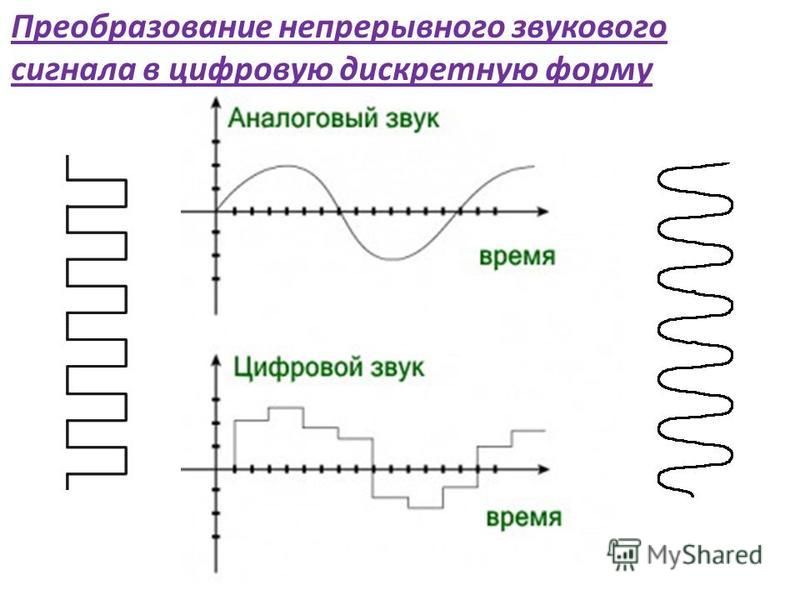 Отношение частоты дискретизации (F S ) к удвоенной ширине полосы сигнала (2f B ) называется коэффициентом передискретизации (OSR).
Отношение частоты дискретизации (F S ) к удвоенной ширине полосы сигнала (2f B ) называется коэффициентом передискретизации (OSR). 
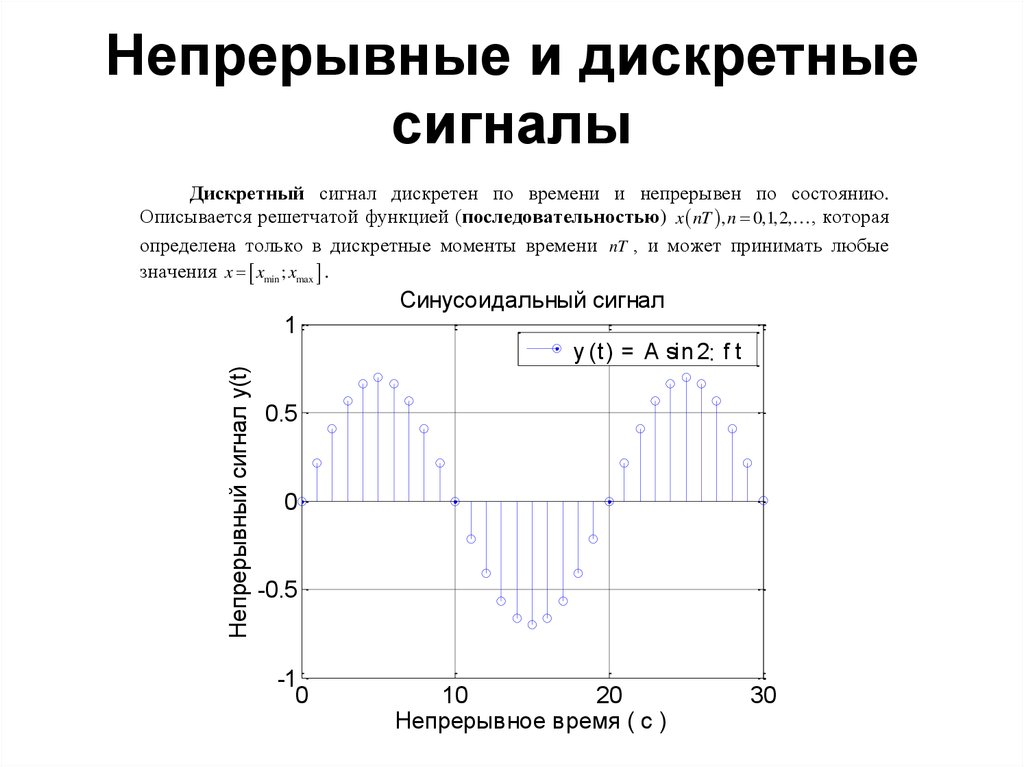 Контурный фильтр теперь является непрерывным с использованием интеграторов непрерывного времени, часто интеграторов RC или gm / C.
Контурный фильтр теперь является непрерывным с использованием интеграторов непрерывного времени, часто интеграторов RC или gm / C.  0499 (рис. 4) . Неопределенность в периоде интегрирования из-за джиттера часов приводит к очень небольшой ошибке в общем заряде, интегрированном в ЦАП с переключаемыми конденсаторами.
0499 (рис. 4) . Неопределенность в периоде интегрирования из-за джиттера часов приводит к очень небольшой ошибке в общем заряде, интегрированном в ЦАП с переключаемыми конденсаторами.  Это связано с тем, что в этой архитектуре ЦАП нет ступенчатых входов для операционного усилителя. В ЦАП с переключаемыми конденсаторами операционный усилитель получает ступенчатый входной сигнал, который должен установиться в течение половины тактового цикла, что приводит к требованиям к высокой пропускной способности, что, в свою очередь, приводит к более высокому энергопотреблению. Кроме того, ЦАП с управлением током более подвержены межсимвольным помехам из-за асимметричного времени нарастания и спада тактового сигнала обратной связи по сравнению с ЦАП с переключаемыми конденсаторами. 2
Это связано с тем, что в этой архитектуре ЦАП нет ступенчатых входов для операционного усилителя. В ЦАП с переключаемыми конденсаторами операционный усилитель получает ступенчатый входной сигнал, который должен установиться в течение половины тактового цикла, что приводит к требованиям к высокой пропускной способности, что, в свою очередь, приводит к более высокому энергопотреблению. Кроме того, ЦАП с управлением током более подвержены межсимвольным помехам из-за асимметричного времени нарастания и спада тактового сигнала обратной связи по сравнению с ЦАП с переключаемыми конденсаторами. 2  Чтобы предотвратить наложение входного сигнала обратно в интересующую полосу пропускания сигнала, входной сигнал должен быть ограничен полосой до F S /2 частота. Для этого требуется фильтр сглаживания перед АЦП с дискретным временем для подавления содержания сигнала вблизи F S и кратных F S .
Чтобы предотвратить наложение входного сигнала обратно в интересующую полосу пропускания сигнала, входной сигнал должен быть ограничен полосой до F S /2 частота. Для этого требуется фильтр сглаживания перед АЦП с дискретным временем для подавления содержания сигнала вблизи F S и кратных F S . 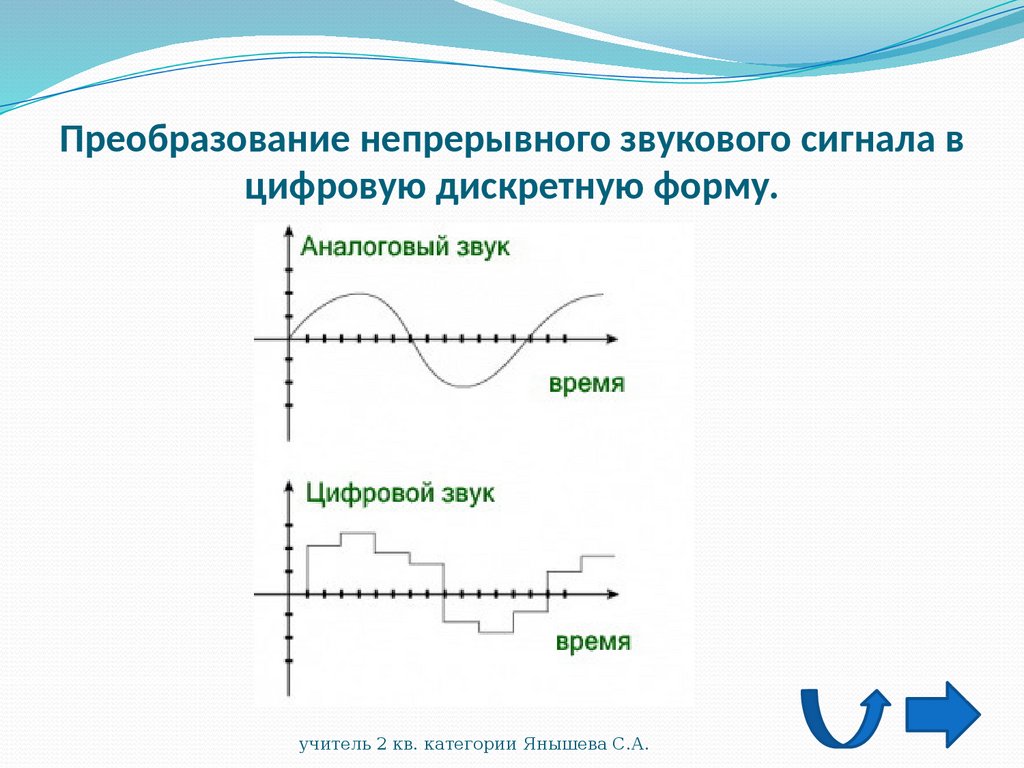 Для петлевых фильтров с прямой связью порядок пути получаемой фильтрации сглаживания уменьшается. Однако, как минимум, всегда получается антиалиасинговая фильтрация первого порядка. 3 Таким образом, АЦП с непрерывным временем можно рассматривать как комбинацию сглаживающего фильтра и АЦП.
Для петлевых фильтров с прямой связью порядок пути получаемой фильтрации сглаживания уменьшается. Однако, как минимум, всегда получается антиалиасинговая фильтрация первого порядка. 3 Таким образом, АЦП с непрерывным временем можно рассматривать как комбинацию сглаживающего фильтра и АЦП. 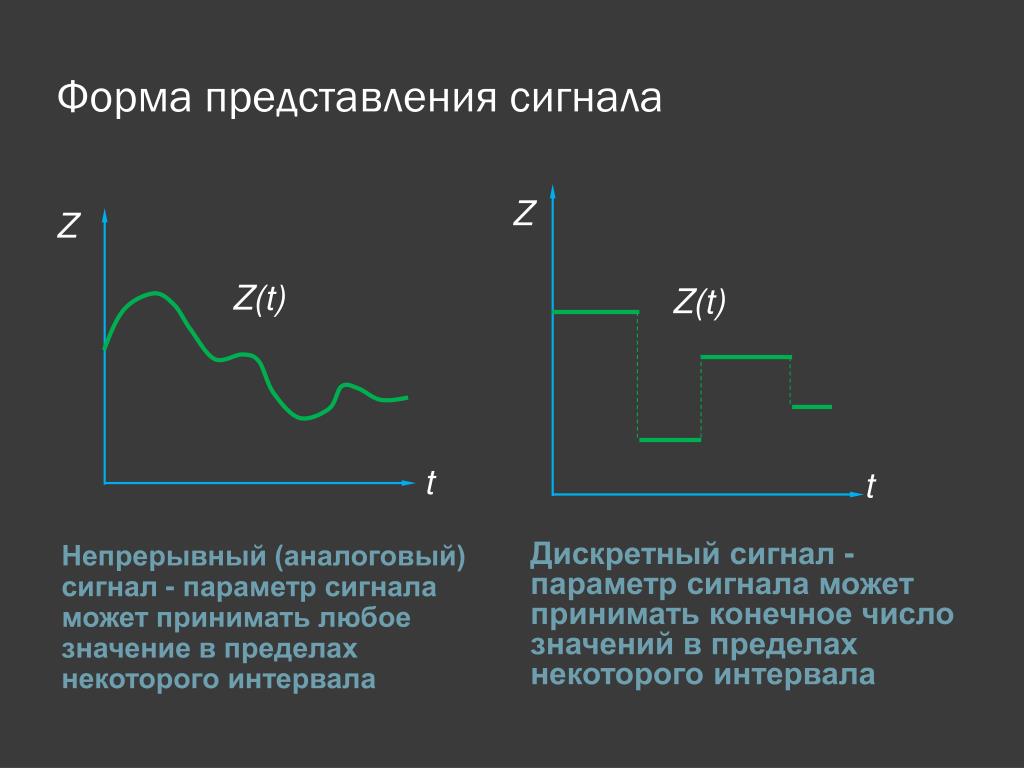 Выходной сигнал драйвера должен установиться за половину тактового периода (1/2*Fs).
Выходной сигнал драйвера должен установиться за половину тактового периода (1/2*Fs). 

 IN ) + 10log 10 (OSR)
IN ) + 10log 10 (OSR) 
 Это может ограничить диапазон синфазных входных сигналов для АЦП непрерывного времени.
Это может ограничить диапазон синфазных входных сигналов для АЦП непрерывного времени. 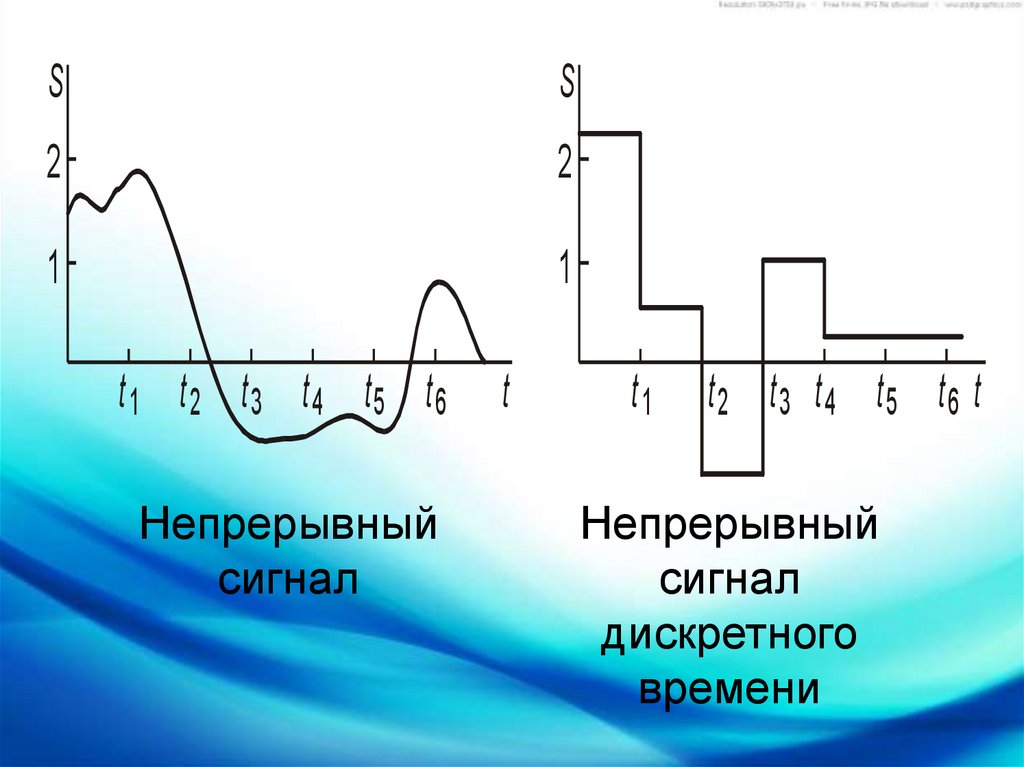 Самый быстрый в отрасли дельта-сигма АЦП с дискретным временем, ADS1610, имеет полосу пропускания сигнала 5 МГц. Технология непрерывного времени позволила использовать такие продукты, как ADC12EU050, которые могут обеспечить полосу дискретизации без наложения частот до 22,5 МГц. Архитектура с непрерывным временем может обеспечить еще более высокую пропускную способность за счет использования передовых технологических узлов.
Самый быстрый в отрасли дельта-сигма АЦП с дискретным временем, ADS1610, имеет полосу пропускания сигнала 5 МГц. Технология непрерывного времени позволила использовать такие продукты, как ADC12EU050, которые могут обеспечить полосу дискретизации без наложения частот до 22,5 МГц. Архитектура с непрерывным временем может обеспечить еще более высокую пропускную способность за счет использования передовых технологических узлов. 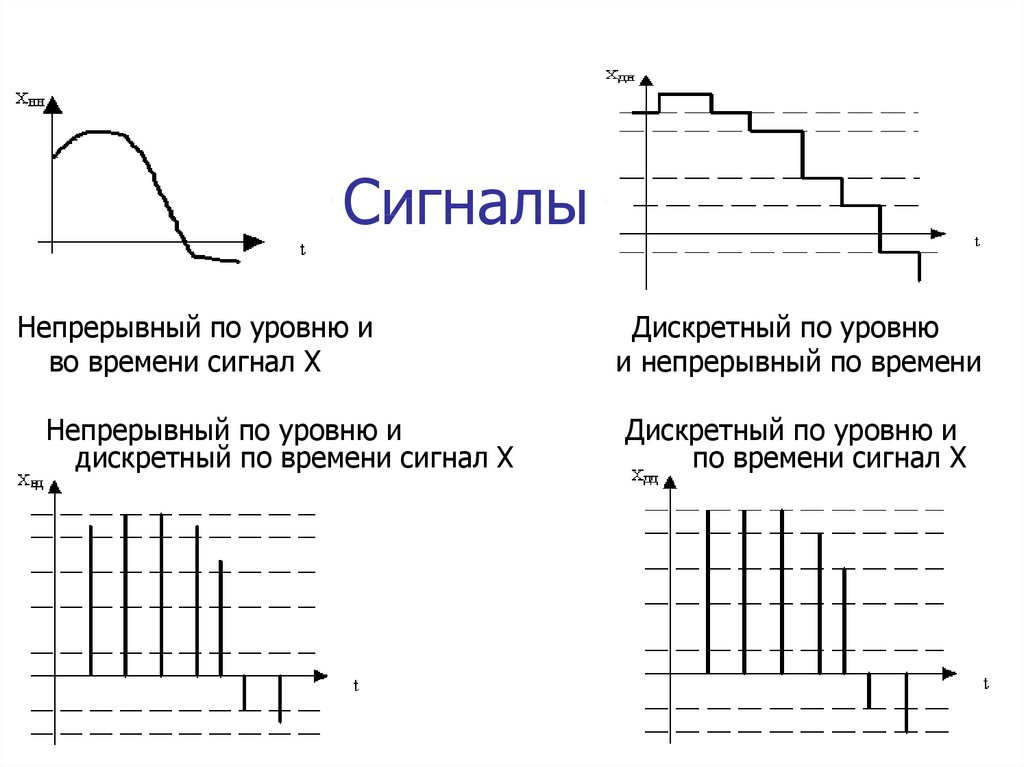 Richard Schreier and Gabor C. Temes, Understanding Delta-Sigma Data Converters , John Wiley and Sons, 2005
Richard Schreier and Gabor C. Temes, Understanding Delta-Sigma Data Converters , John Wiley and Sons, 2005 

