Активная и реактивная составляющие тока. Активная и реактивная мощность в электрических цепях: основные понятия и методы расчета

Что такое активная и реактивная мощность в электрических цепях. Как рассчитываются активная и реактивная составляющие тока. Какие существуют методы компенсации реактивной мощности. Как угловая асимметрия напряжений влияет на расчет мощности.

Активная и реактивная мощность: основные понятия

В электрических цепях переменного тока различают активную и реактивную мощность:

• Активная мощность (P) — это мощность, которая преобразуется в полезную работу или тепло. Измеряется в ваттах (Вт).
• Реактивная мощность (Q) — это мощность, которая циркулирует между источником и нагрузкой, не совершая полезной работы. Измеряется в вольт-амперах реактивных (вар).

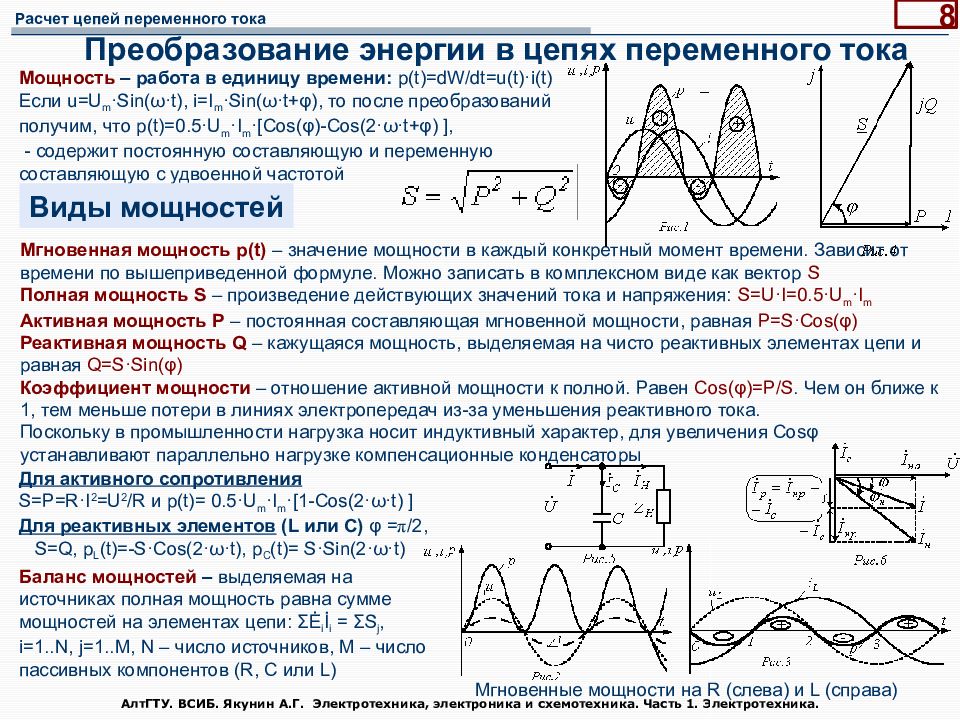
Полная мощность (S) представляет собой векторную сумму активной и реактивной мощностей:

S = √(P² + Q²)

Соотношение между активной и полной мощностью характеризуется коэффициентом мощности cosφ:

cosφ = P / S

Расчет активной и реактивной составляющих тока

Ток в цепи переменного тока можно разложить на активную и реактивную составляющие:

• Активная составляющая тока (Ia) совпадает по фазе с напряжением и определяет активную мощность.
• Реактивная составляющая тока (Ir) сдвинута по фазе на 90° относительно напряжения и определяет реактивную мощность.

Полный ток (I) связан с активной и реактивной составляющими соотношением:

I = √(Ia² + Ir²)

Методы расчета активной и реактивной мощности

Существует несколько подходов к расчету активной и реактивной мощности в электрических цепях:

1. Метод мгновенных значений

При этом методе активная и реактивная мощности определяются по мгновенным значениям напряжения u(t) и тока i(t):

P = (1/T) ∫ u(t)i(t)dt

Q = (1/T) ∫ u(t)i(t-T/4)dt

где T — период сигнала.

2. Метод векторных диаграмм

В этом случае мощности рассчитываются через действующие значения напряжения U и тока I, а также угол сдвига фаз φ между ними:

P = UI cosφ

Q = UI sinφ

3. Метод симметричных составляющих

Для несимметричных трехфазных систем применяется разложение на симметричные составляющие прямой, обратной и нулевой последовательностей. Мощности определяются для каждой последовательности отдельно.

Влияние угловой асимметрии напряжений на расчет мощности

В реальных электрических сетях часто наблюдается угловая асимметрия между векторами фазных напряжений. Это приводит к ошибкам при расчете мощности стандартными методами. Для учета угловой асимметрии применяются следующие подходы:

• Использование отдельных PLL-систем для каждой фазы
• Применение обобщенных методов расчета мгновенной мощности
• Алгоритмы на основе преобразования Кларка и Парка с учетом угловой асимметрии

Точный учет угловой асимметрии особенно важен в микросетях и системах с распределенной генерацией.

Методы компенсации реактивной мощности

Компенсация реактивной мощности позволяет повысить коэффициент мощности и снизить потери в сетях. Основные методы компенсации:

• Применение конденсаторных батарей
• Использование синхронных компенсаторов
• Активные фильтры гармоник
• Статические тиристорные компенсаторы (СТК)
• Активные выпрямители с коррекцией коэффициента мощности

Выбор метода компенсации зависит от характера нагрузки, требуемой скорости регулирования и экономических факторов.

Анализ составляющих мощности с помощью мгновенных векторов

Метод мгновенных векторов позволяет анализировать составляющие мощности в трехфазных системах с несимметричными и искаженными напряжениями и токами. Основные особенности метода:

• Представление трехфазной системы с помощью векторов одной фазы
• Оценка качества электроэнергии по форме траекторий векторов напряжения и тока
• Выделение составляющих основной частоты и прямой последовательности
• Возможность применения для управления компенсаторами реактивной мощности

Метод мгновенных векторов дает наглядное представление о процессах в электрической сети и позволяет разрабатывать эффективные алгоритмы управления.

Проблемы расчета мощности в микросетях

Микросети имеют ряд особенностей, усложняющих расчет и компенсацию реактивной мощности:

• Наличие распределенной генерации на основе возобновляемых источников
• Низкое отношение короткого замыкания
• Значительные колебания параметров режима
• Несимметрия нагрузки по фазам
• Наличие нелинейных нагрузок

Для микросетей требуются адаптивные алгоритмы расчета мощности, учитывающие изменения конфигурации и режима работы системы.

9. Активные и реактивные составляющие токов и напряжений

При расчете электрических цепей переменного тока реальные элементы цепи (при­емники, источники) заменяются эквивалентными схемами замещения, состоящими из ком­бинации идеальных схемных элементов

R, L и С.

Пусть некоторый приемник энергии носит в целом активно-индуктив­ный характер (например, электродвигатель). Такой приемник может быть пред­став­лен двумя простей­шими схемами замещения, состоящими из 2-х схемных эле­ментов R и L: а) последовательной (рис. 53а) и б) параллельной (рис. 53б):

Обе схемы будут эквивалентны друг другу при условии равенства пара­метров ре­жима на входе: , .

Для последовательной схемы (рис. 53а) справедливы соотношения:

,

.

Для параллельной схемы (рис. 53б) справедливы соотношения:

,

.

Сравнивая правые части уравнений для U и I, получим соотношения между пара­метрами эквивалентных схем:

, , , .

Из анализа полученных уравнений следует сделать вывод, что в общем случае и и соответственно и , как это имеет место для цепей постоян­ного тока.

Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.

Последовательной схеме замещения соответствует представление век­тора напряже­ния в виде суммы двух составляющих: активной составляющей U_а, совпадающей с векто­ром тока I, и реактивной составляющей U_р, перпенди­ку­лярной к вектору тока (рис. 54а):

Из геометрии рис. 54а следуют соотношения:

, , .

Треугольник, составленный из векто­ров , , получил назва­ние треугольника напряжений (рис.

54а).

Если стороны треугольника напряжений разделить на ток I, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются полное сопротивление Z, активное сопротивление R и реактивное сопро­тивле­ние X. Треугольник со сторонами Z, R, X называется треугольником со­против­лений (рис. 54б). Из треугольника сопротивлений следуют соотношения: R = Zcosφ, X = Zsinφ, , .

Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей I_а, совпадаю­щей с вектором напряже­ния U, и реактивной составляющей I_р, перпендикуляр­ной к вектору U (рис. 55а).

Из геометрии рисунка следуют соотношения:

, , .

Треугольник, составленный из векторов , , получил название тре­угольника токов (рис.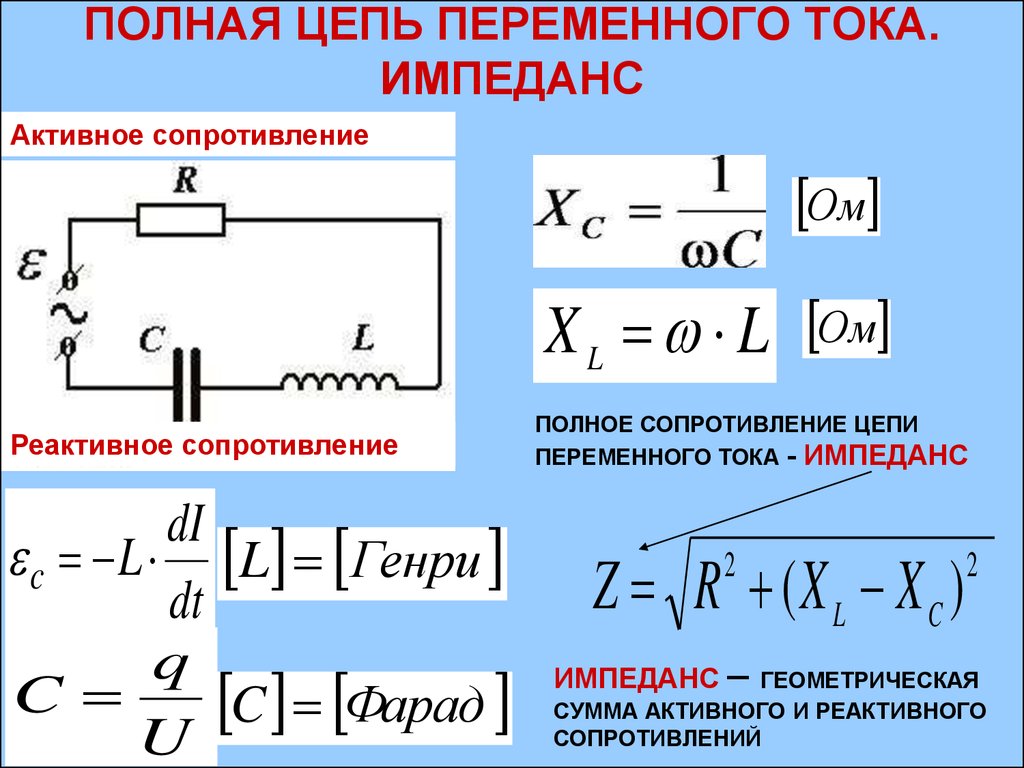 55а).

+1

Если стороны треугольника токов разделить на напряжение U, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются проводимости: пол­ная – Y, активная G, реактивная – B (рис. 55б). Тре­угольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:

, , , .

Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета сравнительно не­сложных цепей пере­менного тока.

Реактивная составляющая — ток — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Реактивная составляющая тока / р / sin 6 определяет реактивную мощность QCT [ Уф 7 sin 8 / ф / р, которую называют намагничивающей мощностью.  [1]

Цепь переменного тока с параллельным соединением элементов. | Треугольники токов. а для р 0. б для р 0.  [2]

Реактивная составляющая тока меняет знак вместе с изменением знака угла ср.  [3]

Реактивная составляющая тока для ветви с г и С также получается отрицательной.  [4]

Реактивная составляющая тока создает продольный магнитный поток, который и является потоком возбуждения машины.  [5]

Реактивная составляющая тока — составляющая, которая в отличие от активной составляющей тока не выделяет энергии в цепи. Это связано с тем, что ток в чисто реактивном сопротивлении сдвинут по фазе на четверть периода по отношению к напряжению, тогда как в чисто активном сопротивлении они совпадают по фазе. В течение той четверти периода, когда напряжение и ток совпадают по знаку и произведение их положительно ( на рис. от до t2), энергия поступает из источника в реактивное сопротивление.  [6]

Реактивная составляющая тока — составляющая, которая в отличие от активной составляющей тока не выделяет энергии в цепи.  [7]

Реактивная составляющая тока — составляющая, которая в отличие от активной составляющей тока не выделяет энергии в цепи. Это связано с тем, что ток в чисто реактивном сопротивлении сдвинут по фазе на четверть периода по отношению к напряжению, тогда как в чисто активном сопротивлении они совпадают по фазе.  [8]

Конструктивные схемы однофазного двигателя с экранированными полюсами и его векторная диаграмма. I — статор, г — обмотка статора, 3 — короткозамкнутый виток, 4 — ротор, 5 — полюс.  [9]

Реактивная составляющая тока / к уменьшает поток Фп2, а активная — смещает его по фазе относительно МДС Fa. Так как поток Фщ не охватывает короткозамкнутый виток, угол YI имеет сравнительно небольшую величину ( 4 — 9) — примерно такую же, как угол сдвига фаз между потоком трансформатора и МДС первичной обмотки в режиме холостого хода.  [10]

Векторная диаграмма.  [11]

С — реактивная составляющая тока, зависящая от емкости диэлектрика; 1Х — полный ток; U — напряжение.  [12]

Было указано, что реактивная составляющая тока первичной обмотки зависит от напряжения сети и индуктивного сопротивления первичной обмотки.  [13]

Выше было указано, что реактивная составляющая тока первичной обмотки зависит от напряжения сети и индуктивного сопротивления первичной обмотки.  [14]

Режим возбуждения СЭМ, при котором реактивная составляющая тока / а равна нулю, называется, режимом полного, или нормального, возбуждения. Такой режим, называется режимом перевозбуждения и используется для компенсации cos t в электрических сетях. Если ток возбуждения / меньше нормального, то / о содержит реактивную составляющую, отстающую на 90 от вектора Ос, что соответствует потреблению машиной реактивной мощности.  [15]

Страницы:      1    2    3    4

Метод компенсации реактивной мощности

Одной из основных задач современной электроэнергетики является симметрирование сетевых напряжений и минимизация потоков реактивной мощности в распределительных сетях. Существует много негативных эффектов, связанных с асимметрией в энергосистемах, таких как повышенные потери в электродвигателях, гармоники, передаваемые в системы постоянного тока, или неравенство фазных токов. С помощью метода компенсации реактивной мощности поток активной мощности может быть уменьшен даже при наличии угловой асимметрии между векторами напряжения коммунальной сети.

1. Введение

Одной из основных задач современной электроэнергетики является симметрирование сетевых напряжений и минимизация потоков реактивной мощности в распределительных сетях. Существует множество негативных эффектов, связанных с асимметрией в энергосистемах, таких как повышенные потери в электродвигателях, гармоники, передаваемые в системы постоянного тока, или неравенство фазных токов [1]. Исследования по четырехпроводным преобразователям и методам компенсации асимметрии напряжения в распределительных сетях уже проводились. Решение, представленное в [2], описывает метод управления инверторами, который характеризуется резистивным поведением при помехах в сети. Искажения напряжения также неразрывно связаны с несимметрией нагрузки. Существуют предложения по компенсации нагрузки при искаженных напряжениях, основанные на теории мгновенных симметричных составляющих с извлечением прямой последовательности [3] или дифференциально вращающихся системах отсчета [4]. Другие подходы связаны с компенсацией тока нейтрали ^[5][6] [5,6] и нечетких нейронных сетей [7]. Однако проблемой, не затронутой в исследованиях ^[7] публикаций, является взаимосвязь между асимметрией фазовых углов и коэффициентом выходной мощности компенсаторов реактивной мощности. Следует подчеркнуть, что нелинейная и асимметричная загрузка распределительных сетей [8,9] вызывает значительную асимметрию напряжения, а также фазовый сдвиг. Эта проблема усугубляется в системах с высоким импедансом короткого замыкания — к ним определенно можно отнести микросети [10,11]. По указанной выше причине требуется разработка методов управления активной и реактивной мощностью в состояниях асимметрии микросети, которые будут невосприимчивы к угловой асимметрии между векторами напряжения.

Распределительная система низкого напряжения характеризуется тем, что к ней подключается большое количество приемников с различными характеристиками [12]. Большинство устройств, подключенных к сети, являются однофазными нагрузками. Все большее их число имеют системы энергоснабжения, основанные на электронных преобразователях [13]. Использование этой технологии вытекает из требований к их размерам, весу и цене. Основная проблема, возникающая при использовании таких преобразователей, заключается в том, что они потребляют ток нелинейным образом [14]. Еще одной проблемой является потребность в реактивной мощности. Из-за представленных факторов ухудшаются параметры электросети ^[15][16] [15,16]. Возникает межфазная асимметрия, увеличиваются суммарные гармонические искажения напряжения (THD) в сети, а увеличение реактивной мощности снижает пропускную способность сети и вызывает падение напряжения. Параметр, который также изменяется, — это угол сдвига фаз между векторами напряжения. Измерения в сетях низкого напряжения с большим количеством потребителей показывают, что фазовые углы несимметричны. Рисунок 1  и Рисунок 2  показывают измерения, выполненные с помощью анализатора качества электроэнергии Kyoritsu KEW6310 (Kyoritsu, Токио, Япония).

Рисунок 1.  Угловая асимметрия между векторами напряжения: измерение опорной сетки.

Рисунок 2.  Угловая асимметрия между векторами напряжения: измерение микросети.

Последующие измерения проводились в микросети, где одна из фаз была сильно загружена. Было замечено, что угловая ошибка становится больше. Асимметрия напряжения между фазой 2 и фазой 3 составляет 11 В. Результаты представлены  Рисунок 2 .

Угловая асимметрия между векторами напряжения оказывает существенное влияние на работу трехфазных систем, содержащих трансформаторы, двигатели и силовые преобразователи. В данной статье рассматривается проблема компенсации реактивной мощности в микросети трехфазным преобразователем при наличии угловых погрешностей. В качестве объекта исследования была выбрана микросетевая система из-за сильного влияния флуктуаций ее параметров на устойчивость и эффективность всей системы. Для решения представленной задачи использовался четырехпроводной трехуровневый преобразователь переменного тока в постоянный. Это решение может быть реализовано, в частности, в радиальных сетях и загородных районах в качестве устройства, поддерживающего параметры электрической сети.

2. Фазонезависимая компенсация реактивной мощности с применением четырехпроводного гибридного преобразователя с пропорционально-резонансными регуляторами

Микросети характеризуются тем, что в их состав входят устройства, работающие как источники тока. Это генераторы на базе двигателей внутреннего сгорания, электрохимические или механические накопители энергии, возобновляемые источники энергии. Все эти устройства связаны друг с другом преобразователями, которые синхронизируются с сетью. Типичная структура такой системы показана на  Рисунок 3 .

Рисунок 3.  ( a ) Типовая структура управления преобразователем, интегрированным с возобновляемыми источниками энергии. ( b ) Блок-схема многорезонансного алгоритма. I ^* _q , I ^* _d — Опорное текущее значение в кадре dq; I _d , I _q —токи обратной связи после преобразования Парка; V _dq — сигналы напряжения в кадре dq; I _{g_abc} , V _{g_abc} — трехфазные мгновенные токи и напряжения. В _{inv_abc} — трехфазные опорные сигналы для модуля ШИМ.

Система трехфазного преобразователя для возобновляемых источников энергии, представленная на Рис.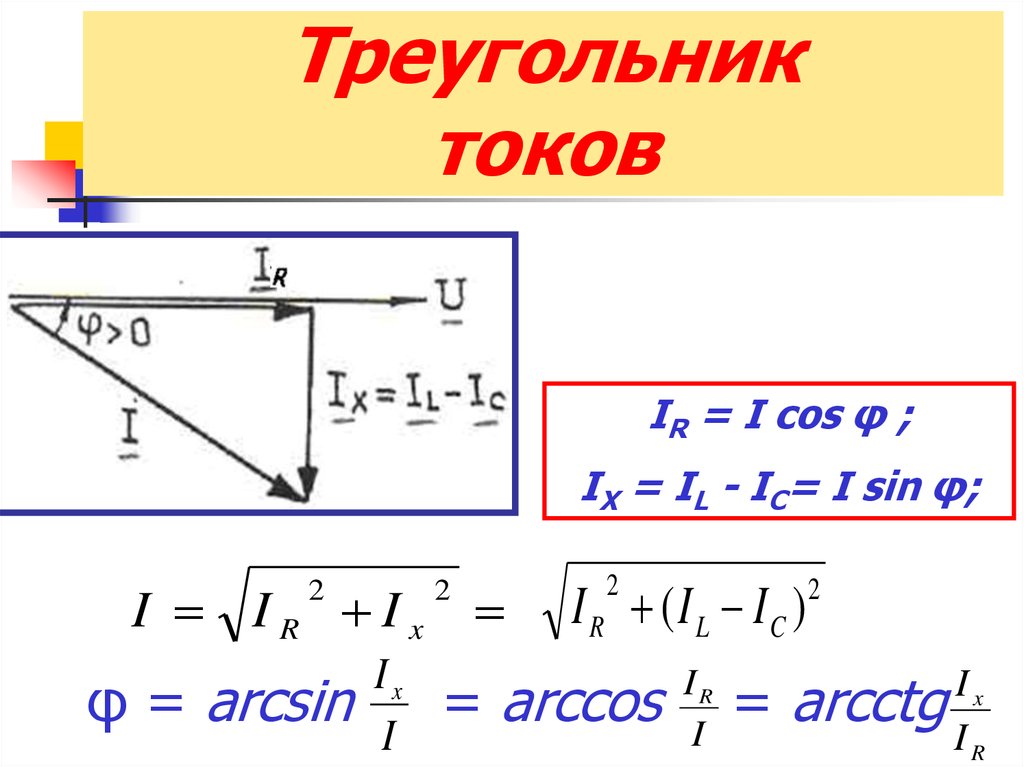 3 , использует системы PLL (петли фазовой автоподстройки частоты) для синхронизации с сетью ^[17][18][19] [17,18,19]. Эти системы можно разделить на системы с системой декомпозиции на симметричные составляющие и без этой функциональности. Общей чертой этих систем является генерация пилообразного сигнала, общего для трех фаз, который отображает фактический угол вектора напряжения сети. К сожалению, системы ФАПЧ, используемые в трехфазных преобразователях, подключенных к микросети, не удовлетворяют надлежащим требованиям синхронизации, связанным с угловой асимметрией между отдельными фазами. Когда эта асимметрия не обнаружена, нежелательное количество энергии будет потребляться или поставляться преобразователями, подключенными к системе микросетей. Следует подчеркнуть, что микросети загружены несимметрично. В результате значение активной и реактивной мощности в каждой из фаз различно. Поэтому разработанный компенсатор реактивной мощности должен обеспечивать фазонезависимую компенсацию реактивной мощности при наличии угловой асимметрии между векторами напряжения. 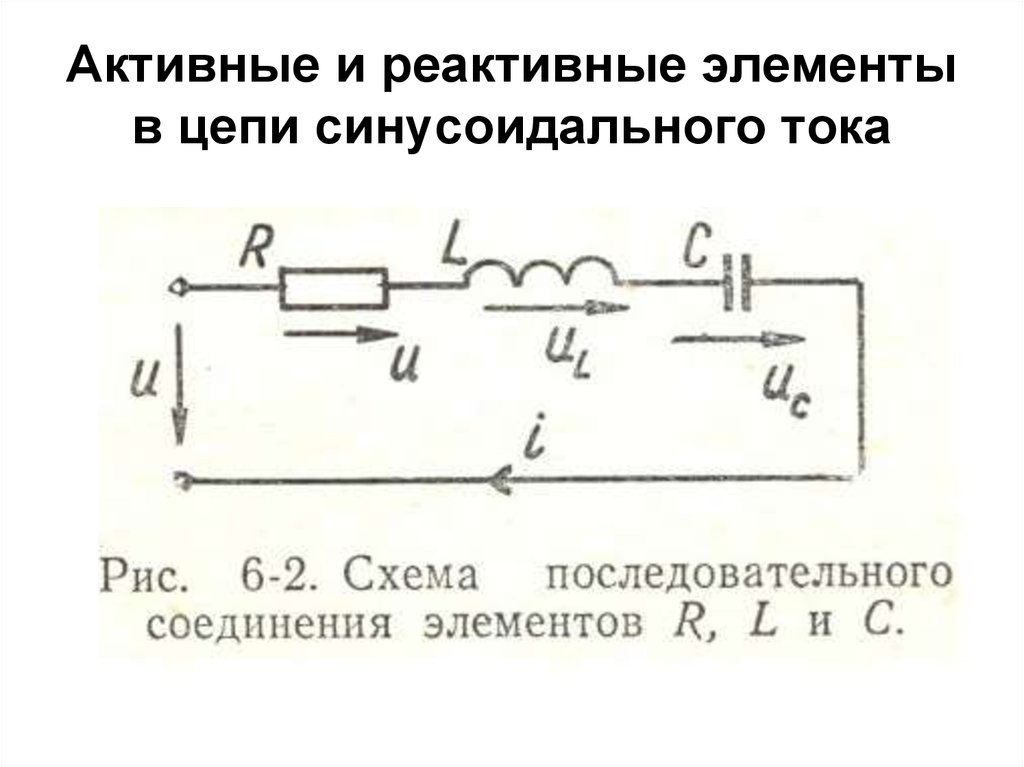Этот тип работы может быть достигнут путем замены классической системы расчета синхронизации и мощности, основанной на классической теории мгновенной мощности, решением, учитывающим фазовые углы отдельных фаз. Система дополняется использованием преобразовательной системы, позволяющей осуществлять независимое регулирование мощности по каждой из фаз, несмотря на наличие возмущений параметров микросети. Блок-схема многорезонансного алгоритма представлена ​​на Рисунок 3 а.

Предлагаемое решение представляет собой четырехпроводной преобразователь переменного тока в постоянный ( рис. 4 ). Его построение основано на трехуровневой топологии Т-типа ^[20][21][22] [20,21,22]. Четвертая ветвь действует как нейтральный провод и обеспечивает независимую от фазы компенсацию реактивной мощности. Это решение реализуется последовательным соединением конденсаторов Сх1 и Сх2. В результате напряжение шины постоянного тока делится на две части. Применение увеличенной емкости на шине постоянного тока улучшает работу системы в динамических состояниях. В этом контексте можно рассматривать использование суперконденсаторов ^[23][24] [23,24]. Индуктивность LN включена между нейтралью и транзисторами Q13–Q14. Это подключение позволяет активную стабилизацию напряжения на разделенной шине постоянного тока. На выходе преобразователя используется индуктивно-емкостно-индуктивный (LCL) фильтр, настроенный на устранение помех от переключающих транзисторов.

Рис. 4.  Гибридный преобразователь в трехфазной трехуровневой четырехпроводной конфигурации для обеспечения независимой от фазы компенсации реактивной мощности.

В связи с тем, что каждая фаза преобразователя управляется независимо, для дальнейшего анализа система управления рассматривалась как однофазная. Впоследствии в ходе моделирования система была расширена до трех фаз.

Основной проблемой, которая не упоминается в литературе, является правильная синхронизация с несбалансированными фазовыми углами и правильный расчет величины выходных токов преобразователя. В базовом методе используется контур фазовой автоподстройки частоты трехфазного синхронного опорного кадра (SRF-PLL) ^[25][26] [25,26]. Метод синхронизации генерирует пилообразный сигнал θ, который имеет значение фазового угла в диапазоне от 0 до 2π.

Угол синхронизации θ используется для расчета значений активного и реактивного тока в кадре dq. Этот расчет реализуется в два этапа: первый заключается в пропускании текущего сигнала через фильтр обобщенного интегратора второго порядка (SOGI), который сдвигает измеренную фазу на 90 градусов на ^[27][28] [27,28]. . Второй – генерация активной и реактивной составляющих тока с помощью преобразования Парка, основанного на предварительно рассчитанном сигнале PLL и сигнале фазного тока.

Метод, представленный в  Рисунок 5 a, прост и эффективен, но приводит к ошибкам расчета тока, если векторы напряжения слабой коммунальной сети больше не смещены на 120 градусов. На рисунке 6 представлены значения сигналов dq в зависимости от угла синхронизации. Решение, позволяющее устранить эти ошибки, представлено на , рис. 5 b. Вместо расчета трех сигналов со сдвигом на 120 градусов с помощью одной системы ФАПЧ используются три отдельные системы ФАПЧ для независимого расчета правильного угла напряжения в каждой фазе. В этом случае проблема, представленная в Рисунок 6  больше не существует: рассчитанные токи являются основой контура управления активным и реактивным током.

Рисунок 5.  Метод расчета активной и реактивной мощности. ( a ) Система со стандартным трехфазным сигналом PLL. ( b ) Система с тремя отдельными сигналами PLL, которая является предлагаемым методом при наличии угловой асимметрии между векторами напряжения.

Рисунок 6.  Изменения компонентов d и q на выходе преобразования Парка в зависимости от фазового угла.

Компоненты активной мощности мгновенных векторов (Конференция)

Компоненты активной мощности мгновенных векторов (Конференция) | ОСТИ.GOV

перейти к основному содержанию

• Полная запись
• Другое связанное исследование

Метод мгновенных векторов, предложенный автором для определения качества электроэнергии и эффективности трехфазных систем с несимметричными и искаженными напряжениями и токами, обладает уникальным свойством симметрии. Векторы одной фазы могут использоваться для представления трех фаз. О качестве электроэнергии трехфазной системы можно судить по округлости траекторий векторов напряжения и тока. Компоненты основной частоты и положительной последовательности непосредственно предыдущего цикла могут быть получены для управления компенсацией текущих значений. Этот подход к улучшению качества электроэнергии отличается от недавней разработки мгновенной реактивной мощности. В данной работе исследуются составляющие активной мощности мгновенных векторов.

Авторов:

Хсу, Дж. С.

Дата публикации:

1998-08-01

Исследовательская организация:

Национальная лаборатория Ок-Ридж. (ORNL), Ок-Ридж, Теннесси (США)

Организация-спонсор:

Управление энергетических исследований Министерства энергетики США, Вашингтон, округ Колумбия (США)

Идентификатор ОСТИ:

666287

Номер(а) отчета:

ОРНЛ/СР-96303; КОНФ-981021-
ПО: DE98007182; РНН: AHC29819%%447

Номер контракта с Министерством энергетики:  

АК05-96ОР22464

Тип ресурса:

Конференция

Отношение ресурсов:

Конференция: Ежегодное собрание Института инженеров по электротехнике и электронике (IEEE)/Общества отраслевых приложений (IAS), Сент-Луис, Миссури (США), 12 октября 1998; Другая информация: PBD: [1998]

Страна публикации:

США

Язык:

Английский

Тема:

24 ПЕРЕДАЧА И РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ; ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ; СИСТЕМЫ РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ; ЭЛЕКТРОЭНЕРГИЯ; КОНТРОЛЬ КАЧЕСТВА; ЭНЕРГОЭФФЕКТИВНОСТЬ

---

Форматы цитирования

• MLA
• АПА
• Чикаго
• БибТекс

Хсу, Дж. С. Компоненты активной мощности мгновенных векторов . США: Н. П., 1998. Веб.

Копировать в буфер обмена

Хсу, Дж. С. Компоненты активной мощности мгновенных векторов . Соединенные Штаты.

Копировать в буфер обмена

Хсу, Дж. С. 1998. «Компоненты активной мощности мгновенных векторов». Соединенные Штаты. https://www.osti.gov/servlets/purl/666287.

Копировать в буфер обмена

@статья{osti_666287,
title = {Компоненты активной мощности мгновенных векторов},
автор = {Хсу, Дж. С},
abstractNote = {Метод мгновенного фазора, созданный автором для определения качества электроэнергии и эффективности трехфазных систем с несимметричными и искаженными напряжениями и токами, обладает уникальным симметричным свойством. Векторы одной фазы могут использоваться для представления трех фаз. О качестве электроэнергии трехфазной системы можно судить по округлости траекторий векторов напряжения и тока. Компоненты основной частоты и положительной последовательности непосредственно предыдущего цикла могут быть получены для управления компенсацией текущих значений. Этот подход к улучшению качества электроэнергии отличается от недавней разработки мгновенной реактивной мощности. В статье исследуются компоненты активной мощности мгновенных векторов.},
дои = {},
URL-адрес = {https://www.osti.gov/biblio/666287}, журнал = {},
номер =,
объем = ,
место = {США},
год = {1998},
месяц = ​​{8}
}

Копировать в буфер обмена

---

Просмотр конференции (1,33 МБ)

Дополнительную информацию о получении полнотекстового документа см. в разделе «Доступность документа».