Что такое активное сопротивление в электрической цепи. Как рассчитывается индуктивное сопротивление проводников. Каковы особенности емкостной проводимости линий электропередач. Как эти параметры влияют на работу электрических сетей.
Активное сопротивление проводников: сущность и расчет
Активное сопротивление является ключевым параметром электрических цепей, определяющим потери энергии в проводниках. Это свойство материала препятствовать прохождению электрического тока, преобразуя его энергию в тепло.
Для проводов из цветных металлов (медь, алюминий) активное сопротивление рассчитывается по формуле:
R = ρ * l / S
где:
- R — активное сопротивление, Ом
- ρ — удельное сопротивление материала, Ом*мм²/м
- l — длина проводника, м
- S — площадь поперечного сечения, мм²
Активное сопротивление зависит от температуры. При нагреве проводника его сопротивление увеличивается. Это учитывается формулой:
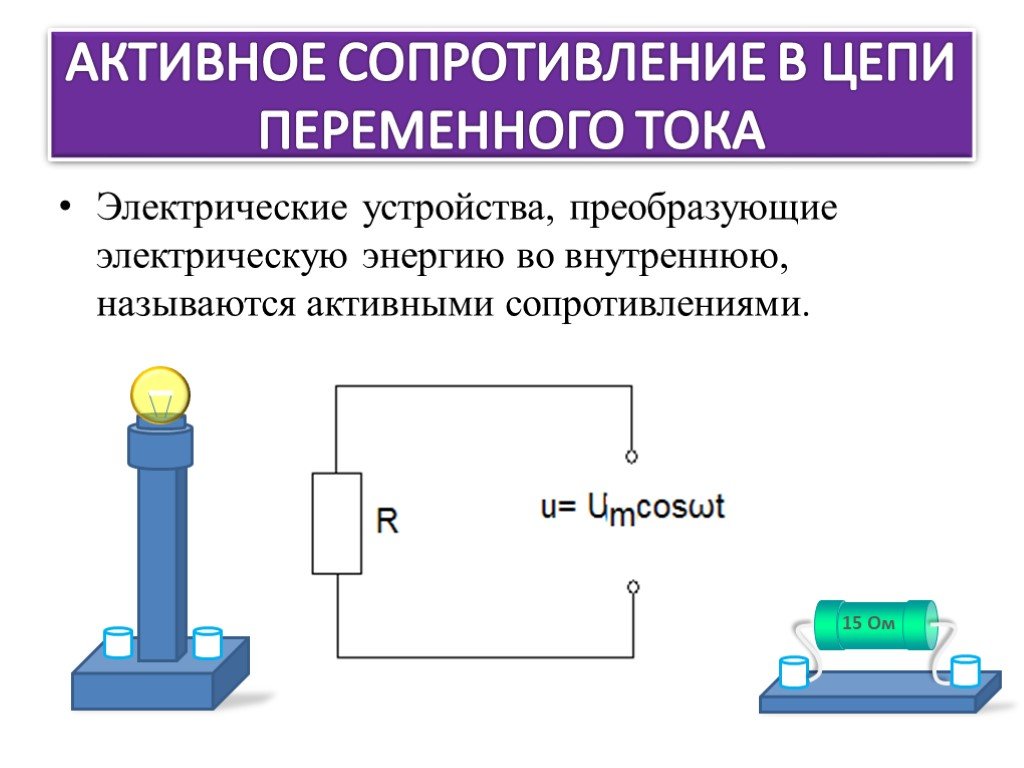
Rt = R20 * (1 + α * (t — 20))
где α — температурный коэффициент сопротивления материала.
Индуктивное сопротивление: природа и особенности
Индуктивное сопротивление возникает в проводниках при протекании переменного тока из-за явления самоиндукции. Оно препятствует изменению тока, но не вызывает потерь энергии.
Индуктивное сопротивление катушки рассчитывается по формуле:
XL = ω * L = 2π * f * L
где:
- XL — индуктивное сопротивление, Ом
- ω — угловая частота, рад/с
- f — частота тока, Гц
- L — индуктивность катушки, Гн
Индуктивное сопротивление линий электропередач зависит от их геометрических параметров и частоты тока. Для воздушных линий оно обычно составляет 0,3-0,4 Ом/км при частоте 50 Гц.
Емкостная проводимость в электрических сетях
Емкостная проводимость обусловлена наличием электрической емкости между проводами линий электропередачи, а также между проводами и землей. Она вызывает появление в сети емкостных токов.
Емкостная проводимость линии рассчитывается по формуле:

B = ω * C = 2π * f * C
где:
- B — емкостная проводимость, См
- C — емкость линии, Ф
Емкостная проводимость особенно важна для линий высокого и сверхвысокого напряжения, где она может существенно влиять на режимы работы сети.
Влияние активного и реактивного сопротивлений на работу электрических цепей
Активное и реактивные (индуктивное и емкостное) сопротивления в совокупности определяют полное сопротивление цепи переменного тока:
Z = √(R² + (XL — XC)²)
Это полное сопротивление влияет на:
- Величину тока в цепи
- Потери напряжения и мощности
- Коэффициент мощности
- Возможность возникновения резонансных явлений
Особенности расчета сопротивлений для кабельных и воздушных линий
- Материал проводников (медь, алюминий, сталь)
- Конструкция линии (воздушная, кабельная)
- Геометрические параметры (сечение проводов, расстояние между ними)
- Частота тока
- Температура окружающей среды
Для воздушных линий индуктивное сопротивление обычно больше, чем для кабельных, из-за большего расстояния между проводами. Емкостная проводимость, напротив, выше у кабельных линий.

Методы снижения потерь в электрических сетях
Для снижения потерь в электрических сетях применяются следующие методы:
- Увеличение сечения проводов для снижения активного сопротивления
- Применение проводов из материалов с низким удельным сопротивлением
- Компенсация реактивной мощности для снижения токов в линиях
- Оптимизация конфигурации сети
- Повышение номинального напряжения сети
Современные тенденции в расчетах и оптимизации электрических сетей
В настоящее время расчеты электрических сетей все чаще выполняются с использованием специализированного программного обеспечения, позволяющего учесть множество факторов и провести комплексный анализ режимов работы сети.
Актуальными направлениями оптимизации являются:
- Применение технологий Smart Grid для интеллектуального управления сетями
- Интеграция возобновляемых источников энергии
- Использование накопителей энергии для сглаживания нагрузки
- Развитие систем мониторинга и диагностики состояния линий электропередачи
Заключение: важность учета всех видов сопротивлений в электрических сетях
Комплексный учет активных и реактивных сопротивлений, а также емкостной проводимости, критически важен для:

- Точного расчета режимов работы электрических сетей
- Минимизации потерь электроэнергии
- Обеспечения надежности электроснабжения
- Оптимального проектирования новых и модернизации существующих электрических сетей
Понимание природы и взаимосвязи различных видов сопротивлений позволяет инженерам-электрикам принимать обоснованные решения при разработке и эксплуатации систем электроснабжения.
Активное и индуктивное сопротивление | У электрика.ру
 Различные факторы играют важную роль для вычисления потерь в линиях транспортировки электрической энергии. Для постоянного тока вполне хватает стандартных данных об омическом сопротивлении. А вот для цепей переменной разновидности необходимо учитывать активное и индуктивное сопротивление в сочетании с емкостной проводимостью токопроводников.
Различные факторы играют важную роль для вычисления потерь в линиях транспортировки электрической энергии. Для постоянного тока вполне хватает стандартных данных об омическом сопротивлении. А вот для цепей переменной разновидности необходимо учитывать активное и индуктивное сопротивление в сочетании с емкостной проводимостью токопроводников.
Можно воспользоваться для вычислений специальными таблицами. В них представлены с большой точностью различные варианты для выполнения расчетов в сетях переменного тока. Но, чтобы быстро разобраться в специфике представленных характеристик, желательно знать природу подобного явления и его основные характеристики.
Особенности активного сопротивления
В общем виде данный параметр выглядит, как противодействие определенного участка цепи проходящему по нему току. Полученная в результате такого процесса величина участвует в преобразовании энергии и ее переходе в какое-то другое состояние.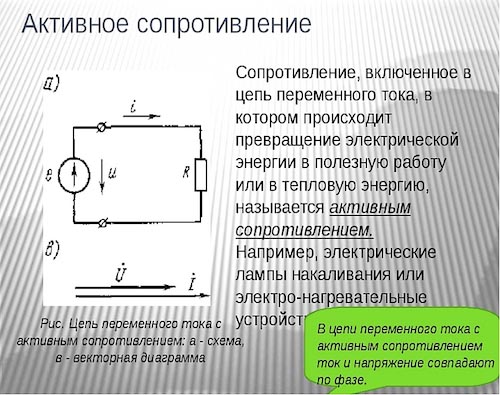
Важно! Это явление наблюдается исключительно в ситуациях с переменным током. Только он способен образовывать в кабелях оба вида противодействия.
Величина активного сопротивления обусловлена эффектом поверхностного типа. Наблюдается процесс своеобразного перемещения тока от центра к поверхности проводника. Сечение кабеля используется не полностью, а возникающее противодействие будет значительно превышать аналогичный омический показатель.
Обратим внимание на такой момент:
- Поверхностный эффект имеет незначительную величину в линиях из металлов, относящихся к категории цветных. Активное сопротивление приравнивают к омическому и считают его при условной температуре в +20°С, без учета фактических показателей окружающей среды. В справочниках имеются данные определения для использования в основном выражении R=r0l, с учетом того, что r0 – это номинальное значение искомой величины для 1 км провода, а l – его фактическая протяженность.
- А вот в стальных изделиях данный показатель намного выше. Обязательно потребуется брать во внимание, зависящее от сечения явление перемагничивания и влияние таких компонентов, как вихревые токи. На практике обычно при больших нагрузках пользуются справочными данными. При этом, само явление ослабевает в проводниках многопроволочного типа.
Индуктивное сопротивление
Созданное в ходе передачи энергии переменное магнитное поле становится источником реактивного сопротивления подобного вида. Индуктивный вариант в основном зависит от характеристик проходящего тока, диаметра и расстояния между проводами.Само сопротивление обычно классифицируют следующим образом:
- зависящее от параметров тока и материала — внутреннее;
- обусловленное геометрическими особенностями линии — внешнее. В этом случае данный показатель будет постоянной величиной, не зависящей от каких-либо других факторов.
Заводы по производству кабельной продукции всегда указывают в своих каталогах информацию об индуктивном сопротивлении.
Данный параметр обычно определяется следующим выражением:

в котором индуктивный показатель для 1 км провода – , а L – протяженность.
Х километрового участка рассчитывается по следующей формуле:

Где: Dср – расстояние среднее по центральной оси имеющихся проводов, мм; d – диаметр рабочего токопроводника, мм; μт –относительная магнитная проницаемость.
Принцип действия индуктивного сопротивления линий
Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.
Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.
Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение 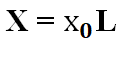
Емкостная проводимость
Одним из эксплуатационных показателей остается данный параметр, обозначающий емкость между проводниками и землей, а также аналогичный показатель между самими токопроводниками.
Для его определения в трехфазной линии воздушных передач применяется выражение: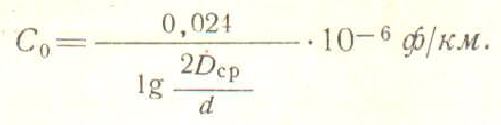
Можно увидеть прямую зависимость рабочей емкости от уменьшения расстояния между кабелями и их сечения. Следовательно, для линий низкого напряжения данная величина всегда будет больше, чем для высокого.
Проводимость подобного вида в воздушных линиях одноцепной конструкции рассчитывается так: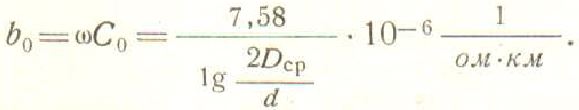 Токи емкостного происхождения существенно влияют на работу линий с рабочими характеристиками напряжения лот 110 кВ и более, а также в магистралях уложенными кабелями с идентичными параметрами выше 10 кВ.
Токи емкостного происхождения существенно влияют на работу линий с рабочими характеристиками напряжения лот 110 кВ и более, а также в магистралях уложенными кабелями с идентичными параметрами выше 10 кВ.
Попытка применить именно подобный способ для самостоятельного выполнения будет весьма непростой задачей, ведь в нем применяются и различные конструктивные нюансы типа геометрических характеристик, и диэлектрическая проницаемость изоляционного слоя, и многие другие вводные. Следовательно, оптимальным решением будет информация из таблиц, составленных производителями для конкретной марки кабеля. В каталогах все данные приведены с учетом номинального напряжения для каждой модификации.
Для начала линии, когда мы имеем дело с холостым ходом, емкостный ток определяется так:
Данный показатель будет объективным только при полностью обесточенных приемниках электричества.
Большое значение обозначенная емкость в любой рассматриваемой конструкции имеет для точного выполнения предварительных расчетов для устройств компонентов защиты и элементов заземления.
Для воздушной линии действительна такая формула: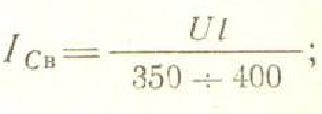
Для кабельных магистралей: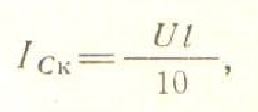
Поделиться ссылкой:
Похожее
|
Емкостное сопротивление в цепи переменного тока |
|
|
При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |
|
|
Мгновенное значение напряжения равно Мгновенное значение силы тока равно: Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2. |
|
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: |
|
|
Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). |
|
|
Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). |
|
|
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. |
|
|
Индуктивное сопротивление в цепи переменного тока |
|
|
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. |
|
|
Мгновенное значение силы тока: |
|
|
Мгновенное значение напряжения можно установить, учитывая, что u = — εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. |
|
|
Следовательно Напряжение опережает ток по фазе на π/2. |
|
|
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой. |
|
|
Величина |
|
|
Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. |
|
|
В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. |
|
|
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
|
57. Активное, индуктивное и емкостное сопротивление.
Активным
сопротивлением R
называется физическая величина, равная
отношению мощности к квадрату силы тока
,
что получается из выражения для мощности
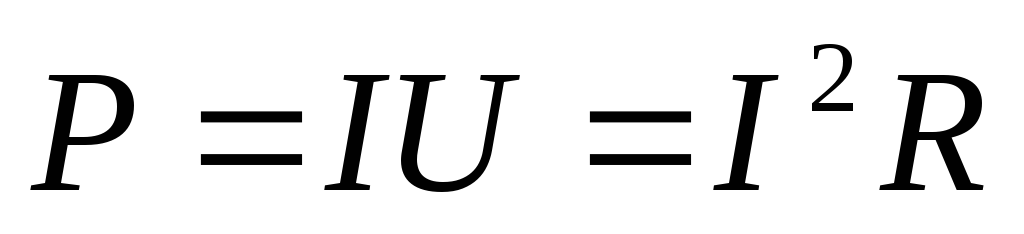 .
При небольших частотах практически не
зависит от частоты и совпадает с
электрическим сопротивлением проводника.
.
При небольших частотах практически не
зависит от частоты и совпадает с
электрическим сопротивлением проводника.
Пусть
в цепь переменного тока включена катушка.
Тогда при изменении силы тока по закону
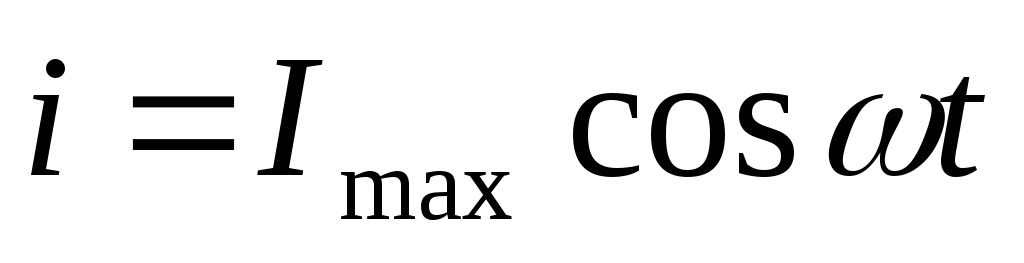 в
катушке возникает ЭДС самоиндукции
в
катушке возникает ЭДС самоиндукции
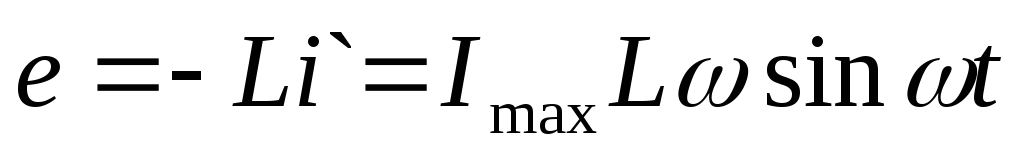 .
Т.к. электрическое сопротивление катушки
равно нулю, то ЭДС равна минус напряжению
на концах катушки, созданному внешним
генератором (???
Каким еще генератором???)
.
Т.к. электрическое сопротивление катушки
равно нулю, то ЭДС равна минус напряжению
на концах катушки, созданному внешним
генератором (???
Каким еще генератором???)
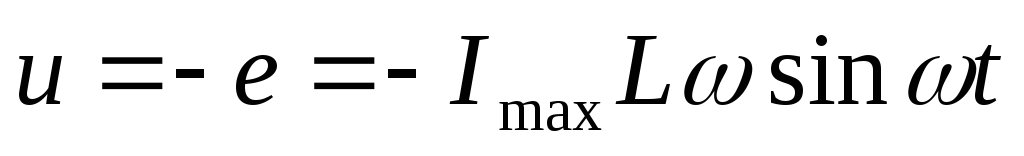 .
Следовательно, изменение силы тока
вызывает изменение напряжения, но со
сдвигом по фазе
.
Следовательно, изменение силы тока
вызывает изменение напряжения, но со
сдвигом по фазе
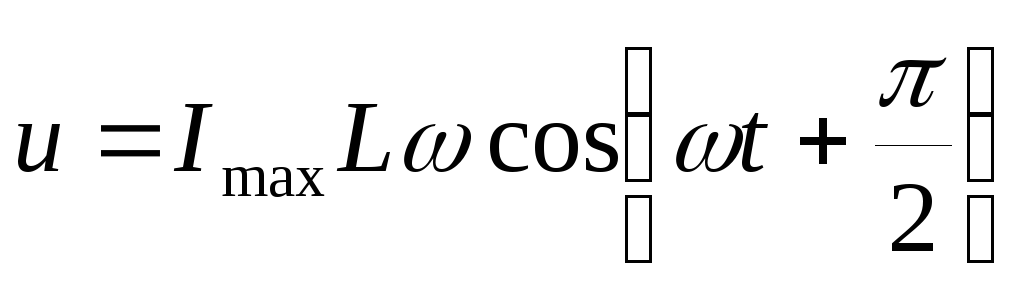 .
Произведение
.
Произведение
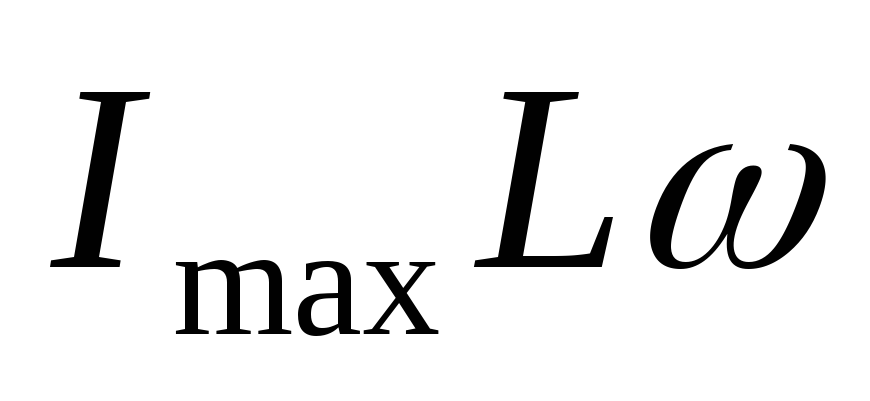 является амплитудой колебаний напряжение,
т.е.
является амплитудой колебаний напряжение,
т.е.
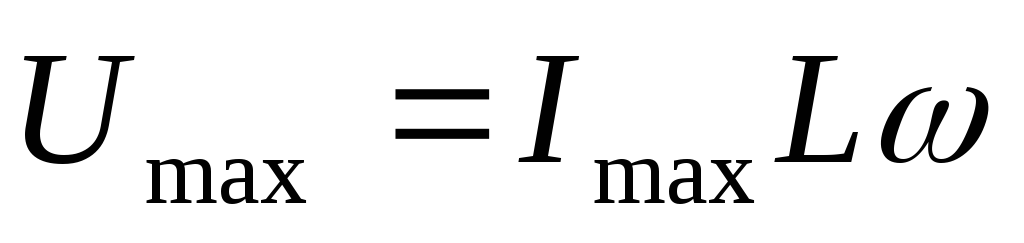 .
Отношение амплитуды колебаний напряжения
на катушке к амплитуде колебаний тока
называется индуктивным сопротивлением
.
Отношение амплитуды колебаний напряжения
на катушке к амплитуде колебаний тока
называется индуктивным сопротивлением
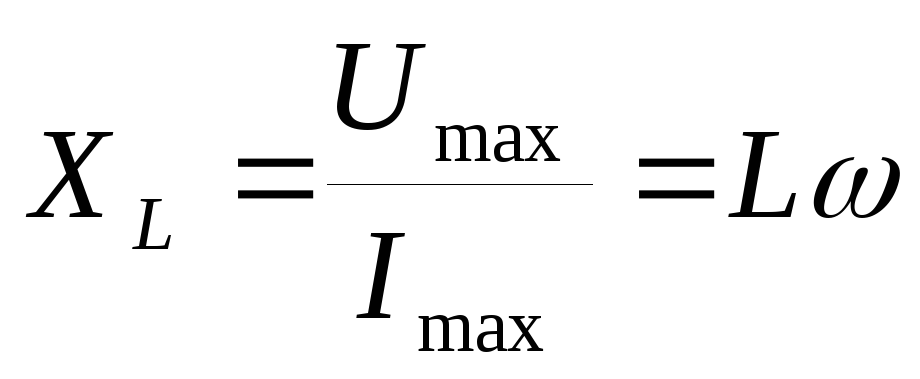 .
.
Пусть
в цепи находится конденсатор. При его
включение он четверть периода заряжается,
потом столько же разряжается, потом то
же самое, но со сменой полярности. При
изменении напряжения на конденсаторе
по гармоническому закону
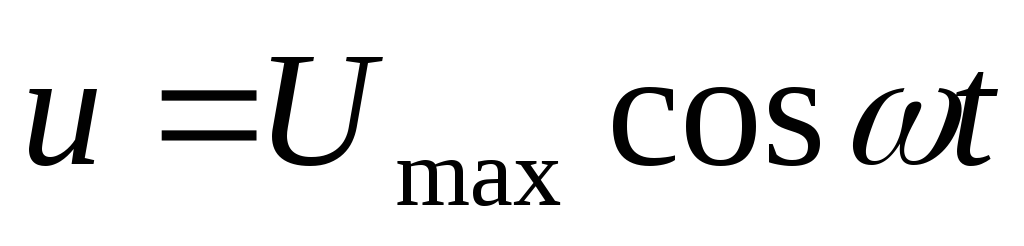 заряд на его обкладках равен
заряд на его обкладках равен
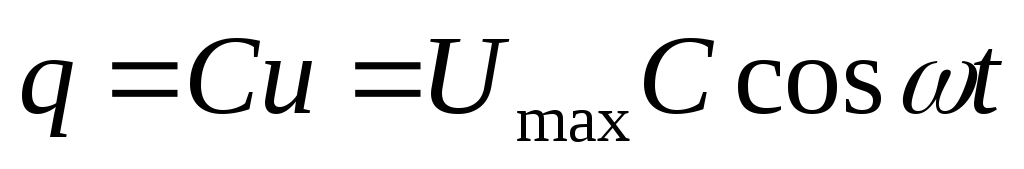 .
Ток в цепи возникает при изменении
заряда:
.
Ток в цепи возникает при изменении
заряда:
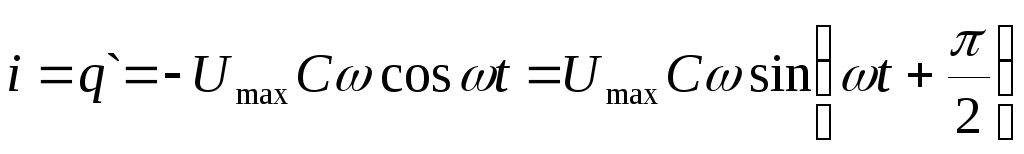 , аналогично случаю с катушкой амплитуда
колебаний силы тока равна
, аналогично случаю с катушкой амплитуда
колебаний силы тока равна
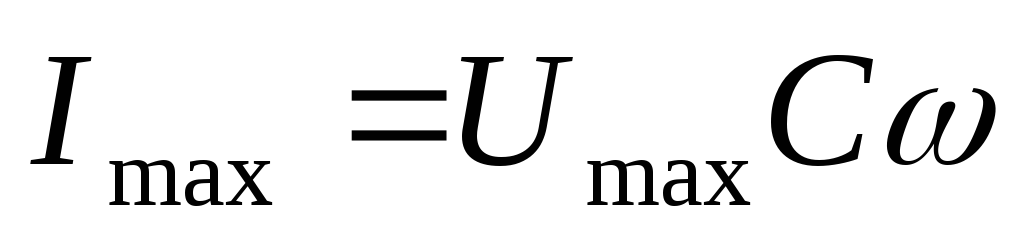 .
Величина, равная отношению амплитуды
к силе тока, называется емкостным
сопротивлением
.
Величина, равная отношению амплитуды
к силе тока, называется емкостным
сопротивлением
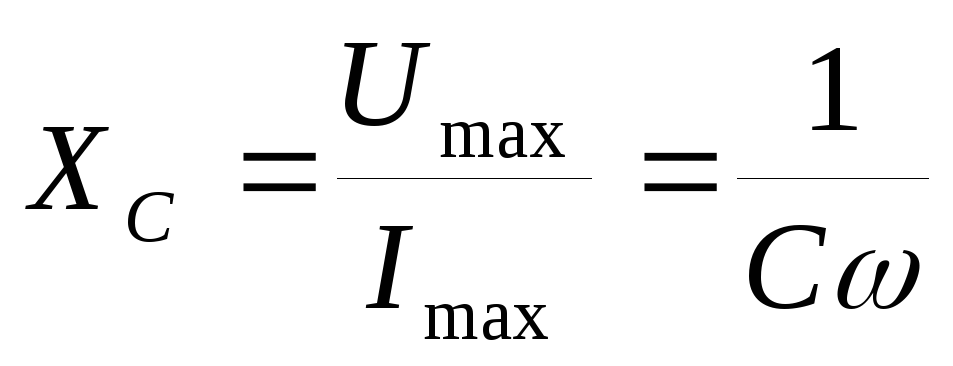 .
.
58. Закон Ома для переменного тока.
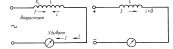
Рассмотрим
цепь, состоящую из последовательно
подключенных резистора, катушки и
конденсатора. В любой момент времени
приложенное напряжение равно сумме
напряжений на каждом элементе. Колебания
силы тока во всех элементах происходят
по закону
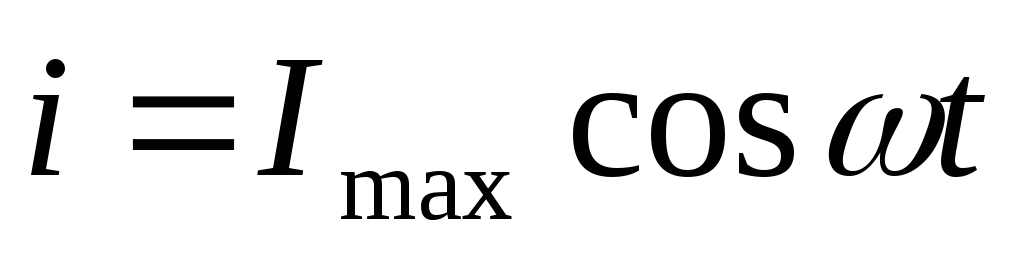 .
Колебания напряжения на резисторе
совпадают по фазу с колебаниями силы
тока, колебания напряжения на конденсаторе
отстают по фазе на
.
Колебания напряжения на резисторе
совпадают по фазу с колебаниями силы
тока, колебания напряжения на конденсаторе
отстают по фазе на
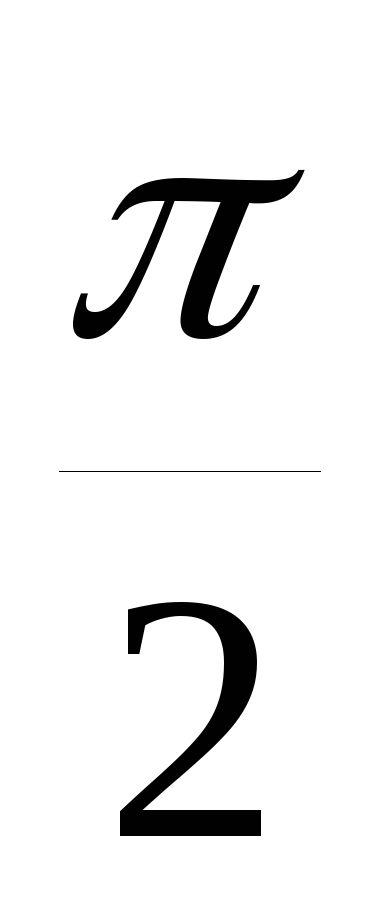 от колебаний тока, колебания напряжения
на катушке опережают по фазе колебания
тока на
от колебаний тока, колебания напряжения
на катушке опережают по фазе колебания
тока на
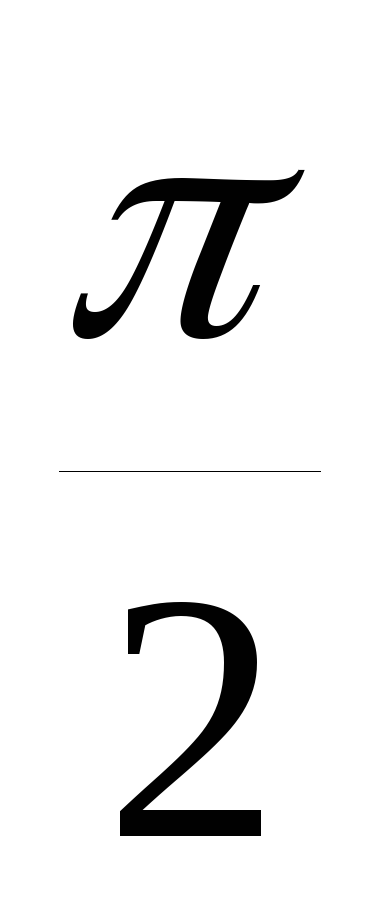 (почему
отстают-то???).
Поэтому условие равенства суммы
напряжений общему можно записать как
(почему
отстают-то???).
Поэтому условие равенства суммы
напряжений общему можно записать как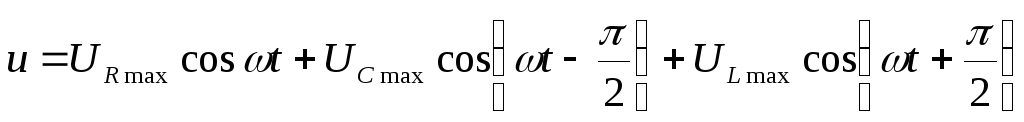 .
Воспользовавшись векторной диаграммой,
можно увидеть, что амплитуда напряжений
в цепи равна
.
Воспользовавшись векторной диаграммой,
можно увидеть, что амплитуда напряжений
в цепи равна
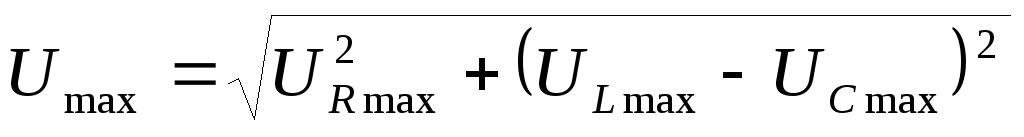 ,
или
,
или
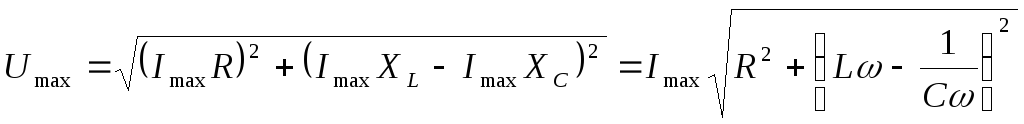 ,
т.е.
,
т.е.
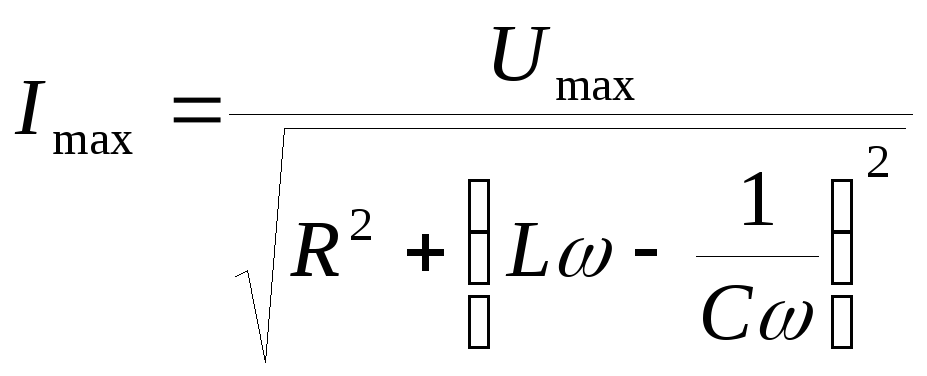 .
Полное сопротивление цепи обозначают
.
Полное сопротивление цепи обозначают
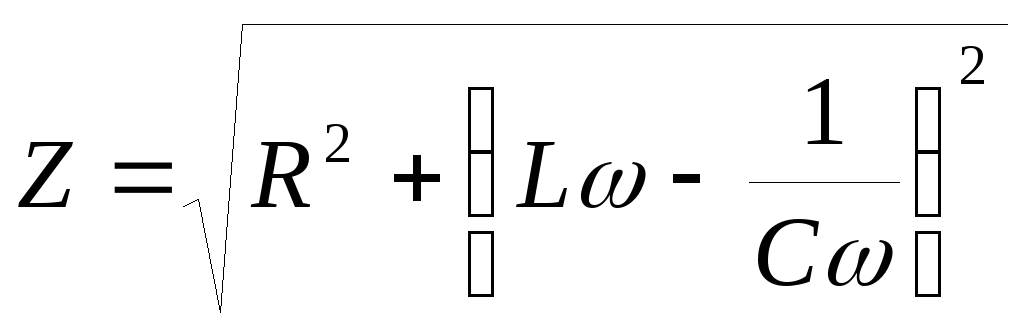 .
Из диаграммы очевидно, что напряжение
также колеблется по гармоническому
закону
.
Из диаграммы очевидно, что напряжение
также колеблется по гармоническому
закону
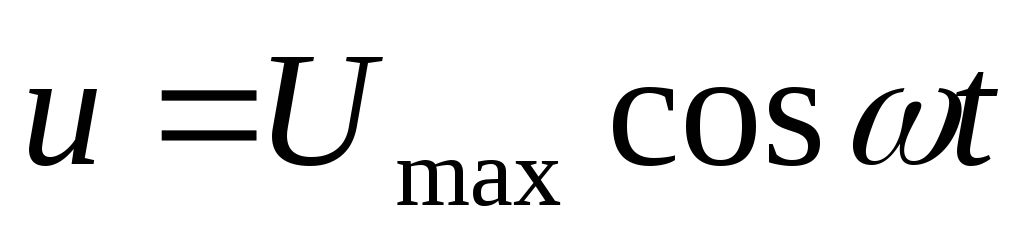 .
Начальную фазу
можно найти по формуле.
Мгновенная мощность в цепи переменного
тока равна
.
Начальную фазу
можно найти по формуле.
Мгновенная мощность в цепи переменного
тока равна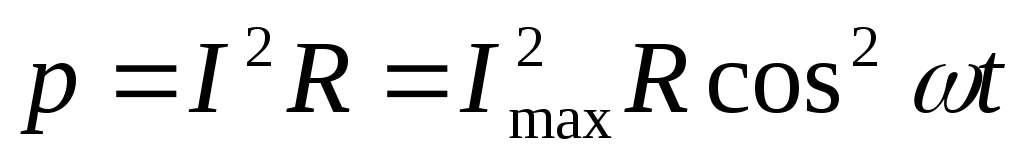 .
Поскольку среднее значение квадрата
косинуса за период равно 0.5,
.
Поскольку среднее значение квадрата
косинуса за период равно 0.5,
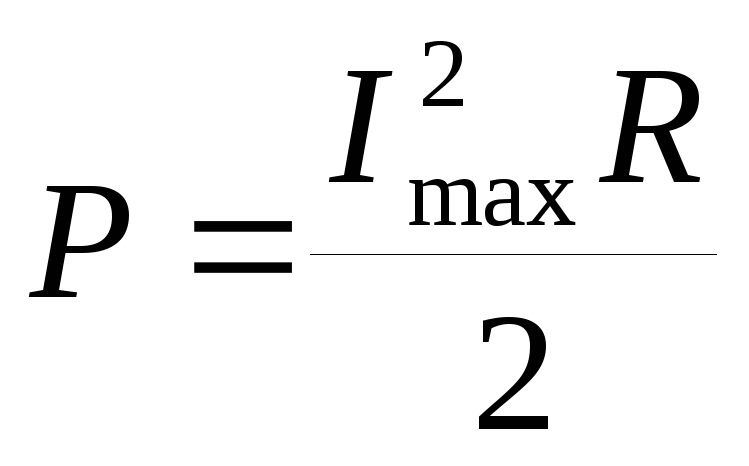 .
Если в цепи присутствует катушка и
конденсатор, то по закону Ома для
переменного тока
.
Если в цепи присутствует катушка и
конденсатор, то по закону Ома для
переменного тока
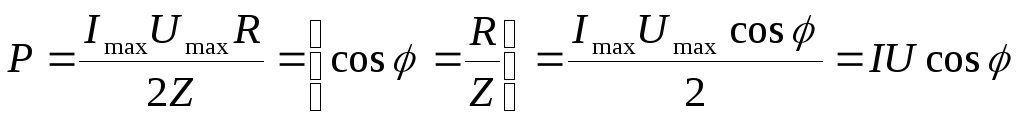 .
Величина
.
Величина
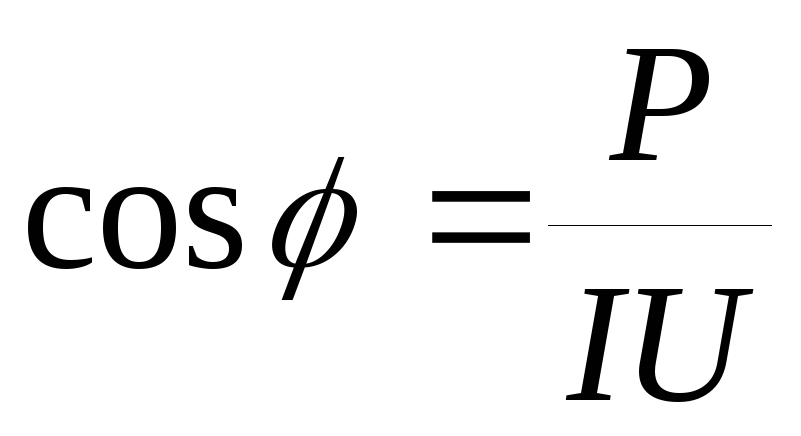 называется коэффициентом мощности.
называется коэффициентом мощности.
59. Резонанс в электрической цепи.
Емкостное
и индуктивное сопротивления зависят
от частоты приложенного напряжения.
Поэтому при постоянной амплитуде
напряжения амплитуда силы тока зависит
от частоты. При таком значении частоты,
при котором
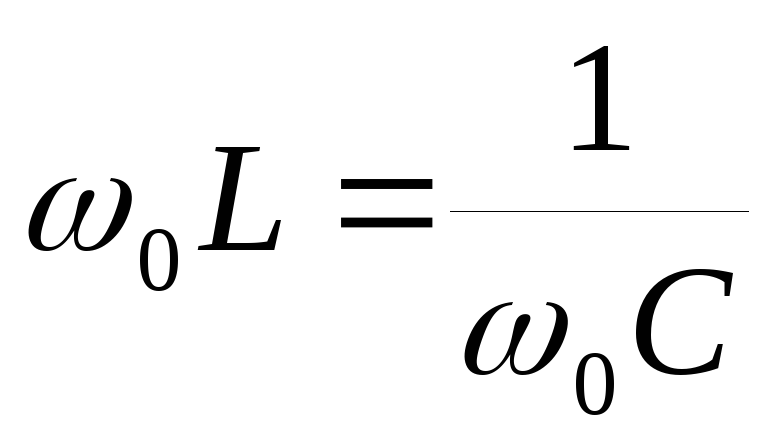 ,
сумма напряжений на катушке и конденсаторе
становится равной нулю, т.к. их колебания
противоположны по фазе. В результате,
напряжение на активном сопротивлении
при резонансе оказывается равным полному
напряжению, а сила тока достигает
максимального значения. Выразим
индуктивное и емкостное сопротивления
при резонансе:
,
сумма напряжений на катушке и конденсаторе
становится равной нулю, т.к. их колебания
противоположны по фазе. В результате,
напряжение на активном сопротивлении
при резонансе оказывается равным полному
напряжению, а сила тока достигает
максимального значения. Выразим
индуктивное и емкостное сопротивления
при резонансе:
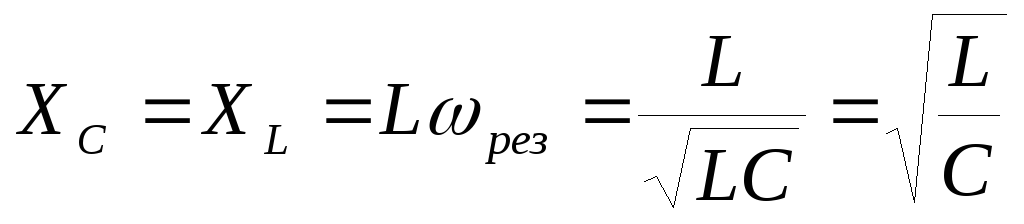 ,
следовательно
,
следовательно
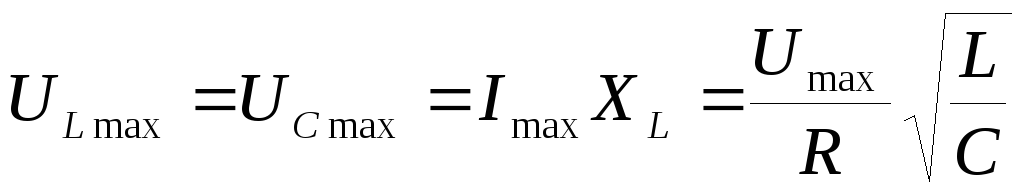 . Это выражение показывает, что при
резонансе амплитуда колебаний напряжения
на катушке и конденсаторе могут
превосходить амплитуду колебаний
приложенного напряжения.
. Это выражение показывает, что при
резонансе амплитуда колебаний напряжения
на катушке и конденсаторе могут
превосходить амплитуду колебаний
приложенного напряжения.
«Активное, индуктивное, емкостное сопротивления в цепи переменного тока»
Инфоурок › Физика ›Презентации›Повторение темы: «Активное, индуктивное, емкостное сопротивления в цепи переменного тока»
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:
Активное, индуктивное, емкостное сопротивления в цепи переменного тока
2 слайд Описание слайда:
Описание слайда:
…переменный ток – это вздор, не имеющий будущего. Я не только не хочу осматривать двигатель переменного тока, но и слышать о нем Томас Эдисон
3 слайд Описание слайда:
Описание слайда:
Электрические устройства, преобразующие электрическую энергию во внутреннюю Высокоомные провода Нагревательные приборы 1. Активное сопротивление
4 слайд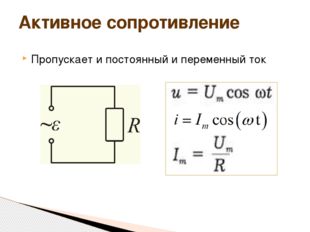 Описание слайда:
Описание слайда:
Пропускает и постоянный и переменный ток Активное сопротивление
5 слайд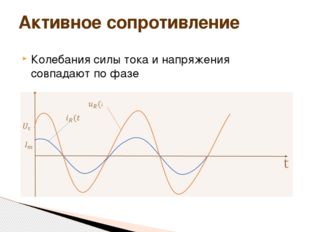 Описание слайда:
Описание слайда:
Колебания силы тока и напряжения совпадают по фазе Активное сопротивление
6 слайд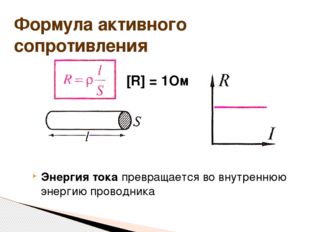 Описание слайда:
Описание слайда:
Энергия тока превращается во внутреннюю энергию проводника Формула активного сопротивления ω [R] = 1Ом
7 слайд Описание слайда:
Описание слайда:
Катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения 2. Индуктивное сопротивление
8 слайд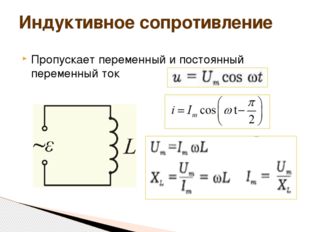 Описание слайда:
Описание слайда:
Пропускает переменный и постоянный переменный ток Индуктивное сопротивление
9 слайд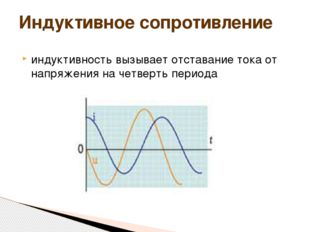 Описание слайда:
Описание слайда:
индуктивность вызывает отставание тока от напряжения на четверть периода Индуктивное сопротивление
10 слайд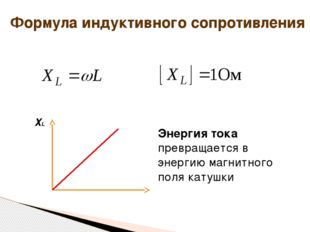 Описание слайда:
Описание слайда:
Формула индуктивного сопротивления ω ХL Энергия тока превращается в энергию магнитного поля катушки
11 слайд Описание слайда:
Описание слайда:
В любой момент времени изменению силы тока противодействуют ЭДС самоиндукции ЭДС самоиндукции — причина индуктивного сопротивления Физический смысл индуктивного сопротивления
12 слайд Описание слайда:
Описание слайда:
Конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока 3. Емкостное сопротивление
13 слайд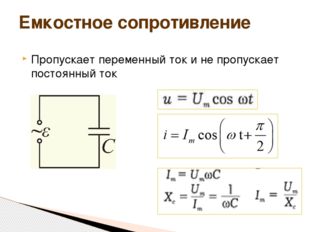 Описание слайда:
Описание слайда:
Пропускает переменный ток и не пропускает постоянный ток Емкостное сопротивление
14 слайд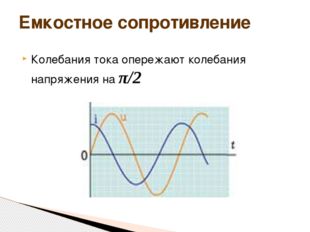 Описание слайда:
Описание слайда:
Колебания тока опережают колебания напряжения на π/2 Емкостное сопротивление
15 слайд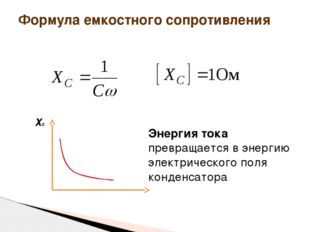 Описание слайда:
Описание слайда:
Формула емкостного сопротивления ω Хс Энергия тока превращается в энергию электрического поля конденсатора
16 слайд Описание слайда:
Описание слайда:
Изменению переменного тока в любое мгновение противодействует электрическое поле между обкладками конденсатора Физический смысл емкостного сопротивления
17 слайд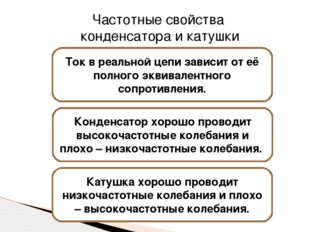 Описание слайда:
Описание слайда:
Ток в реальной цепи зависит от её полного эквивалентного сопротивления. Частотные свойства конденсатора и катушки Конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания. Катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания.
18 слайд Описание слайда:
Описание слайда:
— реактивное сопротивление — полное сопротивление Закон Ома для полной цепи переменного тока
19 слайд Описание слайда:
Описание слайда:
Используемые материалы https://infourok.ru

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Проверен экспертом
Общая информация
Номер материала: ДБ-341145
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Активное и индуктивное сопротивление кабелей и проводов. Емкостная проводимость линий электропередач
Для того, чтобы произвести расчет электрической сети на потерю напряжения необходимо знать параметры линий, а именно их сопротивления и проводимости. Если производятся расчеты цепей постоянного тока, то вполне достаточно знать только омическое сопротивление линии. А вот при расчете линии переменного тока одного омического сопротивления бывает недостаточно, и помимо активных сопротивлений, необходимо знать еще индуктивные сопротивления и емкостные проводимости проводов и кабелей.
Активное сопротивление проводов и кабелей
Из электротехники известно, что полное сопротивление при равных условиях переменному и постоянному току будут отличаться. Касается это также проводов и кабелей. Это вызвано тем, что переменный ток распределяется по сечению неравномерно (поверхностный эффект). Однако для проводов из цветных металлов и с частотой переменного напряжения 50 Гц этот эффект не оказывает слишком большого влияния и им можно пренебречь. Таким образом, при расчете проводников из цветных металлов, их сопротивления переменному и постоянному току принимаются равными.
На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:

Где: l – длина в км, γ – удельная проводимость материала провода м/ом∙мм2, r0 – активное сопротивление 1 км провода на фазу Ом/км, s – площадь поперечного сечения, мм2.
Величина r0, как правило, берется из таблиц справочников.
На активное сопротивление провода влияет и температура окружающей среды. Величину r0 при температуре Θ можно определить по формуле:

Где: α – температурный коэффициент сопротивления; r20 – активное сопротивление при температуре 20 0С, γ20 – удельная проводимость при температуре в 20 0С.
Стальные провода обладают значительно большими активными сопротивлениями, чем аналогичные провода из цветных металлов. Его увеличение обусловлено значительно меньшей величиной удельной проводимости и поверхностным эффектом, который у стальных проводов выражен гораздо более ярко, чем у алюминиевых или медных. Более того, в стальных проводах присутствуют потери активной энергии на вихревые токи и перемагничивание, что в схемах замещения линий учитывают дополнительной составляющей активного сопротивления.
Активное сопротивление стальных проводов (в отличии от проводов из цветных металлов) сильно зависит от величины протекаемого тока, поэтому использовать постоянное значение удельной проводимости при расчетах нельзя.
Активное сопротивление стальных проводов в зависимости от протекающего тока аналитически выразить весьма трудно, поэтому для его определения используют специальные таблицы.
Индуктивное сопротивление проводов и кабелей
Для определения индуктивного сопротивления (обозначается Х) кабельной или воздушной линии определенной протяженности в километрах удобно пользоваться выражением:

Где: Х0 – индуктивное сопротивление одного километра провода или кабеля на фазу, Ом/км.
Х одного километра воздушной или кабельной линии можно определить по формуле:

Где: Dср – расстояние среднее между проводами или центрами жил кабелей, мм; d – диаметр токоведущей жилы кабеля или диаметр провода, мм; μт – относительная магнитная проницаемость материала провода;
Первый член правой части уравнения обусловлен внешним магнитным полем и называется внешним индуктивным сопротивлением Х0/. Из этого выражения видно, что Х0/ зависит только от расстояния между проводами и их диаметра, а так как расстояние между проводами выбирается исходя из номинального напряжения линии, соответственно Х0/ будет расти с ростом номинального напряжения линии. Х0/ воздушных линий больше, чем кабельных. Это связано с тем, что токоведущие жилы кабеля располагаются друг к другу значительно ближе, чем провода воздушных линий.
Для одной фазы:

Где: D1:2 расстояние между проводами.
Для одинарной трехфазной линии при расположении проводов по треугольнику:

При горизонтальном или вертикальном расположении проводов трехфазной линии в одной плоскости:

Увеличение сечения проводов линии ведет к незначительному уменьшению Х0/.
Второй член уравнения для определения X0 обусловлен магнитным полем внутри проводника. Он выражает внутреннее индуктивное сопротивление Х0//.
Таким образом выражение для Х0 можно представить в виде:

Для линий из немагнитными материалов μ = 1 внутреннее индуктивное сопротивление Х0// по сравнению с внешним Х0/ составляет ничтожную величину, поэтому им очень часто пренебрегают.
В таком случае формула для определения Х0 примет вид:

Для практических расчетов индуктивные сопротивления кабелей и проводов определяют по соответствующим таблицам.
В случае приближенных расчетов можно считать для воздушных линий напряжением 6-10 кВ Х0 = 0,3 – 0,4 Ом/км, а для кабельных Х0 = 0,08 Ом/км.
Внутренне индуктивное сопротивление стальных проводов сильно отличается от Х0// проводов из цветных металлов. Это вызвано тем, что Х0// пропорционально магнитной проницаемости μr, которая сильно зависит от величины тока в проводе. Если для проводов из цветных металлов μr = 1, то для стальных проводов μr может достигать величины в 103 и даже выше.
Х0// для линий прокладываемых стальными проводами пренебрегать нельзя. Как правило, данную величину берут из таблиц, составленных на основе экспериментальных данных.
Сопротивления r0 и Х0// при некоторых значениях тока могут достигать максимальных значений, а затем с увеличением тока уменьшатся. Это явление объясняется магнитным насыщением стали.
Емкостная проводимость линий
Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.
Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:

Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.
Емкостная проводимость одноцепной воздушной линии определяется по формуле:

Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.
Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:

Где: U – линейное напряжение сети, В; l – длина линии, км;
Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ. При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.
В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:
- Для воздушной линии:

- Для кабельной линии:

Активное, емкостное, индуктивное сопротивление
Стр 1 из 3Следующая ⇒ПЕРЕМЕННЫЙ ТОК
Переменный электрический ток. Генератор переменного тока
| Рис. 6.1. Вращающаяся рамка в магнитном поле |
Переменный ток — это ток, периодически меняющийся по величине и направлению. Рассмотрим принцип действия генератора переменного тока на примере вращения рамки из проводника в однородном магнитном поле (рис. 6.1).
Пусть рамка имеет площадь S и первоначально расположена в однородном магнитном поле так, что нормаль к плоскости рамки составляет угол a=0 с направлением вектора индукции .
При вращении рамки с угловой скоростью w угол a изменяется по закону , a магнитный поток Ф, пронизывающий рамку, — по закону: . Так как , где Т — период, то .
Изменения магнитного потока возбуждают в рамке ЭДС индукции, согласно закону электромагнитной индукции, равную производной от потока по времени (строчными буквами мы будем обозначать мгновенные значения):
.
Последнее выражение можно переписать в виде: , где — амплитуда ЭДС индукции.
С помощью контактных колец и скользящих по ним щеток концы рамки соединяют с электрической цепью, в которой под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, возникнет переменный ток такой же частоты. Напряжение на выходных зажимах генератора несколько меньше ЭДС (на величину напряжения на внутреннем сопротивлении — см. раздел 2.2): и также изменяется по гармоническому закону и=Umsin(wt). Мгновенное значение силы тока в цепи будет равно: , где Im, — амплитуда колебаний тока, j — разность фаз между колебаниями тока и напряжения. Амплитуда тока и разность фаз зависят от характера сопротивления цепи.
Активное, емкостное, индуктивное сопротивление
| Рис. 6.2. Резистор в цепи переменного тока. Ток и напряжение колеблются в одинаковой фазе |
Активным называется сопротивление, в котором выделяется энергия тока. Таким сопротивлением обладает обычный проводник – резистор. Пусть через резистор (рис. 6.2), подключенный к генератору переменного тока (изображен символом ), протекает ток, изменяющийся по закону . Применим к участку цепи 1,2 закон Ома для мгновенных значений тока и напряжения в виде: . Получаем выражение: , из которого следует, что колебания напряжения на активном сопротивлении совпадают с колебаниями тока по фазе (рис.6.2), так как j = 0. Выражение , стоящее перед знаком синуса, есть амплитуда напряжения . Отсюда следует закон Ома для амплитудных значений:
. (6.1)
Мощность, выделяемая в резисторе, равна: . Это мгновенная мощность, зависящая от времени. Она положительна, поскольку в нее входит . Среднее значение равно ½, поэтому средняя мощность (за период) выразится как:
.
| Рис. 6.3. Конденсатор в цепи переменного тока. Колебания тока опережают колебания напряжения на угол p/2 (четверть периода) |
Действующим (эффективным) значением силы тока называют величину постоянного тока, который на активном сопротивлении за то же время выделяет такое же количество теплоты, как и данный переменный ток. Действующее значение силы тока связано с амплитудным значением соотношением: . Аналогично определяется действующее значение напряжения: . Использование действующих значений приводит полученные выше формулы для мощности к виду (2.17) — такому же, как для постоянного тока. Отметим, что в законе Ома для амплитуд (6.1) можно использовать и действующие значения тока и напряжения (естественно, одновременно).
Рассмотрим конденсатор в цепи переменного тока (рис. 6.3). Постоянный ток не протекает через конденсатор, поскольку тот фактически разрывает цепь постоянного тока. Однако при возникновении колебаний напряжения на конденсаторе происходит его перезарядка и в подводящих проводах возникают колебания тока. Пусть заряд на конденсаторе меняется по гармоническому закону: .
Сила тока является производной заряда по времени:
.
Следовательно, колебания силы токаопережаютколебания напряжения на конденсаторе на p/2. Амплитуда силы тока равна . Если ввести емкостное сопротивление , то из последнего выражения можно получить закон Ома для амплитуд:
(6.2)
Если вместо амплитудных значений использовать действующие, то получим закон Ома для действующих значений:
.
| Рис. 6.4. Индуктивность в цепи переменного тока. Ток отстает от напряжения на угол p/2 |
Индуктивность в цепи переменного тока (рис. 6.4) тоже влияет на величину тока, так как возникает ЭДС самоиндукции. Если активным сопротивлением катушки можно пренебречь, то разность потенциалов на катушке равна . Если ток в цепи меняется по закону , то
Колебания силы тока в катушке отстаютот колебаний напряжения на p/2.Амплитуда напряжения . Амплитудные (и действующие) значения тока и напряжения также связаны между собой законом Ома:
, (6.3)
где — индуктивное сопротивление.
Мгновенное значение мощности переменного тока равно произведению мгновенных значений силы тока и напряжения:
.
Мгновенная мощность колеблется с удвоенной частотой, принимая как положительные, так и отрицательные значения. В эти моменты (когда мощность отрицательна) цепь отдает мощность внешнему источнику. Практический интерес представляет среднее за период значение мощности:
, (6.4)
или через действующие значения тока и напряжения:
. (6.5)
Косинус угла сдвига фаз между током и напряжением называют коэффициентом мощности.
Если в электрической цепи не совершается работа, средняя мощность выделяется в активном сопротивлении в виде тепла. Чем меньше cosj, тем при большем токе выделится заданная мощность. Большие значения тока приводят к бесполезной потере мощности в соединительных проводах, поэтому на практике стараются увеличить коэффициент мощности нагрузки.
При сдвиге фаз j=p/2 (как в конденсаторе или катушке индуктивности без активного сопротивления) средняя выделяемая мощность равна нулю. Поэтому сопротивления XС, XL называются реактивными.
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
| Емкостное сопротивление в цепи переменного тока | |
| При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |  |
Мгновенное значение напряжения равно 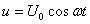 .
Мгновенное значение силы тока равно: .
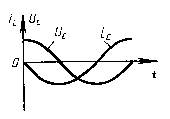
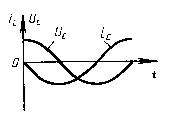
Мгновенное значение силы тока равно: 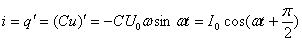 Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
|  |
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: 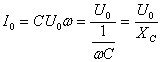 , где , где 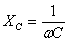 — емкостное сопротивление. — емкостное сопротивление.
| 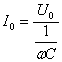 |
| Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). | 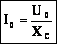 |
| Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). | 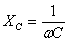 |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. | |
| Индуктивное сопротивление в цепи переменного тока | |
| В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. | |
Мгновенное значение силы тока: 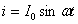 | 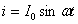 |
| Мгновенное значение напряжения можно установить, учитывая, что u = — εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. | |
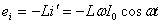 .
Следовательно .
Следовательно 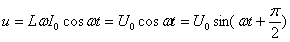 , где , где 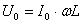 амплитуда напряжения.
Напряжение опережает ток по фазе на π/2. амплитуда напряжения.
Напряжение опережает ток по фазе на π/2.
| 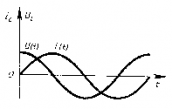 |
| Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой. | 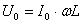 |
Величина 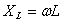 — индуктивное сопротивление. — индуктивное сопротивление.
| 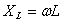 |
| Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. | 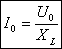 |
| В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. | |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
Индуктивное и емкостное сопротивление
-
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma
- Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к пересмотру класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке
23.11 Реактивное сопротивление, индуктивное и емкостное — College Physics
23.11 Реактивное сопротивление, индуктивное и емкостное — College Physics | OpenStaxSkip to Content- Предисловие
- 1 Введение: Природа науки и физики
- Введение в науку и область физики, физических величин и единиц измерения
- 1.1 Физика: введение
- 1.2 Физические величины и единицы измерения
- 1.3 Точность, прецизионность и значащие цифры
- 1.4 Приближение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
-
- Введение в одномерную кинематику
- 2.1 Смещение
- 2.2 Векторы, скаляры, системы координат и скорости. и скорость
- 2.4 Ускорение
- 2.5 Уравнения движения для постоянного ускорения в одном измерении
- 2.6 Основы решения проблем для одномерной кинематики
- 2.7 падающих объектов
- 2.8 Графический анализ одномерного движения
- Глоссарий
- Сводка раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в двумерную кинематику
- в двух измерениях: введение
- 3.2 Сложение и вычитание векторов: графические методы
- 3.3 Сложение и вычитание векторов: аналитические методы
- 3.4 Движение снаряда
- 3.5 Добавление скоростей
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в динамику
- : законы Ньютона 4 4.1 Развитие концепции силы
- 4.2 Первый закон движения Ньютона: инерция
- 4.3 Второй закон движения Ньютона: концепция системы
- 4.4 Третий закон движения Ньютона: симметрия сил
- 4.5 Нормальные, растягивающие и другие примеры сил
- 4.6 Стратегии решения проблем
- 4.7 Дальнейшие применения законов движения Ньютона
- 4.8 Расширенная тема: Четыре основных силы — Введение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение: дополнительные применения законов Ньютона
- 5.1 Трение
- 5.2 Силы сопротивления
- 5.3 Упругость: напряжение и деформация
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- 6.1 Угол поворота и угловая скорость
- 6.2 Центростремительное ускорение
- 6.3 Центростремительная сила
- 6.4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
- 6.5 Универсальный закон тяготения Ньютона
- 6.6 Спутники и законы Кеплера: аргумент в пользу простоты
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- — Введение от
- Работа, энергия и энергетические ресурсы
Основной принцип работы индуктивного датчика приближения
Вы когда-нибудь задумывались, как индуктивный датчик приближения может обнаруживать металлическую цель? Хотя лежащая в основе электротехника сложна, основной принцип работы понять нетрудно.
В основе индуктивного датчика приближения («prox», «датчик» или «prox sensor» для краткости) лежит электронный генератор, состоящий из индуктивной катушки, состоящей из множества витков очень тонкой медной проволоки, конденсатора для хранения электрического заряда, и источник энергии для электрического возбуждения.Размер индукционной катушки и конденсатора согласован для создания самоподдерживающихся синусоидальных колебаний с фиксированной частотой. Катушка и конденсатор действуют как две электрические пружины с грузом, подвешенным между ними, постоянно толкая электроны вперед и назад между собой. Электрическая энергия подается в цепь, чтобы инициировать и поддерживать колебания. Без поддержания энергии колебания исчезли бы из-за небольших потерь мощности из-за электрического сопротивления тонкой медной проволоки в катушке и других паразитных потерь.
Колебание создает электромагнитное поле перед датчиком, потому что катушка расположена прямо за «лицевой стороной» датчика. Техническое название лицевой панели датчика — «активная поверхность».
Когда кусок проводящего металла входит в зону, определяемую границами электромагнитного поля, часть энергии колебаний передается металлу цели. Эта переданная энергия проявляется в виде крошечных циркулирующих электрических токов, называемых вихревыми токами.Вот почему индуктивные датчики иногда называют вихретоковыми датчиками.
Протекающие вихревые токи сталкиваются с электрическим сопротивлением, пытаясь циркулировать. Это создает небольшую потерю мощности в виде тепла (как маленький электрический нагреватель). Потери мощности не полностью компенсируются внутренним источником энергии датчика, поэтому амплитуда (уровень или интенсивность) колебаний датчика уменьшается. В конце концов, колебания уменьшаются до такой степени, что другая внутренняя цепь, называемая триггером Шмитта, обнаруживает, что уровень упал ниже заранее определенного порога.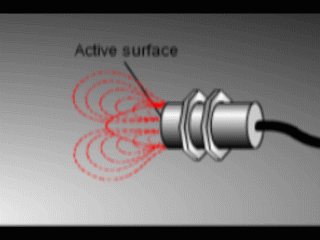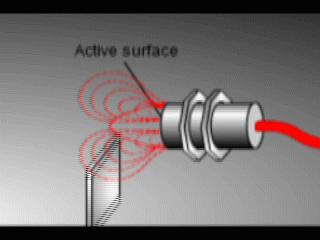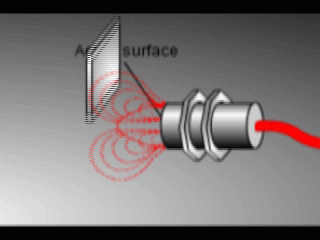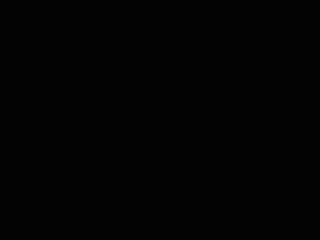 Этот порог — уровень, при котором присутствие металлической цели точно подтверждается. При обнаружении цели триггером Шмитта включается выход датчика.
Этот порог — уровень, при котором присутствие металлической цели точно подтверждается. При обнаружении цели триггером Шмитта включается выход датчика.
На короткой анимации справа показано влияние металлической цели на колеблющееся магнитное поле датчика. Когда вы видите, что кабель, выходящий из датчика, становится красным, это означает, что обнаружен металл и датчик был включен. Когда цель уходит, вы можете видеть, что колебания возвращаются к своему максимальному уровню, и выход датчика снова отключается.
Хотите узнать больше об основных принципах работы индуктивных датчиков приближения? Вот короткое видео на YouTube, посвященное основам:
Как это:
Нравится Загрузка …
Генри Менке
У меня есть электротехническое образование, которое дает мне прочную техническую основу для моей нынешней должности директора по маркетингу продуктов.
.
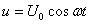 .
.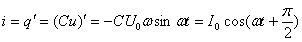
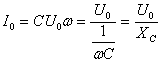 , где
, где 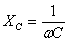 — емкостное сопротивление.
— емкостное сопротивление.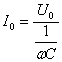
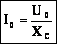
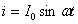
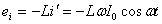 .
.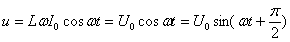 , где
, где 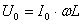 амплитуда напряжения.
амплитуда напряжения.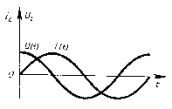
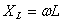 — индуктивное сопротивление.
— индуктивное сопротивление.