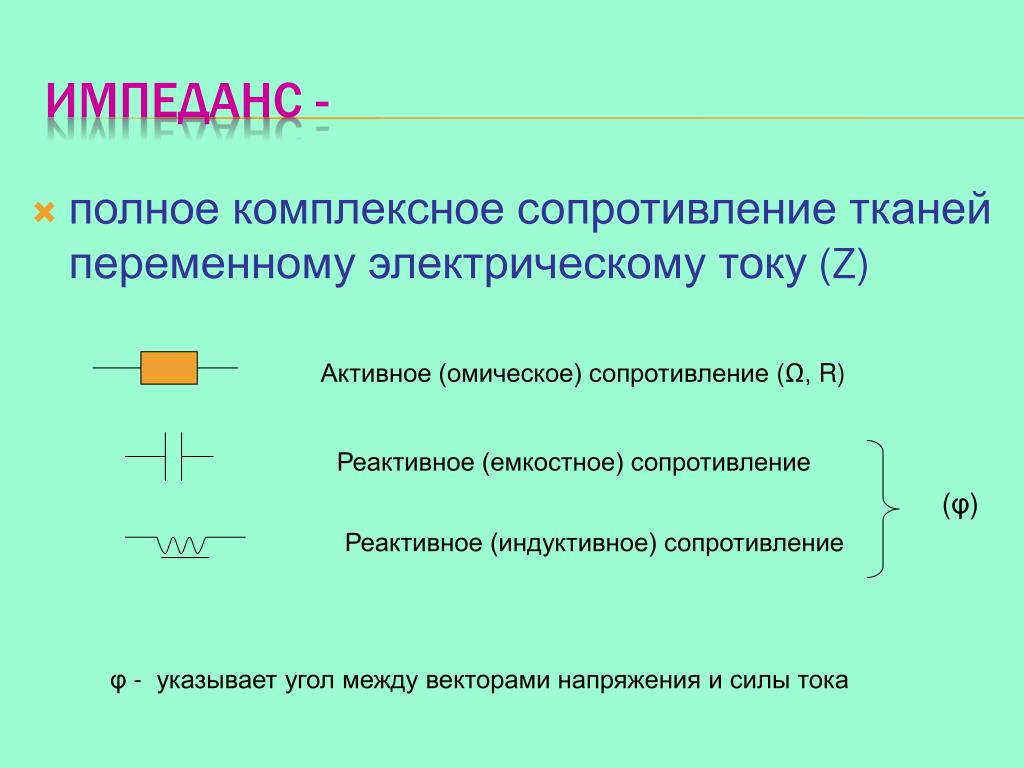
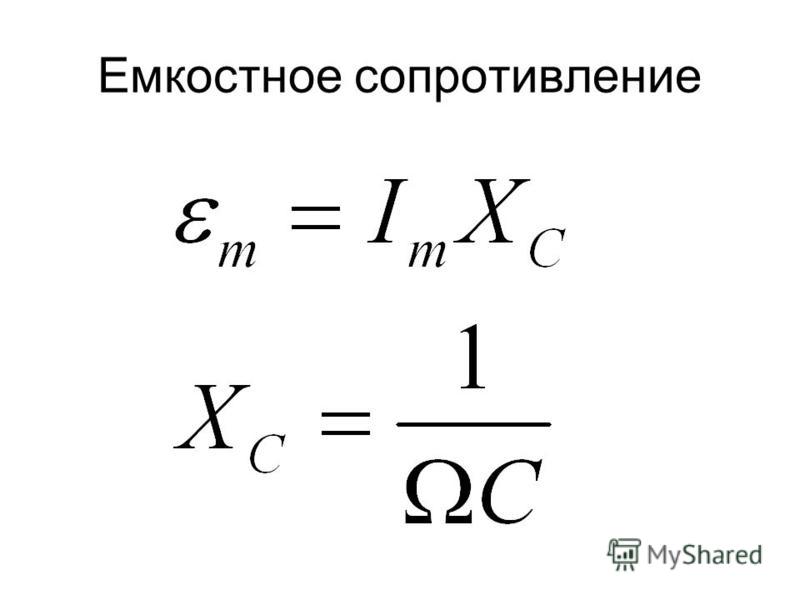Активное емкостное и индуктивное сопротивление: Билет №16. Активное, индуктивное, емкостное сопротивление цепи переменного тока. — Администратор — Каталог статей

Активное, емкостное и индуктивное сопротивление. закон ома для цепей переменного тока — справочник студента

 Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.

Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).

Узнай стоимость своей работы

Бесплатная оценка заказа!

В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.

Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением.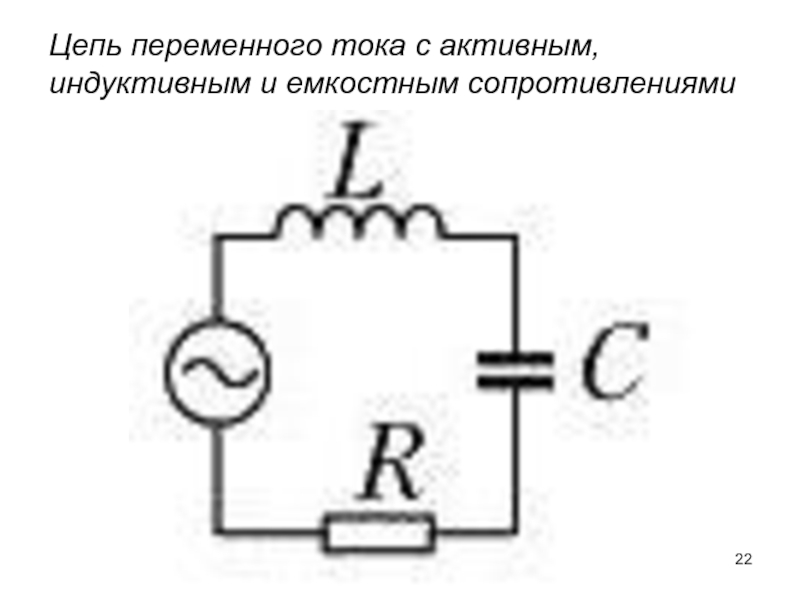 Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю

Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.

Тогда, падение напряжения на активном сопротивлении определяется по формуле:

(1)

• где, U-напряжение на элементе цепи,
• I – ток через элемент цепи
• R – активное сопротивление элемента
• Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:

(2)

1. где, Um-амплитудное значение напряжения на элементе цепи,
2. Im – амплитудное значение тока через элемент цепи
3. R – активное сопротивление элемента

В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис.

2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).

Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.

Узнай стоимость своей работы

Бесплатная оценка заказа!

Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.

Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.

Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:

	(3)
	(4)

• где — UL-падение напряжение на чисто индуктивном сопротивлении ;
• UС—падение напряжения на чисто емкостном сопротивлении;
• I— значение тока в через реактивное сопротивление;
• L— индуктивность реактивного элемента;
• C— емкость реактивного элемента;
• ω— циклическая частота.

Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.

Приведенные выше формулы являются частными случаями закона Ома для переменного тока.

Следовательно, полный закон Ома для переменного тока будет иметь вид:

(5)

Где Z – полное сопротивление цепи переменного тока.

Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.

Закон Ома для различных типовых цепей переменного тока

Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)

Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.

Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:

(6)

1. где —эффективное значение силы тока в А;
2. U—эффективное значение напряжения в В;
3. R—активное сопротивление в Ом;
4. ωL—индуктивное сопротивление в ом.
5. Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.

В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.

Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.

А закон Ома для такой цепи принимает вид:

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),

Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.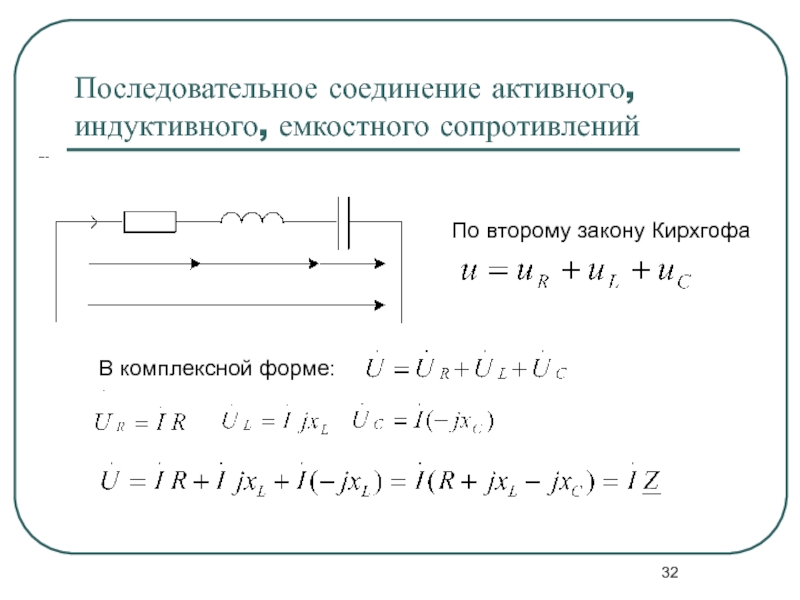

Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:

• где I-сила тока в А;
• U-напряжение в В;
• R-активное сопротивление в Ом;
• ωL-индуктивное сопротивление в Ом;
• 1/ωС-емкостное сопротивление в Ом.
• Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
• Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).

Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.

Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.

Рисунок 8. Эквивалентная схема колебательного контура.

1. Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
2. Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник: http://www.sxemotehnika.ru/zakon-oma-dlia-peremennogo-toka.html

Закон Ома для переменного тока

Когда-то люди жили без электричества. Потом научились делать батарейки, и так появился постоянный электрический ток. Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи. А мы двинемся дальше.

Сейчас вы поймете, почему так важен и что даёт закон Ома для цепи переменного тока. В современной жизни без этого закона никак не обойтись. Поскольку ток, это работа, а работа есть выделение тепла, то существенная задача электротехники в том, чтобы соблюдался термический режим, проще говоря, чтобы не произошло перегрева электроцепей.

Итак, закон Ома гласит, что:

Измерить напряжение довольно просто, для этого понадобится вольтметр, в нашем случае для переменного напряжения.

В цепях постоянного тока измерить сопротивление тоже не составляет сложности, для этого потребуется омметр.

Почему же возникают сложности с переменным током? А проблема, именно, в его переменности, а точнее понятиях емкости и индукции, которые ведут себя при переменном токе несколько иначе, нежели при постоянном.

Формула Закона Ома для переменного тока:

Кому-то эта формула может показаться неожиданной, потому что все привыкли видеть другую формулу:

Теперь давайте разберёмся, что такое полное сопротивление цепи и всё сразу встанет на свои места.

В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями.

Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.

Ёмкостное сопротивление. При подаче напряжения на конденсатор сначала возникает сильный ток и потом поднимается напряжение, то есть в идеальных условиях ток опережает напряжение на угол 90.

Другими словами, ток совершает работу из-за наличия сопротивления в цепи, которое можно посчитать по формуле:

Таким образом, чем выше частота переменного тока и чем выше емкость конденсатора, тем меньше ёмкостное сопротивление.

Индуктивное сопротивление. Здесь все происходит наоборот, сначала возникает напряжение, затем запускается индукционный процесс который препятствует возрастанию тока. Подробнее об этом читайте в статьях про индукцию.

Поэтому здесь мы видим уже обратную картину – чем выше частота и чем больше индуктивность катушки, тем больше индуктивное сопротивление переменному току.

Почему эти понятия не встречаются в цепях постоянного тока? Ответ можно узнать, посмотрев на формулы. Если ток постоянный, то f=0.

То есть, емкостное сопротивление станет бесконечно большим, а это значит, что конденсатор в цепи постоянного тока становится похож на выключатель, который размыкает цепь и ток по ней не идёт, но при этом, конденсатор будет пропускать переменный ток.

А индуктивное сопротивление станет равно нулю, значит, у нас останется просто провод, который имеет свое собственное сопротивление, которое еще называется активным, и его можно измерить обычным омметром.

В отличие от конденсатора, у которого нет активного сопротивления, сопротивление катушки, если оно довольно большое, должно приниматься в расчёт. Как правило, активное сопротивление катушки очень маленькое по сравнению с индуктивным, поэтому его в расчёт не берут, но всё же правильно формула сопротивления катушки выглядит так:

• По такому принципу в электронике изготавливают фильтры, которые должны отсечь переменный ток от постоянного, то есть пропускать только переменный ток или наоборот заглушить переменный ток, оставив только постоянный, или даже заглушить токи какой-то одной или нескольких частот.
• А сейчас совсем вас запутаю… И катушка может иметь ёмкостные свойства и конденсатор – индуктивные, но как правило они слишком малы и носят паразитический характер.
• Ну а сейчас мы рассмотрим закон Ома для электрической цепи переменного тока наглядно.

Допустим, у нас есть цепь из последовательно включенных резистора (активное сопротивление), конденсатора (реактивное ёмкостное сопротивление) и катушка (активно-реактивное индуктивное сопротивление). Теперь, чтобы узнать силу тока в цепи нам нужно правильно посчитать полное сопротивление цепи.

Осталось применить всё изложенное выше.

Реактивное сопротивление Х это разница между индуктивным сопротивлением XL и ёмкостным сопротивлением XC. Ну а дальше векторным сложением можем узнать полное реактивное сопротивление

1. следовательно:
2. дальнейший расчет:
3. или:

Что можно сказать в заключении. Как вы можете видеть, закон Ома для переменного тока точно такой же, как и для постоянного. Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное.

И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях.

Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.

Источник: https://uelektrika.ru/osnovy-yelektrotekhniki/zakon-oma-dlya-peremennogo-toka/

Закон Ома для переменного тока

После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.

При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

где

• I [А] – сила тока,
• U [В] – напряжение,
• Z [Ом] – полное сопротивление цепи.

Полное сопротивление цепи

В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:

где

• — индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
• — емкостное сопротивление, создается конденсатором.

Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.

Рис.1. Треугольник сопротивлений

Учитывая последние равенства, запишем формулу закона Ома для переменного тока:

– амплитудное значение силы тока.

Рис.2. Последовательная электрическая цепь из R, L, C элементов.

Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:

Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?

Дано:
Решение:

Запишем закон Ома для переменного тока — где ω=2πν. Амплитудное значение силы тока связано с действующим значением равенством Аналогично для напряжения Подставим в первую формулу

Источник: https://zakon-oma.ru/dlya-peremennogo-toka.php

Закон РћРјР° для цепей постоянного Рё переменного тока — теория Рё практика

• Онлайн расчёт электрических величин напряжения, тока Рё мощности для: участка цепи, полной цепи СЃ резистивными, ёмкостными Рё индуктивными
• элементами.

— Рђ любите ли Р’С‹ закон РћРјР° так, как люблю его СЏ? — СЃРїСЂРѕСЃРёР» учитель физики стоящего СЂСЏРґРѕРј СЃ щитком Рё разглядывающего СЃРІРѕР№ обугленный палец электрика, — Всеми силами души Вашей, СЃРѕ всем энтузиазмом Рё исступлением, Рє которому только СЃРїРѕСЃРѕР±РЅР° пылкая молодость, — никак РЅРµ угомонялся РѕРЅ, сверкая РёР·-РїРѕРґ очков пытливым взглядом. — Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным РІРѕРїСЂРѕСЃРѕРј электрик Рё пошёл, насвистывая «РљР°Р»РёРЅРєСѓ-Малинку» РІ направлении ближайшего супермаркета — РЅРµ ради пьянства окаянного, Р° дабы залечить СЃРІРѕР№ увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:

I=U/R, I – сила тока в проводнике, измеряемая в амперах [А]; U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В]; R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные РѕС‚ этой формулы приобретают такой же незамысловатый РІРёРґ: R=U/I Рё U=R×I.

Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.

Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:

P(Вт) = U(В)×I(А) = I2(А)×R(Ом) = U2(В)/R(Ом) Можно, конечно, описывая закон Ома обойтись и вообще без формул, а вместо них пользоваться словами или картинками: С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта. Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари! Считайте, учитывайте размерность, не стирайте из памяти, что: 1В=1000мВ=1000000мкВ; 1А=1000мА=1000000мкА; 1Ом=0.001кОм=0.000001МОм; 1Вт=1000мВт=100000мкВт. Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛ�ЦА ДЛЯ ПРОВЕРК� РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить РІ таблицу нужно только РґРІР° имеющихся Сѓ Вас параметра, остальные посчитает таблица.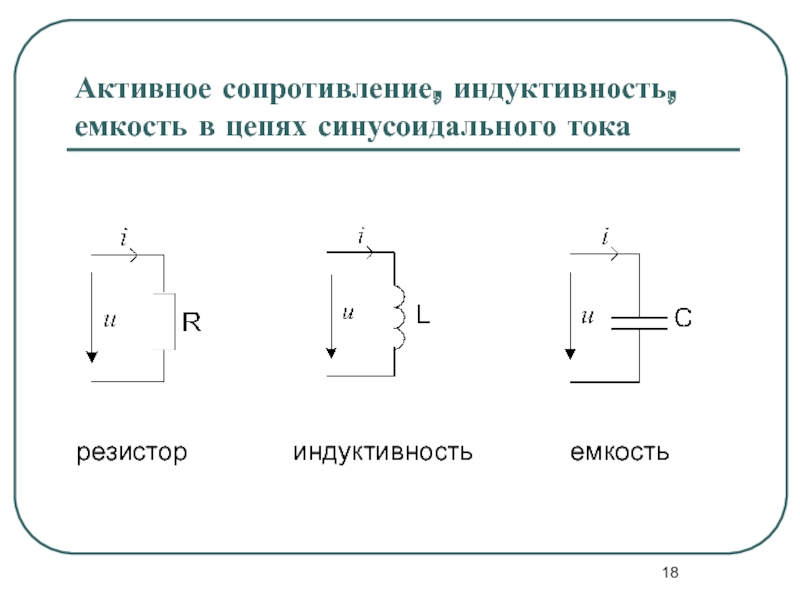 Р’СЃРµ наши расчёты проводились РїСЂРё условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр. Если это условие РЅРµ соблюдается, то РїРѕРґ величиной R следует принять СЃСѓРјРјСѓ внешнего Рё внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон РћРјР° для полной цепи: I=U/(R+r) . Для многозвенных цепей возникает необходимость преобразования её Рє эквивалентному РІРёРґСѓ:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/Rll = 1/R4+1/R5.

А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.

Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.

Единственное, что надо иметь РІ РІРёРґСѓ для правильной интерпретации закона РћРјР° для переменного тока — РїРѕРґ значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

Рђ что такое действующее значение Рё как РѕРЅРѕ связано СЃ амплитудой сигнала переменного тока? Приведём диаграммы для нескольких различных форм сигнала. Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал СЃРѕ скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы. Глядя РЅР° СЂРёСЃСѓРЅРѕРє можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда РІ пределах положительной, или отрицательной (РІ наших случаях РѕРЅРё равны) полуволны. Рассчитываем действующее значение напряжение интересующей нас формы: Для СЃРёРЅСѓСЃР° U = UРґ = UР°/в€љ2; для треугольника Рё пилы U = UРґ = UР°/в€љ3; для меандра U = UРґ = UР°. РЎ этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.

В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.

Поскольку фазы протекающего через эти элементы тока РЅРµ одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись РЅРµ удаётся, Рё формула приобретает РІРёРґ: Реактивные сопротивления конденсаторов Рё индуктивностей РјС‹ СЃ Вами уже рассчитывали РЅР° странице ссылка РЅР° страницу Рё знаем, что величины эти зависят РѕС‚ частоты, протекающего через РЅРёС… тока Рё описываются формулами: XC = 1/(2ПЂЖ’РЎ) ,   XL = 2ПЂЖ’L .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.

Количество вводимых элементов должно быть РЅРµ менее РѕРґРЅРѕРіРѕ, РїСЂРё наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТ�ВЛЕН�Я ЦЕП�.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

Токозадающими цепями РІ данной схеме являются элементы R1 Рё РЎ1. Допустим, нас интересует выходное напряжение Uвых = 12 вольт РїСЂРё токе нагрузки 100 РјРђ. Выбираем стабилитрон Р”815Р” СЃ напряжением стабилизации 12Р’ Рё максимально допустимым током стабилизации 1,4Рђ. Зададимся током через стабилитрон СЃ некоторым запасом — 200РјРђ. РЎ учётом падения напряжения РЅР° стабилитроне, напряжение РЅР° токозадающей цепи равно 220РІ — 12РІ = 208РІ. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200РјРђ: Z = 208РІ/200РјРђ = 1,04РєРћРј. Резистор R1 является токоограничивающим Рё выбирается РІ пределах 10-100 РћРј РІ зависимости РѕС‚ максимального тока нагрузки. Зададимся номиналами R1 — 30 РћРј, РЎ1 — 1 РњРєС„, частотой сети f — 50 Гц Рё подставим РІСЃС‘ это хозяйство РІ таблицу. Получили полное сопротивление цепи, равное 3,183РєРћРј. Многовато будет — надо увеличивать ёмкость РЎ1. Поигрались туда-СЃСЋРґР°, нашли нужное значение ёмкости — 3,18 РњРєС„, РїСЂРё котором Z = 1,04РєРћРј. Р’СЃС‘ — закон РћРјР° выполнил СЃРІРѕСЋ функцию, расчёт закончен, всем спать полчаса!

Источник: https://vpayaem.ru/information11.html

Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока

Определение 1

Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:

[Ileft(t
ight)=I_m{sin left(omega t
ight) left(1
ight). }]

• Рисунок 1.
• Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:

[U=IR=I_m{Rsin left(omega t
ight) left(2
ight), }]

где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:

[U_m=RI_mleft(3
ight),]

где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.

Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

1. Рисунок 2.
2. Мы можем использовать следующие соотношения:

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

• Если $I(t)$ определена уравнением (1), то заряд выражен как:
• где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
• Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac{pi }{2}.$ Амплитуда напряжения на емкости равна:

Величину $X_C=frac{1}{omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $.

Это значит, что постоянный ток не течет через конденсатор.

Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.

Индуктивное сопротивление

Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.

1. Рисунок 3.
2. Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
3. По условию $R=0. mathcal E$ самоиндукции можно выразить как:
4. Из выражений (8), (9) следует, что:
5. Амплитуда напряжения в данном случае равна:
6. где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).2}(13)]

   называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.

   Пример 1

   Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
   u$.

   • Решение:
   • Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
   • Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
   • оно связано с действующим значением силы тока как:
   • В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.2}}.]

     Источник: https://spravochnick.ru/fizika/peremennyy_sinusoidalnyy_tok/aktivnoe_emkostnoe_i_induktivnoe_soprotivlenie_zakon_oma_dlya_cepey_peremennogo_toka/

     Закон Ома для переменного тока: формула

     Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи.

     Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов.

     Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

     Закон ома для участка цепи

     Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

     В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах. Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.

     Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке.

     Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение.

     Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

     Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

     Закон ома для полной цепи

     Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

     Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

     Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта.

     Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания.

     Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

     Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока.

     По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами.

     Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.

     Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела.

     Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r).

     На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.

     Что такое трансформаторы тока

     Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U

     ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока.

     В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы.

     Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

     Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

     Закон ома для цепи переменного тока

     Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.

     Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.

     Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится.

     Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс.

     Для обозначения полного сопротивления контура используется символ Z.

     Мощность короткого замыкания

     Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.

     Источник: https://electric-220.ru/news/zakon_oma_dlja_peremennogo_toka/2018-03-02-1465

     Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями

     По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:

     Пример.  Активное  сопротивление  катушки  составляет  5 ом,  а  ее  полное сопротивление Z=30 ом. Определить угол сдвига фаз.

     Решение.

     При соs =0,25 угол =75°.

     § 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ

     На рис. 57, а изображена цепь переменного тока, в которую  включены  последовательно  активное  сопротивление r,  индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.

     Под действием переменного напряжения в этой цепи протекает переменный ток.

     Выясним, чему равно общее напряжение на за­жимах цепи. Построим векторную диаграмму то­ка и напряжений для рас­сматриваемой цепи (рис. 57, б).

     Так как сопротив­ления соединены последовательно, то в них проте­кает одинаковый ток. Отложим по горизонтали, в  выбранном  масштабе вектор тока I.

     В цепи с активным сопротивлением ток и напряжение совпа­дают  по  фазе,  поэтому вектор напряжения Uа от­кладываем по вектору тока.

     Напряжение на индуктивности опережает ток на угол  = 90°. Поэтому век­тор UL откладываем вверх

     под углом 90° к вектору тока.

     В цепи с емкостью, наоборот, напряжение отстает от тока на угол  = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.

     Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий вектор­ную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор U, изображающий общее напряжение на за­жимах цепи.

     На основании теоремы Пифагора из треугольника напряжений АО Б следует, что

     отсюда общее напряжение

     Определим полное сопротивление цепи переменного тока, со­держащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис. 57, в). Его сторонами являются сопро­тивления r, (ХL — Хс) и полное сопротивление цепи Z.

     Пользуясь теоремой Пифагора, можно написать, что

     Отсюда полное сопротивление цепи

     Силу тока в цепи с активным, индуктивным и емкостным сопро­тивлениями определяют по закону Ома:

     На векторной диаграмме (рис. 57, б) видно, что в рассматри­ваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что

     • Из треугольника сопротивлений
     • § 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ

     На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.

     Полное сопротивление первой катушки

     Полное сопротивление второй катушки

     Напряжение на  зажимах  катушек  равно  напряжению генератора.

     1. Сила  тока в каждой  катушке  определяется  согласно  закону Ома:
     2. Из этих равенств можно сделать вывод, что в такой цепи токи раз­ветвляются обратно пропорционально полным сопротивлениям ветвей.
     3. Для определения угла сдвига фаз между напряжением и током
     4. в каждой катушке вычисляют  и    и по таблице тригонометрических функций находят значения углов 1 и 2.
     5. Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощ­ности (cos ).

     Так как первый закон Кирхгофа справедлив для цепей перемен­ного тока, то в рассматриваемой цепи общий ток определяется гео­метрическим сложением векторов (рис. 58,6).

     По горизонтали в выбранном масштабе отложим вектор напря­жения U. Так как ток в цепи с индуктивностью отстает от напря­жения, то вектор тока  I1 выбранном масштабе отложим с по­мощью транспортира под углом 1 к вектору напряжения U, а век­тор тока I2 и отложим под углом 2. Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбран­ного масштаба.

     • Чтобы найти общий ток, нужно воспользоваться тем, что актив­ная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:
     • а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережаю­щие):
     • После чего определяют общий ток:
     • Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.

     Пример. Три катушки соединены параллельно и к ним подключено перемен­ное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;

     1. Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.
     2. Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.
     3. Решение. Индуктивное сопротивление катушек:
     4. Полное сопротивление катушек:
     5. Сила тока в катушках:

     Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/cep-peremennogo-toka-s-aktivnym-induktivnym-i-emkostnym-soprotivleniyami

     Активное, емкостное и индуктивное сопротивление в цепи переменного тока

     I. Активное сопротивление –R: обычное электрическое сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю.

     — длина проводника, площадь поперечного сечения, -удельное сопротивление.

     — активное сопротивление проводника.

     R  i u  T t

     Рассмотрим электрическую цепь переменного тока с активным сопротивлением. Закон колебания напряжения на резисторе: . Мгновенное значение силы тока можно найти из закона Ома: .

     Выводы:

     II. Емкостное сопротивление –X_C: сопротивление, которым цепь обладает вследствие наличия в ней емкости.

     С  i u  T t 0 1/4 т — емкостное сопротивление.

     Рассмотрим электрическую цепь переменного тока с емкостью С. В цепи переменного тока конденсатор периодически заряжается и разряжается, поэтому переменный ток проходит через конденсатор. Закон колебания напряжения на емкости: . Мгновенное значение силы тока можно найти через первую производную заряда по времени: . Из формулы емкости: . Получаем: . Из выражения  .

     Выводы:

     • Потребляемая энергия за период равна нулю: половину периода конденсатор запасает энергию, вторую половину периода отдает энергию в цепь.

     III. Индуктивное сопротивление- X_L: сопротивление, которым обладает цепь вследствие наличия в ней индуктивности.

     L  i u  0 ¼ T T t — индуктивное сопротивление.

     В цепи переменного тока в катушке возникает ЭДС самоиндукции, которая противодействует изменениям силы тока. Это приводит к появлению дополнительного сопротивления – индуктивного. Рассмотрим электрическую цепь переменного тока с индуктивностью L. Закон колебания силы тока в цепи: . Из закона Ома для участка цепи с ЭДС получаем:. Рассмотрим идеальную катушку, для которой R=0. Из закона э-м индукции — среднее значение ЭДС самоиндукции , что мгновенное значение ЭДС самоиндукции пропорционально первой производной силы тока: . Получаем:  Из выражения .

     Выводы:

     или на ¼ периода.

     • Индуктивное сопротивление пропорционально круговой частоте и индуктивности.

     • Амплитудные и действующие значения связаны формулами: и .

     • Потребляемая энергия за период равна нулю: половину периода энергия накапливается в магнитном поле катушки, вторую половину периода катушка отдает энергию в цепь.

     Активное, индуктивное и емкостное сопротивления в цепи переменного тока

     Сформировать знания учащихся о различных видах сопротивлениях в цепи переменного тока:

     а) цепь переменного тока с активным сопротивлением; б) цепь переменного тока с индуктивным сопротивлением; в) цепь, переменного тока с емкостью.  

     Просмотр содержимого документа
     «Активное, индуктивное и емкостное сопротивления в цепи переменного тока»

     АКТИВНОЕ, ИНДУКТИВНОЕ И ЕМКОСТНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

     СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

     Активное Реактивное

     индуктивное ёмкостное

     АКТИВНОЕ СОПРОТИВЛЕНИЕ

     Активным сопротивлением называется такое сопротивление, в котором электрическая энергия превращается в другие виды энергии. Им обладают реостаты и электронагревательные приборы) лампы накаливания, электропечи, электроплиты и др.).

     ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ

     Индуктивное сопротивление   Х L обусловлено возникновением  ЭДС самоиндукции  в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующую изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности L и  угловой частоты  ω протекающего тока:

     Трансформаторы, электродвигатели, дроссели, кроме активного, обладают также и индуктивным сопротивлением .

     ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ

     Ёмкостное сопротивление Х С — это сопротивление переменному току, которое оказывает проводник, включенный в цепь переменного тока и не имеющий заметного сопротивления и индуктивности, но имеющий заметную емкость С. Элементы, связанные с наличием электрического поля, называются емкостями. Емкостью обладают конденсаторы. Ток в цепи с емкостью опережает напряжение по фазе на 90 градусов. Емкостное сопротивление является реактивным, то есть потерь энергии в нем не происходит как, например, в активном сопротивлении. Емкостное сопротивление обратно пропорционально частоте переменного тока. Измеряется в Омах.

     Дополнить утверждение……

     • Индуктивное сопротивление вызвано тем, что …
     • Сопротивление конденсатора в цепи переменного тока определяется по формуле …
     • Сопротивление, в котором электрическая энергия превращается в другие виды энергии, называется …
     • Противодействие ЭДС самоиндукции периодическим изменениям переменного тока называется …

     Векторные диаграммы

     Контрольные вопросы

     • Какое сопротивление называется активным? Приведите примеры активного сопротивления.
     • Чему равен сдвиг фаз между током и напряжением в цепи переменного тока с активным сопротивлением?
     • Начертите график и векторную диаграмму тока и напряжения для цепи с активным сопротивлением.
     • Запишите формулу закона Ома для цепи переменного тока с индуктивным сопротивлением.
     • Какое сопротивление называется индуктивным, емкостным? Приведите примеры индуктивного и емкостного сопротивления.
     • Чему равен сдвиг фаз между током и напряжением в цепи переменного тока с индуктивным сопротивлением?

     СПАСИБО ЗА ВНИМАНИЕ!

     Активное, ёмкостное и индуктивное сопротивления — презентация на Slide-Share.ru 🎓

     1

     Первый слайд презентации: Активное, ёмкостное и индуктивное сопротивления

     Изображение слайда

     2

     Слайд 2: Активное сопротивление

     Активное сопротивление –R: обычное электрическое сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю. l — длина проводника, s- площадь поперечного сечения, ρ -удельное сопротивление. — активное сопротивление проводника

     Изображение слайда

     3

     Слайд 3

     Рассмотрим электрическую цепь переменного тока с активным сопротивлением. Закон колебания напряжения на резисторе : Мгновенное значение силы тока можно найти из закона Ома: i u  T t R  0

     Изображение слайда

     4

     Слайд 4: Выводы

     Колебания силы тока и напряжения на активном сопротивлении совпадают по фазе. Амплитудные и действующие значения связаны формулой: и. При низких частотах активное сопротивление не зависит от частоты. На активном сопротивлении происходят безвозвратные превращения электрической энергии во внутреннюю.

     Изображение слайда

     5

     Слайд 5: Емкостное сопротивление –X C

     Закон колебания напряжения на емкости: Мгновенное значение силы тока можно найти через первую производную заряда по времени:. Из формулы емкости: Получаем: Из выражения  В цепи переменного тока конденсатор периодически заряжается и разряжается, поэтому переменный ток проходит через конденсатор. i u T t  0 1/4 т  C

     Изображение слайда

     6

     Слайд 6: Выводы

     Колебания силы тока опережают колебания напряжения на емкости по фазе  /2 или на ¼ T. Емкостное сопротивление обратно пропорционально емкости и частоте переменного тока. Амплитудные и действующие значения связаны формулой: и. Потребляемая энергия за период равна нулю: половину периода конденсатор запасает энергию, вторую половину периода отдает энергию в цепь.

     Изображение слайда

     7

     Слайд 7: Индуктивное сопротивление- X L

     В цепи переменного тока в катушке возникает ЭДС самоиндукции, которая противодействует изменениям силы тока. Это приводит к появлению дополнительного сопротивления – индуктивного. — индуктивное сопротивление i u ¼ T T t 0  L ω

     Изображение слайда

     8

     Слайд 8

     Рассмотрим электрическую цепь переменного тока с индуктивностью L. Закон колебания силы тока в цепи: Из закона Ома для участка цепи с ЭДС получаем: Рассмотрим идеальную катушку, для которой R =0. Из закона э-м индукции : , что мгновенное значение ЭДС самоиндукции пропорционально первой производной силы тока: Получаем: Из выражения -среднее значение ЭДС самоиндукции 

     Изображение слайда

     9

     Последний слайд презентации: Активное, ёмкостное и индуктивное сопротивления: Выводы

     Колебания силы тока отстают от колебаний напряжения по фазе на или на ¼ периода. Индуктивное сопротивление пропорционально круговой частоте ω и индуктивности L. Амплитудные и действующие значения связаны формулами: и. Потребляемая энергия за период равна нулю: половину периода энергия накапливается в магнитном поле катушки, вторую половину периода катушка отдает энергию в цепь.

     Изображение слайда

     Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока. Активное, емкостное, индуктивное сопротивление

     В которой генератор переменного тока создает синусоидальное напряжение. Разберем последовательно, что произойдет в цепи, когда мы замкнем ключ. Начальным будем считать тот момент, когда напряжение генератора равно нулю.

     В первую четверть периода напряжение на зажимах генератора будет возрастать, начиная от нуля, и конденсатор начнет заряжаться. В цепи появится ток, однако в первый момент заряда конденсатора, несмотря на то, что напряжение на его пластинах только что появилось и еще очень мало, ток в цепи (ток заряда) будет наибольшим. По мере же увеличения заряда конденсатора ток в цепи убывает и доходит до нуля в момент, когда конденсатор полностью зарядится. При этом напряжение на пластинах конденсатора, строго следуя за напряжением генератора, становится к этому моменту максимальным, но обратного знака, т. е. направлено навстречу напряжению генератора.
     

     
     

     Рис. 1. Изменение тока и напряжения в цепи с емкостью

     Таким образом, ток с наибольшей силой устремляется в свободный от заряда конденсатор, но тут же начинает убывать по мере заполнения зарядами пластин конденсатора и падает до нуля, полностью зарядив его.

     Сравним это явление с тем, что происходит с потоком воды в трубе, соединяющей два сообщающихся сосуда (рис. 2),один из которых наполнен, а другой пустой. Стоит только выдвинуть заслонку, преграждающую путь воде, как вода сразу же из левого сосуда под большим напором устремится по трубе в пустой правый сосуд. Однако тотчас же напор воды в трубе начнет постепенно ослабевать, вследствие выравнивания уровней в сосудах, и упадет до нуля. Течение воды прекратится.

     Рис. 2. Изменение напора воды в трубе, соединяющей сообщающиеся сосуды, сходно с изменением тока в цепи во время заряда конденсатора

     Подобно этому и ток сначала устремляется в незаряженный конденсатор, а затем постепенно ослабевает по мере его заряда.

     С началом второй четверти периода, когда напряжение генератора начнет сначала медленно, а затем все быстрее и быстрее убывать, заряженный конденсатор будет разряжаться на генератор, что вызовет в цепи ток разряда. По мере убывания напряжения генератора конденсатор все больше и больше разряжается и ток разряда в цепи возрастает. Направление тока разряда в этой четверти периода противоположно направлению тока заряда в первой четверти периода. Соответственно этому кривая тока, пройдя нулевое значение, располагается уже теперь ниже оси времени.

     К концу первого полупериода напряжение на генераторе, а также и на конденсаторе быстро приближается к нулю, а ток в цепи медленно достигает своего максимального значения. Вспомнив, что величина тока в цепи тем больше, чем больше величина переносимого по цепи заряда, станет ясным, почему ток достигает максимума тогда, когда напряжение на пластинах конденсатора, а следовательно, и заряд конденсатора быстро убывают.

     С началом третьей четверти периода конденсатор вновь начинает заряжаться, но полярность его пластин, так же как и полярность генератора, изменяется «а обратную, а ток, продолжая течь в том же направлении, начинает по мере заряда конденсатора убывать, В конце третьей четверти периода, когда напряжения на генераторе и конденсаторе достигают своего максимума, ток становится равным нулю.

     В последнюю четверть периода напряжение, уменьшаясь, падает до нуля, а ток, изменив свое направление в цепи, достигает максимальной величины. На этом и заканчивается период, за которым начинается следующий, в точности повторяющий предыдущий, и т. д.

     Итак, под действием переменного напряжения генератора дважды за период происходят заряд конденсатора (первая и третья четверти периода) и дважды его разряд (вторая и четвертая четверти периода). Но так как чередующиеся один за другим сопровождаются каждый раз прохождением по цепи зарядного и разрядного токов, то мы можем заключить, что по цепи с емкостью проходит .
     

     Убедиться в этом можно на следующем простом опыте. Подключите к сети переменного тока через лампочку электрического освещения мощностью 25 Вт конденсатор емкостью 4-6 мкф. Лампочка загорится и не погаснет до тех пор, пока не будет разорвана цепь. Это говорит о том, что по цепи с емкостью проходил переменный ток. Однако проходил он, конечно, не сквозь диэлектрик конденсатора, а в каждый момент времени представлял собой или ток заряда или ток разряда конденсатора.

     Диэлектрик же, как нам известно, поляризуется под действием электрического поля, возникающего в нем при заряде конденсатора, и поляризация его исчезает, когда конденсатор разряжается.

     При этом диэлектрик с возникающим в нем током смещения служит для переменного тока своего рода продолжением цепи, а для постоянного разрывает цепь. Но ток смещения образуется только в пределах диэлектрика конденсатора, и поэтому сквозного переноса зарядов по цепи не происходит.

     Сопротивление, оказываемое конденсатором переменному току, зависит от величины емкости конденсатора и от частоты тока.

     Чем больше емкость конденсатора, тем больший заряд переносится по цепи за время заряда и разряда конденсатора, а следовательно, и тем больший будет ток в цепи. Увеличение же тока в цепи свидетельствует о том, что уменьшилось ее сопротивление.

     Следовательно, с увеличением емкости уменьшается сопротивление цепи переменному току.

     Увеличение увеличивает величину переносимого по цепи заряда, так как заряд (а равно и разряд) конденсатора должен произойти быстрее, чем при низкой частоте. В то же время увеличение величины переносимого в единицу времени заряда равносильно увеличению тока в цепи, а следовательно, уменьшению ее сопротивления.

     Если же мы каким-либо способом будем постепенно уменьшать частоту переменного тока и сведем ток к постоянному, то сопротивление конденсатора, включенного в цепь, будет постепенно возрастать и станет бесконечно большим (разрыв цепи) к моменту появления в .

     Следовательно, с увеличением частоты уменьшается сопротивление конденсатора переменному току.

     Подобно тому как сопротивление катушки переменному току называют индуктивным, сопротивление конденсатора принято называть емкостным.

     Таким образом, емкостное сопротивление тем больше, чем меньше емкость цепи и частота питающего ее тока.

     Емкостное сопротивление обозначается через Хс и измеряется в омах.

     Зависимость емкостного сопротивления от частоты тока и емкости цепи определяется формулой Хс = 1/ ωС, где ω — круговая частота, равная произведению 2 πf , С-емкость цепи в фарадах.

     Емкостное сопротивление, как и индуктивное, является реактивным по своему характеру, так как конденсатор не потребляет энергии источника тока.

     Формула для цепи с емкостью имеет вид I = U/Xc , где I и U — действующие значения тока и напряжения; Хс — емкостное сопротивление цепи.

     Свойство конденсаторов оказывать большое сопротивление токам низкой частоты и легко пропускать токи высокой частоты широко используется в схемах аппаратуры связи.
     

     С помощью конденсаторов, например, достигается необходимое для работы схем разделение постоянных токов и токов низкой частоты от токов высокой частоты.

     Если нужно преградить путь току низкой частоты в высокочастотную часть схемы, последовательно включается конденсатор небольшой емкости. Он оказывает большое сопротивление низкочастотному току и в то же время легко пропускает ток высокой частоты.
     

     Если же надо не допустить ток высокой частоты, например, в цепь питания радиостанции, то используется конденсатор большой емкости, включаемый параллельно источнику тока. Ток высокой частоты в этом случае проходит через конденсатор, минуя цепь питания радиостанции.

     Активное сопротивление и конденсатор в цепи переменного тока

     На практике часто встречаются случаи, когда в цепи последовательно с емкостью Общее сопротивление цепи в этом случае определяется по формуле

     Следовательно, полное сопротивление цепи, состоящей из активного и емкостного сопротивлений, переменному току равно корню квадратному из суммы квадратов активного и емкостного сопротивлений этой цепи.

     Закон Ома остается справедливым и для этой цепи I = U/Z .

     На рис. 3 приведены кривые, характеризующие фазовые соотношения между током и напряжением в цепи, содержащей емкостное и активное сопротивления.
     

     Рис. 3. Ток, напряжение и мощность в цепи с конденсатором и активным сопротивлением

     Как видно из рисунка, ток в этом случае опережает напряжение уже не на четверть периода, а меньше, так как активное сопротивление нарушило чисто емкостный (реактивный) характер цепи, о чем свидетельствует уменьшенный сдвиг фаз. Теперь уже напряжение на зажимах цепи определится как сумма двух слагающих: реактивной слагающей напряжения u с, идущей на преодоление емкостного сопротивления цепи, и активной слагающей напряжения преодолевающей активное ее сопротивление.

     Чем больше будет активное сопротивление цепи, тем меньший сдвиг фаз получится между током и напряжением.

     Кривая изменения мощности в цепи (см. рис. 3) дважды за период приобрела отрицательный знак, что является, как нам уже известно, следствием реактивного характера цепи. Чем менее реактивная цепь, тем меньше сдвиг фаз между током и напряжением и тем большую мощность источника тока эта цепь потребляет.

     Емкостное сопротивление это сопротивление переменному току, которое оказывает электрическая емкость. Ток в цепи с емкостью опережает напряжение по фазе на 90 градусов. Емкостное сопротивление является реактивным, то есть потерь энергии в нем не происходит как, например, в активном сопротивлении. Емкостное сопротивление обратно пропорционально частоте переменного тока.

     Проведем эксперимент, для этого нам понадобится. Конденсатор лампа накаливания и два источника напряжения один постоянного тока другой переменного. Для начала построим цепь, состоящую из источника постоянного напряжения, лампы и конденсатора все это включено последовательно.

     Рисунок 1 — конденсатор в цепи постоянного тока

     При включении тока лампа вспыхнет на короткое время, а потом погаснет. Так как для постоянного тока конденсатор имеет большое электрическое сопротивление. Оно и понятно ведь между обкладками конденсатора находится диэлектрик, через который постоянный ток не способен пройти. А вспыхнет лампа по тому, что в момент включения источника постоянного напряжения идет кратковременный импульс тока, заряжающий конденсатор. А раз ток идет значит и лампа светится.

     Теперь в этой цепи заменим источник постоянного напряжения на генератор переменного. При включении такой цепи мы обнаружим, что лампа буде светится непрерывно. Происходит это по тому, что конденсатор в цепи переменного тока заряжается за четверть периода. Когда напряжение на нем достигнет амплитудного значения, напряжение на нем начинает уменьшаться, и он будет, разряжается следующие четверть периода. В следующие пол периода процесс повторится снова, но напряжение в этот раз уже будет отрицательным.

     Таким образом, в цепи непрерывно течет ток хотя он и меняет при этом свое направление дважды за период. Но через диэлектрик конденсатора заряды не проходят. Как же это происходит.

     Представим себе конденсатор, подключаемый к источнику постоянного напряжения. При включении, источник убирает электроны с одной обкладки, тем самым создавая на ней положительный заряд. А на второй обкладке добавляет электронов, создавая тем самым равный по величине, но противоположный по знаку отрицательный заряд. В момент перераспределения зарядов в цепи протекает ток заряда конденсатора. Хотя электроны при этом не движутся через диэлектрик конденсатора.

     Рисунок 2 — заряд конденсатора

     Если теперь из цепи исключить конденсатор, то лампа будет светить ярче. Это говорит о том, что емкость создает сопротивление, току ограничивая его величину. Происходит это из-за того что при заданной частоте тока значение ёмкости мало и она не успевает накопить достаточно энергии в виде зарядов на своих обкладках. И при разряде будет протекать ток меньше чем способен развить источник тока.

     Опыт показывает, что если последовательно с лампочкой соединить конденсатор и подключить их к генератору постоянного напряжения, то лампочка не горит. Это понятно, так как обкладки конденсатора разделены диэлектриком, и цепь оказывается разомкнутой. При подключении конденсатора к источнику постоянного тока возникает кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Но если эту цепь подключить к источнику переменного напряжения, то лампочка горит. Переменный ток представляет собой вынужденные электромагнитные колебания, происходящие под действием переменного электромагнитного поля генератора. При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается, и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор снова заряжается, но знак заряда на его обкладках изменяется на противоположный и т.д. Через диэлектрик, разделяющий обкладки конденсатора, как и в цепи постоянного тока, электрические заряды не проходят. Но по проводам, соединяющим обкладки конденсатора с источником напряжения, течет переменный ток разрядки и зарядки конденсатора. Поэтому лампочка, включенная последовательно с конденсатором, будет гореть непрерывно. Если теперь конденсатор отсоединить, то лампочка горит ярче. Следовательно, конденсатор оказывает переменному току сопротивление, которое называется емкостным сопротивлением .

     Рассмотрим цепь (рис. 1), состоящую из конденсатора и подводящих проводов, сопротивление которых пренебрежительно мало, и генератора переменного напряжения.

     Пусть напряжение на конденсаторе изменяется по закону \(~U = U_0\sin wt.\) Как известно, заряд на обкладках конденсатора можно определить по формуле \(~q = CU = CU_0\sin wt.\) Сила тока \(~I = q».\) Следовательно,

     \(~I = -wCU_0\cos wt = wCU_0\sin(wt+\frac {\pi}2).\)

     Отсюда \(~I=I_0\sin (wt +\frac {\pi}2),\)

     где \(~I_0=wCU_o\) — амплитудное значение силы тока:

     \(~I_0=\frac {U_0}{\frac 1{wC}}; I_0 =\frac {U_0}{X_C},\)

     где \(~X_C = \frac 1{wC}.\)

     Выразив амплитудные значения через действующие \(~I_0 = \sqrt2 I \) и \(~U_0 = \sqrt2 U,\) получим \(~I= \frac U{X_C}, \) т.е. действующее значение силы тока связано с деиству-Хс ющим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение на участке цепи постоянного тока. Это позволяет рассматривать величину Х с как сопротивление конденсатора переменному току:

     \(~X_C = \frac 1{wC}\) — емкостное сопротивление.

     В СИ единицей емкостного сопротивления является ом (Ом).

     Как видно из полученной выше формулы, если в цепи включено только емкостное сопротивление, колебания силы тока в этой цепи опережают по фазе колебания напряжения на конденсаторе на \(~\frac {\pi}2,\) что изображено на графике и на векторной диаграмме (рис. 2).

     Мгновенная мощность

     \(~P=IU = I_0\sin (wt +\frac {\pi}2)U_0\sin wt = I_0U_0\sin wt \cos wt =\frac {I_0U_0}2 \sin 2wt,\)

     т.е. мощность периодически изменяется с двойной частотой, а среднее значение мощности — за период \(\mathcal h P \mathcal i =0,\) так как \(~\mathcal h \sin 2wt \mathcal i = 0.\) Первую и третью четверти периода, когда конденсатор заряжается, он получает энергию от генератора, а вторую и четвертую четверти периода, когда конденсатор разряжается, он отдает энергию генератору.

     Таким образом, так же, как активное сопротивление, емкостное сопротивление ограничивает силу тока в цепи, но в отличие от активного сопротивления на емкостном сопротивлении электрическая энергия не превращается необратимо в другие виды энергии.

     Литература

     Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 402-404.

     Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

     Элементы, обладающие реактивным сопротивлением, называют реактивными.

     Реактивное сопротивление катушки индуктивности.

     При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
     При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

     В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U , подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

     При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

     Если приложить к выводам катушки индуктивности напряжение U , ток не может начаться мгновенно по причине противодействия ЭДС, равного -U , поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

     Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε ), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt) .
     Отсюда выразим синусоидальный ток .

     Интегралом функции sin(t) будет -соs(t) , либо равная ей функция sin(t-π/2) .
     Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω .
     В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
     Для среднеквадратичных значений U и I в таком случае можно записать .

     В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL , которое и является реактивным сопротивлением:

     Реактивное сопротивлениие индуктивностей называют индуктивным.

     Реактивное сопротивление конденсатора.

     Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

     В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

     В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

     Если приложить к конденсатору напряжение U , мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

     Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt) .
     Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2) .
     Тогда для синусоидального напряжения u = U amp sin(ωt) запишем выражение мгновенного значения тока следующим образом:

     i = U amp ωCsin(ωt+π/2) .

     Отсюда выразим соотношение среднеквадратичных значений .

     Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

     Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

     Онлайн-калькулятор расчёта реактивного сопротивления

     Необходимо вписать значения и кликнуть мышкой в таблице.
     При переключении множителей автоматически происходит пересчёт результата.

     Реактивное сопротивление ёмкости X C = 1 /(2πƒC)

     Конденсатор оказывает определённое сопротивление переменному току и совершенно не проводит постоянный. Это свойство находит применение в различных областях радиоэлектроники и электротехники. Ёмкостное сопротивление в цепи переменного тока зависит от частоты последнего и ёмкости конденсатора.

     Основные понятия

     Ёмкостное сопротивление — это величина , которая создаётся конденсатором, включённым в цепь. Сопротивление подводящих проводов должно быть непренебрежимо большим. При подаче переменного тока возникают процессы, обусловленные периодическим зарядом и разрядом конденсатора.

     Период разбивается на четыре четверти. В течение первой четверти напряжение растёт. В этот момент по цепи проходит зарядный ток, сила которого будет уменьшаться, достигнув нуля, когда электродвижущая сила достигнет положительного максимума. Конденсатор полностью заряжен. После этого начнётся спад напряжения. Конденсатор будет разряжаться через подключённую к нему нагрузку. По цепи потечёт ток.

     К концу полупериода величина напряжения будет равна нулю, а сила тока будет наибольшей. Разрядка завершена. В начале третьей четверти электродвижущая сила будет возрастать, изменив своё направление. Вновь начнётся процесс заряда. Направление зарядного тока в третью четверть будет таким же, как и в предыдущую. По мере зарядки конденсатора эта величина будет убывать. К концу третьей четверти процесс зарядки будет завершён.

     Электродвижущая сила достигнет своего наибольшего отрицательного значения. А на той обкладке, на которой в течение первого полупериода был положительный заряд, теперь будет отрицательный. Во время четвёртой четверти значение электродвижущей силы снова будет стремиться к нулю. Конденсатор будет разряжаться. Соответственно, в цепи появится постепенно нарастающий ток. Процесс повторяется. Таким образом, фаза переменного тока в конденсаторной цепи опережает фазу напряжения на 90 градусов.

     Формула сопротивления

     Формула ёмкостного сопротивления выводится следующим образом:

     Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление.

     Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

     Применение на практике

     Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:

     • Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
     • Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.

     Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

     Благодаря своим свойствам конденсаторы используются в тех случаях, когда необходимо передать и постоянный, и переменный ток по одним и тем же проводам. Источник постоянного напряжения подключается к общему проводу и второму выводу ёмкости , через которую присоединяется источник переменного напряжения. На другой стороне происходит разделение: потребитель переменного подключается через конденсатор той же ёмкости, а потребитель постоянного — напрямую, до выводов детали.

     Распространённый пример подобного использования — это телевизионная наружная антенна с усилителем. Сам телевизор или подключаемое к кабелю устройство, называемое «инжектором», подаёт напряжение питания. В антенном усилителе происходит разделение и фильтрация сигналов. Таким образом, ёмкостное сопротивление конденсатора находит широкое применение . Фильтры обеспечивают задержку одних сигналов и прохождение — других.

     Благодаря этому свойству, можно передавать сразу и переменное, и постоянное напряжение, что имеет немаловажное значение при построении некоторых линий связи.

     Конспект урока по физике. Активное, ёмкостное и индуктивное сопротивление в цепи переменного тока.

     Урок по физике-11 класс. Активное, ёмкостное и индуктивное сопротивление в цепи переменного тока.

     Цели урока.

     Предметные: Сформировать знания учащихся о различных видах сопротивлениях в цепи переменного тока.

     Метапредметные: Развивать элементы творческой деятельности учащихся на уроке. Закрепить умения самостоятельно добывать знания из различных источников, работать с медийной информацией, проводить анализ, исследование.

     Личностные: Воспитывать активную жизненную позицию. Развивать навыки проектной деятельности.

     Учебно-наглядные пособия и оборудование

     1. Плакаты:

     а) цепь переменного тока с активным сопротивлением; 
     б) цепь переменного тока с индуктивным сопротивлением;
     в) цепь, переменного тока с емкостью; 
     2 .Компьютер, интерактивная доска.

     3. Электрические лампы.

     4. Индуктивные катушки, различные виды обмоток.

     План урока:

     1. Организационный момент.

     2. Повторение изученного материала.

     3. Объяснение нового материала.

     4. Обобщение изученного материала.

     5. Домашнее задание.

     Ход урока

     Организационный момент

     Проверяю отсутствующих, внешнее состояния класса и рабочих мест учащихся, создаю психологический настрой учащихся и рабочую обстановку на уроке.

     Повторение изученного материала

     Для определения уровня усвоения предыдущего материала, предлагаю учащимся написать самостоятельную работу, задание которой соответствует уровню В.

     Самостоятельная работа.

     1. Что называется периодом?

     2. Что такое амплитуда?

     3. Что называется частотой переменного тока?

     4. Какой частоты вырабатывается переменный ток?

     5. Какой зависимостью связаны период и частота?

     6. Какими буквами обозначаются частота и период?

     7. Какое явление получило название электромагнитной индукции?

     8. От чего зависит величина индуктивной электродвижущей силы (эдс)?

     9. Кем и когда было открыто явление электромагнитной индукции?

     Последовательность работы над проектом.

     Этапы проектной деятельности

     Формулировка проблемы.

     Изучение большого объёма нового материала за короткий промежуток времени. Подготовка к зачёту.

     Генерирование идей для решения данной проблемы.

     1. 1. Создать презентацию.

        2. Написать опорный конспект.

        3. Создать буклет.

        4. Создать таблицу.

     Постановка цели для решения данной проблемы (определение вида конечного продукта).

     Создать индивидуальную таблицу каждым учащимся по определённым параметрам и заполнить её.

     Разработка плана работы над проектом.

     1. 1. 1. Разделить класс на группы.

           2. Определить количество групп.

           3. Определить учебную задачу каждой группы.

     Формулирование вопросов для исследования.

     1,3 группа

     1.Определение каждого вида сопротивления.

     2.Что является сопротивлением.

     3.Схема цепи.

     4. Графики силы тока и напряжения для различных видов сопротивлений.

     5.Формулы силы тока , напряжения для различных видов сопротивления.

     6.Амплитуда силы тока, напряжения.

     7. Закон Ома.

     8. Формулы сопротивлений.

     9.Выводы.

     Подбор информационных ресурсов для исследований.

     2.4 группа

     1. Подбор презентации в интернете по данной теме.

     2. Работа с учебником «Физика-11».

     3. Консультации у учителя.

     Создание таблицы-продукта , критерии оценивания.

     Обмен информацией между группами.

     Домашнее задание. Оформить в чистовом виде продукт проекта- таблицу «Различные сопротивления в цепи переменного тока».

     Ёмкостное сопротивление. Индуктивное сопротивление

     Физика – какая ёмкость слова,

     Физика для нас не просто звук,

     Физика – опора и основа,

     Всех без исключения наук!

     Задача 1. В цепи переменного тока с частотой 50 Гц при напряжении 220 В возникает сила тока 4 А. Известно, что в эту цепь включена катушка с ничтожно малым активным сопротивлением. Какова индуктивность катушки?

     ДАНО:	РЕШЕНИЕ Индуктивное сопротивление определяется по формуле Циклическую частоту можно рассчитать по выражению Запишем закон Ома для участка цепи Приравняем две последних формулы для расчёта индуктивного сопротивления и выразим индуктивность катушки

     Ответ: 175 мГн.

     Задача 2. . При увеличении частоты от 50 Гц до 60 Гц, ёмкостное сопротивление конденсатора с постоянной ёмкостью уменьшилось на 10 Ом.  Найдите электроёмкость конденсатора.

     ДАНО:	РЕШЕНИЕ Ёмкостное сопротивление определяется по формуле Циклическую частоту можно определить по выражению Тогда ёмкостное сопротивление Применим данную формулу для двух значений частоты Изменение ёмкостного сопротивления конденсатора определяется по формуле Тогда электроёмкость конденсатора

     Ответ: 53 мкФ.

     Задача 3. Известно, что через катушку, включенную в цепь переменного тока с частотой 200 Гц, проходит ток не более 3 А. Найдите напряжение на катушке, в момент времени t = 0,2 мс, если в начальный момент времени оно максимально. Индуктивность катушки равна 5 мГн.

     ДАНО:	СИ	РЕШЕНИЕ Из закона Ома для участка цепи следует Индуктивное сопротивление определяется по формуле Амплитудное напряжение рассчитывается по выражению Запишем уравнение гармонических колебаний напряжения Циклическая частота равна Тогда уравнение гармонических колебаний напряжения будет иметь вид Тогда в момент времени t = 0,2 мс напряжение будет равно

     Ответ: 18,3 В.

     Задача 4. Докажите, что если частота переменного тока равна собственной частоте, то по катушке индуктивности и конденсатору будет протекать одинаковый ток, а также на катушке и на конденсаторе будет одинаковое напряжение.

     ДАНО:

     РЕШЕНИЕ Собственная циклическая частота в колебательном контуре равна По определению, собственная частота – это частота свободных колебаний (то есть, колебаний при отсутствии активного сопротивления) Таким образом, имеется два случая: либо катушка и конденсатор подключены параллельно, либо они подключены последовательно. Активное сопротивление отсутствует. Рассмотрим параллельное соединение Из закона Ома для участка цепи Индуктивное сопротивление определяется по формуле Ёмкостное сопротивление определяется по формуле С учётом двух последних формул и равенства напряжений получаем Теперь рассмотрим последовательное соединение При последовательном соединении Из закона Ома для участка цепи Индуктивное сопротивление определяется по формуле Ёмкостное сопротивление определяется по формуле С учётом двух последних формул и равенства силы тока получаем

     Доказать

     Ответ: доказано.

     Импеданс

     . Как определить, емкостный или индуктивный, учитывая нагрузку?

     Почему это так …

     Импеданс определяется как отношение вектора напряжения и вектора тока . Для получения дополнительной информации о фазорах вы можете проверить здесь.

     По сути, вектор — это комплексное число и, как таковое, поддерживает несколько типов представления, включая прямоугольное (то, что вы выразили) и полярную форму или модуль / угол.Если мы выразим ток и напряжение в виде комплексных чисел, импеданс будет комплексным числом , но вы, , не можете, сказать, что это вектор.

     Фазоры применяются для анализа установившегося состояния электрической цепи . В случае индуктивной цепи ток задерживается по фазе с напряжением , тогда как в емкостной цепи ток опережает фазу с напряжением . Как это связано с импедансом? так как импеданс — это комплексное число, то угол соответствует фазовому сдвигу между напряжением и током .
     Если этот угол положительный, напряжение опережает ток или ток опаздывает по сравнению с напряжением, так что это индуктивная цепь. Аналогичный анализ можно поднять и для емкостной цепи.
     Положительный угол соответствует комплексному числу, действительная и мнимая части которого положительны.

     … что нам делать, когда в нагрузке присутствует как емкость, так и индуктивность (т.е. сеть RLC)?

     В цепи, содержащей как емкостные, так и индуктивные элементы , преобладает один идентификатор , то есть цепь в конечном итоге будет индуктивной или емкостной, в соответствии со значением , эквивалентным общему импедансу .Можно ли убрать каждый индуктивный и емкостной элементы? Да. В этом случае говорят, что цепь находится в резонансе и с точки зрения источника представляет собой чисто резистивную цепь, хотя и содержит реактивные элементы.

     РЕАКТИВНАЯ МОЩНОСТЬ — прикладное промышленное электричество

     Рисунок 6.1 Чисто резистивная цепь переменного тока: напряжение и ток резистора синфазны.

     Если бы мы изобразили ток и напряжение для очень простой цепи переменного тока, состоящей из источника и резистора (рисунок выше), это выглядело бы примерно так: (рисунок ниже)

     Рисунок 6.2 Напряжение и ток «синфазны» для резистивной цепи.

     Поскольку резистор просто и напрямую сопротивляется протеканию тока во все периоды времени, форма волны падения напряжения на резисторе точно совпадает по фазе с формой волны тока через него. Мы можем посмотреть в любой момент времени вдоль горизонтальной оси графика и сравнить эти значения тока и напряжения друг с другом (любой «снимок», показывающий значения волны, обозначается как мгновенных значений , что означает значения при этом момент времени ).Когда мгновенное значение тока равно нулю, мгновенное напряжение на резисторе также равно нулю. Аналогичным образом, в момент времени, когда ток через резистор находится на своем положительном пике, напряжение на резисторе также находится на своем положительном пике, и так далее. В любой момент времени на волнах закон Ома справедлив для мгновенных значений напряжения и тока.

     Мы также можем рассчитать мощность, рассеиваемую этим резистором, и нанести эти значения на тот же график: (рисунок ниже)

     Рисунок 6.3 Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительная. Сопротивление резисторов

     и катушек индуктивности

     Катушки индуктивности ведут себя иначе, чем резисторы. В то время как резисторы просто противодействуют протеканию тока через них (снижая напряжение, прямо пропорциональное току), индукторы противодействуют изменениям тока через них, понижая напряжение, прямо пропорциональное скорости изменения тока . В соответствии с законом Ленца , это индуцированное напряжение всегда имеет такую ​​полярность, чтобы поддерживать ток на его текущем уровне.То есть, если ток увеличивается по величине, индуцированное напряжение будет «противодействовать» току; если ток уменьшается, полярность изменится на противоположную и «подтолкнет» ток, чтобы противодействовать уменьшению. Это противодействие текущему изменению называется реактивным сопротивлением , а не сопротивлением. Выражаясь математически, соотношение между падением напряжения на катушке индуктивности и скоростью изменения тока через катушку индуктивности выглядит следующим образом:

     [латекс] e = L \ frac {d_i} {d_t} [/ латекс]

     Переменный ток в простой индуктивной цепи

     Выражение di / dt получено из расчетов, означающее скорость изменения мгновенного тока (i) во времени в амперах в секунду.Индуктивность (L) измеряется в Генри, а мгновенное напряжение (е), конечно, выражается в вольтах. Иногда вы можете встретить скорость мгновенного напряжения, выраженную как «v» вместо «e» (v = L di / dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктивности:

     Рисунок 6.4 Чистая индуктивная цепь: ток индуктора отстает от напряжения индуктора на 90 °.

     Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:

     Рисунок 6.5 Чистая индуктивная цепь, формы сигналов.

     Помните, что падение напряжения на катушке индуктивности является реакцией на изменение тока через нее. Следовательно, мгновенное напряжение равно нулю всякий раз, когда мгновенный ток достигает пика (нулевое изменение или наклон уровня на синусоидальной волне тока), а мгновенное напряжение находится на пике везде, где мгновенный ток имеет максимальное изменение (точки самый крутой наклон на текущей волне, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, сдвинутой по фазе на 90 ° с волной тока. Глядя на график, кажется, что волна напряжения имеет «фору» по сравнению с волной тока; напряжение «опережает» ток, а ток «отстает» от напряжения.

     Ток отстает от напряжения на 90 ° в чисто индуктивной цепи.

     Все становится еще интереснее, когда мы строим график мощности для этой схемы:

     Рисунок 6.6 В чисто индуктивной цепи мгновенная мощность может быть положительной или отрицательной.

     Поскольку мгновенная мощность является произведением мгновенного напряжения и мгновенного тока (p = ie), мощность равна нулю, когда мгновенный ток или напряжение равно нулю. Если мгновенный ток и напряжение положительные (над линией), мощность положительная. Как и в примере с резистором, мощность также положительна, когда мгновенные ток и напряжение отрицательны (ниже линии). Однако, поскольку волны тока и напряжения сдвинуты по фазе на 90 °, бывают моменты, когда одна из них положительна, а другая — отрицательна, что приводит к одинаково частым случаям отрицательной мгновенной мощности .

     Что такое отрицательная сила?

     Но что означает отрицательная мощность ? Это означает, что катушка индуктивности возвращает мощность в цепь, в то время как положительная мощность означает, что она поглощает мощность из цепи. Поскольку положительные и отрицательные циклы мощности равны по величине и продолжительности с течением времени, индуктор возвращает обратно в цепь столько же мощности, сколько потребляет в течение полного цикла. В практическом смысле это означает, что реактивное сопротивление катушки индуктивности рассеивает нулевую полезную энергию, в отличие от сопротивления резистора, который рассеивает энергию в виде тепла.Имейте в виду, это только для идеальных катушек индуктивности, у которых нет сопротивления провода.

     Реактивное сопротивление в зависимости от сопротивления

     Противодействие катушки индуктивности изменению тока приводит к противодействию переменному току в целом, который по определению всегда изменяется по мгновенной величине и направлению. Это противодействие переменному току аналогично сопротивлению, но отличается тем, что всегда приводит к сдвигу фаз между током и напряжением и рассеивает нулевую мощность. Из-за различий он имеет другое название: реактивное сопротивление .Реактивное сопротивление по переменному току выражается в омах, как и сопротивление, за исключением того, что его математический символ — X вместо R. Чтобы быть конкретным, реактивное сопротивление, связанное с катушкой индуктивности, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X _L .

     Поскольку напряжение на индукторах падает пропорционально скорости изменения тока, они будут снижать большее напряжение при более быстром изменении тока и меньшее напряжение при более медленном изменении тока. Это означает, что реактивное сопротивление в Ом для любой катушки индуктивности прямо пропорционально частоте переменного тока.Точная формула для определения реактивного сопротивления выглядит следующим образом:

     [латекс] X_L = 2πfL [/ латекс]

     Если мы подвергнем индуктор 10 мГн воздействию частот 60, 120 и 2500 Гц, он проявит реактивные сопротивления, указанные в таблице ниже.

     Реактивное сопротивление индуктора 10 мГн:

     Таблица 6.1 Реактивное сопротивление индуктора 10 мГн

     Частота (Герцы)	Реактивное сопротивление (Ом)
     60	3.7699
     120	7,5398
     2500	157.0796

     В уравнении реактивного сопротивления термин «2πf» (все в правой части, кроме L) имеет особое значение. Это количество радиан в секунду, на которое «вращается» переменный ток, если вы представите себе один цикл переменного тока, представляющий вращение полного круга. радиан — это единица измерения угла: в одном полном круге 2π радиана, так же как в полном круге 360 °.Если генератор переменного тока является двухполюсным, он будет производить один цикл на каждый полный оборот вала, что составляет каждые 2π радиан или 360 °. Если эту константу 2π умножить на частоту в герцах (циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.

     Угловая скорость в системах переменного тока

     Угловая скорость может быть представлена ​​выражением 2πf или ее собственным символом — строчной греческой буквой омега, которая похожа на нашу строчную римскую букву «w»: ω.Таким образом, формула реактивного сопротивления X _L = 2πfL также может быть записана как X _L = ωL.

     Следует понимать, что эта «угловая скорость» является выражением того, насколько быстро колеблются формы колебаний переменного тока, полный цикл равен 2π радиан. Это не обязательно отражает фактическую скорость вала генератора переменного тока. Если генератор имеет более двух полюсов, угловая скорость будет кратной скорости вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, а не в (простых) радианах в секунду, чтобы отличить его от механического движения.

     Как бы мы ни выразили угловую скорость системы, очевидно, что она прямо пропорциональна реактивному сопротивлению в катушке индуктивности. По мере увеличения частоты (или скорости вала генератора переменного тока) в системе переменного тока катушка индуктивности будет оказывать большее сопротивление прохождению тока, и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в вольтах), деленному на индуктивное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Пример схемы показан здесь:

     Индуктивное сопротивление

     (Индуктивное сопротивление индуктора 10 мГн при 60 Гц)

     [латекс] X_L = 3,7600 Ом [/ латекс]

     [латекс] I_ {X_ {L}} = \ frac {E} {X} [/ latex]

     [латекс] = \ frac {10 В} {3,7600 Ом} [/ латекс]

     [латекс] \ mathbf {= 2.6526A} [/ латекс]

     Фазовые углы

     Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, напряжение имеет фазовый сдвиг + 90 ° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что сопротивление катушки индуктивности току также имеет фазовый угол:

     [латекс] \ text {Opposition} = \ frac {\ text {Voltage}} {\ text {Current}} [/ latex]

     [латекс] \ text {Opposition} = \ frac {10 V \ angle \ text {90 °}} {2.6526A \ angle \ text {90 °}} [/ латекс]

     [латекс] \ begin {align} \ text {Opposition} = & 3.7699 \ Omega \ angle \ text {90 °} \\ \ text {или} & 0 + j3.7699 \ Omega \ end {align} [/ latex]

     Математически мы говорим, что фазовый угол сопротивления катушки индуктивности току равен 90 °, что означает, что сопротивление катушки индуктивности току является положительной мнимой величиной. Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют. Будет полезно представить любое сопротивление компонента току в терминах комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.

     • Индуктивное реактивное сопротивление — это противодействие, которое индуктор предлагает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его магнитном поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
     • Индуктивное реактивное сопротивление можно рассчитать по следующей формуле: X _L = 2πfL
     • Угловая скорость цепи переменного тока — это еще один способ выразить ее частоту в единицах электрических радиан в секунду вместо циклов в секунду.Его символизирует строчная греческая буква «омега» или ω.
     • Индуктивное реактивное сопротивление увеличивается на с увеличением частоты. Другими словами, чем выше частота, тем сильнее он противодействует потоку электронов переменного тока.

     Возьмем эту схему в качестве примера для работы:

     Цепь индуктивности последовательного резистора : ток отстает от приложенного напряжения от 0 ° до 90 °.

     Резистор будет обеспечивать сопротивление 5 Ом переменному току независимо от частоты, а катушка индуктивности — 3 Ом.Реактивное сопротивление 7699 Ом на переменный ток при 60 Гц.

     Поскольку сопротивление резистора является действительным числом (5 Ом 0 ° или 5 + j0 Ом), а реактивное сопротивление катушки индуктивности — мнимым числом (3,7699 Ом ∠ 90 ° или 0 + j3,7699 Ом), совокупный эффект двух компонентов будет противодействовать току, равному комплексной сумме двух чисел.

     Это комбинированное противодействие будет векторной комбинацией сопротивления и реактивного сопротивления. Чтобы выразить это противопоставление лаконично, нам нужен более полный термин для обозначения сопротивления току, чем просто сопротивление или реактивное сопротивление.

     Этот термин называется импеданс , его символ — Z, и он также выражается в единицах Ом, как сопротивление и реактивное сопротивление. В приведенном выше примере полное сопротивление цепи составляет:

     Сопротивление по закону Ома

     Импеданс связан с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:

     На самом деле, это гораздо более полная форма закона Ома, чем то, чему учили в электронике постоянного тока (E = IR), так же как импеданс является гораздо более полным выражением сопротивления потоку тока, чем сопротивление. Любое сопротивление и любое реактивное сопротивление, отдельно или в комбинации (последовательно / параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока.

     Чтобы вычислить ток в приведенной выше схеме, нам сначала нужно задать опорный фазовый угол для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивного и индуктивного импеданса равны , всегда 0 ° и + 90 °, соответственно, независимо от заданных фазовых углов для напряжения или тока).

     Как и в чисто индуктивной схеме, волна тока отстает от волны напряжения (источника), хотя на этот раз отставание не так велико: всего 37,016 ° вместо полных 90 °, как в случае чисто индуктивного схема.

     Ток отстает от напряжения в последовательной цепи L-R.

     Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось.Напряжение на резисторе синфазно (сдвиг 0 °) с током через него, а напряжение на катушке индуктивности на + 90 ° не совпадает по фазе с током, проходящим через него. Мы можем проверить это математически:

     Напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I находятся в фазе (только для резистора).

     Напряжение на катушке индуктивности имеет фазовый угол 52.984 °, в то время как ток через катушку индуктивности имеет фазовый угол -37,016 °, разница между ними составляет ровно 90 °. Это говорит нам о том, что E и I все еще не совпадают по фазе на 90 ° (только для катушки индуктивности).

     Используйте закон Кирхгофа о напряжении

     Мы также можем математически доказать, что эти комплексные значения в сумме составляют общее напряжение, как и предсказывает закон Кирхгофа:

     Давайте возьмем те же компоненты для нашей схемы последовательного примера и подключим их параллельно:

     Рисунок 6.7 Параллельная цепь R-L.

     Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:

     Таблица 6.2 Таблица анализа импеданса 1

     Единственная разница в нашей методике анализа на этот раз состоит в том, что мы будем применять правила для параллельных цепей вместо правил для последовательных цепей.Принцип такой же, как и для DC. Мы знаем, что напряжение распределяется равномерно между всеми компонентами в параллельной цепи, поэтому мы можем передать цифру общего напряжения (10 вольт 0 °) на все столбцы компонентов:

     Таблица 6.3. Таблица анализа импеданса 2

     Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через катушку индуктивности:

     Таблица 6.4. Таблица анализа импеданса 3

     Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (Закон Кирхгофа по току по-прежнему остается верным для переменного тока, как и для постоянного тока):

     Таблица 6.5 Таблица анализа импеданса 4

     Наконец, общий импеданс можно рассчитать, используя закон Ома (Z = E / I) по вертикали в столбце «Всего». Между прочим, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений.

     [латекс] \ tag {6.1} Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [ / латекс]

     Единственная проблема с использованием этой формулы заключается в том, что она обычно требует выполнения множества нажатий клавиш калькулятора.И если вы полны решимости использовать формулу, подобную этой «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших таблицах анализа, и этот пример ничем не отличается. Независимо от того, каким способом вы рассчитываете полное сопротивление (закон Ома или обратная формула), вы получите одно и то же значение:

     Таблица 6.6 Таблица анализа импеданса 5
     • Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы.Только обязательно выполняйте все вычисления в сложной (не скалярной) форме!

     [латекс] Z_ {parallel} = \ frac {1} {(\ frac {1} {Z1} + \ frac {1} {Z2} +… \ Frac {1} {Zn})} [/ латекс]

     • Закон Ома для цепей переменного тока:

     [латекс] E = {I} {Z} [/ латекс]; [латекс] I = \ frac {E} {Z} [/ latex]; [латекс] Z = \ frac {E} {I} [/ latex]

     • Когда резисторы и индукторы смешаны вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и + 90 °.Ток в цепи будет иметь фазовый угол от 0 ° до -90 °.
     • Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение однородно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.

     В идеальном случае индуктор действует как чисто реактивное устройство. То есть его противодействие переменному току строго основано на индуктивной реакции на изменения тока, а не на трении электронов, как в случае с резистивными компонентами.Однако индукторы не так чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, и мы знаем, что все проволоки обладают некоторой измеримой величиной сопротивления (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было подключено последовательно с идеальной индуктивностью катушки, например:

     Рисунок 6.8 Катушка индуктивности Эквивалентная схема реальной катушки индуктивности.

     Следовательно, полное сопротивление любой реальной катушки индуктивности всегда будет представлять собой сложную комбинацию сопротивления и индуктивного реактивного сопротивления.

     Эту проблему усугубляет то, что называется скин-эффектом , который представляет собой тенденцию переменного тока проходить через внешние области поперечного сечения проводника, а не через середину. Когда электроны движутся в одном направлении (постоянный ток), они используют для движения всю площадь поперечного сечения проводника. С другой стороны, электроны, меняющие направление потока, стремятся избежать прохождения через самую середину проводника, ограничивая доступную эффективную площадь поперечного сечения. Скин-эффект становится более выраженным с увеличением частоты.

     Кроме того, переменное магнитное поле индуктора, питаемого переменным током, может излучаться в космос как часть электромагнитной волны, особенно если переменный ток имеет высокую частоту. Эта излучаемая энергия не возвращается к катушке индуктивности и поэтому проявляется в виде сопротивления (рассеяния мощности) в цепи.

     Помимо резистивных потерь в проводе и излучения, в индукторах с железным сердечником действуют и другие эффекты, которые проявляются как дополнительное сопротивление между выводами.Когда на индуктор подается переменный ток, создаваемые переменные магнитные поля имеют тенденцию индуцировать циркулирующие токи в железном сердечнике, известные как вихревые токи . Эти электрические токи в железном сердечнике должны преодолевать электрическое сопротивление, обеспечиваемое железом, который не так хорош в качестве проводника, как медь. Вихретоковым потерям в первую очередь противодействуют, разделив железный сердечник на множество тонких листов (пластин), каждый из которых отделен от другого тонким слоем электроизоляционного лака.Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого не будет (или будет очень мало) резистивных потерь.

     Как и следовало ожидать, потери на вихревые токи в металлических сердечниках индуктора проявляются в виде тепла. Эффект более выражен на высоких частотах и ​​может быть настолько сильным, что иногда его используют в производственных процессах для нагрева металлических предметов! Фактически, этот процесс «индукционного нагрева» часто используется при литье металлов высокой чистоты, когда металлические элементы и сплавы должны нагреваться в вакууме, чтобы избежать загрязнения воздухом, и, таким образом, стандартная технология нагрева сжиганием была бы бесполезной.Это «бесконтактная» технология, когда нагретое вещество не должно касаться катушки (катушек), создающей магнитное поле.

     В высокочастотной среде вихревые токи могут возникать даже в поперечном сечении самого провода, что способствует дополнительным резистивным эффектам. Чтобы противодействовать этой тенденции, можно использовать специальный провод, сделанный из очень тонких, индивидуально изолированных жил, который называется Litz wire (сокращенно от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.

     Кроме того, любой магнитный гистерезис, который необходимо преодолевать при каждом изменении направления магнитного поля индуктора, представляет собой расход энергии, который проявляется как сопротивление в цепи. Некоторые материалы сердечника (например, феррит) особенно известны своим гистерезисным эффектом. Противодействовать этому эффекту лучше всего за счет правильного выбора материала сердечника и ограничения пиковой напряженности магнитного поля, генерируемой в каждом цикле.

     В целом паразитные резистивные свойства реального индуктора (сопротивление провода, радиационные потери, вихревые токи и гистерезисные потери) выражаются одним термином «эффективное сопротивление»:

     Рисунок 6.9 Эквивалентная схема реального индуктора с потерями на скин-эффект, излучение, вихревые токи и гистерезис.

     Следует отметить, что скин-эффект и потери на излучение применимы к прямым отрезкам провода в цепи переменного тока так же хорошо, как и к спиральному проводу. Обычно их совокупный эффект слишком мал, чтобы его можно было заметить, но на радиочастотах они могут быть довольно большими. Например, антенна радиопередатчика спроектирована специально для рассеивания наибольшего количества энергии в виде электромагнитного излучения.

     Конденсаторы Vs. Резисторы

     Конденсаторы не ведут себя так же, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток при зарядке или разрядке до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе. Это противодействие изменению напряжения представляет собой еще одну форму реактивного сопротивления , но оно прямо противоположно тому, которое демонстрируют индукторы.

     Характеристики цепи конденсатора

     Выражаясь математически, соотношение между током, протекающим через конденсатор, и скоростью изменения напряжения на конденсаторе как таковое:

     [латекс] i = C \ frac {d_e} {d_t} [/ латекс]

     Выражение de / dt получено из расчетов, означающее скорость изменения мгновенного напряжения (e) во времени в вольтах в секунду. Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.Иногда скорость мгновенного изменения напряжения с течением времени выражается как dv / dt вместо de / dt: вместо напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую схему конденсатора:

     Рисунок 6.10 Чистая емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90 °

     Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:

     Рисунок 6.11 Формы сигналов чисто емкостной цепи.

     Помните, что ток через конденсатор — это реакция на изменение напряжения на нем. Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение достигает пика (нулевое изменение или наклон уровня на синусоидальной волне напряжения), а мгновенный ток находится на пике везде, где мгновенное напряжение имеет максимальное изменение (точки самый крутой наклон на волне напряжения, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, которая на -90 ° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна тока имеет «фору» по сравнению с волной напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.

     Рисунок 6.12 Напряжение отстает от тока на 90 ° в чисто емкостной цепи.

     Как вы могли догадаться, та же необычная волна мощности, которую мы видели в простой цепи индуктивности, присутствует и в простой цепи конденсатора:

     Рисунок 6.13 В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.

     Как и в случае с простой схемой индуктивности, сдвиг фазы на 90 градусов между напряжением и током приводит к появлению волны мощности, которая в равной степени чередуется между положительной и отрицательной полярностью. Это означает, что конденсатор не рассеивает мощность, поскольку он реагирует на изменения напряжения; он просто поочередно поглощает и высвобождает энергию.

     Реактивное сопротивление конденсатора

     Противодействие конденсатора изменению напряжения переводится в противодействие переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.Для любой данной величины переменного напряжения на данной частоте конденсатор данного размера будет «проводить» определенную величину переменного тока. Точно так же, как ток через резистор является функцией напряжения на резисторе и сопротивления, предлагаемого резистором, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , обеспечиваемого конденсатором. Как и в случае катушек индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или X _C , если точнее).

     Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больше тока при более быстром изменении напряжения (поскольку они заряжаются и разряжаются до тех же пиков напряжения за меньшее время) и меньший ток при более медленном изменении напряжения. . Это означает, что реактивное сопротивление в Ом для любого конденсатора равно , обратно пропорционально частоте переменного тока.

     [латекс] X_C = \ frac {1} {2πfC} [/ латекс]

     Реактивное сопротивление конденсатора 100 мкФ:

     Частота (Герцы)	Реактивное сопротивление (Ом)
     60	26.5258
     120	13,2629
     2500	0,6366

     Обратите внимание, что отношение емкостного реактивного сопротивления к частоте прямо противоположно отношению индуктивного реактивного сопротивления. Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное реактивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Индукторы противодействуют более быстрому изменению токов, создавая большие падения напряжения; Конденсаторы противодействуют более быстрому изменению падений напряжения, допуская большие токи.

     Как и в случае с индукторами, член 2πf в уравнении реактивного сопротивления может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока. Таким образом, уравнение X _C = 1 / (2πfC) также может быть записано как X _C = 1 / (ωC), где ω приведено в единицах радиан в секунду .

     Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Следующая схема иллюстрирует это математическое соотношение на примере:

     Емкостное реактивное сопротивление.

     [латекс] X_C = 26,5258 Ом [/ латекс]

     [латекс] I = \ frac {E} {X} [/ латекс]

     [латекс] I = \ frac {10} {26,5258 Ом} [/ латекс]

     [латекс] I = 0,3770A [/ латекс]

     Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг + 90 ° по отношению к напряжению.Если мы математически представим эти фазовые углы напряжения и тока, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.

     Напряжение в конденсаторе отстает от тока на 90 °.

     Математически мы говорим, что фазовый угол сопротивления конденсатора току составляет -90 °, что означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. Рисунок выше). Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют.Будет полезно представить любое сопротивление компонента току в виде комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.

     • Емкостное реактивное сопротивление — это противодействие, которое конденсатор предлагает переменному току из-за сдвинутого по фазе накопления и выделения энергии в его электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
     • Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1 / (2πfC)
     • Емкостное реактивное сопротивление уменьшается с увеличением частоты.Другими словами, чем выше частота, тем меньше он противодействует (тем больше «проводит») переменному току.

     Используя компоненты с одинаковыми значениями в нашей схеме последовательного примера, мы подключим их параллельно и посмотрим, что произойдет:

     Рисунок 6.14 Параллельная цепь RC.

     Параллельный резистор и конденсатор

     Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:

     Таблица 6.7

     Сейчас это параллельная схема, мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт ∠ 0 °) во все столбцы:

     Таблица 6.8 Расчет

     по закону Ома

     Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам в таблице, рассчитав ток через резистор и ток через конденсатор:

     Таблица 6.9

     Как и в случае цепей постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа):

     Таблица 6.10

     Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно.Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться. равномерно по той же формуле. И снова формула параллельного импеданса выглядит так:

     [латекс] Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [/ латекс]

     Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами.Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы получим ту же цифру:

     • Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы. Только не забудьте
       • выполнять все вычисления в сложной (не скалярной) форме! ZTotal = 1 / (1 / Z1 + 1 / Z2 +.. 1 / Zn)
       • Закон Ома для цепей переменного тока: E = IZ; I = E / Z; Z = E / I
       • Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °.Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
       • Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение однородно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.

     (Следующий раздел был адаптирован из: Уроки электрических цепей, Том II, Глава 5 — Реактивное сопротивление и импеданс — R, L и C)

     Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.

     Сопротивление

     Это по существу трение против потока тока. В той или иной степени он присутствует во всех проводниках (кроме проводов super !), Особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).

     Реактивное сопротивление

     По сути, это инерция против тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности. Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).

     Импеданс

     Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через полное сопротивление, возникает падение напряжения, которое находится где-то между 0 ° и 90 ° не в фазе с током. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.

     Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.

     Рис. 6.15. Идеальный резистор, катушка индуктивности и конденсатор.

     Фазовый угол импеданса для любого компонента — это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент. Для идеального резистора падение напряжения и ток всегда в фазе друг с другом, поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.

     Полное сопротивление переменного тока ведет себя аналогично сопротивлению в цепях постоянного тока: они складываются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:

     Закон Ома для цепи переменного тока

     [латекс] \ begin {align} \ tag {6.2} \ text {E} & = {I} {Z} \\ \ text {I} & = \ frac {E} {Z} \\ \ text {Z } & = \ frac {E} {I} \ end {align} [/ latex]

     Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:

     Рисунок 6.16 Пример параллельной схемы R, L и C.

     Импеданс в параллельных компонентах

     Тот факт, что эти компоненты соединены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивление вообще не изменится.

     Рисунок 6.17 Пример параллельной цепи R, L и C с импедансами, заменяющими значения компонентов.

     Со всеми значениями компонентов, выраженными как импедансы (Z), мы можем создать таблицу анализа и действовать, как в предыдущем примере задачи, за исключением того, что на этот раз следуя правилам параллельных цепей вместо последовательного.

     Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем перенести цифру для общего напряжения во все столбцы компонентов в таблице:

     Значения компонентов в таблице 6.11 выражаются в виде импеданса изображения 2

     Теперь мы можем применить закон Ома (I = E / Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:

     Таблица 6.12. Значения компонентов выражаются в виде изображения импеданса 3

     Расчет полного тока и полного импеданса

     Существует две стратегии расчета полного тока и полного сопротивления.Во-первых, мы можем рассчитать общий импеданс из всех отдельных параллельных сопротивлений (Z _Total = 1 / (1 / Z _R + 1 / Z _L + 1 / Z _C ), а затем вычислить общий ток путем деления напряжения источника на полное сопротивление (I = E / Z).

     Тем не менее, работа с уравнением параллельного импеданса с комплексными числами — непростая задача, учитывая все взаимные колебания (1 / Z). Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (преобразовать индивидуальные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно в полярную форму для окончательной инверсии, затем инвертировать).Второй способ вычисления общего тока и полного импеданса — это сложить все токи ответвления, чтобы получить общий ток (полный ток в параллельной цепи — переменный или постоянный — равен сумме токов ответвления), а затем использовать закон Ома. для определения полного сопротивления по общему напряжению и общему току (Z = E / I).

     Таблица 6.13 Расчет общего тока и полного импеданса

     Любой из методов, выполненный должным образом, даст правильные ответы.

     За исключением расчетов мощности (P), все расчеты цепей переменного тока основаны на тех же общих принципах, что и расчеты для цепей постоянного тока.Единственное существенное отличие состоит в том, что в расчетах переменного тока используются комплексные величины, а в расчетах постоянного тока используются скалярные величины. Закон Ома, законы Кирхгофа и даже сетевые теоремы, изученные на постоянном токе, остаются верными для переменного тока, когда напряжение, ток и импеданс выражаются комплексными числами. Те же стратегии поиска и устранения неисправностей, которые применяются в цепях постоянного тока, справедливы и для переменного тока, хотя с переменным током, безусловно, может быть труднее работать из-за фазовых углов, которые не регистрируются портативным мультиметром.

     Власть — это отдельная тема, которая будет рассмотрена в отдельной главе этой книги. Поскольку мощность в реактивной цепи одновременно поглощается и высвобождается, а не просто рассеивается, как в случае с резисторами, ее математическая обработка требует более прямого применения тригонометрии для решения.

     При анализе цепи переменного тока первым шагом в анализе является преобразование всех значений компонентов резистора, катушки индуктивности и конденсатора в импедансы (Z) в зависимости от частоты источника питания.После этого выполните те же шаги и стратегии, которые были изучены для анализа цепей постоянного тока, используя новую форму закона Ома: E = IZ; I = E / Z; и Z = E / I

     Помните, что только рассчитанные значения, выраженные в полярной форме , применимы непосредственно к эмпирическим измерениям напряжения и тока. Прямоугольные обозначения — это просто полезный инструмент для сложения и вычитания сложных величин. Полярная запись, где величина (длина вектора) напрямую связана с величиной измеряемого напряжения или тока, а угол напрямую связан с фазовым сдвигом в градусах, является наиболее практичным способом выражения сложных величин для анализа схем.

     Разница между индуктивными и емкостными банками нагрузки

     Знакомы ли вы с различными типами решений для банков реактивной нагрузки? Банк реактивной нагрузки имитирует системы, на которые воздействуют электродвигатели или другие электромагнитные устройства в электросети. Если на объекте находится значительное количество устройств с приводом от двигателя, трансформаторов и конденсаторов, для батарей нагрузки, используемых во время нагрузочных испытаний, потребуется компенсация реактивной мощности.

     Блок реактивной нагрузки может моделировать индуктивную или емкостную нагрузку в зависимости от типа нагрузки, ожидаемой в энергосистеме.Вот разбивка этих двух нагрузок:

     • Реактивная / индуктивная нагрузка — индуктивная нагрузка преобразует ток в магнитное поле. Индуктивное реактивное сопротивление сопротивляется изменению тока, в результате чего ток в цепи отстает от напряжения. Примеры устройств, создающих реактивную / индуктивную нагрузку, включают двигатели, трансформаторы и дроссели.
       При использовании в сочетании с резистивными батареями нагрузки решения для реактивной / индуктивной нагрузки могут моделировать реальные смешанные коммерческие нагрузки, состоящие из освещения, отопления, двигателей, трансформаторов и дросселей.Другими словами, вы можете оценить работу всей энергосистемы, включая генераторы, регуляторы напряжения, проводники, распределительное устройство и другое оборудование.
     • Реактивная / емкостная нагрузка — емкостная нагрузка заряжает и высвобождает энергию. Емкостное реактивное сопротивление сопротивляется изменению напряжения, заставляя ток в цепи опережать напряжение. Емкостная нагрузка аналогична индуктивной нагрузочной батарее по номиналу и назначению. Однако малонагруженные импульсные источники питания (применяемые для уменьшения гармонических токов) и длинные кабельные трассы вызывают энергопотребление системы, ведущий коэффициент мощности, позволяющий подавать реактивную мощность от этих нагрузок в систему.В результате повышается коэффициент мощности.
       
       Батареи реактивной / емкостной нагрузки используются в различных отраслях и сферах применения. Некоторые примеры включают телекоммуникации, информационные технологии, производство и добычу полезных ископаемых.

     Загрузите последнюю электронную книгу ComRent…

     Для более подробного обсуждения тестирования банка нагрузки загрузите последнюю электронную книгу ComRent «Резистивная и реактивная — причины выбора решений для тестирования банка реактивной нагрузки». В этом ресурсе обсуждается важность использования тестирования банка нагрузки для всей системы аварийного производства электроэнергии.В нем будет представлен обзор тестирования банка нагрузки, объяснены различные типы банков нагрузки и описаны наиболее выгодные решения банка нагрузки для большинства приложений.

     Команда экспертов ComRent готова помочь обеспечить успешный ввод вашей системы в эксплуатацию. Мы предлагаем бесплатную консультацию по рассмотрению вашего проекта и предложению правильного решения для банка нагрузки в соответствии с вашими требованиями. Свяжитесь с нами сегодня.

     Цепи переменного тока серии резистивных, емкостных и индуктивных

     Резистивные , емкостные и индуктивные серии переменного тока Цепи Цели: изучение электрического резонанса в цепях переменного тока , наблюдение за действием конденсаторов и индукторов в цепях переменного тока . , для анализа цепей RLC серии AC .Оборудование: 1 — осциллограф Instek GOS-620 со шнуром питания и пробником, 1 — функциональный генератор BK 2831D с шнуром питания и выходным кабелем, 1 — мультиметр BK 4017A со шнуром питания Измерительные провода и , 1 — монтажная плата Pasco Cl-6512 RLC, 2 — провода с зажимом типа «банан», 2 — провода с зажимом «крокодил» (рис. 1). Рисунок 1 Обсуждение: Вы ранее исследовали явление резонанса в своем исследовании скорости звука в воздухе в лаборатории последнего семестра.Все электрические и механические системы имеют естественные режимы вибрации. В прошлом семестре вы сопоставили эти режимы в столбе воздуха с колебаниями камертона, чтобы отправить столб воздуха в резонанс. Когда к системе прикладывается периодическая сила, такая как серия импульсов или ударов, она вибрирует с частотой, равной частоте силы. Этот тип вибрации известен как вынужденное колебание. Обычно реакция на вынужденные колебания довольно мала, но если частота вынужденных колебаний приближается к собственной или резонансной частоте системы, амплитуда колебаний быстро растет.Резонанс возникает всякий раз, когда две частоты совпадают. Теоретически амплитуда колебаний при резонансе должна приближаться к бесконечности. В механических системах трение ограничивает рост амплитуды колебаний, в электрических системах ту же роль играет сопротивление. В этом упражнении вы изучите резонанс в цепях переменного тока RLC (резистивных, индуктивных, емкостных). Аналоговые радиоприемники используют резонанс для настройки приемной схемы на частоту радиовещания настраиваемой станции.Каждая радиостанция вещает на определенной несущей частоте. Когда ваш приемник находится в резонансе на этой частоте, вы настроены на эту станцию. В большинстве случаев это достигается путем изменения емкости приемной цепи при фиксированной индуктивности.

     Разница между сопротивлением и реактивным сопротивлением (со сравнительной таблицей)

     Сопротивление и реактивное сопротивление — два основных термина, которые вместе формируют импеданс электрической цепи. Решающее различие между сопротивлением и реактивным сопротивлением состоит в том, что сопротивление препятствует прохождению электрического тока только через резистор.В отличие от реактивного сопротивления, это сопротивление изменению тока катушкой индуктивности или конденсатора.

     В основном, препятствие для прохождения электрического тока в любой цепи определяется как импеданс . Импеданс — это сложный термин, представляющий собой комбинацию реальных и мнимых значений. В этом разделе мы обсудим различные факторы, различающие сопротивление и реактивное сопротивление, используя сравнительную таблицу.

     Содержание: сопротивление против реактивного сопротивления

     1. Сравнительная таблица
     2. Определение
     3. Ключевые отличия
     4. Заключение

     Сравнительная таблица

     Параметр	Сопротивление	Реактивное сопротивление
     Basic	Это препятствие, препятствующее прохождению тока резистором.	Это противодействие изменяющемуся току в цепи с помощью катушки индуктивности или конденсатора.
     Символическое представление
     Обозначается	R	X
     Выдается
     Тип цепи	Цепи переменного и постоянного тока.	Конкретно цепь переменного тока.
     Элемент схемы	Чистый резистор	Идеальный индуктор или конденсатор.
     Характер значения	Действительная часть импеданса.	Мнимая часть импеданса.
     Зависит от	Размеры, удельное сопротивление и температура проводника.	Частота переменного тока.
     Разность фаз между V и I	V и I находятся в одной фазе. Таким образом, разность фаз составляет 0 градусов.	Существует разность фаз в 90 градусов между V и I.
     Электроэнергия	Общая мощность рассеивается в виде тепла.	Часть потребляемой мощности сохраняется.

     
     

     Определение сопротивления

     Препятствие на пути тока, протекающего по цепи, называется сопротивлением. Мы знаем, что когда к электрической цепи прикладывается определенный потенциал, через цепь течет ток, пропорциональный приложенному напряжению. Однако на пути протекающего тока также существует определенное препятствие. Это свойство противодействия протекающему току известно как сопротивление .

     Сопротивление — это свойство резисторов в электрических цепях. Другими словами, мы можем сказать, что соотношение подаваемого напряжения и протекающего тока в электрической цепи, имеющей резистор в качестве нагрузки, называется сопротивлением. Таким образом, сопротивление цепи определяется как:

     Сопротивление любой электрической цепи измеряется в омах и показывает зависимость от удельного сопротивления и размеров соответствующих проводников. Предлагаемое сопротивление указано как:

     Здесь следует отметить, что сопротивление проводников одинаково для постоянного или переменного тока.В резистивных цепях потребляемая мощность определяется как:

     Поскольку оба термина в продукте являются действительными значениями, потребляемая мощность также будет действительным термином. Тем самым указывается, что подаваемая мощность полностью используется в резистивной цепи.

     Определение реактивного сопротивления

     Препятствие для прохождения переменного или изменяющегося тока в электрических цепях известно как реактивное сопротивление. Реактивное сопротивление цепи — это противодействие протеканию переменного тока.

     Причина, по которой реактивное сопротивление цепи таково, что его значение является фактором наличия конденсатора или индуктора в качестве нагрузки. Таким образом, можно сказать, что отношение приложенного напряжения к изменяющемуся току в электрической цепи с емкостной или индуктивной нагрузкой называется реактивным сопротивлением этой цепи.

     Для индуктивной нагрузки реактивное сопротивление определяется как:

     В случае емкостной нагрузки реактивное сопротивление определяется как:

     Следовательно, в случае индуктивной цепи реактивное сопротивление считается прямо пропорциональным частоте.Пока он обратно пропорционален емкостной схеме.

     Когда переменный ток протекает через цепь с индуктивной или емкостной нагрузкой, изменяющаяся энергия сохраняется либо в электрическом поле, либо в магнитном поле. В случае индуктивной нагрузки возникает изменяющееся магнитное поле. А для емкостной нагрузки есть электрическое поле.

     Как мы уже обсуждали, сопротивление и реактивное сопротивление вместе образуют комплексное значение, называемое импедансом, где реактивное сопротивление действует как мнимая часть комплексного значения.Индуктивное реактивное сопротивление обычно является положительным мнимым значением, поэтому с увеличением индуктивной нагрузки реактивное сопротивление также увеличивается.
     

     Ключевые различия между сопротивлением и реактивностью

     1. Сопротивление — это препятствие для прохождения тока в электрической цепи из-за резистора. В то время как реактивное сопротивление — это противодействие зарядному току из-за индуктивности или конденсатора.
     Сопротивление
     2. — это свойство , связанное с цепью как переменного, так и постоянного тока.Однако реактивное сопротивление собственности связано только с цепями переменного тока.
     3. Чистые резисторы создают сопротивление. В отличие от идеальных катушек индуктивности или конденсаторов возникает реактивное сопротивление в цепи.
     4. Сопротивление связано с действительной частью импеданса. В то время как реактивное сопротивление вносит вклад в мнимую часть значения импеданса.
     5. Разница по фазе между напряжением и током в чисто резистивной цепи равна 0⁰. В то время как разность фаз между напряжением и током в идеальной емкостной или индуктивной цепи составляет 90⁰.В случае индуктивной нагрузки ток отстает от напряжения на 90⁰, а для чисто емкостной нагрузки напряжение отстает от тока на 90⁰.
     6. Сопротивление, обеспечиваемое схемой , зависит от размера, удельного сопротивления и температурных условий проводника. Однако реактивное сопротивление зависит от частотной составляющей переменного тока в цепи. Он показывает пропорциональность с частотой в случае индуктивной нагрузки, тогда как в случае емкостной нагрузки это соотношение является обратным.
     7. В резистивной цепи общая мощность, подаваемая на схему, рассеивается в виде тепла. В то время как в емкостной или индуктивной цепи устройство не полностью потребляет всю подаваемую мощность.

     Заключение

     Итак, из этого обсуждения можно сделать вывод, что и сопротивление, и реактивное сопротивление несут ответственность за противодействие потоку тока и, таким образом, действуют как импеданс для любой электрической цепи, когда они вместе присутствуют в ней.

     видов электрических нагрузок | Активная, индуктивная и емкостная нагрузка

     Если мы посмотрим на природу электрических нагрузок, мы можем разделить их на 3 типа. В этом руководстве вы подробно разберетесь с резистивной, индуктивной и емкостной нагрузкой. Также я выделю одно из очень распространенных заблуждений о конкретном типе нагрузки. Итак, начнем.

     ---

     Рекомендуем прочитать перед тем, как переходить к

     Активная, реактивная и полная мощность

     Что такое электрическая нагрузка?

     ---

     Во-первых, давайте разберемся, что такое электрическая нагрузка? Проще говоря, все, что потребляет электроэнергию, называется электрической нагрузкой .Это включает в себя лампочки, компьютеры, холодильник и т. Д., Все они потребляют электроэнергию, и, следовательно, мы можем назвать их электрической нагрузкой. Теперь, если мы посмотрим на природу такой нагрузки, мы можем разделить ее на три разных типа. И это так.

     1. Активная нагрузка
     2. Индуктивная нагрузка и
     3. Емкостная нагрузка

     Активная нагрузка

     ---

     Давайте сначала разберемся с резистивной нагрузкой. Нагрузка, потребляющая только активную мощность, называется резистивной нагрузкой. И если вы посмотрите на формы сигналов напряжения и тока такой нагрузки, вы обнаружите, что напряжение и ток идеально совпадают по фазе друг с другом.

     Теперь, когда я говорю, что они идеально совпадают по фазе, это означает, что обе формы волны достигают своего пикового значения одновременно. Они также одновременно достигают нулевого значения. Один пример показан выше.

     Поскольку такой тип нагрузки потребляет только активную мощность, мощность передается только от источника к нагрузке. От нагрузки к источнику не будет передаваться мощность.Да, в некоторых случаях мощность также течет от нагрузки к источнику, что я объяснил в моем видео об активной реактивной и полной мощности.

     Поскольку такие нагрузки потребляют только активную мощность, коэффициент мощности таких нагрузок равен единице! И это очень хороший знак. Если вы хотите узнать коэффициент мощности в деталях, вы можете просмотреть мой полный список воспроизведения Power Factor.

     Пример резистивной нагрузки

     ---

     Пример резистивной нагрузки:

     • Фары
     • Нагреватели
       Или любые другие нагрузки, состоящие только из нагревательных элементов.Это примеры резистивной нагрузки.

     Свойства резистивной нагрузки

     ---

     Давайте посмотрим, каковы свойства резистивной нагрузки

     • Эта нагрузка потребляет только активную мощность.
     • Форма кривой напряжения и тока таких нагрузок идеально совпадает по фазе друг с другом.
     • Коэффициент мощности такой нагрузки равен единице
     • Мощность всегда течет от источника к нагрузке

     Индуктивная нагрузка

     ---

     Теперь давайте разберемся с индуктивными нагрузками.

     Нагрузка, потребляющая только реактивную мощность, называется индуктивной нагрузкой . И если вы посмотрите на формы сигналов напряжения и тока такой нагрузки, вы обнаружите, что напряжение и ток не совпадают по фазе друг с другом на 90 градусов.

     Теперь, когда я говорю, что они не в фазе, это означает, что обе формы волны достигают своего пикового значения в разное время. Они также достигают нулевого значения в разное время. Если вы посмотрите на осциллограмму, вы обнаружите, что напряжение имеет преимущество перед током.Мы также можем сказать, что ток отстает от напряжения.

     Поскольку такой тип нагрузки потребляет только реактивную мощность, мощность может течь от источника к нагрузке или даже от нагрузки к источнику. Далее, коэффициент мощности таких нагрузок — это не Unity! Коэффициент мощности таких нагрузок носит отстающий характер. И это не очень хороший знак.

     Пример индуктивной нагрузки

     ---

     Давайте посмотрим на несколько примеров индуктивной нагрузки.

     Электродвигатель
     Вентиляторы
     Стиральная машина или что-нибудь, что имеет двигатель внутри.

     Кроме того, реакторы, используемые в энергосистеме, являются примером индуктивной нагрузки.

     Свойства индуктивных нагрузок

     ---

     Посмотрим, каковы свойства индуктивной нагрузки

     • Эта нагрузка потребляет только реактивную мощность
     • Форма кривой напряжения и тока таких нагрузок не совпадает по фазе друг с другом на 90 градусов.
     • Коэффициент мощности такой нагрузки отстает.
     • Мощность перетекает от источника к нагрузке и от нагрузки к источнику

     Этот тип нагрузки не является простой нагрузкой, как резистивная нагрузка.Они создают множество проблем в системе. Но, конечно, они не менее важны. Поскольку в таких нагрузках ток отстает от напряжения на 90 градусов, переключение такой нагрузки затруднено. Как известно, автоматический выключатель размыкается при текущем нулевом состоянии. Если вы посмотрите на кривые тока и напряжения такой нагрузки, вы обнаружите, что, когда ток равен нулю, напряжение является максимальным.

     Следовательно, когда автоматический выключатель размыкается при нулевом токе, напряжение на контакте выключателя является максимальным.Тогда как в случае резистивной нагрузки и ток, и напряжение одновременно становятся равными нулю. Поэтому переключение индуктивных нагрузок такого типа крайне важно.

     Нагрузка такого типа также сильно влияет на коэффициент мощности системы. Следовательно, счета за электричество растут.

     Емкостная нагрузка

     ---

     Емкостная нагрузка аналогична индуктивной нагрузке. В емкостных нагрузках ток и напряжение не совпадают по фазе друг с другом. Единственное отличие состоит в том, что в емкостной нагрузке ток опережает напряжение на 90 град.А в индуктивной нагрузке ток отстает от напряжения на 90 град.

     Заблуждение о емкостной нагрузке

     ---

     Теперь давайте поговорим о заблуждении, о котором я говорил в начале этого видео.

     Как правило, емкостные нагрузки не существуют в автономном формате. Конденсаторные батареи устанавливаются для повышения коэффициента мощности нагрузки или системы. Их работа — обеспечивать реактивную мощность. Поэтому конденсаторные батареи нельзя назвать емкостной нагрузкой.Потому что нагрузка — это то, что поглощает энергию. Я видел во многих местах в Интернете, что люди называют батарею конденсаторов емкостной нагрузкой. Ну, я думаю, конденсаторная батарея обеспечивает реактивную мощность и, следовательно, ее нельзя классифицировать как емкостную нагрузку. /

     Например, у меня есть генератор переменного тока 230 В и подключенная к нему конденсаторная батарея. Реактивное сопротивление конденсаторной батареи 23 Ом. Следовательно, ток, потребляемый системой, будет составлять 10 А.

     Теперь, если вы подключите измеритель VAR, который используется для расчета реактивной мощности, между генератором и конденсаторной батареей, он даст отрицательное значение.Отрицательная 2300 VAR или 2,3 KVAR. Таким образом, это отрицательное значение указывает на то, что мощность действительно течет от конденсаторной батареи к генератору. / Следовательно, конденсаторную батарею нельзя назвать емкостной нагрузкой. По сути, не существует того, что можно было бы классифицировать как емкостную нагрузку.

     ---

     Итак, это все о типах электрических нагрузок. Эту тему запросил один из моих подписчиков. Надеюсь, сегодня вы узнали что-то новое.

     Калькулятор импеданса параллельной LC-цепи

     • Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц

     Этот калькулятор импеданса параллельной LC-цепи определяет импеданс и угол сдвига фаз идеального индуктора и идеального конденсатора, подключенных параллельно для заданной частоты синусоидальный сигнал.Также определяется угловая частота.

     Пример: Рассчитайте полное сопротивление катушки индуктивности 250 мкГн и конденсатора 100 пФ на частоте 1 МГц. Этот пример показывает очень высокий импеданс, близкий к резонансному, около 120 кОм. Если вы хотите проверить импеданс почти при точном резонансе, введите 101,32 пФ вместо 100 пФ. При такой емкости цепь все еще остается слегка индуктивной, а ее индуктивное реактивное сопротивление меньше ее емкостного реактивного сопротивления. Если ввести чуть большую емкость 101.33 пФ, цепь станет слегка емкостной, ее индуктивное реактивное сопротивление станет выше емкостного реактивного сопротивления, и вы заметите, что угол разности фаз изменился с 90 ° до –90 °.

     Входной

     Индуктивность, л

     генри (H) миллигенри (мГн) микрогенри (мкГн) наногенри (нГн) пикогенри (pH)

     Емкость, C

     фарад (F) мкФ) мкФ (нанофарад) (нФ) пикофарад (пФ)

     Частота, f

     герц (Гц) миллигерц (мГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)

     Выход

     угловая частота рад / ω

     Емкостное реактивное сопротивление X _C = Ом

     Индуктивное реактивное сопротивление X _L = Ом

     Общее полное сопротивление LC | Z _LC | = Ом

     Разность фаз φ = ° = рад

     Резонансная частота

     f ₀ = Гц ω ₀ = рад / с

     Введите значения емкости, индуктивности и частоты, выберите единиц и нажмите или коснитесь кнопки Calculate .Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.

     Для расчета используются следующие формулы:

     φ = 90 °, если 1 / (2 πfL )> 2 πfC

     0

     90 °, если 1 / (2 πfL ) <2 πfC

     φ = 0 °, если 1 / (2 πfL ) = 2 πfC

     13 где
     0 _LC — полное сопротивление цепи LC в омах (Ом),

     ω = 2πf — угловая частота в рад / с,

     f — частота в герцах (Гц),

     L — индуктивность в генри (H),

     C — емкость в фарадах (F),

     ω ₀ — резонансная угловая частота в радианах в секунду (рад / с),

     f ₀ — резонансная частота в герцах (Г),

     φ — фазовый сдвиг между полным напряжением V _T и полным током I _T в градусах (°) и радианах, а

     j — мнимая единица.

     График импеданса нескольких параллельных LC-контуров Z _LC в зависимости от частоты f для заданной индуктивности и емкости показывает бесконечно большой импеданс на резонансных частотах

     Для расчета введите индуктивность, емкость и частоту, выберите единицы измерения и результат для полного сопротивления LC будут показаны в омах, а для разности фаз — в градусах. Также будут рассчитаны емкостное и индуктивное реактивное сопротивление и резонансная частота.Щелкните или коснитесь Рассчитать на резонансной частоте , чтобы увидеть, что произойдет при резонансе.

     График зависимости полного сопротивления нескольких идеальных параллельных LC-контуров Z _LC от частоты f для заданной индуктивности и емкости; резонансная частота 3,559 кГц одинакова для всех LC-цепей

     В параллельной LC-цепи приложенное напряжение одинаково для катушки индуктивности и конденсатора, но отдельные токи в обеих ветвях цепи различны.На векторной диаграмме показано напряжение V _T идеального источника напряжения. Из-за отсутствия сопротивления вектор тока не совпадает по фазе с приложенным напряжением. Вектор тока индуктивности I _L отстает от вектора напряжения на 90 °, поэтому он нарисован под углом –90 °. Вектор емкостного тока I _C опережает вектор напряжения на 90 ° и вычерчивается под углом 90 °. Векторная сумма двух противоположных векторов может быть направлена ​​вниз или вверх в зависимости от тока, протекающего через индуктивность и емкость.Ток в каждой ветви цепи в соответствии с законом Ома зависит от его реактивного сопротивления — чем оно выше, тем меньше ток.

     На резонансной частоте емкостное и индуктивное реактивные сопротивления равны, и если мы посмотрим на уравнение для | Z | выше, мы увидим, что эффективный импеданс бесконечно велик, потому что знаменатель стремится к нулю. Токи, протекающие через катушку индуктивности и конденсатор, равны, потому что их реактивные сопротивления равны. Таким образом, на резонансной частоте ток от источника не поступает.Поскольку ток равен нулю, идеальная параллельная LC-цепь на резонансной частоте, подключенная к источнику напряжения, действует как разомкнутая цепь.

     Векторная диаграмма теоретически идеальной параллельной LC-цепи. 1 — индуктивное реактивное сопротивление меньше емкостного реактивного сопротивления, то есть цепь действует как индуктор, 2 — индуктивное реактивное сопротивление выше емкостного реактивного сопротивления, то есть цепь действует как конденсатор, и 3 — бесконечно большое реактивное сопротивление при резонансе и цепь действует как разомкнутая цепь.От источника берется нулевой ток.

     В то же время мы можем видеть, что ток циркулирует через катушку индуктивности и конденсатор взад и вперед. Это можно сравнить с идеальными качелями, которые могут бесконечно колебаться без трения и без приложения к ним какой-либо внешней силы. Конечно, это может произойти только в идеальной цепи без сопротивления ни в одной из ветвей цепи. В то же время это удивительно близко к тому, что на самом деле происходит во многих практических схемах, в которых индукторы имеют очень маленькое сопротивление.

     На английском языке параллельный LC-контур часто называют контуром резервуара, потому что он может накапливать энергию в форме электрического поля, а магнитное поле с циркулирующим током, как резервуар, может хранить жидкость, не выпуская ее. Величина этого циркулирующего тока зависит от импеданса конденсатора и катушки индуктивности. Если индуктивность высокая, а емкость низкая, их реактивные сопротивления будут высокими, а ток будет небольшим. И наоборот, если индуктивность низкая, а емкость высокая, их реактивные сопротивления будут низкими, а ток будет высоким.

     Катушки индуктивности в ВЧ-модуле

     Режимы отказа

     Что делать, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:

     Неисправный компонент	Режим отказа
     Индуктор	Короткий	Открыть

     Специальные режимы

     Щелкните или коснитесь соответствующей ссылки для просмотра калькулятора в различных специальных режимах:

     Различные режимы постоянного тока

     Короткое замыкание

     Обрыв

     Чисто емкостный контур

     Резонансный контур

     Чисто индуктивный контур

     Индуктивный контур

     Примечания

     34 В наших объяснениях поведения этой схемы нулевая частота означает постоянный ток.