Что такое реактивное сопротивление трансформатора. Как рассчитать импеданс трансформатора. Какие формулы используются для вычисления реактивной мощности трансформатора. Как компенсировать реактивную мощность трансформатора.
Что такое реактивное сопротивление трансформатора
Реактивное сопротивление трансформатора возникает из-за рассеяния магнитных потоков в обмотках. Хотя большая часть магнитного потока проходит через обе обмотки и сердечник, небольшая его часть замыкается только в одной обмотке, создавая так называемый поток рассеяния. Это явление и приводит к появлению реактивного сопротивления рассеяния обмоток трансформатора.
Реактивное сопротивление трансформатора складывается из двух основных составляющих:
- Реактивное сопротивление намагничивания (шунтирующее)
- Реактивное сопротивление рассеяния (последовательное)
Совокупность этих сопротивлений и активного сопротивления обмоток образует полное внутреннее сопротивление трансформатора, называемое импедансом.
Расчет импеданса трансформатора
Импеданс трансформатора для каждой обмотки можно рассчитать по следующим формулам:
- Z1 = R1 + jX1 — для первичной обмотки
- Z2 = R2 + jX2 — для вторичной обмотки
Где:
- Z1, Z2 — импеданс первичной и вторичной обмотки
- R1, R2 — активное сопротивление обмоток
- X1, X2 — реактивное сопротивление рассеяния обмоток
- j — мнимая единица
Для расчета полного импеданса трансформатора используется формула:
Z = √(R² + X²)
Где R — суммарное активное сопротивление, X — суммарное реактивное сопротивление.
Формулы расчета реактивной мощности трансформатора
Реактивная мощность трансформатора складывается из двух составляющих:
- Реактивная мощность намагничивания (Q0)
- Реактивная мощность рассеяния (Qк)
Общая реактивная мощность трансформатора рассчитывается по формуле:
Qt = Q0 + Qк * (S/Sном)²
Где:
- Qt — общая реактивная мощность
- Q0 — реактивная мощность намагничивания
- Qк — реактивная мощность короткого замыкания
- S — фактическая нагрузка трансформатора
- Sном — номинальная мощность трансформатора
Влияние реактивного сопротивления на работу трансформатора
Реактивное сопротивление трансформатора оказывает существенное влияние на его характеристики и работу:
- Вызывает падение напряжения на обмотках
- Снижает коэффициент полезного действия
- Уменьшает пропускную способность трансформатора
- Приводит к дополнительным потерям мощности
Чем выше реактивное сопротивление, тем больше эти негативные эффекты. Поэтому важно учитывать реактивное сопротивление при проектировании и эксплуатации трансформаторов.
Способы компенсации реактивной мощности трансформатора
Для уменьшения потребления реактивной мощности трансформатором применяются следующие методы компенсации:
- Установка конденсаторных батарей на вторичной стороне трансформатора
- Использование синхронных компенсаторов
- Применение статических тиристорных компенсаторов
- Оптимизация режимов работы трансформатора
При выборе способа компенсации необходимо учитывать параметры трансформатора, характер нагрузки и экономическую целесообразность. Важно не допустить перекомпенсации, особенно при малых нагрузках.
Измерение реактивного сопротивления трансформатора
Для определения реактивного сопротивления трансформатора применяются следующие методы измерений:
- Опыт холостого хода — для определения сопротивления намагничивания
- Опыт короткого замыкания — для измерения сопротивления рассеяния
- Измерение импеданса специальными приборами
- Косвенные методы на основе измерения мощности и напряжения
Точное измерение реактивного сопротивления позволяет правильно рассчитать параметры трансформатора и выбрать оптимальные режимы его работы.
Зависимость реактивного сопротивления от параметров трансформатора
Реактивное сопротивление трансформатора зависит от следующих факторов:
- Мощность трансформатора — чем выше мощность, тем меньше относительное реактивное сопротивление
- Напряжение обмоток — с ростом напряжения увеличивается реактивное сопротивление
- Конструкция магнитопровода — влияет на сопротивление намагничивания
- Количество витков и сечение проводов обмоток — определяют сопротивление рассеяния
- Частота сети — реактивное сопротивление прямо пропорционально частоте
Учет этих зависимостей позволяет оптимизировать конструкцию трансформатора для получения требуемых характеристик.
Нормирование реактивного сопротивления трансформаторов
Для силовых трансформаторов устанавливаются нормативные значения реактивного сопротивления:
- Напряжение короткого замыкания (uк) — 4-12% в зависимости от мощности
- Ток холостого хода (i0) — 0,2-3% от номинального
- Потери холостого хода и короткого замыкания
Эти параметры регламентируются стандартами и техническими условиями на трансформаторы. Соблюдение нормативов обеспечивает требуемые эксплуатационные характеристики трансформаторов.
Реактивное сопротивление трансформатора: формулы расчета
Мы привыкли считать, что все магнитные потоки в трансформаторе пронизывают обе обмотки и магнитопровод. Если бы существовал идеальный трансформатор, то это действительно так бы и происходило. К сожалению, в реальности часть магнитного потока преодолевает изоляционное пространство, выходит за пределы обмоток и замыкается в них (см. рис. 1). В результате возникает реактивное сопротивление трансформатора. Такое явление ещё называют рассеиванием магнитных потоков.
Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоковВ катушках существуют и другие сопротивления, являющиеся причинами потерь мощности. Таковыми являются: внутреннее сопротивление материалов обмоток, и рассеивания, вызванные индуктивными сопротивлениями. Совокупность рассеиваний магнитных потоков называют внутренним сопротивлением или импедансом трансформатора.
Потери реактивных мощностей
Вспомним, как работает идеальный двухобмоточный трансформатор (см.
рис. 2). Когда первичная обмотка окажется под переменным напряжением (например, от электрической сети), возникнет магнитный поток, который пронизывает вторичную катушку индуктивности. Под действием магнитных полей происходит возбуждение вторичных обмоток, в витках которых возникает ЭДС. При подключении активной мощности к прибору во вторичной цепи начинает протекать переменный ток с частотой входного тока.
В идеальном трансформаторе образуется прямо пропорциональная связь между напряжениями в обмотках. Их соотношение определяется соотношением числа витков каждой из катушек. Если U1 и U2 – напряжения в первой и второй обмотке соответственно, а w1 и w2 – количество витков обмоток, то справедлива формула: U1 / U2 = w1 / w2.
Другими словами: напряжение в рабочей обмотке во столько раз больше (меньше), во сколько раз количество мотков второй катушки увеличено (уменьшено) по отношению к числу витков, образующих первичную обмотку.
Величину w1 / w2 = k принято называть коэффициентом трансформации. Заметим, что формула, приведённая выше, применима также для автотрансформаторов.
В реальном трансформаторе часть энергии теряется из-за рассеяния магнитных потоков (см. рис. 1). Зоны, где происходит концентрация потоков рассеяния обозначены пунктирными линиями. На рисунке видно, что индуктивность рассеяния охватывает магнитопровод и выходит за пределы обмоток.
Наличие реактивных сопротивлений в совокупности с активным сопротивлением обмоток приводят к нагреванию конструкции. То есть, при расчётах КПД необходимо учитывать импеданс трансформатора.
Обозначим активное сопротивление обмоток символами R1 и R2 соответственно, а реактивное – буквами X1 и X2. Тогда импеданс первичной обмотки можно записать в виде: Z1= R1+jX1. Для рабочей катушки соответственно будем иметь: Z2= R2+jX2, где j – коэффициент, зависящий от типа сердечника.
Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = RL – RC. Учитывая, что RL = ωL, а RC = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления: X = ωL – 1/ωC.
Не прибегая к цепочке преобразований, приведём готовую формулу для расчёта полного сопротивления, то есть, для определения импеданса трансформатора:
Суммарное сопротивление трансформатора необходимо знать для определения его КПД. Величины потерь в основном зависят от материала обмоток и конструктивных особенностей трансформаторного железа. Вихревые потоки в монолитных стальных сердечниках значительно больше, чем многосекционных конструкциях магнитопроводов. Поэтому на практике сердечники изготавливаются из тонких пластин трансформаторной стали. С целью повышения удельного сопротивления материала, в железо добавляют кремний, а сами пластины покрывают изоляционным лаком.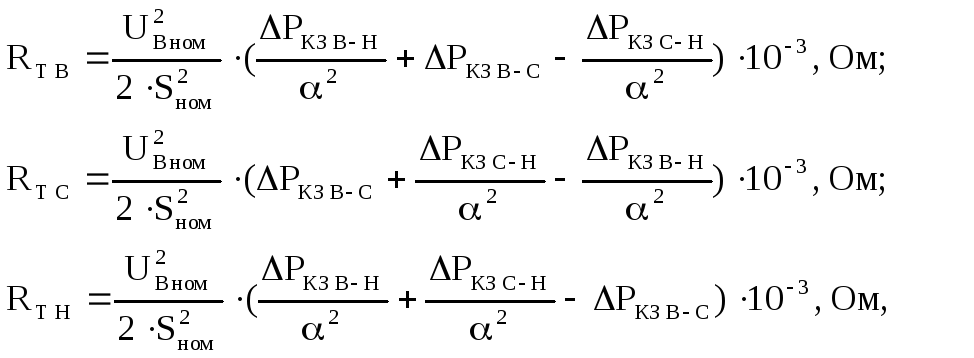
Для определения параметров трансформаторов важно найти активное и реактивное сопротивление, провести расчёты потерь холостого хода. Приведённая выше формула не практична для вычисления импеданса по причине сложности измерений величин индукционного и ёмкостного сопротивлений. Поэтому на практике пользуются другими методами для расчёта, основанными на особенностях режимов работы силовых трансформаторов.
Режимы работы
Двухобмоточный трансформатор способен работать в одном из трёх режимов:
- вхолостую;
- в режиме нагрузки;
- в состоянии короткого замыкания.
Для проведения расчётов режимов электрических цепей проводимости заменяют нагрузкой, величина которой равна потерям при работе в режиме холостого хода. Вычисления параметров схемы замещения проводят опытным путём, переводя трансформатор в один из возможных режимов: холостого хода, либо в состояние короткого замыкания. Таким способом можно определить:
- уровень потерь активной мощности при работе на холостом ходу;
- величины потерь активной мощности в короткозамкнутом приборе;
- напряжение короткого замыкания;
- силу тока холостого хода;
- активное и реактивное сопротивление в короткозамкнутом трансформаторе.
Параметры режима холостого хода
Для перехода в работу на холостом ходу необходимо убрать отсутствует нагрузку на вторичной обмотке, то есть – разомкнуть электрическую цепь. В разомкнутой катушке напряжение отсутствует. Главной составляющей тока в первичной цепи является ток, возникающий на реактивных сопротивлениях. С помощью измерительных приборов довольно просто найти основные параметры переменного тока намагничивания, используя которые можно вычислить потери мощности, умножив силу тока на подаваемое напряжение.
Схема измерений на холостом ходу показана на рисунке 3. На схеме показаны точки для подключения измерительных приборов.
Рис. 3. Схема режима холостого ходаФормула, применяемая для расчётов параметров реактивной проводимости, выглядит так: Вт = Iх%*Sном / 100* Uв ном2 Умножитель 100 в знаменателе применён потому, что величина тока холостого хода Iх обычно выражается в процентах.
Режим короткого замыкания
Для перевода трансформатора на работу в режиме короткого замыкания закорачивают обмотку низшего напряжения. На вторую катушку подают такое напряжение, при котором в каждой обмотке циркулирует номинальный ток. Поскольку подаваемое напряжение существенно ниже номинальных напряжений, то потери активной мощности в проводимости настолько малы, что ими можно пренебречь.
Таким образом, у нас остаются активные мощности в трансформаторе, которые расходуются на нагрев обмоток: ΔPk = 3* I1ном * Rт. Выразив ток I1 ном через напряжение Uка и сопротивление Rт, умножив выражение на 100, получим формулу для вычисления падения напряжения в зонах активного сопротивления (в процентах):
Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:
Подставив значение Rт в предыдущую формулу, получим:
Вывод: в короткозамкнутом трансформаторе падение напряжения в зоне активного сопротивления (выраженная в %) прямо пропорционально размеру потерь активной мощности.
Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:
Отсюда находим:
Величины реактивных сопротивлений в современных трансформаторах гораздо меньше активного. Поэтому можно считать что падение напряжения в зоне реактивного сопротивления Uк р ≈ Uк, поэтому для практических расчётов можно пользоваться формулой: XT = Uk*Uв ном2 / 100*Sном
Рассуждения, приведённые выше, справедливы также для многообмоточных, в том числе и для трёхфазных трансформаторов. Однако вычисления проводятся по каждой обмотке в отдельности, а задача сводится к решению систем уравнений.
Знание коэффициентов мощности, сопротивления рассеивания и других параметров магнитных цепей позволяет делать расчёты для определения величин номинальных нагрузок. Это, в свою очередь, обеспечивает работу трансформатора в промежутке номинальных мощностей.
Список использованной литературы
- Сивухин Д. В. «Общий курс физики» 1975
- Н.А. Костин, О.Г.Шейкина «Теоретические основы электротехники» 2007
- Нейман Л.Р., Демирчян К.С. «Теоретические основы электротехники» 1981
- Бартош А.И. «Электрика для любознательных» 2019
В. «Общий курс физики» 1975Реактивное сопротивление трансформатора или импеданс
- Дартекс
- Cтатьи
- Реактивное сопротивление трансформатора или импеданс
30.11.2021
Когда на трансформатор подается нагрузка, в его обмотках возникают магнитные потоки. Большая часть из них проходит через обе обмотки. Но есть малая часть потоков, которые замыкаются только на одной из обмоток. Последняя часть рассеивается. Этот поток называется реактивным потоком рассеяния.
Наглядно это явление видно на рисунке:
Что такое сопротивление трансформатора?
Обмотки трансформаторов изготавливаются из проводящего материала – меди либо алюминия. Оба металла неплохо проводят электрический ток. Но идеальных проводников просто не существует. Поэтому в обеих обмотках есть определенное сопротивление. Из него и складывается сопротивление трансформатора.
Импеданс трансформатора
Мы выяснили, что в катушках трансформатора есть сопротивление и реактивное сопротивление. Совокупность внутреннего сопротивления и сопротивления рассеивания – это и есть импеданс трансформатора.
Магнитный поток рассеяния в трансформаторах
Если бы существовал идеальный трансформатор, то все магнитные потоки проходили бы через обе обмотки и сердечник. Но на деле такого просто не бывает. Часть магнитного потока выходит из обмотки, проходит через изоляцию и замыкается в этой же обмотке.
Это явление называют реактивным сопротивлением рассеяния обмоток. Оно же является реактивным сопротивлением рассеяния всего трансформатора. Иначе его еще называют рассеянием магнитного потока.
Как рассчитать импеданс трансформатора?
Формулы для расчета импеданса трансформатора для обеих обмоток имеют вид:
Z1 = R1 + jX1 и
Z2 = R2 + jX2,
где R1 и R2 – это сопротивление первичной и вторичной обмотки, X1 и X2 – сопротивление рассеяния обмоток, а Z1 и Z2 – это импеданс обмоток.
Как рассчитать напряжение трансформатора с учетом импеданса обмоток?
Из-за сопротивления рассеяния в обмотках возникают перепады напряжения. Если мы подаем на первичную обмотку ток напряжением V1, то из-за сопротивления рассеяния в ней возникает составляющая I1X1 как самоиндукция. X1 здесь – это реактивное сопротивление рассеяния. Теперь, если учтем падение напряжения из-за сопротивления на первичной обмотке, то уравнение напряжения трансформатора примет вид:
V1 = E1 + I1(R1 + jX1) ⇒ V1 = E1 + I1R1 + jI1X1.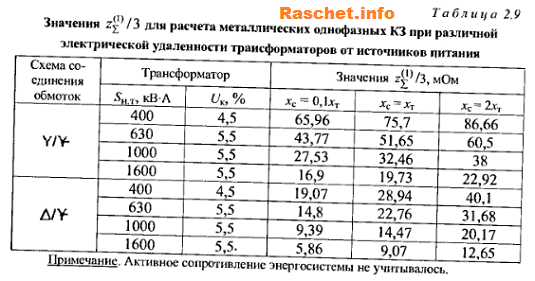
Так же с учетом вторичного реактивного напряжения на вторичной обмотке покажем уравнение напряжения:
V2 = E2 – I2(R2 + jX2) ⇒ V2 = E2 – I2R2 − jI2X2.
Как видите, магнитный поток рассеяния влияет на общее сопротивление трансформатора. Из-за реактивного сопротивления в первичной и вторичной обмотке трансформатора возникают скачки напряжения. Это особенно важно учитывать в электрических сетях, где несколько трансформаторов работают параллельно.
Список статей
Как рассчитать реактивную мощность трансформатора? – Помехи напряжения
Потребление реактивной мощности трансформатораСиловые трансформаторы «потребляют» индуктивную мощность ВАРС во время работы. Это связано с потребностью в реактивной мощности двух отдельных ветвей трансформатора, а именно:
- Реактивное сопротивление намагничивания шунта
- Реактивное сопротивление утечки серии
Реактивная мощность, потребляемая силовым трансформатором, может достигать 5 % от номинальной мощности трансформатора при подаче тока полной нагрузки.
Коэффициент мощности на первичной обмотке трансформатора обычно ниже, чем измеренный на вторичной обмотке из-за этого требования к реактивной мощности трансформатора. Если измерение выполняется при среднем напряжении, то также будет измеряться дополнительная реактивная мощность, потребляемая трансформатором. В подобных случаях важно знать, сколько реактивной мощности потребляет трансформатор, чтобы ее можно было вычесть из потребности в реактивной мощности нагрузки. Обычно это происходит, когда электросчетчик находится на первичной обмотке, а трансформатор также принадлежит коммунальному предприятию. Нет смысла выставлять счет за реактивную мощность, потребляемую трансформатором, принадлежащим коммунальному предприятию, поскольку они могли бы очень хорошо поставить счетчики на стороне низкого напряжения, и потребителю не придется платить за это, если это так. Когда трансформатор принадлежит потребителю, коммунальное предприятие будет измерять реактивную мощность, потребляемую силовым трансформатором.
Конденсаторные батареи обычно меньше рассчитанного значения, так как существует риск перекомпенсации при малой нагрузке. Может быть установлен автоматический конденсатор ступенчатого коэффициента мощности, который будет переключать только необходимые ступени конденсатора, чтобы довести коэффициент мощности до желаемого уровня. Однако для этого необходимо будет выполнить измерение коэффициента мощности на первичной обмотке трансформатора, что не всегда возможно. Чаще всего реактивная мощность, потребляемая силовым трансформатором, составляет лишь небольшой процент реактивной мощности, потребляемой объектом, и точная компенсация может не требоваться.
1.
Реактивное сопротивление намагничивания шунта
Реактивное сопротивление намагничивания шунта отвечает за создание магнитного потока в сердечнике трансформатора. Ток, необходимый для создания этого потока в сердечнике, называется током возбуждения и относительно не зависит от тока нагрузки трансформатора. Ток возбуждения обычно составляет около 0,25-2% от тока полной нагрузки трансформатора. Фактическое значение тока возбуждения можно получить из протокола заводских испытаний или измерить в полевых условиях.
Чтобы рассчитать потребляемую реактивную мощность, сначала рассчитайте приблизительное сопротивление намагничивания шунта по заданному току возбуждения. Ток возбуждения обычно указывается в процентах от тока полной нагрузки трансформатора.
2. Реактивное сопротивление последовательного рассеяния
Сопротивление последовательного рассеяния косвенно относится к величине магнитного потока, который не связан между первичной и вторичной обмотками.
Реактивное сопротивление последовательного рассеяния (также известное как % импеданса) является важным параметром трансформатора, который определяет влияние короткого замыкания, регулирование напряжения и т. д.
Требуемая реактивная мощность из-за реактивного сопротивления последовательного рассеяния изменяется пропорционально квадрату тока нагрузки. Общая индуктивная мощность, потребляемая силовым трансформатором, представляет собой арифметическую сумму потребности обеих вышеперечисленных ветвей. Калькулятор в этой статье рассчитает это за вас.
Компенсация реактивной энергии, потребляемой трансформатором
Потребляемая трансформатором реактивная мощность может быть компенсирована добавлением шунтирующих батарей конденсаторов. Как видно из калькулятора, когда трансформатор загружен, полная реактивная мощность Qt состоит из двух компонентов: реактивной мощности Q0 во время работы вторичной разомкнутой цепи (без нагрузки) и реактивной мощности, вызванной реактивным сопротивлением рассеяния.
Суммарная реактивная мощность, потребляемая трансформатором, описывается следующим уравнением:
Где,
Q t = Общая реактивная мощность, потребляемая трансформатором
Q 0 = Реактивная мощность, потребляемая шунтирующим реактивным сопротивлением намагничивания трансформатора (без нагрузки)
% z= Сопротивление короткого замыкания трансформатора в процентах
кВА T = Номинальная мощность трансформатора кВА
кВА L = Нагрузка кВА
Если для компенсации потребляемой трансформатором реактивной мощности требуется емкостная компенсация, следует соблюдать осторожность, чтобы избежать перекомпенсации при малой нагрузке. В условиях малой нагрузки или без нагрузки реактивная мощность не будет потребляться реактивным сопротивлением последовательного рассеяния, и реактивная мощность будет потребляться только шунтирующим импедансом намагничивания. В случае чрезмерной компенсации это вызовет увеличение напряжения на вторичных клеммах.
Многие коммунальные службы предоставляют документ, в котором указана максимальная емкостная компенсация, которую можно установить на вторичной обмотке служебного трансформатора. Если вам нужна эта информация, обратитесь в местную электроэнергетическую службу.
Чаще реактивная мощность, потребляемая самим трансформатором, очень мала по сравнению с общей реактивной мощностью, потребляемой нагрузкой объекта. В этих случаях предприятие может принять решение об установке конденсаторной батареи большего размера на вторичной обмотке трансформатора. В этом случае необходимо обратить внимание на возможность гармонического резонанса между реактивным сопротивлением трансформатора и конденсатором.
Как измерить реактивную мощность?
Калькулятор коэффициента мощности
Электрическое испытательное оборудование | электростанция к розетке
В этой статье мы рассмотрим некоторые ключевые практические аспекты измерения и оценки качества электроэнергии. Как следует из названия, мы выходим далеко за рамки основ, но для того, чтобы обеспечить прочную основу, мы начнем с краткого обзора некоторых основных понятий, касающихся мощности и качества электроэнергии.
Немного об основах мощности
Мгновенная мощность в цепи, согласно IEEE1459 и, без сомнения, другим аналогичным стандартам во всем мире, определяется как произведение мгновенного напряжения и мгновенного тока в цепи. Мгновенная мощность состоит из двух составляющих: активной мощности и реактивной мощности. Активная мощность создается компонентом тока, который совпадает по фазе с напряжением и течет в одном направлении от источника к нагрузке. Реактивная мощность создается компонентом тока, который не совпадает по фазе с напряжением, и, по сути, он колеблется между источником и нагрузкой. Это означает, что чистая передача энергии от источника к нагрузке за счет реактивной мощности равна нулю.
При проведении измерений активной мощностью является среднее значение мгновенной мощности за интервал времени наблюдения. Математически это можно выразить формулой:
.
где P = активная мощность, T = 1/f в циклах, K = целое число, ԏ = начало измерения и p = мгновенная мощность.
Активная мощность является функцией рассеивающих элементов цепи, которые часто являются сопротивлениями. Активная мощность, измеряемая в ваттах, является однонаправленной и всегда имеет положительное значение. В цепях с синусоидальными формами тока и напряжения активная мощность может быть выражена как
где θ — фазовый угол между напряжением и током.
Рассматривая реактивную мощность аналогичным образом, она является функцией амплитуды колебательной мгновенной мощности, измеренной во времени, что может быть выражено математически по формуле:
Реактивная мощность измеряется в ВАр (реактивный вольт-ампер) и является функцией реактивного сопротивления цепи. Как уже упоминалось, поскольку энергия, связанная с реактивной мощностью, колеблется между источником и нагрузкой, нет средней чистой передачи энергии в нагрузку. В цепях с синусоидальными формами тока и напряжения реактивная мощность может быть выражена как
где θ — фазовый угол между напряжением и током.
Другой важной величиной является полная мощность. Это функция полного импеданса цепи, равная произведению среднеквадратичного (среднеквадратического) тока и среднеквадратичного напряжения. В синусоидальной системе без гармоник взаимосвязь между реактивной мощностью (относительно реактивного сопротивления), активной мощностью (относительно сопротивления) и полной мощностью (относительно импеданса) может быть выражена графически в виде «треугольника мощностей».
Применение к этому треугольнику теоремы Пифагора показывает, что квадрат полной мощности равен сумме квадратов активной и реактивной мощностей или, выражаясь формулой
Коэффициент реактивной мощности
Учитывая треугольник мощности, косинус фазового угла, то есть угол между напряжением и током, обозначается коэффициентом мощности смещения (DPF). Обратите внимание, что DPF действителен только для синусоидальных сигналов и не учитывает гармоники. Когда реактивное сопротивление добавляется в цепь, фазовый угол увеличивается, а DPF уменьшается.
Например, в чисто резистивной цепи фазовый угол равен нулю, а DPF равен 1. Если добавить реактивное сопротивление, увеличивающее фазовый угол до 8º, DPF падает до 0,9.92, а если добавить больше реактивного сопротивления для дальнейшего увеличения фазового угла до 26º, DPF упадет до 0,898.
Поскольку реактивные нагрузки могут быть как индуктивными, так и емкостными, значения DPF могут быть положительными или отрицательными, поскольку индуктивные нагрузки вызывают отставание тока от напряжения, тогда как емкостные нагрузки заставляют ток опережать напряжение. Когда ток отстает от напряжения, DPF положительный, а когда ток опережает напряжение, DPF отрицательный.
Низкие значения DPF указывают на неэффективность энергосистем, поскольку система должна поддерживать подачу реактивной мощности, которая не выполняет полезной работы. Улучшение коэффициента мощности системы позволит ей подавать больше энергии на нагрузку, одновременно снизив общую нагрузку на такие компоненты, как кабели и трансформаторы.
Как показывает этот пример, улучшения могут быть существенными.
Система подавала питание на нагрузку с DPF 0,829. Отдаваемая полная мощность (то есть общая нагрузка на систему) составила 7030 кВА, что составляет 95% мощности системы. Отданная активная мощность составила 5828 кВт, а реактивная мощность – 3931 кВАр. Были предприняты шаги для увеличения DPF до 0,990, что снизило полную мощность до 5960 кВА, что эквивалентно 80,5% мощности системы. Активная мощность, отдаваемая в нагрузку, практически не изменилась и составила 5900 кВт, а реактивная (расходуемая) мощность снизилась до 0,829 кВт.кВАр. Другими словами, улучшение DPF с 0,829 до 0,990 высвободило 15% мощности системы питания!
На практике нагрузки в энергосистеме, скорее всего, будут индуктивными, а не емкостными, поэтому DPF будет положительным. В таких случаях DPF можно улучшить, добавив конденсаторную батарею, которая снижает реактивную мощность и увеличивает активную мощность. Вот пример того, как это работает:
Можно видеть, что когда реактивное сопротивление конденсаторной батареи, добавленной в цепь, равно индуктивному сопротивлению нагрузок в цепи, общее реактивное сопротивление становится равным нулю, и цепь ведет себя так, как если бы она была чисто резистивной нагрузкой.
На практике такая идеальная коррекция коэффициента мощности вряд ли достижима, но к ней можно приблизиться.
Батареи конденсаторов для коррекции коэффициента мощности обычно измеряются в кВАр. Ключевыми значениями на паспортной табличке являются напряжение, частота и кВАр. Полное сопротивление батареи конденсаторов можно рассчитать по формуле
.
где Q — номинальная мощность конденсаторной батареи в кВАр. Например, если банк рассчитан на 10 кВ и 150 кВАр, его импеданс будет 667 Ом.
Суммарный коэффициент мощности
Возвращаясь теперь к треугольнику мощности, важно помнить, что он работает только с чистыми синусоидальными сигналами — отношения, которые он воплощает, не выполняются при наличии гармонических искажений. Это связано с тем, что, когда присутствуют гармоники, они не сдвигают фазовый угол тока, как индуктивная или емкостная нагрузка, а искажают форму волны тока.
Это означает, что в цепях с наличием гармоник DPF не является точным показателем коэффициента мощности, поскольку он учитывает только фазовый сдвиг, а не искажение формы волны.
По этой причине в цепях со значительными уровнями гармоник требуется другая мера коэффициента мощности. Это общий коэффициент мощности (TPF, а иногда и просто PF), который учитывает как искажения, так и фазовый сдвиг.
TPF определяется как мощность, деленная на полную мощность (P/S). Если в цепи нет гармоник, TPF равен DPF. Однако по мере увеличения уровня гармоник увеличивается и разница между TPF и DPF. Связанный параметр, который иногда встречается, — это коэффициент мощности искажения (dPF), который определяется как отношение между TPF и DPF (TPF/DPF).
Силовые системы и измерительные устройства
Теперь давайте перейдем к рассмотрению конфигураций и характеристик некоторых практических систем распределения электроэнергии, а также способов измерения мощности в этих системах. Первая — это четырехпроводная система «звезда», показанная здесь:
Преимущества этой схемы заключаются в том, что подключение нейтрали обеспечивает дополнительную безопасность, напряжения изоляции ниже, чем в большинстве других схем распределения электроэнергии, и можно подключать нагрузки либо между фазами, либо между фазой и нейтралью, что эффективно предлагает выбор.
двух различных напряжений питания. Недостатки заключаются в том, что неисправности могут привести к потере напряжения на одной фазе, а схема чувствительна к гармоникам нулевой последовательности. Кроме того, фазы могут быть несимметричными, что вместе с гармониками нулевой последовательности может привести к высоким токам нейтрали. Поэтому должны быть предусмотрены нейтральные проводники соответствующего номинала, что значительно увеличивает затраты.
Альтернативным вариантом является трехпроводная конфигурация треугольника, показанная здесь:
Преимущество такой схемы заключается в том, что гармоники нулевой последовательности автоматически подавляются, а неисправность не приводит к потере фазы. Кроме того, система останется сбалансированной при наличии несбалансированных однофазных нагрузок, хотя следует отметить, что дисбаланс может быть вызван фазовыми сдвигами. Затраты ниже, чем у четырехпроводной системы, соединенной звездой, поскольку нейтральный проводник не требуется.
Недостатки заключаются в том, что потеря фазы увеличит ток в остальных фазах, а это означает, что требуется более высокая степень изоляции. Кроме того, отсутствие нейтрали снижает безопасность.
Следующее расположение, которое следует рассмотреть, носит разные названия: дельта с красной ногой, дельта с дикой ногой, дельта с высокой ногой и другие. Каким бы ни было название, в этой конструкции используется трансформатор треугольника с центральным ответвлением для обеспечения двух источников 120 В. Подробности показаны на следующей диаграмме; обратите внимание, что угол между фазами составляет 90°, а не 120°, как это обычно бывает в трехфазных системах.
Преимущество трехфазной схемы «красный треугольник» заключается в том, что она может обеспечивать три различных напряжения питания — 240 В, 208 В и 120 В, а также в том, что при небольшой трехфазной нагрузке возможна использовать два отдельных трансформатора вместо трех, что снижает затраты. Недостатки заключаются в том, что такое расположение может привести к дисбалансу из-за несбалансированных однофазных нагрузок, а также в том, что между высшей ветвью и нейтралью может быть подключена только ограниченная нагрузка.
Такое расположение также усложняет проектирование сети.
Последнее, что мы рассмотрим, — это двухфазное питание, которое чаще всего используется для подачи однофазного питания в жилые дома.
Основными преимуществами такой схемы являются простота и низкая стоимость. Кроме того, он обеспечивает два напряжения питания — 240 В и 120 В. Недостатки здесь в том, что он может стать несимметричным, восприимчив к гармоникам нулевой последовательности, а эти гармоники вместе с несимметричными нагрузками могут привести к высоким токам нейтрали.
Теорема Блонделя и преобразования дельта-звезда
Для каждой из рассмотренных нами схем схемы включали соединения ваттметра. Однако полезно знать, что теорема Блонделя утверждает, что общая мощность в системе из N проводников может быть правильно измерена с помощью N ваттметров или ваттметров. N ваттметров подключены отдельно, так что каждый из них измеряет уровень тока в одном из N проводников и уровень потенциала между этим проводником и общей точкой.
Если же общей точкой является один из проводников, то ваттметр на этом проводнике можно убрать, а значит, понадобится всего N-1 ваттметров или ваттметров.
Также полезно знать, что фазные напряжения, измеренные между фазами в системе, соединенной треугольником, можно легко преобразовать в «виртуальное» напряжение между фазами, просто разделив значения между фазами на √ 3. Это позволяет просматривать значения мощности для каждого канала, но важно помнить, что этот расчет действителен только в том случае, если дельта-система, в которой выполняются измерения, сбалансирована. К счастью, дельта-системы обычно остаются сбалансированными даже при наличии несбалансированных нагрузок, но могут стать несбалансированными при введении фазовых сдвигов.
Просмотр данных об энергопотреблении
При просмотре данных об энергопотреблении, собранных приборами контроля качества электроэнергии, или при просмотре этих данных в режиме реального времени, в первую очередь необходимо убедиться, что активная мощность положительна.
Реверсирование активной мощности может произойти, когда мощность подается обратно в систему электроснабжения, когда включаются такие источники, как возобновляемые источники энергии и системы распределенной генерации. Отрицательная активная мощность создает проблемы, поскольку может привести к частому переключению ответвлений трансформатора, что приведет к чрезмерному износу переключателей ответвлений.
Гистограммы, показывающие почасовое энергопотребление в течение тестового интервала, также предоставляют ценную информацию. Стоит отметить моменты, когда потребление энергии достигает своего пика, а также просмотреть общее потребление полной, активной и реактивной энергии за период тестирования.
Данные, касающиеся токов нейтрали, заслуживают внимания, поскольку высокие токи нейтрали указывают либо на плохо сбалансированные нагрузки, либо на гармонические проблемы, оба из которых указывают на необходимость дальнейшего изучения.
Значительная разница между TPF и DPF обычно является надежным индикатором наличия гармоник, но необходимо предостережение.
Если очень малые нагрузки имеют высокие гармоники, это может быть связано с плохим отношением сигнал/шум в измерительной системе. Этой проблемы можно избежать путем соответствующего выбора трансформаторов тока, используемых для проведения измерений. Не используйте, например, ТТ на 6000 А для контроля цепи с током нагрузки 60 А!
Высокие уровни реактивной мощности — еще один призыв к действию, так как часто можно добиться значительной экономии средств за счет емкостной компенсации больших индуктивных нагрузок, тем более что многие энергоснабжающие компании налагают штрафы за низкий коэффициент мощности. Тем не менее, чрезмерная компенсация также может быть проблематичной, и всегда важно убедиться, что коэффициент мощности отстает, а не опережает.
Одна из причин заключается в том, что нагрузки с опережающим коэффициентом мощности могут неблагоприятно влиять на работу генераторов. Регулятор напряжения в генераторе предназначен для поддержания выходного напряжения на заданном уровне.
По мере увеличения отстающего противофазного тока он уменьшается до напряженности поля ротора. Регулятор напряжения компенсирует это за счет увеличения тока на роторе.
Однако, если генератор питает нагрузку с опережающим коэффициентом мощности, то по мере увеличения опережающего противофазного тока увеличивается напряженность поля ротора. Регулятор напряжения уменьшает ток, подаваемый на электромагнит, для компенсации. И, если опережающий противофазный ток становится достаточно большим, регулятор вообще не подает ток, что может привести к отключению из-за перенапряжения.
Нагрузки с опережающим коэффициентом мощности также могут создавать проблемы для источников бесперебойного питания (ИБП). У них есть система постоянного тока, которая выпрямляет переменный ток в постоянный, и система переменного тока, которая инвертирует постоянный ток в переменный. Некоторые конструкции инверторов имеют большие емкостные выходные фильтры. Емкостное реактивное сопротивление этих фильтров компенсирует реактивное сопротивление нагрузок с отстающим коэффициентом мощности, позволяя ИБП отдавать почти всю свою номинальную мощность.
Однако, если нагрузка имеет опережающий коэффициент мощности, реактивное сопротивление фильтров добавляется к реактивному сопротивлению нагрузки, сильно ограничивая мощность, которую может выдавать ИБП.
Проведение энергетических испытаний
Выполнение энергетических испытаний установки состоит из четырех основных этапов: бенчмаркинг, аудит, рекомендации по изменениям и повторное тестирование. Мы рассмотрим каждый из них по очереди.
Этап сравнительного анализа должен начинаться со сбора счетов за электроэнергию за один-три года и с тщательного анализа исторического потребления энергии. Следует определить ежегодные тенденции — потребление энергии неуклонно растет, снижается или остается примерно на том же уровне? Следует также учитывать сезонные тенденции. Это нормально и ожидаемо, но большие изменения могут указывать на проблемы, связанные с отоплением, кондиционированием воздуха или системами управления технологическими процессами, или на необходимость улучшения теплоизоляции здания.
Графики тарифов на коммунальные услуги также должны быть тщательно изучены на случай, если есть возможность сократить затраты на энергию, например, путем изменения графика энергоемких операций.
Сравнительный анализ также должен включать в себя перечисление всего оборудования, потребляющего первичную энергию на объекте, и отметку часов работы каждого элемента оборудования. Особое внимание следует уделить освещению, так как его влияние на общее энергопотребление часто недооценивается. Следует учитывать тип освещения, а также адекватность уровня освещенности в здании.
Следующим шагом является аудит; но прежде чем продолжить, необходимо очень тщательно подумать и обратить внимание на безопасность. Проверьте объект на наличие угроз безопасности, убедитесь, что все системы соответствуют соответствующим кодам и стандартам, и проверьте наличие плохих соединений — для этого может пригодиться тепловизионная камера. Помните, что плохие соединения означают более высокие сопротивления, которые не только представляют угрозу безопасности, но и представляют собой потери энергии.
Аудит будет включать в себя регистрацию энергопотребления всего объекта за определенный период времени, но также важно регистрировать индивидуально энергопотребление основных элементов оборудования, потребляющих энергию. Однако перед началом записи необходимо выбрать соответствующие преобразователи тока.
Выберите датчики с правильным диапазоном: если диапазон слишком низкий, КТ может насытиться, но если он слишком большой, это приведет к плохому разрешению. Также подумайте, нужен ли преобразователь с гибким или разъемным сердечником: подойдет ли он для места, где его нужно установить, и нужны ли ему батареи? Если вы работаете в зоне с высокой ЭДС, то лучшим вариантом будет преобразователь с разъемным сердечником, а если вы записываете постоянный ток, вы должны использовать КТ на эффекте Холла.
При программировании прибора, который будет делать записи для аудита, прежде всего убедитесь, что выбрана правильная конфигурация мощности, затем установите уровень потребления на тот же уровень, что и у счетчика, обращая внимание на то, является ли он фиксированным или скользящая ставка и является ли это тарифом интервала спроса или тарифа ставки спроса.
Обязательно включите гармоническую запись!
После того, как предварительные приготовления завершены, можно приступить к контрольной фазе аудита. При подключении анализатора PQ всегда используйте соответствующие средства индивидуальной защиты (СИЗ). Убедитесь, что выводы напряжения подключены правильно в соответствии с инструкциями производителя анализатора, что диапазоны ТТ установлены правильно и ТТ подключены в правильном направлении. Затем убедитесь, что мощность (кВт) положительна, и проверьте фазовые углы.
Большое преимущество заключается в использовании прибора, который автоматически проверяет правильность настройки перед началом долговременной записи. Досадно и дорого возвращаться к инструменту через неделю только для того, чтобы обнаружить, что запись была прервана из-за простой ошибки. Когда все будет готово, убедитесь, что инструмент заземлен, еще раз проверьте, что он действительно записывает, затем закройте его и оставьте работать. Запись общего энергопотребления объекта и потребления основных единиц оборудования должна продолжаться не менее одной полной недели.
