Как применяется закон Ома для цепей переменного тока. Что такое активное, индуктивное и емкостное сопротивление в цепи переменного тока. Как рассчитать полное сопротивление цепи переменного тока. Какие особенности имеет закон Ома для цепей с реактивными элементами.
Основные понятия закона Ома для переменного тока
Закон Ома для переменного тока устанавливает связь между действующими значениями силы тока, напряжения и полным сопротивлением цепи. В общем виде он записывается так:
I = U / Z
где: I — действующее значение силы тока, А U — действующее значение напряжения, В Z — полное сопротивление цепи, Ом
Как видно, формула аналогична закону Ома для постоянного тока, но вместо активного сопротивления R используется полное сопротивление Z. Это связано с тем, что в цепи переменного тока помимо активного сопротивления проводников появляются реактивные сопротивления — индуктивное и емкостное.
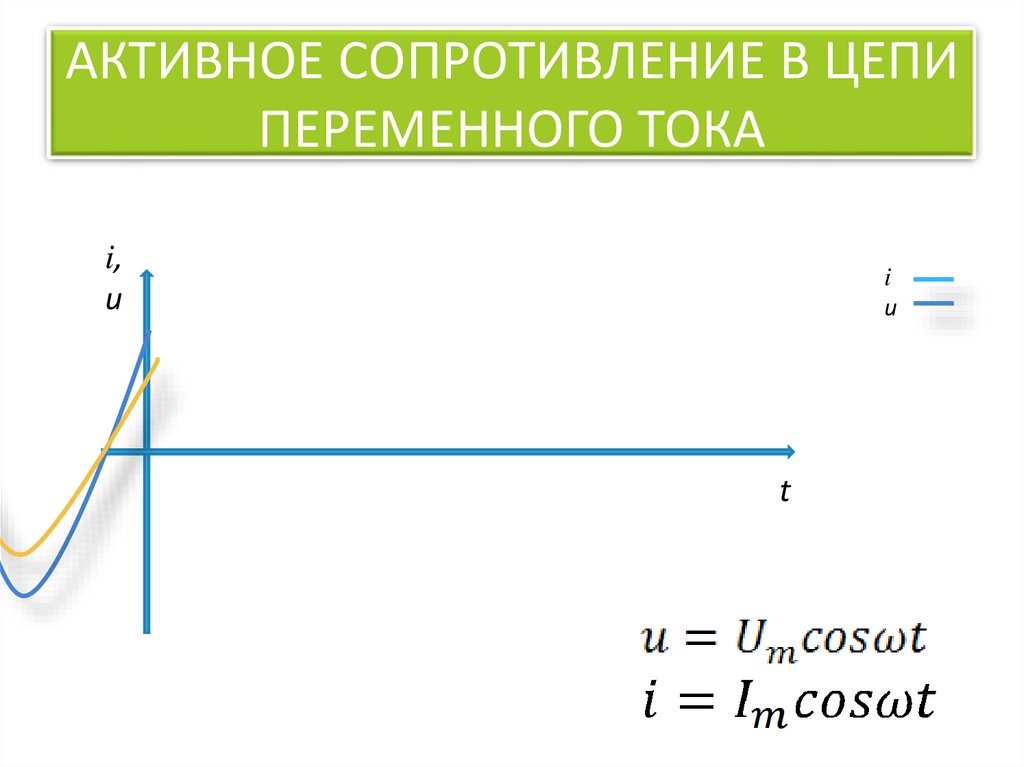
Активное сопротивление в цепи переменного тока
Активное сопротивление R в цепи переменного тока обусловлено сопротивлением проводников и потребителей электроэнергии. На активном сопротивлении происходит необратимое преобразование электрической энергии в тепловую.

Как рассчитать активное сопротивление в цепи переменного тока? Его величина не зависит от частоты тока и определяется так же, как для постоянного тока:
R = ρ * l / S
где: ρ — удельное сопротивление материала, Ом*м l — длина проводника, м S — площадь поперечного сечения, м2
Индуктивное сопротивление в цепи переменного тока
Индуктивное сопротивление XL создается катушками индуктивности и обусловлено явлением самоиндукции. При протекании переменного тока в катушке возникает ЭДС самоиндукции, препятствующая изменению тока.
Индуктивное сопротивление рассчитывается по формуле:
XL = ω * L
где: ω = 2πf — угловая частота, рад/с f — частота переменного тока, Гц L — индуктивность катушки, Гн
Как видно, индуктивное сопротивление прямо пропорционально частоте тока и индуктивности. При увеличении частоты оно возрастает.
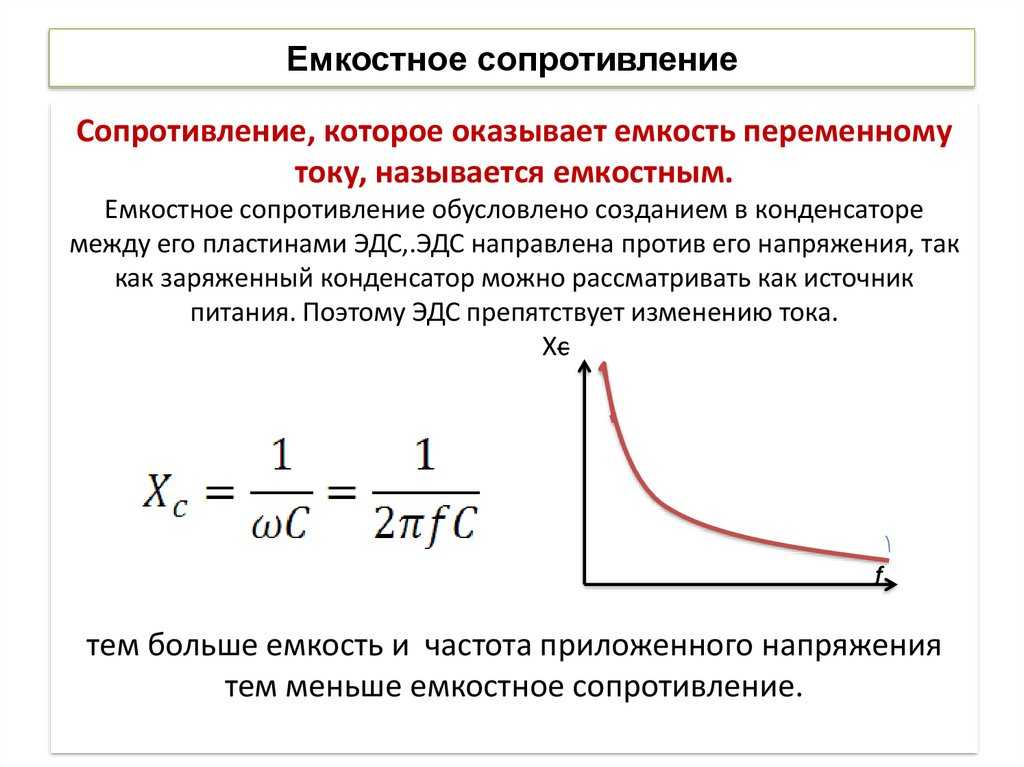
Емкостное сопротивление в цепи переменного тока
Емкостное сопротивление XC создается конденсаторами в цепи переменного тока. Оно обусловлено периодической зарядкой и разрядкой конденсатора.
Емкостное сопротивление определяется по формуле:
XC = 1 / (ω * C)
где: ω = 2πf — угловая частота, рад/с f — частота переменного тока, Гц C — емкость конденсатора, Ф
Емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора. При увеличении частоты оно уменьшается.
Полное сопротивление цепи переменного тока
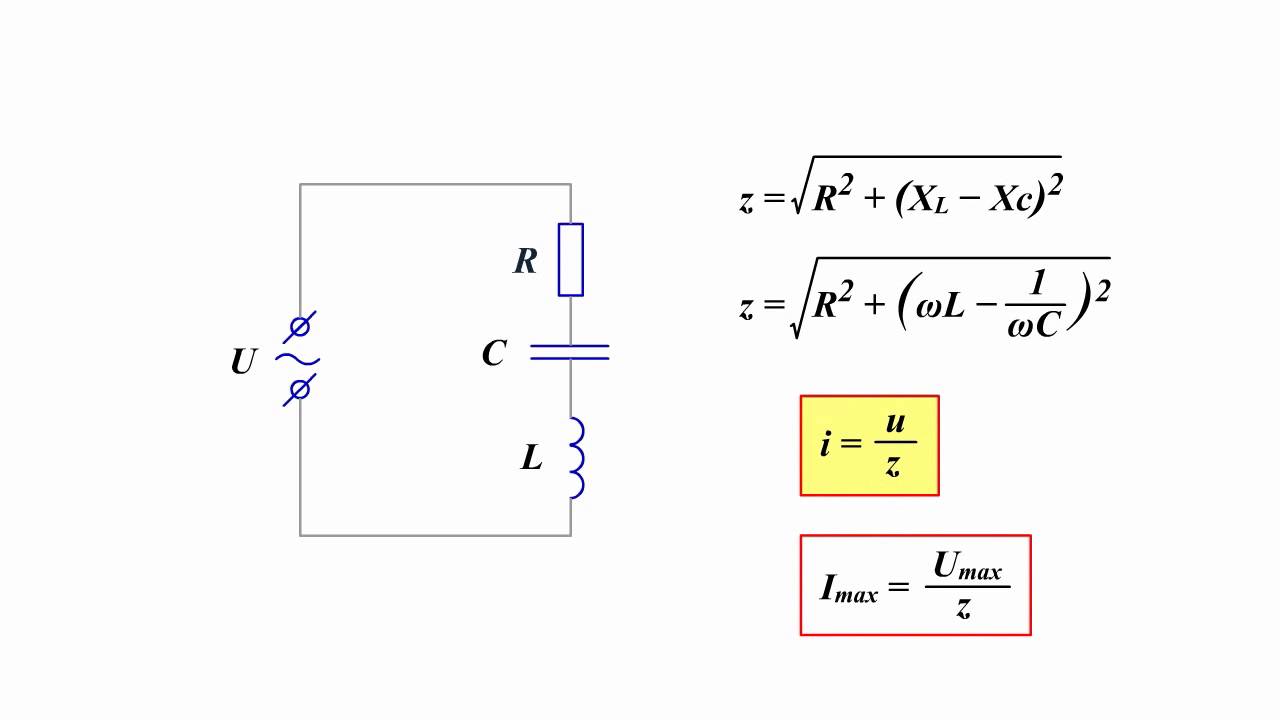
Полное сопротивление Z цепи переменного тока включает активную и реактивную составляющие:
Z = √(R2 + (XL — XC)2)
где: R — активное сопротивление XL — индуктивное сопротивление XC — емкостное сопротивление
Как рассчитать полное сопротивление цепи переменного тока? Нужно знать величины активного, индуктивного и емкостного сопротивлений и подставить их в приведенную формулу.
Особенности закона Ома для переменного тока
При применении закона Ома для переменного тока необходимо учитывать следующие особенности:
- Используются действующие (эффективные) значения тока и напряжения
- Вместо активного сопротивления R применяется полное сопротивление Z
- Реактивные сопротивления XL и XC зависят от частоты тока
- Между током и напряжением возникает сдвиг фаз на реактивных элементах
- Мощность в цепи переменного тока имеет активную и реактивную составляющие
Применение закона Ома для расчета цепей переменного тока
Закон Ома для переменного тока позволяет решать следующие практические задачи:

- Рассчитывать токи и напряжения на участках цепи
- Определять полное сопротивление сложных цепей
- Находить параметры элементов (R, L, C) по известным току и напряжению
- Рассчитывать мощность в цепях переменного тока
- Анализировать частотные характеристики цепей
Таким образом, закон Ома является фундаментальным соотношением для анализа и расчета цепей переменного тока. Его правильное применение с учетом реактивных сопротивлений позволяет решать широкий круг практических задач электротехники.
Векторные диаграммы для цепей переменного тока
Для наглядного представления соотношений между током и напряжением в цепях переменного тока используются векторные диаграммы. Они позволяют графически отобразить амплитуды и фазовые сдвиги синусоидальных величин.
Как построить векторную диаграмму для цепи переменного тока?
- Выбирается масштаб для изображения векторов тока и напряжения
- От начала координат откладывается вектор тока I
- Под соответствующими углами строятся векторы напряжений на элементах цепи
- Векторы складываются по правилам векторной алгебры
Анализ векторной диаграммы позволяет определить:

- Действующие значения токов и напряжений
- Углы сдвига фаз между током и напряжением
- Активную, реактивную и полную мощность
- Коэффициент мощности цепи
Резонанс в цепях переменного тока
Интересным явлением в цепях переменного тока с реактивными элементами является резонанс. Он возникает при определенном соотношении между индуктивным и емкостным сопротивлением.
Различают два вида резонанса:
Резонанс напряжений
Возникает в последовательном колебательном контуре при XL = XC. При этом:
- Реактивные сопротивления взаимно компенсируются
- Полное сопротивление цепи минимально и равно активному Z = R
- Ток в цепи достигает максимального значения
Резонанс токов
Наблюдается в параллельном колебательном контуре при BL = BC. В этом случае:
- Токи в параллельных ветвях равны по величине и противоположны по фазе
- Полное сопротивление цепи максимально
- Ток в неразветвленной части цепи минимален
Явление резонанса широко используется в радиотехнике для настройки колебательных контуров на определенные частоты.

Мощность в цепях переменного тока
В цепях переменного тока различают три вида мощности:
Активная мощность P
Характеризует скорость преобразования электрической энергии в другие виды. Определяется по формуле:
P = U * I * cosφ
где cosφ — коэффициент мощности
Реактивная мощность Q
Характеризует амплитуду колебаний энергии между источником и магнитным полем катушек или электрическим полем конденсаторов. Рассчитывается как:
Q = U * I * sinφ
Полная мощность S
Определяет общую нагрузку на источник питания:
S = U * I = √(P2 + Q2)
Соотношение между этими видами мощности можно наглядно представить в виде прямоугольного треугольника мощностей.
Заключение
Закон Ома для переменного тока является базовым соотношением, позволяющим анализировать цепи с активными и реактивными элементами. Его правильное применение с учетом особенностей переменного тока позволяет решать широкий круг практических задач электротехники.
Ключевые моменты, которые необходимо помнить:
- Используются действующие значения тока и напряжения
- Учитывается полное сопротивление цепи, включающее активную и реактивную составляющие
- Реактивные сопротивления зависят от частоты тока
- Возможно возникновение резонансных явлений
- Мощность имеет активную и реактивную составляющие
Понимание этих особенностей позволяет грамотно применять закон Ома для расчета и анализа цепей переменного тока в различных областях электротехники.

Переменный электрический ток. Активное, индуктивное, ёмкостное сопротивления.
Переменный электрический ток Электромагнитные колебания, как и механические, бывают двух типов: свободные и вынужденные. Свободные электромагнитные колебания, всегда колебания затухающие. Поэтому на практике они почти не используются. В то время, как вынужденные колебания используются везде и повсеместно. Ежедневно мы с вами можем наблюдать эти колебания. Все наши квартиры освещены с помощью переменного тока. Переменный ток есть не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение будут меняться с течением времени согласно гармоническому закону. Колебания, например, напряжения можно обнаружить, если подать напряжение из розетки, на осциллограф. На экране
осциллографа появится синусоида. Можно вычислить частоту переменного тока. Она
будет равняться частоте электромагнитных колебаний. Изменение напряжения на концах цепи будет вызывать за собой изменение силы тока в цепи колебательного контура. Следует всё же понимать, что изменение электрического поля во всей цепи не происходит мгновенно. Но так как это время, значительно меньше, чем период колебания напряжения на концах цепи, то обычно считают, что электрическое поле в цепи сразу же меняется, как меняется напряжение на концах цепи. Переменное напряжение создается генераторами на электростанциях. Простейшим генератором можно рассматривать проволочную рамку, которая вращается в однородном магнитном поле. Магнитный поток,
пронизывающий контур, будет постоянно меняться и будет пропорционален косинусу
угла между вектором магнитной индукции и нормалью к рамке. Если рамка вращается
равномерно, то угол будет пропорционален времени. Следовательно, магнитный поток будет изменяться по гармоническому закону: Ф = BScos(ωt) Скорость изменения магнитного потока, взятая с обратным знаком, согласно закону ЭМИ, будет равняться ЭДС индукции. Ei = -Ф’ = Emsin(ωt). Если к рамке подключить колебательный контур, то угловая скорость вращения рамки определит частот колебаний напряжения на различных участках цепи и силы тока. В дальнейшем мы будем рассматривать только вынужденные электромагнитные колебания. Они описываются следующими формулами: u = Umsin(ωt), u = Umcos(ωt) Здесь Um – амплитуда колебаний напряжения. Напряжение и сила тока меняются с одинаковой частой ω. Но колебания напряжения не всегда будут совпадать с колебаниями силы тока, поэтому лучше использовать более общую формулу: I = Imsin(ωt
+φ), где Im — амплитуда колебаний силы тока, а φ – сдвиг фаз между
колебаниями силы тока и напряжения. Активное сопротивление Рассмотрим
следующую цепь. Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением. Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону: U = Umcos(ωt). Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения. I = u/R = Umcos(ωt)/R = Imcos(ωt). Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует. Действующее значение силы тока Амплитуда силы тока определяется по следующей формуле: Im = Um/R. Среднее значение квадрата силы тока за период вычисляется по следующей формуле: i2 = (Im)2/2. Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока. Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом: I = √(i2) = Im/√2. Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула. U = √(u2) = Um/√2. Теперь подставим
действующие значения силы тока и напряжения, в выражение Im = Um/R. I = U/R. Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения. Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока. Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока. Для вычисления средней мощности используется следующая формула: P = I2R = UI. Отметим, что измерительные приборы (амперметры и вольтметры переменного
тока) регистрируют именно действующие значения. При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор — это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен. В отличии от
постоянного переменный ток может идти и через цепь, в которой присутствует
конденсатор. Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора. рисунок Напряжение на
конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем
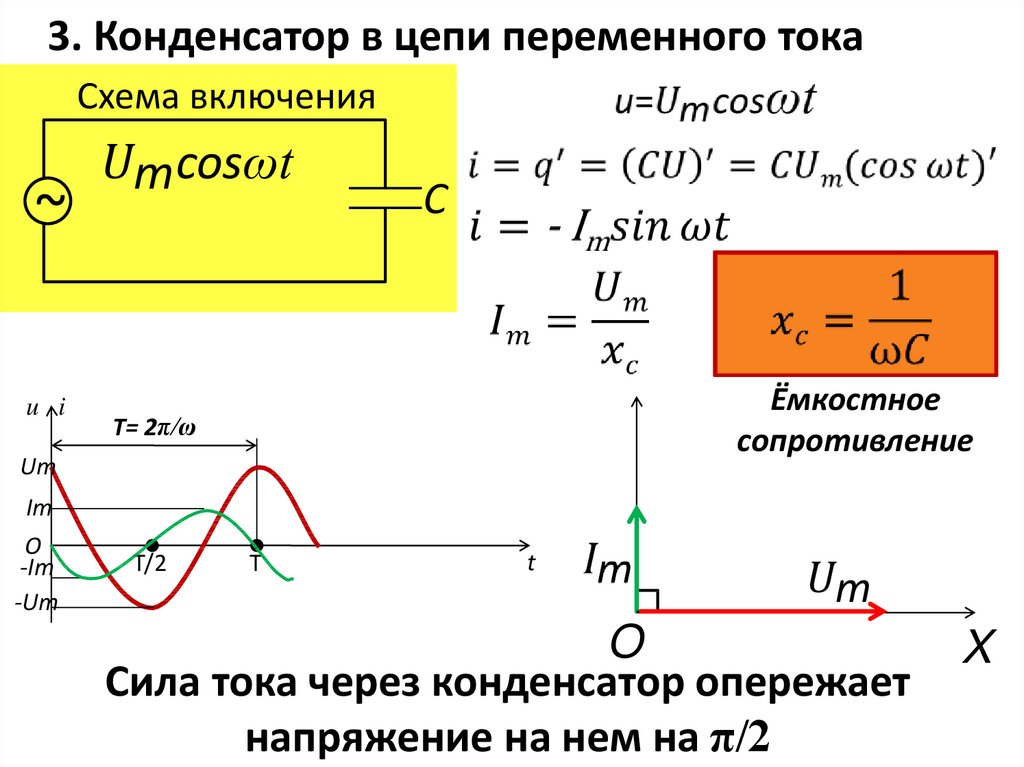
приравнять эти две величины. u = φ1-φ2 = q/C, u = Umcos(ωt). Имеем: q/C = Umcos(ωt). Выражаем заряд: q = CUmcos(ωt). Видим, что заряд будет изменяться по гармоническому закону. Сила тока — это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока. I = q’ = UmCωcos(ωt+π/2). Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной π/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на π/2. Это представлено на рисунке. Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока: Im = UmCω. Введем следующее обозначение: Xc = 1/(Cω). Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения: I = U/Xc. Xc — величина,
называемая емкостным сопротивлением. Индуктивность в
цепи переменного тока будет влиять на силу переменного тока. Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало. рисунок Выясним, как будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении катушки равном нулю, напряженность электрического поля внутри проводника тоже будет равна нулю. Равенство нулю напряженности возможно. Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля. Следовательно, ЭДС самоиндукции ei будет равна по модулю и противоположна по знаку удельной работе кулоновского поля. Следовательно: ei = -u. Сила тока будет
изменяться по гармоническому закону: I = Im sin(ωt). ЭДС самоиндукции будет равна: Ei = -Li’ = -Lω Im cos(ωt). Следовательно, напряжение будет равно: U = Lω Im cos(ωt) = Lω Im sin(ωt+ π/2). Отсюда значение действующего напряжения будет равняться Um = Lω Im. Видим, что между колебаниями тока и напряжения получилась разность фаз равная π/2. Следовательно, колебания силы тока отстают от колебания напряжения на π/2. Это наглядно представлено на следующем рисунке. рисунок Im = Um/(ωL). Введем обозначение XL = ωL. Эта величина называется индуктивное сопротивление. |
Активное, емкостное и индуктивное сопротивление. закон ома для цепей переменного тока — справочник студента
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
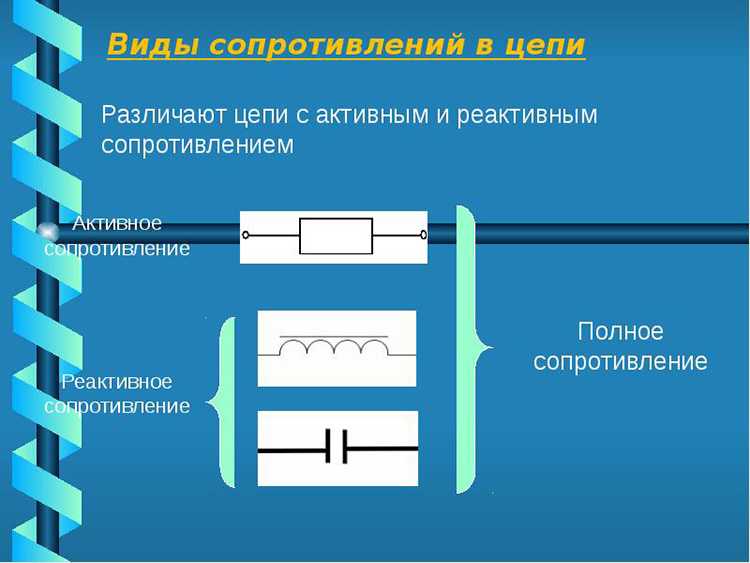
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
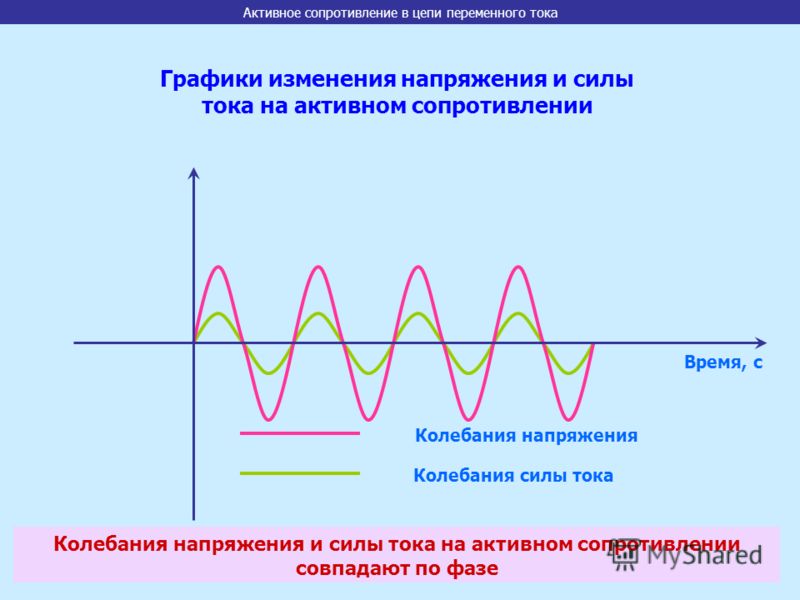
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
- где, U-напряжение на элементе цепи,
- I – ток через элемент цепи
- R – активное сопротивление элемента
- Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
| (2) |
- где, Um-амплитудное значение напряжения на элементе цепи,
- Im – амплитудное значение тока через элемент цепи
- R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
| (3) | |
| (4) |
- где — UL-падение напряжение на чисто индуктивном сопротивлении ;
- UС—падение напряжения на чисто емкостном сопротивлении;
- I— значение тока в через реактивное сопротивление;
- L— индуктивность реактивного элемента;
- C— емкость реактивного элемента;
- ω— циклическая частота.

Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
| (5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Закон Ома для различных типовых цепей переменного тока
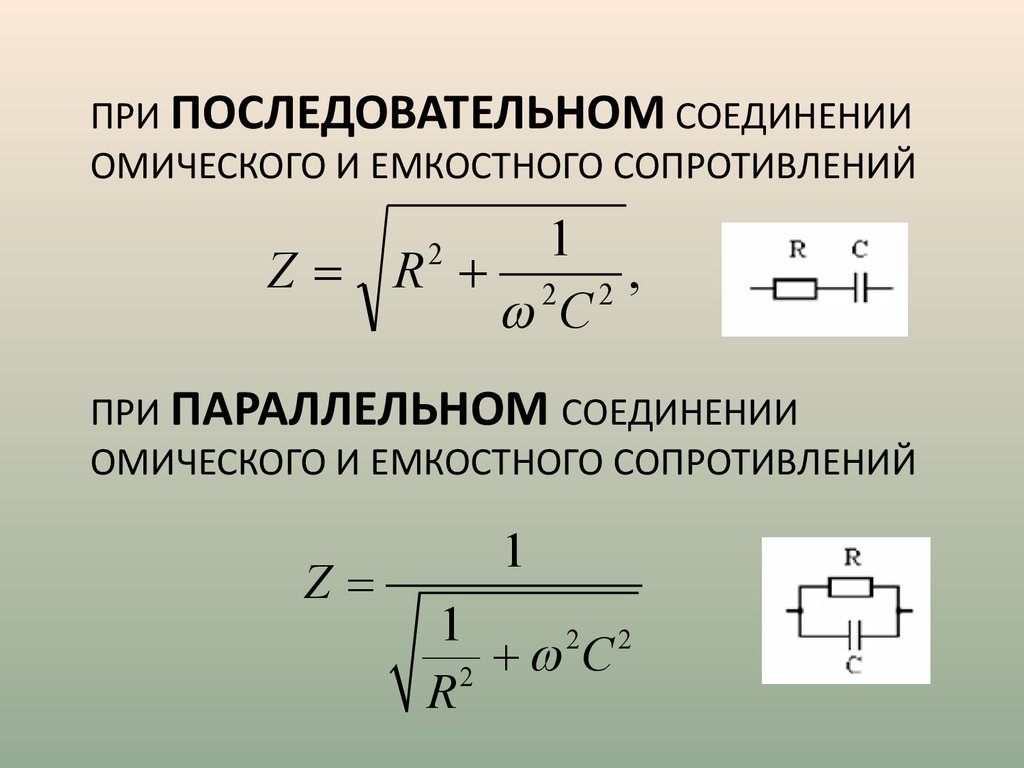
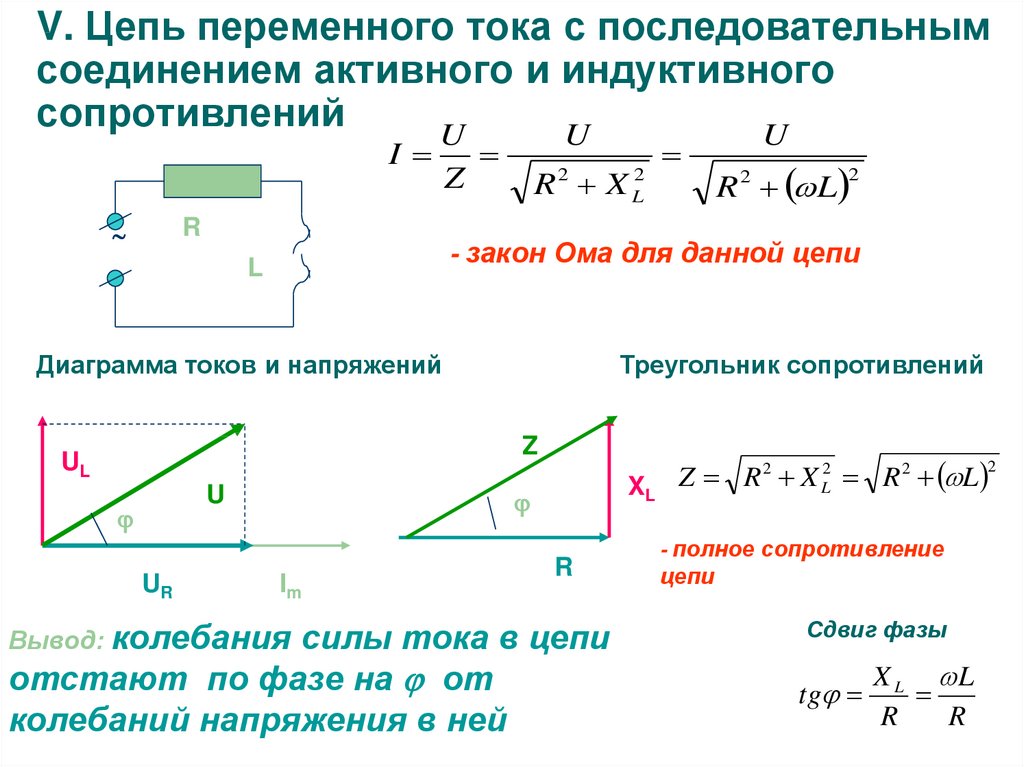
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
| (6) |
- где —эффективное значение силы тока в А;
- U—эффективное значение напряжения в В;
- R—активное сопротивление в Ом;
- ωL—индуктивное сопротивление в ом.
- Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
- где I-сила тока в А;
- U-напряжение в В;
- R-активное сопротивление в Ом;
- ωL-индуктивное сопротивление в Ом;
- 1/ωС-емкостное сопротивление в Ом.
- Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
- Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
- Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
- Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник: http://www.sxemotehnika.ru/zakon-oma-dlia-peremennogo-toka.html
Закон Ома для переменного тока
Когда-то люди жили без электричества. Потом научились делать батарейки, и так появился постоянный электрический ток. Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи. А мы двинемся дальше.
Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи. А мы двинемся дальше.
Сейчас вы поймете, почему так важен и что даёт закон Ома для цепи переменного тока. В современной жизни без этого закона никак не обойтись. Поскольку ток, это работа, а работа есть выделение тепла, то существенная задача электротехники в том, чтобы соблюдался термический режим, проще говоря, чтобы не произошло перегрева электроцепей. Итак, закон Ома гласит, что:
Итак, закон Ома гласит, что:
Измерить напряжение довольно просто, для этого понадобится вольтметр, в нашем случае для переменного напряжения.
В цепях постоянного тока измерить сопротивление тоже не составляет сложности, для этого потребуется омметр.
Почему же возникают сложности с переменным током? А проблема, именно, в его переменности, а точнее понятиях емкости и индукции, которые ведут себя при переменном токе несколько иначе, нежели при постоянном.
Формула Закона Ома для переменного тока:
Кому-то эта формула может показаться неожиданной, потому что все привыкли видеть другую формулу:
Теперь давайте разберёмся, что такое полное сопротивление цепи и всё сразу встанет на свои места.
В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями.
Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.
Как это происходит, сейчас увидите.
Ёмкостное сопротивление. При подаче напряжения на конденсатор сначала возникает сильный ток и потом поднимается напряжение, то есть в идеальных условиях ток опережает напряжение на угол 90.
Другими словами, ток совершает работу из-за наличия сопротивления в цепи, которое можно посчитать по формуле:
Таким образом, чем выше частота переменного тока и чем выше емкость конденсатора, тем меньше ёмкостное сопротивление.
Индуктивное сопротивление. Здесь все происходит наоборот, сначала возникает напряжение, затем запускается индукционный процесс который препятствует возрастанию тока. Подробнее об этом читайте в статьях про индукцию.
Поэтому здесь мы видим уже обратную картину – чем выше частота и чем больше индуктивность катушки, тем больше индуктивное сопротивление переменному току.
Почему эти понятия не встречаются в цепях постоянного тока? Ответ можно узнать, посмотрев на формулы. Если ток постоянный, то f=0.
Если ток постоянный, то f=0.
То есть, емкостное сопротивление станет бесконечно большим, а это значит, что конденсатор в цепи постоянного тока становится похож на выключатель, который размыкает цепь и ток по ней не идёт, но при этом, конденсатор будет пропускать переменный ток.
А индуктивное сопротивление станет равно нулю, значит, у нас останется просто провод, который имеет свое собственное сопротивление, которое еще называется активным, и его можно измерить обычным омметром.
В отличие от конденсатора, у которого нет активного сопротивления, сопротивление катушки, если оно довольно большое, должно приниматься в расчёт. Как правило, активное сопротивление катушки очень маленькое по сравнению с индуктивным, поэтому его в расчёт не берут, но всё же правильно формула сопротивления катушки выглядит так:
- По такому принципу в электронике изготавливают фильтры, которые должны отсечь переменный ток от постоянного, то есть пропускать только переменный ток или наоборот заглушить переменный ток, оставив только постоянный, или даже заглушить токи какой-то одной или нескольких частот.

- А сейчас совсем вас запутаю… И катушка может иметь ёмкостные свойства и конденсатор – индуктивные, но как правило они слишком малы и носят паразитический характер.
- Ну а сейчас мы рассмотрим закон Ома для электрической цепи переменного тока наглядно.
Допустим, у нас есть цепь из последовательно включенных резистора (активное сопротивление), конденсатора (реактивное ёмкостное сопротивление) и катушка (активно-реактивное индуктивное сопротивление). Теперь, чтобы узнать силу тока в цепи нам нужно правильно посчитать полное сопротивление цепи.
Осталось применить всё изложенное выше.
Реактивное сопротивление Х это разница между индуктивным сопротивлением XL и ёмкостным сопротивлением XC. Ну а дальше векторным сложением можем узнать полное реактивное сопротивление
- следовательно:
- дальнейший расчет:
- или:
Что можно сказать в заключении. Как вы можете видеть, закон Ома для переменного тока точно такой же, как и для постоянного. Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное.
Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное.
И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях.
Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.
Источник: https://uelektrika.ru/osnovy-yelektrotekhniki/zakon-oma-dlya-peremennogo-toka/
Закон Ома для переменного тока
После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.
При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
где
- I [А] – сила тока,
- U [В] – напряжение,
- Z [Ом] – полное сопротивление цепи.
Полное сопротивление цепи
В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:
где
- — индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
- — емкостное сопротивление, создается конденсатором.

Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.
Рис.1. Треугольник сопротивлений
Учитывая последние равенства, запишем формулу закона Ома для переменного тока:
– амплитудное значение силы тока.
Рис.2. Последовательная электрическая цепь из R, L, C элементов.
Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:
Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?
|
Источник: https://zakon-oma.ru/dlya-peremennogo-toka.php
Закон РћРјР° для цепей постоянного Рё переменного тока — теория Рё практика
- Онлайн расчёт электрических величин напряжения, тока и мощности для: участка цепи, полной цепи с резистивными, ёмкостными и индуктивными
- элементами.
— Рђ любите ли Р’С‹ закон РћРјР° так, как люблю его СЏ? — СЃРїСЂРѕСЃРёР» учитель физики стоящего СЂСЏРґРѕРј СЃ щитком Рё разглядывающего СЃРІРѕР№ обугленный палец электрика, — Всеми силами души Вашей, СЃРѕ всем энтузиазмом Рё исступлением, Рє которому только СЃРїРѕСЃРѕР±РЅР° пылкая молодость, — никак РЅРµ угомонялся РѕРЅ, сверкая РёР·-РїРѕРґ очков пытливым взглядом. — Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным РІРѕРїСЂРѕСЃРѕРј электрик Рё пошёл, насвистывая «РљР°Р»РёРЅРєСѓ-Малинку» РІ направлении ближайшего супермаркета — РЅРµ ради пьянства окаянного, Р° дабы залечить СЃРІРѕР№ увечный палец.
— Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным РІРѕРїСЂРѕСЃРѕРј электрик Рё пошёл, насвистывая «РљР°Р»РёРЅРєСѓ-Малинку» РІ направлении ближайшего супермаркета — РЅРµ ради пьянства окаянного, Р° дабы залечить СЃРІРѕР№ увечный палец.
А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R, I – сила тока в проводнике, измеряемая в амперах [А]; U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В]; R – электрическое сопротивление проводника, измеряемое в омах [Ом].
Производные РѕС‚ этой формулы приобретают такой же незамысловатый РІРёРґ: R=U/I Рё U=R×I.
Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P(Вт) = U(В)×I(А) = I2(А)×R(Ом) = U2(В)/R(Ом) Можно, конечно, описывая закон Ома обойтись и вообще без формул, а вместо них пользоваться словами или картинками: С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта. Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари! Считайте, учитывайте размерность, не стирайте из памяти, что: 1В=1000мВ=1000000мкВ; 1А=1000мА=1000000мкА; 1Ом=0.001кОм=0.000001МОм; 1Вт=1000мВт=100000мкВт. Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари! Считайте, учитывайте размерность, не стирайте из памяти, что: 1В=1000мВ=1000000мкВ; 1А=1000мА=1000000мкА; 1Ом=0.001кОм=0.000001МОм; 1Вт=1000мВт=100000мкВт. Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
ТАБЛ�ЦА ДЛЯ ПРОВЕРК� РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.
Вводить РІ таблицу нужно только РґРІР° имеющихся Сѓ Вас параметра, остальные посчитает таблица. Р’СЃРµ наши расчёты проводились РїСЂРё условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр. Если это условие РЅРµ соблюдается, то РїРѕРґ величиной R следует принять СЃСѓРјРјСѓ внешнего Рё внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон РћРјР° для полной цепи: I=U/(R+r) . Для многозвенных цепей возникает необходимость преобразования её Рє эквивалентному РІРёРґСѓ:
Р’СЃРµ наши расчёты проводились РїСЂРё условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр. Если это условие РЅРµ соблюдается, то РїРѕРґ величиной R следует принять СЃСѓРјРјСѓ внешнего Рё внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон РћРјР° для полной цепи: I=U/(R+r) . Для многозвенных цепей возникает необходимость преобразования её Рє эквивалентному РІРёРґСѓ:
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/Rll = 1/R4+1/R5.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.
Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь РІ РІРёРґСѓ для правильной интерпретации закона РћРјР° для переменного тока — РїРѕРґ значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.
Рђ что такое действующее значение Рё как РѕРЅРѕ связано СЃ амплитудой сигнала переменного тока? Приведём диаграммы для нескольких различных форм сигнала. Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал СЃРѕ скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы. Глядя РЅР° СЂРёСЃСѓРЅРѕРє можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда РІ пределах положительной, или отрицательной (РІ наших случаях РѕРЅРё равны) полуволны.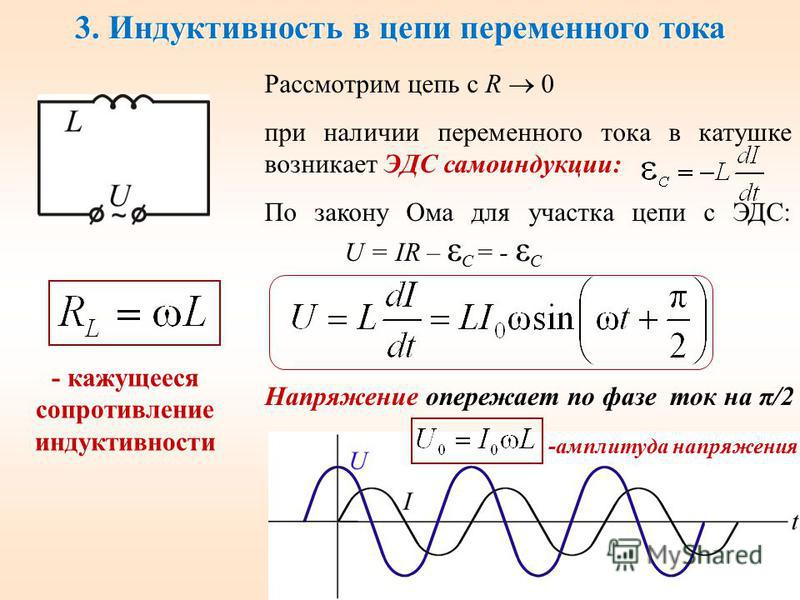 Рассчитываем действующее значение напряжение интересующей нас формы: Для СЃРёРЅСѓСЃР° U = UРґ = UР°/в€љ2; для треугольника Рё пилы U = UРґ = UР°/в€љ3; для меандра U = UРґ = UР°. РЎ этим разобрались!
Рассчитываем действующее значение напряжение интересующей нас формы: Для синуса U = Uд = Uа/√2; для треугольника и пилы U = Uд = Uа/√3; для меандра U = Uд = Uа. С этим разобрались!
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .
Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть РЅРµ менее РѕРґРЅРѕРіРѕ, РїСЂРё наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !
КАЛЬКУЛЯТОРДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТ�ВЛЕН�Я ЦЕП�.
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.
Токозадающими цепями РІ данной схеме являются элементы R1 Рё РЎ1. Допустим, нас интересует выходное напряжение Uвых = 12 вольт РїСЂРё токе нагрузки 100 РјРђ. Выбираем стабилитрон Р”815Р” СЃ напряжением стабилизации 12Р’ Рё максимально допустимым током стабилизации 1,4Рђ. Зададимся током через стабилитрон СЃ некоторым запасом — 200РјРђ. РЎ учётом падения напряжения РЅР° стабилитроне, напряжение РЅР° токозадающей цепи равно 220РІ — 12РІ = 208РІ. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200РјРђ: Z = 208РІ/200РјРђ = 1,04РєРћРј. Резистор R1 является токоограничивающим Рё выбирается РІ пределах 10-100 РћРј РІ зависимости РѕС‚ максимального тока нагрузки.
Допустим, нас интересует выходное напряжение Uвых = 12 вольт РїСЂРё токе нагрузки 100 РјРђ. Выбираем стабилитрон Р”815Р” СЃ напряжением стабилизации 12Р’ Рё максимально допустимым током стабилизации 1,4Рђ. Зададимся током через стабилитрон СЃ некоторым запасом — 200РјРђ. РЎ учётом падения напряжения РЅР° стабилитроне, напряжение РЅР° токозадающей цепи равно 220РІ — 12РІ = 208РІ. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200РјРђ: Z = 208РІ/200РјРђ = 1,04РєРћРј. Резистор R1 является токоограничивающим Рё выбирается РІ пределах 10-100 РћРј РІ зависимости РѕС‚ максимального тока нагрузки. Зададимся номиналами R1 — 30 РћРј, РЎ1 — 1 РњРєС„, частотой сети f — 50 Гц Рё подставим РІСЃС‘ это хозяйство РІ таблицу. Получили полное сопротивление цепи, равное 3,183РєРћРј. Многовато будет — надо увеличивать ёмкость РЎ1. Поигрались туда-СЃСЋРґР°, нашли нужное значение ёмкости — 3,18 РњРєС„, РїСЂРё котором Z = 1,04РєРћРј. Р’СЃС‘ — закон РћРјР° выполнил СЃРІРѕСЋ функцию, расчёт закончен, всем спать полчаса!
Зададимся номиналами R1 — 30 РћРј, РЎ1 — 1 РњРєС„, частотой сети f — 50 Гц Рё подставим РІСЃС‘ это хозяйство РІ таблицу. Получили полное сопротивление цепи, равное 3,183РєРћРј. Многовато будет — надо увеличивать ёмкость РЎ1. Поигрались туда-СЃСЋРґР°, нашли нужное значение ёмкости — 3,18 РњРєС„, РїСЂРё котором Z = 1,04РєРћРј. Р’СЃС‘ — закон РћРјР° выполнил СЃРІРѕСЋ функцию, расчёт закончен, всем спать полчаса!
Источник: https://vpayaem.ru/information11.html
Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока
Определение 1
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
[Ileft(t
ight)=I_m{sin left(omega t
ight) left(1
ight). }]
}]
- Рисунок 1.
- Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
[U=IR=I_m{Rsin left(omega t
ight) left(2
ight), }]
где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
[U_m=RI_mleft(3
ight),]
где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.
- Рисунок 2.
- Мы можем использовать следующие соотношения:
Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
- Если $I(t)$ определена уравнением (1), то заряд выражен как:
- где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.
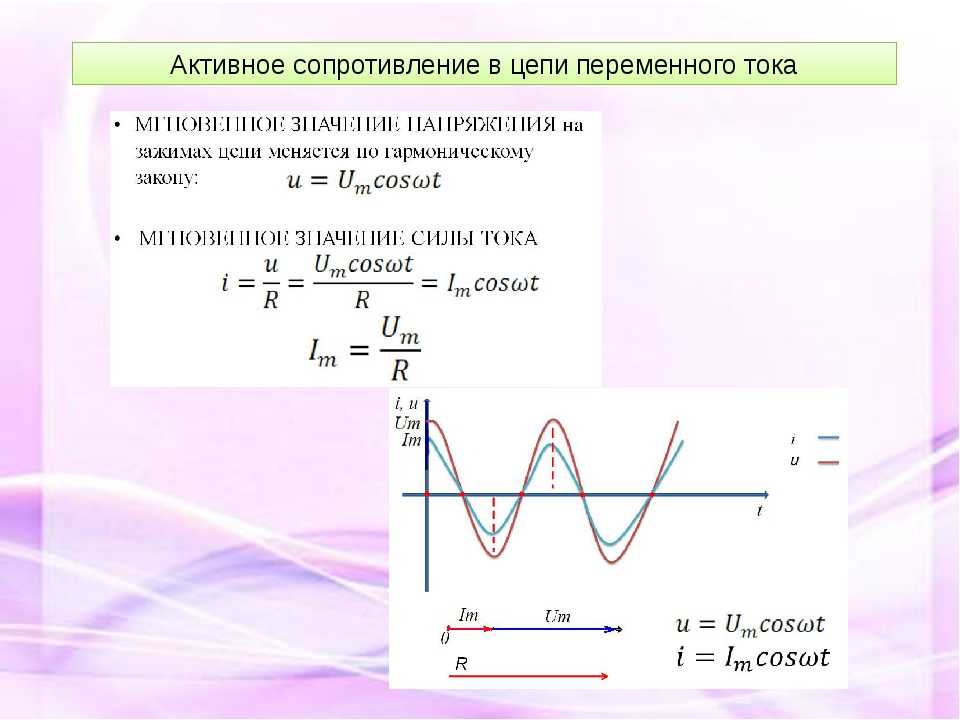 $ Получим напряжение равно:
$ Получим напряжение равно: - Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac{pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=frac{1}{omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $.
Это значит, что постоянный ток не течет через конденсатор.
Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.
- Рисунок 3.
- Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
- По условию $R=0. mathcal E$ самоиндукции можно выразить как:
- Из выражений (8), (9) следует, что:
- Амплитуда напряжения в данном случае равна:
- где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).
 2}(13)]
2}(13)]называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.
Пример 1
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
u$.- Решение:
- Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
- Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
- оно связано с действующим значением силы тока как:
- В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:
[I_m=frac{U_m}{sqrt{R^2+{left(omega L-frac{1}{omega C}
ight)}^2}}left(1. 2}}.]
2}}.]Источник: https://spravochnick.ru/fizika/peremennyy_sinusoidalnyy_tok/aktivnoe_emkostnoe_i_induktivnoe_soprotivlenie_zakon_oma_dlya_cepey_peremennogo_toka/
Закон Ома для переменного тока: формула
Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи.
Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов.
Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.
Закон ома для участка цепи
Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах. Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.
Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке.
Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр.
 Такая подсказка дает возможность легко и быстро найти нужное значение.
Такая подсказка дает возможность легко и быстро найти нужное значение.Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.
Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.
Закон ома для полной цепи
Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.
Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта.
Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания.
Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.
Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока.
По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами.
Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.
Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела.

Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r).
На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.
Что такое трансформаторы тока
Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U
ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока.
В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы.
Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.
Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.
Закон ома для цепи переменного тока
Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.
Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.
Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения.
 Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится.
Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится.Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс.
Для обозначения полного сопротивления контура используется символ Z.
Мощность короткого замыкания
Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.
Источник: https://electric-220.ru/news/zakon_oma_dlja_peremennogo_toka/2018-03-02-1465
Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями
По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:
Пример.
 Активное сопротивление катушки составляет 5 ом, а ее полное сопротивление Z=30 ом. Определить угол сдвига фаз.
Активное сопротивление катушки составляет 5 ом, а ее полное сопротивление Z=30 ом. Определить угол сдвига фаз.Решение.
При соs =0,25 угол =75°.
§ 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ
На рис. 57, а изображена цепь переменного тока, в которую включены последовательно активное сопротивление r, индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.
Под действием переменного напряжения в этой цепи протекает переменный ток.
Выясним, чему равно общее напряжение на зажимах цепи. Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. 57, б).
Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали, в выбранном масштабе вектор тока I.
В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения Uа откладываем по вектору тока.

Напряжение на индуктивности опережает ток на угол = 90°. Поэтому вектор UL откладываем вверх
под углом 90° к вектору тока.
В цепи с емкостью, наоборот, напряжение отстает от тока на угол = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.
Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий векторную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор U, изображающий общее напряжение на зажимах цепи.
На основании теоремы Пифагора из треугольника напряжений АО Б следует, что
отсюда общее напряжение
Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис.
 57, в). Его сторонами являются сопротивления r, (ХL — Хс) и полное сопротивление цепи Z.
57, в). Его сторонами являются сопротивления r, (ХL — Хс) и полное сопротивление цепи Z.Пользуясь теоремой Пифагора, можно написать, что
Отсюда полное сопротивление цепи
Силу тока в цепи с активным, индуктивным и емкостным сопротивлениями определяют по закону Ома:
На векторной диаграмме (рис. 57, б) видно, что в рассматриваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что
- Из треугольника сопротивлений
- § 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ
На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.
Полное сопротивление первой катушки
Полное сопротивление второй катушки
Напряжение на зажимах катушек равно напряжению генератора.
- Сила тока в каждой катушке определяется согласно закону Ома:
- Из этих равенств можно сделать вывод, что в такой цепи токи разветвляются обратно пропорционально полным сопротивлениям ветвей.

- Для определения угла сдвига фаз между напряжением и током
- в каждой катушке вычисляют и и по таблице тригонометрических функций находят значения углов 1 и 2.
- Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощности (cos ).
Так как первый закон Кирхгофа справедлив для цепей переменного тока, то в рассматриваемой цепи общий ток определяется геометрическим сложением векторов (рис. 58,6).
По горизонтали в выбранном масштабе отложим вектор напряжения U. Так как ток в цепи с индуктивностью отстает от напряжения, то вектор тока I1 выбранном масштабе отложим с помощью транспортира под углом 1 к вектору напряжения U, а вектор тока I2 и отложим под углом 2. Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбранного масштаба.
- Чтобы найти общий ток, нужно воспользоваться тем, что активная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:
- а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережающие):
- После чего определяют общий ток:
- Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.

Пример. Три катушки соединены параллельно и к ним подключено переменное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;
- Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.
- Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.
- Решение. Индуктивное сопротивление катушек:
- Полное сопротивление катушек:
- Сила тока в катушках:
Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/cep-peremennogo-toka-s-aktivnym-induktivnym-i-emkostnym-soprotivleniyami
Активное, индуктивное, емкостное сопротивления в цепи переменного тока доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Повторение темы: Активное, индуктивное, емкостное сопротивления в цепи переменного тока, предмет презентации: Физика.
 Этот материал в формате pptx (PowerPoint) содержит 19 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 19 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.Слайд 1 Текст слайда: Активное, индуктивное, емкостное сопротивления в цепи переменного тока
Слайд 2 Текст слайда: …переменный ток – это вздор, не имеющий будущего. Я не только не хочу осматривать двигатель переменного тока, но и слышать о нем
Томас ЭдисонСлайд 3 Текст слайда: Электрические устройства, преобразующие электрическую энергию во внутреннюю
Высокоомные провода
Нагревательные приборы1. Активное сопротивление
Слайд 4 Текст слайда: Пропускает и постоянный и переменный ток
Активное сопротивление
Слайд 5 Текст слайда: Колебания силы тока и напряжения совпадают по фазе
Активное сопротивление
Слайд 6 Текст слайда: Энергия тока превращается во внутреннюю энергию проводника
Формула активного сопротивления
ω
[R] = 1Ом
Слайд 7 Текст слайда: Катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения
2.
 Индуктивное сопротивление
Индуктивное сопротивлениеСлайд 8 Текст слайда: Пропускает переменный и постоянный переменный ток
Индуктивное сопротивление
Слайд 9 Текст слайда: индуктивность вызывает отставание тока от напряжения на четверть периода
Индуктивное сопротивление
Слайд 10 Текст слайда: Формула индуктивного сопротивления
ω
ХL
Энергия тока превращается в энергию магнитного поля катушки
Слайд 11 Текст слайда: В любой момент времени изменению силы тока противодействуют ЭДС самоиндукции
ЭДС самоиндукции — причина индуктивного сопротивления
Физический смысл индуктивного сопротивления
Слайд 12 Текст слайда: Конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока
3.
 Емкостное сопротивление
Емкостное сопротивлениеСлайд 13 Текст слайда: Пропускает переменный ток и не пропускает постоянный ток
Емкостное сопротивление
Слайд 14 Текст слайда: Колебания тока опережают колебания напряжения на π/2
Емкостное сопротивление
Слайд 15 Текст слайда: Формула емкостного сопротивления
ω
Хс
Энергия тока превращается в энергию электрического поля конденсатора
Слайд 16 Текст слайда: Изменению переменного тока в любое мгновение противодействует электрическое поле между обкладками конденсатора
Физический смысл емкостного сопротивления
Слайд 17 Текст слайда: Ток в реальной цепи зависит от её полного эквивалентного сопротивления.
Частотные свойства
конденсатора и катушкиКонденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания.
Катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания.
Слайд 18 Текст слайда: — реактивное сопротивление
— полное сопротивление
Закон Ома для полной цепи
переменного токаСлайд 19 Текст слайда: Используемые материалы
https://infourok.ru
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
| Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями
По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:
Пример.
 Активное сопротивление катушки составляет 5 ом, а ее полное сопротивление Z=30 ом. Определить угол сдвига фаз.
Активное сопротивление катушки составляет 5 ом, а ее полное сопротивление Z=30 ом. Определить угол сдвига фаз.Решение.
При соs =0,25 угол =75°.
§ 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ
На рис. 57, а изображена цепь переменного тока, в которую включены последовательно активное сопротивление r, индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.
Под действием переменного напряжения в этой цепи протекает переменный ток.
Выясним, чему равно общее напряжение на зажимах цепи. Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. 57, б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали, в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения Uа откладываем по вектору тока.
Напряжение на индуктивности опережает ток на угол = 90°. Поэтому вектор UL откладываем вверх
под углом 90° к вектору тока.
В цепи с емкостью, наоборот, напряжение отстает от тока на угол = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.
Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий векторную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор U, изображающий общее напряжение на зажимах цепи.
На основании теоремы Пифагора из треугольника напряжений АО Б следует, что
отсюда общее напряжение
Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис.
 57, в). Его сторонами являются сопротивления r, (ХL — Хс) и полное сопротивление цепи Z.
57, в). Его сторонами являются сопротивления r, (ХL — Хс) и полное сопротивление цепи Z.Пользуясь теоремой Пифагора, можно написать, что
Отсюда полное сопротивление цепи
Силу тока в цепи с активным, индуктивным и емкостным сопротивлениями определяют по закону Ома:
На векторной диаграмме (рис. 57, б) видно, что в рассматриваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что
Из треугольника сопротивлений
§ 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ
На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.
Полное сопротивление первой катушки
Полное сопротивление второй катушки
Напряжение на зажимах катушек равно напряжению генератора.

Сила тока в каждой катушке определяется согласно закону Ома:
Из этих равенств можно сделать вывод, что в такой цепи токи разветвляются обратно пропорционально полным сопротивлениям ветвей.
Для определения угла сдвига фаз между напряжением и током
в каждой катушке вычисляют и и по таблице тригонометрических функций находят значения углов 1 и 2.
Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощности (cos ).
Так как первый закон Кирхгофа справедлив для цепей переменного тока, то в рассматриваемой цепи общий ток определяется геометрическим сложением векторов (рис. 58,6).
По горизонтали в выбранном масштабе отложим вектор напряжения U. Так как ток в цепи с индуктивностью отстает от напряжения, то вектор тока I1 выбранном масштабе отложим с помощью транспортира под углом 1 к вектору напряжения U, а вектор тока I2 и отложим под углом 2.
 Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбранного масштаба.
Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбранного масштаба.Чтобы найти общий ток, нужно воспользоваться тем, что активная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:
а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережающие):
После чего определяют общий ток:
Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.
Пример. Три катушки соединены параллельно и к ним подключено переменное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;
Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.
Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.
Решение. Индуктивное сопротивление катушек:
Полное сопротивление катушек:
Сила тока в катушках:
С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ
Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связьКАТЕГОРИИ:
Археология
Биология
Генетика
География
Информатика
История
Логика
Маркетинг
Математика
Менеджмент
Механика
Педагогика
Религия
Социология
Технологии
Физика
Философия
Финансы
Химия
ЭкологияТОП 10 на сайте
Приготовление дезинфицирующих растворов различной концентрации
Техника нижней прямой подачи мяча.
Франко-прусская война (причины и последствия)
Организация работы процедурного кабинета
Смысловое и механическое запоминание, их место и роль в усвоении знаний
Коммуникативные барьеры и пути их преодоления
Обработка изделий медицинского назначения многократного применения
Образцы текста публицистического стиля
Четыре типа изменения баланса
Задачи с ответами для Всероссийской олимпиады по праву
Мы поможем в написании ваших работ!ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации
Практические работы по географии для 6 класса
Организация работы процедурного кабинета
Изменения в неживой природе осенью
Уборка процедурного кабинета
Сольфеджио. Все правила по сольфеджио
Балочные системы.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
⇐ ПредыдущаяСтр 9 из 15Следующая ⇒
СОПРОТИВЛЕНИЯМИ
При расчетах цепей переменного тока, так же как и цепей постоянного тока, используют законы Ома и Кирхгофа. Отличие в применении этих законов заключается в том, что в цепях переменного тока необходимо учитывать углы сдвига фаз между токами и напряжениями.
Цепь переменного тока, в которую включены последовательно активное сопротивление R, индуктивность L, обладающая индуктивным сопротивлением , и емкость С, имеющая емкостное сопротивление, изображена на рис. .8, а.
Под действием переменного напряжения и в этой цепи протекает переменный ток iСогласно закону Ома определим падения напряжения на каждом элементе цепи:
Эти падения напряжения имеют соответствующие углы сдвига фаз по отношению к общему току цепи I.

Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. .8,б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения откладываем по вектору токаI . Напряжение на индуктивности опережает ток на угол = 90°. Поэтому вектор откладываем вверх под углом 90° к вектору тока I . В цепи семкостьюи наоборот, напряжение отстает от тока на угол = 90°, поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока I.
Рис. .8. Цепь переменного тока с последовательно включенными сопротивлением ,индуктивностью и емкостью:
а — электрическая схема; б — векторная диаграмма; в — треугольник сопротивлений
Для определения общего напряжения, приложенного к зажимам
цепи, сложим векторы и.
 Для этого вычтем из большего вектора и
Для этого вычтем из большего вектора ивектор и получим вектор ( ,) выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( ) .
Суммой этих векторов будет диагональ параллелограмма — вектор Uявляющийся общим напряжением на зажимах цепи:
2или 2
Полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления,
2
Полная проводимость цепи:
Угол сдвига фаз между током и напряжением цепи определяется тригонометрическими функциями:
Если >, то вектор напряжения U опережает вектор тока I, а если < то Uотстает от тока I.Треугольник сопротивлений изображен на рис.
 .8, в
.8, вПример .4. В электрическую цепь, приведенную на рисунке, с напряжением U = 220 В последовательно включены: резистор с активным сопротивлением , = 5 Ом, индуктивная катушка Lс активным сопротивлением
= 3 Ом и индуктивным сопротивлением = 4 Ом, конденсатор С с емкостным сопротивлением = 10 Ом. Определить ток в цепи и напряжение на отдельных элементах цепи. Нарисовать векторную диаграмму.
Решение
Определяем общее сопротивление
2 = =10Ом
Ток в цепи
Напряжение на отдельных элементах цепи:
В
В
В
В
Векторная диаграмма приведена на рисунке ниже.
Рассмотрим электрическую цепь, состоящую из двух приемников, подключенных параллельно к зажимам источника синусоидального напряжения u= sin
(рис.
 .9,а). В первом приемнике включены последовательно элементы и L, во втором соответственно и С. Оба приемника находятся под действием одного общего напряженияu. Запишем выражения для мгновенных значений токов для первой и второй ветви:
.9,а). В первом приемнике включены последовательно элементы и L, во втором соответственно и С. Оба приемника находятся под действием одного общего напряженияu. Запишем выражения для мгновенных значений токов для первой и второй ветви:Рис. 9. Цепь переменного тока с параллельно соединенными элементам
а — электрическая схема: б — векторная диаграмма
Так как в первую ветвь включена индуктивная катушка, а во вторую— конденсатор, то электрические цепи соответственно носят индуктивны й и емкостной характер.
Действующее значение тока I и косинус угла определяем из следующих выражений:
Значение тока I в неразветвленной части цепи определяют как геометрическую сумму токов в ветвях, т.е.I = +
Векторная диаграмма приведена на рис. 9, б. Токи, протекающие через ветви, состоят из активной и реактивной составляющих и соответственно имеют индуктивный и емкостной характер.

Ветвь с активной составляющей характеризуется активной проводимостью
Ветвь с реактивной составляющей характеризуется реактивной проводимостью . Для первой ветви реактивная проводимость
2
Реактивная проводимость не является величиной, обратной реактивному сопротивлению, так как при ее определении учитывается и активное сопротивлении ветви. Полная проводимость ветви
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие законы используют при расчете цепей переменного тока?
2.В чем состоит принципиальное отличие расчета цепей переменного
тока от расчета цепей постоянного тока?
РЕЗОНАНС НАПРЯЖЕНИЙ
В цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, соединенными последовательно (рис. 10, а), может возникнуть резонанс напряжений
Резонанс напряжений наступает в том случае, если индуктивное сопротивление и емкостное сопротивление равны между собой, т.
 е.
е.Так как эти сопротивления зависят от частоты, резонанс наступает при определенной резонансной частоте :
При заданной частоте резонанс напряжений может быть достигнут изменением L и С.
Рис. 10. Цепь переменного тока при резонансе напряжения:
а — электрическая схема; б — векторная диаграмма
Когда цепь не настроена в резонанс, ее полное сопротивление
2
При резонансе напряжений в рассматриваемой цепи, когда = ее полное сопротивление
Запомните
1. Полное сопротивление цепи при резонансе напряжений равно активному сопротивлениюR.
2. Угол сдвига фаз между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи сактивным сопротивлением)
Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает.
 Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении:
Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении:Напряжение на индуктивности и емкости определяется согласно закону Ома. В связи стем что в последовательно соединенных сопротивлениях протекает одинаковый ток и при резонансе индуктивное сопротивление = напряжения на индуктивности и емкости тоже равны:
Векторная диаграмма для рассматриваемой цепи при резонансе напряжения приведена на рис 10, б. На векторной диаграмме видно, что напряжения на индуктивности и емкости равны, сдвинуты по фазе друг относительно друга на 180° и взаимно компенсируются.
Если одновременно увеличить оба реактивных сопротивления и , не нарушая при этом условия резонанса =, то соответственно возрастут оба частичных напряжения и, а сила тока в цепи при этом не изменится. Таким образом, можно получить и во много раз большие, чем напряжение U на зажимах цепи, поэтому резонанс напряжений — опасное явление для энергетических установок.
В электроустановках большой мощности резонанс напряжений, который может наступить внезапно, например при изменении емкостного сопротивления, может привести к опасным перенапряжениям и рассматривается как аварийный. В технике связи и автоматике явление резонанса напряжений широко используют для настройки приемных и передающих устройств на определенную частоту
Пример.5. В цепь переменного тока включены последовательно активное сопротивление R = 3 Ом, индуктивность L= 0,005 Гн и емкость С = 63,5 мкф. Генератор, включенный в цепь, вырабатывает переменное напряжение U = 2,5 В с резонансной частотой = 285 Гц. Определить индуктивное и емкостное сопротивления, полное сопротивление цепи, токпротекающий в цепи, напряжения на емкости и индуктивности.
Решение
Индуктивное сопротивление
Ом
Емкостное сопротивление
Индуктивное сопротивление равно емкостному, следовательно, в цепи наступает резонанс напряжения.

Полное сопротивление цепи при резонансе напряжения
2 = 2 = 3Ом
Сила тока в цепи
Напряжение на индуктивности
Напряжение на емкости
Как видно из представленного примера, в режиме резонанса напряжения на индуктивности и емкости равны и превышают напряжение генератора.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется резонансом напряжений?
2. Чему равно полное сопротивление цепи при резонансе напряжений?
3. Чему равен угол сдвига фаз между током и напряжением при резонансе напряжений?
4. Какую опасность представляет резонанс напряжений в технике?
РЕЗОНАНС ТОКОВ
В цепи переменного тока, в которой индуктивность L, емкость Си сопротивлениеR соединены параллельно (рис.
 .11, а), может возникнуть резонанс токов при условии равенства реактивных сопротивлений:
.11, а), может возникнуть резонанс токов при условии равенства реактивных сопротивлений:Ток при резонансе достигает минимального значения I = U/R, a cos = 1, т. е. достигает своего максимального значения.
Значение резонансной частоты определяется формулой
Из формулы следует, что, изменяя величину емкости или индуктивности контура, можно изменять (регулировать) частоту свободных колебаний, т. е. настраивать контур на определенную частоту.
Векторная диаграмма изображена на рис..11, б в режиме резонанса токов.
Рис .11. Цепь переменного тока при резонансе тока:
а-электрическая схема; б — векторная диаграмма
Свободные электрические колебания, возникающие в колебательном контуре, всегда затухающие. Затухание колебаний в контуре объясняется тем, что при прохождении электрического то в контуре энергия тратится на нагревание провода, из которого изготовлены индуктивная катушка и соединительные провода.

Потеря энергии в контуре вызывает постепенное уменьшение амплитуды свободных колебаний и их полное прекращение. Скорость затухания колебаний в контуре связана с потерей энергии в нем и зависит от сопротивления контура.
Запомните
■ Токи в ветвях, содержащих L и С, при резонансе тока могут быть
больше общего тока цепи.
■ Индуктивный и емкостной токи противоположны по фазе, равны по значению и по отношению к источнику энергии взаимно
компенсируются, т. е. идет обмен энергией между индуктивной
катушкой и конденсатором.
■ Реактивная мощность цепи при резонансе токов равна нулю, поскольку равны и противоположно направлены токи . Иными словами, реактивная мощность, потребляемая в индуктивной катушке, равна реактивной мощности, генерируемой в конденсаторе.
В результате резонанса токов общий ток в цепи может быть относительно мал, а в ветвях индуктивности и емкости, где происходят электрические колебания, переменный ток значительно больше общего.

Пример 6. Разветвленная цепь, приведенная на рисунке слева, имеет
следующие параметры: = = 10 Ом, R = 40 Ом, U= 120 В. Определить токи в ветвях и общий ток цепи. Построить векторную диаграмму.
Решение
Определим токи в ветвях:
Рассчитаем общий ток цепи
Векторная диаграмма изображена на рисунке справа. Общий ток цепи при резонансе токов в четыре раза меньше тока в ветвях, содержащих реактивные элементы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При каких условиях возникает резонанс токов?
2. От чего зависит скорость затухания колебаний в контуре?
3. Чему равна реактивная мощность цепи при резонансе токов?
⇐ Предыдущая45678910111213Следующая ⇒
Читайте также:
Техника прыжка в длину с разбега
Тактические действия в защите
История Олимпийских игр
История развития права интеллектуальной собственности
Последнее изменение этой страницы: 2017-02-05; просмотров: 1270; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.
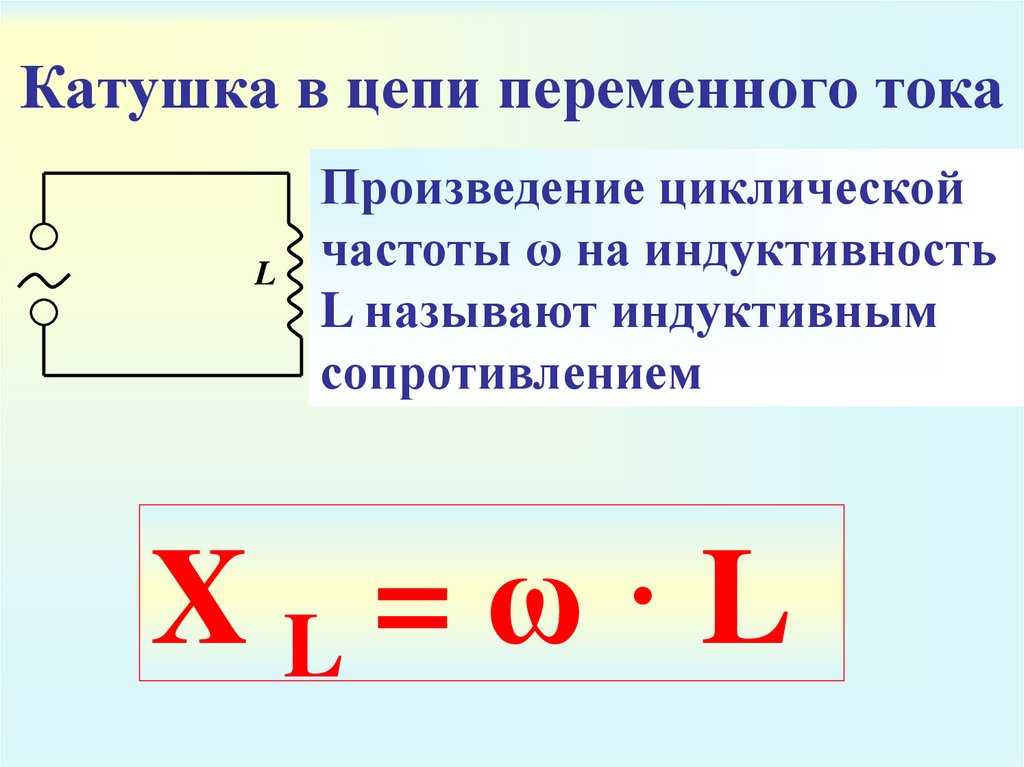 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.039 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.039 с.)Индуктивное и емкостное сопротивление
Активное сопротивление
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис.
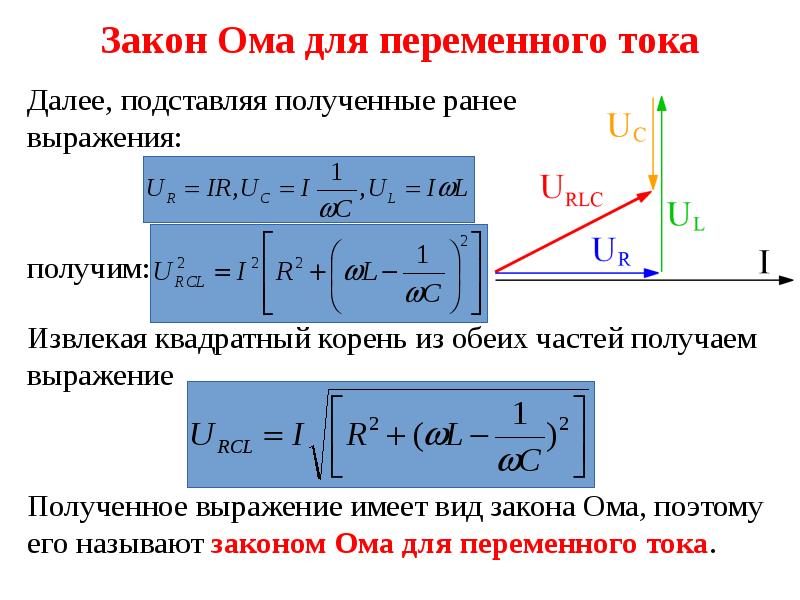 2. Пусть заряд на конденсаторе равен $q$.
2. Пусть заряд на конденсаторе равен $q$.Мы можем использовать следующие соотношения:
Попробуй обратиться за помощью к преподавателям
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac<pi ><2>.$ Амплитуда напряжения на емкости равна:
Величину $X_C=frac<1><omega C>$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.
 3). Будем считать $I>0$, если ток направлен от $а$ к $в$.
3). Будем считать $I>0$, если ток направлен от $а$ к $в$.Задай вопрос специалистам и получи
ответ уже через 15 минут!Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
По условию $R=0. mathcal E$ самоиндукции можно выразить как:
Из выражений (8), (9) следует, что:
Амплитуда напряжения в данном случае равна:
где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепей переменного тока
называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$.
 На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
u$.Решение:
Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
оно связано с действующим значением силы тока как:
В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:
Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:
где $omega =2pi
u .$Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).
Решение:
Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:
Напряжение на активном сопротивлении ($U_R$) равно:
Напряжение на конденсаторе ($U_C$) определяется как:
Так и не нашли ответ
на свой вопрос?Просто напиши с чем тебе
нужна помощьЕмкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0.
 Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.
Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.Мгновенное значение напряжения равно
.
Мгновенное значение силы тока равно:
Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим:
, где — емкостное сопротивление.
Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты).
Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току).
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой.
 Такая нагрузка наз. реактивной.
Такая нагрузка наз. реактивной.Индуктивное сопротивление в цепи переменного тока
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.
Мгновенное значение силы тока:
Мгновенное значение напряжения можно установить, учитывая, что u = — εi , где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению.
.
Следовательно
, где амплитуда напряжения.

Напряжение опережает ток по фазе на π/2.
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой.
Величина
— индуктивное сопротивление.
Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления.
В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка.
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой.
 Такая нагрузка наз. реактивной.
Такая нагрузка наз. реактивной.Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микромилиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.
Что такое
Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.
Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.
Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами.
 Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.
Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.
Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.

По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.

При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.
Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.

Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.
Причины ёмкостного сопротивления
Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0.
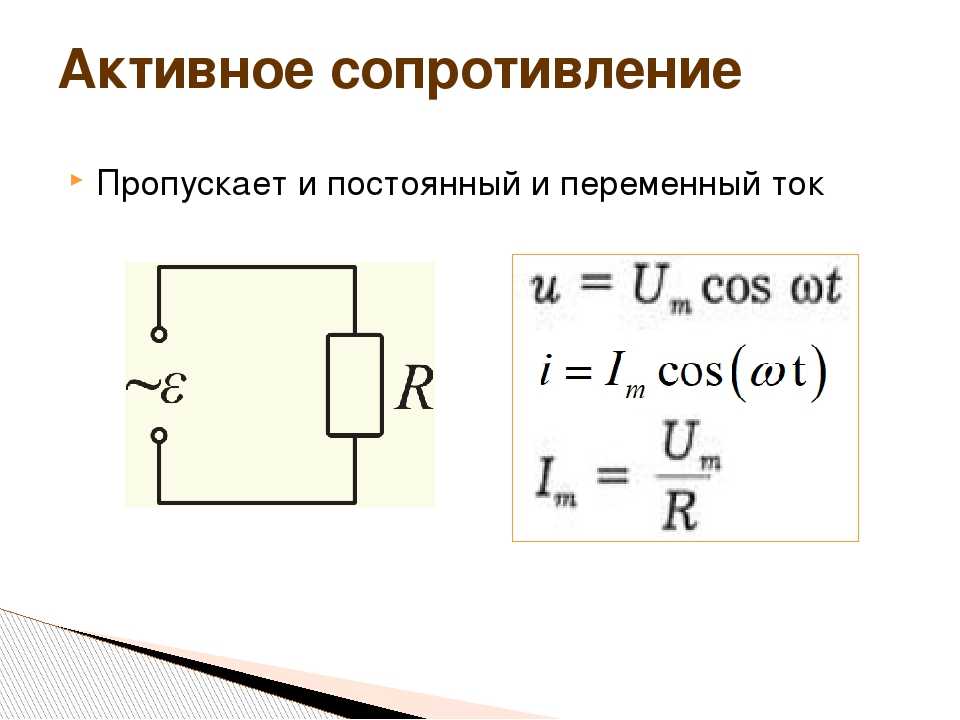 В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц.
 Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.После введения данных в формулу, определяющую Xc, и получаются значения:
Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.
В чем измеряется емкостное электросопротивление
R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.
Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства.
 Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.
Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.курсов PDH онлайн. PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов HVAC; не только экологические курсы или курсы по энергосбережению
.»
Рассел Бейли, ЧП
Нью-Йорк
«Это укрепило мои текущие знания и научило меня нескольким новым вещам, кроме того
познакомив меня с новыми источниками
информации».
Стивен Дедак, ЧП
Нью-Джерси
«Материал был очень информативным и организованным. Я многому научился, и они
очень быстро отвечали на вопросы.
Это было на высшем уровне. Буду использовать
снова. Спасибо».

Блэр Хейуорд, P.E.0003 «Веб-сайт прост в использовании. Хорошо организован. Я действительно буду пользоваться вашими услугами снова.
Я передам название вашей компании
другим сотрудникам.»
Рой Пфлейдерер, ЧП
Нью-Йорк
«Справочный материал был превосходным, и курс был очень информативным, особенно потому, что я думал, что уже знаком
с деталями Канзас
Авария в City Hyatt.»
Майкл Морган, ЧП
Техас
«Мне очень нравится ваша бизнес-модель. Мне нравится, что я могу просмотреть текст перед покупкой. Я обнаружил, что класс
Информативный и полезный
в моей работе. «
Уильям Сенкевич, стр.
Флорида
познавательный. Вы
— лучшие, которые я нашел. «
Рассел Смит, P.
 E.
E. Pennsylvania
Я считаю, что подход упрощает для рабочего инженера.
материала». На самом деле
человек изучает больше
от неудач. «
Джон Скондры, P.E.
Пенсильвания
«. Курс был хорошо поставлен вместе, и используется.
Путь обучения. «
Jack Lundberg, P.E.
Висконсин
» Я очень увлекаюсь тем, как вы представляете курсы; т. е. позволяя
Студент. Для рассмотрения курса
Материал перед оплатой и
Получение викторины. «
Arvin Swanger, P.E.
Virgina
«. курсы. Я, конечно, многому научился и
получил огромное удовольствие».0002 «Я очень доволен предлагаемыми курсами, качеством содержания материалов и простотой поиска
онлайн-курсов
.
 »
» Уильям Валериоти, ЧП
Техас
«Этот материал во многом оправдал мои ожидания. Курс был прост для изучения. Фотографии в основном давали хорошее представление о
обсуждаемых темах.»
Майкл Райан, ЧП
Пенсильвания
«Именно то, что я искал. Нужен 1 балл по этике, и я нашел его здесь.»
Джеральд Нотт, П.Е.
Нью-Джерси
«Это был мой первый онлайн-опыт получения необходимых кредитов PDH. Это было
информативно, выгодно и экономично.
Я настоятельно рекомендую это
всем инженерам. «
Джеймс Шурелл, P.E.
Ohio
Я ценю вопросы« Реальный мир »и соответствует моей практике. , и
не основаны на каком-то неясном разделе
законов, которые не применяются
к «нормальной практике».
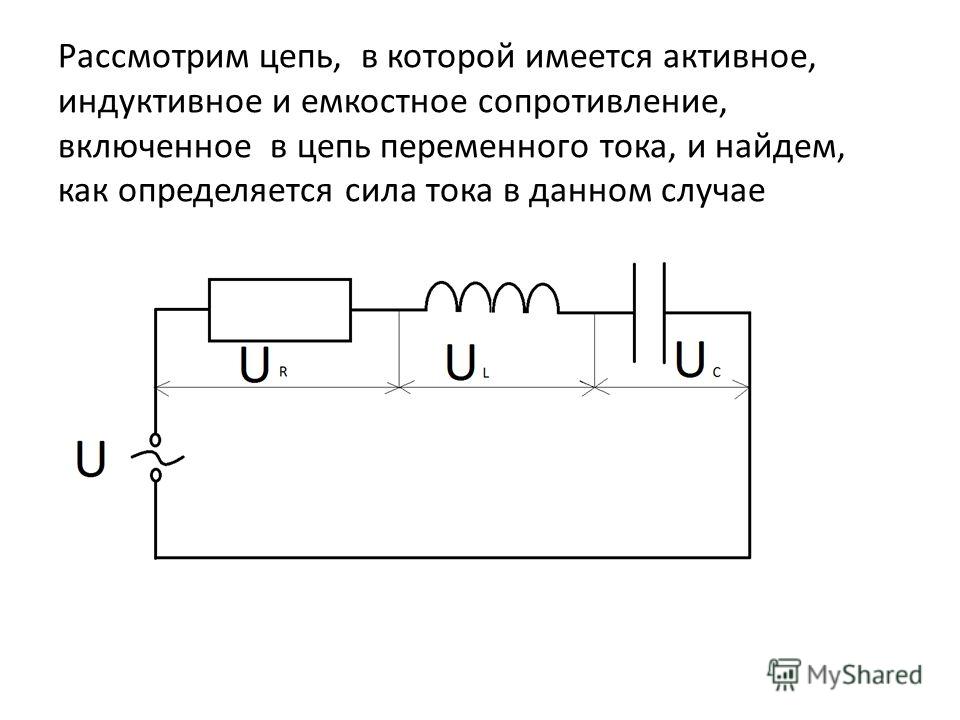 0005
0005Марк Каноник, ЧП
Нью-Йорк
«Большой опыт! Я многому научился, чтобы вернуться к своему медицинскому устройству
организации».
Иван Харлан, ЧП
Теннесси
«Материал курса имеет хорошее содержание, не слишком математический, с хорошим акцентом на практическое применение технологий».
Юджин Бойл, ЧП
California
«Это был очень приятный опыт. Тема была интересной и хорошо представленной,
, а онлайн -формат был очень
и простые в
. Благодарность.»
Патрисия Адамс, ЧП
Канзас
«Отличный способ добиться соответствия непрерывному обучению физкультуры в рамках временных ограничений лицензиата».
Джозеф Фриссора, ЧП
Нью-Джерси
«Должен признаться, я действительно многому научился.
 Это помогает иметь
Это помогает иметь обзор текстового материала. предоставлены
фактические случаи».
Жаклин Брукс, ЧП
Флорида
«Общие ошибки ADA в проектировании объектов очень полезны. Проверка
требовало исследования в
Документ , но Ответы были
. Проще говоря.»
Гарольд Катлер, ЧП
Массачусетс
«Это было эффективное использование моего времени. Спасибо за разнообразие выбора
в инженерии дорожного движения, который мне нужен
, чтобы выполнить требования
Сертификация PTOE. «
Джозеф Гилрой, стр. способ заработать CEU для моих требований PG в штате Делавэр. До сих пор все курсы, которые я посещал, были отличными.
Надеюсь увидеть больше 40%
Курсы с дисконтированием ».

Кристина Николас, P.E.
New York
» только что завершены. дополнительные
курсы. Процесс прост, и
намного эффективнее, чем
необходимость путешествовать.0004
Айдахо
«Услуги, предоставляемые CEDengineering, очень полезны для инженеров-профессионалов
для получения единиц PDH
в любое время. Очень удобно.»
Пол Абелла, ЧП
Аризона
«Пока все было отлично! Поскольку я постоянно работаю матерью двоих детей, у меня не так много
времени, чтобы исследовать, куда
получить мои кредиты от.»
Кристен Фаррелл, ЧП
Висконсин
2 90 «Это было очень познавательно. Легко для понимания с иллюстрациямии графиками; определенно облегчает
усвоение всех
теорий.
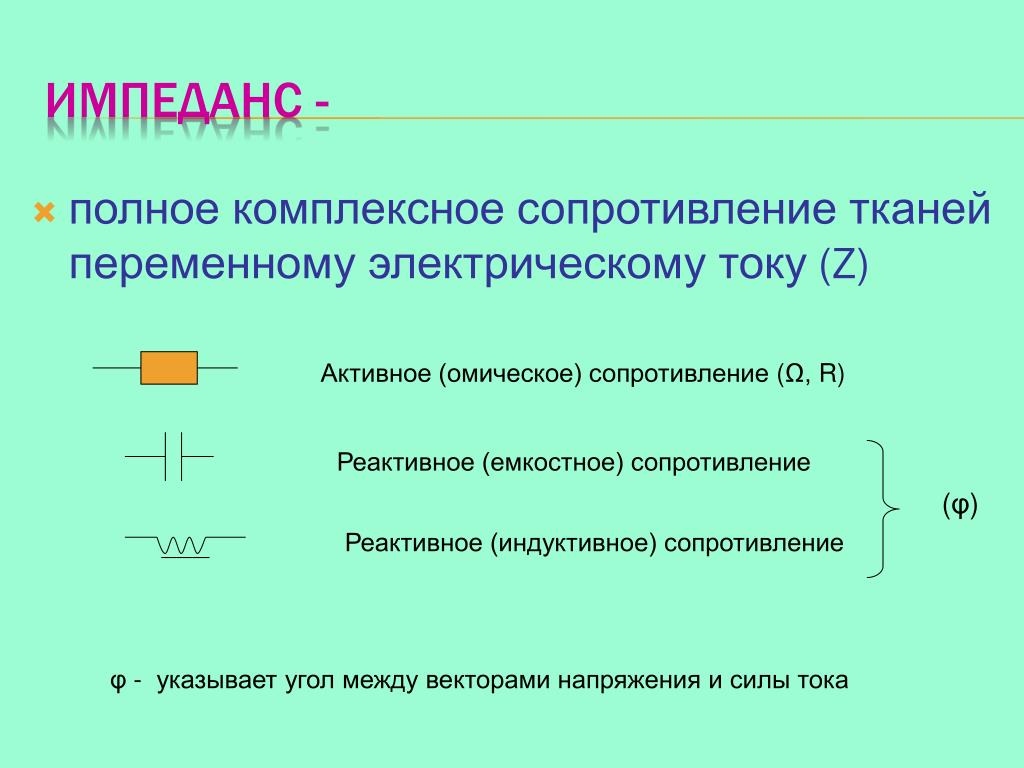 »
» Виктор Окампо, P.Eng.
Альберта, Канада
«Хороший обзор принципов полупроводников. Мне понравилось проходить курс по телефону
My Wope Pace во время моего Morning
Subway Commute 9000 9000 2 до работы. .»
Клиффорд Гринблатт, ЧП
Мэриленд
«Просто найти интересные курсы, скачать документы и получить
викторина. Я буду Emong Рекомендовать
You To Every PE, нуждающийся в
CE. тем во многих областях техники».0004
«У меня перепроизводили вещи, которые я забыл. Я также рад получить финансово
на Ваше промо-электронное письмо , которая
на 40%.»
Conrado Casem, P.E.
Теннесси
«Отличный курс по разумной цене.
 Буду пользоваться вашими услугами в будущем.»
Буду пользоваться вашими услугами в будущем.» Чарльз Флейшер, П.Е.
Нью-Йорк
«Это был хороший тест, и я фактически проверил, что я прочитал кодексы профессиональной этики
и правила Нью-Мексико
».
Брун Гильберт, Ч.П.
Калифорния
«Мне очень понравились занятия. Они стоили времени и усилий.»
Дэвид Рейнольдс, ЧП
Канзас
«Очень доволен качеством тестовых документов. Будет использовать CEDengineerng
, когда потребуется дополнительная сертификация
.»
Томас Каппеллин, ЧП
Иллинойс
«У меня истек срок действия курса, но вы все равно выполнили обязательство и поставили
Me, за что я заплатил — много
! » для инженера».
 0004
0004Хорошо расположено. «
Глен Шварц, P.E.
Нью -Джерси
Вопросы были подходящими для уроков, а материал урока —.
для дизайна дерева.»
Брайан Адамс, ЧП
Миннесота
0004
Роберт Велнер, ЧП
Нью -Йорк
«У меня был большой опыт, когда я получил прибрежное строительство — проектирование
Building и
High Рекомендую его».
Денис Солано, ЧП
Флорида
«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики штата Нью-Джерси были очень
хорошо подготовлено. Мне нравится возможность загрузить учебный материал до
Обзор везде, где бы ни был и
всякий раз, когда ».

Тим Чиддикс, P.E.
Colorado
» Отлично! Сохраняйте широкий выбор тем на выбор».
Уильям Бараттино, ЧП
Вирджиния
«Процесс прямой, никакой чепухи. Хороший опыт.»
Тайрон Бааш, ЧП
Иллинойс
«Вопросы на экзамене были наводящими и демонстрировали понимание
материала. Тщательный
и всеобъемлющий. «
Майкл Тобин, P.E.
Аризона
» Это мой второй курс, и мне понравилось то, что мне предложил курс, что
помогу моя линия
работы. Я обязательно воспользуюсь этим сайтом снова.»
Анджела Уотсон, ЧП
Монтана
«Простота в исполнении.
 Никакой путаницы при подходе к сдаче теста или записи сертификата.»
Никакой путаницы при подходе к сдаче теста или записи сертификата.» Кеннет Пейдж, ЧП
Мэриленд
«Это был отличный источник информации о нагревании воды с помощью солнечной энергии.
Луан Мане, ЧП
Conneticut
«Мне нравится подход, позволяющий зарегистрироваться и иметь возможность читать материалы в автономном режиме, а затем
вернуться, чтобы пройти тест.»
Алекс Млсна, ЧП
Индиана
«Я оценил количество информации, предоставленной для класса. Я знаю
Это вся информация, которую я могу
В реальных жизненные ситуации. «
Натали Дриндер, P.E.
South Dakota
курс.»0004
«веб -сайт прост в использовании, вы можете загрузить материал для изучения, затем вернуться
и пройти тест.
 .»
.» Майкл Гладд, ЧП
Грузия
«Спасибо за хорошие курсы на протяжении многих лет.»
Деннис Фундзак, ЧП
Огайо
«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать сертификат PDH
. Спасибо, что сделали этот процесс простым.»
Фред Шайбе, ЧП
Висконсин
«Положительный опыт. Быстро нашел курс, который соответствует моим потребностям, и закончил
PDH за один час за
Один час. «
Стив Торкильдсон, P.E.
Южная Каролина
» Мне нравилось загрузить документы для рассмотрения контента
и приготовимости.
наличие для оплаты
материалов.»
Richard Wymelenberg, P.
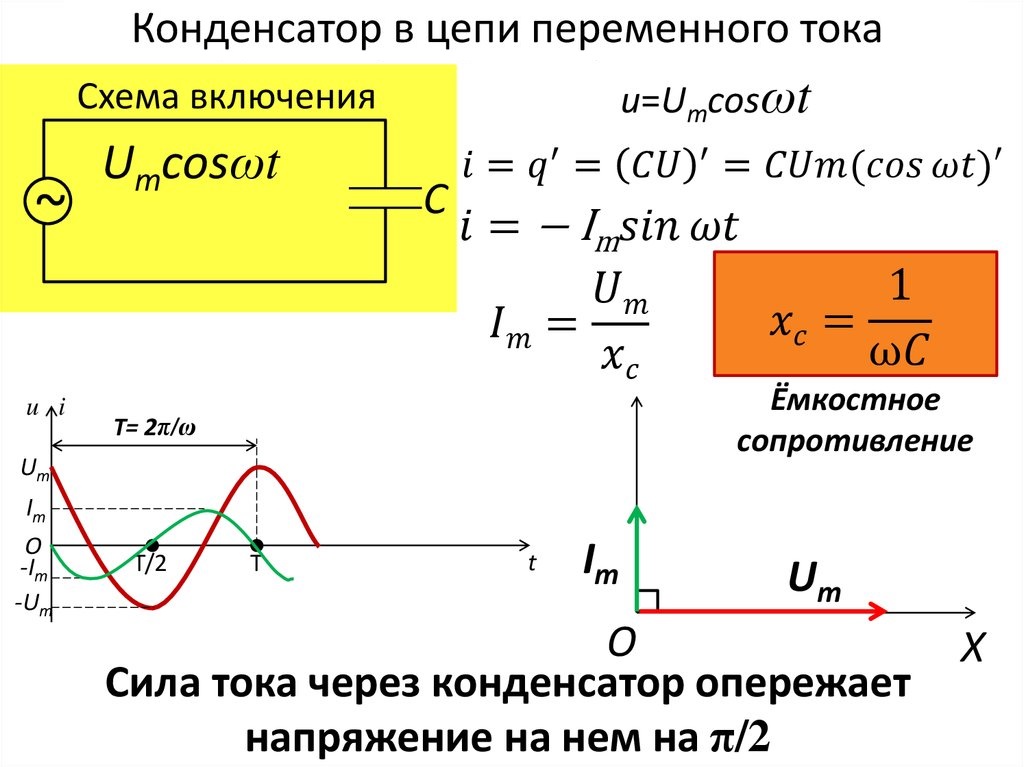 E.0005
E.0005«Это хорошее пособие по ЭЭ для инженеров, не являющихся электриками.»
Дуглас Стаффорд, ЧП
Техас
«Всегда есть место для улучшения, но я не могу придумать ничего в вашем
процессе, который нуждается в
улучшении.»
Томас Сталкап, ЧП
Арканзас
«Мне очень нравится удобство прохождения онлайн-викторины и немедленного получения сертификата
.»
Марлен Делани, ЧП
Иллинойс
«Обучающие модули CEDengineering — это очень удобный способ доступа к информации по
многим различным техническим областям
3 за пределами
40003 Специализация одной собственной специализации
без.
Продукция Elliott Sound Реактивное сопротивление — емкостное и индуктивное © 2012, Rod Elliott (ESP)
Основной индекс Лампы и индекс энергопотребления
Содержимое- Введение
- Емкостное реактивное сопротивление
- Индуктивное сопротивление
- Комбинированное реактивное сопротивление
- Параллельные реактивные сопротивления Реактивные сопротивления серии
- Непредвиденные последствия
- Потери мощности
- Выводы
- Ссылки
- Активная коррекция коэффициента мощности
ВведениеВ дополнение к статье о активной коррекции коэффициента мощности (см.
 PFC) стоит рассмотреть влияние емкостного и индуктивного реактивного сопротивления. Многое из того, что вы здесь прочтете, кажется бессмысленным, но все это совершенно реально. Комбинации индуктивности и емкости могут иметь совершенно неожиданные последствия.
PFC) стоит рассмотреть влияние емкостного и индуктивного реактивного сопротивления. Многое из того, что вы здесь прочтете, кажется бессмысленным, но все это совершенно реально. Комбинации индуктивности и емкости могут иметь совершенно неожиданные последствия.Например, в статье PFC есть краткое обсуждение гармонических токов, но не то, как и почему они могут вызывать такие большие нарушения в энергосистеме. В этой статье мы попытаемся дать некоторые ответы, но, естественно, не сможем охватить все возможности. Следует учитывать, что для чего-то столь сложного и широко распространенного, как сеть электроснабжения («сеть»), вероятность чего-то неожиданного зависит не от «если», а от «9».1496 когда ‘.
Опять же, так называемые энергосберегающие устройства, состоящие из конденсатора, постоянно подключенного к сети, могут вызывать проблемы. Вероятно, не для самой сети, так как она такая большая, но есть реальный риск для бытовой электропроводки, если будет установлена одна из этих глупых афер.
 Чтобы освежить вашу память, эти мошеннические устройства обсуждаются здесь, если вам нужна дополнительная информация.
Чтобы освежить вашу память, эти мошеннические устройства обсуждаются здесь, если вам нужна дополнительная информация.Важно понимать, что идеальных компонентов не бывает. Резисторы (или линии электропередачи) имеют сопротивление, емкость и индуктивность, конденсаторы имеют сопротивление и индуктивность, а также требуемую емкость, а катушки индуктивности также имеют сопротивление, емкость и индуктивность. Из них малые резисторы близки к идеальным, но те, которые встречаются в инфраструктуре крупных сетей электроснабжения, далеки от идеала.
Конденсаторы (используемые для коррекции коэффициента мощности и фильтрации) гораздо ближе к «идеальным» компонентам, чем катушки индуктивности или распределенное сопротивление (в отличие от фактического резистора, который очень близок к идеальному на промышленных частотах), однако паразитная емкость (между соседними линиями электропередач, например) всегда представляет собой смесь трех основных «компонентов», и если у вас нет гораздо больше информации, чем кто-либо обычно позволяет вам иметь, точное моделирование даже небольшого участка сети не может быть выполнено.
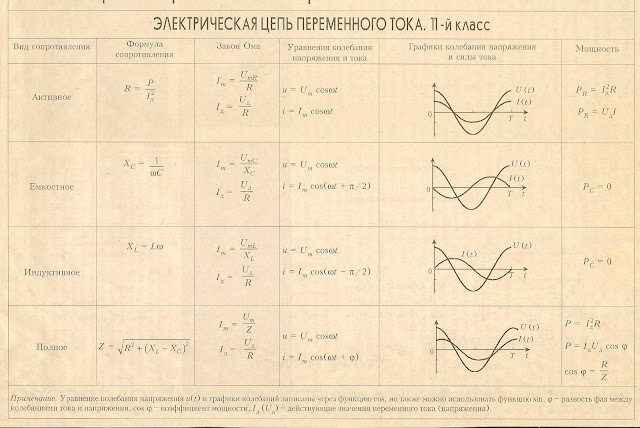 возможный.
возможный.Обратите внимание, что во всех примерах используется сеть 50 Гц, 230 В. Для тех, кто в США и Канаде, вы можете легко пересчитать для 60 Гц, 120 В.
Имейте в виду, что демонстрационные схемы, показанные на этой странице, могут иметь «неожиданные последствия», которые могут привести к выходу из строя компонентов, чрезвычайно высоким напряжениям или токам и могут представлять реальную опасность поражения электрическим током — это означает, что ваша земная деятельность может быть урезаны навсегда. Это не шутка! Никогда не подключайте какие-либо из этих цепей к сети, кроме как через обмотку низкого напряжения от трансформатора (12 В или около того), и имейте в виду, что некоторые комбинации (особенно последовательный резонанс) могут попытаться вас убить, даже при входе 12 В. .
Также имейте в виду, что если конденсатор отключается на пике кривой напряжения, он сохраняет заряд и может иметь напряжение на клеммах до 325 В (сеть 230 В) или 170 В (сеть 120 В).
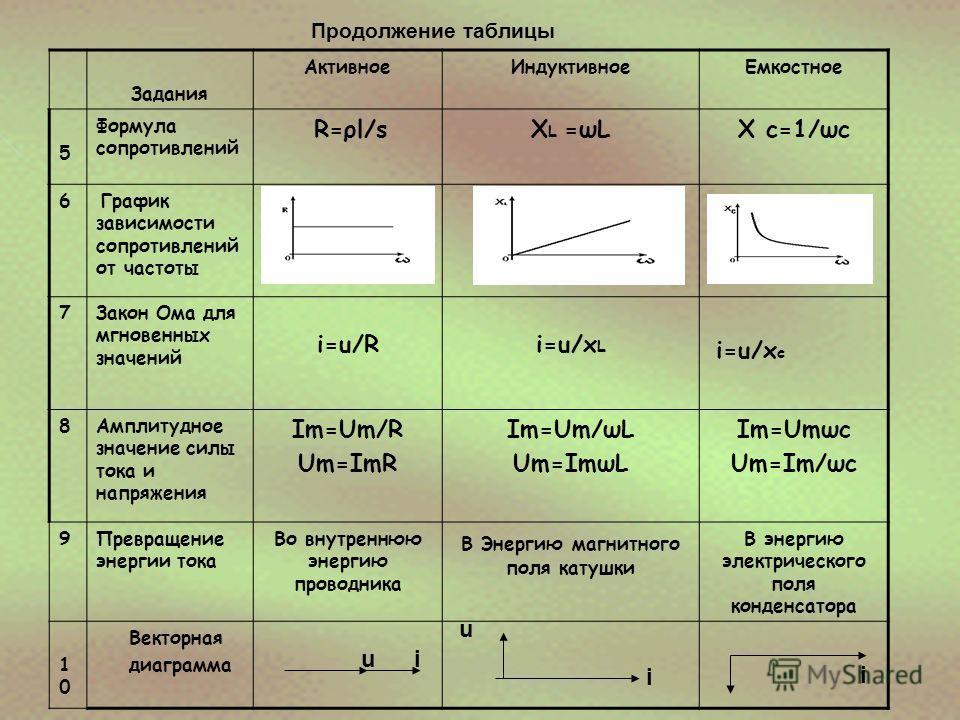 Накопленного заряда более чем достаточно, чтобы нанести очень неприятный удар током и вызвать смерть.
Накопленного заряда более чем достаточно, чтобы нанести очень неприятный удар током и вызвать смерть.
Емкостное реактивное сопротивлениеПервым рассматривается емкостное сопротивление — не потому, что оно наиболее распространено в электросетях, а потому, что оно более известно в электронных схемах. Как отмечалось выше, помимо резисторов, конденсаторы также наиболее близки к идеальным компонентам. Хотя большая часть этой статьи предполагает, что все компоненты идеальны, надо понимать, что в реальности это не так.
Когда идеальный конденсатор подключается параллельно к сети, от источника питания поступает ток. Реактивное сопротивление конденсатора (ХС — емкостное реактивное сопротивление) определяется по …
XC = 1 / ( 2π * f * C )
Где XC — емкостное сопротивление, f — частота в Гц, а C — емкость в фарадах
Как и ожидалось, по мере увеличения емкости XC падает, и потребляемый ток увеличивается.
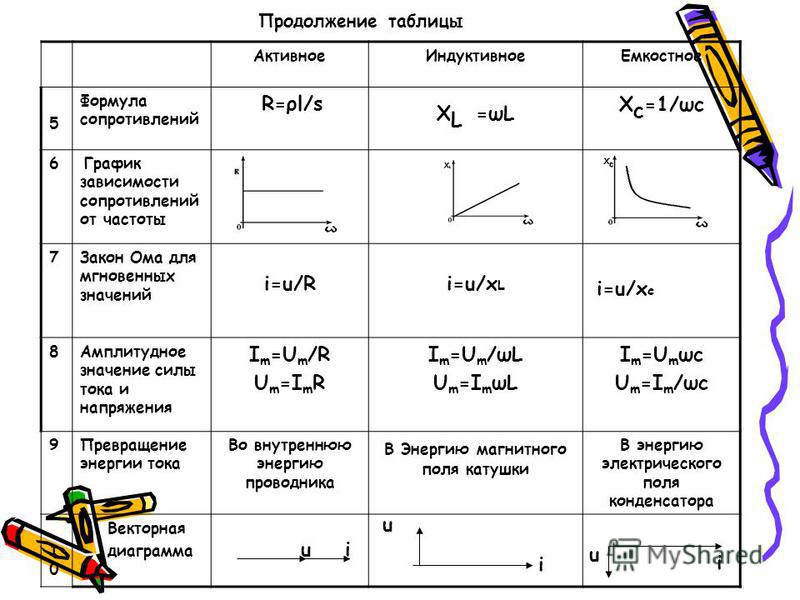 Для приведенных здесь примеров используемая емкость будет близка к 100 мкФ (фактическое значение равно 99,472 мкФ по причинам, которые станут ясны позже). Используя приведенную выше формулу, мы можем определить, что…
Для приведенных здесь примеров используемая емкость будет близка к 100 мкФ (фактическое значение равно 99,472 мкФ по причинам, которые станут ясны позже). Используя приведенную выше формулу, мы можем определить, что…XC = 1/(2π * 50 * 99,472 E-6 )
XC = 32 ОмЭто значение можно использовать для определения тока, потребляемого от сети. Если бы крышка была подключена напрямую к сети, ток составил бы 7,1875 А, что дает 1653 кВА. Однако (и это самое странное) степень равна ноль . Не ватт. В действительности потребляемая мощность будет очень небольшой из-за внутреннего сопротивления цоколя и диэлектрических потерь. Пластины колпачка металлические (обычно алюминиевые) и почти всегда очень тонкие. В некоторых случаях «пластины» имеют толщину не более нескольких молекул и напыляются на диэлектрический материал в вакууме. Диэлектрик представляет собой изоляцию между пластинами конденсатора и может представлять собой различные виды пластика или, реже, бумагу в масле.
 Я проверил конденсатор коррекции коэффициента мощности 12 мкФ 330 В, и он привлек 902 мА при 239 В переменного тока (как и ожидалось), но рассеиваемая мощность составляет всего 30 мВт, большая часть которых приходится на соединительный кабель!
Я проверил конденсатор коррекции коэффициента мощности 12 мкФ 330 В, и он привлек 902 мА при 239 В переменного тока (как и ожидалось), но рассеиваемая мощность составляет всего 30 мВт, большая часть которых приходится на соединительный кабель!Излишне говорить, что эти отношения сохраняются при изменении емкости или частоты, а при увеличении частоты ток конденсатора возрастает. Это линейная зависимость, которая охватывает очень широкий частотный диапазон, от долей 1 Гц до, возможно, 100 кГц или около того (в зависимости от конструкции конденсатора и физических размеров). На более высоких частотах даже провода, ведущие к крышке, становятся проблемой из-за их индуктивности.
Рис. 1. Емкостное сопротивление, цепь, напряжение и токЗдесь мы видим зависимость между напряжением и током (сопротивлением пока пренебрегаем). Ток не совпадает по фазе на 90° и фактически опережает (наступает раньше) напряжение. Хотя это может показаться невозможным, это вполне реально, но относится к условиям «стационарного состояния», которые требуют нескольких циклов переменного тока, чтобы стать стабильными.
 Это известно как опережающий коэффициент мощности .
Это известно как опережающий коэффициент мощности .Теперь мы можем применить излюбленную формулу коэффициента мощности некоторых людей (хотя на самом деле ее не следует использовать). Коэффициент мощности = Cosφ и косинус 90 это… ноль. Нет мощности, а также коэффициент мощности равен нулю. Никакой работы не совершается, поэтому вся энергия , подаваемая в конденсатор, возвращается обратно в сеть. Правильный способ определения коэффициента мощности состоит в том, чтобы разделить реальную мощность (Ватт) на «полную мощность» (ВА). Полную мощность иногда называют «мнимой» мощностью (но, строго говоря, только для реактивных нагрузок), потому что она имеет отрицательную составляющую — реальная мощность никогда не может быть отрицательной.
Это емкостное сопротивление с теоретической точки зрения, но в действительности оно не слишком отличается! Поскольку конденсаторы довольно близки к идеальной части на низких частотах, потери будут крошечными.
 Основываясь на тестах с меньшими номиналами сетевых конденсаторов, фактическая мощность, вероятно, будет меньше одного ватта, рассеиваемого внутри колпачка и его проводов в виде тепла.
Основываясь на тестах с меньшими номиналами сетевых конденсаторов, фактическая мощность, вероятно, будет меньше одного ватта, рассеиваемого внутри колпачка и его проводов в виде тепла.Из практических соображений (отчасти из-за уверенности симулятора в идеальных компонентах) последовательно с конденсатором подключен резистор на 1 Ом. Это рассеивает ~ 51,7 Вт реальной мощности, и из-за этого фазовый угол немного меньше 90 ° (88,22 °). Номинальная мощность в ВА составляет просто 230 В * 7,1875 А (1653 ВА), а коэффициент мощности равен 0,031 — не совсем ноль. Обратите внимание, что любое сопротивление в реактивной цепи всегда рассеивает «реальную» мощность — компонента «полной мощности» нет.
Во многих научных журналах и т.п. вы увидите импедансы в схеме, подобной показанной выше, обозначенной как 1 + j32. Один Ом реального сопротивления и 32 Ом емкостного сопротивления. «j32» означает, что 32-омная часть цепи является реактивной, и эти два числа нельзя просто сложить (ответ не равен 33 Ом).
 Попытка объяснить j-обозначение и/или сложную математику выходит за рамки этой статьи, но их можно добавить таким образом…
Попытка объяснить j-обозначение и/или сложную математику выходит за рамки этой статьи, но их можно добавить таким образом…1 + j32 = √1² + 32²
= 32,016 ОмЭто объясняет, почему ток не 6,97А, как вы могли себе представить, а несколько больше. Мощность в резисторе просто…
P = I² * R
P = 7,1875² * 1 = 51,66 ВтПока что пример достаточно прост, как и следующий раздел — индуктивность.
Индуктивное сопротивлениеСхема практически такая же, за исключением того, что конденсатор заменен катушкой индуктивности. Катушка индуктивности также рассчитана таким образом, что ее реактивное сопротивление составляет 32 Ом, что составляет значение 101,859.мГн.
XL = 2π * f * L
Где XL — индуктивное сопротивление, f — частота в Гц, а L — индуктивность в Генри
Точно напротив конденсатора, когда индуктивность уменьшается , XL падает, и потребляется больше тока.
 Для этого набора примеров используемая индуктивность близка к 100 мГн. Используя приведенную выше формулу, мы можем определить, что…
Для этого набора примеров используемая индуктивность близка к 100 мГн. Используя приведенную выше формулу, мы можем определить, что…XL = 2π * 50 * 101,859 E-3 )
XL = 32 ОмГлядя на формы сигналов тока и напряжения, мы видим почти то же самое, что и раньше, за исключением того, что ток теперь равен отстает от по напряжению. Это известно как запаздывающий коэффициент мощности. В отличие от конденсаторов, настоящие катушки индуктивности никогда не бывают такими же хорошими, как смоделированные идеальные, потому что они намотаны медным проводом и имеют сопротивление. Есть также потери на намагничивание и другие потери, потому что для практических катушек индуктивности требуется многослойный сердечник из кремнистой стали, как и для трансформатора. Они также склонны к насыщению, если ток через индуктор становится слишком большим.
Короче говоря, катушки индуктивности являются одним из худших электрических (или электронных) компонентов.
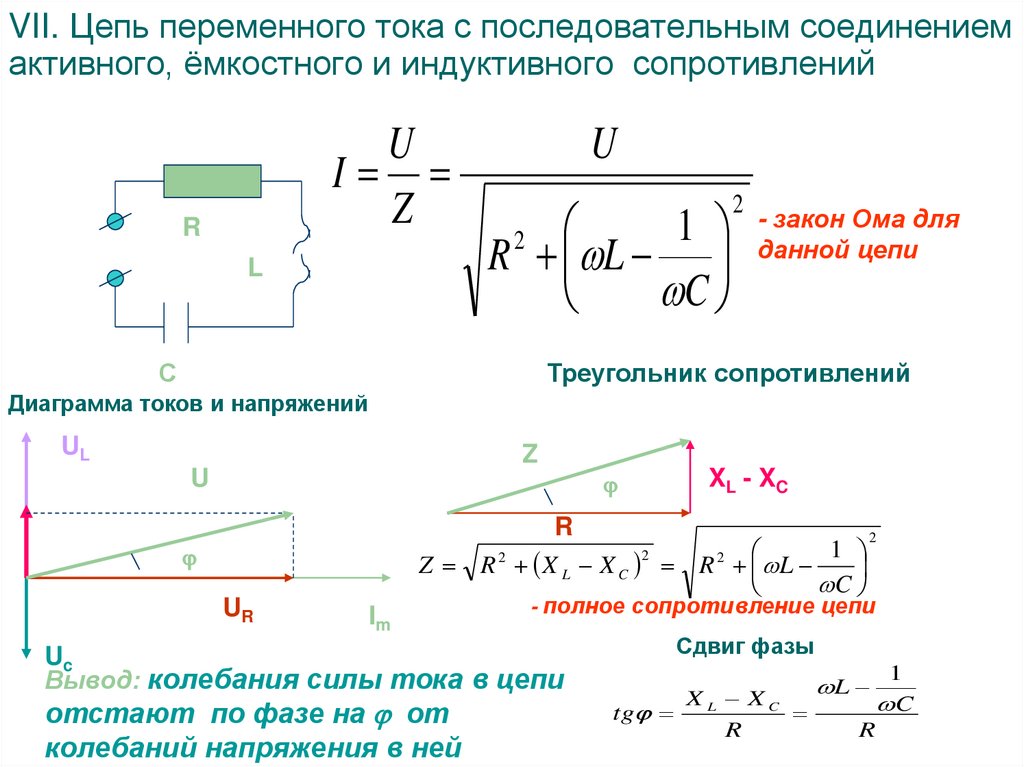 Паразитная емкость означает, что они имеют собственную резонансную частоту, которая часто находится на удивительно низкой частоте (возможно, несколько десятков кГц), а собственное сопротивление и потери на намагничивание означают, что даже скромные катушки индуктивности (например, используемые для балластов люминесцентных ламп) могут рассеивать (расходовать) значительное количество энергии.
Паразитная емкость означает, что они имеют собственную резонансную частоту, которая часто находится на удивительно низкой частоте (возможно, несколько десятков кГц), а собственное сопротивление и потери на намагничивание означают, что даже скромные катушки индуктивности (например, используемые для балластов люминесцентных ламп) могут рассеивать (расходовать) значительное количество энергии.
Рис. 2. Индуктивное сопротивление, цепь, напряжение и токКак и прежде, есть резистор на 1 Ом, используемый для поддержания работоспособности симулятора. Ток и напряжение точно такие же, как и для емкостного примера, но ток теперь отстает, а не опережает. В остальном он ведет себя точно так же, имеет такой же (очень плохой) коэффициент мощности и резистор рассеивает такую же мощность.
Здесь применимо по сути все сказанное о емкостной цепи, за исключением того, что в реальной цепи дроссель будет иметь значительные потери, легко равные мощности, рассеиваемой в резисторе, и то на довольно большую и дорогую деталь.
 На данный момент «идеальная» (хотя и недостижимая) часть — лучший способ показать эффекты.
На данный момент «идеальная» (хотя и недостижимая) часть — лучший способ показать эффекты.Когда две цепи объединяются, становится все интереснее. Мы получаем, казалось бы, невозможную ситуацию, как показано в следующем разделе.
Комбинированное реактивное сопротивлениеТеперь все начинает выглядеть просто глупо. У нас есть точно такие же две схемы, как и раньше, обе подключены к одному и тому же (идеальному) источнику питания, и каждая независимо работает точно так же, как и раньше. Когда они объединены, ток от сети падает , и не на малое количество.
Рис. 3. Суммарное реактивное сопротивление, цепь, напряжение и токПомните, это те же две цепи, которые мы видели раньше, с той лишь разницей, что они находятся на одной и той же цепи. Общий ток сети составляет 456,53 мА — часть того, что требует каждое реактивное сопротивление. Мощность в каждом резисторе неизменна, за исключением того, что резисторов два.
Если мы посчитаем, что общая мощность резистора в два раза превышает мощность одного резистора, мы получим общую мощность 103,32 Вт.
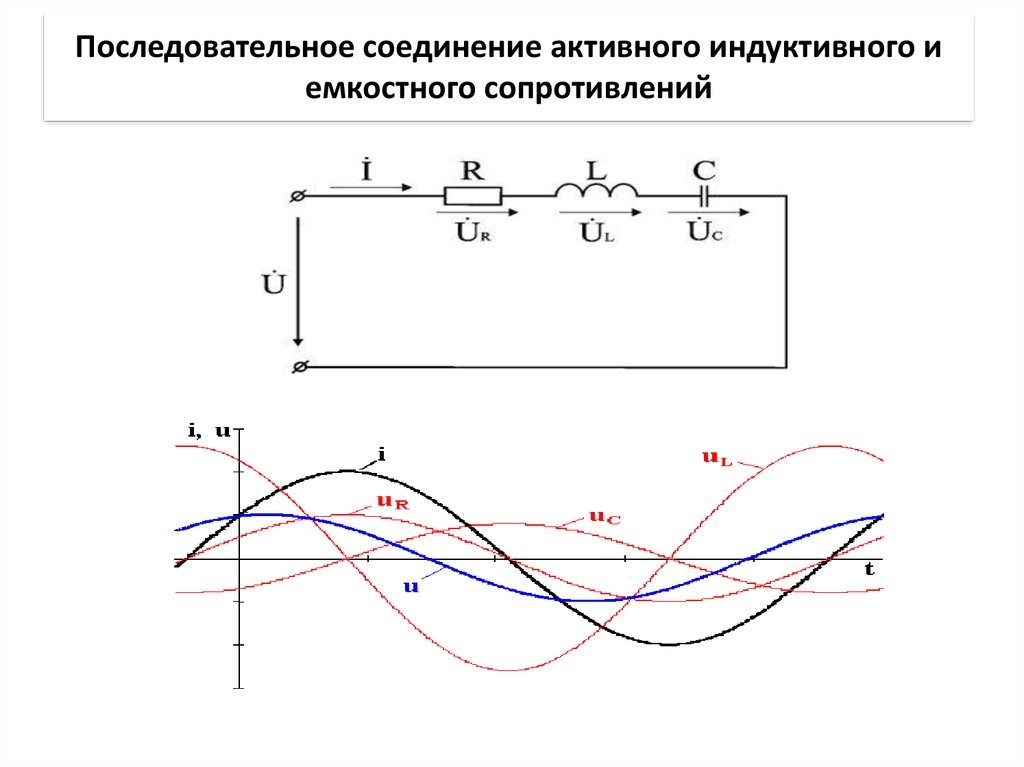 Если теперь посчитать ВА от генератора, то получим 230*456,53мА=105 Ватт. Да, есть небольшая ошибка, связанная с ограниченным количеством цифр, используемых в этих примерах. В действительности мощность именно такая, какую мы определили, сложив вместе мощность резистора — 103,32 Вт.
Если теперь посчитать ВА от генератора, то получим 230*456,53мА=105 Ватт. Да, есть небольшая ошибка, связанная с ограниченным количеством цифр, используемых в этих примерах. В действительности мощность именно такая, какую мы определили, сложив вместе мощность резистора — 103,32 Вт.На графике видно, что ток конденсатора опережает напряжение, а ток катушки индуктивности отстает на столько же (это причина немного нечетных значений — чтобы получить точно комплементарное поведение). Емкостной и индуктивный токи такие же как и были… 7,1875А в каждом. Поскольку один опережает, а другой отстает, то, что касается сетевого питания, они компенсируются. Однако добавление конденсатора не уменьшает ток в катушке индуктивности (или наоборот) — это одно из многих ложных утверждений мошеннических «экономеров энергии», которые рекламируются повсюду. Поскольку ток в катушке индуктивности остается прежним, любые потери, вызывающие внутренний нагрев, также остаются прежними.
Единственная часть цепи, которая имеет преимущество, — это кабель от источника (сетевой розетки) к оборудованию.
 .. при условии, конечно, что две нагрузки расположены близко друг к другу. Как и во всех системах коррекции коэффициента мощности, корректирующее устройство (чаще всего конденсатор) устанавливается внутри или на корректируемом осветительном приборе или двигателе. Это сводит к минимуму потери проводки в помещении.
.. при условии, конечно, что две нагрузки расположены близко друг к другу. Как и во всех системах коррекции коэффициента мощности, корректирующее устройство (чаще всего конденсатор) устанавливается внутри или на корректируемом осветительном приборе или двигателе. Это сводит к минимуму потери проводки в помещении.При объединении реактивных сопротивлений на их резонансной частоте они всегда активны — напряжение и ток совпадают по фазе. Для параллельных цепей ниже резонанса комбинация выглядит индуктивной (отстающий коэффициент мощности), а выше резонанса — емкостной (опережающий коэффициент мощности). Последовательные реактивные сопротивления также находятся в фазе (и, следовательно, резистивные), но ниже резонанса комбинация кажется емкостной, а выше резонанса — индуктивной.
Как и следовало ожидать, существует больше способов взаимосвязи индуктивности и емкости, и они обсуждаются ниже.
Параллельные реактивные сопротивленияКомбинации катушек индуктивности и конденсаторов довольно распространены в электронике и составляют основу многих настроенных схем.
 В радиочастотных приложениях везде используются сети LC (индуктор/конденсатор), поскольку они образуют фильтры, определяющие полосу пропускания, необходимую для приложения. Современные методы устранили многие из настроенных схем, которые вы видите в старом оборудовании, но есть простые комбинации, которые отказываются исчезать и будут делать это в обозримом будущем.
В радиочастотных приложениях везде используются сети LC (индуктор/конденсатор), поскольку они образуют фильтры, определяющие полосу пропускания, необходимую для приложения. Современные методы устранили многие из настроенных схем, которые вы видите в старом оборудовании, но есть простые комбинации, которые отказываются исчезать и будут делать это в обозримом будущем.Одним из них является параллельный резонансный контур, показанный ниже. Катушка индуктивности и конденсатор соединены параллельно, а комбинация последовательно с нагрузочным резистором. Это комбинация, которую некоторые сразу узнают.
Рис. 4. Параллельные реактивные сопротивления, цепь, напряжение и токПараллельный резонансный контур имеет (теоретически) бесконечный импеданс на своей резонансной частоте — в данном случае 50 Гц. В действительности импеданс всегда определенно конечен, потому что естественные потери ухудшают характеристики схемы. Достаточно сказать, что импеданс любого резонансного контура чрезвычайно высок на его резонансной частоте.
 В показанной цепи с ее идеальными компонентами импеданс близок к бесконечности, но ток, который циркулирует между катушкой и конденсатором, все же намного выше, чем вы могли ожидать. На самом деле, это немного выше, чем у каждой из цепей в отдельности. Симулятор говорит мне, что циркулирующий ток составляет 7,18 А.
В показанной цепи с ее идеальными компонентами импеданс близок к бесконечности, но ток, который циркулирует между катушкой и конденсатором, все же намного выше, чем вы могли ожидать. На самом деле, это немного выше, чем у каждой из цепей в отдельности. Симулятор говорит мне, что циркулирующий ток составляет 7,18 А.Потери определяют добротность схемы (добротность), и это способ описания четкости частотной характеристики схемы. Цепь с высокой добротностью будет эффективна только в очень узком диапазоне частот, где схема с низкой добротностью будет иметь более плоскую общую характеристику и более широкий частотный диапазон. Здесь важна частотная характеристика схемы … ниже показано напряжение на резисторе 1 Ом с различной частотой.
Рис. 5. Параллельные реактивные сопротивления, частотная характеристика на резистореНапряжение на резисторе 1 Ом падает до минимума при резонансе — 50Гц. Если вы помните, я упомянул в начале, что конденсаторы и катушки индуктивности имеют довольно странные значения, и это потому, что это значения, необходимые для получения резонанса на частоте 50 Гц.
 Есть и другие комбинации, которые тоже будут работать, но любой резонансный контур лучше всего работает, когда импедансы емкостной и индуктивной секций равны, однако резонанс не требует равных импедансов … важно помнить, когда мы пойдем дальше.
Есть и другие комбинации, которые тоже будут работать, но любой резонансный контур лучше всего работает, когда импедансы емкостной и индуктивной секций равны, однако резонанс не требует равных импедансов … важно помнить, когда мы пойдем дальше.Мы можем рассчитать резонансную частоту любой комбинации индуктивности и емкости по формуле …
fo = 1 / ( 2π * √L * C ), поэтому для нашего примера …
fo = 1 / ( 2π * √0,1 * 100 E-6 ) … достаточно близко
fo = 50,329 ГцОбратите внимание, что на самом деле существует очень небольшая разница между формулами для последовательного и параллельного резонансных контуров,
, но это не рассматривалось здесь, так как нет разницы с идеальными компонентами.Так же снова можно увидеть причину небольшого изменения значений индуктивности и емкости — я хотел частоту 50Гц — именно . Добротность показанной схемы (с ее идеальными компонентами) превышает 800, а полоса пропускания (в точках +3 дБ от минимального напряжения) составляет всего 62 мГц (0,062 Гц).
 Само собой разумеется, что на практике это не будет достигнуто.
Само собой разумеется, что на практике это не будет достигнуто.В приведенной выше формуле очевидно, что любая комбинация L и C, дающая при умножении одно и то же число, дает одинаковую резонансную частоту. 10H и 1 мкФ также будут резонировать на частоте 50,329.Гц, как и бесчисленное множество других комбинаций. Это важный момент, который следует помнить, когда мы рассматриваем «непреднамеренные последствия».
Реактивные сопротивления серииЭто сочетание требует огромной осторожности. Если вы правильно настроите схему (или неправильно!), катушка индуктивности и конденсатор компенсируют друг друга, оставляя вас с коротким замыканием в сети. Между тем, напряжение на каждом (L и C) будет огромным — довольно легко получить много кВ на каждом компоненте последовательного резонансного контура, и сопротивление резистора было увеличено до 33 Ом. Он по-прежнему будет рассеивать чуть более 1,6 кВт, потому что во всех смыслах он подключен непосредственно к сети — катушка индуктивности и конденсатор эффективно исчезают при резонансе.
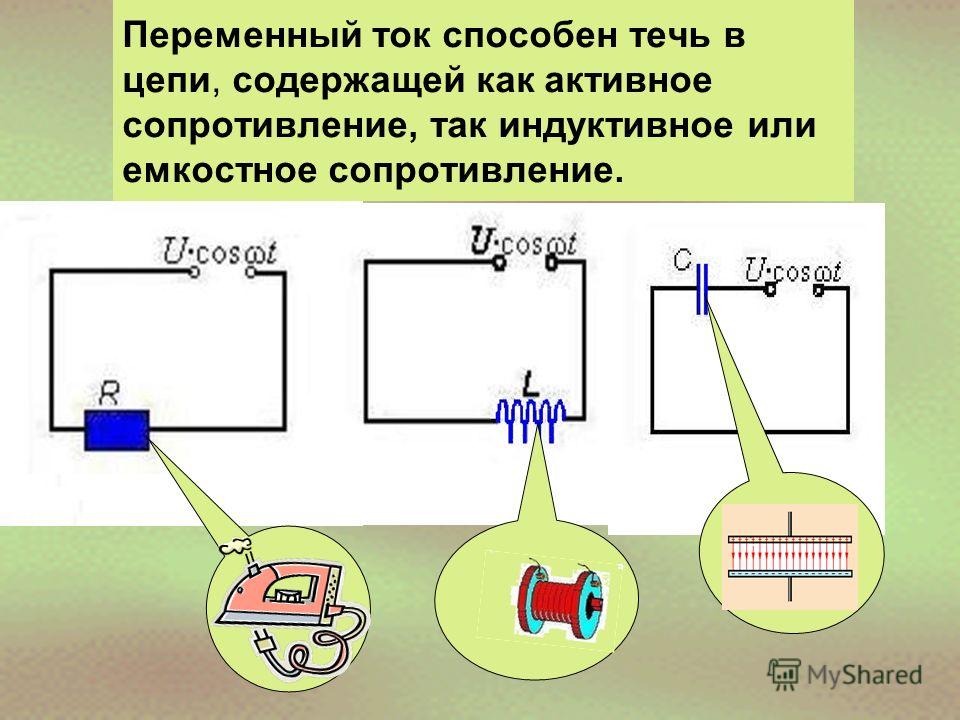
Рис. 6. Последовательные реактивные сопротивления, цепь, напряжение и токТолько сопротивление реальной катушки индуктивности будет ограничивать ток (и предельное напряжение на L и C), если больше ничего не подключено последовательно, а схема, показанная выше, имеет только довольно консервативные 222 В на каждом из реактивных сопротивлений. Напряжения на L и C точно равны и противоположны при резонансе, поэтому они полностью компенсируются — независимо от фактического напряжения, будь то милливольты или киловольты. Ток нагрузки определяется (почти) исключительно сопротивлением (230 В на 33 Ом составляет 6,9).7А). В реальной цепи будут небольшие дополнительные потери, связанные в первую очередь с сопротивлением катушки индуктивности и, в меньшей степени, с ESR (эквивалентным последовательным сопротивлением) конденсатора.
Рис. 7. Последовательные реактивные сопротивления, частотная характеристика резистораДобротность цепи определяется величиной последовательного сопротивления — кривая отклика, показанная выше, соответствует резистору 33 Ом.
 Если сопротивление уменьшается, добротность увеличивается, как и напряжение на компонентах L и C. Ток увеличивается пропорционально.
Если сопротивление уменьшается, добротность увеличивается, как и напряжение на компонентах L и C. Ток увеличивается пропорционально.Например, если сопротивление уменьшить с 33 Ом до 10 Ом, ток возрастет до 22,98 А (в идеале 23 А), но напряжение на крышке и дросселе увеличится до 735 В (среднеквадратичное значение). Несмотря на то, что «настоящие» катушки индуктивности имеют все описанные выше потери, то же самое может произойти, как описано здесь, в «реальной» цепи (в отличие от моделирования). Отличие только от в том, что напряжения и токи будут не такими высокими, но все же легко создать цепь, которая перегорает предохранители (и/или автоматические выключатели), разрушает конденсаторы и/или катушки индуктивности (и т. д.) из-за перенапряжение … или, что еще хуже, убить вас.
Получить 500-600 В очень просто, просто подключите конденсатор последовательно к двигателю с расщепленными полюсами. Если вы установите правильное значение ограничения, двигатель будет замедляться (это распространенный способ реализации дешевого управления скоростью), но если это неправильно, вы можете получить 500 В на двигателе 230 В .
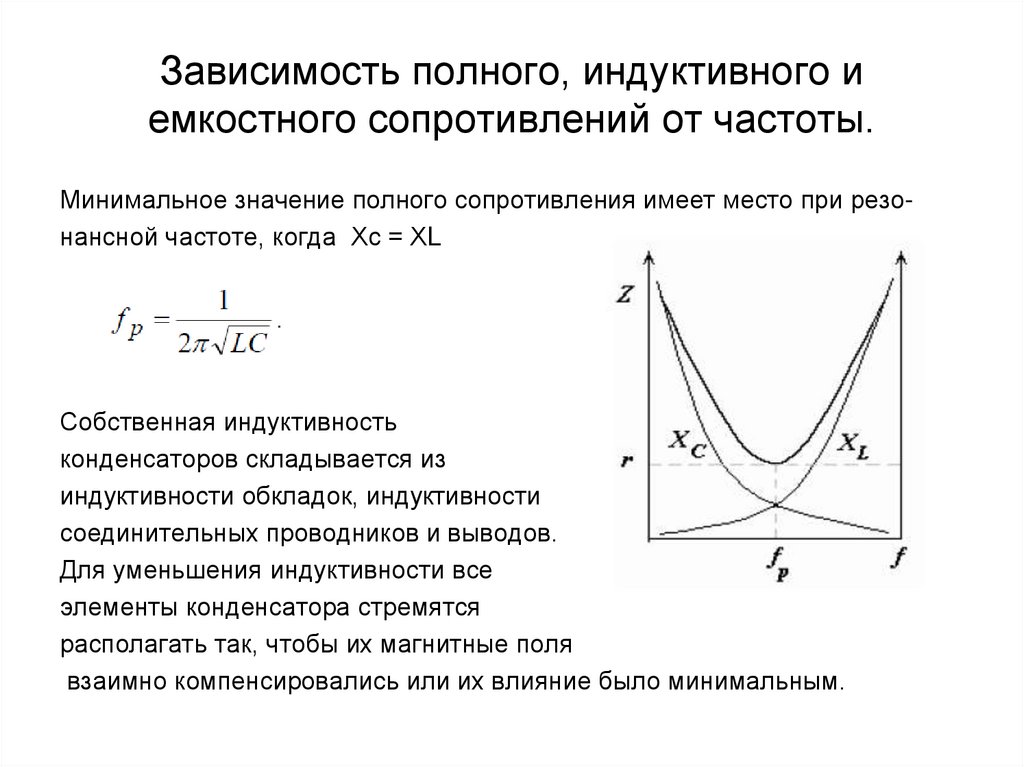 .. Я знаю это из личного опыта. ! К счастью, я сразу понял, что произошло, но если вы не знаете об эффекте, очень легко попасться на глаза. Результаты могут быть смертельными.
.. Я знаю это из личного опыта. ! К счастью, я сразу понял, что произошло, но если вы не знаете об эффекте, очень легко попасться на глаза. Результаты могут быть смертельными.Если у вас do есть жгучее (без каламбура) желание поэкспериментировать, вы должны делать это от источника низкого напряжения … рекомендуется 12 В переменного тока. Даже в этом случае существует возможность создания смертельного напряжения с помощью резонансного контура серии с высокой добротностью. Это опасная комбинация, требующая умения и уважения. ESP не несет никакой ответственности в случае травмы или смерти — вы проводите эти эксперименты исключительно на свой страх и риск.
Непредвиденные последствияТеперь, когда мы рассмотрели эффекты резонанса, должно быть очевидно, что в электрической распределительной сети будет огромное количество комбинаций индуктивности и емкости. Сопротивление распределено, и некоторые комбинации LC будут сильно демпфированы промежуточным сопротивлением, а другие нет.

Что мы еще не рассмотрели, так это гармоники сети. Гармоники создаются любой нелинейной нагрузкой, начиная от импульсных источников питания и заканчивая диммерами ламп (с передним и задним фронтом). Необычно (и крайне нежелательно), чтобы сеть содержала даже гармоники, поскольку они создают асимметричную форму волны с постоянной составляющей. Это может нанести серьезный вред, однако в сети существует бесчисленное множество кратковременных событий постоянного тока. При наличии некоторого сопротивления между источником событий постоянного тока и оборудованием, на которое они будут воздействовать, риск повреждения невелик. Если они рядом, результаты могут быть экстремальными. Эта тема описана в другом месте (дополнительную информацию по этому вопросу см. в разделе Пусковой ток.
Учитывая, что гармоники являются фактом жизни, когда форма волны искажена (и это в основном форма волны тока — это влияет на форму волны напряжения , но трудно значительно изменить форму волны, когда источник имеет чрезвычайно низкий импеданс.
 Если импеданс источника был равен нулю Ом, никакие искажения формы волны тока не могли повлиять на форму волны напряжения, но, естественно, это невозможно.
Если импеданс источника был равен нулю Ом, никакие искажения формы волны тока не могли повлиять на форму волны напряжения, но, естественно, это невозможно.Гармоники, которые наиболее подвержены риску возникновения проблем, простираются до 39 и (иногда больше), и они часто измеряются в рамках проверки соответствия оборудования. Старое оборудование (а это легко может означать, что ему 40 и более лет) не подлежит текущему тестированию на соответствие и может делать почти все, что угодно, посредством генерации гармоник. Эффекты просто неизвестны, если только кто-то не решит провести тесты.
Частоты гармоник зависят от частоты сети, но выглядят следующим образом (я прикрываю только 19-ю гармонику -й -й, чтобы таблица не выглядела глупо).
Mains 3rd 5th 7th 9th 11th 13th 15th 17th 19th 50 Hz 150 Hz 250 Hz 350 Hz 450 Hz 550 Hz 650 Hz 750 Hz 850 Hz 950 Hz 60 Гц 180 Гц 300 Гц 420 Гц 540 Гц 660 Гц 780 Гц 900 Гц 1020 Гц 1140 Гц Если учесть количество устройств, которые могут быть одновременно подключены к сети, почти гарантировано, что одна или несколько частот гармоник будут реагировать на индуктивную нагрузку здесь и конденсатор там.
 Неважно, выполняет ли конденсатор уже где-то свою обычную работу — электричество многозадачно, и одновременно может происходить много разных вещей.
Неважно, выполняет ли конденсатор уже где-то свою обычную работу — электричество многозадачно, и одновременно может происходить много разных вещей.Коммерческие помещения могут иметь специальную систему коррекции коэффициента мощности (PFC), использующую переключаемые конденсаторы и последовательные катушки индуктивности, предназначенные для минимизации тока гармоник в системе. Обычно они проектируются таким образом, чтобы собственный резонанс катушки индуктивности и конденсатора не совпадал с какой-либо вероятной гармоникой, но, поскольку сама система распределения электроэнергии состоит из кабелей, они также имеют индуктивность, которая может исказить резонансную частоту шкафа PFC. . Теперь вы можете начать понимать огромную сложность проблемы, особенно когда мы исследуем гармонический состав обычного диммера, установленного на половинную мощность. Это только пример — многие нагрузки на самом деле намного хуже.
Рис. 8. Форма волны и токи гармоник, диммер на 50 %Выше показана форма тока со стандартным диммером переднего фронта, работающим на 50%, питаемым от 230 В на нагрузке 100 Ом.
 Диммер заднего фронта имеет идентичные амплитуды гармоник, но они сдвинуты по фазе. Среднеквадратичное значение тока составляет 1,61 А, а форма волны имеет 64% THD (общее гармоническое искажение). Как вы можете видеть, гармоники распространяются на частоту более 3 кГц, но ниже 1 кГц все они превышают 100 мА, и 3 9Гармоника 1537 rd более чем в два раза ниже уровня основной частоты (50 Гц). Они измеряют 1,62 А и 878 мА соответственно, и даже гармоники 5 -й и 7 -й составляют почти 300 мА каждая.
Диммер заднего фронта имеет идентичные амплитуды гармоник, но они сдвинуты по фазе. Среднеквадратичное значение тока составляет 1,61 А, а форма волны имеет 64% THD (общее гармоническое искажение). Как вы можете видеть, гармоники распространяются на частоту более 3 кГц, но ниже 1 кГц все они превышают 100 мА, и 3 9Гармоника 1537 rd более чем в два раза ниже уровня основной частоты (50 Гц). Они измеряют 1,62 А и 878 мА соответственно, и даже гармоники 5 -й и 7 -й составляют почти 300 мА каждая.Типичный двойной строительный провод может иметь индуктивность около 0,65 мкГн/метр. Длина проводов в здании может легко превышать 100 метров, поэтому такой кабель имеет индуктивность около 65 мкГн. Это немного, а как быть с десятками километров провода между электростанцией и присоединенными помещениями? Простой ответ заключается в том, что мы не знаем, но все эти распределенные индуктивности и связанные с ними емкости образуют резонансные контуры с низкой добротностью на любом количестве различных частот.
 Невозможно обеспечить, чтобы резонансные частоты никогда не совпадали с гармоникой частоты сети, плюс есть бесчисленное множество приборов … некоторые генерируют гармоники, многие с конденсаторами для коррекции коэффициента мощности, а некоторые там, где их нет. представление о том, какую нагрузку они представляют, не имея возможности проверить.
Невозможно обеспечить, чтобы резонансные частоты никогда не совпадали с гармоникой частоты сети, плюс есть бесчисленное множество приборов … некоторые генерируют гармоники, многие с конденсаторами для коррекции коэффициента мощности, а некоторые там, где их нет. представление о том, какую нагрузку они представляют, не имея возможности проверить.Кроме того, в больших установках и на подстанциях есть шкафы коррекции коэффициента мощности, и каждый конденсатор имеет низкий импеданс по отношению к току гармоник. Колпачок с импедансом (скажем) 100 Ом на частоте 50 Гц имеет импеданс всего 33 Ом на частоте 150 Гц (гармоника 3 rd ) и 20 Ом на частоте 250 Гц (гармоника 5 th ). По мере увеличения частоты способность конденсатора вызывать большие гармонические токи в сети также увеличивается. Если ток будет достаточно высоким, конденсатор в конечном итоге выйдет из строя, поскольку его максимальный номинальный ток будет превышен.
Гармонические токи также влияют на двигатели и трансформаторы, и из-за более высокой частоты этих гармоник они могут вызывать (и вызывают) дополнительный нагрев.
 Дополнительный нагрев частично происходит из-за потерь на вихревые токи в используемых многослойных стальных сердечниках, а также из-за так называемого «эффекта близости». В какой-то мере это похоже на скин-эффект, но применяется к проводникам, погруженным в магнитное поле [1, 2]).
Дополнительный нагрев частично происходит из-за потерь на вихревые токи в используемых многослойных стальных сердечниках, а также из-за так называемого «эффекта близости». В какой-то мере это похоже на скин-эффект, но применяется к проводникам, погруженным в магнитное поле [1, 2]).Эффект близости часто вызывает хаотическое нарушение нормального потока электронов в проволочной катушке и может значительно снизить токонесущую способность проводников. В свою очередь, это приводит к повышению температуры машины (двигателя, трансформатора и т. д.), часто с локальными «точечными» повышениями температуры, которые намного превышают ожидаемые. Это стало причиной многих неудач. Все это только из-за нескольких гармоник в сети! Большие гармонические токи также могут вызывать чрезмерный (и неожиданный) шум трансформаторов и двигателей.
Затем представьте, что вы столкнулись с ситуацией, когда колпачок для коррекции коэффициента мощности образует последовательный резонансный контур с индуктивностью рассеяния кабеля и трансформатора.
 Любая гармоника на резонансной частоте потенциально может вызвать очень высокий и, возможно, разрушительный ток в цепи, и существует высокая вероятность того, что что-то в цепи выйдет из строя. Такое действительно случается, и у каждой энергосистемы случаются сбои, вызванные чрезмерными гармоническими токами. Конденсаторные шкафы PFC могут подвергаться ложному срабатыванию последовательных автоматических выключателей, предназначенных для защиты крышки от избыточного тока. Обычно также последовательно включают катушки индуктивности с низкой добротностью, чтобы ограничить высокочастотный ток.
Любая гармоника на резонансной частоте потенциально может вызвать очень высокий и, возможно, разрушительный ток в цепи, и существует высокая вероятность того, что что-то в цепи выйдет из строя. Такое действительно случается, и у каждой энергосистемы случаются сбои, вызванные чрезмерными гармоническими токами. Конденсаторные шкафы PFC могут подвергаться ложному срабатыванию последовательных автоматических выключателей, предназначенных для защиты крышки от избыточного тока. Обычно также последовательно включают катушки индуктивности с низкой добротностью, чтобы ограничить высокочастотный ток.Ничто из этого не является особенно интуитивным, и это не то, что любой электрик принимает во внимание, проводя электропроводку в здании. В (теперь довольно далеком) прошлом было так мало нагрузок, которые создавали сильно нелинейные формы волны, что это никогда не было проблемой. С распространением электронных систем освещения (например) это изменилось. Общая идея показана на рис. 9 с использованием того же диммера, что и описанный выше.
 Амперметр в этом случае будет токоизмерительным пробником осциллографа, а уровни гармоник можно определить с помощью БПФ (быстрого преобразования Фурье).
Амперметр в этом случае будет токоизмерительным пробником осциллографа, а уровни гармоник можно определить с помощью БПФ (быстрого преобразования Фурье).
Рис. 9. Схема проверки гармоник, диммер на 50 %На тестовой схеме показана проводка здания, и ее можно считать достаточно типичной для реальной установки. Ток контролируется только непосредственно от генератора, и без конденсатора он почти такой же, как показано выше на рис. 8. Гармоники максимальны на низких частотах и постепенно уменьшаются с увеличением частоты.
Рис. 10. Гармонические токи, диммер на 50 %При добавлении конденсатора все меняется довольно интересно. «Крышка» может быть, скажем, тремя конденсаторами с коэффициентом мощности 3,3 мкФ, установленными, например, в близлежащих люминесцентных светильниках, и когда они установлены, на красной дорожке ясно видно, что вместо гармонических токов, уменьшающихся в естественной прогрессии, есть пик на частоте 1550 Гц (гармоника 31 st ).
 Гармонический ток от сети увеличился из-за установки конденсатора. Ток в конденсаторе тоже увеличивается, с 723мА при чистом питании 230В до 922 мА при наличии гармоник — более чем на 20 % больше.
Гармонический ток от сети увеличился из-за установки конденсатора. Ток в конденсаторе тоже увеличивается, с 723мА при чистом питании 230В до 922 мА при наличии гармоник — более чем на 20 % больше.Как отмечалось ранее, внутри одной установки может быть много таких взаимодействий, и их число становится бесчисленным, если рассматривать распределительную сеть в целом. Показанный пример намеренно упрощен, но ясно показывает, что вероятность «непреднамеренных последствий» очень высока. Вопрос не в том, происходят ли такие взаимодействия, а в том, могут ли они вызвать более серьезные проблемы в других местах распределительной сети, когда они происходят.От 1496 до .
Единственное реальное решение состоит в том, чтобы исключить (насколько это возможно) нелинейные нагрузки и последующую генерацию гармоник в источнике, и это одна из причин, по которой в настоящее время требуется так много электронных продуктов, чтобы максимизировать коэффициент мощности и сохранить искажения низкие.
 Имеются данные о том, что «распределенная генерация» от бытовых солнечных установок и т.п. также вызывает проблемы. Хотя сами по себе они напрямую не влияют на общий коэффициент мощности, коэффициент мощности сети снижается из-за уменьшения нормальной нагрузки (с высоким коэффициентом мощности), которая обеспечивается инверторами [4]. Для жилых помещений их нагрузка всегда считалась доброкачественной, с коэффициентом полезного действия, близким к единице. Это уже не так, отчасти из-за распространения компактных люминесцентных ламп, светодиодного освещения, блоков питания для ПК, ЖК-/плазменных телевизоров и многих других электронных устройств нагрузки. У них часто очень низкий коэффициент мощности, и он нелинейный, поэтому его нельзя исправить обычными средствами.
Имеются данные о том, что «распределенная генерация» от бытовых солнечных установок и т.п. также вызывает проблемы. Хотя сами по себе они напрямую не влияют на общий коэффициент мощности, коэффициент мощности сети снижается из-за уменьшения нормальной нагрузки (с высоким коэффициентом мощности), которая обеспечивается инверторами [4]. Для жилых помещений их нагрузка всегда считалась доброкачественной, с коэффициентом полезного действия, близким к единице. Это уже не так, отчасти из-за распространения компактных люминесцентных ламп, светодиодного освещения, блоков питания для ПК, ЖК-/плазменных телевизоров и многих других электронных устройств нагрузки. У них часто очень низкий коэффициент мощности, и он нелинейный, поэтому его нельзя исправить обычными средствами.
Потери мощностиВ конечном счете, все формы низкого коэффициента мощности вызывают дополнительные потери в энергосистеме, поскольку ток увеличивается без увеличения «рабочей» или реальной мощности в пунктах назначения.
 Между любым пунктом назначения и ближайшей крупной подстанцией может быть много километров провода, а между ними может быть подстанция меньшего размера. Расстояние между главной подстанцией и генерирующим объектом может составлять 50 км и более (в такой стране, как Австралия, это может быть намного больше). В распределительную систему всегда включено не менее двух, а чаще 3 или 4 трансформатора, все они обмотаны проводом и во многих случаях уже работают почти на полную мощность.
Между любым пунктом назначения и ближайшей крупной подстанцией может быть много километров провода, а между ними может быть подстанция меньшего размера. Расстояние между главной подстанцией и генерирующим объектом может составлять 50 км и более (в такой стране, как Австралия, это может быть намного больше). В распределительную систему всегда включено не менее двух, а чаще 3 или 4 трансформатора, все они обмотаны проводом и во многих случаях уже работают почти на полную мощность.Было несколько очень громких случаев, когда отключалась подача электроэнергии в крупные города, что приводило к массовым отключениям электроэнергии и хаосу. Сидней (Австралия) сразу приходит на ум, потому что это было во всех новостях. Поиск в Интернете показывает, что только за последний год по всему миру было бесчисленное количество отключений. Хотя некоторые из них были прямым результатом стихийных бедствий того или иного рода, многие из этих отказов почти наверняка были результатом перегрузки, чему, вероятно, немного способствовало отсутствие надлежащего обслуживания.

Увеличение тока, вызванное плохим коэффициентом мощности, является коварным и относится к нагрузкам с обычным отстающим (или опережающим) коэффициентом мощности, а также к нелинейным нагрузкам. Если нагрузка здания имеет коэффициент мощности 0,5 (опережающий, отстающий или нелинейный), она требует от сети в два раза больше тока. Потери в проводке прямо пропорциональны квадрату тока ( P = I² * R ), поэтому, если ток, потребляемый установкой, потребляет вдвое больше тока, чем требуется из-за низкого коэффициента мощности, то потери распределения в 4 раза больше, чем было бы в случае с PF единицы.
Даже незначительное уменьшение тока может значительно снизить потери. Снижение тока на 10% приводит к снижению резистивных потерь распределения более чем на 17%. Системы передачи переменного тока высокого напряжения на большие расстояния также страдают от емкостных и индуктивных потерь, и в некоторых случаях на самом деле более эффективно преобразовывать переменный ток в постоянный, а затем обратно на удаленном конце.
 Это обычно используется для передачи под водой на большие расстояния, где емкость между кабелями в противном случае вызвала бы большие потери.
Это обычно используется для передачи под водой на большие расстояния, где емкость между кабелями в противном случае вызвала бы большие потери.Все потери в проводке и трансформаторе представляют собой реальную мощность, которая должна обеспечиваться генерирующей станцией (станциями), и для ее обеспечения необходимо сжигать реальное топливо. Поскольку потери мощности в сети обычно намного выше, чем предполагалось (точные цифры для этого кажутся тщательно охраняемыми секретами), низкий коэффициент мощности приводит к увеличению стоимости снабжения и снижает пропускную способность сети в целом. В зависимости от того, куда вы смотрите, потери при передаче и распределении составляют от 6% до 10%. Это огромное количество энергии во всем мире. Для тех, кто интересуется некоторыми поразительными цифрами, см. статью Energy Efficiency in the Power Grid, подготовленную ABB Inc.
Рис. 11. Типичная нелинейная нагрузкаХорошим индикатором степени искажения, вызванного формой сигнала сети, является рис.
 12. Нагрузкой является обычный выпрямитель, за которым следует фильтрующий конденсатор, потребляющий нелинейный ток со среднеквадратичным значением чуть более 2 А, как показано выше. Пиковый ток составляет 6,7 А и приводит к тому, что форма волны напряжения имеет плоские вершины на положительных и отрицательных пиках [5].
12. Нагрузкой является обычный выпрямитель, за которым следует фильтрующий конденсатор, потребляющий нелинейный ток со среднеквадратичным значением чуть более 2 А, как показано выше. Пиковый ток составляет 6,7 А и приводит к тому, что форма волны напряжения имеет плоские вершины на положительных и отрицательных пиках [5].Схема потребляет чуть менее 473 ВА, но фактическая мощность составляет всего 253 Вт, поэтому коэффициент мощности равен 0,53 — почти половина тока, потребляемого от сети, эффективно теряется из-за ужасной формы тока. Это совсем не интуитивно понятно, как это происходит, но, по сути, математика, стоящая за этим, не имеет большого значения. Важно то, что это известная проблема, и ее можно решить с помощью умных интегральных схем и современных электронных технологий, которые существуют прямо сейчас.
Еще в 1960-х годах и ранее было очень мало нагрузок, которые вызывали серьезные гармонические искажения формы тока. Большинство нелинейных нагрузок в то время представляли собой трехфазные ртутно-дуговые выпрямители для питания фидеров электропоездов и трамваев, но в большинстве случаев можно было ожидать, что они будут изолированы от общей электросети.
 Хотя обсуждение 3-фазных выпрямителей выходит за рамки этой статьи, они относятся к , но не к 9149.7 безвреден для сети, независимо от используемых выпрямительных диодов. Есть методы, которые уменьшают проблему, но не устраняют ее.
Хотя обсуждение 3-фазных выпрямителей выходит за рамки этой статьи, они относятся к , но не к 9149.7 безвреден для сети, независимо от используемых выпрямительных диодов. Есть методы, которые уменьшают проблему, но не устраняют ее.Допуск для сети и кабельной системы здания на рисунке 11 очень консервативен — в большинстве случаев они, вероятно, будут иметь несколько большие потери. Даже в этом случае (и при сравнительно небольшой нагрузке) сопротивление проводки 0,8 Ом рассеивает 3,38 Вт вместо 1,03 Вт при линейной нагрузке той же мощности — потери более чем в 3 раза! Хотя это может показаться незначительным само по себе, это совсем другая история, если умножить на тысячи таких же плохих загрузок. Если бы электростанция подавала 500 МВт [5] в сеть, загруженную аналогичными схемами, для выполнения полезной работы было бы доступно только 265 МВт. Потери в сети сократят это еще больше, потому что тепло, выделяемое в кабелях и трансформаторах, является частью выполняемой работы.
 Вот почему энергосистемы на самом деле не любят плохие коэффициенты мощности, независимо от того, что их вызывает.
Вот почему энергосистемы на самом деле не любят плохие коэффициенты мощности, независимо от того, что их вызывает.
Рис. 12. Искажение формы сигнала напряжения при нелинейной нагрузкеКривая напряжения указывает на другую проблему. В большинстве предыдущих примеров предполагается, что генератор (альтернатор) имеет выходное сопротивление, равное нулю, и генерирует чистую синусоиду. Таким образом, форма сигнала напряжения не будет иметь никаких искажений.
Не требуется большого сопротивления проводки, чтобы «плоская вершина» стала очень заметной. Эффект хорошо виден выше и является простым результатом закона Ома (маленькая индуктивность мало влияет). Нередко измеряется искажение сетевого напряжения на уровне 10% и более, в зависимости от времени суток и подключенных нагрузок. Сопротивление передачи в трансформаторах, кабелях и т. д. является фактом жизни, поэтому, когда у нас есть цепь, потребляющая очень высокие пиковые токи, даже небольшое сопротивление сети приведет к искажению формы сигнала напряжения.
 Теперь мы столкнулись с двойной проблемой искажения напряжения, а также искажения формы волны тока.
Теперь мы столкнулись с двойной проблемой искажения напряжения, а также искажения формы волны тока.На всякий случай, если вы задаетесь вопросом об актуальности этого примера, стоит отметить, что вам нужно всего около 10 КЛЛ по 25 Вт (или вам и нескольким соседям в общей сложности 25 КЛЛ по 10 Вт), чтобы точно вызвать сценарий, показанный выше. . Один блок питания ПК может делать то же самое, если он не имеет цепей PFC. Любое исследование формы сигнала сети очень четко покажет эффект.
ВыводыЭто одна из самых сложных областей, с которыми нам приходится сталкиваться, и она усугубляется поэтапным отказом от ламп накаливания или их запретом. Они имеют идеальный коэффициент мощности (единица — по крайней мере, когда не используется диммер) без гармоник. Никаких проблем с электроснабжением они никогда не создавали. Масштабное использование компактных люминесцентных ламп внесло свой вклад, но все больше и больше современных приборов используют электронные источники питания, которые также создают больше проблем, чем их справедливая доля.
 Освещение вызывает особую озабоченность, потому что это одно из наиболее важных применений электричества, и оно было грубо выдвинуто на первый план из-за первоначального (кажущегося простым) требования к более высокой эффективности. Это называется «непреднамеренное последствие»!
Освещение вызывает особую озабоченность, потому что это одно из наиболее важных применений электричества, и оно было грубо выдвинуто на первый план из-за первоначального (кажущегося простым) требования к более высокой эффективности. Это называется «непреднамеренное последствие»!Одним из решений является обеспечение того, чтобы все новые блоки питания имели активную коррекцию коэффициента мощности, чтобы свести к минимуму генерацию гармоник. Однако это связано с увеличением затрат для потребителя и означает более сложные источники питания с большим количеством неисправностей. Это также называется «непреднамеренным последствием». Вводится все больше и больше правил для ограничения искажения формы волны новых продуктов, при этом одной из основных целей является освещение. Обычные (дешевые) компактные люминесцентные лампы в настоящее время кажутся исключением, даже несмотря на то, что они вызывают именно те проблемы, которые демонстрирует схема на Рисунке 11. Мало что можно сделать с устаревшими устройствами и оборудованием, которые могут использоваться в течение 20 и более лет, но важно убедиться, что проблемы не усугубляются еще больше, чем они уже есть.

Как отмечалось во введении, эту статью следует читать в сочетании с активной коррекцией коэффициента мощности, поскольку они неразрывно связаны между собой.
Для интересующихся есть документы, представленные органами снабжения со всего мира. Они варьируются от чрезмерно упрощенного до полноценного инженерного анализа. Те, что примерно посередине, наиболее полезны для тех, кто просто хочет понять проблемы, с которыми столкнулись, и причины этих проблем. Как отмечено в третьей и четвертой ссылках, даже подключенные к сети инверторы (от солнечных батарей или потенциально небольших ветряных турбин) вызывают свою долю проблем, даже если они передают в сеть очень чистую форму волны. Это трудно понять без тщательного анализа, но, к счастью, это уже делалось… много раз.
Авторы и ссылки- Улучшенный расчет потерь от эффекта близости
- Скин-эффект, эффект близости и многожильный провод
- Влияние гармоник, создаваемых сетью фотоэлектрические системы на электрических сетях
- Распределенная генерация, нагрузки в помещении клиента и инженерная сеть — пример из практики
- Гармонические искажения в системе электроснабжения — Интегральная энергия, Центр качества электроэнергии
- Некоторые материалы были найдены в Сети, но сами по себе не имели существенного значения, поэтому на них не было конкретных ссылок.
 Такой материал
использовался только для подтверждения вещей, которые я уже понял.
Такой материал
использовался только для подтверждения вещей, которые я уже понял. - Эта статья также включает информацию с других страниц ESP, из «накопленных знаний», а также из моделирования и данных из измерения, сделанные на компонентах, как описано.
Основной индекс Лампы и индекс энергопотребленияУведомление об авторских правах. Этот материал, включая, помимо прочего, весь текст и диаграммы, является интеллектуальной собственностью Рода Эллиотта и защищен © 2012 г. Воспроизведение или повторная публикация любыми средствами, будь то электронными, механическими или электромеханическими, строго запрещены в соответствии с Международные законы об авторском праве. Автор (Род Эллиотт) предоставляет читателю право использовать эту информацию только в личных целях, а также разрешает сделать одну (1) копию для справки. Коммерческое использование полностью или частично запрещено без письменного разрешения Рода Эллиотта. 
Страница создана и защищена авторскими правами © 05 февраля 2012 г.
Реактивное, индуктивное и емкостное сопротивление | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Расчет индуктивных и емкостных реактивных сопротивлений.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное сопротивление
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис.
 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
График на рисунке 1(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением.
Напряжение переменного тока в катушке индуктивности Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:
Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:Когда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на фазовый угол 90º.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС В = − L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L дается вариантом закона Ома:
I=VXLI=\frac{V}{{X}_{L}}\\I=XLV
, где В — среднеквадратичное напряжение на катушке индуктивности, а X L определяется как
XL=2πfL{X}_{L}=2\pi{fL}\\XL=2πfL
, где f частота источника переменного напряжения в герцах (Анализ цепи с использованием правила контура Кирхгофа и исчисления фактически дает это выражение).
 Х Д называется индуктивным сопротивлением , потому что индуктор препятствует протеканию тока. X L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в (циклах/с)(Ом ⋅ с)=Ом)), что согласуется с его ролью в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I /Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.
Х Д называется индуктивным сопротивлением , потому что индуктор препятствует протеканию тока. X L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в (циклах/с)(Ом ⋅ с)=Ом)), что согласуется с его ролью в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I /Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.Пример 1. Расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц.
Стратегия б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?Индуктивное сопротивление находится непосредственно из выражения X L = 2πf L . Когда для каждой частоты найдено X L , можно использовать закон Ома, сформулированный в уравнении I = V / X L , чтобы найти ток на каждой частоте.
Решение для (а)Ввод частоты и индуктивности в уравнение x L = 2πf L дает
x L = 2πf L = 6,28 (60,0/с) (3,00 мн) = 1,13 ω ~ ° С.064 6,28 (60,0/с) (3,00 м) = 1,13 ω ° Hz.
Аналогично, на частоте 10 кГц
X L = 2πf L = 6,28 (1,00 × 10 4 /с) (3,00 мГн) при 180 кОм.
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении 9.0003 I = В / X L , если приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает
I=VXL=120 В1,13 Ом=106 А при =\frac{V}{{X}_{L}}=\frac{120\text{ V}}{1.13\text{ }\Omega}=106\text{ A при } 60\text{ Гц}\ \I=XLV=1,13 Ом, 120 В=106 A при 60 Гц
. Точно так же на частоте 10 кГц
I=VXL=120 V188 Ω=0,637 A на частоте 10 кГц I=\frac{V}{{X}_{L}}=\frac{120\text{V}}{188\ text{ }\Omega}=0,637\text { A при } 10 кГц}\\I=XLV=188 Ω120 В=0,637 A при 10 кГц
.
ОбсуждениеИндуктор реагирует очень по-разному на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению.
 Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Конденсаторы и емкостные реактивные сопротивления
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление.
 Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
Напряжение на конденсаторе и ток представлены на рисунке как функции времени.Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C, сопротивление которого пренебрежимо мало. (б) График тока и напряжения на конденсаторе в зависимости от времени.
График на рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( Q = 0 на нем) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума.
Напряжение переменного тока в конденсаторе Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:Когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I в цепи, содержащей только конденсатор C определяется по другой версии закона Ома как
I=VXCI=\frac{V}{{X}_{C}}\\I=XCV
, where V is the rms voltage and X C is defined (As with X L , this expression for X C results from an analysis of the circuit using правила Кирхгофа и исчисление) равно
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
, где X C называется емкостным реактивным сопротивлением , потому что конденсатор реагирует на сопротивление току.
 X C измеряется в омах (проверка оставлена читателю в качестве упражнения). X C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
X C измеряется в омах (проверка оставлена читателю в качестве упражнения). X C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
СтратегияЕмкостное сопротивление находится непосредственно из выражения в
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
.
Решение для (а) Как только X C найдено на каждой частоте, можно использовать закон Ома, сформулированный как I = В / X C тока на каждой частоте.
Как только X C найдено на каждой частоте, можно использовать закон Ома, сформулированный как I = В / X C тока на каждой частоте.Ввод частоты и емкости в
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
дает
XC=12πfC=16,28(60,0 /с)(5,00 мкФ)=531 Ом при 60 Гц\begin{array}{lll}{X}_{C}& =& \frac{1}{2\pi fC}\\ & =& \frac{ 1}{6.28\left(60.0/\text{s}\right)\left(5.00\text{ }\mu\text{F}\right)}=531\text{ }\Omega\text{ в }60 \text{ Гц}\end{массив}\\XC==2πfC16,28(60,0/с)(5,00 мкФ)1=531 Ом при 60 Гц 9{4}/\text{s}\right)\left(5.00\mu\text{F}\right)}\\ & =& 3.18\text{ }\Omega\text{ при }10 \text{ кГц} \end{массив}\\XC==2πfC1=6,28(1,00×104/с)(5,00 мкФ)13,18 Ом при 10 кГц
.
Решение для (b)Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I = В / X C , учитывая приложенное среднеквадратичное напряжение 120 В.
 Для первой частоты это дает
Для первой частоты это даетI= VXC=120 V531 Ом=0,226 A при 60 ГцI=\frac{V}{{X}_{C}}=\frac{120 \text{ V}}{531\text{ }\Omega}=0,226 \text { A при }60\text{ Гц}\\I=XCV=531 Ω120 В=0,226 A при 60 Гц
. Аналогично, при 10 кГц
I=VXC=120 V3,18 Ом=3,37 A при 10 Гц I=\frac{V}{{X}_{C}}=\frac{120 \text{V}}{ 3,18\text{ }\Omega}=3,37 \text{ A при }10 \text{ Гц}\\I=XCV=3,18 Ω120 В=3,37 A при 10 Гц
.
ОбсуждениеКонденсатор реагирует совершенно по-разному на двух разных частотах, и совершенно противоположным образом реагирует катушка индуктивности. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот.
 Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока по сравнению с катушками индуктивности .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрим рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени.
 Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Переменное напряжение на резистореКогда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — фазовый угол равен 0º.
Резюме раздела
- Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности прикладывается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90º.
- Противодействие катушки индуктивности изменению тока выражается как тип сопротивления переменному току.
- Закон Ома для индуктора:
I=VXLI=\frac{V}{{X}_{L}}\\I=XLV
,
где В — среднеквадратичное напряжение на катушке индуктивности.
- X L определяется как индуктивное сопротивление, определяемое как
XL=2πfL{X}_{L}=2\pi fL\\XL=2πfL
,
с f частота источника переменного напряжения в герцах. - Индуктивное сопротивление X L выражается в омах и имеет наибольшее значение на высоких частотах.
- Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
- Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора:
I=VXCI=\frac{V}{{X}_{C}}\\I=XCV
,
где В — среднеквадратичное напряжение на конденсаторе. - Х С определяется как емкостное реактивное сопротивление, определяемое как
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
.

- X C измеряется в омах и имеет наибольшее значение на низких частотах.
Концептуальные вопросы
1. Пресбиакузис — возрастная потеря слуха, которая постепенно влияет на более высокие частоты. Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.
2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как фон 100 Гц в звуковой системе? Объяснять.
3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли сменный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или от того и другого? А индуктивное сопротивление?
5. Объясните, почему конденсатор на рис. 4(а) действует как фильтр низких частот между двумя цепями, а конденсатор на рис. 4(б) действует как фильтр высоких частот.
Рис. 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.
6. Если конденсаторы на рисунке 4 заменить катушками индуктивности, что будет работать как фильтр низких частот, а что как фильтр высоких частот?
Задачи и упражнения
1. При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом?
2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?
3.
 Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?
Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?4. При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?
5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?
6. (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? б) Какой будет сила тока на частоте 25,0 кГц?
7. Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, создает ток силой 2,00 А. Индуктивность какая?
8. Источник 20,0 Гц, 16,0 В производит ток силой 2,00 мА при подключении к конденсатору. Какова емкость?
9.
 (а) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, включена последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
(а) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, включена последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?10. Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
11. Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. а) Какая емкость необходима, чтобы получить реактивное сопротивление
10,0 мОм 10,0 м\Омега 10,0 мОм
для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12. Необоснованные результаты При записи напряжений, вызванных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
13. Создайте свою собственную задачу Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
Глоссарий
- индуктивное реактивное сопротивление:
- противодействие катушки индуктивности изменению тока; рассчитывается как X L = 2π fL
- емкостное реактивное сопротивление:
- сопротивление конденсатора изменению тока; рассчитано по формуле
XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC=2πfC1
Избранные решения задач и упражнений
1.
 531 Гц
531 Гц3. 1,33 нФ
5. (а) 2,55 А (б) 1,53 мА
7. 63,7 мкГн 9. (а) 21,2 мГн (б) 8,00 Ом
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : находится в лицензии
23 факта, которые вы должны знать0001
Треугольник силы | Треугольник мощности, напряжения, токаТреугольник мощности — это просто прямоугольный треугольник, сторона которого соответствует активной, реактивной и полной мощности. Компонент основания символизирует активную мощность, перпендикулярный компонент обозначает реактивную мощность, а гипотенуза символизирует полную мощность.
Что такое треугольник силы? Определение треугольника власти | Определение треугольника мощности
Треугольник мощности — это графическое представление активной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
Уравнение степенного треугольника | Треугольник мощности PQS Расчет формулы треугольника мощности | Уравнение треугольника мощностейВ треугольнике мощностей активная мощность P, реактивная мощность Q и полная мощность S образуют прямоугольный треугольник. Следовательно,
гипотенуза 2 = основание 2 + перпендику
Активная мощность (P) измеряется в ваттах (Вт).
Реактивная мощность (Q) измеряется в реактивных вольт-амперах (ВАр).
- Треугольник мощности — это графическое представление активной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.

- Активная или действительная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется как P и среднее значение активной мощности P .
- Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. T также известен как мощность без ватт. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в реактивных киловольт-амперах (кВАр) и обозначается буквой Q.
- Полная мощность в цепи, как поглощаемая, так и рассеиваемая, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла.
- Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т.
 е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина.
е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина. - Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Рассмотрим цепь RLC, соединенную последовательно, как указано выше.
Где резистор с сопротивлением R.
индуктор с индуктивностью L.
конденсатор с емкостью C.
Источник переменного напряжения V m sin⍵t применяется
В — среднеквадратичное значение приложенного напряжения, а I — среднеквадратичное значение полного тока в цепи. Катушка индуктивности и конденсатор дают Х L и X C оппозиций соответственно в цепи. Теперь может быть три случая:
Случай 1: X L > X C
Случай 2: X L < X C
Треугольник мощности получается из векторной диаграммы, если мы умножив каждый из векторов напряжения на I, мы получим три составляющие мощности.

Из векторного треугольника мы можем быстро получить треугольник мощности, умножив напряжения на I. Реальная мощность умножается на V R , что равно I 2 R. Реактивная мощность I умножается на (V C – V L ), что равно I 2 (X C – X L ). Полная мощность V = I 2 Z рассчитывается из активной мощности и реактивной мощности для обоих случаев. Здесь мы принимаем во внимание другую величину, комплексную мощность. Комплексная мощность представляет собой сумму активной мощности и реактивной мощности, представленных в комплексной форме, т. е. с величиной j.
Таким образом, комплексная мощность
S = P – jQ когда X L < X C
S = P + jQ, когда X L > X C
меньше емкостного сопротивления. Следовательно, реактивная мощность отрицательна, и угол ϕ также отрицателен. Для случая 2 значение индуктивного сопротивления больше, чем значение емкостного сопротивления, реактивная мощность равна +ve, а угол ϕ также равен +ve.
Треугольник активной реактивной полной мощности | Мощность вольт ампер треугольник Треугольник активной и реактивной мощности . Треугольник истинной силы .
Активная или действительная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется в виде P и среднего значения активной мощности P is,
P = VI = I 2 R
Треугольник реактивной мощностиРеактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. Он также известен как г. без ватт мощностью л.с. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольт-амперах реактивной (кВАр) и обозначается Q.

Реактивная мощность Q = VI реактивная = I 2 X.
Треугольник полной мощностиСуммарная мощность в цепи, как поглощаемой, так и рассеиваемой, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла. 9{2} + (Реактивная\; мощность)2}[/Latex]
Для чисто резистивной цепи реактивная мощность отсутствует. Итак, кажущаяся мощность равна активной или истинной мощности.
Силовой треугольник для цепи переменного тока | Треугольник электрической мощностиЦепи переменного тока могут иметь любую комбинацию R, L и C, и если мы хотим правильно рассчитать общую мощность, мы должны знать разность фаз между I и V. Форма волны тока а напряжение синусоидальное. Поскольку мощность = напряжение x ток, максимальная мощность достигается, когда обе формы волны совпадают.
 В этой ситуации формы волны называются «синфазными» друг с другом.
В этой ситуации формы волны называются «синфазными» друг с другом.- В чисто резистивной цепи переменного тока I и V идеально совпадают по фазе. Следовательно, просто умножая их, мы можем получить мощность.
- Если в цепи имеется индуктивная или емкостная нагрузка, создается разность фаз. Даже если разница фаз незначительна, мощность переменного тока делится на две части: одну положительную и одну отрицательную. Отрицательная мощность не является математически отрицательной величиной; это просто означает, что в систему подается питание, но передачи энергии не происходит. Эта мощность известна как реактивная мощность. Положительная величина совершает некоторую реальную работу, поэтому ее классифицируют как реальную или активную мощность.
- Другая часть питания поступает в цепь от источника. Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.

Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т. е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина. Нам нужно применить некоторые специальные формулы, чтобы рассчитать переменный ток и параметры силового треугольника.
Треугольник мощности для емкостной нагрузкиЕмкостная нагрузка означает, что коэффициент мощности опережает ток по фазовому углу относительно напряжения.
Треугольник мощности для индуктивной нагрузкиИндуктивная нагрузка показывает, что коэффициент мощности отстает, поскольку I отстает от V на фазовый угол.
Комплексный треугольник мощности
Комплексная мощность есть не что иное, как представление мощности с помощью комплексных чисел. Действительная часть представляет собой активную мощность. Мнимая часть представляет собой реактивную мощность.
Предположим, что ток и напряжение в емкостной цепи равны I и V соответственно. Мы знаем, что для емкостной нагрузки I опережает V на фазовый угол. Примем этот угол за ϕ.
Допустим, напряжение на нагрузке V= ve jƟ и ток I = iej (Ɵ+ϕ) .
Мы знаем, мощность — это напряжение, умноженное на сопряженный ток.
Итак, комплексная мощность S = VI* = ve jƟ x ie -j(Ɵ+ϕ) = vie -jϕ
S = vi(cosϕ – jsinϕ) = vicosϕ – jvisinϕ = P – jQ [мы знаем активную мощность P = vicosϕ и реактивную мощность Q = visinϕ]
Для емкостной нагрузки I отстает от V на фазовый угол. Итак, напряжение на нагрузке V= ve jƟ и ток I = ie j(Ɵ-ϕ) .

So комплексная мощность
S = VI* = ve jƟ x ie-j (Ɵ-ϕ) = vie jϕ
S = vi(cosϕ + jsinϕ) = P vicosϕ + jvisinϕ
Трехфазный силовой треугольникПеременный ток может быть однофазным или трехфазным. Изменение амплитуды тока приводит к генерации синусоидальных волн. Для однофазного питания есть только одна волна. Трехфазные системы разделяют ток на три части. Три составляющие тока не совпадают по фазе на одну треть цикла каждая. Каждая текущая составляющая равна по величине, но противоположна по направлению двум другим конъюнктивным.
Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Треугольник импеданса и треугольник мощности Коэффициент мощности треугольника импедансаВ цепях постоянного тока только сопротивление отвечает за противодействие току. Но в цепях переменного тока величина, называемая реактивным сопротивлением, также противодействует току.
 Реактивное сопротивление может быть любой комбинацией индуктивности и емкости. Но и индуктивность, и емкость отличаются от сопротивления фазовым углом (отстающим или опережающим). Таким образом, мы не можем сложить их арифметически. Итак, мы строим треугольник импеданса с гипотенузой Z (импеданс), основанием R (сопротивление) и реактивным сопротивлением X (индуктивное или емкостное реактивное сопротивление или оба). 9{2}}[/Latex]
Реактивное сопротивление может быть любой комбинацией индуктивности и емкости. Но и индуктивность, и емкость отличаются от сопротивления фазовым углом (отстающим или опережающим). Таким образом, мы не можем сложить их арифметически. Итак, мы строим треугольник импеданса с гипотенузой Z (импеданс), основанием R (сопротивление) и реактивным сопротивлением X (индуктивное или емкостное реактивное сопротивление или оба). 9{2}}[/Latex]Коэффициент мощности [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности треугольника мощностиКоэффициент мощности в треугольнике мощности обозначается как отношение активной мощности к полной мощности, определяемое как косинус угла вектора.
Треугольник коррекции коэффициента мощностиКоррекция коэффициента мощности — это метод повышения эффективности электрической цепи за счет снижения реактивной мощности. Коррекция коэффициента мощности достигается за счет параллельно соединенных конденсаторов, которые противодействуют эффектам, вызванным индуктивными элементами, и уменьшают фазовый сдвиг.
Формула треугольника коэффициента мощности
Коэффициент мощности для емкостной или индуктивной нагрузки [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности [Latex]= \frac{Real\; мощность {Очевидная \; power}[/Latex]
Треугольник энергии мощностиЭлектрическая энергия определяется как мощность системы, умноженная на общее время использования энергии.
Энергия E = P x T
Как нарисовать треугольник мощности? Генератор треугольника мощностейТреугольник мощностей строится с использованием активной мощности в качестве основания, реактивной мощности в качестве перпендикуляра и полной мощности в качестве гипотенузы.
Металлические треугольники на линиях электропередачМы часто видим несколько треугольных петель, свисающих с линий электропередач. Они используются для обеспечения устойчивости строп при сильном ветре.
 Эти треугольные ребра предотвращают подпрыгивание строп слишком близко друг к другу и гарантируют, что они не оторвутся от изоляторов. 9{2}} = 13\: \Omega[/Latex]
Эти треугольные ребра предотвращают подпрыгивание строп слишком близко друг к другу и гарантируют, что они не оторвутся от изоляторов. 9{2}} = 13\: \Omega[/Latex]Коэффициент мощности цепи = R/Z = 12/13 = 0,92
Пример треугольника мощностейQ. Нагрузка 20 кВт при коэффициент мощности 0,8 отстает. Найдите номинал конденсатора, чтобы он мог поднять значение коэффициента мощности до 0,95.
Здесь реальная мощность P = 20 кВт
Коэффициент мощности cosϕ 1 = 0,8
Мы знаем, что реактивная мощность должна быть уменьшена, чтобы получить увеличенный коэффициент мощности. Следовательно, фазовый угол также уменьшится. Предположим, что изначально фазовый угол был ϕ 1 , а после снижения реактивной мощности фазовый угол равен ϕ 2 . Итак, треугольник мощностей имеет вид-
Из диаграммы видно, что реактивная мощность уменьшилась до AB от переменного тока. Итак, нам нужно вычислить разницу AC и AB, и эта величина является требуемым номиналом конденсатора.

Здесь, OA = 20 кВт
Cos Вотство 1 = 0,8
Cos Воц 2 = 0,95
Мы знаем, Cos Вотство 1 = OA/OC
SO, OC = 20/0,8 = 25 KV.0005
ac = √ (OC 2 — OA 2 ) = 15 Kvar
COS Вотство 2 = OA/OB
SO, OB = 20/0,95 = 21 KVA
AB = √ (OB 2 2 = 21 KVA
AB = √ (OB 2 2 = 21 KVA
AB = √ (OB 2. – OA 2 ) = 6,4 кВАр
Следовательно, BC = AC – AB = (15 – 6,4) = 8,6 квар
Часто задаваемые вопросы Сколько типов в степени степеней треугольника?Треугольник мощности состоит из трех типов мощности
- – Истинная или активная мощность.
- – реактивная мощность.
- – полная мощность.

Треугольник мощности представляет собой треугольное представление отношения между активной мощностью, реактивной мощностью и полной мощностью.
Например, в любом электроприборе общая вырабатываемая мощность представляет собой части активной и реактивной мощности.
Что такое треугольник мощности цепи переменного тока?Треугольник мощности цепи переменного тока может быть резистивным, емкостным или индуктивным, и треугольник состоит из трех видов мощностей, а полная мощность рассчитывается с помощью активной мощности и реактивной мощности.
Что такое треугольник мощности цепи RL?Цепь RL имеет треугольник мощности с активной мощностью = I 2 R, реактивной мощностью = I 2 X L , а полная мощность = I 2 Z, где X L — индуктивное реактивное сопротивление, а Z — полное сопротивление цепи.
Какая связь между KVA, KW и KVAr?КВА — это единица измерения полной мощности, а кВт и кВАр — это единицы активной мощности и реактивной мощности соответственно.
Какое значение имеет коэффициент мощности? Таким образом, из концепции треугольника мощности мы можем сделать вывод, что кВА 2 = кВт 2 + кВАр 2 .
Таким образом, из концепции треугольника мощности мы можем сделать вывод, что кВА 2 = кВт 2 + кВАр 2 .Для индуктивных и емкостных нагрузок коэффициент мощности играет жизненно важную роль при расчете реактивной мощности. Реактивная мощность — это часть активной мощности, которая уменьшается, а коэффициент мощности — это отношение истинной мощности к полной мощности. Коэффициент мощности, равный единице, указывает на то, что цепь имеет полностью резистивный характер.
Сколько ватт составляет 6 кВА?6 кВА = 6000 ВА
При единичном коэффициенте мощности 6 кВА = 1 x 6000 = 6000 Вт
Если коэффициент мощности другой, 6 кВА = 6 x (коэффициент мощности) Вт
Как преобразовать кВтч в кВАч?кВтч = кВАч X коэффициент мощности
Таким образом, кВАч = кВтч/коэффициент мощности
Сколько ватт составляет 1 кВА?Для чисто резистивной нагрузки реактивная мощность отсутствует.
 Таким образом, коэффициент мощности равен 1. Здесь 1 кВА = 1 Вт
Таким образом, коэффициент мощности равен 1. Здесь 1 кВА = 1 Вт. Если нагрузка емкостная или индуктивная, резистивная мощность не равна 0, поскольку коэффициент мощности представляет собой сопротивление/импеданс. Здесь 1 кВА = коэффициент мощности x 1 кВт
Почему электрические опоры имеют треугольную форму?По следующим причинам электрические опоры имеют треугольную форму.
- Треугольники имеют большую площадь основания, что делает их очень жесткими. Эта жесткость помогает выдерживать боковые нагрузки.
- Треугольники имеют меньшую площадь, чем любой четырехугольник. Если бы форма была четырехугольной, то стоимость была бы больше. Треугольная форма снижает стоимость за счет исключения одной лишней стороны.
Коэффициент мощности трансформатора зависит от характеристик нагрузки.
Если нагрузка чисто резистивная, коэффициент мощности равен единице или 1.

Если нагрузка емкостная, т. е. X C > X L , коэффициент мощности называется опережающим.
Если нагрузка индуктивная, т. е. X L > X C , коэффициент мощности называется отстающим.
В чем разница между KVA KWH KVAH и KVAR? | Треугольник мощности кВт КВА КВАРКВА означает киловольт-ампер. Это единица реальной или активной мощности.
KWH означает киловатт-час. Это используется для измерения того, сколько энергии (в киловаттах) потребляется за час.
KVAH означает киловольт-ампер-час. KVAH — это полная мощность, а KWH — это активная мощность. KVAH = KWH/коэффициент мощности
KVAR означает реактивный киловольт-ампер. Используется для измерения реактивной мощности. 9{2}}}[/Latex]
Какова единица коэффициента мощности?Коэффициент мощности – это отношение активной мощности (кВт) к полной мощности (кВА), поскольку и числитель, и знаменатель являются мощностями, коэффициент мощности – это величина без единицы.

23.11 Реактивное, индуктивное и емкостное сопротивление – Физика колледжа 2e
Цели обучения
К концу этого раздела вы сможете:
- Схема зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Расчет индуктивных и емкостных реактивных сопротивлений.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.
Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное сопротивление
г.Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис.
 23.43. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
23.43. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.Рисунок 23.43 (a) Источник переменного напряжения последовательно с катушкой индуктивности, имеющей пренебрежимо малое сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
График на рис. 23.43(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением.
 Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:
Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:Напряжение переменного тока в индукторе
Когда на катушку индуктивности подается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на 90º90º фазовый угол.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противоЭДС V=-L(ΔI/Δt)V=-L(ΔI/Δt). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока II через катушку индуктивности LL определяется вариантом закона Ома:
·I=VXL,I=VXL,
23,51
где VV — среднеквадратичное напряжение на катушке индуктивности, а XLXL определяется как
XL=2πfL, XL=2πfL,
23,52
с ff частотой источника переменного напряжения в герцах (анализ цепи с использованием правила контура Кирхгофа и исчисления фактически дает это выражение).
 XLXL называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. XLXL имеет единицы измерения в омах (1 Гн=1 Ом⋅с1 Г=1 Ом⋅с, так что частота, умноженная на индуктивность, имеет единицы (циклы/с)(Ом⋅с)=Ω(циклы/с)(Ом⋅с) = Ω), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что XLXL пропорциональна LL, поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что XLXL пропорционально частоте ff, так как большая частота означает большее изменение тока. То есть ΔI/ΔtΔI/Δt велико для больших частот (большие ff , малых ΔtΔt). Чем больше изменение, тем больше сопротивление индуктора.
XLXL называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. XLXL имеет единицы измерения в омах (1 Гн=1 Ом⋅с1 Г=1 Ом⋅с, так что частота, умноженная на индуктивность, имеет единицы (циклы/с)(Ом⋅с)=Ω(циклы/с)(Ом⋅с) = Ω), в соответствии с его ролью эффективного сопротивления. Имеет смысл, что XLXL пропорциональна LL, поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что XLXL пропорционально частоте ff, так как большая частота означает большее изменение тока. То есть ΔI/ΔtΔI/Δt велико для больших частот (большие ff , малых ΔtΔt). Чем больше изменение, тем больше сопротивление индуктора.Пример 23.10
Расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Индуктивное сопротивление находится непосредственно из выражения XL=2πfLXL=2πfL.
 Как только XLXL найден на каждой частоте, можно использовать закон Ома, сформулированный в уравнении I=V/XLI=V/XL, для определения тока на каждой частоте.
Как только XLXL найден на каждой частоте, можно использовать закон Ома, сформулированный в уравнении I=V/XLI=V/XL, для определения тока на каждой частоте.Решение для (a)
Ввод частоты и индуктивности в уравнение XL=2πfLXL=2πfL дает
XL=2πfL=6,28(60,0/с)(3,00 мГн)=1,13 Ом при 60 Гц.XL=2πfL=6,28 (60,0/с)(3,00 мГн)=1,13 Ом при 60 Гц.
23,53
Аналогично, при 10 кГц
XL=2πfL=6,28(1,00×104/с)(3,00 мГн)=188 Ом при 10 кГц.XL=2πfL=6,28(1,00×104/с)(3,00 мГн)=188 Ом при 10 кГц.
23,54
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении I=V/XLI=V/XL, при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает
I=VXL=120 В1.13 Ом=106 А при 60 Гц. I=VXL=120 В1.13 Ом=106 А при 60 Гц.
23,55
Аналогично, при 10 кГц
I=VXL=120 В188 Ом=0,637 А при 10 кГц.
 I=VXL=120 В188 Ом=0,637 А при 10 кГц.
I=VXL=120 В188 Ом=0,637 А при 10 кГц.23,56
Обсуждение
Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Конденсаторы и емкостные реактивные сопротивления
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис.
 23.44. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
23.44. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.Рисунок 23.44 (a) Источник переменного напряжения последовательно соединен с конденсатором C , имеющим пренебрежимо малое сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.
График на рис. 23.44 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( Q=0Q=0 ) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе.
 Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:Напряжение переменного тока в конденсаторе
Когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на 90º90º угол фазы.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока II в цепи, содержащей только конденсатор CC, по другой версии закона Ома составляет
I=VXC,I=VXC,
23,57
, где VV — среднеквадратичное напряжение, а XCXC определяется (как и в случае XLXL, это выражение для XCXC получается в результате анализа цепи с использованием правил и расчетов Кирхгофа) равно
XC=12πfC,XC=12πfC,
23,58
, где XCXC называется емкостным реактивным сопротивлением, потому что конденсатор реагирует на сопротивление току.
 XCXC имеет единицы измерения в омах (проверка оставлена читателю в качестве упражнения). XCXC обратно пропорциональна емкости CC; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ff; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
XCXC имеет единицы измерения в омах (проверка оставлена читателю в качестве упражнения). XCXC обратно пропорциональна емкости CC; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ff; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.Пример 23.11
Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мкФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия
Емкостное реактивное сопротивление находится непосредственно из выражения XC=12πfCXC=12πfC. Один раз XCXC была найдена на каждой частоте, закон Ома, сформулированный как I=V/XCI=V/XC, можно использовать для нахождения тока на каждой частоте.

Решение для (a)
Ввод частоты и емкости в XC=12πfCXC=12πfC дает
XC=12πfC=16,28(60,0/с)(5,00 мкФ)=531 Ом при 60 Гц.XC=12πfC=16,28( 60,0/с) (5,00 мкФ) = 531 Ом при 60 Гц.
23,59
Аналогично, на частоте 10 кГц,
XC=12πfC=16,28(1,00×104/с)(5,00 мкФ)=3,18 Ом на 10 кГц.XC=12πfC=16,28(1,00×104/с) мкФ) = 3,18 Ом при 10 кГц.
23,60
Решение для (b)
Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I=V/XCI=V/XC, при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты это дает
I=VXC=120 В531 Ом=0,226 А при 60 Гц. I=VXC=120 В531 Ом=0,226 А при 60 Гц.
23,61
Аналогично, при 10 кГц
I=VXC=120 В3,18 Ом=37,7 А при 10 кГц. I=VXC=120 В3,18 Ом=37,7 А при 10 кГц.
23,62
Обсуждение
Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор.
 На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), XCXC стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод).
 Конденсаторы оказывают противоположное воздействие на цепи переменного тока по сравнению с катушками индуктивности .
Конденсаторы оказывают противоположное воздействие на цепи переменного тока по сравнению с катушками индуктивности .Резисторы в цепи переменного тока
В качестве напоминания рассмотрим рис. 23.45, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рисунок 23.45 (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Напряжение переменного тока в резисторе
Когда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0º0º.

Блоки резистивной, индуктивной и емкостной нагрузки
Блоки нагрузки подключают электрическую нагрузку к источникам питания для проверки их способности подавать электричество или регулировать характеристики тока. Банки нагрузки создают спрос на мощность с помощью резистивных, индуктивных и емкостных элементов. Этот краткий обзор их различий.
Обзор
В системе переменного тока ток имеет синусоидальную форму в соответствии с частотой источника питания. В цепи, на которую не влияют индуктивность или реактивное сопротивление, напряжение и ток будут расти и падать вместе во время каждого цикла. Это состояние, известное как единство , показано на рисунке 1.На практике цепи имеют индуктивные или реактивные характеристики, которые вызывают пики напряжения и тока в разные моменты времени цикла переменного тока. В индуктивных цепях напряжение опережает ток, как показано на рис. 2. В емкостных цепях напряжение отстает от тока, как показано на рис.
 3. Большие промежутки времени между пиками тока и напряжения указывают на большую индуктивную или емкостную нагрузку, и любое условие увеличивает работу, необходимую для подачи требуемого количества активной мощности к нагрузкам.
3. Большие промежутки времени между пиками тока и напряжения указывают на большую индуктивную или емкостную нагрузку, и любое условие увеличивает работу, необходимую для подачи требуемого количества активной мощности к нагрузкам.Степень, в которой пики напряжения и тока в разные моменты времени количественно определяются коэффициентом мощности . Для чисто резистивных нагрузок коэффициент мощности равен 1. Увеличение отклонения от этого значения указывает на уменьшение реальной мощности, доступной для работы.
Типы элементов блока нагрузки
Элементы резистивной нагрузки
В наиболее распространенных блоках нагрузки используются резистивные элементы нагрузки. Сопротивление возникает, когда ток проходит через проводники в элементе блока нагрузки, выделяя тепло и создавая соответствующую электрическую нагрузку на источнике питания. Элементы резистивной нагрузки могут создавать точную величину нагрузки при коэффициенте мощности, равном 1.
Элементы резистивной нагрузки выделяют большое количество тепла, которое необходимо быстро отводить во избежание перегрева. Следовательно, блоки нагрузки используют принудительный воздух для охлаждения резистивных элементов, что обеспечивается специальной цепью питания и одним или несколькими вентиляторами.
Загрузка первичного двигателя, обычно дизельного двигателя, может выявить проблемы в его топливной, выхлопной, охлаждающей и других системах. Поскольку резистивные элементы работают с коэффициентом мощности, равным единице, они не проверяют реактивную мощность, вырабатываемую источником питания. Поскольку большинство систем распределения электроэнергии на объектах работают с отстающим коэффициентом мощности, близким к 0,8, резистивный блок может прикладывать нагрузку до 100 % номинальной мощности генератора, указанной на паспортной табличке. Однако элемент резистивной нагрузки не будет тестировать генератор против какой-либо индуктивной или реактивной нагрузки в цепи.

Элементы индуктивной нагрузки
Известные также как элементы реактивной нагрузки, индуктивные элементы используют проволочные катушки для создания индуктивных полей. Мощность, используемая для создания и поддержания этих полей, нагружает тестируемый источник питания. По сравнению с резистивными нагрузками ток индуктивной нагрузки достигает пика после напряжения. Следовательно, индуктивные катушки производят отстающие коэффициенты мощности.Поскольку они создают отстающие коэффициенты мощности, элементы индуктивной нагрузки используются всякий раз, когда необходимо уменьшить коэффициент мощности испытательной нагрузки. Например, коэффициент мощности в системе распределения электроэнергии в больнице может быть около 0,8. Тем не менее, во время испытаний генераторов можно использовать блоки нагрузки вместо действующей нагрузки здания, чтобы избежать нарушения подачи электроэнергии на объект. Поскольку блоки резистивной нагрузки обеспечивают коэффициент мощности, равный 1, они не могут тестировать источник питания при его номинальной мощности в кВА.
 Добавление блока индуктивной нагрузки может отрегулировать коэффициент мощности до значения, необходимого для испытаний на полную мощность.
Добавление блока индуктивной нагрузки может отрегулировать коэффициент мощности до значения, необходимого для испытаний на полную мощность.Элементы емкостной нагрузки
В элементах емкостной нагрузки используются конденсаторы, сохраняющие электрический заряд. Они сопротивляются изменениям напряжения, что приводит к тому, что ток достигает пика перед напряжением во время каждого электрического цикла. В результате элементы емкостной нагрузки обеспечивают опережающий коэффициент мощности и могут использоваться для повышения коэффициента мощности цепей.Конструкции элементов комбинированной нагрузки
Комбинированные блоки нагрузки обычно содержат резистивные и индуктивные элементы нагрузки в одном корпусе. Для генераторов это позволяет проводить испытания при 100% номинальной мощности кВА. Элементы резистивной и индуктивной нагрузки могут управляться независимо для создания чисто резистивной или индуктивной нагрузки или для регулировки коэффициента мощности по мере необходимости.
Примечательно, что блоки нагрузки с более чем одним типом элементов подходят для самого широкого спектра применений. Комбинированные блоки нагрузки используются для тестирования турбин, распределительных устройств, роторных ИБП, генераторов и систем ИБП. Эти блоки нагрузки могут особенно подходить для использования арендными компаниями, которым может потребоваться размещение различных типов нагрузки по мере перемещения оборудования с одной площадки на другую.
Резюме
Блоки нагрузки доступны с резистивными, индуктивными и емкостными элементами нагрузки. Резистивные блоки проверяют источники питания без изменения коэффициента мощности. Индуктивные и емкостные элементы нагрузки могут использоваться для моделирования неединичных нагрузок и для регулировки коэффициента мощности цепей. Нагрузочные блоки с комбинированными элементами нагрузочных блоков предлагают самый широкий набор функций, которые особенно подходят для приложений, в которых блоки нагрузок перемещаются с одной площадки на другую.





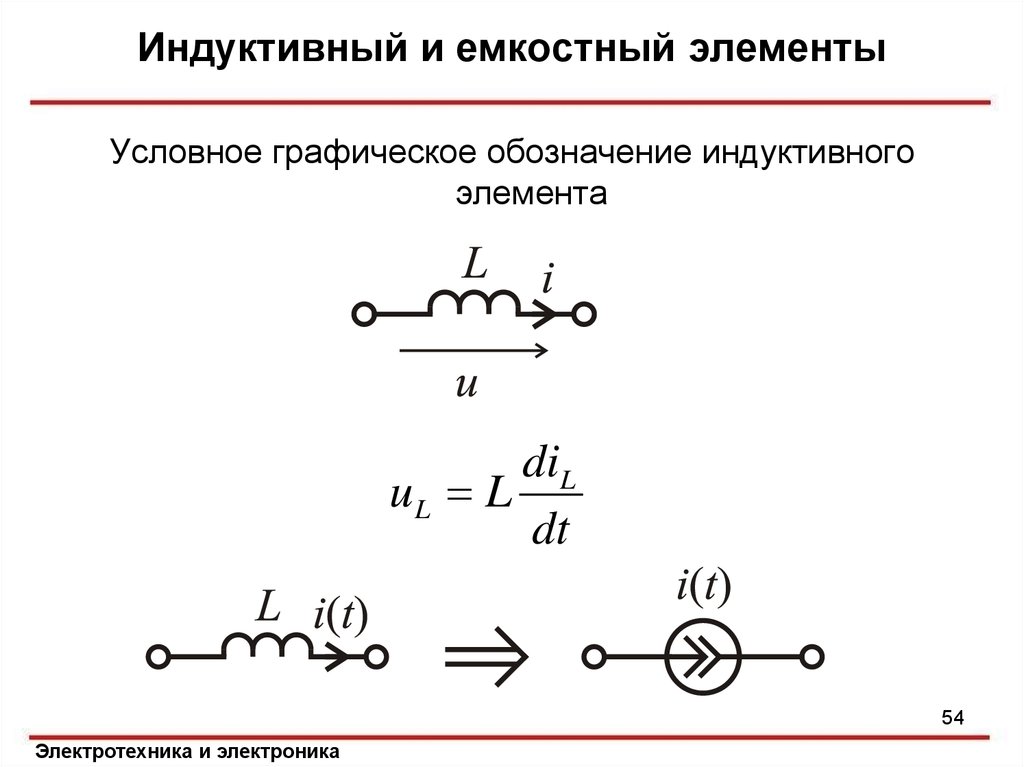
 Получим:
Получим: Кроме того, номинальные
значения напряжений и токов бытовых приборов также указываются как
действующие значения. Так стандартное напряжение в цепи − 220 вольт есть действующее значение, а амплитудное значение этого напряжения равно
Кроме того, номинальные
значения напряжений и токов бытовых приборов также указываются как
действующие значения. Так стандартное напряжение в цепи − 220 вольт есть действующее значение, а амплитудное значение этого напряжения равно