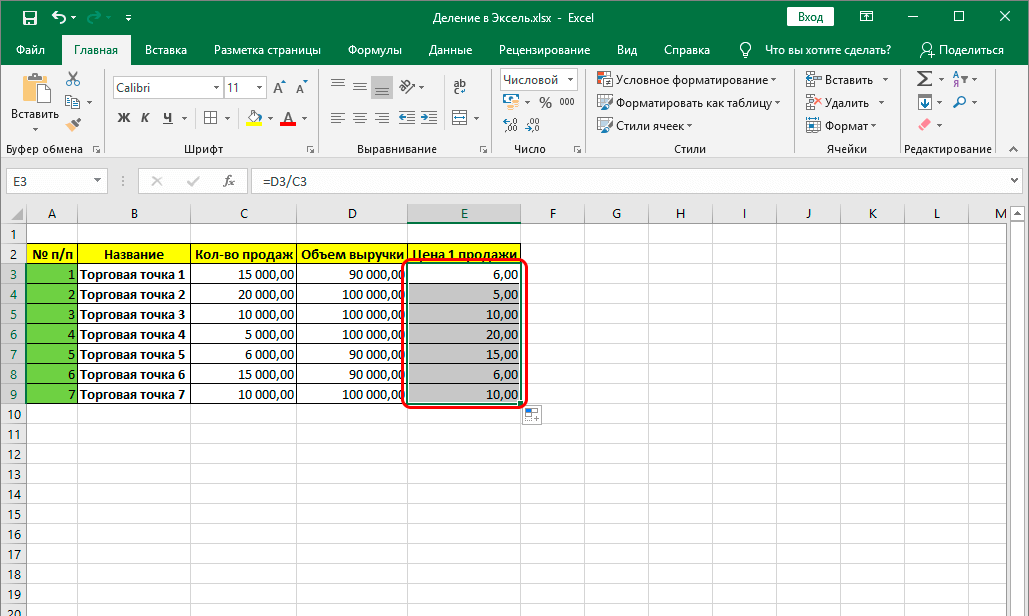
Как получить целую часть от деления чисел в 1С 8. Какие встроенные функции использовать для целочисленного деления. Чем отличается целочисленное деление от обычного. Как избежать ошибок при делении на ноль.
Основные способы целочисленного деления в 1С 8
В 1С 8 существует несколько эффективных способов выполнить целочисленное деление:
- Использование функции Цел()
- Применение оператора \
- Комбинация функций Окр() и /
Рассмотрим каждый из этих методов подробнее и разберем их особенности.
Функция Цел() для целочисленного деления
Функция Цел() возвращает целую часть числа, отбрасывая дробную. Ее можно использовать в комбинации с обычным делением для получения целочисленного результата:
Результат = Цел(Делимое / Делитель);
Например:
ЦелаяЧасть = Цел(10 / 3); // Вернет 3
Этот способ прост и интуитивно понятен. Однако у него есть недостаток — выполняется два действия: деление и округление, что может быть менее эффективно при больших объемах вычислений.

Оператор \ для целочисленного деления
В 1С 8 существует специальный оператор \ для целочисленного деления:
Результат = Делимое \ Делитель;
Пример использования:
ЦелаяЧасть = 10 \ 3; // Вернет 3
Этот способ является наиболее эффективным, так как выполняется за одну операцию. Он рекомендуется для использования в большинстве случаев.
Функция Окр() в сочетании с обычным делением
Еще один способ получить целую часть от деления — использовать функцию Окр() в сочетании с обычным делением:
Результат = Окр(Делимое / Делитель, 0, РежимОкругления.Отсечение);
Пример:
ЦелаяЧасть = Окр(10 / 3, 0, РежимОкругления.Отсечение); // Вернет 3
Этот метод дает корректный результат, но использует два действия и дополнительный параметр, что делает его менее предпочтительным по сравнению с оператором \.
Особенности целочисленного деления в 1С 8
При использовании целочисленного деления в 1С 8 следует учитывать некоторые важные особенности:
- Результат всегда округляется в меньшую сторону
- При делении отрицательных чисел результат может отличаться от математического
- Деление на ноль вызывает ошибку выполнения
Рассмотрим эти моменты подробнее на примерах.
Округление результата целочисленного деления
При целочисленном делении результат всегда округляется в меньшую сторону, отбрасывая дробную часть:
ЦелаяЧасть = 10 \ 3; // Вернет 3 ЦелаяЧасть = 11 \ 3; // Вернет 3 ЦелаяЧасть = 12 \ 3; // Вернет 4
Это нужно учитывать при вычислениях, где важна точность. В таких случаях может потребоваться дополнительная проверка остатка от деления.
Целочисленное деление отрицательных чисел
При делении отрицательных чисел результат целочисленного деления может отличаться от математического:
ЦелаяЧасть = -10 \ 3; // Вернет -3 ЦелаяЧасть = 10 \ -3; // Вернет -3 ЦелаяЧасть = -10 \ -3; // Вернет 3
Это связано с тем, что результат всегда округляется в сторону минус бесконечности. Важно помнить об этом при работе с отрицательными числами.
Обработка деления на ноль
Деление на ноль при использовании оператора \ вызывает ошибку выполнения. Чтобы избежать этого, необходимо добавить проверку делителя перед выполнением операции:
Если Делитель <> 0 Тогда Результат = Делимое \ Делитель; Иначе // Обработка ошибки деления на ноль ВызватьИсключение «Деление на ноль недопустимо»; КонецЕсли;

Такая проверка поможет избежать аварийного завершения программы и корректно обработать ошибочную ситуацию.
Сравнение целочисленного и обычного деления
Чем отличается целочисленное деление от обычного в 1С 8? Основные различия:
- Целочисленное деление всегда возвращает целое число
- Обычное деление может вернуть дробный результат
- Целочисленное деление быстрее из-за отсутствия операций с плавающей точкой
- При целочисленном делении теряется точность за счет отбрасывания остатка
Выбор между целочисленным и обычным делением зависит от конкретной задачи и требований к точности вычислений.
Оптимизация производительности при целочисленном делении
Для оптимизации производительности при использовании целочисленного деления в 1С 8 можно применить следующие приемы:
- Использовать оператор \ вместо функций Цел() или Окр()
- Избегать повторных вычислений, сохраняя промежуточные результаты в переменных
- Применять битовые операции для деления на степени двойки
Рассмотрим пример оптимизации с использованием битовых операций:

// Деление на 2 Результат = Число >> 1; // Эквивалентно Число \ 2, но быстрее // Деление на 4 Результат = Число >> 2; // Эквивалентно Число \ 4 // Деление на 8 Результат = Число >> 3; // Эквивалентно Число \ 8
Такой подход особенно эффективен при работе с большими объемами данных и в циклах.
Примеры использования целочисленного деления в 1С 8
Рассмотрим несколько практических примеров использования целочисленного деления в 1С 8:
Расчет количества полных комплектов
КоличествоДеталей = 100; ДеталейВКомплекте = 3; ПолныхКомплектов = КоличествоДеталей \ ДеталейВКомплекте; // Вернет 33 ОстатокДеталей = КоличествоДеталей % ДеталейВКомплекте; // Вернет 1
Преобразование секунд в часы и минуты
ОбщееКоличествоСекунд = 3665; Часы = ОбщееКоличествоСекунд \ 3600; // Вернет 1 Минуты = (ОбщееКоличествоСекунд % 3600) \ 60; // Вернет 1 Секунды = ОбщееКоличествоСекунд % 60; // Вернет 5
Распределение элементов по столбцам
КоличествоЭлементов = 10; КоличествоСтолбцов = 3; ПолныхСтрок = КоличествоЭлементов \ КоличествоСтолбцов; // Вернет 3 ЭлементовВПоследнейСтроке = КоличествоЭлементов % КоличествоСтолбцов; // Вернет 1
Эти примеры демонстрируют практическое применение целочисленного деления в различных сценариях разработки на 1С 8.
К вопросу о делении / Хабр
Нам подвернулась возможность провести небольшое, но крайне интересное тактическое учение
В процессе исследований нового МК от известной фирмы на основе архитектуры Cortex-М4 (я об этом обязательно еще напишу) возник вопрос, насколько быстро может работать операция целочисленного деления в аппаратной реализации. Натурный эксперимент дал несколько неожиданный результат: деление 32-разрядного числа на 32-разрядное выполняется за 3 такта частоты процессора — ну ни фига ж себе, как быстро. Выяснилось, что это имеет место только с определенными операндами, но дальнейшие исследования показали, что никогда время выполнения деления не превосходит 7 тактов. Полученные результаты вызвали легкую оторопь («и это не некая фигура речи, которая неизвестно что означает, а вполне конкретный глагол» — Дивов, как всегда, бесподобен).
Ну нельзя же просто так взять и быстро поделить такие длинные числа, странно как то, но факты — упрямая вещь.
И стало мне грустно, что в ARM сидят ребята намного умнее меня, и пошел я с тоской во взоре подглядеть в Инете, как они это делают. На сайте ARM никакой информации по времени исполнения не нашел, в одном из материалов по STM32 было указано, что деление занимает от 2 до 7 тактов, что соответствует наблюдениям, но информации о том, как это делается, нет.
В общем, Инет всемогущий особо не помог, есть трюки с делением на константу, сам о них писал в одном из постов, но у нас иная ситуация, есть алгоритм Ньютона и ускоренная его версия, но это явно не по делу, есть алгоритм на основе преобразования Фурье, но это для очень больших чисел и вряд ли выполнится за 7 тактов даже на архитектуре ARM. Пришлось придумывать самому и решение было найдено, причем настолько простое и очевидное, что становится несколько неловко от того, что это не было сделано мгновенно после формулировки задачи.
Пришлось придумывать самому и решение было найдено, причем настолько простое и очевидное, что становится несколько неловко от того, что это не было сделано мгновенно после формулировки задачи.
Прежде, чем смотреть мое решение, предлагаю Вам найти свое самостоятельно, а потом сравните с моим, и, если они отличаются то жду Вас в комментариях.
Итак, как нам быстро (не более, чем за 7 тактов) поделить два 32-разрядных числа с получением 32-разрядного результата.
Для начала вспомним, как вообще осуществляется деление в двоичной арифметике в
 Таким образом, мы получаем за один такт один бит результата и вся операция продлится 32 такта. В этом процессе есть еще начальный сдвиг, но на оценку ситуации в целом он не влияет. Будем ускорять, но как?
Таким образом, мы получаем за один такт один бит результата и вся операция продлится 32 такта. В этом процессе есть еще начальный сдвиг, но на оценку ситуации в целом он не влияет. Будем ускорять, но как?Обратим внимание, что полученный алгоритм сильно напоминает работу АЦП с последовательным приближением и вспоминаем, что есть и другой метод преобразования, намного более быстрый — параллельное преобразование. А что, если…
Будем вычитать из делителя не только делимое, но и делимое*2 и делимое*3 (одновременно, на трех сумматорах), тогда мы получим три бита (знаки результатов) информации, которые принимают 4 различных значения, значит из них можно извлечь сразу 2 бита результата. Далее экстраполируем подобный подход для 3,4,5 бит результата.
Чтобы получить 5 бит информации за один такт, нам потребуется 31 сумматор, на каждом из которых будет выполняться операция Делимое-Делитель*н(1-31), знаки результата пропускаем через шифратор и получаем сразу 5 бит результата. Затем сдвигаем делимое на 5 разрядов влево и повторяем до готовности. Тогда нам потребуется 32/5=6.4=>7 тактов для полного завершения операции.
Затем сдвигаем делимое на 5 разрядов влево и повторяем до готовности. Тогда нам потребуется 32/5=6.4=>7 тактов для полного завершения операции.
Для работы нам потребуется 31+х сумматоров, вроде бы немало, но они у нас уже есть, ведь у нас есть операция умножения 32*32 за один такт, а для ее реализации без 32 сумматоров не обойтись (ну я так думаю …), так что необходимая аппаратура у нас уже имеется, вопрос только в построении схемы контроля и кучи мультиплексоров для реализации быстрого сдвига, но это вполне решаемо.
Так что задача поделить за 7 тактов решена, остается вопрос – как можно ли сократить данное время, ведь в исследуемом МК оно бывает меньше 7. Напрашивающееся решение — на этапе подготовки алгоритма определить номер старшего значащего разряда делимого (Ч) и делителя (З) и сразу станет ясно, сколько старших битов частного равны нулю, так что мы можем пропустить первую либо несколько фаз алгоритма. Например, если Ч<З, то результат сразу равен нулю и мы завершаем операцию, наверняка можно вывести формулу для количества тактов, но мне уже стало скучно.
Интересно, что операция udiv дает только частное, хотя остаток явно где-то внутри остается лежать. В принципе, получить его нетрудно за два такта, что и делалось в исследуемом фрагменте машинного кода, выполнив псевдокод Делимое-Частное*Делитель, но это по любому 2 такта, почему не бы выдать его сразу в регистровой паре – я не знаю ответа на этот вопрос.
В общем, встретите ВВП, передайте ему, что блок деления в МК мы точно сделаем не хуже, если ему это по-прежнему интересно.
P.S.: Кстати, когда искал КДПВ (как вы заметили, так и не нашел), то заметил одну с откровенно неправильной надписью «На ноль делить нельзя». Должен сказать со всей определенностью, что на ноль делить можно, разделить нельзя. А если серьезно, то в разных архитектурах на ноль делят по разному, в х86 получаем исключение (о это незабвенная ошибка 200), в некоторых получаем делимое либо ноль, но я еще не разу не видел максимального целого. В ARM н/0 = 0/0 и получается 0.
Двоичная целочисленная арифметика — Двоичная арифметика и устройсто управления ЭВМ
Устройство управления руководит прохождением и обработкой информации в системе, память хранит эту информацию для дальнейшего использования, арифметическое устройство выполняет арифметические и логические операции над ней, периферийные устройства преобразуют ее из внешней формы представления во внутреннюю и наоборот. В этом разделе мы рассмотрим двоичную и шестнадцатеричную системы счисления, которые лежат в основе внутреннего представления информации, а затем перейдем к обсуждению двоичной целочисленной арифметики, одной из арифметик, применяющихся в современных ЭВМ.
В этом разделе мы рассмотрим двоичную и шестнадцатеричную системы счисления, которые лежат в основе внутреннего представления информации, а затем перейдем к обсуждению двоичной целочисленной арифметики, одной из арифметик, применяющихся в современных ЭВМ.
Двоичная и шестнадцатиричная системы счисления
Двоичная система счисления. Наша десятичная система счисления является позиционной в том смысле, что величина числа зависит от порядка цифр в нем. Например, число 534.686 в 10 раз больше, чем
53.4686, поскольку позиции одних и тех же цифр относительно десятичной точки различны. На самом деле, когда мы пишем 534.686, мы имеем в виду число
Положение цифры относительно десятичной точки определяет степень числа 10, на которую эта цифра будет умножена при вычислении суммы.
Отметим фундаментальное значение числа 10 в десятичной системе. Основанием позиционной системы счисления называется число, возводимое в соответствующие степени в развернутом представлении чисел этой системы. Таким образом, основанием десятичной системы счисления является число 10.
Таким образом, основанием десятичной системы счисления является число 10.
То, что мы используем десятичную систему, до некоторой степени является случайностью. Если бы у человека было 8 пальцев, а не 10, мы, вероятно, использовали бы восьмеричную систему, что, надо отметить, облегчило бы изобретение вычислительных машин и их изучение.
Информация в большинстве современных ЭВМ хранится и обрабатывается в двоичной форме. В двоичной системе существует всего две цифры, или бита, 0 и 1. Одной из причин использования именно этой системы в программировании является то, что обычные электронные переключатели могут находиться только в одном из двух состояний — включенном или выключенном. Кроме того, логика, которую мы используем, по своему существу является двоичной логикой: любое предложение в ней либо истинно, либо ложно. Таким образом, мы употребляем биты для обозначения 1 или 0, состояний «включено» или «выключено», истины или лжи.
В нашей повседневной жизни мы используем десятичную арифметику. В программировании более естественной является двоичная система. Значит, нам придется часто преобразовывать числа из двоичной системы в десятичную и наоборот.
В программировании более естественной является двоичная система. Значит, нам придется часто преобразовывать числа из двоичной системы в десятичную и наоборот.
Поскольку основанием двоичной системы является число 2, мы можем определить десятичное значение двоичного числа, расписывая двоичное число в виде суммы степеней двойки и вычисляя полученную сумму, используя десятичную арифметику. Например, для преобразования числа
11011.1001
в десятичную форму можно записать
В результате мы получили
Иными словами, система, в которой записано число, определяется подстрочным указанием основания этой системы в конце числа.
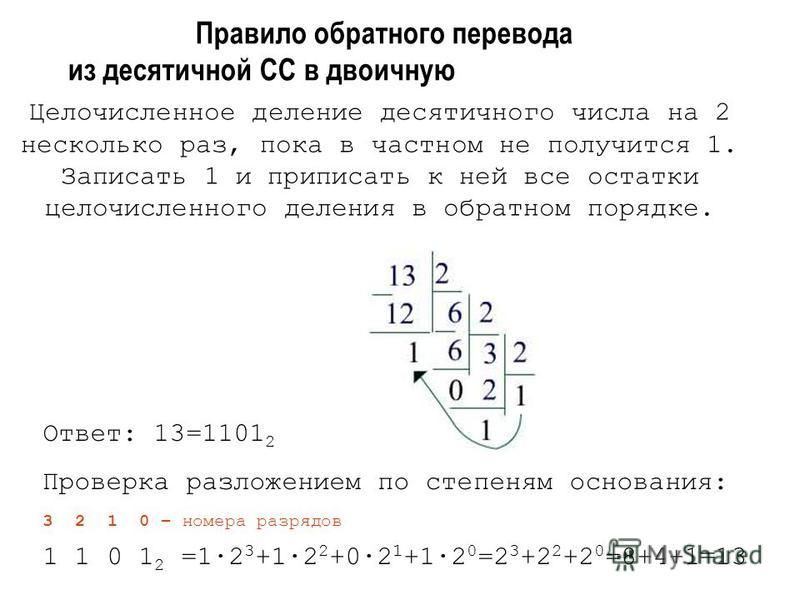
Теперь рассмотрим обратное преобразованием дано десятичное число. Как перевести его в двоичную форму? Предлагаемый алгоритм очень напоминает алгоритм деления в столбик и может быть хорошо проиллюстрирован на примере.
Мы хотим перевести число в его двоичный эквивалент. Выполним преобразование в две стадии, преобразуя целую и дробную части исходного числа по отдельности.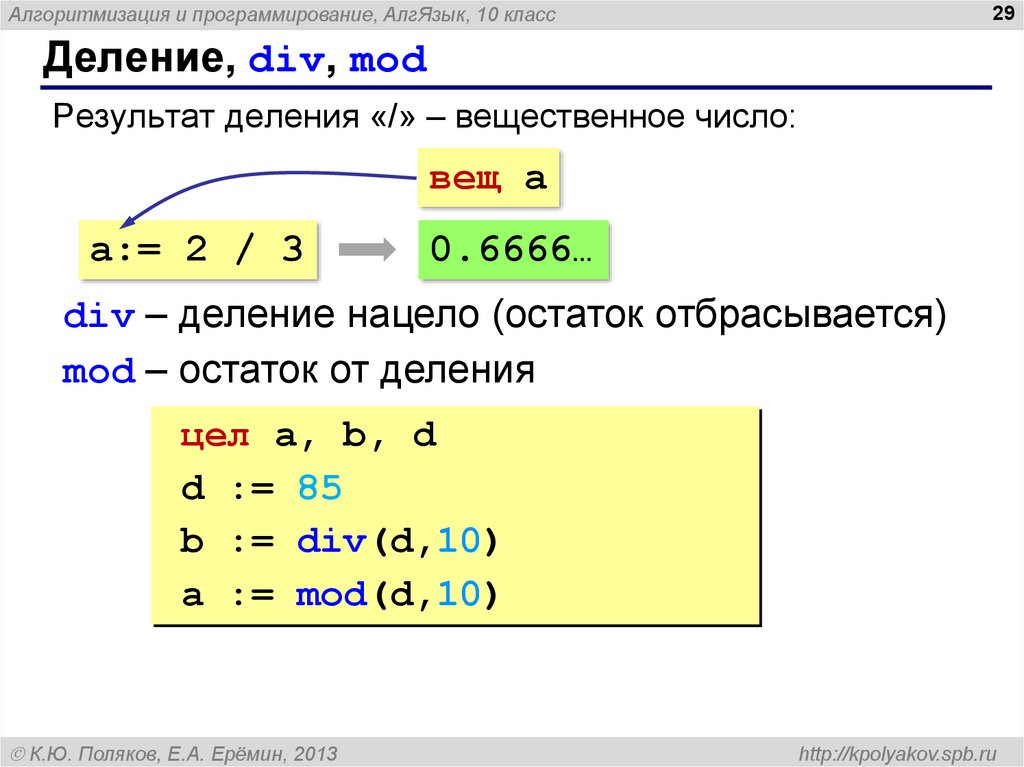
Для преобразования целого десятичного числа в двоичное будем последовательно делить исходное число и результаты деления на 2, сохраняя остатки от каждого деления; последовательность остатков будет представлять собой результат преобразования. В нашем примере
Теперь для получения результата осталось лишь записать остатки в порядке «снизу вверх». Получим
(Проверьте этот результат, проделав обратное преобразование.)
Для соответствующего преобразования десятичной дроби в двоичную мы последовательно будем умножать десятичную дробь на 2, записывая 1 каждый раз при получении числа, по модулю большего 1 (перенос в целую часть), и 0 в противном случае. При последующих умножениях используется только дробная часть полученного числа. В нашем примере мы имеем
Очевидно, этот процесс можно продолжить до бесконечности; двоичное представление десятичного числаявляется периодической дробью. Для получения ответа необходимо выписать все переносы в порядке «сверху вниз». То есть
То есть
и в конечном итоге мы получаем
с бесконечной дробной частью.
Замечание по поводу полученного результата. Большинство десятичных дробей, например, такие, как 1, 2, 06, не могут быть представлены в виде конечных двоичных. Но ЭВМ оперируют лишь числами, представленными конечными наборами цифр. Это ведет к неизбежным ошибкам округления, возникающим при отбрасывании младших разрядов числа, необходимом для записи его в виде конечного машинного слова.
Чем больше разрядов используется для представления дробей, тем больше точность получаемого приближения. Так, используя всего 4 двоичных разряда для представления числа 2, мы имели бы
при использовании 8 битов мы получаем более точный результат
Шестнадцатеричная система счисления. Вы могли уже заметить, что перевод в двоичную систему несколько утомителен; для представления десятичной дроби в двоичном виде требуется приблизительно в три раза больше цифр. Поэтому для краткой записи двоичной информации в программировании используется система с большим основанием. Главным требованием, предъявляемым к такой системе, является то, что перевод из этой системы в двоичную и обратно должен быть достаточно прост, т. е. эта система и двоичная должны быть в некотором смысле эквивалентны.
Поэтому для краткой записи двоичной информации в программировании используется система с большим основанием. Главным требованием, предъявляемым к такой системе, является то, что перевод из этой системы в двоичную и обратно должен быть достаточно прост, т. е. эта система и двоичная должны быть в некотором смысле эквивалентны.
Шестнадцатеричная система, или система с основанием 16, обладает этим свойством и широко используется в тех случаях, когда двоичная информация легко представима в виде групп по 4 бита в каждой. Поскольку основание системы равно 16, то в ней должны существовать 16 различных цифр. У нас есть 10 цифр нашей десятичной системы счисления, их мы и используем в качестве первых 10 цифр шестнадцатеричной системы. В качестве остальных шести цифр мы используем буквыА, В, С, D, Е, F.
На рис. 2.1 изображены первые десятичные числа и их двоичное и шестнадцатеричное представление. Отметим, что каждое 4-разрядное двоичное число соответствует определенной цифре шестнадцатеричной системы. Именно это позволяет легко проводить преобразования из одной системы в другую. Для преобразования двоичного числа в шестнадцатеричное нужно разбить двоичное число на группы, по 4 бита в каждой, двигаясь вправо и влево от десятичной точки. Затем нужно добавить к крайним группам нули для дополнения их до 4 разрядов,
Именно это позволяет легко проводить преобразования из одной системы в другую. Для преобразования двоичного числа в шестнадцатеричное нужно разбить двоичное число на группы, по 4 бита в каждой, двигаясь вправо и влево от десятичной точки. Затем нужно добавить к крайним группам нули для дополнения их до 4 разрядов,
|
Десят. |
Двоичн. |
Шестн. |
|
0 |
0000 |
0 |
|
1 |
0001 |
1 |
|
2 |
0010 |
2 |
|
3 |
0011 |
3 |
|
4 |
0100 |
4 |
|
5 |
0101 |
5 |
|
6 |
0110 |
6 |
|
7 |
0111 |
7 |
|
8 |
1000 |
8 |
|
9 |
1001 |
9 |
|
10 |
1010 |
А |
|
11 |
1011 |
в |
|
12 |
1100 |
С. |
|
13 |
1101 |
D |
|
14 |
1110 |
Е |
|
15 |
1111 |
F |
|
16 |
10000 |
10 |
|
17 |
10001 |
11 |
|
18 |
10010 |
12 |
|
19 |
10011 |
13 |
|
20 |
10100 |
14 |
Рис. 2.1. Десятичные, двоичные и шестнадцатеричные числа.
2.1. Десятичные, двоичные и шестнадцатеричные числа.
если это потребуется. Например, для преобразования
в шестнадцатеричное, нужно записать
Теперь мы находим каждую группу из четырех цифр, рассматриваемую как двоичное целое, в таблице, изображенной на рис. 2.1, и выписываем соответствующие шестнадцатеричные цифры для каждой группы (после небольшой практики поиск в таблице станет ненужным). В нашем примере
Для проведения обратного преобразования мы просто проводим описанный выше процесс в обратной последовательности, сопоставляя теперь уже каждому шестнадцатеричному числу группу из четырех битов. Например,
Процесс преобразования из шестнадцатеричной системы в десятичную может быть осуществлен расписыванием исходного числа по степеням 16 и вычислением полученной суммы в десятичной системе. Так
Наконец, перевод десятичного целого в шестнадцатеричное может быть выполнен примерно так же, как и перевод десятичного целого в двоичное; разница заключается в том, что на каждом шаге мы делим десятичное число на 16 и записываем остатки в шестнадцатеричном виде.
Вот процесс перевода 638.0 в шестнадцатеричную форму:
И в результате получаем
Для перевода десятичной дроби в шестнадцатеричную форму обычно используется та же процедура, которую мы использовали для перевода десятичной дроби в двоичную, только теперь умножение производится на 16 и числа, получающиеся в целой части при умножении, записываются в шестнадцатеричной форме.
Умножение и деление на 16 гораздо более сложны, чем умножение и деление на 2. Поэтому для перевода десятичного числа в шестнадцатеричное гораздо удобнее сначала перевести десятичное число в двоичное и лишь затем перевести результат в шестнадцатеричную форму. Наиболее же просто можно произвести преобразования из десятичной системы в шестнадцатеричную, используя таблицы приложения 4 или справочные карты фирмы IBM.
Двоичная арифметика в дополнительных кодах
Рассмотрев преобразования десятичных чисел в двоичные и шестнадцатеричные, познакомимся теперь с арифметическими действиями в этих системах. Поскольку над двоичными дробями и смешанными числами можно производить арифметические действия, используя арифметику с плавающей точкой (см. гл. 19), ограничимся рассмотрением арифметики целых чисел, иначе говоря арифметики с фиксированной точкой.
Поскольку над двоичными дробями и смешанными числами можно производить арифметические действия, используя арифметику с плавающей точкой (см. гл. 19), ограничимся рассмотрением арифметики целых чисел, иначе говоря арифметики с фиксированной точкой.
Сложение. Сложение в двоичной системе счисления выполняется точно так же, как и в десятичной. Мы можем использовать следующую таблицу для определения сумм всевозможных пар одноразрядный двоичных чисел:
Если справедливость результатов таблицы вызывает сомнения, переведите все числа в десятичную систему, выполните указанные сложения и вновь переведите результаты в двоичную систему (это вообще один из возможных методов реализации двоичной арифметики). Сложим два двоичных целых
и
Получим
где числа в кружочках обозначают переносы. Как и в десятичной арифметике, мы начинаем с младших разрядов и производим сложение шаг за шагом, справа налево, получая по одной цифре на каждом шаге:
Проверьте правильность проделанных вычислений переводом в десятичную систему.
При проверке и отладке программ на языке ассемблера часто требуется сложение пар шестнадцатеричных чисел. При этом используется тот же алгоритм, что и в десятичной системе, только необходимо иметь в виду, что , т. е. если имеет место перенос, то переносится число 16, а не 10. Рассмотрим простой пример и вычислим
Совершенно верным (и наиболее часто используемым опытными программистами) способом является следующий: шестнадцатеричные числа переводятся по столбцам в десятичные, выполняется сложение, и результат снова приводится к шестнадцатеричному виду с переносом единиц в старший разряд, если полученная сумма больше (десятичного) 16. Возвращаясь к нашему примеру, мы должны рассуждать так: «есть,есть, сумма равна. Далее, больше , поэтому мы должны вычесть из результата, получим 2, но теперь необходимо произвести перенос 1, компенсируя таким образом вычитание 16». Рассмотрим более сложный пример:
Опять номера в кружочках представляют собой переносы. Для вычисления суммы необходимо последовательно выполнить следующие шаги:
Для вычисления суммы необходимо последовательно выполнить следующие шаги:
Мы могли бы так же использовать методы вычисления в десятичной системе для вычитания двоичных и шестнадцатеричных чисел. Необходимо было бы только помнить, что, занимая единицу старшего разряда для вычитания, мы занимаем соответственно 2 и 16, а не 10. Тем не менее на современных вычислительных машинах, и в частности на машинах Систем 360 и 370, операция вычитания выполняется совсем по-другому. Поскольку в дальнейшем мы будем тесно связаны с машинной арифметикой, познакомимся поближе с машинными методами выполнения арифметических операций.
Из соображений экономии современные арифметические устройства не содержат отдельных схем для выполнения операций сложения и вычитания. Обе эти операции выполняются одной и той же схемой, сумматором, способной выполнять только операцию сложения чисел. Для вычитания числа bиз числа а ЭВМ производит сложение а с — b. Иными словами, ЭВМ вычисляет не а—b, а+(—b),
где минус означает не операцию вычитания, а отрицательность числа, следующего за ним.
В Системе 360 числа обычно хранятся и обрабатываются в форме полных слов. Каждое слово состоит из 32 двоичных разрядов, или битов. Таким образом, реальным содержимым ячейки, содержащей, например, число 5, будет
Отметим также, что мы можем представить содержимое ячейки в форме шестнадцатеричного числа, в нашем случае
00000005
Для представления отрицательных чисел используется так называемый дополнительный код. Покажем теперь, как определить дополнительный код для заданного числа и как выполняется сложение с его использованием. После этого будет показано, как можно применить это понятие при выполнении арифметических операций над целыми числами со знаками.
Для вычисления дополнительного кода целого числа получим сначала его логическое дополнение. Логическое дополнение (обратный код) числа получается заменой каждой 1 в машинном представлении этого числа на 0 и каждого 0 на 1. Терминология станет ясной, как только вы поймете, что логическим дополнением истины является ложь, и наоборот.
Таким образом, логическим дополнением слова 11010101110110100011100001010111
является слово
00101010001001011100011110101000
Дополнительный код целого числа получается добавлением 1 к обратному коду этого числа, т. е.
дополнительный код = обратный код + 1
Возвращаясь к нашему предыдущему примеру, мы увидим, что дополнительный код для слова, содержащего число 5, вычисляется так:
Все это может быть гораздо более удобно записано в шестнадцатеричной системе счисления. Только нужно проявить аккуратность при вычислении логических дополнений шестнадцатеричных чисел. В этой форме записи предыдущий пример мог выглядеть так:
Обычно мы пользуемся шестнадцатеричным представлением двоичной информации. Если вы сомневаетесь в правильности полученных результатов, проделайте обратное преобразование шестнадцатеричных чисел в двоичные и выполните необходимые операции в двоичной системе. Отметим, что совершенно безразлично, в шестнадцатеричной или двоичной форме мы записываем машинную информацию; двоичная и шестнадцатеричная системы действительно эквивалентны.
Отметим, что совершенно безразлично, в шестнадцатеричной или двоичной форме мы записываем машинную информацию; двоичная и шестнадцатеричная системы действительно эквивалентны.
Утверждается, что дополнительный код некоторого числа при выполнении арифметических операций, если, конечно, эти операции выполняются правильно, ведет себя так же, как это число, взятое с обратным знаком. Продемонстрируем это на примере вычисления разности 13—13 с использованием дополнительного кода. Имеем в виде полного машинного слова, тогда как дополнительным кодом числа 13 (проверьте) является
опять же в 32-разрядном машинном представлении.
Вычислим теперь сумму
Мы получили правильный ответ 0, но как быть с последней переносимой единицей, не умещающейся в 32-разрядное машинное слово? Ответ на этот вопрос таков:
В арифметике в дополнительных кодах единица, выносящаяся влево за разрядную сетку, не учитывается.
Отсюда мы заключаем, что дополнительный код числа при выполнении арифметических операций ведет себя как это же число, взятое с обратным знаком. Почему это на самом деле так, легко понять, взглянув на вопрос с несколько иной точки зрения. Предположим, что мы имеем двоичное число А. Легко видеть, что дополнительный код
Почему это на самом деле так, легко понять, взглянув на вопрос с несколько иной точки зрения. Предположим, что мы имеем двоичное число А. Легко видеть, что дополнительный код
В двоичном видезаписывается как 1 с 32 нулями. Пытаясь теперь представитьв виде машинного слова, мы получим 32 нуля и 1, не вошедшую в разрядную сетку. Отбрасывая 1, мы получим, чтопредставляется машинным 0. Теперь для вычисленияВ — А можно формально записать
1
Математик сказал бы нам, что наша арифметика в дополнительных кодах для 32-разрядных чисел есть не что иное, как арифметика по модулю
Абсолютная величина двоичного числа. Для суммирующей схемы не существует разницы между сложением и вычитанием. Знак операции определяют сами числа, подающиеся на вход схемы. Если второй операнд на самом деле является лишь дополнительным кодом истинного, результатом сложения будет разность двух чисел. Однако во многих других случаях, и в частности при интерпретации результатов арифметических операций, необходимо различать положительные и отрицательные числа и быть в состоянии вычислить их абсолютные значения, или модули.
Для определения знака числа необходимо посмотреть на первый(0-й) бит, или, как его часто называют, знаковый разряд числа. Если 1 знаковый разряд равен 0, то число положительно, т. е. если мы добавим его к другому числу, то результат будет больше исходного числа. Абсолютной величиной такого числа является просто оно само.
Если, с другой стороны, знаковый разряд содержит 1, число может рассматриваться как отрицательное, т. е. если мы сложим его с положительным числом, то результат будет меньше последнего.
Абсолютной величиной отрицательного числа является его представление в дополнительном коде. В заключение надо сказать, что модуль числаА есть не что иное, как его абсолютная величина | А |.
ЕслиА — число, записанное в машинной форме, то
Переполнение. Мы видели, что в машине двоичные числа представлены в форме слов, содержащих 31 разряд и один знаковый разряд. Но что произойдет при сложении чисел, сумма которых не помещается в машинное слово, т. е. модуль которой больше чем—1? В этом
е. модуль которой больше чем—1? В этом
случае обычно фиксируется ошибка, ситуация, возникающая при этом, называется арифметическим переполнением. Предположим, что нам нужно вычислить
причем работает рассмотренное выше правило. Суммой этих двух положительных чисел будет отрицательное число
(подсчитайте его абсолютную величину). ЭВМ производит проверку и прекращает выполнение программы, если происходит переполнение.
Умножение и деление. Каждый, кто хоть раз пытался выполнить эти операции в шестнадцатеричной системе счисления, знает, что лучшим способом получения результата является приведение операндов к двоичному и десятичному виду, выполнение необходимых действий в этих системах и обратное преобразование результатов.
Умножение и деление двоичных чисел производится так же, как умножение и деление десятичных, только сами арифметические действия производятся в двоичной системе. К примеру, для вычисления произведения на необходимодействоватьтак:
Отметим, что длина произведения равна сумме длин сомножителей. Следовательно, при умножении двух 32-разрядных слов может получиться 64-разрядный результат. Как мы увидим в дальнейшем, в действительности при выполнении операции умножения содержимое некоторого регистра умножается на содержимое другого регистра или слова памяти. Результат занимает два регистра, содержимое которых рассматривается как 64-разрядное двоичное число.
Следовательно, при умножении двух 32-разрядных слов может получиться 64-разрядный результат. Как мы увидим в дальнейшем, в действительности при выполнении операции умножения содержимое некоторого регистра умножается на содержимое другого регистра или слова памяти. Результат занимает два регистра, содержимое которых рассматривается как 64-разрядное двоичное число.
Деление двоичных целых чисел может выполняться с помощью хорошо известного алгоритма деления в столбик. Для выполнения деления 111011101 на 11011 можно записать:
То есть частное равно, остаток — .
Частное и остаток при делении полных слов занимают по одному слову. Если делитель представляет собой полное слово, то мы имеем возможность разделить на него содержимое двух слов, рассматриваемых как единое 64-разрядное число. Как мы увидим позднее, такая возможность предусматривается командой деления.
На этом заканчивается наше формальное обсуждение двоичной целочисленной арифметики, хотя мы еще не раз встретимся с ней в примерах и упражнениях в других частях книги. Хорошее знание двоичной арифметики значительно облегчает составление и отладку программ. Проверьте себя, освоили ли вы простейшие арифметические действия в шестнадцатеричной «системе счисления и арифметику в дополнительных кодах.
Хорошее знание двоичной арифметики значительно облегчает составление и отладку программ. Проверьте себя, освоили ли вы простейшие арифметические действия в шестнадцатеричной «системе счисления и арифметику в дополнительных кодах.
Integer Division — Algorithmica
По сравнению с другими арифметическими операциями, деление очень плохо работает на x86 и компьютерах в целом. Общеизвестно, что как с плавающей запятой, так и с целым числом деление сложно реализовать на аппаратном уровне. Схема занимает много места в АЛУ, вычисления состоят из множества стадий, и в результате div и его собратья обычно занимают 10-20 циклов, при этом задержка немного меньше при меньших размерах данных.
#Деление и модуль в x86
Поскольку никто не хочет дублировать весь этот беспорядок для отдельной операции по модулю, инструкция div служит обеим целям. Чтобы выполнить 32-битное целочисленное деление, вам нужно поместить делимое , а именно , в регистр eax и вызвать div с делителем в качестве единственного операнда. После этого частное будет храниться в
После этого частное будет храниться в eax , а остаток будет храниться в edx .
Единственная оговорка заключается в том, что дивиденд на самом деле должен храниться в два регистра , eax и edx : этот механизм обеспечивает деление 64 на 32 или даже 128 на 64, аналогично тому, как работает 128-битное умножение. При выполнении обычного знакового деления 32 на 32 нам нужно расширить знак eax до 64 бит и сохранить его старшую часть в edx :
div(int, int):
мов акс, эди
компакт-диск
идив эси
рет
Для беззнакового деления можно просто установить edx в ноль, чтобы не мешало:
div(без знака, без знака):
мов акс, эди
xor эдкс, эдкс
див эси
рет
В обоих случаях в дополнение к частному в eax вы также можете получить доступ к остатку как edx :
mod(без знака, без знака):
мов акс, эди
xor эдкс, эдкс
див эси
движение eax, edx
рет
Вы также можете разделить 128-битное целое число (хранящееся в rdx:rax ) на 64-битное целое число:
div(u128, u64):
; а = rdi + rsi, b = rdx
мов rcx, rdx
мов ракс, рди
мов rdx, rsi
раздел edx
рет
Старшая часть делимого должна быть меньше делителя, иначе произойдет переполнение. Из-за этого ограничения трудно заставить компиляторы создавать этот код самостоятельно: если вы разделите 128-битный целочисленный тип на 64-битное целое число, компилятор заполнит его дополнительными проверками, которые на самом деле могут быть ненужными.
Из-за этого ограничения трудно заставить компиляторы создавать этот код самостоятельно: если вы разделите 128-битный целочисленный тип на 64-битное целое число, компилятор заполнит его дополнительными проверками, которые на самом деле могут быть ненужными.
#Division by Constants
Целочисленное деление мучительно медленное, даже если оно полностью аппаратно реализовано, но в некоторых случаях его можно избежать, если делитель постоянный. Хорошо известным примером является деление на степень двойки, которое можно заменить двоичным сдвигом в один цикл: двоичный алгоритм GCD — восхитительная демонстрация этой техники. 99 + 7)$:
; ввод (rdi): х ; вывод (rax): x mod (m=1e9+7) мов ракс, рди movabs rdx, -8543223828751151131 ; загрузить магическую константу в регистр мул рдкс ; выполнить умножение мов ракс, rdx Шр Ракс, 29 лет; двоичный сдвиг результата
Этот метод называется Редукция Барретта , и он называется «редукция», потому что он в основном используется для операций по модулю, которые могут быть заменены одним делением, умножением и вычитанием в силу этой формулы: 9с})$. Левая граница максимально близка к целому числу, а размер всего диапазона является вторым из возможных. И вот кульминация: если $s \ge n$, то единственное целое число, содержащееся в этом диапазоне, равно $1$, и поэтому алгоритм всегда будет возвращать его.
Левая граница максимально близка к целому числу, а размер всего диапазона является вторым из возможных. И вот кульминация: если $s \ge n$, то единственное целое число, содержащееся в этом диапазоне, равно $1$, и поэтому алгоритм всегда будет возвращать его.
#Lemire Reduction
Сокращение по Барретту немного сложно, а также генерирует последовательность команд длины для модуля, поскольку она вычисляется косвенно. Существует новый (2019 г.) метод, который в некоторых случаях проще и на самом деле быстрее по модулю. У него пока нет общепринятого названия, но я буду называть его редукцией Лемира.
Вот основная идея. Рассмотрим представление с плавающей запятой некоторой целой дроби:
$$ \frac{179}{6} = 11101,1101010101\ldots = 29\tfrac{5}{6} \приблизительно 29,83 $$Как мы можем «разобрать» его, чтобы получить нужные нам части?
- Чтобы получить целую часть (29), мы можем просто уменьшить или обрезать ее до точки.
- Чтобы получить дробную часть (⅚), мы можем просто взять то, что стоит после точек.

- Чтобы получить остаток (5), мы можем умножить дробную часть на делитель. 964/г)
uint32_t мод (uint32_t х) {
uint64_t младшие биты = m * x;
return ((__uint128_t) младшие биты * y) >> 64;
}
uint32_t дел (uint32_t х) {
return ((__uint128_t) m * x) >> 64;
}
Мы также можем проверить делимость $x$ на $y$ всего одним умножением, используя тот факт, что остаток от деления равен нулю тогда и только тогда, когда дробная часть (младшие 64 бита $m \cdot x$) не превосходит $m$ (иначе оно стало бы ненулевым числом при обратном умножении на $y$ и сдвиге вправо на 64).
логическое значение is_divisible (uint32_t x) { вернуть м * х < м; }Единственным недостатком этого метода является то, что для выполнения умножения требуются целочисленные типы, в четыре раза превышающие исходный размер, в то время как другие методы сокращения могут работать только с двойным числом.
Существует также способ вычисления 64x64 по модулю путем тщательного манипулирования половинками промежуточных результатов; реализация оставлена читателю в качестве упражнения.

#Дополнительная литература
Ознакомьтесь с libdivide и GMP, чтобы узнать о более общих реализациях оптимизированного целочисленного деления.
Также стоит прочитать Hacker’s Delight, в котором есть целая глава, посвященная целочисленному делению.
Что означает // в Python?
Что делает оператор Python
//? Чем он отличается от оператора/?Оператор
/Оператор
/является оператором деления в Python.Когда между двумя числами используется
/, вы всегда получите точный (настолько точный, насколько Python может управлять) результат:>>> 5 / 2 2,5
В отличие от некоторых языков программирования,
/в Python не действуют иначе при использовании между целыми числами; в Python 3 то есть. В Python 2 при делении двух целых чисел результат будет уменьшаться до ближайшего целого числа:>>> 5 / 2 # Python 2 2
Но в Python 3 деление двух целых чисел всегда возвращает число с плавающей запятой с точным результатом:
>>> 4 / 2 2.
 0
0
Оператор
//между целыми числамиОператор
//— это оператор деления пола в Python. Когда//используется между двумя целыми числами, вы всегда получите целое число:>>> 5 // 2 2
Оператор
//обеспечивает деление при округлении результата до ближайшего целого числа. Это часто называют целочисленным делением или делением пола .При использовании
//с числом с плавающей запятой, вы получите обратно число с плавающей запятой:>>> 5.0 // 2 2.0
Но, как и в случае с целыми числами, это число с плавающей запятой будет , а будет округленным в меньшую сторону до ближайшего целого числа .
Когда следует использовать
//в Python?Если вы когда-нибудь видели такой код:
>>> n = 5 >>> целое(n / 2) 2
Тогда вы, вероятно, видели возможность использовать
//оператор. Если вы делите, а затем сразу же конвертируете результат в целое число, вы, вероятно, могли бы использовать вместо этого оператор
Если вы делите, а затем сразу же конвертируете результат в целое число, вы, вероятно, могли бы использовать вместо этого оператор //.В этой функции
split_in_halfмы используем функциюint, чтобы убедиться, что значениеmid_pointявляется целым числом:def split_in_half(sequence): """Вернуть две половины заданной последовательности (список, строка и т.д.)""" mid_point = int (len (последовательность) / 2) возвращаемая последовательность[:mid_point], последовательность[mid_point:]Оба числа, которые мы делим, являются целыми, поэтому мы могли бы использовать
//, чтобы получить целочисленный результат:def split_in_half(sequence): """Вернуть две половины заданной последовательности (список, строка и т.д.)""" mid_point = len(последовательность) // 2 возвращаемая последовательность[:mid_point], последовательность[mid_point:]Это немного эффективнее, чем деление для получения точного числа с плавающей запятой, а затем деление этого числа с плавающей запятой, чтобы вернуться к целому числу.

Обратите внимание, что
//всегда округляется в меньшую сторонуПрежде чем вы замените все случаи использования
int(a / b)в вашем коде наa // b, вы должны заметить, что эти два значения действуют по-разному, когда результат деление является отрицательным числом:Допустим, мы делим и получаем
-2,5:>>> a = -5 >>> б = 2 >>> а/2 -2,5
При использовании
/иintмы получим-2, но при делении на//мы получим-3вместо:>>> int(a / 2) -2 >>> а // 2 -3
Оператор
//всегда округляет в меньшую сторону. Он действует не столько как встроенная функцияint, сколько какmath.floor:>>> from math import floor >>> этаж(а/2) -3 >>> а // 2 -3
Также помните, что
a // bвозвращает число с плавающей запятой, когда либоa, либоb— числа с плавающей запятой.
>>> а = 52,0 >>> б = 4 >>> а // б 13,0
Таким образом, вы, скорее всего, захотите использовать
//только для деления между положительными целыми числами .Использование
divmodвместоЧто делать, если вам нужно целочисленное деление (с
//) и остаток от этого деления (с%):>>> duration = 500 >>> минуты = продолжительность // 60 >>> секунды = продолжительность % 60 >>> print(f"{минуты}:{секунды}") 8:20Вместо того, чтобы использовать
//и%по отдельности, вы можете использовать функциюdivmod, чтобы получить оба результата одновременно:>>> duration = 500 >>> минуты, секунды = divmod(длительность, 60) >>> print(f"{минуты}:{секунды}") 8:20Теоретически это можно оптимизировать для одновременного выполнения обеих операций, но на практике CPython не выполняет эту оптимизацию, поэтому в первую очередь касается удобочитаемости .
Иногда
divmodможет значительно улучшить читаемость кода. Например, здесь мы используем//и%, чтобы получить часы, минуты и секунды:>>> duration = 9907 >>> часы = продолжительность // (60 * 60) >>> минуты = (длительность // 60) % 60 >>> секунды = продолжительность % 60 >>> print(f"{часы}:{минуты:02d}:{секунды:02d}") 2:46:07Но вместо этого мы могли бы дважды использовать
divmod:>>> продолжительность = 9907 >>> минуты, секунды = divmod(длительность, 60) >>> часы, минуты = divmod(минуты, 60) >>> print(f"{часы}:{минуты:02d}:{секунды:02d}") 2:46:07Я считаю, что подход
divmodнамного понятнее, чем альтернативное использование//и%. Если вам нужно как частное (если использовать математический термин), так и остаток от деления, рассмотрите возможность использованияdivmod.Примечание : если вам это интересно 9Синтаксис 0003 :02d выше, см.