Цена деления штангенциркуля. Штангенциркуль: устройство, принцип работы и применение — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое штангенциркуль. Как устроен штангенциркуль. Как пользоваться штангенциркулем. Какие бывают виды штангенциркулей. Для чего используется штангенциркуль.

Содержание

Что такое штангенциркуль и для чего он используется

Штангенциркуль — это высокоточный измерительный инструмент, который позволяет определять линейные размеры с точностью до десятых и сотых долей миллиметра. Он широко применяется в машиностроении, приборостроении и других отраслях промышленности для контроля качества деталей и изделий.

Основные области применения штангенциркуля:

Измерение наружных и внутренних размеров деталей
Измерение глубины отверстий и пазов
Разметка заготовок
Проверка соответствия размеров деталей чертежам
Контроль качества в процессе производства

Штангенциркуль позволяет быстро и точно производить измерения, что делает его незаменимым инструментом для инженеров, технологов, контролеров ОТК и рабочих на производстве.

Устройство и конструкция штангенциркуля

Штангенциркуль состоит из следующих основных частей:

Штанга с основной миллиметровой шкалой
Рамка с нониусом, перемещающаяся по штанге
Губки для наружных измерений
Губки для внутренних измерений
Линейка глубиномера
Стопорный винт для фиксации рамки

Главный измерительный узел — это сочетание основной шкалы на штанге и нониуса на подвижной рамке. Именно наличие нониуса позволяет повысить точность отсчета до десятых и сотых долей миллиметра.

Принцип действия штангенциркуля

Принцип действия штангенциркуля основан на использовании нониуса — вспомогательной шкалы, позволяющей повысить точность отсчета. Как это работает:

Длина нониуса немного меньше определенного числа делений основной шкалы
Это создает небольшую разницу между делениями основной шкалы и нониуса
При совмещении нулевого деления нониуса с делением основной шкалы можно определить доли миллиметра

Например, если 9 делений основной шкалы равны 10 делениям нониуса, то цена деления нониуса составляет 0,1 мм. Это позволяет измерять размеры с точностью до 0,1 мм.

Как правильно пользоваться штангенциркулем

Чтобы правильно использовать штангенциркуль и получать точные результаты измерений, необходимо придерживаться следующего алгоритма:

Проверьте инструмент на отсутствие повреждений и загрязнений
Убедитесь, что при сомкнутых губках нулевые отметки шкал совпадают
Плотно охватите измеряемую деталь губками штангенциркуля
Зафиксируйте рамку стопорным винтом
Считайте показания по основной шкале до нулевой отметки нониуса
Определите, какое деление нониуса совпадает с делением основной шкалы
Сложите показания основной шкалы и нониуса

При измерении важно не прилагать чрезмерных усилий, чтобы не деформировать деталь или сам инструмент. Измерения рекомендуется проводить несколько раз для повышения точности.

Виды штангенциркулей

Существует несколько основных видов штангенциркулей, различающихся по конструкции и назначению:

Штангенциркуль ШЦ-I — самый простой, для наружных и внутренних измерений
Штангенциркуль ШЦ-II — универсальный, с глубиномером
Штангенциркуль ШЦ-III — с удлиненными губками для измерения пазов
Цифровой штангенциркуль — с электронным отсчетным устройством
Штангенглубиномер — для измерения глубины отверстий
Штангенрейсмас — для разметочных работ

Выбор конкретного вида штангенциркуля зависит от специфики выполняемых измерений и требуемой точности.

Преимущества и недостатки штангенциркуля

Штангенциркуль имеет ряд преимуществ по сравнению с другими измерительными инструментами:

Высокая точность измерений (до 0,01 мм)
Универсальность применения
Простота использования
Надежность конструкции
Относительно невысокая стоимость

Однако у штангенциркуля есть и некоторые недостатки:

Сложность измерения очень малых размеров
Необходимость определенных навыков для точного снятия показаний
Возможность погрешностей из-за параллакса при считывании

Несмотря на эти ограничения, штангенциркуль остается одним из самых востребованных измерительных инструментов в промышленности.

Уход и хранение штангенциркуля

Для обеспечения долгой и точной работы штангенциркуля необходимо соблюдать правила ухода и хранения:

Протирайте инструмент после каждого использования
Смазывайте направляющие штанги тонким слоем масла
Храните в сухом месте при комнатной температуре
Используйте специальный футляр для хранения

Избегайте падений и ударов инструмента
Периодически проводите калибровку

При правильном обращении штангенциркуль может служить долгие годы, сохраняя высокую точность измерений.

Штангенциркуль, 150 мм, цена деления 0.02 мм, металлический, с глубиномером Matrix

Главная
Каталог
Измерительный инструмент
Штангенциркули

Артикул:

316315

Скачать фото

Скачать все архивом

Группа товаров: Ручной инструмент
Длина, мм: 150
Бренд: MATRIX
Размер шага, мм: 0. 02
Вес, кг: 0,308

Станьте нашим партнером и получите уникальные условия сотрудничества

Стать партнеромВойти в аккаунт

С этим товаром покупают

Нож ремонтно-монтажный, трехкомпонентная рукоятка, кнопочный автовыброс, возврат лезвия, 175 мм, 5 запасных лезвий Gross

Степлер мебельный регулируемый (Handwerker), стальной корпус, тип скобы 53, 4-14 мм Gross

Рулетка Autostop,3 м х 16 мм,двухкомпонентный корпус,автоматическая фиксация,Pro Matrix

Угольник, 250 мм, алюминиевый, литой Matrix

Перчатки универсальные комбинированные STYLISH, L Gross

Штангенциркуль ШЦ-II цена деления 0,1. Паспорт

Содержание

1 Назначение.
2 Технические характеристики.
3 Условия эксплуатации.
4 Комплектность.
5 Устройство и принцип работы.
6 Указание мер безопасности.
7 Подготовка к работе.
8 Порядок работы и техническое обслуживание.
9 Правила хранения.
10 Методы и средства поверки.
11 Сведения о консервации.
12 Гарантийные обязательства.

Назначение.

Штангенциркуль ШЦ-II с двусторонним расположением губок предназначен для измерения наружных и внутренних размеров и для разметочных работ.

Применяется для измерений, не требующих высокой точности, абсолютным методом. Допускается оснащать штангенциркули приспособлениями или вспомогательными измерительными поверхностями для расширения функциональных возможностей (измерения высот, уступов и др. ).

Пример обозначения штангенциркуля со значением отсчета по нониусу 0,05мм:

ШЦ-II-200-0,05

Технические характеристики.

2.1. Штангенциркули изготавливаются из углеродистой или нержавеющей стали, со значением отсчёта по нониусу 0,02; 0,05 мм и 0,1 мм, 1 и 2 классов точности с метрической шкалой. Твёрдость измерительных поверхностей инструментальной и конструкционной стали не менее 51,5 HRC. Штангенциркуль оснащен стопорным винтом.

2.2. Технические характеристики приведены в таблице 1.

Таблица 1 — Технические характеристики штангенциркулей ШЦ-II

Модель	Диапазон измерения, мм	Вылет губок для измерения размеров, мм, не менее:		Значение отсчета по нониусу, мм	Предел допускаемой погрешности при значении нониуса, мм
		наружных (верхние губки)	внутренних (нижние губки)		0,02	0,05	0,1 для класса точности
		наружных (верхние губки)	внутренних (нижние губки)		0,02	0,05	1	2
ШЦ-II-200	0-200	37	60	0,02; 0,05; 0,1	±0,02	±0,05	±0,05	±0,1
ШЦ-II-300	0-300	37	60	0,02; 0,05; 0,1	±0,02	±0,05	±0,05	±0,1
ШЦ-II-500	0-500	55	100	0,02; 0,05; 0,1	±0,02	±0,05	±0,1	±0,1
ШЦ-II-600	0-600	55	100	0,02; 0,05; 0,1	±0,02	±0,1	±0,1	±0,1
ШЦ-II-800	0-800	64	125	0,02; 0,05; 0,1	±0,02	±0,1	±0,1	±0,1
ШЦ-II-1000	0-1000	64	125	0,02; 0,05; 0,1	±0,04	±0,1	±0,1	±0,2
ШЦ-II-1500	0-1500	64	125	0,02; 0,05; 0,1	±0,04	±0,1	±0,1	±0,2
ШЦ-II-2000	0-2000	73	150	0,02; 0,05; 0,1	±0,04	±0,1	±0,1	±0,2

Условия эксплуатации.

3.1. Температура рабочего пространства в процессе измерения должна быть (20±15)˚С.

3.2. Относительная влажность воздуха не более 80% при температуре 20˚С.

3.3. Содержание в окружающей среде агрессивных газов и паров не допускается.

Комплектность.

В комплект прибора входят:

штангенциркуль;
футляр;
паспорт.

Устройство и принцип работы.

5.1. Штангенциркуль имеет две шкалы и микровинтовое устройство для тонкой регулировки рамки. Основная шкала нанесена на штанге

c делениями через 1 мм, вторая шкала – на нониусе, который закреплен на рамке. Фиксация рамки производится при помощи стопорного винта. Плавное перемещение рамки обеспечивается пру-жиной, расположенной внутри рамки.

5.2. Наружные размеры измеряются при помощи обеих пар губок. Верхние губки применяются для разметочных работ. Для измерения внутренних размеров используются нижние губки. При таких замерах измеряемый размер равен величине отсчета по шкале штангенциркуля плюс величина губок штангенциркуля.

5.3. Отсчет размеров производится методом непосредственной оценки совпадения деления шкалы с делениями нониуса.

Указание мер безопасности.

Во избежание травматизма необходимо осторожно обращаться с острыми разметочными губками, не проводить измерения на ходу станка, при движении режущего инструмента и при вращении измеряемой детали.

Подготовка к работе.

7.1. Ознакомиться перед началом работы с паспортом на штангенциркуль.

7.2. Протереть штангенциркуль, удалить смазку ветошью, смоченной в бензине (особенно тщательно с измерительных поверхностей), насухо протереть тканью.

7.3. Проверить установку нониуса на ноль. При необходимости совместить нулевые штрихи шкал и нониуса.

Порядок работы и техническое обслуживание.

8.1. В процессе работы и по окончании ее протирать штангенциркуль салфеткой, смоченной в водно-щелочном растворе СОЖ, а затем насухо чистой салфеткой.

8.2. По окончании работы нанести на поверхности штангенциркуля тонкий слой любого технического масла и поместить в футляр.

8.3. В процессе эксплуатации не допускать грубых ударов или падения во избежание изгибов штанги и других повреждений, царапин на измерительных поверхностях, трения измерительных поверхностей об контролируемую деталь.

Правила хранения.

9.1. Хранить штангенциркуль в футляре в сухом отапливаемом помещении при температуре воздуха от +5 до +40˚С и относительной влажности не более 80% при температуре +20˚С.

9.2. При длительном хранении изделия, во избежание возникновения коррозии, помимо смазки штангенциркуля маслом, его необходимо завернуть в бумагу с водоотталкивающей пропиткой.

9.3. Воздух в помещении не должен содержать примесей агрессивных паров и газов.

Методы и средства поверки.

10.1. Поверка штангенциркуля должна производиться методами и средствами, указанными в ГОСТ 8113-85.

10.2. Межповерочный интервал устанавливается потребителем в зависимости от интенсивности эксплуатации штангенциркуля.

Сведения о консервации.

11.1. Штангенциркуль подвергнут консервации в соответствии требованиям ГОСТ 9014-76. Наименование и марка консерванта – масло консервационное К-17.

11.2. Срок хранения прибора без переконсервации – 2 года, при условии хранения в условиях по ГОСТ 15150-69.

Гарантийные обязательства.

Гарантийный срок эксплуатации изделия – 1 год, со дня продажи (получения покупателем) прибора, при условии соблюдения потребителем правил хранения и эксплуатации прибора.

Вверх

Скачать технический паспорт бесплатно можно по ссылке ниже.

Формат: Doc.

Штангенциркуль ШЦ-2 цена деления 0,1. Паспорт

Пожалуйста, введите Ваш E-mail, чтобы получить ссылку для скачивания этого файла

Штангенциркули Made Easy

Содержимое

Что мы знаем о штангенциркуле Вернье?
Проработанные примеры 1 | 2 | 3 | 4 | 5
Решенные проблемы IIT JEE 2003 | 2005 | 2010 | 2013 | 2015 | 2016
Проблемы с упражнениями
Более…

Что мы знаем о штангенциркуле?

Измерение является фундаментальной частью всех научных экспериментов, в том числе Физика.

С одной стороны, наша необъятная Вселенная расширяет это упражнение по измерению до световых лет, а расстояния настолько огромны, что мы не можем видеть их невооруженным глазом. На другая крайность мельчайших расстояний, новые открытия толкают ее до фемтометров (10 ^-15 м) или даже меньше. Эти расстояния так малы что мы не можем видеть их своими глазами. На каждые 1-2 порядка изменение расстояния, наши инструменты для точного измерения расстояний может отличаться. Когда расстояния, которые мы хотим измерить, находятся в диапазоне 10 ^-2 мм до 1 мм, мы используем штангенциркуль и винтовой калибр для точной измерение. В этой статье мы сосредоточимся на этих измерительных приборах. Только.

В классе 11 ^th Physics lab нас учили отвечать на следующие вопросы:

Как найти наименьший счет (LC) или постоянную нониуса?
Как читать показания основной шкалы (MSR) и показания шкалы нониуса (ВСР)?
Как найти ошибку нуля?
Как использовать приведенные выше данные для получения окончательного измерения?

Ответы на эти вопросы «как на вопросы» держали нас довольными в течение 22 лет. Но это не было достаточно для решения проблемы IIT JEE 2016. Нам нужно было выяснить еще кое-что интересно почему такие вопросы:

Почему наименьший счет — это отношение «значения 1 деления основной шкалы» к «общему количеству делений на нониусной шкале».
Почему измеренное значение определяется как: Наблюдаемое значение = MSR + LC×VSR.
Почему ошибка нуля вычитается из наблюдаемого значения, т. е. истинное значение = измеренное значение — ошибка нуля.

Начнем наше путешествие с штангенциркуля без нулевой погрешности. Когда двое челюсти закрыты, отметка 0 ^th на шкале нониуса совмещена с отметкой 0 ^th отметка на основной шкале, как показано на рисунке 1. Также обратите внимание, что 10 ^th отметка на нониусной шкале совпадает с отметкой 9 ^th на основной шкале.

Одно главное деление шкалы (МСД) – это расстояние между двумя последовательными отметки на основной шкале. На рисунке 1 указано, что 1 СКО равен до 1 мм. Одно деление шкалы Вернье (VSD) — это расстояние между двумя последовательные отметки по шкале нониуса. Принято, что 10 ВСД = 9 МСД. Таким образом, 1 ВСД = (9/10) СКО = 0,9мм, т. е. расстояние между двумя последовательными отметок по шкале нониуса составляет 0,9 мм.

Рисунок 1: Штангенциркули без ошибки нуля

Теперь давайте воспользуемся этим штангенциркулем для измерения диаметра D мраморного шара. (мраморные шары обычно имеют D = 1/2 дюйма). Измерение показано на рисунке 2. Здесь x _m0 — расстояние между губкой, прикрепленной к основной шкале (левая челюсть), и отметкой 0 ^th на основной шкале, а x _v0 — расстояние между челюсть прикреплена к шкале Вернье (правая челюсть) и 0,^th отметка по нониусной шкале. Обратите внимание, что диаметр определяется выражением \начать{выравнивать} Д=х_{м0}+х \end{выравнивание} где x — расстояние между отметкой 0 ^th на основной шкале и правой челюстью.

Теперь обратите внимание, что отметка 7 ^th на нониусной шкале совпадает с 1,9 см на основной шкале. Эта точка называется точкой совпадения . Расстояние между отметкой 0 ^th на главной шкале и точкой совпадения составляет x _м, а расстояние между отметкой 0 ^й отметка по шкале нониуса и точка совпадения х _v . Таким образом, \начать{выравнивать} х+х_{v0}+х_в=х_м \end{выравнивание} Подставьте x из приведенного выше уравнения в первое уравнение, чтобы получить \начать{выравнивать} D=(x_m-x_v)-(x_{m0}-x_{v0}) \end{выравнивание}

Величина ($x_{m0}-x_{v0}$) называется ошибкой нуля штангенциркуля. Отрицательная нулевая ошибка называется коррекция нуля . Обратите внимание, что $x_{m0}=x_{v0}$ в штангенциркуле без нулевой ошибки (что верно в данном случае). Также, $x_m=19\mathrm{MSD}=19$ мм и $x_v=7\mathrm{VSD}=7(9/10)=6,3$ мм. Подставьте эти значения в приведенное выше уравнение, чтобы получить D = 12,7 мм = 1,27 см (полдюйма мрамора).

Рисунок 2: Измерение диаметра мраморного шара

Есть еще один более простой способ получить измеренное значение. Показание основной шкалы (MSR) – это первое показание на основной шкале непосредственно слева от нуля Шкала нониуса (в данном примере MSR = 12 мм). Показание нониуса (VSR) – это отметка на нониусной шкале, точно совпадающая с отметкой на основной масштаб (VSR = 7 в этом примере). Обратите внимание, что на основной шкале между отметкой MSR (т.е. отметка на основной шкале сразу слева от нуля шкалы нониуса) и точка совпадения. Таким образом, \начать{выравнивать} x_v&=\mathrm{VSR}\times\mathrm{VSD},\\ x_m&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{MSD} \end{выравнивание} Соответствующие значения параметров для ошибок нуля равны \начать{выравнивать} x_{v0}&=\mathrm{VSR_0}\times\mathrm{VSD},\\ x_{m0}&=\mathrm{MSR_0}+\mathrm{VSR_0}\times\mathrm{MSD} \end{выравнивание} Подставьте в выражение вместо D, чтобы получить \начать{выравнивать} D=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}-\mathrm{Ноль\,Ошибка} \end{выравнивание} где LC = MSD — VSD называется наименьший счет или постоянная Вернье . Это наименьшая длина, которую можно точно измерить штангенциркулем. Для данных штангенциркулей \начать{выравнивать} \mathrm{LC}&=\mathrm{MSD}-\mathrm{VSD} \без номера\\ &=1-9/10=0,1\,\mathrm{мм}, \\ D&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}\nonumber\\ &=12+7(0,1)=1,27\,\mathrm{мм} \end{выравнивание}

Обратите внимание, что штангенциркуль можно использовать для измерения (1) внешних размеров, таких как диаметр сферы или грани куба (2) внутренние размеры, такие как внутренний диаметр полого цилиндра и (3) глубина полого цилиндра.

Разработанные примеры

Пример 1

Губки штангенциркуля, показанного на рисунке, соприкасаются друг с другом. Найдите погрешность нуля этого штангенциркуля.

Рисунок 3: (Пример 1) Штангенциркули с положительной погрешностью нуля

Решение: Наименьшее количество заданных штангенциркулей равно \начать{выравнивать} \mathrm{LC}&=\mathrm{MSD}-\mathrm{VSD} \\ &=1-9/10=0,1\,\mathrm{мм} \end{выравнивание}

Показание основной шкалы MSR ₀ = 0 мм, а показания шкалы нониуса ВСР ₀ = 3. Таким образом, \начать{выравнивать} \mathrm{Ноль\, Ошибка}&=\mathrm{MSR_0}+\mathrm{VSR_0}\times\mathrm{LC} \\ &=0+3\умножить на 0,1=0,3\,\mathrm{мм} \end{выравнивание}

Пример 2

Штангенциркуль из примера 1 используется для измерения ребра куба. Показания показаны на рисунке 4. Найдите длину ребра куб.

Рисунок 4: (Пример 2) Измерение ребра куба

Решение: Показания MSR = 25 мм и VSR = 7. Таким образом, \начать{выравнивать} a&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}- \mathrm{Ноль\, Ошибка} \\ &=25+7\times 0,1-0,3=25,4,\mathrm{мм}. \end{выравнивание}

Пример 3

Губки штангенциркуля, показанного на рис. 5, соприкасаются с друг друга. Найдите погрешность нуля этого штангенциркуля.

Рисунок 5: (Пример 3) Штангенциркули с отрицательной погрешностью нуля

Решение: Это интересная проблема. Что такое MSR ₀? Это первое показание на основной шкале сразу слева от нуля шкалы нониуса. Но на основной шкале нет отметок перед нулем шкалы нониуса. Мы утверждаем, что MSR ₀ = -1 мм (обратите внимание, почему MSR ₀ не равно -2 мм? Показания нониуса VSR ₀ = 4, а наименьшее значение LC = 0,1 мм. Подставьте эти значения получить, \начать{выравнивать} \mathrm{Ноль\, Ошибка}&=\mathrm{MSR_0}+\mathrm{VSR_0}\times\mathrm{LC}\\ &=-1+4\умножить на 0,1=-0,6\,\mathrm{мм}. \end{выравнивание}

Пример 4

Штангенциркуль из примера 3 используется для измерения ребра куба. Показания показаны на рисунке 6. Найдите длину ребра куба.

Рисунок 6: (Пример 4) Измерение длины ребра куба

Решение: Показания MSR = 24 мм и VSR = 8. Таким образом, \начать{выравнивать} a&=\mathrm{MSR+VSR\times LC-Zero\,Error} \\ &=24+8(0,1)-(-0,6)=25,4\,\mathrm{мм}. \end{выравнивание}

Пример 5

Чему равен LC штангенциркуля, изображенного на рисунке 7?

Рисунок 7: (Пример 5) Наименьшее количество штангенциркулей

Решение: Одно деление основной шкалы равно 1 СКО = 1 мм. Поскольку 5 VSD = 4 MSD, мы получаем 1 ВСД = (4/5) СКО = 0,8. Таким образом, наименьшее количество этих суппортов LC = MSD — VSD = 1 — 0,8 = 0,2 мм.

Решенные проблемы IIT JEE

Проблема IIT JEE 2003

N делений на основной шкале штангенциркуля совпадают с (N + 1) делениями на его шкале. Если каждое деление на основной шкале соответствует единице, определите наименьшее количество инструментов.

Решение: Учитывая, что главное деление шкалы (МСД) штангенциркуля равно $N=a$. Так как (N + 1) делений нониуса (VSD) равны N делениям основной шкалы, получаем \начать{выравнивать} 1\,\mathrm{VSD}=\frac{N}{N+1}\mathrm{MSD}=\frac{Na}{N+1} \end{выравнивание} Наименьшее количество дается \начать{выравнивать} \mathrm{LC}=1\mathrm{MSD}-1\mathrm{VSD}=a/(N+1). \end{выравнивание}

Проблема от IIT JEE 2005

Ребро куба измеряется штангенциркулем (9 делений основная шкала равна 10 делениям шкалы Вернье и 1 основной шкале деление 1 мм). Показания основного деления шкалы – 10, а первое деление Шкала нониуса оказалась совпадающей с основной шкалой. Масса куб 2,736 г. Рассчитайте плотность в г/см ³ с точностью до значащих цифр.

Решение> Из приведенных данных одно главное деление шкалы (СКО) равно 1 СКО = 1 мм. Поскольку 10 делений шкалы Вернье (VSD) равны 9СКО, получаем 1 СКО = 9/10 ССО = 0,9 мм. Наименьшее количество (LC) определяется как LC = 1 MSD — 1 VSD = 1,0 — 0,9 = 0,1 мм.

Учитывая, что показание основной шкалы (MSR) равно 10, а показание шкалы Vernier (VSR) равно 1. Измеренное значение края определяется выражением \начать{выравнивать} a&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC}\\ &=10+1\умножить на 0,1=10,1\,\mathrm{мм}. \end{выравнивание}

Измерение a имеет три значащих цифры. Объем куба V = a ³ = 1,03 см ^{3}
\end{выравнивание}
(после округления до трех значащих цифр).}

Проблема из IIT JEE 2010

Штангенциркули имеют отметки 1 мм на основной шкале. имеет 20 равных деления шкалы нониуса, соответствующие 16 делениям основной шкалы. Для этого Штангенциркули, наименьшее количество

0,02 мм
0,05 мм
0,1 мм
0,2 мм

Решение: Для данных штангенциркулей одно главное деление шкалы (MSD) 1 СКО = 1 мм.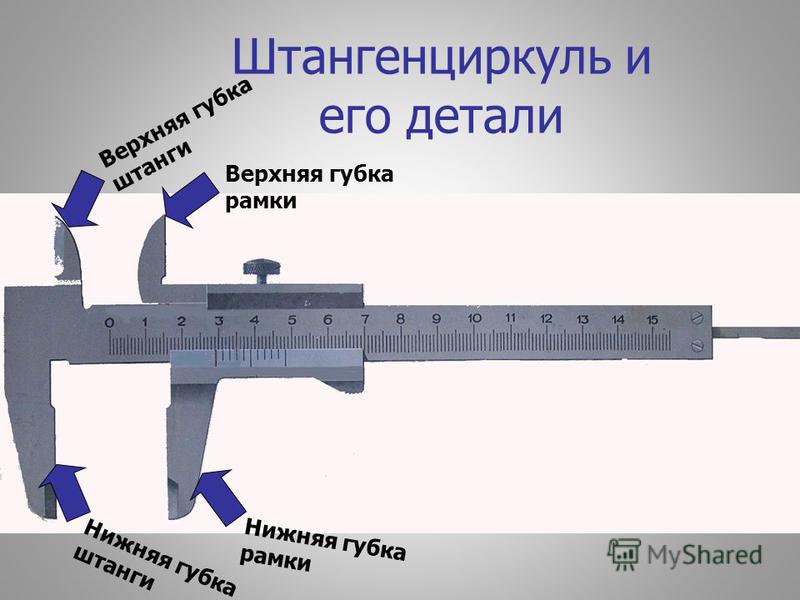 Так как 20 делений шкалы нониуса (ЧД) равны 16 СКО, то получаем 1 ДСП = 16/20 СКО = 0,8 мм. Количество лизингов определяется как LC = 1 MSD — 1 VSD = 1 — 0,8 = 0,2 мм.

Проблема от IIT JEE 2013

Диаметр цилиндра измеряют штангенциркулем без нулевая ошибка. Установлено, что ноль шкалы нониуса лежит между 5,10 см и 5,15 см основной шкалы. Шкала нониуса имеет 50 делений, соответствующих 2,45 см. 24 деление шкалы нониуса в точности совпадает с одним из основных делений шкалы. Диаметр цилиндра

5,112 см
5,124 см
5,136 см
5,148 см

Решение: Из приведенных данных одно деление основной шкалы (СКО) и одно деление шкалы нониуса (ЧС) составляют 1 СКО = 5,15 — 5,10 = 0,05 см и 1 СКО = 2,45/50 = 0,049 мм. Наименьшее количество данных штангенциркулей составляет LC = 1 MSD — 1 VSD = 0,001 см.

Для данного измерения показание основной шкалы (MSR) составляет 5,10 см, а Отсчет нониуса (VSR) равен 24. Следовательно, диаметр D цилиндра равен \начать{выравнивать} D&=\mathrm{MSR}+\mathrm{VSR}\times\mathrm{LC} \\ &=5,10+24\умножить на 0,001=5,124\,\mathrm{см}. \end{выравнивание}

Проблема от IIT JEE 2015

Рассмотрим штангенциркуль, у которого каждый 1 см на основной шкале равен разделенный на 8 равных делений и винтовой датчик со 100 делениями на его круглая шкала. В штангенциркуле совпадают 5 делений шкалы нониуса с 4 делениями на основной шкале и на винтовом манометре, один полный вращение круговой шкалы перемещает ее на два деления по линейной шкале. Затем,

Если шаг калибра в два раза больше наименьшего значения штангенциркуля, наименьшее значение калибра составляет 0,01 мм.
Если шаг калибра винта в два раза меньше наименьшего значения нониуса штангенциркуль, наименьший отсчет калибра 0,005 мм.
Если наименьший отсчет линейной шкалы винтового калибра в два раза больше наименьшего количество штангенциркулей, наименьшее количество винтовых калибров составляет 0,01 мм.
Если наименьшее значение линейной шкалы калибра-винта в два раза превышает наименьшее значение шкалы штангенциркуля, наименьшее значение калибра-винта составляет 0,005 мм.

Решение: В данных штангенциркулях каждый 1 см делится поровну на 8 основных делений шкалы (СКО). Таким образом, 1 СКО = 1/8 = 0,125 см. Далее 4 основных деления шкалы совпадают с 5 делениями шкалы нониуса (VSD), т. е. 4 MSD = 5 VSD. Таким образом, 1 ВСД = 4/5 СКО = 0,1 см. Наименьшее количество штангенциркулей нониус определяется как LC = 1 MSD — 1 VSD = 0,125 — 0,1 = 0,025 см.

В винтовом калибре пусть l будет расстоянием между двумя соседними делениями на линейной шкала. Шаг p винтового калибра — это пройденное расстояние по линейной шкале. когда он делает один полный оборот. Так как круговая шкала смещается на два деления по линейный масштаб, когда он делает один полный оборот, мы получаем p = 2l. Наименьшее количество калибра винта определяется как отношение шага к числу делений на круговая шкала (n), т. е. \начать{выравнивать} \mathrm{lc}=p/n=2l/100=l/50. \end{выравнивание}

Если $p=2\mathrm{LC}=2(0,025)=0,05$ см, то $l=p/2=0,025$ см. Подставьте в приведенное выше уравнение, чтобы получить наименьшее значение калибра винта lc = 0,005 мм.

Если $l=2\mathrm{LC}=2(0,025)=0,05$ см, то приведенное выше уравнение дает lc = 0,01 мм.

Проблема из IIT JEE 2016

Есть два штангенциркуля, каждый из которых имеет 1 см, разделенный на 10. равные деления на основной шкале. Шкала нониуса одного из штангенциркулей (C ₁) имеет 10 равных делений, соответствующих 9деления основной шкалы. Вернье шкала другого штангенциркуля (C ₂ ) имеет 10 равных делений, соответствующих 11 основных делений шкалы. Показания двух штангенциркулей показаны на фигура. Измеренные значения (в см) штангенциркулем C ₁ и C ₂ соответственно равны

2,85 и 2,82
2,87 и 2,83
2,87 и 2,86
2,87 и 2,87

Решение: В обоих суппортах C ₁ и C ₂ , 1 см делится на 10 равных деления на основной шкале. Таким образом, 1 деление по основной шкале равно $x_{m1}=x_{m2}=1/10=0,1$ см. В штангенциркуле С ₁ 10 равных делений шкалы нониуса равны 9 делениям основной шкалы. Таким образом, 1 деление по шкале нониуса C ₁ равно $x_{v1}=9x_{m1}/10=0,09$ см. В штангенциркуле С ₂ 10 равных делений шкалы нониуса равны 11 делениям основной шкалы. Таким образом, 1 деление по шкале нониуса С ₂ равно $x_{v2}=11x_{м2}/10=0,11$ см.

Пусть отсчет основной шкалы равен MSR и v ^-е-е деление шкалы нониуса совпадает с m ^-м-м делением основной шкалы (m отсчитывается за MSR). Значение, измеренное этим штангенциркулем, равно \начать{выравнивать} X&=\mathrm{MSR}+x &=\mathrm{MSR}+mx_m-vx_v \end{выравнивание}

В суппортах C ₁, MSR ₁ = 2,8 см, m ₁ = 7 и v ₁ = 7, а в суппортах C ₂ , MSR ₂ = 2,8 см, м ₂ = 8 и v ₂ = 7. Подставьте эти значения в приведенное выше уравнение, чтобы получить \начать{выравнивать} X_1&=\mathrm{MSR}_1+m_1 x_{m1} -v_1 x_{v1}=2,87\,\mathrm{см}\\ X_2&=\mathrm{MSR}_2+m_2 x_{m2} -v_2 x_{v2}=2,83. \end{выравнивание}

Упражнения

Губки штангенциркуля, показанного на рис. 8, соприкасаются с друг друга. Найдите погрешность нуля этого штангенциркуля. Рисунок 8: Нулевая погрешность штангенциркуля
Ответ: 1,9 мм
Губки штангенциркуля, показанного на рисунке 9, соприкасаются друг с другом. Найдите погрешность нуля этого штангенциркуля. Рисунок 9: Нулевая погрешность штангенциркуля
Ответ: -1,2 мм
Погрешность нуля штангенциркуля, показанного на рис. 10, составляет 0,9 мм. Какой диаметр сферы измеряется на рисунке 10. Рисунок 10: Измерение диаметра сферы ошибочным штангенциркулем
Ответ: 3,14 см.
Погрешность нуля штангенциркуля, показанного на рис. 11, составляет -0,5 мм. Какой диаметр измеряемого шара на рисунке? Рисунок 11: Измерение диаметра сферы ошибочным штангенциркулем
Ответ: 3,14 см.
Выберите неверное утверждение для нулевой ошибки и нулевой коррекции
1. Если ноль шкалы нониуса не совпадает с нулем основной шкале, то говорят, что прибор имеет нулевую ошибку.
2. Ошибка нуля положительна, если ноль шкалы нониуса лежит слева от ноль основной шкалы.
3. Коррекция нуля имеет величину, равную ошибке нуля, но противоположный знак к нулевой ошибке.
4. Все вышеперечисленное неверно.
Ответ: (В)
Что такое постоянная Вернье?
1. Это значение одного основного деления шкалы, деленное на общее количество деления на основной шкале.
2. Это значение одного деления шкалы Вернье, деленное на общее количество деления по шкале Вернье.
3. Это разница между значением одного деления основной шкалы и одного деления шкалы нониуса.
4. Это также наименьшее значение шкалы Вернье.
Ответ: (С), (Д)
Наименьшее деление на основной шкале штангенциркуля – 1 мм. 10 делений шкалы нониуса совпадают с 9деления основной шкалы. При измерении длины линии нулевая отметка шкалы нониуса находится между 10,2 см и 10,3 см. и третье деление шкалы нониуса совпадают с делением основной шкалы. (а) Определите наименьшее количество штангенциркулей и (б) длину линии.
Ответ: 0,01 см, 10,23 см.
Основная шкала штангенциркуля откалибрована в миллиметрах. 19 делений основной шкалы по длине равны 20 делениям нониуса. В при измерении этим прибором диаметра цилиндра основная шкала показывает 35 деления и 4-е деление нониуса совпадает с делением основной шкалы. Найдите (а) наименьшее количество штангенциркулей и (б) радиус цилиндра.
Ответ: 0,005 см, 1,76 см.
Наименьший отсчет штангенциркуля — 0,01 см. Когда две челюсти инструмента соприкасаются друг с другом 5 деление нониуса совпадают с делением основной шкалы, а ноль шкалы нониуса лежит левее нуля основной шкалы. Кроме того, при измерении диаметра сферы нулевая отметка шкалы нониуса лежит между 2,4 см и 2,5 см, а деление 6 ^th нониуса совпадает с делением основной шкалы. Вычислите диаметр шара.
Ответ: 2,51 см.
В эксперименте углы должны быть измерены с помощью инструмент. 29 делений основной шкалы точно совпадают с 30 делениями шкале Вернье. Если наименьшее деление основной шкалы составляет полградуса (= 0,5 градуса), то наименьшее значение инструмента равно (AIEEE 2009).
1. одна минута
2. полминуты
3. один градус
4. полградуса
Ответ: (А)
Ученик измерил длину стержня и написал, что она равна 3,50 см. Какой прибор он использовал для измерения?
1. Измерительная шкала
2. Штангенциркуль, у которого 10 делений шкалы нониуса совпадают с 9 делений в основной шкале и основная шкала имеет 10 делений в 1 см
3. Винтовой калибр, имеющий 100 делений по круговой шкале и шаг, как 1 мм
4. Винтовой калибр с 50 делениями по круговой шкале и шагом 1 мм
Ответ: (В)
19 делений на основной шкале штангенциркуля совпадают с 20 делений по шкале Вернье. Если каждое деление на основной шкале равно 1 см, определяют наименьший счет прибора.
Ответ: 0,05 см
Угол призмы измеряется спектрометром. Основная шкала показание составляет 58,5 градусов, а по шкале Вернье – 9подразделения. Учитывая, что 1 дивизия по основной шкале соответствует 0,5 градуса, а 30 делений по шкале Вернье соответствуют с 29 делениями на основной шкале. Угол призмы из приведенных выше данных есть (AIEEE 2012)
1. 58,59 градуса
2. 58,77 градуса
3. 58,65 градусов
4. 59 градусов
Ответ: (С)
1 см по основной шкале штангенциркуля делится на 10 равных части. Если 10 делений нониуса совпадают с 8 малыми делениями основной шкалы, то наименьшее количество штангенциркулей равно
1. 0,01 см
2. 0,05 см
3. 0,005 см
4. 0,02 см
Ответ: (Г)
Губки штангенциркуля нониуса касаются внутренней стенки калориметра. без излишнего давления. Положение нуля шкалы нониуса на основной шкале читает 3,48 см. 6-е деление шкалы нониуса совпадает с делением основной шкалы. Нониусная постоянная штангенциркуля равна 0,01 см. Найдите фактический внутренний диаметр калориметра, если видно, что погрешность нуля шкалы нониуса составляет -0,03 см.
1. 3,37 см
2. 3,57 см
3. 3,42 см
4. 3,54 см
Ответ: (В)
В передвижном микроскопе 1 см по основной шкале делится на 20 равных делений, а на шкале нониуса 50 делений. Каков наименьший счет микроскопа?
Ответ: 0,001 см
Постоянная Вернье передвижного микроскопа равна 0,001 см. Если 49 делений основной шкалы совпадают с 50 делениями шкалы Вернье, то значение 1 основное деление шкалы
1. 0,1 мм
2. 0,4 мм
3. 0,5 мм
4. 1 мм
Ответ: (С)
Тонкая металлическая полоска штангенциркуля нониуса движется сверху вниз до дна таким образом, чтобы он едва касался поверхности стакана. Главный отсчет шкалы штангенциркуля составляет 6,4 см, тогда как его постоянная нониуса составляет 0,1 мм. Четвертое деление шкалы нониуса совпадает с делением основной шкалы. фактическая глубина стакана (при совпадении нуля нониуса с нулем основного шкала)
1. 6,64 см
2. 6,42 см
3. 6,44 см
4. 6,13 см
Ответ: (С)
В инструменте есть 25 делений по шкале нониуса, которые совпадает с 24 делениями основного масштаба. 1 см по основной шкале делится на 20 равных частей. Наименьшее количество инструментов
1. 0,002 см
2. 0,05 см
3. 0,001 см
4. 0,02 см
Ответ: (А)
1 см основной шкалы штангенциркуля разделен на 10 делений. Если наименьшее количество штангенциркулей составляет 0,005 см, то шкала нониуса должна иметь
1. 10 отделов
2. 20 дивизий
3. 25 дивизий
4. 50 делений
Ответ: (В)
В штангенциркуле есть 10 делений на шкале нониуса и 1 см по основной шкале делится на 10 частей. При измерении длины, ноль шкалы Вернье находится сразу перед отметкой 1,8 см и 4-м делением шкалы Вернье совпадает с основным делением шкалы. Значение длины является
1. 1,804 см
2. 1840 см
3. 1800 см
4. Ни один из этих
Ответ: (D)
Диаметр стального шарика измеряют штангенциркулем, который имеет деления 0,1 см на основной шкале (MS), а 10 делений на его нониусной шкале (VS) соответствуют 9 делам на основной шкале. Три таких измерения для мяча: (1) MSR = 0,5 см, VSD = 8 (2) MSR = 0,5 см, VSD = 4 (3) MSR = 0,5 см, VSD = 6. Если погрешность нуля составляет -0,03 см, то средний скорректированный диаметр равен
1. 0,53 см
2. 0,56 см
3. 0,59 см
4. 0,52 см
Ответ: (С)
Каждое деление на основной шкале равно 1 мм. Который из перечисленных Весы нониуса дают константу нониуса, равную 0,01 мм?
1. 9 мм разделен на 10 делений
2. 90 мм, разделенный на 100 делений
3. 99 мм, разделенный на 100 делений
4. 9 мм, разделенный на 100 делений
Ответ: (К)
В штангенциркуле 1 см основной шкалы делится на 20 равных части. 19 делений основной шкалы совпадают с 20 делениями нониусной шкалы. Найдите наименьшее количество инструментов.
Ответ: 0,025 см
В штангенциркуле одно основное деление шкалы — это х см и n делений. нониуса совпадают с (n-1) делениями основной шкалы. Наименьшее количество (в см) суппортов составляет (АМУ ПМТ 2009 г.)
1. $(n-1)x/n$
2. $nx/(n-1)$
3. $x/n$
4. $x/(n-1)$
Ответ: (С)

Подробнее…

Вы можете сделать недорогие штангенциркули, нарисовав основную шкалу и шкалу нониуса на полоски бумаги и т. д. Линии на основной шкале могут быть разделены на 1 см. Чтобы получить линии на шкале нониуса, вы можете разделить 9 делений основной шкалы на 10 равных делений (это проверка ваших знаний по геометрии).

Возьмите чешую длиной 30 см и другую чешуйку длиной 15 см. Более крупный масштаб — это основная шкала ваших штангенциркулей, а меньшая шкала — шкала нониуса. Ничья 30 параллельные линии на основной шкале на расстоянии 1 см каждая. Нарисуйте 10 параллельных линий на Шкала нониуса по 0,9 см каждая. Ваш штангенциркуль готов (см. рис. 12). Возьмите другую шкалу (или любую другую прямоугольную деталь) в качестве опоры. Объект, длина которого измеряется, помещается между опорой и нониусной шкалой.

Рисунок 12: Ваши штангенциркули

Вернье-двигатель — это ракетный двигатель, используемый на космическом корабле для точной регулировки скорость космического корабля. Название происходит от штангенциркуля нониуса (названного в честь Pierre Vernier), которые имеют первичную шкалу для валовых измерений и вторичную шкала для точных измерений.

Каталожные номера

Как пользоваться штангенциркулем. https://www.miniphysics.com/how-to-read-a-vernier-caliper.html. Доступ: 2017-07-15.
С помощью штангенциркуля и микрометрического винта измерять. http://www.phy.uct.ac.za/courses/phylab1/vernier. Доступ: 2017-07-15.
Проблемы с штангенциркулем и решениями. https://examinationsecrets.wordpress.com/2017/04/28/vernier-callipers-problems/. Доступ: 2017-07-15.
Штангенциркули в онлайн-лабораториях университета Амрита. http://amrita.olabs.edu.in/?sub=1&brch=5&sim=16&cnt=1. Доступ: 2017-07-15.
Видео на Youtube о штангенциркуле Edunovus. https://youtu.be/ySRN3yuZUT0. YouTube.

Как считывать показания штангенциркуля (дюймы и мм) 0,05 мм, 0,001 дюйма, 1/128 дюйма и т. д.

Для считывания показаний штангенциркуля требуется больше действий, чем для считывания показаний штангенциркуля со шкалой или считывания показаний цифрового штангенциркуля. Пользователям приходится вручную рассчитывать обе шкалы (основную шкалу и нониусную шкалу ). Вычисление шкалы нониуса, в частности, контрастирует с чтением этих двух типов штангенциркуля.

Ваши глаза должны быть внимательны при определении того, какая из них является выровненной линией. Это основная вещь, когда вы читаете штангенциркуль. Это требует хорошего зрения. Если вы этого не сделаете, ваши измерения будут неверными.

Во многих случаях вы можете увидеть наш список рекомендуемых штангенциркулей, один штангенциркуль обычно имеет градуировку в дюймах и миллиметрах. Это означает, что вы можете получить две версии показаний, будь то в миллиметрах или дюймах. Но некоторые продукты также могут поставляться только с миллиметровой или дюймовой градуировкой.

Если вы видите на рынке, модели с дюймовым отсчетом обеспечивают разрешение до 0,001 дюйма или 1/128 дюйма (британская единица измерения). С другой стороны, метрические модели обеспечивают разрешение до 0,02 мм, 0,05 мм или 0,1 мм (метрическая единица измерения). Изменение этих разрешений приводит к различным системам градуировки. Более того, при одном и том же разрешении система градации также может быть разной.

В этом посте мы обсудим, как считывать показания штангенциркуля с такими системами деления. Будь то мм (миллиметры) или дюймы, мы рассмотрим их здесь. Из этого поста вы узнаете о системах градации, которые мы имеем в виду. Прежде чем идти дальше, вы должны сначала узнать, что такое общая формула и как читать нулевую ошибку.

Общая формула

В основном правило большого пальца при считывании показаний штангенциркуля одинаково как для дюймовой, так и для миллиметровой шкалы.

Окончательный результат = показание основной шкалы + показание нониусной шкалы – ошибка нуля

Показание основной шкалы – это количество делений нониусной шкалы, которые полностью проходят через нулевую линию нониусной шкалы. В то время как показание нониусной шкалы — это количество делений нониусной шкалы от 0 до выровненной линии.

Вы могли видеть следующую картину. Первая (левая) желтая линия показывает, сколько делений прошло отметку нониуса 0. При этом прошло 42 дивизии. В то время как вторая (правая) пожелтевшая линия показывает выровненную линию. Основная шкала — красная; нониусная шкала синяя. Нажмите на картинку для увеличения в новой вкладке.

Таким образом, показание основной шкалы зависит от шкалы нониуса, а показание шкалы нониуса зависит от выровненной линии. Что такое выровненная линия? Всякий раз, когда вы перемещаете нониусную шкалу, должны быть две линии (одна от основной шкалы и одна от нониусной шкалы), которые полностью образуют единую прямую линию.

Нониусная шкала делит наименьшее деление основной шкалы на определенное количество делений, чтобы обеспечить желаемое разрешение.

Если основная шкала имеет 40 делений на дюйм, это означает, что каждое наименьшее деление на основной шкале имеет значение 0,025″.

Наименьшее значение деления основной шкалы = 1″ : 40 делений = 0,025″

Для получения разрешения 0,001″ нониусная шкала должна обеспечивать 25 делений. Это потому, что наименьшее деление основной шкалы, деленное на 25, составляет 0,001 дюйма.

Наименьшее значение деления нониусной шкалы = 0,025″ : 25 делений = 0,001″

Кроме того, расчет основного и нониусного показаний учитывает нулевую ошибку, хотя в большинстве случаев нулевая ошибка равна «0», и вы можете избегай это.

Что такое нулевая ошибка?

Перед считыванием показаний штангенциркуля необходимо проверить, существует ли ошибка нуля или нет. Если он появляется, вы должны выяснить это при расчете / чтении окончательного измерения. Продолжайте измерять, не принимая во внимание погрешность нуля, вы измеряете неправильно.

Ошибка нуля — это состояние, при котором нулевые отметки обеих шкал (основной шкалы и нониуса) не образуют совпадающую линию. Это происходит, когда вы правильно закрываете обе челюсти (неподвижную и подвижную).

а. Отсутствие ошибки нуляb. Отрицательная ошибка нуля c. Ошибка положительного нуля

Возможны 3 варианта: отсутствие ошибки нуля, отрицательная ошибка нуля и положительная ошибка нуля.

Отрицательная ошибка нуля – это когда нулевая отметка нониусной шкалы находится слева от нулевой отметки основной шкалы.
Положительная ошибка нуля — это когда нулевая отметка нониусной шкалы находится справа от нулевой отметки основной шкалы.
Нет ошибки нуля означает, что это полностью выровненная линия.

Если вы обнаружите несоосность (положительную или отрицательную ошибку нуля), вы должны включить ее в расчет окончательного измерения.

Как считывать ошибку нуля штангенциркуля

По сути, считывать ошибку нуля — это то же самое, что и считывать показания штангенциркуля, как обычно. Для измерения требуется как основная, так и нониусная шкала. Однако это может сбивать с толку, когда вы сталкиваетесь с ошибкой отрицательного нуля. К счастью, создав воображаемую дополнительную шкалу, как на следующем изображении, вы можете начать помещать измерение в фиксированную формулу. Как прочитать погрешность нуля штангенциркуля; нажмите на картинку для увеличения в новой вкладке.

Первый шаг , который вам необходимо сделать, это определить значение каждого наименьшего деления как для основной шкалы, так и для нониуса. Определите, является ли масштаб имперским (дюймы) или метрическим (мм). В этом случае указанная выше шкала — дюймы. Глядя на градуировку, мы знаем, что основная шкала имеет 20 делений на дюйм, а нониусная шкала имеет 50 делений. Затем

Основное значение шкалы/деление = 1 дюйм : 20 делений = 0,05″/деление

Вернье значение шкалы/деление = 0,05″ : 50 делений = 0,001″/деление

Второй шаг заключается в подсчете основной и нониусной шкалы, а затем их суммировании.

Основная шкала = −1 × 0,05″/дел = −0,05″

Нониусная шкала = 47 × 0,001″/дел = 0,047″ есть более короткий способ чтения нулевой ошибки. Но мы просто хотим убедиться, что вы знаете это основное измерение, прежде чем переходить к упрощенному методу.

Более короткий путь — чтение в обратном порядке. Если вы обнаружите, что шкала нониуса градуирована слева направо. Вы можете себе представить, что приращение (от 0 до 50) градуировано справа налево. Просто измерьте нулевую погрешность непосредственно по нулевой отметке нониусной шкалы, и вы получите ответ. Но этот метод работает только тогда, когда погрешность нуля меньше наименьшего значения деления основной шкалы.

Как читать показания штангенциркуля в миллиметрах (метрические)

Когда речь идет о метрическом штангенциркуле, доступны несколько разрешений: 0,02 мм, 0,05 мм и 0,1 мм. Разное разрешение имеет разную модель градации. Вскоре вы узнаете модели выпускных, которые мы имеем в виду, и как их читать.

Мы называем их модель 1 (разрешение 0,02 мм), модель 2 (разрешение 0,05) и модель 3 (разрешение 0,1 мм). Среди этих моделей модель 1 является наиболее используемой и легкодоступной на рынке.

1. Показания штангенциркуля модели 1 (разрешение 0,02 мм)

Эта модель имеет 10 делений на см на основной шкале и 50 делений на нониусной шкале . Примером штангенциркуля, поставляемого с этой моделью, является штангенциркуль Mitutoyo 532-119.

См. следующее изображение, когда эта градуированная модель не показывает ошибку нуля. Как прочитать ошибку нуля штангенциркуля; нажмите на картинку, чтобы открыть ее в новой вкладке.

Следовательно, наименьшее показание на основной шкале:

1 см : 10 делений = 1 мм

И наименьшее значение шкалы нониуса:

1 мм : 50 делений = 0,02 мм

погрешность)

Основная шкала = 10 × 1 мм = 10 мм

Нониусная шкала = 3 × 0,02 мм = 0,06 мм

Ошибка нуля = 0 мм

Окончательное показание = 10 мм + 0,06 мм − 0,06 мм 10,06 мм

Показания метрического штангенциркуля Модель 1 Случай 2 (с отрицательной погрешностью нуля)

Основная шкала = −1 × 1 мм = −1 мм

Нониусная шкала = 47 × 0,02 мм = 0,94 мм

Ошибка нуля = −1 мм + 0,94 мм = −0,06 мм

3 Основная шкала = 12 × 1 мм = 12 мм

Нониусная шкала = 13 × 0,02 мм = 0,26 мм

Ошибка нуля = −0,06 мм

Итоговое значение = 12 мм + 0,26 мм − (−0,06 мм) = 12,32 мм Показания метрического штангенциркуля, модель 1, случай 3 (с положительной погрешностью нуля)

Основная шкала = 0 × 1 мм = 0 мм

Нониусная шкала = 3 × 0,02 мм = 0,06

Ошибка нуля = 0 мм + 0,06 мм = 0,06 мм

Основная шкала = 18 × 1 мм = 18 мм

Нониусная шкала = 37 × 0,02 мм = 0,74 мм

Ошибка нуля = 0,06 мм

Окончательное показание = 18 мм + 0,74 мм − 0,06 мм = 18,68 мм )