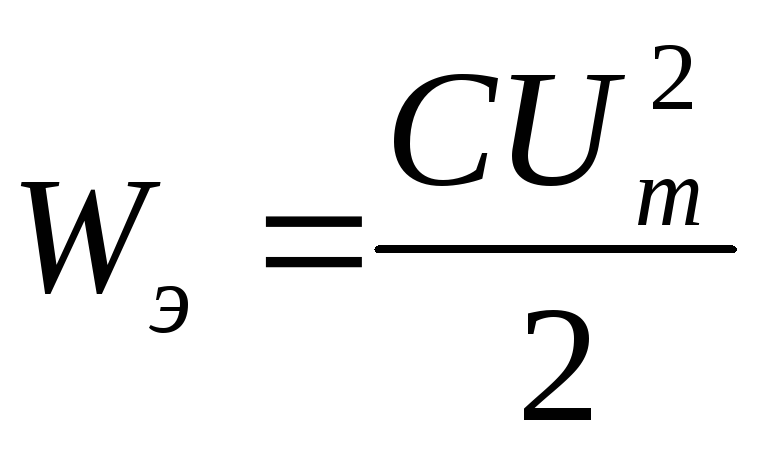Что такое колебательный LC-контур. Как работает параллельный LC-контур. Как рассчитать резонансную частоту LC-контура. Где применяются LC-контуры в электронике. Какие формулы используются для расчета параметров LC-контура.
Что такое колебательный LC-контур и как он устроен
Колебательный LC-контур представляет собой электрическую цепь, состоящую из катушки индуктивности (L) и конденсатора (C), соединенных параллельно или последовательно. В такой цепи могут возникать свободные электромагнитные колебания за счет периодического обмена энергией между магнитным полем катушки и электрическим полем конденсатора.
Основные компоненты LC-контура:
- Катушка индуктивности L — накапливает энергию в магнитном поле
- Конденсатор C — накапливает энергию в электрическом поле
- Соединительные провода (обладают некоторым активным сопротивлением R)
В идеальном LC-контуре (без потерь энергии) колебания могли бы продолжаться бесконечно долго. Но в реальных контурах всегда присутствуют потери энергии на активном сопротивлении проводов и других элементов, поэтому колебания постепенно затухают.
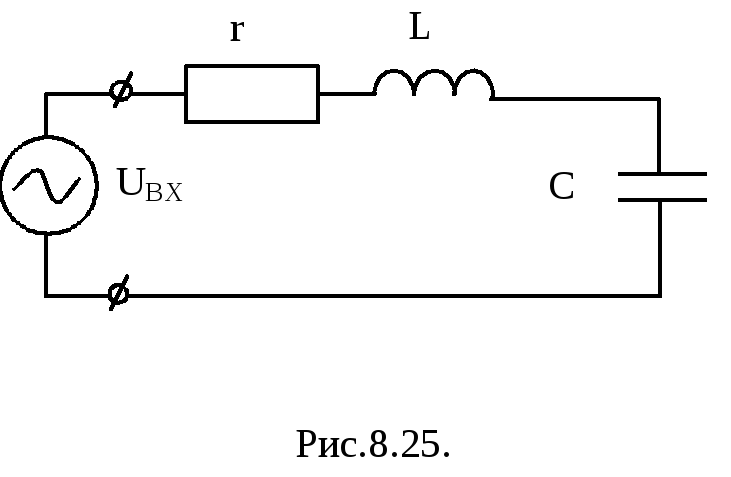
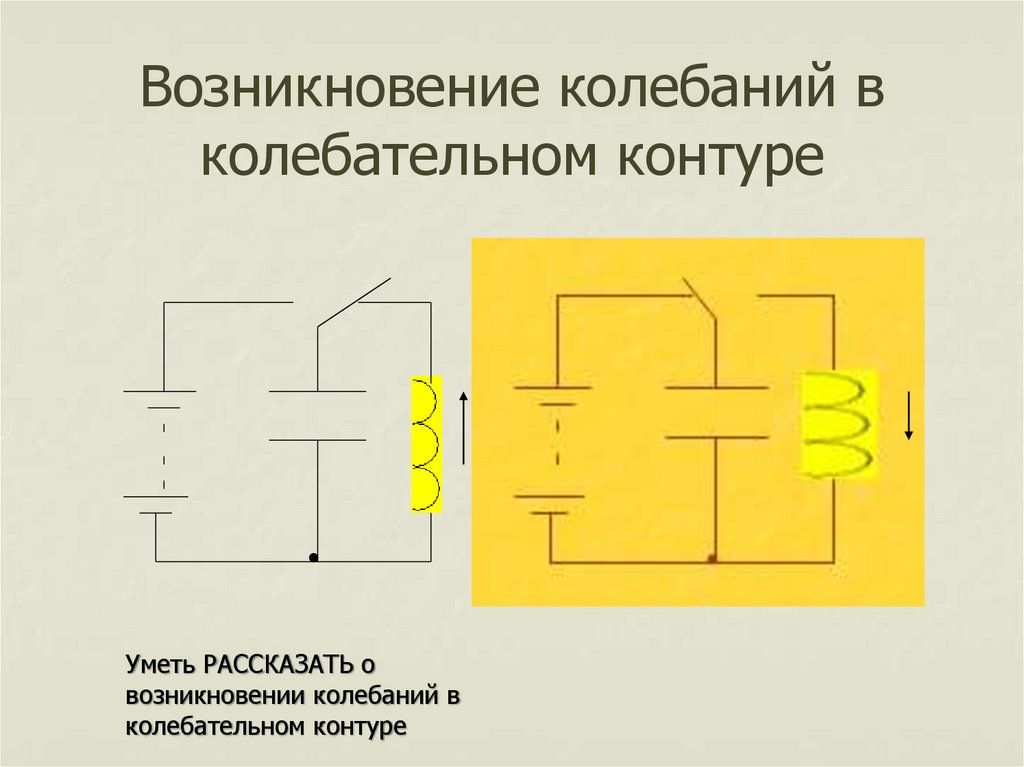
Принцип работы параллельного LC-контура
Рассмотрим принцип работы параллельного LC-контура на примере:
- Изначально конденсатор заряжен до некоторого напряжения U
- При замыкании цепи конденсатор начинает разряжаться через катушку индуктивности
- Ток разряда создает в катушке магнитное поле
- Когда конденсатор полностью разрядится, магнитное поле катушки достигнет максимума
- Магнитное поле катушки начинает уменьшаться, индуцируя ЭДС самоиндукции
- Индуцированный ток заряжает конденсатор, но уже с обратной полярностью
- Процесс повторяется, образуя колебания
Таким образом, в LC-контуре происходит периодическое преобразование энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно.
Расчет резонансной частоты LC-контура
Резонансная частота LC-контура — это частота свободных колебаний, возникающих в контуре. Она зависит только от величин индуктивности L и емкости C.
Формула для расчета резонансной частоты:
f = 1 / (2π√LC)
где:
- f — резонансная частота (Гц)
- L — индуктивность катушки (Генри)
- C — емкость конденсатора (Фарад)
Пример расчета: Если L = 100 мкГн, C = 100 пФ, то резонансная частота составит:
f = 1 / (2π√(100*10^-6 * 100*10^-12)) ≈ 1.59 МГц
Добротность колебательного контура
Добротность Q — важный параметр LC-контура, характеризующий его качество. Чем выше добротность, тем меньше потери энергии в контуре и тем медленнее затухают колебания.
Добротность определяется по формуле:
Q = (1/R) * √(L/C)
где R — активное сопротивление контура.
Высокодобротные контуры (Q > 100) имеют узкую полосу пропускания и позволяют точно выделять нужную частоту. Низкодобротные контуры имеют широкую полосу и используются, например, в широкополосных фильтрах.
Применение LC-контуров в электронике
LC-контуры широко применяются в различных областях радиоэлектроники:
- Колебательные системы генераторов
- Частотные фильтры в радиоприемниках
- Резонансные усилители
- Полосовые фильтры
- Системы настройки антенн
- Частотные модуляторы и демодуляторы
- Измерительные приборы
Одно из важнейших применений — использование LC-контуров в качестве частотно-избирательных цепей в радиоприемниках для выделения сигнала нужной частоты.
Параметры реальных LC-контуров
При расчете и проектировании реальных LC-контуров необходимо учитывать ряд дополнительных параметров:
- Активное сопротивление катушки и проводов
- Собственная емкость катушки
- Индуктивность выводов конденсатора
- Потери в диэлектрике конденсатора
- Влияние температуры на параметры компонентов
Эти факторы приводят к отклонению реальной резонансной частоты от расчетной и снижению добротности контура. Их необходимо учитывать при разработке высокочастотных и прецизионных устройств.
Настройка LC-контуров
Для точной настройки резонансной частоты LC-контуров применяются различные методы:
- Использование переменных конденсаторов
- Применение катушек с подстроечным сердечником
- Подключение дополнительных подстроечных конденсаторов
- Изменение числа витков катушки
- Использование варикапов (емкость меняется под действием напряжения)
Выбор метода настройки зависит от требуемой точности, диапазона перестройки и конкретного применения LC-контура.
Как настроить LC-контур на нужную частоту?
Для настройки LC-контура на заданную частоту можно использовать следующий алгоритм:
- Рассчитать требуемые номиналы L и C по формуле резонансной частоты
- Выбрать ближайшие стандартные номиналы компонентов
- Собрать контур и измерить его реальную резонансную частоту
- Провести точную подстройку частоты одним из методов
- Проверить добротность контура и при необходимости оптимизировать ее
При настройке высокочастотных контуров важно учитывать паразитные параметры компонентов и монтажа.
Моделирование LC-контуров
Для анализа работы LC-контуров широко применяется компьютерное моделирование с использованием специализированных программ:
- LTspice — бесплатный SPICE-симулятор для моделирования аналоговых схем
- Multisim — профессиональная среда схемотехнического моделирования
- QucsStudio — открытое ПО для моделирования ВЧ-схем
- MATLAB/Simulink — мощный инструмент для системного моделирования
Моделирование позволяет проанализировать частотные характеристики, переходные процессы, влияние паразитных параметров и оптимизировать конструкцию LC-контуров.
Какие параметры LC-контура можно исследовать с помощью моделирования?
С помощью компьютерного моделирования можно исследовать следующие характеристики LC-контуров:
- Амплитудно-частотная характеристика (АЧХ)
- Фазо-частотная характеристика (ФЧХ)
- Переходная характеристика
- Импульсная характеристика
- Добротность контура
- Полоса пропускания
- Влияние паразитных параметров
- Нелинейные эффекты при больших сигналах
Моделирование позволяет оптимизировать параметры контура без изготовления множества физических прототипов.
Калькулятор параллельного колебательного LC-контура
Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L,
обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром.
В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот.
Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока.
При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает.
При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное — растет.
При некоторой частоте ƒ0, емкостное сопротивление конденсатора и индуктивное сопротивление катушки
становятся численно равными: Xc = XL.
При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.
Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве
емкостного и индуктивного сопротивлений, называют режимом резонанса токов.
Расчет частоты резонанса параллельного LC-контура описывается формулами:
XL =
2πƒL
XC =
1
2πƒC
ƒ0 =
1
2π√LC
XL — индуктивное реактивное сопротивление, Ом;
XС — ёмкостное реактивное сопротивление, Ом;
ƒ0 — резонансная частота, Гц;
Расчет частоты резонанса LC-контура
Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура, или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.
IC
IL
Iƒ
мкФнФпФ
ГнмГнмкГн
МГцкГцГц
XL = XC = ƒ0 = φ = °
XL
>
XC
Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного. Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°
Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°
Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс, тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.
Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.
Подбор конденсатора на сайте
Подбор катушки индуктивности на сайте
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Колебательный LC контур: определение, принцип действия, расчет
Сегодня нас интересует простейший колебательный контур, его принцип работы и применение.
За полезной информацией по другим темам переходите на наш телеграм-канал.
Колебания – процесс, повторяющийся во времени, характеризуется изменением параметров системы около точки равновесия.
Первое, что приходит на ум — это механические колебания математического или пружинного маятников. Но ведь колебания бывают и электромагнитными.
По определению колебательный контур (или LC-контур) – это электрическая цепь, в которой происходят свободные электромагнитные колебания.
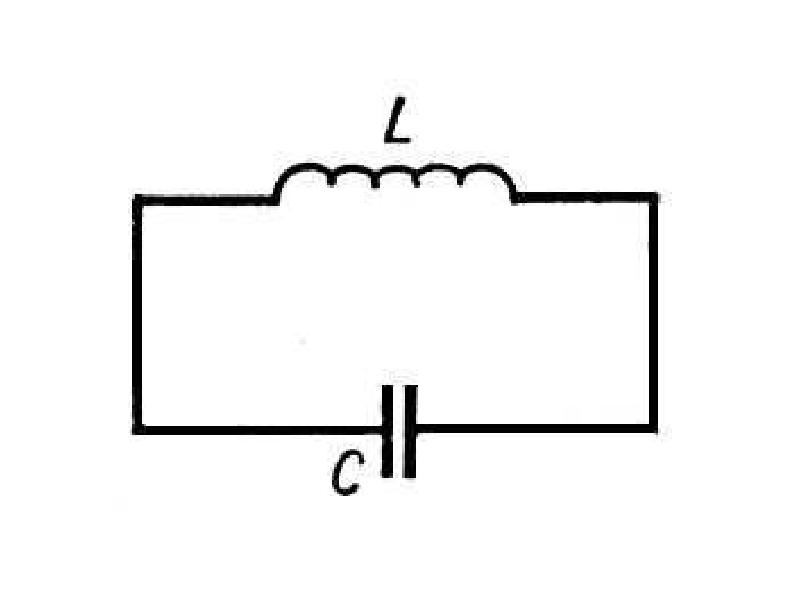
Такой контур представляет собой электрическую цепь, состоящую из катушки индуктивностью L и конденсатора емкостью C. Соединены эти два элемента могут быть лишь двумя способами — последовательно и параллельно. Покажем на рисунке ниже изображение и схему простейшего колебательного контура.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Принцип действия колебательного контура
Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.
Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.
Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны.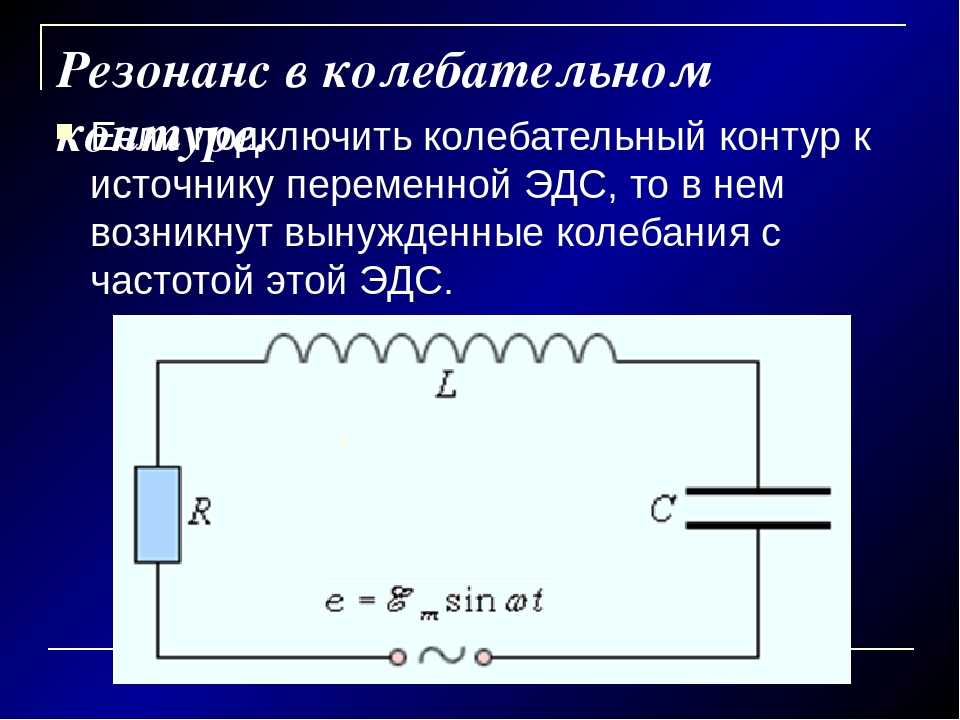 В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.
В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.
Еще одна важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.
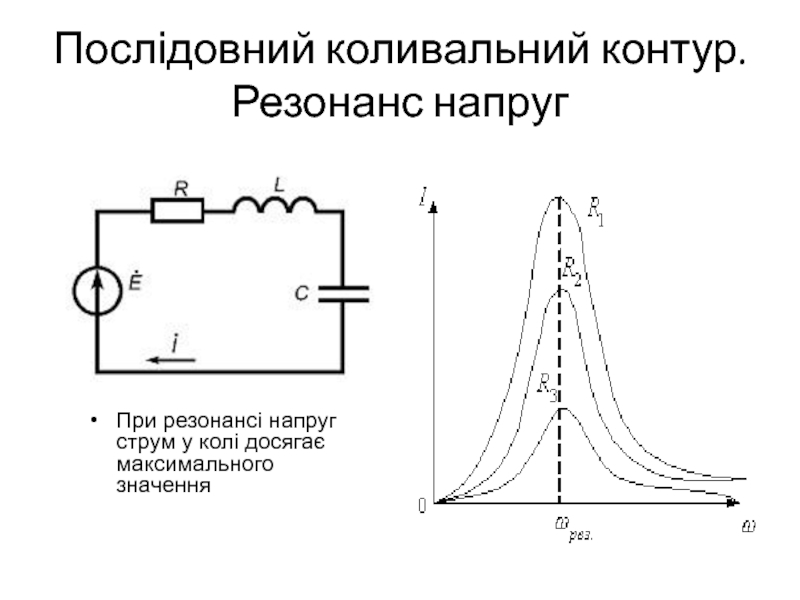
Резонанс LC-контура
Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс – в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура).
Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу:
Применение колебательного контура
Колебательный контур широко применяется на практике.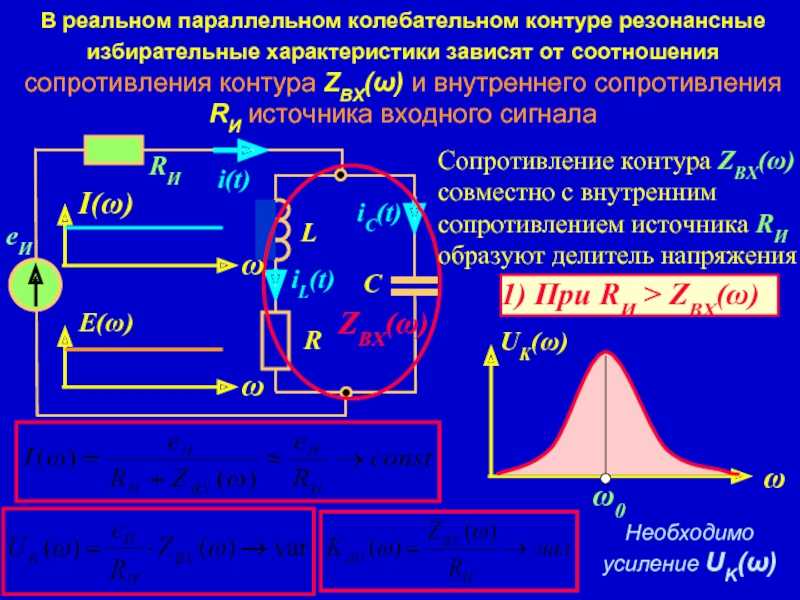 На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис. Качественная и быстрая помощь в решении любых задач не заставит себя ждать!
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
LC Circuits — Гиперучебник по физике
[закрыть]
схема LC
Начните с правила Кирхгофа.
| В = Л | ДИ | + | q |
| дт | С |
Возьмем производную от каждого члена.
| дВ | = Д | г 2 I | + | 1 | дк | |
| дт | дт 2 | С | дт |
Напряжение батареи постоянно, поэтому производная равна нулю. Производная заряда — это ток, что дает нам дифференциальное уравнение второго порядка.
| 0 = L | г 2 I | + | 1 | я |
| дт 2 | С |
Немного переставить…
| д 2 | I = — | 1 | я |
| дт 2 | ЛК |
, а затем сделайте паузу, чтобы обдумать решение.
Нам нужна функция, вторая производная которой равна самой себе со знаком минус. У нас есть два варианта: синус и косинус. Любая из них хороша, поскольку они в основном идентичны с фазовым сдвигом между ними на 90°. Без ограничения общности я выберу синус с произвольным фазовым углом (φ), который может быть равен 90°, если мы позволим. Или он может быть равен какому-то другому углу. Другими параметрами общей синусоидальной функции являются амплитуда ( I 0 ) и угловой частоты (ω).
Основной метод, который я начал, называется « угадать и проверить «. Моя догадка состоит в том, что функция выглядит как обычная синусоидальная функция…
I = I 0 sin(ω t + φ)
и проверка состоит в том, чтобы снова включить его в дифференциальное уравнение и посмотреть, что произойдет.
| д 2 | I 0 sin(ω t + φ) | = − | 1 | I 0 sin(ω t + φ) |
| дт 2 | ЛК | |||
| − ω 2 I 0 sin(ω t + φ) | = − | 1 | I 0 sin(ω t + φ) | |
| ЛК | ||||
Отменяется в принципе все, кроме одного параметра — угловой частоты.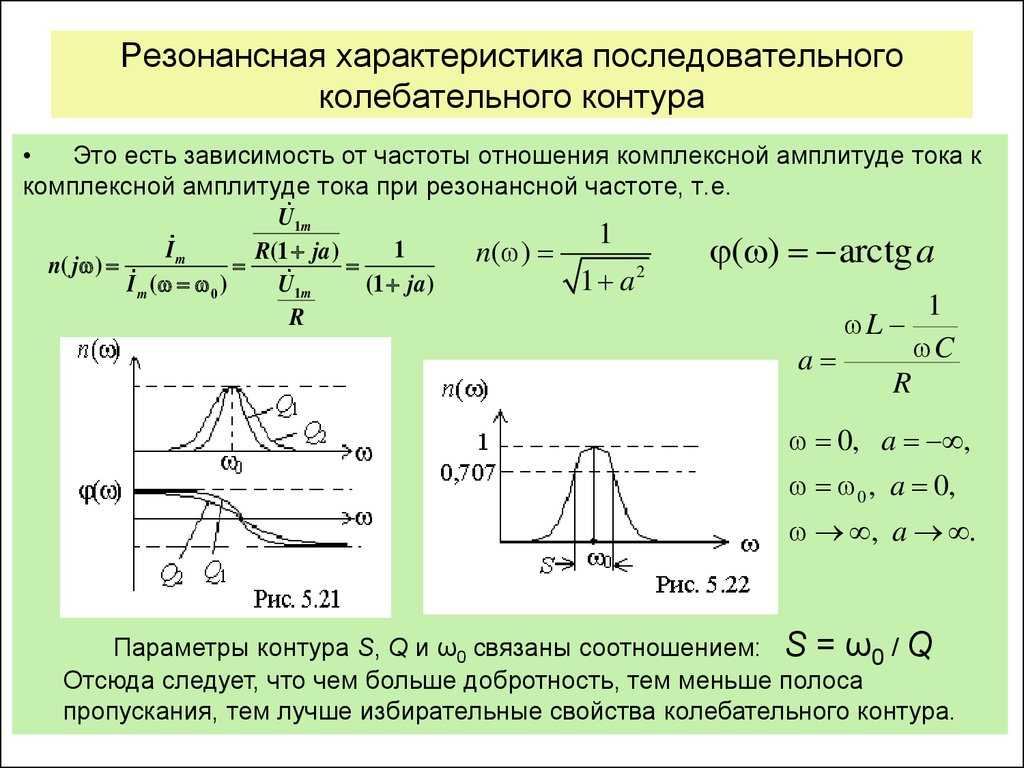
| ω = | 1 |
| √ ЛК |
Таким образом, LC-контур является колебательным контуром. Частота такой цепи (в отличие от ее угловой частоты) равна…
| f = | ω | = | 1 |
| 2π | 2π√ ЛК |
И что? Чем это полезно?
Справа показана схема аудиокроссовера, состоящая из трех LC-цепей, каждая из которых настроена на свою собственную частоту. Катушки индуктивности ( L ) находятся в верхней части схемы, а конденсаторы ( C ) – в нижней части. Слева схема «низкочастотного динамика», настроенная на низкую звуковую частоту, справа схема «твитера», настроенная на высокую звуковую частоту, а между ними схема «среднечастотного динамика», настроенная на частоту в середине звукового спектра.
Цепи RC в основном являются фильтрами.
RCL Circuit
Мне нужно написать эту часть.
LC-контур (он же бак или резонансный контур)
LC-цепь состоит из катушки и конденсатора, которые резонируют. друг с другом, передавая энергию туда и обратно между ними (цепь показано ниже). Этот происходит на определенной частоте, называемой резонансной частотой. L — это символ индуктивности, которая является свойством катушки. C — это символ емкости, которая является свойством конденсатора. Примеры на фотографиях ниже показывают кристаллические радиоприемники, каждый со своим катушка и конденсатор соединены параллельно.
Схема цепи LC.
LC-цепь в кварцевом радиоприемнике с цилиндрическим конденсатором.
LC-цепь в кварцевом радиоприемнике с плоским конденсатором.
Цепи LC используются для ряда вещей, таких как генерация
сигналов на резонансной частоте и для выделения конкретной
частота (резонансная частота) от цепи со многими частотами. Выделение определенной частоты — вот что происходит в кристаллическом радиоприемнике.
где катушка и конденсатор соединены параллельно.
Выделение определенной частоты — вот что происходит в кристаллическом радиоприемнике.
где катушка и конденсатор соединены параллельно.
На самом деле сопротивление тоже играет роль, но часто при выполнении расчетах сопротивлением пренебрегаем. При включении сопротивления, вместо этого мы говорим о цепи RLC, где R представляет собой сопротивление.
Принцип работы LC-цепи
Индуктивность катушки (L) и емкость конденсатора (C) равны
выбираются таким образом, чтобы они резонировали на определенной частоте. Формула
дается раздел ниже, показывающий, как это сделать. Как показано
в анимации они обмениваются энергией туда и обратно на этой частоте.
В то время, когда ток течет через катушку, либо
увеличиваясь или уменьшаясь, вокруг него создается магнитное поле.
По мере увеличения тока увеличивается напряженность магнитного поля.
По мере уменьшения тока магнитное поле ослабевает.
Когда нет больше тока, больше нет магнитного поля.
Конденсатор действует противоположно току.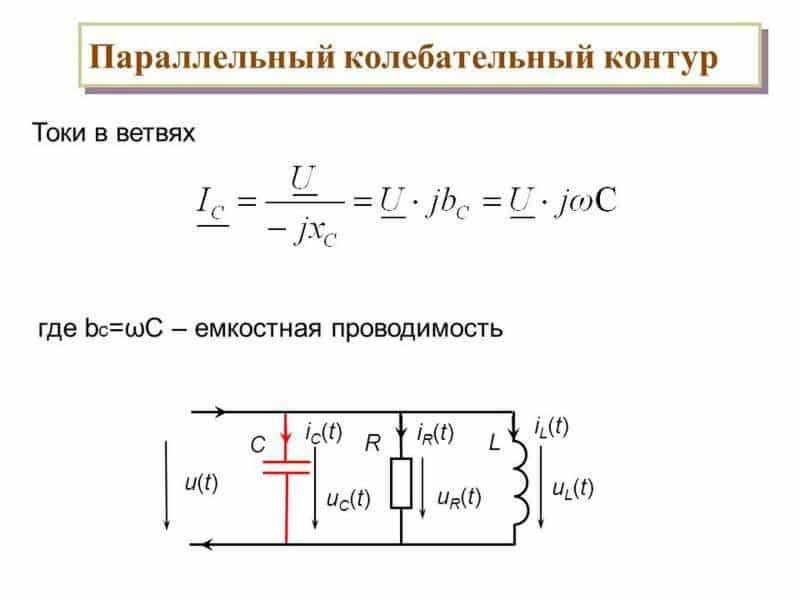 Пока ток увеличивается, конденсатор разряжается.
Пока ток уменьшается, конденсатор заряжается.
Когда тока больше нет, конденсатор полностью заряжен.
Пока ток увеличивается, конденсатор разряжается.
Пока ток уменьшается, конденсатор заряжается.
Когда тока больше нет, конденсатор полностью заряжен.
LC-контур резонирует.
Кривые заряда/разряда конденсатора.
Все это имеет смысл. Если ток все еще течет, то конденсатор
не будет полностью заряжен — его заряд будет меняться.
Но как только он заряжен, ничто не держит его заряженным, и поэтому
этот заряд циркулирует обратно по цепи, обеспечивая ток.
Конденсатор не разряжается с постоянной скоростью (см. график).
Это начинается
разрядка медленно и быстро ускоряется, что означает, что ток также
начинается медленно и быстро ускоряется.
Ток, проходящий через катушку, создает
магнитное поле, поэтому пока конденсатор разряжается,
магнитное поле увеличивается в силе. Но когда больше нет заряда
на конденсаторе тока больше нет, а значит магнитный
поле схлопывается. Изменяющееся магнитное поле индуцирует ток
течет по контуру, и пока поле схлопывается, оно меняется.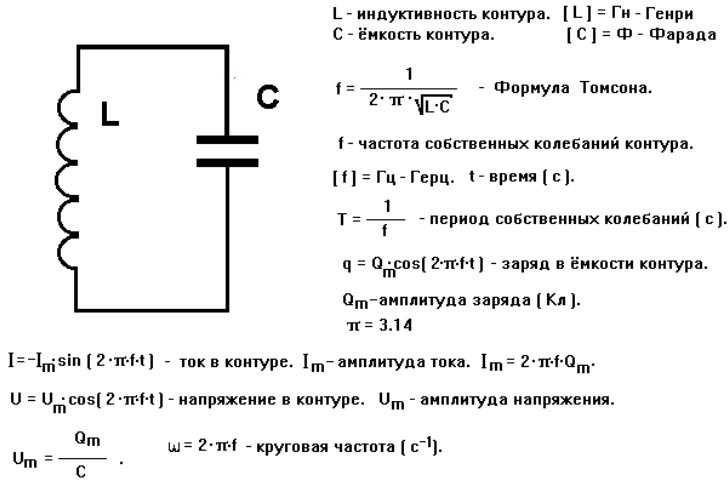 И так в цепи течет ток. Этот ток заряжает
конденсатор снова, и мы начинаем сначала.
И так в цепи течет ток. Этот ток заряжает
конденсатор снова, и мы начинаем сначала.
Калькулятор резонансной частоты LC и варианты
Вот калькулятор для расчета резонансной частоты. формулы ниже, если вам интересно.
Заполните следующие поля и нажмите кнопку «Рассчитать»…Если вы не знаете индуктивность и вам нужно вычислить ее, вы можете использовать калькулятор индуктивности, или формула на этой странице.
Если вы не знаете емкость и вам нужно вычислить ее, вы можете используйте калькулятор емкости, или формула на этой странице.
Индуктивность (л):
Генримиллигенримикрогенри
Емкость (С):
Фарадмиллифарадмикрофараднанофарадпикофарад
Результат:
Резонансная частота
Гц
Однако иногда вы знаете, какая частота вам нужна, и либо не знаете, знать, что емкость или индуктивность вам нужно, чтобы получить эту частоту. Поэтому ниже приведены калькуляторы для этих двух.
Чтобы получить индуктивность, заполните следующее и нажмите кнопку «Рассчитать».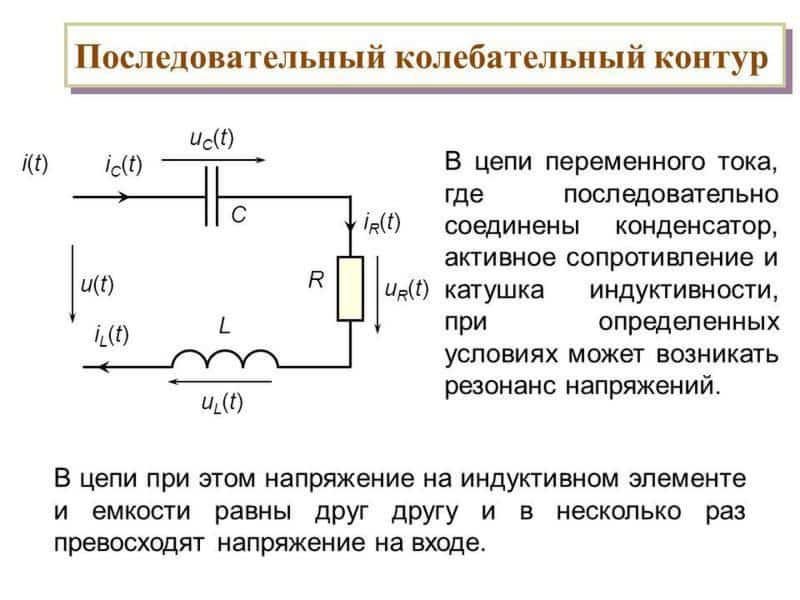
Если вы не знаете емкость и вам нужно вычислить ее, вы можете используйте калькулятор емкости, или формула на этой странице.
Частота (f):
Гц (Герц) или циклов в секунду
Емкость (С):
Фарадмиллифарадмикрофараднанофарадпикофарад
Результат:
Индуктивность
микрогенри
Чтобы получить емкость, заполните следующее и нажмите кнопку «Рассчитать»…
Если вы не знаете индуктивность и вам нужно вычислить ее, вы можете использовать калькулятор индуктивности, или формула на этой странице.
Частота (f):
Гц (Герц) или циклов в секунду
Индуктивность (л):
Генримиллигенримикрогенри
Результат:
Емкость
микрофарады
Расчет резонансной частоты ЖК
Формула, необходимая для расчета резонансной частоты параллельная LC-цепь выглядит следующим образом:
L в приведенной выше формуле резонансной частоты представляет собой индуктивность
катушка. Если вы не знаете индуктивность, вы можете ее рассчитать
с помощью онлайн-калькулятора или формулы на
эта страница о конструкции катушки и
индукция.