Частота ню. Частота колебаний в физике: формулы, примеры и практическое применение

Что такое частота колебаний в физике. Как рассчитать частоту колебаний по формуле. Какие бывают виды частот колебаний. Где используется понятие частоты в науке и технике.

Что такое частота колебаний и как она определяется в физике

Частота колебаний — это фундаментальная физическая величина, характеризующая периодические процессы. Она показывает, сколько полных колебаний совершается за единицу времени.

Математически частота определяется следующей формулой:

ν = 1/T

где:

• ν (ню) — частота колебаний
• T — период колебаний, то есть время одного полного колебания

Единица измерения частоты в Международной системе единиц (СИ) — герц (Гц). 1 Гц означает, что за 1 секунду происходит одно полное колебание.

Какие основные характеристики частоты колебаний необходимо знать.

• Частота обратно пропорциональна периоду колебаний
• Чем выше частота, тем быстрее происходят колебания
• Частота всегда положительная величина
• Частота не зависит от амплитуды колебаний

Основные формулы для расчета частоты колебаний

Помимо базовой формулы ν = 1/T, существует несколько других важных формул для расчета частоты колебаний в различных системах:

Формула для математического маятника

ν = (1/2π) * √(g/l)

где:

• g — ускорение свободного падения
• l — длина маятника

Формула для пружинного маятника

ν = (1/2π) * √(k/m)

где:

• k — жесткость пружины
• m — масса груза

Формула для колебательного контура

ν = (1/2π) * √(1/LC)

где:

• L — индуктивность катушки
• C — емкость конденсатора

Эти формулы позволяют рассчитать частоту колебаний в различных физических системах, зная их параметры.

Виды частот колебаний и их особенности

В физике выделяют несколько видов частот колебаний, каждая из которых имеет свои особенности:

Циклическая частота

Циклическая частота (ω) связана с обычной частотой соотношением:

ω = 2πν

Циклическая частота измеряется в радианах в секунду и часто используется в теоретических расчетах.

Собственная частота

Собственная частота — это частота свободных колебаний системы при отсутствии внешних воздействий. Она определяется только параметрами самой колебательной системы.

Резонансная частота

Резонансная частота — это частота вынужденных колебаний, при которой амплитуда колебаний достигает максимального значения. Она близка к собственной частоте системы.

Практическое применение понятия частоты колебаний

Частота колебаний находит широкое применение во многих областях науки и техники:

• В акустике — для характеристики звуковых волн
• В оптике — для описания электромагнитных волн видимого света
• В радиотехнике — для настройки радиоприемников и передатчиков
• В электронике — при разработке колебательных контуров
• В механике — при расчете вибраций машин и механизмов
• В сейсмологии — для анализа колебаний земной коры

Как частота колебаний используется в повседневной жизни. Несколько примеров:

• Настройка музыкальных инструментов по эталонной частоте
• Выбор частоты процессора компьютера
• Установка частоты кадров в видео
• Настройка частоты сотовой связи и Wi-Fi

Измерение частоты колебаний: приборы и методы

Для измерения частоты колебаний используются различные приборы и методы:

Частотомеры

Частотомеры — это специализированные электронные приборы для прямого измерения частоты электрических сигналов. Они могут быть аналоговыми или цифровыми.

Осциллографы

Осциллографы позволяют визуально наблюдать форму колебаний и измерять их параметры, включая частоту.

Стробоскопический метод

Стробоскопический метод основан на визуальном наблюдении колеблющегося объекта при периодическом освещении. Когда частота вспышек света совпадает с частотой колебаний, объект кажется неподвижным.

Резонансный метод

Резонансный метод использует явление резонанса для определения собственной частоты колебательной системы.

Влияние различных факторов на частоту колебаний

Частота колебаний может изменяться под влиянием различных физических факторов:

Температура

Повышение температуры обычно приводит к увеличению частоты колебаний из-за изменения упругих свойств материалов.

Давление

Изменение давления может влиять на частоту колебаний газовых и жидкостных систем.

Масса колеблющейся системы

Увеличение массы приводит к уменьшению частоты колебаний.

Жесткость упругих элементов

Повышение жесткости пружин или других упругих элементов увеличивает частоту колебаний.

Внешние воздействия

Внешние силы могут изменять частоту колебаний, например, при вынужденных колебаниях.

Частота колебаний в природных явлениях

В природе можно наблюдать множество колебательных процессов с различными частотами:

• Колебания маятника — от долей герца до нескольких герц
• Звуковые волны — от 20 Гц до 20 кГц (слышимый диапазон)
• Радиоволны — от нескольких килогерц до сотен мегагерц
• Видимый свет — от 430 до 750 ТГц
• Рентгеновское излучение — от 30 ПГц до 30 ЭГц

Как частота колебаний проявляется в биологических системах.

• Сердечные сокращения — около 1 Гц
• Альфа-ритмы мозга — 8-13 Гц
• Взмахи крыльев колибри — до 80 Гц

Понимание частоты природных колебаний важно для изучения различных физических, химических и биологических процессов.

Формула частоты в физике

Формула частоты в физике Определение

Частота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.

Чаще всего в физике частоту обозначают буквой $\nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

\[\nu =\frac{1}{T}\left(1\right).\]

Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:

\[\nu =\frac{N}{\Delta t}\left(2\right),\]

где $\Delta t$ — время за которое происходят $N$ колебаний.

Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:

\[\left[\nu \right]=с^{-1}=Гц. \]

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]

Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:

\[{\omega }_0=2\pi \nu \left(4\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right).\]

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(6\right),\]

где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(8\right). \]

Единицей измерения частоты дискретных событий является обратная секунда:

\[\left[n\right]=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:

\[n=\frac{1}{\tau }\left(9\right).\]

Примеры задач с решением

Пример 1

Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?

Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.

\[\nu =\frac{N}{\Delta t}\left(1.1\right).\]

Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $\Delta t=1\ мин=60\ с$. Вычислим частоту:

\[\nu =\frac{600}{60}=10\ \left(Гц\right).\]

Ответ. $\nu =10Гц$

Пример 2

Задание. На рис.1 изображен график колебаний некоторого параметра $\xi \ (t)$, Какова амплитуда и частота колебаний этой величины?

Решение. Из рис.1 видно, что амплитуда величины $\xi \ \left(t\right)={\xi }_{max}=5\ (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:

\[T=2\ \left(c\right).\]

Частота — величина обратная периоду колебаний, значит:

\[\nu =\frac{1}{T}=0,5\ \left(Гц\right).\]

Ответ. 1) ${\xi }_{max}=5\ (м)$. 2) $\nu =0,5$ Гц

Читать дальше: формулы математического маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Частота колебаний – величина, формула, график

4. 6

Средняя оценка: 4.6

Всего получено оценок: 129.

4.6

Средняя оценка: 4.6

Всего получено оценок: 129.

Частота колебаний – это один из параметров, описывающих колебательные процессы в природе. Многие явления зависят от частоты, и происходят по-разному при ее изменении. Рассмотрим это понятие подробнее.

Колебания в природе

Колебания различных величин очень широко распространены в природе. Явление колебаний заключается в том, что измеряемый параметр меняет свое значение вокруг некоторого среднего.

Рис. 1. Колебания в природе.

Колебания могут быть периодическими (маятник), а могут быть непериодическими (флаг на ветру). Поскольку любое непериодическое колебание может быть представлено в виде бесконечной суммы периодических, то в первую очередь изучаются периодические колебания. График таких колебаний представляет собой синусоиду, которая хорошо изучена в математике.

Маятник

Для рассмотрения базовых понятий колебательных процессов в качестве примера удобно взять маятник – подвешенную на тонкой легкой нити небольшую массу. Если ее качнуть, она начнет совершать равномерные движения.

Рис. 2. Колебания маятника.

Каждое движение маятника, начинающееся от крайней точки, и заканчивающееся в ней же, называется колебанием.

Частота колебаний

Если взять несколько маятников разной длины, можно убедиться, что они будут совершать колебания «с разной скоростью» (хотя линейная скорость груза при этом может быть одинаковой). То есть «скорость колебаний» и скорость движения груза маятника – это не одно и то же.

Для характеристики «скорости колебаний» используют специальное понятие – частоту колебаний.

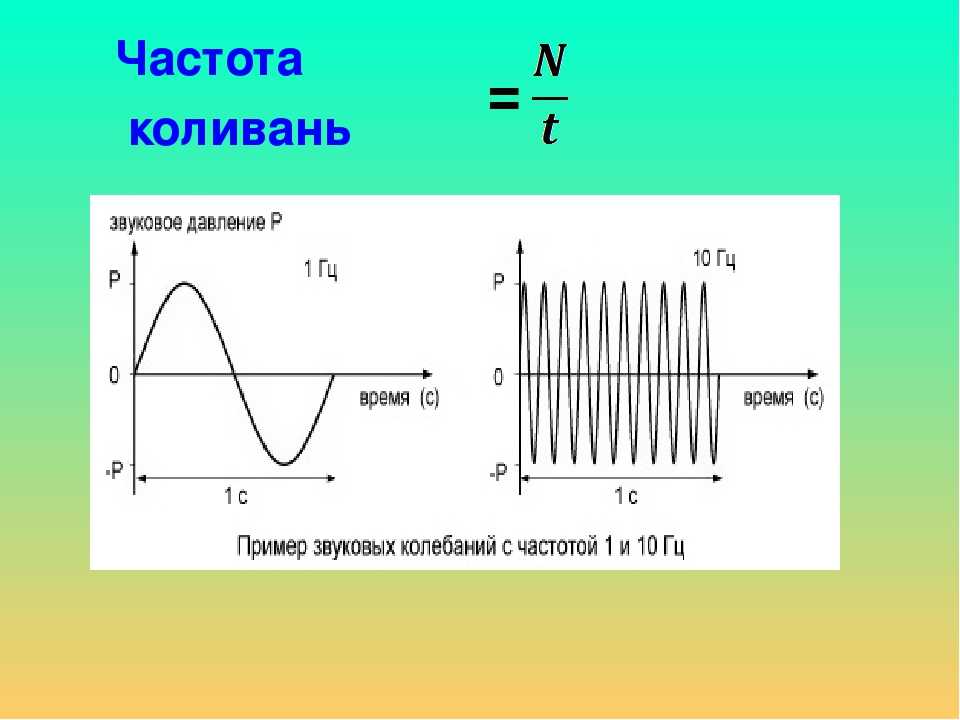
Число колебаний, которое совершается за единицу времени, называется частотой колебаний. Для обозначения используется греческая буква $\nu$ («ню»).

Единица частоты колебаний в системе СИ – Герц (Гц). Один Герц – это число колебаний, происходящих в одну секунду.

Для измерения частоты колебаний подсчитывают число колебаний за некоторый отрезок времени, и делят его на длительность отрезка:

$$\nu={N\over t},$$

где:

• N – число колебаний;
• t – время, за которое эти колебания были совершены (сек).
  {25}$ Гц (жесткое гамма-излучение).
  Рис. 3. Высокая и низкая частота.

  Что мы узнали?

  Колебание – это изменение измеряемой величины от начальной точки до точки максимального отклонения и дальнейшее возвращение в исходную точку. Число колебаний, происходящих в единицу времени, называется частотой колебаний.

  Тест по теме

  Доска почёта

  Чтобы попасть сюда — пройдите тест.

  • Егор Князев

    4/5

  Оценка доклада

  4.6

  Средняя оценка: 4.6

  Всего получено оценок: 129.

  ---

  А какая ваша оценка?

  Частота | Определения, символы и формулы

  Связанные темы:

  угловая частота собственная частота основная частота диапазон частот мода третьей гармоники

  Просмотреть весь связанный контент →

  Популярные вопросы

  Что такое частота в физике?

  В физике термин

  частота относится к числу волн, которые проходят фиксированную точку в единицу времени. Он также описывает количество циклов или колебаний, совершаемых в единицу времени телом, находящимся в периодическом движении.

  Что такое символ частоты?

  Чаще всего для обозначения частоты используются символы f и греческие буквы ню (ν) и омега (ω). Nu чаще используется при описании электромагнитных волн, таких как свет, рентгеновские лучи и гамма-лучи. Омега обычно используется для описания угловой частоты.

  Как выражается частота?

  Частота обычно выражается в герцах, сокращенно Гц. Один килогерц (кГц) равен 1000 Гц, а один мегагерц (МГц) равен 1 000 000 Гц. В спектроскопии иногда используется еще одна единица частоты — волновое число, число волн на единицу расстояния.

  частота , в физике количество волн, проходящих фиксированную точку в единицу времени; также число циклов или колебаний, совершаемых в единицу времени телом, находящимся в периодическом движении. Говорят, что тело в периодическом движении претерпело один цикл или одну вибрацию после прохождения ряда событий или положений и возвращения в исходное состояние. См. также угловая скорость; простые гармонические колебания.

  Если период или интервал времени, необходимый для завершения одного цикла или вибрации, составляет 1/2 секунды, частота составляет 2 раза в секунду; если период равен 1/100 часа, частота равна 100 в час. В общем, частота является обратной величиной периода или временного интервала; т. е. частота = 1/период = 1/(интервал времени). Частота обращения Луны вокруг Земли чуть больше 12 оборотов в год. Частота струны ля скрипки составляет 440 колебаний или циклов в секунду.

  Викторина «Британника»

  Физика и естественное право

  Чаще всего для обозначения частоты используются символы f и греческие буквы ню (ν) и омега (ω). Nu чаще используется при описании электромагнитных волн, таких как свет, рентгеновские лучи и гамма-лучи. Омега обычно используется для описания угловой частоты, то есть того, насколько объект вращается или вращается в радианах в единицу времени. Обычно частота выражается в герцах, названных в честь 19немецкий физик 19-го века Генрих Рудольф Герц, один герц равен одному циклу в секунду, сокращенно Гц; один килогерц (кГц) равен 1000 Гц, а один мегагерц (МГц) равен 1 000 000 Гц. В спектроскопии иногда используют другую единицу частоты — волновое число — число волн на единицу расстояния.

  Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена ​​Эриком Грегерсеном.

  Seiichi Yamamoto: Обзор альбома Nu Frequency

  Слишком много информации не обязательно должно приводить к перегруженной обратной связи статики и путаницы, хотя в музыке это часто происходит. Представление натиска глобальной культуры, средств массовой информации и технологий вызывает искушение перенасытиться, и хотя это может быть один точный портрет (пост)современного мира, я не уверен, что он самый реалистичный.

  Такие исполнители, как Джон Освальд, Джон Зорн и Отомо Ёсихидэ, специализировались на своего рода карикатуре на этот мир в своей музыке: собирая вокруг себя обрывки информации и развлечений, они собирали воедино довольно пугающие документы о том, что могло бы дезориентировать окружающую среду. мягко говоря. Вспышки света, крики, разряды электричества, зазубренные, отрывистые сэмплы, проносящиеся мимо, прежде чем мы успеваем понять, что нас поразило: если бы каждая ночь была кануном Нового года на Таймс-сквер, а все это время на площади бушевали убийства, роды и война. улицы, это был бы идеальный саундтрек. Но каждый день не такой.

  Бывший гитарист группы Boredoms Сейичи Ямамото, кажется, осознал пустоту между хаосом. Это не из-за отсутствия активности в его мире: помимо 15-летнего пребывания в Boredoms, он руководил собственными группами Omoide Hatoba, Rashinban и Akabushi и выступал с Rovo, Most, Novo Tono и Ontoko. Он также владеет влиятельным клубом Bears в Осаке, где десятки полных надежд молодых любителей нойза каждую ночь пытаются доказать свой диссонанс. Кроме того, Ямамото выпустил несколько сольных гитарных альбомов, в которых он присоединился к цепляющимся и царапающимся рядам коллег-импровизаторов Фреда Фрита и Юджина Чедборна. Его музыкальный опыт столь же разнообразен, сколь и давний, и я бы не стал винить его за то, что он время от времени обращается к скронку.

  Nu Frequency , четвертый сольный релиз Ямамото, демонстрирует, что вам не нужно взрываться шизофреническим нойзом, чтобы испытать всю гамму живых ощущений. Работая с великолепной барабанщицей Чайной, Ямамото придумывает обширную смесь ансамблевого взаимодействия в стиле фри-джаз, пост-рока (вспомните To Rococo Rot, а не Sigur Ros) и своей собственной мерцающей, беспокойной гитары. Всякий раз, когда появляется мелодия, ее быстро затмевает мошенническая перкуссия или внезапный басовый всплеск. Во всем, вместо того, чтобы подчеркивать традиционное, он выбирает крайность, но вместо часа избиения истерики, Nu Frequency — это продолжительное путешествие в неразрешенное и приземленное. «Частота» может быть временами пронзительной, рокочущей или успокаивающей, но в целом звуковой спектр Ямамото ровный и неконфронтационный.

  После короткого блестящего вступления «Convergence» начинается «Acceleration», словно небольшой оркестр современных джазовых духов. Вечно стучащие китайские тарелки предлагают размер, который не ограничен реальным временем, в то время как несколько гитар играют на расстоянии. Синтезированные флейты плачут над глубокими, повторяющимися басовыми партиями, которые уступают место группам аккордов Ямамото. Если это звучит как беспорядок, это, вероятно, больше, чем вы думаете. Тем не менее, мне кажется, что это совершенно естественная квинтэссенция почти всего, что композитор делал в музыкальном плане за последние несколько лет, только все сразу. «Seed» продолжает необычный микс, но предлагает пассивную мелодию через гитары и фортепианную партию, которая находится где-то между контрапунктом и просто потерянной. Взбалмошная, тяжелая перкуссия заставляет вещи казаться более неорганизованными, чем они есть на самом деле, и почти так же, как басовые партии Скотта ЛаФаро дали Биллу Эвансу пространство для растяжки, Ямамото предлагает себе достаточно холста, по которому можно разбрызгаться.

  Есть моменты эклектичной красоты, как, например, в «Yarn», где композитор использует только гитару для создания слабой, спокойной тональности, под которой щелчки, треск и реверберация танцуют, как последние искры угасающего огня.