Частоты дпс москва. Теория и алгоритмы DPS-кластеризации: новые подходы к анализу многомерных данных

Что такое DPS-кластеризация. Как работают алгоритмы DPS-кластеризации. Какие новые подходы предлагаются для улучшения DPS-кластеризации. Как применять итеративный DPS и третий этап DPS-алгоритма.

Основы DPS-кластеризации и ее преимущества

DPS-кластеризация (Discrete Perfect Sets) — это современный подход к анализу многомерных данных, основанный на концепции дискретных совершенных множеств. Ключевые особенности DPS-кластеризации:

• Использует нечеткую математику и логику
• Вводит понятие плотности как меры связи между подмножеством и точкой
• Определяет кластеры как α-совершенные множества
• Состоит из двух основных этапов: топологической фильтрации и разбиения на компоненты связности

Преимущества DPS-кластеризации по сравнению с классическими алгоритмами:

• Предварительная очистка данных от шума
• Возможность обнаружения кластеров произвольной формы
• Меньшая чувствительность к выбросам
• Отсутствие необходимости задавать число кластеров заранее

Благодаря этим особенностям, DPS-кластеризация позволяет более точно выделять структуры в многомерных данных, особенно в сложных случаях.

Алгоритмы DPS-кластеризации: принцип работы

Базовый алгоритм DPS-кластеризации состоит из следующих шагов:

1. Задание плотности P и уровня α
2. Топологическая фильтрация: выделение максимального α-совершенного подмножества X(α)
3. Разбиение X(α) на компоненты r-связности

Рассмотрим подробнее каждый из этих этапов:

1. Задание плотности и уровня

Плотность P определяет степень связи между подмножеством и точкой. Она должна быть монотонной по подмножеству. Уровень α задает порог плотности для выделения кластеров.

2. Топологическая фильтрация

На этом этапе итеративно вырезается максимальное α-совершенное подмножество X(α). Оно состоит из точек, для которых плотность не меньше α.

3. Разбиение на компоненты связности

Полученное подмножество X(α) разбивается на r-связные компоненты, которые и считаются кластерами. Радиус r определяет локальность связей.

Таким образом, DPS-алгоритм сначала очищает данные от шума, а затем выделяет плотные и связные области — кластеры.

Итеративный DPS: расширение базового алгоритма

Базовый DPS-алгоритм имеет ограничение: он может пропускать некоторые значимые кластеры из-за глобального подхода к определению уровня плотности. Для решения этой проблемы предлагается итеративный DPS.

Суть итеративного DPS заключается в следующем:

1. Применение базового DPS-алгоритма к исходному множеству X
2. Применение DPS к дополнению полученного результата X(β)
3. Повторение шага 2 для каждого следующего дополнения

Преимущества итеративного подхода:

• Обнаружение кластеров разной плотности
• Выявление иерархической структуры кластеров
• Более полный анализ данных без снижения уровня плотности

Итеративный DPS позволяет находить «скрытые» кластеры, которые не были обнаружены на первой итерации из-за наличия более плотных областей.

Третий этап DPS: объединение кластеров

Для дальнейшего улучшения результатов кластеризации предлагается добавить третий этап к DPS-алгоритму — объединение кластеров. Его цель — выявить более крупные структуры, состоящие из нескольких близких кластеров.

Основные шаги третьего этапа:

1. Определение расстояния между кластерами
2. Анализ связности кластеров (d-кластеризация)
3. Построение мер близости между точками разных кластеров
4. Выбор значимых объединений кластеров

Преимущества добавления третьего этапа:

• Выявление глобальных структур в данных
• Уменьшение фрагментации результатов кластеризации
• Учет экспертных знаний при объединении кластеров

Третий этап позволяет получить более интерпретируемые результаты кластеризации, особенно для сложных многомерных данных.

Практическое применение усовершенствованной DPS-кластеризации

Рассмотренные улучшения DPS-кластеризации — итеративный подход и третий этап — позволяют существенно расширить возможности анализа данных. Области применения усовершенствованной DPS-кластеризации:

• Анализ сложных научных данных (биоинформатика, астрономия)
• Сегментация клиентов в маркетинге
• Обнаружение аномалий в системах безопасности
• Анализ социальных сетей и сообществ
• Классификация текстов и изображений

При использовании усовершенствованной DPS-кластеризации важно:

1. Правильно выбрать начальные параметры (плотность, уровень, радиус)
2. Определить оптимальное число итераций
3. Задать критерии значимости для объединения кластеров
4. Интерпретировать результаты с учетом специфики данных

Корректное применение новых подходов позволяет получить более полную и точную картину структуры данных по сравнению с базовым DPS-алгоритмом.

Сравнение DPS с другими алгоритмами кластеризации

Чтобы лучше понять преимущества DPS-кластеризации, сравним ее с другими популярными алгоритмами:

DPS vs K-means

• DPS не требует заранее задавать число кластеров
• DPS может находить кластеры произвольной формы, K-means — только сферические
• DPS менее чувствителен к выбросам

DPS vs DBSCAN

• DPS использует более гибкое понятие плотности
• DPS лучше работает с кластерами разной плотности (особенно итеративный вариант)
• DPS позволяет объединять близкие кластеры на третьем этапе

DPS vs Иерархическая кластеризация

• DPS эффективнее для больших объемов данных
• DPS не требует построения полного дерева кластеров
• DPS лучше справляется с шумом в данных

Таким образом, DPS-кластеризация, особенно с предложенными улучшениями, обладает рядом преимуществ перед классическими алгоритмами, что делает ее мощным инструментом анализа многомерных данных.

Заключение: перспективы развития DPS-кластеризации

DPS-кластеризация — перспективное направление в области анализа данных. Рассмотренные в статье улучшения — итеративный подход и третий этап — значительно расширяют ее возможности. Дальнейшие направления развития DPS-кластеризации могут включать:

• Разработку эффективных методов автоматического подбора параметров
• Создание параллельных и распределенных версий алгоритма для работы с большими данными
• Интеграцию с методами глубокого обучения для анализа сложных структур данных
• Расширение теоретической базы и доказательство свойств DPS-кластеров

Усовершенствованная DPS-кластеризация имеет большой потенциал для применения в различных областях науки и индустрии, где требуется глубокий анализ многомерных данных и выявление нетривиальных структур.

Минцифры готово бесплатно предоставить операторам частоты для 5G — 15 января 2022

Общество

15 января 2022, 15:24

16 комментариев

Государственная комиссия по радиочастотам рассматривает вопрос предоставления операторам связи частоты для 5G без взимания платы. Об этом 15 января, как пишет ТАСС, сообщил министр цифрового развития, связи и массовых коммуникаций РФ Максут Шадаев.

«Мы используем диапазон 4,8–4,9 Ггц, где требуется значительно больше частота установки базовых станций, чем в диапазоне классическом — 3,4–3,5 Ггц, то мы сейчас вышли с инициативой обнулить плату за спектр», — сказал он.

В конце прошлого года в Государственной комиссии по радиочастотам объявили о том, что диапазон для 5G в городах-миллионниках будет расширен до 4,8–4,99 ГГц.

С лета ежемесячный объем интернет-трафика, который сгенерировали петербуржцы в сетях пятого поколения, вырос в два раза, заявляли в ноябре прошлого года в МТС. Весной компания Apple представит новый телефон, который будет поддерживать 5G.

По теме

• Сотовые операторы повысят стоимость архивных тарифов

  19 января 2022, 12:49

УДИВЛЕНИЕ0

ПЕЧАЛЬ0

Комментарии 16

читать все комментариидобавить комментарий

ПРИСОЕДИНИТЬСЯ

Самые яркие фото и видео дня — в наших группах в социальных сетях

ВКонтактеТелеграмДзен

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

Новости СМИ2

сообщить новость

Отправьте свою новость в редакцию, расскажите о проблеме или подкиньте тему для публикации. Сюда же загружайте ваше видео и фото.

• Группа вконтакте

Новости компаний

Комментарии

16

Новости компаний

01.06.2023 17:10

БСПБ ко Дню защиты детей участвует в событии «Белый цветок» — большое добро для самых маленьких

1 июня, в Международный День защиты детей, Банк «Санкт-Петербург» в одиннадцатый раз принимает участие в благотворительном мероприятии «Белый цветок». Событие приурочено ко Дню рождения Санкт-Петербургского Детского хосписа, который Банк, его клиенты, партнеры и сотрудники поддерживают с 2012 года. Детский хоспис и одноименный благотворительный фонд — учреждение, которое помогает детям с тяжёлыми и неизлечимыми заболеваниями по всей стране. Благодаря инициативе Фонда, поддержке государства и неравнодушию людей Детский хоспис сегодня — это…

11.04.2023 17:10

ГК «Ленстройтрест» приняла участие в спортивных соревнованиях Кубка «Над Невой»

В Санкт-Петербурге завершились соревнования Кубка «Над Невой», организованные Комитетом по физической культуре и спорту Санкт-Петербурга и РОО «Федерация футбола лиц с заболеванием церебральным параличом». ГК «Ленстройтрест» выступила партнером мероприятия. В соревнованиях приняли участие команды из разных регионов России: Санкт-Петербург, Москва, Екатеринбург, Ижевск и другие. В составе команд — юноши и девушки в возрасте от 12 до 18 лет. «Мы много лет занимаемся социальными проектами по различным направлениям — иппотерапия, улучшение…

18.04.2023 13:06

ГК «Ленстройтрест» запустила социально-образовательный проект совместно с волонтерами «Школы ЛизыАлерт»

Волонтеры добровольческого поисково-спасательного отряда «ЛизаАлерт» побывали в жилых комплексах компании. На площадке Соседских центров для жителей голландского квартала «Янила», финского городка «Юттери» и квартала «Окла» в Приморском районе прошли лекции проекта «Школа ЛизыАлерт». Застройщик пригласил волонтеров провести образовательные встречи с детьми во время весенних каникул. По словам ГК «Ленстройтрест», такое время запуска проекта выбрано не случайно. Именно в этот период дети остаются без постоянного присмотра, у них возникает…

ТОП 5

1Российская семья протаранила шлагбаум, прорываясь из Польши в Белоруссию

132 158

2182Песков рассказал, что такое атака беспилотников на Москву

103 734

1713Ответочка: Германия закрывает почти все российские генконсульства

89 507

1774По Москве ударили восемь беспилотников, Шойгу назвал потери украинской армии: главные новости СВО за 30 мая78 907

495Финны сказали, что будет с запретом на въезд для россиян

76 204

104Новости компаний

68585-17: БС-ДПС/М Блоки связи — Производители, поставщики и поверители

Назначение

Блоки связи БС-ДПС/М (далее — БС-ДПС/М) входят в состав безопасных локомотивных объединенных комплексов и предназначены для измерений количества импульсов и частоты их следования, которые преобразовываются в значение пройденного пути и скорости.

Описание

Принцип действия БС-ДПС/М заключается в преобразовании электрических импульсов, поступающих от датчиков угла поворота универсальных ДПС-У, и программном вычислении дальности по количеству импульсов, а скорости — по их частоте следования.

БС-ДПС/М рассчитан на работу с двумя датчиками угла поворота, имеющими по два выхода каждый, диаметрами бандажей колёсных пар от 800 до 1300 мм и количеством зубьев на датчике скорости 42.

БС-ДПС/М также вычисляет и передает в линию связи направление вращения обоих датчиков угла поворота, сигналы исправности по каждому и номер выбранного в данный момент датчика.

БС-ДПС/М имеет две модификации:

—    БС-ДПС/М-CAN;

—    БС-ДПС/М-БЗС-CAN.

Блок БС-ДПС/М-БЗС-CAN имеет дополнительную плату с устройством защиты от скольжения.

Общий вид БС-ДПС/М (модификация БС-ДПС/М-БЗС-CAN) и место пломбировки от несанкционированного доступа представлены на рисунке 1.

Программное обеспечение

Программное обеспечение (ПО) обеспечивает управление режимами работы БС-ДПС/М, и на основе данных, полученных от датчиков угла поворота, рассчитывает фактические значения скорости и дальности (пути).

Уровень защиты ПО «высокий» в соответствии с Р 50.2.077-2014.

Идентификационные данные метрологически значимого ПО, представлены в таблице 1.

Таблица 1 — Идентификационные данные ПО БС-ДПС/М

Идентификационные признаки	Значение
Идентификационное наименование	БС-ДПС-CAN
Номер версии ПО	не ниже 1.0
Цифровой идентификатор	05*
*Значение цифрового идентификатора ПО может меняться в зависимости от версии ПО

Технические характеристики

Таблица 2 — Метрологические характеристики БС-ДПС/М

Наименование параметра	Значение
Диапазон измерения частоты следования импульсов, Гц	от 1 до 2000*
Диапазон измерения количества импульсов, шт.	от 0 до 113255864*
Коэффициент преобразования частоты следования импульсов в скорость	269,279- 10-6 D**
Коэффициент преобразования количества импульсов в пройденный путь	74,799 10-6 D**
Диапазон преобразования скорости, км/ч	от 0 до 300
Диапазон преобразования пройденного пути, м	от 0 до 6777215
Пределы допускаемой абсолютной погрешности преобразования скорости, км/ч	±1,2
Пределы допускаемой абсолютной погрешности преобразования пройденного пути, м	±(2+1,25- 10-3-Бизм***)
* в зависимости от диаметра бандажа; **D — диаметр бандажа, мм; ***§изм — преобразованное значение пройденного пути, м.

Таблица 3 — Технические характеристики БС-ДПС/М

Наименование параметра	Значение
Количество каналов связи RS-485, шт.	1
Количество каналов связи CAN, шт.	1
Масса, кг, не более	1,6
Г абаритные размеры, мм, не более	260x210x45
Диапазон рабочих температур, °С	от -40 до +60
Напряжение питания, В	50±5

Знак утверждения типа

наносится на переднюю панель блока БС-Д11С/М лазерным способом, а также на титульный лист паспорта в центре типографским способом.

Комплектность

Таблица 4 — Комплектность БС-ДПС/М

Наименование	Обозначение	Количество
БС-ДПС/М-CAN (БС-ДПС/М-БЗС-САК )	04Б.13.00.00-03 (04Б.13.00.00-06)	1 шт.
Паспорт	04Б. 13.00.00-03 ПС (04Б.13.00.00-06 ПС)	1 шт.
Руководство по эксплуатации	04Б.13.00.00 РЭ	по заявке потребителя
Методика поверки	04Б.13.00.00 МП	по заявке потребителя

Поверка

осуществляется по документу 04Б.13.00.00 МП «Блок связи БС-ДПС/М. Методика поверки», утвержденному ФБУ «УРАЛТЕСТ» 19.04.2017 г.

Основное средство поверки:

— частотомер электронно-счетный Ч3-85/3 (регистрационный номер в Федеральном информационном фонде № 32359-06).

Допускается применение аналогичных средств поверки, обеспечивающих определение метрологических характеристик поверяемых СИ с требуемой точностью.

Знак поверки наносится на свидетельство о поверке.

Сведения о методах измерений

приведены в эксплуатационном документе.

Нормативные документы

01Б.01.00.00 ТУ Блок связи с ДПС БС-ДПС.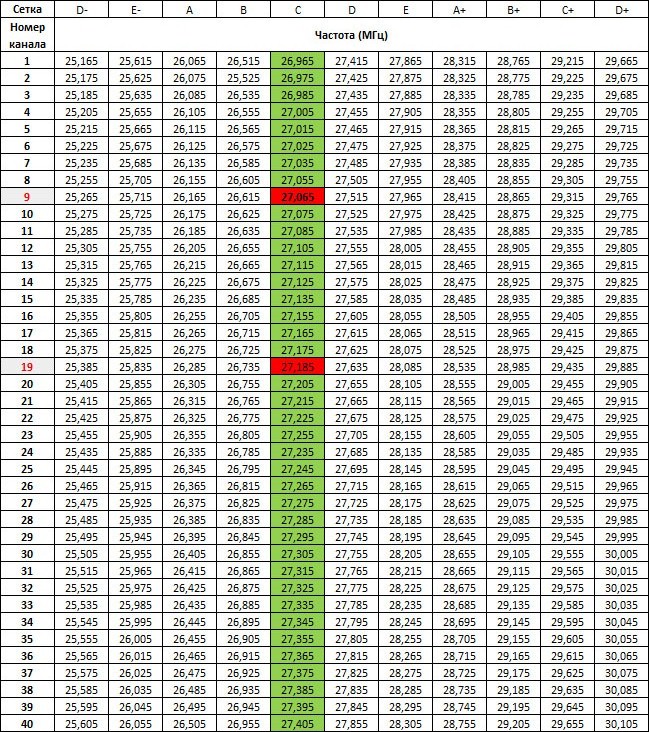 Технические условия.

Прикладные науки | Free Full-Text

1. Введение

Одним из наиболее интересных и широко используемых подходов к анализу многомерных данных является кластерный анализ или методы кластеризации. В настоящее время существует множество алгоритмов кластеризации. Несмотря на существенные различия между ними, все они опираются на исходный постулат компактности: в пространстве объектов все «близкие» объекты должны принадлежать одному кластеру, а все разные объекты, соответственно, должны находиться в разных кластерах. Понятия «близости» интерпретируются по-разному в разных алгоритмах кластеризации.

В рамках дискретного математического анализа (ДМА) — оригинального подхода к анализу данных, использующего нечеткую математику и нечеткую логику [1], разрабатываются методы так называемой DPS-кластеризации. Настоящее исследование посвящено кластеризации DPS и продолжает серию работ по этой проблеме [2,3,4,5,6,7].

Первоначальное понятие DPS-кластеризации представляет собой нечеткую модель фундаментального математического свойства «предел». Она называется плотностью и представляет собой неотрицательную функцию, зависящую от произвольного подмножества и любой точки исходного пространства, в которой предполагается кластеризация.

Значение плотности можно понимать как силу связи между подмножеством и точкой, как степень влияния подмножества на точку или двойственно, как степень ограничения точки подмножеством. Такой взгляд на плотность автоматически требует ее монотонности по подмножеству: чем больше подмножество, тем сильнее его влияние на точку, и оно более ограничивает ее.

Нетривиальные плотности всегда существуют в конечном метрическом пространстве (КМП). Каждая плотность на БМС дает новый взгляд на нее и новую программу ее изучения, так что плотность есть новое математическое понятие.

Фиксируя уровень плотности α и интерпретируя его как предельный уровень, можно ввести понятие дискретного совершенства с уровнем α: подмножество называется дискретно совершенным с уровнем α (α-DPS- или просто DPS-множество), если оно состоит ровно всех точек исходного пространства α-предела к нему. В рамках DMA построена строгая теория DPS-множеств. В частности, показано, что DPS-множества обладают свойствами кластеров. Это, а также сравнение DPS-кластеризации с современными алгоритмами кластерного анализа и его приложениями подробно описано в [5].

Созданные к настоящему времени алгоритмы DPS-кластеризации работают в конечных метрических пространствах, зависят от трех параметров (плотность P, уровень плотности α и радиус локального покрытия r) и состоят из двух этапов.

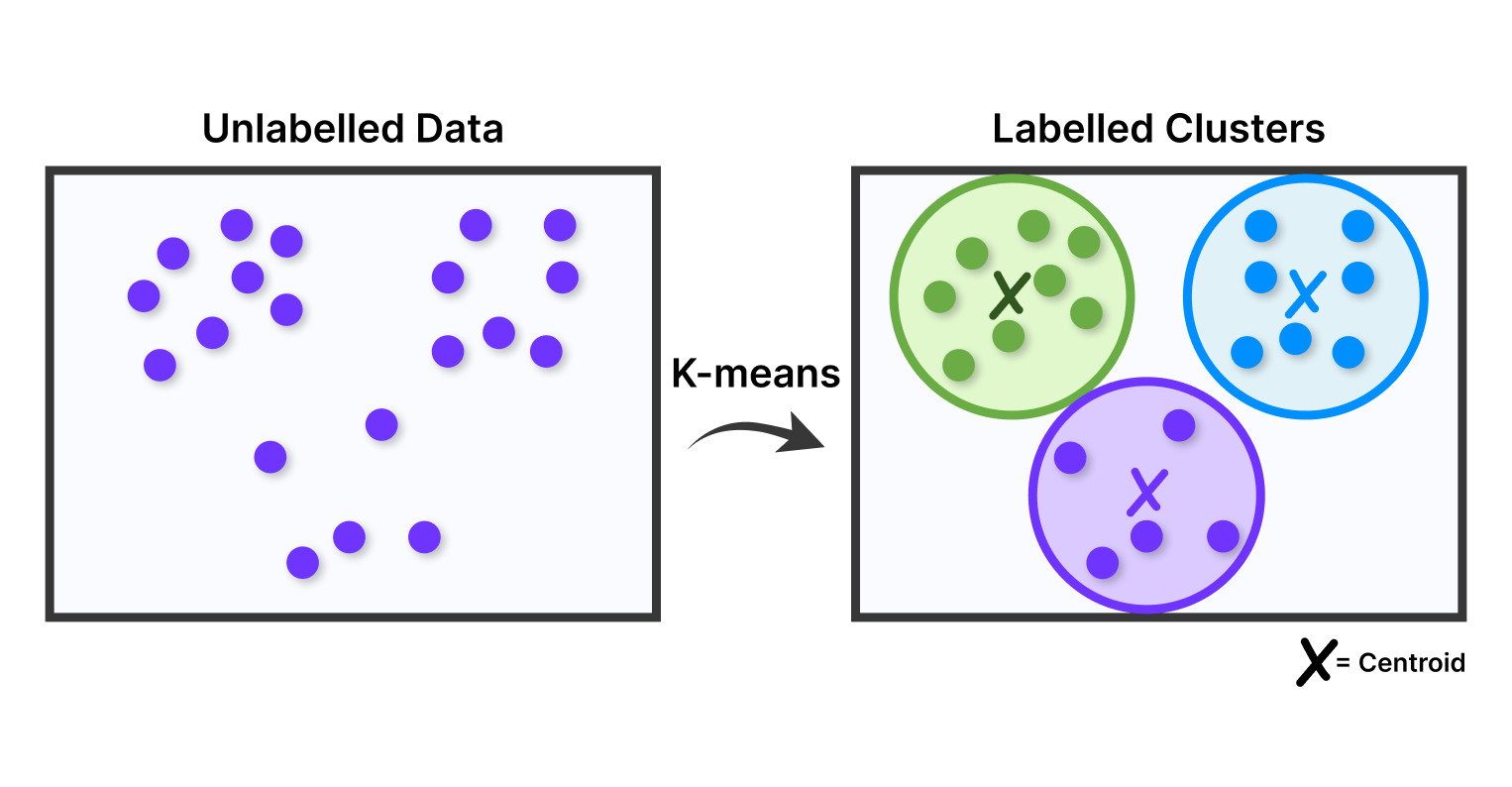
На первом этапе осуществляется топологическая фильтрация исходного пространства. Чистится от шума. DPS-алгоритм итеративно вырезает из исходного пространства (рис. 1а) максимальное α-совершенное подмножество (рис. 1б).

На втором этапе DPS-алгоритм разбивает результат второго этапа на r-связные компоненты, которые он считает кластерами (рис. 1в).

Для массива на рис. 1а и для алгоритма SDPS, наиболее известного из алгоритмов DPS Раздел 2.2.2, кластеры показаны на рис. 1б разными цветами. Аналогичные кластеры, полученные в результате работы на заданном массиве известных алгоритмов кластерного анализа DBSCAN [8] и OPTICS [9], практически совпадают и представлены на рис. 1в. Это позволяет сделать вывод, что DPS-алгоритмы, как и алгоритмы DBSCAN и OPTICS, представляют собой новый этап в кластерном анализе, поскольку не только разбивают исходное пространство на однородные части, но и предварительно очищают его от шума (фильтруют).

Исследования показывают, что бывают ситуации, когда результат первого этапа не включает все заслуживающие внимания кластеры. Снижение уровня ограничения а приводит к снижению качества распознавания кластера и не является выходом из ситуации.

Кроме того, из-за локальности радиуса разбиение на r-связные компоненты максимального α-совершенного подмножества на втором этапе часто бывает слишком мелким и подробным и требует расширения, как видно на рис. 1б. .

Исправлению этих недостатков посвящена настоящая работа.

2.

Материалы и методы

В этом разделе определяются DPS-наборы и описываются алгоритмы DPS-кластеризации.

2.1. Дискретные совершенные множества

DMA имеет строгую теорию дискретных совершенных множеств (DPS-множеств) в конечных пространствах, которая кратко изложена в [5]. Полное строгое обоснование можно найти в [3].

Пусть X — конечное множество, а A, B,… и x, y,… — его подмножества и точки соответственно.

При фиксированном x функция PA(x) является ненормированной нечеткой мерой на X, поэтому плотность P представляет собой семейство таких мер, параметризованных самим X.

Фиксируя уровень плотности α и интерпретируя его как предельный уровень, можно определить любые топологические понятия в X, в частности, дискретное совершенство с уровнем α.

Многочисленные исследования и приведенные ниже примеры показывают, что DPS-множества являются кластерами в X и тесно связаны с кластеризацией в X.

В работах [2,3,5] приведена конструкция, допускающая подмножество A(α) ⊂X построить по подмножеству A в пространстве X и уровню α плотности P. При условии нетривиальности это будет α-DPS-множество в X. Оно не обязано лежать в A, но если само A является α-DPS-множеством в X, то построенное для него множество A(α) будет совпадать с ним. Таким образом, конструкция A⇒A(α) зависит от пространства X, подмножества A, плотности P и уровня α. Чтобы подчеркнуть этот факт, введем обозначение

Свойства конструкции A⇒AP(α|X) сформулированы в утверждении 1, доказанном в [3].

2.2. DPS-алгоритмы

В случае всего пространства X переход X⇒X(α) является итерационным разрезом:

α-совершенство наследуется компонентами связности множества X(α). Именно они наиболее точно соответствуют в первом приближении эмпирическим кластерам.

Далее на пространстве X задана метрика d, так что (X,d) является КМП.

2.2.1. Топологическое отступление

Две точки x и y в A называются r-связными, если существует цепочка из r-близких друг к другу точек x0,…,xn в A с началом x0=x, а концом xn=y и расстояния d(xi,xi+1)≤r, i=0,…,n−1. Отношение r-связности представляет собой эквивалентность, разбивающую множество A на компоненты r-связности, которые в зависимости от контекста будут обозначаться cA(k)=crA(k), k=1,…,k*=k*( А, р). Обозначим их набор через C(A)=Cr(A)={cA=crA(k)|1k*}. Таким образом:

где знак ∨ обозначает несвязное объединение множеств.

Для x∈X, A⊂X обозначим через DA(x,r) замкнутый шар в A с центром в x и радиусом r: DA(x,r)={a∈A:d(x,a) ≤r}.

Доказательство.  

Согласно (2) для любого k=1,…,k* необходимо установить равенство компоненты crX(α)(k) с множеством {x∈X:PcrX(α)( k)(x)≥α}, которую обозначим через crX(α)(k)1.

Включение crX(α)(k)⊆{x∈X:PcrX(α)(k)(x)≥α}. x∈crX(α)(k)⇒x∈X(α)⇒PX(α)(x)≥α. Кроме того, DX(α)(x,r)=DcrX(α)(k)(x,r), так как d(x,crX(α)(k¯))>r при k¯≠k. В силу r-локальности P PcrX(α)(k)(x)=PDcrX(α)(k)(x,r)(x)=PDX(α)(x,r)(x)=PX( α)(x)≥α, x∈crX(α)(k)1.

Включение crX(α)(k)⊇{x∈X:PcrX(α)(k)(x)≥α}.

Первый случай (x∉crX(α)(k))∧(x∉X(α)). Тогда PcrX(α)(k)(x)≤PX(α)(x)<α⇒x∉crX(α)(k)1.

Второй случай (x∉crX(α)(k))∧(x∈X(α)). Тогда (x∈crX(α)(k¯)) и d(x,crX(α)(k¯))>r, поэтому DcrX(α)(k)(x,r)=⌀.

С учетом нормировки плотности P и ее r-локальности PcrX(α)(k)(x)=0. Таким образом, в этом случае x∉crX(α)(k)1. □

Далее по тексту DPS(P,α,r) обозначает, в зависимости от контекста, либо сам алгоритм, либо его первую стадию.

Приведем блок-схему DPS-алгоритма (рис. 2).

Подытожим сказанное с точки зрения кластерного анализа: 1-й этап DPS(P,α,r) вырезает из исходного пространства X максимально плотное на общем фоне подмножество X(α); 2-й этап DPSc(P,α,r) разбивает X(α) на компоненты r-связности cX(α), каждая из которых сочетает в себе плотность на фоне и связность, т. е. формально выражает эмпирическую кластеризацию [5].

DPS-кластеризация разработала методы выбора параметров α, r, которые подробно описаны в [5] (см. также раздел 4.3.1). В частности, показатель плотности α определяется через уровень его окончания β(α), что отвечает на вопрос по шкале [−1,1]: «Насколько α можно считать большим на фоне всех значений плотность P на X?».

При построении β(α) используется нечеткое сравнение n между неотрицательными числами. Он выражает по шкале [−1,1] степень превосходства большего из них над меньшим (левая часть в (7))

В силу свойств n соответствие α⇒β(α) единственно, а обратная зависимость β⇒α(β) неявно задается правой частью (7). Таким образом, алгоритм DPS имеет вторую параметризацию, которая будет использоваться в дальнейшем:

2.2.2. SDPS-алгоритм

Исторически первым в ряду DPS-алгоритмов был теоретико-множественный SDPS. В его основе лежит плотность S, имеющая название «Количество точек» («Количество пространства») [2,3,6] и передающая степень концентрации пространства X вокруг каждой его точки x (наиболее естественное понимание плотности X в x).

Плотность SA(x) зависит от радиуса локализации r и неотрицательного параметра p, учитывающего расстояние до x в шаре DA(x,r):

При p=0 получаем обычное количество точек, что объясняет название S:

Плотность S является r-локальной, а SDPS-алгоритм является работой DPS-схемы, основанной на S: SDPS=DPS(S,β,r).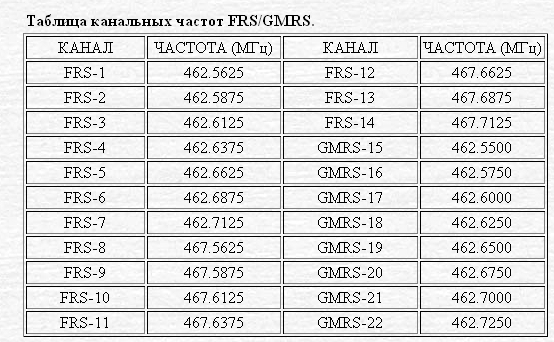

Результат SDPS-уплотнения в множествах X⇔, локально содержащих «много X». Формально они наиболее согласуются с эмпирическими кластерами. Варьируя параметры SDPS, можно получить достаточно полное представление об иерархии кластеров в X.

SDPS-алгоритм послужит полигоном, на котором будут проверены и показаны новые результаты для алгоритмов серии DPS.

3. Результаты: Итеративный DPS

Первый DPS-этап алгоритма DPS(P,β,r) вырезает максимальное совершенное подмножество X(β), β-экстремально P-плотное на фоне X в каждой из его точки из пространства X.

Обратимся к рис. 3б: на нем красным цветом показан результат X(β) алгоритма DPS на массиве X (рис. 3а) при β=0,02. Легко видеть, что не все заслуживающие внимания конденсации из X были включены. Причина их невключения в результат X(β) объясняется противоречием между r-локальным характером представления X и глобальным подходом к определению уровня α(β) плотности P по ее уровню экстремальности β на основе всего образа PX(X) (7) и (8): уровень плотности достойных сгущений в дополнении X(β)¯ оказывается ниже α(β).

Чтобы включить их в конечный результат, нужно понизить уровень экстремума β: β⇒β¯<β и перейти от алгоритма DPS(P,β,r) к алгоритму DPS(P,β¯,r). В контрольном примере первый уровень β¯, для которого результат X(β¯) будет включать все достойные сгущения, будет β¯=−0,25. Результат показан красным на рис. 3в: мы видим, что результат X(β¯) алгоритма DPS(P,β¯,r), наряду с X(β) и достойными уплотнениями из X(β)¯, включал слабые места r-ореола множества X(β), и это помогло им в этом.

Можно поступить иначе: сохранить уровень экстремума β, но изменить исходное пространство переходом от X к X(β)¯. Результат DPS(P,β,r) на X(β)¯ показан зеленым цветом на рисунке 3b. Если мы сделаем еще один подобный переход, на рис. 3b появится синий кластер.

Такой способ использования схемы DPS называется «итеративным алгоритмом DPS».

3.1. Итерации по экстремальности

Напомним, что уровень α(β) плотности P по уровню экстремальности β определяется в алгоритме DPS(P,β,r)=DPS(P,α(β),r) из уравнения (8). Введем разбиение X=X(β)∨X(β)¯. Согласно (7) и (8),

Из свойств выпуклости, отсюда и неравенство

Однако левое среднее ≤0, поскольку ∀x∈X(β)⇒PX(x)≥PX(β)(x)≥α(β). Следовательно, если β≥0, то правое среднее должно быть ≥β:

Тогда из неравенств ∀x∈X⇒PX(β)¯(x)≤PX(x) и свойств нечеткого сравнения n имеем :

Отсюда следует, что уровень плотности α1(β), необходимый для работы алгоритма DPS(P,β,r) на пространстве X(β)¯:

не превосходит уровня α(β), который будем считать нулевым: α(β)=α0(β), и может быть строго меньше его. Кроме того, это, в свою очередь, означает возможную нетривиальность такой операции, т. е. множества X(β)¯(β). Обозначим его через X1(β).

В ситуации нетривиальности X1(β) можно определить первую итерацию на конце X(β,1) множества X(β), которую естественно считать его нулевой итерацией, полагая X(β ,0)=Х(β).

Прямая проверка показывает, что PX(β,1)(x)≥α1(β)∀x∈X(β,1), поэтому, повторяя приведенный выше вывод с заменой α0(β)⇒α1(β), X(β,0)⇒X(β,1), получаем уровень α2(β)≤α1(β) алгоритма DPS(P,β,r) на дополнении X(β,1)¯ и возможная нетривиальность его результата X2(β)=X(β,1)¯(β).

Если все это можно продолжить до i-го шага включительно, т. е. множества X1(β),…,Xi(β) будут нетривиальны, то их объединение с X(β,0)=X (β) будем называть i-й итерацией X по уровню экстремума β:

3.2. Итерации алгоритма DPS

Рассматривая алгоритмы DPS(P,β,r) и DPSc(P,β,r) как их нулевые итерации: DPS0(P,β,r)=DPS(P,β,r), DPSc0(P,β,r)=DPSc(P,β,r), их i-ю итерацию определим как процессы построения для пространства X его i-й итерации X(β,i) и последующего разбиения ее на r- компоненты подключения:

Ввиду дизъюнктивного характера разложения (10) индекс итерации ind корректно определен на i-й итерации X(β,i):

Индекс ind переходит от точек к компонентам связности c=cX( β,i), становясь таким образом многозначным:

Кроме того, это, в свою очередь, позволяет для любого подмножества I∈[0,i] определить условный вариант алгоритма DPSI:

4. Результаты: Третий этап DPS

Первый этап алгоритма DPS⇔DPS(P,α,r) вырезает из исходной FMS X максимальное α-совершенное подмножество X(α):DPS(X)=X(α). Второй этап алгоритма DPSC⇔DPSC(P,α,r) считается его результатом и представляет собой совокупность всех компонент r-связности множества X(α):DPSC(X)=CrX(α ). Каждая компонента crX(α) считается DPS-кластером, так как в силу исходного предположения о r-локальности начальной плотности P является DPS-множеством в X и, в частности, α-плотно в каждой из его точек.

На данном этапе результат DPSC(X) принимается как заданный и дальнейшему преобразованию не подлежит. Радиус r предполагается бесконечно малым, а уровень α функции P бесконечно большим. Как следствие, каждая компонента cX(α) считается единым и неделимым пятном (большой точкой).

Пятна cX(α) интерпретируются как фрагментарные проявления (выходы) глобальных аномальных сущностей в X. Для понимания их истинных масштабов, по возможности, необходимо дальнейшее соединение пятен. Это третий и последний этап DPS-алгоритма.

4.1. Логика и план действий

Набор пятен C⊂DPSc(X) рассматривается экспертом как единое целое, если степень преимущества в близости внутренних переходов (путей) между любыми его пятнами перед внешними переходами из C в C ¯, позволяет эксперту заключить, что C неслучайна.

Таким образом, скопление пятен C должно иметь более тесную внутреннюю связь между собой на общем фоне всех пятен из DPSc(X). Других ограничений на C, в частности на форму, нет.

Ввиду α-совершенности пятен cX(α)(k) минимальное расстояние между ближайшими точками в них естественно рассматривать как расстояние между ними:

Это уже не будет метрикой, так как не являются неравенствами треугольника для d (13), как показывает следующий пример:

На основе расстояния d строится формализация экспертной логики соединения пятен: в каждом кластере пятен C любые два пятна можно соединить цепочка точек, расстояние d между соседними звеньями которых будет меньше, чем расстояние d от C до C¯. Это условие d-кластеризации, необходимое для C. Его формальный анализ будет первой частью работающей программы по алгоритмизации третьего этапа DPS. Обратите внимание, что d-кластеризация и DPS-кластеризация — это разные интерпретации кластеризации: первая основана на связности, а вторая — на ограничении.

Вторая часть этой программы состоит в построении на основе начального расстояния d в исходном пространстве X мер близости и расстояния между точками, выражающих в этом эксперт. На их основе из d-кластеров пятен выбираются только те пятна, в которых преимущество близости внутренних переходов над размахом внешних будет, по мнению эксперта, неслучайным.

4.2. Первая часть: Теория d-кластеров

Исходные данные и обозначения: X — конечное множество, d — квазиметрика в X ((X,d) — квазиметрическое пространство)

4.2.1. Обозначение

d(x) представляет собой числовую последовательность расстояний di(x)=dXi−1(x),Xi−1(x)¯:

Другими словами, в случае d-кластеризации имеется теоретико-множественное равенство Xk(x)=Xk(y), т. е. для любого y∈Ck(x) первые k+1 слагаемых в нумерации X(y) будут лежать в Ck(x).

D-кластеры Ck(x) являются собственными неточечными подмножествами в X. Удалим это ограничение на k в определении 7, используя понятие показателя связности, которое развивает и продолжает тему конечной связности раздела 2. 2.1.

Для собственного d-кластера C (определение 7) доказанное утверждение означает выполнение необходимого условия

Оно инвариантно не только от начала перечисления, но и от самого перечисления, обязательного на данном этапе для определения C. Поэтому естественно проверить это условие на достаточность d-кластеризации.

Результатом определения 8, утверждения 4 и утверждения 5 является новый инвариант и более полное определение d-кластера.

К собственным кластерам C(1<|C|<|X|) будут добавлены все точки x∈X: x=C0(x) и все пространство X: X=C|X|−1(x)∀ х∈Х.

Таким образом, ограничения в определении 7 на k(1≤k≤|X|−2) снимаются:

•

x⇔d-кластер, поскольку 0=r(x)

•

X⇔d-кластер, поскольку r(X)

4.2.2. Выводы

Набор d-кластеров C(X,d) образует иерархию множеств на X, основанную на понятии дискретной связности и отличающуюся от традиционных иерархий иерархического кластерного анализа, обычно бинарных [10].

C(X,d) — первая часть формализации третьего этапа ДПС.

4.3. Вторая часть: окончательный отбор D-кластеров

Благодаря (14)–(16) поиск d-кластеров в пространстве компонент r-связности DPSC(X) относительно расстояния (13), т. е. формирование пространства C(DPSC(X),d) конструктивно. Каждый d-кластер C∈C(DPSC(X),d) имеет две характеристики: внутреннюю r(C) и внешнюю e(C) (17). На основании этой информации эксперт Е должен решить: нужно ли объединять пятна из С в единое целое или нет?

Пусть DPSf(X)=DPSf(X|E) обозначает множество максимальных d-кластеров в DPSC(X), полученных после объединения пятен экспертом E. Согласно Следствию 1, все они не пересекаются.

При условии нетривиальности DPSf(X) в множестве X(α) в общем случае появляется разбиение большее, чем разбиение (5), на компоненты r-связности:

Обозначим его также через DPSf(X ) и считать его третьим и последним этапом алгоритма DPS. Полная история представлена ​​на рисунке 6.

Таким образом, для каждой компоненты crX(α) может произойти одно из трех:

• crX(α)∈DPSf(X)⇔ компонент crX(α) достаточно изолирован от остальных, чтобы представлять интерес для эксперт, это единственный выход из стоящей за ним глобальной сущности на X;

• crX(α)∉DPSf(X), но crX(α)⊂C∈DPSf(X)⇔ компонента crX(α) входит в состав d-кластера C, представляющего интерес для эксперта и в команда представляет глобальную сущность в X;

• crX(α)∉C∀C∈DPSf(X)⇔ любой d-кластер, содержащий crX(α), не представляет интереса для эксперта: либо он недостаточно внутренне плотен, либо внешне сепарабельен. По мнению эксперта, если crX(α) является фрагментом выхода глобальной сущности на X, то это недостаточно ясно.

Кроме того, пример 3 покажет, что возможны все варианты crX(α).

На этапе 3.2 (рисунок 6) эксперт может действовать по-разному. Приведем простейший булев вариант действий по формированию DPSf(X).

4.

3.1. Булев вариант

Эксперт E решает, включен ли d-кластер C в окончательный результат DPSf(X) на основе сравнения r(C) и e(C) с их порогами близости и расстояния rE и eE: C∈DPSf(X )⇔r(C)≤rE и e(C)≥eE.

Эксперт E считает параметр r DPS-алгоритма очень малым (бесконечно малым), много меньше rE, который, в свою очередь, согласно E, много меньше eE:

Порог rE, как и радиус r в DPS-алгоритме, строится с помощью колмогоровского усреднения нетривиальных расстояний ФМС X [5]

Для параметра r многочисленные применения алгоритмов серии DPS установили, что выбор q(r)∈[−3,−2] можно считать оптимальным. Исследования, проведенные в рамках настоящей статьи, показывают, что q(rE)∈[−2,5,−1,5]. Пересечение областей параметров r, rE объясняется как нечетким восприятием близости экспертом, так и разнообразием в расположении произвольной ФМС.

Порог eE получается из rE путем формализации экспертной оценки «rE≪eE» с использованием нечеткого сравнения. Для сравнения, приведенного в примере 1, это будет неравенство eE/rE≥5/3.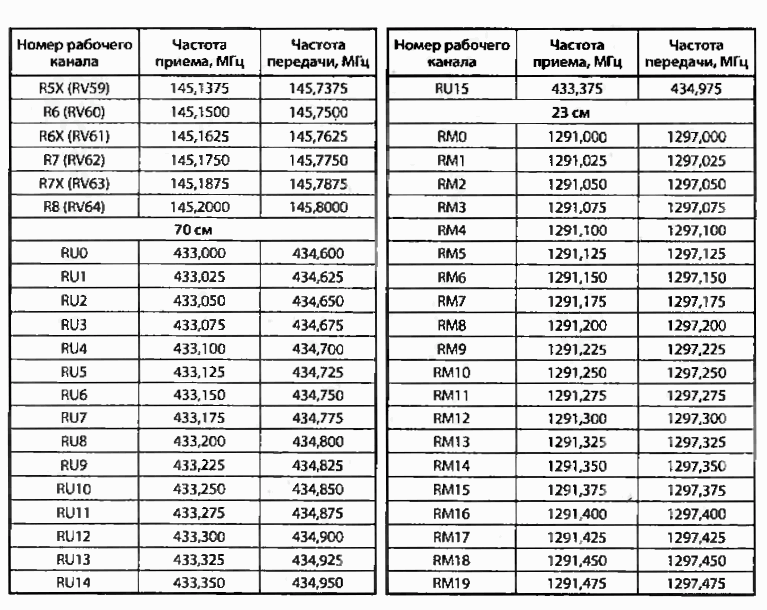

5. Обсуждение

Плотность P на конечном пространстве X есть определение в X на языке нечеткой математики свойства предельности. С формальной точки зрения P — нечеткая структура на прямом произведении 2X×X, монотонная по первому аргументу (1).

Зафиксировав уровень α∈[0,1] для P, мы можем определить оператор замыкания на 2X и через него обычную топологию τα на X. Таким образом, растущее семейство топологий {τα,α∈[0, 1]}, возникает на X, начиная с нуля с тривиально неотделимой минимальной топологией склеивания точек и заканчивая тривиально отделимой максимальной топологией всех подмножеств.

Каждая плотность на пространстве X дает свой взгляд на него и свою программу его изучения. Это концепция, которой нет в классической математике.

Помимо плотности S Раздел 2.2.2, в конечном метрическом пространстве всегда существуют нетривиальные плотности. Описание наиболее важных плотностей и их значение для анализа данных приведены в [5,11].

Изучение пространства X с помощью заданной на нем плотности P началось с изучения совершенных множеств в топологии τα. Объяснение этому следующее: установка P на X определяет кластеризацию в X: K является кластером (P-кластером) в X, если он состоит ровно из всех точек, которые являются P-предельными для него. Если α — предельный порог, то формальное выражение сказанного совпадает с α-совершенством: K={x∈X:PK(x)≥α}.

DPS-алгоритм строит все такие кластеры, но их слишком много для полноценного кластерного анализа в X: в первую очередь нам нужны «компоненты связности» максимального α-совершенного подмножества X(α) в X .

Все это существует, когда X есть БМЗ и плотность P локальна на нем. Именно в этой ситуации и работает DPS-алгоритм. Это зависит от конструкции плотности P, ее уровня α и радиуса локализации r: DPS=DPS(P,α,r). ДПС работает в два этапа: сначала он вырезает подмножество X(α) в X (первый этап), а затем разбивает его на r-связные компоненты, которые считает ДПС-кластерами в X (второй этап).

Несмотря на в целом хорошие результаты и эффективность приложений [4,5,11,12,13], DPS-алгоритм в его текущей версии имеет недостатки: на первом этапе разрез X⇒X(α) не всегда тщательный и высокого качества; на втором этапе разбиение X(α) на компоненты r-связности слишком мало и детализировано из-за локальности радиуса r. Правильное разбиение X(α) должно происходить из глобального представления X(α), индуцированного всем пространством X.

В настоящей статье мы предприняли попытки исправить или смягчить эти недостатки: наши ответы были этап — итерационная схема разрезания DPSi(X), на втором — ее третий этап DPSf(X) соединения компонент r-связности.

Итерации позволили DPS-алгоритму на первом этапе добиться полноты своего результата DPS(X) при сохранении высокого уровня экстремальности резания.

На данный момент результатом DPSC(X) второго этапа DPS-алгоритма считается его окончательный результат. Предлагаемые в статье дополнительные соединения компонентов из DPSC(X) происходят в два этапа. На первом из них, имеющем необходимый характер, в DPSC(X) ищутся d-кластеры. По результатам статьи их поиск носит конструктивный характер. d-кластеризация является необходимым условием соединения компонентов из DPSC(X) в единое целое. Набор d-кластеров C(DPSC(X),d) служит основой для второго этапа, которого уже достаточно. Главное здесь — эксперт: его критерии формируют окончательный выбор ДФСf(X) в C(DPSC(X),d) и одновременно финальное разбиение ВРСК(X). В DMA существуют различные формальные варианты этого выбора. Самый простой из них приведен в разделе 4.3.1.

Алгоритмы серии DPS активно применяются во многих геолого-геофизических исследованиях (анализ сейсмических каталогов, поиск сигналов на геофизических записях, в задаче захоронения радиоактивных отходов и др.) [1,4,5,7,11, 12,13]. Представляется, что новая версия DPS, разработанная в настоящей статье, позволит улучшить это приложение.

Добавление третьего каскада к ДПС по мнению авторов делает его архитектуру достаточной. Дальнейшее развитие DPS-алгоритмов должно происходить через их параметры: новые конструкции плотностей и их связь с нечеткой логикой дадут (и уже дают [5]) возможность глубокого изучения конечных метрических пространств. Кроме того, принципиально следующее обстоятельство: в отличие от евклидова пространства БМП X локальна в каждой своей точке x; как правило, устроен по-разному; поэтому параметры α, r DPS-алгоритма, имеющие локальный характер, должны зависеть от x: r=r(x), α=α(x). Итеративная схема карвинга только смягчает дело.

Способы взаимодействия Dps Escherichia coli с ДНК по данным атомно-силовой микроскопии

1. Азам Т.А., Исихама А. Двенадцать видов нуклеоид-ассоциированного белка из Escherichia coli . Специфичность распознавания последовательности и аффинность связывания ДНК. Дж. Биол. Хим. 1999; 274: 33105–33113. 10.1074/jbc.274.46.33105 [PubMed] [CrossRef] [Google Scholar]

2. Дорман Си Джей. Нуклеоидассоциированные белки и физиология бактерий. Adv Appl Microb. 2009; 67: 47–64. 10.1016/С0065-2164(08)01002-2 [PubMed] [CrossRef] [Академия Google]

3. Азам Т.А., Ивата А., Нисимура А., Уэда С., Исихама А. Зависящие от фазы роста изменения белкового состава нуклеоида Escherichia coli . J Бактериол. 1999; 181: 6361–6370. [Бесплатная статья PMC] [PubMed] [Google Scholar]

4. Гудман С.Д., Вельтен Н.Дж., Гао К., Робинсон С., Сегалл А.М. In vitro Выбор сайтов связывания интеграционного фактора хозяина. J Бактериол. 1999; 181: 3246–3255. [Бесплатная статья PMC] [PubMed] [Google Scholar]

5. Чо Б.К., Найт Э.М., Барретт К.Л., Палссон Б.О. Полногеномный анализ связывания Fis в Escherichia coli указывает на причинную роль A-/AT-трактов. Генерал рез. 2008; 18: 900–910. 10.1101/гр.070276.107 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

6. Чо Б.К., Барретт К.Л., Найт Э.М., Парк Ю.С., Палссон Б.О. Реконструкция в масштабе генома регуляторной сети Lrp у Escherichia coli . Proc Natl Acad Sci USA. 2008; 105: 19462–19467. 10.1073/пнас.0807227105 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

7. Bouffartiques E, Buckle M, Badaut C, Travers A, Rimsky S. Совместное связывание H-NS с высокоаффинными сайтами в регуляторном элементе приводит к подавлению транскрипции. Nat Struct Mol Biol. 2007; 14: 441–448. 10.1038/nsmb1233 [PubMed] [CrossRef] [Академия Google]

8. Ueguchi C, Kakeda M, Yamada H, Mizumo T Аналог молекулярного шаперона DnaJ в Escherichia coli . Proc Nati Acad Sci USA. 1994; 91: 1054–1058. 10.1073/пнас.91.3.1054 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

9. Блох В., Ян Ю., Марже Э., Шаванье А., Ож М.Т., Роберт Б. и другие. Домен димеризации H-NS определяет новую складку, способствующую распознаванию ДНК. Nat Struct Mol Biol. 2003; 10: 212–218. 10.1038/нсб904 [PubMed] [CrossRef] [Академия Google]

10. Sonnenfield JM, Burns CM, Higgins CF, Hinton JCD. Нуклеоид-ассоциированный белок StpA связывается с искривленной ДНК, обладает большей аффинностью связывания с ДНК, чем H-NS, и присутствует в значительных количествах у мутантов hns . Биохимия. 2001; 83: 243–249. [PubMed] [Google Scholar]

11. Боннефой Э., Такахаши М., Янив Ю.Р. Параметры ДНК-связывания белка HU Escherichia coli с крестообразной ДНК. Дж Мол Биол. 1994; 242: 116–129. 10.1006/jmbi.1994.1563 [PubMed] [CrossRef] [Академия Google]

12. Castaing B, Zelwer C, Laval J, Boiteux S. Белок HU Escherichia coli специфически связывается с ДНК, которая содержит одноцепочечные разрывы или разрывы. Дж. Биол. Хим. 1995; 270: 10291–10296. 10.1074/jbc.270.17.10291 [PubMed] [CrossRef] [Google Scholar]

13. Лавуа Б.Д., Шоу Г.С., Милнер А., Чаконас Г. Анатомия комплекса сгибатель-ДНК внутри промежуточного соединения транспозиции более высокого порядка. Клетка. 1996; 85: 761–771. 10.1016/С0092-8674(00)81241-6 [PubMed] [CrossRef] [Академия Google]

14. Альмирон М.А., Линк Дж., Ферлонг Д., Колтер Р. Новый ДНК-связывающий белок с регулирующей и защитной ролью у голодающих Escherichia coli . Гены Дев. 1992;6: 2646–2654. 10.1016/0168-9525(93)

-5 [PubMed] [CrossRef] [Google Scholar]

15. Ceci P, Cellai S, Falvo E, Rivetti C, Rossi GL, Chiancone E. Конденсация ДНК и самоагрегация Escherichia coli Dps являются связанными явлениями, связанными со свойствами N-конца. Нукл Кислоты Res. 2004;32:5935–5944. 10.1093/нар/гх915 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

16. Грант Р.А., Filman DJ, Finkel SE, Kolter R, Hogle JM. Кристаллическая структура Dps, гомолога ферритина, который связывает и защищает ДНК. Nat Struct Biol. 1998;5: 294–303. 10.1038/нсб0498-294 [PubMed] [CrossRef] [Google Scholar]

17. Де лос Риос С, Перона Дж. Структура лейцин-чувствительного регуляторного белка Lrp Escherichia coli раскрывает новую октамерную сборку. Дж Мол Биол. 2007;366:1589–1602. 10.1016/j.jmb.2006.12.032 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

18. Ceci P, Ilari A, Falvo E, Giangiacomo L, Chiancone E. Переоценка стабильности белка, связывания ДНК и защиты Mycobacterium smegmatis Dps. Дж. Биол. Хим. 2005; 280: 34776–34785. 10.1074/jbc.M502343200 [PubMed] [CrossRef] [Google Scholar]

19. Рой С., Сарасвати Р., Чаттерджи Д., Виджаян М. Структурные исследования второго Mycobacterium smegmatis Dps: инвариантные и изменчивые особенности структуры, сборки и функции. Дж Мол Биол. 2008;375:948–959. Доступно: http://www.ncbi.nlm.nih.gov/pubmed/17543333. [PubMed] [Google Scholar]

20. Юань Х.С., Финкель С.Э., Фэн Дж.А., Качор-Гржесковяк М., Джонсон Р.С., Дикерсон Р.Э. Молекулярная структура дикого типа и мутантного белка FIS: взаимосвязь между мутационными изменениями и функцией рекомбинационного энхансера или связыванием ДНК. Proc Natl Acad Sci USA. 1991; 88: 9558–9562. 10.1073/пнас.88.21.9558 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

21. Кавамура Т., Вартанян А.С., Чжоу Х., Далквист Ф.В. Конструкция, связанная с регуляцией PapI и Lrp оперона pap. Дж Мол Биол. 2011;409: 311–332. 10.1016/j.jmb.2011.01.05 [PubMed] [CrossRef] [Google Scholar]

22. Кордейро Т.Н., Шмидт Х., Мадрид С., Хуарес А., Бернадо П., Гризингер С. и другие. Непрямое считывание ДНК белком, родственным H-NS: структура комплекса ДНК С-концевого домена Ler. Путь PLoS. 2011;7: e1002380 10.1371/журнал.ppat.1002380 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

23. Райс П.А., Ян С.В., Мизуучи К., Нэш Х.А. Кристаллическая структура комплекса IHF-ДНК: разворот ДНК, индуцированный белком. Клетка. 1996;87: 1295–1306. 10.1016/S0092-8674(00)81824-3 [PubMed] [CrossRef] [Google Scholar]

24. Стелла С., Касио Д., Джонсон Р.С. Форма малой бороздки ДНК определяет связывание ДНК-изгибающего белка Fis. Генерал Дев. 2010; 24: 814–826. 10.1101/гад.1

0 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

25. Ceci P, Ilari A, Falvo E, Chiancone E. Белок Dps Agrobacterium tumefaciens не связывается с ДНК, но защищает ее от окислительного расщепления: рентгеновская кристаллическая структура, связывание железа и свойства удаления гидроксильных радикалов. Дж. Биол. Хим. 2003;278:20319–20326. 10.1074/jbc.M302114200 [PubMed] [CrossRef] [Google Scholar]

26. Стиллман Т.Дж., Упадхьяй М., Норте В.А., Седельникова С.Е., Каррадус М., Цоков С. и соавт. Кристаллические структуры белков Lactococcus lactis MG1363 Dps обнаруживают наличие N-концевой спирали, необходимой для связывания ДНК. Мол микробиол. 2005; 57: 1101–1112. 10.1111/j.1365-2958.2005.04757.x [PubMed] [CrossRef] [Google Scholar]

27. Chiancone E, Ceci P. Многогранная способность белков Dps бороться с бактериальными стрессовыми состояниями: детоксикация железа и перекиси водорода и связывание ДНК. Биохим Биофиз Акта. 2010;18:00:798–805. 10.1016/j.bbagen.2010.01.013 [PubMed] [CrossRef] [Google Scholar]

28. Ceci P, Mangiarotti L, Rivetti C, Chiancone E. Активирующий нейтрофилы белок Dps Helicobacter pylori , HP-NAP, использует механизм, отличный от Escherichia coli Dps, для связывания и конденсации ДНК. Нукл Кислоты Res. 2007; 35: 2247–2256. 10.1093/нар/гкм077 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

29. Гупта С., Чаттерджи Д. Бимодальная защита ДНК с помощью Mycobacterium smegmatis ДНК-связывающий белок из клеток стационарной фазы. Дж. Биол. Хим. 2003; 278: 5235–5241. 10.1074/jbc.M208825200 [PubMed] [CrossRef] [Google Scholar]

30. Вольф С.Г., Френкель Д., Арад Т., Финкель С.Е., Колтер Р., Мински А. Защита ДНК с помощью стресс-индуцированной биокристаллизации. Природа. 1999; 400: 83–85. 10.1038/21918 [PubMed] [CrossRef] [Google Scholar]

31. Френкил-Криспин Д., Левин-Зайдман С., Шимони Э., Вольф С.Г., Вахтель Э.Дж., Арад Т. и другие. Регулируемые фазовые переходы бактериального хроматина: неферментативный путь общей защиты ДНК. EMBO J. 2001; 20: 1184–119.1. 10.1093/emboj/20.5.1184 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

32. Френкил-Криспин Д., Бен-Авраам И., Энгландер Дж., Шимони Э., Вольф С.Г., Мински А. Реструктуризация нуклеоидов в стационарных бактериях. Мол микробиол. 2004; 51: 395–405. 10.1046/j.1365-2958.2003.03855.x [PubMed] [CrossRef] [Google Scholar]

33. Азам Т.А., Хирага С., Исихама А. Два типа локализации ДНК-связывающих белков в нуклеоиде Escherichia coli . Клетки генов. 2000;5: 613–626. 10.1046/j.1365-2443.2000.00350.x [PubMed] [CrossRef] [Академия Google]

34. Френкил-Криспин Д., Мински А. Организация нуклеоидов и поддержание целостности ДНК в E . кишечная палочка , В . subtilis и D . радиодуранс . J Struct Biol. 2006; 156: 311–319. 10.1016/j.jsb.2006.05.014 [PubMed] [CrossRef] [Google Scholar]

35. Huergo LF, Rahman H, Ibrahimovic A, Day CJ, Korolika V. Campylobacter jejuni Белок Dps связывается с ДНК в присутствии железа или перекиси водорода. J Бактериол. 2013;195: 1970–1978. 10.1128/ДЖБ.00059-13 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

36. Zeth K. Биоминерализующие белки Dps: многофункциональные архитекторы природы. Биохим Дж. 2012; 445: 297–311. 10.1042/БДЖ20120514 [PubMed] [CrossRef] [Google Scholar]

37. Сальгадо Х., Перальта-Хиль М., Гама-Кастро С., Сантос-Завалета А., Муньис-Раскадо Л., Гарсия-Сотело Х.С. и другие. RegulonDB v8.0: наборы данных omics, эволюционное сохранение, нормативные фразы, перекрестная проверка золотых стандартов и многое другое. Нукл Кислоты Res. 2013;41(Выпуск базы данных): Д203–213. 10.1093/нар/гкс1201 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

38. Калхун Л.Н., Ким Дж.Н., Рен И, Сонг Дж.Дж., Квон Ю.М. ДНК-связывающий белок Dps функционирует как глобальный регулятор при голодании Salmonella enterica сероварного энтеритита во время голодания. Int J Microb Res. 2011;3: 136–147. 10.9735/0975-5276.3.3.136-147. [CrossRef] [Google Scholar]

39. Пуртов Ю.А., Глазунова О.А., Антипов С.С., Покусаева В.О., Фесенко Е.Е., Преображенская Е.В. и другие. Промоторные островки как платформа для взаимодействия с нуклеоидными белками и факторами транскрипции. J Bioinform Comput Biol. 2014;12:1441006 10.1142/S0219720014410066 [PubMed] [CrossRef] [Google Scholar]

40. Илари А., Сеси П., Феррари Д., Росси Г.Л., Чианконе Э. Включение железа в Escherichia coli Dps приводит к образованию ферритиноподобного микрокристаллического ядра. Дж. Биол. Хим. 2002; 277: 37619–37623. 10.1074/jbc.M206186200 [PubMed] [CrossRef] [Google Scholar]

41. Ивахори К., Эномото Т., Фурушо Х., Миура А., Нисио К., Мисима Ю. и др. Синтез наночастиц сульфида кадмия в белке Dps из Listeria innocua . Хим Матер. 2007;19: 3105–3111. 10.1021/см0628799 [CrossRef] [Google Scholar]

42. Игараси К., Исихама А. Двудольная функциональная карта E . coli Альфа-субъединица РНК-полимеразы: участие С-концевой области в активации транскрипции с помощью цАМФ-СРБ. Клетка. 1991; 65: 1015–1022. 10.1016/0092-8674(91)90553-Б [PubMed] [CrossRef] [Google Scholar]

43. Тутукина М.Н., Шавкунов К.С., Масулис И.С., Озолин О. Н. Антисмысловая транскрипция в пределах hns локус Escherichia coli . Мол Биол (Моск). 2010; 44: 439–447. 10.1134/S002689331003012X [PubMed] [CrossRef] [Google Scholar]

44. Маниатис Т., Фриш Э.Ф., Сэмбрук Дж. Молекулярное клонирование: Лабораторное руководство. Колд-Спринг-Харбор, Нью-Йорк: Лаборатория Колд-Спринг-Харбор. Нажимать; 1982. [Google Scholar]

45. Рогулин Е.А., Перевязова Т.А., Железная Л.А., Матвиенко Н.И. Плазмида pRARE в качестве вектора для клонирования с целью конструирования суперпродуцента сайт-специфичной никазы N.BspD6I. Биохимия (Москва). 2004;69: 1123–1127. 10.1023/Б:БИРИ.0000046886.19428.d5 [PubMed] [CrossRef] [Google Scholar]

46. Антипов С.С., Покусаева В.О., Мелехов В.В., Озолин О.Н. Зависимость образования нуклеопротеидных комплексов с белком Dps от физико-химических свойств ДНК. Вопросы биологической медицинской и фармацевтической химии. 2013;7: 24–28. Доступно: http://www.radiotec.ru/catalog.php?cat=jr19&art=13161 [Google Scholar]

47. Altuvia S, Almiron M, Huisman G, Kolter R, Storz G. Промотор dps активируется OxyR во время роста, а также IHF и σ ^S в стационарной фазе. Мол микробиол. 1994; 13: 265–272. 10.1111/j.1365-2958.1994.tb00421.x [PubMed] [CrossRef] [Google Scholar]

48. Лакур С., Ландини П. SigmaS-зависимая экспрессия генов в начале стационарной фазы у Escherichia coli : функция sigmaS-зависимых генов и идентификация их промоторных последовательностей. J Бактериол. 2004; 186: 7186–7195. 10.1128/JB.186.21.7186-7195.2004 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

49. Швырева У.С., Тутукина М.Н., Озолин О.Н. Бактериоферритин: свойства, структурно-функциональная организация регуляторной области гена dps . Биофизика. 2011; 56: 795–802. 10.1134/S0006350911050204 [PubMed] [CrossRef] [Google Scholar]

50. Мачулин А.В., Дерюшева В.И., Юнусова А.К., Железная Л.А., Сердюк И.Н. Исследование сайт-специфического связывания ДНК с разрывной эндонуклеазой Nt. BspD6I на уровне одной молекулы с помощью атомно-силовой микроскопии. Биофизика. 2012; 57: 314–317. 10.1134/S0006350912030128 [PubMed] [CrossRef] [Google Scholar]

51. Мартинес А., Колтер Р. Защита ДНК во время окислительного стресса с помощью неспецифического ДНК-связывающего белка Dps. J Бактериол. 1997; 179: 5188–5194. Доступно: http://jb.asm.org/content/179/16/5188.full.pdf+html. [Бесплатная статья PMC] [PubMed] [Google Scholar]

52. Guex N, Peitsch MC. SWISS-MODEL и Swiss-PdbViewer: среда для сравнительного моделирования белков. Электрофорез. 1997; 18: 2714–2723. 10.1002/элпс.1150181505 [PubMed] [CrossRef] [Академия Google]

53. Инглстон С.М., Дикман М.Дж., Грасби Дж.А., Хорнби Д.П., Шарплс Г.Дж., Ллойд Р.Г. Связывание и процессинг соединения Холлидея белком RuvA Mycoplasma pneumoniae . Евр Дж Биохим. 2002; 269: 1525–1533. Доступно: http://www.ncbi.nlm.nih.gov/pubmed/11874468. [PubMed] [Google Scholar]

54. Хомякова Е.Б., Петрова М.В., Минят Е.