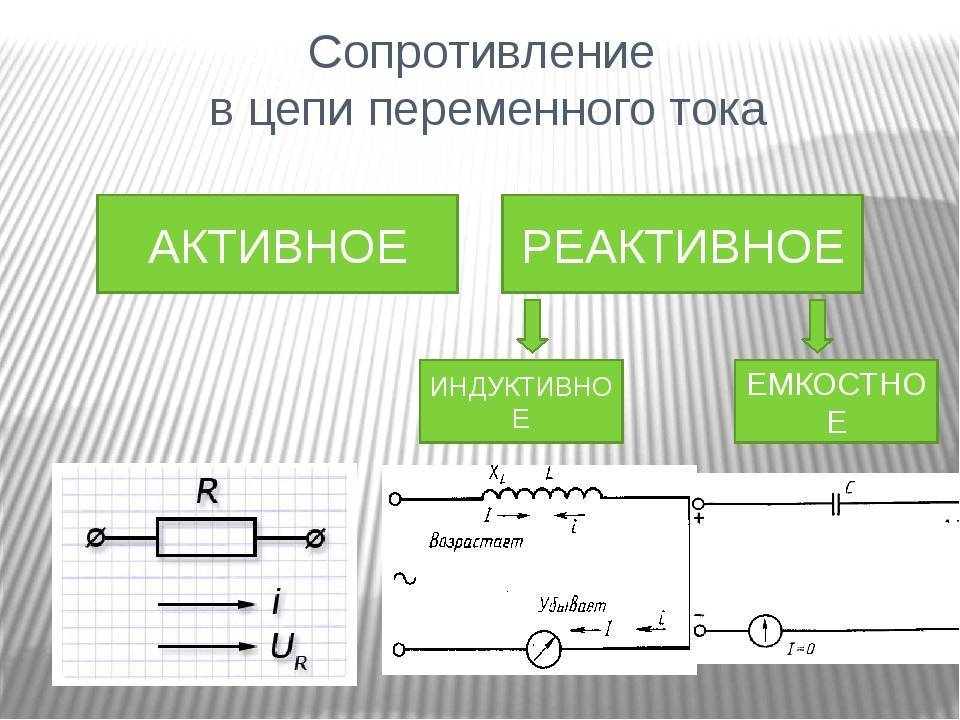
Чему равно полное сопротивление цепи переменного тока. Полное сопротивление цепи переменного тока: расчет и характеристики — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Как рассчитать полное сопротивление цепи переменного тока. Что такое активное и реактивное сопротивление. От каких параметров зависит полное сопротивление. Как построить векторную диаграмму для цепи переменного тока.

Содержание

Что такое полное сопротивление цепи переменного тока

Полное сопротивление цепи переменного тока (импеданс) — это комплексная величина, характеризующая сопротивление электрической цепи переменному току. Оно обозначается буквой Z и измеряется в Омах.

Полное сопротивление включает в себя две составляющие:

Активное сопротивление R — вызывает потери энергии в цепи
Реактивное сопротивление X — не вызывает потерь энергии, но создает сдвиг фаз между током и напряжением

Реактивное сопротивление в свою очередь может быть индуктивным XL (создается катушками индуктивности) или емкостным XC (создается конденсаторами).

Формула расчета полного сопротивления

Полное сопротивление цепи переменного тока рассчитывается по формуле:

Z = √(R² + X²)

Где:

Z — полное сопротивление, Ом
R — активное сопротивление, Ом
X — реактивное сопротивление, Ом

При этом реактивное сопротивление X равно разности индуктивного и емкостного сопротивлений:

X = XL — XC

От чего зависит полное сопротивление цепи

Полное сопротивление цепи переменного тока зависит от следующих параметров:

Активного сопротивления R элементов цепи
Индуктивности L катушек
Емкости C конденсаторов
Частоты f переменного тока

При этом индуктивное и емкостное сопротивления рассчитываются по формулам:

XL = 2πfL

XC = 1 / (2πfC)

Как видно, индуктивное сопротивление прямо пропорционально частоте, а емкостное — обратно пропорционально.

Треугольник сопротивлений

Для наглядного представления соотношения активного, реактивного и полного сопротивлений используется треугольник сопротивлений:

[Здесь должен быть рисунок треугольника сопротивлений]

Из этого треугольника можно получить следующие соотношения:

Z = √(R² + X²)
R = Z * cos φ
X = Z * sin φ

Где φ — угол сдвига фаз между током и напряжением.

Векторная диаграмма цепи переменного тока

Для анализа цепей переменного тока удобно использовать векторные диаграммы. На них изображаются векторы тока, напряжения и сопротивлений.

Рассмотрим построение векторной диаграммы на примере последовательной RLC-цепи:

За базовый вектор принимаем вектор тока I, направленный вправо
Вектор напряжения на активном сопротивлении UR совпадает по фазе с током
Вектор напряжения на индуктивности UL опережает ток на 90°
Вектор напряжения на емкости UC отстает от тока на 90°
Суммарное напряжение U получается геометрическим сложением векторов UR, UL и UC

[Здесь должен быть рисунок векторной диаграммы]

Особенности расчета полного сопротивления для разных цепей

Последовательное соединение

При последовательном соединении элементов полное сопротивление равно геометрической сумме сопротивлений отдельных элементов:

Z = √((R1 + R2)² + (XL1 + XL2 — XC1 — XC2)²)

Параллельное соединение

Для параллельного соединения удобнее оперировать проводимостями. Полная проводимость Y равна:

Y = √(G² + B²)

Где G — активная проводимость, B — реактивная проводимость.

Резонанс в цепи переменного тока

Резонанс — это режим работы электрической цепи, при котором реактивное сопротивление равно нулю. Различают:

Резонанс напряжений — в последовательном колебательном контуре
Резонанс токов — в параллельном колебательном контуре

При резонансе полное сопротивление цепи становится равным активному сопротивлению.

Практическое применение расчета полного сопротивления

Расчет полного сопротивления цепи переменного тока имеет важное практическое значение:

Позволяет определить ток и напряжение в цепи
Необходим при проектировании электрических фильтров
Используется для согласования нагрузки с источником питания
Применяется при расчете линий электропередач

Методы измерения полного сопротивления

Для измерения полного сопротивления цепи переменного тока используются следующие методы:

Вольтметра-амперметра
Мостовой метод
Резонансный метод
Использование специальных приборов — измерителей RLC

Выбор конкретного метода зависит от требуемой точности измерений и доступного оборудования.

Заключение

Расчет полного сопротивления — важная задача при анализе цепей переменного тока. Понимание соотношения активного и реактивного сопротивлений позволяет правильно проектировать и эксплуатировать электрические устройства. Использование векторных диаграмм дает наглядное представление о процессах в цепи переменного тока.

Полное сопротивление цепей переменного тока

При последовательном
соединении приборов с активным и индуктивным сопротивлениями полное сопротивление цепи нельзя находить арифметическим суммированием.

Полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Для упрощения расчетов
полезно знать, что если одно из сопротивлений (r или xL) превосходит
другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и
считать, что z равно большему сопротивлению. При параллельном соединении ветвей, имеющих активные и реактивные сопротивления …

При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:

Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то

т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.

Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению. Ошибка весьма невелика.

Например, если r = 1 Ом и xL = 10 Ом, то

Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.

Итак, если

То

а если

То

При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости

и реактивной проводимости

Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:

А полное сопротивление цепи является величиной, обратной у,

Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:

Эта формула напоминает известную формулу

но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.

Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.

Решение.

При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %

Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением

Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением

Следовательно, если

То

а если

То

Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:

При параллельном соединении (рис. 2) складываются токи:

Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.

При любой цепи переменного тока закон Ома можно писать в следующем виде:

где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.

Коэффициент мощности cos для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:

При параллельном соединении получим:

10.12.2016 Без рубрики

6.4. Сопротивление в цепи синусоидального тока

Если напряжение подключить к сопротивлению R, то через него протекает ток

(6.7)

Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.
Формула (6.7) в комплексной форме записи имеет вид

(6.8)

где и — комплексные амплитуды тока и напряжения.
Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).

Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.

Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением.

Рис.6.4
Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

6.5. Индуктивная катушка в цепи синусоидального тока

Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

(6.9)

Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

(6.10)

Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.
Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

(6.11)

Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^oo), величина которого зависит от соотношения R и L. Выражение (6.11) в комплексной форме записи имеет вид:

(6.12)

где Z_L — полное комплексное сопротивление индуктивной катушки ;
Z_L — модуль комплексного сопротивления;
— начальная фаза комплексного сопротивления;
— индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

Рис. 6.5

Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.
В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически.
Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

Из треугольника сопротивлений получим несколько формул:
; ;
Рис. 6.6

;

; .

6.6. Емкость в цепи синусоидального тока

Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

. (6.13)

Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

Выражение (6.13) в комплексной форме записи имеет вид:

, (6.14)

где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

Если комплексное сопротивление индуктивности положительно
, то комплексное сопротивление емкости отрицательно

На рис. 6.7 изображена векторная диаграмма цепи с емкостью.
Вектор тока опережает вектор напряжения на 90^o.

Рис. 6.7

6.7. Последовательно соединенные реальная индуктивная

катушка и конденсатор в цепи синусоидального тока

Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.6.8). В схеме протекает синусоидальный ток

Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,

(6.15)

Подставим эти формулы в уравнение (6.15). Получим:

(6.16)

Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
Запишем уравнение (6.16) в комплексной форме:

(6.17)

Рис. 6.8

Поделим левую и правую части уравнения (6.17) на √2.
Получим уравнение для комплексов действующих значений токов и напряжений

, (6.18)

где — комплексное сопротивление цепи;
— модуль комплексного сопротивления, или полное сопротивление цепи;
— начальная фаза комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.6.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

Условие возникновения резонанса: , отсюда резонансная частота равна

Из формулы следует, что режима резонанса можно добиться следующими способами:

изменением частоты;
изменением индуктивности;
изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀ (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

Рис. 6.9 Рис. 6.10 Рис. 6.11

6.8. Параллельно соединенные индуктивность, емкость

и активное сопротивление в цепи синусоидального тока

К схеме на рис. 6.12 подключено синусоидальное напряжение . Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.
Определим ток на входе схемы.

В соответствии с первым законом Кирхгофа:
, (6.19)
где
— активная проводимость.

Рис. 6.12

Подставим эти формулы в уравнение (6.19). Получим:

, (6.20)

где — индуктивная проводимость;
— емкостная проводимость.

Из уравнения (6.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.
Запишем уравнение (6.20) в комплексной форме.

, (6.21)

где — комплексная проводимость;
— полная проводимость;
— начальная фаза комплексной проводимости.

Построим векторные диаграммы, соответствующие комплексному уравнению (6.21).

Рис. 6.13 Рис. 6.14 Рис. 6.15

В схеме на рис. 6.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.
Из условия возникновения резонанса тока получим формулу для резонансной частоты тока

В режиме резонанса тока полная проводимость цепи — минимальна, а полное сопротивление — максимально. Ток в неразветвленной части схемы в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

и .

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.

6.9. Резонансный режим в цепи, состоящей

из параллельно включенных реальной индуктивной
катушки и конденсатора

Комплексная проводимость индуктивной ветви

где — активная проводимость индуктивной катушки;
   — полное сопротивление индуктивной катушки;
   — индуктивная проводимость катушки;
   — емкостная проводимость второй ветви.

В режиме резонансов токов справедливо уравнение:

или

Из этого уравнения получим формулу для резонанса частоты

(6.22)

На рисунке 6.16 изображена векторная диаграмма цепи в резонансном режиме.

Вектор тока I₂ опережает вектор напряжения на 90^o. Вектор тока I₁ отстает от вектора напряжения на угол φ,

где .

Разложим вектор тока I₁ на две взаимно перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения, называется активной составляющей тока I_а1, другая — реактивной составляющей тока I_р1.

Рис. 6.16

В режиме резонанса тока реактивная составляющая тока I_р1 и емкостный ток I₂ , направленные в противоположные стороны, полностью компенсируют друг друга, активная составляющая тока I_а1 совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной части схемы совпадает по фазе с напряжением.

Рис. 6.17

общие сведения, зависимость от других величин и формулы расчета

Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.

Физический смысл

Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.

Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.

Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.

Зависимость электропроводимости

R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.

Электрические величины

К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.

Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).

Геометрические параметры и тип вещества

Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.

Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.

Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:

Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.

П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.

Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:

Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.

Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:

Визуально определить геометрическую фигуру при разрезе П.
Найти в справочнике формулу S.
Произвести измерения при помощи ШЦ необходимых величин.
Подставить в формулу и вычислить S.

Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.

Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.

Температура проводника

Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.

На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.

В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:

для металлов а > 0;
для электролитов a < 0.

Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.

В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.

Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.

Цепь переменного тока

Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:

активным;
индуктивным;
емкостным;
полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).

Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.

Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.

При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:

w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.

Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:

геометрии П;
типа вещества, из которого сделан П;
температуры;
деформации различного вида;
электрических показателей I, U, f, L, C и R.

Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.

Измерение сопротивления

На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.

Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.

Полное сопротивление — цепь — переменный ток

Cтраница 1

Полное сопротивление цепи переменного тока равно 15 ом, активное 12 ом. [1]

Полное сопротивление цепи переменного тока равно гипотенузе прямоугольного треугольника. [2]

Полное сопротивление цепи переменного тока, состоящей из контактной сети, рельсового пути и грунта, является величиной неопределенной. При одном и том же сечении контактной сети сопротивление изменяется в зависимости от расположения различных элементов подвески, характера почвы, наличия соседних рельсовых путей и других факторов. [3]

Полное сопротивление цепи переменного тока равно 120 ом, а индуктивное 72 ом. [4]

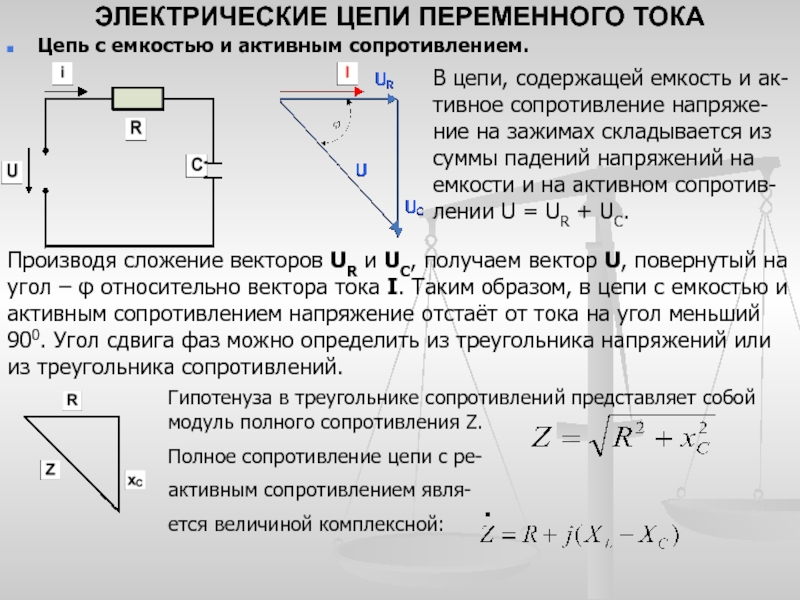
Полное сопротивление цепи переменного тока с активным, индуктивным и емкостным сопротивлениями определяется из треугольника напряжений ОАВ. [5]

Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. [6]

Что называется активным, индуктивным, емкостным и полным сопротивлением цепи переменного тока. [7]

Сопротивление г называется полным сопротивлением цепи переменного тока. [8]

Это и есть, полное сопротивление цепи переменного тока или импеданс. [9]

Расчет показывает, что для получения величины полного сопротивления цепи переменного тока надо построить прямоугольный треугольник, сторонами которого служили бы величины омического и индуктивного сопротивлений. Если, например, омическое сопротивление цепи равно 3 ом, а индуктивное 4 ом, то полное сопротивление будет равно 5 ом. [10]

Сопротивление цепи с омическим и реактивным сопротивлениями, полученное путем деления напряжения на полный ток, протекающий по цепи, называют полным сопротивлением цепи. Полное сопротивление цепи переменного тока обозначают буквой z и измеряют в омах. [11]

Какие сопротивления называют реактивными. Чем они отличаются от активного сопротивления. По какой формуле определяют полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. [12]

Что называется активным сопротивлением цепи. Запишите формулу для определения полного сопротивления цепи переменного тока, состоящей из последовательно соединенных конденсатора, катушки индуктивности и резистора. [13]

Страницы: 1

7 «Б»

Урок
1/1	Что изучает физика. Физические термины. Наблюдения и опыты.	§ 1 — 3, Л № 5, 12
2/2	Физические величины. Измерение физических величин. Погрешность и точность измерений	§ 4, 5, упр.1
3/3	Определение цены деления измерительного прибора	§ 4, 5
4/4	Физика и техника	§ 6,
	Первоначальные сведения о строении вещества
5/1	Строение вещества. Молекулы	§ 7, 8
6/2	Определение размеров малых тел	§ 7, 8
7/3	Движение молекул. Диффузия в газах, жидкостях и твердых телах	§ 9,
8/4	Взаимодействие молекул
9/5	Три состояния вещества	§ 11, 12
10/6	Повторение. Контрольная работа №1 «Первоначальные сведения о строении вещества»	§ 12

Цепь переменного тока с R, L и С сопротивлениями

Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями

На рис. 60, а изображена цепь переменного тока, в которую включены последовательно активное сопротивление r, индуктивность L, обладающая индуктивным сопротивлением Х_L и емкость С, обладающая емкостным сопротивлением Х_c. Под действием переменного напряжения в этой цепи протекает переменный ток.
Выясним, чему равно общее напряжение на зажимах цепи. Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. 60, б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения откладываем по вектору тока.
Напряжение на индуктивности опережает ток на угол φ = 90°. Поэтому вектор откладываем вверх под углом 90° к вектору тока.
В цепи с емкостью, наоборот, напряжение отстает от тока на угол φ = 90°. Поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока.
Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы и . Для этого отнимем от большего вектора вектор и получим вектор — , выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( — ) и . Суммой этих векторов будет диагональ параллелограмма — вектор , изображающий общее напряжение на зажимах цепи.
На основании теоремы Пифагора из треугольника напряжений АОБ следует, что

отсюда общее напряжение

Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I, выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А′О′Б′ (рис. 59, в). Его сторонами являются сопротивления r, (Х_L — Х_c) и полное сопротивление цепи Z. Пользуясь теоремой Пифагора, можно написать, что

Z² =r² + (Х_L — Х_c)².

Отсюда полное сопротивление цепи Формула (70) может применяться и в частных случаях, когда Х_L = 0 или Х_c = 0.
Силу тока в цепи с активным, индуктивным и емкостным сопротивлениями определяют по закону Ома: На векторной диаграмме (рис. 59, б) видно, что в рассматриваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что Из треугольника сопротивлений

Пример решения контрольной по электротехнике

Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.

На рисунке, изображён магнитопровод с воздушным зазором. Материал сердечника — электротехническая сталь. Размеры сердечника по средней магнитной линии в мм : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм. Толщина сердечника 50 мм. В сердечнике требуется создать магнитный поток Ф=0,0048 Вб. Определить ток, который должен проходить по обмотке катушки, если она имеет w=800 витков. Вычислить, также ток катушки, для создания заданного магнитного потока, если в сердечнике будет отсутствовать воздушный зазор.

Дано : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм ; d=50 мм ; w=800 ; Ф=0,0048 Вб.

Найти : I

Решение.

1. Начертим схему замещения магнитной цепи.

Цепь содержит три участка : первый состоит из одного участка – электротехнической стали ; второй из одного участка – электротехнической стали ; третий из двух участков — электротехнической стали и воздушного зазора.

Найдём длины и площади сечения участков.

Первый участок : S1=0.05×0.1=5×10-3 м2 ; ℓ1=280 мм=0,28 м

Второй участок : S2=0.05×0.08=4×10-3 м2 ; ℓ2=330 мм=0,33 м ;

Третий участок : S3=0.05×0.08=4×10-3 м2 ; ℓ3=370 мм=0,37 м.

2. Составим для магнитной цепи уравнения по законам Кирхгофа.

По второму закону Кирхгофа составляем одно уравнение.

Ф(Rм1+Rм2+Rм3+R0)=F (1)

Найдём магнитные индукции на каждом участке : B1=Ф/S1=0.0048/0.005=0.96 Тл ;

B2=B3=B0=Ф/S2=Ф/S3=0.0048/0.004=1.2 Тл

Найдём напряжённости магнитного поля на каждом участке : на участках из электротехнической стали напряжённость поля находим по кривой намагничивания

h2=600 А/м ; h3=h4=1400 А/м.

Напряжённость магнитного поля находим по формуле : H0=B0/μ0=1.2/(4π×10-7)=9.6×105 А/м

(где μ0=4π×10-7 Гн/м – магнитная постоянная).

Запишем уравнение (1) :

F=Iw=h2ℓ1+h3ℓ2+h4ℓ3+H0ℓ0=600×0.28+1400×0.33+1400×0.37+9.6×105×0.002=3068 А

Откуда находим ток, который должен проходить по обмотке : I=3068/800=3.8 А

Найдём ток в обмотке катушки, необходимый для создания магнитного потока Ф=0,0048 Вб, если воздушный зазор отсутсвует.

F=Iw=h2ℓ1+h3ℓ2+h4(ℓ3+ℓ0)=600×0.28+1400×(0.33+0.37+0.002)=1150.8

Откуда ток катушки : I=1150.8/800=1.4 А

Ответ : 1) I=3.8 A ; 2) I=1.4 A.

Задача 7.

К переменному напряжению U=150 В частотой f=50 Гц подключены последовательно соединённые резистор и конденсатор. По цепи проходит ток I=3 А, при этом на резисторе возникает падение напряжения Ua=90 В. Начертить схему цепи. Определить полное сопротивление цепи z, сопротивление резистора R, сопротивление XC и ёмкость С конденсатора, коэффициент мощности cosφ, напряжение UC на ёмкостном сопротивлении. Построить в масштабе mu=20 В/см векторную диаграмму напряжений, отложив горизонтально вектор тока.

Дано : U=150 В ; f=50 Гц ; I=3 А ; Ua=90 В.

Найти : z , R , XC , C , cosφ , UC.

Решение.

Находим полное сопротивление цепи : z=U/I=150/3=50 Ом.

Сопротивление резистора : R=Ua/I=90/3=30 Ом.

Находим сопротивление XC : XC==40 Ом.

Находим ёмкость конденсатора : C=1/(2πfXC)=1/(2×50×3.14×40)=79.6×10-6 Ф=79,6 мкФ.

Находим коэффициент мощности цепи : cosφ=R/z=30/50=0.6

Находим напряжение на ёмкости : UC=IXC=3×40=120 В.

Для построения векторной диаграммы, найдём длины векторов : ℓUa=Ua/mu=90/20=4.5 см ;

ℓUc=UC/mu=120/20=6 см.

Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua откладываем параллельно вектору тока I. От конца вектора Ua откладываем вектор напряжения UC перпендикулярно вектору тока I, в сторону его опережения. Геометрическая сумма векторов Ua и UC даёт вектор U.

Схема цепи и векторная диаграмма построены на рисунке.

Ответ : z=50 Ом ; R=30 Ом ; XC=40 Ом ; C=79,6 мкФ ; cosφ=0.6 ; UC=120 В.

Задача 13.

Последовательно с катушкой, активное сопротивление которой R=5 Ом и индуктивное XL=

=26 Ом, включен конденсатор, ёмкостное сопротивление которого XC=14 Ом. Ток в цепи I=12 А, частота f=50 Гц. Начертить схему цепи. Определить полное сопротивление цепи z ; коэффициент мощности cosφ и напряжение на зажимах цепи U. Вычислить индуктивность катушки L0, при которой в цепи наступает резонанс напряжений. Для режима резонанса напряжений определить полное сопротивление цепи z0 ; ток I0 ; падение напряжения на активном Ua0 и ёмкостном UC0 сопротивлениях ; коэффициент мощности цепи cosφ0 ; полную S, активную P и реактивную Q мощности цепи. Построить в масштабе mu=50 В/см векторную диаграмму напряжений для режима резонанса, отложив горизонтально вектор тока.

Дано : R=5 Ом ; XL=260 Ом ; XC=14 Ом ; I=12 A ; f=50 Гц.

Найти : z ; cosφ ; U ; L0 ; z0 ; I0 ; Ua0 ; UC0 ; cosφ0 ; S ; P ; Q.

Решение.

Схема цепи приведена на рисунке.

Полное сопротивление цепи : z==13 Ом

Коэффициент мощности цепи : cosφ=R/z=5/13=0,38

Напряжение, приложенное к цепи : U=Iz=12×13=156 В

Найдём индуктивность катушки, которую нужно включить в сеть с конденсатором, чтобы в цепи возник резонанс напряжений. Условие резонанса :

XL0=XC=14 Ом

Индуктивность катушки : L0=XL0/(2πf)=14/(2×3.14×50)=0.045 Гн=45 мГн.

Полное сопротивление цепи в режиме резонанса напряжений равно активному сопротивлению : z0=R=5 Ом.

Ток в цепи в режиме резонанса напряжений : I0=U/z0=156/5=31,2 А.

Падение напряжения на активном сопротивлении в режиме резонанса напряжений : Ua0=I0R=31.2×5=156 В.

Падение напряжения на ёмкостном сопротивлении в режиме резонанса напряжений :

UC0=I0XC=31.2×14=436.8 В.

Коэффициент мощности цепи в режиме резонанса напряжений : cosφ0=R/z0=5/5=1

Активная P, реактивная Q и полная S мощности цепи в резонансе напряжений :

P=I02R=31.22×5=4867.2 Вт ; Q=0 ; S=P=4867.2 В∙А.

Для построения векторной диаграммы найдём длины векторов : ℓUa=156/50=3.1 см ;

ℓUc0=436.8/50=8.7 см.

Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua0 откладываем параллельно вектору тока I. От конца вектора Ua0 откладываем вектор напряжение UC0 перпендикулярно вектору тока I в сторону отставания от него. От конца вектора UC0 откладываем вектор напряжения UL0 перпендикулярно вектору тока I в сторону его опережения (по модулю вектора UC0 и UL0 равны).

Геометрическая сумма векторов Ua0 , UC0 и UL0 даёт вектор напряжения U, приложенного к цепи (U=Ua0).

Ответ : z=13 Ом ; cosφ=0.38 ; U=156 В ; L0=45 мГн ; z0=5 Ом ; I0=31.2 A ; Ua0=156 В ; UC0=

=436.8 В ; cosφ0=1 ; P=4867.2 Вт ; Q=0 ; S=4867.2 В∙А.

№ 19

Цепь переменного тока состоит из двух параллельных ветвей. В первую ветвь включены последовательно активное и индуктивное сопротивления : R1=12 Ом ; XL=9 Ом. Вторая ветвь состоит из последовательно соединённых активного и ёмкостного сопротивлений : R2=12 Ом ; XC=16 Ом. Напряжение на зажимах цепи U=220 В. Начертить схему цепи. Определить токи I1 , I2 в параллельных ветвях и ток I в неразветвленной части цепи ; коэффициент мощности всей цепи ; активную P , реактивную Q и полную S мощности цепи. Задачу решить методом разложения токов на активные и реактивные составляющие. Построить векторную диаграмму токов в масштабе mi=2 А/см. Вычислить активную g и реактивную bc проводимости второй ветви.

Дано : R1=12 Ом ; XL=9 Ом ; R2=12 Ом ; XC=16 Ом ; U=220 В.

Найти : I1 , I2 , I , cosφ , P , Q , S , g2 , bc.

Решение.

Схема цепи изображена на рисунке.

Находим полные сопротивления параллельных ветвей.

Z1==15 Ом ; Z2= =20 Ом.

Находим токи в параллельных ветвях : I1=U/Z1=220/15=14.7 A ; I2=U/Z2=220/20=11 A

Найдём углы сдвига фаз между токами I1 и I2 и напряжением U.

φ1=arctg[XL/R1]=arctg[9/12]=37°

φ2=arctg[-XC/R2]=arctg[-16/12]=-53°

Находим активные составляющие токов I1, I2 и I.

Ia1=I1cosφ1=14.7×cos(37°)=11.7 A ; Ia2=I2cosφ2=11×cos(-53°)=6.6 A ;

Ia=Ia1+Ia2=11.7+6.6=18.3 A

Находим реактивные составляющие токов I1 , I2 и I.

Ip1=I1sinφ1=14.7×sin(37°)=8.84 A ; Ip2=I2sinφ2=11×sin(-53°)=-8.78 A

Ip=Ip1+Ip2=8.84-8.78=0,06 А

Полный ток в неразветвленной части цепи : I==18.3 A.

Найдём коэффициент мощности цепи : cosφ=Ia/I=18.3/18.3=1

В цепи имеет место резонанс токов.

Найдём активную P, реактивную Q и полную S мощности цепи.

P=I12R1+I22R2=14.72×12+112×12=4045.08 Вт

Q=I12XL-I22XC=14.72×9-112×16=8.8 вар

S=UI=220×18.3=4026 В∙А , или S==4045 В∙А.

Вычислим активную g2 и реактивную bc составляющие второй ветви.

g2=R2/Z22=12/202=0.05 сим ; bc=-XC/Z22=-16/202=-0.04 сим.

Для построения векторной диаграммы найдём длины векторов :

ℓIa1=Ia1/mI=11.7/2=5.9 см ; ℓIp1=Ip1/mI=8.84/2=4.4 см ; ℓI1=I1/mI=14.7/2=7.4 см ;

ℓIa2=Ia2/mI=6.6/2=3.3 см ; ℓIp2=Ip2/mI=8.78/2=4.4 см ; ℓI2=I2/mI=11/2=5.5 см.

ℓIa=Ia/mI=18.3/2=9.2 см ; ℓIp=Ip/mI=0.06/2=0.03 см ; ℓI=I/mI=18.3/2=9.2 см.

Построение векторной диаграммы начинаем с построения вектора напряжения U , который откладываем горизонтально. Вектор тока Ia1 откладываем параллельно вектору напряжения U. От конца вектора Ia1 откладываем вектор тока Ip1 перпендикулярно вектору U в сторону отставания от него. Геометрическая сумма векторов Ia1 и Ip1 дают вектор I1. Вектор тока Ia2 откладываем параллельно вектору напряжения U. От конца вектора Ia2 откладываем вектор тока Ip2 перпендикулярно вектору напряжения U в сторону его опережения. Геометрическая сумма векторов Ia2 и Ip2 дают вектор I2. Вектор I строим как геометрическая сумма векторов I1 и I2 , или как геометрическую сумму векторов Ia и Ip.

Ответ : I1=14.7 A ; I2=11 A ; I=18.3 A ; cosφ=1 ; P=4045 Вт ; Q=8.8 вар ; S=4045 В∙А ; g2=0.05 сим ; bc=-0.04 сим.

№ 21

Три одинаковых приёмника с сопротивлениями ZA=ZB=ZC=12+j16 Ом, соединены звездой и питаются от трёхфазной сети с линейным напряжением Uл=220 В. Начертить схему цепи. Определить фазное напряжение Uф ; фазные Iф и линейные Iл токи ; полную S , активную P и реактивную Q мощности ; коэффициент мощности cosφ трёхфазного потребителя. Построить в масштабе mu=40 В/см , mI=2 А/см векторную диаграмму напряжений и токов.

Дано : ZA=ZB=ZC=12+j16 Ом ; Uл=220 В

Найти : Uф , Iф , Iл , S , P , Q , cosφ.

Решение.

Так как приёмник симметричный, то полное сопротивление фаз :

Z=ZA=ZB=ZC===20 Ом.

Фазное напряжение : Uф=Uл/=220/=127 В

Так как приёмник соединён звездой, то фазные и линейные токи равны :

Iф=Iл=Uф/Z=127/20=6.35 А.

Коэффициент мощности цепи : cosφ=R/Z=12/20=0.6 ; угол сдвига фаз между током Iф и напряжением Uф : φ=arccos(0.6)=53°

Активная мощность цепи : P=3Iф2R=3×6.352×12=1452 Вт.

Реактивная мощность цепи : Q=3Iф2X=3×6.352×16=1935 вар

Полная мощность цепи : S==2419 В∙А.

Для построения векторной диаграммы найдём длины векторов :

ℓUф=Uф/mu=127/40=3.2 см ; ℓIф=Iф/mI=6.35/2=3.2 см.

Построение диаграммы начинаем с построения векторов фазных напряжений UA, UB и UC , которые откладываем под углом 120° относительно друг – друга, предварительно отложив вектор UA вдоль вещественной оси.

Вектора фазных токов откладываем под углом φ=53° от соответствующих фазных напряжений. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений.

Ответ : Uф=127 В ; Iф=6,35 А ; S=2419 В∙А ; P=1452 Вт ; Q=1935 вар ; cosφ=0.6.

№ 30

Конденсатор С=30 мкФ, соединённый последовательно с резистором R=0.5 МОм, заряжается от сети с постоянным напряжением U=220 В. Определить постоянную времени цепи τ и значение разрядного тока и напряжения в конденсаторе для моментов времени t=0, τ, 2τ, 3τ, 4τ, 5τ. Начертить схему цепи. Построить в масштабе кривые iзар=f(t) ; uc=f(t).

Дано : С=30 мкФ ; R=0.5 МОм ; U=220 В.

Найти : τ ; iзар=f(t) ; uc=f(t).

Решение.

Постоянная времени цепи : τ=RC=0.5×106×30×10-6=15 c

Напряжение на конденсаторе при заряде : uc=U(1-e-t/τ)=220(1-e-t/τ) В

Вычислим значение напряжения на конденсаторе в моменты времени : t=0, τ, 2τ, 3τ, 4τ, 5τ. Вычисления сведём в таблицу.

t, c	0	τ	2τ	3τ	4τ	5τ
e-t/τ	1	0.37	0.14	0.05	0.02	0.01
uc , В	0	138.6	189.2	209	215.6	217.8

По результатам расчёта строим кривую : uc=f(t).

Ток переходного режима, или зарядный ток : i=Ie-t/τ===440e-t/τ мкА

Вычислим значение зарядного тока в моменты времени : t=0, τ,2τ, 3τ, 4τ, 5τ.

Вычисления сведём в таблицу.

t, c	0	τ	2τ	3τ	4τ	5τ
e-t/τ	1	0,37	0,14	0,05	0,02	0,01
I, мкA	440	162,8	61,6	22	8,8	4,4

По результатам расчёта строим кривую : i=440e-t/τ мкА.

Ответ : τ=15 с ; uc=220(1-e-t/τ) В ; i=440e-t/τ мкА.

Цепи переменного тока серии

RLC | Физика

Цели обучения

К концу этого раздела вы сможете:

Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
Нарисуйте принципиальную схему последовательной цепи RLC.
Объясните значение резонансной частоты.

Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току.Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом этого раздела. Суть анализа цепи RLC — это частотная зависимость X _L и X _C, а также влияние, которое они оказывают на фазу напряжения в зависимости от тока (установлено в предыдущий раздел).Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.

Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.

Комбинированный эффект сопротивления R , индуктивного реактивного сопротивления X _L и емкостного реактивного сопротивления X _C определяется как полное сопротивление , аналог сопротивления в цепи постоянного тока по переменному току.Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:

[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].

Здесь I ₀ — пиковый ток, В ₀ — пиковое напряжение источника, а Z — полное сопротивление цепи. Единицы измерения импеданса — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток.Чтобы получить выражение для Z в терминах R , X _L и X _C, мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение. Эти напряжения обозначены на Рисунке 1: В, , _{, , R, ,}, В, , _{, , L, ,} и В, , _{, , C, ,}. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны.Но мы знаем из предыдущего раздела, что напряжение на катушке индуктивности В _L опережает ток на одну четверть цикла, напряжение на конденсаторе В _C следует за током на единицу. -четвертый цикл, и напряжение на резисторе В, _R точно совпадает по фазе с током. На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи В = В _R + В _L + В _C, где все четыре напряжения — мгновенные значения.Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. Из рисунка 2 видно, что в то время как В _R находится в фазе с током, В _L опережает на 90 °, а В _C следует на 90 °. Таким образом, V _L и V _C сдвинуты по фазе на 180 ° (от пика до впадины) и имеют тенденцию к компенсации, хотя и не полностью, если они не имеют одинаковой величины.{2}}} \\ [/ latex],

, где V _{0 R}, V _{0 L} и V _{0 C} — пиковые напряжения на R , L и C , соответственно. {2}} \\ [/ latex],

, который является сопротивлением цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора — X _L = 0; а для тех, у кого нет конденсатора, возьмем X _C = 0.

Рис. 2. На этом графике показаны отношения напряжений в цепи RLC к току. Напряжения на элементах схемы в сумме равняются напряжению источника, которое, как видно, не совпадает по фазе с током.

Пример 1.Расчет импеданса и тока

Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела «Реактивное, индуктивное и емкостное». (b) Если источник напряжения имеет В _{действующее значение} = 120 В, что будет I _{среднеквадратичное значение} на каждой частоте?

Стратегия

Для каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} — {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {kHz} \ end {array} \\ [/ latex]

Обсуждение для (а)

В обоих случаях результат почти такой же, как и наибольшее значение, а импеданс определенно не является суммой отдельных значений. Понятно, что X _L доминирует на высокой частоте, а X _C доминирует на низкой частоте.

Решение для (b)

Текущее значение I _{действующее значение} можно найти, используя версию закона Ома для переменного тока в уравнении I _{среднеквадратичное значение} = В _{среднеквадратичное значение}/ Z :

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц

Наконец, на частоте 10,0 кГц мы находим

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц

Обсуждение для (а)

Ток при 60,0 Гц такой же (до трех цифр), что и для одного конденсатора в примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь незначительно отличается от тока, обнаруженного для одной катушки индуктивности в Примере 1 из разделов «Реактивное сопротивление, индуктивность и емкость».{2}}} \\ [/ latex]

Реактивные сопротивления изменяются в зависимости от частоты: X _L большие на высоких частотах и X _C большие на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f ₀ реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса и максимальное значение для I _rms результатов .Мы можем получить выражение для f ₀, взяв

X _L = X _C.

Замена определений X _L и X _C,

[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].

Решение этого выражения для f ₀ дает

[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],

, где f ₀ — это резонансная частота последовательной цепи RLC .Это также собственная частота , на которой цепь будет колебаться, если не будет управляться источником напряжения. При f ₀ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R , а I _{среднеквадратичное значение} является максимальным.

Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызываемое источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется на ее f ₀. Переменный конденсатор часто используется для регулировки f ₀, чтобы получить желаемую частоту и отклонить другие. На рисунке 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в I _{среднеквадратичное значение} при f ₀. Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.

Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс f ₀, но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В ₀.

Пример 2. Расчет резонансной частоты и тока

Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I _{среднеквадратичное значение} при резонансе, если В _{среднеквадратичное значение} равно 120 В.

Стратегия

Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]

Обсуждение для (а)

Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.

Решение для (b)

Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40.0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].

Обсуждение для (б)

В резонансе ток больше, чем на более высоких и низких частотах, рассмотренных для той же цепи в предыдущем примере.

Питание в цепях переменного тока серии

RLC

Если ток изменяется в зависимости от частоты в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника В и током I существует фазовый угол ϕ , который можно найти из

[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]

Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I _{среднеквадратичное значение} ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность составляет

[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],

Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.

Пример 3. Расчет коэффициента мощности и мощности

Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В _{действующее значение} 120 В: (a) Рассчитайте коэффициент мощности и фазу угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.

Стратегия и решение для (a)

Коэффициент мощности при 60,0 Гц находится из

[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].

Мы знаем Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что

[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].

Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].

Обсуждение для (а)

Фазовый угол близок к 90º, что соответствует тому факту, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90º).

Стратегия и решение для (b)

Средняя мощность при 60,0 Гц —

P _средн. = I _{среднеквадратичное значение} В _{среднеквадратичное значение} cos ϕ .

I _{среднеквадратичное значение} оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает

P _средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.

Стратегия и решение для (c)

На резонансной частоте мы знаем, что cos ϕ = 1, и I _{среднеквадратичное значение} оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P _средн. = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)

Обсуждение

Как ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на высоких и низких частотах.

Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, хранящейся в автомобильной пружине (аналогично отсутствию тока и энергии, хранящейся в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.

Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.

Чистая цепь LC с пренебрежимо малым сопротивлением колеблется на f ₀, на той же резонансной частоте, что и цепь RLC . Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.

Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и без движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.

Исследования PhET: комплект для конструирования цепей (AC + DC), виртуальная лаборатория

Создавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

Аналогом сопротивления переменного тока является сопротивление Z , комбинированное действие резисторов, катушек индуктивности и конденсаторов, определяемое версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],
, где I _o — пиковый ток, а В _o — пиковое напряжение источника.{2}} \\ [/ латекс].
Резонансная частота f ₀, при которой X _L = X _C , составляет
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]
В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],
ϕ = 0º для чисто резистивной цепи или цепи RLC при резонансе.
Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.

Концептуальные вопросы

1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.

2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.

Задачи и упражнения

1. Цепь RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.

2. Цепь RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.

3. Цепь LC состоит из индуктора 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.

4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?

5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?

6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?

7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?

8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?

9. Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?

10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В _{действующее значение} = 5,60 В, что будет I _{среднеквадратичное значение} на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I _rms в резонансе?

11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В _{действующее значение} = 408 В, что будет I _{среднеквадратичное значение} на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I _rms в резонансе?

12. Цепь серии RLC имеет 2.Резистор 50 Ом, катушка индуктивности 100 мкГн и конденсатор 80,0 мкФ. (а) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.

13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.

14. Последовательная цепь RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. {2}} \\ [/ latex]

резонансная частота:: — частота, при которой полное сопротивление в цепи минимально, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]

фазовый угол:: обозначается как ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи

Коэффициент мощности:: — величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ

Избранные решения проблем и упражнения

1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.

3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой — индуктор. доминирует.Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.

5. От 9,30 нФ до 101 нФ

7. 3,17 пФ

9. (а) 1,31 мкГн (б) 1,66 пФ

11. (a) 12,8 кОм (b) 1,31 кОм (c) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (d) 82,2 кГц (e) 0,408 A

13. (а) 0,159 (б) 80,9 ° (в) 26,4 Вт (г) 166 Вт

15. 16.0 Вт

Импеданс

Импеданс

Полное противодействие току в цепи переменного тока называется импедансом и обозначается буквой Z.Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное сопротивление току в цепи переменного тока). Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.

Рисунок 9-22. Применение постоянного и переменного тока в цепи.

Правила и уравнения для цепей постоянного тока применимы к цепям переменного тока только в том случае, если эта цепь содержит только сопротивление, а не индуктивность или емкость.Как в последовательной, так и в параллельной цепях, если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как и сопротивление, а закон Ома для цепи переменного тока, I = E / Z, точно такой же, как для цепи постоянного тока. схема. На рис. 9-22 показана последовательная схема, содержащая нагревательный элемент с сопротивлением 11 Ом, подключенный к источнику 110 В. Чтобы определить, какой ток протекает при подаче переменного тока 110 В, решается следующий пример:

Рисунок 9-23. Два значения сопротивления, подключенные параллельно к источнику переменного тока.Импеданс равен общему сопротивлению цепи.

Если есть два значения сопротивления, подключенных параллельно к напряжению переменного тока, как показано на Рисунке 9-23, полное сопротивление равно общему сопротивлению цепи. Еще раз, вычисления будут производиться так же, как если бы это была цепь постоянного тока, и применимо следующее:

Так как это чисто резистивная цепь R _T = Z (сопротивление = импеданс)

To Определите ток в цепи, используя уравнение:

Импеданс — это полное сопротивление току в цепи переменного тока.Если цепь имеет индуктивность или емкость, необходимо учитывать сопротивление (R), индуктивное реактивное сопротивление (X _L) и / или емкостное реактивное сопротивление (X _C) для определения полного сопротивления (Z). В этом случае Z не равно R _T. Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником.[Рис. 9-24] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон. Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.

Рисунок 9-24. Треугольник импеданса Рисунок 9-25. Цепь, содержащая сопротивление и индуктивность.

На практике, если последовательная цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 9-25, соотношение между сторонами может быть указано как:

Квадратный корень из обеих частей уравнения дает:

Эту формулу можно использовать для определения импеданса, если известны значения индуктивного реактивного сопротивления и сопротивления.Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X _C вместо X _L. В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):

или

Пример 1 показан на рисунке 9-25.Здесь последовательная цепь, содержащая резистор и катушку индуктивности, подключена к источнику 110 вольт при 60 циклах в секунду. Резистивный элемент представляет собой простой измерительный элемент 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какое значение импеданса и тока в цепи?

Решение:

Сначала вычисляется индуктивное реактивное сопротивление катушки:

Затем вычисляется полное сопротивление:

Помните, что при расчетах для Z всегда используйте индуктивное реактивное сопротивление, а не индуктивность, и используйте емкостное реактивное сопротивление. , а не емкость.

После определения полного сопротивления можно рассчитать общий ток.

Так как эта цепь резистивная и индуктивная, там есть фазовый сдвиг, когда напряжение ведет к току.

Пример 2 — это проиллюстрированная последовательная схема, в которой конденсатор емкостью 200 мкФ соединен последовательно с резистором 10 Ом. [Рисунок 9-26] Какое значение имеет импеданс, ток и падение напряжения на резисторе?

Рисунок 9-26. Цепь, содержащая сопротивление и емкость.

Решение:

Сначала емкость изменяется с микрофарад на фарады. Так как 1 миллион микрофарад равен 1 фараду, то 200 мкФ = 0,000200 фарад

Далее решаем емкостное реактивное сопротивление:

Чтобы найти полное сопротивление,

Поскольку эта цепь резистивная и емкостная, существует фазовый сдвиг, при котором ток напряжение проводов:

Чтобы найти ток:

Чтобы найти падение напряжения на резисторе (E _R):

Чтобы найти падение напряжения на конденсаторе (E _C):

Сумма этих двух напряжений не равна приложенному напряжению, поскольку ток опережает напряжение.Используйте следующую формулу, чтобы найти приложенное напряжение:

Если цепь содержит сопротивление, индуктивность и емкость, для определения полного сопротивления используется следующее уравнение.

Пример 3: Каково полное сопротивление последовательной цепи, состоящей из конденсатора с емкостным сопротивлением 7 Ом, катушки индуктивности с индуктивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 9-27] Рисунок 9-27. Цепь, содержащая сопротивление, индуктивность и емкость.

Решение:

Чтобы найти полный ток:

Помните, что индуктивные и емкостные сопротивления могут вызвать сдвиг фаз между напряжением и током. В этом примере индуктивное реактивное сопротивление больше емкостного, поэтому напряжение ведет к току.

Следует отметить, что, поскольку индуктивное реактивное сопротивление, емкостное реактивное сопротивление и сопротивление влияют друг на друга под прямым углом, падения напряжения в любой последовательной цепи переменного тока следует складывать с использованием векторного сложения.На рисунке 9-28 показаны падения напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.

Рисунок 9-28. Падение напряжения.

Чтобы рассчитать отдельные падения напряжения, просто используйте уравнения:

Чтобы определить общее приложенное напряжение для цепи, каждое отдельное падение напряжения должно быть добавлено с использованием векторного сложения.

Параллельные цепи переменного тока

При решении параллельных цепей переменного тока необходимо также использовать производную теоремы Пифагора.Уравнение для определения полного сопротивления в цепи переменного тока выглядит следующим образом:

Чтобы определить полное сопротивление параллельной цепи, показанной на рисунке 9-29, сначала нужно определить емкостное и индуктивное реактивные сопротивления. (Не забудьте перевести микрофарады в фарады.)

Рисунок 9-29. Полный импеданс параллельной цепи.

Затем можно найти полное сопротивление:

Для определения протекания тока в цепи:

Чтобы определить протекание тока через каждый параллельный путь цепи, вычислите I _R, I _L и I _C.

Следует отметить, что общий ток в параллельных цепях определяется с помощью векторного сложения отдельных потоков тока следующим образом:

Мощность в цепях переменного тока

Поскольку напряжение и ток определяют мощность , есть сходства в мощности, потребляемой цепями переменного и постоянного тока. Однако в переменном токе ток зависит как от сопротивления, так и от реактивного сопротивления цепи. Мощность, потребляемая любой цепью переменного тока, является функцией приложенного напряжения, а также сопротивления и реактивного сопротивления цепи.Цепи переменного тока имеют два различных типа мощности: один создается сопротивлением цепи, а другой — реактивным сопротивлением цепи.

Истинная мощность

Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность — это мощность, потребляемая участком сопротивления цепи, и измеряется в ваттах (Вт). Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:

Полная мощность

Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи.Полная мощность — это мощность, потребляемая всей цепью, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Полная мощность — это произведение эффективного напряжения на эффективный ток. Полная мощность рассчитывается по формуле:

Коэффициент мощности

Как видно на Рисунке 9-30, резистивная мощность и реактивная мощность влияют на схему под прямым углом друг к другу.Коэффициент мощности в цепи переменного тока создается этим эффектом прямого угла.

Рисунок 9-30. Соотношения сил в цепи переменного тока.

Коэффициент мощности можно определить как математическую разницу между истинной мощностью и полной мощностью. Коэффициент мощности (PF) — это коэффициент и всегда измеряется в диапазоне от 0 до 100. Коэффициент мощности напрямую связан с фазовым сдвигом цепи. Чем больше фазовый сдвиг цепи, тем ниже коэффициент мощности. Например, цепь переменного тока, которая является чисто индуктивной (содержит только реактивное сопротивление и не имеет сопротивления), имеет фазовый сдвиг 90 ° и коэффициент мощности 0.0. Цепь переменного тока, которая является чисто резистивной (без реактивного сопротивления), имеет фазовый сдвиг 0 и коэффициент мощности 100. Коэффициент мощности рассчитывается по следующей формуле:

Пример расчета коэффициента мощности: Рисунок 9-31 показывает нагрузку переменного тока, подключенную к источнику питания на 50 В. Потребляемый в цепи ток составляет 5 ампер, а общее сопротивление цепи составляет 8 Ом. Определите истинную мощность, полную мощность и коэффициент мощности для этой цепи.

Рисунок 9-31. Нагрузка переменного тока подключена к источнику питания на 50 В.

Решение:

Коэффициент мощности также может быть представлен в процентах. Используя процентное соотношение для отображения коэффициента мощности, схема в предыдущем примере будет иметь коэффициент мощности 80 процентов.

Следует отметить, что низкий коэффициент мощности нежелателен. Цепи с более низким коэффициентом мощности создают избыточную нагрузку на источник питания и снижают эффективность системы. Генераторы переменного тока для самолетов обычно должны работать с коэффициентом мощности от 90 до 100 процентов.Поэтому очень важно тщательно учитывать коэффициент мощности при проектировании электрической системы самолета.

Летный механик рекомендует

В чем разница между сопротивлением, реактивным сопротивлением и импедансом?

Цепи постоянного тока относительно легко анализировать, поскольку ток течет в одном направлении, а сопротивление является основным элементом цепи. Цепи переменного тока, с другой стороны, более сложны, поскольку напряжение и ток меняют направление с заданной частотой.В то время как цепи постоянного тока имеют сопротивление, цепи переменного тока часто имеют сопротивление и другое свойство, известное как реактивное сопротивление. Импеданс — это комбинация сопротивления и реактивного сопротивления.

Компоненты, известные как резисторы, предотвращают протекание тока — другими словами, они обладают свойством сопротивления. Резисторы присутствуют как в цепях переменного, так и в постоянном токе, а энергия, которая не может течь, отводится в виде тепла. Математически сопротивление — это просто напряжение, разделенное на ток.

R = сопротивление (Ом)

В = напряжение (вольт)

I = ток (амперы)

Реактивное сопротивление — это свойство, которое противодействует изменению тока и присутствует как в катушках индуктивности, так и в конденсаторах. Поскольку это влияет только на , изменяя ток , реактивное сопротивление зависит от мощности переменного тока и зависит от частоты тока. Когда присутствует реактивное сопротивление, оно создает сдвиг фазы на 90 градусов между напряжением и током, причем направление сдвига зависит от того, является ли компонент катушкой индуктивности или конденсатором.

Реактивное сопротивление, возникающее в катушке индуктивности, известно как индуктивное реактивное сопротивление . Когда присутствует индуктивное реактивное сопротивление, энергия накапливается в форме изменяющегося магнитного поля, и форма волны тока отстает от формы волны напряжения на 90 градусов. Индуктивное реактивное сопротивление возникает из-за устройств, в которых провод намотан по кругу, таких как катушки (включая линейные реакторы), дроссели и трансформаторы.

X _L = индуктивное реактивное сопротивление (Ом)

f = частота (Гц)

L = индуктивность (Генри)

Реактивное сопротивление конденсатора известно как емкостное реактивное сопротивление .Емкостное реактивное сопротивление накапливает энергию в виде изменяющегося электрического поля и вызывает ток в отведении напряжения на 90 градусов. Емкость создается при размещении двух проводящих пластин параллельно друг другу с небольшим расстоянием между ними, заполненных диэлектрическим материалом (изолятором).

X _C = емкостное реактивное сопротивление (Ом)

C = емкость (фарады)

Импеданс — это комбинация сопротивления и реактивного сопротивления (как индуктивного, так и емкостного) и является комплексным числом, содержащим как действительную, так и мнимую части.(Действительная часть импеданса — это сопротивление, а мнимая часть — реактивное сопротивление.) Импеданс имеет как величину, так и фазу.

Z = величина импеданса (Ом) в последовательной цепи

X _T = полное реактивное сопротивление (Ом) = X _L — X _C

θ = фаза полного сопротивления (градусы)

Треугольников мощности и импеданса — тригонометрия и генерация однофазного переменного тока для электриков

Это тот момент, когда я попрошу вас взять меня за руку и поверить мне.Хорошо, тебе не нужно брать меня за руку, но ты должен мне доверять. Мы собираемся начать использовать некоторые термины, прежде чем полностью углубиться в их теорию. Я обещаю, что мы более подробно рассмотрим эти концепции в будущих уроках.

При работе с цепями постоянного тока единственное, что препятствует току, — это сопротивление в цепи.

Рис. 20. Резистивная цепь постоянного тока

Как мы узнаем в последующих разделах, переменный ток добавляет компонент, который также противодействует току.Это называется реактивным сопротивлением и проходит под углом 90 градусов к сопротивлению цепи. Это означает, что их невозможно арифметически сложить; это должно быть сделано с использованием теоремы Пифагора. Когда вы складываете эти два вместе, вы получаете полное противодействие потоку тока, называемое импедансом .

Рис. 21. Индуктивная цепь постоянного тока

Треугольник, который образуется при добавлении сопротивления к реактивному сопротивлению, известен как треугольник импеданса .

Рисунок 22.Треугольник полного сопротивления

В треугольнике полного сопротивления сопротивление (r) всегда находится в нижней части треугольника, реактивное сопротивление (x) всегда идет сбоку, а гипотенуза всегда является сопротивлением (z).

При работе с чисто резистивной схемой рассеиваемая мощность находится в форме тепла или света и измеряется в ваттах и известна как истинная или активная мощность . Это продукт I ² R.

Рис. 23. Цепь резистивной мощности

В цепи переменного тока с индуктивностью все еще присутствуют ватты.При прохождении тока через реактивное сопротивление также присутствует реактивная мощность. Эта мощность называется реактивной мощностью , а также мощностью Вт или квадратурной мощностью . Его единица — варс.

Рис. 24. Индуктивная цепь питания

Подобно треугольнику импеданса, мы не можем просто сложить две мощности вместе, чтобы получить общую мощность. Их необходимо добавить, используя теорему Пифагора. Их сумма равна полной мощности (ВА).

Рис. 25. Треугольник мощности

При расчете реактивной мощности мы все еще можем использовать формулы мощности. Нам просто нужно использовать их с реактивным сопротивлением вместо сопротивления.

I ² X = Вар
E ² (напряжение индуктора) / X = Вар
I x E (напряжение индуктора) =

Помните

При построении треугольника импеданса или мощности резистивная составляющая всегда идет в нижней части треугольника, а реактивная составляющая всегда идет сбоку.

Что такое реактивное сопротивление и импеданс в цепи переменного тока?

Реактивное сопротивление определяется как электрическая величина, из-за которой переменному току противодействует индуктор, конденсатор или их комбинация в цепи. Импеданс — это чистый фактор, противодействующий переменному току. Реактивное сопротивление также можно назвать импедансом индуктивности или конденсатора. Реактивное сопротивление обозначено X, а полное сопротивление Z. В этой статье мы подробно обсудим реактивное сопротивление и импеданс.

Что такое реактивность?

Реактивность — это сопротивление протеканию переменного тока. Это противодействие может быть вызвано либо индуктором (L), либо конденсатором (C). Значение реактивного сопротивления индуктора с индуктивностью L равно ωL, тогда как его значение составляет (1 / ωC) для конденсатора с емкостью C.

Объяснение реактивного сопротивления:

Давайте рассмотрим схему для лучшего понимания. В цепи индуктивность с индуктивностью L Генри подключена к источнику переменного тока V = V _м Sinωt.Здесь ω — угловая частота в радианах / сек. ω = 2πf, где f — частота питающей сети в Гц. Сила тока в цепи I.

Ток I, протекающий по цепи, равен [V _m Sin (ωt — π / 2) / (ωL)]. Следовательно, максимальное значение этого тока равно

I _м = (V _м / ωL)

= (V _м / X _L)

где X _L = ωL

Внимательно наблюдайте за приведенным выше выражением тока и сравните его с законом Ома (I = V / R).Вы заметите, что здесь X _L выполняет работу R. То есть X _L = ωL противостоит потоку тока, как и сопротивление. Это причина; это называется реактивным сопротивлением. Поскольку он обеспечивается индуктором, он называется индуктивным реактивным сопротивлением и обозначается символом X _L.

Давайте теперь рассмотрим другую схему, состоящую из конденсатора и переменного источника, как показано ниже.

Ток в цепи равен (В _м ωC) Sin (ωt + π / 2).Следовательно, максимальное значение тока будет иметь место, когда Sin (ωt + π / 2) = 1, и это значение указано ниже.

I _м = V _м / (1 / ωC)

= V _м / X _C

При сравнении вышеуказанного значения тока I _m с законом Ома (I = V / R) становится ясно, что X _C противодействует потоку тока и действует как сопротивление. Это X _C = (1 / ωC) называется емкостным реактивным сопротивлением.

Что такое импеданс?

Импеданс в цепи переменного тока определяется как чистый противодействующий фактор протеканию тока. Это противодействие может быть связано с сопротивлением и индуктивностью, или сопротивлением и емкостью, или сопротивлением, индуктивностью и емкостью. Обозначается символом Z. Z часто выражается как Z = R + jX, где X — реактивное сопротивление.

Описание импеданса:

Чтобы иметь четкое представление об импедансе, давайте рассмотрим схему, показанную ниже.В этой цепи последовательно соединены чистое сопротивление R и чистая индуктивная катушка с индуктивностью L.

Пусть, V = действующее значение приложенного напряжения

I = действующее значение тока цепи

В _R = падение напряжения на R

В _L = падение напряжения на катушке

Предположим, что ток цепи является опорным вектором. Падение напряжения на сопротивлении будет синфазным с током I. Однако падение напряжения в индуктивной катушке опережает ток I на 90 °.Эти падения напряжения показаны в треугольнике напряжения OAB.

Вектор OA, AB и OB представляет падение напряжения в сопротивлении (V _R), индуктивное падение напряжения (V _L) и напряжение питания (V) соответственно. Напряжение питания (В) — это гипотенуза этого треугольника напряжений. Следовательно, напряжение питания можно рассчитать, как показано ниже.

Величина Z — это полное сопротивление цепи переменного тока. Напряжение питания также можно записать из треугольника напряжения с помощью оператора j.Это показано ниже.

В = (ИК) + j (IX _L)

I = V / (R + jX _L)

= В / З

Таким образом, импеданс Z = R + jX . Таким образом, импеданс — это сложная величина. Угол, который образует Z относительно опорного вектора, рассчитывается как tanƟ = (X / R).

Импеданс | Инжиниринг | Fandom

Электрический импеданс или просто импеданс — это мера сопротивления синусоидальному электрическому току.Концепция электрического импеданса обобщает закон Ома для анализа цепей переменного тока. В отличие от электрического сопротивления, полное сопротивление электрической цепи может быть комплексным числом. Оливер Хевисайд ввел термин импеданс в июле 1886 года.

В общем, решения для напряжений и токов в цепи, содержащей резисторы, конденсаторы и катушки индуктивности (короче говоря, все компоненты с линейным поведением), являются решениями линейного обыкновенного дифференциального уравнения. Можно показать, что если источники напряжения и / или тока в цепи являются синусоидальными и имеют постоянную частоту, решения имеют тенденцию к форме, называемой установившимся режимом переменного тока.Таким образом, все напряжения и токи в цепи синусоидальны и имеют постоянную пиковую амплитуду, частоту и фазу.

Пусть v (t) будет синусоидальной функцией времени с постоянной пиковой амплитудой Vp, постоянной частотой f и постоянной фазой φ.

Где: v (t) — функция напряжения

— максимальная амплитуда напряжения

, где f — постоянная частота, — постоянная фаза, ω — угловая скорость (в радианах в секунду), ω = 2π f , j представляет мнимую единицу (), и означает действительную часть комплексного числа z .

Теперь позвольте комплексному числу V быть задано следующим образом:

V называется векторным представлением v (t) . V — постоянное комплексное число. Для цепи в установившемся режиме переменного тока все напряжения и токи в цепи имеют векторные представления, если все источники имеют одинаковую частоту. То есть каждое напряжение и ток можно представить как постоянное комплексное число. Для анализа цепи постоянного тока каждое напряжение и ток представлены постоянным действительным числом.Таким образом, разумно предположить, что правила, разработанные для анализа цепей постоянного тока, можно использовать для анализа цепей переменного тока, используя комплексные числа вместо действительных чисел.

Определение электрического импеданса [править | править источник]

Импеданс элемента схемы определяется как отношение векторного напряжения на элементе к векторному току через элемент:

Следует отметить, что, хотя Z — это отношение двух векторов, Z сам по себе не является вектором.То есть Z не связано с некоторой синусоидальной функцией времени.

Для цепей постоянного тока сопротивление определяется законом Ома как отношение постоянного напряжения на резисторе к постоянному току через резистор:

где и выше — постоянные действительные значения.

Так же, как закон Ома обобщается на цепи переменного тока с помощью векторов, другие результаты анализа цепей постоянного тока, такие как деление напряжения, деление тока, теорема Тевенина и теорема Нортона, обобщаются на цепи переменного тока.

Импеданс различных устройств [править | править источник]

Резистор

[править | править источник]

Для резистора имеем соотношение:

То есть отношение мгновенного напряжения и тока, связанного с резистором, представляет собой значение сопротивления постоянному току, обозначенное R. Поскольку R является постоянным и действительным, отсюда следует, что если v (t) синусоидальный , i (t) также является синусоидальным с той же частотой и фазой. Таким образом, мы имеем, что сопротивление резистора равно R:

Конденсатор [редактировать | править источник]

Для конденсатора имеем соотношение

.Теперь позвольте

Отсюда следует, что

Используя векторную нотацию и результат выше, запишите наше первое уравнение как:

Отсюда следует, что полное сопротивление конденсатора равно

Индуктор [редактировать | править источник]

Для индуктора имеем:

По тем же соображениям, что и в приведенном выше примере конденсатора, следует, что полное сопротивление на катушке индуктивности составляет:

См. Основную статью: Электрическое реактивное сопротивление

Термин реактивное сопротивление относится к мнимой части импеданса.Несколько примеров:

Сопротивление резистора составляет R (его сопротивление) , а его реактивное сопротивление равно 0 .

Полное сопротивление с конденсатора составляет Дж (-1 / ωC) , а его реактивное сопротивление составляет -1 / ωC .

Полное сопротивление с индуктора составляет Дж ω L , а его реактивное сопротивление составляет Ом L .

Важно отметить, что импеданс конденсатора или катушки индуктивности является функцией частоты f и является мнимой величиной, однако, безусловно, является реальным физическим явлением, связывающим сдвиг фаз между векторами напряжения и тока из-за к наличию конденсатора или катушки индуктивности.Ранее было показано, что сопротивление резистора является постоянным и действительным, другими словами, резистор не вызывает сдвига фаз между напряжением и током, как конденсаторы и катушки индуктивности.

Когда резисторы, конденсаторы и катушки индуктивности объединены в цепи переменного тока, импедансы отдельных компонентов могут быть объединены таким же образом, как сопротивления объединены в цепи постоянного тока. Результирующий эквивалентный импеданс, как правило, является сложной величиной. То есть эквивалентный импеданс имеет действительную и мнимую части.Действительная часть обозначается R, а мнимая часть обозначается X. Таким образом:

называется резистивной частью импеданса, а реактивной частью импеданса. Поэтому конденсатор или катушку индуктивности принято называть реактивным сопротивлением или, что эквивалентно, реактивным компонентом (элементом схемы). Кроме того, импеданс емкости отрицательный мнимый, в то время как импеданс катушки индуктивности является положительным мнимым.Таким образом, емкостное реактивное сопротивление относится к отрицательному реактивному сопротивлению, а индуктивное реактивное сопротивление относится к положительному реактивному сопротивлению.

Реактивный компонент отличается тем, что синусоидальное напряжение на компоненте находится в квадратуре с синусоидальным током, протекающим через компонент. Это означает, что компонент попеременно поглощает энергию из цепи, а затем возвращает энергию в цепь. То есть, в отличие от сопротивления, реактивное сопротивление не рассеивает мощность.

Поучительно определить значение емкостного реактивного сопротивления на крайних частотах. Когда частота приближается к нулю, емкостное реактивное сопротивление неограниченно возрастает, так что конденсатор приближается к разомкнутой цепи для очень низкочастотных синусоидальных источников. По мере увеличения частоты емкостное реактивное сопротивление приближается к нулю, так что конденсатор приближается к короткому замыканию для очень высокочастотных синусоидальных источников.

И наоборот, индуктивное реактивное сопротивление приближается к нулю, когда частота приближается к нулю, так что индуктор приближается к короткому замыканию для очень низкочастотных синусоидальных источников.По мере увеличения частоты индуктивное реактивное сопротивление увеличивается, так что катушка индуктивности приближается к разомкнутой цепи для очень высокочастотных синусоидальных источников.

Объединение импедансов последовательно, параллельно или в конфигурациях треугольник-звезда такое же, как для резисторов. Разница в том, что комбинирование импедансов включает в себя манипуляции с комплексными числами.

Последовательно [править | править источник]

Последовательное объединение импедансов просто:

Параллельно [править | править источник]

Параллельное объединение импедансов намного сложнее, чем объединение простых свойств, таких как сопротивление или емкость, из-за члена умножения.

В рационализированном виде эквивалентное сопротивление:

См. Также Последовательные и параллельные схемы.

Схемы с общими источниками [править | править источник]

Импеданс определяется отношением двух векторов, где вектор — это комплексная пиковая амплитуда синусоидальной функции времени. Для более общих периодических источников и даже непериодических источников все же можно использовать понятие импеданса.Можно показать, что практически все периодические функции времени можно представить рядом Фурье. Таким образом, общий периодический источник напряжения можно рассматривать как (возможно, бесконечную) последовательную комбинацию источников синусоидального напряжения. Точно так же общий периодический источник тока можно рассматривать как (возможно, бесконечную) параллельную комбинацию источников синусоидального тока.

Используя технику суперпозиции, каждый источник активируется по одному, и решение цепи переменного тока находится с использованием импедансов, рассчитанных для частоты этого конкретного источника.Окончательные решения для напряжений и токов в цепи вычисляются как суммы членов, рассчитанных для каждого отдельного источника. Однако важно отметить, что фактические напряжения и токи в цепи не имеют представления вектора. Фазоры можно складывать вместе, только если каждый из них представляет временную функцию той же частоты . Таким образом, векторные напряжения и токи, которые вычисляются для каждого конкретного источника, должны быть преобразованы обратно в их представление во временной области до того, как произойдет окончательное суммирование.

Этот метод можно обобщить на непериодические источники, в которых дискретные суммы заменены интегралами. То есть вместо ряда Фурье используется преобразование Фурье.

Величина и фаза импеданса [редактировать | править источник]

Комплексные числа обычно выражаются в двух различных формах. Прямоугольная форма — это просто сумма действительной части с произведением j и мнимой части:

Полярная форма комплексного числа — это произведение действительного числа, называемого величиной, и другого комплексного числа, называемого фазой:

Где величина определяется по формуле:

, а угол определяется по формуле:

Эквивалентно величина определяется по формуле:

Где Z * обозначает комплексное сопряжение Z:.

Пиковый вектор против среднеквадратичного фазора [править | править источник]

Синусоидальное напряжение или ток имеет пиковое значение амплитуды, а также среднеквадратичное значение. Можно показать, что действующее значение синусоидального напряжения или тока определяется выражением:

Во многих случаях анализа переменного тока среднеквадратичное значение синусоиды более полезно, чем пиковое значение. Например, чтобы определить количество мощности, рассеиваемой резистором из-за синусоидального тока, необходимо знать действующее значение тока.По этой причине источники напряжения вектора и тока часто указываются как среднеквадратичное значение вектора. То есть величина вектора — это среднеквадратичное значение соответствующей синусоиды, а не пиковая амплитуда. Обычно среднеквадратичные векторы используются в электроэнергетике, тогда как векторы пиковых значений часто используются при анализе цепей малой мощности.

В любом случае, импеданс явно один и тот же независимо от того, используются ли векторы пиков или среднеквадратичные векторы, поскольку коэффициент масштабирования компенсируется при измерении соотношения векторов.

При установке компонентов вместе для передачи электромагнитных сигналов важно согласовать импеданс, который может быть достигнут с помощью различных согласующих устройств. Несоблюдение этого правила называется рассогласованием импеданса и приводит к потере сигнала и отражениям. Наличие отражений позволяет использовать рефлектометр во временной области для обнаружения несовпадений в системе передачи.

Например, обычная радиочастотная антенна для телевещания в Северной Америке была стандартизирована до 300 Ом с использованием сбалансированной неэкранированной плоской проводки.Однако системы кабельного телевидения представили использование несимметричной экранированной круглой проводки сопротивлением 75 Ом, которую нельзя было подключить к большинству телевизоров той эпохи. Чтобы использовать новую проводку на старом телевизоре, были широко доступны небольшие устройства, известные как балуны . Сегодня большинство телевизоров просто стандартизированы на питание с сопротивлением 75 Ом.

Величина, обратная нереактивному сопротивлению, называется проводимостью. Точно так же величина, обратная импедансу, называется проводимостью. Проводимость — это действительная часть допуска, а мнимая часть называется восприимчивостью.Проводимость и восприимчивость — это , а не , обратные сопротивлению и реактивному сопротивлению в целом, а только для чисто резистивных или чисто реактивных импедансов.

Электромагнитный импеданс [править | править источник]

В задачах распространения электромагнитных волн в однородной среде полное сопротивление среды определяется как:

где μ и ε — проницаемость и диэлектрическая проницаемость среды соответственно.

Акустический импеданс [редактировать | править источник]

В полной аналогии с обсуждаемым здесь электрическим импедансом также определяется акустический импеданс, комплексное число, которое описывает, как среда поглощает звук, связывая амплитуду и фазу приложенного звукового давления с амплитудой и фазой результирующего звукового потока.

Импеданс передачи данных [править | править источник]

Другая аналогичная чеканка — использование импеданса компьютерными программистами для описания того, насколько легко или сложно передавать данные и поток управления между частями системы, обычно написанными на разных языках. Обычно используется описание двух программ или языков / сред как имеющих несоответствие с низким или высоким импедансом.

Приложение к физическим устройствам [править | править источник]

Обратите внимание, что приведенные выше уравнения применимы только к теоретическим устройствам.Реальные резисторы, конденсаторы и катушки индуктивности более сложны, и каждый из них может быть смоделирован как сеть теоретических резисторов, конденсаторов и катушек индуктивности. Номинальные импедансы реальных устройств на самом деле являются номинальными импедансами и точны только для узкого частотного диапазона и обычно менее точны для более высоких частот. Даже в пределах номинального диапазона сопротивление катушки индуктивности может быть отличным от нуля. Выше номинальных частот резисторы становятся индуктивными (в большей степени силовые резисторы), конденсаторы и катушки индуктивности могут становиться более резистивными.Соотношение между частотой и импедансом может даже не быть линейным вне номинального диапазона устройства.

Противодействие текущему потоку переменного тока

Емкость — это способность тела удерживать электрический заряд. Обычно конденсатор состоит из двух параллельных пластин, разделенных изолятором. Изолятор обычно называют диэлектриком. Пластины конденсатора обладают способностью накапливать электроны при зарядке от источника напряжения. Конденсатор разряжается, когда подаваемое напряжение больше не присутствует, и конденсатор подключается к пути тока.В электрической цепи конденсатор служит резервуаром или хранилищем электроэнергии.

Базовая единица емкости — фарад, обозначается буквой F. По определению, один фарад — это один кулон заряда, накопленного с одним вольт на пластинах конденсатора. На практике одна фарада — это большая емкость. Обычно в электронике используются блоки гораздо меньшего размера. Две более распространенные единицы меньшего размера — это микрофарад (мкФ), который составляет 10-6 фарад, и пикофарад (пФ), который составляет 10-12 фарад.

Когда в цепи подается переменный ток, заряд на пластинах постоянно меняется. [Рис. 5] Это означает, что электричество должно течь сначала от Y по часовой стрелке к X, затем от X против часовой стрелки к Y, затем от Y по часовой стрелке к X и так далее. Хотя ток не течет через изолятор между пластинами конденсатора, он постоянно течет в оставшейся части цепи между X и Y. По мере того, как этот ток попеременно поступает в конденсатор и от него, создается определенная задержка по времени.Когда конденсатор заряжается или разряжается через сопротивление, требуется определенное время для полной зарядки или разрядки. Напряжение на конденсаторе не меняется мгновенно. Скорость зарядки или разрядки определяется постоянной времени цепи. Такая скорость заряда и разряда создает противодействие протеканию тока в цепях переменного тока, известное как емкостное реактивное сопротивление. Емкостное реактивное сопротивление обозначается XC и измеряется в омах. Эта характеристика конденсатора также может создавать фазовый сдвиг между напряжением и током в цепи.Фазовый сдвиг, создаваемый емкостным реактивным сопротивлением, всегда приводит к тому, что ток ведет к напряжению. То есть ток емкостной цепи достигает своих пиковых значений до того, как напряжение достигает пиковых значений.

Рисунок 5. Конденсатор в цепи переменного тока

Емкостное реактивное сопротивление — это мера того, насколько емкостная цепь противодействует приложенному току. Емкостное реактивное сопротивление измеряется в омах. Емкостное реактивное сопротивление цепи косвенно пропорционально емкости цепи и приложенной к цепи частоте.При увеличении емкости или приложенной частоты емкостное реактивное сопротивление уменьшается, и наоборот. Это соотношение задается как:

Где: XC = емкостное реактивное сопротивление в омах, C = емкость в фарадах, f = частота в циклах в секунду и π = 3,1416.

На рисунке 5 показана последовательная схема, в которой приложенное напряжение составляет 110 вольт при 400 гц, а емкость конденсатора составляет 80 мФ. Найдите емкостное реактивное сопротивление и ток.

Чтобы найти емкостное реактивное сопротивление, воспользуйтесь следующим уравнением:

Во-первых, емкость 80 мкф заменяется на фарады путем деления 80 на 1000000, поскольку 1 миллион микрофарад равен 1 фараду.Это частное равно 0,000080 фарада. Это подставляется в уравнение:

Импеданс

Полное противодействие протеканию тока в цепи переменного тока называется импедансом и обозначается буквой Z. Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное противодействие протеканию тока в цепи переменного тока). Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением.Импеданс измеряется в омах.

Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только в том случае, если эта цепь содержит только сопротивление, а не индуктивность или емкость. Как в последовательной, так и в параллельной цепях, если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как и сопротивление, а закон Ома для цепи переменного тока, I = E / Z, точно такой же, как для цепи постоянного тока. схема. На рисунке 6 показана последовательная схема, содержащая нагревательный элемент с сопротивлением 11 Ом, подключенный к источнику 110 В.Чтобы определить, какой ток протекает при подаче переменного тока 110 вольт, решается следующий пример:

Рис. 6. Применение постоянного и переменного тока в цепи

Если два значения сопротивления параллельно подключены к источнику переменного тока, как показано на рисунке 7, полное сопротивление равно общему сопротивлению цепи. Еще раз, вычисления будут производиться так же, как если бы это была цепь постоянного тока, и применимо следующее:

Рисунок 7.
Два значения сопротивления, подключенные параллельно к источнику переменного тока. Импеданс равен общему сопротивлению цепи

Импеданс — это полное сопротивление току в цепи переменного тока. Если цепь имеет индуктивность или емкость, необходимо учитывать сопротивление (R), индуктивное реактивное сопротивление (XL) и / или емкостное реактивное сопротивление (XC) для определения полного сопротивления (Z). В этом случае Z не равно RT. Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу.Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником. [Рис. 8] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон. Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.

Рисунок 8.Треугольник полного сопротивления

На практике, если последовательная цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 9, соотношение между сторонами может быть указано как:

Эту формулу можно использовать для определения импеданса, если известны значения индуктивного реактивного сопротивления и сопротивления. Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив XC в формулу вместо XL. В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):

Рисунок 9.Цепь, содержащая сопротивление и индуктивность

На рисунке 9 показан пример 1. Здесь последовательная цепь, содержащая резистор и катушку индуктивности, подключена к источнику 110 вольт с частотой 60 циклов в секунду. Резистивный элемент представляет собой простой измерительный элемент 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какое значение импеданса и тока в цепи?

Решение:

Сначала вычисляется индуктивное реактивное сопротивление катушки:

Помните, что при расчете Z всегда используйте индуктивное реактивное сопротивление, а не индуктивность, и используйте емкостное реактивное сопротивление, а не емкость.

После определения полного сопротивления можно рассчитать общий ток.

Так как эта цепь резистивная и индуктивная, там есть фазовый сдвиг, когда напряжение ведет к току.

Пример 2 представляет собой проиллюстрированную последовательную схему, в которой конденсатор емкостью 200 мкФ соединен последовательно с резистором 10 Ом. [Рисунок 10] Каково значение импеданса, тока и падения напряжения на резисторе?

Рисунок 10.Цепь, содержащая сопротивление и емкость

Решение:

Во-первых, емкость изменяется с микрофарад на фарады. Поскольку 1 миллион микрофарад равен 1 фараду, то 200 мкф = 0,000200 фарад

Следующее решение для емкостного реактивного сопротивления:

Поскольку эта цепь резистивная и емкостная, существует фазовый сдвиг в точках, где ток ведет к напряжению:

Чтобы узнать ток:

Когда схема содержит сопротивление, индуктивность и емкость, для определения полного сопротивления используется следующее уравнение.

Пример 3: Каково полное сопротивление последовательной цепи, состоящей из конденсатора с емкостным реактивным сопротивлением 7 Ом, катушки индуктивности с индуктивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 11]

Рисунок 11.Цепь, содержащая сопротивление, индуктивность и емкость

Помните, что индуктивное и емкостное сопротивление могут вызвать сдвиг фаз между напряжением и током. В этом примере индуктивное реактивное сопротивление больше емкостного, поэтому напряжение ведет к току.

Следует отметить, что, поскольку индуктивное реактивное сопротивление, емкостное реактивное сопротивление и сопротивление влияют друг на друга под прямым углом, падения напряжения в любой последовательной цепи переменного тока следует складывать с помощью векторного сложения.На рисунке 12 показано падение напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.

Рисунок 12. Падения напряжения

Чтобы рассчитать отдельные падения напряжения, просто используйте уравнения:

Чтобы определить общее приложенное напряжение для цепи, каждое отдельное падение напряжения должно быть добавлено с помощью векторного сложения.

Параллельные цепи переменного тока

Чтобы определить полное сопротивление параллельной цепи, показанной на рисунке 13, сначала нужно определить емкостное и индуктивное реактивные сопротивления. (Не забудьте перевести микрофарады в фарады.)

Рисунок 13. Полный импеданс параллельной цепи

Для определения протекания тока в цепи:
Чтобы определить ток, протекающий через каждый параллельный путь цепи, рассчитайте IR, IL и IC.
Следует отметить, что полный ток в параллельных цепях определяется путем сложения векторов отдельных потоков тока следующим образом:

Питание в цепях переменного тока
Поскольку напряжение и ток определяют мощность, есть сходства в мощности, потребляемой цепями переменного и постоянного тока. Однако в переменном токе ток зависит как от сопротивления, так и от реактивного сопротивления цепи. Мощность, потребляемая любой цепью переменного тока, является функцией приложенного напряжения, а также сопротивления и реактивного сопротивления цепи.Цепи переменного тока имеют два различных типа мощности: один создается сопротивлением цепи, а другой — реактивным сопротивлением цепи.
Истинная сила
Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность — это мощность, потребляемая участком сопротивления цепи, и измеряется в ваттах (Вт). Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:
Полная мощность
Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи.Полная мощность — это мощность, потребляемая всей цепью, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Полная мощность — это произведение эффективного напряжения на эффективный ток. Полная мощность рассчитывается по формуле:
СВЯЗАННЫЕ ЗАПИСИ
.

Что такое полное сопротивление цепи переменного тока

Формула расчета полного сопротивления

От чего зависит полное сопротивление цепи

Треугольник сопротивлений

Векторная диаграмма цепи переменного тока

Особенности расчета полного сопротивления для разных цепей

Последовательное соединение

Параллельное соединение

Резонанс в цепи переменного тока

Практическое применение расчета полного сопротивления

Методы измерения полного сопротивления

Заключение

Полное сопротивление цепей переменного тока

6.4. Сопротивление в цепи синусоидального тока

6.5. Индуктивная катушка в цепи синусоидального тока

6.6. Емкость в цепи синусоидального тока

6.7. Последовательно соединенные реальная индуктивная

6.8. Параллельно соединенные индуктивность, емкость

6.9. Резонансный режим в цепи, состоящей

общие сведения, зависимость от других величин и формулы расчета

Физический смысл

Зависимость электропроводимости

Электрические величины

Геометрические параметры и тип вещества

Температура проводника

Цепь переменного тока

Измерение сопротивления

Полное сопротивление — цепь — переменный ток

Полное сопротивление — цепь — переменный ток

7 «Б»

Цепь переменного тока с R, L и С сопротивлениями

Пример решения контрольной по электротехнике

RLC | Физика

Цели обучения

Пример 1.Расчет импеданса и тока

Пример 2. Расчет резонансной частоты и тока

Питание в цепях переменного тока серии

Пример 3. Расчет коэффициента мощности и мощности

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Избранные решения проблем и упражнения

Импеданс

Летный механик рекомендует

В чем разница между сопротивлением, реактивным сопротивлением и импедансом?

Треугольников мощности и импеданса — тригонометрия и генерация однофазного переменного тока для электриков

Помните

Что такое реактивное сопротивление и импеданс в цепи переменного тока?

Импеданс | Инжиниринг | Fandom

Определение электрического импеданса [править | править источник]

Импеданс различных устройств [править | править источник]

[править | править источник]

Конденсатор [редактировать | править источник]

Индуктор [редактировать | править источник]

Последовательно [править | править источник]

Параллельно [править | править источник]

Схемы с общими источниками [править | править источник]

Величина и фаза импеданса [редактировать | править источник]

Пиковый вектор против среднеквадратичного фазора [править | править источник]

Электромагнитный импеданс [править | править источник]

Акустический импеданс [редактировать | править источник]

Импеданс передачи данных [править | править источник]

Приложение к физическим устройствам [править | править источник]

Противодействие текущему потоку переменного тока

Импеданс

Параллельные цепи переменного тока

Питание в цепях переменного тока

Истинная сила

Полная мощность

Похожие записи

Первая обувь для ребенка: советы доктора Комаровского

Как вызвать настоящего Деда Мороза: магические ритуалы и современные способы

Развивающие занятия для детей от 1,5 до 5 лет: игры, упражнения и советы родителям

Добавить комментарий Отменить ответ