Что такое индуктивное сопротивление и как оно рассчитывается. От каких параметров зависит индуктивное сопротивление катушки. Как применяется индуктивное сопротивление в электрических цепях и устройствах. Формулы для расчета индуктивного сопротивления.
Что такое индуктивное сопротивление и его физическая сущность
Индуктивное сопротивление — это реактивное сопротивление, которое оказывает катушка индуктивности переменному току. Физическая сущность индуктивного сопротивления заключается в следующем:
- При протекании переменного тока через катушку в ней возникает переменное магнитное поле
- Изменяющееся магнитное поле наводит в катушке ЭДС самоиндукции
- ЭДС самоиндукции препятствует изменению тока в катушке
- Это препятствие изменению тока и воспринимается как сопротивление катушки переменному току
Таким образом, индуктивное сопротивление является следствием явления электромагнитной индукции в катушке. Чем больше индуктивность катушки, тем больше ее индуктивное сопротивление.

Формула для расчета индуктивного сопротивления
Основная формула для расчета индуктивного сопротивления катушки:
XL = ωL = 2πfL
где:
- XL — индуктивное сопротивление, Ом
- ω — угловая частота, рад/с
- f — частота переменного тока, Гц
- L — индуктивность катушки, Гн
Из этой формулы видно, что индуктивное сопротивление:
- Прямо пропорционально частоте переменного тока
- Прямо пропорционально индуктивности катушки
От каких параметров зависит индуктивное сопротивление
Основные параметры, влияющие на величину индуктивного сопротивления катушки:
- Частота переменного тока — при увеличении частоты индуктивное сопротивление растет
- Индуктивность катушки — чем больше индуктивность, тем больше сопротивление
- Число витков обмотки — увеличение числа витков повышает индуктивность и сопротивление
- Геометрические размеры катушки — влияют на индуктивность
- Магнитная проницаемость сердечника — повышает индуктивность
Важно отметить, что индуктивное сопротивление не зависит от силы тока, в отличие от активного сопротивления проводника.

Применение индуктивного сопротивления в электротехнике
Индуктивное сопротивление катушек находит широкое применение в различных областях электротехники и электроники:
- Фильтрация сигналов — катушки используются для создания фильтров высоких и низких частот
- Колебательные контуры — в сочетании с конденсаторами образуют резонансные LC-контуры
- Трансформаторы — индуктивная связь между обмотками позволяет преобразовывать напряжение
- Дроссели — ограничивают пульсации тока в выпрямителях и импульсных источниках питания
- Электродвигатели — обмотки статора и ротора обладают индуктивностью
Знание принципов индуктивного сопротивления необходимо для расчета и проектирования многих электротехнических устройств.
Сравнение индуктивного и емкостного сопротивлений
Индуктивное и емкостное сопротивления являются двумя типами реактивного сопротивления в цепях переменного тока. Основные отличия между ними:
- Индуктивное сопротивление увеличивается с ростом частоты, а емкостное — уменьшается
- Напряжение на индуктивности опережает ток на 90°, а на емкости — отстает на 90°
- Индуктивность накапливает энергию в магнитном поле, а емкость — в электрическом
- Формулы расчета: XL = ωL для индуктивности, XC = 1/(ωC) для емкости
При последовательном соединении индуктивности и емкости их сопротивления вычитаются. Это явление используется для создания резонансных контуров.
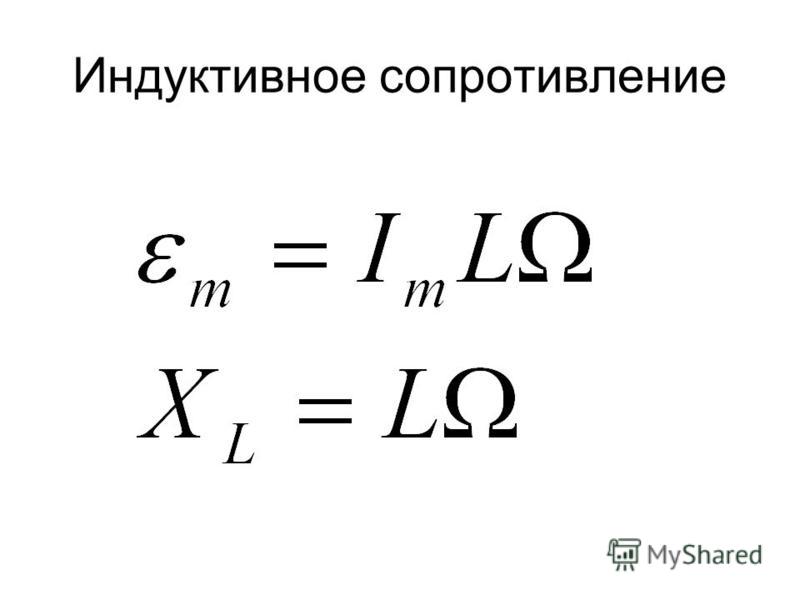
Расчет индуктивного сопротивления в сложных цепях
При расчете сложных электрических цепей с несколькими индуктивностями необходимо учитывать следующие правила:
- При последовательном соединении катушек их индуктивные сопротивления складываются: XL общ = XL1 + XL2 + … + XLn
- При параллельном соединении суммируются проводимости: 1/XL общ = 1/XL1 + 1/XL2 + … + 1/XLn
- В цепи с активным сопротивлением R и индуктивностью L полное сопротивление рассчитывается по формуле: Z = √(R2 + XL2)
- Для расчета мощности в цепи с индуктивностью используются формулы: S = UI — полная мощность P = UI cosφ — активная мощность Q = UI sinφ — реактивная мощность
При анализе сложных цепей переменного тока удобно использовать метод комплексных чисел, представляя индуктивное сопротивление в виде jωL.
Способы изменения индуктивного сопротивления
На практике часто возникает необходимость регулировать величину индуктивного сопротивления. Основные способы изменения индуктивного сопротивления катушки:
- Изменение числа витков — используются катушки с отводами или переменные индуктивности
- Изменение геометрии катушки — применяются катушки с подвижным сердечником
- Подмагничивание сердечника — изменяется магнитная проницаемость материала сердечника
- Изменение частоты тока — при фиксированной индуктивности меняется сопротивление
- Включение/выключение секций катушки — для ступенчатого изменения индуктивности
Выбор конкретного способа зависит от требуемого диапазона регулирования и особенностей применения катушки индуктивности в электрической схеме.

Формула расчета реактивного сопротивления проводника: калькулятор расчетов
Реактивное сопротивление относится к числу явлений, наблюдаемых в цепях переменного тока. Тем, кто занимается ремонтом и эксплуатацией таких цепей, будет полезно знать, как определяется эта величина, и каким образом она влияет на процессы, происходящие в электросети.
Соленоид – устройство, обладающее индуктивностью
Понятие реактивного сопротивления
Данная разновидность репрезентирует взаимоотношение электротока и напряжения на определенных типах подключенных в сеть нагрузок (дросселях, конденсаторных компонентах), не сопряженное с объемами электроэнергии, используемыми потребителем. Измерительной единицей, как и для других разновидностей, выступает ом. Рассматриваемое явление обнаруживает себя только при переменном электротоке. В расчетах оно обозначается латинской литерой Х.
Различия между активным и реактивным сопротивлением
Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию.
Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.
Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг. При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.
Виды и свойства реактивного сопротивления
Данная величина может иметь две формы:
- емкостную – присущую конденсаторным элементам;
- индуктивную – характерную для катушек, соленоидов и обмоток.

Важно! Если к трансформатору подключить активную нагрузку, реактивное сопротивление понизится, так как упадет значение того типа мощности, который его вызывает. В некоторых цепях с несколькими индуктивными или емкостными нагрузками имеет место взаимоуничтожение фазовых сдвигов, приходящихся на разные детали, тогда комплексная величина будет равной нулю.
Треугольник сопротивлений
Виды пассивных элементов
Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.
Катушка индуктивности
Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.
Подключение катушки в электрическую цепь
Емкостной элемент
Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.
Подсоединение конденсатора в электроцепь
Конденсатор в цепи переменного тока
Конденсаторные устройства характеризуются неспособностью пропускать константный электроток. Так что если устройство подсоединить последовательно к источнику такого тока, в цепи электроток идти не будет. В переменных цепях дело обстоит иначе. Если цепочка содержит только емкостной компонент, в ней будет проходить ток, обгоняющий по фазе напряжение на 90°.
Важно! Величина электротока определяется его частотой и емкостной характеристикой использованного конденсатора.
Реактивное сопротивление конденсатора
Его можно узнать, воспользовавшись формулой:
Х=1/(C*w).
Здесь С – емкостная величина рассматриваемой детали, а w – угловая частота. При параллельном подключении элементов будет справедлива формула:
1/Хобщ = 1/Х1 + 1/Х2 +…
Если конденсаторы объединены последовательно, для нахождения комплексного показателя системы потребуется сложить значения для всех компонентов:
Хобщ = Х1 + Х2 +…
Катушка индуктивности в цепи переменного тока
В отличие от предыдущего случая, при подключении катушечного элемента идущий по нему электроток будет отставать от напряжения. Однако величина фазового сдвига будет аналогичной – 90°. При этом за препятствование быстрому увеличению тока ответственна ЭДС. Элемент способен играть роль безваттного резистора.
Реактивное сопротивление катушки индуктивности
В его расчете поможет выражение:
X = L*w.
Здесь L – показатель индуктивности подсоединенного элемента. При последовательном включении в сеть серии катушек индуктивная компонента сопротивления такой композиции может быть выражена как сумма таковых для всех деталей. Если применено параллельное соединение, справедливым будет выражение:
Если применено параллельное соединение, справедливым будет выражение:
1/Хобщ = 1/Х1 + 1/Х2 +…
Как для катушки, так и для конденсаторных деталей будет верной запись закона Ома:
X = U/I, в которой U – величина падения напряжения на элементе.
Почему не сгорает первичная обмотка трансформатора
Иногда при эксплуатации трансформаторов возникает вопрос, почему не происходит сгорание обмотки, если ее сопротивляемость оказывается малой. Обмоточный компонент по своему устройству может быть приравнен к катушке. Соответственно, искомый показатель может быть вычислен с помощью выражения:
X = 2*π*L*F, где L – частота, F – индуктивность.
Поскольку последняя у трансформатора оказывается достаточно большой, таковым будет и итоговое число.
Мощность в цепи с реактивными радиоэлементами
При подключении таких элементов в цепь в четных четвертях периода мощность будет иметь отрицательное значение (в это время компонент направляет накопленную энергию в источник напряжения). В итоге использование энергии элементом за весь цикл оказывается равным нулю. Это означает, что на нем не происходит выделения энергии, так что на электросхемах такие детали изображаются холодными. На деле положение вещей может быть немного иным (это зависит от параметров конкретного элемента), бывает, что небольшие тепловые потери на конденсаторе или соленоиде все-таки имеют место. Но они не будут значительными, измеряющимися в кв.
В итоге использование энергии элементом за весь цикл оказывается равным нулю. Это означает, что на нем не происходит выделения энергии, так что на электросхемах такие детали изображаются холодными. На деле положение вещей может быть немного иным (это зависит от параметров конкретного элемента), бывает, что небольшие тепловые потери на конденсаторе или соленоиде все-таки имеют место. Но они не будут значительными, измеряющимися в кв.
Компенсация реактивной мощности
При подключении большого числа индуктивных компонентов генерируемая ими реактивная мощность создает избыточную нагрузку на трансформаторы и в целом ведет к бесполезной потере энергии. Чтобы это нивелировать, параллельно можно подсоединить конденсатор. Если правильно подобрать номинал, можно скомпенсировать фазовый сдвиг, что сильно снизит энергетические потери. Емкость этого устройства С равна 1/(2*π*f*X), где Х – параметр сопротивляемости подключенной нагрузки, равный U2/Q (Q – реактивная мощность).
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
Видео
Определение активных и индуктивных сопротивлений проводов
Доброго времени суток. В данной статье речь пойдет о расчете активных и индуктивных сопротивлений для воздушных и кабельных линий из цветных металлов, таких как медь и алюминий. Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.
Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.
Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см.
 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30].
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
Определение индуктивного сопротивления проводов
Индуктивное сопротивление воздушных линий для стандартной частоты f = 50 Гц и относительной магнитной проницаемости для цветных металлов µ = 1, определяется по известной всем формуле [Л1.с.19]:
где:
- Dср. – среднее геометрическое расстояние между проводами, мм;
- dр – расчетный диаметр провода (мм2), определяется по ГОСТ 839-80, таблицы 1 -4;
Среднее геометрическое расстояние между проводами определяется по формуле [Л1.с.19]:
где:
- D1-2 — расстояние между проводами первой и второй фазы;
- D2-3 — расстояние между проводами второй и третей фазой;
- D1-3 — расстояние между первой и третей фазой.

Данные значения определяются по чертежам опор линий электропередачи.
Для упрощения расчетов индуктивного сопротивления проводов рекомендуется использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
Если же нужно выполнить приближенный расчет, то можно использовать в расчетах средние значения сопротивлений:
- для линий 0,4 – 10 кВ х = 0,3 Ом/км;
- для линий 35 кВ х = 0,4 Ом/км;
- для стальных проводов использовать приложение П6 [Л1.с.70];
Индуктивное сопротивление кабелей рассчитать довольно сложно, из-за различной их конструкции. Поэтому активные и индуктивные сопротивления кабелей рекомендуется принимать по справочникам, приложение П7 [Л1.с.70].
Если же нужно выполнить приближенный расчет, можно принять индуктивные сопротивления:
- для кабелей сечением 16 – 240 мм2 х = 0,06 Ом/км для напряжения до 1000 В;
- для кабелей сечением 16 – 240 мм2 х = 0,08 Ом/км для напряжения 6 – 10 кВ;
- для проводов проложенных на роликах х = 0,20 Ом/км;
- для проводов проложенных на изоляторах х = 0,25 Ом/км;
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Поделиться в социальных сетях
Определение сопротивления кабелей на напряжение 6
В данной статье приводятся таблицы активного и индуктивного сопротивления кабелей на напряжение 6 — 35 кВ взятые из различных справочников по проектированию электрических сетей и руководящих указаний.
Значения активного и индуктивного сопротивления кабелей необходимы при расчете токов короткого замыкания и проверки кабеля на потери напряжения.
Сопротивление кабелей с бумажной, резиновой и поливинилхлоридной изоляцией на напряжение 6 — 35 кВ
1. РД 153-34.0-20.527-98 – Руководящие указания по расчету токов короткого замыкания и выбору электрооборудования. 2002 г. Таблица П.8, страница 145.
2. Проектирование кабельных сетей и проводок. Хромченко Г.Е. 1980 г. Таблица 2-5, страница 48.
Хромченко Г.Е. 1980 г. Таблица 2-5, страница 48.
3. Справочник по проектированию электроснабжению. Ю.Г. Барыбина. 1990 г. Таблица 2.63, страницы 175-176.
4. Справочная книга электрика. Григорьева В.И. 2004г. Таблицы 3.9.7; 3.9.11; страницы 448-449
Если значения активных и реактивных сопротивлений кабелей, вы не нашли в приведенных таблицах. В этом случае, сопротивление кабеля можно определить по приведенным формулам с подстановкой в них фактических параметров кабелей.
Методика расчета представлена в книге: «Проектирование кабельных сетей и проводок. Хромченко Г.Е. 1980 г, страницы 45-48».
Активное сопротивление кабеля
1. Активное сопротивление однопроволочной жилы, определяется по формуле 2-1, Ом:
где:
- l — длина жилы, м;
- s – поперечное сечение жилы, мм2, определяется по формуле: π*d2/4;
- d – диаметр жилы кабеля;
- α20 – температурный коэффициент сопротивления, равный при 20 °С:
- 0,00393 1/град – для меди;
- 0,00403 1/град – для алюминия;
- ρ20 – удельное сопротивление материала жилы при 20 °С (температура изготовления жилы), можно принять согласно книги «Справочная книга электрика.
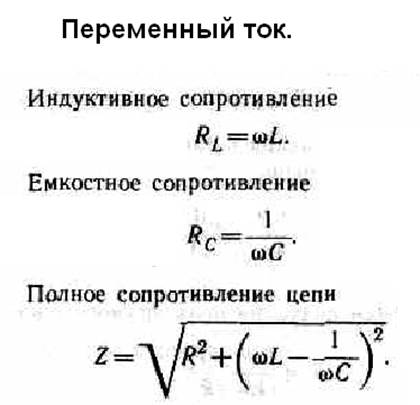 Григорьева В.И. 2004г.» Таблица 1.14, страница 30.
Григорьева В.И. 2004г.» Таблица 1.14, страница 30.
- tж – допустимая температура нагрева жилы, согласно ПУЭ п.1.3.10 и 1.3.12.
2. Активное сопротивление многопроволочной жилы определяется также по формуле 2-1, но из-за конструктивных особенностей многопроволочной жилы, вместо значений ρ20 вводиться в формулу ρр равное:
- 0,0184 Ом*мм2/м – для медных жил;
- 0,031 Ом*мм2/м – для алюминиевых жил.
3. Удельное активное сопротивление жилы, отнесенное к единице длины линии 1 км, определяется из следующих зависимостей, Ом/км:
Индуктивное сопротивление кабеля
1. Удельное реактивное (индуктивное) сопротивление кабеля определяется по формуле 2-8, Ом/км:
где:
- d – диаметр жилы кабеля.
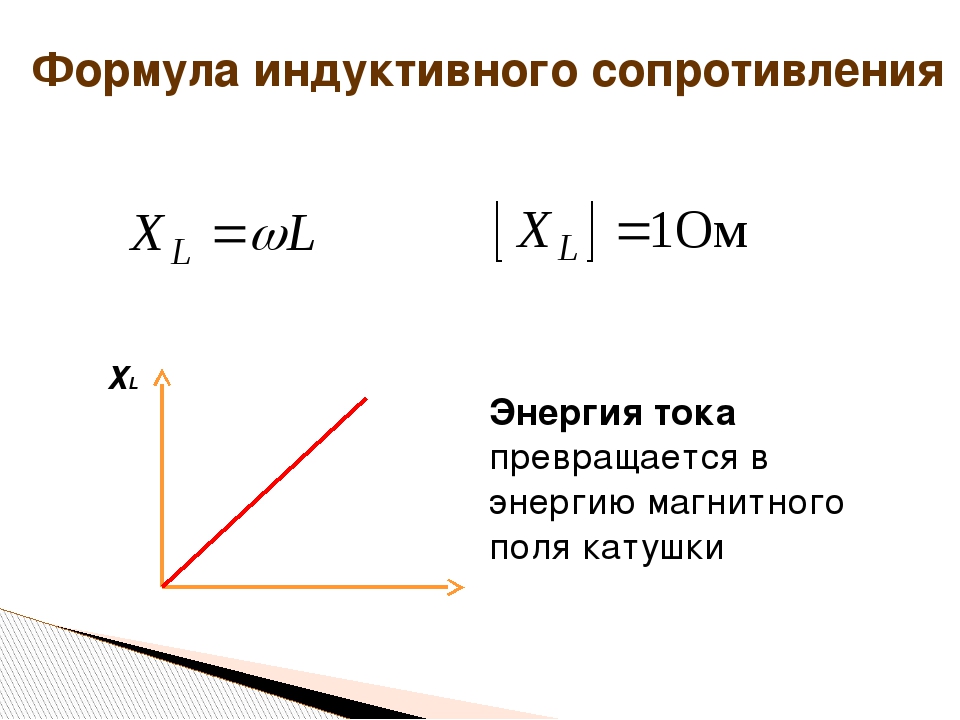
- lср – среднее геометрическое расстояние между центрами жил кабеля определяется по формуле [Л1.с.19]:
где:
- lА-В — расстояние между центрами жил фаз А и В;
- lВ-С — расстояние между центрами жил фаз В и С;
- lС-А — расстояние между центрами жил фаз С и А.
Пример
Определить активное и индуктивное сопротивление кабеля марки АВВГнг(А)-LS 3х120 на напряжение 6 кВ производства «Электрокабель» Кольчугинский завод». Длина кабельной линии L = 300 м.
Решение
1. Определяем поперечное сечение токопроводящей жилы кабеля имеющую круглую форму:
S = π*d2/4 = 3,14*13,52/4 = 143 мм2
Расчет поперечного сечение секторной жилы, а также размеры секторных жил на напряжение 0,4 — 10 кВ представлен в статье: «Расчет поперечного сечения секторной жилы кабеля«.
где: d = 13,5 мм – диаметр жилы кабеля (многопроволочные уплотненные жилы), определяется по ГОСТ 22483— 2012 таблица С.3 для кабеля с токопроводящей жилой класса 2. Класс токопроводящей жилы указывается в каталоге завода-изготовителя кабельной продукции.
Ниже представлена классификация жил кабелей, согласно ГОСТ 22483— 2012:
2. Определяем удельное активное сопротивление кабеля марки АВВГнг(А)-LS 3х120, отнесенное к единице длины линии 1 км, Ом/км:
где:
- l = 1000 м – длина жилы, м;
- α20 – температурный коэффициент сопротивления, равный при 20 °С:
- 0, 00393 1/град – для меди;
- 0,00403 1/град – для алюминия;
- ρр – удельное сопротивление материала многопроволочной жилы, равное:
- 0,0184 Ом*мм2/м – для медных жил;
- 0,031 Ом*мм2/м – для алюминиевых жил;
- tж = 65 °С — допустимая температура нагрева жилы, для кабеля напряжением 6 кВ, согласно ПУЭ п.
 1.3.10.
1.3.10.
3. Определяем удельное активное сопротивление кабеля, исходя из длины кабельной трассы:
где: L = 0,3 км – длина кабельной трассы, км;
4. Определяем среднее геометрическое расстояние между центрами жил кабеля, учитывая что жилы кабеля расположены в виде треугольника.
где:
- lА-В = 20,3 мм — расстояние между центрами жил фаз А и В;
- lВ-С = 20,3 мм — расстояние между центрами жил фаз В и С;
- lС-А = 20,3 мм — расстояние между центрами жил фаз С и А.
Что бы определить расстояние между центрами жил кабеля, нужно знать диаметр жил кабеля d = 13,5 мм и толщину изоляции жил из поливинилхлоридного пластиката dи.ж = 3,4 мм, согласно ГОСТ 16442-80 таблица 4. Определяем расстояние между центрами жил фаз равное 20,3 мм (см.рис.1).
5. Определяем удельное реактивное (индуктивное) сопротивление кабеля марки АВВГнг(А)-LS 3х120, Ом/км:
где: d = 13,5 мм – диаметр жилы кабеля;
6. Определяем удельное реактивное сопротивление кабеля, исходя из длины кабельной трассы:
Определяем удельное реактивное сопротивление кабеля, исходя из длины кабельной трассы:
Сопротивление кабелей с изоляцией из сшитого полиэтилена на напряжение 6 — 35 кВ
Значения активного и реактивного (индуктивного) сопротивления кабелей с изоляцией из сшитого полиэтилена приводятся в каталогах завода-изготовителя. Для ознакомления приведу лишь некоторых производителей кабельной продукции.
«Электрокабель» Кольчугинский завод» – Каталог кабельной продукции.
В таблице 12 – приводятся значения активного сопротивления кабелей согласно ГОСТ 22483-2012
Компания «Estralin» — Каталог силовые кабели и кабельные системы 6 – 220 кВ.
Компания «Камкабель» — Настольная книга проектировщика. Кабели с изоляцией из сшитого полиэтилена на напряжение 6-35 кВ.
Справочники по проектированию электрических сетей и руководящие указания, которые упомянуты в данной статье, вы сможете найти, скачав архив.
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Формула индуктивного сопротивления катушки индуктивности: что это такое и от чего зависит
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением.
Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока.
Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
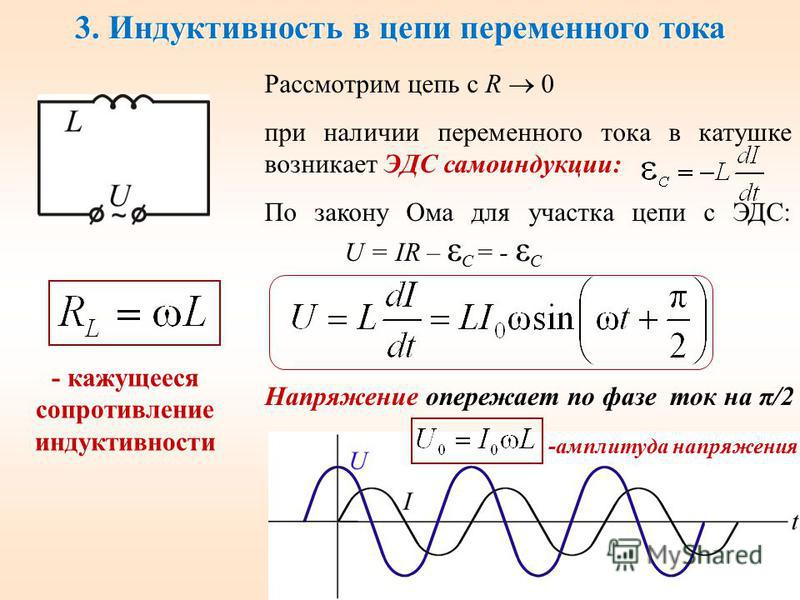
- Добротность катушки индуктивности может быть найдена через следующую формулу:
- где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
- Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
- Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.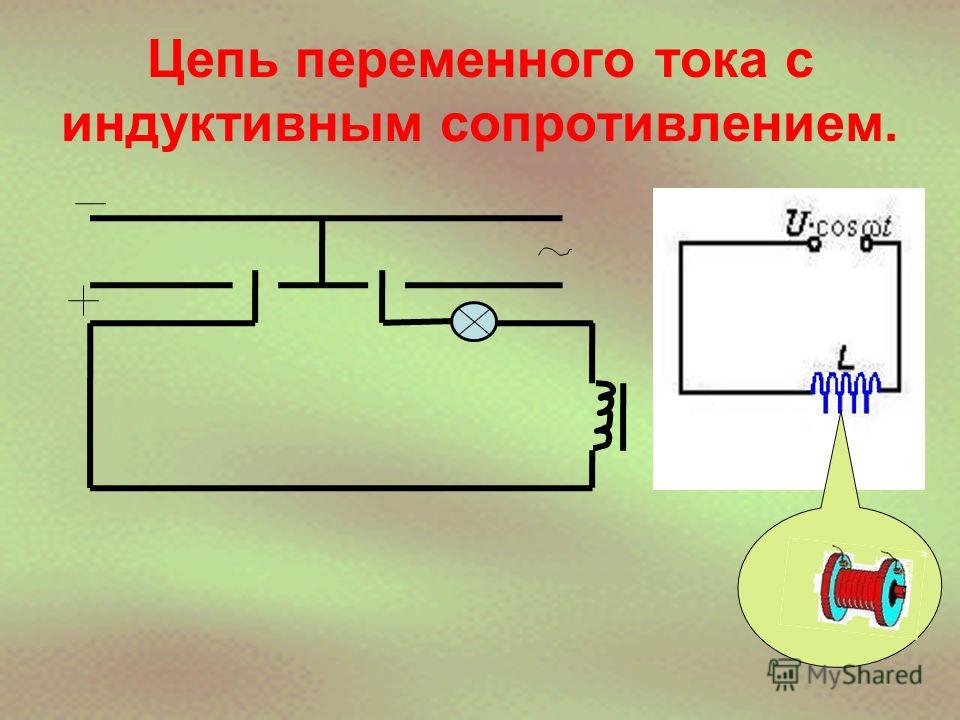
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
- По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
- Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Источник: http://fornk.ru/1970-katushka-induktivnosti-opisanie-xarakteristiki-formula-rascheta/
Индуктивное реактивное сопротивление: формулы, схемы
В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.
Введение
Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.
Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения.
Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока.
Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи.
Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .
Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.
Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока.
В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o .
В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).
Схема индуктивности переменного тока
В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0о и 180о вдоль синусоиды.
Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.
Векторная диаграмма индуктора переменного тока
Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Мы можем также написать это заявление как, V L = 0 ö и I L = -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:
Где: ω в радианах в секунду, а
t в секундах.
Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o .
Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o .
Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:
Где: ƒ — частота, L — индуктивность катушки и
2πƒ = ω .
Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.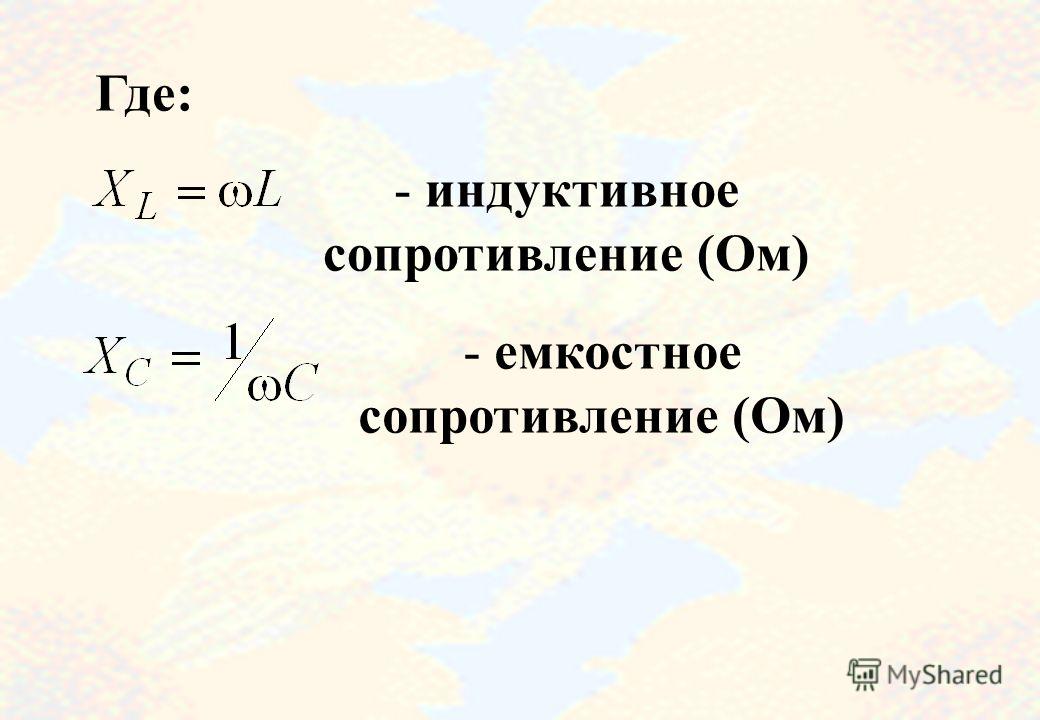
Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.
Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.
Индуктивное сопротивление от частоты
Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).
Питание от сети переменного тока серии LR
До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).
Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).
В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V R и V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V R и V L .
Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .
Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент.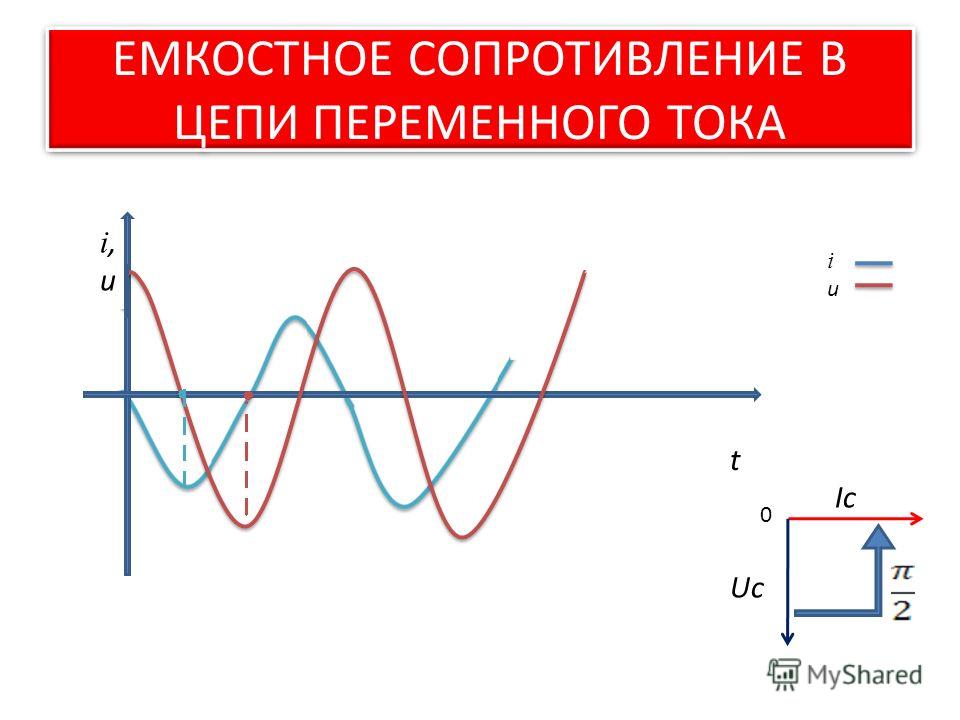 Вектор этой эталонной величины обычно рисуется горизонтально слева направо.
Вектор этой эталонной величины обычно рисуется горизонтально слева направо.
Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.
Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.
Цепь переменного тока серии LR
На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:
Треугольник напряжения выводится из теоремы Пифагора и имеет вид:
Треугольник сопротивления
В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».
Силовой треугольник индуктора переменного тока
Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник».
Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах.
В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .
В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания.
Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью.
Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.
Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.
Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.
Источник: https://meanders.ru/induktivnoe-soprotivlenie.shtml
Индуктивное сопротивление: обозначение, сопротивление катушки формула
Когда в цепи нарастает или уменьшается ток, электромагнитное поле создает противодействующую электродвижущую силу. Это явление порождается индуктивностью катушки. Индуктивное сопротивление воздействует только на переменный ток, быстрые изменения которого порождают противодействующую силу. В статье будет более подробно рассказано о природе этого явления.
Что зовется индуктивным сопротивлением
Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.
Схема для измерения
В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.
Они обозначаются, соответственно, как R и XL.
На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.
В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.
Определение индуктивности
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.
Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.
Принцип действия электродвижущей силы
Катушка индуктивности
Он представляет собой изолированный провод, многократно намотанный вокруг сердечника.
Обычно каркас имеет цилиндрическую или тороидальную форму.
Индуктивность рассматривается в качестве основной характеристики катушки. Это качество выражает способность элемента осуществлять преобразование переменного тока в магнитное поле.
Важно! Магнитные свойства существуют даже у одиночного провода, при условии, что изменяется проходящий через него ток. Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.
Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.
Катушки индуктивности
- Определение направления силовых линий подчиняется «правилу большого пальца»: если у сжатой в кулак руки большой палец указывает в направлении изменения силы тока, то сомкнутые пальцы подсказывают направление силовых линий поля.
- Таким образом в том случае, если провод многократно намотан на цилиндрическое основание, то силовые линии от разных витков складываются и проходят через ось.
- Для того, чтобы многократно увеличить индуктивность, в центр цилиндра помещают сердечник из ферромагнитного материала.
Индуктивное сопротивление – единицы измерения
Измерение этой величины производится в омах. Здесь используются такая же единица измерения, как и для резистора, несмотря на то, что у них различная природа. Рассматриваемая величина порождается электродвижущей силой, противодействующей происходящему изменению. Обычное возникает в связи с рассеиванием энергии при прохождении электронов по проводнику.
Обычное возникает в связи с рассеиванием энергии при прохождении электронов по проводнику.
Магнитное поле индуктивного элемента
Индуктивное сопротивление – как его найти
- Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:
- XL=2*П*v*L
- Здесь употреблены следующие обозначения:
- XL – рассматриваемая величина.
- Символом «П» обозначено число Пи.
- V представляет собой частоту.
- L — это обозначение величины индуктивности.
Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».
Катушки с различными сердечниками
- Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:
- I = U / XL
- I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.
Конфигурация магнитного поля катушки
Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.
При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.
При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.
Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.
Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.
Магнитное поле провода
К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.
Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.
При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.
Источник: https://rusenergetics.ru/polezno-znat/induktivnoe-soprotivlenie
Индуктивное сопротивление катушки — Основы электроники
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.
Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот.
Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки.
Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
- Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
- Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
- XL=2π• f •L
- где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
- Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
- XL=ω•L
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.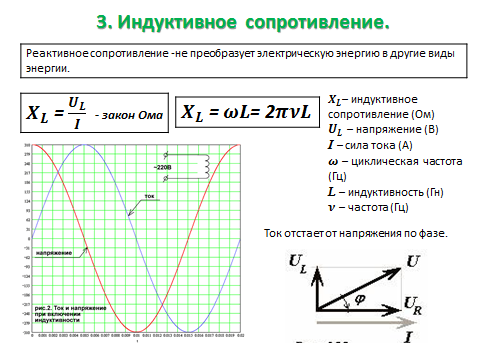
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник: http://www.sxemotehnika.ru/induktivnoe-soprotivlenie-katushki.html
Формула индуктивного сопротивления
При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока.
В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока.
Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.
От чего зависит индуктивное сопротивление
Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.
Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.
Формула электрической мощности
Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.
На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов.
Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%.
Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.
Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.
Индуктивное сопротивление в цепи переменного тока
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов.
Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным.
Длина каждого катета соответствует действующему значению того или иного сопротивления.
Применение электрического тока в металлах
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока.
В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L).
Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени.
Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси.
При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси).
Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности.
В результате, между током и напряжением происходит смещение фаз.
Индуктивное сопротивление катушки
Катушка индуктивности относится к категории пассивных компонентов, используемых в электронных схемах. Она способна сохранять электроэнергию, превращая ее в магнитное поле. В этом и состоит ее основная функция. Катушка индуктивности по своим характеристиками и свойствам напоминает конденсатор, сохраняющий энергию в виде электрического поля.
Индуктивность, измеряемая в Генри, заключается в появлении вокруг проводника с током магнитного поля.
В свою очередь, связано с электродвижущей силой, которая противодействует приложенному переменному напряжению и силе тока в катушке.
Данное свойство и есть индуктивное сопротивление, находящееся в противофазе с емкостным сопротивлением конденсатора. Индуктивность катушки возможно повысить за счет увеличения количества витков.
Для того чтобы выяснить, чему равно индуктивное сопротивление катушки, следует помнить, что оно, в первую очередь, противодействует переменному току. Как показывает практика, каждая индуктивная катушка сама по себе имеет определенное сопротивление.
Прохождение переменного синусоидального тока через катушку, приводит к возникновению переменного синусоидального напряжения или ЭДС. В результате, возникает индуктивное сопротивление, определяемое формулой: XL = ωL = 2πFL, в которой ω является угловой частотой, F – частотой в герцах, L – индуктивностью в генри.
Источник: https://electric-220.ru/news/formula_induktivnogo_soprotivlenija/2017-05-03-1254
Что такое катушка индуктивности и для чего она нужна?
Я получил письма от многих из вас с просьбой рассказать простыми словами о катушке индуктивности.
Это действительно хорошая просьба и желание). Потому что катушка индуктивности — это довольно странный компонент. Её невероятно легко сделать. Но немного сложнее понять как она работает.
Катушка индуктивности
Катушка индуктивности (иногда называют ее индуктором или дросселем) — это просто катушка проволоки, которая намотана вокруг какого-нибудь сердечника. Ядро сердечника может быть просто воздухом или магнитом.
Когда вы подаете ток через катушку, вокруг неё создается магнитное поле.
При использовании магнитного сердечника магнитное поле будет намного сильнее.
Как работает катушка индуктивности?
Ток через любой провод создаст магнитное поле. Катушка индуктивности имеет проволочную форму, поэтому магнитное поле будет намного сильнее.
Причина, по которой индуктор работает так, как он работает, заключается в этом магнитном поле. Отсюда вытекают и следующие свойства катушки.
Свойства катушки индуктивности:
- Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
- Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
- Катушка индуктивности при протекании тока запасает энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.
Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое (активное) сопротивление, но и реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.
Более детально о принципе работы катушек индуктивности вы можете почитать на сайте.
Для чего вы можете использовать их?
Я почти никогда не использую катушки индуктивности. Главным образом потому, что я работаю в основном с цифровыми схемами. Но я использовал их иногда для создания фильтров, генераторов и блоков питания.
Вы часто найдете катушки индуктивности в аналоговой электронике переменного тока, такой как радиооборудование.
Источник: https://zen.yandex.ru/media/id/5d38230cd5135c00ad1384d4/5d613819ec575b00ad6dce12
Переменный ток. Полное и индуктивное сопротивление.
⇐ ПредыдущаяСтр 3 из 14Следующая ⇒
Это электрический ток, который периодически изменяется по модулю и направлению.
Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.
В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока.
Полное сопротивление (Z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.
полное сопротивление цепи.
индуктивное сопротивление — это сопротивление проводника, включенного в цепь переменного тока и неимеющего заметного активного сопротивления и емкости, но имеющий заметную индуктивность L.
— индуктивное сопротивление проводника переменному току. Где: омега- частота, L- индуктивность (Гн)
Мощность выделяемая в цепи переменного тока, принцип действия теплового амперметра.
мгновенное значение мощности переменного тока, которое равно произведению мгновенных значений напряжения и силы тока:
где U(t)=Umcosωt, I(t)=Imcos(ωt-φ) .
Средняя мощность, выделяемая в цепи переменного тока
Тепловой амперметр
Тепловой амперметр основанный на свойстве тока нагревать провода, устроен так: к двум неподвижным зажимам присоединена тонкая проволока. Эта проволока оттянута книзу шелковой нитью, связанной с пружиной. По пути Эта нить петлей охватывает подвижную ось, на которой укреплена стрелка.
Измеряемый ток подводится к неподвижным зажима.м и проходит через проволоку (путь тока показан стрелками). Под действием тока проволока немного нагреется. От нагревания она чуть-чуть удлинится, и шелковая нить, np i-Крепленная к проволоке, оттянется пружинкой. Движение Нити повернет ось и сидящую на ней стрелку.
По отклонению стрелки и определяют величину тока: чем больше ток, тем больше нагревается нить, тем больше поворачивается стрелка.
20. Введение в теорию волновых процессов, основные понятия. Математическое описание синусоидальной волны. Волновое уравнение.
Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры.
В связи с этим волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO3 ), электромагнитную (электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д.
Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и оно.
Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов. Об этих законах говорят в таком случае как о волновых уравнениях. Для непрерывных систем это обычно дифференциальные уравнения в частных производных в фазовом пространстве системы, для сред часто сводимые к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений[2]. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.
По своему характеру волны подразделяются на:
По признаку распространения в пространстве: стоячие, бегущие.
По характеру волны: колебательные, уединённые (солитоны).
По типу волн: поперечные, продольные, смешанного типа.
По законам, описывающим волновой процесс: линейные, нелинейные.
По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.
По геометрии: сферические (пространственные), одномерные (плоские), спиральные.
Отличие колебания от волны.
Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»).
В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков.
Математическое описание:
Волновое уравнение — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики
Рекомендуемые страницы:
Активные и индуктивные сопротивления проводов
Активное сопротивление проводов rо на единицу длины (погонное) 1 км (Ом/км) одной фазы линии трехфазного тока определяется по формуле
Ом/м (9)
где ρ – удельное сопротивление материала провода, Ом/м; F – сечение провода, м2; γ – удельная проводимость, м/Ом∙мм2.
Индуктивное сопротивление на единицу длины (погонное) одной фазы линии трехфазного тока определяют по уравнению
Ом/км (10)
где x¢o – внешнее индуктивное сопротивление, Ом/км; x²o – внутреннее индуктивное сопротивление, Ом/км; dпр – диаметр провода, мм; Дср – среднее геометрическое расстояние между проводами линии:
мм;
μ – относительная магнитная проницаемость (для проводов из цветных металлов μ = 1).
Задача 2.1
Сравнить индуктивные и активные сопротивления двух линий одинаковой протяженности (по 20 км). Первая линия напряжением 10 кВ выполнена проводами АС70 со среднегеометрическим расстоянием между проводами Дср = 1,25 м; вторая линия напряжением 110 кВ – проводами АС150 со среднегеометрическим расстоянием Дср = 5 м.
Активные сопротивления линий, Ом, определяют по формуле
(11)
где rо – сопротивление 1 км провода, Ом/км; ℓ – длина линии, км; ρ – удельное сопротивление материала провода, Ом∙м2; F – сечение провода, м2.
Табличное значение алюминиевой части сечения сталеалюминевого провода (по приложению 10.3):
F = 68 мм2 = 68 ∙ 10–6 м2.
Удельное сопротивление сталеалюминевого провода принимается таким же, как и у алюминиевого (проводимостью стальных проводов пренебрегают):
ρ = 31,2 ∙ 10–3 Ом∙м2.
Тогда
Ом.
Сопротивление 1 км провода АС70
Ом/км.
Правильность ответа проверяется по приложению 10.3. Разница в 0,04 Ом/км находится в допустимых пределах.
Активное сопротивление линии 110 кВ, выполненной проводом АС150:
Ом.
Ом/км.
Сравнение активных сопротивлений линий, выполненных разными сечениями проводов:
раза.
Индуктивные сопротивления 1 км находят по формуле
где dпр – диаметр провода, мм; μ – магнитная проницаемость материала (для цветных металлов μ = 1).
Сравниваем индуктивные сопротивления линий
Задача 2.2
Определить активные и индуктивные (внешнее и внутреннее) сопротивления линий 10 кВ длиной 5 км, выполненной многопроволочными стальными проводами марки ПС50 при токе I = 20 А и среднем геометрическом расстоянии между проводами – 1, 2 м.
Активное сопротивление линии rПС50 = rоПС50ℓ.
Активное погонное (на 1 км) сопротивление берется из приложения 12 в зависимости от значения протекающего тока:
rоПС50 = 2,85 Ом/км, rПС50 = 2,85 ∙ 5 = 14 Ом.
Индуктивное погонное сопротивление состоит из внешнего, не зависящего от тока и внутреннего, зависящего от тока:
[2]
По приложению 16 Ом/км (при I = 20 А):
Ом/км,
Ом/км,
Ом,
dпр = 9,2 мм.
Определение потерь энергии в электрических сетях
Потери электрической энергии за год в трехфазной линии с нагрузкой в конце определяются по одной из формул
Вт×ч, (12)
где r – сопротивление фазного провода, Ом; I – ток в проводе, А; Imax = максимальный ток, А; Iср.кв – среднеквадратичный ток, А; t – период времени, за который определяются потери, ч; τ – время потерь, ч.
Время потерь τ находят по графику электрической нагрузки или по уравнению
(13)
или по формулам:
τ = (0,124 + Т/1000)2 ∙ 8760; (14)
τ = 0,69Т – 584.
Среднеквадратичный ток находится по уравнению
(15)
Время использования максимальной нагрузки
(16)
или берется из приложения 17.
Потери энергии в трансформаторах:
кВт×ч,(17)
где Ркз – потери короткого замыкания, кВт; Рхх – потери холостого хода, кВт; Smax, Sном – максимальная нагрузка и номинальная мощность трансформатора, кВ∙А; n – число работающих на подстанции трансформаторов.
Задача 2.3
Определить годовые потери электрической энергии в трехфазной воздушной линии 10 кВ, выполненной проводом АС70, длина линии 12 км, нагрузка изменяется по заданному графику (рис. 2.1). Определить также для этого графика число часов использования максимальной нагрузки Т, время потерь τ и среднеквадратичный ток Iср.кв.
I, А
40 0 2000 4000 6000 8760 t, ч
Рис. 2.1. Годовой график электрической нагрузки
Сопротивление линии
rл = roℓ = 0,42 ∙ 12 = 5,04 Ом (rо = 0,42, см. приложение 10.3).
Потери электрической энергии определены по формуле (12).
В соответствии с графиком электрических нагрузок (рис. 2.1):
ΔW = 3 ∙ 5,04 (902 ∙ 2000 + 802 ∙ 2000 + 602 ∙ 2000 + 402 ∙ 2760) ∙ 10–3 =
= 15,12 (162 ∙ 105 + 128 ∙ 105 + 72 ∙ 105 + 44,16 ∙ 105) ∙ 10–3 =
= 614050 кВт∙ч = 614 МВт∙ч.
Число часов использования максимальной нагрузки определяется по формуле (16):
ч.
Время потерь рассчитано по уравнению (13)
ч.
Среднеквадратичный ток определен по формуле (15):
А.
Потери электрической энергии находят через
среднеквадратичный ток:
МВт×ч.
время потерь:
МВт×ч.
Задача 2.4
Определить потери активной энергии за год в трехфазной воздушной линии напряжением 10 кВ, длиной 15 км, выполненной проводами АС70, если за год через линию передано 3600 мВт∙ч и максимальная замеренная нагрузка составляет 52 А. Коэффициент мощности нагрузки 0,9. Потери энергии выразить в процентах по отношению к энергии, переданной за год.
Потери определяем по формуле (12):
кВт×ч.
Сопротивление линии находим по выражению
rл = rol = 0,42 ∙ 15 = 6,3 Ом (rо = 0,42, см. приложение 10.3).
Максимальная мощность
(17)
Число часов использования максимальной мощности
ч. (18)
Время потерь находят по формуле
τ = 0,69Т – 584 = 0,69 ∙ 4444 – 584 = 2483 ч.
Потери электроэнергии за год
кВт×ч,
или в процентах:
Задача 2.5
Определить годовые потери электрической энергии, МВт∙ч и %, в трансформаторе ТМН мощностью 2500 кВ∙А с высшим напряжением 35 кВ, если максимальная нагрузка составляет 3000 кВ∙А при cosj = 0,9 и Т = 5000 ч.
Номинальные потери в меди и стали трансформатора (из приложения 18) Рм = 25,5 кВт; Рст = 5,1 кВт.
Время потерь находим по формуле (14): τ = 3650 ч.
Годовые потери энергии рассчитываются по формуле (17):
= 1 23516 + 44676 = 168192 кВт∙ч = 168,22 МВт∙ч.
Всего за год передано активной энергии:
МВт×ч.
Потери энергии за год
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Самоиндуктивность и индуктивное сопротивление
Самоиндуктивность и индуктивное реактивное сопротивление
Самоиндуктивность — это особая форма электромагнитной индукции. Самоиндукция определяется как индукция напряжения в токоведущем проводе, когда ток в самом проводе изменяется. В случае самоиндукции магнитное поле, создаваемое изменяющимся током в цепи, само индуцирует напряжение в той же цепи.Следовательно, напряжение самоиндуцировано.
Термин «индуктор» используется для описания элемента схемы, обладающего свойством индуктивности, а катушка с проводом является очень распространенной катушкой индуктивности. В принципиальных схемах для обозначения индуктивного компонента обычно используется катушка или провод. Более пристальный взгляд на катушку поможет понять причину, по которой в проводе, по которому проходит изменяющийся ток, возникает напряжение. Переменный ток, проходящий через катушку, создает магнитное поле внутри и вокруг катушки, которое увеличивается и уменьшается по мере изменения тока.Магнитное поле образует концентрические петли, которые окружают провод и соединяются, образуя более крупные петли, окружающие катушку, как показано на изображении ниже. Когда ток увеличивается в одной петле, расширяющееся магнитное поле пересекает некоторые или все соседние петли провода, вызывая напряжение в этих петлях. Это вызывает индуцирование напряжения в катушке при изменении тока.
Изучая это изображение катушки, можно увидеть, что количество витков в катушке будет влиять на величину напряжения, которое индуцируется в цепи.Увеличение числа витков или скорости изменения магнитного потока увеличивает величину индуцированного напряжения. Следовательно, Закон Фарадея должен быть изменен для катушки с проволокой и станет следующим.
Где:
VL = индуцированное напряжение в вольтах
N = количество витков в катушке
dø / dt = скорость изменения магнитного потока в
интервалах в секунду
Уравнение просто утверждает, что величина индуцированного напряжения (VL) пропорциональна количеству витков в катушке и скорости изменения магнитного потока (dø / dt).Другими словами, когда увеличивается частота магнитного потока или количество витков в катушке, величина индуцированного напряжения также увеличивается.
В цепи намного проще измерить ток, чем измерить магнитный поток, поэтому следующее уравнение можно использовать для определения индуцированного напряжения, если известны индуктивность и частота тока. Это уравнение также можно реорганизовать, чтобы можно было рассчитать индуктивность, когда можно определить величину наведенного напряжения и известна частота тока.
Где:
VL = индуцированное напряжение в вольтах
L = значение индуктивности в генри
di / dt = скорость изменения тока в амперах в секунду
Закон Ленца
Вскоре после того, как Фарадей предложил свой закон индукции, Генрих Ленц разработал правило для определения направления индуцированного тока в контуре.По сути, закон Ленца гласит, что индуцированный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного поля, которое индуцировало ток . Это означает, что ток, индуцированный в проводнике, будет противодействовать изменению тока, которое вызывает изменение магнитного потока. Закон Ленца важен для понимания свойства индуктивного реактивного сопротивления, которое является одним из свойств, измеряемых при вихретоковом контроле.
Индуктивное реактивное сопротивление
Уменьшение протекания тока в цепи из-за индукции называется индуктивным реактивным сопротивлением . При более внимательном рассмотрении катушки с проводом и применении закона Ленца можно увидеть, как индуктивность уменьшает протекание тока в цепи. На изображении ниже направление первичного тока показано красным цветом, а магнитное поле, создаваемое током, показано синим. Направление магнитного поля можно определить, взяв правую руку и указав большим пальцем в направлении тока. Затем ваши пальцы будут указывать в направлении магнитного поля. Можно видеть, что магнитное поле от одной петли провода будет пересекать другие петли в катушке, и это вызовет протекание тока (показано зеленым цветом) в цепи.Согласно закону Ленца, индуцированный ток должен течь в направлении, противоположном первичному току. Индуцированный ток, работающий против первичного тока, приводит к уменьшению тока в цепи.
Следует отметить, что индуктивное реактивное сопротивление будет увеличиваться, если количество витков в катушке увеличивается, поскольку магнитное поле от одной катушки будет иметь больше катушек для взаимодействия.
Подобно сопротивлению, индуктивное реактивное сопротивление уменьшает протекание тока в цепи.Тем не менее, можно различать сопротивление и индуктивное реактивное сопротивление в цепи, глядя на синхронизацию между синусоидальными волнами напряжения и тока переменного тока. В цепи переменного тока, содержащей только резистивные компоненты, напряжение и ток будут синфазными, что означает, что пики и спады их синусоидальных волн будут происходить одновременно. Когда в цепи присутствует индуктивное реактивное сопротивление, фаза тока будет сдвинута так, чтобы ее пики и спады не возникали одновременно с пиками напряжения.Более подробно об этом будет сказано в разделе, посвященном схемам.
Индуктивный подход против дедуктивного исследования (с примерами)
Опубликован в 18 апреля 2019 г., по Раймо Стрефкерк. Пересмотрено 11 ноября 2019.
Основное различие между индуктивным и дедуктивным рассуждением состоит в том, что индуктивное рассуждение направлено на развитие теории , в то время как дедуктивное рассуждение направлено на проверку существующей теории .
Индуктивное рассуждение переходит от конкретных наблюдений к широким обобщениям, а дедуктивное рассуждение — наоборот.
Оба подхода используются в различных типах исследований, и нередко их комбинируют в одном большом исследовании.
Индуктивный подход к исследованию
Когда литературы по теме мало или совсем нет, обычно проводят индуктивные исследования, потому что нет теории для проверки. Индуктивный подход состоит из трех этапов:
- Наблюдение
- Задерживается рейс лоукостера
- У собак A и B есть блохи
- Существование слонов зависит от воды
- Соблюдайте схему
- Еще 20 рейсов лоукостеров задерживаются
- У всех наблюдаемых собак есть блохи
- Существование всех наблюдаемых животных зависит от воды
- Развивайте теорию
- Бюджетные авиакомпании всегда задерживают
- У всех собак есть блохи
- Вся биологическая жизнь зависит от воды
Ограничения индуктивного подхода
Вывод, сделанный на основе индуктивного метода, никогда не может быть доказан, но его можно опровергнуть.
Пример
Вы наблюдаете 1000 рейсов бюджетных авиакомпаний. Все они испытывают задержку, что соответствует вашей теории. Однако никогда нельзя доказать, что рейс 1001 также будет задержан. Тем не менее, чем больше ваш набор данных, тем надежнее будет вывод.
Дедуктивный исследовательский подход
При проведении дедуктивного исследования вы всегда начинаете с теории (результат индуктивного исследования). Дедуктивное рассуждение означает проверку этих теорий.Если теории еще нет, дедуктивное исследование проводить нельзя.
Дедуктивный исследовательский подход состоит из четырех этапов:
- Начните с существующей теории
- Бюджетные авиакомпании всегда задерживают
- У всех собак есть блохи
- Вся биологическая жизнь зависит от воды
- Сформулируйте гипотезу на основе существующей теории
- Если пассажиры летят бюджетной авиакомпанией, они всегда будут испытывать задержки.
- У всех домашних собак в моем многоквартирном доме есть блохи
- Существование всех наземных млекопитающих зависит от воды
- Собрать данные для проверки гипотезы
- Сбор данных о рейсах лоукостеров
- Проверить всех собак в здании на блох
- Изучите все виды наземных млекопитающих, чтобы узнать, зависят ли они от воды
- Проанализируйте результаты: данные отвергают или поддерживают гипотезу?
- 5 из 100 рейсов лоукостеров не задерживаются = отвергнуть гипотезу
- У 10 из 20 собак не было блох = отвергнуть гипотезу
- Все виды наземных млекопитающих зависят от воды = поддержка гипотезы
Ограничения дедуктивного подхода
Выводы дедуктивного рассуждения могут быть верными только в том случае, если все предпосылки, установленные в индуктивном исследовании, верны и термины ясны.
Пример
- У всех собак блохи (помещение)
- Бенно собака (помещение)
- У Бенно блохи (заключение)
На основании имеющихся у нас посылок заключение должно быть верным. Однако, если первая посылка окажется ложной, нельзя полагаться на вывод о том, что у Бенно блохи.
Какая у вас оценка за плагиат?
Сравните свою статью с более чем 60 миллиардами веб-страниц и 30 миллионами публикаций.
- Лучшая программа проверки плагиата 2020 года
- Отчет о плагиате и процентное содержание
- Самая большая база данных о плагиате
Scribbr Проверка на плагиат
Сочетание индуктивного и дедуктивного исследования
Многие ученые, проводящие более крупный исследовательский проект, начинают с индуктивного исследования (разработки теории). После индуктивного исследования проводится дедуктивное исследование для подтверждения или опровержения вывода.
В приведенных выше примерах вывод (теория) индуктивного исследования также используется в качестве отправной точки для дедуктивного исследования.
Насколько полезна эта статья?
1151 130 Вы уже проголосовали.Благодаря 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса …определение индуктивного реактивного сопротивления и синонимы индуктивного реактивного сопротивления (английский)
индуктивное реактивное сопротивление: определение индуктивного реактивного сопротивления и синонимы индуктивного реактивного сопротивления (английский)
арабский болгарский китайский язык хорватский чешский язык Датский Голландский английский эстонский Финский французский язык Немецкий Греческий иврит хинди венгерский язык исландский индонезийский Итальянский Японский корейский язык Латышский Литовский язык Малагасийский Норвежский Персидский Польский португальский румынский русский сербский словацкий словенский испанский язык Шведский Тайский турецкий вьетнамский
арабский болгарский китайский язык хорватский чешский язык Датский Голландский английский эстонский Финский французский язык Немецкий Греческий иврит хинди венгерский язык исландский индонезийский Итальянский Японский корейский язык Латышский Литовский язык Малагасийский Норвежский Персидский Польский португальский румынский русский сербский словацкий словенский испанский язык Шведский Тайский турецкий вьетнамский
содержание сенсагента
- определения
- синонимы
- антонимы
- энциклопедия
Решение для веб-мастеров
Александрия
Всплывающее окно с информацией (полное содержимое Sensagent), вызываемое двойным щелчком по любому слову на вашей веб-странице.Предоставьте контекстные объяснения и перевод с вашего сайта !
Попробуйте здесь или получите код
SensagentBox
С помощью SensagentBox посетители вашего сайта могут получить доступ к надежной информации на более чем 5 миллионах страниц, предоставленных Sensagent.com. Выберите дизайн, который подходит вашему сайту.
Бизнес-решение
Улучшите содержание своего сайта
Добавьте новый контент на свой сайт из Sensagent by XML.
Сканировать продукты или добавлять
Получите доступ к XML, чтобы найти лучшие продукты.
Индексирование изображений и определение метаданных
Получите доступ к XML, чтобы исправить значение ваших метаданных.
Напишите нам, чтобы описать вашу идею.
Lettris
Lettris — любопытная игра-тетрис-клон, в которой все кубики имеют одинаковую квадратную форму, но разное содержание. На каждом квадрате есть буква. Чтобы квадраты исчезли и сэкономили место для других квадратов, вам нужно собрать английские слова (left, right, up, down) из падающих квадратов.
болт
Boggle дает вам 3 минуты, чтобы найти как можно больше слов (3 буквы и более) в сетке из 16 букв. Вы также можете попробовать сетку из 16 букв. Буквы должны располагаться рядом, и более длинные слова оцениваются лучше. Посмотрите, сможете ли вы попасть в Зал славы сетки!
Английский словарь
Основные ссылки
WordNet предоставляет большинство определений на английском языке.
Английский тезаурус в основном является производным от The Integral Dictionary (TID).
English Encyclopedia лицензирована Википедией (GNU).
Перевод
Измените целевой язык, чтобы найти перевод.
Советы: просмотрите семантические поля (см. От идей к словам) на двух языках, чтобы узнать больше.
5826 онлайн посетителей
вычислено за 0,047 с
.
