Что такое полное сопротивление цепи переменного тока. Как рассчитать полное сопротивление. Какие факторы влияют на полное сопротивление цепи. Где применяется понятие полного сопротивления на практике.
Что такое полное сопротивление цепи переменного тока
Полное сопротивление (импеданс) — это комплексная величина, характеризующая сопротивление электрической цепи переменному току. Оно учитывает как активное сопротивление цепи, так и реактивное сопротивление, создаваемое индуктивностью и емкостью.
Полное сопротивление обозначается буквой Z и измеряется в Омах (Ом). В отличие от активного сопротивления, которое всегда положительно, полное сопротивление может иметь как положительную, так и отрицательную мнимую часть в зависимости от преобладания индуктивного или емкостного сопротивления в цепи.
Формула расчета полного сопротивления
Для расчета полного сопротивления цепи переменного тока используется следующая формула:

Z = √(R² + (XL — XC)²)
Где:
- Z — полное сопротивление (Ом)
- R — активное сопротивление (Ом)
- XL — индуктивное сопротивление (Ом)
- XC — емкостное сопротивление (Ом)
Как видно из формулы, полное сопротивление зависит от трех составляющих — активного, индуктивного и емкостного сопротивлений.
Активное сопротивление в цепи переменного тока
Активное сопротивление R в цепи переменного тока обусловлено наличием резистивных элементов — проводников, резисторов и т.д. Оно не зависит от частоты тока и определяется по закону Ома:
R = U / I
Где U — напряжение, а I — сила тока.
Активное сопротивление вызывает нагрев проводников и преобразование электрической энергии в тепловую. Оно всегда положительно и измеряется в Омах.
Реактивное сопротивление: индуктивное и емкостное
Реактивное сопротивление в цепи переменного тока создается катушками индуктивности и конденсаторами. Оно зависит от частоты тока и бывает двух типов:
- Индуктивное сопротивление XL = 2πfL, где f — частота, L — индуктивность
- Емкостное сопротивление XC = 1 / (2πfC), где C — емкость
Индуктивное сопротивление увеличивается с ростом частоты, а емкостное — уменьшается. При этом индуктивное сопротивление вызывает отставание тока от напряжения по фазе, а емкостное — опережение.

Треугольник сопротивлений
Для наглядного представления соотношения между активным, реактивным и полным сопротивлениями используется треугольник сопротивлений:
«` «`Где:
- Катет R — активное сопротивление
- Катет X — реактивное сопротивление
- Гипотенуза Z — полное сопротивление
Из этого треугольника легко увидеть, что полное сопротивление всегда больше активного и реактивного по отдельности.
Факторы, влияющие на полное сопротивление цепи
На величину полного сопротивления цепи переменного тока влияют следующие факторы:
- Активное сопротивление проводников и нагрузки
- Индуктивность катушек и проводников
- Емкость конденсаторов
- Частота переменного тока
- Взаимное расположение элементов (последовательное или параллельное)
При изменении любого из этих параметров будет меняться и полное сопротивление цепи. Например, увеличение частоты приведет к росту индуктивного сопротивления и уменьшению емкостного.
Расчет полного сопротивления для различных схем
Рассмотрим расчет полного сопротивления для наиболее распространенных схем включения элементов:

Последовательное соединение R, L и C
При последовательном соединении активного сопротивления R, индуктивности L и емкости C полное сопротивление рассчитывается по формуле:
Z = √(R² + (ωL — 1/ωC)²)
Где ω = 2πf — угловая частота.
Параллельное соединение R и L
Для параллельного соединения активного сопротивления R и индуктивности L полное сопротивление равно:
Z = (R * ωL) / √(R² + (ωL)²)
Параллельное соединение R и C
При параллельном соединении R и C полное сопротивление вычисляется как:
Z = R / √(1 + (ωCR)²)
Для более сложных схем расчет полного сопротивления проводится с использованием методов теории цепей.
Практическое применение понятия полного сопротивления
Понятие полного сопротивления широко используется в электротехнике и радиотехнике для решения следующих задач:
- Расчет токов и напряжений в цепях переменного тока
- Анализ частотных характеристик электрических фильтров
- Согласование импедансов источника сигнала и нагрузки
- Расчет резонансных контуров
- Проектирование антенн и линий передачи
Знание полного сопротивления позволяет правильно выбирать элементы схем и прогнозировать поведение цепей на разных частотах.

Измерение полного сопротивления
Для измерения полного сопротивления цепей переменного тока используются специальные приборы — измерители импеданса. Они позволяют определить как модуль, так и аргумент комплексного сопротивления на различных частотах.
Современные цифровые измерители импеданса обеспечивают высокую точность измерений в широком диапазоне частот и сопротивлений. Они широко применяются при разработке и тестировании электронных устройств.
Заключение
Полное сопротивление является важной характеристикой цепей переменного тока, учитывающей как активную, так и реактивную составляющие. Его знание необходимо для правильного расчета и проектирования электрических схем. Понимание факторов, влияющих на полное сопротивление, позволяет эффективно управлять характеристиками цепей переменного тока.
Полное сопротивление | Формулы и расчеты онлайн
В любой цепи переменного тока наряду с чисто реактивным сопротивлением присутствует омическое (активное) сопротивление, которое нужно учитывать при определении полного сопротивления.
Если
| Z | полное сопротивление, | Ом |
|---|---|---|
| R | омическое (активное) сопротивление, | Ом |
| X | реактивное сопротивление, | Ом |
| Y = 1/Z | полная проводимость, | сименс |
| G | активная проводимость, | сименс |
| B | реактивная проводимость, | сименс |
| U | полное напряжение (эффективное значение), | Вольт |
| I | полный ток (эффективное значение), | Ампер |
то имеем:
Полное сопротивление при последовательном соединении R и X

полное сопротивление векторная диаграмма тока и напряжений
При последовательном соединении активное и реактивное сопротивления складываются геометрически

полное сопротивление векторная диаграмма
\[ Z = \sqrt{R^{2} + X^{2}} \]
и
\[ U = \sqrt{U^{2}_{R} + U^{2}_{X}} = IZ \]
Полное сопротивление при параллельном соединение R и X

полное сопротивление векторная диаграмма тока и напряжений
При параллельном соединении активная и реактивная проводимости складываются геометрически

полное сопротивление векторная диаграмма
\[ Y = \sqrt{G^{2} + B^{2}} \]
и
\[ I = \sqrt{I^{2}_{R} + I^{2}_{X}} = UY \]
Полное сопротивление |
стр. 689 |
|---|
Переменный электрический ток. Полное сопротивление цепи переменного тока
Электрический ток называется переменным, если он в течение времени меняет свое направление и непрерывно изменяется по величине
Переменный ток, который используется для подключения бытовых или производственных электрических приборов, изменяется по синусоидальному закону:i = Imsin(2πft)
· i – мгновенное значение тока
· Im – амплитудное или наибольшее значение тока
· f – значение частоты переменного тока
· t – время
· Переменный однофазный электрический ток имеет следующие основные характеристики:
· f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц (Гц):
Τ – период – время одного полного изменения переменной величины.
ω – угловая скорость
Помимо частоты f при изучении цепей переменного тока вводится понятие угловой скорости ω. Угловая скорость ω связана с частотой f следующим соотношением:
ω=2πf
Стандартная частота промышленного переменного тока в России равна 50 Гц. Переменное напряжение между контактами розетки электрической сети создаётся с помощью генераторов, находящихся на электростанциях. Упрощённой моделью генератора переменного тока является проволочная рамка площадью S, вращающаяся с круговой частотой w в постоянном однородном магнитном поле с индукцией В (рис. 10а). Если считать, что угол a между нормалью к рамке n и вектором магнитной индукции изменяется во времени t какa = wt, то поток магнитной индукции Ф, проходящий через рамку, будет равен:
Ф = BS.cos(a) = BS.cos(wt) .
Переменным током называется электрический ток, сила которого каким-либо образом меняется со временем. Обычный способ получения переменного тока заключается в том, что при вращении рамки в однородном магнитном поле в ней возникает электродвижущая сила, которая по закону Фарадея равна
.
Если рамка вращается в магнитном поле с частотой , то поток вектора магнитной индукции через поверхность, ограниченную контуром рамки, меняется со временем по закону:
,
где – максимальное значение потока вектора индукции через плоскость контура. Возникающая при этом электродвижущая сила равна
.
Величина называется амплитудой электродвижущей силы и представляет ее наибольшее значение.
Электродвижущая сила максимальна, когда угол . В этом положении поток равен нулю, а скорость изменения магнитного потока максимальна. Когда , поток максимален, а электродвижущая сила равна нулю. За один период электродвижущая сила дважды меняет знак. Периодически действующая электродвижущая сила вызывает в замкнутом проводнике переменный ток, также изменяющийся по периодическому закону.
Гармонически изменяющаяся электродвижущая сила – это идеализация. Такой закон изменения электродвижущей силы получается в том случае, когда магнитное поле однородно, а рамка вращается равномерно. Если хотя бы одно из этих условий нарушается, в контуре возникает электродвижущая сила, изменяющаяся по более сложному закону. Однако при равномерном вращении изменение электродвижущей силы происходит всегда по периодическому закону. Теория синусоидальных токов наиболее проста и хорошо разработана. Преимущество этого подхода подтверждается и тем, что все технические генераторы переменного тока имеют электродвижущую силу, изменяющуюся по синусоидальному закону. На этом основании при изучении переменных токов предпочтение отдается теории синусоидальных токов.
Обычно цепь переменного тока включает в себя и активное сопротивление, и емкость, и индуктивность.
Полное сопротивление (Z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.
— полное сопротивление цепи.
Здесь:
— активное сопротивление.
— емкостное сопротивление.
— индуктивное сопротивление.
— полное сопротивление определяет силу тока в цепи по закону Ома.
35)ток смещения. Уравнение Максвелла
Ток смещения или абсорбционный ток — величина, прямо пропорциональная быстроте изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.
Введение тока смещения позволило устранить противоречие[1] в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.
Строго говоря, ток смещения не является[2] электрическим током, но измеряется в тех же единицах, что и электрический ток.
Точная формулировка[править]
В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения (с точностью до универсального постоянного коэффициента) называется[3] поток вектора быстроты изменения электрического поля через некоторую поверхность[4] :
(СИ)
(СГС)
В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:
(СИ)
(СГС),
где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)
Соответственно, плотностью тока смещения в вакууме называется величина
(СИ)
(СГС)
а в диэлектриках — величина
(СИ)
(СГС)
В некоторых книгах плотность тока смещения называется просто «током смещения».
Ток смещения и ток проводимости[править]
В природе можно выделить два вида токов: ток связанных зарядов и ток проводимости.
Ток связанных зарядов — это перемещение средних положений связанных электронов и ядер, составляющих молекулу, относительно центра молекулы.
Ток проводимости — это направленное движение на большие расстояния свободных зарядов (например, ионов или свободных электронов). В случае, если этот ток идёт не в веществе, а в свободном простанстве, нередко вместо термина «ток проводимости» употребляют термин «ток переноса». Иначе говоря, ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля.
Во времена Максвелла ток проводимости мог быть экспериментально зарегистрирован и измерен (например, амперметром, индикаторной лампой), тогда как движение связанных зарядов внутри диэлектриков могло быть лишь косвенно оценено.
Сумма тока связанных зарядов и быстроты изменения потока электрического поля была названа током смещения в диэлектриках.
При разрыве цепи постоянного тока и включении в неё конденсатора ток в разомкнутом контуре отсутствует. При питании такого разомкнутого контура от источника переменного напряжения в нём регистрируется переменный ток (при достаточно высокой частоте и ёмкости конденсатора загорается лампа, включённая последовательно с конденсатором). Для описания «прохождения» переменного тока через конденсатор (разрыв по постоянному току) Максвелл ввёл понятие тока смещения.
Ток смещения существует и в проводниках, по которым течёт переменный ток проводимости, однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучившим магнитное поле тока поляризации, который является частью тока смещения. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:
где j — плотность тока проводимости, jD — плотность тока смещения[5].
В диэлектрике (например, в диэлектрике конденсатора) и в вакууме нет токов проводимости. Поэтому приведенная выше формула Максвелла пишется так —
36)Шкала электромагнитных волн представляет собой непрерывную последовательность частот и длин электромагнитных излучений, представляющих собой распространяющееся в пространстве переменное магнитное поле. Теория электромагнитных явлений Джеймса Максвелла позволила установить, что в природе существуют электромагнитные волны разных длин.
Экспериментальные работы немецкого ученого Г. Герца и русского ученого П. Н. Лебедева подтвердили теорию Максвелла и доказали, что световое излучение представляет собой очень короткие электромагнитные волны, создаваемые естественными вибраторами – атомами и молекулами.
В зависимости от способа получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн). Между соседними диапазонами шкалы нет четких границ. Диапазоны волн различных типов перекрывают друг друга, следовательно, волны таких длин можно получить двумя способами.
Принципиального различия между отдельными излучениями нет, так как все они представляют электромагнитные волны, порождаемые заряженными частицами. Но в зависимости от длины волны они обладают различными свойствами: например, проникающей способностью, видимостью, коэффициентом отражения и т.д.
Эти различия определяются общей закономерностью шкалы электромагнитных волн: по мере уменьшения длины волны волновые свойства света, такие как интерференция, дифракция и поляризация, проявляются слабее, а квантовые свойства света, связанные со свойствами частиц, проявляются сильнее.
Шкала электромагнитных излучений
| Название диапазона | Длины волн, λ | Частоты, ν | Источники | |
| Радиоволны | Сверхдлинные | более 10 км | менее 30 кГц | Атмосферные имагнитосферныеявления. Радиосвязь. |
| Длинные | 10 км — 1 км | 30 кГц — 300 кГц | ||
| Средние | 1 км — 100 м | 300 кГц — 3 МГц | ||
| Короткие | 100 м — 10 м | 3 МГц — 30 МГц | ||
| Ультракороткие | 10 м — 1 мм | 30 МГц — 300 ГГц[4] | ||
| Инфракрасное излучение | 1 мм — 780 нм | 300 ГГц — 429 ТГц | Излучение молекул и атомов при тепловых и электрических воздействиях. | |
| Видимое (оптическое) излучение | 780—380 нм | 429 ТГц — 750 ТГц | ||
| Ультрафиолетовое | 380 — 10 нм | 7,5·1014 Гц — 3·1016 Гц | Излучение атомов под воздействием ускоренных электронов. | |
| Рентгеновские | 10 нм — 5 пм | 3·1016 — 6·1019 Гц | Атомные процессы при воздействии ускоренных заряженных частиц. | |
| Гамма | менее 5 пм | более 6·1019 Гц | Ядерные и космические процессы, радиоактивный распад. |
Источники ЭМП естественные: атмосферное электричество, космические лучи, излучение солнца. Искусственные: генераторы, трансформаторы, антенны, лазерные установки, микроволновые печи, мониторы компьютеров и др. Источники электромагнитных полей промышленной частоты — это все электрические приборы, линии электропередач.
Переменное ЭМП является совокупностью двух взаимосвязанных полей: электрического (Е, В/м) и магнитного (Н, A/м).
Характеристики ЭМП: длина волны λ, [м]; частота колебаний f, [Гц]; скорость распространения С, м/с.
λ = C/f.
37)теплово́е излуче́ние или лучеиспускание — передача энергии от одних тел к другим в виде электромагнитных волн за счёт их тепловой энергии. Тепловое излучение в основном приходится на инфракрасный участок спектра, т.е на длины волн от 0,74 мкм до 1000 мкм. Отличительной особенностью лучистого теплообмена является то, что он может осуществляться между телами, находящимися не только в какой-либо среде, но и вакууме.
Примером теплового излучения является свет от лампы накаливания.
Мощность теплового излучения объекта, удовлетворяющего критериям абсолютно чёрного тела, описывается законом Стефана — Больцмана.
Отношение излучательной и поглощательной способностей тел описывается законом излучения Кирхгофа.
Тепловое излучение является одним из трёх элементарных видов переноса тепловой энергии (помимо теплопроводности и конвекции).
Равновесное излучение — тепловое излучение, находящееся в термодинамическом равновесии с веществом.
Фотометрическая светимость [править]
В фотометрии, светимость — это световая величина, представляющая собой световой поток излучения, испускаемого с малого участка светящейся поверхности единичной площади. Она равна отношению светового потока, исходящего от рассматриваемого малого участка поверхности, к площади этого участка[1]:
,
где dΦv — световой поток, испускаемый участком поверхности площадью dS. Светимость в Международной системе единиц (СИ) измеряется в лм/м². 1 лм/м² — это светимость поверхности площадью 1 м2, излучающей световой поток, равный 1 лм.
Аналогом светимости в системе энергетических фотометрических величин является энергетическая светимость (излучательность). Её определение аналогично определению светимости, но вместо светового потока Φv используется поток излучения Фe. Единица энергетической светимости в СИ — Вт/м².
Cветимость небесного тела [править]
Светимость в астрономии — полная энергия, излучаемая астрономическим объектом (планетой, звездой, галактикой и т. п.) в единицу времени. Измеряется в абсолютных единицах (СИ — Вт; СГС — эрг/с) либо в единицах светимости Солнца (L☉ = 3,86·1033 эрг/с).[2]
Светимость не зависит от расстояния до объекта, от него зависит только видимая звёздная величина. Светимость — одна из важнейших звёздных характеристик, позволяющая сравнивать между собой различные типы звёзд на диаграммах «спектр — светимость», «масса — светимость». Светимость звезды можно рассчитать по формуле:
где R — радиус звезды, T — температура её поверхности, σ — коэффициент Стефана-Больцмана.
Светимость ускорителя [править]
В экспериментальной физике элементарных частиц светимостью называют параметр ускорителя, характеризующий интенсивность столкновения частиц пучка с частицами фиксированной мишени (интенсивность столкновения частиц двух встречных пучков в случае коллайдеров). Светимость L измеряется в см−2·с−1. При умножении сечения реакции на светимость получается средняя частота протекания этого процесса на данном коллайдере .
иСПУСКАТЕЛЬНАЯ СПОСОБНОСТЬ (лучеиспускательная способность, излучательная способность) — осн. характеристикатеплового излучения, испускаемого с поверхности нагретого тела, мерой к-рой является поток энергии излучения, испускаемого за единицу времени с единицы поверхности тела. И. с. в данном направлении В (наз. также энергетич. яркостью поверхности) рассчитывается на единицу телесного угла; И. с. во всех направлениях е (наз. также светимостью) при выполнении Ламберта закона равна pВ. И. с. зависит от темп-ры поверхности Т и характеризуется при каждой темп-ре определ. спектральным составом испускаемого излучения. Спектральную И. с. рассчитывают на единицу интервала частот v (или длин волн l) и соответственно обозначают Bv,Т и ev,T (или Вl,T и el,T). Полная (интегральная) И. с. ВT и eT получается интегрированием спектральной И. с. по всему спектру. Спектральная И. с. связана Кирхгофа законом излучения с поглощательной способностью тела, для абсолютно чёрного тела она определяется Планка законом излучения (см. также Излучение равновесное). Наряду с И. с. поверхности нагретого тела в теории переноса излучения рассматривается объёмная И. с. (коэф. испускания). М. А. Елъяшевич.
ПОГЛОЩАТЕЛЬНАЯ СПОСОБНОСТЬ тела — отношение поглощаемого телом потока излучения к падающему на него монохроматич. потоку излучения частоты v; то же, что монохроматический поглощения коэффициент. П. с. зависит от вещества, из к-рого тело состоит, от формы тела и от его темп-ры. Если П. с. тела в нек-ром диапазоне частот и темп-р равна 1, говорят, что оно при этих условиях является абсолютно чёрным телом. П. с. наряду со спектральной испускателъной способностью входит вКирхгофа закон излучения и характеризует отклонение поглощающих свойств данного тела от свойств абсолютно чёрного тела. П. с. — важнейшая характеристика теплового излучения. Сумма П. с., пропускания коэффициента и отражения коэффициента тела равна 1.
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравненийотносительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил [править]
Определения[править]
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило[править]
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4
Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило[править]
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для постоянных напряжений
для переменных напряжений
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
38) Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.
Важность абсолютно чёрного тела в вопросе о спектре теплового излучения любых (серых и цветных) тел вообще, кроме того, что оно представляет собой наиболее простой нетривиальный случай, состоит ещё и в том, что вопрос о спектре равновесного теплового излучения тел любого цвета и коэффициента отражения сводится методами классической термодинамики к вопросу об излучении абсолютно чёрного тела (и исторически это было уже сделано к концу XIX века, когда проблема излучения абсолютно чёрного тела вышла на первый план).
Наиболее чёрные реальные вещества, например, сажа, поглощают до 99 % падающего излучения (то есть имеют альбедо, равное 0,01) в видимом диапазоне длин волн, однако инфракрасное излучение поглощается ими значительно хуже. Среди тел Солнечной системы свойствами абсолютно чёрного тела в наибольшей степени обладает Солнце.
Термин был введён Густавом Кирхгофом в 1862 году.
Практическая модель[править]
Модель абсолютно чёрного тела
Абсолютно чёрных тел в природе не существует, поэтому в физике для экспериментов используется модель. Она представляет собой замкнутую полость с небольшим отверстием. Свет, попадающий внутрь сквозь это отверстие, после многократных отражений будет полностью поглощён, и отверстие снаружи будет выглядеть совершенно чёрным. Но при нагревании этой полости у неё появится собственное видимое излучение. Поскольку излучение, испущенное внутренними стенками полости, прежде, чем выйдет (ведь отверстие очень мало), в подавляющей доле случаев претерпит огромное количество новых поглощений и излучений, то можно с уверенностью сказать, что излучение внутри полости находится в термодинамическом равновесии со стенками. (На самом деле, отверстие для этой модели вообще не важно, оно нужно только чтобы подчеркнуть принципиальную наблюдаемость излучения, находящегося внутри; отверстие можно, например, совсем закрыть, и быстро приоткрыть только тогда, когда равновесие уже установилось и проводится измерение).
Законы излучения абсолютно чёрного тела[править]
Классический подход[править]
Изначально к решению проблемы были применены чисто классические методы, которые дали ряд важных и верных результатов, однако полностью решить проблему не позволили, приведя в конечном итоге не только к резкому расхождению с экспериментом, но и к внутреннему противоречию — так называемой ультрафиолетовой катастрофе.
Изучение законов излучения абсолютно чёрного тела явилось одной из предпосылок появления квантовой механики.
Первый закон излучения Вина[править]
В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу:
·
где uν — плотность энергии излучения,
ν — частота излучения,
T — температура излучающего тела,
f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.
Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина.
Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы.
Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином «закон смещения Вина» называют закон максимума.
Второй закон излучения Вина[править]
В 1896 году Вин на основе дополнительных предположений вывел второй закон:
где C1, C2 — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.
Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C1 и C2. С учётом этого, второй закон Вина можно записать в виде:
где h — постоянная Планка,
k — постоянная Больцмана,
c — скорость света в вакууме.
Закон Рэлея — Джинса[править]
Основная статья: закон Рэлея — Джинса
Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса:
Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможность термодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой.
Тем не менее закон излучения Рэлея — Джинса справедлив для длинноволновой области спектра и адекватно описывает характер излучения. Объяснить факт такого соответствия можно лишь при использовании квантово-механического подхода, согласно которому излучение происходит дискретно. Исходя из квантовых законов можно получить формулу Планка, которая будет совпадать с формулой Рэлея — Джинса при .
Этот факт является прекрасной иллюстрацией действия принципа соответствия, согласно которому новая физическая теория должна объяснять всё то, что была в состоянии объяснить старая.
Закон Планка[править]
Основная статья: Формула Планка
Зависимость мощности излучения чёрного тела от длины волны.
Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:
где — мощность излучения на единицу площади излучающей поверхности в единичном интервале частот в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·Гц−1·ср−1).
Эквивалентно,
где — мощность излучения на единицу площади излучающей поверхности в единичном интервале длин волн в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·м−1·ср−1).
Полная (т.е. испускаемая во всех направлениях) спектральная мощность излучения с единицы поверхности абсолютно чёрного тела описывается этими же формулами с точностью до коэффициента π: ε(ν, T) = πI(ν, T), ε(λ, T) = πu(λ, T)[1].
Закон Стефана — Больцмана[править]
Основная статья: Закон Стефана — Больцмана
Общая энергия теплового излучения определяется законом Стефана — Больцмана, который гласит:
Мощность излучения абсолютно чёрного тела (интегральная мощность по всему спектру), приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:
где — мощность на единицу площади излучающей поверхности, а
Вт/(м²·К4) — постоянная Стефана — Больцмана.
Таким образом, абсолютно чёрное тело при = 100 K излучает 5,67 ватт с квадратного метра своей поверхности. При температуре 1000 К мощность излучения увеличивается до 56,7 киловатт с квадратного метра.
Для нечёрных тел можно приближённо записать:
где — степень черноты (для всех веществ , для абсолютно чёрного тела ).
Константу Стефана — Больцмана можно теоретически вычислить только из квантовых соображений, воспользовавшись формулой Планка. В то же время общий вид формулы может быть получен из классических соображений (что не снимает проблемы ультрафиолетовой катастрофы).
Закон смещения Вина[править]
Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:
где — температура в кельвинах, а — длина волны с максимальной интенсивностью в метрах.
Так, если считать в первом приближении, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 К) лежит на длине волны 9400 нм (в инфракрасной области спектра).
Видимый цвет абсолютно чёрных тел с разной температурой представлен на диаграмме.
39) Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.
Общий вид закона смещения Вина [править]
λmax = b/T ≈ 0,002898 м·К × T −1 (K),
где T — температура, а λmax — длина волны с максимальной интенсивностью. Коэффициент b, называемыйпостоянной Вина, в системе СИ имеет значение 0,002898 м·К.
Для частоты света (в герцах) закон смещения Вина имеет вид:
где
α ≈ 2,821439… Гц/К — постоянная величина,
k — постоянная Больцмана,
h — постоянная Планка,
T — температура (в кельвинах).
Вывод закона [править]
Для вывода можно использовать выражение закона излучения Планка для абсолютно чёрного тела, записанного для длин волн:
Чтобы найти экстремумы этой функции в зависимости от длины волны, её следует продифференцировать по и приравнять дифференциал к нулю:
Из этой формулы сразу можно определить, что производная приближается к нулю, когда или когда , что выполняется при . Однако, оба эти случая дают минимум функции Планка , которая для указанных длин волн достигает своего нуля (см. рисунок вверху). Поэтому анализ следует продолжить лишь с третьим возможным случаем, когда
Используя замену переменных , данное уравнение можно преобразовать к виду
Численное решение этого уравнения даёт:[1]
Таким образом, используя замену переменных и значения постоянных Планка, Больцмана и скорости света, можно определить длину волны, на которой интенсивность излучения абсолютно чёрного тела достигает своего максимума, как
где температура дана в кельвинах, а — в метрах.
40) Квант (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике. В основе понятия лежит представление квантовой механики о том, что некоторые физические величины могут принимать только определённые значения (говорят, что физическая величина квантуется). В некоторых важных частных случаях эта величина или шаг её изменения могут быть только целыми кратными некоторого фундаментального значения[1] — и последнее называют квантом. Например, энергиямонохроматического электромагнитного излучения угловой частоты может принимать значения , где — редуцированная постоянная Планка, а — целое число. В этом случае имеет смысл энергии кванта излучения (иными словами, фотона), а — смысл числа́ этих квантов (фотонов). В смысле, близком к этому, термин квант был впервые введен Максом Планком в его классической работе 1900 года — первой работе по квантовой теории, заложившей её основу. Вокруг идеи квантования с начала 1900-х годов развилась полностью новая физическая концепция, обычно называемая квантовой физикой.
Ныне прилагательное «квантовый» используется в названии ряда областей физики (квантовая механика, квантовая теория поля, квантовая оптика и т. д.). Широко применяется термин квантование, означающий построение квантовой теории некоторой системы или переход от её классического описания к квантовому. Тот же термин употребляется для обозначения ситуации, в которой физическая величина может принимать только дискретные значения — например, говорят, что энергия электрона ватоме «квантуется».
Сам же термин «квант» в настоящее время имеет в физике довольно ограниченное применение. Иногда его употребляют для обозначения частиц или квазичастиц, соответствующих бозонным полям взаимодействия (фотон — квант электромагнитного поля, фонон — квант поля звуковых волн в кристалле, гравитон — гипотетический квант гравитационного поля и т. д.), также о таких частицах говорят как о «квантах возбуждения» или просто «возбуждениях» соответствующих полей.
Кроме того, по традиции «квантом действия» иногда называют постоянную Планка. В современном понимании это название может иметь тот смысл, что постоянная Планка является естественной единицей измерения действия и других физических величин такой же размерности (например, момента импульса).
Формула Планка — выражение для спектральной плотности мощности (Спектральной Плотности Энергетической Светимости) излучения абсолютно чёрного тела, которое было получено Максом Планком. Для плотности энергии излучения :
Формула Планка («форма» зависимости от частоты и температуры) первоначально была «выведена» эмпирически. Формула Планка была получена после того, как стало ясно, что формула Рэлея—Джинса, которая следует из классической теории электромагнитного поля, удовлетворительно описывает излучение только в области длинных волн. С убыванием длин волн формула Рэлея—Джинса сильно расходится с эмпирическими данными. Более того, в пределе она даёт расхождение — бесконечную энергию излучения (ультрафиолетовая катастрофа). В связи с этим Планк в 1900 году сделал предположение, противоречащее классической физике, о том, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:
Коэффициент пропорциональности впоследствии назвали постоянной Планка, = 1.054 · 10−27 эрг·с. Это предположение позволило объяснить наблюдаемый спектр излучения теоретически.
Правильность формулы Планка подтверждается не только непосредственной эмпирической проверкой, но и следствиями из данной формулы, в частности из неё следуетзакон Стефана-Больцмана, также эмпирически подтверждённый. Кроме того, из неё выводятся также и приблизительные формулы, полученные до формулы Планка, — формула Вина и формула Рэлея-Джинса
41) Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Законы фотоэффекта:
Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока.
Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света (или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если , то фотоэффект уже не происходит.
Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода φ, покидает металл: где — максимальная кинетическая энергия, которую имеет электрон при вылете из металла.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Карла Вильгельма Озеена, получил Нобелевскую премию) на основе гипотезы Макса Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк в 1900 году предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
где φ — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), — максимальная кинетическая энергия вылетающего электрона, — частота падающего фотона с энергией , h —постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты ( ), ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из металла. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества и на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Исследования фотоэффекта были одними из самых первых квантовомеханических исследований.
46. Полное сопротивление в цепи переменного тока.
Обычно
цепь переменного тока включает в себя
и активное сопротивление, и емкость, и
индуктивность.
Полное
сопротивление (Z)
— это векторная сумма всех сопротивлений:
активного, емкостного и индуктивного.
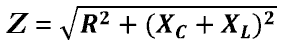 —
полное сопротивление цепи.
—
полное сопротивление цепи.
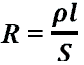 —
активное сопротивление.
—
активное сопротивление.
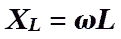 —
индуктивное сопротивление.
—
индуктивное сопротивление.
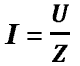 —
полное сопротивление определяет силу
тока в цепи по закону Ома.
—
полное сопротивление определяет силу
тока в цепи по закону Ома.
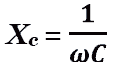 —
емкостное сопротивление.
—
емкостное сопротивление.
I — действующее значение силы тока (един.измер. А)
U— действующее значение напряжения(един.измер. В)
XL — индуктивное сопротивление(един.измер. Ом)
ω — циклическая частота переменного тока(един.измер. рад/с)
L – индуктивность(ед.из. Гн)
C – емкость (ед.из. Ф)
XC — индуктивное сопротивление (ед.из. Ом)
Z — полное сопротивление (Ом)
R — активное сопротивление (Ом)
ρ — удельное сопротивление проводника (Ом/м)
l — длина проводника (м)
S — площадь сечения проводника (м2
47.Импеданс тканей. Физические основы реографии.
Импеданс – основные понятия.
При прохождении через ткани переменного тока, изменяющегося по гармоническому закону
I(t) =I0 cos ωt,
падение напряжения на биологической ткани изменяется по закону
U (t)=Uo⋅cos (ωt+ϕ).
Величиной, определяющей соотношение между напряжением и силой переменного тока, является импеданс — полное электрическое сопротивление цепи переменному току.
На опыте напряжение отстает по фазе от тока (ϕ<0), что характерно для электрических цепей, состоящих из резисторов и конденсаторов.
Для биологического объекта импеданс носит составной (комплексный) характер Z=(R,X). Его активная составляющая R связана, в первую очередь, с проводимостью внутренних жидких сред, являющихся электролитами. Различные процессы в тканях, сопровождающиеся необратимыми потерями энергии, также дают вклад в величину активной составляющей импеданса. Реактивная компонента X определяется емкостными свойствами исследуемой ткани, в частности, емкостью биологических мембран. Кроме того, в емкостную составляющую импеданса дает вклад и область контакта стимулирующих электродов с биологическими тканями.
Абсолютная величина (модуль) электрического импеданса определяется выражением .22XRZ+=
На опыте величина импеданса может быть определена по измерениям амплитудных (или эффективных) значений напряжения Uo и силы тока Io
⏐Z⏐ = Uo/Io (или ⏐Z⏐ = Uэфф/Iэфф).
Фазовый сдвиг ϕ определяет отношение реактивной и активной составляющих импеданса
tg ϕ = X/R.
Значения угла сдвига фаз, полученные при частоте 1 кГц для различных биологических объектов, приведены в таблице 1.
Таблица 1. Угол сдвига фаз (в градусах) для различных видов тканей.
|
Объект |
ϕ , град. |
|
Кожа человека, лягушки Нерв лягушки Мышцы кролика |
-55 -64 -65 |
Составную (комплексную) величину Z принято изображать в виде векторной диаграммы, на которой ось абсцисс — величина активного сопротивления, ось ординат — величина реактивного сопротивления.
Абсолютная величина импеданса ⏐Z⏐ и фазовый сдвиг ϕ являются функциями частоты переменного тока. Зависимость электрического импеданса от частоты носит название дисперсии импеданса.
Физические основы реологии.
Величина импеданса тканей зависит от их физиологического состояния, в частности от их кровоснабжения. При кровенаполнении сосудов происходит изменение величины импеданса в такт с работой сердца. По величине изменений импеданса можно судить о состоянии сердечно-сосудистой системы.
Реология — диагностический метод, основанный на регистрации изменения величины импеданса тканей в процессе сердечной деятельности.
Величина импеданса тканей |Z| состоит из двух составляющих |Z| = |Zo| + |z(t)|: постоянной — |Zo| и изменяющейся во времени в соответствии с работой сердца – |z(t)|.
На практике, на исследуемый участок тела накладывают электроды площадью несколько см2 и пропускают переменный ток частотой ≈ 30 − 40 кГц. Выбор частоты определяется несколькими факторами: электробезопасностью, исключением влияния электродов и емкости их контакта с кожей, уменьшением зависимости величины импеданса от механических воздействий на исследуемую ткань. Наполнение сосудов кровью изменяет расстояния между отдельными участками ткани, что должно приводить к изменению ёмкостного сопротивления. Но вклад макроскопических объемов тканей в реактивную составляющую импеданса существенен только в области α- дисперсии. Следовательно, изменения импеданса во времени обусловлены влиянием притока и оттока крови на активную составляющую полного сопротивления.
При прохождении через ткани электрического тока I = Io⋅cos ωt величина напряжения будет изменяться по закону
U = Uο cos (ωt + ϕ) = Io⋅( ⏐Zo⏐ + ⏐z(t)⏐ )⋅cos (ωt +ϕ ).
Электрическими методами выделяют из регистрируемого сигнала составляющую, пропорциональную |z(t)|, содержащую информацию о состоянии кровоснабжения изучаемого участка тканей − реограмму.
Для парных анатомических образований проводят запись реограммы на правой и левой стороне тела.
|
Закон Ома для полной цепи переменного тока. |
|
|
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае:
|
|
|
|
|
|
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: |
|
|
Сдвиг фаз в цепи переменного тока определяется характером нагрузки:
|
|
|
Мощность в цепи переменного тока. |
|
|
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): |
|
|
или, переходя к действующим значениям, |
|
|
Величина |
коэффициент мощности |
|
Резонанс в электрической цепи. |
|
|
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии
|
|
|
Следовательно, |
|
|
Амплитуды колебаний напряжения на индуктивности и емкости будут равны и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
|
Следовательно, |
|
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением |
|
|
При этом если величина то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! |
|
|
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. |
|
|
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа |
|
|
В случае резонанса |
|
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). |
|
Полное сопротивление цепи переменного — Студопедия
тока. Резонанс напряжений.
Рассмотрим цепь, в которой последовательно соединены резистор, катушка индуктивности и конденсатор(рис.4)

В общем случае сила тока в цепи и напряжение изменяются не в одной фазе, поэтому
I = Imsin (ωt-φ),
где φ – разность фаз напряжения и силы тока.
Сумма напряжений на отдельных участках цепи равна внешнему напряжению:
U= IR+ IXL+ IXC = UR + UL + UС, (9)
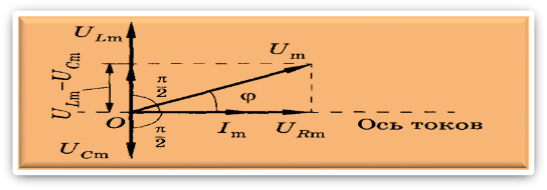
На рис.5 по оси токов направлен вектор амплитуды силы тока Im .
Так как по всей цепи амплитуда силы тока одинакова, то амплитуды напряжений на участках цепи отложены относительно этого вектора: вектор URm – в одной фазе с силой тока; вектор ULm– с опережением силы тока по фазе на , вектор UCm –c отставанием от силы тока по фазе на . Используя теорему Пифагора, имеем U2м=U2Rm+(ULm-UCm)2
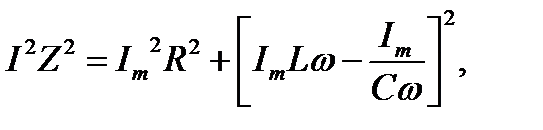 Подставляя в (10) выражения этих амплитуд из (5)-(7) и учитывая закон Ома, находим
Подставляя в (10) выражения этих амплитуд из (5)-(7) и учитывая закон Ома, находим
(11)
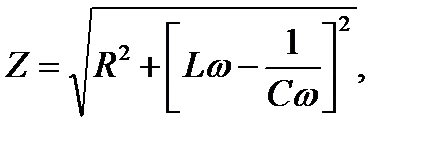 где Z – полное сопротивление цепи переменного тока, называемое импедансом. Из (11) получаем
где Z – полное сопротивление цепи переменного тока, называемое импедансом. Из (11) получаем
(12)
Омическое сопротивление R цепи называют также активным, оно обусловливает выделение теплоты в цепи в соответствии с законом Джоуля—Ленца. Разность индуктивного и емкостного сопротивлений (XL — Хс) называют реактивным сопротивлением. Оно не вызывает нагревания элементов электрической цепи.
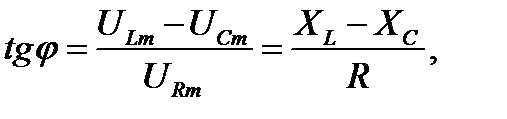 Из рис.5 выразим значение tgφ:
Из рис.5 выразим значение tgφ:
Если Xc =XL , то tgϕ=0 и ϕ=0. Это означает, что сила тока и приложенное напряжение изменяются в одной фазе так, как будто в цепи имеется только омическое сопротивление; напряжения на индуктивности и емкости одинаковы по амплитуде, но противоположны по фазе.
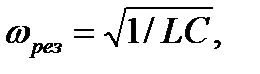 Этот случай вынужденных электрических колебаний называют резонансом напряжения и резонансная частота равна:
Этот случай вынужденных электрических колебаний называют резонансом напряжения и резонансная частота равна:
(14)
При этом условии полное сопротивление Z цепи имеет наименьшее значение, равное R, а сила тока достигает наибольшего значения. Векторная диаграмма для резонанса напряжений в цепи показана на рис. 6.а.

а) б)
Рис.6
Если Lω>1/Сω, то tgϕ>0 и ϕ>0; сила тока отстает по фазе от приложенного напряжения (рис.5). Если Lω<1/Сω , то tgϕ<0 и ϕ<0 — сила тока опережает по фазе приложенное напряжение. Этому случаю соответствует векторная диаграмма на рис.6 б.
Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
где, U-напряжение на элементе цепи,
I – ток через элемент цепи
R – активное сопротивление элемента
Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
| (2) |
где, Um-амплитудное значение напряжения на элементе цепи,
Im – амплитудное значение тока через элемент цепи
R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
| (3) | |
| (4) |
где — UL-падение напряжение на чисто индуктивном сопротивлении ;
UС—падение напряжения на чисто емкостном сопротивлении;
I— значение тока в через реактивное сопротивление;
L— индуктивность реактивного элемента;
C— емкость реактивного элемента;
ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
| (5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Закон Ома для различных типовых цепей переменного тока
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
| (6) |
где —эффективное значение силы тока в А;
U—эффективное значение напряжения в В;
R—активное сопротивление в Ом;
ωL—индуктивное сопротивление в ом.
Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
| (7) |
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
| (8) |
где I-сила тока в А;
U-напряжение в В;
R-активное сопротивление в Ом;
ωL-индуктивное сопротивление в Ом;
1/ωС-емкостное сопротивление в Ом.
Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
ПОЛНОЕ СОПРОТИВЛЕНИЕ — это… Что такое ПОЛНОЕ СОПРОТИВЛЕНИЕ?
- ПОЛНОЕ СОПРОТИВЛЕНИЕ
- ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: ,где r и x — активное и реактивное сопротивления. Измеряется в омах.
Большой Энциклопедический словарь. 2000.
- ПОЛНОЕ СОБРАНИЕ РУССКИХ ЛЕТОПИСЕЙ
- ПОЛНОЕ ТОВАРИЩЕСТВО
Смотреть что такое «ПОЛНОЕ СОПРОТИВЛЕНИЕ» в других словарях:
Полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи, где r и x активное и реактивное сопротивления.… … Википедия
полное сопротивление — Параметр пассивного двухполюсника, равный отношению действующего значения электрического напряжения на выводах этого двухполюсника к действующему значению электрического тока через двухполюсник при синусоидальных электрическом напряжении и… … Справочник технического переводчика
ПОЛНОЕ СОПРОТИВЛЕНИЕ — (6, м) … Большая политехническая энциклопедия
полное сопротивление КЗ — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN closed end impedance … Справочник технического переводчика
полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: , где r и х активное и реактивное сопротивления.… … Энциклопедический словарь
полное сопротивление — pilnutinė varža statusas T sritis automatika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. полное сопротивление, n pranc. impédance, f … Automatikos terminų žodynas
полное сопротивление — pilnutinė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Visuminė elektrinės grandinės varža kintamajai srovei. atitikmenys: angl. apparent resistance; impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полное сопротивление — pilnutinė varža statusas T sritis fizika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное сопротивление, n pranc. impédance, f … Fizikos terminų žodynas
ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрич. цепи току. П. с. синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: Z=U/I = корень из (r2 + х2), где r и х активное и реактивное сопротивления … Естествознание. Энциклопедический словарь
полное сопротивление нулевой последовательности (трехфазной обмотки) — Полное сопротивление обмотки фазы в омах при номинальной частоте между соединенными вместе линейными выводами трехфазной обмотки, соединенной по схеме «звезда» или «зигзаг», и выводом ее нейтрали (МЭС 421 07 04).… … Справочник технического переводчика
Введение, Генерация переменного тока, переменного и постоянного тока и трансформаторы
Введение
Электрическая цепь — это полный проводящий путь, по которому электроны текут от источника к нагрузке и обратно к источнику. Однако направление и величина потока электронов зависят от типа источника. В «Электротехника » в основном есть два типа источника напряжения или тока (электрическая энергия), которые определяют вид цепи, и они есть; переменного тока (или напряжения) и постоянного тока .
В следующих двух статьях мы сосредоточимся на переменном токе и рассмотрим темы от , что такое переменный ток до , формы волны переменного тока и так далее.
Цепи переменного тока
Цепи переменного тока, как следует из названия («Переменный ток»), — это просто цепи, питаемые от переменного источника напряжения или тока. Переменный ток или напряжение — это тот, в котором значение либо напряжения, либо тока изменяется около определенного среднего значения и периодически меняет направление.
Большинство современных бытовых и промышленных устройств и систем питаются от переменного тока. Все подключаемые к сети электроприборы и устройства на базе аккумуляторных батарей технически работают от переменного тока, поскольку все они используют некоторую форму постоянного тока, получаемую от переменного тока, либо для зарядки своих батарей, либо для питания системы. Таким образом, переменный ток — это форма, через которую энергия передается в сеть.
Схема переменного тока возникла в 1980-х годах, когда Тесла решил решить проблему неспособности генераторов постоянного тока Томаса Эдисона на больших расстояниях.Он искал способ передачи электроэнергии с высоким напряжением, а затем использовал трансформаторы для повышения или понижения, что может потребоваться для распределения, и, таким образом, смог минимизировать потери мощности на большом расстоянии, что было основной проблемой Direct Текущий в то время.
Переменный ток и постоянный ток (переменный и постоянный)
переменного тока и постоянного тока различаются несколькими способами от поколения к передаче и распределению, но для простоты мы сохраним сравнение их характеристик в этом посте.
Основное различие между переменным и постоянным током, которое также является причиной их разных характеристик, заключается в направлении потока электрической энергии. В постоянном токе электроны движутся в одном направлении или вперед, в то время как в переменном токе электроны периодически меняют направление потока. Это также приводит к изменению уровня напряжения, поскольку он переключается с положительного на отрицательный в соответствии с током.


Ниже приведена сравнительная таблица, чтобы выделить некоторые из различий между переменного и постоянного тока.Другие различия будут выделены, когда мы углубимся в изучение цепей переменного тока.
|
Основание для сравнения |
переменного тока |
постоянного тока |
|
Мощность передачи энергии |
Путешествует на большие расстояния с минимальными потерями энергии |
Большое количество энергии теряется при передаче на большие расстояния |
|
Основы поколения |
Вращение магнита по проволоке. |
Устойчивый магнетизм вдоль проволоки |
|
Частота |
Обычно 50 Гц или 60 Гц в зависимости от страны |
Частота равна нулю |
|
Направление |
Периодически меняет направление при прохождении через контур |
Это устойчивый постоянный поток в одном направлении. |
|
Текущий |
Его величина меняется со временем |
Постоянная звездная величина |
|
Источник |
Все виды генераторов переменного тока и сети |
Элементы, батареи, преобразование из AC |
|
Пассивные параметры |
Импеданс (RC, RLC и т. Д.) |
Только сопротивление |
|
Коэффициент мощности |
Лежит между 0 и 1 |
Всегда 1 |
|
Форма волны |
Синусоидальная, трапецеидальная, треугольная и квадратная |
Прямая, иногда пульсирующая. |
Базовый источник переменного тока (генератор переменного тока с одной катушкой)
Принцип в отношении поколения переменного тока прост. Если магнитное поле или магнит вращается вдоль стационарного набора катушек (проводов) или вращение катушки вокруг стационарного магнитного поля, переменный ток генерируется с помощью генератора переменного тока (генератора переменного тока).
Самая простая форма генератора переменного тока состоит из проволочной петли, которая механически вращается вокруг оси, находясь между северным и южным полюсами магнита.
Обратите внимание на изображение ниже.

Когда катушка якоря вращается в магнитном поле, создаваемом магнитами северного и южного полюсов, магнитный поток через катушку изменяется, и заряды, таким образом, проталкиваются через провод, вызывая эффективное напряжение или индуцированное напряжение. Магнитный поток через петлю зависит от угла петли относительно направления магнитного поля. Рассмотрите изображения ниже;





Из изображений, показанных выше, мы можем сделать вывод, что определенное количество линий магнитного поля будет обрезано при вращении якоря, количество «обрезанных линий» определяет выходное напряжение .С каждым изменением угла поворота и результирующим круговым движением якоря относительно магнитных линий также изменяется величина «перерезания магнитных линий», следовательно, изменяется и выходное напряжение. Например, линии магнитного поля, обрезанные под нулевым градусом, равны нулю, что делает результирующее напряжение равным нулю, но при 90 градусах почти все линии магнитного поля обрезаются, таким образом, максимальное напряжение в одном направлении генерируется в одном направлении. То же самое относится к 270 градусам, только если они генерируются в противоположном направлении.Таким образом, возникает результирующее изменение напряжения при вращении якоря в магнитном поле, что приводит к формированию синусоидальной формы волны . Результирующее индуцированное напряжение, таким образом, имеет синусоидальную форму с угловой частотой ω, измеряемой в радианах в секунду.
Наведенный ток в приведенной выше схеме определяется уравнением:
I = V / R
Где V = NABwsin (вес)
Где N = Скорость
A = Площадь
B = Магнитное поле
w = Угловая частота.
Настоящие генераторы переменного тока, очевидно, сложнее этого, но они работают на основе тех же принципов и законов электромагнитной индукции, которые описаны выше. Переменный ток также генерируется с помощью определенных типов преобразователей и схем генераторов, которые можно найти в инверторах.
Трансформаторы
Принципы индукции, на которых основан переменный ток, не ограничиваются только его производством, но также и его передачей и распределением .Как и в то время, когда переменный ток приходил в расчет, одной из основных проблем было то, что постоянный ток не мог передаваться на большие расстояния, поэтому одной из основных проблем, которую необходимо было решить, чтобы переменный ток стал жизнеспособным, была возможность для безопасной доставки генерируемых высоких напряжений (KV) потребителям, которые используют напряжения в диапазоне V, а не KV. Это одна из причин, по которой трансформатор описывается как один из основных компонентов переменного тока, и о нем важно говорить.

В трансформаторе две катушки соединены таким образом, что, когда к одной подается переменный ток, он индуцирует напряжение в другой.Трансформаторы — это устройства, которые используются для понижения или повышения напряжения, подаваемого на одном конце (первичная катушка), для создания более низкого или более высокого напряжения соответственно на другом конце (вторичная катушка) трансформатора. Наведенное напряжение во вторичной обмотке всегда равно напряжению, приложенному к первичной обмотке, умноженному на отношение количества витков вторичной обмотки к первичной обмотке.
Трансформатор, являющийся понижающим или повышающим трансформатором, таким образом, зависит от отношения числа витков на вторичной катушке к числу витков проводника на первичной обмотке.Если на первичной обмотке на витков больше, чем на вторичной, трансформатор понижает напряжение на , но если первичная обмотка имеет меньшее количество витков по сравнению с вторичной обмоткой, трансформатор увеличивает напряжение на применяется на первичной.
Трансформаторы сделали распределение электроэнергии на большие расстояния очень возможным, рентабельным и практичным. Чтобы уменьшить потери при передаче, электроэнергия передается от генерирующих станций с высоким напряжением и низким током, а затем распределяется по домам и офисам с низким напряжением и высоким током с помощью трансформаторов.
На этом мы остановимся, чтобы не перегружать статью слишком большим количеством информации. Во второй части этой статьи мы обсудим формы сигналов переменного тока и рассмотрим некоторые уравнения и расчеты. Быть в курсе.
.Electronics Club — Импеданс и реактивное сопротивление
Electronics Club — Импеданс и реактивное сопротивление — входное сопротивление, выходное сопротивление
Импеданс | Реактивное сопротивление | Входное сопротивление | Выходное сопротивление | Импеданс делителя напряжения
Следующая страница: Аналоговые и цифровые
См. Также: Емкость | Сопротивление
Импеданс
Импеданс (символ Z) — это мера полного сопротивления цепи току,
другими словами: насколько цепь препятствует потоку заряда.Это похоже на сопротивление, но также учитывает влияние емкости и индуктивности.
Импеданс измеряется в омах ( ).
).
Импеданс более сложен, чем сопротивление, потому что влияние емкости и индуктивность зависит от частоты тока, проходящего через цепь, и это означает, что импеданс изменяется с частотой . Эффект сопротивления постоянен независимо от частоты.
В = напряжение в вольтах (В)
I = ток в амперах (А)
Z = полное сопротивление в Ом ( )
)
R = сопротивление в Ом ( )
)
Импеданс в простых цепях
Термин «импеданс» часто используется (вполне правильно) для простых цепей. которые не имеют емкости или индуктивности, например, для обозначения их «входной импеданс» или «выходной импеданс».Сначала это может показаться запутанным, но для этих простых схем вы можете предположить, что это просто другое слово для обозначения сопротивления.
Импеданс можно разделить на две части:
- Сопротивление R (часть, которая постоянна независимо от частоты)
- Реактивное сопротивление X (часть, которая зависит от частоты из-за емкости и индуктивности)

Емкость и индуктивность вызывают сдвиг фазы (см. Примечание) между ток и напряжение, что означает, что сопротивление и реактивное сопротивление нельзя просто сложить для получения полного сопротивления.Вместо этого они должны быть добавлены как векторы с реактивным сопротивлением под прямым углом к сопротивлению, как показано на диаграмме.
Четыре электрические величины определяют полное сопротивление (Z) цепи: сопротивление (R), емкость (C), индуктивность (L) и частота (f).
В следующем разделе о реактивном сопротивлении объясняется, как емкость, индуктивность и частота влияют на импеданс.
Что означает «фазовый сдвиг»?
Фазовый сдвиг означает, что ток и напряжение не совпадают друг с другом.Подумайте о зарядке конденсатора. Когда напряжение на конденсаторе равно нулю, ток максимален; когда конденсатор заряжен и напряжение максимальное, ток минимальный. Зарядка и разрядка происходят постоянно с переменным током, и ток вскоре достигает максимума. прежде, чем напряжение достигнет своего максимума: мы говорим, что ток опережает напряжение.
Реактивное сопротивление, X
Реактивное сопротивление (символ X) — это мера противостояния емкости и индуктивности.
к текущему.Реактивное сопротивление зависит от частоты электрического сигнала.
Реактивное сопротивление измеряется в омах ( ).
).
Существует два типа реактивного сопротивления: емкостное реактивное сопротивление (Xc) и индуктивное реактивное сопротивление (X L ).
Полное реактивное сопротивление (X) — это разница между двумя:
| Полное реактивное сопротивление, X = X L — Xc |
Емкостное реактивное сопротивление Xc
Емкостное реактивное сопротивление (Xc) велико на низких частотах и мало на высоких частотах.Для постоянного постоянного тока с нулевой частотой (f = 0 Гц) Xc бесконечно (полное противодействие), Это означает, что конденсаторы пропускают переменный ток, но блокируют постоянный ток .
| Емкостное реактивное сопротивление, Xc = | 1 |
2  fC fC |
Xc = реактивное сопротивление в Ом ( )
)
f = частота в герцах (Гц)
C = емкость в фарадах (F)
Например: конденсатор 1 мкФ имеет реактивное сопротивление
3.2k  для сигнала 50 Гц,
но когда частота выше 10 кГц, его реактивное сопротивление составляет всего 16
для сигнала 50 Гц,
но когда частота выше 10 кГц, его реактивное сопротивление составляет всего 16  .
.
Индуктивное реактивное сопротивление, X L
Индуктивное реактивное сопротивление, X L мало на низких частотах и большое на высоких. Для установившегося постоянного тока (нулевая частота) X L равно нулю (нет противодействия), Это означает, что индукторы пропускают постоянный ток, но блокируют высокочастотный переменный ток .
Индуктивное реактивное сопротивление, X L
= 2  фЛ фЛ |
X L = реактивное сопротивление в Ом ( )
)
f = частота в герцах (Гц)
L = индуктивность в Генри (Гн)
Например: индуктор 1 мГн имеет реактивное сопротивление всего 0.3  для сигнала 50 Гц,
но когда частота выше 10 кГц, его реактивное сопротивление составляет 63
для сигнала 50 Гц,
но когда частота выше 10 кГц, его реактивное сопротивление составляет 63  .
.
Входное сопротивление Z IN
Входное сопротивление (Z IN ) — это импеданс, «видимый» всем, что подключено ко входу. схемы или устройства (например, усилителя). Это совокупный эффект всего сопротивления, емкость и индуктивность, подключенные к входу внутри схемы или устройства.
Термин «входной импеданс» является нормальным даже в простых случаях, когда есть только сопротивление. и вместо этого можно использовать термин «входное сопротивление».На самом деле обычно разумно предположить что входное сопротивление — это просто сопротивление, при условии, что входной сигнал имеет низкую частоту (менее 1 кГц).

Влияние емкости и индуктивности зависит от частоты, поэтому, если они присутствуют, входное сопротивление будет меняться в зависимости от частоты. Влияние емкости и индуктивности обычно наиболее значимо на высоких частотах.
Обычно входной импеданс должен быть высоким , как минимум в десять раз превышающим выходной импеданс схемы (или компонента), подающей сигнал на вход.Это гарантирует, что вход не будет «перегружен». источник сигнала и значительно уменьшите силу (напряжение) сигнала.
Выходное сопротивление Z OUT
Выход любой цепи или устройства эквивалентен выходному сопротивлению (Z OUT ) последовательно с идеальным источником напряжения (В ИСТОЧНИК ). Это называется эквивалентная схема и представляет собой совокупное влияние всех источников напряжения, сопротивления, емкость и индуктивность, подключенные к выходу внутри схемы или устройства.Обратите внимание, что V SOURCE обычно , а не то же самое, что и напряжение питания Vs.
Термин «выходной импеданс» является нормальным даже для простых случаев, когда имеется только сопротивление. вместо этого можно использовать термин «выходное сопротивление». На самом деле обычно разумно предположить что выходное сопротивление — это просто сопротивление, при условии, что выходной сигнал имеет низкую частоту (менее 1 кГц).

Схема замещения любого выхода
Влияние емкости и индуктивности зависит от частоты, поэтому, если они присутствуют, выходное сопротивление будет меняться в зависимости от частоты.Влияние емкости и индуктивности обычно наиболее значимо на высоких частотах.
Обычно выходное сопротивление должно быть низким , менее одной десятой полного сопротивления нагрузки подключен к выходу. Если выходной импеданс слишком высок, он не сможет обеспечить достаточно сильный сигнал на нагрузку, потому что большая часть напряжения сигнала будет « потеряна » внутри цепи, управляющей током через выходное сопротивление Z OUT . Нагрузкой может быть отдельный компонент или входное сопротивление другой цепи.
Низкое выходное сопротивление , Z ВЫХ << Z НАГРУЗКА
Большая часть В ИСТОЧНИК появляется через нагрузку, очень небольшое напряжение «теряется»
управляя выходным током через выходное сопротивление. Обычно это лучшая аранжировка.
Согласованные импедансы , Z ВЫХ = Z НАГРУЗКА
Половина V ИСТОЧНИК появляется в нагрузке, другая половина «теряется»
управляя выходным током через выходное сопротивление.Такое расположение полезно в некоторых
ситуации (например, усилитель, управляющий громкоговорителем), потому что он обеспечивает максимальную мощность
нагрузка . Обратите внимание, что равное количество энергии тратится впустую, управляя выходным током через
Z OUT , КПД 50%.
Высокое выходное сопротивление , Z ВЫХ >> Z НАГРУЗКА
Лишь небольшая часть V SOURCE появляется в нагрузке, большая часть «теряется»
управляя выходным током через выходное сопротивление.Такое расположение неудовлетворительно.

Нагрузка может быть однокомпонентной или
входным сопротивлением другой цепи
Выходное сопротивление делителя напряжения
Делители напряженияшироко используются в электронике, например, для подключения входного преобразователя, такого как LDR, к входу схемы.
Для успешного использования выходное сопротивление делителя напряжения должно быть намного меньше. чем входное сопротивление подключенной к нему цепи.
В идеале выходное сопротивление должно быть меньше одной десятой входного сопротивления.

В эквивалентной схеме делителя напряжения выходное сопротивление — это просто сопротивление и можно использовать термин «выходное сопротивление». R OUT равно к двум параллельно подключенным сопротивлениям (R1 и R2):
| Выходное сопротивление, R OUT = | R1 × R2 | |
| R1 + R2 |
Источник напряжения V ИСТОЧНИК в эквивалентной схеме является значением выходное напряжение Vo, когда к выходу ничего не подключено (и, следовательно, нет выходного тока).Иногда его называют напряжением холостого хода.
| Источник напряжения, В ИСТОЧНИК = | Vs × R2 | |
| R1 + R2 |

Схема замещения делителя напряжения

Делитель напряжения с LDR
Следующая страница: Аналоговый и цифровой | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет используется только для ответа на ваше сообщение, оно не будет передано никому. На этом веб-сайте отображается реклама, если вы нажмете на рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден. Рекламодателям не передается никакая личная информация. Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов. (включая этот), как объяснил Google. Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста посетите AboutCookies.org.
electronicsclub.info © Джон Хьюс 2020
Веб-сайт размещен на Tsohost
.Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовательская работа
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
-
Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
.Что такое метод допуска? — Входной треугольник
Метод полной проводимости используется для решения параллельных цепей переменного тока. Проводимость показывает надежность электрической цепи, позволяющую пропускать электрический ток через нее. Прежде всего, мы должны знать значения некоторых терминов, используемых в методе допуска.
Вход
Величина, обратная импедансу цепи переменного тока, известна как полная проводимость цепи. Поскольку импеданс — это полное противодействие протеканию переменного тока в цепи переменного тока.
Таким образом, адмиттанс определяется как эффективная способность цепи, благодаря которой она позволяет переменному току проходить через нее. Он представлен (Y). Старая единица доступа — mho (Ʊ). Его новый блок — Siemens .
Схема с полным сопротивлением 1 Ом имеет проводимость 1 Сименс. Старый блок был mho.
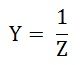
В комплекте:
Применение метода допуска
Рассмотрим 3-разветвленную схему, показанную на рисунке ниже.Полная проводимость определяется простым сложением проводимости трех ветвей. Точно так же полная восприимчивость находится путем алгебраического сложения индивидуальной восприимчивости различных ветвей.
 Общая проводимость G = g 1 + g 2 + g 3 +… ..
Общая проводимость G = g 1 + g 2 + g 3 +… ..
Общая проводимость B = (-b 1 ) + (-b 2 ) + b 3 … .
Общий допуск Y = (G 2 + B 2 )
Общий ток I = VY; Коэффициент мощности cosΦ = G / Y
шагов для решения схемы методом допуска
Рассмотрим параллельную цепь переменного тока, в которой сопротивление и емкость соединены последовательно, а сопротивление и индуктивность также соединены последовательно, как показано на рисунке ниже.
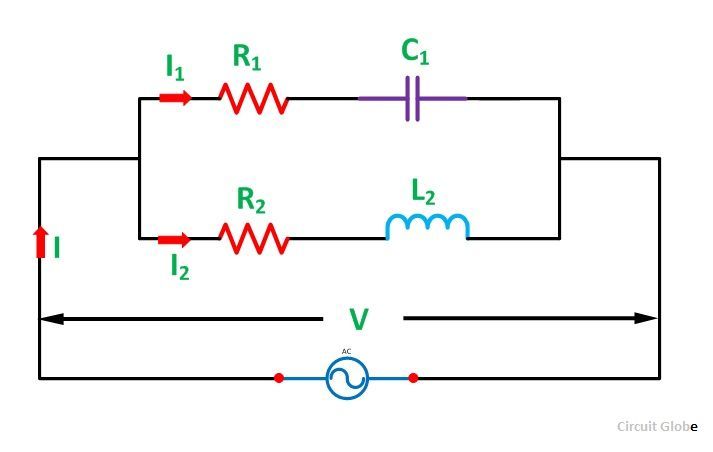 Шаг 1 — Нарисуйте схему согласно заданной задаче.
Шаг 1 — Нарисуйте схему согласно заданной задаче.
Шаг 2 — Найдите полное сопротивление и фазовый угол каждой ветви.
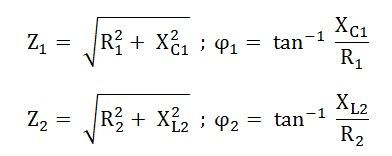
Шаг 3 — Теперь найдите Проводимость, Приемлемость и Допуск каждого отделения.
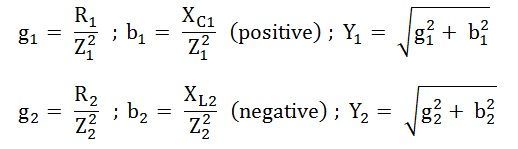
Шаг 4 — Найдите алгебраическую сумму проводимости и восприимчивости.
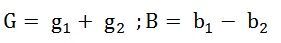
Шаг 5 — Найдите полную проводимость (Y) цепи.
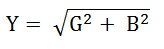
Шаг 6 — Найдите различные токи ответвления цепи.
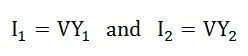
Шаг 7 — Теперь найдите полный ток I цепи.
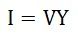
Шаг 8 — Найдите фазовый угол всей цепи.
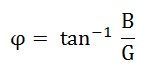
Фазовый угол будет запаздывать, если B отрицательное.
Шаг 9 — Теперь найдите коэффициент мощности цепи.
.

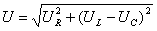
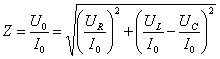 — полное сопротивление переменному току.
— полное сопротивление переменному току.
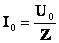
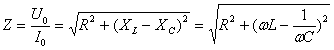 .
.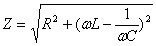
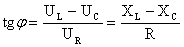 или
или 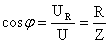 .
.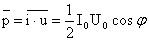
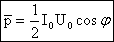
 .
.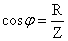 наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.
наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.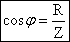
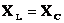 или
или 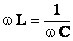 .
.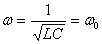 — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.
— т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.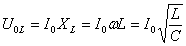
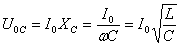
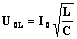
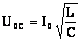
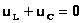 .
.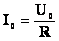 . В этом и состоит смысл явления резонанса.
. В этом и состоит смысл явления резонанса.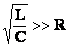 ,
,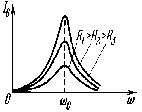
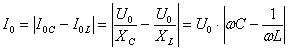 .
.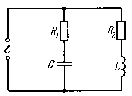
 . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.