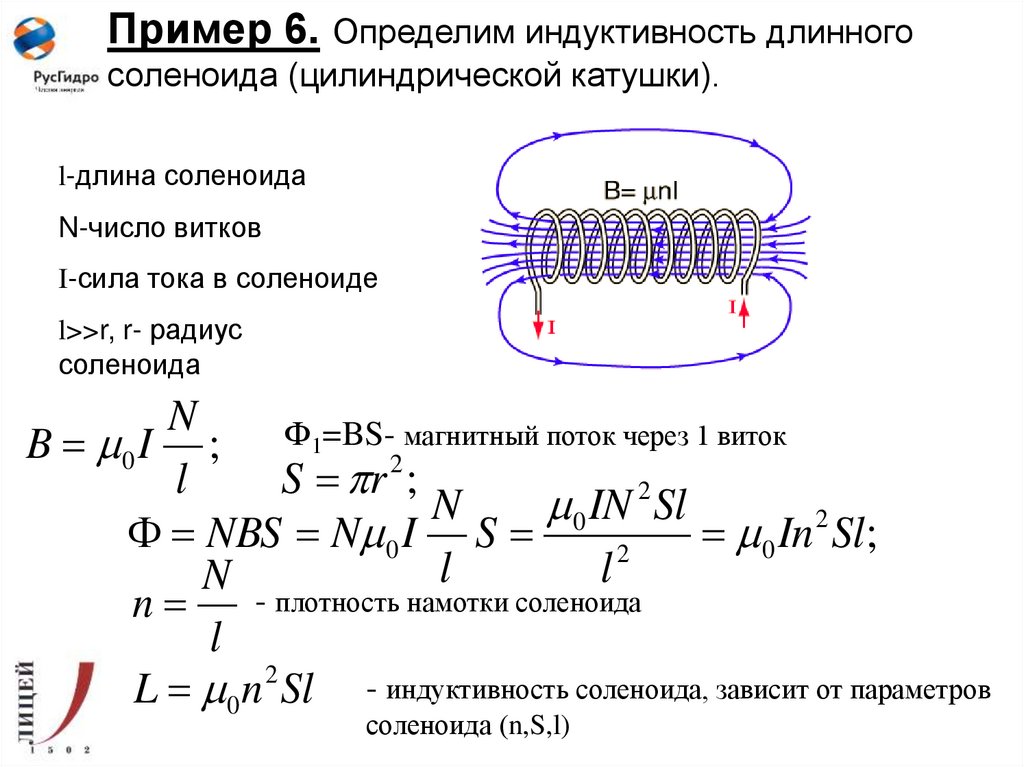
Как рассчитать число витков соленоида по формуле. Какие параметры влияют на число витков. Как применить формулу на практике. Какие типичные задачи решаются с помощью формулы числа витков соленоида.
Что такое соленоид и для чего он используется
Соленоид представляет собой катушку из провода, намотанную на цилиндрический каркас. При протекании электрического тока через витки соленоида внутри него создается магнитное поле. Соленоиды широко применяются в различных областях техники:
- В электромагнитах и реле
- В электродвигателях и генераторах
- В измерительных приборах
- В медицинском оборудовании
- В научных исследованиях
Ключевой характеристикой соленоида является число витков провода на единицу длины. Именно от этого параметра во многом зависит сила создаваемого магнитного поля.
Формула для расчета числа витков соленоида
Основная формула для расчета числа витков соленоида выглядит следующим образом:
n = N / L
где:
- n — число витков на единицу длины (м^-1)
- N — общее число витков соленоида
- L — длина соленоида (м)
Эта формула позволяет найти плотность намотки соленоида, зная общее число витков и длину. Также ее можно использовать для расчета общего числа витков, если известна требуемая плотность намотки и длина соленоида.

Параметры, влияющие на число витков соленоида
На число витков соленоида влияют следующие ключевые параметры:
- Длина соленоида — чем длиннее соленоид, тем больше витков можно разместить при той же плотности намотки
- Диаметр провода — чем тоньше провод, тем больше витков помещается на единицу длины
- Требуемая индуктивность — для получения большей индуктивности нужно увеличивать число витков
- Максимальный ток — для работы с большими токами требуется провод большего сечения, что уменьшает число витков
- Напряжение питания — влияет на выбор диаметра провода и числа витков
При проектировании соленоида необходимо учитывать все эти факторы для получения оптимальных характеристик.
Как применить формулу числа витков на практике
Рассмотрим пошаговый алгоритм применения формулы числа витков соленоида на практике:
- Определите требуемые характеристики соленоида (индуктивность, максимальный ток и т.д.)
- Выберите длину соленоида L и диаметр намоточного провода
- Рассчитайте требуемое общее число витков N исходя из индуктивности
- Подставьте значения N и L в формулу n = N / L
- Получите число витков на единицу длины n
- При необходимости скорректируйте параметры и повторите расчет
Такой подход позволяет спроектировать соленоид с нужными характеристиками.

Типичные задачи с использованием формулы числа витков
Формула числа витков соленоида применяется для решения следующих типовых задач:- Расчет плотности намотки соленоида по его длине и общему числу витков
- Определение общего числа витков по заданной длине и плотности намотки
- Расчет длины соленоида при известном числе витков и плотности намотки
- Проектирование соленоида с заданными электрическими параметрами
- Оптимизация конструкции соленоида для получения максимальной индуктивности
Рассмотрим несколько примеров решения таких задач.
Пример 1: Расчет плотности намотки
Дано: соленоид длиной 10 см имеет 500 витков. Найти плотность намотки.
Решение:
- Используем формулу n = N / L
- Подставляем значения: n = 500 / 0.1 м
- Получаем: n = 5000 витков/м
Пример 2: Определение общего числа витков
Дано: требуется намотать соленоид длиной 20 см с плотностью 2000 витков/м. Найти общее число витков.
Решение:
- Преобразуем формулу: N = n * L
- Подставляем значения: N = 2000 * 0.2 м
- Получаем: N = 400 витков
Особенности расчета числа витков для разных типов соленоидов
При расчете числа витков важно учитывать особенности конструкции соленоида:
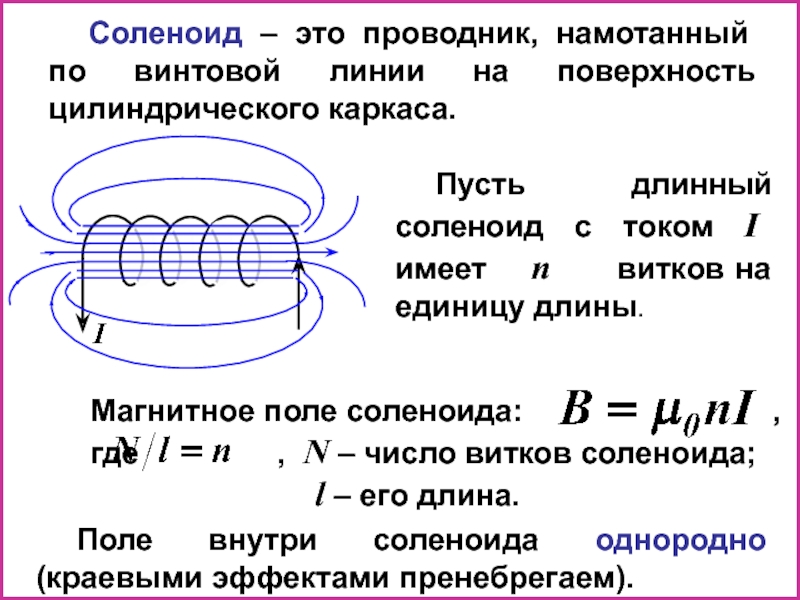
- Для многослойных соленоидов число витков увеличивается пропорционально числу слоев
- В тороидальных соленоидах число витков распределяется по окружности сердечника
- Соленоиды с ферромагнитным сердечником требуют меньшего числа витков для создания того же поля
- В импульсных соленоидах число витков ограничено из-за высоких токов
Эти факторы необходимо принимать во внимание при проектировании конкретных типов соленоидов.
Влияние числа витков на характеристики соленоида
Число витков оказывает существенное влияние на ключевые характеристики соленоида:
- Индуктивность — растет пропорционально квадрату числа витков
- Сопротивление — увеличивается линейно с ростом числа витков
- Собственная емкость — возрастает с увеличением числа витков
- Максимальный ток — уменьшается при росте числа витков из-за увеличения сопротивления
- Быстродействие — снижается с ростом числа витков из-за увеличения индуктивности
Поэтому выбор оптимального числа витков — это всегда компромисс между различными параметрами соленоида.
Практические рекомендации по расчету числа витков
При расчете числа витков соленоида рекомендуется придерживаться следующих правил:
- Начинайте с приблизительной оценки числа витков на основе требуемой индуктивности
- Учитывайте ограничения по размерам и массе конструкции
- Принимайте во внимание тепловой режим работы соленоида
- Проверяйте, не превышает ли рассчитанное число витков максимально допустимое для выбранного каркаса
- При необходимости корректируйте число витков, изменяя другие параметры (длину, диаметр провода и т.д.)
- Для точных расчетов используйте специализированное программное обеспечение
Следование этим рекомендациям позволит получить оптимальную конструкцию соленоида для конкретной задачи.
Количество витков в соленоиде Калькулятор
✖МП магнитного поля создаются электрическими токами, которые могут быть макроскопическими токами в проводах или микроскопическими токами, связанными с электронами на атомных орбитах.ⓘ Магнитное поле МП [Bmf] | ГаммаГаусскилотеслаЛиния на квадратный сантиметрМаксвелл на квадратный сантиметрМегатесламикротеслаМиллитеслананотеслапикотеслатеслаВебер на квадратный метр | +10% -10% | |
✖Длина соленоида — это длина соленоида.ⓘ Длина соленоида [Los] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Электрический ток Магнитное поле — это временная скорость потока заряда через площадь поперечного сечения. | AbampereАмперАттоамперБайотсантиамперСГС ЭМБлок ЭС СГСДециамперДекаампереEMU текущегоESU текущегоExaampereФемтоамперГигаамперГилбертгектоамперкилоамперМегаампермикроамперМиллиампернаноамперПетаамперПикоамперStatampereтераамперЙоктоампереЙоттаампереZeptoampereZettaampere | +10% -10% |
|
✖Количество витков катушки в данной токовой петле.ⓘ Количество витков в соленоиде [n] |
⎘ копия |
👎
Формула
сбросить
👍
Количество витков в соленоиде Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Магнитное поле МП: 4.763 тесла —> 4.763 тесла Конверсия не требуется
Длина соленоида: 11.55 метр —> 11.55 метр Конверсия не требуется
Электрический ток Магнитное поле: 0.573 Ампер —> 0.573 Ампер Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
96.0081151832461 —> Конверсия не требуется
< 10+ МАГНИТНОЕ ПОЛЕ Калькуляторы
Радиус от центра полюса до центра диска
Радиус от центра полюса до центра диска = ЭДС, индуцированная в части ниже магнитного поля/(Магнитное поле МП*Глубина постоянного магнита*Угловая скорость диска) Идти
ЭДС, индуцированная в области ниже магнитного поля
ЭДС, индуцированная в части ниже магнитного поля = Магнитное поле МП*Длина бывшего*Ширина бывшего магнитного поля*Угловая скорость бывшего Идти
Длина бывшего
Длина бывшего = ЭДС, генерируемая в бывшем/(2*Магнитное поле МП*Ширина бывшего магнитного поля*Угловая скорость бывшего) Идти
Сила магнитного поля
Магнитное поле МП = ЭДС, генерируемая в бывшем/(2*Длина бывшего*Ширина бывшего магнитного поля*Угловая скорость бывшего) Идти
ЭДС, генерируемая в бывшем
ЭДС, генерируемая в бывшем = 2*Магнитное поле МП*Длина бывшего*Ширина бывшего магнитного поля*Угловая скорость бывшего Идти
Количество витков в соленоиде
Количество витков катушки = Магнитное поле МП*Длина соленоида/Электрический ток Магнитное поле Идти
Ток через соленоид
Электрический ток Магнитное поле = Магнитное поле МП*Длина соленоида/Количество витков катушки Идти
Длина соленоида
Длина соленоида = Электрический ток Магнитное поле*Количество витков катушки/Магнитное поле МП Идти
Потоковые связи вторичной катушки
Потоковые связи вторичной катушки = Магнитное поле МП*Площадь вторичной катушки Идти
Площадь вторичной катушки
Площадь вторичной катушки = Потоковые связи вторичной катушки/Магнитное поле МП Идти
Количество витков в соленоиде формула
Количество витков катушки = Магнитное поле МП*Длина соленоида/Электрический ток Магнитное поле
n = Bmf*Los/i
Что такое преобразователь?
Преобразователи в основном представляют собой датчики первичного элемента, которые преобразуют механическую энергию в электрический сигнал, обычно милливольт. Обычно это те, кто находится в контакте с окружающей средой или самим материалом, который нужно измерить.
Обычно это те, кто находится в контакте с окружающей средой или самим материалом, который нужно измерить.
Share
Copied!
Магнитное поле однослойного соленоида
Соленоид – это цилиндрическая обмотка из провода по которой протекает постоянный или переменный электрический ток. Обмотка может наноситься в один или несколько слоёв виток к витку. Если длинна соленоида значительно превышает его диаметр, то поле, создаваемое постоянным током сосредоточено внутри него и практически однородно.
Рис. 1: Магнитное поле, создаваемое серией кольцевых токов
Для вычисления индукции магнитного поля $\vec B$ внутри однослойного соленоида представим его в виде суперпозиции кольцевых токов лежащих на одной оси – оси соленоида (Рис. 1) и воспользуемся теоремой о циркуляции:
\[\oint_{ABCD} B_l\,dl=\int_{AB} B_l\,dl + \int_{BC} B_l\,dl + \int_{CD} B_l\,dl + \int_{DA} B_l\,dl = \mu_0
\sum_{i=1}^{N} I_i. \]
\]
(1)
Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая приближение однородности поля получим:
\[B_l L=\mu_0 NI,\]
(2)
где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:
\[B=\mu_0 nI.\]
(3)
Рис. 2: Соленоид с произвольными размерами $L$ и $R$.
Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:
\[B=\frac12\mu_0 nI (\cos\alpha_2-\cos\alpha_1).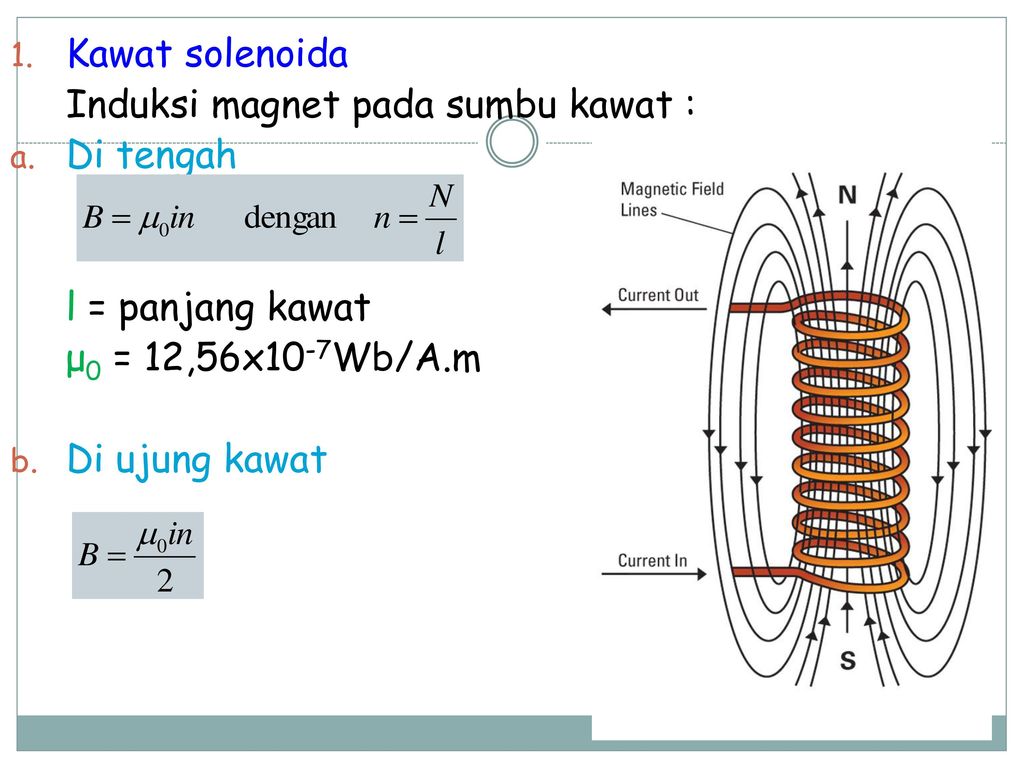 2}},\]
2}},\]
(5)
где $R$ – радиус соленоида. А на краю полубесконечного соленоида:
\[B=\frac12 \mu_0 nI.\]
(6)
Индукция магнитного поля бесконечного соленоида (3)
Плотность намотки n (м-1)
Сила тока соленоида I (A)
B = Тл
Индукция магнитного поля конечного соленоида (5)
Плотность намотки n (м-1)
Радиус намотки R (м)
Длина соленоида L (м)
Сила тока соленоида I (A)
B = Тл
Распределение индукция магнитного внутри конечного соленоида (4)
Плотность намотки n (м-1)
Радиус намотки R (м)
Длина соленоида L (м)
Сила тока соленоида I (A)
Соленоиды
как источники магнитного поля Соленоиды
как источники магнитного поля|
Длинная прямая катушка проволоки может быть использована для создания почти однородного магнитного поля, подобного магнитному стержню. В приведенном выше выражении для магнитного поля B n = N/L — это число витков на единицу длины, иногда называемое «плотностью витков». Магнитное поле B пропорционально току I в катушке. Выражение представляет собой идеализацию соленоида бесконечной длины, но дает хорошее приближение к полю длинного соленоида.
|
Индекс Концепции магнитного поля Токи как источники магнитного поля | ||||||||||||||||||||||||||
|


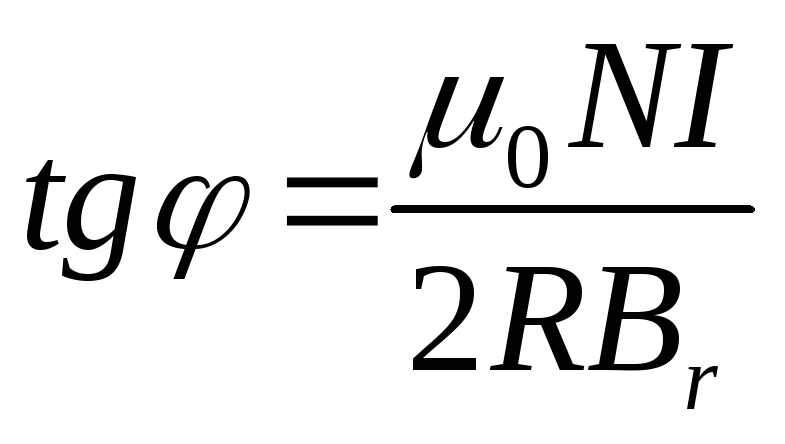 Такие катушки, называемые соленоидами, обладают огромным
количество
практичный
Приложения.
Поле может
быть очень
усиленный
посредством
добавление
железное ядро.
Такие ядра
типичный в
электромагниты.
Такие катушки, называемые соленоидами, обладают огромным
количество
практичный
Приложения.
Поле может
быть очень
усиленный
посредством
добавление
железное ядро.
Такие ядра
типичный в
электромагниты.  Поле
по сути
перпендикулярно к
стороны
путь, давая
незначительный
вклад. Если
конец взят до сих пор
от катушки, которая
поле пренебрежимо мало, то
длина внутри катушки
является доминирующим вкладом.
Поле
по сути
перпендикулярно к
стороны
путь, давая
незначительный
вклад. Если
конец взят до сих пор
от катушки, которая
поле пренебрежимо мало, то
длина внутри катушки
является доминирующим вкладом.

 Его можно интерпретировать как круговую петлю, если расстояние между витками меньше. Однородность внутреннего магнитного поля соленоида возрастает с увеличением его длины. Полное магнитное поле соленоида равно сумме магнитных полей, создаваемых на каждом его витке. Идеальный соленоид имеет нулевое внешнее поле и однородное внутреннее поле, так как его длина намного больше радиуса витков.
Его можно интерпретировать как круговую петлю, если расстояние между витками меньше. Однородность внутреннего магнитного поля соленоида возрастает с увеличением его длины. Полное магнитное поле соленоида равно сумме магнитных полей, создаваемых на каждом его витке. Идеальный соленоид имеет нулевое внешнее поле и однородное внутреннее поле, так как его длина намного больше радиуса витков.