Что такое конденсатор в физике. Конденсатор в физике: устройство, принцип работы и применение

Что такое конденсатор в физике. Как устроен конденсатор. Какой принцип работы конденсатора. Где применяются конденсаторы. Какие бывают виды конденсаторов. Как рассчитать емкость конденсатора.

Что такое конденсатор и как он устроен

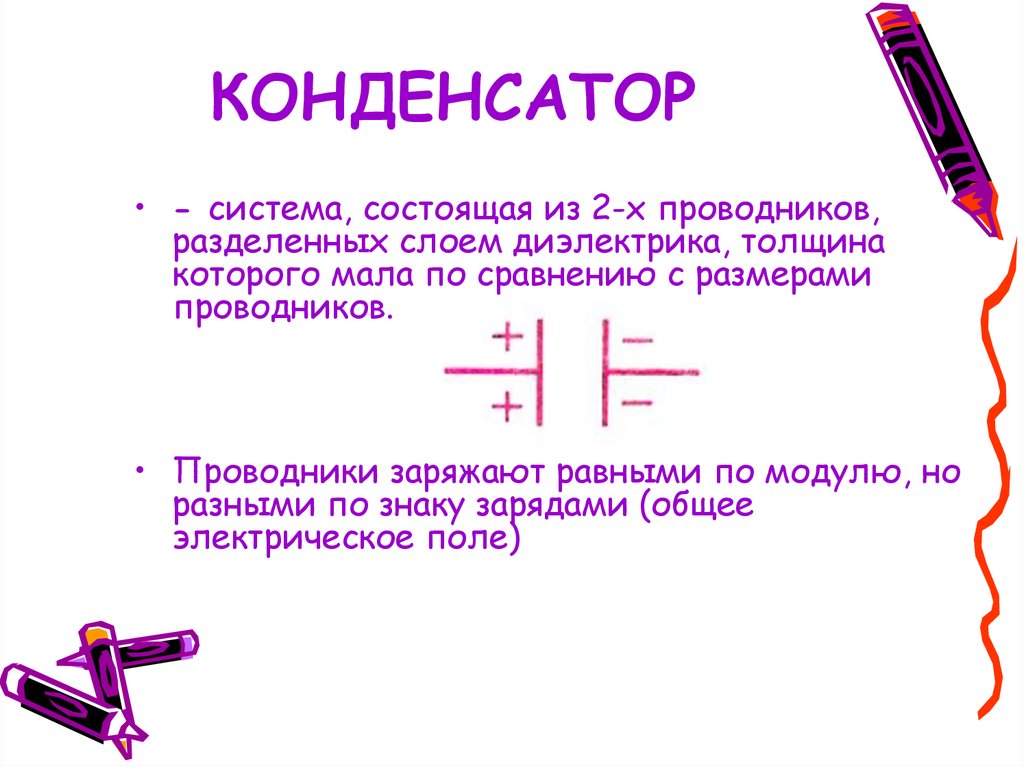
Конденсатор — это электронный компонент, способный накапливать и хранить электрический заряд. Простейший конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком:

• Обкладки — это проводящие пластины, на которых накапливается электрический заряд
• Диэлектрик — это изолирующий слой между обкладками, препятствующий их соприкосновению

Такая конструкция позволяет накапливать на обкладках разноименные электрические заряды. Чем больше площадь обкладок и чем меньше расстояние между ними, тем больше заряда может накопить конденсатор.

Принцип работы конденсатора

Принцип работы конденсатора основан на способности накапливать и отдавать электрический заряд. При подключении к источнику напряжения на обкладках конденсатора накапливаются противоположные по знаку заряды:

• На положительной обкладке — положительный заряд
• На отрицательной обкладке — отрицательный заряд

При этом в диэлектрике возникает электрическое поле. Когда конденсатор отключают от источника, заряды остаются на обкладках — конденсатор сохраняет накопленную энергию. При замыкании обкладок происходит разряд конденсатора — накопленная энергия высвобождается.

Основные характеристики конденсаторов

Главной характеристикой конденсатора является его электрическая емкость. Емкость показывает, какой заряд накапливает конденсатор при заданном напряжении:

• C = Q / U, где C — емкость, Q — заряд, U — напряжение
• Единица измерения емкости — Фарад (Ф)

Другие важные параметры конденсаторов:

• Рабочее напряжение — максимальное напряжение, которое выдерживает конденсатор
• Ток утечки — ток, протекающий через конденсатор в заряженном состоянии
• Температурный коэффициент емкости — изменение емкости при изменении температуры

Виды конденсаторов

Существует множество видов конденсаторов, различающихся конструкцией и применяемыми материалами:

• Керамические — компактные и недорогие, для высокочастотных цепей
• Пленочные — с пластиковым диэлектриком, стабильные характеристики
• Электролитические — большая емкость, для фильтрации в блоках питания
• Танталовые — миниатюрные и надежные, для мобильной электроники
• Слюдяные — для высокочастотных и высоковольтных применений

Выбор типа конденсатора зависит от требований конкретной схемы — рабочего напряжения, требуемой емкости, стабильности параметров и других факторов.

Применение конденсаторов

Благодаря способности накапливать заряд, конденсаторы широко применяются в электронике и электротехнике:

• Фильтрация пульсаций напряжения в блоках питания
• Разделение постоянной и переменной составляющих сигнала
• Накопление энергии для мощных импульсных схем
• Создание резонансных LC-контуров в радиотехнике
• Сглаживание колебаний напряжения в сети

Конденсаторы используются практически во всех электронных устройствах — от простейших до самых сложных. Их применение позволяет улучшить качество электропитания, стабилизировать работу схем и реализовать многие функции в радиоэлектронной аппаратуре.

Как рассчитать емкость конденсатора

Емкость плоского конденсатора можно рассчитать по формуле:

C = εε0S / d

Где:

• ε — диэлектрическая проницаемость диэлектрика
• ε0 — электрическая постоянная (8.85 * 10^-12 Ф/м)
• S — площадь перекрытия пластин
• d — расстояние между пластинами

Из формулы видно, что емкость конденсатора:

• Прямо пропорциональна площади пластин
• Обратно пропорциональна расстоянию между пластинами
• Зависит от диэлектрической проницаемости материала между пластинами

Таким образом, увеличить емкость конденсатора можно за счет увеличения площади обкладок, уменьшения расстояния между ними или использования диэлектрика с большей диэлектрической проницаемостью.

Последовательное и параллельное соединение конденсаторов

При соединении нескольких конденсаторов в батарею их общая емкость зависит от способа соединения:

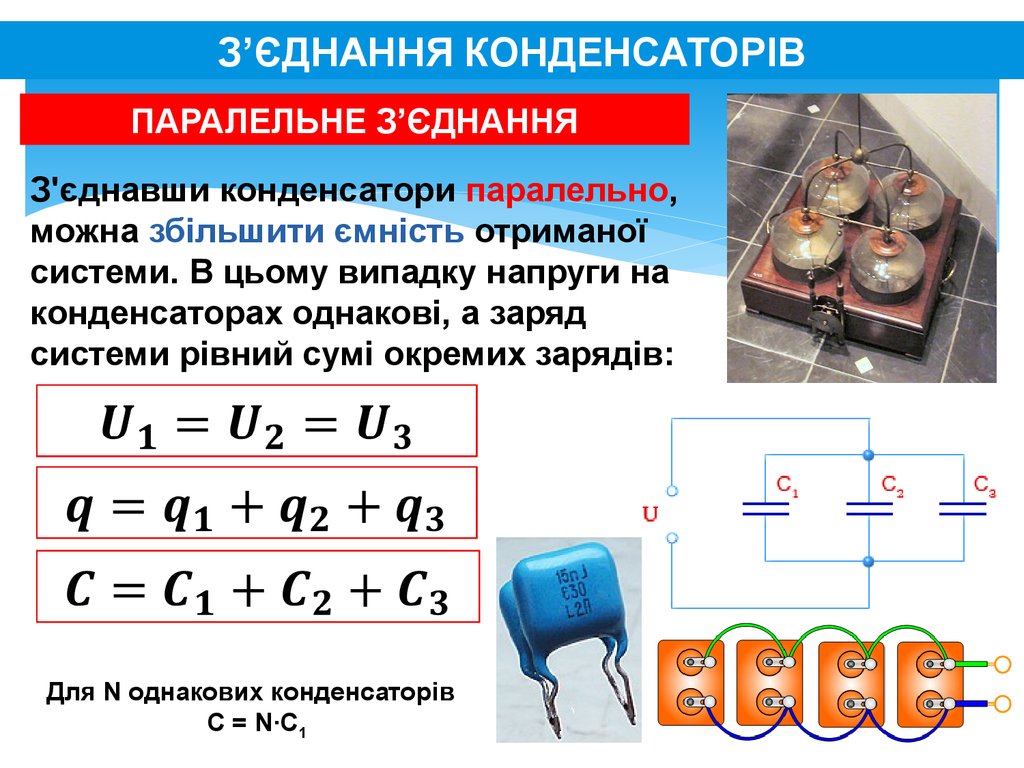
Параллельное соединение

При параллельном соединении общая емкость равна сумме емкостей отдельных конденсаторов:

C = C1 + C2 + C3 + …

Таким образом, параллельное соединение позволяет увеличить общую емкость батареи конденсаторов.

Последовательное соединение

При последовательном соединении обратная величина общей емкости равна сумме обратных величин емкостей конденсаторов:

1/C = 1/C1 + 1/C2 + 1/C3 + …

Общая емкость при последовательном соединении всегда меньше емкости наименьшего из конденсаторов. Такое соединение позволяет получить конденсатор с большим рабочим напряжением.

Энергия заряженного конденсатора

Заряженный конденсатор обладает потенциальной энергией электрического поля. Эту энергию можно рассчитать по формуле:

W = CU^2 / 2 = Q^2 / (2C) = QU / 2

Где:

• W — энергия конденсатора
• C — емкость конденсатора
• U — напряжение на обкладках
• Q — заряд конденсатора

Энергия заряженного конденсатора пропорциональна квадрату напряжения на его обкладках. Это свойство используется в импульсных схемах для получения мощных кратковременных импульсов тока.

Конденсатор — урок. Физика, 9 класс.

Конденсатор — это устройство, предназначенное для накопления заряда и энергии электрического поля (от лат. kondensator — «уплотнять», «сгущать»).

Простейший плоский конденсатор состоит из двух одинаковых металлических пластин — обкладок — и  слоя диэлектрика, толщина которого мала по сравнению с размерами пластин.

 

 

На схемах электрических цепей  конденсатор обозначается:  .

 

Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника тока. При зарядке обе обкладки получают заряды, равные по модулю, но противоположные по знаку. Под зарядом конденсаторов понимают модуль заряда одной из его обкладок. Свойство конденсатора накапливать электрический заряд характеризуется физической величиной — электроёмкостью.

Электроёмкость  обозначается буквой \(C\) и определяется по формуле:

C=qU, где  \(q\) — заряд конденсатора, \(U\) — напряжение между обкладками конденсатора.

                

Электроёмкость конденсатора зависит от площади перекрытия пластин и расстояния между ними, а также от свойств используемого диэлектрика:

 

C∼Sd, где \(S\) — площадь каждой обкладки, \(d\) — расстояние между обкладками.

За единицу электроёмкости в СИ принимается Фарад (Ф).   

Она названа в честь Майкла Фарадея — английского физика. \(1\) Фарад равен ёмкости конденсатора, при которой заряд \(1\) Кулон создаёт между его обкладками напряжение \(1\) Вольт:  1 Фарад=1 Кулон1 Вольт.

 

 

\(1\) Ф — это очень большая ёмкость для конденсатора. Чаще всего конденсаторы имеют электроёмкость, равную дольным единицам Ф: микрофарад (мкФ) — 10−6Ф,  пикофарад (пФ) — 10−12 Ф.

 

Для получения требуемой ёмкости конденсаторы соединяют в батареи.

 

Если конденсаторы соединены параллельно, то общая ёмкость равна сумме ёмкостей: Cоб=C1+C2+C3.

 

  

Если конденсаторы соединены последовательно, то общая ёмкость будет равна: 1Cоб=1C1+1C2+1C3.

 

  

При зарядке конденсатора внешними силами совершается работа по разделению положительных и отрицательных зарядов. По закону сохранения энергии работа внешних сил равна энергии поля конденсатора. При разрядке конденсатора за счёт этой энергии может быть совершена работа. Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Энергию электрического поля конденсатора можно рассчитать по формуле: Eэл=q22C.

Из формулы видно, что энергия конденсатора данной электроёмкости тем больше, чем больше его заряд.

Конденсатор | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Электроемкость тела, как и его потен­циал, трудно определить однозначно. Для этого необходимо создать условия, при ко­торых полностью исключалось бы влияние окружающих тел. В реальных условиях ок­ружающие тела влияют на исследуемое те­ло, изменяя его потенциал и емкость.

Укрепим на стержне заземленного элект­рометра металлический шар и сообщим ему определенный заряд. Стрелка электрометра отклонится от положения равновесия и по­кажет значение потенциала шара относи­тельно земли. Поднесем к шару металли­ческую пластину, соединенную проволокой с землей (рис. 4.63). Показания электрометра уменьшатся. Поскольку заряд шара не из­менился, то уменьшение потенциала свиде­тельствует об увеличении электроемкости шара. Изменения потенциала и соответственно емкости будут наблюдаться в случае изменения расстояния между шаром и пла­стиной.

Таким образом, определяя емкость отдель­ного тела, необходимо учитывать размеще­ние всех окружающих тел.

Рис. 4.63. Влияние заземленной метал­лической пластины на емкость шара

Поскольку практически этого сделать не­возможно, то используют устройство, кото­рое называется конденсатором. Простейшей для изучения и расчетов является система из двух проводящих пластин, разделенных диэлектриком.

Конденсатор — это система из двух про­водников, разделенных диэлектриком.

Размеры этих пластин (длина и ширина) намного больше расстояния между ними. Электрические свойства такой системы про­водников не зависят от размещения окружа­ющих тел. Если пластинам сообщить разно­именные заряды, то они разместятся на внутренних поверхностях пластин вследст­вие взаимного притяжения.

Соответственно и поле заряженных пла­стин будет сосредоточено в пространстве между пластинами. Это можно объяснить на основе принципа суперпозиции полей.

На рис. 4.64 показана структура элект­рического поля пластины, заряженной поло­жительным зарядом. Силовые линии парал­лельные и направлены в противоположные от пластины направления.

Рис. 4.64. Электрическое поле положи­тельно заряженной металлической пла­стины

Рис. 4.65. Электрическое поле отрица­тельно заряженной металлической пла­стины

На рис. 4.65 — подобная структура элект­рического поля отрицательно заряженной пластины. Силовые линии параллельные, а направление — противоположное предшест­вующему (рис. 4.64).

Если пластины разместить на расстоянии d, намного меньшем, чем линейные разме­ры пластин, то в пространстве между ними силовые линии обеих пластин будут иметь одинаковое направление (рис. 4.66), а потому напряженность электрического поля бу­дет равна сумме напряженностей обоих полей:

E’ = Е₁ + E₂.

Вне пластин линии напряженности име­ют противоположное направление, а потому

E’ = E₁ — E₂.

Поскольку E₁ = E₂, то E’ = 0 (рис. 4.67). Материал с сайта http://worldofschool.ru

Рис. 4.66. Электрическое поле двух раз­ноименно заряженных пластин

Рис. 4.67. Напряженность электрического поля за пределами заряженного конден­сатора равна нулю

Конденсатор может накапливать значи­тельный заряд даже при небольшой раз­ности потенциалов между пластинами. В случае отдельного тела большой заряд со­здает большой потенциал, который приво­дит к автоэлектронной эмиссии или «стеканию зарядов».

Емкость конденсатора в отличие от ем­кости отдельного тела определяется разно­стью потенциалов между обкладками.

C = Q / (φ₁ — φ₂) = Q / Δφ.

где Q — заряд одной из пластин; (φ₁ — φ₂) — разность потенциалов между пластинами.

Для измерения емкости конденсатора ис­пользуется 1 фарад:

1Ф = 1 Кл/ 1 В.

На этой странице материал по темам:

• Почему емкость конденсатора не зависит от окружающих тел

• Конденсатор физические законы

• Почему емкость не зависит от окружающих тел

• Конденсатор физическое явление

• История развития конденсаторов

Вопросы по этому материалу:

• Как устроен конденсатор?

• Какое главное свойство конденсатора?

• Почему емкость конденсатора не зависит от влияния окружающих тел?

Конденсатор. Энергия электрического поля — материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах

.

Но прежде введём понятие электрической ёмкости.

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

(1)

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит

фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Ф.

Так легче запомнить, не правда ли?

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

или

(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

(6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

(8)

Соответственно, напряжение на конденсаторе:

(9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где — напряжённость поля первой обкладки:

Следовательно,

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

где

Это можно переписать следующим образом:

где

(12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

(13)

(14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но — объём конденсатора. Получаем:

(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

(17)

(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве

Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.

Проводники и диэлектрики в электростатическом поле

Вещества в природе можно разделить на проводники и диэлектрики.

Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.

Типичные проводники — металлы.

Диэлектрическая проницаемость вещества

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

Физическая величина, равная отношению модуля напряженности \(\vec{E}_0\) внешнего электрического поля в вакууме к модулю напряженности \(\vec{E}\) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества \(\varepsilon\).

\[\varepsilon=\dfrac{\vec{E}_0}{\vec{E}}\]

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда \(q\) одного из проводников к разности потенциалов \(\Delta \varphi\) между ними:

\[\fbox{$C=\dfrac{q}{\Delta \varphi}$}\]

Единицы измерения: \(\displaystyle [\text{Ф}]\) (фарад).

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.

Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

Разность потенциалов \(\Delta \varphi\) между пластинами в однородном электрическом поле равна \(Ed\), где \(d\) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

\[C=\dfrac{q}{\Delta \varphi}=\dfrac{\sigma S}{Ed}=\dfrac{\varepsilon_0S}{d}\]

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в \(\varepsilon\) раз:

\[\fbox{$C=\dfrac{\varepsilon_0\varepsilon S}{d}$}\]

Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

• Последовательное соединение конденсаторов

  При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

  Напряжение на данном участке цепи соотносятся следующим образом:

  \[\fbox{$U=U_1+U_2$}\]

  Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

  \[\dfrac{q}{C}=\dfrac{q}{C_1}+\dfrac{q}{C_2}\]

  Сократив выражение на \(Q\), получим формулу:

  \[\fbox{$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}$}\]

  Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

  \[\fbox{$C=\dfrac{C_1C_2}{C_1+C_2}$}\]

• Параллельное соединение конденсаторов

  При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

  Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

  \[\fbox{$q=q_1+q_2$}\]

  Так как заряд конденсатора

  \[q=CU\]

  А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

  \[CU=C_1U+C_2U\]

  \[\fbox{$C=C_1+C_2$}\]

• По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.

Вычислим эту энергию: начнём с плоского воздушного конденсатора.

Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора \(q\), площадь обкладок \(S\). Возьмём на второй обкладке настолько маленькую площадку, что заряд \(q_0\) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

\[F_0 = q_0E_1,\]

где \(E_1\) — напряжённость поля первой обкладки:

\[E_1=\dfrac{\sigma}{2\varepsilon_0}=\dfrac{q}{2\varepsilon_0S}\]

Значит

\[F_0=\dfrac{qq_0}{2\varepsilon_0S}\]

Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила \(F\) притяжения второй обкладки к первой складывается из всех этих сил \(F_0\), с которыми притягиваются к первой обкладке всевозможные маленькие заряды \(q_0\) второй обкладки. При этом суммировании постоянный множитель \(\displaystyle\dfrac{q}{2\varepsilon_0S}\) вынесется за скобку, а в скобке просуммируются все \(q_0\) и дадут \(q\).2}{2}$}, (3)\]

Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Виды конденсаторов, теория и примеры задач

Определение и основные виды конденсаторов

Любой конденсатор состоит из двух металлических обкладок, которые разделяет диэлектрик. Допустим, что обкладками конденсатора являются две замкнутые металлические оболочки: наружная и внутренняя. При этом внутренняя обкладка полностью окружена наружной. В таком случае электрическое поле внутри этой системы абсолютно не зависимо от внешних электрических полей. Заряды, распределенные по поверхностям данных обкладок, обращенных одна к другой по теореме Фарадея, будут равны по модулю и противоположны по знаку. Описанная выше картина для реального конденсатора является приближенной, так как его обкладки не являются полностью замкнутыми, однако, следует отметить, что приближение к идеальной картине довольно большое. На практике независимости внутреннего поля внутри конденсатора от внешних полей добиваются тем, что пластины конденсатора располагают на очень малом расстоянии. Тогда заряды будут находится на внутренних поверхностях обкладок.

Основной характеристикой конденсатора является его емкость (C):

   

q – заряд одной из обкладок конденсатора, – разность потенциалов между обкладками конденсатора. Емкость конденсатора – величина зависящая только от размеров, устройства конденсатора.

Конденсаторы делят по разным параметрам. Так, например, существуют:

1. Конденсаторы с постоянной и переменной емкостью и подстроечные.
2. Конденсаторы с различным типом диэлектрика (электролит, поликарбонат, воздух, тефлон и тд).
3. По типу материала корпуса: керамические, пластиковые, металлические.
4. В соответствии с геометрическим строением (плоские, цилиндрические, шаровые (сферические) конденсаторы).

Кроме этого конденсаторы можно разделить по их предназначению, способу монтажа (для печатного, навесного, поверхностного монтажа; с защелкивающимися выводами; выводами под винт), принципам защиты от внешних воздействий (с защитой и без нее; изолированные и неизолированные; уплотненные и герметизированные).

В задачах по общей физике рассматривают обычно три типа конденсаторов: плоские, цилиндрические и сферические. Кроме того могут варьироваться типы диэлектрика между обкладками.

Формулы емкости базовых видов конденсаторов

Емкость плоского конденсатора:

   

Емкость цилиндрического конденсатора:

   

где l – высота цилиндров; – радиус внешнего цилиндра; – радиус внутреннего цилиндра. По формуле (3) вычисляют емкость коаксиального кабеля.

Емкость сферического конденсатора:

   

где – радиусы обкладок конденсатора.

Примеры решения задач

Электроемкость конденсатора — формула и определение

Электроемкость проводников

Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.

Электроемкость C = q/φ С — электроемкость [Ф] q — электрический заряд [Кл] φ — потенциал [В]

Особенность этой величины в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости. Самая популярная — формула электроемкости шара.

Электроемкость шара C = 4πεε0r С — электроемкость [Ф] ε — относительная диэлектрическая проницаемость среды [-] ε0 — электрическая постоянная ε0 = 8,85 × 10-12 Ф/м r — радиус шара [м]

Конденсаторы

Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.

Конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.

Когда заряд накапливается на обкладках, происходит процесс под названием зарядка конденсатора. Заряды на разных обкладках равны по величине и противоположны по знаку.

Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:

Электроемкость конденсатора C = q/U С — электроемкость [Ф] q — электрический заряд [Кл] U — напряжение (разность потенциалов) [В]

По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.

Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо через диэлектрик. Такой конденсатор больше работать не будет.

Виды конденсаторов

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

Энергия электростатического поля Wp = qEd Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] E — напряженность электрического поля [В/м] d — расстояние от заряда [м]

В случае с конденсатором d будет представлять собой расстояние между пластинами.

Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

W_p = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

Поэтому:

W_p = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора Wp = qU/2 Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] U — напряжение на конденсаторе [В]

Энергия конденсатора Wp = q2/2C Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] C — электроемкость конденсатора [Ф]

Энергия конденсатора Wp = CU2/2 Wp — энергия электростатического поля [Дж] C — электроемкость конденсатора [Ф] U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Без него не будет работать ни один прибор. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Пример два — тачскрин

Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.

Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.

В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.

Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.

Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.

Виды конденсаторов и их применение презентация. Презентация по физике на тему «Конденсаторы. Электроемкость». Конденсаторы переменной электроемкости

Сформировать понятие электроемкости; Ввести новую характеристику – электроемкость конденсатора, и ее единицу измерения. Рассмотреть виды конденсаторов и где они применяются

Повторим… 1 вариант 1) Кем и когда была создана теория электромагнитного поля и в чем заключается ее суть. 2) Перечислите виды электромагнитных волн. Инфракрасное излучение, его свойства и влияние на организм человека. 2 вариант 1) Что называют электромагнитной волной?. Какими основными свойствами обладает электромагнитная волна? 2) Перечислите виды электромагнитных волн. Рентгенвоское излучение, его свойства и влияние на организм человека.

Конденсатор представляет собой два проводника, разделенные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Электроемкость конденсатора равна где q – заряд положительной обкладки, U – напряжение между обкладками. Электроемкость конденсатора зависит от его геометрической конструкции и электрической проницаемости заполняющего его диэлектрика и не зависит от заряда обкладок. Конденсатор

Электроёмкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между этим проводником и соседним. Единица измерения ёмкости – фарад – [ Ф ] Это надо знать:

Электроемкость плоского конденсатора равна где S– площадь каждой из обкладок, d– расстояние между ними, ε – диэлектрическая проницаемость вещества между обкладками. При этом предполагается, что геометрические размеры пластин велики по сравнению с расстоянием между ними. Запомните, что…

В настоящее время широко применяются бумажные конденсаторы для напряжений в несколько сот вольт и ёмкостью в несколько микрофарад. В таких конденсаторах обкладками служат две длинные ленты тонкой металлической фольги, а изолирующей прокладкой между ними – несколько более широкая бумажная лента, пропитанная парафином. Бумажной лентой покрывается одна из обкладок, затем ленты туго свёртываются в рулон и укладываются в специальный корпус. Такой конденсатор, имея размеры спичечного коробка, обладает ёмкостью 10мкФ (металлический шар такой ёмкости имел бы радиус 90км). Бумажный конденсатор

Керамический конденсатор В радиотехнике применяют керамические конденсаторы. Диэлектриком в них служит специальная керамика. Обкладки керамических конденсаторов изготавливаются в виде слоя серебра, нанесённого на поверхность керамики и защищённого слоем лака. Керамические конденсаторы изготавливаются на ёмкости о единиц до сотен пикофарад и на напряжения от сотен до тысяч вольт.

Запишите какова их электроемкость.

Слайд 14

Какова электроемкость конденсатора, если заряд конденсатора 10 нКл, а разность потенциалов 20 кВ. А теперь задача…

Слайд 15

Конденсатору емкостью 10 мкФ сообщили заряд 4 мкКл. Какова энергия заряженного конденсатора. А теперь задача…

Муниципальное автономное общеобразовательное учреждение

«Лицей № 7» г. Бердск

Конденсаторы

8 класс

Учитель физики

И.В.Торопчина

Конденсатор

Конденсатор- это устройство, предназначенное для накопления электрического заряда и энергии электрического поля.

Конденсатор

Конденсатор представляет собой два

проводника (обкладки), разделенных слоем

диэлектрика, толщина которого мала по

сравнению с размерами проводников.

Все электрическое поле сосредоточено внутри конденсатора и однородно.

Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.

— по виду диэлектрика : воздушные,

слюдяные, керамические,

электролитические. — по форме обкладок : плоские,

сферические, цилиндрические. — по величине емкости:

постоянные, переменные.

• В зависимости от назначения конденсаторы имеют различное устройство.

• Обычный технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свернуты в пакет небольшого размера

Конденсаторы переменной электроемкости

Обозначение конденсаторов

Конденсатор постоянной ёмкости

Конденсатор переменной ёмкости

Электроемкость

Физическая величина, характеризующая способность двух проводников накапливать электрический заряд называется электроёмкостью, или ёмкостью.

При увеличении заряда в 2, 3, 4 раза соответственно в 2, 3, 4

раза увеличатся показания электрометра, т. е. увеличится

напряжение между пластинами конденсатора.

Отношение заряда к напряжению будет оставаться

постоянным:

Электроёмкость конденсатора

• Величина, измеряемая отношением заряда ( q) одной из пластин конденсатора к напряжению ( U) между пластинами, называется электроёмкостью конденсатора .
• Электроёмкость конденсатора вычисляется по формуле:

C = q / U

Единицы электроемкости

Электроемкость измеряется в фарадах(Ф)

[ С ] = 1Ф (фарад)

Электроемкость двух проводников численно

равна единице, если при сообщении им зарядов

+1 Кл и -1 Кл между ними возникает разность

потенциалов 1В

1Ф = 1Кл/В

Единицы электроемкости

1 мкФ (микрофарад)=10 -6 Ф

1 нФ (нанофарад)=10 -9 Ф

1 пФ (пикофарад)=10 -12 Ф

• Чем больше площадь пластин, тем больше ёмкость конденсатора.
• При уменьшении расстояния между пластинами конденсатора при неизменном заряде ёмкость конденсатора увеличивается.
• При внесении диэлектрика ёмкость конденсатора увеличивается.

Емкость конденсатора зависит от площади пластин, расстояния между пластинами, от свойств внесённого диэлектрика.

Электроемкость

от геометрических

размеров проводников

Зависит

от формы проводников и

их взаимного расположения

от электрических свойств

среды между проводниками

Энергия конденсатора

• Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. В соответствии с законом сохранения энергии, совершённая работа А равна энергии конденсатора Е, т. е

А = Е,

где Е — энергия конденсатора.

• Работу электрическое поле конденсатора, можно найти по формуле: А = qU cp ,

где U ср — это среднее значение напряжения.

U ср = U/2; тогда А = qU ср = qU/2, так как q = CU, то А = CU 2 /2.

• Энергия конденсатора ёмкостью С равна:

W = CU 2 /2

• Конденсаторы могут длительное время накапливать энергию, а при разрядке они отдают её почти мгновенно.
• Свойство конденсатора накапливать и быстро отдавать электрическую энергию широко используется в электротехнических и электронных устройствах, в медицинской технике (рентгеновская техника, устройства электротерапии), при изготовлении дозиметров, аэрофотосъёмке.

• Лампа-вспышка питается электрическим током разрядки конденсатора.
• Газоразрядные трубки зажигаются при разрядки батареи конденсаторов.
• Радиотехника .

Первый конденсатор был изобретен в 1745 г. немецким юристом и учёным Эвальд Юрген фон Клейстом

Первый конденсатор: одна обкладка-ртуть, другая обкладка- рука экспериментатора, державшая банку.

• Почти такой же опыт и почти в то же время был поставлен в голландском городе Лейдене профессором университета Питером ван Мушенбруком.
• Зарядив воду и взяв банку в одну руку, он прикоснулся другой рукой к металлическому стержню, служившему для подвода заряда к воде. При этом Мушенбрук ощутил такой сильный удар в руки, плечи и грудь, что потерял сознание, и два дня приходил в себя.
• Эксперимент ван Мушенбрука получил большую известность, поэтому конденсатор стал известен как «лейденская банка».

Домашнее задание

§ 54, Упражнение 38

«Конденсатор физика» — Виды конденсаторов. — Бумажный конденсатор — слюдяной конденсатор электролитический конденсатор. Воздушный конденсатор. Соединения конденсаторов. — Воздушный конденсатор. Определение конденсатора. При подключении электролитического конденсатора необходимо соблюдать полярность. Назначение конденсаторов.

«Использование конденсаторов» — Опыты с конденсатором. Конденсатор используется в схемах зажигания. Формулы энергии. Применение конденсаторов. Особенности применения конденсаторов. Конденсатор используется в медицине. Светильники с разрядными лампами. Емкостная клавиатура. Конденсатор. Мобильные телефоны. Применяется в телефонии и телеграфии.

«Электроемкость и конденсаторы» — В клавиатуре компьютера. Конденсатор переменной емкости. Соединение конденсаторов. Электроемкость. Последовательное. Фотовспышки. Схемы соединения конденсаторов. Обозначение на электрических схемах: Конденсаторы. Электроемкость плоского конденсатора. Все электрическое поле сосредоточено внутри конденсатора.

«Применение конденсаторов» — Для аккумуляторов последних время регенерации принципиально важно. Полимерные конденсаторы с твёрдым электролитом на чипсете. Схема телефонного «жучка». Схема выпрямителя тока. Конденсатор CTEALTG STC — 1001. Микрофон конденсаторный. Удачная ассоциация есть на сайте Sciencentral. Студийный конденсаторный направленный микрофон широкого применения.

«Конденсатор» — Емкость конденсатора. Отношение заряда. Энергия конденсатора. Конденсатор переменной емкости. Бумажный конденсатор. Площадь. Конденсатор. Применение конденсаторов. Урок физики в 9 классе

Cлайд 1

Выполнил: Каретко Дима, ученик 10 «А» Руководитель: Попова Ирина Александровна, учитель физики Белово 2011 Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 30 г. Белово» Конденсаторы Миипроект по физике

Cлайд 2

План Введение Конденсаторы Основные параметры конденсатора Классификация конденсаторов Применение конденсаторов Вывод Литература

Cлайд 3

Введение Систему проводников очень большой электроемкости вы можете обнаружить в любом радиоприемнике или купить в магазине. Называется она конденсатором. Сейчас вы узнаете, как устроены подобные системы и от чего зависит их электроемкость.

Cлайд 4

Конденсаторы Конденсатор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля.

Cлайд 5

Основные параметры конденсатора: 1)Ёмкость: в обозначении конденсатора фигурирует ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость- определяет по электрическим свойствам. 2)Удельною емкостью называют отношением ёмкости к объёму (или массе) диэлектрика. 3) Номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. 4)Полярность: многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком.

Cлайд 6

Классификация конденсаторов Конденсаторы вакуумные (обкладки без диэлектрика находятся в вакууме). Конденсаторы с газообразным диэлектриком. Конденсаторы с жидким диэлектриком. Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические), слюдяные, тонкослойные из неорганических плёнок. Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные. Электролитические и оксидно-полупроводниковые конденсаторы (Такие конденсаторы отличаются от всех прочих типов прежде всего своей огромной удельной ёмкостью). Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости. Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости. Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке.

Cлайд 7

Применение конденсаторов Конденсаторы используются для построения различных цепей с частотно-зависимыми свойствами При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках. Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии. В промышленной электротехнике конденсаторы используются для компенсации реактивной мощности и в фильтрах высших гармоник. Измерительный преобразователь (ИП) малых перемещений: малое изменение расстояния между обкладками очень заметно сказывается на ёмкости конденсатора. ИП влажности воздуха (изменение состава диэлектрика приводит к изменению емкости) ИП влажности древесины В схемах РЗиА конденсаторы используются для реализации логики работы некоторых защит.

Конденсаторы и диэлектрики | Физика

Цели обучения

К концу этого раздела вы сможете:

• Опишите действие конденсатора и определите емкость.
• Объясните, что такое конденсаторы с параллельными пластинами и их емкости.
• Обсудите процесс увеличения емкости диэлектрика.
• Определите емкость при заданном заряде и напряжении.

Конденсатор — это устройство, используемое для хранения электрического заряда.Конденсаторы имеют различные применения: от фильтрации статического электричества при радиосигнале до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 1. (В большинстве случаев между двумя пластинами используется изолятор для обеспечения разделения — см. Обсуждение диэлектриков ниже). Клеммы батареи подключены к первоначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, + Q и — Q , разделены на его две пластины.Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд Q .

Рис. 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них есть разделенные заряды + Q и — Q на своих двух половинах. (а) Конденсатор с параллельными пластинами. (b) Скрученный конденсатор с изоляционным материалом между двумя проводящими листами.

Конденсатор

Конденсатор — это устройство, используемое для хранения электрического заряда.

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Q конденсатор может хранить

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Рис. 2. Линии электрического поля в этом конденсаторе с параллельными пластинами, как всегда, начинаются с положительных зарядов и заканчиваются отрицательными.Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для конденсатора с параллельными пластинами, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поля будет больше. линии, если есть больше заряда.(Рисование одной силовой линии для каждого заряда — это только удобство. Мы можем нарисовать много силовых линий для каждого заряда, но их общее количество пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна Ом. .

Поле пропорционально начислению:

E ∝ Q ,

, где символ ∝ означает «пропорционально». Из обсуждения в разделе «Электрический потенциал в однородном электрическом поле» мы знаем, что напряжение на параллельных пластинах равно

.

V = Ed .

Таким образом, V ∝ E . Отсюда следует, что V ∝ Q , и, наоборот,

Q ∝ V .

В целом это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.

Различные конденсаторы будут накапливать разное количество заряда для одного и того же приложенного напряжения, в зависимости от их физических характеристик. Мы определяем их емкость C так, чтобы заряд Q , хранящийся в конденсаторе, был пропорционален C .Заряд, накопленный в конденсаторе, равен

.

Q = CV .

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Переставляя уравнение, мы видим, что емкость C — это количество заряда, сохраненного на вольт, или

.

[латекс] C = \ frac {Q} {V} \\ [/ latex].

Емкость

Емкость C — это количество хранимого заряда на вольт, или

[латекс] C = \ frac {Q} {V} \\ [/ latex]

Единица измерения емкости — фарад (Ф), названная в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

.

[латекс] 1 \ text {F} = \ frac {1 \ text {C}} {1 \ text {V}} \\ [/ latex].

Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольт. Таким образом, одна фарада — это очень большая емкость. Типичные конденсаторы варьируются от долей пикофарада (1 пФ = 10 ⁻¹² Ф) до миллифарадов (1 мФ = 10 ⁻³ Ф).

На рисунке 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типичные конденсаторы. Размер и значение емкости не обязательно связаны. (Источник: Windell Oskay)

Конденсатор с параллельными пластинами

Рис. 4. Конденсатор с параллельными пластинами, разделенные пластинами на расстояние d. Каждая пластина имеет площадь A.

Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A, , разделенных расстоянием d (без материала между пластинами).Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость зависит от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, в отличие от зарядов притягиваются, и сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут расходиться больше. Таким образом, C должен быть больше для большего A .Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Значит, C должно быть больше для меньшего d .

Можно показать, что для конденсатора с параллельными пластинами есть только два фактора ( A, и d ), которые влияют на его емкость C . Емкость конденсатора с параллельными пластинами в форме уравнения равна

.

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].

Емкость параллельного пластинчатого конденсатора

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex]

A — это площадь одной пластины в квадратных метрах, а d — это расстояние между пластинами в метрах.Константа ε ₀ — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε ₀ = 8,85 × 10 ⁻¹² Ф / м. Единицы измерения Ф / м эквивалентны C ² / Н · м ² . Небольшое числовое значение ε ₀ связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фараду. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как обсуждается ниже.)

Пример 1. Емкость и заряд в параллельном пластинчатом конденсаторе

1. Какова емкость конденсатора с параллельными пластинами, каждая из которых имеет площадь 1,00 м ² , разделенных расстоянием 1,00 мм?
2. Какой заряд сохраняется в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 ³ В?

Стратегия

Определение емкости C представляет собой прямое приложение уравнения [латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].{-9} \ text {F} = 8.85 \ text {nF} \ end {array} \\ [/ latex]

Обсуждение части 1

Это небольшое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонких пленок очень большой площади, расположенных близко друг к другу.

Решение для Части 2

Заряд любого конденсатора определяется уравнением Q = CV . Ввод известных значений в это уравнение дает

[латекс] \ begin {array} {lll} Q & = & CV = \ left (8.{3} \ text {V} \ right) \\\ text {} & = & 26.6 \ mu \ text {C} \ end {array} \\ [/ latex]

Обсуждение части 2

Этот заряд лишь немного больше, чем у обычного статического электричества. Поскольку воздух разрывается при примерно 3,00 × 10 ⁶ В / м, на этом конденсаторе не может быть накоплено больше заряда за счет увеличения напряжения.

Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам выборочно входить и выходить из клетки.Существует разность потенциалов на мембране около –70 мВ. Это связано с преобладанием отрицательно заряженных ионов в клетке и преобладанием положительно заряженных ионов натрия (Na ⁺ ) снаружи. Все меняется, когда нервная клетка стимулируется. Ионы Na ⁺ проходят через мембрану в клетку, создавая положительный мембранный потенциал — нервный сигнал. Клеточная мембрана имеет толщину от 7 до 10 нм. {6} \ text {V / m} \\ [/ latex]

Этого электрического поля достаточно, чтобы вызвать пробой в воздухе.

Диэлектрик

Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если d сделать меньше, чтобы обеспечить большую емкость, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс] E = \ frac {V} {d} \\ [/ latex]). Важным решением этой проблемы является размещение изоляционного материала, называемого диэлектриком , между пластинами конденсатора и обеспечение минимально возможного размера d .Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем сломаться.

Есть еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем заданная уравнением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], на коэффициент κ , называемый диэлектрическая проницаемость . Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, равную [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex] (конденсатор с параллельными пластинами с диэлектриком).

Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума равно 1, поэтому приведенное выше уравнение справедливо и в этом случае. Если использовать диэлектрик, например, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в κ раз, что для тефлона составляет 2,1.

Эксперимент на вынос: создание конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут из алюминиевой фольги, а разделитель (диэлектрик) между ними — из бумаги.

Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC
Материал	Диэлектрическая проницаемость κ	Электрическая прочность (В / м)
Вакуум	1,00000	–
Воздух	1.00059	3 × 10 6
Бакелит	4,9	24 × 10 6
Плавленый кварц	3.78	8 × 10 6
Неопреновый каучук	6,7	12 × 10 6
Нейлон	3,4	14 × 10 6
Бумага	3,7	16 × 10 6
Полистирол	2,56	24 × 10 6
Стекло Pyrex	5,6	14 × 10 6
Кремниевое масло	2.5	15 × 10 6
титанат стронция	233	8 × 10 6
Тефлон	2,1	60 × 10 6
Вода	80	–

Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится равной. слишком большой.(Напомним, что [латекс] E = \ frac {V} {d} \\ [/ latex] для конденсатора с параллельными пластинами.) Также в таблице 1 показаны максимальные напряженности электрического поля в В / м, которые называются диэлектрической прочностью , для нескольких материалов. Это поля, над которыми материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного расстояния между пластинами. 6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]

Однако предел для расстояния 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку диэлектрическая прочность тефлона составляет 60 × 10 ⁶ В / м. Таким образом, тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для конденсатора с параллельными пластинами, заполненного воздухом, мы обнаружили, что конденсатор с тефлоновым заполнением может хранить максимальный заряд

[латекс] \ begin {array} {lll} Q & = & CV \\\ text {} & = & \ kappa {C} _ {\ text {air}} V \\\ text {} & = & (2.4 \ text {V}) \\\ text {} & = & 1.1 \ text {mC} \ end {array} \\ [/ latex]

Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.

Диэлектрическая прочность

Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется его диэлектрической прочностью.

Микроскопически, как диэлектрик увеличивает емкость? За это отвечает поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .Вода, например, представляет собой полярную молекулу и , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды обуславливает ее относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации лучше всего объясняется характеристиками кулоновской силы. На рис. 5 схематично показано разделение зарядов в молекулах диэлектрического материала, помещенных между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень сильна, поскольку они расположены очень близко друг к другу.Это притягивает больше заряда к пластинам, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии d друг от друга.

Рис. 5. (a) Молекулы изоляционного материала между пластинами конденсатора поляризованы заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда на пластину, увеличивая ее емкость. (б) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к уменьшению напряжения между пластинами при одинаковом заряде.Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — это рассмотреть его влияние на электрическое поле внутри конденсатора. На рисунке 5 (b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются зарядами в диэлектрике, их меньше, идущих от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, даже если бы на пластинах был одинаковый заряд.Напряжение между пластинами составляет В, = Ед, , поэтому оно тоже снижается за счет диэлектрика. Таким образом есть меньшее напряжение В, для того же заряда Q ; поскольку [латекс] C = \ frac {Q} {V} \\ [/ latex], емкость C больше.

Диэлектрическая проницаемость обычно определяется как [латекс] \ kappa = \ frac {E_0} {E} \\ [/ latex], или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и в конечном итоге связанных с поляризуемостью материала.

Великие и малые вещи: субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома описывает его как имеющее положительное ядро, вращающееся вокруг отрицательных электронов, аналогично планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.

Рис. 6. Художественное представление о поляризованном атоме. Орбиты электронов вокруг ядра слегка смещены внешними зарядами (показаны в преувеличении). Получающееся разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что непохожий заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью обнаружения электрона в этом месте (в отличие от определенных положений и путей движения планет на их орбитах). вокруг Солнца).Это облако сдвигается кулоновской силой, так что в среднем атом имеет разделенный заряд. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому они называются полярными молекулами. На рисунке 7 показано разделение зарядов в молекуле воды, которая имеет два атома водорода и один атом кислорода (H ₂ O).Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец — слегка положительным. Внутреннее разделение зарядов в полярных молекулах облегчает их выравнивание с внешними полями и зарядами. Следовательно, полярные молекулы обладают более сильными поляризационными эффектами и имеют более высокие диэлектрические проницаемости.Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов, чтобы притягивать заряды обоих знаков. Кроме того, как было показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рис. 7. Художественная концепция молекулы воды. Существует внутреннее разделение зарядов, поэтому вода — полярная молекула.Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда около двух ядер водорода. (Обратите внимание, что схема справа является приблизительной иллюстрацией распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

Исследования PhET: лаборатория конденсаторов

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.Измените напряжение и посмотрите, как на пластинах накапливаются заряды. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

• Конденсатор — это устройство для накопления заряда.
• Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
• Емкость C, — это количество заряда, накопленного на вольт, или [латекс] C = \ frac {Q} {V} \\ [/ latex].
• Емкость конденсатора с параллельными пластинами составляет [латекс] C = {\ epsilon} _ {0} \ frac {A} {d} \\ [/ latex], когда пластины разделены воздухом или свободным пространством. [latex] {\ epsilon} _ {\ text {0}} [/ latex] называется диэлектрической проницаемостью свободного пространства.
• Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], где κ — диэлектрик. постоянная материала.
• Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется электрической прочностью.

Концептуальные вопросы

1. Зависит ли емкость устройства от приложенного напряжения? А как насчет хранящегося в нем заряда?
2. Используйте характеристики кулоновской силы, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Аналогичным образом объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
3. Объясните причину, по которой диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора.Какова независимая причина того, что диэлектрический материал также позволяет приложить большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает большее значение V .)
4. Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. Рисунок 7.)
5. Искры возникают между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем когда сухой. Объясните почему, учитывая полярный характер молекул воды.
6. Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
7. Мембраны в живых клетках, в том числе в человеческих, характеризуются разделением заряда через мембрану. Таким образом, мембраны представляют собой заряженные конденсаторы, важные функции которых связаны с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизм пищевой энергии или каким-либо другим источником?

Рисунок 8.Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K ⁺ (калий) и Cl ^— (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na ⁺ (ионы натрия).

Задачи и упражнения

1. Какой заряд сохраняется в конденсаторе 180 мкФ, когда к нему приложено 120 В?
2. Найдите накопленный заряд, когда 5.50 В подается на конденсатор емкостью 8,00 пФ.
3. Какой заряд хранится в конденсаторе в Примере 1?
4. Рассчитайте напряжение, приложенное к конденсатору 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
5. Какое напряжение необходимо подать на конденсатор емкостью 8,00 нФ, чтобы накопить заряд 0,160 мкКл?
6. Какая емкость необходима для хранения заряда 3,00 мкКл при напряжении 120 В?
7. Какая емкость терминала большого генератора Ван-де-Граафа, учитывая, что он хранит 8?00 мкКл заряда при напряжении 12,0 МВ?
8. Найдите емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 5,00 м ² , разделенных слоем тефлона 0,100 мм.
9. (a) Какова емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 1,50 м ² , разделенных 0,0200 мм неопреновой резины? (b) Какой заряд он держит, когда к нему приложено 9,00 В?
10. Интегрированные концепции. Шутник подает 450 В на 80.Конденсатор 0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обгорел от разряда конденсатора через 0,200 г мяса. Какое повышение температуры мяса? Разумно ли предполагать отсутствие изменения фазы?
11. Необоснованные результаты. (a) Определенный конденсатор с параллельными пластинами имеет пластины площадью 4,00 м ² , разделенные 0,0100 мм нейлона, и накапливает 0,170 Кл заряда. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие допущения являются ответственными или противоречивыми?

Глоссарий

конденсатор: устройство, накапливающее электрический заряд

емкость: количество заряда на единицу вольт

диэлектрик: изоляционный материал

диэлектрическая прочность: максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить

Конденсатор с параллельными пластинами: две идентичные проводящие пластины, разделенные расстоянием

полярная молекула: молекула с внутренним разделением заряда

Избранные решения проблем и упражнения

1.21,6 мК

3. 80.0 мС

5. 20,0 кВ

7. 667 пФ

9. (а) 4,4 мкФ; (б) 4.0 × 10 ⁻⁵ C

11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз выше напряжения пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.

Что такое емкость? | Fluke

Емкость — это способность компонента или схемы собирать и накапливать энергию в виде электрического заряда.

Конденсаторы — это устройства накопления энергии, доступные во многих размерах и формах. Они состоят из двух пластин из проводящего материала (обычно тонкого металла), зажатых между изолятором из керамики, пленки, стекла или других материалов, даже воздуха.

Изолятор, также известный как диэлектрик , увеличивает зарядную емкость конденсатора. Конденсаторы иногда называют конденсаторами в автомобильной, морской и авиационной промышленности.

Внутренние пластины подключены к двум внешним клеммам, которые иногда бывают длинными и тонкими и могут напоминать крошечные металлические антенны или ножки.Эти клеммы можно включить в цепь.

Конденсаторы и батареи накапливают энергию. В то время как батареи выделяют энергию постепенно, конденсаторы разряжают ее быстро.

Как работает конденсатор?

Конденсатор собирает энергию (напряжение), когда ток течет по электрической цепи. Обе пластины содержат одинаковые заряды, и когда положительная пластина накапливает заряд, равный заряд стекает с отрицательной пластины.

Когда цепь отключена, конденсатор сохраняет собранную энергию, хотя обычно происходит небольшая утечка.

Различные конденсаторы (показаны цветом) в печатной плате.

Емкость выражается как отношение электрического заряда на каждом проводе к разности потенциалов (т. Е. Напряжению) между ними.

Значение емкости конденсатора измеряется в фарадах (Ф), единицах, названных в честь английского физика Майкла Фарадея (1791–1867).

Фарад — это большая емкость. Большинство бытовых электрических устройств содержат конденсаторы, которые производят только доли фарада, часто тысячные доли фарада (или микрофарады, мкФ) или даже пикофарады (триллионные доли, пФ).

Суперконденсаторы, тем временем, могут хранить очень большие электрические заряды в тысячи фарад.

Как увеличить емкость

Емкость можно увеличить, если:

• Пластины (проводники) конденсатора расположены ближе друг к другу.
• Пластины большего размера обеспечивают большую площадь поверхности.
• Диэлектрик — лучший изолятор для данной области применения.

Конденсаторы бывают разных форм.

В электрических цепях конденсаторы часто используются для блокировки постоянного тока (dc), позволяя протекать переменному току (ac).

Некоторые цифровые мультиметры предлагают функцию измерения емкости, поэтому технические специалисты могут:

• Определить неизвестный или немаркированный конденсатор.
• Обнаружение обрыва или короткого замыкания конденсаторов.
• Измерьте конденсаторы напрямую и отобразите их значение.

Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.

Конденсатор — Конструкция и работа

Что такое конденсатор?

Конденсаторы

являются наиболее широко используемыми электронные компоненты после резисторов.Мы находим конденсаторы в телевизорах, компьютерах и во всех электронных устройствах. схемы. Конденсатор — это электронное устройство, которое хранит электрический заряд или электричество при подаче напряжения и при необходимости высвобождает накопленный электрический заряд.

Конденсатор действует как небольшая батарея, которая быстро заряжается и разряжается. Любой объект, на котором можно хранить электрический заряд, представляет собой конденсатор.Конденсатор тоже иногда называется конденсатор.

Что такое электрический заряд?

Электрический заряд — основное свойство частицы, такие как электроны и протоны. Этот электрический заряд заставляет их испытывать притягательную или отталкивающую силу, когда помещен в электромагнитное поле.

Электрические заряды бывают двух типов: положительные. и отрицательный.Электроны имеют отрицательный заряд, а протоны имеют отрицательный заряд. положительный заряд.

Как гравитационная энергия, присутствующая вокруг планет, таких как Земля, электрическая энергия присутствует вокруг заряженные частицы, такие как электроны и протоны. Однако заряженные частицы проявляют силу только на небольшом расстоянии вокруг их и сверх того они не могут применить силу. Область до сила, действующая на заряженные частицы, называется электрической поле.Если мы поместим любую заряженную частицу внутрь этого регион, он испытает силу. Эта сила может быть отталкивающей или притягательной.

Электроэнергия или электрический заряд присутствующий вокруг заряженной частицы представлен электрическим силовые линии. Направление этих электрических линий сила различна для положительного и отрицательного заряда. Для положительный заряд, электрические силовые линии начинаются от центр заряженной частицы и улетает от него.Для отрицательный заряд, электрические силовые линии начинаются вдали от заряженная частица и движется к ее центру. В В электронике дырка считается положительным зарядом.

Когда отрицательно заряженная частица (электрон) находится в электрическом поле положительно заряженного частица (протон), она притягивается. С другой стороны, когда положительно заряженная частица (протон) помещается в электрическое поле другого протона, он отталкивается.В простом словами, противоположные электрические заряды притягиваются друг к другу и одинаковы электрические заряды отталкивают друг друга.

Строительство конденсатора

Базовая конструкция всех конденсаторов похожий. Конструкция конденсатора очень проста. А Конденсатор состоит из двух электропроводящих пластин, размещенных близко друг к другу, но не касаются друг друга.Эти токопроводящие пластины обычно изготавливаются из таких материалов, как алюминий, латунь или медь.

Проводящие пластины конденсатора разделены небольшим расстоянием. Пустое пространство между этими пластины заполнены непроводящим материалом или электрическим изолятор или диэлектрическая область. Непроводящий материал или область между двумя пластинами может быть воздухом, вакуумом, стеклом, жидкий или твердый.Этот непроводящий материал называется диэлектрик.

Две токопроводящие пластины конденсатора хорошие проводники электричества. Поэтому они легко могут пропускают через них электрический ток. Электропроводящие пластины конденсатор также удерживает электрический заряд. В конденсаторах эти пластины в основном используются для удержания или хранения электрических плата.

Плохой диэлектрический материал или среда проводник электричества. Они не могут пропускать электрический ток через них. В конденсаторах диэлектрическая среда или материал блокировать поток носителей заряда (особенно электронов) между проводящие пластины. В результате электрические заряды, которые попытаться перейти с одной пластины на другую пластина будет в ловушке внутри пластины из-за сильного сопротивления со стороны диэлектрик.

Если поместить проводящую среду между эти пластины, электрические заряды легко перетекают от одной пластины к другая тарелка. Однако между пластинами течет электрический ток. не желательно. Это указывает на выход из строя конденсатора.

Мы знаем, что электрический ток — это поток носителями заряда, тогда как электрическая сила или электрическое поле являются свойство электрических зарядов.Диэлектрический материал не позволяет поток носителей заряда, но они допускают электрическую силу, электрический заряд или электрическое поле, создаваемое заряженным частицы (электроны). В результате при накоплении заряда на две пластины, сильное электрическое поле создается между две тарелки.

Как конденсатор работает?

Конденсатор без источника напряжения

Когда на конденсатор не подается напряжение, общее количество электронов и протонов в левой пластине конденсатор равны.Мы знаем, что любой объект, имеющий равное количество электронов и протонов считается электрически нейтральный. Следовательно, полный заряд левой пластины компенсирует и становится электрически нейтральным. Следовательно, левая пластина конденсатор называется электрической нейтралью.

С другой стороны, правая пластина также имеет равное количество электронов и протонов.Таким образом, общая заряд правой пластины отменяется и становится электрически нейтральный.

Отсутствие электрического заряда означает отсутствие электрического поля. Следовательно, конденсатор не накапливает заряд при отсутствии напряжения. применяется.

Зарядка конденсатор

Заряд будет построен на объекте, имеющем избыточное количество электронов или протонов.Чтобы произвести избыточное количество электронов или протонов, нам нужно подать напряжение на конденсатор.

Когда напряжение подается на конденсатор таким образом, чтобы положительный полюс аккумуляторной батареи подключен к левой стороне пластина конденсатора и отрицательный вывод аккумуляторной батареи подключен к правой боковой пластине конденсатора, происходит зарядка конденсатора.

Из-за этого напряжения питания большой количество электронов начинают двигаться от отрицательной клеммы аккумулятор через токопроводящий провод. Когда эти электроны достигают правой боковой пластины конденсатора, они испытывают сильное сопротивление диэлектрического материала. Диэлектрик материал или среда, присутствующие между пластинами, будут сильно противодействовать движению электронов с правой боковой пластины.Как в результате большое количество электронов захватывается или накапливается на правая боковая пластина конденсатора.

Из-за накопления избыточных электронов извне количество электронов (отрицательных носителей заряда) на правой боковой пластине станет больше, чем количество протоны (носители положительного заряда). В итоге правая сторона пластина конденсатора заряжается отрицательно.

С другой стороны, электроны слева боковая пластина испытывает сильную притягивающую силу от положительный полюс аккумуляторной батареи. В результате электроны оставьте левую боковую пластину и привлечете или переместите в сторону положительный полюс аккумуляторной батареи.

Отрицательный заряд на правой стороне пластина создает сильное отрицательное электрическое поле.Этот сильный отрицательное электрическое поле также толкает подобные заряды или электроны на левой пластине.

Из-за потери большого количества электронов с левой боковой пластины, количество протонов (носителей положительного заряда) станет больше, чем количество электроны (носители отрицательного заряда). В результате левая сторона пластина конденсатора заряжается положительно.Таким образом, оба проводящие пластины конденсатора заряжены.

Положительный и отрицательный заряды на обоих пластины оказывают друг на друга силу. Однако они не трогают друг с другом.

Из-за избыточного количества электронов на одна пластина и нехватка электронов на другой пластине, разность потенциалов или напряжение устанавливается между тарелки.Как конденсатор продолжает заряжаться, напряжение между пластинами увеличивается.

Напряжение между пластинами противостоит источнику напряжения. В результате, когда конденсатор полностью заряжен (напряжение между пластинами равно источнику напряжение) конденсатор перестает заряжаться. Потому что на данный момент энергия напряжения источника и напряжение конденсатора равны равный.В результате электроны или электрическое поле справа боковая пластина отталкивает электроны, идущие от источника напряжения.

Поэтому для дальнейшей зарядки конденсатора нам нужно увеличить напряжение на более высокий уровень. Когда напряжение подается на конденсатор повышен до более высокого уровня. Зарядка снова начинается наращивая проводящие пластины конденсатора, пока он выходит на новый уровень напряжения.Когда напряжение между пластины достигают нового уровня напряжения источника, он снова останавливается зарядка. Конденсаторы

спроектированы и изготовлены для работают при определенном максимальном напряжении. Если напряжение приложено к конденсатор превышает максимальное напряжение, электроны начинают перемещение между пластинами. Это приведет к необратимому повреждению конденсатора.

Разрядка конденсатор

Если внешний источник напряжения подключен к конденсатор удаляется, конденсатор остается заряженным.Однако, когда конденсатор подключен к любому электрическому устройству например, электрическая лампочка через проводящий провод, он запускается разрядка.

Когда конденсатор подключен к электрическая лампочка через проводящий провод, электроны захвачены на правой боковой пластине начинает протекать контур. Мы знать, что электрический ток — это поток носителей заряда (бесплатно электроны).Следовательно, когда свободные электроны или электрические ток достигает лампочки, она светится с большой силой.

Электроны, которые начали вытекать из правая боковая пластина через проводящий провод, наконец, достигла левую боковую пластину и заполните отверстия левой боковой пластины. Как В результате заряд на левой боковой пластине и правой боковой пластине начинает уменьшаться.Это снижает интенсивность электрического лампочку, потому что электрический ток, протекающий через электрическую лампочка уменьшается.

Наконец, заряд хранится на левой пластине и правая пластина полностью освобождается. В результате лампочка выключится, потому что электрический ток не течет через лампочка. Таким образом, заряд хранится на левой пластине, а на правой. пластина конденсатора разряжена.

Конденсатор условное обозначение

Обозначение схемы основного конденсатора: показано на рисунке ниже. Обозначение конденсатора представлено проведя две параллельные линии близко друг к другу, но не трогательно. Он состоит из двух терминалов. Эти терминалы используются подключить в схему.

Емкость

Способность конденсатора накапливать электрическую заряд называется емкостью.Конденсаторы с большой емкостью будет хранить большое количество электрического заряда, тогда как конденсаторы с низкой емкостью сохранят небольшое количество электрический заряд.

Емкость конденсатора может быть по сравнению с размером резервуара для воды: чем больше объем воды резервуар, тем больше воды он может вместить. Аналогичным образом чем больше емкость, тем больше электрического заряда или электричества он может хранить.

Емкость конденсатора в основном зависит от размера пластин, обращенных друг к другу, расстояние между двумя проводящими пластинами, а диэлектрическая проницаемость материал между пластинами.

Емкость конденсатора напрямую пропорционально размеру токопроводящих пластин и обратно пропорционально пропорционально расстоянию между двумя пластинами.

Иными словами, конденсатор с большой проводящие пластины хранят большое количество электрического заряда, тогда как конденсатор с небольшими токопроводящими пластинами накапливает небольшое количество электрического заряда. С другой стороны, конденсатор с большой расстояние между пластинами имеет низкую емкость (малая накопитель заряда), тогда как конденсатор с малым разделением расстояние между пластинами имеет высокую емкость (высокий заряд место хранения).

Емкость конденсатора измеряется в фарад. Он представлен символом Ф. Фарад назван в честь Английский физик Майкл Фарадей. Заряженный конденсатор емкостью 1 фарад с 1 кулоном электрического заряда имеет разность потенциалов или напряжение между его пластинами 1 вольт.

Один фарад — очень большая сумма емкость. Следовательно, в большинстве случаев мы используем очень маленькую единицу емкость.Наиболее распространенные единицы емкости, которые мы используем сегодня микрофарады (мкФ), нано фарад (нФ), пикофарад (пФ) и фемофарад (фФ).

1 микрофарад = 10 ^-6 фарад

1 нанофарад = 10 ^-9 фарад

1 пикофарад = 10 ^-12 фарад

1 фемофарад = 10 ^-15 фарад

Заряд на конденсаторе

Электрический заряд, накопленный конденсатором. зависит от напряжения, приложенного к конденсатору.

Если на конденсатор подается высокое напряжение, большой заряд передается пластинам конденсатора. В результате конденсатор накапливает большой заряд.

С другой стороны, если применяется низкое напряжение на конденсатор передается только небольшой заряд к обкладкам конденсатора. В результате конденсатор хранит только небольшая сумма заряда.Однако емкость конденсатор остается постоянным. Мы не можем увеличить емкость конденсатора.

Взаимосвязь заряда, напряжения и емкость можно математически записать в трех формах:

Конденсаторы Physics A-Level

Изучив этот раздел, вы должны уметь:

• описать действие конденсатора и рассчитать накопленный заряд
• Свяжите энергию, запасенную в конденсаторе, с графиком зависимости заряда от напряжения
• объясните значение постоянной времени цепи, содержащей конденсатор и резистор

В этом разделе рассматриваются следующие темы

Действие конденсатора

Конденсаторы накапливают заряд и энергию.У них есть много применений, включая сглаживание переменных постоянных токов, электронные схемы синхронизации и питание памяти для хранения информации в калькуляторах, когда они выключены.

Конденсатор состоит из двух параллельных проводящих пластин, разделенных изолятором.

Когда он подключен к источнику напряжения, заряд течет на пластины конденсатора до тех пор, пока разность потенциалов на них не станет такой же, как у источника питания. Поток заряда и окончательный заряд на каждой пластине показаны на диаграмме.

Когда конденсатор заряжается, заряд протекает во всех частях цепи, кроме между пластинами.

По мере заряда конденсатора:

• заряд –Q течет на пластину, подключенную к отрицательной клемме источника питания
• заряд –Q стекает с пластины, подключенной к положительному выводу источника питания, оставляя на ней заряд + Q
• пластины конденсатора всегда имеют одинаковое количество заряда, но противоположного знака
• между пластинами конденсатора не течет заряд.

Емкость

Считается, что конденсатор, показанный на диаграмме выше, накапливает заряд Q, что означает, что это количество заряда на каждой пластине. Когда конденсатор заряжен, величина накопленного заряда зависит от:

• напряжение на конденсаторе
• его емкость: то есть чем больше емкость, тем больше заряда сохраняется при заданном напряжении.

КЛЮЧЕВЫЙ МОМЕНТ — Емкость конденсатора C определяется как: где Q — это заряд, накопленный, когда напряжение на конденсаторе равно V.Емкость измеряется в фарадах (Ф). 1 фарад — это емкость конденсатора, который накапливает 1 Кл заряда, когда п.д. поперёк — 1 В.

Поскольку обкладки конденсатора имеют одинаковое количество заряда противоположного знака, общий заряд фактически равен нулю. Однако, поскольку заряды разделены, они обладают энергией и могут работать, когда собраны вместе.

Один фарад — очень большое значение емкости. Общие значения емкости обычно измеряются в пикофарадах (1 пФ = 1.0 × 10 ^–12 F) и микрофарад (1 мкФ = 1,0 × 10 ^–6 F).

Конденсаторы комбинированные

Подобно резисторам, конденсаторы можно подключать последовательно или параллельно для достижения различных значений емкости.

При последовательном подключении конденсаторов к источнику напряжения:

• независимо от того, каково значение его емкости, каждый конденсатор в комбинации хранит одинаковое количество заряда, поскольку любая пластина может только терять или получать заряд, полученный или потерянный пластиной, к которой она подключена
• общий заряд, накопленный последовательной комбинацией, является зарядом на каждой из двух внешних пластин и равен заряду, накопленному на каждом отдельном конденсаторе
• поскольку приложенная разность потенциалов распределяется между конденсаторами, общий накопленный заряд меньше, чем заряд, который мог бы накапливать любой из конденсаторов, индивидуально подключенных к источнику напряжения.

Последовательное добавление конденсаторов приводит к уменьшению емкости. При добавлении дополнительного конденсатора p.d. меньше. по каждому из них сохраняется меньше заряда.

На схеме показан заряд пластин трех последовательно соединенных конденсаторов.

Это приводит к тому, что эффективное значение последовательной комбинации конденсаторов меньше, чем конденсатор наименьшего номинала в комбинации.

КЛЮЧЕВЫЙ МОМЕНТ — Емкость C ряда конденсаторов, соединенных последовательно, определяется выражением:

Распространенной ошибкой при использовании этого отношения является то, что забывают выполнить окончательный ответ, давая ответ, равный 1 / C вместо C.

В отличие от этого, эффект параллельного соединения конденсаторов заключается в увеличении емкости, так что эффективное значение количества конденсаторов, подключенных параллельно, всегда больше, чем наибольшее значение комбинации.

При параллельном подключении конденсаторов:

• все конденсаторы заряжены до одинаковой разности потенциалов
• каждый конденсатор сохраняет такое же количество заряда, как если бы он был подключен сам по себе к тому же напряжению
• добавление дополнительного конденсатора увеличивает общий накопленный заряд.

КЛЮЧЕВЫЙ МОМЕНТ — Емкость C нескольких конденсаторов, подключенных параллельно, определяется выражением: C = C ₁ + C ₂ + C ₃

Выражения для конденсаторов, соединенных последовательно и параллельно, аналогичны выражениям для резисторов, но наоборот.

Энергия, запасенная в конденсаторе

Для зарядки конденсатора необходима энергия от источника питания или другого источника.Заряженный конденсатор может поставлять энергию, необходимую для поддержания памяти в калькуляторе или тока в цепи, когда напряжение питания слишком низкое.

Количество энергии, хранящейся в конденсаторе, зависит от:

• количество заряда на обкладках конденсатора
• напряжение, необходимое для размещения этого заряда на пластинах конденсатора, то есть емкость конденсатора.

График ниже показывает, как напряжение на пластинах конденсатора зависит от накопленного заряда.

Когда к конденсатору добавляется заряд ΔQ при разности потенциалов V, выполняемая работа равна ΔQV. Общая работа, выполняемая при зарядке конденсатора, составляет ΣΔQV.

Заштрихованная область между линией графика и осью заряда представляет энергию, запасенную в конденсаторе.

КЛЮЧЕВЫЙ ТОЧЕК — Энергия E, запасенная в конденсаторе, определяется выражением E = ½ QV = ½ CV ² где Q — заряд накапливается на конденсаторе емкости C, когда напряжение на нем равно V.

Зарядка и разрядка конденсатора

Когда конденсатор заряжается путем прямого подключения к источнику питания, в цепи очень мало сопротивления, и кажется, что конденсатор заряжается мгновенно. Это потому, что процесс происходит за очень короткий промежуток времени.

Установка резистора в цепь зарядки замедляет процесс. Чем больше значения сопротивления и емкости, тем больше времени требуется для зарядки конденсатора.

На приведенной ниже диаграмме показано, как ток изменяется со временем при зарядке конденсатора.

Наличие резистора в цепи означает, что для зарядки конденсатора необходимо проделать дополнительную работу, поскольку при прохождении заряда через резистор всегда происходит передача энергии в тепло.

Этот график показывает, что:

• зарядный ток падает по мере увеличения заряда конденсатора, а напряжение на конденсаторе увеличивается
• зарядный ток уменьшается в той же пропорции через равные промежутки времени.

Второй пункт списка показывает, что изменение тока происходит по той же схеме, что и активность радиоактивного изотопа. Это пример экспоненциального изменения , зарядный ток уменьшается экспоненциально.

График, показанный выше, можно использовать для определения количества заряда, протекающего на конденсатор, путем оценки площади между линией графика и осью времени. Поскольку ток = скорость потока заряда , отсюда следует, что:

КЛЮЧ. На графике зависимости тока от времени область между линией графика и осью времени представляет поток заряда.

Для расчета расхода заряда:

• оцените количество целых квадратов между линией графика и осью времени
• умножьте это на «значение заряда» каждого квадрата, полученное путем вычисления ΔQ × Δt для одного квадрата.

Постоянная времени

Когда конденсатор заряжается или разряжается, количество заряда на конденсаторе изменяется экспоненциально. Графики на схеме показывают, как заряд конденсатора изменяется со временем, когда он заряжается и разряжается.

Графики, показывающие изменение напряжения во времени, имеют такую ​​же форму. Поскольку В = Q / C , отсюда следует, что единственная разница между графиком заряда-времени и графиком напряжение-время — это метка и масштаб по оси ординат.

Эти графики показывают, что заряд конденсатора приближается к окончательному значению, нулю в случае разряда конденсатора, но никогда не достигает его.

Скорость, с которой изменяется заряд конденсатора, зависит от постоянной времени цепи зарядки или разрядки.

КЛЮЧ — Постоянная времени τ цепи заряда или разряда конденсатора является произведением сопротивления и емкости:
τ = RC. τ измеряется в с.

Чем больше значения R и C , тем дольше длится процесс заряда или разряда. Знание значений R и C позволяет рассчитать величину заряда конденсатора в любое время после того, как конденсатор начал заряжаться или разряжаться.Это полезно в схемах синхронизации, где переключатель срабатывает после того, как заряд и, следовательно, p.d. достигли определенного значения.

Постоянная времени τ представляет:

• время, необходимое для того, чтобы заряд конденсатора упал до 1 / e от его начального значения, когда конденсатор разряжается
• время, необходимое для повышения заряда конденсатора до 1–1 / e от его окончательного значения, когда конденсатор заряжается

Роль постоянной времени аналогична периоду полураспада при радиоактивном распаде.Когда конденсатор разряжается, 1 / e ² начального заряда остается после времени 2τ и 1 / e ³ остается после 3τ .

Экспоненциальная функция e используется для вычисления заряда, оставшегося на разряжающемся конденсаторе.

КЛЮЧЕВЫЙ МОМЕНТ — Заряд Q на конденсаторе емкости C, оставшееся время t после начала разряда задается выражением Q = Q ₀ e ^{–t / τ} , где Q ₀ — это начальный заряд конденсатора.

Здесь e — экспоненциальная функция, обратная натуральному логарифму, ln. Не путайте это с кнопкой EXP на калькуляторе, которая используется для ввода степеней 10.

Это выражение показывает, что когда t равно τ , т.е. после истечения одной постоянной времени, оставшийся заряд равен Q ₀ e ^–1 , или Q ₀ / e

ПРОВЕРКА ПРОГРЕССА

Конденсатор

Конденсатор

Конденсатор

Емкость

Конденсатор — это устройство для хранения разделенного заряда.Нет единого электронного компонента сегодня играет более важную роль, чем конденсатор. Это устройство используется для хранить информацию в памяти компьютера, регулировать напряжение в источниках питания, для создания электрических полей, для хранения электрической энергии, для обнаружения и производить электромагнитные волны и измерять время. Любые два проводника, разделенные изолирующей средой, образуют конденсатор.

А Параллельно-пластинчатый конденсатор состоит из двух пластин, разделенных тонкой изоляционной материал, известный как диэлектрик .В параллельной пластине Электроны конденсатора переносятся с одной параллельной пластины на другую.

Мы уже показали, что электрическое поле между пластинами постоянно с величиной E = σ / ε ₀ и указывает от положительной пластины к отрицательной.

Следовательно, разность потенциалов между отрицательной и положительной пластинами равна предоставлено

∆U = U _пол. — U _отриц. = -q ∫ _отриц. ^пол. E · d r = q E d.

При интегрировании d r указывает с отрицательной на положительную пластину в противоположном направлении от E . Следовательно, E · d r = -Edr, и знаки минус отменяют.
Положительный пластина имеет более высокий потенциал, чем отрицательная пластина.

Силовые линии и эквипотенциальные линии для Постоянное поле между двумя заряженными пластинами показано справа. Одна пластина конденсатора удерживает положительный заряд Q, а другая — отрицательный заряд -Q.Заряд Q на пластинах пропорционален потенциалу разность V на двух пластинах. Модель емкость C — пропорциональная константа,

Q = CV, C = Q / V.

C зависит от геометрии конденсатора и типа диэлектрического материала использовал. Емкость параллельного пластинчатого конденсатора с двумя пластинами площадью А расстояние d и отсутствие диэлектрического материала между пластинами составляет

C = ε ₀ A / d.

(Электрическое поле E = σ / ε ₀ . Напряжение V = Ed = σd / ε ₀ . Заряд Q = σA. Следовательно, Q / V = σAε ₀ / σd = Aε ₀ / d.)
Единица измерения емкости в системе СИ — Кулон / Вольт = Фарад (Ф).
Типичный конденсаторы имеют емкость в диапазоне от пикофарад до микрофарад.

Емкость говорит нам, сколько заряда устройство хранит для данного Напряжение. Диэлектрик между проводниками увеличивает емкость конденсатор.Молекулы диэлектрического материала поляризованы в поле между двумя проводниками. Весь отрицательный и положительный заряд диэлектрик смещен на небольшую величину друг относительно друга. Этот приводит к эффективному положительному поверхностному заряду на одной стороне диэлектрика. и отрицательный поверхностный заряд на другой стороне диэлектрика. Эти эффективные поверхностные заряды на диэлектрике создают электрическое поле, которое противостоит полю, создаваемому поверхностными зарядами на проводниках, и, таким образом, снижает напряжение между проводниками.Чтобы поддерживать напряжение, больше заряда необходимо надеть на проводники. Таким образом, конденсатор сохраняет больше заряда для заданное напряжение. Диэлектрическая проницаемость κ — это отношение напряжения V ₀ между проводниками без диэлектрика к напряжение V с диэлектриком, κ = V ₀ / V, для данного количества заряда Q на проводниках.

На диаграмме выше такое же количество заряда Q на проводников приводит к меньшему полю между пластинами конденсатора с диэлектрик.Чем выше диэлектрическая проницаемость κ, тем больше заряда может хранить конденсатор при заданном напряжении. Для параллельной пластины конденсатор с диэлектриком между пластинами, емкость

C = Q / V = ​​κQ / V ₀ = κε ₀ A / d = εA / d,

, где ε = κε ₀ . Статическая диэлектрическая проницаемость любого материала всегда больше 1.

Типичная диэлектрическая проницаемость

Материал Диэлектрическая проницаемость Воздух 1.00059 силикат алюминия от 5,3 до 5,5 Бакелит 3,7 Пчелиный воск (желтый) 2,7 Бутилкаучук 2,4 Formica XX 4,00 Германий 16 Стекло от 4 до 10 Гуттаперча 2.6 Масло Halowax 4,8 Кел-Ф 2,6 Люцит 2,8 Слюда от 4 до 8 Микарта 254 от 3,4 до 5,4 Майлар 3,1 Неопреновый каучук 6,7 Нейлон 3.00

Материал Диэлектрическая проницаемость Бумага 1,5 к 3 Парафин от 2 до 3 Оргстекло 3,4 Полиэтилен 2,2 Полистирол 2,56 Фарфор 5-7 Стекло Pyrex 5.6 кварцевый от 3,7 до 4,5 Силиконовое масло 2,5 Стеатит от 5,3 до 6,5 титанат стронция 233 Тефлон 2,1 Tenite от 2,9 до 4,5 Вакуум 1,00000 Вазелин 2.16 Вода (дистиллированная) от 76,7 до 78,2 Дерево от 1,2 до 2,1

Если диэлектрик с диэлектрической проницаемостью κ вставляется между пластинами параллельной пластины конденсатора, а напряжение поддерживается постоянным аккумулятором, заряд Q на пластинах увеличивается в κ раз. Батарея перемещает больше электронов с положительной пластины на отрицательную. Величина электрического поля между пластинами E = V / d остается неизменной. тем же.

Если диэлектрик вставлен между пластинами параллельной пластины конденсатор, и заряд на пластинах остается прежним, потому что конденсатор отключается от АКБ, то напряжение V уменьшается в раз из κ, а электрическое поле между пластиной E = V / d уменьшается в 2 раза. κ.

---

Энергия, запасенная в конденсаторе

Энергия U, запасенная в конденсаторе, равна работе W сделано при разделении заряды на проводниках.Чем больше заряда уже накоплено на пластинах, тем необходимо проделать больше работы по разделению дополнительных сборов из-за сильного отталкивание между одноименными зарядами. При заданном напряжении требуется бесконечно малое объем работы ∆W = V∆Q для отделения дополнительной бесконечно малой суммы заряда ∆Q.
(Напряжение V — это количество работы на единицу заряда.)
Поскольку V = Q / C, V увеличивается линейно с Q. Общая работа, выполняемая при зарядке конденсатора является

W = ∫ ₀ ^Qf VdQ = ∫ ₀ ^Qf (Q / C) dQ = ½ (Q _f ² / C) = ½VQ _F = V _{среднее} Q _f
Используя Q = CV, мы также можем написать U = ½ (Q ² / C) или U = ½CV ² .

Задача:

Каждая ячейка памяти компьютера содержит конденсатор для хранения заряда. Сохраняемый или не сохраняемый заряд соответствует двоичным цифрам 1 и 0. Для более плотной упаковки ячеек в траншейных конденсаторах часто используются пластины конденсатора установлены вертикально вдоль стенок траншеи выгравирован на кремниевом чипе. Если у нас емкость 50 фемтоФарад = 50 * 10 ^-15 F и каждая пластина имеет площадь 20 * 10 ^-12 м ² (траншеи микронного размера), что такое разделение пластин?

Решение:

• Рассуждение:
  Емкость параллельного пластинчатого конденсатора с двумя пластинами площадью А разделенных расстоянием d и отсутствием диэлектрического материала между пластинами C = ε ₀ A / d.
• Детали расчета:
  C = ε ₀ A / d, d = ε ₀ A / C = (8,85 * 10 ^-12 * 20 * 10 ^-12 / (50 * 10 ^-15 )) м = 3,54 * 10 ^-9 м.
  Типичные атомные размеры порядка 0,1 нм, поэтому траншея находится на порядка 30 атомов в ширину.

Ссылка: PhET Конденсаторная лаборатория (базовая)

---

Для любого изолятора существует максимальное поддерживаемое электрическое поле без ионизации молекул.Для конденсатора это означает, что есть максимально допустимое напряжение, которое может быть приложено к проводникам. Этот максимальное напряжение зависит от диэлектрика в конденсаторе. Соответствующие максимальное поле E _b называется диэлектрической прочностью материала. Для более сильных полей конденсатор « выходит из строя » (аналогично коронный разряд) и обычно разрушается. Большинство конденсаторов, используемых в электрических схемы имеют как емкость, так и номинальное напряжение.Это напряжение пробоя V _b относится к диэлектрической прочности E _b . Для параллельной пластины конденсатор имеем V _b = E _b d.

Материал	Диэлектрическая прочность (В / м)
Воздух	3 * 10 6
Бакелит	24 * 10 6
Неопреновый каучук	12 * 10 6
Нейлон	14 * 10 6
Бумага	16 * 10 6
Полистирол	24 * 10 6
Стекло Pyrex	14 * 10 6
кварцевый	8 * 10 6
Силиконовое масло	15 * 10 6
титанат стронция	8 * 10 6
Тефлон	60 * 10 6

---

Последовательные или параллельные конденсаторы

Конденсатор — это устройство для хранения разделенного заряда и, следовательно, для хранения электростатическая потенциальная энергия.Цепи часто содержат более одного конденсатора.

Рассмотрим два конденсатора, подключенных параллельно , как показано справа

Когда батарея подключена, электроны будут течь до тех пор, пока потенциал точки А не станет равным. такой же, как потенциал положительной клеммы аккумулятора и потенциал точки B равен потенциалу отрицательной клеммы аккумулятора. Таким образом, разность потенциалов между пластинами обоих конденсаторов составляет V _A — V _B = V _bat .Имеем C ₁ = Q ₁ / V _bat и C ₂ = Q ₂ / V _bat , где Q ₁ — заряд конденсатора C ₁ , а Q ₂ — заряд конденсатора С ₂ . Пусть C — эквивалентная емкость двух конденсаторов. параллельно, то есть C = Q / V _bat , где Q = Q ₁ + Q ₂ . Тогда C = (Q ₁ + Q ₂ ) / V _bat = C ₁ + C ₂ .

Для конденсаторов, включенных параллельно, емкости складываются. Более двух конденсаторы у нас
C = C ₁ + C ₂ + C ₃ + С ₄ + ….

---

Рассмотреть два конденсатора серии , как показано справа.
Пусть Q представляют собой общий заряд на верхней пластине C ₁ , который затем вызывает заряд -Q на его нижней пластине. Заряд на нижней пластине С ₂ будет -Q, что, в свою очередь, индуцирует заряд + Q на своей верхней пластине, как показано.
Пусть V ₁ и V ₂ представляют собой разности потенциалов между пластины конденсаторов С ₁ и С ₂ соответственно.
Затем V ₁ + V ₂ = V _bat , или (Q / C ₁ ) + (Q / C ₂ ) = Q / C или (1 / C ₁ ) + (1 / C ₂ ) = 1 / C.

Более двух конденсаторы последовательно имеем
1 / C = 1 / C ₁ + 1 / C ₂ + 1 / К ₃ + 1 / К ₄ +….
где C эквивалентно емкость двух конденсаторов.
Для конденсаторов последовательно величина, обратная их эквивалентной емкости, равна сумме обратных величин их индивидуальные емкости.

Задача:

Какую общую емкость можно получить, подключив 5 мкФ и 8 мкФ конденсатор вместе?

Решение:

• Рассуждение:
  Мы можем подключать конденсаторы последовательно или параллельно.
  Чтобы получить наибольшую емкость, мы необходимо подключить конденсаторы параллельно.
  Чтобы получить наименьшую емкость, мы должны подключить конденсаторы последовательно.
• Детали расчета:
  Параллельное подключение конденсаторов:
  C _{наибольший} = (5 + 8) мкФ = 13 мкФ.
  Последовательное соединение конденсаторов.
  1 / C _{наименьшее} = (1/5 + 1/8) (мкФ) ^-1 = 13 / (40 мкФ) = 0,325 / мкФ.
  C _{наименьшее} = 40/13 мкФ = 3.077 мкФ.

---

Модуль 5: Вопрос 2:

(a) Конденсатор с параллельными пластинами изначально имеет напряжение 12 В и остается подключенным к батарее. Если теперь расстояние между пластинами увеличено вдвое, что бывает?
(b) Конденсатор с параллельными пластинами первоначально подключается к батарее, а пластины удерживают заряд ± Q. Затем аккумулятор отключается. Если расстояние между пластинами равно теперь вдвое, что происходит?

Подсказка: аккумулятор является зарядным насосом.Может качать заряд с одной пластины к другому, чтобы поддерживать постоянную разность потенциалов.
Нет батареи <--> нет зарядного насоса. Заряд не может перемещаться с одной пластины на Другие.

Обсудите это со своими однокурсниками на дискуссионном форуме!

Что такое емкость? — Определение, уравнения и примеры — Видео и стенограмма урока

Упражнение «Истина или ложь» емкости

Проверьте свои знания урока об определении и примерах емкости, определив, верны ли следующие утверждения.

Проезд

Распечатайте следующие вопросы на чистом листе бумаги и подчеркните или округлите ответ.

1. Емкость обратно пропорциональна напряжению и выражается в кулонах.

Верно | Ложь

2. Конденсатор емкостью 10 Фарад, подключенный к 12-вольтовой батарее, может хранить заряд 100 кулонов.

Верно | Ложь

3. В организме человека клеточная мембрана служит диэлектриком.

Верно | Ложь

4.Протоны текут к положительной клемме батареи и от отрицательной клеммы.

Верно | Ложь

5. Каучук — хороший пример диэлектрического материала.

Верно | Ложь

6. Нервная клетка может накапливать электрическую энергию и выделять ее в виде импульса.

Верно | Ложь

7. Проводящий материал, зажатый между двумя пластинами конденсатора, известен как диэлектрик.

Верно | Ложь

8. Две металлические пластины конденсатора будут заряжаться положительно при подключении через батарею.

Верно | Ложь

9. Источник напряжения, например аккумулятор, может создавать электрическое поле в конденсаторе.

Верно | Ложь

10. Конденсатор, накапливающий 12 кулонов заряда, подключенный к 3-вольтовой батарее, может давать емкость 4 фарада.

Верно | Ложь

Ключ ответа

1. Неверно, поскольку правильное утверждение гласит: «Емкость прямо пропорциональна напряжению и выражается в фарадах».

2.Неверно, потому что правильное утверждение звучит так: «Конденсатор емкостью 10 Фарад, подключенный к 12-вольтовой батарее, может хранить заряд 120 кулонов».

3. Верно

4. Неверно, потому что правильное утверждение звучит так: «Электроны текут к положительной клемме батареи и от отрицательной клеммы».

5. Верно

6. Верно

7. Неверно, потому что правильное утверждение звучит так: «Изолирующий материал, зажатый между двумя проводящими пластинами конденсатора, называется диэлектриком».

8. Неверно, потому что правильное утверждение звучит так: «Одна пластина конденсатора заряжена положительно, а другая — отрицательно при подключении к батарее».

9. верно

10. Верно

Емкость конденсатора Formula

Емкость конденсатора — это способность конденсатора накапливать электрический заряд на единицу напряжения на своих пластинах конденсатора. Емкость определяется делением электрического заряда на напряжение по формуле C = Q / V.Его единица — Фарад.

Формула

Его формула выглядит так:

C = Q / V

Где C — емкость, Q — напряжение, а V — напряжение. Мы также можем найти заряд Q и напряжение V, переписав приведенную выше формулу как:

Q =

CV

В = Q / C

Фарад — единица измерения емкости. Один фарад — это величина емкости, когда один кулон заряда хранится с одним вольт на пластинах.

Большинство конденсаторов, которые используются в электронике, имеют значения емкости, указанные в микрофарадах (мкФ) и пикофарадах (пФ).Микрофарад — это одна миллионная фарада, а пикофарад — одна триллионная фарада.

Какие факторы влияют на емкость конденсатора?

Зависит от следующих факторов:

Площадь плит

Емкость прямо пропорциональна физическому размеру пластин, определяемому площадью пластины A. Большая площадь пластины дает большую емкость и меньшую емкость. На рисунке (а) показано, что площадь пластины конденсатора с параллельными пластинами равна площади одной из пластин.Если пластины перемещаются относительно друг друга, как показано на рис (b), площадь перекрытия определяет эффективную площадь пластины. Это изменение эффективной площади пластины является основным для определенного типа переменного конденсатора.

Пластины разделительные

`Емкость обратно пропорциональна расстоянию между пластинами. Разделение пластин обозначено буквой d, как показано на рис. (А). Чем больше разделение пластин, тем меньше емкость, как показано на рис. (B).Как обсуждалось ранее, напряжение пробоя прямо пропорционально расстоянию между пластинами. Чем дальше разделены пластины, тем больше напряжение пробоя .

Диэлектрическая проницаемость материала

Как известно, изоляционный материал между пластинами конденсатора называется диэлектриком. Диэлектрические материалы имеют тенденцию уменьшать напряжение между пластинами при заданном заряде и, таким образом, увеличивать емкость. Если напряжение фиксировано, из-за наличия диэлектрика может храниться больше заряда, чем может храниться без диэлектрика.Мера способности материала создавать электрическое поле называется диэлектрической постоянной или относительной диэлектрической проницаемостью и обозначается как ∈ _r .

Емкость прямо пропорциональна диэлектрической проницаемости. Диэлектрическая проницаемость вакуума определяется как 1, а диэлектрическая проницаемость воздуха очень близка к 1. Эти значения используются в качестве справочных, а для всех других материалов значения ∈r указаны по отношению к таковым для вакуума или воздуха. Например, материал с εr = 8 может иметь емкость в восемь раз большую, чем у воздуха, при прочих равных условиях.

Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала, ∈r, к абсолютной диэлектрической проницаемости вакуума, ∈ ₀ , которое выражается следующей формулой:

∈ _r = ∈ / ∈ ₀

Ниже приведены некоторые общие диэлектрические материалы и типичные диэлектрические постоянные для каждого из них. Значения могут варьироваться, поскольку зависят от конкретного состава материала.

Материал Типичные значения ∈r

• Воздух 1.0
• Тефлон 2.0
• Бумага 2.5
• Нефть 4.0
• Слюда 5,0
• Стекло 7,5
• Керамика 1200

Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала, ∈r, к абсолютной диэлектрической проницаемости вакуума, ∈0, которое выражается следующей формулой:

∈r = ∈ / ∈0

Значение ∈0 равно 8.85 × 10-12 Ф / м.

Формула емкости по физическим параметрам

Вы видели, как емкость напрямую связана с площадью пластины, A, и диэлектрической проницаемостью, ∈r, и обратно пропорциональна расстоянию между пластинами, d. Точная формула для расчета емкости по этим трем величинам:

C = A ∈ _r ∈ / d

где ∈ = ∈ _r ∈ ₀ = ∈r (8,85 × 10-12F / м)

Емкость параллельных обкладок конденсатора вывода

Рассмотрим конденсатор с параллельными пластинами.Размер пластины большой, а расстояние между пластинами очень маленькое, поэтому электрическое поле между пластинами однородно.

Электрическое поле «E» между конденсаторами с параллельными пластинами составляет:

Емкость цилиндрических конденсаторов физика

Рассмотрим цилиндрический конденсатор длиной L, образованный двумя коаксиальными цилиндрами с радиусами «a» и «b». Предположим, что L >> b, так что на концах цилиндров отсутствует окаймляющее поле.

Пусть «q» — это заряд конденсатора, а «V» — это разность потенциалов между пластинами. Внутренний цилиндр заряжен положительно, а внешний цилиндр — отрицательно. Мы хотим узнать выражение емкости для цилиндрического конденсатора. Для этого мы рассматриваем цилиндрическую гауссовскую поверхность радиуса «r», такую ​​что a << b.

Если «E» — напряженность электрического поля в любой точке цилиндрической гауссовой поверхности, то по закону Гаусса:

Если «V» — разность потенциалов между пластинами, тогда

Это соотношение для емкости цилиндрического конденсатора.

Емкость сферического конденсатора

Емкость изолированного сферического конденсатора

Внешний источник
https://en.wikipedia.org/wiki/Capacitance

.