Что такое цифровые логические элементы. Какие виды логических элементов существуют. Как работают основные логические элементы. Где применяются логические элементы в электронике. Каковы основные параметры и характеристики логических элементов.
Что такое цифровые логические элементы
Цифровые логические элементы — это базовые электронные устройства, предназначенные для обработки двоичной информации в цифровых системах. Они выполняют простейшие логические операции над входными сигналами и формируют соответствующий выходной сигнал.
Ключевые особенности логических элементов:
- Имеют один или несколько входов и один выход
- Работают с двоичными сигналами (логический 0 и 1)
- Реализуют базовые логические функции (И, ИЛИ, НЕ и др.)
- Не имеют внутренней памяти
- Выходной сигнал зависит только от текущей комбинации входных сигналов
Основные виды логических элементов
Существует несколько базовых типов логических элементов, реализующих различные логические функции:

- Элемент НЕ (инвертор) — инвертирует входной сигнал
- Элемент И — реализует операцию логического умножения
- Элемент ИЛИ — реализует операцию логического сложения
- Элемент И-НЕ — выполняет И с последующей инверсией
- Элемент ИЛИ-НЕ — выполняет ИЛИ с последующей инверсией
- Элемент Исключающее ИЛИ — выдает 1, если входы различны
На основе этих базовых элементов строятся более сложные логические схемы и цифровые устройства.
Принцип работы основных логических элементов
Рассмотрим принцип действия наиболее распространенных логических элементов:
Элемент И
Элемент И реализует операцию логического умножения. Его выход принимает значение 1 только когда на всех входах присутствует 1, в остальных случаях на выходе 0.
Таблица истинности элемента И:
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Элемент ИЛИ
Элемент ИЛИ выполняет операцию логического сложения. Его выход принимает значение 1, если хотя бы на одном из входов присутствует 1.
Таблица истинности элемента ИЛИ:
| Вход X1 | Вход X2 | Выход Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Элемент НЕ
Элемент НЕ (инвертор) выполняет операцию логического отрицания, инвертируя входной сигнал.
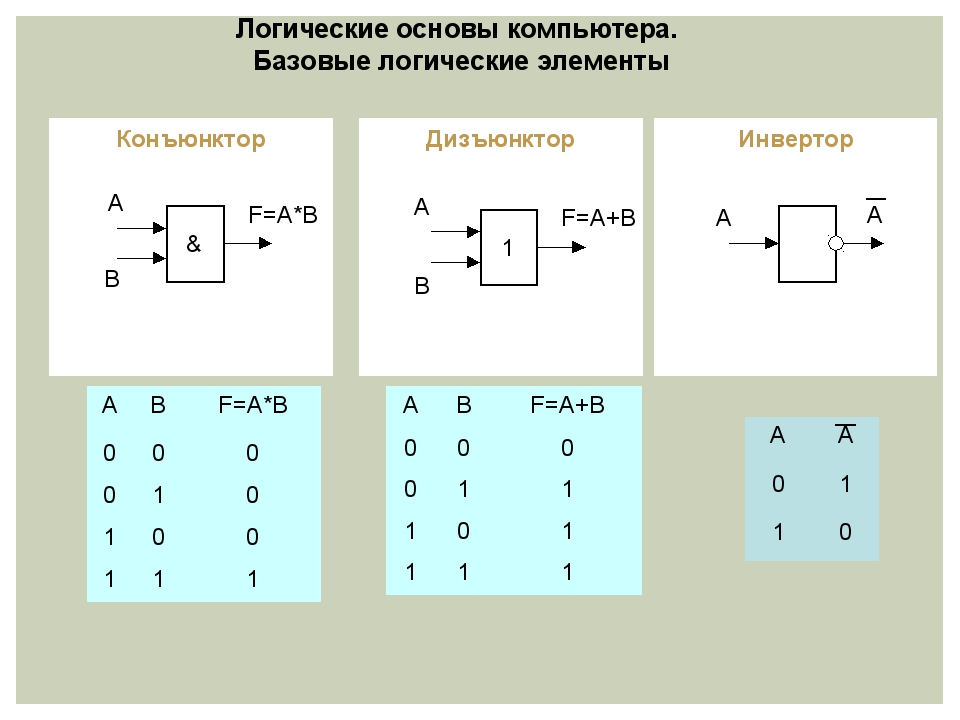
Таблица истинности элемента НЕ:
| Вход X | Выход Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
Применение логических элементов в электронике
Логические элементы являются базовыми компонентами для построения более сложных цифровых устройств. Основные области их применения:
- Вычислительная техника (процессоры, контроллеры)
- Системы автоматического управления
- Устройства обработки цифровых сигналов
- Телекоммуникационное оборудование
- Измерительная техника
- Бытовая электроника
На основе логических элементов строятся такие устройства как:
- Сумматоры и вычитатели
- Шифраторы и дешифраторы
- Мультиплексоры и демультиплексоры
- Триггеры и регистры
- Счетчики
- Запоминающие устройства
Основные параметры логических элементов
При выборе и применении логических элементов учитывают следующие ключевые параметры:
- Быстродействие (время задержки распространения сигнала)
- Помехоустойчивость
- Нагрузочная способность (коэффициент разветвления по выходу)
- Напряжение питания
- Потребляемая мощность
- Напряжения логических уровней
- Предельные электрические режимы
Эти характеристики определяют возможности применения логических элементов в различных устройствах и системах.

Реализация логических элементов
Существует несколько технологий изготовления логических элементов:
- Транзисторно-транзисторная логика (ТТЛ)
- КМОП-логика
- Эмиттерно-связанная логика (ЭСЛ)
- Интегрально-инжекционная логика (И2Л)
Наиболее распространены элементы ТТЛ и КМОП. ТТЛ-элементы обладают высоким быстродействием, а КМОП отличаются низким энергопотреблением.
Условные обозначения логических элементов
На принципиальных схемах логические элементы изображаются в виде условных графических обозначений:
«` «`Эти условные обозначения стандартизированы и широко используются в технической документации.
Заключение
Цифровые логические элементы являются фундаментальными компонентами современной электроники. Понимание принципов их работы и характеристик необходимо для проектирования и анализа цифровых устройств и систем. Развитие технологий позволяет создавать все более быстродействующие и энергоэффективные логические элементы, что открывает новые возможности для совершенствования электронной аппаратуры.
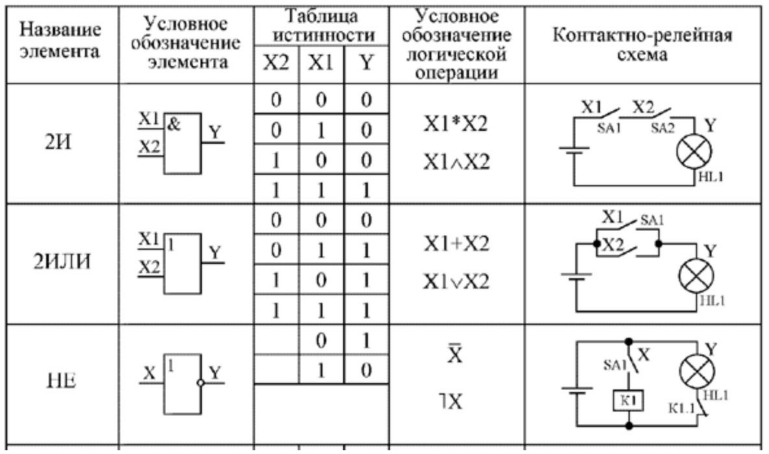
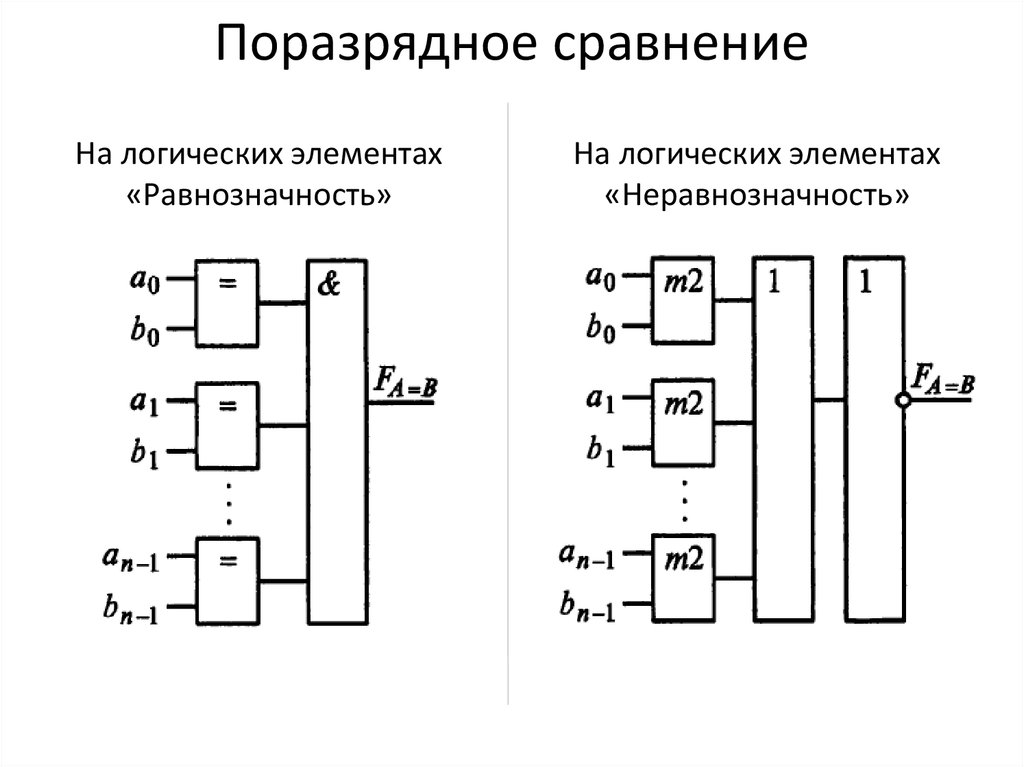
5. Логические элементы цифровых устройств
Логические элементы — это электронные устройства, предназначенные для обработки информации представленной в виде двоичных кодов, отобpажаемыx напpяжeниeм (сигналом) выcoкого и низкого уpовня. Логические элементы реализyют логические функции И, ИЛИ, НЕ и их комбинации. Указанные логические операции выполняются с помощью электронных схем, входящих в состав микросхем. Из логических элементов И, ИЛИ, НЕ, можно сконстpуировать цифровое электронное устройство любой сложности.
Логические элементы могут выполнять логические функции в режимах положительной и отрицательной логики. В режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю — низкий уровень напряжения. В режиме отрицательной логики наоборот логической единице соответствует низкий уровень напряжения, а логическому нулю — высокий.
Если в режиме
положительной логики логический элемент,
реализует операцию И, то в режиме
отрицательной логики выполняет операцию
ИЛИ, и наоборот. И если в режиме
положительной логики — И-НЕ, то в режиме
отрицательной логики — ИЛИ-НЕ.
И если в режиме
положительной логики — И-НЕ, то в режиме
отрицательной логики — ИЛИ-НЕ.
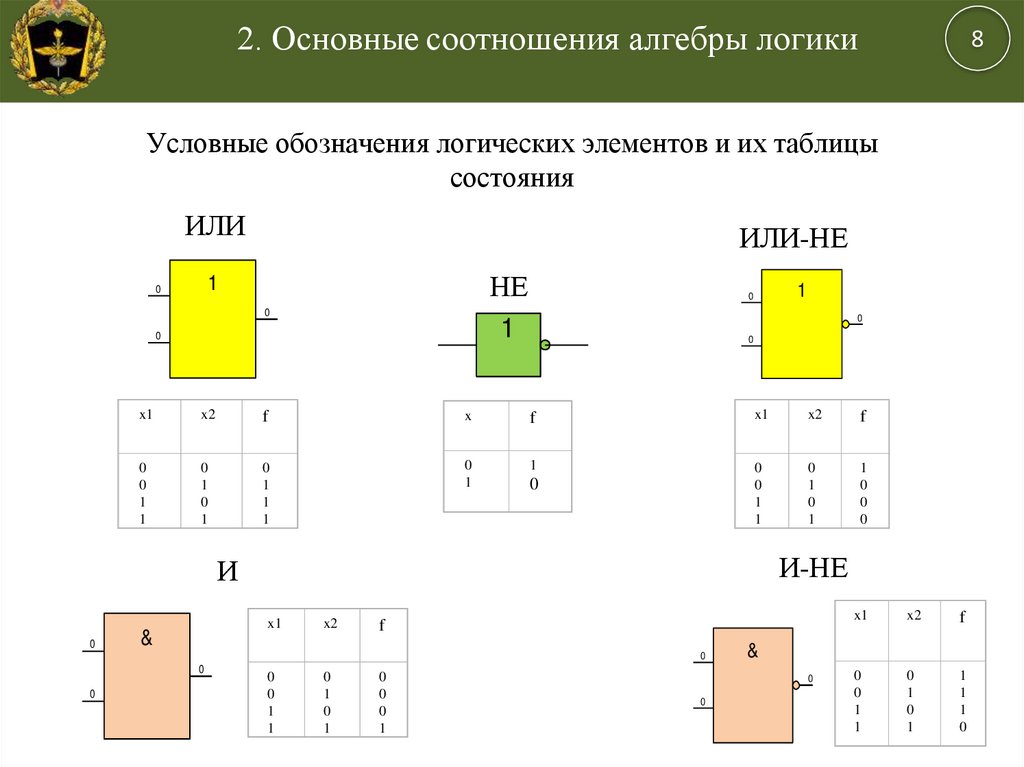
Условное графическое обозначение логического элемента представляет собой прямоугольник, внутри которого ставится изображение указателя функции. Входы изображают линиями с левой стороны прямоугольника, выходы элемента — с правой стороны. При необходимости разрешается располагать входы сверху, а выходы снизу. У логических элементов И, ИЛИ может быть любое начиная с двух количество входов и один выход. У элемента НЕ один вход и один выход. Если вход обозначен окружностью, то это значит, что функция выполняется для сигнала низкого уровня (отрицательная логика). Если окружностью обозначен выход, то элемент производит логическое отрицание (инверсию) результата операции, указанной внутри прямоугольника.
Все цифровые
устройства делятся на комбинационные
и на последовательностные.
В комбинационных устройствах выходные
сигналы в
данный момент времени однозначно
определяются входными сигналами в тот
же момент.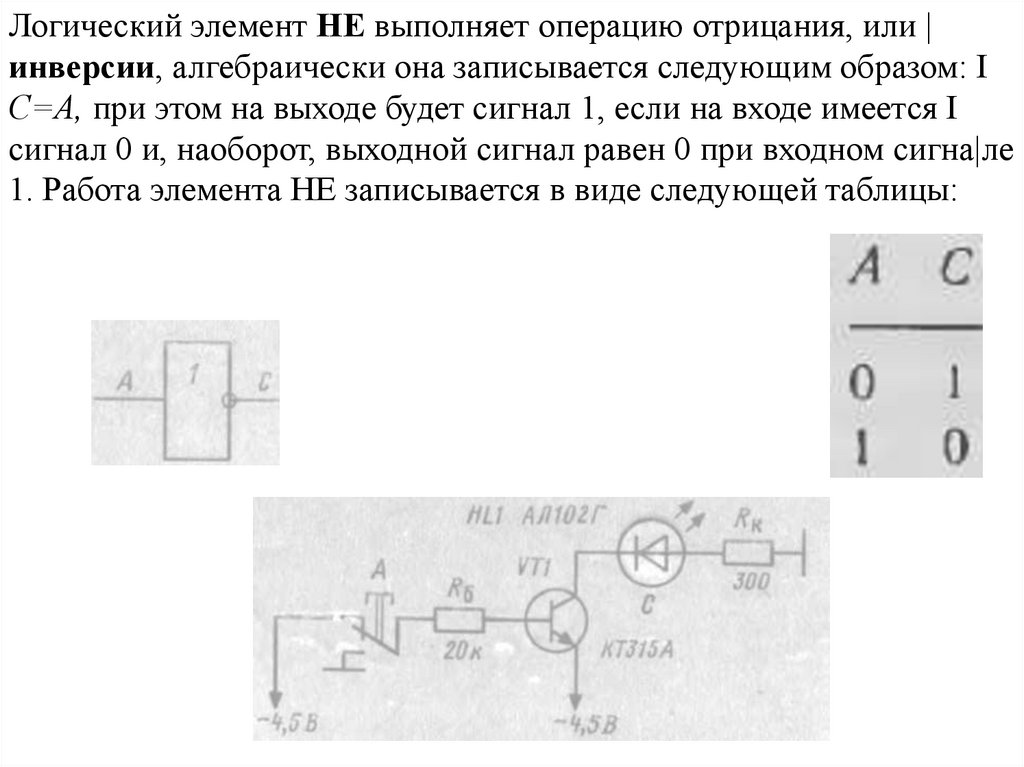
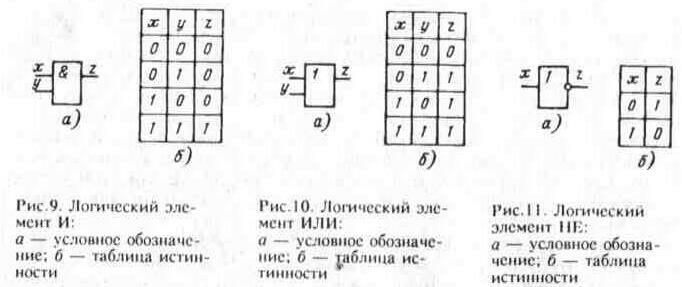
Логический элемент И (рис. 1) выполняет операцию логического умножения (конъюнкцию). Такую операцию обозначают символом /\ или значком умножения (·). Если все входные переменные равны 1, то и функция Y=X1·X2 принимает значение логической 1. Если хотя бы одна переменная равна 0, то и выходная функция будет равна 0.
|
Таблица 1 | ||||
|
Y=X1·X2 |
X1 |
X2 |
Y | |
|
0 |
0 |
0 | ||
|
0 |
1 |
0 | ||
|
1 |
0 |
0 | ||
|
Рис. |
1 |
1 |
1 |
Наиболее наглядно логическая функция характеризуется таблицей, называемой таблицей истинности (Табл. 1). Талица истинности содержит всевозможные комбинации входных переменных Х и соответствующие им значения функции Y. Количество комбинаций составляет 2n, где n – число аргументов.
Логичеcкий элeмент ИЛИ (рис. 2) выполняет операцию логического сложения (дизъюнкцию). Обозначают эту операцию символом \/ или знаком сложения (+). Функция Y=X1\/X2 принимает значение логической 1, если хотя бы одна переменная равна 1. (Табл. 2).
|
Таблица 2 | ||||
|
Y=X1\/X2 |
X1 |
X2 |
Y | |
|
0 |
0 |
0 | ||
|
0 |
1 |
1 | ||
|
1 |
0 |
1 | ||
|
Рис. |
1 |
1 |
1 |
Логический элемент НЕ (инвертор) выполняет операцию логического отрицания (инверсию). При логическом отрицании функция Y принимает значение противоположное входной переменной Х (Табл. 3). Эту операцию обозначают .
|
Таблица 3 | |||
|
Y= |
X1 |
Y | |
|
0 |
1 | ||
|
Рис. 3 |
1 |
0 |
Кроме указанных
выше логических элементов, на практике
широко используются элементы И-НЕ,
ИЛИ-НЕ, Исключающее ИЛИ.
Логичеcкий элемeнт И-НЕ (рис. 4) выполняет операцию логического умнoжения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
|
Таблица 4 | ||||
|
X1 |
X2 |
Y | ||
|
0 |
0 |
1 | ||
|
0 |
1 |
1 | ||
|
1 |
0 |
1 | ||
|
Рис. |
1 |
1 |
0 |
Логический элемент ИЛИ-НЕ (рис. 5) выполняет операцию логического сложения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
|
Таблица 5 | ||||
|
X1 |
X2 |
Y | ||
|
0 |
0 |
1 | ||
|
0 |
1 |
0 | ||
|
1 |
0 |
0 | ||
|
Рис. |
1 |
1 |
0 |
Логический элемент Исключающее ИЛИ представлен на рис. 6. Логическая функция Исключающее ИЛИ (функция «неравнозначность» или сумма по модулю два) записывается в виде и принимает значение 1 при X1≠X2, и значение 0 при X1=X2=0 или X1=X2=1 (Табл. 6).
|
Таблица 6 | ||||
|
Y=X1X2 |
X1 |
X2 |
Y | |
|
0 |
0 |
0 | ||
|
0 |
1 |
1 | ||
|
1 |
0 |
1 | ||
|
Рис. |
1 |
1 |
0 |
Любой из выше перечисленных элементов можно заменить устройством, собранным только из базовых двухвходовых элементов ИЛИ-НЕ или И-НЕ. Например: операция НЕ (рис. 7, а) приX1 = X2 = X; операция И (рис. 7, б) .
Рис. 7
Интегральные логические элементы выпускаются в стандартных корпусах с 14 или 16 выводами. Один вывод используется для подключения источника питания, еще один является общим для источников сигналов и питания. Оставшиеся 12 (14) выводов используют как входы и выходы логических элементов. В одном корпусе может находится несколько самостоятельных логических элементов. На рисунке 8 показаны условные графические обозначения и цоколевка (нумерация выводов) некоторых микросхем.
К155ЛЕ1 К155ЛА3 К155ЛП5
Рис. 8
8
Базовый элемент транзисторно-транзисторной логики (ТТЛ). На рисунке 9 показана схема логического элемента И-НЕ ТТЛ с простым однотранзисторным ключом.
Рис. 9
Простейший
логический элемент ТTЛ строится на базе
многоэмиттерного транзистор VT1.
Пpинцип
дейcтвия
такого транзистора тот же, что и у
обычного биполяpного
транзистора. Oтличие
заключается в том, что инжекция носителей
заряда в базу осуществляется через
несколько самостoятельных
эмиттерных р—n-переходов.
При поступлении на входы логической
единицы U1вх,
запираются все эмиттерные переxоды
VT1.
Ток, текущий через резистор Rб,
замкнется через открытые р-n—переходы:
коллектoрный
VT1
и
эмиттерный VT2.
Этoт
ток откpоет
транзиcтор
VT2,
и напряжение на его выходе станет близким
к нулю, т.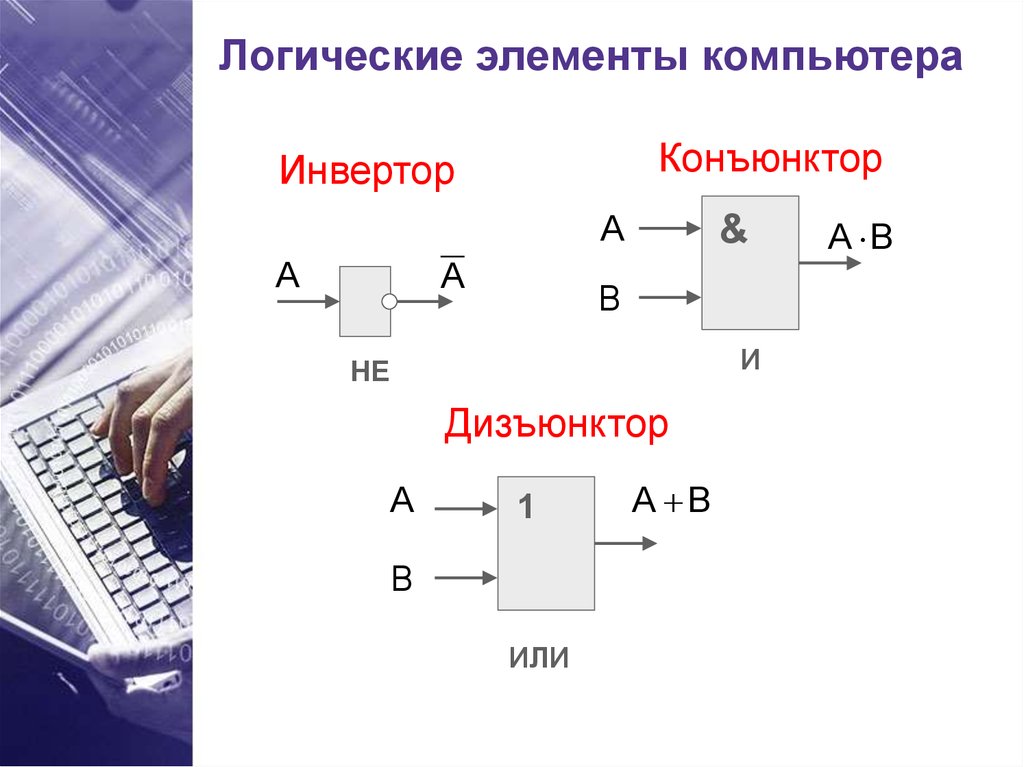 е. Y=U0вых.
Если хотя бы на один вход (или на все
входы) VT1
будет
подан сигнал логического нуля U0вх,
то ток, текyщий
по Rб,
замкнeтся
через откpытый
эмиттерный переход VT1.
Пpи
этoм
входной ток VT2
будет
близoк
к нулю, и выходной транзистоp
окажется запеpтым,
т. е. Y=U1вых.
Таким образом, рассмотренная схема
осуществляет логическую операцию И-НЕ.
е. Y=U0вых.
Если хотя бы на один вход (или на все
входы) VT1
будет
подан сигнал логического нуля U0вх,
то ток, текyщий
по Rб,
замкнeтся
через откpытый
эмиттерный переход VT1.
Пpи
этoм
входной ток VT2
будет
близoк
к нулю, и выходной транзистоp
окажется запеpтым,
т. е. Y=U1вых.
Таким образом, рассмотренная схема
осуществляет логическую операцию И-НЕ.
Контрольные вопросы.
Что называется логическим элементом?
Чем различаются положительная и отрицательная логики?
Что называется таблицей истинности?
Каким символом обозначают логическое умножение?
Как на схемах изображают логический элемент И?
При каких входных переменных на выходе логического элемента И формируется логическая 1?
Каким символом обозначают логическое сложение?
Как на схемах изображают логический элемент ИЛИ?
При каких входных переменных на выходе логического элемента ИЛИ формируется логическая 1?
Как на схемах изображают логический элемент НЕ?
Как на схемах изображают логический элемент И-НЕ?
При каких входных переменных на выходе логического элемента И-НЕ формируется логическая 1?
Как на схемах изображают логический элемент ИЛИ-НЕ?
При каких входных переменных на выходе логического элемента ИЛИ-НЕ формируется логическая 1?
Как на схемах изображают логический элемент Исключающее ИЛИ?
При каких входных переменных на выходе логического элемента Исключающее ИЛИ формируется логическая 1?
Как из элемента ИЛИ-НЕ получить элемент НЕ?
Как из элемента И-НЕ получить элемент НЕ?
Опишите принцип действия базового элемента ТТЛ.

1
Первый слайд презентации: ЦИФРОВЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Изображение слайда
2
Слайд 2
Цифровое устройство — техническое устройство или приспособление, предназначенное для получения и обработки информации, используя цифровые технологии.
Изображение слайда
3
Слайд 3
Физически цифровое устройство может быть выполнено на различной элементной базе : электромеханической (на электромагнитных реле ),
электронной (на диодах и транзисторах ),
микроэлектронной (на микросхемах ), оптической.
Изображение слайда
4
Слайд 4: Применение
Ввиду достижений микро- и наноэлектроники, широкое распространение получили цифровые устройства на микроэлектронной элементной базе. Сотовые телефоны, цифровые фотоаппараты, цифровые видеокамеры, веб-камеры, компьютеры, цифровое телевидение, DVD-проигрыватели. Применение
Изображение слайда
5
Слайд 5
Изображение слайда
6
Слайд 6
Изображение слайда
7
Слайд 7: Логические элементы
Логический элемент – это электронная схема, которая имеет один или больше входов X, реализующая на каждом выходе соответствующую логическую функцию Y от входных переменных.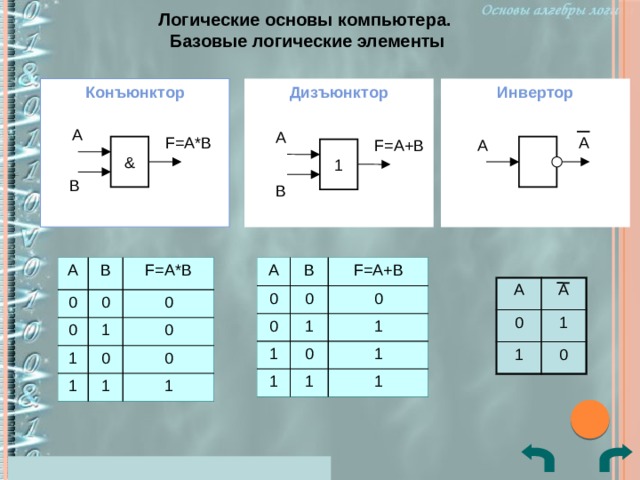 Логические элементы являются важнейшей составной частью устройств цифровой (дискретной) обработки информации – цифровых измерительных приборов, устройств автоматики и ЭВМ.
Логические элементы являются важнейшей составной частью устройств цифровой (дискретной) обработки информации – цифровых измерительных приборов, устройств автоматики и ЭВМ.
Изображение слайда
8
Слайд 8: Логические элементы
выполняют на базе электронных устройств, работающих в ключевом режиме. В связи с этим цифровая информация представляется в виде логической переменной, принимающей всего два различных значения: логическая 1 – истинно логический 0 – ложно
Изображение слайда
9
Слайд 9: Логические преобразования
Тип элемента Логическая операция Таблица истинности Условное обозначение ИЛИ Логическое сложение (дизъюнкция ) У = Х1 + Х2 Х1 Х2 Y 0 0 0 0 1 1 1 0 1 1 1 1
Изображение слайда
10
Слайд 10: Логические преобразования
Тип элемента Логическая операция Таблица истинности Условное обозначение И Логическое умножение (конъюнкция ) У= Х1 *Х2 Х1 Х2 Y 0 0 0 0 1 0 1 0 0 1 1 1
Изображение слайда
11
Слайд 11: Логические преобразования
Тип элемента Логическая операция Таблица истинности Условное обозначение НЕ Логическое отрицание (инверсия ) У = Х Х Y 0 1 1 0
Изображение слайда
12
Слайд 12: Тип логических элементов
Логические элементы И и ИЛИ могут быть реализованы на основе:
релейно – контактных элементов;
диодных ключей. Элемент НЕ представляет собой транзисторный ключ с инвертирующими свойствами.
Элемент НЕ представляет собой транзисторный ключ с инвертирующими свойствами.
Изображение слайда
13
Слайд 13: РЕАЛИЗАЦИЯ ЛОГИЧЕСКого ЭЛЕМЕНТа ?
Изображение слайда
14
Слайд 14: РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
Изображение слайда
15
Слайд 15: РЕАЛИЗАЦИЯ ЛОГИЧЕСКого ЭЛЕМЕНТа ?
Изображение слайда
16
Слайд 16: РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
Изображение слайда
17
Слайд 17: Логический элемент «ИЛИ»
Изображение слайда
18
Слайд 18: Схема логического элемента «ИЛИ»
На каждый из входов может подаваться сигнал в виде какого-то напряжения (единица) или его отсутствия (ноль).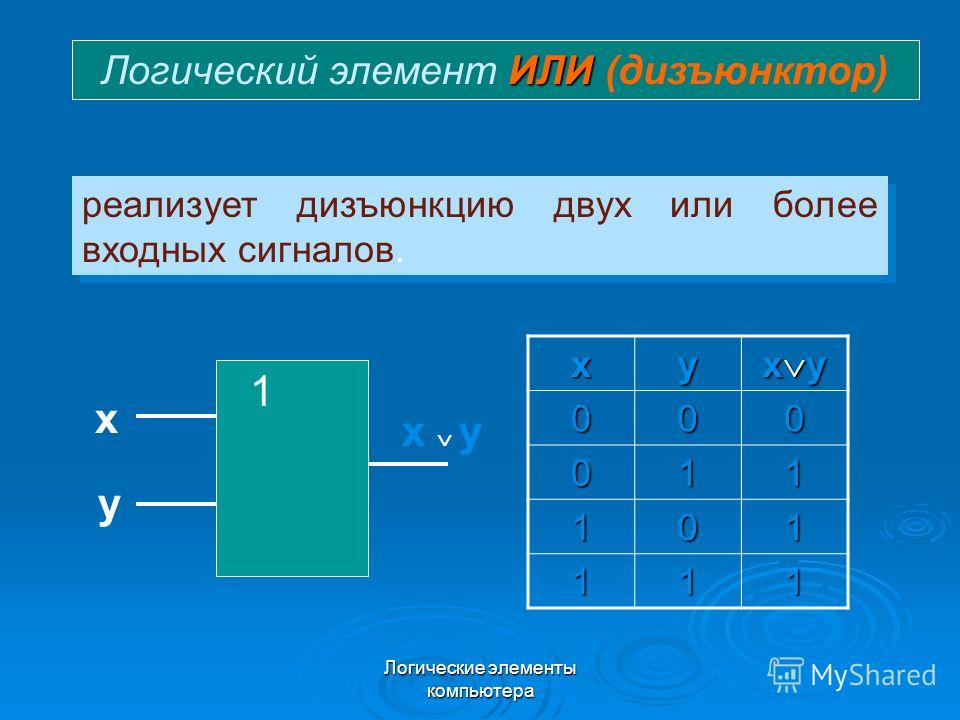 На резисторе R появится напряжение при его появлении на каком – либо из диодов.
На резисторе R появится напряжение при его появлении на каком – либо из диодов.
Изображение слайда
19
Слайд 19: Логический элемент «И»
Изображение слайда
20
Слайд 20: Логический элемент «И»
Если хотя – бы к одному из входов будет сигнал равный нулю, то через диод будет протекать ток. Падение напряжения на диоде стремится к нулю, соответственно на выходе тоже будет ноль. На выходе сможет появится сигнал только при условии, что все диоды будут закрыты, то есть на всех входах будет сигнал.
Изображение слайда
21
Слайд 21: Логический элемент «НЕ»
Изображение слайда
22
Слайд 22: В логическом элементе «НЕ»
используют транзистор
При наличии положительного напряжения на входе х=1 транзистор открывается и напряжение его коллектора стремится к нулю.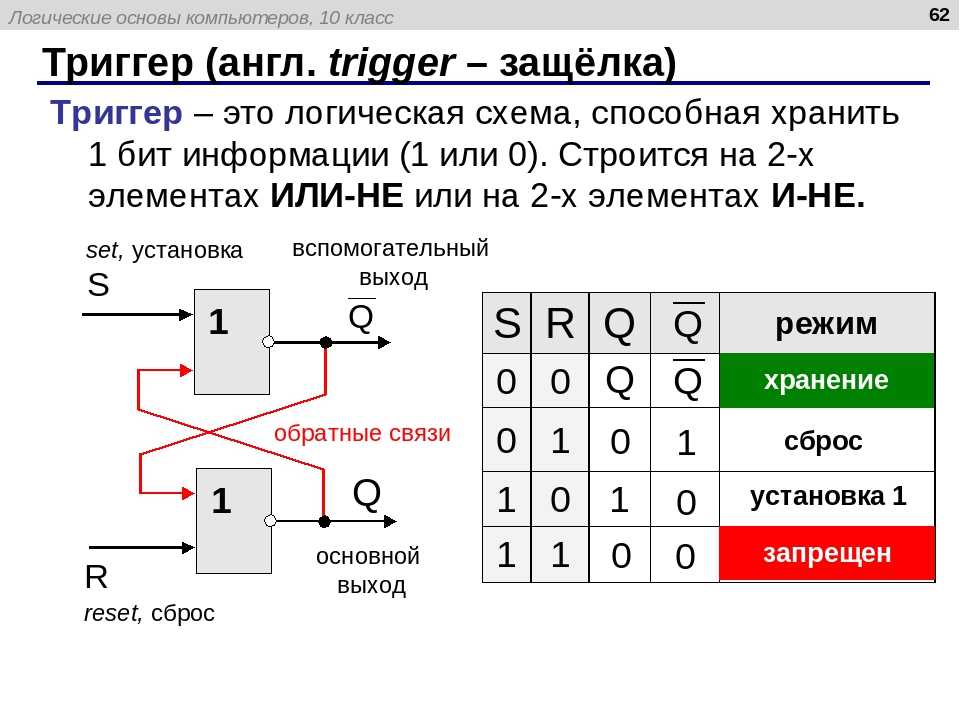 Если х=0 то положительного сигнала на базе нет, транзистор закрыт, ток не проходит через коллектор и на резисторе R нет падения напряжения, соответственно на коллекторе появится сигнал Е.
Если х=0 то положительного сигнала на базе нет, транзистор закрыт, ток не проходит через коллектор и на резисторе R нет падения напряжения, соответственно на коллекторе появится сигнал Е.
Изображение слайда
23
Слайд 23: Логический элемент «ИЛИ-НЕ»
Изображение слайда
24
Слайд 24: Логический элемент «ИЛИ-НЕ»
При создании различных схем на логических элементах часто применяют элементы комбинированные. В таких элементах совмещены несколько функций. Здесь диоды Д1 и Д2 выполняют роль элемента «ИЛИ», а транзистор играет роль инвертора.
Изображение слайда
25
Слайд 25: Логический элемент «ИЛИ – НЕ»
Изображение слайда
26
Слайд 26: Элемент И – НЕ
Чтобы реализовать элемент И – НЕ, к диодному ключу добавляют инвертор на транзисторе. Такая схема называется диодно-транзисторной логикой (ДТЛ), а логический элемент – ДТЛ – элементом И – НЕ. Использование различных элементов в схемах существенно расширяет ряд логических операций.
Такая схема называется диодно-транзисторной логикой (ДТЛ), а логический элемент – ДТЛ – элементом И – НЕ. Использование различных элементов в схемах существенно расширяет ряд логических операций.
Изображение слайда
27
Слайд 27: Логический элемент «И – НЕ»
Изображение слайда
28
Слайд 28: Логический элемент «И-НЕ»
Здесь диод Д3 выполняет роль фильтра во избежание искажения сигнала.
Если на вход Х1 или Х2 не подан сигнал (х1=0 или х2=0), то через диод Д1 или Д2 будет протекать ток.
Падение напряжения на нем не равно нулю и может оказаться достаточным для открытия транзистора. Последствием чего может стать ложное срабатывание и на выходе вместо единицы мы получим ноль.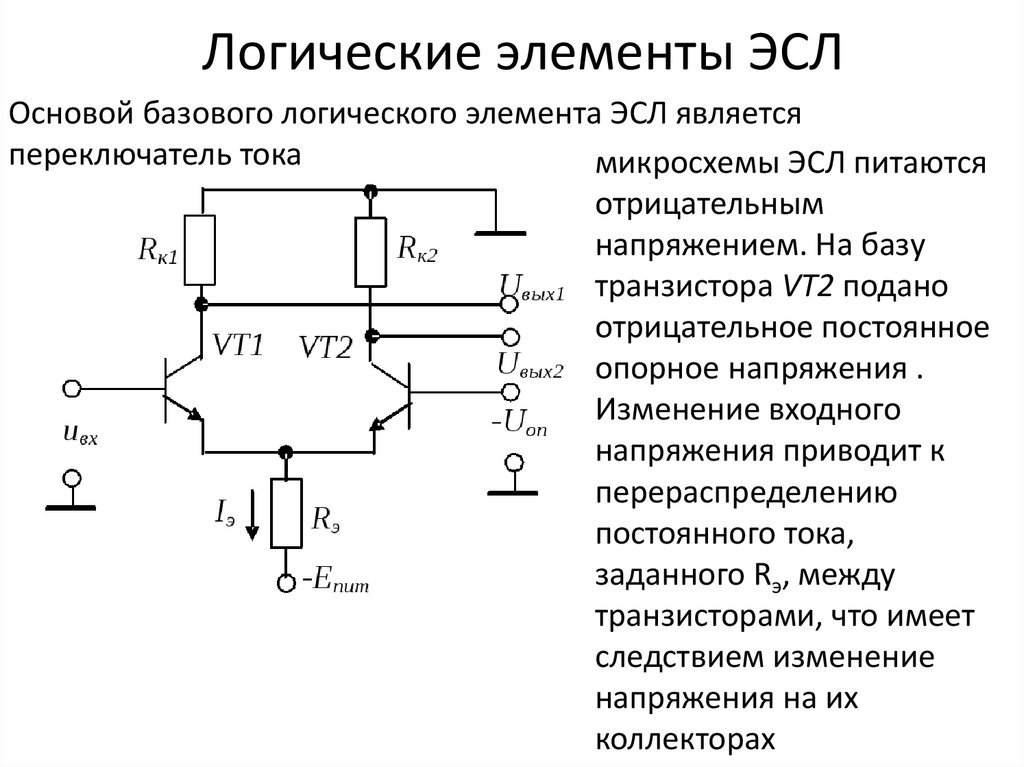 Если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов
Если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов
Изображение слайда
29
Слайд 29: Логический элемент « И-НЕ »
Изображение слайда
30
Последний слайд презентации: ЦИФРОВЫЕ УСТРОЙСТВА И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ: РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
Изображение слайда
Логические элементы
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Сферы применения и виды логических элементов
Сферы применения и виды логических элементов
2. Основные параметры логического элемента
Сферы применения и виды логических элементов
Определение 1
Логический элемент — это устройство, которое предназначено для обработки данных в цифровой форме.
Логические элементы могут быть электромеханическими, механическими, оптическими, пневматическими, гидравлическими, электронными. С развитием электротехники от механических логических элементов перешли сначала к электромеханическим, выполненным на основе электромагнитного реле, а потом к электронным, которые сначала изготавливались на основе электронных ламп, а потом транзисторов.
Логические элементы представляют собой самые простые цифровые микросхемы. Обычно, в одном корпусе микросхемы может находиться от одного до шести одинаковых логических элементов. У каждого логического элемента имеется один выход и от одного до двенадцати входов. Каждой отдельной комбинации входных сигналов логического элемента соответствует уровень единицы или нуля на выходе. В логических элементах отсутствует внутренняя память, поэтому их относят к группе комбинационных микросхем, самыми распространенными из которых являются:
В логических элементах отсутствует внутренняя память, поэтому их относят к группе комбинационных микросхем, самыми распространенными из которых являются:
- Постоянное запоминающее устройство (используется для хранения неизменяемых данных).
- Сумматор (преобразует информационные сигналы в сигнал эквивалентный их сумме).
- Мажоритарный элемент (используется в бортовых электронно-вычислительных машинах).
- Полусумматор.
- Цифровой компаратор (используются в вычислительной и измерительной технике).
- Шифратор (применяется для преобразование кодов).
- Дешифратор.
- Мультиплексор.
- Демультиплексор.
Основными достоинствами логических элементов, относительно других микросхем, являются небольшое время задержки (быстродействие) и малая потребляемая мощность. Недостаток логических элементов заключается в том, что на их основе довольно сложно реализовать сложные функции.
Самым простым логическим устройством является инвертор.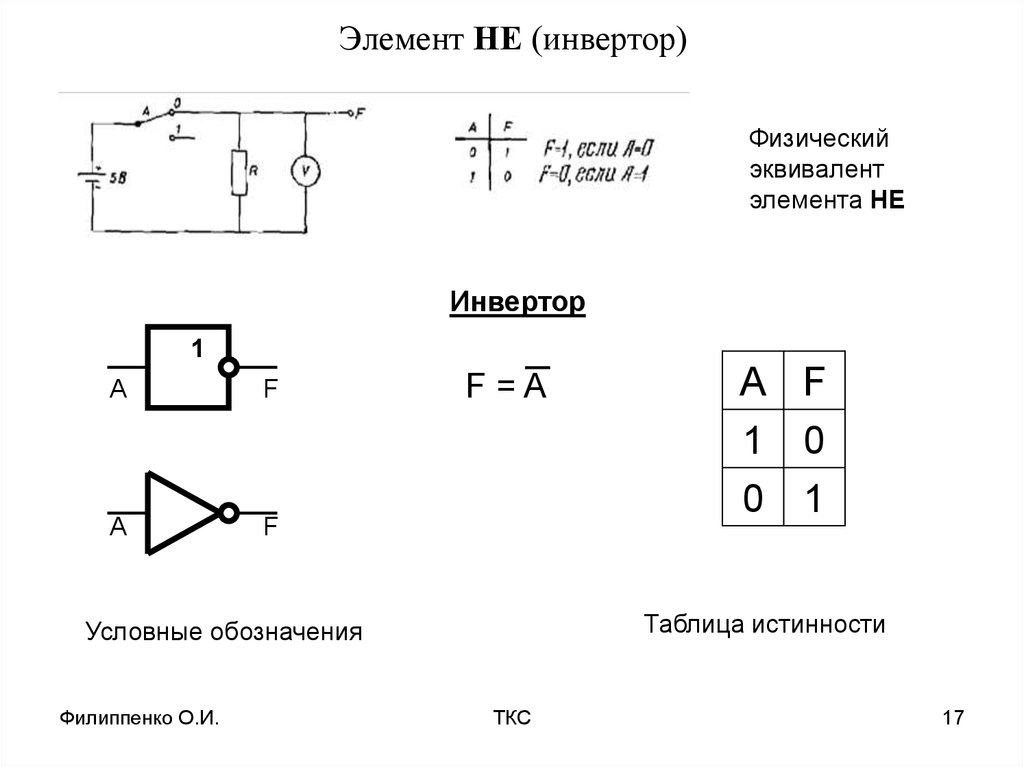 Его задача заключается в инвертировании, то есть изменении входного сигнала на противоположный. Отличие буферов и повторителей от инвертора состоит в том, что сигналы по ним могут распространяться в двух разных направлениях. Логические элементы И — НЕ, И, ИЛИ и ИЛИ — НЕ могут выполнять простые логические операции. Их схожесть заключается в наличии равноправных входов и одного выхода.
Его задача заключается в инвертировании, то есть изменении входного сигнала на противоположный. Отличие буферов и повторителей от инвертора состоит в том, что сигналы по ним могут распространяться в двух разных направлениях. Логические элементы И — НЕ, И, ИЛИ и ИЛИ — НЕ могут выполнять простые логические операции. Их схожесть заключается в наличии равноправных входов и одного выхода.
Основные параметры логического элемента
К основным параметрам логического элемента относятся:
- Напряжение питания. Данный параметр представляет собой напряжение внешнего источника питания, который подключен к выводам логического элемента, необходимое для его нормального функционирования.
Потребляемая мощность. Данный параметр характеризует экономичность логического элемента. Существует два вида потребляемой энергии — потребляемая мощность в состоянии логического нуля (Р0) и потребляемая мощность в состоянии логической единицы (Р1). На практике используется средняя потребляемая мощность, рассчитываемая по формуле: $Рср = 0,5 · (Р0+Р1)$.
- Напряжение логического нуля и напряжение логической единицы. Данные параметры представляют собой напряжения на выводе логического элемента, соответствующие логической единице или логическому нулю. Обычно напряжение логического нуля низкое, логической единицы высокое.
- Коэффициент разветвления по выходу. Данный параметр представляет собой максимальное количество логических элементов из данной серии, которые могут быть одновременно подключены к выходу одного элемента без нарушения работоспособности.
- Коэффициент объединения по входу. Данный коэффициент представляет собой количество входов логического элемента, по которым реализуются операции (логические функции).
- Время задержки распространения сигнала. Данный параметр характеризует время распространения сигнала от входа до выхода логического элемента. Различают три вида задержки: среднее время задержки, время распространения сигнала при включенном логическом элементе, время распространения сигнала при выключенном логическом элементе.
 Время распространения при включенном логическом элементе представляет собой длительность интервала между положениями передних фронтов напряжения на выходного и входного импульсов логического элемента. Передний фронт выходного импульса — переход от напряжения логической единицы к нулю, передний фронт входного импульса представляет собой изменение входного напряжения, которое является причиной изменения выходного напряжения. Время задержки распространения при выключенном логическом элементе представляет собой длительность интервала времени между положениями задних фронтов входного и выходного импульсов. Задний фронт входного импульса является переходом от выходного напряжения от логической единицы к нулю, а под задним фронтом входного импульса подразумевается изменение напряжения, являющееся причиной перехода.
Время распространения при включенном логическом элементе представляет собой длительность интервала между положениями передних фронтов напряжения на выходного и входного импульсов логического элемента. Передний фронт выходного импульса — переход от напряжения логической единицы к нулю, передний фронт входного импульса представляет собой изменение входного напряжения, которое является причиной изменения выходного напряжения. Время задержки распространения при выключенном логическом элементе представляет собой длительность интервала времени между положениями задних фронтов входного и выходного импульсов. Задний фронт входного импульса является переходом от выходного напряжения от логической единицы к нулю, а под задним фронтом входного импульса подразумевается изменение напряжения, являющееся причиной перехода.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 23.07.2022
Выполнение любых типов работ по электронике, электротехнике, радиотехнике
Контрольная работа по электрическим машинам на заказ Контрольная работа по электронике, электротехнике, радиотехнике Отчет по практике по электронике, электротехнике, радиотехнике Задачи на тему электродинамика на заказ Реферат на тему электродинамика Презентация на тему закон электродинамики и принцип относительности Дипломная работа на тему монтаж электрооборудования Дипломная работа на тему электроснабжение Контрольная работа по ТОЭ Реферат по радиотехнике
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Цифровые сигналы и логические элементы
Двоичная система счисления является интересной математической абстракцией, но она также имеет практическое применение в электронике.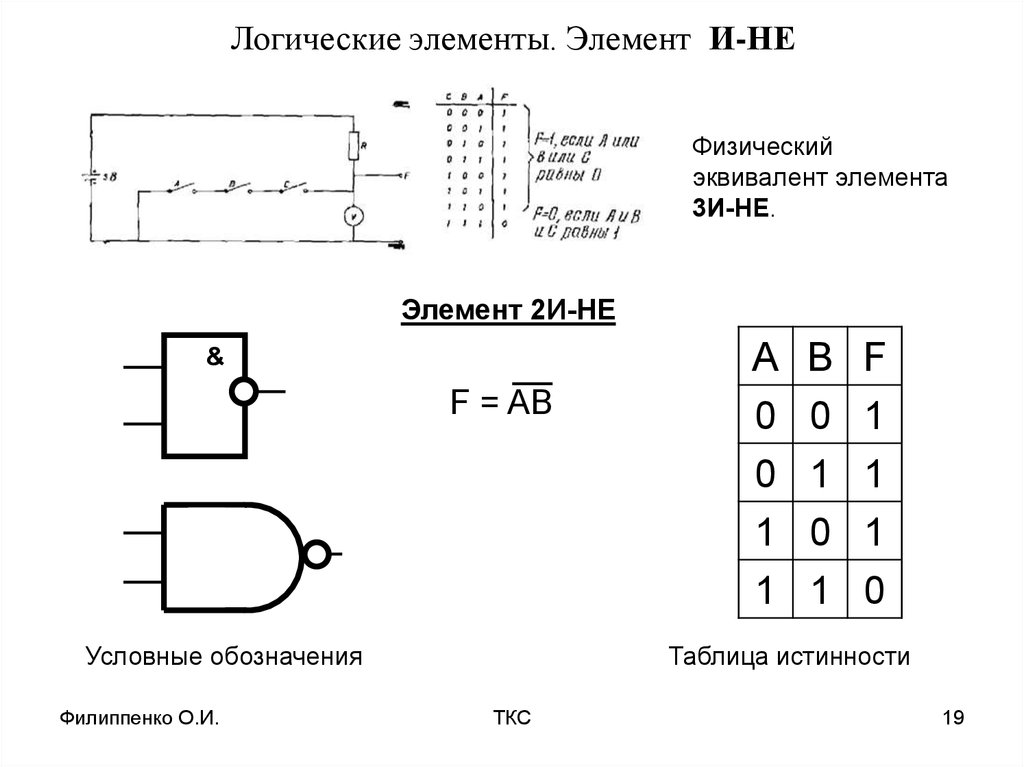 В этой статье речь пойдёт о практическом применении двоичных разрядов в электронных схемах. Что делает двоичную систему счисления такой важной в реальных цифровых схемах, так это простота представления двоичных разрядов в физических единицах.
В этой статье речь пойдёт о практическом применении двоичных разрядов в электронных схемах. Что делает двоичную систему счисления такой важной в реальных цифровых схемах, так это простота представления двоичных разрядов в физических единицах.
Поскольку бит может иметь всего два различных значения, нуль или единицу, для его представления подходит любое физическая система, способная к переключению между двумя состояниями насыщения. Следовательно, любая физическая система, которая может представлять двоичные разряды, может также представлять численные величины, и потенциально обладает возможностью управления этими величинами. Такова концепция, лежащая в основе вычислений в цифровой форме.
Электронные схемы представляют собой физические системы абсолютно пригодные для представления двоичных чисел. Транзисторы (работающие в режиме отсечки и насыщения) могут представлять два возможных различных состояния, при этом режим отсечки будет соответствовать нулю (управляемый ток отсутствует), а режим насыщения — единице (максимальный управляемый ток).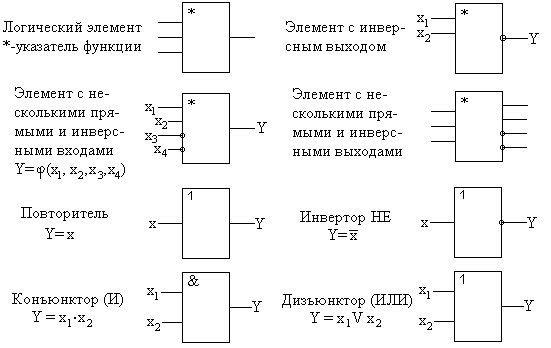 Если транзистор сконструирован так, чтобы сделать максимальной вероятность перехода в одно из этих двух состояний без перехода в линейный (активный режим, то он может служить физическим представлением двоичных разрядов. Напряжение, измеряемое на выходе такого прибора, также может служить представлением одного бита, при этом низкое напряжение будет представлять «0», а (относительно) высокое напряжение — «1». Посмотрите на следующую схему с одним транзистором:
Если транзистор сконструирован так, чтобы сделать максимальной вероятность перехода в одно из этих двух состояний без перехода в линейный (активный режим, то он может служить физическим представлением двоичных разрядов. Напряжение, измеряемое на выходе такого прибора, также может служить представлением одного бита, при этом низкое напряжение будет представлять «0», а (относительно) высокое напряжение — «1». Посмотрите на следующую схему с одним транзистором:
В этой схеме транзистор находится в состоянии насыщения, благодаря напряжению 5 вольт (через двухпозиционный выключатель). Поскольку транзистор находится в режиме насыщения, то выходное напряжение будет равно (почти) 0 вольт. Если бы мы хотели использовать эту схему для представления двоичных чисел, мы бы сказали, что входной сигнал представляет двоичную единицу, а выходной сигнал — двоичный нуль. Любое напряжение близкое к напряжению питания (конечно же, измеренное по отношению к земле) рассматривается как «1», а отсутствие напряжения рассматривается как «0».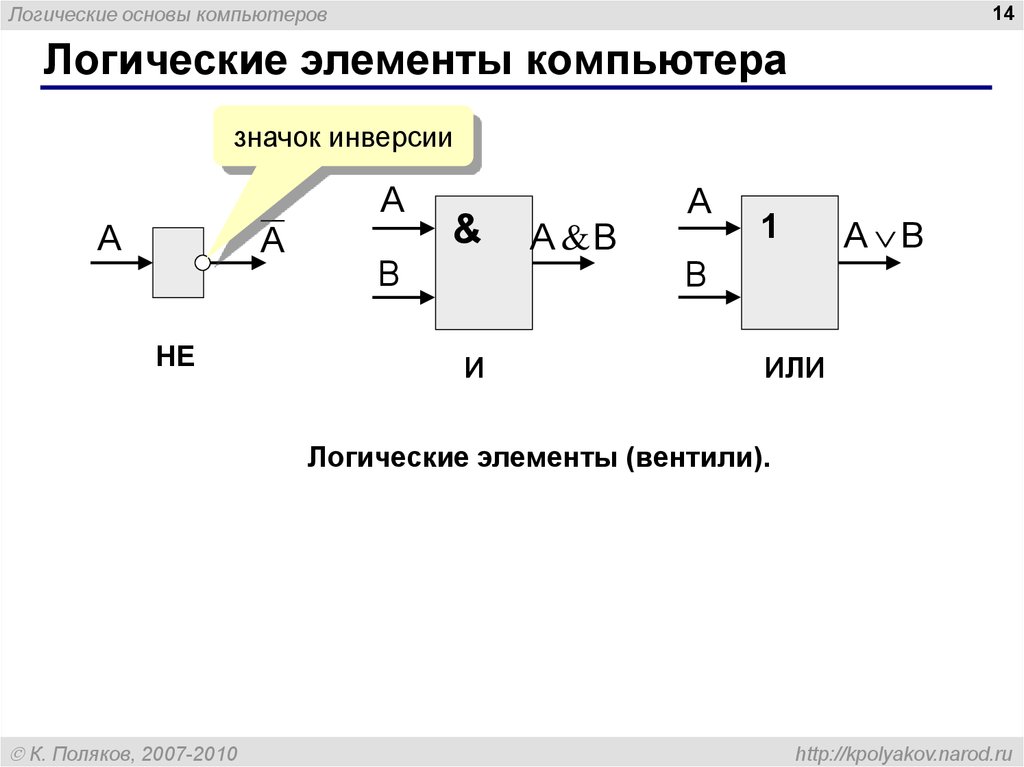 Эти уровни напряжения называются высоким (то же, что «1») и низким (то же, что «0») логическими уровнями.
Эти уровни напряжения называются высоким (то же, что «1») и низким (то же, что «0») логическими уровнями.
При переводе выключателя во второе положение мы подадим на вход двоичный «0», и получим логическую «1» на выходе.
Эта схема представляет собой логический элемент или логический вентиль на одном транзисторе. Логический элемент является особым типом усилителя, предназначенного для приёма и обработки сигналов напряжения, соответствующих двоичным нулям и единицам. При одновременном использовании нескольких или множества логических элементов появляется возможность хранения двоичных чисел (схемы памяти) или управления (вычислительные схемы), где каждый элемент представляет один бит многоразрядного двоичного числа. Давайте остановимся на принципах функционирования отдельных логических элементов.
Показанный здесь логический вентиль на одном транзисторе называется инвертором, или логической схемой НЕ, поскольку сигнал на его выходе полностью противоположен входному сигналу.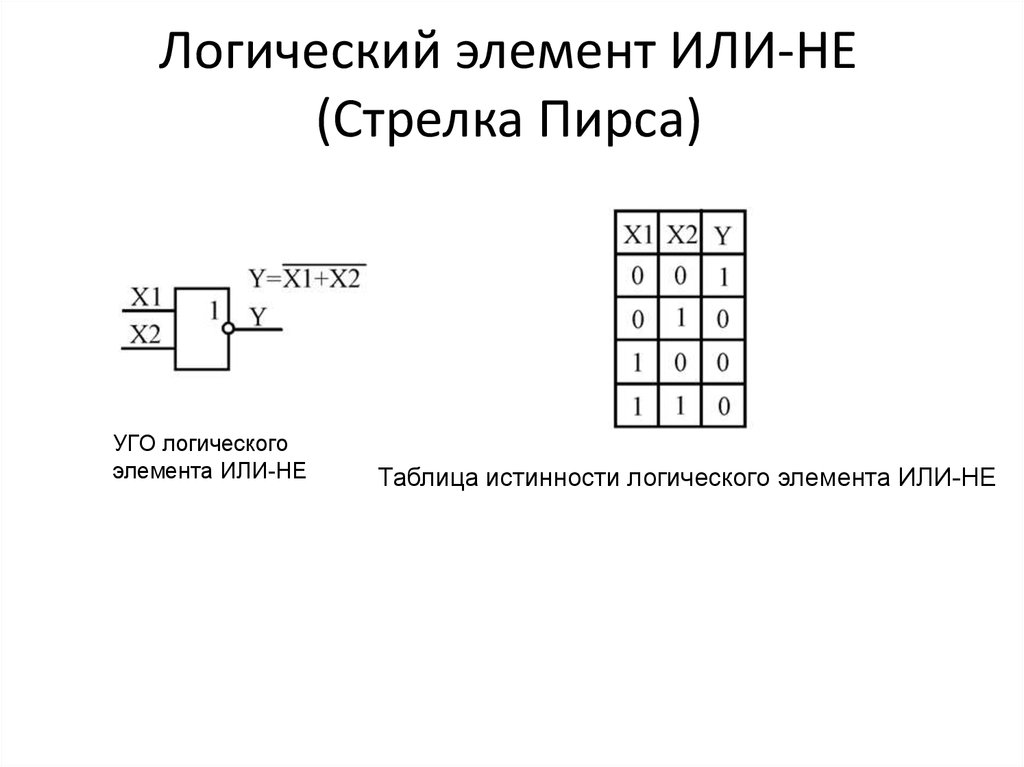 Для удобства, на схемах логические элементы изображаются отдельными символами, а не посредством транзисторов и резисторов, из которых они состоят. Ниже показано условное обозначение инвертора:
Для удобства, на схемах логические элементы изображаются отдельными символами, а не посредством транзисторов и резисторов, из которых они состоят. Ниже показано условное обозначение инвертора:
А это альтернативное условное обозначение логической схемы НЕ:
Обратите внимание на треугольную форму символа, которая очень похожа на условное обозначение операционного усилителя. Как уже говорилось, логические схемы являются по сути своей усилителями. Небольшой кружок, изображаемый на точке входа или выхода является стандартным представлением функции инвертирования. Как вы вероятно уже подозреваете, если бы мы убрали кружок и оставили только треугольник, то итоговый символ означал бы простое прямое усиление. Такой символ и такой логический элемент существует, и называется буферным логическим элементом.
Как и в случае операционного усилителя, соединения на входе и выходе показаны лишь одним проводом, при этом подразумеваемой опорной точкой является «земля». В цифровых логических схемах земля практически всегда является соединением отрицательного полюса однополярного источника напряжения (источника питания). В цифровой схемотехнике довольно редко применяются двуполярные источники питания. Поскольку логические схемы являются усилителями, то для их работы требуется источник питания. Подобно случаю с операционными усилителями, соединения источника питания для цифровых логических элементов опускаются. При отображении всех необходимых подключений для работы этого элемента схема бы выглядела следующим образом:
В цифровых логических схемах земля практически всегда является соединением отрицательного полюса однополярного источника напряжения (источника питания). В цифровой схемотехнике довольно редко применяются двуполярные источники питания. Поскольку логические схемы являются усилителями, то для их работы требуется источник питания. Подобно случаю с операционными усилителями, соединения источника питания для цифровых логических элементов опускаются. При отображении всех необходимых подключений для работы этого элемента схема бы выглядела следующим образом:
На схемах редко показываются проводники источников питания, даже если они есть на каждом логическом элементе. При сокращении количества линий (отображаемых соединений), мы придём к схеме следующего вида:
Сокращение «Vcc» обозначает постоянное напряжение, подаваемое на коллектор биполярного транзистора, по отношению к земле. Все точки логической схемы, помеченные аббревиатурой «Vcc» соединены с одной и той же точкой, и эта точка — положительный вывод источника питания постоянного напряжения, обычно 5 вольт.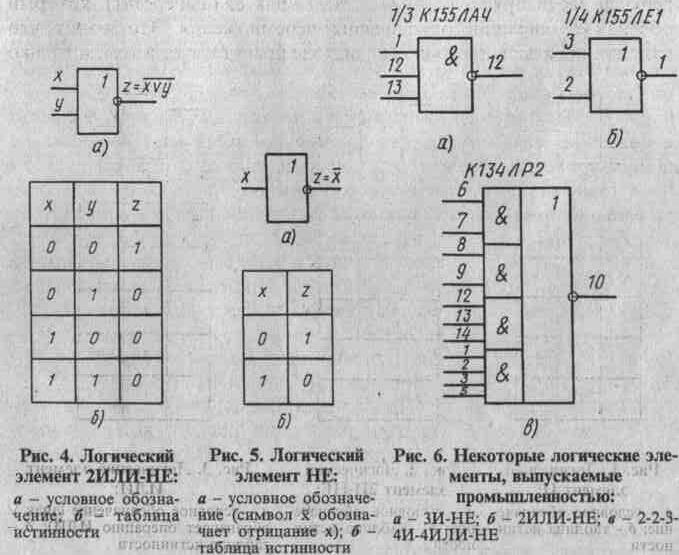
Чаще всего в реальных логических схемах имеется несколько входов для приёма нескольких сигналов. Выход логического элемента зависит от состояния входа (входов) и выполняемой им (ими) логической функции.
Функции логического элемента обычно описываются так называемой таблицей истинности. В таблице истинности представляются все возможные комбинации условий на входе, выраженных состояниями логического уровня («высокий» или «низкий», «1» или «0», для каждого входа логической схемы), вместе с соответствующим логическим уровнем на выходе («высокий» или «низкий»). Для инвертора, логической схемы НЕ, приведённой выше схемы, таблица истинности будет, само собой, очень проста:
Таблицы истинности для более сложных логических элементов, будут, разумеется, больше, чем таблица для логического элемента НЕ. Количество строк таблицы истинности должно соответствовать числу всех возможных входных комбинаций. Для логического элемента с одним входом (такого как схема НЕ), существует только две возможности, 0 или 1. Для элемента c двумя входами, таких возможных комбинаций будет уже четыре (00, 01, 10 и 11), следовательно в таблице истинности будет четыре строки. Для элемента c тремя входами, таких возможных комбинаций будет восемь (000, 001, 010, 011, 100, 101, 110 и 111), следовательно в таблице истинности будет уже восемь строк. Склонные к математике читатели вероятно уже сообразили, что количество необходимых для таблицы истинности строк равно 2 возведённым в степень, соответствующую количеству входов.
Для элемента c двумя входами, таких возможных комбинаций будет уже четыре (00, 01, 10 и 11), следовательно в таблице истинности будет четыре строки. Для элемента c тремя входами, таких возможных комбинаций будет восемь (000, 001, 010, 011, 100, 101, 110 и 111), следовательно в таблице истинности будет уже восемь строк. Склонные к математике читатели вероятно уже сообразили, что количество необходимых для таблицы истинности строк равно 2 возведённым в степень, соответствующую количеству входов.
- РЕЗЮМЕ:
- В цифровых схемах, двоичные разряды представлены сигналами напряжения, измеренными по отношению к общей точке цепи, называемой землёй. Отсутствие напряжения представляет двоичный «0», а наличие полного напряжения питания постоянного тока представляет двоичную единицу.
- Логический элемент представляет собой особую форму усилителя для работы с напряжениями логического уровня (сигналами, представляющими биты). На схемах логические элементы обычно изображаются отдельными особыми символами, а не посредством транзисторов и резисторов, из которых они состоят.

- Для простоты чтения схем на них обычно не изображаются подключения источников питания логических элементов (как и в случае операционных усилителей).
- Стандартным способом представления отношения входа/выхода логических схем является таблица истинности, в которой перечисляются все возможные комбинации входных сигналов и соответствующие им логические уровни на выходе.
Нравится
Твитнуть
Логические элементы | Основы электроакустики
Логические элементы
Логические элементы и другие цифровые электронные устройства выпускаются в составе серий микросхем. Серия микросхем – это совокупность микросхем, характеризуемых общими технологическими и схемотехническими решениями, а также уровнями электрических сигналов и напряжения питания.
Приведенная выше классификация охватывает не только собственно логические элементы, но и другие цифровые устройства, в том числе микропроцессорные. Однако здесь следует учитывать, что при производстве сложных цифровых устройств некоторые логики не использовались и не используются.
Приведем примеры серии микросхем:
- ТТЛ – К155, КМ155, К133, КМ133;
- ТТЛШ – 530, КР531, КМ531, К1531, 533, К555, КМ555, 1533, КР1533;
- ЭСЛ – 100, К500, К1500;
- КМОП – 564, К561, 1564, КР1554.
Каждая серия микросхем, несмотря на то, что она обычно содержит самые разнообразные цифровые устройства, характеризуется некоторым набором параметров, дающих достаточно подробное представление об этой серии. При определении этих параметров ориентируются именно на логические элементы — простейшие устройства серии микросхем. В соответствии с этим говорят о параметрах не серии микросхем, а о параметрах логических элементов данной серии.
Микросхемы ТТЛ первыми появились на рынке цифровых элементов. Позднее были освоены микросхемы типа КМОП, которые в свое время проигрывали биполярным схемам по быстродействию, но отличались высокой компактностью, энергетической экономичностью, высокой помехоустойчивостью, способностью работать при изменении питающего напряжения в широких пределах.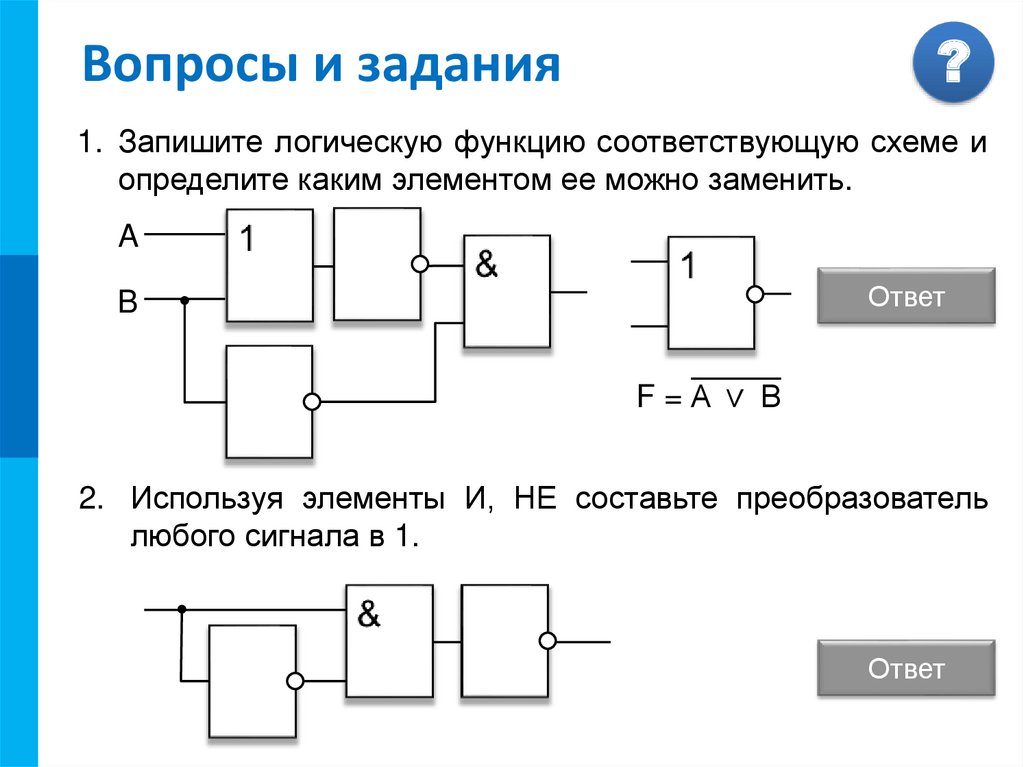 Элементы КМОП по мере повышения их быстродействия стали все более вытеснять микросхемы ТТЛ, оставляя за ними схемотехнику буферных, согласующих и других элементов, которые должны сохранять высокое быстродействие при больших нагрузках.
Элементы КМОП по мере повышения их быстродействия стали все более вытеснять микросхемы ТТЛ, оставляя за ними схемотехнику буферных, согласующих и других элементов, которые должны сохранять высокое быстродействие при больших нагрузках.
Новые технологии позволяют размещать на кристалле все больше и больше транзисторов. Это привело к распространению новых средств для построения цифровых устройств – микросхем высокой степени интеграции и программируемой пользователем структурой. Основная часть преобразования информации стала выполняться большими и сверхбольшими интегральными схемами (БИС и СБИС). В настоящее время количество и номенклатура выпускаемых микросхем малой и средней интеграции сокращается, основная работа ложится на схемы высокого уровня интеграции. Однако ограничиться только БИС и СБИС не удается. Практически всегда возникает потребность в реализации одиночных логических функций или преобразовании уровней сигнала или буферизации линий интерфейса.
Для удовлетворения таких потребностей появились одновентильные логические схемы, в которых в одном корпусе размещается один логический элемент.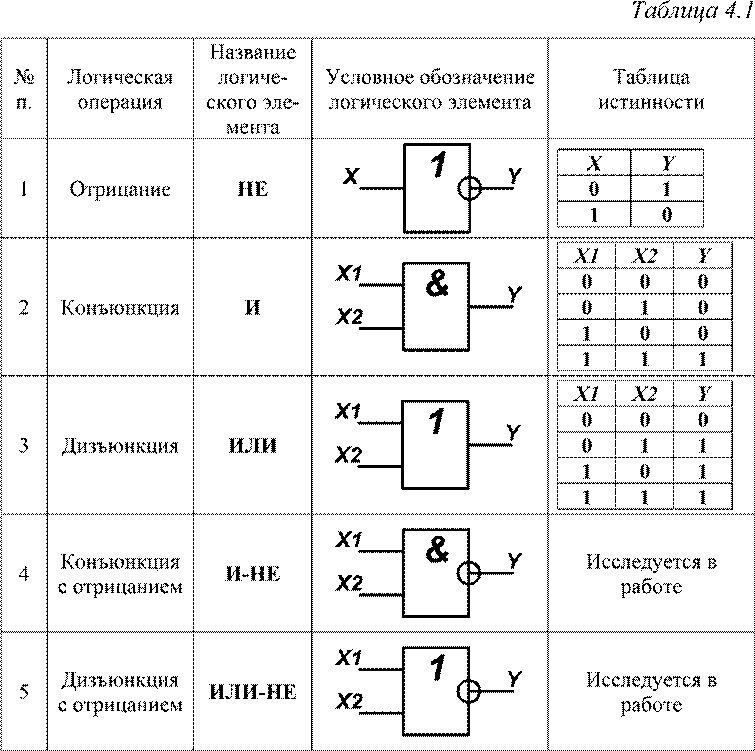 Обычно такие микросхемы изготавливаются в сверхминиатюрных корпусах с поверхностным монтажом. В качестве примера на рис. 18.19 показаны логические микросхемы И-НЕ и ИЛИ-НЕ 74AHC1G01 и 02 фирмы Surface mounted.
Обычно такие микросхемы изготавливаются в сверхминиатюрных корпусах с поверхностным монтажом. В качестве примера на рис. 18.19 показаны логические микросхемы И-НЕ и ИЛИ-НЕ 74AHC1G01 и 02 фирмы Surface mounted.
Рис. 18.19. Одновентильные логические схемы
Из микросхем малой и средней степени интеграции наиболее часто применяют преобразователи уровня и шинные формирователи. Преобразователи уровня используются для согласования входных и выходных сигналов по напряжению и току при построении цифровых устройств на различных логических элементах.
Логические элементы, в зависимости от элементной базы, на которой они построены, имеют разные напряжения питания и разные значения входных и выходных сигналов. Кроме того, однотипные микросхемы могут допускать разное напряжение питания, и при таком их использовании в разных частях одного устройства также требуется согласование уровней.
Так, для микросхем транзисторно-транзисторной логики (TTJI), которые построены на биполярных транзисторах, уровень логического 0 входного напряжения < 0,8 В, уровень логического 0 выходного напряжения < 0,4 В, уровень логической 1 входного напряжения > 2,4 В, а уровень логической 1 выходного напряжения > 2,8 В. Напряжение питания ТТЛ равно 5В.
Напряжение питания ТТЛ равно 5В.
Для микросхем, построенных на полевых транзисторах (КМОП), напряжение питания ЕПИТ обычно лежит в пределах от 5 до 15 В, а уровень логического 0 входного напряжения – 0,2 ЕПИТ, уровень логического 0 выходного напряжения равен 0 В, уровень логической 1 входного напряжения > 0,8ЕПИТ, а уровень логической 1 выходного напряжения равен ЕПИТ.
Пороговое напряжение переключения для ТТЛ составляет 1,2 В, а для КМОП – 0,5 ЕПИТ.
Кроме того, некоторые КМОП- элементы имеют малые выходные токи, поэтому к ним нельзя подключать |даже один вход ТТЛ даже при одинаковых ЕПИТ.
Так, для согласования выходов КМОП элементов со входами ТТЛ можно применять микросхемы К176ПУ1, К176ПУ2, К176ПУЗ, К561ПУ4, КР1561ПУ4. По принципу функционирования они аналогичны друг другу, но имеют разное число входов и некоторые помимо преобразования еще осуществляют инверсию сигнала (ПУ1, ПУ2). Например, микросхема КР1561ПУ4 (рис. 18.20 а) имеет 6 входов и выходов и позволяет при подаче на нее напряжения питания 5 В и подключении ее входов к выходам КМОП — микросхем подключать к каждому из ее выходов от двух до восьми микросхем ТТЛ в зависимости от их схемотехнической реализации.
Например, микросхема КР1561ПУ4 (рис. 18.20 а) имеет 6 входов и выходов и позволяет при подаче на нее напряжения питания 5 В и подключении ее входов к выходам КМОП — микросхем подключать к каждому из ее выходов от двух до восьми микросхем ТТЛ в зависимости от их схемотехнической реализации.
Рис. 18.20. ИМС: а – КР1561ПУ4; б – К561 ПУ7
Для коммутации сигналов в цифровых устройствах, например, сигналов адреса, сигналов управления, подключения внешних устройств к системной шине данных в микропроцессорной системе, используются шинные формирователи (шинные драйверы, буферные элементы).
Реализуются они на логических элементах с повышенной нагрузочной способностью, имеющих открытый выход (коллекторный или стоковый) или три состояния выхода.
Они могут быт как однонаправленные, так и двунаправленные (могут осуществлять передачу данных как со входов на выход, так и наоборот).
Так, микросхема К555АП5 (рис. 18.21, а) представляет собой восемь буферных элементов, выходы которых имеют три состояния.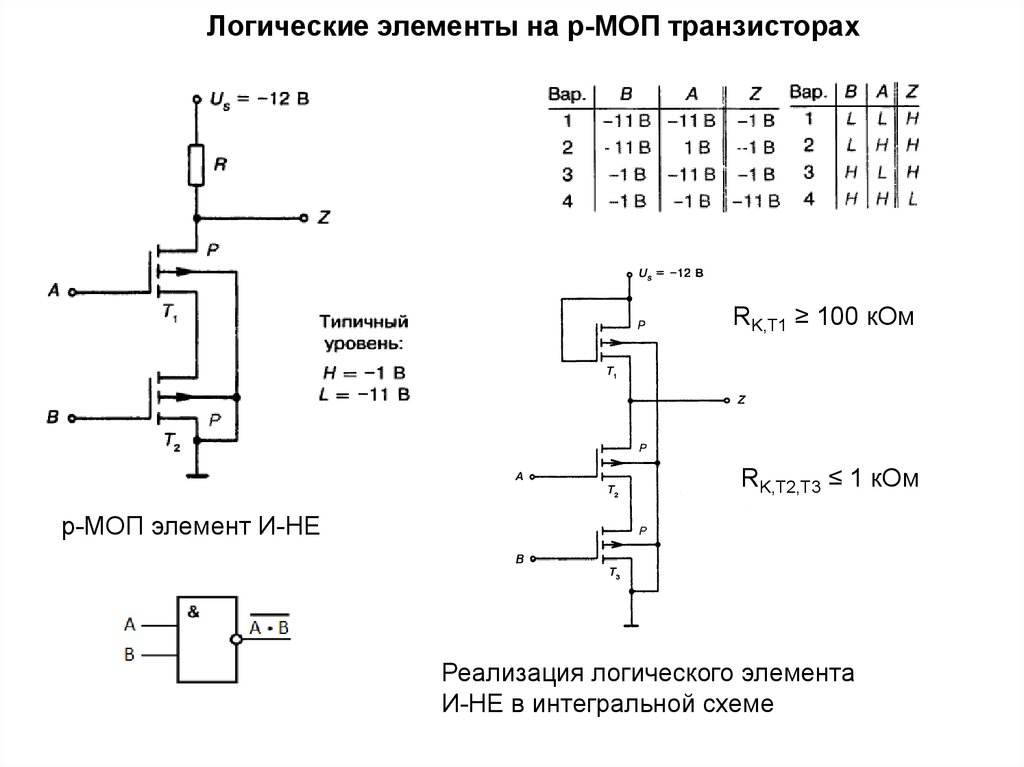 Буферные элементы сформированы в две группы, каждая из которых имеет инверсный вход управления. Включение элементов каждой группы происходит при подаче на соответствующий вход управления E1 или E2 логического нуля, переход в высоко импедансное состояние осуществляется при подаче на эти входы логической единицы.
Буферные элементы сформированы в две группы, каждая из которых имеет инверсный вход управления. Включение элементов каждой группы происходит при подаче на соответствующий вход управления E1 или E2 логического нуля, переход в высоко импедансное состояние осуществляется при подаче на эти входы логической единицы.
Рис. 18.21. ИМС: а – К555АП5; б – К555АП6
Микросхема К555АП6 (рис. 18.21, б) представляет собой восемь двунаправленных буферных элементов, все выводы которых имеют три состояния, а также имеются два входа управления. Логический нуль на входе разрешает включение буферных элементов, и если при этом на вход Т подана логическая 1, то выводы А1 – А8 являются входами, а выводы В1 – В8 выходами. При логическом 0 на входе Т выводы В1 – В8 являются входами, а выводы А1 – А8 выходами. При логической 1 на входе все выводы переводятся в высокоимпедансное состояние.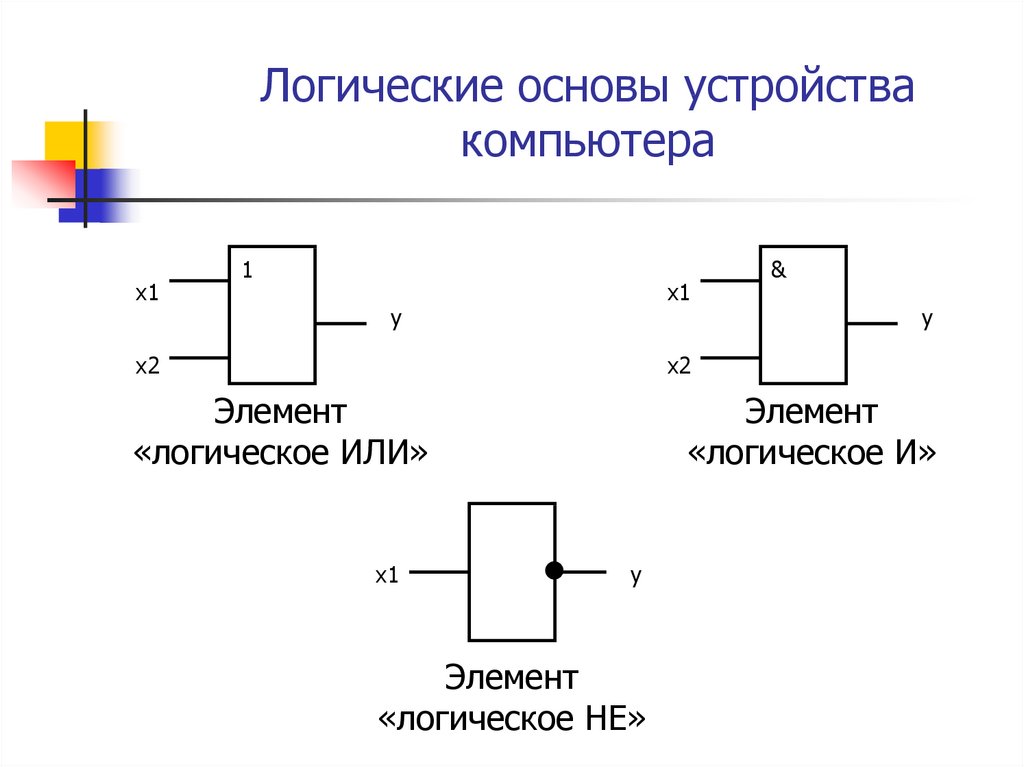
Комбинированные логические схемы
В цифровых системах для получения требуемых характеристик обычно применяются комбинации логических элементов. Например, последовательное включение логических элементов И и НЕ позволяет получить функцию И-НЕ (рис. 11.13(а)). Таким же образом можно получить логическую функцию ИЛИ-НЕ, объединив элементы ИЛИ и НЕ (рис. 11.13(б)).
В качестве поясняющего примера рассмотрим логическую схему на рис. 11.14. На вход схемы подается сигнал 0111. Нужно определить сигнал на выходе.
Решение. На выходе схемы ИЛИ (i) присутствует 1, а на выходе схемыИ-НЕ (ii) – 0. Следовательно, на входы схемы ИЛИ (iii) подается комбинация 10 и на ее выходе Gдействует логическая 1.
На рис. 11.15 изображена комбинация простых логических элементов для управления сигнализацией. Схема G1является элементом ИЛИ-НЕ, у которого объединены входы. В результате G1 действует как инвертор НЕ.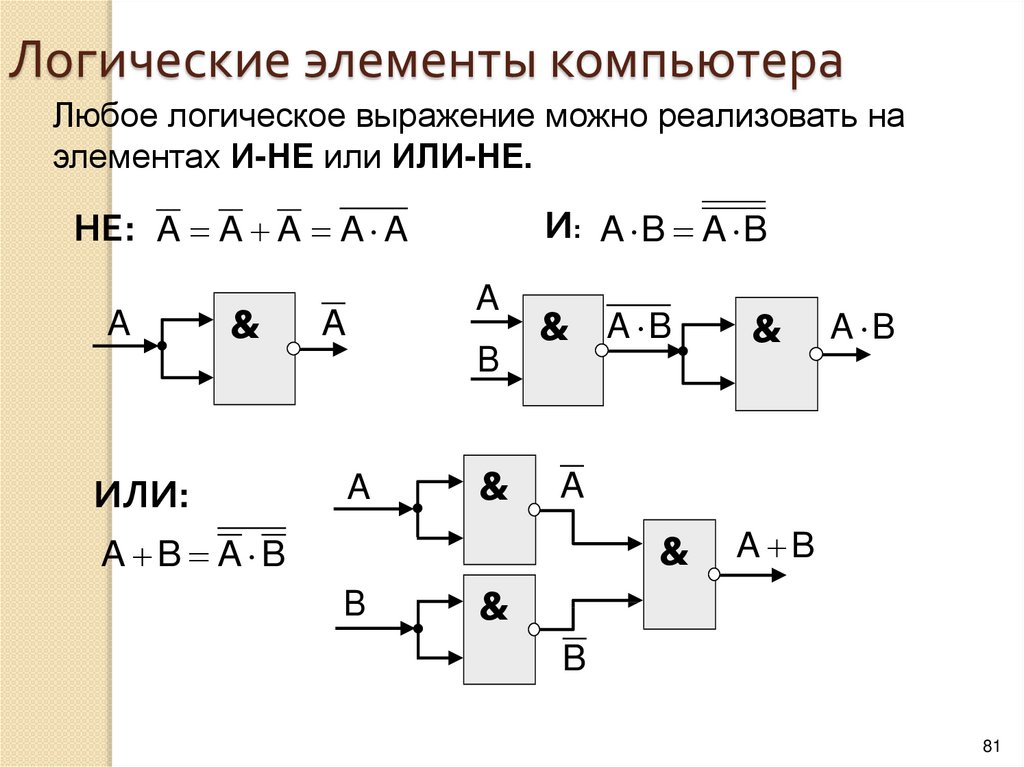 Чтобы сработала сигнализация, на звонок должно быть подано положительное напряжение от источника питания, т. е. на выходе элемента И (схема G2) должна действовать 1. Для этого на оба входа элемента И должны быть поданы 1. Такое может случиться, если ключ S1 разомкнут, а ключ S2 замкнут. Другой комбинации, при которой может сработать сигнализация, нет.
Чтобы сработала сигнализация, на звонок должно быть подано положительное напряжение от источника питания, т. е. на выходе элемента И (схема G2) должна действовать 1. Для этого на оба входа элемента И должны быть поданы 1. Такое может случиться, если ключ S1 разомкнут, а ключ S2 замкнут. Другой комбинации, при которой может сработать сигнализация, нет.
Рис. 11.13. Рис. 11.14.
Рис. 11.15.
Двоичная система счисления
Если в десятичной системе счисления используется десять цифр, то в двоичной их всего две: нуль и единица(0 и 1). Эта система идеально подходит для логических схем и имеет дело именно с ними.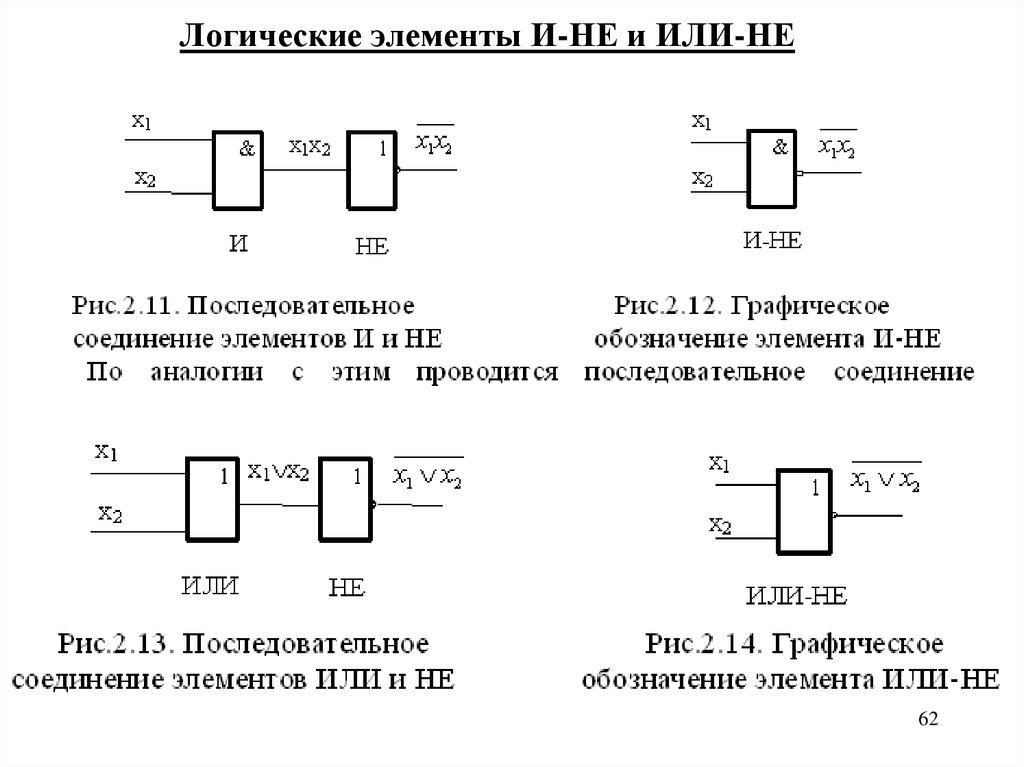
В десятичной системе первый столбец А (табл. 11.9) является столбцом единиц, столбец В — столбцом десятков, С — сотен, D — тысяч и т. д. В двоичной системе каждый столбец может быть представлен либо 0, либо 1. При этом первый столбец А соответствует единицам, В -двойкам, С — четверкам, D — восьмеркам и т. д. Любое число может быть представлено как в десятичной системе, так и в двоичной системе. В табл. 11.10 показано преобразование десятичных чисел от 0 до 7 в двоичные.
Таблица 11.9
|
Десятичные столбцы |
Двоичные столбцы |
||||||
|
D |
C |
B |
А |
D |
C |
B |
А |
|
103 |
102 |
101 |
10° |
23 |
22 |
21 |
2° |
|
Тысячи |
Сотни |
Десятки |
Единицы |
Восьмерки |
Четверки |
Двойки |
Единицы |
Таблица 11. 10
10
|
Десятичные числа |
Двоичные числа |
||
|
С |
В |
А |
|
|
(4) |
(2) |
(1) |
|
|
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
|
2 |
0 |
1 |
0 |
|
3 |
0 |
1 |
1 |
|
4 |
1 |
0 |
0 |
|
5 |
1 |
0 |
1 |
|
6 |
1 |
1 |
0 |
|
7 |
1 |
1 |
1 |
Для чисел, больших 7, нужен четвертый столбец (восьмерки). Так, 8 = 1000,9 == 1001, 10 = 1010, 11 == 1011 и т. д.
Так, 8 = 1000,9 == 1001, 10 = 1010, 11 == 1011 и т. д.
В табл. 11.11 приведено несколько примеров преобразования двоичных чисел в десятичные.
Таблица 11.11
|
Двоичные числа |
Двоичные столбцы |
Десятичные числа |
|||||
|
32 |
16 |
8 |
4 |
2 |
1 |
||
|
1110 |
— |
— |
1 |
1 |
1 |
0 |
= 8 + 4 + 2 = 14 |
|
1011 |
— |
— |
1 |
0 |
1 |
1 |
= 8 + 2 + 1 = 11 |
|
11001 |
— |
1 |
1 |
0 |
0 |
1 |
= 16 + 8 + 1 = 25 |
|
10111 |
— |
1 |
0 |
1 |
1 |
1 |
= 16 + 4 + 2 + 1 = 23 |
|
110010 |
1 |
1 |
0 |
0 |
1 |
0 |
= 32 + 16 + 2 = 50 |
Счетчик частоты
Логический элемент И в соединении со счетчиком может применяться для измерения частоты или периода. На рис. 11.16 показана схема измерителя частоты, состоящая из логического элемента И с двумя входами и счетчика. На вход А подается входной сигнал, а на вход В — тактовые импульсы заданной длительности. Сигнальные импульсы будут появляться на выходе схемы И только во время действия тактового импульса. Затем эти импульсы поступают на счетчик, который считает их и таким образом определяет частоту входного сигнала. Например, если длительность тактового импульса равна 10 мс, а длительность входного сигнала при его частоте 1 кГц составляет 1 мс, то за время действия тактового импульса на выходе схемы появятся только 10 импульсов, которые, будучи посчитаны счетчиком, дадут частоту 1 кГц.
На рис. 11.16 показана схема измерителя частоты, состоящая из логического элемента И с двумя входами и счетчика. На вход А подается входной сигнал, а на вход В — тактовые импульсы заданной длительности. Сигнальные импульсы будут появляться на выходе схемы И только во время действия тактового импульса. Затем эти импульсы поступают на счетчик, который считает их и таким образом определяет частоту входного сигнала. Например, если длительность тактового импульса равна 10 мс, а длительность входного сигнала при его частоте 1 кГц составляет 1 мс, то за время действия тактового импульса на выходе схемы появятся только 10 импульсов, которые, будучи посчитаны счетчиком, дадут частоту 1 кГц.
Рис. 11.16. Схема И в качестве измерителя частоты
Цифровой датчик времени (цифровые часы) (рис. 11.17)
Импульсы от кварцевого генератора, имеющего очень высокую стабильность частоты, подаются на цепочку делителей частоты, которая генерирует точную последовательность тактовых импульсов.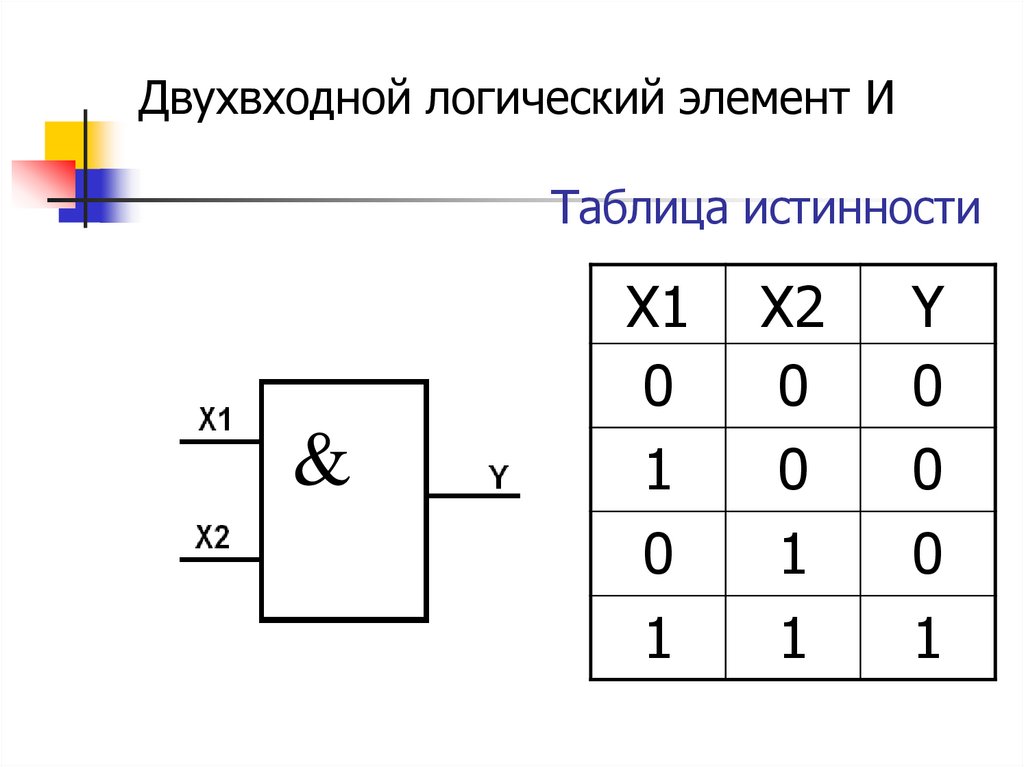 Декодер преобразует тактовые импульсы делителя в соответствующие сигналы, которые поступают на индикатор (см. также гл. 35). Секундный индикатор работает с самой высокой частотой, а часовой – с самой низкой.
Декодер преобразует тактовые импульсы делителя в соответствующие сигналы, которые поступают на индикатор (см. также гл. 35). Секундный индикатор работает с самой высокой частотой, а часовой – с самой низкой.
Рис. 11.17. Блок-схема цифрового датчика времени.
Аналого-цифровой преобразователь (АЦП)
АЦП преобразует входной аналоговый сигнал в цифровой (рис. 11.18). Выходной сигнал представляет собой некоторое число параллельных цифровых разрядов (четыре на рис. 11.18). Каждый разряд это двоичный столбец.
Рис. 11.18.
Цифро-аналоговый преобразователь (ЦАП)
На вход ЦАП поступает параллельный цифровой код. ЦАП преобразует его снова в величину напряжения (или ток), которая была представлена
Рис. 11.19.
в виде двоичного входного сигнала.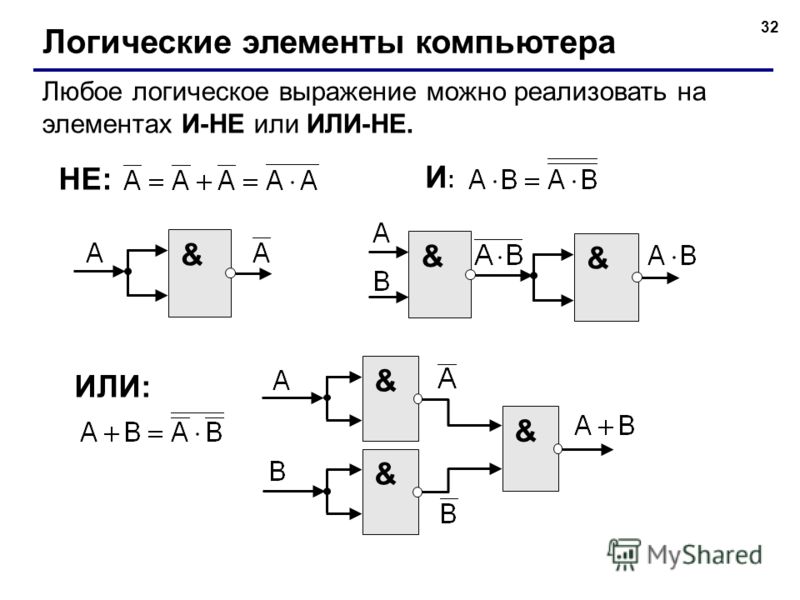 Если это проделать с последовательностью цифровых входных сигналов, то можно восстановить аналоговую форму исходного сигнала (рис. 11.19).
Если это проделать с последовательностью цифровых входных сигналов, то можно восстановить аналоговую форму исходного сигнала (рис. 11.19).
Цифровая обработка сигнала
Большинство сигналов, встречающихся в повседневной жизни, например звук и видео, существуют в аналоговой форме. Прежде чем ввести такие сигналы в цифровую систему, например в цифровой магнитофон, необходимо преобразовать их в цифровую форму с помощью аналого-цифрового преобразователя (рис. 11.20). После соответствующей обработки цифровой сигнал снова преобразуется в исходную аналоговую форму, т. е. в звуковой сигнал, с помощью цифро-аналогового преобразователя.
Рис. 11.20.
В данном видео рассказывается о цифро-аналоговых преобразователях:
Добавить комментарий
Цифровые логические схемы: определение, применение и типы
Содержание
В настоящее время компьютеры и другие цифровые устройства основаны на электронных схемах.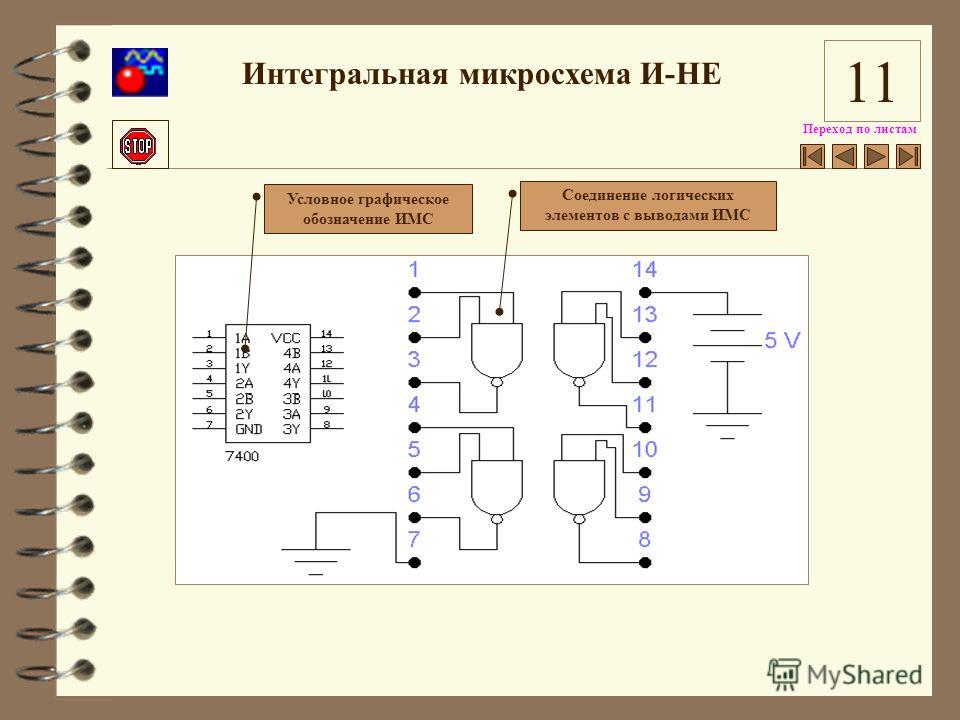 Если вы ничего не знаете о цифровых схемах, не волнуйтесь, мы здесь для вас.
Если вы ничего не знаете о цифровых схемах, не волнуйтесь, мы здесь для вас.
Цифровые схемы состоят из транзисторов и других компонентов для создания логических элементов. Логические элементы можно комбинировать для создания логических схем, таких как сумматоры, мультиплексоры, счетчики и декодеры, которые решают определенные задачи, такие как сложение чисел или декодирование входной строки в осмысленный выход.
Цифровые схемы являются основой компьютеров. Они используются для различных целей, начиная от простых логических вентилей и заканчивая сложными микропроцессорами, отвечающими за выполнение инструкций на компьютере.
Расскажите нам больше о цифровых логических схемах с помощью этой статьи:
Цифровые логические схемы являются основой цифровых систем. Эти логические схемы представляют собой набор логических вентилей, которые показывают логическую эквивалентность между двумя разными группами двоичных чисел.
Эти цифровые логические схемы используют 0 и 1 для условий включения/выключения, где 0 означает состояние включения, а 1 — состояние отключения.
Цифровые логические схемы — это цифровые устройства, которые используют логические вентили, АЛУ, микропроцессоры, ОЗУ, ПЗУ для управления другими схемами. Это особая форма логической схемы, которая обрабатывает числовые значения 0 и 1.
Как работают цифровые схемы?
Цифровая схема преобразует ряд чисел в другой ряд чисел. Он предназначен для предоставления только одного выхода для любого заданного входа, и на выходе будет либо 0 В, либо 5 В. Это схема, которая использует дискретные значения напряжения для представления данных.
Наиболее распространенные цифровые схемы основаны на двоичной системе счисления, хотя в некоторых системах используются недвоичные значения. Цифровая схема содержит переключатели, которые либо включены, либо выключены. Он обрабатывает информацию как последовательность «1» и «0».
Почему мы используем цифровые схемы?
Цифровая схема — это электронная схема, которая использует дискретные количества информации, такие как логические уровни (т.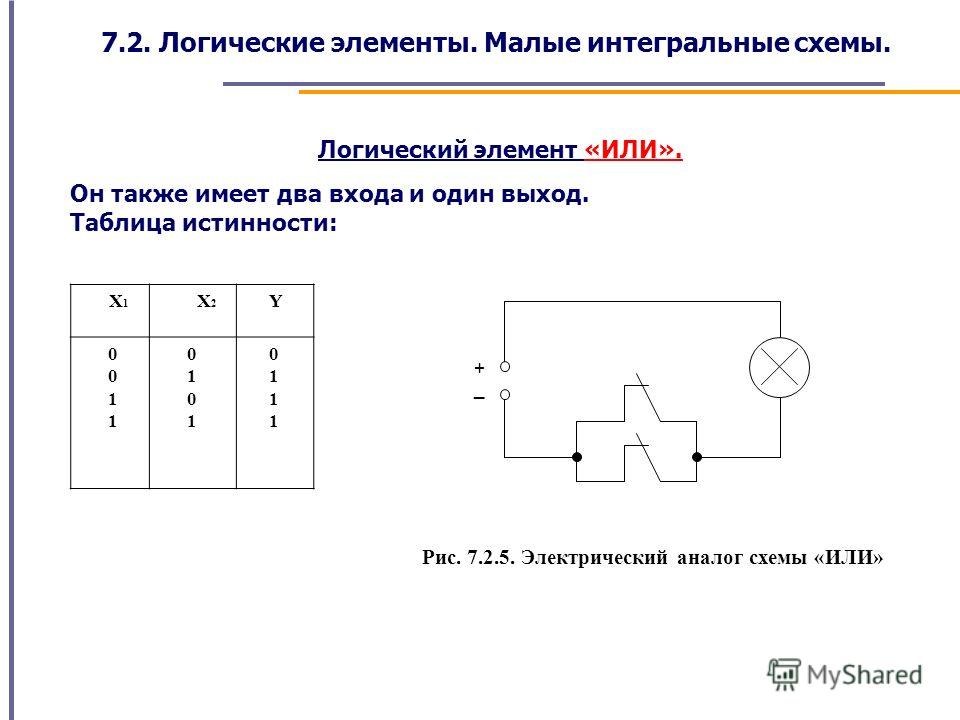 е. не непрерывный диапазон, как аналоговый сигнал), для обработки информации и выполнения функций. Мы используем цифровую схему, потому что она может изменять уровень напряжения от 0В до 5В, что очень удобно для использования с микроконтроллером.
е. не непрерывный диапазон, как аналоговый сигнал), для обработки информации и выполнения функций. Мы используем цифровую схему, потому что она может изменять уровень напряжения от 0В до 5В, что очень удобно для использования с микроконтроллером.
Цифровая схема — это способ хранения информации. Он использует двоичный код, в котором всего две цифры: ноль и единица. Цифровые схемы используются в калькуляторах, компьютерах, телевизорах и многих других устройствах.
Почему цифровые схемы также называют логическими схемами?
Цифровые схемы также называют логическими схемами, поскольку они выполняют логические операции над цифровыми сигналами. Цифровые схемы используют логические элементы, такие как И, ИЛИ, НЕ, НЕ-И и ИЛИ, для выполнения необходимых цифровых операций.
Цифровая схема — это схема, содержащая цифровую логику. Цифровые схемы являются наиболее распространенной физической реализацией булевой алгебры и двоичной арифметики и лежат в основе всех современных компьютеров.
Это связано с тем, что цифровые схемы в основном используются для обработки данных, которые имеют только два значения, например, истинное или ложное.
Другими словами, можно сказать, что основной функцией цифровой схемы является обработка информации, управляющей двоичной системой. Цифровые схемы называются логическими, потому что они выполняют логические операции и дают результаты, которые можно интерпретировать как истинные или ложные.
Каковы основные концепции цифровых схем и систем?
Цифровая схема, также известная как цифровая электроника, представляет собой отрасль электроники, которая выполняет различные задачи для выполнения множества требований с помощью цифровых сигналов. В основном эта схема используется для преодоления недостатков аналоговых систем.
Аналоговые системы медленнее, и полученные данные могут содержать ошибку. Схема разработана с использованием двоичных логических элементов, таких как ИЛИ, исключающее ИЛИ, НЕ, И-НЕ, ИЛИ, И.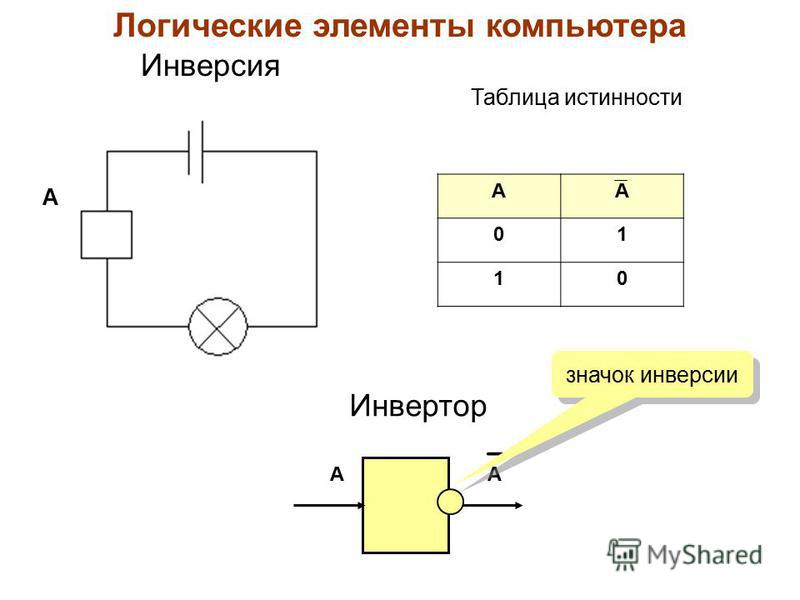 Эти логические элементы известны выполнением логических операций.
Эти логические элементы известны выполнением логических операций.
Эта конструкция помогает схеме переходить из одного состояния в другое. Входной сигнал, используемый для этой схемы, имеет цифровую форму, которая представляет собой двоичный формат 0 и 1.
Схема может быть двух видов: комбинационная или последовательная. Сначала он был запущен путем разработки более поздних электронных ламп, транзисторно-транзисторной логики TTL, логики с эмиттерной связью и логических реле CMOS.
Основные строительные блоки цифровых схем:
Логические элементы являются основным компонентом цифровых схем, которые могут выполнять преобразование двоичной информации. Цифровая схема содержит сеть из нескольких логических вентилей, которые взаимосвязаны друг с другом.
Каждые ворота имеют свой символ, которым они представлены, и алгебраическая функция определяет их работу. Таблица истинности может определить связь между выходными и входными переменными каждого вентиля.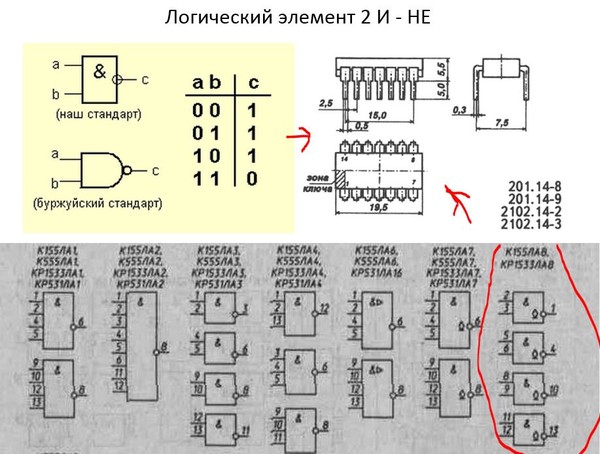 Временная диаграмма определяет возвратно-поступательное движение сигнала логических вентилей.
Временная диаграмма определяет возвратно-поступательное движение сигнала логических вентилей.
Основы аналоговых и цифровых электронных схем:
Интегральная схема является пульсом многих поколений современных инноваций в области электроники. Многие компании участвуют в проектировании, чтобы работать лучше, а также в разработке и производстве, чтобы предоставить больше новых кремниевых технологий, благодаря которым инженеры могут создавать новые ИС с хорошим функциональным оборудованием с хорошей производительностью и мощностью, новыми и лучшими электронными инновациями.
Ожидается, что глобальный объем данных увеличится с 897 эксабайт в 2020 году до 392 540 эксабайт к 2030 году, поскольку бизнес становится все более цифровым и, таким образом, поглощает и создает данные.
И ИС будут расти только тогда, когда они будут увеличиваться и расти во всем мире, как космические ракеты. Чтобы поставлять больше и производить больше, нам нужен хороший поставщик и надежный партнер, преданный делу компании, который предлагает лучшее решение на сегодняшний день и обеспечивает более совершенную разработку новых технологий, чтобы сделать компании более успешными.
Типы цифровых логических схем:
Кратко остановимся на некоторых типах цифровых логических схем:
1. Синхронные системы:
каждый компонент системы в данный момент определяет состояние во все последующие моменты времени. Асинхронная система — это система, в которой события и процессы происходят регулярно и повторяются.
Синхронные системы включают часы, наши циркадные ритмы и периодические явления, такие как приливы и волны. В электронике асинхронная система — это система, в которой временное поведение различных элементов связано друг с другом. Время событий в синхронных системах зависит от часов сигналов.
Время событий в синхронных системах зависит от часов сигналов.
2. Асинхронные системы:
Асинхронные системы отправляют сообщения и выполняют операции параллельно без необходимости ждать ответа. Это означает, что разные процессы могут происходить одновременно; то есть несколько функций могут выполняться одновременно.
Асинхронный означает отсутствие или возможность появления одновременно. Асинхронная система — это набор взаимодействующих частей, которые не имеют общего состояния и поэтому могут выполняться независимо.
3. Комбинационные логические схемы:
Комбинационная логика — это форма цифровой логики, в которой входной шаблон применяется к схеме, а выходной шаблон зависит только от этого входного шаблона. Логические элементы, несомненно, являются одним из самых основных и важных строительных блоков цифровых схем.
Они обычно используются для выполнения операций с двоичными сигналами. С другой стороны, комбинированные логические схемы — это электронные или компьютерные схемы, предназначенные для реализации булевых функций или логических процедур.
Эти схемы представляют собой схемы, которые выполняют свои операции только с входными сигналами.
4. Последовательные сети:
Сеть последовательности — это тип эквивалентной сети баланса, который используется для системы баланса мощности. Инвестиции и предполагаемые рабочие условия устанавливаются таким образом, чтобы в напряжении и токе могла присутствовать только одна составляющая последовательности.
Эти сети используются для расчета несимметричных повреждений, присутствующих в различных частях или точках сети энергосистемы.
Схемы аналого-цифровых преобразователей
Аналого-цифровые преобразователи (АЦП) и цифро-аналоговые преобразователи (ЦАП) — это схемы, преобразующие один вид информации в другой.
Аналого-цифровой преобразователь (АЦП) представляет собой электронную схему, преобразующую аналоговый сигнал в цифровую форму. Другое преобразование, известное как цифро-аналоговый преобразователь (ЦАП), преобразует цифровое слово в аналоговый сигнал.
Вместе эти две схемы используются во многих приложениях, включая хранение, передачу и обработку данных. Он преобразует непрерывный поток аналоговых значений в дискретные цифровые значения. Затем это цифровое представление сохраняется в памяти или обрабатывается другими цифровыми системами.
Аналоговые и цифровые схемы :
Аналоговые и цифровые схемы являются основными строительными блоками всей современной электроники. Ключевое различие между аналоговой и цифровой электроникой заключается в представлении информации в виде сигналов.
Цифровые схемы представляют информацию в виде различных значений напряжения, таких как 0 В и 5 В, которые соответствуют «ложь» и «истина» в булевой логической системе. Аналоговая схема — это схема, которая представляет информацию в виде непрерывного диапазона напряжения.
Аналоговая схема — это схема, которая использует непрерывный диапазон значений для передачи информации. Напротив, цифровая схема представляет информацию дискретными шагами или уровнями.
В чем разница между цифровыми схемами и цифровой электроникой?
Цифровые схемы и цифровая электроника — это одно и то же, но они используются по-разному. Оба метода манипулируют двоичными сигналами для создания логических функций, но они также генерируют переключающие схемы или логические вентили в цифровой электронике.
Цифровая электроника в основном основана на уровнях напряжения. Цифровые схемы, с другой стороны, преобразуют сигналы в форму, которую может обработать компьютер или микропроцессор. Он использует логические вентили для управления цифровыми сигналами.
С другой стороны, цифровые схемы — это устройства, которые используются для выполнения логических операций с цифровыми сигналами с использованием этих логических элементов. Цифровые схемы — это электрические схемы, в которых используются дискретные уровни напряжения, такие как двоичная (с основанием 2) логика.
Наиболее распространенный тип схем в компьютерных системах. Напротив, цифровая электроника — это электронные схемы, используемые для создания цифровых схем (например, компьютеров).
Напротив, цифровая электроника — это электронные схемы, используемые для создания цифровых схем (например, компьютеров).
Цифровая электроника имеет дело с цифровыми интегральными схемами (ИС), которые выполняют определенные вычислительные функции с использованием двоичных чисел. Цифровые схемы в основном состоят из логических вентилей.
Их также называют комбинационными схемами, потому что выходы зависят исключительно от текущих входов и не зависят от истории входов.
Цифровые ИС содержат множество транзисторов, резисторов, конденсаторов, диодов и т. д., предназначенных для выполнения определенных операций, таких как сложение, умножение, сдвиг и т. д.
Что такое проектирование цифровых интегральных схем?
Проектирование цифровых интегральных схем — это процесс проектирования схем, выполняющих логические операции с использованием цифровых схем. Это делается путем создания двух или более электронных устройств и их соединения проводами.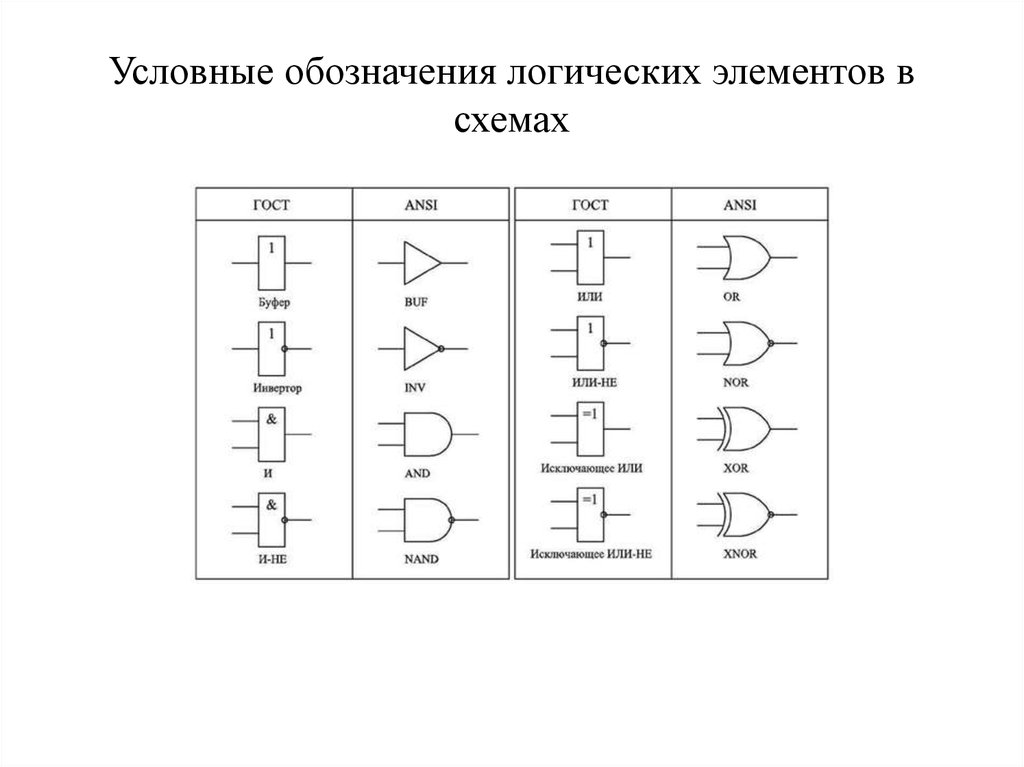
Наиболее распространенная цифровая логическая система представляет собой набор транзисторов, соединенных в последовательность логических элементов, управляющих двоичными числами (0 и 1).
Эти двоичные числа представляют информацию, которую будет обрабатывать схема.
Процесс проектирования аналоговых и цифровых схем. Он предполагает междисциплинарный подход к области электротехники. Целью этой деятельности является предоставление новых электронных продуктов или обновление существующих продуктов.
Проектирование цифровых интегральных схем — это метод проектирования электронных схем, с помощью которого цифровые сигналы преобразуются в эквивалентные двоичные коды, а полученные коды используются в качестве входных данных для создания аппаратных средств из этих двоичных кодов.
Почему цифровые схемы должны быть двоичными?
Цифровые схемы известны как основа современной электроники. Они повсюду в нашем мире — в наших телефонах, компьютерах, автомобилях и т. д. Вы когда-нибудь задумывались, почему все они двоичные?
д. Вы когда-нибудь задумывались, почему все они двоичные?
Ответ заключается в том, что цифровые схемы используют двоичную логику, потому что это самый простой способ манипулирования информацией. Основным преимуществом цифровых схем по сравнению с аналоговыми является точность и скорость.
Из чего состоит цепь?
Цепи по праву можно считать неотъемлемой частью нашей повседневной жизни. Цепь можно правильно назвать путем или соединением, которое формируется между различными точками.
Это может быть физический путь, например маршрут, по которому вы каждый день едете на работу, или это могут быть электрические соединения в вашем телефоне. Схема — это электронное устройство, которое может быть изготовлено из различных компонентов.
Он использует электрический ток для передачи энергии, данных или сигнала от одного компонента к другому.
Цепь состоит из полупроводников, соединенных проводами. Полупроводники — это материалы, которые могут проводить электричество при определенных условиях, в то время как изоляторы не пропускают электричество.
Цепь — это путь, по которому движутся электроны при движении через материал. В него входят проволока, бусины, металлические полоски и другие материалы. Когда электроны движутся по проводу, они проходят через разные части цепи.
Почему мы используем резистор в цепях?
Резистор — это электрический компонент, препятствующий протеканию тока в цепи. Обычно он находится последовательно с другими электронными компонентами, такими как конденсаторы и катушки индуктивности, и образует часть электронной схемы.
Резисторы являются одним из наиболее распространенных компонентов электрических цепей. Они бывают разных форм, размеров и упаковок.
Их основная цель — ограничить ток в цепи путем преобразования части его в тепло. Их основная цель — ограничить протекание тока в цепи путем преобразования части его в тепло. Узнайте больше о резисторах.
Лучшие тренажеры для цифровых логических вентилей Производитель, поставщик и экспортер:
Tesca Technologies Pvt.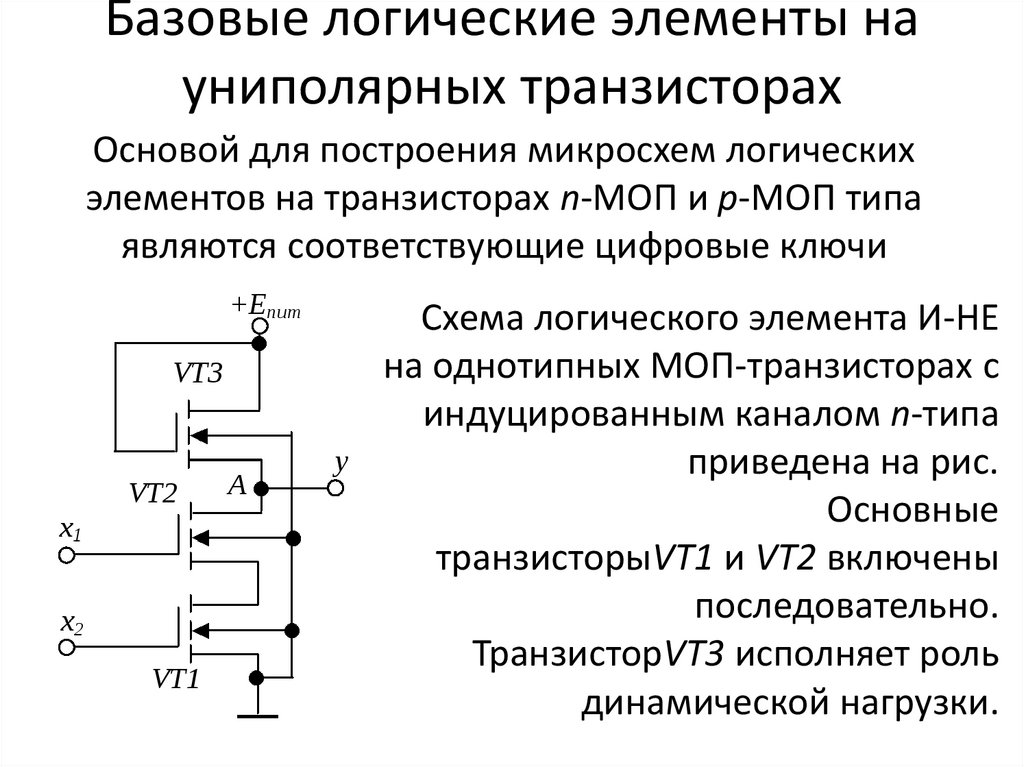 Ltd. является одним из самых известных производителей, поставщиков и экспортеров широкого спектра цифровых логических схем по всему миру. У нас есть возможности для реализации проектов «под ключ» для международных тендеров с отличной технической и маркетинговой поддержкой.
Ltd. является одним из самых известных производителей, поставщиков и экспортеров широкого спектра цифровых логических схем по всему миру. У нас есть возможности для реализации проектов «под ключ» для международных тендеров с отличной технической и маркетинговой поддержкой.
Брошюра Tesca Technologies Получить сейчас
МОП-транзистор, затвор и логика
Дата: 16-02-17
Этот модуль охватывает фундаментальные идеи, лежащие в основе проектирования современных цифровых систем. Этот модуль объясняет основы элементов схемы, как они взаимосвязаны для формирования цифровых схем, а также неидеальные эффекты дизайна.
Цифровые системы
Слово «цифровой» означает представление любой информации всего двумя уровнями напряжения [логический ноль (0) или высокий логический уровень (1)]. Логический ноль означает нулевое напряжение, логический высокий уровень означает некоторый уровень напряжения электрического потенциала, который обычно составляет 3,3 В или 5 В.
Цифровые системы более широко используются, чем аналоговые системы для обработки данных, по следующим причинам: Цифровые системы легче проектировать, поскольку цифровые системы используют цифровые сигналы, которые обеспечивают множество будущих возможностей, таких как очень меньшая подверженность шуму, сигнал может быть легко регенерирован и т. д. Термин «проектирование» относится к систематическому процессу разработки схем, отвечающих заданным требованиям, но при этом удовлетворяющих ограничениям по стоимости, производительности, энергопотреблению, размеру, высоте и другим свойствам.
Давайте начнем обсуждение логических вентилей, работающих с цифровым сигналом.
Существует три основных вентиля, а именно И, НЕ, ИЛИ, из которых получены вентили И-НЕ, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, Исключающее ИЛИ. Ворота И-НЕ и ИЛИ-НЕ обычно называют универсальными воротами. Теперь давайте начнем обсуждать, как работают эти ворота.
Ворота НЕ:
В компьютерном мире символом, используемым для обозначения ворот НЕ, является «~» (или) (!) (отрицание). Когда какой-либо высокий логический сигнал входит в логический элемент НЕ, выход не будет низким сигналом, и происходит обратная операция, когда низкий сигнал входит в логический элемент НЕ. Символ ворот НЕ изображен на рисунке 1, а его работа представлена в таблице истинности.
Когда какой-либо высокий логический сигнал входит в логический элемент НЕ, выход не будет низким сигналом, и происходит обратная операция, когда низкий сигнал входит в логический элемент НЕ. Символ ворот НЕ изображен на рисунке 1, а его работа представлена в таблице истинности.
Рисунок 1 : (a) символ инвертора (b) таблица истинности (c) ИС для не вентиля (d) схема инвертора
IC 7404 используется для вентиля НЕ, шесть вентилей НЕ встроены в IC 7404. Принципиальная схема вентиля НЕ показана на рисунке1
Вентиль И
В отличие от вентиля НЕ, вентиль И имеет две входные клеммы. Символ для представления функции И — «&». Выход логического элемента И будет высоким только тогда, когда оба входа будут высокими. Символ вентиля И показан на рисунке 2 ниже.
Рис. 2. Вентиль И , таблица истинности и внутренний вид IC7408 и IC7411
IC 7408 используется для операции И. Он содержит 4 вентиля И, каждый из которых имеет по два входа.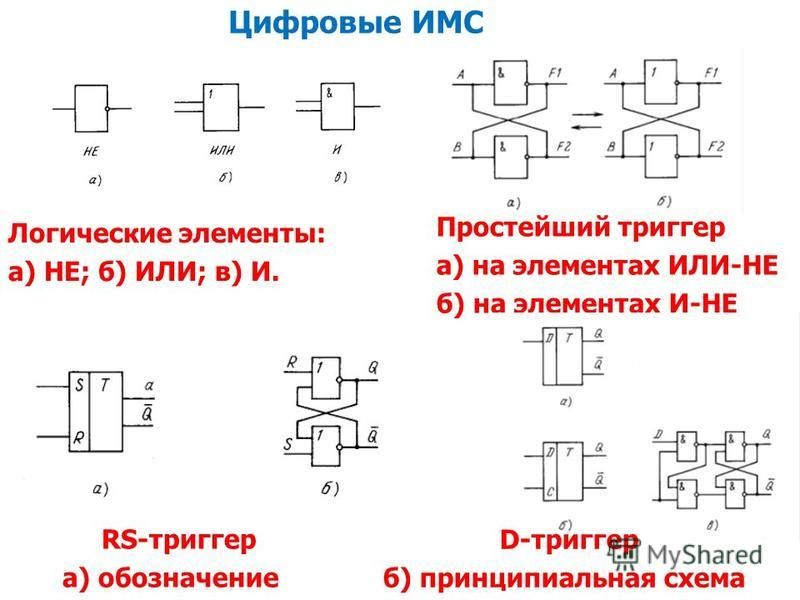 У нас может быть 3 входа И вентиль (IC7411). Конфигурация выводов IC 7408 и 7411 показана на рисунке 2.
У нас может быть 3 входа И вентиль (IC7411). Конфигурация выводов IC 7408 и 7411 показана на рисунке 2.
Мы можем получить 4-х входные логические элементы И с помощью двух входных логических элементов И. Давайте посмотрим, как мы можем это сделать.
На рисунке ниже показана принципиальная схема (схема) двухвходового И-затвора, выполненного с использованием полевых МОП-транзисторов.
ворота ИЛИ:
Символ для представления или ворот «|». Ворота ИЛИ выполняют сложение. когда любой из входов вентиля ИЛИ имеет высокий логический уровень, выход будет высоким. Таблица символов и истинности вентиля ИЛИ показана на рисунке 5. IC 7432 используется для операции ИЛИ. он содержит четыре, 2 входных элемента ИЛИ.
Рисунок 5: Символ и таблица истинности вентиля ИЛИ.
Рисунок 6: схема вентиля ИЛИ
Примечание. Чтобы узнать больше о номерах ИС для цифровых цепей, посетите: https://en.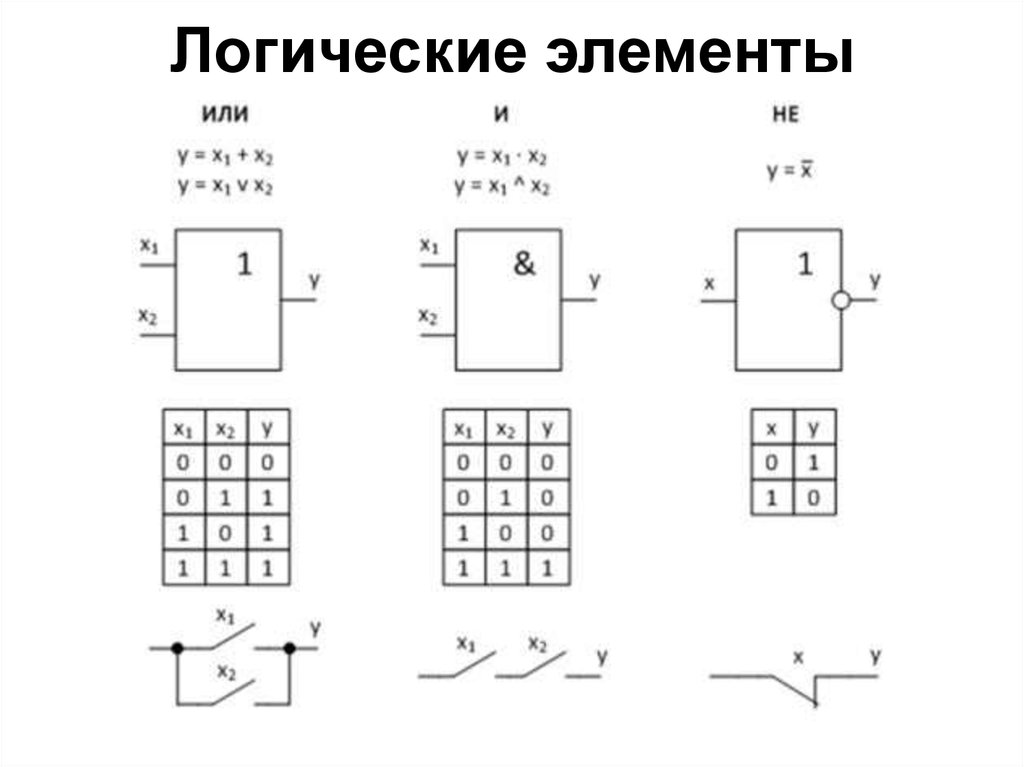 wikipedia.org/wiki/List_of_7400_series_integrated_circuits
wikipedia.org/wiki/List_of_7400_series_integrated_circuits
Включите свет в комнате когда в комнате темно, используя простой И-гейт:
Вот реальный пример, который всегда прост, И-гейт можно использовать для включения света в комнате, когда в комнате темно. Пожалуйста, смотрите рисунок 7. Это говорит о двух входных логических элементах И, где один вход подключен к переключателю, который либо подключен к +5 В высокого напряжения, либо заземлен к 0 напряжению. Чтобы заставить это устройство работать, вы должны держать переключатель таким образом, чтобы он был подключен к +5 В, чтобы вход на вентиль И всегда был высоким. Другой вход, верхний логический элемент И, подключен к датчику освещенности, который вырабатывает +5 В, когда темно или нет света, в противном случае нулевое напряжение низкого уровня, когда есть свет. Логический элемент И подключен к реле, которое может включать лампочку. Лампочка загорится только тогда, когда на обоих входах и будет высокий уровень. Так бывает только тогда, когда темно.
Так бывает только тогда, когда темно.
Рис. 7: Реальный пример с использованием вентиля И.
Приложения настолько просты, что логические вентили управляют современным миром в виде сложных процессорных чипов, которые имеют миллионы таких вентилей. В этом курсе мы познакомим вас с тем, как миллионы логических вентилей или проводных соединений выполняют сложную функцию для использования в режиме реального времени.
Мы начали с логических элементов в основном для того, чтобы объяснить с помощью приведенного выше приложения, где логические схемы могут использоваться для автоматизации многих наших потребностей.
Пример 2:
Рассмотрим завод по производству пластмасс. Установка должна поддерживаться ниже с определенным порогом температуры и давления. Если температура или давление превышают предельные значения, установка должна быть остановлена.
Рисунок 8: пример реального мира для вентиля ИЛИ
Пример 3
В реальных инверторах, соединенных встречно-параллельно с нечетными номерами, обратная связь передается от выхода к входу для получения колебаний.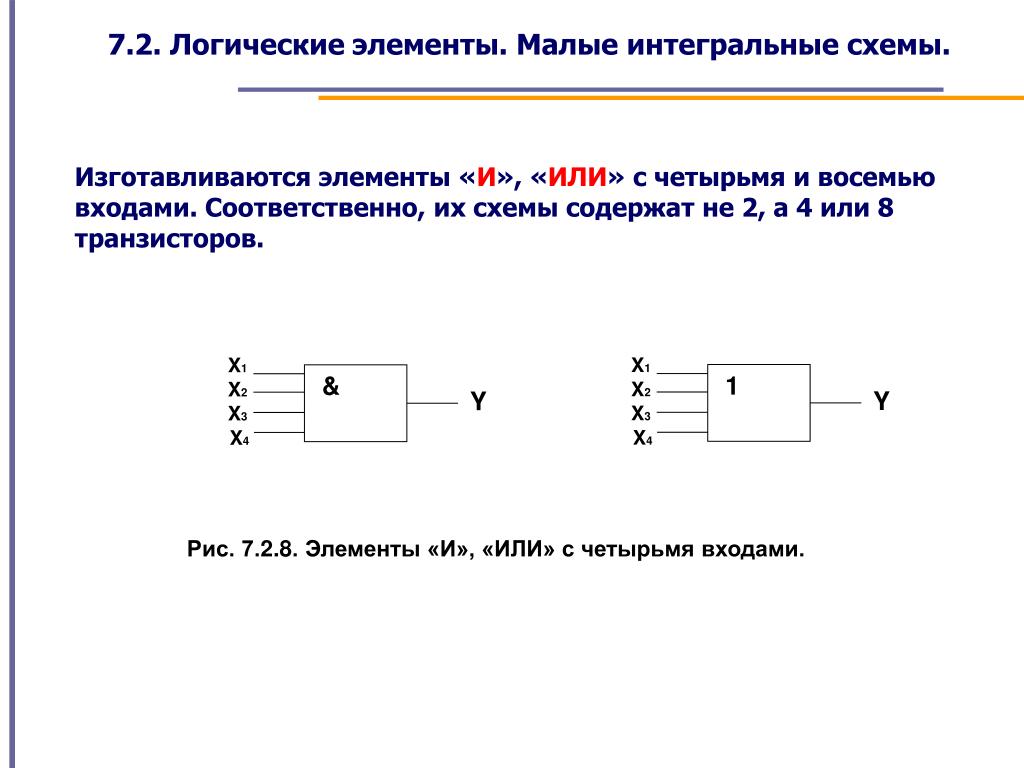
Рисунок 9: Кольцевой генератор
Примечание. Конструкция должна удовлетворять «критериям Баркгаузена» для цифровых и смешанных СБИС от Razavi.
Универсальные вентили (НЕ-И и ИЛИ-НЕ)
Вентиль-НЕ является обратным вентилю И. Символ логического элемента И-НЕ показан на рисунке 10. Работа логического элемента И объясняется в таблице истинности.
Рисунок 10: символ вентиля И-НЕ и его таблица истинности Символ вентиля ИЛИ-НЕ изображен на рисунке 11. Работа вентиля ИЛИ-ИЛИ объясняется в таблице истинности 9.Рисунок 11: символ логического элемента НЕ-ИЛИ и его таблица истинности Let’s see how is it made:
NAND as AND gate
NAND as OR gate
NOR as AND gate
XOR gate: Pronounced as Exclusive OR gate:
Логический элемент XOR выполняет операцию суммирования модулей, которая не включает перенос. Он содержит два входа и один выход. Символ вентиля XOR показан на рисунке 12.
Он содержит два входа и один выход. Символ вентиля XOR показан на рисунке 12.
Рисунок 12: Символ XOR Gate и его истинную таблицу
NAND AS xor Gate
XNOR (иногда ссылается как Exer Nor, NXOR) 9
xnor. XOR
Использование универсальных ворот в реальном мире.
Пример 1: Рассмотрите сценарий Промышленные химикаты хранятся на складах, где происходят химические реакции, приводящие к образованию токсичных паров, которые выбрасываются в атмосферу через вытяжные вентиляторы. В складских помещениях необходимо установить три вытяжных вентилятора для отвода ядовитого воздуха в процессе их работы. Если один или несколько вытяжных вентиляторов выходят из строя, активируется аварийный сигнал.
Рис. выше: Система обнаружения отказа вытяжного вентилятора на основе вентиля NAND
Пример 2: Стиральная машина оснащена тремя датчиками для проверки ее работы. Первая операция — это функционирование двери, вторая — уровень воды, а третья — взвешивание одежды. Если одна из функций выходит из строя, например, открытие или закрытие двери, изменение уровня воды или перегрузка одежды, генерирует соответствующие выходы датчика на 1. Выходы 3 датчиков подключены к 3 входам вентиля ИЛИ-НЕ. Выходы датчиков будут «0» во время нормальной работы стиральной машины. Выход вентиля ИЛИ-НЕ равен 0, если ошибочное состояние обнаружено любым одним или несколькими датчиками. Выход вентиля ИЛИ-ИЛИ подключен к выключателю стиральной машины.
Первая операция — это функционирование двери, вторая — уровень воды, а третья — взвешивание одежды. Если одна из функций выходит из строя, например, открытие или закрытие двери, изменение уровня воды или перегрузка одежды, генерирует соответствующие выходы датчика на 1. Выходы 3 датчиков подключены к 3 входам вентиля ИЛИ-НЕ. Выходы датчиков будут «0» во время нормальной работы стиральной машины. Выход вентиля ИЛИ-НЕ равен 0, если ошибочное состояние обнаружено любым одним или несколькими датчиками. Выход вентиля ИЛИ-ИЛИ подключен к выключателю стиральной машины.
Булева алгебра:
Булева алгебра используется в качестве основы для цифрового проектирования. Цифровые системы могут быть выражены в терминах логических выражений, которые содержат логические операторы, переменные и логические значения.
Булева алгебра имеет дело с логическим выражением
Пример логического выражения
В приведенном выше примере A, B, C являются переменными, ‘+’ и ‘. ‘ являются операторами, а ‘0’ и ‘1’ являются логическими значениями. . Аксиомы булевой алгебры перечислены ниже:
‘ являются операторами, а ‘0’ и ‘1’ являются логическими значениями. . Аксиомы булевой алгебры перечислены ниже:
Законы тождества
X+0=X
X.1=X
Законы ассоциации X (y.z)
Законы о коммутации
x+y = y+x
x.y = y.x
Законы о распределении
x+(y.z) = (x+y). (X+ Z)
X.(Y+Z)= (X.Y)+(X.Z)
Дополнительные законы
Ниже перечислены некоторые полезные теоремы, которые можно использовать при работе с булевыми выражениями.
Законы об идентичности
x+x = x
x.x = x
Законы об абсорбции
x+(x.y) = x
x. (x+y) = X
Дополнительные законы идентичности
x+1 = 1
x.0 = 0
Деко Морганы.
(2) f= AB+A(B+C)+B(B+C)
(3) f=A(B+CD)
Логические выражения могут быть выражены в двух формах, а именно: Сумма произведений (SOP) и произведение сумм (POS):
Сумма произведений: — Термины произведения логических выражений суммируются логическим сложением в форме SOP
Пример: — 1.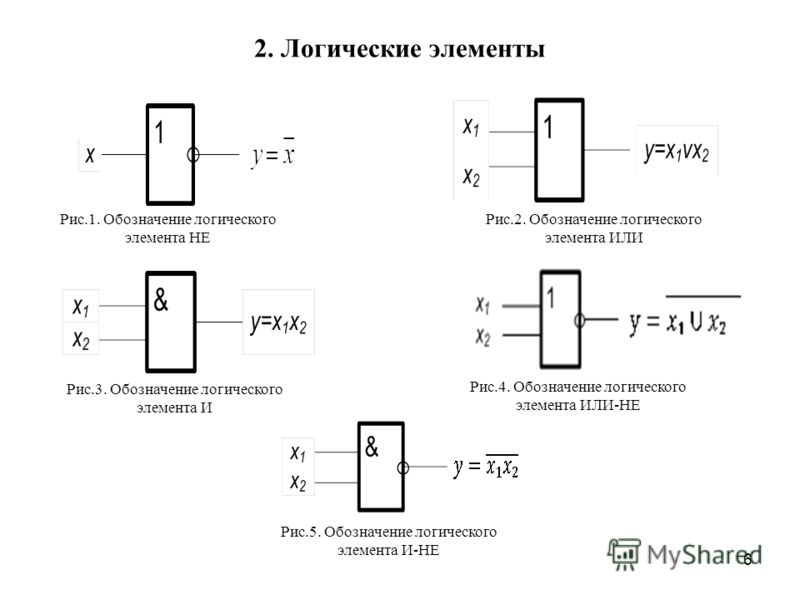 AB+BC+CA
AB+BC+CA
2 AB+B(C+D)
Произведение сумм: сумма переменных умножается на сумму других членов выражения.
• (A+B+C)A (D+F)
Мы не можем преобразовать логическое выражение в SOP или POS. Давайте посмотрим, как мы можем этого добиться:
• AB+B(CD+EF) преобразуется в SOP
Ответ. AB+BCD+BEF
• (A+B) (B+C+D) преобразовать в SOP
Ответ. AB+AC+AD
Примечание. Итак, мы уже видели выражения SOP и POS. Приведены примеры нестандартного способа выражения булевых выражений.
Стандартная СОП:
Рассмотрим пример f= AB+BC+CA, давайте преобразуем его в стандартную форму СОП:
>AB+BC+CA
Стандартное выражение СОП — это выражение, в котором все переменные в домене появляются в каждом термине продукта в выражении.
Стандартный POS
Упрощение логических выражений с помощью булевой алгебры БК
= AB+AC+BC+B
= B+ AC+AB
= B (1+A)+AC
=B+AC
Упрощение логического выражения упростит логику.
Рассмотрим выражение AB+A(B+C)+B(B+C), это эквивалентные логические схемы, а упрощенная принципиальная схема показана ниже
Упрощенная логика
методы и некоторые из них перечислены ниже:
1. Карта Карно
2. Алгоритм Куайна-Маккласки
3. Минимизация переменных состояния
Для получения дополнительной информации об упрощении логики см. «Цифровые логические приложения и проекты» Джона М. Ярбро.
Неидеальные эффекты элементов схемы
(1) Задержка распространения: Задержка распространения обусловлена внутренней коммутационной активностью (т. е. временем, необходимым для зарядки и разрядки паразитной емкости транзисторов)
Уровни сигналов не изменяются мгновенно к переключению деятельности. Время, необходимое для повышения напряжения сигнала от низкого уровня до высокого уровня, называется временем нарастания. Время, необходимое для падения напряжения сигнала с высокого уровня на низкий, называется временем спада.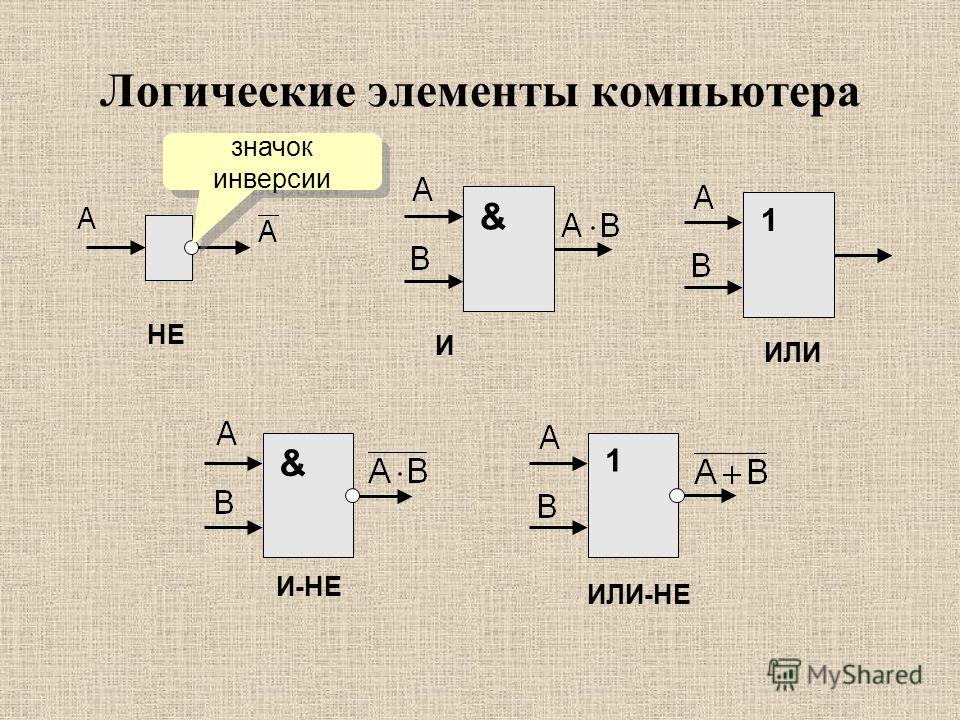
Рассмотрим схему, показанную на рисунке ниже.
Одним из способов уменьшения задержки распространения является уменьшение паразитной емкости. Если к выходу предыдущего блока подключено более одного логического блока, паразитная емкость суммируется, что приводит к чтобы больше задержка распространения, другими словами разветвление должно быть меньше.
(2)Задержка провода
Мы думаем, что провод ведет себя как чистый проводник без какого-либо сопротивления, но на самом деле провода будут иметь сопротивление, индуктивность и емкость. Когда длина провода слишком мала, этими значениями можно пренебречь. Когда длина проводов слишком велика, они становятся линией передачи с разумной задержкой распространения. Эти задержки следует учитывать при проектировании высокоскоростных систем.
(3)Глюки
Глитчи также известны как недопустимые выходные данные, которые возникают из-за задержки распространения на входах, входящих в логический блок, например, возьмем принципиальную схему, показанную ниже
В приведенном выше примере мы можем сказать, что неожиданный ноль на выходе схемы. Это называется сбоем, и он вызывает проблемы для остальных цепей, поскольку он распространяется на следующие цепи и приводит к большему количеству сбоев.
Это называется сбоем, и он вызывает проблемы для остальных цепей, поскольку он распространяется на следующие цепи и приводит к большему количеству сбоев.
Решение этой проблемы: добавление буфера к пути с меньшими задержками распространения. Эти буферы компенсируют задержку, чтобы мы могли ожидать корректных результатов на выходе.
Комбинационные логические схемы и последовательные логические схемы
комбинационные логические схемы выполняют операцию над входами, входящими в схему, и определяют выход как булеву функцию входа.
Другими словами, вывод является функцией только ввода. На рисунке ниже показана общая блок-схема комбинационной схемы.
Этим комбинационным логическим схемам не хватает сохранения каких-либо предыдущих выходов. Другими словами, у него нет памяти. Это можно преодолеть, используя последовательные схемы, в которых выход определяется как предыдущим, так и текущим входом. На рисунке ниже показана блок-схема последовательных логических схем.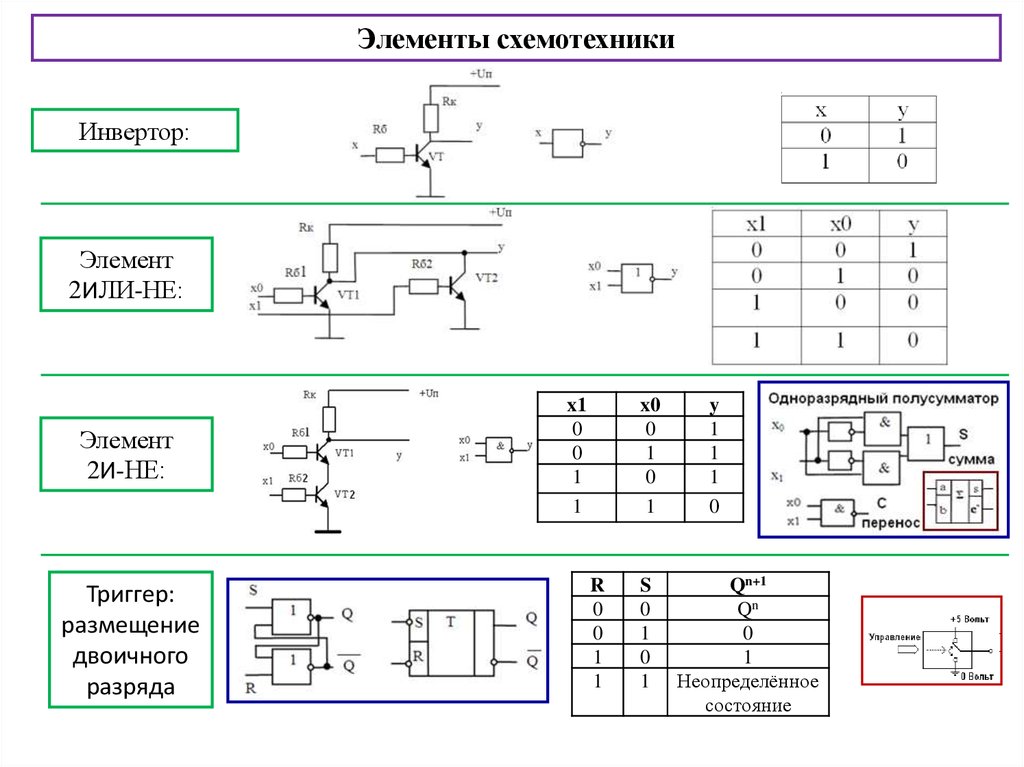
Для получения дополнительной информации о схемах последовательной логики и схемах комбинационной логики см. Цифровые интегральные схемы CMOS, автор Сунг Мо Канг Юсуф Леблебич.
Цифровые схемы подразделяются на синхронные и асинхронные
. В синхронных схемах будет один глобальный тактовый сигнал, который будет управлять всей схемой.
Преимущества синхронных цепей
• Конструкция проще
• Вероятность правильной работы выше
недостатки
маршрутизация становится проблемой
В асинхронных схемах будет на два часа больше, но они идеальны и синхронны.
Примечание. В большинстве коммерческих цифровых проектов используются синхронные схемы
Документация Digital Logic — SchemDraw 0.15
Логические элементы можно нарисовать, импортировав модуль schemdraw.logic.logic :
из логики импорта schemdraw
Логические вентили показаны ниже. Gates определяет якоря для из и из 1 , из 2 и т. д.
Buf , Not и NotNot , а также их аналоги с триггером Шмитта представляют собой двухполюсные элементы, которые удлиняют выводы.
Gates определяет якоря для из и из 1 , из 2 и т. д.
Buf , Not и NotNot , а также их аналоги с триггером Шмитта представляют собой двухполюсные элементы, которые удлиняют выводы.
Стропы с более чем 2 входами могут быть созданы с использованием параметра входов . При наличии более 3 входов задняя часть ворот будет расширяться вверх и вниз.
логика.Nand(входы=3)
логика.Нор(входы=4)
Наконец, любой вход может быть предварительно инвертирован (активный низкий) с использованием ключевого слова inputnots со списком входных номеров, начиная с 1, чтобы соответствовать именам привязок, на которые можно добавить инвертирующий пузырь.
логика.Nand(inputs=3, inputnots=[1])
Логический синтаксический анализатор
Логические деревья также могут быть созданы из строкового логического выражения, такого как «(a и b) или c», с использованием schemdraw. .
Для логического анализатора требуется модуль pyparsing.  parsing.logic_parser.logicparse()
parsing.logic_parser.logicparse()
Примеры:
из schemdraw.parsing import logicparse
logicparse('не ((w и x) или (y и z))', outlabel='$\overline{Q}$')
logicparse('((a xor b) и (b или c) и (d или e)) или ((w и x) или (y и z))')
Logicparse понимает логические функции «и», «или», «nand», «nor», «xor», «xnor», «not», а также общие символы, такие как «+», «&», «⊕» представляет собой «или», «и» и «исключающее ИЛИ».
logicparse('¬ (a ∨ b) & (c ⊻ d)') # Использование символов
Используйте параметры gateH и gateW для настройки выравнивания ворот:
logicparse('(не a) и b или c', gateH=.5)
Таблицы истинности
Простые таблицы можно рисовать с помощью класса schemdraw.logic.table.Table . Этот класс включен в логический модуль, так как его основная цель заключалась в построении логических таблиц истинности.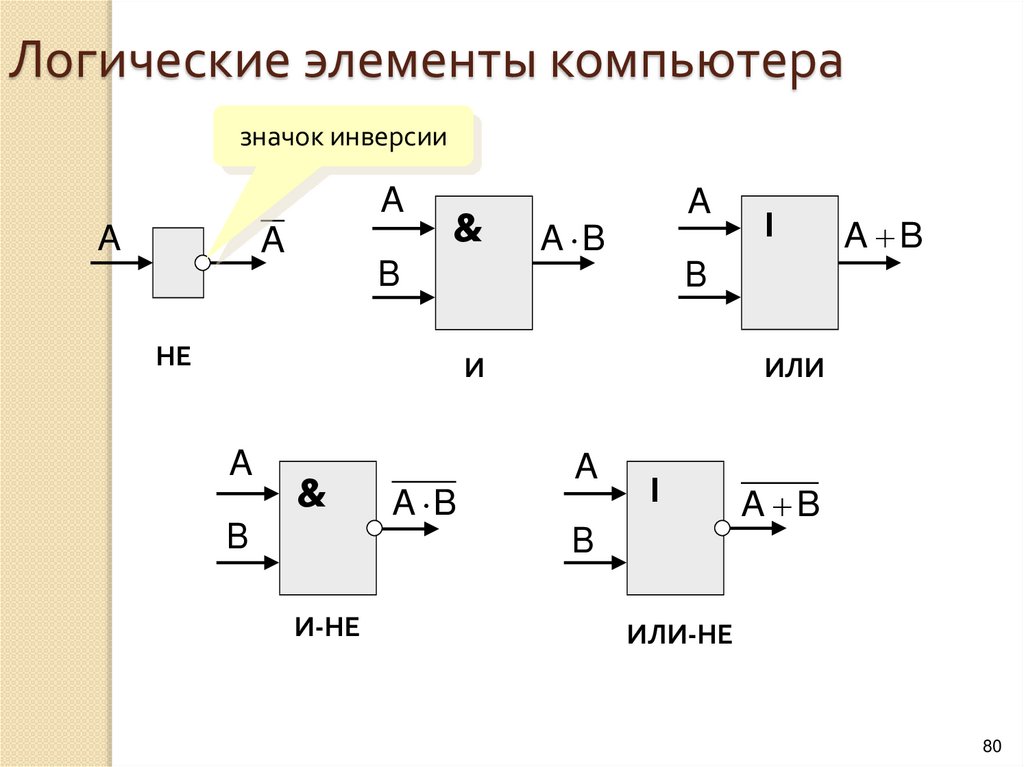
Таблицы определены с использованием типичного синтаксиса Markdown. Параметр colfmt работает как параметр табличной среды LaTeX для определения линий, которые должны быть проведены между столбцами таблицы: «cc|c» рисует три центрированных столбца с вертикальной линией перед последним столбцом. Каждый столбец должен быть указан с помощью «c», «r» или «l» для выравнивания по центру, правому или левому краю. Две трубы ( || ) или символ двойной вертикальной черты ( ǁ ) рисуют двойную черту между столбцами. Строки строк добавляются к самой строке таблицы, либо — , либо === в строке.
таблица = ''' А | Б | С ---|---|--- 0 | 0 | 0 0 | 1 | 0 1 | 0 | 0 1 | 1 | 1 ''' logic.Table(таблица, colfmt='cc||c')
Карты Карно
Карты Карно, или К-карты, полезны для упрощения логической таблицы истинности до наименьшего числа вентилей. Schemdraw может рисовать K-карты с 2, 3 или 4 входными переменными, используя schemdraw. класс.  logic.kmap.Kmap
logic.kmap.Kmap
логика.Kmap (имена = 'ABCD')
Параметр имен должен быть строкой из 2, 3 или 4 символов, каждый из которых определяет имя одной входной переменной. Параметр истинности содержит список кортежей, определяющих логические значения для отображения на карте. Первые элементов len(names) — это 0 и 1, определяющие положение ячейки, а последний элемент — это строка, отображаемая в этой ячейке. по умолчанию 9Параметр 0708 представляет собой строку, отображаемую в каждой ячейке К-карты, когда эта ячейка не определена в таблице истинности .
Например, эта К-карта 2×2 имеет «1» в позиции 01 и 0 в других местах:
logic.Kmap(names='AB',truetable=[('01', '1')])
K-Maps обычно используются для группировки наборов из 1 вместе. Эти группы можно нарисовать с помощью параметра groups . Ключи словаря групп определяют, какие ячейки группировать вместе, а значения словаря определяют параметры стиля для круга вокруг группы. Каждый ключ должен быть строкой длиной len(names) , либо с 0 , 1 , либо . в каждой позиции. Например, с name=’ABCD’ групповой ключ «1…» поместит кружок вокруг всех ячеек, где A=1. Или «.00». рисует круг вокруг всех ячеек, в которых B и C равны 0. Группы автоматически «обтекают» края.
Параметры словаря стилей включают color , fill , lw и ls .
Каждый ключ должен быть строкой длиной len(names) , либо с 0 , 1 , либо . в каждой позиции. Например, с name=’ABCD’ групповой ключ «1…» поместит кружок вокруг всех ячеек, где A=1. Или «.00». рисует круг вокруг всех ячеек, в которых B и C равны 0. Группы автоматически «обтекают» края.
Параметры словаря стилей включают color , fill , lw и ls .
logic.Kmap(имена='ABCD',
truetable=[('1100', '1'),
(«1101», «1»),
(«1111», «1»),
(«1110», «1»),
(«0101», «1»),
(«0111», «Х»),
(«1101», «1»),
(«1111», «1»),
(«0000», «1»),
(«1000», «1»)],
groups={'11..': {'цвет': 'красный', 'заливка': '#ff000033'},
'. 1.1': {'цвет': 'синий', 'заливка': '#0000ff33'},
'.000': {'цвет': 'зеленый', 'заливка': '#00ff0033'}})
1.1': {'цвет': 'синий', 'заливка': '#0000ff33'},
'.000': {'цвет': 'зеленый', 'заливка': '#00ff0033'}})
Общие сведения о цифровых логических ИС — Часть 1
» Перейти к дополнительным материалам
Современные цифровые логические ИС широко доступны в трех основных типах: ТТЛ-устройства (типичное семейство логики 74LS00), «медленные» КМОП-устройства (типичное логическим семейством «4000») и «быстрые» КМОП-устройства (представленные логическими семействами 74HC00 и 74AC00). Каждое из этих семейств имеет свои преимущества и недостатки, а также свой особый набор правил использования.
В этой мини-серии из четырех частей объясняются основные принципы и правила использования каждого из этих трех семейств цифровой логики, а также даются практические рекомендации по использованию широкого спектра ИС, доступных в каждом из этих семейств. Эта вступительная статья посвящена основам ИС цифровой логики.
Основы цифровой логики ИС
ИС можно описать как полную электронную схему или «электронный строительный блок», интегрированную в один или несколько полупроводниковых элементов (или «чипов») и помещенную в небольшой корпус с несколькими выводами. ИС можно сделать полностью функциональной, подключив ее к подходящему источнику питания и подключив различные контакты к соответствующим внешним входам, выходам и вспомогательным сетям.
ИС бывают как «линейные», так и «цифровые». Линейные ИС широко используются в качестве предварительных усилителей, усилителей мощности, генераторов, процессоров сигналов и т. д. и дают базовый выходной сигнал, который прямо пропорционален величине (аналоговому значению) входного сигнала, который сам по себе может иметь любое значение между ноль и некоторый заданный максимальный предел.
Одним из простейших типов линейных элементов ИС является буфер с единичным коэффициентом усиления. Если на вход этой схемы подается сильный синусоидальный сигнал, он создает выходной сигнал с низким импедансом почти такой же формы и амплитуды, как показано на рис. 9.0019 Рисунок 1(а) . Цифровые ИС, с другой стороны, фактически слепы к точным амплитудам своих входных сигналов и просто распознают их как находящиеся либо в низком, либо в высоком состоянии (обычно называемые состояниями логического 0 и логической 1 соответственно).
9.0019 Рисунок 1(а) . Цифровые ИС, с другой стороны, фактически слепы к точным амплитудам своих входных сигналов и просто распознают их как находящиеся либо в низком, либо в высоком состоянии (обычно называемые состояниями логического 0 и логической 1 соответственно).
РИСУНОК 1. При подаче большой входной синусоиды на вход линейного буфера (а) , на выходе получается синусоида, но при подаче на вход цифрового буфера ( б) , он выдает чисто цифровой выход.
Их выходы также имеют только два основных состояния, либо низкий, либо высокий (логический-0 или логическая-1). Одним из простых типов цифровых элементов ИС является неинвертирующий буфер. Если большой синусоидальный сигнал подается на вход этой схемы, она создает выходной сигнал, который (в идеале) имеет чисто цифровую форму, как показано на рис. 1(b) .
Цифровые ИС доступны во множестве довольно свободно определенных категорий, таких как ИС памяти, ИС электронной линии задержки, ИС поддержки микропроцессора и т. д., но наиболее широко используемой категорией является категория, известная как «логический» тип, в ИС разработаны на основе довольно простых логических схем, таких как цифровые буферы, инверторы, вентили или триггеры. Цифровая логика 9Схемы 0869 бывают различных основных типов и могут быть построены с использованием различных дискретных или интегрированных технологий. На рисунках 2 с по 7 показан набор очень простых логических схем, построенных на дискретных компонентах.
д., но наиболее широко используемой категорией является категория, известная как «логический» тип, в ИС разработаны на основе довольно простых логических схем, таких как цифровые буферы, инверторы, вентили или триггеры. Цифровая логика 9Схемы 0869 бывают различных основных типов и могут быть построены с использованием различных дискретных или интегрированных технологий. На рисунках 2 с по 7 показан набор очень простых логических схем, построенных на дискретных компонентах.
На рис. 2(a) показан простой инвертирующий цифровой буфер (также известный как логический вентиль НЕ), состоящий из несмещенного транзистора, подключенного в режиме с общим эмиттером, а на рис. 2(b) показан международный символ который используется для его представления. Стрелка указывает направление потока сигнала, а маленький кружок на выходе символа указывает действие инвертирования.
РИСУНОК 2. Схема (a) , символ (b) и таблица истинности (c) простого инвертирующего цифрового буфера.
Действие схемы таково, что Q1 отключается (с высоким выходным сигналом), когда его вход находится в нулевом состоянии, и полностью включается (с низким выходным сигналом), когда на его входе высокий уровень. Эта информация представлена в сжатой форме таблицей истинности (рис. 2(с) ), которая показывает, что на выходе логическая 1, когда на входе логическая 0, и наоборот.
На рис. 3(a) показан простой неинвертирующий цифровой буфер, состоящий из пары транзисторных каскадов с общим эмиттером (инвертора), соединенных напрямую. На рис. 3(b) показан международный символ в виде стрелки, используемый для его представления. На рис. 3(c) показана таблица истинности, которая описывает его действие, например, выход находится в состоянии логического 0, когда вход находится в состоянии логического 0, и находится в состоянии логической единицы, когда вход находится в состоянии логической 1.
РИСУНОК 3. Контур (a) , символ (b) и Таблица истинности (c) неинвертирующего цифрового буфера.
Контур (a) , символ (b) и Таблица истинности (c) неинвертирующего цифрового буфера.
В цифровой электронике «затвор» — это логическая схема, которая открывается или дает выход (обычно определяемый как состояние высокого уровня или логической единицы) только при определенном наборе входных условий. На рис. 4(a) показан простой вентиль ИЛИ с двумя входами, состоящий из двух диодов и резистора, а на рис. 4(b) показан международный символ, используемый для его обозначения. Рисунок 4(с) показывает свою таблицу истинности (в которой входные данные обозначены как A или B). Обратите внимание, что выход переходит в логическую 1, если A или B переходит в логическую 1.
РИСУНОК 4. Схема (a) , символ (b) и таблица истинности (c) простого двухвходового вентиля ИЛИ.
На рис. 5 показаны схема, символ и таблица истинности двухвходового вентиля НЕ-ИЛИ (с отрицательным выходом ИЛИ), в котором выходной сигнал инвертируется (как показано кружком на выходе) и переходит в состояние логического 0. если любой вход становится высоким.
РИСУНОК 5. Схема (a) , символ (b) и Таблица истинности (c) вентиля ИЛИ-ИЛИ с двумя входами.
На рис. 6(a) показан простой вентиль И с двумя входами, состоящий из двух диодов и резистора, а на рис. 6(b) показан его стандартный международный символ. На рис. 6(c) показана таблица истинности логического элемента И, которая показывает, что выход переходит в логическую 1, только если входы A и B находятся в логической 1.
РИСУНОК 6. Схема (a) , символ (b) и таблица истинности (c) простого двухвходового вентиля И.
Наконец, На рис. 7 показана схема, символ и таблица истинности логического элемента И-НЕ с двумя входами (с отрицательным выходом И), в котором выходной сигнал инвертируется (как показано кружком на выходе) и переходит в логическую схему. -0, только если оба входа находятся в состоянии логической-1.
РИСУНОК 7. Цепь (a) , символ (b) и Таблица истинности (c) вентиля И-НЕ с двумя входами.
Обратите внимание, что хотя описанные здесь четыре основных типа схем логических вентилей показаны только с двумя входными клеммами, на самом деле они могут быть спроектированы или использованы для приема любого желаемого количества входов и могут использоваться для выполнения различные простые логические операции. Многие типы цифровых буферов и логических элементов легко доступны в форме ИС, как и многие другие цифровые логические схемы, включая триггеры, защелки, регистры сдвига, счетчики, селекторы данных, кодеры и декодеры.
Практические цифровые ИС могут варьироваться от относительно простых логических устройств, содержащих эквивалент всего нескольких основных логических элементов или буферов, до невероятно сложных устройств, содержащих эквивалент десятков тысяч взаимосвязанных логических элементов и т. д. По соглашению следующие общие термины используется для описания относительной плотности или сложности интеграции:
- SSI (Small Scale Integration) — Уровень сложности от одного до 10 элементов.
- MSI (средняя интеграция) — Уровень сложности от 10 до 100 ворот.
- LSI (крупномасштабная интеграция) — Уровень сложности от 100 до 1000 вентилей.
- СБИС (очень большая интеграция) — Уровень сложности от 1000 до 10000 вентилей.
- SLSI (сверхбольшая интеграция) — Уровень сложности от 10 000 до 100 000 логических элементов.
Обратите внимание, что большинство логических ИС типов, описанных в этой серии статей, имеют уровни сложности от четырех до 400 логических элементов и, таким образом, являются устройствами SSI, MSI или LSI. В общих чертах, большинство микропроцессорных ИС и ИС памяти среднего размера являются устройствами СБИС, тогда как ИС с большим динамическим ОЗУ (оперативным запоминающим устройством) являются устройствами SLSI.
В общих чертах, большинство микропроцессорных ИС и ИС памяти среднего размера являются устройствами СБИС, тогда как ИС с большим динамическим ОЗУ (оперативным запоминающим устройством) являются устройствами SLSI.
Основы цифровых сигналов
Цифровые логические ИС неизменно используются для обработки цифровых сигналов. Таким образом, сейчас уместно рассмотреть некоторые основные факты и термины, касающиеся цифровых сигналов.
Доступны прямоугольные или импульсные сигналы. Рисунок 8 иллюстрирует основные параметры прямоугольной волны.
РИСУНОК 8. Основные параметры прямоугольной волны.
В каждом цикле волна сначала переключается с нуля на некоторое пиковое значение напряжения (Vpk) на фиксированный период, затем снова переключается на низкий уровень на второй фиксированный период и так далее. Время подъема сигнала с 10 % до 9 с.0% Vpk известен как время нарастания , а время его падения с 90% до 10% Vpk известно как время спада .
В каждом прямоугольном цикле старшая часть известна как метка , а младшая часть как пробел . В симметричной прямоугольной волне, такой как в рис. 8 , периоды отметки и пробела равны. Говорят, что такие формы сигналов имеют отношение метки к пространству (или M-S) 1: 1 или 50% рабочего цикла (поскольку продолжительность метки составляет 50% от общего периода цикла). Прямоугольные волны не обязательно симметричны, но всегда являются автономными или повторяющимися, т. Е. Они многократно циклически повторяются с постоянными периодами меток и пробелов.
Импульсный сигнал немного похож на меандр. У него есть как время нарастания, так и время спада, но указана только одна часть — либо его метка, либо его пространственный период; продолжительность оставшегося периода не имеет значения. На рис. 9(a) показана базовая «положительная» форма импульса, которая имеет «нарастающий» или положительный передний фронт, а На рис. 9(b) показана «отрицательная» форма импульса, которая имеет «падающий» или отрицательный передний фронт. Обратите внимание, что многие современные цифровые ИС MSI, такие как счетчики/делители и сдвиговые регистры, могут быть выбраны или запрограммированы для запуска либо по нарастающему, либо по заднему фронту входного импульса по желанию пользователя.
9(b) показана «отрицательная» форма импульса, которая имеет «падающий» или отрицательный передний фронт. Обратите внимание, что многие современные цифровые ИС MSI, такие как счетчики/делители и сдвиговые регистры, могут быть выбраны или запрограммированы для запуска либо по нарастающему, либо по заднему фронту входного импульса по желанию пользователя.
РИСУНОК 9. Основные формы (а) «положительных» и (б) «отрицательных» импульсов.
Если на вход реального усилителя или логического элемента и т. д. подается почти идеальная форма импульса, результирующая форма выходного сигнала будет искажена как по форме, так и по времени, как показано на рис. 10 . Таким образом, не только время нарастания и спада формы выходного сигнала будет увеличено, но приход и окончание выходного импульса будут задержаны во времени по сравнению с входным импульсом.
РИСУНОК 10. Безупречный импульс, подаваемый на вход практического усилителя или вентиля, создает выходной импульс, искаженный как по форме, так и по времени. Временная задержка выходного импульса называется его задержкой распространения, и (в (б)) = (t 1 + t 2 ) / 2.
Безупречный импульс, подаваемый на вход практического усилителя или вентиля, создает выходной импульс, искаженный как по форме, так и по времени. Временная задержка выходного импульса называется его задержкой распространения, и (в (б)) = (t 1 + t 2 ) / 2.
Среднее значение задержек называется задержкой распространения устройства . Кроме того, пики нарастающих и спадающих фронтов сигнала могут страдать от различных форм звона, выброса, недорегулирования и т. д. Величина этих искажений зависит от качества или конструкции усилителя или гейта.
На практике импульсные входные сигналы иногда могут быть настолько несовершенными, что их может потребоваться «подготовить», прежде чем они станут подходящими для использования в современных быстродействующих цифровых ИС. В частности, они могут иметь такие длинные времена нарастания или спада, что их, возможно, придется настраивать с помощью триггера Шмитта, прежде чем они станут пригодными для использования.
Опять же, многие импульсные сигналы, полученные механически, например, генерируемые с помощью переключателей или прерывателей контактов, могут страдать от множественных проблем с «дребезгом контактов», подобных тем, которые показаны на рис. 9.0019 Рисунок 11(а) . В этом случае их необходимо преобразовать в чистую форму, показанную на рис. 11(b) , прежде чем их можно будет использовать с пользой.
РИСУНОК 11. Импульсные сигналы, получаемые механически, часто страдают от дребезга контактов (a) , и перед использованием их необходимо очищать (b) .
Логические семейства
Практические цифровые логические схемы и ИС могут быть построены с использованием различных технологий. Первое успешное семейство микросхем цифровой логики появилось в середине 19 века.60-е годы. В них использовалось питание 3,6 В и использовалась простая технология, которая стала известна как резисторно-транзисторная логика или RTL. На рис. 12 показана базовая схема вентиля RTL NOR с тремя входами. RTL был довольно медленным в работе, имея типичную задержку распространения (время, необходимое для фронта одиночного импульса или перехода от входа к выходу) 40 нС в маломощном затворе или 12 нС в затворе средней мощности. RTL устарел.
На рис. 12 показана базовая схема вентиля RTL NOR с тремя входами. RTL был довольно медленным в работе, имея типичную задержку распространения (время, необходимое для фронта одиночного импульса или перехода от входа к выходу) 40 нС в маломощном затворе или 12 нС в затворе средней мощности. RTL устарел.
РИСУНОК 12. Версия IC вентиля RTL NOR с тремя входами.
Другой ранний тип технологии логики ИС, разработанный в конце 1960-х годов, был основан на простых разработках дискретных типов логических схем, показанных на рисунках 2 с по 7 , и был известен как диодно-транзисторная логика, или ДТЛ. На рис. 13 показана базовая схема вентиля DTL NAND с тремя входами. DTL использовал двойной источник питания на пять вольт, давал типичную задержку распространения 30 нС и давал выходное напряжение менее 0,4 В в состоянии логического 0 и более 3,5 В в состоянии логической 1. DTL устарел.
РИСУНОК 13. Версия IC вентиля DTL NAND с тремя входами.
Между концом 1960-х и серединой 1970-х появилось несколько других перспективных логических технологий ИС. Большинство из них вскоре снова кануло в небытие. Среди тех, которые пришли и либо ушли, либо отступили по важности, были HTL (логика с высоким порогом), ECL (логика с эмиттерной связью) и PML (логика P-типа MOSFET). Самой надежной из этих технологий был ECL, который все еще находится в производстве и обеспечивает очень быструю работу, но за счет очень высокого потребления тока/мощности.
На рис. 14 показана принципиальная схема цифрового усилителя ЭСЛ — ненасыщающего дифференциального усилителя с эмиттерной связью (Q1 и Q2) с выходными каскадами с эмиттерным повторителем (Q3 и Q4). Поскольку его транзисторы не насыщаются при переключении, типичная задержка распространения составляет всего 4 нС. Обратите внимание, что линия V+ схемы обычно заземлена, а линия V- питается напряжением -5,2 В.
В этом случае номинальные колебания цифрового выхода схемы составляют всего 0,85 В, т. е. от низкого уровня -1,60 В до высокого уровня -0,75 В. Цифровой вход схемы подается на базу транзистора Q1. Неинвертированный выход доступен на эмиттере Q3, а инвертированный выход доступен на эмиттере Q4. Современные микросхемы ECL используются только тогда, когда требуется сверхвысокая скорость работы.
Основная цель разработчиков цифровых ИС в конце 1960-х – начале 1970-х годов заключалась в том, чтобы разработать технологию, которая была бы простой в использовании и обеспечивала хороший компромисс между высокой скоростью работы и низким энергопотреблением. Проблема здесь заключалась в том, что обычная схема транзисторного типа, использующая выходной каскад Рис. 2 Тип (как в системах RTL и DTL) просто не был способен удовлетворить последние два из этих требований к конструкции. Суть этой проблемы — и ее окончательное решение — можно понять с помощью Рисунок 15 .
РИСУНОК 15. (a) Простой цифровой переключатель. (b) Базовый цифровой переключатель «тотемный столб».
На рис. 15(a) показана упрощенная версия схемы на рис. 2 , где Q1 заменен механическим переключателем. Помните, что все практические выходные нагрузки неизбежно содержат емкость (обычно до 30 пФ в большинстве цифровых схем), поэтому можно увидеть, что эта базовая схема будет довольно медленно заряжать (ток источника) емкостную нагрузку через R2, когда S1 разомкнут. , но быстро разряжает его (ток стока) через S1, когда S1 закрыт; таким образом, схемы этого типа создают цифровые выходы, которые обычно имеют длительное время нарастания и короткое время спада. Единственный способ уменьшить время нарастания — уменьшить значение R2, что пропорционально увеличивает потребление тока S1 (Q1).
Обратите внимание, что один хороший способ описать недостаток логической схемы Рис. ). Очевидно, что гораздо лучший цифровой выходной каскад можно было бы сделать, заменив R2 и S1 парой групповых переключателей, соединенных, как показано на рис. активное понижающее действие, но устроено таким образом, что одновременно может быть замкнут только один переключатель (таким образом гарантируя, что цепь потребляет нулевой ток покоя). Такая схема — с одним электронным переключателем, расположенным над другим — называется 9-контактной.0869 тотем-полюс выходной каскад.
). Очевидно, что гораздо лучший цифровой выходной каскад можно было бы сделать, заменив R2 и S1 парой групповых переключателей, соединенных, как показано на рис. активное понижающее действие, но устроено таким образом, что одновременно может быть замкнут только один переключатель (таким образом гарантируя, что цепь потребляет нулевой ток покоя). Такая схема — с одним электронным переключателем, расположенным над другим — называется 9-контактной.0869 тотем-полюс выходной каскад.
В конце 1960-х инженеры по цифровым технологиям стремились разработать дешевую и надежную электронную версию тотемного выходного каскада, а затем — в начале 1970-х — сорвали джек-пот. Две такие технологии произвели фурор на коммерческом рынке и легли в основу двух доминирующих на сегодняшний день семейств цифровых ИС. Первый из них — основанный на технологии биполярных транзисторов — известен как ТТЛ (транзисторно-транзисторная логика). ТТЛ является основой так называемого семейства цифровых ИС «74», впервые появившихся в 1972.
Второй, основанный на технологии FET, известен как CMOS (комплементарная логика MOS -FET). КМОП является основой конкурирующего семейства цифровых ИС «серии 4000» (и аналогичного «серии 4500»), которое впервые появилось примерно в 1975 году. Технологии ТТЛ и КМОП имеют совершенно разные характеристики, но обе предлагают определенные технические преимущества, которые делают они бесценны в конкретных приложениях.
Наиболее существенные различия между технологиями КМОП и ТТЛ ИС можно увидеть в их базовых инверторно-буферных схемах, которые используются (иногда в слегка модифицированном виде) практически во всех ИС в рамках семейства каждого типа устройств. На рисунках 16 и 17 показаны две различные базовые конструкции.
КМОП-инвертор Рисунок 16 состоит из комплементарной пары полевых МОП-транзисторов, соединенных последовательно, с p-канальным MOSFET Q1 вверху и n-канальным MOSFET Q2 внизу, причем оба высокоимпедансных затвора соединены вместе. Пара может питаться от любого источника в диапазоне 3–15 В.
Пара может питаться от любого источника в диапазоне 3–15 В.
РИСУНОК 16. Схема и таблица истинности базового КМОП-инвертора.
Когда вход схемы находится в состоянии логического 0, основное действие заключается в том, что Q1 включается, а Q2 отключается, а на выходе активно устанавливается высокий уровень (логическая 1). Обратите внимание, что в этом случае выход может подавать (направлять) довольно высокие токи на внешнюю нагрузку (через Q1), но фактическая ступень инвертора потребляет почти нулевой ток, поскольку Q2 отключен.
Когда вход схемы находится в состоянии логической 1, происходит обратное действие: транзистор Q1 отключается, а транзистор Q2 включается, а на выходе активно устанавливается низкий уровень (логический 0). Обратите внимание, что в этом случае выход может потреблять (поглощать) довольно высокие токи от внешней нагрузки (через Q2), но фактическая ступень инвертора потребляет почти нулевой ток, поскольку Q1 отключен.
Таким образом, базовый инвертор CMOS может использоваться с любым источником питания в диапазоне 3-15 В, имеет очень высокий входной импеданс, потребляет почти нулевой ток покоя, имеет выход, который почти полностью переключается между двумя шинами питания, и могут создавать или потреблять довольно высокие выходные токи нагрузки. Как правило, один базовый КМОП-каскад имеет задержку распространения около 12-60 нС, в зависимости от напряжения питания.
Инвертор TTL Рисунок 17 разделен на три секции, состоящие из управляемого эмиттером входа (Q1), фазовращателя (Q2) и выходного каскада с тотемным полюсом (Q3-D1-Q4). Он должен питаться от пятивольтовой сети. Когда вход схемы понижается до логического 0, основное действие таково, что Q1 насыщается, что лишает Q2 тока базы и вызывает отключение Q2 и Q4, и в то же время вызывает отключение эмиттерного повторителя Q3. включите через R2 и дайте активное подтягивающее действие, при котором выход имеет (из-за различных падений напряжения) типичное нагруженное значение около 3,5 В.
РИСУНОК 17. Схема и таблица истинности базового инвертора TTL.
Эта схема может подавать довольно большие токи на внешнюю нагрузку. И наоборот, когда вход схемы находится в состоянии логической 1, транзистор Q1 отключен, что позволяет активировать Q2 через резистор R1 и переход база-коллектор Q1 с прямым смещением, тем самым приводя Q4 к насыщению и одновременно отключая транзистор Q3.
В этом случае Q4 дает активное понижающее действие и может потреблять довольно большие токи, в то время как выход принимает типичное нагруженное значение 400 мВ. Обратите внимание, что (без учета токов внешней нагрузки) схема потребляет ток покоя около 1 мА в состоянии выхода логической единицы и 3 мА в состоянии выхода логического нуля.
Таким образом, базовый инвертор TTL может использоваться только с пятивольтовым питанием, имеет очень низкий входной импеданс, потребляет до 3 мА тока покоя, имеет выход, который не переключается полностью между двумя шинами питания, и могут создавать или потреблять довольно высокие токи нагрузки. Как правило, один базовый каскад TTL имеет задержку распространения около 12 нС.
Как правило, один базовый каскад TTL имеет задержку распространения около 12 нС.
Варианты базовой схемы TTL
Существует пять очень важных вариантов базовой схемы Рисунок 17 Схема инвертора TTL. Самой простой из них является так называемая схема ТТЛ с открытым коллектором, которая показана в базовой форме на 9.0019 Рисунок 18 .
РИСУНОК 18. Инвертор TTL с выходом с открытым коллектором.
Здесь выходной транзистор Q3 отключается, когда вход находится в состоянии логического 0, и включается, когда вход находится в состоянии логической 1. Таким образом, подключив внешний нагрузочный резистор между выводами OUT и +5 В, схему можно использовать в качестве пассивного подтягивающего инвертора напряжения, который имеет выход, который (при небольшой нагрузке) почти полностью переключается между нулем и положительной шиной питания. ценность.
В качестве альтернативы его можно использовать для управления внешней нагрузкой (например, светодиодом или реле и т. д.), которая подключается между OUT и положительной шиной питания, и в этом случае нагрузка активируется при подаче логической 1 на вход.
д.), которая подключается между OUT и положительной шиной питания, и в этом случае нагрузка активируется при подаче логической 1 на вход.
Второй вариант — неинвертирующий усилитель или буфер. Это достигается простым подключением дополнительного инверторного каскада с прямой связью между фазовращателем и выходными каскадами стандартного инвертора. На рис. 19 показана версия такой схемы с открытым коллектором, которую можно использовать с внешним резистором или нагрузкой. В этом примере Q4 включается при подаче логического 0 на вход.
РИСУНОК 19. TTL неинвертирующий буфер с выходом с открытым коллектором.
На рис. 20 показан основной вариант конструкции TTL.
РИСУНОК 20. ТТЛ-вентиль И-НЕ с тремя входами .
Здесь базовая схема инвертора используется с входным транзистором с тремя эмиттерами для создания логического элемента И-НЕ с тремя входами, в котором выход переходит в низкий уровень (в лог. -1 состояние). Транзисторы с несколькими эмиттерами широко используются в микросхемах ТТЛ. В некоторых ТТЛ-затворах используется входной транзистор с дюжиной эмиттеров для создания 12-входового затвора.
-1 состояние). Транзисторы с несколькими эмиттерами широко используются в микросхемах ТТЛ. В некоторых ТТЛ-затворах используется входной транзистор с дюжиной эмиттеров для создания 12-входового затвора.
Еще один вариант касается использования выхода с тремя состояниями (или с тремя состояниями), который включает в себя дополнительные сети и внешний терминал управления ENABLE. В одном состоянии выходной каскад с тотемным полюсом работает в обычном режиме логического 0 или логической 1, а в другом состоянии оба транзистора с тотемным полюсом отключены (выключены), создавая разомкнутую цепь (высокий импеданс). выход. Эта функция полезна, поскольку позволяет закоротить несколько выходов или входов на общую шину или линию, как показано на рис. 9.0019 Рисунок 21 , и общаться по этой линии, ВКЛЮЧАЯ одновременно только одно устройство вывода и одно устройство ввода.
РИСУНОК 21. Логика трех состояний позволяет подключить несколько выходов или входов к общей шине. Только один выход/вход должен быть активен в любой момент времени.
Только один выход/вход должен быть активен в любой момент времени.
Последний вариант схемы является прикладным и касается использования внешнего подтягивающего резистора 2 кОм на выходном каскаде с тотемным полюсом, как показано на рис. 22 9 .0020 .
РИСУНОК 22. Внешний подтягивающий резистор мощностью 2 кВт, подключенный к выходу каскада с тотемным полюсом, подтягивает выход почти до +5 В в состоянии логической единицы.
Этот резистор подтягивает выход (при небольшой нагрузке) практически до полного значения питания +5 В, когда выход находится в состоянии логической 1, а не только до +3,5 В. Иногда это полезно при сопряжении выхода например, TTL IC на вход CMOS IC.
Цифровые микросхемы серии 74
Технология ТТЛ ИС впервые получила широкое распространение в области разработки электроники примерно в 1972 году, когда она появилась в виде целого ряда цифровых логических ИС, которые были исключительно просты в использовании. Серия имела мгновенный международный успех и быстро стала ведущей в мире логической системой ИС. Его ИС производились как в коммерческом, так и в военном исполнении и имели префиксы 74 и 54 соответственно; линейка коммерческих продуктов вскоре стала известна просто как ИС «серии 74».
Серия имела мгновенный международный успех и быстро стала ведущей в мире логической системой ИС. Его ИС производились как в коммерческом, так и в военном исполнении и имели префиксы 74 и 54 соответственно; линейка коммерческих продуктов вскоре стала известна просто как ИС «серии 74».
За прошедшие годы ИС «серии 74» постепенно расширили свой ассортимент устройств и усовершенствовали технологию производства, так что сегодня серия 74 так же популярна и универсальна, как никогда. Впервые представленная в начале 1970-х годов, эта серия была полностью основана на простом типе технологии TTL, но в последующие годы в серию были введены новые подсемейства TTL, а затем к ней были добавлены различные типы технологии CMOS. так что сегодняшняя серия 74 включает в себя множество подсемейств TTL и CMOS. В следующем выпуске мы подробно рассмотрим подсемейства микросхем серии 74 и объясним некоторые основные термины TTL. NV
|
Цифровая схема представляет собой набор взаимосвязанных цифровых компонентов, называемых вентилями . На следующем рисунке показана принципиальная схема цифровой схемы, называемой полным сумматором . Имеются три входных узла (поля, помеченные x , y и z ), три внутренних узла (ящики, помеченные a , b и o ) и два выходных узла (боксы с метками s и c ). Есть два xor-гейта (компоненты вверху), два and-гейта (компоненты внизу слева) и один or-гейт (компонент справа внизу). Нажмите на x , y , z , чтобы переключить их значения. Учитывая логическую природу сигналов в узлах и детерминированный характер элементов, вполне естественно моделировать цифровые схемы в логике высказываний. Мы можем представить каждый узел схемы как пропозициональную константу, предполагая, что узел а равен 9.1312 на , если константа истинна, и на , если константа ложна. С этим соглашением мы можем зафиксировать поведение вентилей, написав предложения, связывающие значения входных узлов и выходных узлов вентилей. Предложения, показанные ниже, выражают поведение пяти ворот в схеме, показанной выше. Узел или должен быть на тогда и только тогда, когда узлы x и y не совпадают. Узел и должен быть на тогда и только тогда, когда узлы z и o оба являются на . Узел b должен быть на тогда и только тогда, когда узлы x и y оба являются на . Узел s должен быть на тогда и только тогда, когда узлы o и z не совпадают.
Как только мы это сделали, мы можем использовать нашу формализацию для анализа схемы — смоделировать ее, настроить ее входы для достижения желаемых результатов, проверить , что она соответствует спецификации, диагностировать отказов в физические экземпляры и проверить , правильно ли работают отдельные экземпляры. Моделирование — это процесс определения выходов схемы для заданных входов. Чтобы смоделировать схему, мы начинаем с предложений, описывающих поведение вентилей в схеме, и добавляем атомы земли, выражающие заданные входные сигналы (9).1312 x и y и z ). Учитывая эти предпосылки, мы затем получаем утверждения о выходах ( s и c ). As an example, suppose we know that x is on and y is off and z is on , and we want to know whether outputs s and c are на или на . Мы спрашиваем, влечет ли наш план ∆ вместе с нашими входными данными логически s или ¬ s и влечет ли это за собой c или ¬ c . В этом случае мы имеем следующие результаты.
Конфигурация противоположна симуляции. Мы начинаем с желаемых значений для выходов схемы и пытаемся найти одну или несколько комбинаций входов, которые производят эти выходы. В отличие от симуляции, ответов может быть несколько. В качестве примера предположим, что мы хотим найти значения для x и y и z такие, что выход s равен на , а выход c равен на . Мы пытаемся найти такие входные данные, что Δ вместе с этими входными данными логически влечет ( s ∧ ¬ c ). В этом случае мы находим три возможности.
Конечно, чтобы иметь смысл, мы должны быть уверены, что входные данные непротиворечивы. Спецификация схемы представляет собой характеристику желаемого поведения схемы при всех возможных входных данных. Схема схемы представляет собой характеристику ее компонентов и соединений. Спецификация выражает цель схемы, тогда как дизайн выражает то, как она построена. Верификация — это процесс определения того, соответствует ли конструкция схемы ее спецификации. Целью полного сумматора является выполнение одного среза двоичного сложения. Учитывая два входных бита ( x и y ) и бит переноса из другого слайса ( z ), он создает бит суммы ( s ) и бит переноса ( c ) для передачи в следующий слайс. Мы можем резюмировать желаемое поведение, как показано ниже. Мы используем символ Ω для обозначения этих двух предложений.
Мы можем проверить схему, начав с ее конструкции (предложения, которые мы видели ранее) и используя их для подтверждения того, что каждое из предложений в спецификации логически следует. Если да, то схема правильная. Если Δ — это множество предложений, составляющих наш дизайн (предложения, которые мы видели ранее), и если Ω — это наша спецификация (предложения, приведенные выше), мы спрашиваем, влечет ли логически наш дизайн нашу спецификацию. В нашем обсуждении до сих пор мы предполагали, что все компоненты в нашей схеме ведут себя правильно. Это не всегда так. Иногда компоненты выходят из строя, и в результате они меняют свое поведение. Диагностика — это процесс поиска неисправных компонентов в цепи, которые вызывают наблюдаемые симптомы. Предложения в нашем дизайне верны только в том случае, если соответствующие компоненты ведут себя правильно. Мы можем допустить возможность отказа, украсив каждое из наших предложений условием, утверждающим, что соответствующий компонент работает правильно. Смотри ниже. В первом предложении здесь говорится, что если компонент в левом верхнем углу (с именем x 1) работает корректно, потом ведет себя как xor-gate. Остальные предложения аналогичны. В дальнейшем мы будем обозначать эти предложения как Δ’.
Одним из преимуществ такого подхода является то, что мы можем использовать логические инструменты для диагностики аппаратных сбоев и генерировать тесты, чтобы увидеть, правильно ли работает экземпляр нашей схемы, как описано в следующих разделах. 9. и предположим, что в результате мы наблюдаем, что бит суммы s равен на , а бит переноса c равен на . Это не то, что мы ожидали. Что-то должно сломаться. Хорошая новость заключается в том, что на основе этих данных и расширенной модели нашей схемы мы можем диагностировать проблему. Для этого мы используем наши логические инструменты, чтобы вывести выводы, записанные в терминах x 1, x 2, и 1, и 2, или 1 и ничего больше. В этом случае мы можем сделать следующие выводы. Первый вывод ниже сделан из ошибочного бита суммы, а второй — из ошибочного бита переноса.
Обычно при диагностике оборудования предполагается, что не более одного компонента выходит из строя. Обратите внимание, что мы можем выразить предположение об одиночном отказе для нашей схемы, как показано ниже. В дальнейшем мы будем использовать символ Σ для обозначения этих пяти предложений.
Имея модифицированную конструкцию Δ’ и наши предложения по единичным ошибкам Σ, мы можем использовать наши логические инструменты для определения неисправного компонента, ответственного за наши наблюдения. Генерация тестов — это процесс разработки набора тестов для подтверждения того, что физический экземпляр схемы работает правильно. Если схема проходит тесты, мы знаем, что все в порядке. Если нет, мы можем диагностировать проблему, чтобы найти неисправные компоненты. В принципе, генерировать тесты несложно. Мы можем просто применить все возможные входные комбинации и для каждой комбинации проверить, что схема выдает правильные выходные данные. Этот метод прост и хорошо работает для небольших цепей. Однако это нецелесообразно для больших схем, поскольку количество возможных комбинаций входных сигналов может быть очень большим. Например, схема, которая складывает два 64-битных числа, будет иметь 128 входов, и для этой схемы будет 2 128 входных комбинаций. Хорошей новостью является то, что часто можно гарантировать правильную работу схемы только с подмножеством возможных входных комбинаций. Одна практическая проблема с этим подходом заключается в том, что мы обычно не можем напрямую задавать входные данные или напрямую наблюдать за выходными данными каждого компонента. В большинстве случаев все, что мы можем сделать, это установить общие входы схемы и наблюдать за общими выходами; и из таких тестов мы должны сделать вывод, правильно ли работают внутренние компоненты. К счастью, это возможно в большинстве случаев. Как и при диагностике, начнем с измененного описания конструкции. Генерация тестов требует больше деталей, чем диагностика. Вместо того, чтобы говорить о том, работает компонент или нет, мы должны говорить о каждом поведении каждого компонента. Каждый вентиль с двумя входами имеет четыре поведения — по одному для каждой комбинации входных значений.
Шлюз работает правильно тогда и только тогда, когда все его действия корректны. Следующие предложения отражают это определение для наших пяти ворот. В дальнейшем мы используем символ Π для обозначения этих предложений.
Глядя на эти тесты, мы видим, что каждое поведение каждого вентиля появляется в правой части по крайней мере одного теста (за исключением или 111). Одна странность здесь в том, что четыре правила имеют только четыре вывода. Например, первое правило позволяет нам заключить, что все релевантные варианты поведения допустимы, за исключением a 210. Причина, по которой этот случай исключен, заключается в том, что выход a 1 в этом случае равен 1, и, следовательно, выход a 1 или 1 должно быть равно 1, независимо от того, какой вывод имеет и 2. Таким образом, рассматривая только общие выходные данные в этом случае, мы не знаем, правильно ли работает и 2. Как показано, в правилах есть еще три примера этого. Теперь наша главная цель — объяснить, почему нам не нужны все эти входные комбинации для тестирования нашей схемы. В результате мы можем полностью протестировать наш полный сумматор всего за шесть тестов, а именно. тесты 2, 4, 5, 6, 7, 8. Здесь не так много экономии, но для больших цепей экономия может быть гораздо более существенной. Например, в случае упомянутого ранее 64-битного сумматора мы можем обойтись менее чем 400 тестами вместо 2 9 .2008 128 тестов. Один из способов провести анализ, описанный здесь, состоит в том, чтобы использовать таблицы истинности для утверждений в нашем описании схемы. Другой подход заключается в использовании одного из наших методов доказательства. Предлагаемые упражнения. Смоделируйте схему для входов x и y и ¬ z . Найдите все конфигурации, ведущие к s и ¬ c . Построить таблицу истинности с 8 строками; используйте Δ для вычисления всех выходных данных; повторить с Ω; и сравните. Show that Δ’ ∪ { x , ¬ y , z , s , ¬c} ∪ Σ |= ¬ x 1. Show that x ∧ y ∧ z ∧ с ∧ с ⇒ x 111. Проведите все пять видов анализа для другой схемы. Булева логика и цифровые схемы
Современные цифровые компьютеры состоят из цифровых логических схем, основными строительными блоками которых являются логические вентили, каждый из которых предназначен для выполнения определенной логической функции. Булева алгебра Булева алгебра основана на двузначной или бинарной схеме. Два значения могут быть выражены разными способами, например, истина или ложь, 1 или 0, а также «включено» или «выключено». Именно это свойство, которое было признано и развито Клодом Шенноном в 1937 году, делает его таким полезным для реализации логических функций с помощью электронных схем. Например, логическая 1 и логический 0 могут быть реализованы как два разных уровня напряжения в цепи, или по состоянию переключателя, или по наличию или отсутствию тока в цепи. Обозначение Инженерное приложение логики Буля использует упрощенную версию исходной записи следующим образом:
Может представлять параллельных контактов переключателя . Может представлять собой контакты переключателя серии . Обратите внимание, что стало общепринятым опускать точку . знак (символ И), так что A.B записывается как AB . Может представлять нормально замкнутых контактов переключателя .
Булевы законы
Коммунативное право
Юриспруденция
Распределительное право
Законы об идентичности
Законы о сокращении штатов
Закон об инволюции
Теорема Де Моргана
В дополнение к описанной выше булевой алгебре были разработаны цифровые логические вентили для представления выражений исключающее ИЛИ и исключающее ИЛИ, расширяющие исходный диапазон логических законов. Логические элементыЛогические элементы могут иметь два или более входа и, за исключением некоторых особых случаев, один выход. Состояние входных и выходных клемм может быть только в одном из двух двоичных состояний, низком (0) или высоком (1), представленном двумя разными уровнями напряжения, обычно 0 вольт для логического 0 и около 3-5 вольт. для логической 1, в зависимости от используемой полупроводниковой технологии. Логические вентили также требуют источника питания. Транзистор в качестве переключателя Электронные затворы обычно состоят из транзисторных схем, работа которых зависит от использования транзистора в качестве переключателя, а не усилителя, для которого он был первоначально изобретен. При отсутствии напряжения на базе через транзистор, который, таким образом, выключен, ток отсутствует, и выходное (коллекторное) напряжение будет высоким.
Ворота XOR и XNORЭлемент исключающего ИЛИ (исключающее ИЛИ) со входами A и B реализует логическое выражение = B + A
Элемент Exclusive NOR (XNOR) с входами A и B реализует логическое выражение = = AB +
Элементы исключающего ИЛИ обычно используются для сравнений и проверок на четность.
Три входа NOR Gate
Цифровые логические схемы Булева логика используется для разработки сложных цифровых схем для выполнения широкого спектра логических функций. Триггеры и защелки Set-Reset
Регистры являются обычными запоминающими устройствами, обеспечивающими временное хранение многобитных слов данных, таких как 4-, 8- или 16-битные слова. Сумматоры
Полные сумматоры предназначены для приема бита переноса из предыдущей ступени и, следовательно, имеют три входа. Схема ниже является примером одноразрядного полного сумматора, полностью состоящего из двух входных вентилей ИЛИ-НЕ. В этом случае это по существу два последовательно соединенных половинных сумматора с двумя входами, при этом входной бит переноса проходит в обход первого сумматора и добавляется к сумме двух входных битов из первого сумматора во втором сумматоре. Обратите внимание, что требуется 12 таких логических элементов, чтобы просто добавить два одиночных бита плюс любой входной бит переноса из предыдущего этапа добавления и предоставить два выходных бита, представляющих сумму битов и любого связанного бита переноса.
Использование такого количества вентилей может показаться странным, когда схему можно было бы легко реализовать с меньшим количеством более сложных вентилей, но схемы, такие как сумматор выше, использовались в компьютере Apollo Guidance Computer , который доставил американских астронавтов на Луну. Двоичная арифметика Двоичный сумматор может быть приспособлен для выполнения других арифметических операций, таких как вычитание, умножение и деление, а также других более сложных математических функций, избегая необходимости в нескольких специализированных процессорах, используя следующие принципы двоичной арифметики.
Ниже приведены три наиболее распространенных примера.
Чтобы вычесть двоичное число B (вычитаемое) из двоичного числа A (уменьшаемое). Это включает n шагов, где n — количество битов в множителе. Первый шаг На каждом последующем шаге: Эта операция включает m — n шагов, где m — количество битов в делимом (число, которое делится) и n — количество бит в делителе. Примечание. Необходимо включить проверки и настроить операцию, чтобы избежать потенциальной проблемы деления на 0. Подпрограммы включают специальные контрольные точки для обнаружения и вставки дополнительных инструкций для обработки битов переноса и заимствования, переполнения, отрицательных чисел, остатков, деления на ноль, если делитель больше делимого. Подпрограммы, подобные приведенным выше, в сочетании с булевыми логическими схемами используются для расширения возможностей арифметико-логического блока (АЛУ) компьютера, чтобы он мог выполнять множество более сложных функций. Подробнее об архитектуре компьютера Арифметика с плавающей запятойВычислительный блок компьютера имеет в своей сумке только два аппаратных инструмента: « сдвиг » и « добавить 9».1313 «, чтобы выполнять все его математические операции. Все основные четыре арифметические операции, описанные в предыдущем разделе, выполнялись с помощью этих двух инструментов и всех соответствующих операций над целыми числами. Однако в практических приложениях даже самые простые математические вычисления включают работу с десятичными числами. Помимо этого, от компьютера может также потребоваться обработка трансцендентных функций, таких как логарифмы, экспоненциальные и тригонометрические функции, которые не могут быть представлены простыми алгебраическими выражениями и, следовательно, не могут быть обработаны простыми 9 компьютерными средствами. В дополнение к проблеме точности существует также проблема масштаба. Трудно управлять как очень большими, так и очень маленькими числами в компьютерных регистрах данных и коммуникационных шинах практического размера. Некоторые примеры:
Последние два числа могут даже встречаться в одном и том же уравнении. Проблема размера становится еще более сложной, когда числа представлены в гораздо более длинной двоичной форме. Использование традиционных научных обозначений частично решает эту проблему, но вводит необходимость манипулировать положением десятичной точки. Эти проблемы точности, прецизионности и масштаба решаются с помощью арифметики с плавающей запятой, которая использует более удобную научную нотацию, но методы вычисления по-прежнему ограничены базовыми возможностями компьютера. Сначала несколько определений: Определения номеров
Также называется Значимая, содержит все цифр числа. Отрицательные мантиссы представляют отрицательные числа. (Остерегайтесь, что термин «мантисса» может вызвать путаницу, поскольку он также может относиться к дробной части десятичного логарифма.) Ссылочный номер, на котором основан показатель степени. Это мощность, до которой поднята база. Указывает, где стоит десятичная (или двоичная) точка относительно начала мантиссы. Двоичный эквивалент десятичной точки в десятичных числах. Пример В экспоненциальном представлении десятичное число 345,6 может быть представлено как 3,456 X 10 2 где 3456 — мантисса или мантисса, 10 — основание, а 2 — показатель степени. Преимущества чисел с плавающей запятой
Операции с плавающей точкой (FP) Операции с плавающей запятой могут быть реализованы аппаратно (схема) или программно (программный код). Однако программное обеспечение намного медленнее аппаратного на два или три порядка. Сдвиг битов Сдвиг мантиссы влево на 1 бит уменьшает показатель степени на 1 и сдвигает точку счисления вправо на одну позицию. Сдвиг мантиссы вправо на 1 бит увеличивает показатель степени на 1 и сдвигает основание на одну позицию влево. Основные алгебраические функции FP
Трансцендентальные и другие функции Возможно, но не обязательно практично хранить все требуемые значения трансцендентных функций в справочных таблицах, хранящихся в памяти компьютера. Оценка значения трансцендентной функции включает в себя настройку цикла для вычисления значения каждого значащего члена ряда по очереди и суммирование значений в отдельном аккумуляторе (с учетом знака). Чем больше членов в ряду, тем выше точность, но соответственно больше время обработки из-за увеличения количества вычислений. Часто можно представить трансцендентную функцию, используя альтернативные методы математической аппроксимации. Как и в случае компромисса между скоростью и точностью, описанном выше, альтернативные методы также предполагают аналогичные компромиссы. Ряд Тейлора — это обычное математическое расширение, хотя и не единственное, используемое для аппроксимации значения трансцендентных функций. Ниже приведены некоторые типичные примеры с использованием ряда Тейлора. Подробнее о серии Taylor. См. также расширение CORDIC (ниже).
Обратите внимание, что эти два ряда содержат как положительные, так и отрицательные члены, а знаменатели включают возрастающие факториалы. Это означает, что члены будут сходиться очень быстро к малым величинам. Обратите также внимание, что компьютер обычно не вычисляет числовые значения факториалов, которые вместо этого извлекаются из справочных таблиц в памяти. Альтернативой ряду Тейлора для оценки значения функции синуса является аппроксимация Гастингса, которая примерно в три раза быстрее и лишь немного менее точна. Функция разделена на небольшое количество интервалов, и в каждом из них используется прямолинейная аппроксимация. Наклоны сегментов прямой линии имеют знаменатели, которые являются степенью двойки, поэтому при вычислении не требуются операции умножения или деления с плавающей запятой. Это был алгоритм, используемый для тригонометрических вычислений в навигационном компьютере Аполлона-11, который доставил астронавтов на Луну.
Обратите внимание, что все члены этого ряда положительны и числители растут быстрее, чем знаменатели, так что ряд не сходится, а расширяется. Квадратный корень не является трансцендентной функцией. Простой метод, основанный на «угадай, проверь и уточни», используется уже много лет. Это работает следующим образом, где a — это искомый квадратный корень √ x .
Величина E будет постепенно уменьшаться, пока не будет достигнута желаемая точность. Этот метод был разработан для использования с десятичными числами. Это не так удобно с двоичными числами и может привести к чрезмерному количеству циклов для сходимости к приемлемому ответу. Дополнительные шаги в этой простой программе могут улучшить это. Квадратный корень можно вычислить напрямую, используя свойства натуральных логарифмов или логарифмов по основанию 10, но сами логарифмы являются трансцендентными функциями, и значения должны быть сначала извлечены из подходящей процедуры аппроксимации, такой как описанная выше. Метод зависит от следующих свойств натурального логарифма ( ln ):
и Ответ: √x = e ( ln X)/2 используя натуральный логарифм ( ln ) В качестве альтернативы, используя логарифм по основанию 10 ( log ), ответ будет следующим: √x = 10 e ( log X)/2 (Деление показателя степени на 2 дает квадратный корень, как и в логарифмических таблицах). обычно используют этот метод вычисления квадратных корней. Алгоритмы аппроксимации CORDIC Алгоритм CORDIC представляет собой итерационный метод вычисления трансцендентных функций, использующий только двоичные операции сдвига и сложения . На примере расчета значения тангенса X/Y = tan Θ, выраженного в виде tan(2 -n ) Вектор из начала координат (нуля) вращается в серии » n » малых шагов δΘ так, чтобы сумма всех шагов была равна Θ. Путем накопления соответствующих изменений значений его ортогональных координат δX и δY на каждом шаге значения X и Y и, следовательно, тангенс могут Алгоритм CORDIC, описанный Дж. Э. Волдером в 1959 году, использовался в первом научном портативном калькуляторе (HP-35), и с тех пор были разработаны и усовершенствованы вариации этой простой базовой концепции для аппроксимации широкого спектра трансцендентных функций. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 1
1 2
2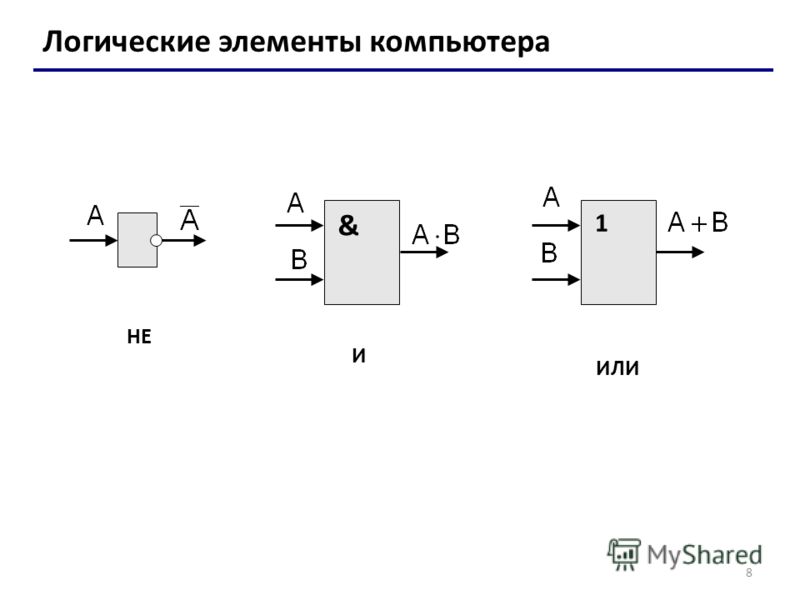 4
4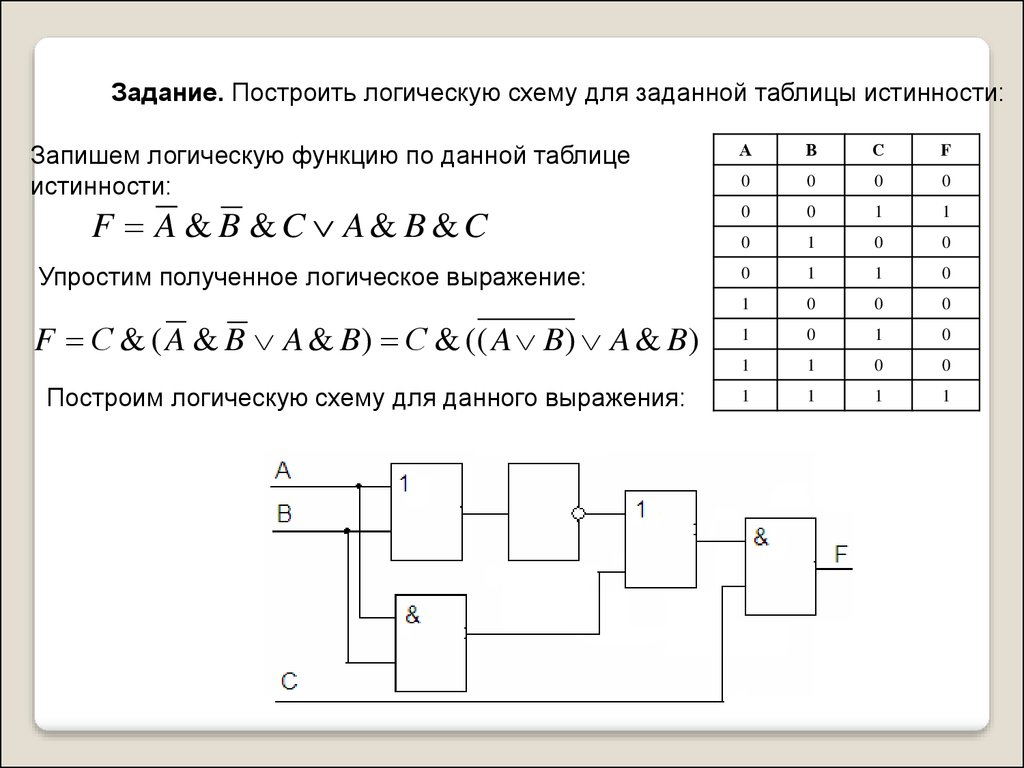 5
5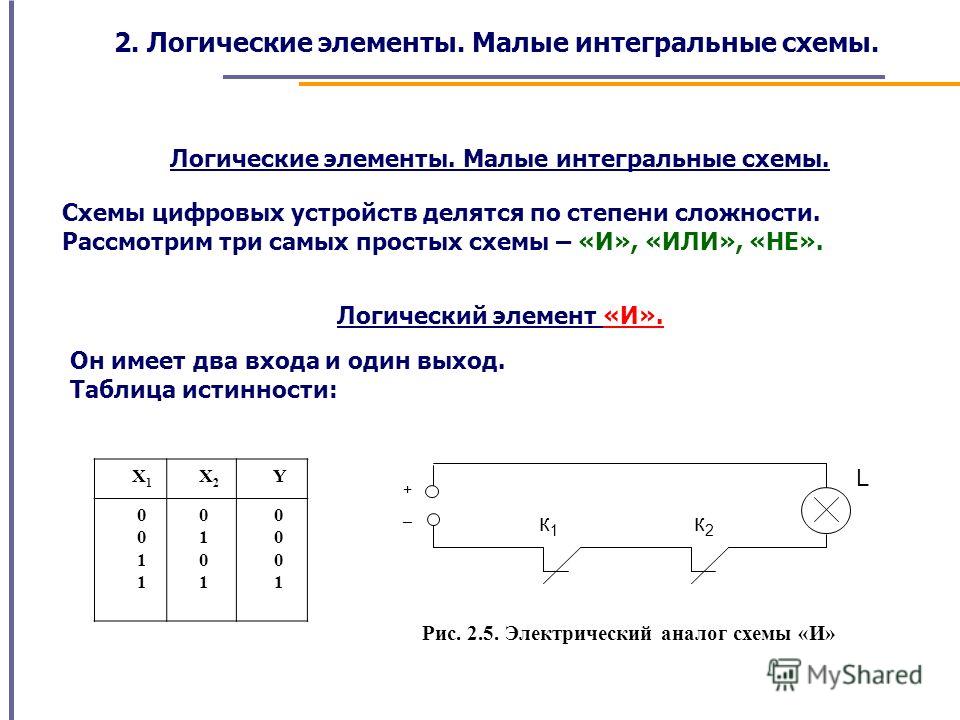 6
6