Делитель напряжения на диодах. Делители напряжения: принцип работы, виды и применение в электронике

Что такое делитель напряжения. Как работают резистивные, емкостные и индуктивные делители. Для чего используются делители напряжения в электронных схемах. Какие бывают виды делителей и как рассчитать их параметры.

Принцип работы делителя напряжения

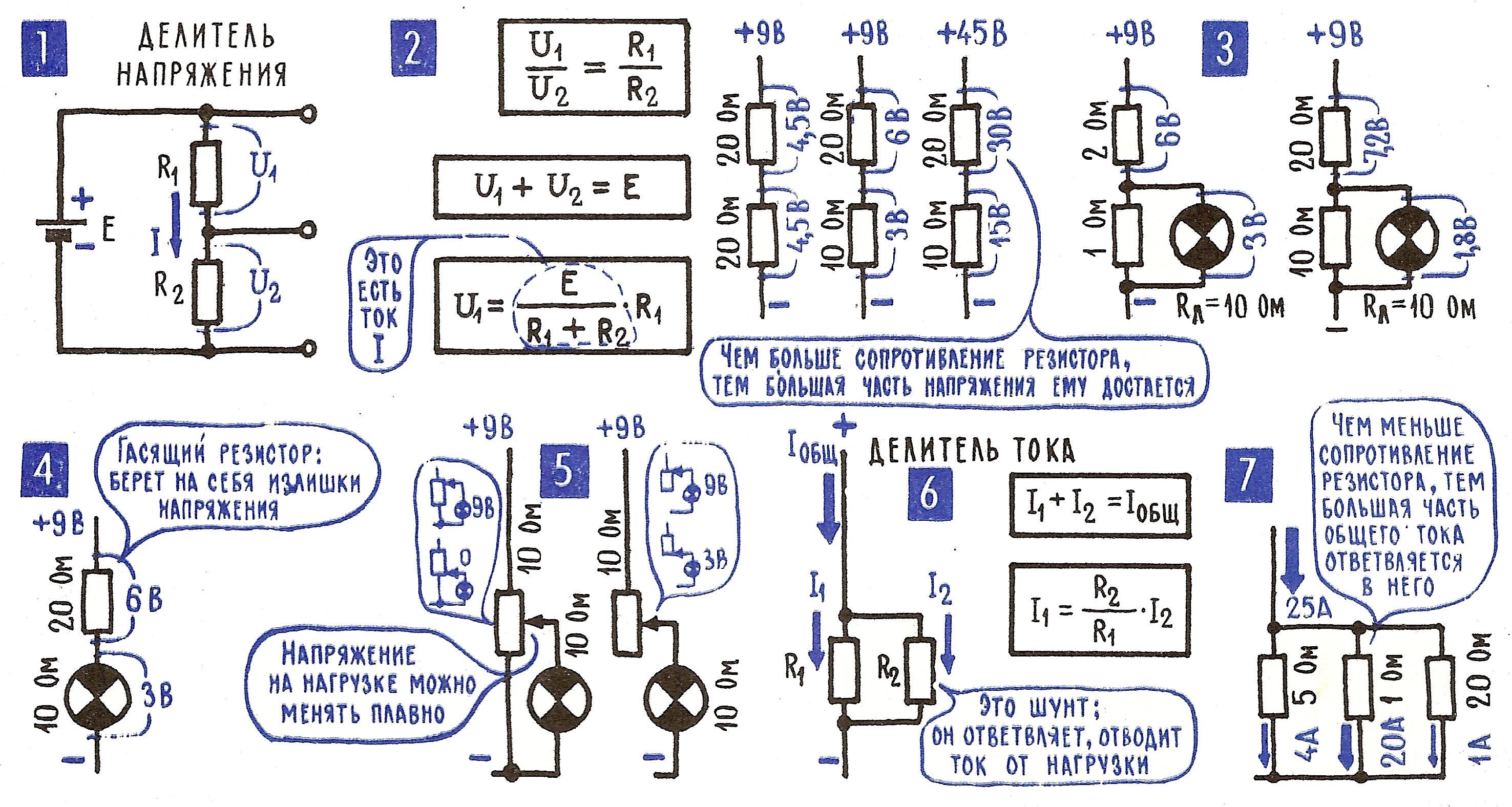
Делитель напряжения — это электрическая схема, позволяющая получить часть входного напряжения на выходе. Простейший делитель состоит из двух последовательно соединенных резисторов. Выходное напряжение снимается с одного из резисторов и определяется соотношением их сопротивлений.

Основная характеристика делителя — коэффициент деления K, равный отношению входного напряжения к выходному:

K = U_вх / U_вых = (R1 + R2) / R2

где R1 и R2 — сопротивления резисторов делителя.

Виды делителей напряжения

В зависимости от используемых элементов различают следующие виды делителей напряжения:

• Резистивные — на основе резисторов
• Емкостные — на основе конденсаторов
• Индуктивные — на основе катушек индуктивности
• Комбинированные — сочетающие разные элементы

Также делители бывают:

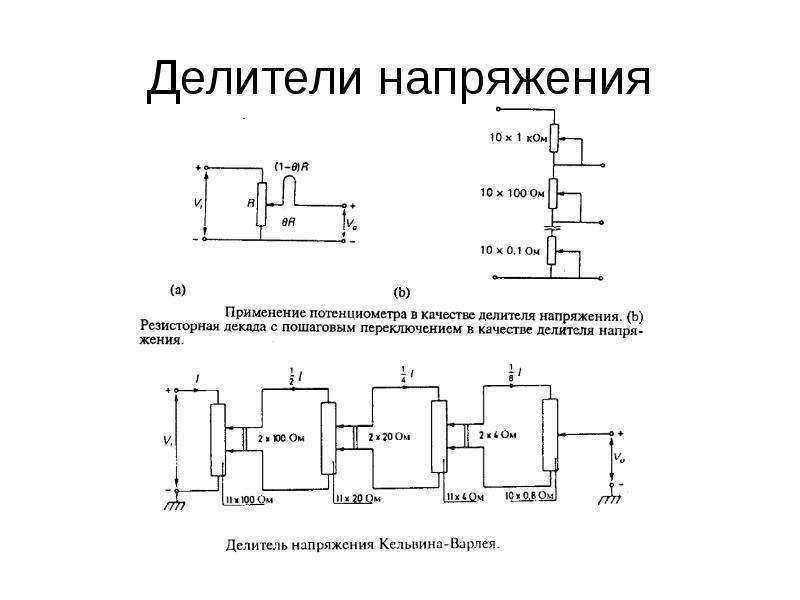
• Однопредельные — с фиксированным коэффициентом деления
• Многопредельные — с несколькими коэффициентами деления
• Регулируемые — с возможностью плавной или ступенчатой регулировки

Резистивный делитель напряжения

Резистивный делитель — самый простой и распространенный вид. Его схема состоит из двух последовательно соединенных резисторов R1 и R2. Входное напряжение подается на всю цепочку, а выходное снимается с резистора R2.

Коэффициент деления такого делителя:

K = (R1 + R2) / R2

Выходное напряжение:

U_вых = U_вх * R2 / (R1 + R2)

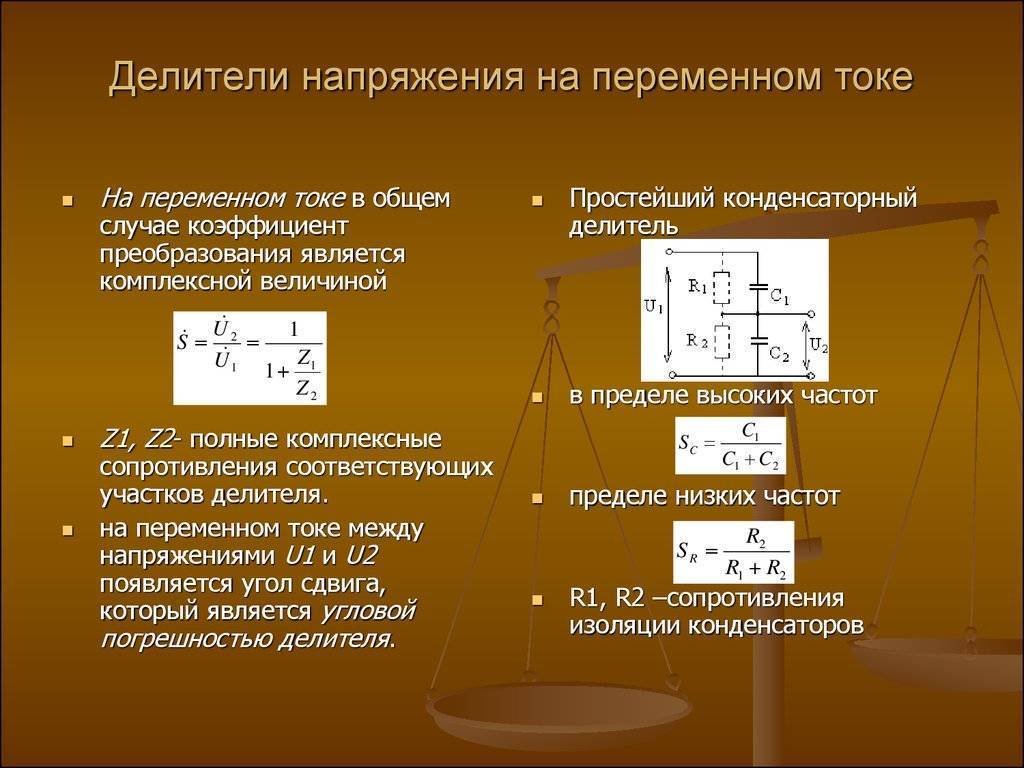
Емкостный делитель напряжения

Емкостный делитель состоит из двух последовательно соединенных конденсаторов. Он применяется в цепях переменного тока. Коэффициент деления определяется соотношением емкостей:

K = (C1 + C2) / C2

где C1 и C2 — емкости конденсаторов.

Емкостные делители используются для измерения высоких напряжений в линиях электропередач.

Индуктивный делитель напряжения

Индуктивный делитель содержит две последовательно включенные катушки индуктивности. Коэффициент деления зависит от соотношения индуктивностей:

K = (L1 + L2) / L2

где L1 и L2 — индуктивности катушек.

Примером индуктивного делителя является автотрансформатор.

Применение делителей напряжения

Делители напряжения широко используются в электронике для следующих целей:

• Получение опорных напряжений в схемах
• Согласование уровней сигналов
• Расширение пределов измерения вольтметров
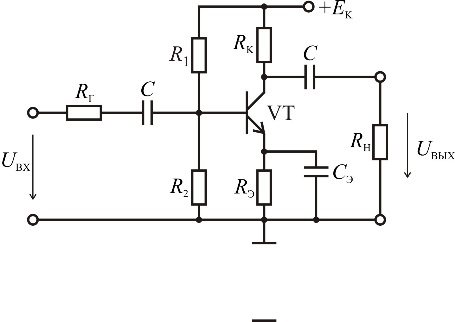
• Смещение рабочей точки транзисторов
• Регулировка громкости в аудиотехнике
• Измерение высоких напряжений

Расчет делителя напряжения

При расчете делителя напряжения необходимо учитывать следующие факторы:

1. Требуемый коэффициент деления K
2. Входное напряжение U_вх
3. Выходное напряжение U_вых
4. Ток нагрузки I_нагр
5. Мощность резисторов P

Порядок расчета:

1. Определить коэффициент деления K = U_вх / U_вых
2. Задать ток делителя I_д (обычно в 10 раз больше тока нагрузки)
3. Рассчитать сопротивления R2 = U_вых / I_д и R1 = R2 * (K — 1)
4. Проверить мощность резисторов P = I_д^2 * R

Особенности применения делителей напряжения

При использовании делителей напряжения следует учитывать ряд особенностей:

• Нагрузка, подключенная к выходу, изменяет коэффициент деления
• Необходимо учитывать допуски на номиналы резисторов
• Температурный дрейф сопротивлений влияет на стабильность
• На высоких частотах проявляются паразитные емкости
• При больших напряжениях возможен пробой резисторов

Для повышения точности и стабильности применяют прецизионные резисторы, температурную компенсацию и другие методы.

Делитель напряжения на потенциометре

Регулируемый делитель напряжения можно реализовать на основе потенциометра. Потенциометр представляет собой переменный резистор с тремя выводами. При вращении ручки изменяется соотношение сопротивлений между средним и крайними выводами.

Коэффициент деления такого делителя плавно регулируется от 0 до 1. Потенциометры широко применяются для регулировки громкости, яркости и других параметров в бытовой электронике.

Многоступенчатые делители напряжения

Для получения нескольких уровней напряжения применяют многоступенчатые делители. Они состоят из цепочки последовательно соединенных резисторов. Напряжения снимаются с отводов между резисторами.

Такие делители позволяют получить несколько фиксированных уровней напряжения от одного источника. Они часто используются в измерительной технике и системах электропитания.

Защита делителей напряжения

При работе с высокими напряжениями необходимо обеспечить защиту делителей напряжения. Для этого применяют следующие меры:

• Использование высоковольтных резисторов
• Последовательное включение нескольких резисторов
• Применение защитных разрядников
• Экранирование делителя
• Изоляция высоковольтной части

Правильно спроектированный делитель обеспечивает безопасное измерение высоких напряжений.

схема и расчёт [Амперка / Вики]

Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов.

В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе V_out? Или эквивалентный вопрос: какое напряжение покажет вольтметр?

Ток, протекающий через R1 и R2 одинаков пока к выходу V_out ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:

Таким образом, сила тока протекающая через резисторы

Теперь, когда нам известен ток в R2, расчитаем напряжение вокруг него:

Или если отавить формулу в общем виде:

Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.

Применение делителя для считывания показаний датчика

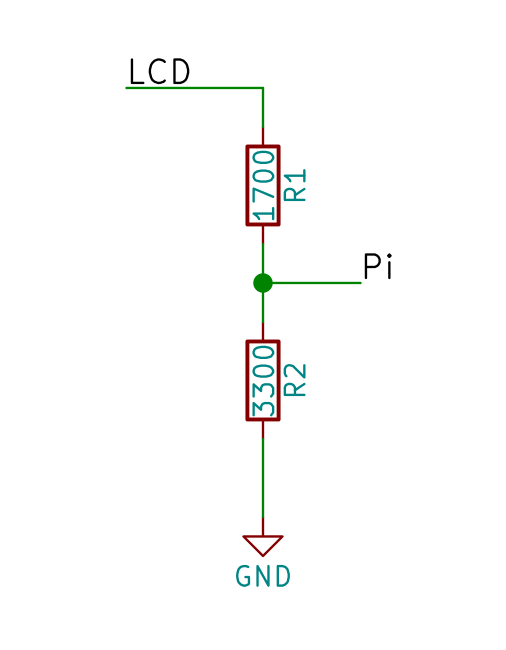
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т.д.

Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V_out будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.

Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта V_out.

Подключение нагрузки

С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):

В этом случае V_out уже не может быть расчитано лишь на основе значений V_in, R1 и R2: сама нагрузка провоцирует дополнительное падение напряжения (voltage drop).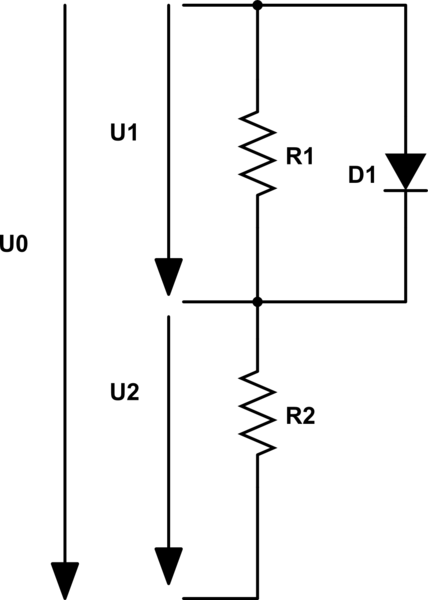 Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление

В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:

Подставив значение в общую формулу расчёта

V_out, получим:

Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.

Пропорция сохраняется, V_out не меняется:

А потери уменьшатся:

Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.

Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на

R1 равна:

А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.

Применимость

Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.

Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.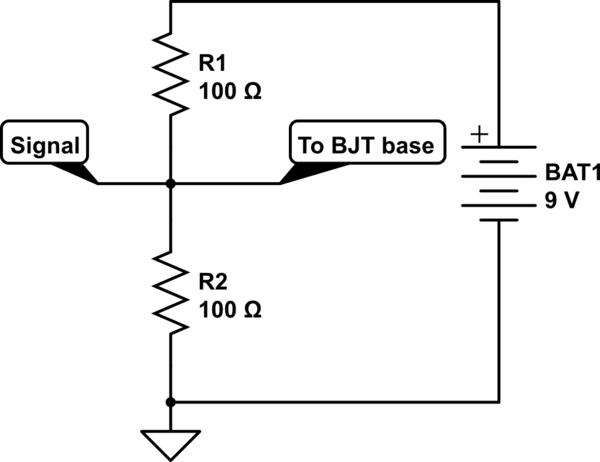

Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.

Если потребление тока нагрузкой неравномерно во времени, V_out также будет неравномерным.

Делитель напряжения в цепи обратной связи

Добавлено 22 ноября 2018 в 23:36

Сохранить или поделиться

Если мы добавим делитель напряжения в схему отрицательной обратной связи так, чтобы на инвертирующий вход подавалась только часть выходного напряжения, а не полная его величина, выходное напряжение будет кратно входному напряжению (помните, схема подключения питания к операционному усилителю снова пропущена для простоты):

Эффект отрицательной обратной связи с делителем напряжения

Если R₁ и R₂ равны, а V_вх равно 6 вольт, операционный усилитель будет выдавать любое напряжение, необходимое для падения 6 вольт на резисторе R

1 (чтобы сделать напряжение на инвертирующем входе равным 6 вольтам, а также сохранить разность напряжений между входами равной нулю). С делителем напряжения 1:2 из резисторов R₁ и R₂ для выполнения этого условия потребуется напряжение 12 вольт на выходе усилителя.

Другой способ анализа этой схемы – начать с вычисления величины и направления тока через R₁, зная напряжение на обеих сторонах (и, следовательно, при помощи вычитания напряжение на R₁) и сопротивление R₁. Так как левая сторона R₁ связана с землей (0 вольт), а правая сторона имеет потенциал 6 вольт (из-за отрицательной обратной связи, поддерживающей эту точку, равной V_вх), мы видим, что имеем на R₁ напряжение 6 вольт. Это дает нам ток 6 мА через R₁ слева направо. Поскольку мы знаем, что оба входа операционного усилителя имеют чрезвычайно высокий импеданс, мы можем с уверенностью предположить, что они не будут добавлять или вычитать какой-либо ток через делитель. Другими словами, мы можем рассматривать R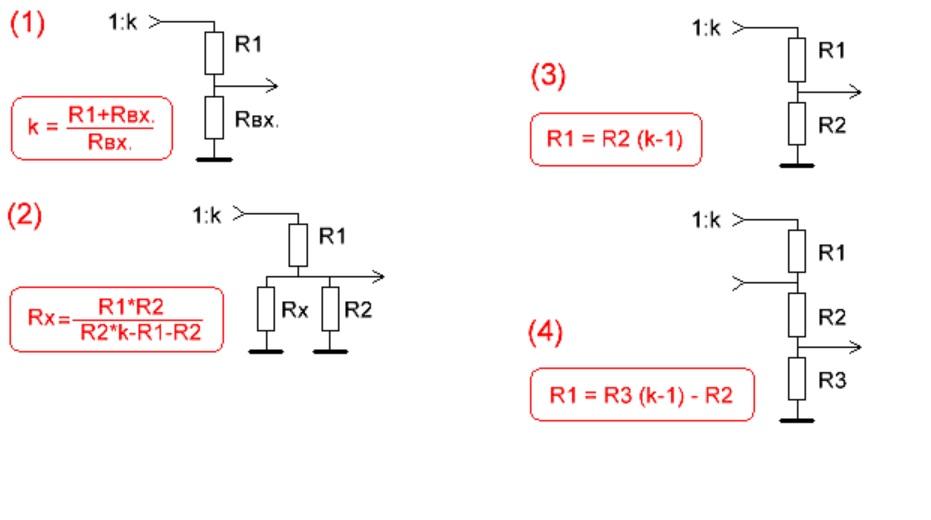

1 и R₂ как включенные последовательно друг с другом: все электроны, протекающие через R₁, должны проходить и через R₂. Зная ток через R₂ и сопротивление R₂, мы можем рассчитать напряжение на R₂ (6 вольт) и его полярность. Подсчитывая напряжения от земли (0 вольт) до правой стороны R₂, мы получаем на выходе 12 вольт.

Исследуя последнюю иллюстрацию, можно задаться вопросом: «Где проходит этот ток 6 мА?». Последняя иллюстрация не показывает весь путь прохождения тока, но на самом деле он начинается с положительного вывода источника питания постоянного напряжения, через выходной транзистор(ы) операционного усилителя, через выходной вывод операционного усилителя, через R

2, через R₁, через землю, а затем к отрицательному выводу источника питания постоянного напряжения.

Отрицательная обратная связь с делителем напряжения на примере модели операционного усилителя

6-вольтовый источник питания не должен обеспечивать схему каким-либо током: он просто управляет операционным усилителем для баланса напряжения между инвертирующим (-) и неинвертирующим (+) входными выводами и при этом создает выходное напряжение, которое в два раза больше входного сигнала из-за деления на двух резисторах по 1 кОм.

Мы можем изменить коэффициент усиления по напряжению в этой схеме, просто регулируя значения R₁ и R₂ (изменяя часть выходного напряжения, которая подается обратно на инвертирующий вход). Коэффициент усиления можно рассчитать по следующей формуле:

\[A_V = {R_2 \over R_1} + 1\]

Обратите внимание, что коэффициент усиления по напряжению для этой схемы усилителя никогда не может быть меньше 1. Если бы мы должны были понизить значение R₂ до нуля ом, наша схема была бы идентична повторителю напряжения, при этом выход напрямую подключался бы к инвертирующему входу. Поскольку повторитель напряжения имеет коэффициент усиления 1, это устанавливает нижний предел коэффициента усиления этого неинвертирующего усилителя. Однако коэффициент усиления может быть увеличен далеко выше 1 с помощью увеличения R₂ относительно R₁.

Также обратите внимание, что полярность выходного сигнала совпадает с полярностью входного сигнала, как и в повторителе напряжения. Положительное входное напряжение приводит к положительному выходному напряжению и наоборот (относительно земли). По этой причине эта схема называется неинвертирующим усилителем.

Как и с повторителем напряжения, мы видим, что дифференциальный коэффициент усиления ОУ не имеет значения, если он очень велик. Напряжения и токи в этой схеме вряд ли изменились бы вообще, если бы коэффициент усиления ОУ составлял бы 250000 вместо 200000. Это резко контрастирует со схемами усилителей на отдельных транзисторах, где бета отдельных транзисторов сильно влияла на общий коэффициент усиления усилителя. С отрицательной обратной связью у нас есть система самокорректирования, которая усиливает напряжение в соответствии с соотношением, установленным резисторами обратной связи, а не коэффициентами усиления, внутренними для операционного усилителя.

Давайте посмотрим, что произойдет, если мы сохраним отрицательную обратную связь через делитель напряжения, но подадим входное напряжение в другое место:

Схема усилителя с отрицательной обратной связью с делителем напряжения и подачей входного сигнала на инвертирующий вход

При соединении неинвертирующего входа с землей отрицательная обратная связь также удерживает напряжение на инвертирующем входе на нуле вольт.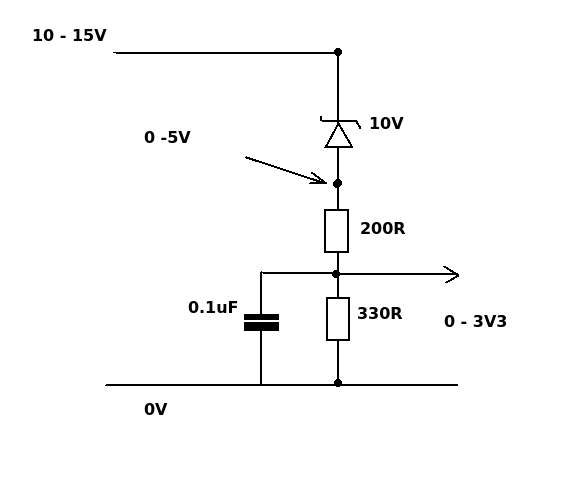 По этой причине инвертирующий вход упоминается в этой схеме как виртуальная земля, которая удерживается обратной связью на потенциале земли (0 вольт), но напрямую не соединена (электрически) с землей. Входное напряжение на этот раз снова подается на левый конец делителя напряжения (снова R₁ = R₂ = 1 кОм), поэтому выходное напряжение должно раскачиваться до -6 вольт, чтобы уравновешивать среднюю точку с потенциалом земли (0 вольт). Используя те же методы, что и для неинвертирующего усилителя, мы можем проанализировать работу этой схемы, определив величины и направления токов, начиная с R₁, и продолжая определением выходного напряжения.

Мы можем изменить общий коэффициент усиления по напряжению этой схемы, просто регулируя значения R₁ и R₂ (изменяя часть выходного напряжения, которая подается обратно на инвертирующий вход). Коэффициент усиления можно рассчитать по следующей формуле:

\[A_V = -{R_2 \over R_1}\]

Обратите внимание, что коэффициент усиления этой схемы может быть меньше 1, в зависимости от отношения R₂ к R₁.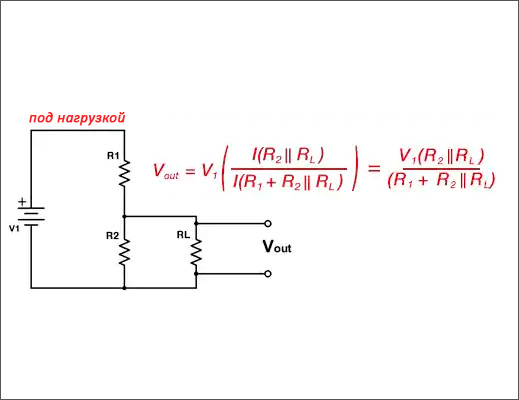 Также обратите внимание, что выходное напряжение всегда имеет полярность, противоположную полярности входного напряжения. Положительное входное напряжение приводит к отрицательному выходному напряжению и наоборот (относительно земли). По этой причине данная схема называется инвертирующим усилителем. Иногда эта формула коэффициента усиления содержит знак минуса (перед дробью R₂/R₁), чтобы отразить изменение полярности.

Эти две схемы усилителей, которые мы только что исследовали, служат для умножения или деления величины напряжения входного сигнала. Именно так математические операции умножения и деления обычно обрабатываются в аналоговой компьютерной схемотехнике.

Резюме

• Подключая инвертирующий (-) вход операционного усилителя напрямую к выходу, мы получаем отрицательную обратную связь, которая дает нам схему повторителя напряжения. Подключая эту отрицательную обратную связь через резисторный делитель напряжения (подавая часть выходного напряжения на инвертирующий вход), выходное напряжение становится кратным входному напряжению.
• Схема операционного усилителя с отрицательной обратной связью и подачей входного сигнала на неинвертирущий (+) вход называется неинвертирующим усилителем. Выходное напряжение будет такой же полярности, как и входное. Коэффициент усиления по напряжению определяется следующей формулой: A_V = (R₂/R₁) + 1.
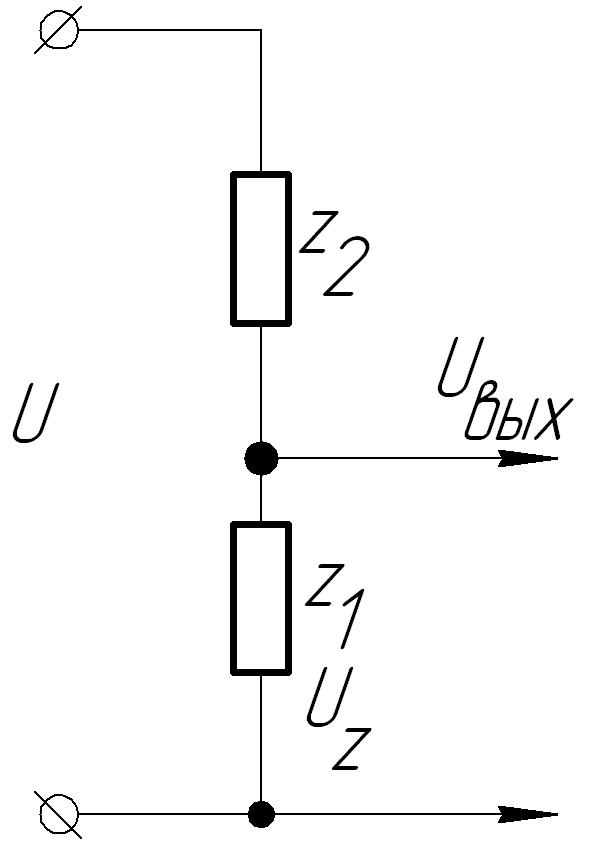
• Схема операционного усилителя с отрицательной обратной связью и подачей входного сигнала на «нижнюю часть» резисторного делителя напряжения, с неинвертирующим (+) входом, соединенным с землей, называется инвертирующим усилителем. Его выходное напряжение будет противоположной полярности, чем входное напряжение. Коэффициент усиления по напряжению определяется следующей формулой: A_V = -R₂/R₁.

Оригинал статьи:

Теги

Делитель напряженияИнвертирующий усилительНеинвертирующий усилительОбучениеОтрицательная обратная связьОУ (операционный усилитель)Повторитель напряженияЭлектроника

Сохранить или поделиться

1. Делители напряжения | 5. Схемы делителей и законы Кирхгофа | Часть1

1. Делители напряжения

Делители напряжения

 

Давайте проанализируем простую последовательную цепь и определим напряжения на каждом из ее резисторов:

 

 

Зная сопротивления каждого из резисторов, мы можем вычислить общее сопротивление цепи (которое для последовательной цепи будет равно сумме отдельных сопротивлений):

 

 

Теперь, используя закон Ома (I = U/R), определяем общую силу тока, которая будет одинакова на всех компонентах нашей последовательной цепи:

 

 

И наконец, зная общую силу тока (2 миллиампера), давайте рассчитаем напряжение на каждом из резисторов:

 

 

Из этой таблицы видно, что напряжения на резисторах пропорциональны их сопротивлениям (учитывая, что сила тока через все резисторы одинакова). Заметьте, напряжение на резисторе R₂ в два раза больше напряжения на резисторе R₁, так же как и сопротивление R₂ в два раза больше сопротивления R₁.

Если мы изменим общее напряжение цепи, то увидим, что эта пропорциональность сохранится:

 

 

Несмотря на увеличение напряжение источника питания, напряжение на резисторе R2 по прежнему в два раза больше напряжения на резисторе R1.

Произведя несколько подобных наблюдений становится очевидным, что напряжение на каждом из резисторов составляет фиксированную пропорцию от общего напряжения. Например, при напряжении батареи 45 вольт, напряжение на резисторе R₁ составляло 10 вольт. Когда напряжение батареи было увеличено до 180 вольт (в 4 раза), напряжение на резисторе R1 так же увеличилось в 4 раза (с 10 до 40 вольт).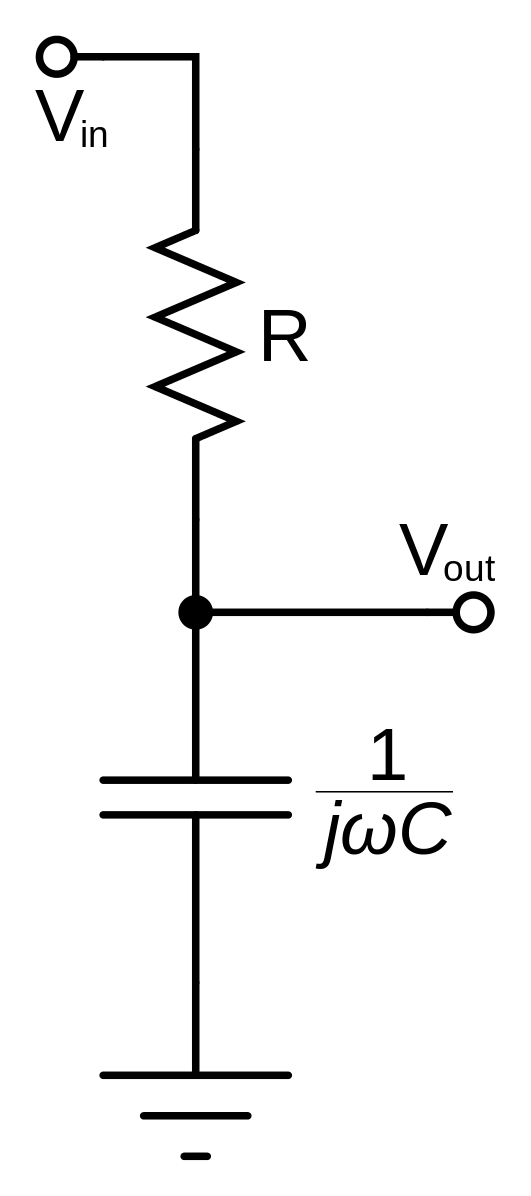 Как видите, соотношение между напряжением на резисторе R₁ и общим напряжением не изменилось:

 

 

Соотношения других напряжений с увеличением напряжения питания так же не изменятся:

 

 

Из за способности последовательной цепи пропорционально распределять общее напряжение по резистивным компонентам, ее часто называют делителем напряжения. Немного поколдовав с математикой, можно получить формулу для определения напряжения на любом резисторе, имея только значения сопротивлений отдельных резисторов, общего напряжения и общего сопротивления:

 

 

Полученная нами формула известна как формула делителя напряжения, с ее помощью легче рассчитывать напряжения последовательной цепи, чем производить аналогичные расчеты с использованием закона Ома.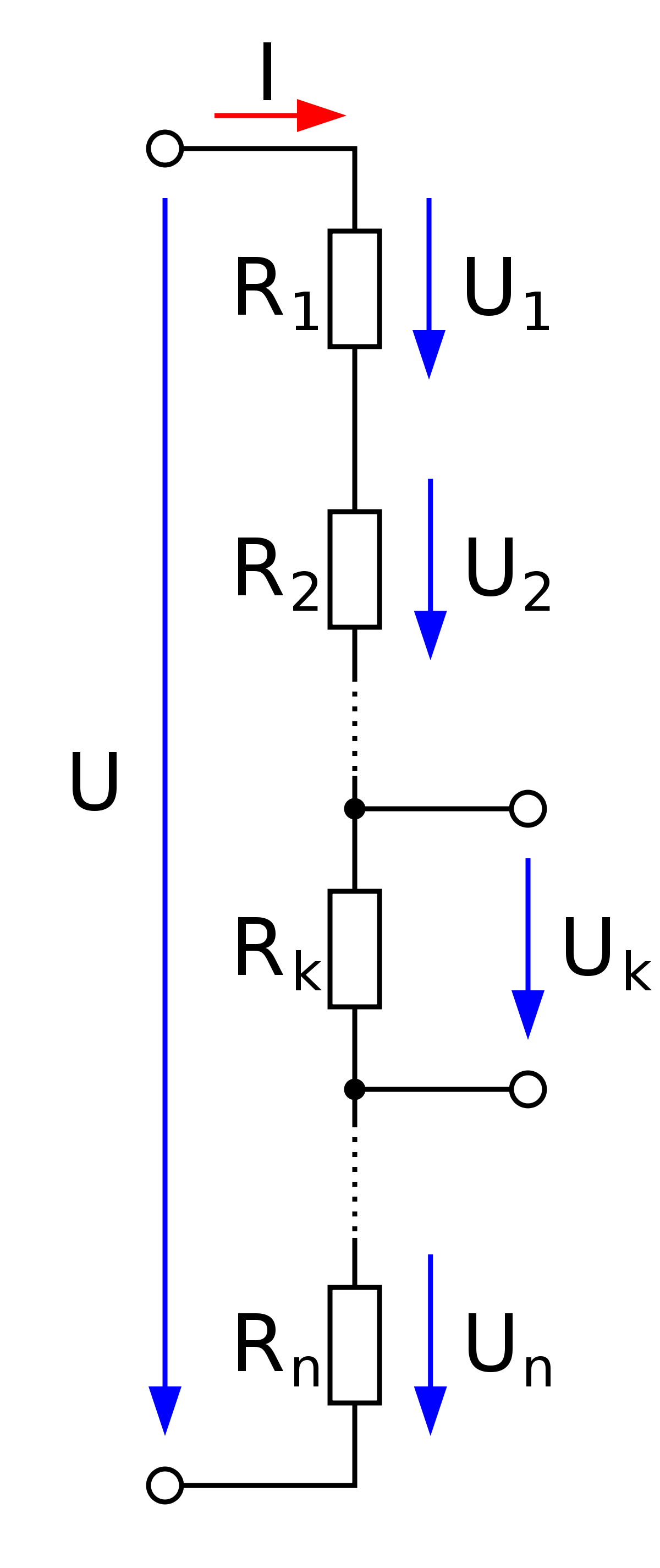

Используя эту формулу можно повторно проанализировать приведенную выше схему, и определить ее напряжения произведя меньшее количество действий:

 

 

 

Делители напряжения нашли широкое применение в схемах измерительных приборов, где определенные комбинации соединенных последовательно резисторов используются для «деления» напряжения на нужные пропорции, необходимые для измерения разных величин того же напряжения.

 

 

Одним из устройств, часто используемых в качестве делителя напряжения, является потенциометр. Потенциометр представляет собой проводник с большим омическим сопротивлением (резистор), снабженный скользящим контактом:

 

 

Условное обозначение потенциометра представляет собой вертикальный символ резистора с примыкающей к нему стрелкой — скользящим контактом. Если скользящий контакт переместить ближе к контакту 1, то сопротивление между ними будет меньше, чем сопротивление между скользящим контактом и контактом 2. Если скользящий контакт переместить ближе к контакту 2, то эффект будет противоположным. Сопротивление между контактами 1 и 2 будет постоянным, независимо от положения скользящего контакта:

 

 

На рисунке ниже показана конструкция двух типов потенциометров, роторного и линейного:

 

 

 

Некоторые линейные потенциометры приводятся в действие посредством прямолинейного движения рычага или слайд-кнопки. Другие, как тот, который изображен на рисунке — посредством отвертки, для более точной настройки. Такие потенциометры называют еще «подстроечными».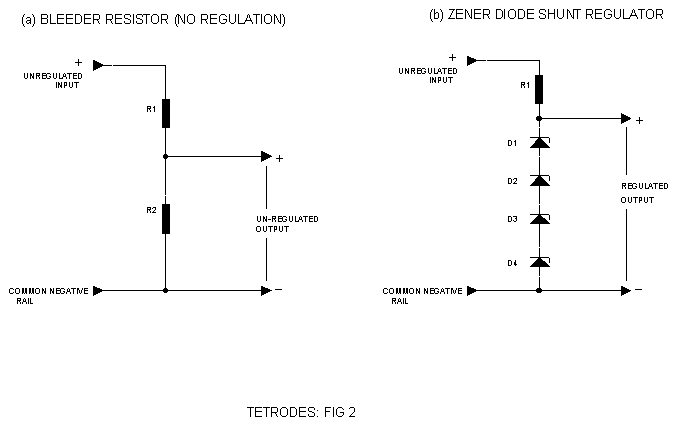 Следует отметить, что не у всех линейных потенциометров назначение выводов соответствует показанным на рисунке. У некоторых, вывод скользящего контакта находится посередине, между выводами конечных контактов.

На следующей фотографии изображен реальный ротационный потенциометр с открытыми для просмотра скользящим контактом и резистивным элементом. Рукоятка этого потенциометра повернута таким образом, что его скользящий контакт почти касается левого вывода резистивного элемента:

А здесь показан тот же самый потенциометр, но его скользящий контакт повернут против часовой стрелки в другую сторону:

Если постоянное напряжение приложить к контактам резистивного элемента потенциометра, то скользящий контакт выступит в роли своеобразного «крана», с помощью которого можно регулировать величину этого напряжения на выходе прибора:

 

 

По аналогии с фиксированным делителем напряжения, пропорциональность деленного потенциометром напряжения является исключительно функцией сопротивления, а не приложенного напряжения.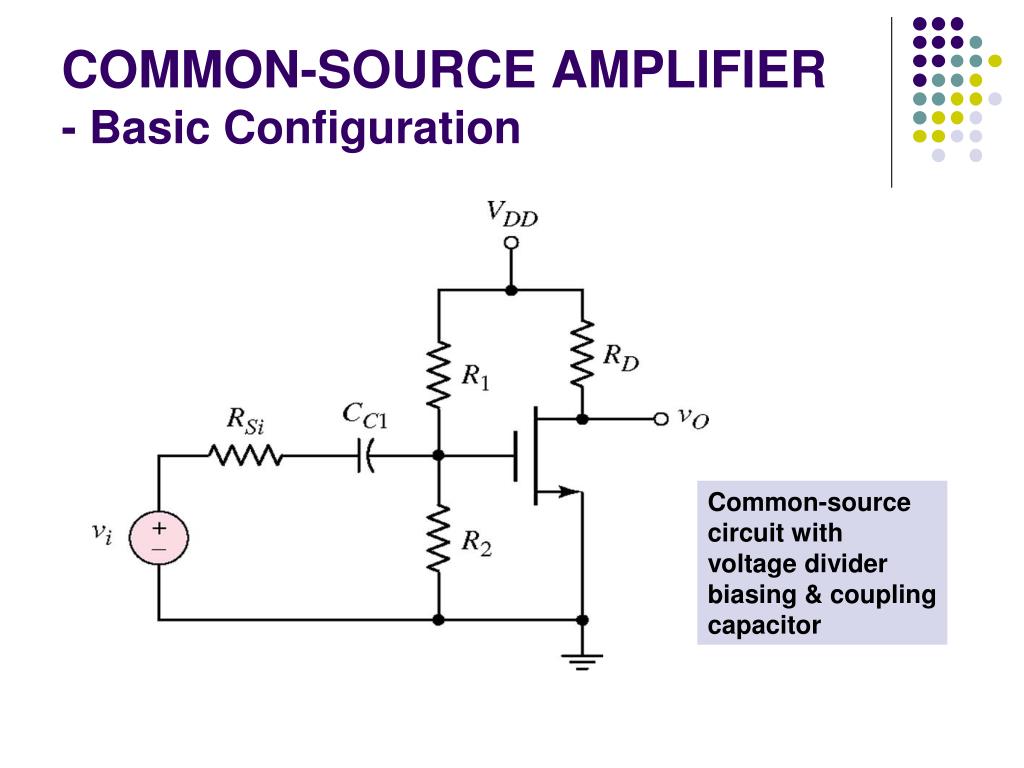 Иными словами, если ручкой потенциометра установить его скользящий контакт строго посередине резистивного элемента, то на выходе мы получим ровно половину от приложенного напряжения, независимо от его величины. Можно сказать, что потенциометр функционирует как регулируемый делитель напряжения, в котором пропорциональность деленного напряжения устанавливается положением скользящего контакта.

Такая функция потенциометра очень полезна для получения регулируемого напряжения от фиксированного источника, например батареи. Если собранная вами схема требует напряжение, которое меньше напряжения имеющейся батареи, то вы можете подключить к этой батарее выводы резистивного элемента потенциометра, и  ручкой «выставить» нужное напряжение между скользящим контактом и одним из конечных контактов:

 

 

Такое применение потенциометра при проектировании электрических схем пользуется большой популярностью.

На следующей фотографии показаны небольшие потенциометры, которые обычно применяются в бытовых электроприборах и различных радиолюбительских схемах:

Самый левый и самый правый потенциометры могут устанавливаться непосредственно на макетную или печатную плату. Средние устройства предназначены для установки на плоскую панель, со схемой они соединяются при помощи проводов.

Ниже показаны специализированные потенциометры:

ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ • Большая российская энциклопедия

Схемы низковольтных делителей напряжения: а – резистивного; б – ёмкостного; в – индуктивного; u и U – напряжения; r и R – резисторы; C1 и C2 – конденсаторы; L1 и L2…

ДЕЛИ́ТЕЛЬ НАПРЯЖЕ́НИЯ, элек­тро­тех­нич. уст­рой­ст­во, по­зво­ляю­щее сни­мать (ис­поль­зо­вать) толь­ко часть имею­ще­го­ся по­сто­ян­но­го или пе­ре­мен­но­го на­пря­же­ния по­сред­ст­вом эле­мен­тов элек­трич. це­пи, со­стоя­щей из ре­зи­сто­ров, кон­ден­са­то­ров или ка­ту­шек ин­дук­тив­но­сти. Обыч­но при­ме­ня­ет­ся для из­ме­ре­ния на­пря­же­ния. Осн. ха­рак­те­ри­сти­ка Д. н. – ко­эф. де­ле­ния, оп­ре­де­ляе­мый от­но­ше­ни­ем вход­но­го (из­ме­ряе­мо­го) на­пря­же­ния к вы­ход­но­му (сни­мае­мо­му). Про­стей­ший Д. н. пред­став­ля­ет со­бой два по­сле­до­ва­тель­но со­еди­нён­ных ре­зи­сто­ра (два пле­ча де­ли­те­ля), на ко­то­рые по­да­ёт­ся вход­ное на­пря­же­ние $U$ (рис., а). Ко­эф. де­ле­ния при от­сут­ст­вии на­груз­ки оп­ре­де­ля­ет­ся фор­му­лой $$K=U/u=R/(R+r),$$ где $R$ и $r$ – со­про­тив­ле­ния ре­зи­сто­ров, $u$ – сни­мае­мое нап­ря­же­ние. От­кло­не­ния $R$ и $r$ (а сле­до­ва­тель­но, и $K$) от но­ми­наль­ных зна­че­ний обу­слов­ли­ва­ют по­греш­ность де­ли­те­ля. В Д. н. вы­со­кой точ­но­сти при­ме­ня­ют ре­зи­сто­ры с ма­лым тем­пе­ра­тур­ным ко­эф. со­про­тив­ле­ния и вы­со­кой вре­мен­нóй ста­биль­но­стью (напр., из ман­га­ни­но­вой про­во­ло­ки). В це­пях пе­ре­мен­но­го то­ка по­ми­мо ре­зи­стив­ных Д.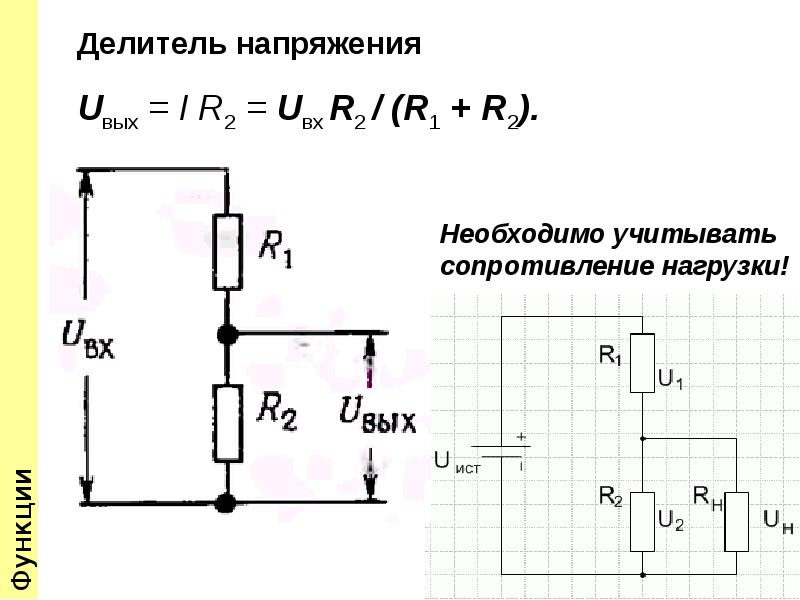  н. ис­поль­зу­ют­ся так­же ём­ко­ст­ные с кон­ден­са­то­ра­ми по­сто­ян­ной или пе­ре­мен­ной ём­ко­сти (рис., б) и ин­дук­тив­ные (рис., в).

Д. н. мо­гут быть од­но­пре­дель­ны­ми (с од­ним но­ми­наль­ным $K$) и мно­го­пре­дель­ны­ми; с по­сто­ян­ным и ре­гу­ли­руе­мым (плав­но, дис­крет­но или ком­би­нир. спо­со­бом) от­но­ше­ни­ем плеч. Д. н. вхо­дят в со­став мн. средств из­ме­ре­ния в ка­че­ст­ве зве­на из­ме­рит. це­пи. Напр., ре­зи­стив­ные де­ли­те­ли с но­ми­наль­ны­ми зна­че­ния­ми $K$, рав­ны­ми 10, 100 и 1000, при­ме­ня­ют­ся во вход­ных це­пях мно­го­пре­дель­ных ана­ло­го­вых и циф­ро­вых вольт­мет­ров. Ём­ко­ст­ные Д. н., со­стоя­щие из не­сколь­ких по­сле­до­ва­тель­но со­еди­нён­ных кон­ден­са­то­ров вы­со­кой точ­но­сти, слу­жат для от­бо­ра мощ­но­стей от ЛЭП вы­со­ко­го на­пря­же­ния (до 500 кВ). При­ме­ром Д. н. на ин­дук­тив­ных со­про­тив­ле­ни­ях яв­ля­ет­ся ав­то­транс­фор­ма­тор.

Делитель напряжения — HomoFaciens

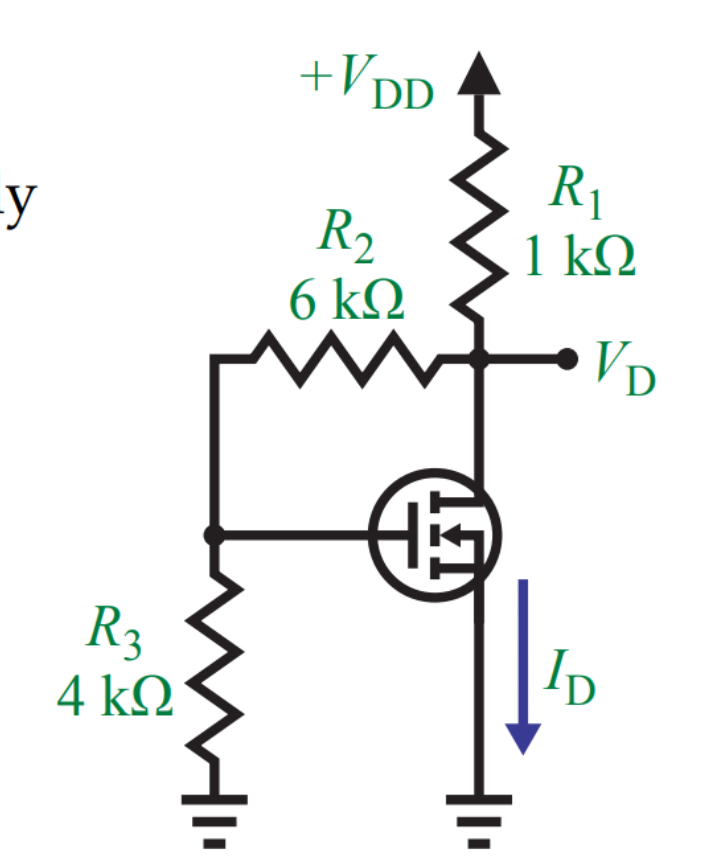
Новости Проект Технологии РобоСпатиум Способствовать Предметный указатель Скачать Ответы Игры Советы по покупкам Связаться с нами <<< RC-схема операционного усилителя >>> Постоянное сопротивление Рисунок 1: В главе о сетях постоянного сопротивления мы познакомились с теорией делителей напряжения.Теперь я хотел бы представить некоторые практические преимущества этих простых сетей. Делители напряжения очень полезны, если вам нужна фиксированная часть напряжения питания для специального устройства в электронной схеме. Например, в главе об усилительных схемах мы приложили напряжение смещения к выводу базы биполярного переходного транзистора. Напряжение смещения составляло около 0,67 В, а номинальное напряжение использованной батареи составляло 12 В. Таким образом, соотношение напряжений составляет 0,67 В: 12,00 В. При использовании резистора 1 кОм значение второго составляет: R 2 = (1 кОм * 0.67 В) / (12,00 В — 0,67 В) = 59 Ом. Что произойдет, если изменится выходное напряжение батареи? Конечное напряжение заряда свинцово-кислотных аккумуляторов 12 В составляет 14 В, и вы должны прекратить их разряжать при напряжении 11,2 В, следовательно, падение напряжения при R 2 варьируется в пределах U max = 14,0 В * 59 Ом / (59 Ом + 1000 Ом. ) = 0,78 В и U мин. = 11,2 В * 59 Ом / (59 Ом + 1000 Ом) = 0,62 В. Поэтому, если вы собираетесь создать высококачественный усилитель, вам следует позаботиться о более постоянном входном напряжении, чем может обеспечить свинцово-кислотная батарея. Рисунок 2: Делитель напряжения может быть построен с использованием более чем 2 резисторов. Внизу требуется напряжение 0,75 В при входном напряжении 12 В, в то время как общее сопротивление сети должно быть 528 Ом, следовательно, резисторы 33 Ом и 495 Ом должны справиться с этой задачей, но вы не сможете купить Резистор 495 Ом. Решение проблемы состоит в том, чтобы вместо этого использовать один резистор 470 Ом, один 15 Ом и один 10 Ом (вы также не сможете купить резистор 25 Ом). Падение напряжения на одиночном резисторе: R x = 12 В * R x / R Всего Итак, получаем 10.68 В при 1 рандов, 0,34 В при 2 рандов, 0,23 В при 3 рандов и, наконец, 0,75 В при 4 рандов. Выходное сопротивление При использовании делителя напряжения в качестве источника напряжения для специального устройства следует учитывать сдвиг напряжения при подключении нагрузки параллельно одному из резисторов. Из главы об электронных переключателях мы узнали, что базового напряжения 0,75 В на BD135 достаточно для включения электродвигателя. Делитель напряжения 2.7 кОм и сопротивление 180 Ом обеспечивают это напряжение, если никакая нагрузка не подключена параллельно к R 2 . При подключении транзистора к схеме падение напряжения на R 2 снижается до 0,68 В, что недостаточно для переключения электродвигателя. Сопротивление линии эмиттер-база транзисторов составляет примерно 1800 Ом. Чтобы получить более стабильное выходное напряжение, необходимо уменьшить общее сопротивление делителя напряжения. При использовании резистора 495 Ом и 33 Ом (см. Пример выше) падение напряжения на R 2 равно 0. 75В без нагрузки и 0,74В при подключении транзистора к сети. Недостатком уменьшения общего сопротивления является то, что большая часть входного напряжения уходит в виде тепла. 256 мВт рассеивается при R 1 и 17 мВт при R 2 , тогда как на транзисторе потребляется всего 375 мкВт. Потенциометр Рисунок 3: В принципе, потенциометр — это регулируемый делитель напряжения. Обычно они состоят из резистивного элемента, образованного дугой окружности, немного меньше полного витка.Выходное напряжение на скользящем контакте находится между нулем вольт и входным напряжением делителя. Кусок резистивного провода с зажимом, используемый в качестве скользящего контакта, можно использовать как очень простую конструкцию линейного потенциометра. Выходное напряжение делителя может использоваться как входное значение схемы управления, следовательно, потенциометры могут использоваться в качестве датчиков для целей позиционирования. Сервоприводы обычно используют однооборотные потенциометры для управления вращательным движением.Соответственно, выходное напряжение линейного скользящего потенциометра может использоваться для определения соответствующей регулировки линейного движения. Рисунок 4: При укорачивании среднего штифта, соединенного изнутри со скользящим контактом и одного из внешних штифтов, потенциометр превращается в регулируемый резистор. Это может быть полезно, если для специального применения требуется немного изменяющееся выходное напряжение. Отрегулировать напряжение смещения от 0,6 В до 0,7 В при входном напряжении 12 В легко при использовании потенциометра 1 кОм (P1) и постоянного резистора 100 кОм, соответственно, 10 кОм (R1, R2). Н мост Рисунок 5: Н-мост — это электронная схема, которая позволяет приложить напряжение к нагрузке в любом направлении. Очень простой H-мост состоит из двух потенциометров с нагрузкой, подключенной к двум скользящим контактам. 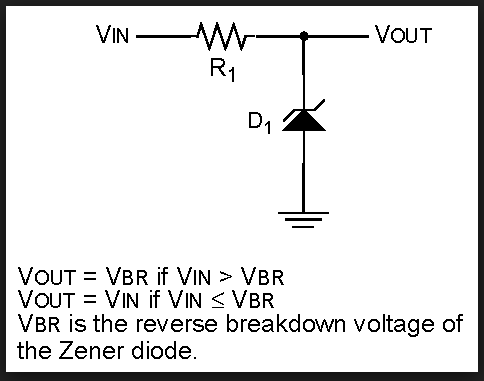Если выходное напряжение потенциометра номер один равно выходному напряжению потенциометра номер два (например, оба находятся в их среднем положении), на нагрузку не подается напряжение. Рисунок 6: Если выходное напряжение потенциометра номер два более положительное, чем выходное напряжение потенциометра номер один, положительный вывод находится на правой стороне нагрузки. Рисунок 7: Если выходное напряжение потенциометра номер два меньше положительного, чем выходное напряжение потенциометра номер один, положительный вывод находится на левой стороне нагрузки. Диоды Рисунок 8: Вольт-амперная характеристика полупроводникового диода отличается от характеристики омического резистора. Сопротивление кремниевого диода, смещенного в прямом направлении, значительно уменьшается при падении напряжения примерно на 0.6В. При замене R 2 на диод с прямым смещением падение напряжения не превышает 0,6 В, даже если входное напряжение явно выше. При последовательном включении двух или более диодов с прямым смещением падение напряжения кратно 0,6 В. Например, результирующее падение напряжения составляет примерно 1,8 В при использовании трех диодов. Рисунок 9: Особым видом диодов является стабилитрон . При использовании прямой полярности характеристики идентичны характеристикам обычного диода.Однако стабилитрон также позволяет току течь, когда он смещен в обратном направлении, а напряжение выше определенного значения, известного как напряжение пробоя или напряжение стабилитрона . Падение напряжения на стабилитроне 3,0 В незначительно превышает этот потенциал при обратном смещении, поэтому на общий ток, протекающий через делитель напряжения, влияет сопротивление R 1 при входных напряжениях выше 3,0 В. При подключении нагрузки параллельно стабилитрону практически не наблюдается сдвига напряжения до тех пор, пока значение сопротивления нагрузки не падает ниже определенного значения: R нагрузка = U стабилитрон * R 1 / (U всего — U стабилитрон ) Делитель напряжения выполнен из постоянного резистора и стабилитрона поэтому идеально подходит для формирования опорного напряжения, или в качестве стабилизатора напряжения для слаботочных применений. Переменное сопротивление Рисунок 10: Сопротивление некоторых устройств значительно зависит от температуры или света. В качестве датчика можно использовать делитель напряжения с одним постоянным и одним переменным резистором. Падение напряжения на переменном резисторе зависит от наблюдаемой физической величины. На чертеже фототранзистор и постоянный резистор используются для преобразования переменной силы света в переменное падение напряжения. Когда светится фототранзистор, падение напряжения на устройстве уменьшается. <<< RC-схема операционного усилителя >>> Новости Проект Технологии РобоСпатиум Способствовать Предметный указатель Архивы Скачать Ответы Игры Ссылки Советы по покупкам Связаться с нами Отпечаток

Регуляторы напряжения на стабилитронах — инструментальный инструмент

Стабилитроны могут использоваться для получения стабилизированного выходного напряжения с низкой пульсацией в условиях переменного тока нагрузки. Пропуская небольшой ток через диод от источника напряжения через подходящий токоограничивающий резистор (R _S ), стабилитрон будет проводить ток, достаточный для поддержания падения напряжения Vout.

Стабилитроны

широко используются в качестве шунтирующих регуляторов напряжения для регулирования напряжения на небольших нагрузках. Стабилитроны имеют резкое обратное напряжение пробоя, и напряжение пробоя будет постоянным для широкого диапазона токов. Таким образом, мы подключим стабилитрон параллельно нагрузке, чтобы приложенное напряжение сместило его в обратном направлении.Таким образом, если напряжение обратного смещения на стабилитроне превышает напряжение перегиба, напряжение на нагрузке будет постоянным.

Здесь мы обсуждаем устранение неисправностей стабилизаторов напряжения на основе стабилитронов.

Источник питания постоянного тока с стабилитроном

На рисунке ниже показан источник питания постоянного тока с фильтром, который выдает постоянное напряжение 24 В перед тем, как стабилизатор стабилизирует его до 15 В.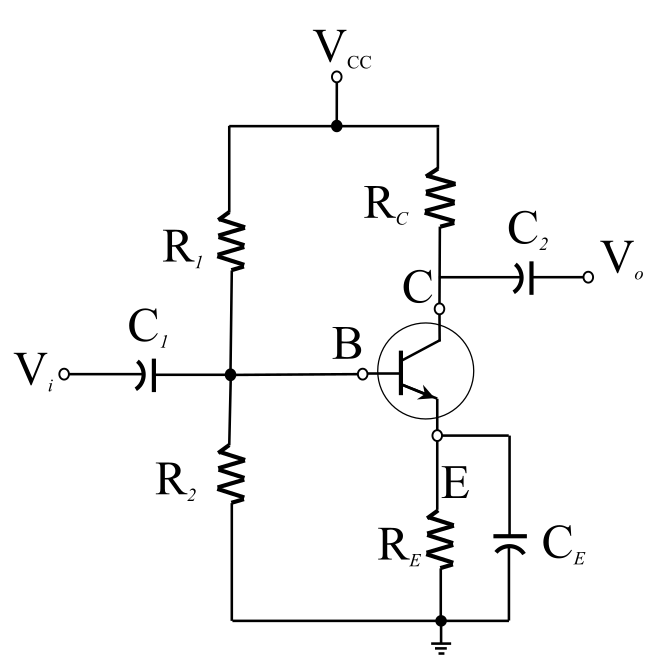 Используется стабилитрон 1N4744A. Проверка регулируемого выходного напряжения без нагрузки показывает 15.5 В, как указано в части (а). Типичное напряжение, ожидаемое при испытательном токе стабилитрона для этого конкретного диода, составляет 15 В.

Рис: Тест стабилитрона

В части (b) подключен потенциометр для обеспечения переменного сопротивления нагрузки. Оно устанавливается на минимальное значение для испытания при полной нагрузке, как определено следующими расчетами. Испытание при полной нагрузке проводится при минимальном токе стабилитрона (IZK). Показание счетчика 14,8 В указывает приблизительно на ожидаемое выходное напряжение 15.0 В.

Корпус 1:

Обрыв стабилитрона Если стабилитрон выходит из строя, проверка источника питания дает приблизительные результаты, указанные на рисунке. При проверке холостого хода, показанной в части (а), выходное напряжение составляет 24 В, потому что между фильтрованным выходом источника питания и выходной клеммой нет падения напряжения. Это определенно указывает на разрыв между выходной клеммой и землей. При проверке полной нагрузки напряжение 14,8 В является результатом действия делителя напряжения последовательного резистора на 180 Ом и нагрузки 291 Ом.В этом случае результат слишком близок к нормальному показанию, чтобы быть надежным индикатором неисправности, но проверка холостого хода позволит выявить проблему. Кроме того, если RL изменяется, VOUT будет изменяться, если стабилитрон открыт.

Рис: Показания открытого стабилитрона

Корпус 2:

Неправильное напряжение стабилитрона Как показано на рисунке ниже, проверка холостого хода, которая приводит к выходному напряжению, превышающему максимальное напряжение стабилитрона, но меньшему, чем выходное напряжение источника питания, указывает на то, что стабилитрон вышел из строя, так что его внутреннее сопротивление больше, чем оно. должно быть.Выходное напряжение 20 В в этом случае на 4,5 В выше ожидаемого значения 15,5 В. Это дополнительное напряжение указывает на неисправность стабилитрона или установку неправильного типа. Выход 0 В, конечно, указывает на короткое замыкание.

▷ Последовательно и параллельно подключенные диоды

Это следующая статья руководства по полупроводниковым коммутационным устройствам. Вы также можете написать статью и отправить ее нам по почте.

Диоды включаются внутри схемы в двух конфигурациях.Это следующие конфигурации:

• Конфигурация серии
• Параллельная конфигурация

Обе схемы подключения широко используются и будут подробно рассмотрены в этой статье вместе со схемами.

Конфигурация серии

Соединение серии

означает параллельное соединение. Когда два компонента соединены последовательно, они имеют одно общее соединение. Изменение напряжения и тока при последовательном соединении выглядит следующим образом:

• Разница потенциалов для каждого компонента различна.
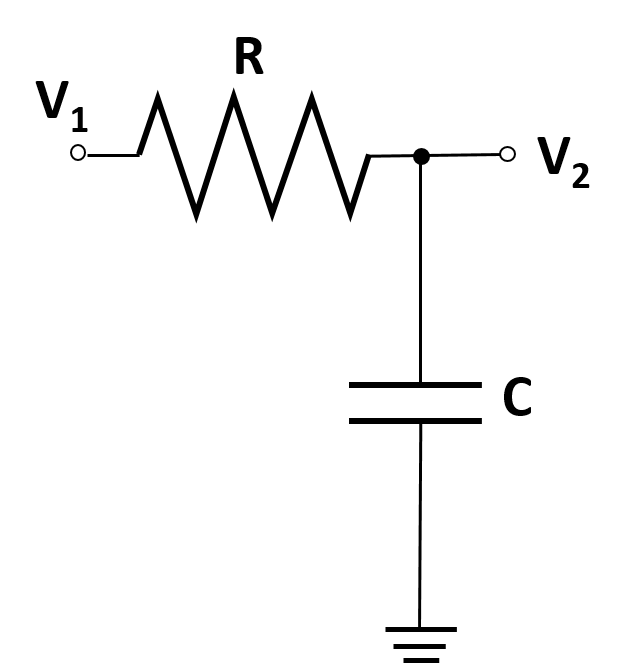
• Ток на всех последовательно подключенных компонентах остается неизменным.

Те же свойства сохраняются и для диодов, когда они соединены последовательно.

Характеристики диода

в последовательной конфигурации

При последовательном соединении мы наблюдаем следующие свойства диодов:

• Результирующее прямое напряжение на диоде увеличивается.
• При последовательном включении диоды увеличивают обратную блокировку.

Рассмотрим два диода, включенных последовательно. Здесь следует иметь в виду, что все диоды, подключенные последовательно, не будут иметь таких же характеристик, как показано на графике ниже.

Характеристики

V-I показывают, что диоды имеют разное напряжение блокировки. В прямом смещенном состоянии падение напряжения и прямой ток на диодах будут одинаковыми. При обратном смещении напряжение блокировки другое, поскольку диоды должны нести одинаковый ток утечки.

Эту проблему можно решить подключением сопротивлений к каждому диоду.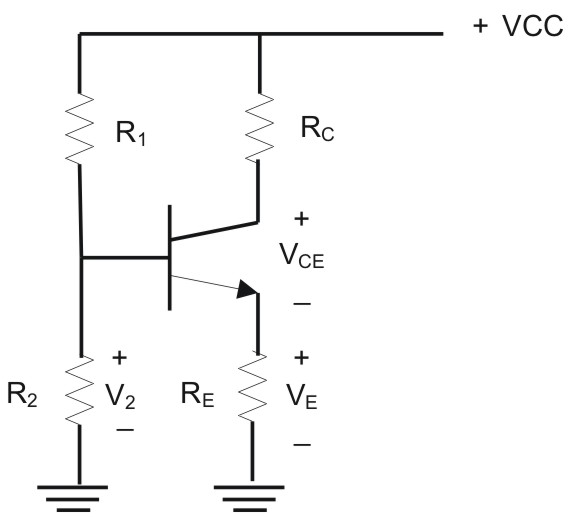 Напряжение будет распределяться поровну; следовательно, ток утечки будет другим.

Общий ток утечки теперь будет:

Наше требование:

Мы знаем,

Итак, получаем,

Область применения

Один диод не может соответствовать требованиям более высокого напряжения, если он не подключен последовательно.Итак, основные области применения:

• Линии передачи постоянного тока высокого напряжения (HVDC).
• Коммерческие помещения, где требуется регулируемое напряжение.

Параллельная конфигурация

Параллельное соединение означает, что компоненты соединены друг с другом, имея две общие точки. Ток различается для каждого компонента, а падение напряжения одинаково. При параллельном подключении диодов наблюдается такая же тенденция.

Характеристики диодов в параллельной конфигурации

• Увеличивается допустимая нагрузка по току.
• Отсутствие проводимости в результирующем диоде с обеих сторон.

Рассмотрим два диода, включенных параллельно. Ток будет разделен между двумя диодами. Чтобы сделать это деление равным, подключаются катушки индуктивности (с одинаковой индуктивностью). Когда ток на D1 увеличивается, падение напряжения на L1 увеличивается, создавая значение противоположной полярности на L2.

Катушки индуктивности используются в динамических условиях. Катушки индуктивности обычно громоздкие и дорогие, а также генерируют выбросы, которые могут вызвать проблемы.

Диоды одного типа с одинаковым падением напряжения могут использоваться в установившемся режиме. В этом случае параллельные диоды будут иметь одинаковые обратные запирающие напряжения. Следует помнить о некоторых мерах предосторожности при использовании диодов с одинаковым падением прямого напряжения, а именно:

• Диоды должны иметь одинаковые радиаторы.
• При необходимости их следует охлаждать одинаково.