Делитель напряжения расчет резисторов. Делитель напряжения: расчет и применение резисторов в электронных схемах

Как рассчитать делитель напряжения на резисторах. Какие формулы использовать для расчета выходного напряжения. Как подобрать номиналы резисторов для делителя напряжения. Где применяются резистивные делители напряжения в электронике.

Принцип работы делителя напряжения на резисторах

Делитель напряжения — это простая электрическая схема, позволяющая получить на выходе напряжение меньше входного. Классический делитель напряжения состоит из двух последовательно соединенных резисторов, подключенных к источнику входного напряжения.

Принцип работы делителя основан на падении напряжения на резисторах при протекании через них тока. Выходное напряжение снимается с нижнего резистора и всегда меньше входного.

Формула расчета делителя напряжения

Для расчета выходного напряжения делителя используется следующая формула:

Uвых = Uвх * R2 / (R1 + R2)

где:

• Uвых — выходное напряжение
• Uвх — входное напряжение
• R1 — сопротивление верхнего резистора
• R2 — сопротивление нижнего резистора

Как видно из формулы, выходное напряжение зависит от соотношения сопротивлений резисторов. Чем больше сопротивление нижнего резистора R2 по отношению к R1, тем ближе выходное напряжение к входному.

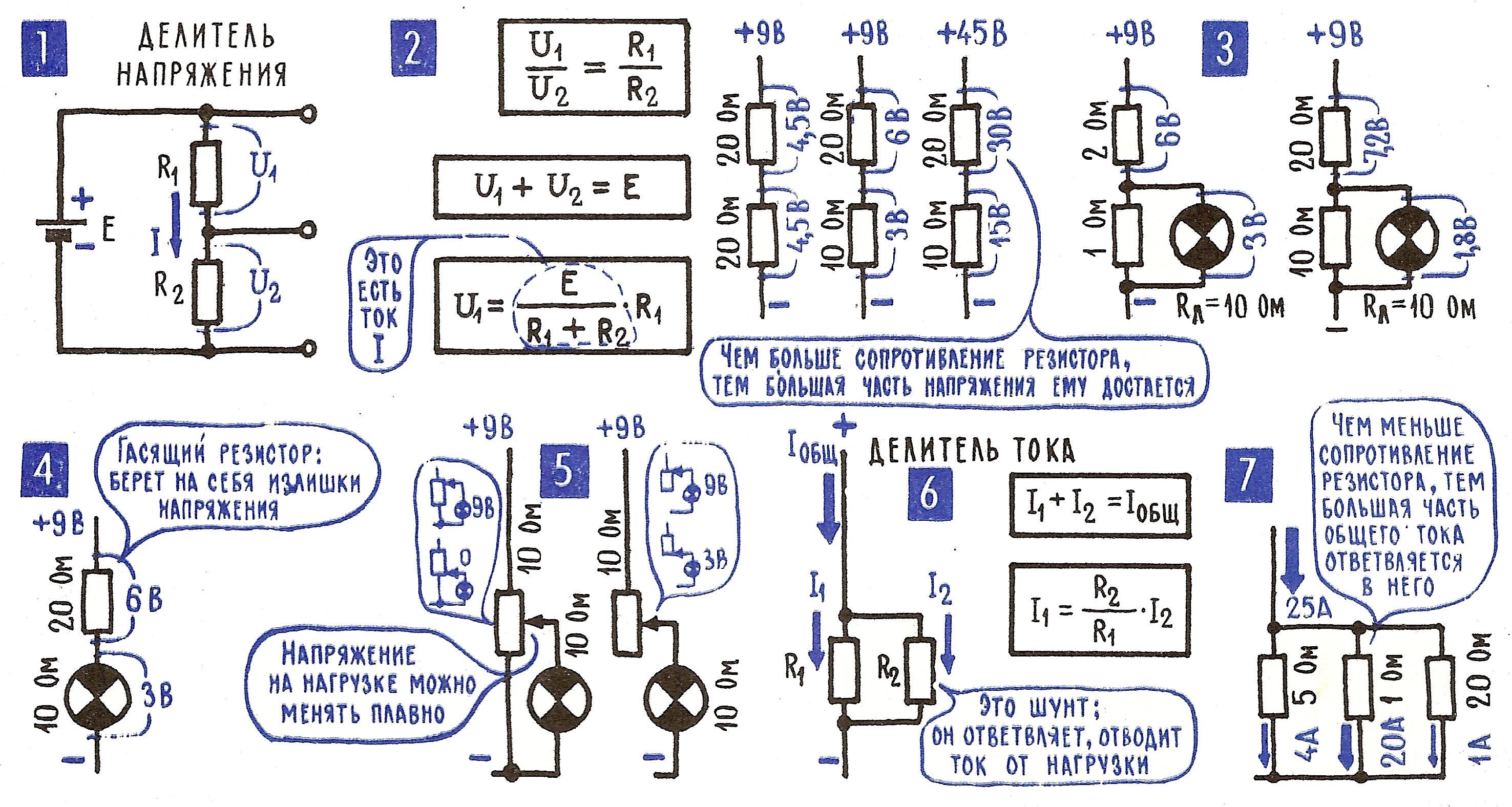
Выбор номиналов резисторов для делителя напряжения

При выборе номиналов резисторов для делителя напряжения нужно учитывать несколько факторов:

• Требуемое выходное напряжение
• Входное сопротивление нагрузки
• Допустимый ток через делитель
• Мощность рассеивания на резисторах

Чтобы обеспечить стабильное выходное напряжение, суммарное сопротивление делителя должно быть в 10-100 раз меньше входного сопротивления нагрузки. При этом, чем меньше сопротивление резисторов, тем больше ток через делитель и рассеиваемая мощность.

Оптимальным решением часто является выбор резисторов в диапазоне 1-100 кОм. Для маломощных схем подойдут резисторы 10-100 кОм, для более мощных — 1-10 кОм.

Расчет делителя напряжения онлайн

Для быстрого расчета делителя напряжения удобно использовать онлайн-калькуляторы. Они позволяют легко подобрать номиналы резисторов по заданному входному и выходному напряжению.

Вот несколько популярных калькуляторов делителя напряжения:

• Calculator.net
• Ohms Law Calculator
• Digi-Key

С помощью онлайн-калькуляторов можно быстро рассчитать оптимальные номиналы резисторов для любого делителя напряжения.

Применение делителей напряжения в электронике

Делители напряжения на резисторах широко применяются в различных электронных устройствах и схемах:

• Снижение напряжения питания для микросхем и других компонентов
• Формирование опорного напряжения
• Измерение напряжения с помощью АЦП микроконтроллеров
• Регулировка громкости в аудиотехнике
• Подстройка и калибровка измерительных приборов
• Смещение рабочей точки транзисторов и других активных элементов

Простота и универсальность делают резистивный делитель напряжения очень распространенным элементом электронных схем.

Потенциометр как регулируемый делитель напряжения

Потенциометр представляет собой регулируемый делитель напряжения на основе переменного резистора. Он позволяет плавно изменять выходное напряжение в определенном диапазоне.

Устройство потенциометра:

• Резистивный элемент с тремя выводами
• Подвижный контакт (движок)
• Корпус с ручкой управления

При вращении ручки движок перемещается по резистивному элементу, изменяя соотношение сопротивлений. Это приводит к изменению выходного напряжения, снимаемого с движка.

Потенциометры широко применяются для регулировки громкости, яркости, напряжения и других параметров в электронных устройствах.

Делитель напряжения на резисторах: плюсы и минусы

Резистивный делитель напряжения имеет ряд преимуществ и недостатков:

Преимущества:

• Простота схемы
• Низкая стоимость
• Отсутствие активных компонентов
• Линейность характеристики
• Работа в широком диапазоне напряжений

Недостатки:

• Зависимость от нагрузки
• Постоянное потребление тока
• Нестабильность при изменении температуры
• Невысокая точность
• Низкий КПД при больших токах нагрузки

Несмотря на недостатки, простота и надежность делают резистивный делитель очень распространенным решением во многих электронных схемах.

Параллельное и последовательное соединение резисторов

При расчете делителей напряжения важно учитывать правила соединения резисторов:

Последовательное соединение:

• Общее сопротивление: R = R1 + R2 + … + Rn
• Ток одинаковый через все резисторы
• Напряжение распределяется пропорционально сопротивлениям

Параллельное соединение:

• Общее сопротивление: 1/R = 1/R1 + 1/R2 + … + 1/Rn
• Напряжение одинаковое на всех резисторах
• Ток распределяется обратно пропорционально сопротивлениям

Зная эти правила, можно рассчитывать более сложные схемы делителей напряжения с несколькими резисторами.

Применение делителя напряжения с операционным усилителем

Для повышения стабильности выходного напряжения делитель часто используется совместно с операционным усилителем (ОУ):

• Делитель подключается к неинвертирующему входу ОУ
• Выход ОУ соединяется с инвертирующим входом (отрицательная обратная связь)
• ОУ компенсирует изменения нагрузки, поддерживая постоянное выходное напряжение

Такая схема позволяет получить стабильный источник опорного напряжения с низким выходным сопротивлением.

Применение ОУ значительно расширяет возможности простого резистивного делителя напряжения.

Делитель напряжения на резисторах ⋆ diodov.net

05.08.2018

HomeШкола электроникиДелитель напряжения на резисторах

By Дмитрий Забарило Школа электроники  0 Comments

Рассмотрим, как рассчитать практически любой делитель напряжения на резисторах. Преимущественное большинство радиоэлектронных элементов и микросхем питаются относительно низким напряжением – 3…5 В. А многие блоки питания выдают U = 9 В, 12 В или 24 В. Поэтому для надежной и стабильной работы различных электронных элементов необходимо снижать величину напряжения до приемлемого уровня. В противном случае может наступить пробой радиоэлектронных элементов. Особенно следует уделять внимание микросхемам – наиболее чувствительным элементам к повышенному напряжению.

Существуют много способов, как снизить напряжение. Выбор того или другого способа зависит от конкретной задачи, что в целом определяет эффективность всего устройства. Мы рассмотрим самый простой способ – делитель напряжения на резисторах, который, тем не менее, довольно часто применяется на практике, но исключительно в маломощных цепях, что поясняется далее.

Расчет делителя напряжения на резисторах

Чтобы сделать и рассчитать простейший делитель напряжения достаточно соединить последовательно два резистора и подключить их источнику питания. Такая схема очень распространенная и применяется более чем в 90 % случаев.

Вход схемы имеет два вывода, а выход – три. При одинаковых значения сопротивлений R₁ и R₂ выходные напряжения U_вых1 и U_вых2 также равны и по величине вдвое меньше входного U_вх. Причем выходное U можно сниматься с любого из резисторов – R₁ или R₂. Если сопротивления не равны, то выходное U будет на резисторе большего номинала.

Точное соотношение U_вых1 к U_вых2 рассчитаем, обратившись к закону Ома. Резисторы вместе с источником питания образуют последовательную цепь, поэтому величина электрического тока, протекающего через R₁ и R₂ определяется отношением напряжения источника питания U_вх к сумме сопротивлений:

Следует обратить внимание, чем больше сумма сопротивлений, тем меньший ток I при том же значении U_вх.

Далее, согласно закону Ома, подставив значение тока, находим U_вых1 и U_вых2:

Путем подстановки в две последние формулы значение из самой первой формулы, находим значение выходного U в зависимости от входного и сопротивлений двух резисторов:

Применяя  делитель напряжения на резисторах, необходимо понимать и помнить следующее:

1. 1. Коэффициент полезного действия такой схемы довольно низкий, поскольку только часть мощности источника питания поступает к нагрузке, а остальная мощность преобразуется в тепло, выделяемое на резисторах. Чем больше понижается напряжение, тем меньше мощности от источника питания поступит к нагрузке.

1. Так как нагрузка подключается параллельно к одному из резисторов делителя, то есть шунтирует его, то общее сопротивление цепи снижается и происходит перераспределение падений напряжений. Поэтому сопротивление нагрузки должно быть гораздо больше сопротивления резистора делителя. В противном случае схема будет работать нестабильно с отклонением от заданных параметров.
2. Распределение U между R₁ и R₂ определяется исключительно их относительными значениями, а не абсолютными величинами. В данном случае неважно, будут ли R₁ и R₂ иметь значение 2 кОм и 1 кОм или 200 кОм и 100 кОм. Однако при более низких значениях сопротивлений можно получить большую мощность на нагрузке, но следует помнить, что и больше мощности преобразуется в тепло, то есть израсходуется невозвратно впустую.

Также иногда находят применение и более сложные делители напряжений, состоящие из нескольких последовательно соединенных резисторов.

Делитель напряжения на переменном резисторе

Схему делителя напряжения на переменном резисторе называют схемой потенциометра. Вращая рукоятку громкости музыкального центра или автомагнитолы, вы таким действием плавно изменяете напряжение, подаваемое на усилитель модности звуковой частоты. Принцип работы и сборка простейшего усилителя мощности уже были ранее рассмотрены здесь.

При перемещении (вращении) ручки переменного резистора сверху вниз по чертежу происходит плавное изменение U от значения источника питания до нуля.

В звуковой технике главным образом применяются переменные резисторы с логарифмической зависимостью, поскольку слуховой аппарат человек воспринимает звуки с данной зависимостью. Для регулирования уровня звука одновременно по двум каналам используют сдвоенные переменные резисторы.

В качестве делителя напряжения находят применение переменные резисторы, имеющие следующие зависимости сопротивления от угла поворота ручки: логарифмическую, линейную и экспоненциальную. Конкретный тип зависимости применяется для решения отдельной задачи.

Делитель напряжения на резисторах ⋆ diodov.net

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Электрический паяльник с регулировкой температуры

Мощность: 60/80 Вт, температура: 200’C-450’C, высококачествен…

Подробнее

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом виде: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Соединение резисторов

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно, параллельно и смешанно.

Последовательное соединение резисторов

Последовательное соединение.

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее. То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток. Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.

Интересно почитать: принцип действия и основные характеристики варисторов.

Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает. Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле: Rобщ = R1 + R2 + R3+…+ Rn.

Последовательное и параллельное соединение резисторов.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)

Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn. Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток.

Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.

Каждый вид соединения находится под одинаковым напряжением:

• U = U1 = U2; Суммарная сила тока равняется суммарному значению тока каждого участка
• I = I1 + I2; Сопротивление цепи равно сумме величина обратных сопротивлению участка:
• 1/R = 1/R1 + 17R2 + . . . + 1/Rn; Сила тока пропорциональна сопротивлению каждого участка
• I1/I2=R2/R1.

Будет интересно➡ Как прочитать обозначение (маркировку) резисторов

Примеры расчета

Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В. А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.

Смешанное соединение резисторов

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением. На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.

Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:

• Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
• Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
• После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
• Рассчитывают сопротивления полученной схемы.

Схема смешанного подключения.

Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.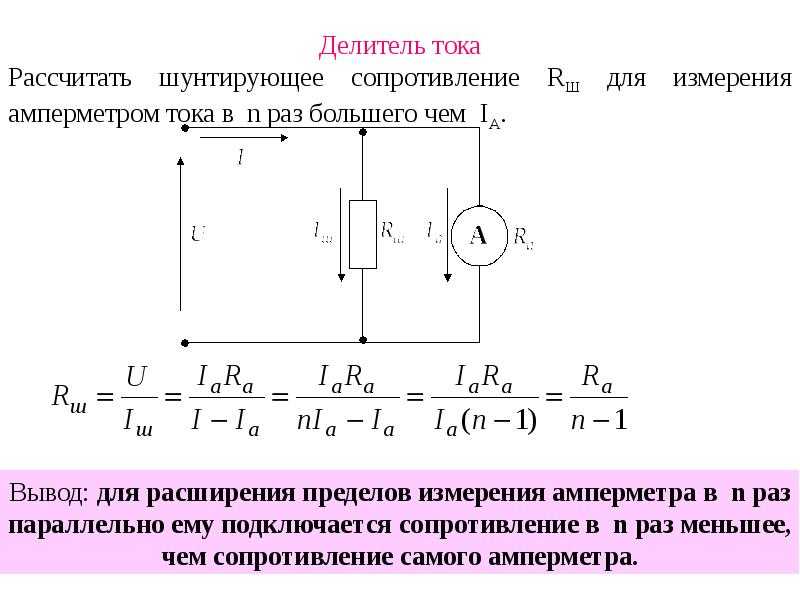

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Расчет гасящего резистора

В схемах аппаратуры связи часто возникает необходимость подать на потребитель меньшее напряжение, чем дает источник. В этом случае последовательно с основным потребителем включают дополнительное сопротивление, на котором гасится избыток напряжения источника. Такое сопротивление называется гасящим.

Будет интересно➡ Как рассчитать резистор для светодиода?

Напряжение источника тока распределяется по участкам последовательной цепи прямо пропорционально сопротивлениям этих участков. Рассмотрим схему включения гасящего сопротивления:

1. Полезной нагрузкой в этой цепи является лампочка накаливания, рассчитанная на нормальную работу при величине напряжения Uл= 80 в и тока I =20 ма.
2. Напряжение на зажимах источника тока U=120 в больше Uл, поэтому если подключить лампочку непосредственно к источнику, то через нее пройдет ток, превышающий нормальный, и она перегорит.
3. Чтобы этого не случилось, последовательно с лампочкой включено гасящее сопротивление R гас.

Схема включения гасящего сопротивления резистора.

Расчет величины гасящего сопротивления при заданных значениях тока и напряжения потребителя сводится к следующему:

– определяется величина напряжения, которое должно быть погашено:

Uгас = Uист – Uпотр,

Uгас = 120 – 80 = 40в

определяется величина гасящего сопротивления

Rгас = Uгас / I

Rгас = 40 / 0,020 = 2000ом = 2 ком

Далее необходимо рассчитать мощность, выделяемую на гасящем сопротивлении по формуле

P = I2 * Rгас

P = 0,0202 * 2000 = 0,0004 * 2000 = 0,8вт

Зная величину сопротивления и расходуемую мощность, выбирают тип гасящего сопротивления.

Как подобрать номинал резистора в делителе напряжения?

Главное актуально.

Взгляните на эту схему. Наведите указатель мыши на символ заземления, и вы увидите, что ток равен 25 мА. Теперь взгляните на эту схему, и вы увидите, что выходной ток составляет \$ 2,5 \mbox{ } \mu A \$.

Теперь посмотрим, как схемы ведут себя под нагрузкой. Вот первая схема с нагрузкой. Как вы можете видеть, ток 2,38 мА проходит через нагрузочный резистор справа, и напряжение на нем уже не ожидаемое 2,5 В, а вместо этого 2,38 В (поскольку два нижних резистора включены параллельно). Если мы посмотрим на вторую схему здесь, мы увидим, что теперь верхний резистор падает примерно на 5 В, а два нижних резистора имеют напряжение 4,9 В.9 мВ. Это потому, что соотношение резисторов было изменено здесь. Поскольку два нижних резистора теперь соединены параллельно, и у нас есть один резистор со значительно большим сопротивлением, чем другой, их суммарное сопротивление ничтожно мало по сравнению с сопротивлением только нижнего правого резистора (вы можете проверить это, используя формулы для параллельных резисторов). Так что теперь выходное напряжение значительно отличается от 2,5 В, которые мы получаем в случае холостого хода.

Теперь рассмотрим противоположную ситуацию: Два маленьких резистора в делителе напряжения и один большой в качестве нагрузки здесь. Опять же, общее сопротивление двух нижних резисторов меньше, чем сопротивление меньшего резистора из двух. Однако в данном случае это не оказывает большого влияния на напряжение, воспринимаемое нагрузкой. Он по-прежнему имеет напряжение 2,5 В, и пока все в порядке.

Итак, суть в том, что при определении сопротивления резисторов мы должны учитывать входное сопротивление нагрузки, а два резистора делителя напряжения должны быть как можно меньше.

С другой стороны, сравним ток, проходящий через делитель в цепи с большими резисторами на делителе и в цепи с маленькими резисторами на делителе. Как видите, через большие резисторы проходит ток всего \$2,5 \mbox{ }\mu A\$, а через маленькие резисторы ток составляет 25 мА. Дело в том, что делитель напряжения тратит ток впустую, и если бы он был, например, частью устройства с батарейным питанием, это негативно повлияло бы на срок службы батареи. Таким образом, резисторы должны быть как можно большего размера, чтобы снизить потери тока.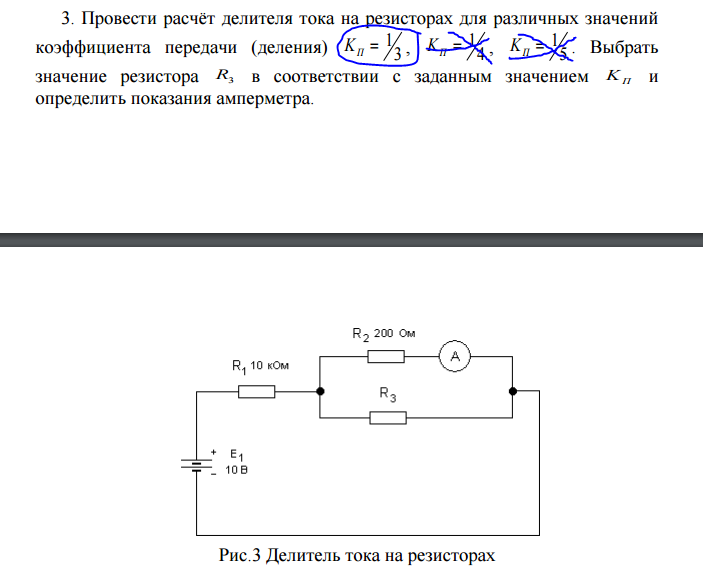

Это дает нам два противоположных требования: иметь как можно меньшие резисторы, чтобы обеспечить лучшую стабилизацию напряжения на выходе, и как можно большие резисторы, чтобы получить как можно меньший потребляемый ток. Таким образом, чтобы получить правильное значение, мы должны увидеть, какое напряжение нам нужно на нагрузке, насколько точным оно должно быть, и получить входное сопротивление нагрузки, и на его основе рассчитать размер резисторов, которые нам нужны, чтобы получить нагрузку с приемлемым значением. Напряжение. Затем нам нужно поэкспериментировать с более высокими значениями резисторов делителя напряжения и посмотреть, как они повлияют на напряжение, и найти точку, в которой мы не можем иметь большее изменение напряжения в зависимости от входного сопротивления. На данный момент у нас (в целом) есть хороший выбор резисторов делителя напряжения.

Другим моментом, который необходимо учитывать, является номинальная мощность резисторов. Это идет в пользу резисторов с большим сопротивлением, потому что резисторы с меньшим сопротивлением будут рассеивать больше энергии и больше нагреваться. Это означает, что они должны быть больше (и обычно дороже), чем резисторы с большим сопротивлением.

На практике, как только вы сделаете несколько делителей напряжения, вы увидите несколько популярных значений для резисторов делителя напряжения. Многие просто выбирают один из них и не слишком заморачиваются расчетами, если только с выбором не возникает проблем. Например, для меньших нагрузок вы можете выбрать резисторы в диапазоне \$100 \mbox{ } k \Omega\$, а для больших нагрузок вы можете использовать \$10 \mbox{ } k \Omega\$ или даже \$1 \mbox{ } k \Omega\$ резисторов, если у вас есть запасной ток.

резисторов — какие значения для делителя напряжения

Лучший способ увидеть различия — использовать эквивалент Thevenin для резисторного делителя, установленного между двумя идеальными (без собственного сопротивления источника) источниками напряжения. Часто это просто какое-то напряжение питания и земля.

Давайте посмотрим на очевидный случай:

^{смоделируйте эту схему – Схема создана с помощью CircuitLab}

На левой стороне есть резистивный делитель между идеальным источником напряжения и землей и, без какой-либо нагрузки, висящей на \$V_ \text{OUT}\$ (он просто открыт, как видите), напряжение легко вычислить как \$V_\text{OUT}=V_\text{IN}\cdot\frac{R_2}{R_1+ Р_2}\$. Однако в этом простом вычислении отсутствует тот факт, что \$V_\text{OUT}\$ больше не равно 9.0033 идеал . Теперь у него есть сопротивление источника, которое делает его неидеальным. Это связано с тем, что любой ток, требуемый нагрузкой (в настоящее время отсутствующей), подключенной между \$V_\text{OUT}\$ и землей, должен вызывать дополнительное падение напряжения на \$R_1\$, что меняет напряжение, которое испытывает нагрузка. Итак, снова \$V_\text{OUT}\$ больше не является идеальным .

Эффективная неидеальность \$V_\text{OUT}\$ выражается сначала установкой вымышленного \$V_\text{TH}\$, равного незагруженному \$V_\text{OUT }\$, а затем вставить последовательный резистор между этими вымышленными \$V_\text{TH}\$ и \$V_\text{OUT}\$. Это показано справа вверху. Этот резистор, представляющий неидеальность источника напряжения, имеет вид \$R_\text{TH}=\frac{R_1\cdot R_2}{R_1+R_2}\$.

Результатом всего этого является то, что теперь у вас есть более простой способ просмотра резисторного делителя, и вы можете легко увидеть, насколько он неидеален , просто изучив значение \$R_\text{TH} \$. Чем ближе это значение к нулю, тем более идеальным является источник напряжения. Но цена, которую вы платите за приближение к нулю, — это быстро увеличивающаяся рассеиваемая мощность, которая тратится впустую в самом резистивном делителе.

---

Чтобы полностью обобщить вышеизложенное, давайте рассмотрим резистивный делитель, расположенный между двумя разными идеальными источниками напряжения, один из которых НЕ равен нулю. (В любом случае это просто произвольная точка отсчета.)

^{имитировать эту схему}

Единственная разница здесь в том, что теперь оба напряжения могут быть ненулевыми. В этом случае единственным новым вычислением является более общая версия: \$V_\text{TH}=\frac{V_\text{B}\cdot R_1+V_\text{A}\cdot R_2}{R_1+R_2 }\$. Это сводится к уравнению, которое я дал выше, когда \$V_\text{B}=0\:\text{V}\$.

---

Выбор номиналов резисторов будет зависеть от диапазона импедансов нагрузки, которые вы хотите разрешить при подключении к \$V_\text{OUT}\$, и от того, какие колебания напряжения могут выдержать ваши нагрузки.

Например, предположим, что у вас есть шина питания \$5\:\text{V}\$ и вы хотите использовать делитель напряжения для создания источника напряжения \$3,3\:\text{V}\$. Предположим также, что максимальный ток, требуемый устройством, которое вы подключите к \$V_\text{OUT}\$, составляет \$10\:\text{мА}\$. Предположим, что устройство не должно работать больше \$3.6\:\text{V}\$ и меньше \$3.1\:\text{V}\$, иначе оно не будет работать должным образом. И, наконец, минимальный ток, требуемый устройством в наихудшем случае, составляет \$100\:\mu\text{A}\$.

Учитывая эти спецификации, мы хотим наихудшего случая \$\Delta V=3.6\:\text{V}-3.1\:\text{V}=500\:\text{мВ}\$ с наихудшим случаем текущее изменение \$\Delta I=10\:\text{мА}-100\:\mu\text{A}=9,9\:\text{мА}\$. Это предполагает эффективное сопротивление источника \$R_\text{TH}=R_\text{SRC}=\frac{500\:\text{мВ}}{9,9\:\text{мА}}\примерно 50,5\: \Омега\$.

Теперь у вас есть два уравнения и два неизвестных:

$$\begin{align*} 50,5\:\Omega &= \frac{R_1\cdot R_2}{R_1+R_2}\\\\ 5\:\text{V}\cdot\frac{R_2}{R_1+R_2} &=3.