Что такое диэлектрики и как они работают. Какие бывают виды диэлектриков. Где применяются изоляционные материалы в электротехнике и электронике. Основные характеристики и свойства диэлектриков.
Что такое диэлектрики и как они работают
Диэлектрики — это вещества, плохо проводящие электрический ток. Их основное свойство — способность поляризоваться во внешнем электрическом поле. При этом связанные электрические заряды в диэлектрике смещаются, образуя электрические диполи.
Как происходит поляризация диэлектрика.
- В отсутствие поля заряды в диэлектрике распределены равномерно
- При помещении в электрическое поле положительные и отрицательные заряды смещаются в противоположные стороны
- Возникает наведенный дипольный момент, направленный вдоль поля
- Диэлектрик становится поляризованным
Степень поляризации диэлектрика характеризуется диэлектрической проницаемостью ε. Чем она выше, тем сильнее поляризуется материал.
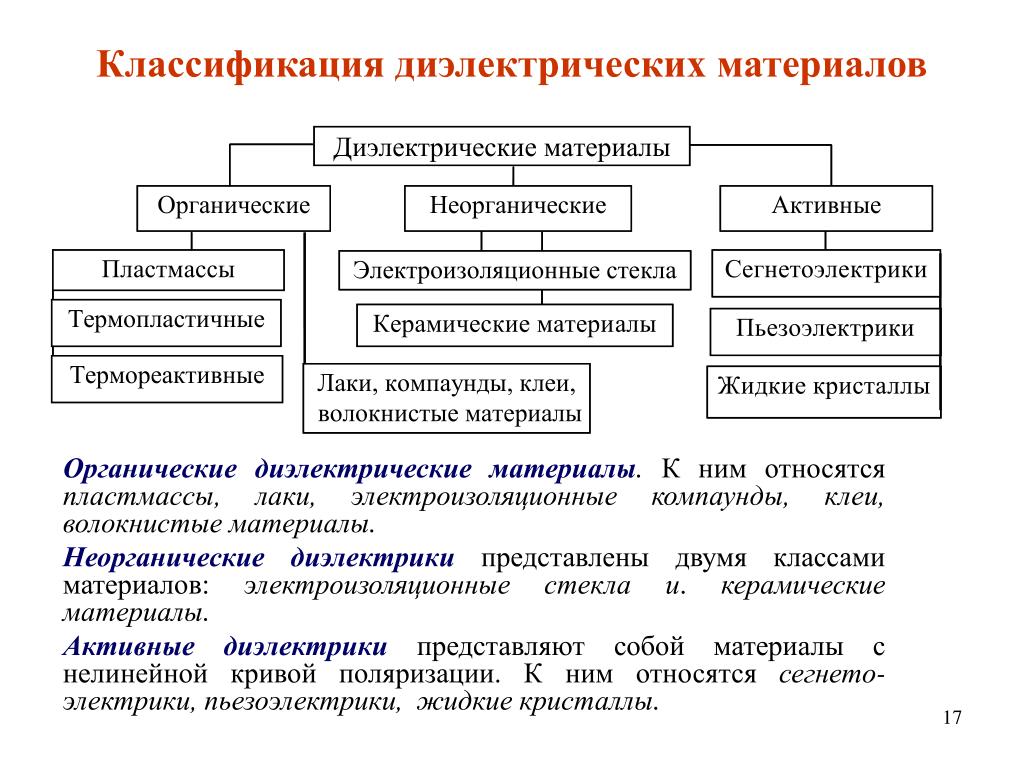
Основные виды диэлектриков

1. Неполярные диэлектрики
Состоят из симметричных молекул без собственного дипольного момента (например, N2, O2). Поляризуются за счет смещения электронных оболочек относительно ядер.
2. Полярные диэлектрики
Содержат молекулы с постоянным дипольным моментом (H2O, NH3). При поляризации диполи ориентируются вдоль внешнего поля.
3. Ионные диэлектрики
Имеют ионную кристаллическую решетку (NaCl, KCl). Поляризуются за счет смещения ионов относительно положений равновесия.
4. Сегнетоэлектрики
Обладают спонтанной поляризацией в отсутствие внешнего поля (BaTiO3). Характеризуются очень высокой диэлектрической проницаемостью.
Основные характеристики диэлектриков
Какие параметры характеризуют диэлектрические свойства материалов.
- Диэлектрическая проницаемость ε — степень поляризации вещества
- Электрическая прочность — максимальная напряженность поля, которую выдерживает диэлектрик
- Тангенс угла диэлектрических потерь tgδ — характеризует потери энергии в диэлектрике
- Удельное объемное сопротивление ρv — способность материала проводить ток
Чем выше ε и электрическая прочность и ниже tgδ и ρv, тем лучше диэлектрические свойства материала.
Где применяются диэлектрики
Основные области применения диэлектриков в технике:
Электроизоляционные материалы
Используются для изоляции токоведущих частей в электрических устройствах. Примеры:
- Изоляция проводов и кабелей
- Электротехнический картон, гетинакс, текстолит
- Керамические и полимерные изоляторы
Конденсаторные диэлектрики
Применяются в качестве диэлектриков в конденсаторах:
- Слюда, керамика, полимерные пленки
- Электролиты для электролитических конденсаторов
- Сегнетоэлектрики для высокоемких конденсаторов
Активные диэлектрики
Используют особые свойства некоторых диэлектриков:
- Пьезоэлектрики в датчиках и актуаторах
- Электреты в микрофонах
- Жидкие кристаллы в дисплеях
Как выбрать диэлектрик для конкретного применения
При выборе диэлектрического материала учитывают следующие факторы:
- Требуемые электрические характеристики (ε, tgδ, электрическая прочность)
- Механические свойства (прочность, эластичность)
- Температурный диапазон работы
- Химическая стойкость
- Технологичность обработки
- Стоимость
Для каждого конкретного применения подбирают оптимальный диэлектрик с учетом всех этих параметров.

Часто задаваемые вопросы о диэлектриках
Чем отличаются диэлектрики от проводников?
Диэлектрики практически не проводят электрический ток, так как в них отсутствуют свободные носители заряда. Проводники, напротив, содержат большое количество свободных электронов и хорошо проводят ток.
Какой диэлектрик самый распространенный?
Самым распространенным диэлектриком в природе является воздух. Из твердых диэлектриков наиболее широко применяются различные полимеры — полиэтилен, поливинилхлорид, фторопласты.
Могут ли диэлектрики проводить ток?
При очень высоких напряженностях поля в диэлектриках может возникать электрический пробой — резкое увеличение проводимости. Но в нормальных условиях диэлектрики практически не проводят ток.
Таким образом, диэлектрики играют важнейшую роль в электротехнике и электронике как изоляционные и функциональные материалы. Понимание их свойств и правильный выбор необходимы для создания надежных электрических устройств.
Диэлектрики: что это такое, примеры
Определение 1Диэлектриками называют вещества, не обладающие способностью проводить электрический ток.
Стоит отметить, что данное определение лишь приблизительно выражает физический смысл приведенного понятия.
Абсолютных изоляторов, то есть веществ, которые совсем не проводят ток, в природе не существует. Диэлектрики по сравнению с проводниками в 1015−1020 раз хуже проводят ток. Данный факт основывается на том, что в диэлектриках отсутствуют свободные заряды.
Что такое диэлектрики и их примеры
Определение 2Если диэлектрик поместить в электрическое поле, то, как диэлектрик, так и само поле значительно изменятся. В диэлектриках, в которых до контакта с полем не было заряда, возникают электрические заряды. Это явление объясняется процессом поляризации вещества, другими словами, в поле диэлектрик обретает электрические полюсы. Возникающие при этом заряды называются поляризационными.
Разделить такие заряды невозможно, чем они существенно отличаются от индукционных зарядов в проводниках. Данное отличие основывается на том факте, что в металлах присутствуют электроны, имеющие возможность перемещаться на относительно большие расстояния. В диэлектриках положительные и отрицательные заряды связаны между собой, и их перемещение ограничено пределами одной молекулы, что является крайне малым расстоянием.
Данное отличие основывается на том факте, что в металлах присутствуют электроны, имеющие возможность перемещаться на относительно большие расстояния. В диэлектриках положительные и отрицательные заряды связаны между собой, и их перемещение ограничено пределами одной молекулы, что является крайне малым расстоянием.
Диэлектрики состоят либо из нейтральных молекул, либо из закрепленных в положении равновесия, к примеру, в узлах кристаллической решетки заряженных ионов. Ионные кристаллические решетки могут быть разбиты на, в целом, нейтральные «элементарные ячейки».
Действие электрического поля на заряды, принадлежащие диэлектрику, провоцирует лишь легкое смещение относительно изначального положения, тогда как заряды проводников, испытывающие такое же влияние, срываются с места. В условиях отсутствующего электрического поля диэлектрик может быть условно представлен в виде совокупности молекул, в каждой из которых положительные и отрицательные заряды равные по величине распределены по всему объему вещества.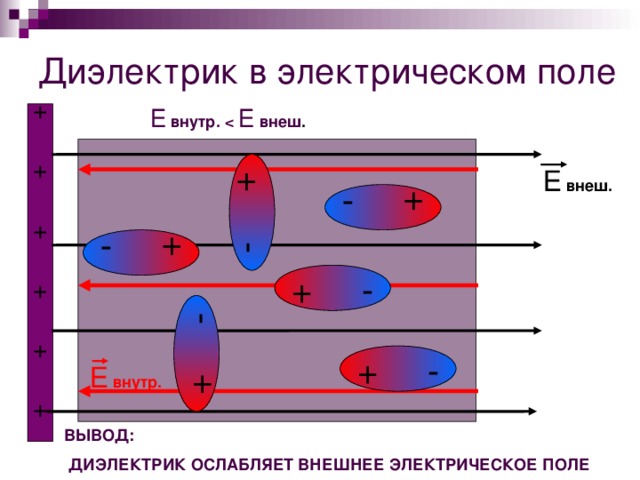
В процессе поляризации заряды каждой отдельной молекулы диэлектрика смещаются в противоположные ее стороны. Соответственно, одна часть молекулы становиться положительно заряженной, а другой — отрицательно, что, в общем, дает возможность заявить:
Равнодействующая электрических сил, в однородном поле оказывающих влияние на нейтральную молекулу диэлектрика, эквивалентна нулю. Этот факт основывается на том, что центр тяжести молекулы не передвигается ни в одну из сторон. Молекула просто претерпевает деформирование.
Определение 4Существуют такие диэлектрики, в которых в условиях отсутствующего электрического поля молекулы имеют дипольный момент (полярные молекулы).
В случае, когда поле отсутствует, такие молекулы, принимающие непосредственное участие в тепловом движении, ориентированы беспорядочно. Если же диэлектрик находится в поле, молекулы, в основном, ориентируются по его направлению. Соответственно, диэлектрик проходит процесс поляризации.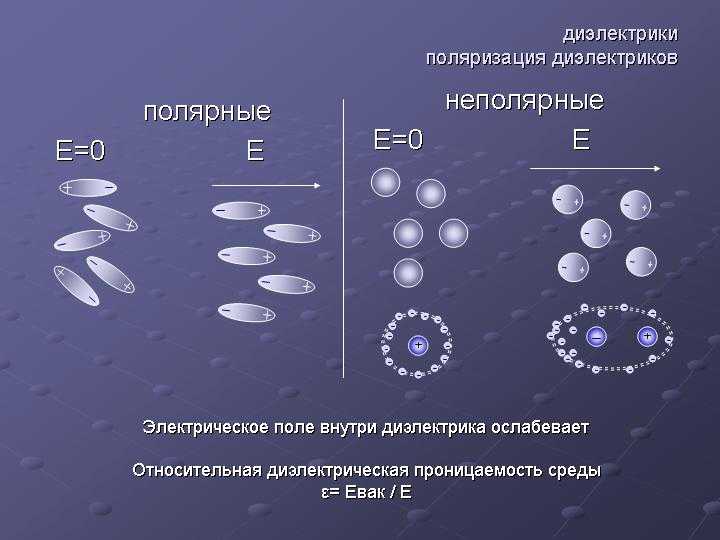
У симметричных молекул, таких как, к примеру, O2, N2, в отсутствие поля центры тяжести отрицательных и положительных зарядов одинаковы. По этой причине собственного дипольного момента у молекул нет (неполярные молекулы). У несимметричных же молекул (возьмем в качестве примера h3O, CO) центры тяжести сдвинуты друг относительно друга, в результате чего молекулы имеют дипольный момент и носят название полярных.
Также существуют диэлектрические или же ионные кристаллы, которые формируются при помощи ионов с противоположным знаком. Такой кристалл состоит из пары “вдвинутых” друг в друга кристаллических решеток, одна из которых является положительной, а вторая — отрицательной. В целом кристалл условно можно принять за подобие гигантской молекулы. Процесс наложения электрического поля провоцирует сдвиг одной решеток относительно друг друга, вследствие чего и происходит поляризация ионных кристаллов. Существует также тип поляризованных без участия поля кристаллов.
Вектор поляризации диэлектрика
Определение 6Поляризованность P→ или, другими словами, вектор поляризованности характеризует степень поляризации диэлектрика:
P→=∆ρ→∆V,
где ∆ρ представляет собой дипольный момент элемента диэлектрика.
В условиях неполярных молекул вектор поляризованности может быть определен в следующем виде:
P→=1∆V∑∆Vρi→=Nρ0→,
где сложение идет относительно всех молекул в объеме △V. N — концентрация молекул,
ρ0→ является индуцированным дипольным моментом (Он один и тот же у всех молекул). ρ0→↑↑E→.
Формула поляризованности в условиях полярных молекул принимает вид следующего выражения:
P→=1∆V∑∆Vρi→=Np→,
в котором P→ представляет собой среднее значение дипольных моментов, которые равнозначны по модулю, но обладают разными направлениями.
В изотропных диэлектриках средние дипольные моменты по направлению идентичны напряженности внешнего электрического поля. У диэлектриков с молекулами полярного типа, вклад в поляризованность от наведенных зарядов значительно ниже вклада от переориентации поля.
Определение 9Ионная решеточная поляризации может быть описана следующей формулой: P→=1∆V∑∆Vρi→=Np→.
В большей части случаев подобная поляризация является анизотропной.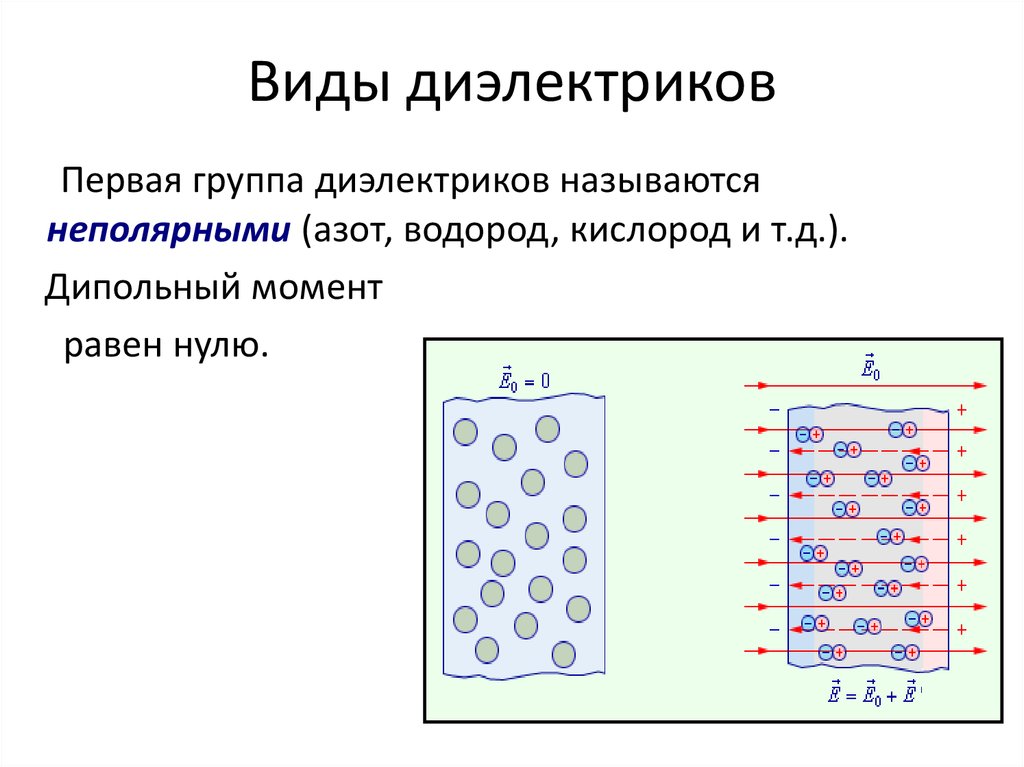
Если представить плоский конденсатор, который заполнен диэлектриком так, как это проиллюстрировано на рисунке 1, то на принадлежащей ему левой обкладке расположен положительный заряд, а на правой — отрицательный. По причине того факта, что разноименные заряды притягиваются друг к другу, у положительной обкладки на поверхности диэлектрика появится отрицательный заряд, а у правой, то есть отрицательной – положительный заряд диэлектрика. Выходит, что поле, формирующееся поляризационными зарядами, имеет противоположное направлению поля направление, которое создают обкладки, соответственно, диэлектрик ослабляет поле.
Рисунок 1
+q,−q представляют собой заряды на обкладках конденсатора.
E→ является напряженностью поля, которое формируется обкладками конденсатора.
−q′, +q′- это заряды диэлектрика.
E→’ — напряженность поля, которое создается как результат поляризации диэлектрика.
Явление влияния вещества на магнитное и электрическое поля было эмпирическим путем открыто Фарадеем.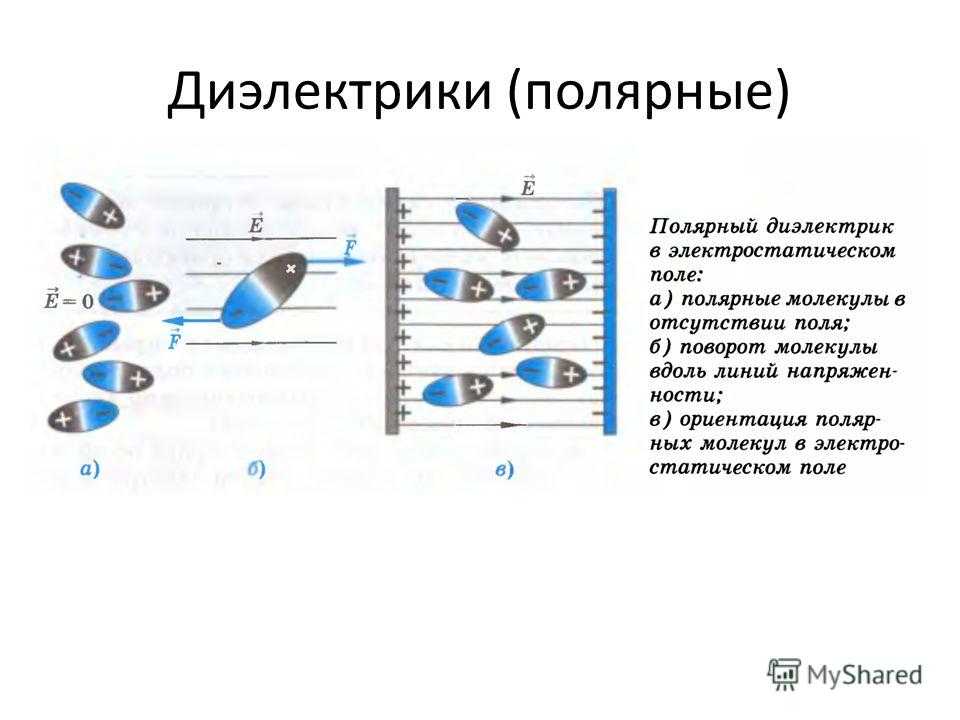 Именно этим ученым было в науку были введены такие термины, как диэлектрик и диэлектрическая постоянная.
Именно этим ученым было в науку были введены такие термины, как диэлектрик и диэлектрическая постоянная.
В случае если однородный изотропный диэлектрик полностью заполняет собой объем, ограниченный эквипотенциальными поверхностями поля сторонних зарядов, то напряженность поля внутри него в ε раз меньше напряженности поля сторонних зарядов.
E→’=E→ε,
где ε определяет диэлектрическую проницаемость среды.
Напряженность поля точечного заряда, который расположен в диэлектрике с некоторой диэлектрической проницаемостью ε, может быть выражена в виде следующего выражения:
E→=14πεε0qr3r→.
Закон Кулона для зарядов, находящихся в жидком и газообразном диэлектрике принимает такой вид:
F→=14πεε0q1q2r3r→.
Пример 2Задание: Бесконечную плоскую пластину из однородного изотропного диэлектрика разместили в однородном электростатическом поле с напряженностью E=200 Вм, направленной под прямым углом силовым линиям поля. Диэлектрическая проницаемость диэлектрика равняется 2. Какова напряженность поля внутри диэлектрика?
Какова напряженность поля внутри диэлектрика?
Решение
Поле в вакууме в ε раз сильнее, чем поле в диэлектрике, по этой причине запишем, что:
E→’=E→ε.
Произведем некоторые расчеты:
E→’=2002=100 Вм.
Ответ: Напряженность поля в пластине будет 100 Вм.
Пример 3Задание: Заряженные шарики обладают массойm1=m2=m. Они подвешены на нитях, имеющих одинаковые значения длины, в одной точке, их заряды эквивалентны q1 и q2( смотри рисунок 1). Изначально они располагаются в воздухе (диэлектрическая проницаемость ε1), после этого погружаются в жидкость ε2. Каково отношение диэлектрических проницаемостей ε2ε1, если при погружении в жидкость системы из шариков угол расхождения нитей не претерпел изменений? Отношение плотности шариков к плотности диэлектрика ρshρd=b.
Решение
Рисунки 2 и 3
Запишем условие равновесия шарика в симметричной системе в воздухе:
Fe1→+mg→+N1→=0.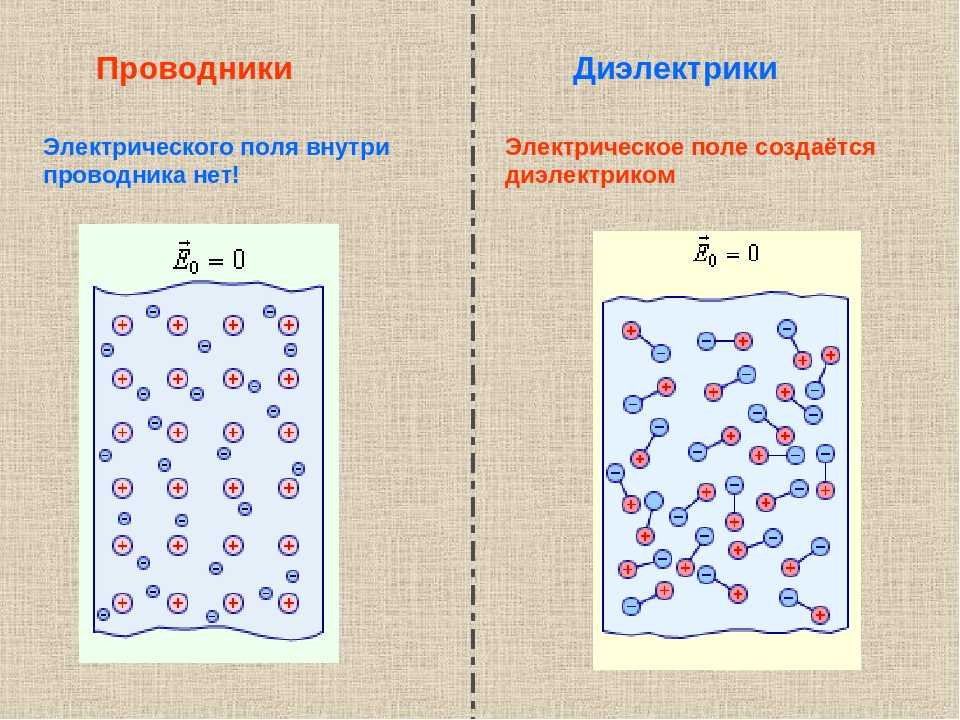
Теперь выразим условие равновесия одного шарика в жидкости:
Fe2→+mg→+N2→+FA→=0.
Запишем проекции уравнения Fe1→+mg→+N1→=0 на оси:
Ох: Fe1-N1sina2=0,
Oy: mg-N1cosα2=0.
Проекции уравнения Fe2→+mg→+N2→+FA→=0 на оси:
Ох: Fe2-N2sinα2=0,
Oy: mg-N2cosα2-FA=0.
Берем отношение уравнения Fe1-N1sina2=0 и mg-N1cosa2=0, в качестве результата получаем:
tga2=Fe1mg.
Уравнение Fe2-N2sina2=0 на уравнение mg-N2cosa2-FA=0, получаем:
tga2=Fe2mg-FA→Fe1mg=Fe2mg-FA.
Основываясь на законе Кулона, запишем такое выражения для Fe1, Fe2:
Fe1=q1q24πε1ε0r2 и Fe2=q1q24πε2ε0r2.
Модуль силы Архимеда равняется следующему выражению:
FA=ρdVg=ρdmρshg.
Подставим в уравнение tga2=Fe2mg-FA→Fe1mg=Fe2mg-FA уравнения Fe1=q1q24πε1ε0r2 и
Fe2=q1q24πε2ε0r2, в результате получим:
q1q24πε1ε0r2mg=q1q24πε2ε0r2mg-ρdmρshg→1ε11=1ε21-ρdρsh→ε2ε1=11-ρdρsh=11-b.
Ответ: Диэлектрическая проницаемость жидкости должна быть ε2e1=11-b.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.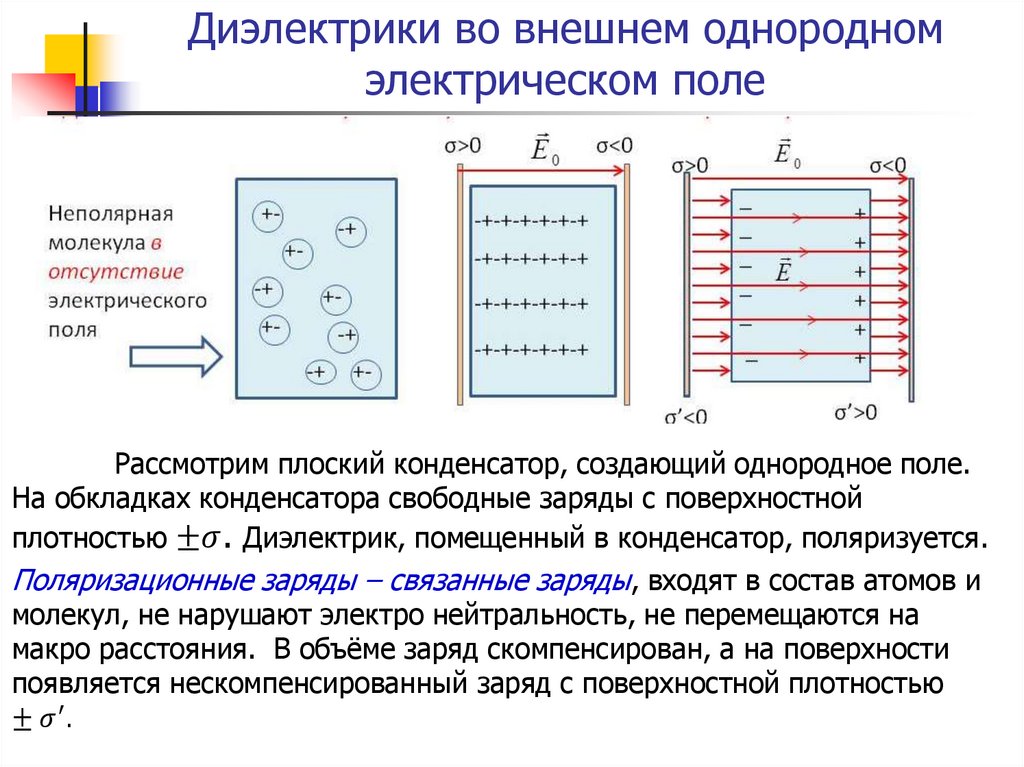
Диэлектрики — изоляционные материалы | Кабели Atlas
Теоретически идеальный кабель представляет собой неизолированный проводник в свободном воздушном пространстве. Однако на практике не все так просто.
Поверхностный эффект
Чтобы понять важность используемого в кабеле изоляционного материала, рассмотрим прохождение переменного тока через проводник. Различные частоты занимают в проводнике различные радиальные позиции. Низкочастотные сигналы занимают центр проводника, высокочастотные сигналы передаются по его поверхностным слоям. Таким образом, высокочастотные сигналы «вынуждены» протекать по области проводника с меньшим поперечным сечением, чем низкочастотные сигналы, а значит, эффективное сопротивление кабеля для них больше, чем для низкочастотных. Поэтому потери в кабелях зависят от частоты сигнала, и наибольшие потери терпят высокочастотные сигналы. Это явление известно как «поверхностный эффект». В кругах аудиофилов ведется ожесточенная дискуссия на эту тему, поскольку многие утверждают, что поверхностный эффект затрагивает только частоты за пределами человеческого слуха. Однако это не совсем верно – сопротивление проводника начинает расти из-за поверхностного эффекта в районе 20 кГц.
Это явление известно как «поверхностный эффект». В кругах аудиофилов ведется ожесточенная дискуссия на эту тему, поскольку многие утверждают, что поверхностный эффект затрагивает только частоты за пределами человеческого слуха. Однако это не совсем верно – сопротивление проводника начинает расти из-за поверхностного эффекта в районе 20 кГц.
Высокие частоты «отвечают» за тембр, пространственность и чистоту.
См. ниже, слева направо.
- Радиальные позиции частот в проводнике.
- Область, занимаемая верхними частотами в витом проводнике.
- Область, занимаемая верхними частотами в цельном проводнике.
Низкие и средние частоты занимают центр проводника. Оптимизация низкочастотных составляющих сигнала особенно важна в акустических кабелях. Обширные тестовые исследования доказывают, что для чистого звучания басов проводник должен иметь поперечное сечение от 3,00 до 4,5 мм2. Кроме того, «большие» кабели должны быть витыми, в них должен использоваться высококачественный диэлектрик, такой как полиэтилен, тефлон или микропористый тефлон.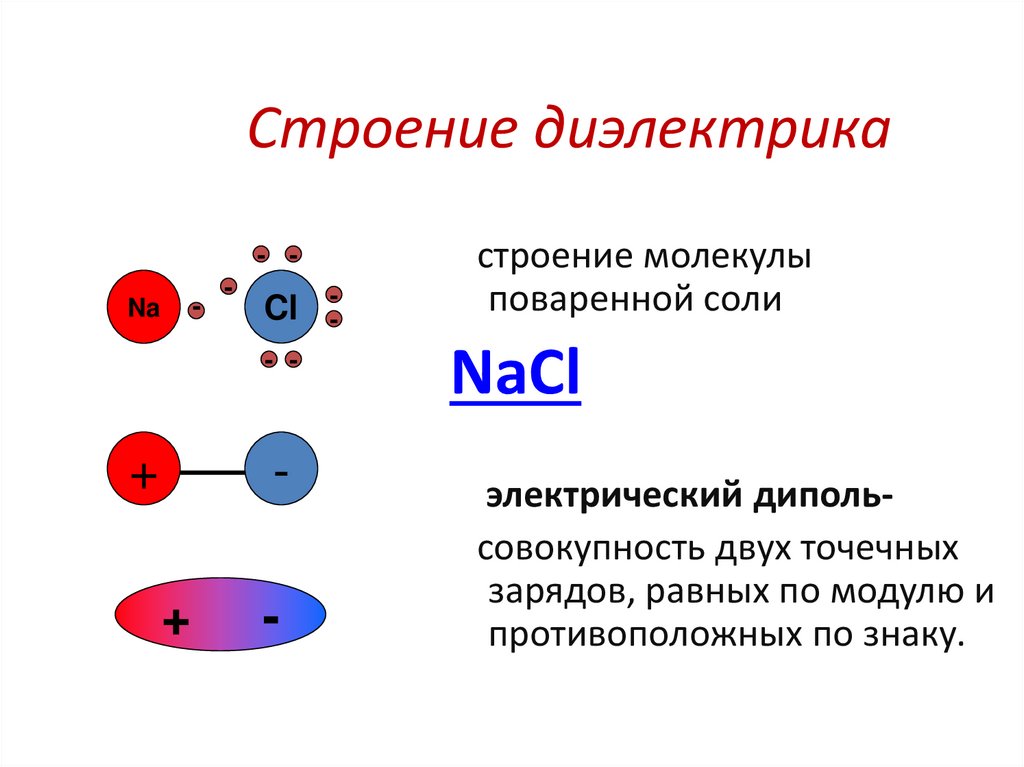 На качество звучания также влияют и другие факторы, не поддающиеся измерению.
На качество звучания также влияют и другие факторы, не поддающиеся измерению.
Конструкции с применением множественных изолированных жил преодолевают проблемы, связанные с увеличением сопротивления из-за поверхностного эффекта, однако такие низкоиндуктивные кабели имеют более высокую емкость. Кабели с низкой емкостью и низким сопротивлением не будут влиять на устройства, к которым они подключены в той степени, насколько кабели с высокой емкостью; акустические кабели должны иметь низкое сопротивление во избежание потерь сигнала, а межблочные кабели должны обладать низкой емкостью для увеличения скорости распространения сигнала.
Аудиосистемы, которые звучат в акустическом диапазоне ярче других, могут работать на грани нестабильности из-за использования кабелей высокой емкости. Яркость часто ошибочно принимается за улучшенную динамику, но «улучшения» динамического диапазона не должны достигаться за счет низкочастотной информации, поскольку это может вызвать нестабильность усилителя.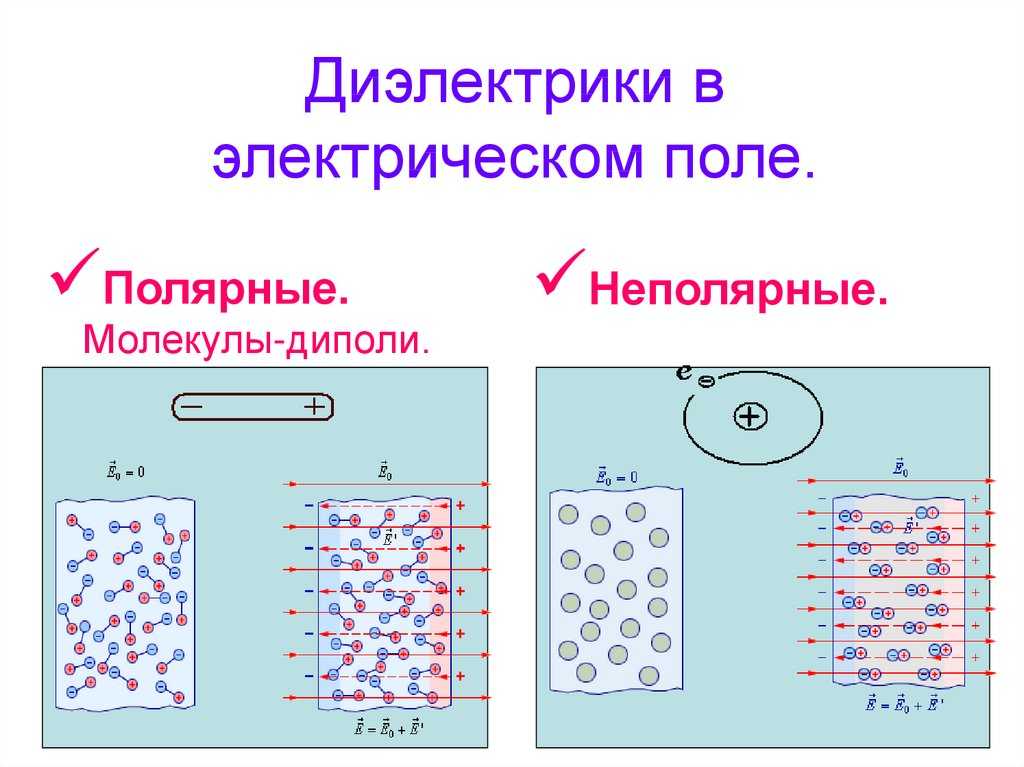 Нежелательная яркость также свойственна посеребренным кабелям, которые через некоторое время утомляют слушателей. Atlas никогда не использует для аудиоприложений посеребренные кабели или кабели из различных металлов с разным сопротивлением и разными характеристиками.
Нежелательная яркость также свойственна посеребренным кабелям, которые через некоторое время утомляют слушателей. Atlas никогда не использует для аудиоприложений посеребренные кабели или кабели из различных металлов с разным сопротивлением и разными характеристиками.
Три вышеприведенных рисунка иллюстрируют, слева направо, радиальные области, занимаемые сигналом в проводнике в зависимости от частоты. Низкие частоты занимают центр проводника. Отсюда следует, что «толстый» проводник обладает меньшим сопротивлением в низкочастотном диапазоне и обеспечивает больше басов. Вот почему Atlas выпускает кабели разного сечения – например, акустические кабели Hyper выпускаются сечением 1,5, 2,0 и 3,0 мм2. В тех случаях, когда необходимы мощные басы, требуется применение кабеля большого сечения. Кроме того, при большой длине акустических кабелей лучше использовать более «толстые» кабели.
На втором рисунке показана область, занимаемая верхними частотами в витом проводнике.
На третьем рисунке показана область, занимаемая верхними частотами в цельном проводнике. Она больше, чем в витом проводнике, поэтому высокочастотный сигнал в цельном проводнике встречает меньшее сопротивление, в связи с чем в этом случае обеспечивается лучшая передача верхних частот. Во всех акустических кабелях bi-wire, производимых Atlas, используются витые проводники для передачи басов и цельные проводники – для передачи верхних частот. Напрашивается вопрос: почему не использовать цельный проводник и для тех, и других частот? Если взять, к примеру, цельный проводник сечением 3,00 мм2, при изгибе он будет не сгибаться, а ломаться, так что это непрактично. Это еще одна из причин использования витых проводников. Приблизительное оптимальное сечение цельного проводника – 1,5 мм2. Акустические кабели bi-wire, производимые Atlas, на стороне, подключаемой к колонкам, имеют четыре вывода неравной длины. Два более длинных вывода подключаются к верхнечастотным разъемам колонок (конечно, при условии, что они поддерживают режим bi-wire!), а два коротких – к низкочастотным разъемам.
Она больше, чем в витом проводнике, поэтому высокочастотный сигнал в цельном проводнике встречает меньшее сопротивление, в связи с чем в этом случае обеспечивается лучшая передача верхних частот. Во всех акустических кабелях bi-wire, производимых Atlas, используются витые проводники для передачи басов и цельные проводники – для передачи верхних частот. Напрашивается вопрос: почему не использовать цельный проводник и для тех, и других частот? Если взять, к примеру, цельный проводник сечением 3,00 мм2, при изгибе он будет не сгибаться, а ломаться, так что это непрактично. Это еще одна из причин использования витых проводников. Приблизительное оптимальное сечение цельного проводника – 1,5 мм2. Акустические кабели bi-wire, производимые Atlas, на стороне, подключаемой к колонкам, имеют четыре вывода неравной длины. Два более длинных вывода подключаются к верхнечастотным разъемам колонок (конечно, при условии, что они поддерживают режим bi-wire!), а два коротких – к низкочастотным разъемам.
Высокочастотные сигналы занимают периферийные слои проводника (см. выше). Низкокачественные диэлектрики уменьшают скорость распространения этих сигналов, что в результате приводит к звучанию, смещенному в сторону нижних и средних диапазонов акустического спектра. Плохое звучание часто связано с применением кабелей с низкокачественной изоляцией.
выше). Низкокачественные диэлектрики уменьшают скорость распространения этих сигналов, что в результате приводит к звучанию, смещенному в сторону нижних и средних диапазонов акустического спектра. Плохое звучание часто связано с применением кабелей с низкокачественной изоляцией.
Изоляция из поливинилхлорида (PVC) дешева в производстве и наиболее часто используется в аудио и видео кабелях. Поливинилхлорид – низкокачественный диэлектрик, один из худших для аудио и видео сигналов, часто вызывающий большие потери из-за существенного снижения скорости распространения сигнала. Поливинилхлорид гораздо лучше подходит для силовых кабелей, а в аудио и видео кабелях его применения следует избегать.
Другие распространенные диэлектрики – полиэтилен, полипропилен и политетрафторэтилен (ПТФЭ), более известный под названием «тефлон». Недавно компания Atlas создала новый уникальный диэлектрик – микропористый тефлон.
Тефлон имеет высокую температуру плавления (327°C), которая идеально подходит для нанесения тефлонового покрытия на непригарные сковороды, но вызывает трудности при покрытии обработанной меди – при высоких температурах медь OFC и OCC возвращаются к гранулярному состоянию, теряя свою монокристаллическую структуру и превращаясь в технически чистую медь. Последние несколько лет компания Atlas совместно со своими поставщиками исследовала способы нанесения тефлоновых покрытий на обработанную медь, не дающие вышеописанных негативных эффектов. Благодаря этим развернутым исследованиям теперь стало возможным наносить на обработанную медь покрытие из одного из типов тефлона под названием «фторированный этилен-пропилен» (ФЭП), температура плавления которого – 275°. При нанесении покрытия медь одновременно охлаждается.
Последние несколько лет компания Atlas совместно со своими поставщиками исследовала способы нанесения тефлоновых покрытий на обработанную медь, не дающие вышеописанных негативных эффектов. Благодаря этим развернутым исследованиям теперь стало возможным наносить на обработанную медь покрытие из одного из типов тефлона под названием «фторированный этилен-пропилен» (ФЭП), температура плавления которого – 275°. При нанесении покрытия медь одновременно охлаждается.
ФЭП существенно снижает диэлектрические потери в кабелях, сохраняя при этом все преимущества низкозернистых медных проводников. Этот вид тефлона используется во всех продуктах серии Atlas Ascent, в акустических кабелях Hyper и других.
Дальнейшие исследования привели к использованию в качестве диэлектрика микропористого тефлона (ПТФЭ). Первые продукты Atlas, в которых применяется этот изоляционный материал – межблочные и акустические кабели Mavros и Asimi.
Микропористый тефлон – это уникальный материал с низким удельным весом и существенно лучшими характеристиками по сравнению с обычным тефлоном. Микропористый тефлон содержит значительно большее количество воздуха, чем цельный тефлон. Воздух содержится в микроскопических (менее половины микрона диаметром) пузырьках внутри материала. Благодаря этому достигается чрезвычайно низкая диэлектрическая проницаемость – от 1,3 до 1,5 (следующий по качеству диэлектрик, тефлон, имеет диэлектрическую проницаемость от 2,1 до 2,3). Скорость распространения сигнала в кабелях с изоляцией из микропористого тефлона на 70-80% выше, чем в обычных кабелях, и примерно на 30% выше, чем в кабелях с изоляцией из обычного тефлона.
Микропористый тефлон содержит значительно большее количество воздуха, чем цельный тефлон. Воздух содержится в микроскопических (менее половины микрона диаметром) пузырьках внутри материала. Благодаря этому достигается чрезвычайно низкая диэлектрическая проницаемость – от 1,3 до 1,5 (следующий по качеству диэлектрик, тефлон, имеет диэлектрическую проницаемость от 2,1 до 2,3). Скорость распространения сигнала в кабелях с изоляцией из микропористого тефлона на 70-80% выше, чем в обычных кабелях, и примерно на 30% выше, чем в кабелях с изоляцией из обычного тефлона.
Микропористый тефлон (ПТФЭ) отличается повышенной фазовой стабильностью при температурных колебаниях. Фазовая стабильность кабеля зависит от коэффициента теплового расширения диэлектрика и проводников. Поскольку микропористый тефлон имеет более низкий коэффициент теплового расширения по сравнению с обычным тефлоном, его использование улучшает фазовую стабильность при колебаниях температуры.
При одинаковом внешнем диаметре кабели с изоляцией из микропористого тефлона обеспечивают меньшие потери сигнала, чем кабели с изоляцией из обычного тефлона. Во-первых, это связано с тем, что низкий коэффициент затухания самого диэлектрика уменьшает ослабление сигнала, особенно на высоких частотах. Во-вторых, с тем, что низкая диэлектрическая проницаемость микропористого тефлона позволяет использовать проводники большего диаметра. Так, в кабелях Mavros улучшение передачи низкочастотной информации (то есть звучание басов) достигается путем применения проводников увеличенного диаметра в изоляции из микропористого тефлона.
Во-первых, это связано с тем, что низкий коэффициент затухания самого диэлектрика уменьшает ослабление сигнала, особенно на высоких частотах. Во-вторых, с тем, что низкая диэлектрическая проницаемость микропористого тефлона позволяет использовать проводники большего диаметра. Так, в кабелях Mavros улучшение передачи низкочастотной информации (то есть звучание басов) достигается путем применения проводников увеличенного диаметра в изоляции из микропористого тефлона.
Термическое расширение цельного тефлона оказывает неблагоприятные механические воздействия на кабель, поскольку с расширением тефлона при нагревании может уменьшиться воздушный зазор между изоляцией кабеля и контактом разъема, что изменяет характеристики импеданса разъема. При применении микропористого тефлона, минимально расширяющегося при нагревании, эти эффекты практически несущественны.
Вышеописанные различия между микропористым и обычным тефлоном могут показаться незначительными, однако кумулятивный эффект этих маленьких различий приводит к ухудшению передачи аудиосигналов и не позволяет полностью раскрыть все нюансы музыкальных записей.
В нижеприведенной таблице приведены свойства ряда диэлектриков. Поливинилхлорид (PVC), хотя и не используется в кабелях Atlas, приведен для сравнения.
В нижеприведенной таблице приведены свойства ряда диэлектриков. Поливинилхлорид (PVC), хотя и не используется в кабелях Atlas, приведен для сравнения
| Диэлектрик | |||||
| Характеристики | Поливинилхлорид | Пористый полиэтилен | Полипропилен | Тефлон (ФЭП) | Микропористый тефлон (PTFE) |
| Диэлектрическая проницаемость (50-106 Гц) |
4-8 | 2.3 | 2.25 | 2.1 | 1.3 |
| Диэлектрическая прочность (кВ мм-1) |
23-30 | 30-50 | 30-50 | 20-25 | н/д |
| Тангенс угла потерь (в % при 50-106 Гц) |
8-15 | 0.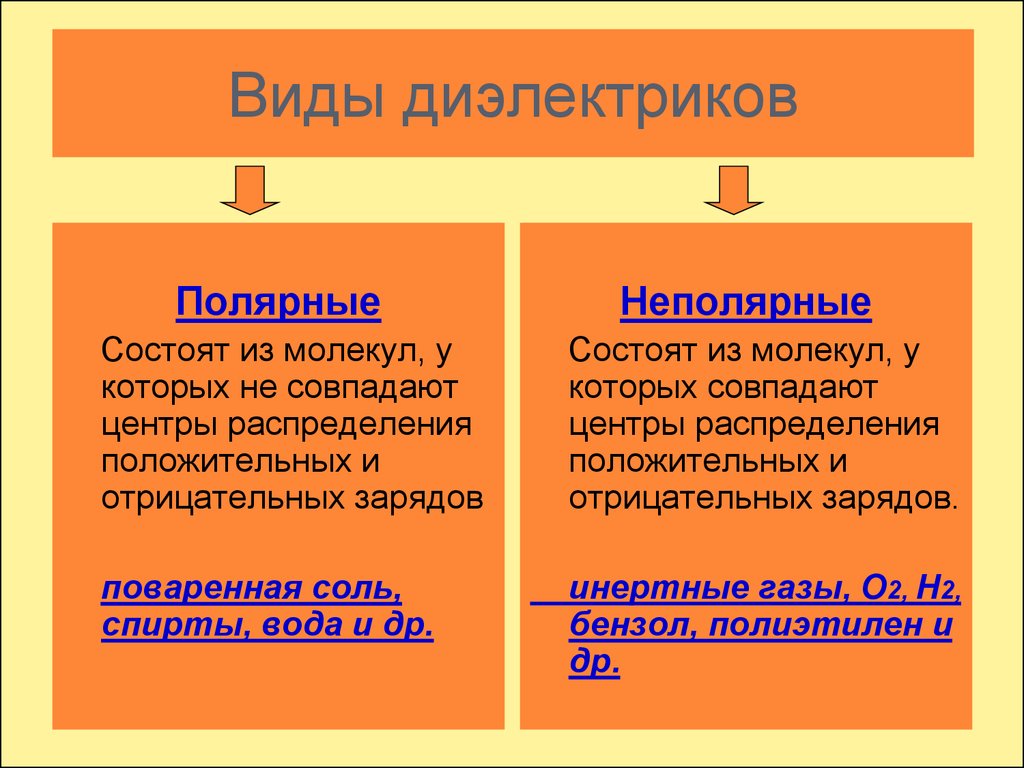 02-0.05 02-0.05 |
0.02 — 0.06 (@ 106 Hz) |
0.02-0.07 | н/д |
| Объемное удельное сопротивление (Ом/см cm при 20°C) |
1012-15 | > 1017 | 6.5 x 1014 | > 1016 | н/д |
| Прочность на разрыв (кг/мм2) |
1.0-2.5 | 1.0-2.0 | 3.0-4.0 | 1.9-2.2 | 1.0 |
| Температура плавления (°C) |
-130 | 112-120 | 155-160 | 275 | 275 |
| Максимальная постоянная рабочая температура (°C) |
60 | 75 | 90 | 200 | 260 |
| Минимальная рабочая температура (°C) |
от -15 до -40 | <-60 | от -5 до -45 | <-60 | -250 |
Диэлектрики
Диэлектрики
Если материал содержит полярные молекулы, они обычно будут иметь случайную ориентацию, когда не будет приложено электрическое поле. Приложенное электрическое поле поляризует материал, ориентируя дипольные моменты полярных молекул. Приложенное электрическое поле поляризует материал, ориентируя дипольные моменты полярных молекул.
Наличие диэлектрика уменьшает электрическое поле, создаваемое данной плотностью заряда. Коэффициент k, на который эффективное поле уменьшается из-за поляризации диэлектрика, называется диэлектрической проницаемостью материала.
|
Индекс Концепции конденсаторов Концепции диполей | |||
|
Назад |
|
Емкость набора заряженных параллельных пластин увеличена за счет вставки диэлектрического материала.
|
Индекс Концепции конденсаторов | |||||||||||
|

 Емкость обратно пропорциональна электрическому полю между пластинами, а наличие диэлектрика снижает эффективное электрическое поле. Диэлектрик характеризуется диэлектрической проницаемостью k, и емкость умножается на этот коэффициент.
Емкость обратно пропорциональна электрическому полю между пластинами, а наличие диэлектрика снижает эффективное электрическое поле. Диэлектрик характеризуется диэлектрической проницаемостью k, и емкость умножается на этот коэффициент.  Диэлектрическая проницаемость — это характеристика пространства, а относительная диэлектрическая проницаемость или «диэлектрическая постоянная» — это способ охарактеризовать уменьшение эффективного поля из-за поляризации диэлектрика. Емкость параллельного расположения пластин увеличивается в k раз.
Диэлектрическая проницаемость — это характеристика пространства, а относительная диэлектрическая проницаемость или «диэлектрическая постоянная» — это способ охарактеризовать уменьшение эффективного поля из-за поляризации диэлектрика. Емкость параллельного расположения пластин увеличивается в k раз.
 Что ж, наверное, неудивительно, что в действительности вещества обычно находятся между этими двумя крайностями. Сейчас мы сосредоточимся на изоляционной стороне спектра. Представьте себе вещество, которое не позволяет зарядам перемещаться, куда им заблагорассудится, но позволяет атомам или молекулам, связывающим эти заряды, изменять свою форму. Такие вещества называются диэлектрики , и они на самом деле обеспечивают эффект, аналогичный тому, который наблюдается в проводниках, хотя он недостаточно экстремальный, чтобы полностью нейтрализовать поле.
Что ж, наверное, неудивительно, что в действительности вещества обычно находятся между этими двумя крайностями. Сейчас мы сосредоточимся на изоляционной стороне спектра. Представьте себе вещество, которое не позволяет зарядам перемещаться, куда им заблагорассудится, но позволяет атомам или молекулам, связывающим эти заряды, изменять свою форму. Такие вещества называются диэлектрики , и они на самом деле обеспечивают эффект, аналогичный тому, который наблюдается в проводниках, хотя он недостаточно экстремальный, чтобы полностью нейтрализовать поле.  0177 поляризационный заряд .
0177 поляризационный заряд . 
 Она равна 1 для вакуума (где нет зарядов для поляризации) или идеального изолятора (который вообще не допускает движения зарядов). ).
Она равна 1 для вакуума (где нет зарядов для поляризации) или идеального изолятора (который вообще не допускает движения зарядов). ).  Отсюда мы можем следовать вычислениям, выполненным в примере 2.4.1. Там было отмечено, что изменение энергии зависит от того, что остается постоянным при изменении емкости — заряд на обкладках или разность потенциалов, и это надо учитывать и здесь. Единственное отличие здесь состоит в том, что емкость изменяется в результате изменения диэлектрической проницаемости, а не изменения расстояния между пластинами.
Отсюда мы можем следовать вычислениям, выполненным в примере 2.4.1. Там было отмечено, что изменение энергии зависит от того, что остается постоянным при изменении емкости — заряд на обкладках или разность потенциалов, и это надо учитывать и здесь. Единственное отличие здесь состоит в том, что емкость изменяется в результате изменения диэлектрической проницаемости, а не изменения расстояния между пластинами.  Поляризационный заряд на поверхности диэлектрика, находящейся между пластинами, будет притягиваться к свободному заряду на части пластин, которые еще разделены вакуумом:
Поляризационный заряд на поверхности диэлектрика, находящейся между пластинами, будет притягиваться к свободному заряду на части пластин, которые еще разделены вакуумом:  Насколько она изменится, опять-таки зависит от того, остается ли заряд на пластинах или разность потенциалов постоянными во время процесса (зависимость выполненной работы от того, какая величина поддерживается постоянной, также характерна для примера 2.4.1). Таким образом, все, что нужно сделать, это записать потенциальную энергию конденсатора в любом положении, в котором находится диэлектрик, пересчитать ее для диэлектрика, помещенного на дополнительное расстояние \(dy\), взять разницу, чтобы получить \(dU\), затем разделить на \(dy\). Важной частью этого процесса является то, что конденсатор с частично вставленным диэлектриком эквивалентен двум отдельным конденсаторам, один с вакуумом между пластинами, а другой с диэлектриком между ними. Полная энергия системы представляет собой сумму энергии в этих двух конденсаторах, и нужно иметь в виду, что, поскольку каждая пластина является эквипотенциальной, разность потенциалов между двумя пластинами для двух отдельных конденсаторов одинакова.
Насколько она изменится, опять-таки зависит от того, остается ли заряд на пластинах или разность потенциалов постоянными во время процесса (зависимость выполненной работы от того, какая величина поддерживается постоянной, также характерна для примера 2.4.1). Таким образом, все, что нужно сделать, это записать потенциальную энергию конденсатора в любом положении, в котором находится диэлектрик, пересчитать ее для диэлектрика, помещенного на дополнительное расстояние \(dy\), взять разницу, чтобы получить \(dU\), затем разделить на \(dy\). Важной частью этого процесса является то, что конденсатор с частично вставленным диэлектриком эквивалентен двум отдельным конденсаторам, один с вакуумом между пластинами, а другой с диэлектриком между ними. Полная энергия системы представляет собой сумму энергии в этих двух конденсаторах, и нужно иметь в виду, что, поскольку каждая пластина является эквипотенциальной, разность потенциалов между двумя пластинами для двух отдельных конденсаторов одинакова.
 Однако здесь следует иметь в виду одну важную деталь.
Однако здесь следует иметь в виду одну важную деталь.  поверхность диэлектрика. Чистый поток от гауссовой поверхности (весь поток проходит через левую сторону показанной поверхности) ниже, чем он был бы без диэлектрика, потому что поляризационный заряд компенсирует часть свободного заряда. Различие в потоках происходит исключительно из-за различия в электрическом поле, которое мы уже знаем, как выразить:
поверхность диэлектрика. Чистый поток от гауссовой поверхности (весь поток проходит через левую сторону показанной поверхности) ниже, чем он был бы без диэлектрика, потому что поляризационный заряд компенсирует часть свободного заряда. Различие в потоках происходит исключительно из-за различия в электрическом поле, которое мы уже знаем, как выразить: 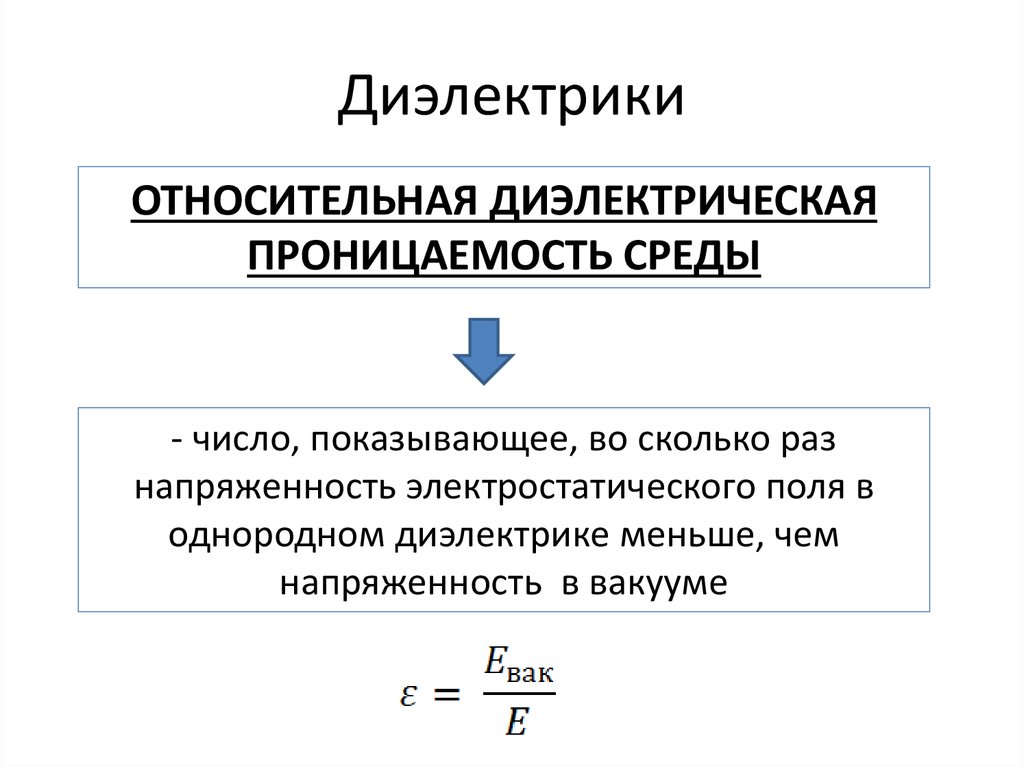 Если диэлектрик теперь удален, опишите, как изменяются следующие величины:
Если диэлектрик теперь удален, опишите, как изменяются следующие величины: 
