Для чего предназначены таблицы истинности. Таблицы истинности: назначение, применение и основные принципы в математической логике — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Для чего нужны таблицы истинности в логике. Как составлять таблицы истинности. Какие логические операции можно представить с помощью таблиц истинности. Где применяются таблицы истинности на практике.

Содержание

Что такое таблица истинности и для чего она нужна

Таблица истинности — это инструмент математической логики, который позволяет наглядно представить все возможные комбинации значений истинности для логических высказываний и операций над ними. По сути, это таблица, в которой отображаются все варианты истинности или ложности составных логических выражений в зависимости от истинности или ложности входящих в них простых высказываний.

Основные цели использования таблиц истинности:

Определение истинности сложных логических выражений
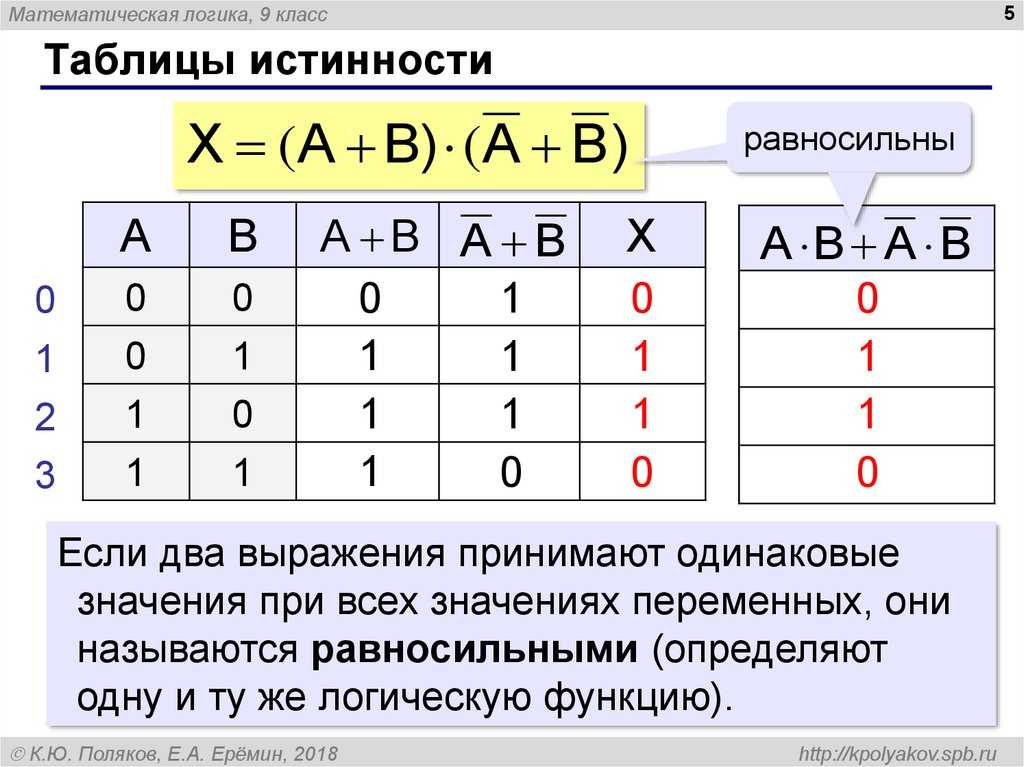
Проверка эквивалентности логических формул
Анализ логических схем и цепей
Изучение свойств логических операций
Упрощение и преобразование логических выражений

Основные компоненты таблицы истинности

Любая таблица истинности состоит из следующих ключевых элементов:

Простые высказывания (обычно обозначаются буквами P, Q, R и т.д.)
Логические операции над высказываниями (И, ИЛИ, НЕ и др.)
Все возможные комбинации значений истинности простых высказываний
Результирующие значения истинности для каждой комбинации

Количество строк в таблице истинности зависит от числа простых высказываний и равно 2^n, где n — число высказываний. Так, для 2 высказываний таблица будет содержать 4 строки, для 3 высказываний — 8 строк и т.д.

Основные логические операции и их таблицы истинности

Рассмотрим наиболее часто используемые логические операции и их представление в виде таблиц истинности:

Отрицание (НЕ)

Операция отрицания меняет значение высказывания на противоположное:

P	НЕ P
0	1
1	0

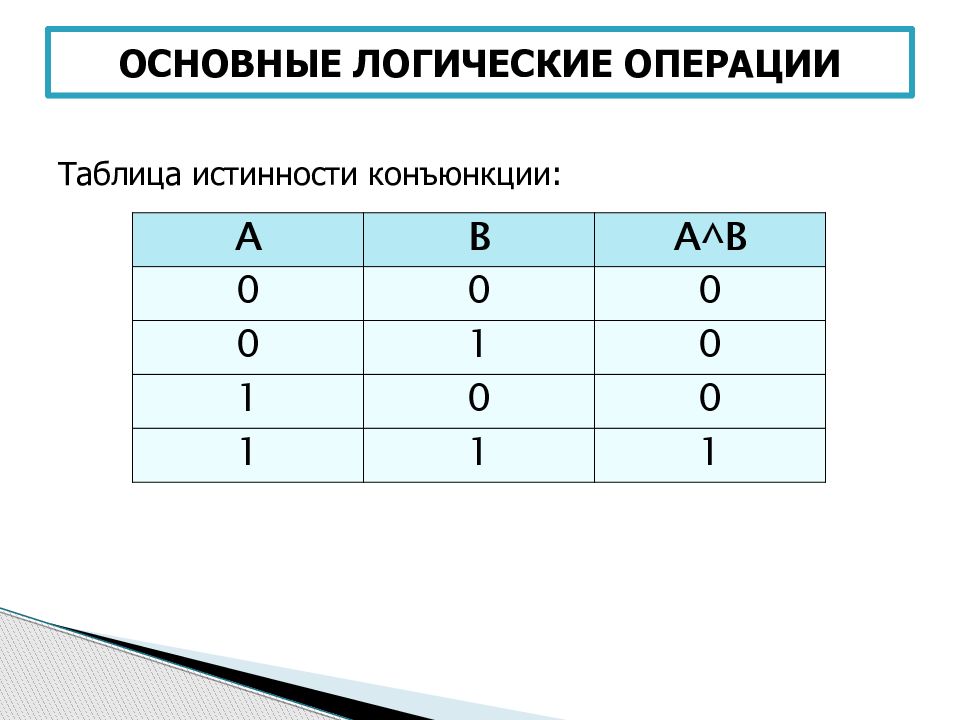
Конъюнкция (И)

Конъюнкция истинна только когда истинны оба высказывания:

P	Q	P И Q
0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкция (ИЛИ)

Дизъюнкция истинна, если истинно хотя бы одно из высказываний:

P	Q	P ИЛИ Q
0	0	0
0	1	1
1	0	1
1	1	1

Как составить таблицу истинности

Процесс составления таблицы истинности включает следующие шаги:

Определить все простые высказывания в логическом выражении
Создать столбцы для каждого простого высказывания
Заполнить все возможные комбинации значений истинности (0 и 1) для простых высказываний
Создать столбцы для промежуточных логических операций
Вычислить значения для промежуточных операций, используя соответствующие правила
Создать столбец для итогового выражения
Вычислить итоговые значения, используя результаты промежуточных операций

Практическое применение таблиц истинности

Таблицы истинности находят широкое применение в различных областях:

Проектирование цифровых схем и логических цепей
Анализ алгоритмов в программировании
Проверка корректности логических рассуждений

Оптимизация булевых функций
Синтез комбинационных схем
Верификация протоколов безопасности

Понимание принципов работы с таблицами истинности является важным навыком для специалистов в области информатики, электроники и математической логики.

Преимущества использования таблиц истинности

Таблицы истинности обладают рядом преимуществ:

Наглядность представления логических зависимостей
Простота проверки логических выражений
Возможность анализа всех возможных комбинаций
Удобство сравнения различных логических формул
Помощь в выявлении логических ошибок и противоречий

Ограничения таблиц истинности

Несмотря на свою полезность, таблицы истинности имеют некоторые ограничения:

Сложность работы с большим количеством переменных
Невозможность представления бесконечных множеств значений

Трудности в анализе временных логических зависимостей
Ограниченность применения для нечеткой логики

Альтернативные методы представления логических зависимостей

Помимо таблиц истинности, существуют и другие способы представления логических зависимостей:

Карты Карно
Диаграммы Венна
Логические схемы
Булевы формулы
Бинарные деревья решений

Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного способа зависит от решаемой задачи и предпочтений исследователя.

Заключение

Таблицы истинности являются мощным и наглядным инструментом для работы с логическими выражениями и операциями. Они позволяют систематически анализировать все возможные комбинации значений истинности и находят широкое применение в различных областях науки и техники. Освоение навыков работы с таблицами истинности является важным этапом в изучении математической логики и ее практических приложений.

Таблицы истинности | Презентация к уроку на тему:

Опубликовано 23.11.2017 — 21:28 — Сальникова Юлия Анатольевна

Понятие таблица истинности, алгорит составления таблиц истинности

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Таблицы истинности Информатика для студентов 2 курса

Слайд 2

Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций. Таблица состоит из строк и столбцов

Слайд 3

Алгоритм построения таблиц истинности Определить количество строк в таблице истинности Количество строк равно 2 n , где n — количество логических переменных. 2. Определить количество столбцов в таблице истинности Количество столбцов равно количеству логических переменных плюс количество логических операций.

Слайд 4

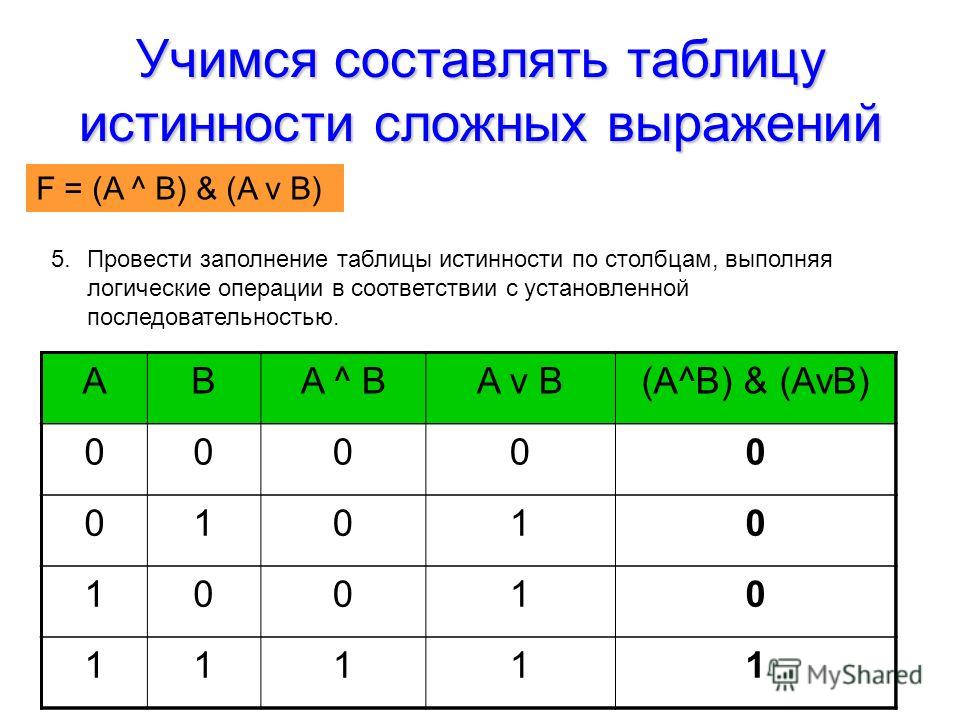
Построить таблицу истинности с указанным количеством строк и столбцов Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов; Заполнить столбцы входных переменных наборами значений; Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Слайд 5

Порядок выполнения логических операций Действия в скобках Инверсия Конъюнкция Дизъюнкция

Слайд 6

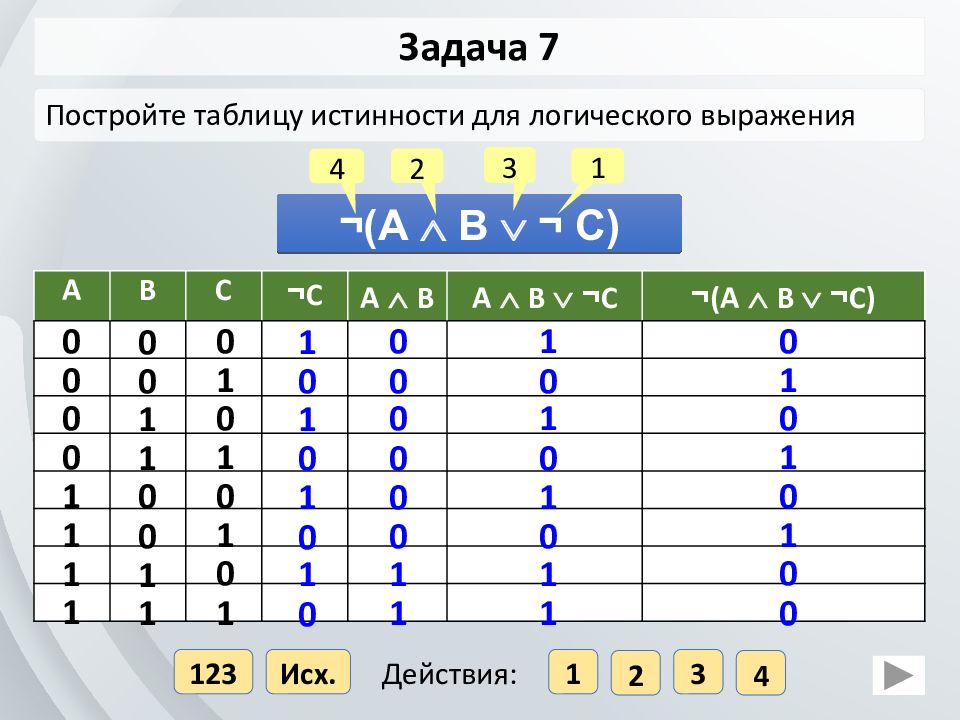
построить таблицу истинности для следующего сложного (составного) логического выражения : А & (B V C)

Слайд 7

Алгоритм выполнения Простые выражения (логические переменные): А, В, С ; (3) Количество логических операций: ¬ А — инверсия; B  C — операция дизъюнкции; ¬ А & (B  C) . операция конъюнкции. Всего: 3 Количество строк: на входе три простых высказывания: А, В, С , поэтому a=3 и количество строк = 2 ³ +1 = 9. Количество столбцов: 3+3=6 Заполняем столбцы с учетом таблиц истинности логических операций.

Слайд 8

А B C A B V C А & (B V C) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 0 1 1 1 0 1 1 1 0 0 0 0 Таблица истинности :

Слайд 9

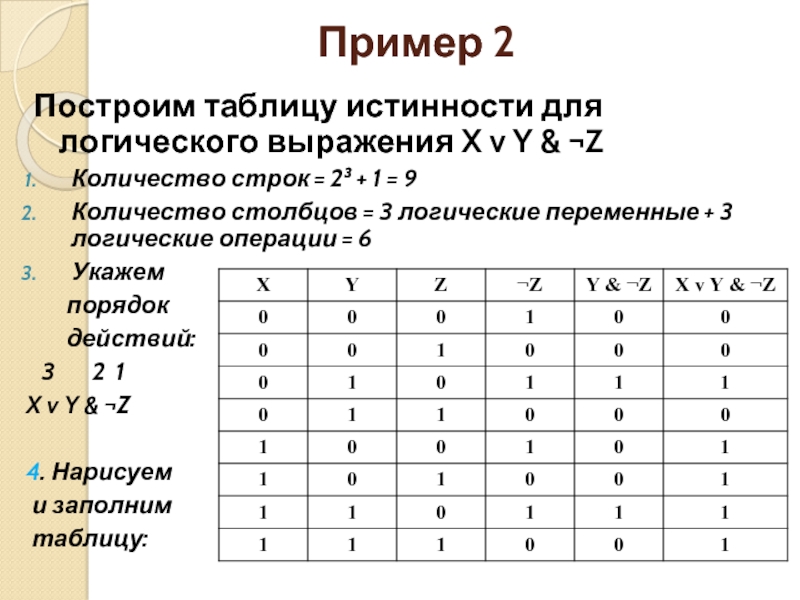
Задание для самостоятельной работы Постройте таблицу истинности для логического выражения: D=А V B & C

По теме: методические разработки, презентации и конспекты

Элементы математической логики — Практическое занятие №2 — Составление таблиц истинности

Цель работы: закрепить основные понятия алгебры высказываний, отработать навыки составления таблицы истинности для высказываний, сформировать умения определять равносильность формул. …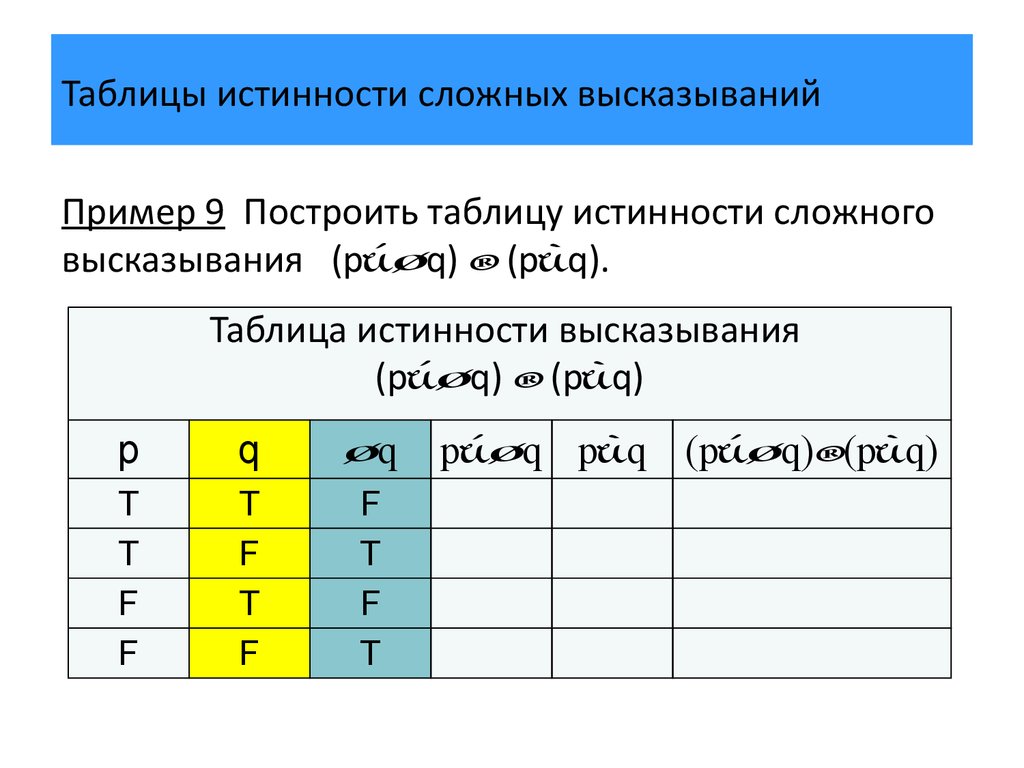

Построение таблиц истинности

закрепить умение строить истинные сложные высказывания из простых с использованием логических операций, сформировать навыки построения таблиц истинности…

Проверочная работа по теме «Таблицы истинности»

Проверочная работа по теме «Основы логики» предназначена для использования на уроках информатики для студентов 1 курса. Работа состоит из 8 вопросов разного характера. Разработан в программе MS Word….

Контрольная работа на тему: Проектирование логических схем, построение таблиц истинности.

Контрольная работа на тему: Проектирование логических схем, построение таблиц истинности.Контрольная работа содержит задания 24 варианта по 2 задания.Есть ответы….

4 раздел — итоговая таблица, таблица для графической части

4 раздел — итоговая таблица, таблица для графической части…

Основные логические операции, таблицы истинности

презентация основные логические операции, таблицы истинности…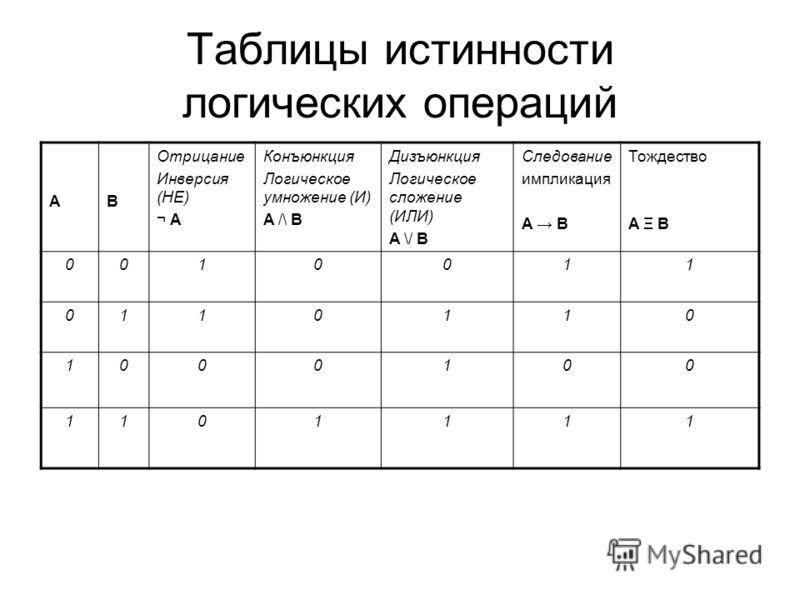

Технологическая карта. Основные логические операции, построение таблиц истинности простых высказываний.

ТЕХНОЛОГИЧЕСКАЯ КАРТАФ. И. О. преподавателя: Денисенко Яна СергеевнаДата проведения занятия: __.__.2018 г.Тема занятия: Основные логические операции, построение таблиц истинности простых высказываний…

Лабораторная работа №3 (1)

Цель работы:

Познакомиться с терминологией и символикой алгебры логики, рассмотреть логические операции с высказываниями.

Теоретическая часть

Логика высказываний – это наука о законах и формах мышления, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других.

Высказывание – это сообщение, выраженное повествовательным предложением, о котором можно сказать истинно оно или ложно.

Логическое выражение – простое или сложное высказывание, представленное в виде символов.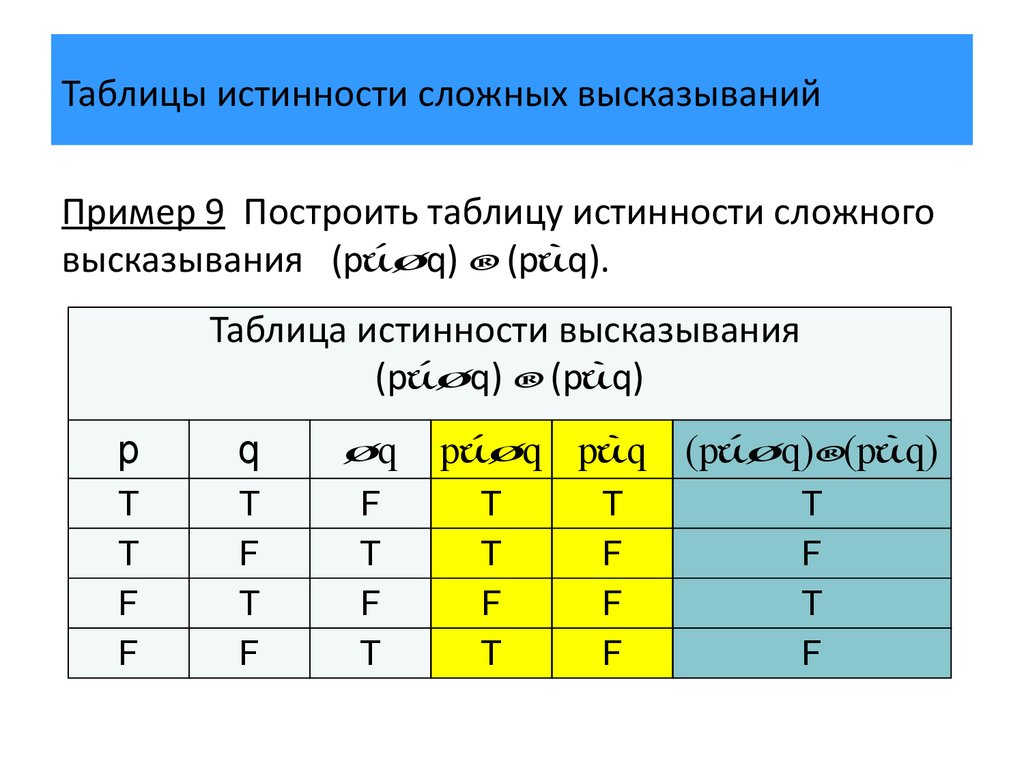

Значение истинного высказывания – истина (1).

Значение ложного высказывания – ложь (0).

Высказываниям ставятся в соответствие логические переменные (заглавные буквы латинского алфавита). Например, А – «Клавиатура – устройство для ввода информации в системный блок» (А=1) и В – «ВЗУ располагается внутри системного блока» (В=0).

Таблица истинности – это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.

Таблица 1. Логические операции

Логические операции	Связка (союз)	Обозначение
Конъюнкция логическое умножение	И	л, &, •
Дизъюнкция логическое сложение	Или	V, +
Инверсия логическое отрицание	Не	¯, ﹁
Импликация логическое следование	Если …, то …	→, ⇒
Эквивалентность	Тогда … только тогда, когда …	↔, ~, ⇔

Таблица 2.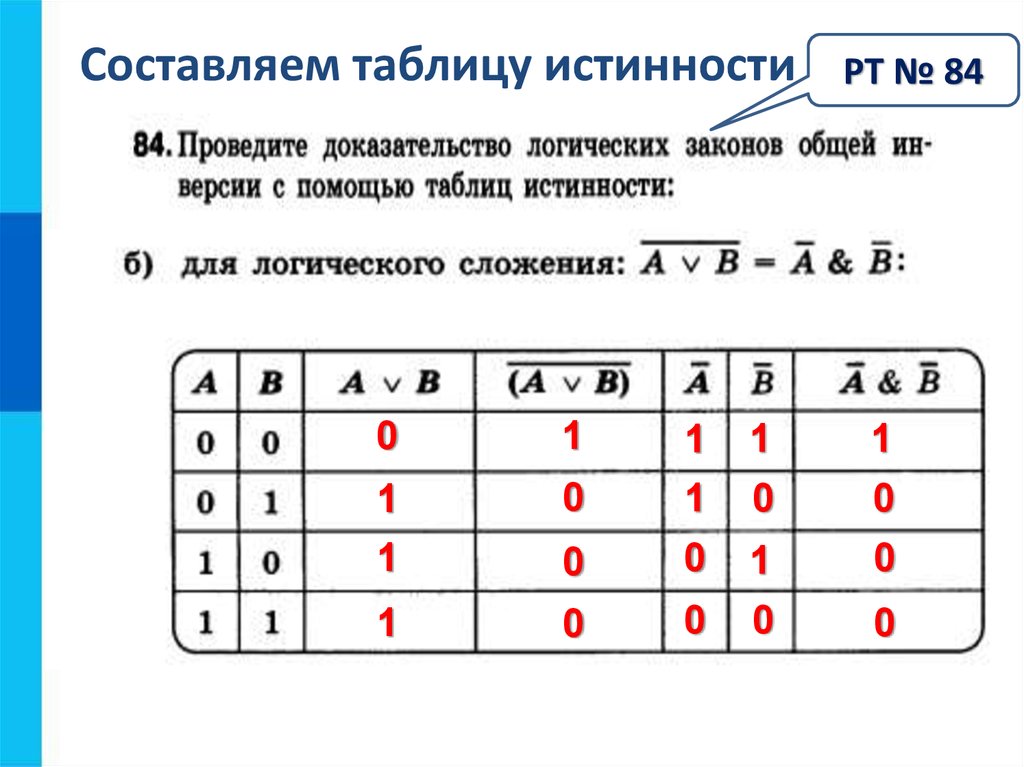 Таблица истинности логических операций

Инверсия	Конъюнкция	Дизъюнкция	Импликация	Эквивалентность
﹁А	А&В	АVВ	А⇒В	А⇔В
1	0	0	1	1
0	0	1	0	0
1	0	1	1	0
0	1	1	1	1

Логические операции имеют следующий приоритет:

Действия в скобках
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность

Общая постановка задачи

В данной лабораторной работе необходимо выполнить все разобранные в теоретической части примеры, параллельно знакомясь с теорией.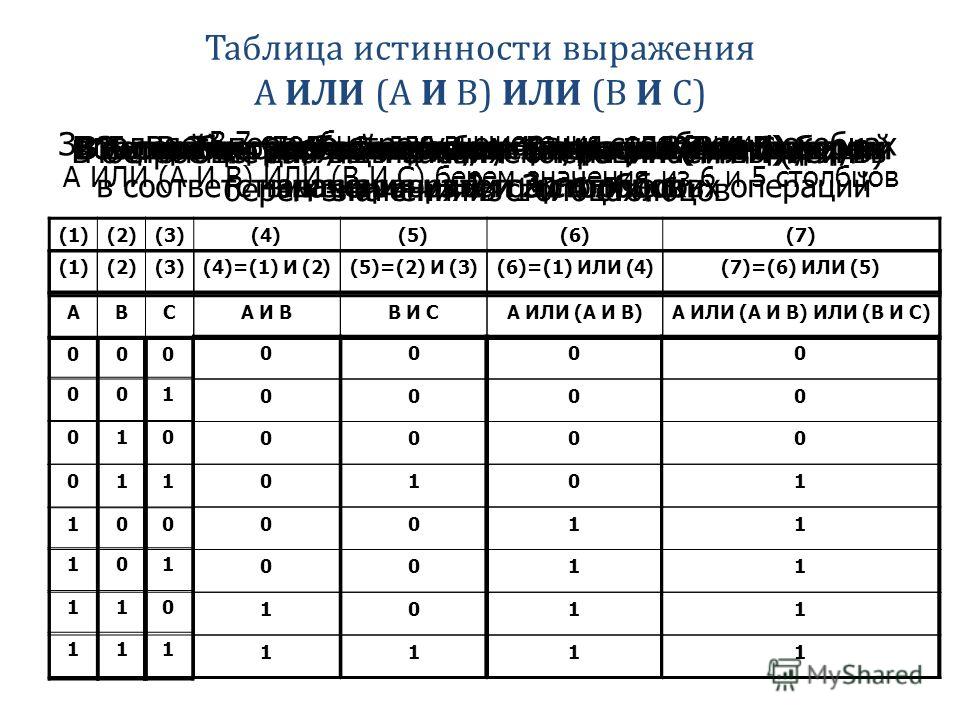

Затем выполнить все задания, представленные ниже.

Список индивидуальных данных

Задание 1. Найти значения логического выражения:

1.	(1 V 1) V (1 V 0)	7.	(1 V 0) & (1 V 0) & (1 → 0)
2.	((0 & 1) & 1) л 0 V 1	8.	﹁(1 & 1 V 0) ↔ (﹁1 V 1)
3.	((1 V 0) & (1 & 1)) & (0 V 1)	9.	((1 V 0) л (1 & 1)) л (0 л 1)
4.	(0 V 1) → (1 & 1)	10.	((0 V 1) & 1) л 0 V 1
5.	(1 & 1 V 0) ↔ (﹁1 & 1)	11.	(1 V ﹁1) & (1 л 0)
6.	﹁((1 → 0) ↔ (1 & 1) V 1)	12.	((1 → 0) ↔ (1 л 1) V 1)

Задание 2. Поставить знак конъюнкции или дизъюнкции вместо знака «?» (если это возможно), чтобы логическое выражение при любых значениях а и в всегда принимала значение «истина»:

1.	(а V в)? (﹁в V в)	7.	(﹁а V а)? (﹁в V ﹁в)
2.	(а V а) ? (﹁в V а)	8.	(а л а) ? (﹁в л ﹁в)
3.	(а л а) ? (﹁в V в)	9.	(﹁а л ﹁а)? (﹁в л ﹁в)
4.	(﹁а л ﹁а)? (﹁в V в)	10.	(в V в) ? (а л а)
5.	(а л а) ? (﹁в V ﹁в)	11.	(﹁а V ﹁а)? (﹁в V ﹁в)
6.	(﹁в л ﹁в)? (﹁а V в)	12.	(в л ﹁а) ? (а V ﹁в)

Задание 3. Для исходной логической функции построить таблицу истинности:

1.	(А V В) & (А V С) & (В → С)	7.	(С V ﹁А) V (﹁В V А)
2.	((А & С) & ﹁В) V (В & А)	8.	(﹁А & В V С) ↔ ﹁(В V А)
3.	((С V ﹁В) & (А & С)) & (А V В)	9.	((В V В) л (С & С)) л (А л С)
4.	((В V А) & А) л (С V ﹁С)	10.	(В & В) → ((А & А) л (С&﹁С))
5.	(С & ﹁А) V (﹁В & А)	11.	(А & В V А) ↔ ( С & ﹁С)
6.	((В л С) & (﹁А л А)) & (С V ﹁В)	12.	((﹁А → В) ↔ (С л С) V В)

Пример выполнения работы

Задание 1. Найти значения логического выражения:

(﹁0 V ﹁1) л (1 л 0) = (1 V 0) л 0= 1 л 0 = 0.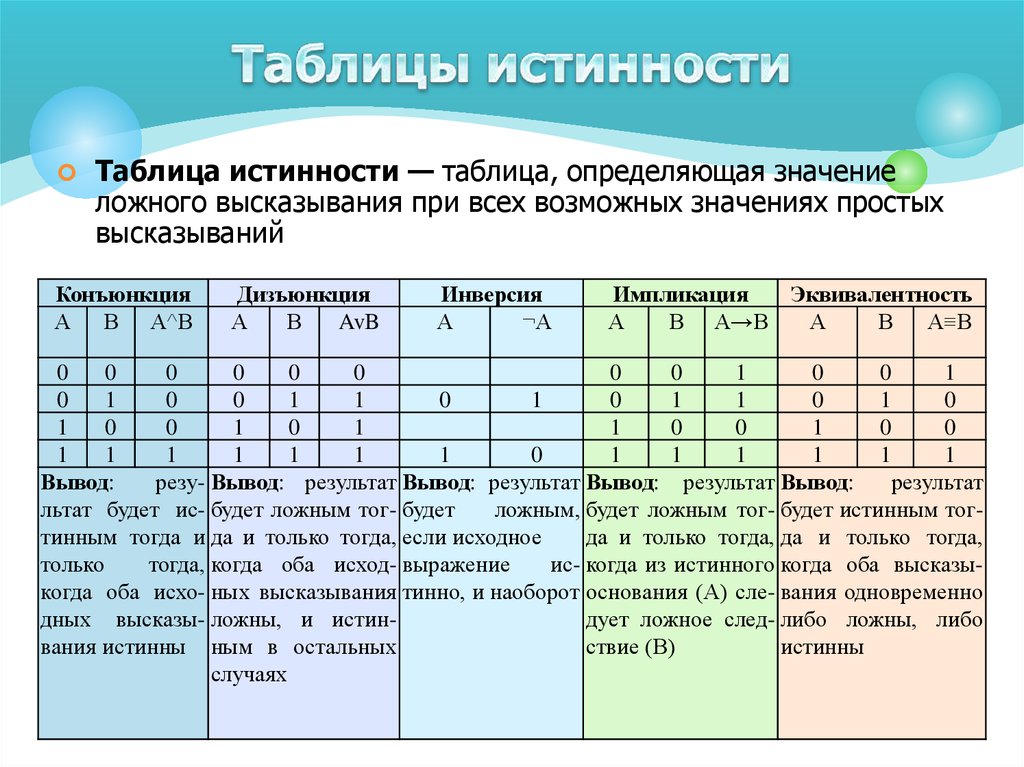

Ответ: 0.

Задание 2. Поставить знак конъюнкции или дизъюнкции вместо «?», если это возможно, чтобы логическое выражение при любых значениях а и в всегда принимала значение «истина».

(а л а) ? (﹁в л ﹁в): а л а.

Ответ: а л а.

Задание 3. Для исходной логической функции построить таблицу истинности.

((А & В) → (А → С)) V А.

1) Необходимо внести в таблицу возможные наборы значений исходных логических переменных А, В, С.

2) Определить последовательность выполнения логических операций (приоритет).

3) Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

А	В	С	А & В	А → С	(А & В) → (А → С)	((А & В) → (А → С)) V А
0	0	0	0	1	1	1
0	0	1	0	1	1	1
0	1	0	0	1	1	1
1	0	0	0	0	1	1
0	1	1	0	1	1	1
1	1	0	1	0	0	1
1	0	1	0	1	1	1
1	1	1	1	1	1	1

Контрольные вопросы к защите

Для чего предназначены таблицы истинности?
Что такое высказывание?
Установите приоритет следующим логическим операциям: дизъюнкция, инверсия, конъюнкция.
Приведите пример ложного высказывания.
Приведите пример истинного высказывания.

О таблицах истинности — Таблицы истинности

A Таблица истинности — это тип правила, которое сравнивает пользовательские данные с несколькими комбинациями входных данных, используемых в условиях, для вывода правильного результата или результата. Каждая строка настроена с несколькими правилами операторов на основе входных данных, используемых в таблице истинности. Эти Правила оператора затем приводят к набору результатов. Если в таблице истинности возвращено несколько строк, будут разные комбинации, которые логика будет оценивать при сравнении входных данных пользователя.

Столбцы представляют данные ввода/вывода в каждой строке. Например, таблица истинности с именем и адресом электронной почты в качестве входных данных будет иметь один столбец для правила утверждения имени и другой для адреса электронной почты, а затем столбец результатов для этой строки.

На приведенном ниже снимке экрана Марка, Модель и Год являются входными данными для Правила с условиями, настроенными для каждой строки. Вводимые пользователем данные сравниваются с каждой строкой, чтобы найти строку, в которой данные соответствуют критериям, которые затем выводят соответствующие данные.

Правило возврата данных (множественный, составной тип) : Создает новый тип данных на основе полей, указанных в возвращаемых данных. Это позволяет разработчику динамически создавать типы данных для вывода таблицы истинности на основе определенных полей.

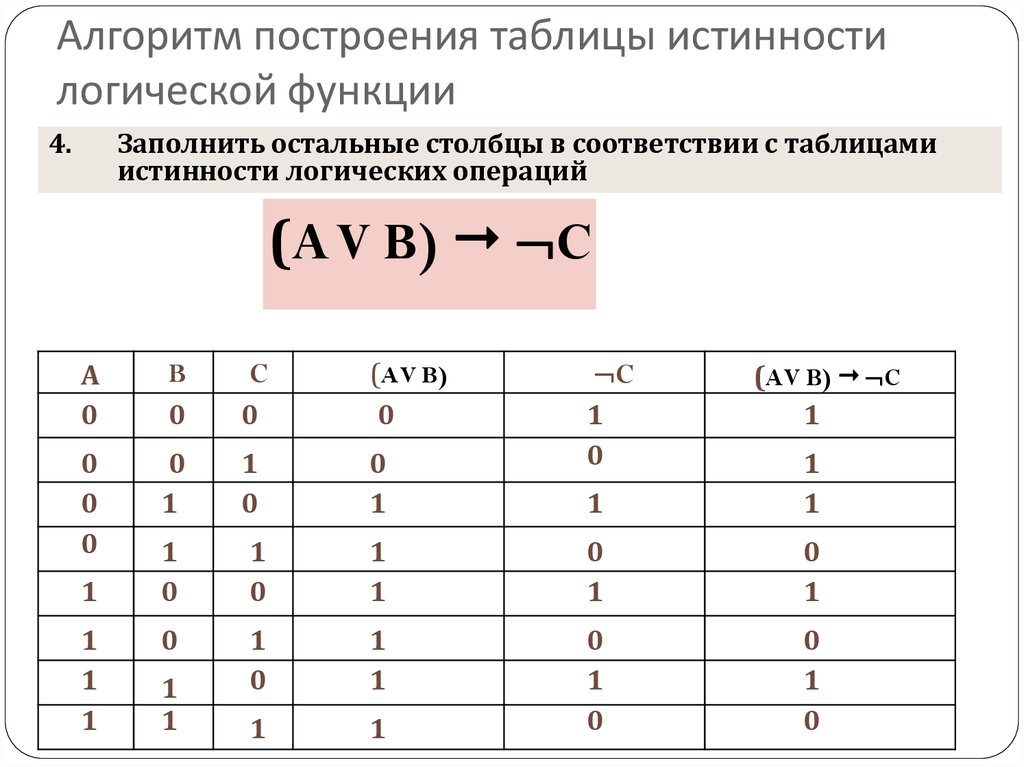
Таблицы истинности можно использовать для самых разных вариантов использования. Таблицы истинности лучше всего использовать для случаев, в которых используются правила , в которых используются вложенные операторы «если».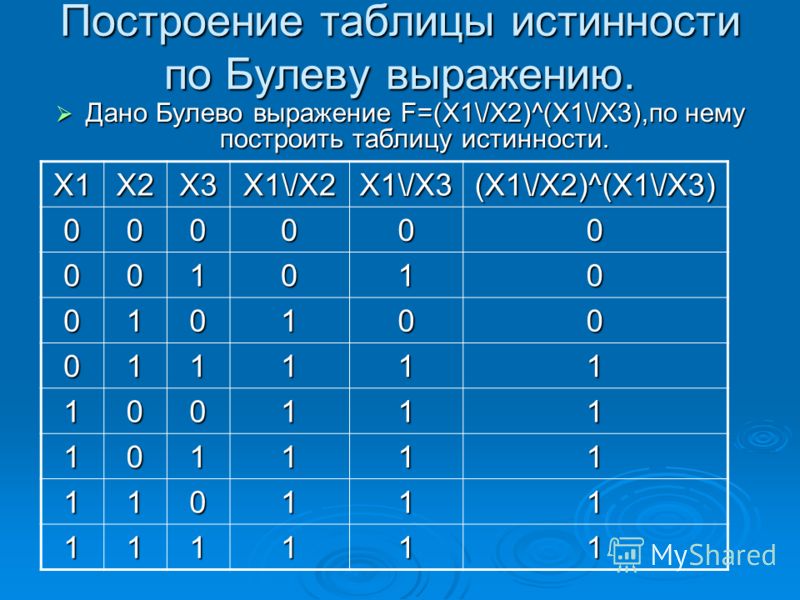 Одна из таких реализаций может включать проверку данных, таких как оценка того, когда следует утвердить аренду автомобиля для компании, путем просмотра времени аренды автомобиля, стоимости для компании и должности лица, запрашивающего аренду. Таким образом, если запрос сделан человеком X, и если он арендован на X дней и стоит компании X долларов, то запрос будет одобрен.

Благодаря тому, что их можно создавать с использованием внутренних или внешних данных, они могут быть полезны для отслеживания данных, относящихся к Системе и/или Учетным записям этой Системы, таким как разрешения Учетной записи. Этого можно добиться, оценив конкретное разрешение в качестве входных данных и сравнив его с учетными записями в системе, которые имеют эти разрешения в качестве выходных данных. Это может быть введено статически через конструктор правил или динамически путем создания таблицы истинности извне через отчет.

Была ли эта статья полезной?
Что дальше
Действия таблицы истинности
Введение в таблицы истинности, утверждения и коннективы
Поиск
Таблица истинности — это одна из тех вещей в математике, которую гораздо легче понять, когда вы видите, как она выглядит и как она работает, чем изучать ее определение. В любом случае, мы попытаемся дать ему определение, чтобы иметь базовое или базовое понимание того, что это такое.
Определение таблицы истинности
В математической логике таблица истинности представляет собой диаграмму строк и столбцов, показывающую истинностное значение (либо «T» для «Истина», либо «F» для «Ложь») каждой возможной комбинации заданные операторы (обычно представленные заглавными буквами P, Q и R), управляемые логическими связками.
Два компонента таблицы истинности
I. Утверждение
Определение: Утверждение — это предложение или математическое выражение, которое либо определенно истинно, либо определенно ложно, но не то и другое одновременно. Обычно обозначается заглавной буквой или переменной. Обычными являются P, Q, R и S.
II. Логическая связка
Определение : Логическая связка — это слово, обычно записываемое как символ, который несет определенную логическую инструкцию о том, как выполнять оператор или составной оператор.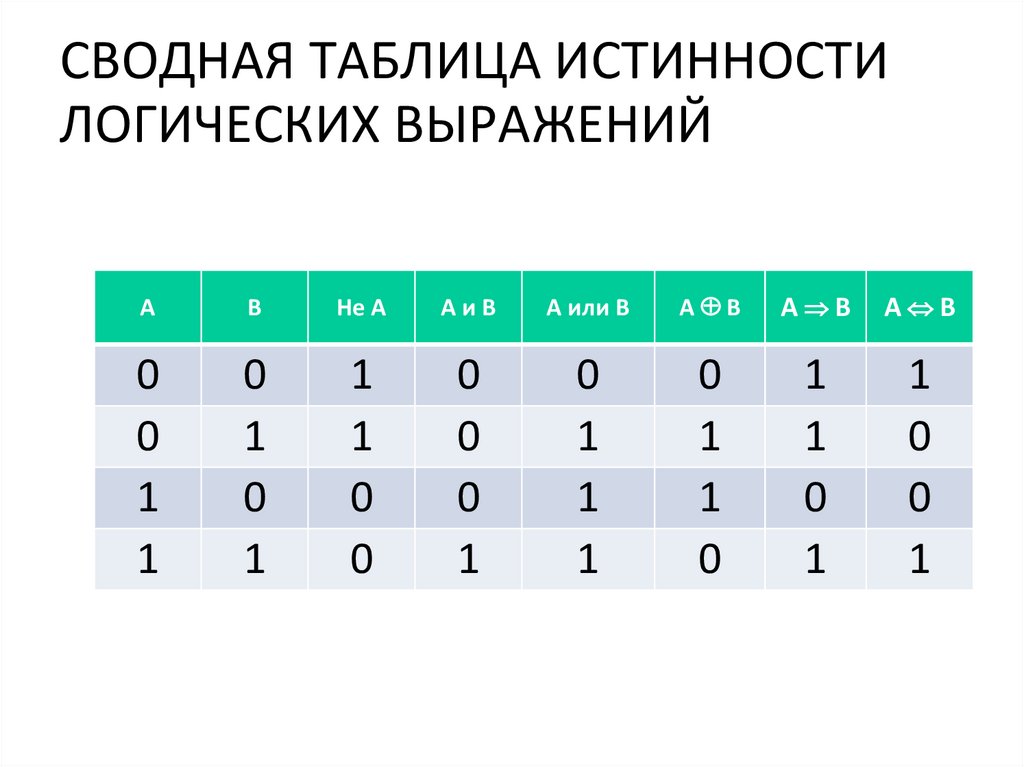 Логические связки также можно использовать для соединения или объединения двух или более утверждений для формирования нового утверждения.
Примеры утверждений
Утверждения, которые определенно верны.
Заведомо ложные утверждения.
ОТКРЫТОЕ ПРЕДЛОЖЕНИЕ
Открытое предложение — это предложение, которое является либо истинным, либо ложным в зависимости от значения переменной (переменных). Этот тип предложения НЕ является утверждением, потому что оно должно быть определенно истинным или определенно ложным.
Примеры:
Число \color{red}k четно.
Обратите внимание, предложение истинно, если k=4, или ложно, если k=7. Поскольку истинность предложения может быть истинной или ложной в зависимости от значения переменной k, то это открытое предложение и, следовательно, не высказывание. 92=0. Помните, что 0 не является ни положительным, ни отрицательным. Таким образом, это предложение НЕ высказывание, а простой падеж открытого предложения.
Общие логические связки
В этой части урока моя цель — кратко познакомить вас с пятью общими логическими связками , которые также известны как логические операторы. Вы также узнаете символ, используемый для каждого оператора, и что он означает.
Примечание: \large{P} и \large{Q} являются операторами.
1) Отрицание
Символ: ~ или \neg читается как НЕ
Пример: ~P или \neg P переводится как «не P» или «неверно, что P»
2 ) Соединение
Символ: \клин читается как И
Пример: P \клин Q переводится как «P и Q»
читается как ИЛИ
Пример: P \vee Q переводится как «P или Q“
4) Импликация или условность
Символ: \Стрелка вправо читается как ПОДРАЗУМЕВАЕТ
Пример: P \Стрелка вправо Q обозначает утверждение «P подразумевает 90 184 Q» 90 Двойная импликация или биусловие
Символ: \Leftrightarrow читается как ЕСЛИ И ТОЛЬКО ЕСЛИ
Пример: P \Leftrightarrow Q означает утверждение «P тогда и только тогда, когда Q»
Таблицы истинности для отрицания, соединения , и дизъюнкция
Я намерен охватить только три основных логических оператора, а именно: отрицание , конъюнкция и дизъюнкция . В этой части урока вы познакомитесь с тем, как может выглядеть таблица истинности.
У меня есть отдельный урок, в котором подробно обсуждается, как строить таблицы истинности упомянутых здесь логических связок и остальных.
А пока давайте сосредоточим наше внимание на приведенных ниже таблицах истинности:
1. Таблица истинности отрицания
Правило логического оператора отрицания
Значение истинности инвертированного утверждения полностью противоположно истинному значению исходного утверждения.
2. Таблица истинности конъюнкции
Правило конъюнкции или логического оператора «И»
Составное высказывание P и Q, записанное как P \wedge Q, является ИСТИННЫМ, если высказывания P и Q равны и истинный. В противном случае утверждение P\wedge Q является ЛОЖНЫМ.
3. Таблица истинности дизъюнкции
Правило дизъюнкции или логический оператор «ИЛИ»
Составное утверждение P или Q, записанное как P \vee Q, является ИСТИННЫМ, если хотя бы одно из утверждений P и Q истинно.