Что такое дополнение до двух. Как работает дополнение до двух. Зачем нужно дополнение до двух. Как представляются положительные и отрицательные числа в памяти компьютера. Какие преимущества дает использование дополнения до двух.
Что такое дополнение до двух
Дополнение до двух — это способ представления целых чисел со знаком в двоичной системе счисления. Это наиболее распространенный метод представления отрицательных чисел в компьютерах. Дополнение до двух позволяет использовать одну и ту же схему для выполнения сложения и вычитания как положительных, так и отрицательных чисел.
Как работает дополнение до двух
Принцип работы дополнения до двух следующий:
- Положительные числа представляются обычным двоичным кодом, с 0 в старшем бите.
- Для получения представления отрицательного числа нужно:
- Взять абсолютное значение числа в двоичном виде
- Инвертировать все биты (заменить 0 на 1 и наоборот)
- Прибавить 1 к результату
- Старший бит используется как знаковый — 0 для положительных чисел, 1 для отрицательных.
Примеры представления чисел в дополнительном коде
Рассмотрим, как будут представлены числа в 8-битном формате с использованием дополнения до двух:
- +5: 00000101
- -5: 11111011
- +1: 00000001
- -1: 11111111
- 0: 00000000
Как видно, положительные числа представлены обычным двоичным кодом, а отрицательные получены путем инвертирования и прибавления единицы.
Зачем нужно дополнение до двух
Использование дополнения до двух дает ряд преимуществ:
- Упрощает схемы сложения и вычитания чисел в компьютере
- Позволяет использовать одни и те же схемы для операций с положительными и отрицательными числами
- Исключает необходимость хранить знак числа отдельно
- Обеспечивает уникальное представление нуля (в отличие от прямого кода)
Диапазон представимых чисел
При использовании n бит для представления числа в дополнительном коде, диапазон представимых значений составляет от -2^(n-1) до 2^(n-1) — 1.
Например, для 8-битных чисел:
- Минимальное число: -128 (10000000 в двоичной системе)
- Максимальное число: 127 (01111111 в двоичной системе)
Особенности арифметики в дополнительном коде
При выполнении арифметических операций с числами в дополнительном коде нужно учитывать следующие особенности:
- Сложение выполняется обычным образом, игнорируя перенос из старшего разряда
- Вычитание заменяется сложением с дополнительным кодом вычитаемого
- При переполнении результат может быть некорректным
Преимущества дополнения до двух перед другими методами
По сравнению с другими методами представления отрицательных чисел (например, прямым или обратным кодом), дополнение до двух имеет ряд преимуществ:
- Единственное представление нуля (в отличие от прямого кода)
- Симметричный диапазон представимых чисел
- Простота реализации арифметических операций
- Отсутствие необходимости в дополнительной логике для обработки знака
Как выполняется сложение в дополнительном коде
Сложение чисел в дополнительном коде выполняется так же, как и обычное двоичное сложение. Рассмотрим пример:
Сложим числа 5 и -3 в 8-битном представлении:
- 5: 00000101
- -3: 11111101
Складываем эти числа:
00000101 + 11111101 ----------- 00000010
Результат: 00000010, что соответствует числу 2 в десятичной системе. Как видим, 5 + (-3) = 2, что верно.
Ограничения и проблемы дополнения до двух
Несмотря на все преимущества, у метода дополнения до двух есть некоторые ограничения:
- Ограниченный диапазон представимых чисел
- Возможность переполнения при арифметических операциях
- Сложность интуитивного понимания представления отрицательных чисел
Как решается проблема переполнения при использовании дополнения до двух? В большинстве современных процессоров реализованы специальные флаги, которые устанавливаются при возникновении переполнения. Программист может проверять эти флаги и предпринимать соответствующие действия.
Применение дополнения до двух в современных компьютерах
Дополнение до двух широко используется в современных компьютерных системах. Вот несколько примеров его применения:
- Представление целых чисел со знаком в большинстве языков программирования
- Реализация арифметико-логических устройств в процессорах
- Обработка аудио и видео сигналов в цифровой форме
- Реализация алгоритмов машинного обучения и компьютерного зрения
Понимание принципов работы дополнения до двух важно для разработчиков низкоуровневого программного обеспечения, специалистов по цифровой обработке сигналов и инженеров-электронщиков.
Что такое «Дополнение 2»?
Как и большинство объяснений, которые я видел, приведенные выше ясно показывают, как работать с дополнением 2, но на самом деле не объясняют, что это такое математически. Я постараюсь сделать это, по крайней мере, для целых чисел, и расскажу о некоторой предыстории, которая, вероятно, будет знакома первой.
Вспомните, как работает десятичное число:
2345
— это способ записи
2 × 10 3 + 3 × 10 2 + 4 × 10 1 + 5 × 10 0 .
Таким же образом, двоичный код — это способ записи чисел, использующий только 0 и 1, следуя той же общей идее, но заменяя те 10, которые указаны выше, на 2. Затем в двоичном коде
1111
является способом записи
1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0,
и если вы решите это, получится равным 15 (основание 10).
Это потому что
8 + 4 + 2 + 1 = 15.
Это все хорошо и хорошо для положительных чисел. Это даже работает для отрицательных чисел, если вы хотите просто поставить знак минус перед ними, как люди делают с десятичными числами. Это даже можно сделать с помощью компьютеров, но я не видел такого компьютера с начала 1970-х годов. Я оставлю причины для другого обсуждения.
Для компьютеров оказывается более эффективным использовать дополнение для отрицательных чисел. И вот кое-что, что часто упускается из виду. Обозначения дополнения включают в себя некоторый вид обращения цифр числа, даже подразумеваемых нулей, которые предшествуют нормальному положительному числу. Это неловко, потому что возникает вопрос: все они? Это может быть бесконечное количество цифр для рассмотрения.
К счастью, компьютеры не представляют бесконечности. Числа ограничены определенной длиной (или шириной, если вы предпочитаете). Итак, давайте вернемся к положительным двоичным числам, но с определенным размером.
Я буду использовать 8 цифр («бит») для этих примеров. Таким образом, наше двоичное число будет действительно
00001111
или
0 × 2 7 + 0 × 2 6 + 0 × 2 5 + 0 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
Чтобы сформировать отрицание дополнения 2, мы сначала добавляем все (двоичные) цифры в форму
и добавляем 1 к форме
11110001
но как нам понять, что это означает -15?
Ответ в том, что мы меняем значение старшего бита (самого левого). Этот бит будет 1 для всех отрицательных чисел. Изменение будет состоять в том, чтобы изменить знак своего вклада в значение числа, в котором он появляется. Итак, теперь наш 11110001, как предполагается , представляет
— 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
Заметьте, что «-» перед этим выражением? Это означает, что знаковый бит имеет вес -2 7 , то есть -128 (основание 10).
Все остальные позиции сохраняют тот же вес, что и в двоичных числах без знака.
Выработка нашего -15, это
-128 + 64 + 32 + 16 + 1
Попробуйте на своем калькуляторе. это -15.
Из трех основных способов, с помощью которых я видел отрицательные числа, представленные в компьютерах, дополнение 2 выигрывает для удобства в общем использовании. Это странно, хотя. Поскольку это двоичный код, должно быть четное количество возможных битовых комбинаций. Каждое положительное число может быть соединено с его отрицательным, но есть только один ноль. Отрицание нуля дает вам ноль. Так что есть еще одна комбинация, число с 1 в знаковый бит и 0 везде. Соответствующее положительное число не будет соответствовать количеству используемых битов.
Что еще более странно в этом числе, так это то, что если вы попытаетесь сформировать его положительное число, дополнив и добавив одно, вы получите то же отрицательное число обратно. Кажется естественным, что ноль сделал бы это, но это неожиданное и совсем не то поведение, к которому мы привыкли, поскольку помимо компьютеров мы обычно думаем о неограниченном количестве цифр, а не об этой арифметике фиксированной длины.
Это как верхушка айсберга странностей. Под поверхностью еще больше подстерегает, но этого достаточно для обсуждения. Возможно, вы найдете больше, если исследуете «переполнение» для арифметики с фиксированной точкой. Если вы действительно хотите войти в это, вы можете также исследовать «модульную арифметику».
Коды двоичных чисел
В принципы работы вычислительных машин заложен принцип двоичного кодирования: все данные представлены в виде закодированных некоторым образом двоичных чисел. коды двоичных чисел необходимы для того, чтобы производить над данными логические и арифметические операции.
В статье «Системы счисления» мы рассматривали только положительные числа. При записи двоичных чисел со знаком
в их формате необходимо предусмотреть два поля: поле, определяющее знак числа, и поле, характеризующее модуль числа.
Под знак числа отводится специальный знаковый бит (двоичный разряд). Остальные разряды определяют
модуль числа.
В истории развития компьютеров использовались три основных варианта представления знаковых чисел:
- прямой код или знак и величина;
- обратный код или код с дополнением до единицы;
- дополнительный код или код с дополнением до двух.
Во всех трёх кодах положительные числа выглядят одинаково. Различия в форме записи отрицательных чисел в обратном и дополнительном кодах касаются только способа представления модуля числа, а способ кодирования и место расположения знакового бита остаются неизменными.
В системе представления в прямом коде число состоит из кода знака и модуля числа, причём обе эти части обрабатываются по отдельности.
Примеры прямого кода для правильных дробей:
Примеры прямого кода для целых чисел:
Представление чисел в прямом коде имеет существенный недостаток — формальное
суммирование чисел с различающимися знаками даёт неверный результат.
Пример — сложение двух чисел
и .
В прямом коде эти числа имеют вид: и .
Очевидно, что результат должен быть равен -2, что в прямом коде может быть записано как 1.010. В
то же время при непосредственном сложении получаем
,
Процедура для корректного сложения чисел в прямом коде всё же существует, но она очень громоздка. Прямой код имеет ещё один недостаток — нуль имеет два различных представления, а именно и , что математически не имеет смысла.
По причине отмеченных недостатков в вычислительных машинах используется не прямой код, а обратный и дополнительный коды.
В этих системах кодирования чисел место расположения знакового разряда и способ кодирования
остаются теми же, что и в прямом кодировании. Однако знаковый разряд уже не рассматривается как обособленный,
а считается неотъемлемой частью числа аналогично разрядам модуля числа и совместно с ними.
Для отрицательных двоичных чисел процедура получения обратного кода следующая: в знаковой разряд записывается единица, а в цифровых разрядах прямого кода единицы заменяются нулями, а нули единицами.
Примеры обратного кода для правильных дробей:
.
Примеры обратного кода для целых чисел:
.
Как нетрудно заметить, положительные числа в прямом и обратном кодах выглядят одинаково.
Хотя обратный код и позволяет решить проблему сложения и вычитания чисел с различными знаками, он имеет и недостатки. Во-первых, процесс суммирования чисел является двухэтапным, что увеличивает время выполнения этой операции. Во-вторых, как и в прямом коде, в обратном — два представления нуля: и .
Дополнительный код отрицательного двоичного числа
формируется по следующему правилу: в цифровых разрядах прямого кода единицы заменить нулями, а нули —
единицами, после чего к младшему разряду прибавить единицу.
Для примера рассмотрим число X, которое в прямом коде имеет вид:
.
Тогда обратный код можно записать как
.
Для получения дополнительного кода прибавим 1 к младшему разряду обратного кода:
.
Примеры дополнительного кода для правильных дробей:
.
Примеры дополнительного кода для целых чисел:
.
Положительные числа в дополнительном коде записываются так же, как и в прямом. При представлении чисел в дополнительном коде есть только одна форма записи нуля: 0.0…00, причём ноль считается положительным числом, так как его знаковый бит равен 0.
В большинстве вычислительных машин отрицательные числа представлены в дополнительном коде.
Сложение и вычитание чисел в обратном и дополнительном кодах
Вычитание производится как сложение чисел, одно из которых с отрицательным знаком.
При выполнении алгебраического сложения знаковый разряд и цифры модуля рассматриваются как единое целое и обрабатываются совместно. Перенос из старшего (знакового) разряда в обратном и дополнительном кодах учитывается по-разному. В случае обратного кода единица переноса из знакового разряда прибавляется к младшему разряду суммы. При использовании дополнительного кода единица переноса из знакового разряда отбрасывается.
Пример 1. Сложить числа и
При использовании обратного кода получим:
При использовании дополнительного кода получим:
Если знаковый разряд результата равен нулю, это означает, что получено положительное число,
которое выглядит так же, как и в прямом коде. Единица в знаковом разряде означает, что результат отрицательный
и его запись соответствует представлению в том коде, в котором производилась операция.
Дополнение — число — Большая Энциклопедия Нефти и Газа, статья, страница 1
Дополнение — число
Cтраница 1
Дополнение числа 011111012 до числа 2 образуется путем прибавления 1 к обратному коду числа. [1]
Образование дополнения числа до двух осуществляется простым прибавлением единицы к дополнению его до единицы. [2]
Операцию получения дополнения числа В выполняют просто, если предварительно найти обратный код этого числа В. Обратный код В получают заменой во всех разрядах числа В цифры 0 на 1 и наоборот. [3]
Для образования дополнения Af-разрядного числа до величины 2N необходимо инверсное значение кода числа увеличить на единицу младшего разряда. [5]
Для образования дополнения отрицательного д-разряд-ного числа до величины 2п необходимо инверсное значение кода числа увеличить на единицу младшего разряда.
[7]
Комплементное число и арифметическое дополнение числа принято рассматривать как код отрицательных чисел. [8]
Мы видим, что дополнение числа до десяти всегда на единицу больше его дополнения до девяти. В основном дополнения до девяти используют для формирования дополнения до десяти. [9]
Обратный код используется при формировании дополнения вычитаемого числа для замены вычитания сложением. [10]
Как видим, дополнительный код совпадает с арифметическим дополнением числа и не выходит за пределы разрядной сетки машины. [11]
При этом необходимо иметь в виду, что дополнение числа до 10 ( два, двоичное число) равно его дополнению до единицы плюс единица. [12]
При этом необходимо иметь в виду, что дополнение числа до двух можно получить, беря дополнение каждого разряда двоичного числа до единицы и добавляя затем единицу в младший разряд.
Это дает возможность получать дополнение до единицы, в каждом двоичном разряде простым обращением ( инверсией) этих разрядов.
[13]
Дополнительный код лежит в пределах разрядной сетки машины и совпадает с арифметическим дополнением числа. В этом коде вычитание заменяется сложением с кодом числа. [14]
Если нужно сбросить восьмой бит, можно использовать побитовую операцию И с дополнением числа 128 до единицы. При выполнении побитовой операции И с этими числами исходное число не изменяется, за исключением восьмого разряда, который сбрасывается в нуль. [15]
Страницы: 1 2 3
Отрицательные числа
Главная / Ассемблер / Для чайников / Введение / Представление данных /
Мы разобрались, как в памяти компьютера представлены
положительные числа,
то есть числа без знака.
Но ведь числа бывают и отрицательными, то есть числа со знаком минус.
Чтобы применять те же самые байты и слова для представления отрицательных чисел,
существует специальная операция, которая называется
дополнение до двух. Но прежде чем рассмотреть эту операцию, покажем,
как отрицательное число отличить от положительного.
Для того чтобы указать знак числа, достаточно одного разряда (бита). Обычно знаковый бит занимает старший разряд числа. Если старший бит числа равен 0, то число считается положительным. Если старший разряд числа равен 1, то число считается отрицательным. Пример байта со знаком приведён на рис. 2.3.
| Разряды | Число | |||||||
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | -110 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | +110 |
Рис.
2.3. Отрицательное число в памяти компьютера.
Как вы успели заметить, для представления числа со знаком требуется использовать старший бит для определения знака числа. Это означает, что этот старший бит уже нельзя использовать для записи самого числа, то есть максимальное значение, которое мы сможем записать в байт, будет уже не 255, а всего 127. Диапазоны возможных значений чисел со знаком приведены в таблице 2.5.
Таблица 2.5. Диапазоны возможных значений чисел со знаком.
| Тип числа | Диапазон значений | Степени двойки |
| Байт | –128…+127 | -27…(27 – 1) |
| Слово | –32 768…+32 767 | -215…(215 – 1) |
| Двойное слово | –2 147 483 648… +2 147 483 647 |
-231…(231 – 1) |
| Учетверённое слово | –9 223 372 036 854 775 808… +9 223 372 036 854 775 807 |
-263…(263 – 1) |
А теперь разберёмся с загадочной операцией дополнение до двух.
Для изменения знака числа выполняется инверсия, то есть для числа
в двоичном представлении все нули заменяются единицами, а все единицы – нулями.
Затем к полученному результату прибавляют 1. Возьмём, например, десятичное число 110
(в двоичной системе это число 01101110). Тогда
| Исходное число | 0110 | 1110 |
| Инверсия | 1001 | 0001 |
| Прибавляем 1 | 1001 | 0010 |
Как видим, после выполнения этих преобразований в старшем разряде у нас 1,
то есть число отрицательное. А теперь проверим, что это число действительно отрицательное.
Как это сделать? Вспомним, что (–110 + 110 = 0). То есть сложение полученных нами
двоичных чисел тоже должно дать в результате ноль.
Итак
01101110 + 10010010 = 100000000То есть у нас получилось девятиразрядное число 100000000 (десятичное 256). Однако мы работаем с байтом, а в байте, как известно, только 8 бит (от 0 до 7). То есть единица у нас перешла в 8-й бит, которого в байте попросту нет. То есть для байта это эквивалентно числу 0.
В некоторых источниках дополнение до двух носит название двоичный дополнительный код.
Подведём итоги
Преобразования положительного десятичного числа со знаком в двоичное число выполняется также как и для чисел без знака.
Преобразования отрицательного десятичного числа со знаком в отрицательное двоичное число выполняется при помощи операции дополнение до двух (с использованием двоичного дополнительного кода). То есть сначала число преобразовывается в двоичное, а потом используется двоичный дополнительный код.
Преобразования положительного двоичного числа со знаком (в старшем бите 0) в десятичное
число выполняется также как и для чисел без знака.
Преобразование отрицательного двоичного числа (в старшем бите 1) в десятичное число выполняется путём нахождения его дополнительного кода. То есть для двоичного числа 10010010 операция будет следующей:
| Исходное число | 1001 | 0010 |
| Инверсия | 0110 | 1101 |
| Прибавляем 1 | 0110 | 1110 |
В итоге получаем число 110, но поскольку в исходном числе старший бит был равен 1, то это отрицательное число, то есть –110.
binary — Дополнение до двух наиболее отрицательного числа
Я сомневаюсь, как поступить с самым отрицательным числом в представлении с дополнением до двух. Для простоты я опишу проблему в 1-байтовом представлении. Самое положительное число
01111111
Что равно 127 в десятичной системе.
Его дополнение до двух легко вычислить. Просто меняя биты, которые мы получаем
10000000
Затем добавьте единицу
10000001
Что равно -127 в десятичной системе счисления. Нулевое число ведет себя особым образом, поскольку оно является двойным дополнением самого себя, что хорошо известно. Однако у меня были трудности, когда я увидел, что самое отрицательное число также дополняет само себя. Самый отрицательный результат — -128, что составляет 10000000. Дополнение — 01111111. И если мы добавим единицу, мы получим 10000000, что, конечно же, неверный результат. У меня вопрос, если этот номер никогда не используется или никогда не достигается
0
Fabio Paolini 7 Фев 2021 в 22:19
1 ответ
Лучший ответ
Его используют, но в каком-то смысле это «самое странное число».
Иногда его выбирают не использовать или зарезервировать для указания состояния ошибки. Это просто соглашения, которые иногда используются, нет ничего, что препятствует нормальному использованию наиболее отрицательного целого числа. Во многих случаях число не будет инвертировано, и тогда это особое свойство просто не появится.
Это странное свойство двух дополнительных целых чисел означает, что в некоторых сценариях, где принято брать абсолютное значение и вычислять с неотрицательными числами, имеет смысл вместо этого брать отрицательное абсолютное значение (которое отрицает положительное входы, а не отрицательные входы) и вычислить с неположительными числами. Это помогает, потому что обычное абсолютное значение имеет причуду, заключающуюся в том, что самое отрицательное целое число не имеет положительного эквивалента, но для положительных чисел такой особенности нет, поэтому все они могут быть безопасно отвергнуты. Этот прием не всегда применим.
-128 отрицание самого себя — не всегда что-то плохое.
Несмотря на кажущийся неверным результат, по-прежнему (с использованием стандартного определения сложения) x + (-x) = 0 для всех значений , включая -128, так что это алгебраически разумно. Он также, по крайней мере, в некоторой степени разумно взаимодействует с принятием абсолютного значения: хотя верно, что abs(x) может таким образом дать отрицательный результат (что часто нежелательно), переинтерпретация результата как беззнакового числа того же размера делает результат правильный, (unsigned 8 bit)abs(-128) = 128.
Наиболее отрицательное целое число относительно часто используется в коде битовой манипуляции. Здесь его арифметические свойства менее важны, что делает число «менее странным».
0
harold 7 Фев 2021 в 20:11
Дополнительный код (представление числа) — это.
.. Что такое Дополнительный код (представление числа)?Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2N для N-битного дополнения до 2).
Представление отрицательного числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым.
Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно , что равно 127.
Примеры:
| Десятичное представление | Код двоичного представления (8 бит) | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 01111111 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | — |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -7 | 10000111 | 11111000 | 11111001 |
| -8 | 10001000 | 11110111 | 11111000 |
| -9 | 10001001 | 11110110 | 11110111 |
| -10 | 10001010 | 11110101 | 11110110 |
| -11 | 10001011 | 11110100 | 11110101 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | — | — | 10000000 |
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1.
Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) | 10-ричная система счисления, дополнительный код |
|---|---|
| … | … |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| … | … |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| … | … |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
. .. | … |
Преобразование в дополнительный код
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
- Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
- Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
101
Инвертируем все разряды числа, получая таким образом обратный код:
010
Добавим к результату 1
011
Допишем слева знаковый единичный разряд
1011
Для обратного преобразования используется тот же алгоритм. А именно:
1011
Инвертируем все разряды числа, получая таким образом обратный код:
0100
Добавим к результату 1 и проверим, сложив с дополнительным кодом
0101 + 1011 = 10000, пятый разряд выбрасывается.
p-адические числа
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000… (1) равно 4444…. (−1).
Реализация алгоритма преобразования в обратный код (для 8-битных чисел)
Pascal
if a<0 then a:=((not a) or 128) + 1;
C/C++
if (a < 0) a = ( (~(-a))|128 ) + 1;
Преимущества и недостатки
Преимущества
- Один и тот же регистр может хранить как n-битовое положительное число, так и (n−1)-битовое число со знаком, с общими для обоих форматов операциями сложения, вычитания и левого сдвига.
- Более удобная упаковка чисел в битовые поля.
- Отсутствие числа «минус ноль».
Недостатки
- Дополнительный код неочевиден для новичков.
- В сложных форматах (таких, как плавающая запятая или двоично-десятичный код) большинство преимуществ аннулируются.
- Модуль наибольшего числа не равен модулю наименьшего числа. Пример: знаковое целое 8-битовое. Максимальное число: 12710 == 7F16 == 011111112. Минимальное число: -12810 == 8016,дополнительный код == 100000002,дополнительный код. Соответственно, не для любого числа существует противоположное. Операция изменения знака может потребовать дополнительной проверки.
- Сравнение. В отличие от сложения, числа в дополнительном коде нельзя сравнивать, как беззнаковые, или вычитать без расширения разрядности. Один из методов состоит в сравнении как беззнаковые исходных чисел с инвертированным знаковым битом.
Пример программного преобразования
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными. b2) — c; //Результат остаётся 121, потому что знаковый разряд — нуль.
См. также
Литература
- Behrooz Parhami 2.3. Complement Representation, 2.4. Two’s- and 1’s-complement numbers // Computer Arithmetic: Algorithms and Hardware Designs. — New York: Oxford University Press, 2000. — P. 22-27. — 510 p. — ISBN 0-19-512583-5
- Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К.: Вища школа, 1987. — 375 с.
Ссылки
- ↑ К.Г.Жуков «Справочное руководство пользователя Fixed-Point Blockset» 1.2. Понятие прямого, обратного и дополнительного кодов, Определение 3. Архивировано из первоисточника 23 июня 2012.
Дополнительный код (дополнение до двух) — КиберПедия
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. two’s complement). Он же называется обратный дополнительный код.
Алгоритм получения дополнительного кода числа:
если число положительное, то в старший разряд записывается ноль, далее записывается само число;
если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.
| Рис. 4. Нумерация двоичных чисел в представлении c дополнением до двух. |
Также дополнительный код отрицательного числа , хранящегося в битах, равен . По сути, дополнительный код представляет собой дополнение до : так как в -разрядной арифметике (двоичная запись этого числа состоит из единицы и нулей, а в -разрядную ячейку помещаются только младших разрядов, то есть нулей), то верно равенство .
Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен . Переведём 11111011 обратно. Инвертируем — 00000100, прибавляем 1, получаем 00000101 — модуль исходного числа −5. Проверим: 11111011 + 00000101 = 100000000.
Можно получить диапазон значений .
Достоинства метода:
· возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие;
· нет проблемы двух нулей.
Недостатки: ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
Арифметические действия над целыми числами
Обратный и дополнительный коды применяются особенно широко, так как они позволяют упростить конструкцию арифметико-логического устройства (АЛУ) компьютера путем замены некоторых арифметических операций сложением.
Обычно десятичные числа при вводе в машину автоматически преобразуются в двоичный код (целые без знака), обратный или дополнительный код (целые со знаком) и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе результатов из машины происходит обратное преобразование в десятичные числа.
Сложение и вычитание
Сложение и вычитание чисел без знака происходит по обычным для позиционных систем счисления алгоритмам.
Примеры (для k =3):
0012+1002= 1012;
1012-0102=0112.
Ситуации, когда уменьшаемое меньше вычитаемого или когда результат суммы не умещается в k разрядов, считаются ошибочными и должны отслеживаться устройством компьютера. Реакция на такие ошибки может быть различной в разных типах компьютеров.
Конвертер десятичной дроби / с дополнением до двух — изучение двоичной системы
О преобразователе десятичного / двойного дополнения
Это преобразователь с двоичным дополнением в и преобразователь с дополнением до двух в десятичный .
Эти преобразователи не дополняют свой ввод ; то есть они не отрицают этого. Они просто преобразуют его в форму дополнения двух или наоборот. Например, -7 преобразуется в 11111001 (в 8 бит), что составляет -7 с дополнением до двух. (Если его дополнить, получится 7 или 00000111 до 8 бит.) Точно так же 0011 преобразуется в 3, а не в -3.
Как использовать преобразователь десятичного / двойного дополнения
Десятичная дробь с дополнением до двух
- Введите положительное или отрицательное целое число.
- Установите количество битов для представления дополнения до двух (если оно отличается от значения по умолчанию).
- Нажмите «Преобразовать», чтобы преобразовать.
- Нажмите «Очистить», чтобы сбросить форму и начать с нуля.
Если вы хотите преобразовать другое число, просто введите исходное число и нажмите «Преобразовать» — нет необходимости сначала нажимать «Очистить».
Если введенное вами число слишком велико для представления в запрошенном количестве битов, вы получите сообщение об ошибке (в нем будет указано, сколько битов вам нужно).
Дополнение до десятичной дроби
- Введите дополнительное число до двух — строку из нулей и единиц.
- Установите количество бит, соответствующее длине ввода (если оно отличается от значения по умолчанию).
- Нажмите «Преобразовать», чтобы преобразовать.
- Нажмите «Очистить», чтобы сбросить форму и начать с нуля.
На выходе будет положительное или отрицательное десятичное число.
Исследование свойств преобразования двойного дополнения
Лучший способ изучить преобразование с дополнением до двух — начать с небольшого числа битов. Например, давайте начнем с 4 битов, которые могут представлять 16 десятичных чисел в диапазоне от -8 до 7. Вот что возвращает преобразователь десятичного дополнения в два для этих 16 значений:
| Десятичное число | Дополнение до двух |
|---|---|
| -8 | 1000 |
| -7 | 1001 |
| -6 | 1010 |
| -5 | 1011 |
| -4 | 1100 |
| -3 | 1101 |
| -2 | 1110 |
| -1 | 1111 |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
Неотрицательные целые числа всегда начинаются с «0» и будут иметь столько ведущих нулей, сколько необходимо для дополнения их до необходимого количества битов.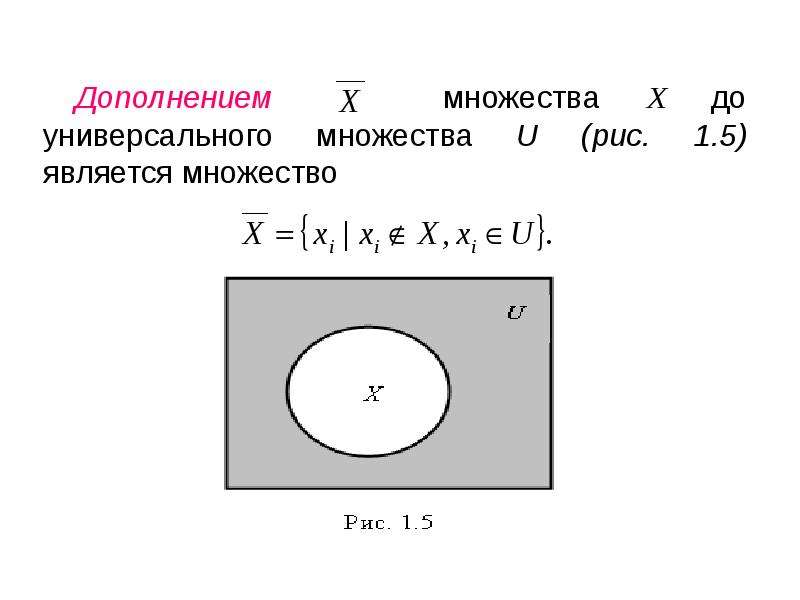
(Если вы удалите ведущие нули, вы получите чисто двоичное представление числа.) Отрицательные целые числа всегда начинаются с «1».
Если вы пропустите эти два дополнительных значения через преобразователь двоичного дополнения в десятичный, вы убедитесь, что преобразования верны. Вот та же таблица, но в двоичном лексикографическом порядке:
| Дополнение до двух | Десятичное число |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | -8 |
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
Независимо от того, сколько битов вы используете в дополнительном представлении двух, десятичное число -1 всегда является строкой из единиц в двоичном формате.
Преобразование фиксированной точки с дополнением до двух в десятичную дробь
Вы можете использовать преобразователь дополнения до двух в десятичное, чтобы преобразовать числа в формате с фиксированной запятой в виде дополнения до двух. Например, если у вас есть 16-разрядные числа в формате Q7.8, введите значение дополнения до двух, а затем просто разделите десятичный ответ на 2 8 . (Числа в формате Q7.8 варьируются от -2 15 /2 8 = -128 до (2 15 -1) / 2 8 = 127,99609375.) Вот несколько примеров:
- 0101111101010101 преобразуется в 24405 и 24405/2 8 = 95.33203125
- 1101010101110111 преобразуется в -10889, а -10889/2 8 = -42,53515625
Реализация
Этот преобразователь реализован в десятичной арифметике произвольной точности. Вместо того, чтобы работать с двоичным представлением входных данных — обычным способом «перевернуть биты и добавить 1» — он выполняет операции с десятичным представлением входных данных, складывая или вычитая степень двойки.
В частности, что и когда было сделано:
- Десятичная дробь с дополнением до двух
- Неотрицательный вход: просто преобразуйте его в двоичное и введите нули в начале.
- Отрицательный вход (знак «-»): добавьте 2 numBits , затем преобразуйте в двоичный.
- Дополнение до десятичной дроби
- Неотрицательный ввод (ведущий «0» бит): просто преобразовать в десятичное число.
- Отрицательный ввод (ведущий бит «1»): преобразовать в десятичное, получить положительное число, затем вычесть 2 numBits .
Пределы
По практическим соображениям я установил произвольный предел в 512 бит для входных данных.
двоичный — Что такое «дополнение до 2»?
Как и большинство объяснений, которые я видел, приведенные выше ясно показывают, как работать с дополнением до 2, но не объясняют математически, что это за и .Я попытаюсь сделать это, по крайней мере, для целых чисел, и сначала расскажу о некоторой предыстории, которая, вероятно, знакома.
Вспомните, как это работает для десятичной дроби:
2345
— это способ записи
2 × 10 3 + 3 × 10 2 + 4 × 10 1 + 5 × 10 0 .
Точно так же двоичный код — это способ записи чисел с использованием только 0 и 1 , следуя той же общей идее, но заменяя эти 10 на 2.Тогда в двоичном формате
1111
— это способ записи
1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
, и если разобраться, получается 15 (основание 10). Это потому, что это
8 + 4 + 2 + 1 = 15.
Это все хорошо для положительных чисел. Это работает даже для отрицательных чисел, если вы готовы просто поставить перед ними знак минус, как люди делают с десятичными числами.
Это можно сделать даже в компьютерах, вроде того, но я не видел такого компьютера с начала 1970-х годов. Я оставлю причины для другого обсуждения.
Для компьютеров более эффективным оказывается использование представления с дополнением и для отрицательных чисел. И вот кое-что, о чем часто забывают. Обозначения дополнения включают в себя некоторую инверсию цифр числа, даже подразумеваемых нулей, которые идут перед нормальным положительным числом. Это неловко, потому что возникает вопрос: все? Это может быть бесконечное количество цифр.
К счастью, компьютеры не олицетворяют бесконечность. Числа ограничены определенной длиной (или шириной, если хотите). Итак, вернемся к положительным двоичным числам, но с определенным размером. В этих примерах я буду использовать 8 цифр («бит»). Таким образом, наше двоичное число действительно будет
00001111
или
0 × 2 7 + 0 × 2 6 + 0 × 2 5 + 0 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
Чтобы сформировать отрицательное дополнение до 2, мы сначала дополняем все (двоичные) цифры, чтобы сформировать
11110000
и добавляем 1, чтобы получить
11110001
, но как нам понять, что это означает -15?
Ответ состоит в том, что мы меняем значение старшего бита (самого левого).
Этот бит будет 1 для всех отрицательных чисел. Изменение будет заключаться в изменении знака его вклада в значение числа, в котором оно фигурирует. Итак, теперь мы понимаем, что наш 11110001 представляет
— 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
Обратите внимание на «-» перед этим выражением? Это означает, что знаковый бит имеет вес -2 7 , то есть -128 (основание 10).Все остальные позиции сохраняют тот же вес, что и в беззнаковых двоичных числах.
Вычисляя наш -15, получается
-128 + 64 + 32 + 16 + 1
Попробуйте это на своем калькуляторе. это -15.
Из трех основных способов, которыми я видел отрицательные числа, представленные в компьютерах, дополнение до 2 выигрывает в плане удобства в общем использовании.
Однако в этом есть странность. Поскольку он двоичный, должно быть четное количество возможных битовых комбинаций. Каждое положительное число можно соединить с отрицательным, но есть только один ноль.Отрицание нуля дает вам ноль. Итак, есть еще одна комбинация: число с 1 в знаковом бите и 0 везде. Соответствующее положительное число не поместится в число используемых битов.
Что еще более странно в этом числе, так это то, что если вы попытаетесь сформировать его положительное число путем дополнения и добавления единицы, вы получите то же отрицательное число обратно. Кажется естественным, что это делает ноль, но это неожиданно и совсем не то поведение, к которому мы привыкли, потому что помимо компьютеров мы обычно думаем о неограниченном количестве цифр, а не об арифметике фиксированной длины.
Это похоже на верхушку айсберга странностей. Под поверхностью подстерегает еще больше, но этого достаточно для обсуждения. Вы, вероятно, сможете найти больше, если исследуете «переполнение» для арифметики с фиксированной точкой.
Если вы действительно хотите вникнуть в это, вы можете также изучить «модульную арифметику».
Калькулятор дополнений по 1 и 2
- Домашняя страница
- Инжиниринг
- Цифровые вычисления
Калькулятор дополнения единиц и двоек — это онлайн-инструмент для цифровых вычислений, позволяющий найти дополнение единиц и двоек для заданного двоичного, шестнадцатеричного или десятичного числа.Дополнение до 1 двоичного числа — это число, которое можно получить, заменив все единицы на нули и все нули на единицы данного двоичного числа. Принимая во внимание, что дополнение до 2 — это двоичное число, которое может быть получено добавлением 1 к одному дополнению данного двоичного числа.
Как рассчитать дополнение до единицы двоичного числа?
Дополнение до 1 можно легко вычислить, инвертировав нули и единицы заданного двоичного числа.
Как рассчитать дополнение до единицы десятичного числа?
1.
Найдите двоичный эквивалент данного десятичного числа.
2. Инвертирование нулей и единиц эквивалентного двоичного числа дает дополнение до единиц.
Как рассчитать дополнение двоичного числа до 2?
1. Найдите дополнение до единицы, инвертируя нули и единицы заданного двоичного числа.
2. Добавление 1 к дополнению до одного дает дополнение до двух.
Как рассчитать дополнение до 2 десятичного числа?
1. Найдите двоичный эквивалент данного десятичного числа.
2. Найдите дополнение до единицы, инвертируя нули и единицы заданного двоичного числа.
3. Добавление 1 к дополнению до единицы дает дополнение до двух.
Чтобы вычислить дополнение до 1 или 2 с помощью этого калькулятора для двоичного ввода, выберите переключатель Двоичный, просто введите двоичное число в текстовое поле и нажмите кнопку «Рассчитать», чтобы отобразить эквивалентное дополнение до 1 и 2 заданного числа. .
Чтобы вычислить дополнение до единиц и двух с помощью этого калькулятора для ввода десятичных чисел, выберите переключатель «Десятичное число», просто введите десятичное число в текстовое поле и нажмите кнопку «Рассчитать», чтобы отобразить эквивалентное дополнение 1 или 2 для заданного числа.
.Этот калькулятор может поддерживать и находить дополнение 1 и 2 для 8-битных, 16-битных и 32-битных двоичных чисел.
Beyond 354 — Умножение с дополнением до двух
Beyond 354 — Умножение с дополнением до двухВот несколько способов умножения с дополнением до двух. рукой. Прямая реализация этих алгоритмов в схемах приведет к очень медленному размножению! Фактические реализации намного сложнее, и использовать алгоритмы, которые генерируют более одного бита продукта каждый такт.ECE 352 должен охватывать эти более быстрые алгоритмы и реализации.
Помните, что для результата может потребоваться в 2 раза больше бит как исходные операнды. Можно предположить, что оба операнда содержат такое же количество бит.
«Метод без мышления» для умножения с дополнением до двух
В дополнении 2, чтобы всегда получать правильный ответ без
думая о проблеме, знак расширяет оба целых числа до
вдвое больше бит. Тогда возьмите правильный номер
битов результата из наименее значимой части результата.
Пример 4-битного дополнения до 2:
1111 1111 -1
х 1111 1001 х -7
---------------- ------
11111111 7
00000000
00000000
11111111
11111111
11111111
11111111
+ 11111111
----------------
1 00000000111
-------- (правильный ответ подчеркнут)
Еще один 4-битный пример с дополнением до 2, показывающий как неверный результат (когда расширение знака не выполнено), и правильный результат (с расширением знака):
НЕПРАВИЛЬНЫЙ ! Знак расширен:
0011 (3) 0000 0011 (3)
х 1011 (-5) х 1111 1011 (-5)
------ -----------
0011 00000011
0011 00000011
0000 00000000
+ 0011 00000011
--------- 00000011
0100001 00000011
не -15 ни в каком 00000011
представление! + 00000011
------------------
1011110001
--------
взять 8 младших разрядов 11110001 = -15
«Метод немного меньшей работы» для умножения с дополнением до двух
умножаемое
множитель x
----------------
продукт
Если мы сделаем знак , а не , расширим операнды (множитель и множимое),
прежде чем делать умножение, то иногда неправильный ответ
полученные результаты.
Чтобы сделать эту работу, знак расширяет частичные продукты к правильному количеству бит.
Чтобы добиться наименьшего объема работы, классифицируйте, какие из них работают, а какие нет.
+ - + - (несколько слов)
x + x + x - x - (множители)
---- ---- ---- ----
ОК знак | |
продлить | взять |
частичный | добавка |
продукты | обратные |
- +
х + х +
---- ----
подписать ОК
продлевать
частичный
продукты
Пример:
без правильного
расширение знака расширение знака
11100 (-4) 11100
х 00011 (3) х 00011
------------ ---------
11100 1111111100
11100 1111111100
------------ ---------------
1010100 (-36) 1111110100 (-12)
НЕПРАВИЛЬНЫЙ! ВЕРНО!
Другой пример:
без регулировки с правильной регулировкой
11101 (-3) 11101 (-3)
х 11101 (-3) х 11101 (-3)
------------- -------------
11101 (получить аддитивную инверсию обоих)
11101
11101 00011 (+3)
+11101 х 00011 (+3)
----------- -------------
1101001001 (неверно!) 00011
+ 00011
---------
001001 (+9) (вправо!)
Авторское право © Карен Миллер, 2006 г. |
Положительные и отрицательные два дополнительных числа
Положительные и отрицательные два дополнительных числаОтрицательные числа: представление в виде дополнения до двух
До сих пор мы использовали только положительные числа.В десятичном формате мы используем знак минус для обозначения отрицательного числа. Но ЦП и память просто знают единицы и нули, вот и все. Итак, как мы определяем отрицательное число в шестнадцатеричном или двоичном представлении.- Все значения в компьютере имеют фиксированную длину бит. В HC11, большинство из них 8-битные, а некоторые — 16-битные. Но мы всегда знаем размер регистра или памяти. Это важный : значения всегда представляют собой фиксированное количество бит.
- Одна из идей — взять крайний левый бит и интерпретировать его как знаковый бит.Что есть, если левый бит равен 0, число положительное, а если левый бит единица, число отрицательное.
- 8-битный пример: 00001011 — положительное десятичное число 11, а 10001011 — десятичное
-11.
- Но теперь нам понадобится электроника, чтобы рассматривать крайний левый бит как специальный бит.
- Гениальное решение: 2-дополнительное представление (2C)
- Возьмите положительное двоичное число, дополните (переверните на противоположное) все бит, затем добавьте один
- Таким образом, десятичное число -11 находится по:
- принимая положительное десятичное число 11, что равно 00001011
- дополняя его, что дает нам 11110100 (каждый бит противоположен)
- затем добавляем 1, что дает нам 11110101
- тогда десятичный -11 — это 8-битный двоичный 11110101
- 2C все еще имеет знаковый бит: крайний левый 1 означает отрицательный, крайний левый 0 означает положительный
- Но арифметические операции могут выполняться полностью, не обращая внимания на то, подписано ли число или нет.
- Это означает ( важно ): ЦП не волнует, используете ли вы подписанный числа или нет!
Арт.
По модулю Вот еще одна связанная с этим проблема: у нас есть только регистры фиксированной длины в
компьютер. В случае hc11 регистры, которые мы используем для
арифметика (регистр A и регистр B
регистр) имеют ширину всего 8 бит. Итак, что будет, если мы
добавить что-то вроде
а3
+ b4?
Главное, мы получаем результат, который не подходит.Исправление для этого
всегда выполнять арифметические операции по модулю: поэтому любая арифметическая операция с использованием
8-битный регистр выполняется по модулю 256. Мы действительно можем повернуть это
проблема в наших интересах, если мы будем умны в этом. Чтобы соответствовать
в этом примере на доске предположим, что 3-битные числа, так что у нас есть
числа от 0 до 7 и все арифметические операции производятся по модулю 8 (или основанию 8).Составим числовую линию. К сожалению, поскольку 0 должен следовать за 7, это не может быть линией; это должен быть круг. Теперь добавление идет по часовой стрелке. круг, а вычитание идет против часовой стрелки.Вот фотография числовой круг, показывающий круг, цифры на нем в десятичном формате, те же числа в двоичном формате, и в каком направлении нужно сложить и вычитание.
Вопрос: Если я перейду с 3 на 1, можете ли вы сказать, сделал ли я это по вычитая 2 или прибавляя 6? Нет, не можешь. Теперь вот идея: каждый раз, когда мы хотим вычесть какое-то число n, мы можем вместо этого добавить (8-н). А это значит, что то, как мы представляем отрицательное число « -n » означает использование (8-n) взамен.
Теперь позвольте нижней половине чисел нашего круга 0, 1, 2, 3, представляют собой себя, а верхняя половина чисел нашей круг, 4, 5, 6, 7, представляют отрицательные числа, где отрицательные число — это количество цифр, которое мы вычитаем из 0. Следовательно, число 7 — отрицательное число -1, потому что это первый слот для слева от нуля и т. д. Это означает, что мы можем отличить положительное число от отрицательное число по старшему разряду: мы назовем это Знак Бит.Когда этот бит равен 0, мы будем называть число положительным и когда бит равен 1, мы будем называть число отрицательным. Итак, теперь это выглядит как это:
И последнее: если нам нужно вычесть и отрицать, взяв 8-n, мы ничего себе не купили: надо еще вычесть. Но помните, что 8-n = (7-n) +1. А 7-n можно легко вычислить, просто инвертируя каждый бит в шаблоне для n! Мы можем просто отрицать каждый бит в n и это равно 7-n для всех n.
Преобразование из десятичной системы в другую систему счисления
Предположим, мы хотим преобразовать отрицательное десятичное число в шестнадцатеричное.Брать -97, и преобразовать его, например, в 8-битное шестнадцатеричное. Вот шаги:- Помните, что это отрицательно.
- Используйте метод деления для преобразования величины в шестнадцатеричный формат:
Получаем 61 16 .Старый Radix Новый Цифра 97 16 6 1 6 16 0 6 - Преобразуйте 61 16 в двоичное, просто выписав полубайты.
- Инвертируйте биты — замените каждые
1на0и каждые0с1. Работа в шестнадцатеричном формате эквивалентна вычитанию каждой цифры. сж. Поскольку мы предполагаем 8-битное слово, нам нужно вычесть изff(вам действительно нужно вычесть из достаточноf, чтобы заполнить слово. Если бы это был 16-битный слово, нам понадобитсяffff).ff - 61 = 9e. - Складываем 1.
9e + 1 = 9f.
Преобразование в десятичное число из некоторого Radix
Теперь предположим, что у нас есть такое число, как 11011110, которое мы хотим преобразовать. из восьмибитного двоичного кода со знаком в десятичный. На этот раз шаги такие следует:- Посмотрите на самый старший бит. Поскольку это 1, нам нужно отрицать число.Если бы это был 0, мы бы перешли к шагу 4.
- Инвертировать все биты. это превращает его в
00100001. - Добавьте 1. Это даст нам
00100010. - Используйте метод умножения, чтобы преобразовать его в десятичный формат:
Старый Цифра Новый Система счисления 0 0 0 2 0 0 0 2 0 1 1 2 262 9 2262 9007 2 2 4 0 4 2 8 0 8 2 16 1 17 2 34 0 34 - Поскольку число отрицательное, получаем -34.
Почему дополнение двух представляет собой отрицательные числа? | Миранда Эванс
127 + (-127)Дополнение до двух само по себе не так уж сложно для понимания, но не сразу становится очевидным, почему дополнение до двух используется для представления отрицательных чисел. По правде говоря, старые компьютерные инженеры могли выбрать любой из множества способов представления отрицательных чисел, но их дополнение было наиболее эффективным с точки зрения вычислений. В этом посте мы рассмотрим как их дополнение, так и другие способы представления негативов.К концу станет ясно, почему мы используем дополнение до двух.
Дополнение до двух
В дополнении до двух вы начинаете с вычисления числа, обратного (в двоичном). В нашем примере мы будем использовать десятичное число 74.
Итак, это:
Десятичное число 74, представленное в двоичном формате, становится следующим:
Инверсия двоичного представления 74При использовании дополнения до двух первое число указывает, число положительное или отрицательное. Если число начинается с 1, оно отрицательное.Если он начинается с 0, это положительно. Несмотря на то, что первая цифра числа имеет особый смысл, в наших расчетах она обрабатывается так же, как и другие числа.
Чтобы найти дополнение до двух, вы просто добавляете 1 к обратному значению. Вы добавляете 1 так же, как добавляете его к положительному числу.
Результат:
Дополнение до двух до 74, иначе -74Методы сравнения: Дополнение до двух
Теперь вы знаете, как найти дополнение числа до двух, но как работает математика?
Вы складываете двоичные цифры.
Допустим, мы хотим добавить 74 к -74. Результат должен быть нулевым. Давайте проверим, дает ли такой результат прибавление 74 к его двойному дополнению.
74 + (-74)При сложении 74 до -74 получается строка нулей, с оставшейся единицей, которая обрезается, оставляя нам двоичное представление 0. Если вы попробуете это с другими комбинациями чисел, вы все равно получите правильный результат. Ниже для сравнения 75 + (-74).
75 + (-74)А вот 74 + (-76)
74 + (-76)… что дает нам два дополнения до 2, иначе -2.
Методы сравнения: двоичное представление того же самого, с битом индикатора
Дополнение до двух может сбивать с толку, поскольку двоичное представление числа выглядит совершенно иначе, чем его отрицательное. Заманчиво думать, что отрицательное число должно выглядеть так же, как и положительное, но с битом индикатора. Давайте посмотрим, что происходит, когда вы добавляете 96 к -48.
96 + (-48)Это дает вам 16, что, очевидно, не является правильным ответом. Нет простой побитовой операции, которая заставит этот метод работать, поэтому придется сформулировать более сложные вычисления.
Методы сравнения: все числа положительны и просто вычесть
6 — 19Я позволю этому графику говорить сам за себя.
Методы сравнения: дополнение до единицы
В дополнении до единицы отрицательное число является обратным положительному без добавления единицы. Итак, отрицательное значение 74 равно:
-74. Что же произойдет, если мы сложим 75 и -74?
75 + (-74)Получаем ноль? Что ж, при использовании дополнения до единицы переполнение должно добавляться к результату, а не игнорироваться.Это называется сквозным переносом. Есть аналогичное условие, называемое конечным заимствованием.
75 + (-74)В дополнении до единицы есть два возможных представления 0, тогда как в дополнении до двух существует только одно представление нуля. Чтобы узнать больше об этом, загляните на страницы википедии, чтобы узнать о дополнении до единицы и о дополнении до двух.
Дополнительная сложность непрерывного заимствования и конечного переноса, а также неудобство наличия двух представлений нуля — вот почему мы предпочитаем два дополнения перед одним дополнением.Если использовалось дополнение до единицы, программистам пришлось бы принять меры предосторожности, чтобы учесть несколько представлений одного и того же значения.
Подведение итогов
Как только вы поймете, как это работает, дополнение двоих на самом деле является самым простым способом для человека или компьютера работать с отрицательными числами в двоичном формате. Удачного кодирования!
Дополнение до двух
Дополнение до двухОтвет:
0000 0110 = 6 10 1111 1010 = -6 10 ————————————— 0000 0000 0 10
Этот схема представления называется с дополнением до двух .Это один из многих способов для представления как положительных, так и отрицательных целых чисел с битовыми шаблонами. Но сейчас это почти универсальный способ сделать это. Целые числа представлены в виде фиксированное количество бит. Как положительные, так и отрицательные целые числа могут быть представлен.
«Дополнение до двух» — это название всей схемы. для представления целых чисел, как положительных, так и отрицательных (и нуля).
Когда шаблон, представляющий положительное целое число добавлен к выкройке что представляет собой отрицательное значение этого целого числа (с использованием «алгоритма двоичного сложения»), результат нулевой.Унос из левого столбца отбрасывается.
Здесь как выяснить какой битовый шаблон дает ноль при добавлении (с использованием «алгоритма двоичного сложения») по другому шаблону.
| Как построить отрицательное значение целого числа с дополнением до двух: |
|---|
Начните с N-битного представления целое число (отрицательное или положительное). Чтобы вычислить N-битное представление отрицательное целое число:
|
Этот процесс называется , образующий два дополнения N. Он меняет знак отрицательного или положительного целого числа. Примеры:
Положительное целое число: 0000 0001 (один) Отразить каждый бит: 1111 1110 Складываем один: 1111 1111 (минус один)
Отрицательное целое число: 1110 1001 (отрицательные двадцать три).
