Двоичные в десятичные онлайн. Системы счисления: перевод чисел между двоичной, восьмеричной, десятичной и шестнадцатеричной

Как перевести число из одной системы счисления в другую. Какие существуют способы перевода чисел между двоичной, восьмеричной, десятичной и шестнадцатеричной системами счисления. Как выполнить перевод чисел с дробной частью между разными системами счисления. Какие особенности нужно учитывать при переводе чисел между системами счисления с разными основаниями.

Что такое системы счисления и для чего они нужны

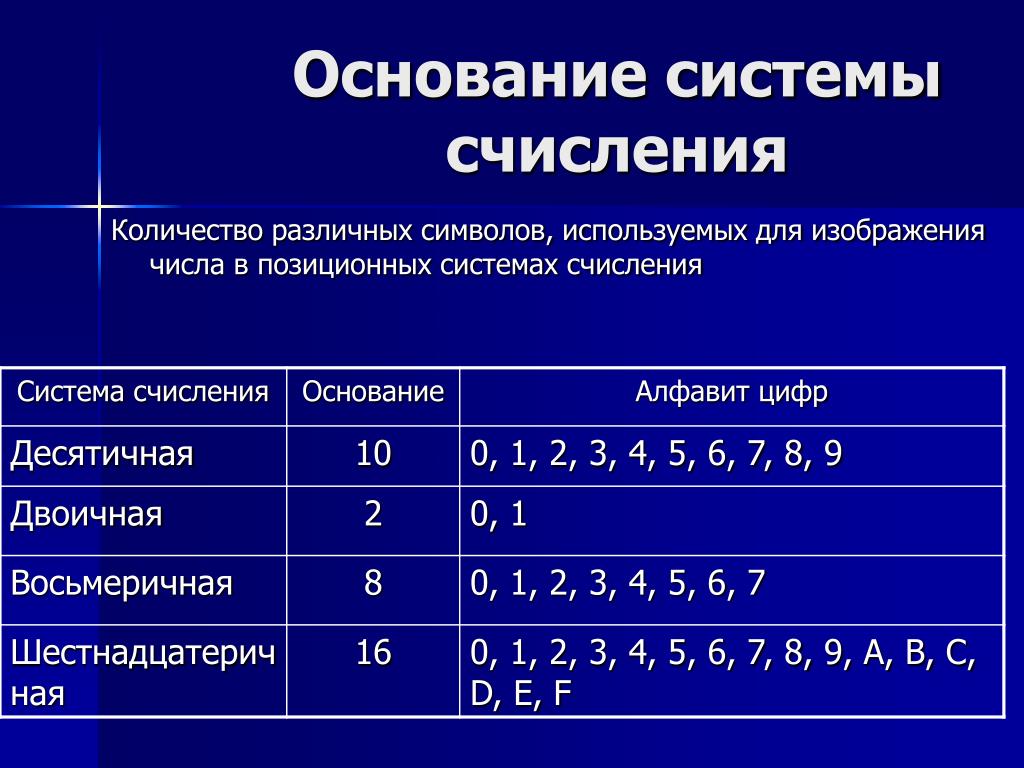
Система счисления — это способ представления чисел с помощью письменных знаков. Существуют позиционные и непозиционные системы счисления. В позиционных системах значение цифры зависит от ее позиции в числе, а в непозиционных — нет.

Основные позиционные системы счисления:

• Двоичная (основание 2) — используется в компьютерной технике
• Восьмеричная (основание 8) — применялась ранее в вычислительной технике
• Десятичная (основание 10) — используется в повседневной жизни
• Шестнадцатеричная (основание 16) — часто применяется в программировании

Умение переводить числа между системами счисления необходимо программистам, инженерам и другим специалистам, работающим с вычислительной техникой.

Перевод целых чисел из десятичной системы в другие

Для перевода целого десятичного числа в другую систему счисления используется метод последовательного деления на основание новой системы. Алгоритм:

1. Делим число на основание новой системы
2. Записываем остаток от деления
3. Делим частное на основание
4. Повторяем шаги 2-3, пока частное не станет равным 0
5. Записываем остатки в обратном порядке — это и будет число в новой системе

Пример перевода числа 75 из десятичной в двоичную систему:

75 / 2 = 37 остаток 1
37 / 2 = 18 остаток 1
18 / 2 = 9  остаток 0
9 / 2 = 4   остаток 1
4 / 2 = 2   остаток 0
2 / 2 = 1   остаток 0
1 / 2 = 0   остаток 1

Записываем остатки в обратном порядке: 75

10 = 1001011₂

Перевод дробных чисел из десятичной системы в другие

Для перевода правильной десятичной дроби в другую систему счисления используется метод умножения на основание новой системы. Алгоритм:

1. Умножаем дробную часть на основание новой системы
2. Записываем целую часть результата
3. Берем дробную часть результата и повторяем шаги 1-2
4. Процесс продолжаем до получения нужной точности

Пример перевода числа 0.625 из десятичной в двоичную систему:

0.625 * 2 = 1.25  записываем 1
0.25 * 2 = 0.5    записываем 0
0.5 * 2 = 1.0     записываем 1

Результат: 0.625₁₀ = 0.101₂

Перевод из двоичной системы в десятичную

Для перевода двоичного числа в десятичное нужно:

1. Пронумеровать разряды справа налево, начиная с 0
2. Умножить каждую цифру на 2 в степени номера разряда
3. Сложить полученные значения

Пример: переведем 1011₂ в десятичную систему

1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11

Результат: 1011₂ = 11₁₀

Перевод между недесятичными системами счисления

Для перевода числа между недесятичными системами счисления (например, из двоичной в шестнадцатеричную) удобно использовать десятичную систему как промежуточную:

1. Переводим число из исходной системы в десятичную
2. Переводим полученное десятичное число в целевую систему

Также можно использовать специальные таблицы соответствия для быстрого перевода между системами счисления с основаниями 2ⁿ (2, 4, 8, 16).

Особенности перевода чисел между разными системами счисления

При переводе чисел между системами счисления с разными основаниями важно учитывать следующие особенности:

• Чем больше основание системы счисления, тем компактнее запись числа
• При переводе из системы с меньшим основанием в систему с большим основанием число может стать короче
• При переводе из системы с большим основанием в систему с меньшим основанием число может стать длиннее
• Некоторые дробные числа, конечные в одной системе, могут стать бесконечными периодическими дробями в другой системе

Практическое применение систем счисления

Различные системы счисления широко применяются в информатике и вычислительной технике:

• Двоичная система используется для представления информации в компьютерах
• Восьмеричная и шестнадцатеричная системы упрощают работу с двоичными данными
• Шестнадцатеричная система применяется для записи адресов памяти, цветовых кодов
• Системы счисления с разными основаниями используются в криптографии

Умение свободно переводить числа между системами счисления — важный навык для специалистов в области информационных технологий.

Онлайн-калькуляторы для перевода чисел между системами счисления

Для быстрого перевода чисел между различными системами счисления можно использовать онлайн-калькуляторы. Они позволяют:

• Переводить целые и дробные числа
• Выполнять перевод между любыми системами счисления
• Получать подробное решение с пояснениями
• Проверять правильность собственных расчетов

Однако важно понимать принципы перевода чисел и уметь выполнять его вручную, а калькуляторы использовать для проверки и экономии времени.

Перевод чисел в различные системы счисления с решением | Онлайн калькулятор

Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую. Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку «Получить запись».

Исходное число записано в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.

Хочу получить запись числа в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.

Получить запись

---

=

Выполнено переводов:

Также может быть интересно:

Системы счисления

Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.

Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:

Число:	5	9	2	1
Позиция:	3	2	1	0

Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 = 5·103+9·102+2·101+1·100. Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.

Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:

Число:	1	2	3	4	5	6	7
Позиция:	3	2	1	0	-1	-2	-3

Число 1234.567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·103+2·102+3·101+4·100+5·10-1

+6·10-2+7·10-3.

Перевод чисел из одной системы счисления в другую

Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:

1. Перевести число 1001101.11012 в десятичную систему счисления.
Решение: 10011.11012 = 1·24+0·23+0·22+1·21+1·20+1·2-1+1·2-2+0·2-3+1·2-4 = 16+2+1+0.5+0.25+0.0625 = 19.812510
Ответ: 10011.1101

2 = 19.812510

2. Перевести число E8F.2D16 в десятичную систему счисления.
Решение: E8F.2D16 = 14·162+8·161+15·160+2·16-1+13·16-2 = 3584+128+15+0.125+0.05078125 = 3727.1757812510
Ответ: E8F.2D16 = 3727.1757812510

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.

Перевод целой части числа из десятичной системы счисления в другую систему счисления

Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.

3. Перевести число

27310 в восьмиричную систему счисления.
Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421
Проверка: 4·82+2·81+1·80 = 256+16+1 = 273 = 273, результат совпал. Значит перевод выполнен правильно.
Ответ: 27310 = 4218

Рассмотрим перевод правильных десятичных дробей в различные системы счисления.

Перевод дробной части числа из десятичной системы счисления в другую систему счисления

Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.

4. Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 — целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 — вторая цифра результата), 0.5·2 = 1.0 (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
Ответ: 0.12510 = 0.0012

Калькулятор систем счисления

Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.

Система счисления — это способ представления числа. Одно и то же число может быть представлено в различных видах. Например, число 200 в привычной нам десятичной системе может иметь вид 11001000 в двоичной системе, 310 в восьмеричной и C8 в шестнадцатеричной.

Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.

Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
200₁₀ = 11001000₂ = 310₈ = C8₁₆

Кратко об основных системах счисления

Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.

Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.

Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.

Шестнадцатеричная система счисления. Наиболее распространена в современных компьютерах. При помощи неё, например, указывают цвет. #FF0000 — красный цвет. Для записи числа используются цифры от 0 до 9 и буквы A,B,C,D,E,F, которые соответственно обозначают числа 10,11,12,13,14,15.

Перевод в десятичную систему счисления

Преобразовать число из любой системы счисления в десятичную можно следующим образом: каждый разряд числа необходимо умножить на Xⁿ, где X — основание исходного числа, n — номер разряда. Затем суммировать полученные значения.

abc_x = (a*x² + b*x¹ + c*x⁰)₁₀

Примеры:

567₈ = (5*8² + 6*8¹ + 7*8⁰)₁₀ = 375₁₀

110₂ = (1*2² + 1*2¹ + 0*2⁰)₁₀ = 6₁₀

A5₁₆ = (10*16¹ + 5*16⁰)₁₀ = 165₁₀

Перевод из десятичной системы счисления в другие

Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.

Переведем число 375₁₀ в восьмеричную систему:

375 / 8 = 46 (остаток 7)

46 / 8 = 5 (остаток 6)

5 / 8 = 0 (остаток 5)

Записываем остатки и получаем 567₈

Перевод из двоичной системы в восьмеричную

Способ 1:

Для перевода в восьмеричную систему нужно разбить двоичное число на группы по 3 цифры справа налево. В последней (самой левой) группе вместо недостающих цифр поставить слева нули. Для каждой полученной группы произвести умножение каждого разряда на 2ⁿ, где n — номер разряда.

1101₂ = (001) (101) = (0*2² + 0*2¹ + 1*2⁰) (1*2² + 0*2¹ + 1*2⁰) = (0+0+1) (4+0+1) = (1) (5) = 15₈

Способ 2:

Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:

Триада	000	001	010	011	100	101	110	111
Цифра	0	1	2	3	4	5	6	7

10111010₂ = (010) (111) (010) = 272₈

Перевод из двоичной системы в шестнадцатеричную

Способ 1:

Разбиваем число на группы по 4 цифры справа налево. Последнюю (левую) группу дополним при необходимости ведущими нулями. Внутри каждой полученной группы произведем умножение каждой цифры на 2ⁿ, где n — номер разряда, и сложим результаты.

11010₂ = (0001) (1010) = (0*2³ + 0*2² + 0*2¹ + 1*2⁰) (1*2³ + 0*2² + 1*2¹ + 0*2⁰) = (0+0+0+1) (8+0+2+0) = (1) (10) = 1A₁₆

Способ 2:

Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:

Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

101111100₂ = (0001) (0111) (1100) = 17C₁₆

Перевод из восьмеричной системы в двоичную

Способ 1:

Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.

Возьмем число 43₈.
Делим последовательно 4 на 2 и получаем остатки 0,0,1. Записываем их в обратном порядке. Получаем 100.
Делим последовательно 3 на 2 и получаем остатки 1,1. Записываем их в обратном порядке и дополняем ведущими нулями до трех разрядов. Получаем 011.
Записываем вместе и получаем 100011₂

Способ 2:

Используем таблицу триад:

Цифра	0	1	2	3	4	5	6	7
Триада	000	001	010	011	100	101	110	111

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

351₈ = (011) (101) (001) = 011101001₂ = 11101001₂

Перевод из шестнадцатеричной системы в двоичную

Способ 1:

Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.

Способ 2:

Используем таблицу тетрад:

Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.

D8₁₆ = (1101) (1000) = 11011000₂

Перевод из восьмеричной системы в шестнадцатеричную и наоборот

Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.

Онлайн калькулятор систем счисления с решением онлайн

Переведем целую часть 12 числа 12.3₁₀ в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

12	:	2	=	6	остаток: 0
6	:	2	=	3	остаток: 0
3	:	2	=	1	остаток: 1
1	:	2	=	0	остаток: 1

12₁₀ = 1100₂

Переведем дробную часть 0.3 числа 12.3₁₀ в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

0.3	·	2	=	0.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2
0.2	·	2	=	0.4
0.4	·	2	=	0.8
0.8	·	2	=	1.6
0.6	·	2	=	1.2

0.3₁₀ = 0.010011001100110011001100110011₂
12.3₁₀ = 1100.010011001100110011001100110011₂

Перевод чисел из одной системы счисления в другую онлайн

С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.

 Результат уже получен!

Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения

Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:

число	6	3	7	2
позиция	3	2	1	0

Тогда число 6372 можно представить в следующем виде:

6372=6000+300+70+2 =6·10³+3·10²+7·10¹+2·10⁰.

Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.

Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:

число	1	2	8	7	.	9	2	3
позиция	3	2	1	0		-1	-2	-3

Тогда число 1287.923 можно представить в виде:

1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10³ +2·10² +8·10¹+7·10⁰+9·10^-1+2·10^-2+3·10^-3.

В общем случае формулу можно представить в следующем виде:

Ц_n·sⁿ+Ц_n-1·s^n-1+…+Ц₁·s¹+Ц₀·s⁰+Д_-1·s^-1+Д_-2·s^-2+…+Д_-k·s^-k

(1)

где Ц_n-целое число в позиции n, Д_-k— дробное число в позиции (-k), s — система счисления.

Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.

В таблице Таб.1 представлены числа в разных системах счисления.

Таблица 1
Система счисления
10	2	8	16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

Перевод чисел из одной системы счисления в другую

Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.

Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:

1·2⁶+0·2⁵+1·2⁴+1·2³+1·2² +0·2¹+1·2⁰+0·2^-1+0·2^-2+1·2^-3 =64+16+8+4+1+1/8=93.125

Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:

Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:

Здесь A -заменен на 10, B — на 11, C— на 12, F — на 15.

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.

Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.

Пример 4. Переведем число 159 из десятичной СС в двоичную СС:

159	2
158	79	2
1	78	39	2
	1	38	19	2
		1	18	9	2
			1	8	4	2
				1	4	2	2
					0	2	1
						0

Рис. 1

Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:

159₁₀=10011111₂.

Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.

615	8
608	76	8
7	72	9	8
	4	8	1
		1

Рис. 2

При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:

615₁₀=1147₈.

Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.

19673	16
19664	1229	16
9	1216	76	16
	13	64	4
		12

Рис. 3

Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.

Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.

Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).

Рассмотрим вышеизложенное на примерах.

Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.

		0.214
	x	2
0		0.428
	x	2
0		0.856
	x	2
1		0.712
	x	2
1		0.424
	x	2
0		0.848
	x	2
1		0.696
	x	2
1		0.392

Рис. 4

Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.

Следовательно можно записать:

0.214₁₀=0.0011011₂.

Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.

		0.125
	x	2
0		0.25
	x	2
0		0.5
	x	2
1		0.0

Рис. 5

Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:

0.125₁₀=0.001₂.

Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.

		0.214
	x	16
3		0.424
	x	16
6		0.784
	x	16
12		0.544
	x	16
8		0.704
	x	16
11		0.264
	x	16
4		0.224

Рис. 6

Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:

0.214₁₀=0.36C8B4₁₆.

Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.

		0.512
	x	8
4		0.096
	x	8
0		0.768
	x	8
6		0.144
	x	8
1		0.152
	x	8
1		0.216
	x	8
1		0.728

Рис. 7

Получили:

0.512₁₀=0.406111₈.

Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:

159.125₁₀=10011111.001₂.

Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:

19673.214₁₀=4CD9.36C8B4₁₆.

Двоичный преобразователь в десятичный

Чтобы использовать этот новый инструмент для преобразования двоичных чисел в десятичные числа , введите любое двоичное значение, например 1010, в левое поле ниже, а затем нажмите кнопку «Преобразовать». Вы можете увидеть результат в правом поле ниже. В десятичные числа можно преобразовать до 63 двоичных символов.

Результат преобразования двоичного числа в десятичный в базовых числах

Двоичная система

Двоичная система счисления использует число 2 как основание (основание).Как система счисления с основанием 2, она состоит только из двух чисел: 0 и 1.

Хотя она применялась в Древнем Египте, Китае и Индии для различных целей, двоичная система стала языком электроники и компьютеров в мире. современный мир. Это наиболее эффективная система для обнаружения состояния выключения (0) и включения (1) электрического сигнала. Это также основа для двоичного кода, который используется для компоновки данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.

Двоичное число читать проще, чем кажется: это позиционная система; следовательно, каждая цифра в двоичном числе возводится в степень двойки, начиная с самого правого с 2 ⁰ . В двоичной системе каждая двоичная цифра относится к 1 биту.

Десятичная система

Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. В качестве основы (системы счисления) используется число 10. Следовательно, в нем 10 символов: числа от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями. Сложность представления очень больших чисел в десятичной системе была преодолена с помощью индийско-арабской системы счисления. Индусско-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степеней основания 10; цифры возводятся в степень n ^th в соответствии с их положением.

Например, возьмите номер 2345.67 в десятичной системе:

• Цифра 5 стоит на позиции единиц (10 ⁰ , что равно 1),
• 4 находится на позиции десятков (10 ¹ )
• 3 находится в позиции сотен (10 ² )
• 2 в тысячах (10 ³ )
• Между тем цифра 6 после десятичной запятой находится в десятых долях (1/10, что составляет 10 ^-1 ), а 7 — в сотых (1/100, что составляет 10 ^-2 ) позиции
• Итак, число 2345.67 также можно представить следующим образом: (2 * 10 ³ ) + (3 * 10 ² ) + (4 * 10 ¹ ) + (5 * 10 ⁰ ) + (6 * 10 ^-1 ) + (7 * 10 ^-2 )

Как читать двоичное число

Для преобразования двоичного числа в десятичное могут помочь базовые знания о том, как читать двоичное число. Как упоминалось выше, в позиционной системе двоичного числа каждый бит (двоичная цифра) представляет собой степень 2. Это означает, что каждое двоичное число может быть представлено как степень двойки, причем крайнее правое число находится в позиции 2 ⁰ .

Пример : Двоичное число (1010) ₂ также можно записать следующим образом: (1 * 2 ³ ) + (0 * 2 ² ) + (1 * 2 ¹ ) + (0 * 2 ⁰ )

Как преобразовать двоичное в десятичное

Существует два метода преобразования двоичного числа в десятичное. Первый использует позиционное представление двоичного файла, описанное выше. Второй метод называется double dabble и используется для более быстрого преобразования длинных двоичных строк.Он не использует позиции.

Метод 1: Использование позиций

Шаг 1 : Запишите двоичное число.

Шаг 2 : Начиная с младшего разряда (LSB — крайний правый), умножьте цифру на значение позиции. Продолжайте делать это, пока не дойдете до самой значащей цифры (MSB — крайний левый).

Шаг 3 : сложите результаты, и вы получите десятичный эквивалент данного двоичного числа.

Теперь применим эти шаги, например, к приведенному выше двоичному числу (1010) ₂

• Шаг 1 : Запишите (1010) ₂ и определите позиции, а именно степени двойки, которым принадлежит цифра.
• Шаг 2 : Представьте число с точки зрения его позиций. (1 * 2 ³ ) + (0 * 2 ² ) + (1 * 2 ¹ ) + (0 * 2 ⁰ )
• Шаг 3 : (1 * 8) + (0 * 4) + (1 * 2) + (0 * 1) = 8 + 0 + 2 + 0 = 10
• Следовательно, (1010) ₂ = (10) ₁₀

(Обратите внимание, что цифры 0 в двоичном формате дают нулевые значения и в десятичном.)

Метод 2: Двойное прикосновение

Также называемый удвоением, этот метод на самом деле является алгоритмом, который может применяться для преобразования любого заданного основания в десятичное. Double dabble помогает преобразовывать более длинные двоичные строки в голове, и единственное, что нужно помнить, — это «удвоить сумму и добавить следующую цифру».

• Шаг 1: Запишите двоичное число. Начиная слева, вы будете удваивать предыдущую сумму и добавлять текущую цифру. На первом этапе предыдущая сумма всегда равна 0, потому что вы только начинаете.Следовательно, удвойте сумму (0 * 2 = 0) и добавьте самую левую цифру.
• Шаг 2: Удвойте сумму и добавьте следующую самую левую цифру.
• Шаг 3: Удвойте сумму и добавьте следующую крайнюю левую цифру. Повторяйте это, пока у вас не закончатся цифры.
• Шаг 4: Результат, который вы получите после добавления последней цифры к предыдущей удвоенной сумме, является десятичным эквивалентом.

А теперь применим метод двойного приближения к тому же двоичному числу (1010) ₂

• Ваша предыдущая сумма 0.Ваша крайняя левая цифра 1. Удвойте сумму и добавьте крайнюю левую цифру
  (0 * 2) + 1 = 1
.
• Шаг 2: Удвойте предыдущую сумму и добавьте следующую крайнюю левую цифру.
  (1 * 2) + 0 = 2
• Шаг 3: Удвойте предыдущую сумму и добавьте следующую крайнюю левую цифру.
  (2 * 2) + 1 = 5
• Шаг 4: Удвойте предыдущую сумму и добавьте следующую крайнюю левую цифру.
  (5 * 2) + 0 = 10

Это то место, где в этом примере у вас заканчиваются цифры. Следовательно, (1010) ₂ = (10) ₁₀

Примеры преобразования двоичного числа в десятичное

Пример 1 : (1110010) ₂ = (114) ₁₀

Метод 1:
(0 * 2 ⁰ ) + (1 * 2 ¹ ) + (0 * 2 ² ) + (0 * 2 ³ ) + (1 * 2 ⁴ ) + (1 * 2 ⁵ ) + (1 * 2 ⁶ )
= (0 * 1) + (1 * 2) + (0 * 4) + (0 * 8) + (1 * 16) + (1 * 32) + (1 * 64)
= 0 + 2 + 0 + 0 + 16 + 32 + 64 = 114

Метод 2:
0 (предыдущая сумма в начальной точке)
(0 + 1) * 2 = 2
2 + 1 = 3
3 * 2 = 6
6 + 1 = 7
7 * 2 = 14
14 + 0 = 14
14 * 2 = 28
28 + 0 = 28
28 * 2 = 56
56 + 1 = 57
57 * 2 = 114

Пример 2 : (11011) ₂ = (27) ₁₀

Метод 1:
(0 * 2 ⁰ ) + (1 * 2 ¹ ) + (0 * 2 ² ) + (1 * 2 ³ ) + (1 * 2 ⁴ )
= (1 * 1) + (1 * 2) + (0 * 4) + (1 * 8) + (1 * 16)
= 1 + 2 + 0 + 8 + 16 = 27

Метод 2:
(0 * 2) + 1 = 1
(1 * 2) + 1 = 3
(3 * 2) + 0 = 6
(6 * 2) + 1 = 13
(13 * 2) + 1 = 27

Сопутствующие преобразователи:
Десятичный преобразователь в двоичный

Таблица двоичных десятичных преобразований

00275 000001006 902 902 902 00002902 9027 11902 9027 11902 9022 902 902

Двоичный	Десятичный
00000001	1
00000010	2
00000011	3
00000100	4	4
00000111	7
00001000	8
00001001	9
00001010	10
00001010	10
13
00001110	14
00001111	15
00010000	16
00010003	0				00010001			19
0 0010100	20
00010101	21
00010110	22
00010111	23
	26
00011011	27
00011100	28
00011101	29
00011110				00011110
00100001	33
00100010	34
00100011	35
00100100	36
36
00100100	36
00100111 9027 6	39
00101000	40
00101001	0041
00101010	42
00101011		00101011	2	45
00101110	46
00101111	47
00110000	48
00110001	6
00110001	3 49
00110001	3 49
00110100	52
00110101	53
00110110	54
00110111	3 55		00111010	58
00111011	59
00111100	60
00111101	61
00111110
6
00111110	6

960 119

01

902 902

Двоичный	Десятичный
01000001	65
01000010	66
01000011	67
01000100	68		01000111	71
01001000	72
01001001	73
01001010
01001010	74
3	2		77
01001110	78
01001111	79
01010000	80
01010006
01010006 83
01010100	84
01010101	85
01010110	86
01010111	87
01011000	88
01011001	89
01011010	90
01011011	91
01011100	92
01011101	93
01100001	97
01100010	98
01100011	99
01100100	3
01100100	3 100
01100100	3 100
01100100	3 100
0 1100111	103
01101000	104
01101001	105
01101010	106
106
6 9011 9011	109
01101110	110
01101111	111
01110000	112
01110003			01110003
01110100	116
01110101	117
01110110	118
01110111	00 9011	01110111	00
01111010	122
01111011	123
01111100	124
01111101	125	125	128

100003 1000032 10100000

8

8 902 75166 902 902 902 902 902 902 10111001 902 76 191

Двоичный	Десятичный
10000001	129
10000010	130
10000011	131
10000100	132
	132
		10000111	135
10001000	136
10001001	137
10001010	138
10001010	138
1402751						141
10001110	142
10001111	143
10010000	144
1001000756
1001000751	147
10010100	148
10010101	149
10010110	150
10010111	6
10011010	154
10011011	155
10011100	156
10011101	157
160
10100001	161
10100010	162
10100011	163
163
10100111	167
10101000	168
10101001	169
10101010
10101010	10101010
10101101	173
10101110	174
10101111	175
10110000
10110000	6
10110000	6
10110011	179
10110100	180
10110101	181
10110110	182	10110110	182
185
10111010	186
10111011	187
10111100	188
101111075 9011 9011 9011 9027 10276
11000000	192

8

8

Двоичный	Десятичный
11000001	193
11000010	194
11000011	195
11000100	196	11000100		196	902	11000111	199
11001000	200
11001001	201
11001010	202
11001011	203
11001100	204
11001101	205
11001110	206
11001111	207
11010000	208
110106 211
11010100	212
11010101	213
11010110	214
11010111	215
11010111	2 902
11011010	218
11011011	219
11011100	220
11011101	221	1102 902 11100000	224
11100001	225
11100010	226
11100011	227
227
227
6 902 75 230
11100111	231
11101000	232
11101001	233
11101010
11101010
11101101	237
11101110	238
11101111	239
11110000	240
11110001	241
11110010	242
11110011	243
11110100	244
11110101	245
11110110	246
11110111	247
11111000	248
11111001 902 76	249
11111010	250
11111011	251
11111100	252
111111075 75 252
11111107 255

.

Десятичный преобразователь в двоичный

Чтобы использовать этот инструмент преобразования десятичных чисел в двоичные , вы должны ввести десятичное значение, например 308, в левое поле ниже, а затем нажмите кнопку «Преобразовать». Таким образом, вы можете преобразовать до 19 десятичных символов (максимальное значение 9223372036854775807) в двоичное значение .

Результат преобразования десятичных чисел в двоичные в базовых числах

Десятичная система

Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни.В качестве основы (системы счисления) используется число 10. Следовательно, в нем 10 символов: числа от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями. Сложность представления очень больших чисел в десятичной системе была преодолена с помощью индийско-арабской системы счисления. Индусско-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степеней основания 10; цифры возводятся в степень n ^th в соответствии с их положением.

Например, возьмите число 2345,67 в десятичной системе счисления:

• Цифра 5 стоит на позиции единиц (10 ⁰ , что равно 1),
• 4 находится на позиции десятков (10 ¹ )
• 3 находится в позиции сотен (10 ² )
• 2 в тысячах (10 ³ )
• Между тем цифра 6 после десятичной точки находится в десятых долях (1/10, что составляет 10 ^-1 ), а 7 — в сотых (1/100, что составляет 10 ^-2 ) позиции
• Таким образом, число 2345.67 также можно представить следующим образом: (2 * 10 ³ ) + (3 * 10 ² ) + (4 * 10 ¹ ) + (5 * 10 ⁰ ) + (6 * 10 ^-1 ) + (7 * 10 ^-2 )

Двоичная система

Двоичная система счисления использует число 2 в качестве основания (основание). Как система счисления с основанием 2, она состоит только из двух чисел: 0 и 1.

Хотя она применялась в Древнем Египте, Китае и Индии для различных целей, двоичная система стала языком электроники и компьютеров в мире. современный мир.Это наиболее эффективная система для обнаружения состояния выключения (0) и включения (1) электрического сигнала. Это также основа для двоичного кода, который используется для компоновки данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.

Двоичное число читать проще, чем кажется: это позиционная система; следовательно, каждая цифра в двоичном числе возводится в степень двойки, начиная с самого правого с 2 ⁰ . В двоичной системе каждая двоичная цифра относится к 1 биту.

Примеры преобразования десятичных чисел в двоичные

• (51) ₁₀ = (110011) ₂
• (217) ₁₀ = (11011001) ₂
• (8023) ₁₀ = (1111101010111) ₂

Таблица преобразования десятичных чисел в двоичные

Десятичное	Двоичное
1	00000001
2	00000010
3	00000011
4	00000100

0 00101

7 00000111 8 00001000 9 00001001 10 00001010 0000109 0000109 00001101 14 00001110 15 00001111 16 00010000 16 00010000 170 170 0009 00010011 2 0 00010100 21 00010101 22 00010110 23 00010111 0 9011 9011 00011010 27 00011011 28 00011100 29 00011101 300 300 00011 33 00100001 34 00100010 35 00100011 36 00100100 901 09 00100111 39 40 00101000 41 00101001 42 00101010 430 46 00101110 47 00101111 48 00110000 49 001100010 52 00110100 53 00110101 54 00110110 55 00110111 00101 58 00111010 59 00111011 60 00111100 61 00111101 62 0010117 62 00111110 62 00111110 62 00111110 Десятичное Двоичное 65 01000001 66 01000010 67 01000011 68 01000100 9010 9010 9010 9010 71 01000111 72 01001000 73 01001001 74 01001010 01001101 78 01001110 79 01001111 80 9010 9010 01010000 9010 9010 9010 9010 01010011 84 01010100 85 01010101 86 01010110 87 01010111 9010 9010 01011010 91 +01011011 92 +01011100 93 +01011101 94 01011110 95 01011111 96 01100000 97 01100001 98 01100010 99 01100011 10001101 1 03 01100111 104 01101000 105 01101001 106 01101010 01101101 110 01101110 111 01101111 112 01110000 112 01110000 11310 11310 11310 116 01110100 117 01110101 118 01110110 9010 9011 9010 9011 9011 122 01111010 123 01111011 124 01111100 125 011111012725 01111101 128102 10000000 9010 10107 Десятичное Двоичное 129 10000001 130 10000010 131 10000011 132 10000100 10000100 135 10000111 136 10001000 137 10001001 138 10001010 1000101 10001101 142 10001110 143 10001111 144 10010000 0010145107 10010011 148 10010100 149 10010101 150 10010110 151 100101 160 10100000 161 10100001 162 10100010 163 10100011 9010 10 100110 167 10100111 168 10101000 169 10101001 170 10101010 171 10101011 172 10101100 173 10101101 174 10101110 175 10101111 176 1011100000 176 1011100000 179 10110011 180 10110100 181 10110101 182 10110110 9 0109 10111001 186 10111010 187 10111011 188 10111100 189 10111101 190 10111110 191 10111111 192 11000000 Десятичное Двоичное 193 11000001 194 11000010 195 11000011 196 1100010010 199 11000111 200 11001000 201 11001001 202 11001010 11001010 11001101 206 11001110 207 11001111 208 11010000 1101 1101 11010011 212 11010100 213 11010101 214 11010110 215 0 110101 218 11011010 219 11011011 220 11011100 221 11011101 224 11100000 225 11100001 226 11100010 227 9010 9010 11100011 11 100110 231 11100111 232 11101000 233 11101001 234 11101010 235 11101011 236 11101100 237 11101101 238 11101110 239 11101111 240 11110000 241 11110001 242 11110010 243 11110011 244 11110100 245 11110101 246 11110110 9 0109 11111001 250 11111010 251 11111011 252 11111100 253 11111101 254 11111110 255 11111111 . Калькулятор двоичного шестнадцатеричного десятичного преобразователя Используя наши новые эффективные инструменты преобразования, вы можете легко преобразовать двоичные, шестнадцатеричные, десятичные, двоичные и ascii числа друг другу. Все, что вам нужно, — это открыть страницу своей пары конверсий и ввести число в соответствующее поле. В дополнение к этому мы также поможем вам с основной информацией, которую вам нужно знать об этих преобразованиях. Попробуйте наш новый отличный и удобный двоичный, шестнадцатеричный и десятичный калькулятор онлайн прямо сейчас! Обновления В конвертеры добавлена ​​опция заполнения.12 сентября 2020 г. Своп конверсионные ссылки добавлены в конвертеры. 15 апреля 2020 г. Добавлен новый инструмент Octal To Binary Converter. 14 апреля 2020 г. Добавлен новый инструмент Конвертер Hex в Ascii (String). 14 апреля 2020 г. Добавлен новый инструмент Конвертер двоичных файлов в восьмеричные. 14 апреля 2020 г. Добавлен новый инструмент «Конвертер восьмеричного в десятичный». 12 апреля 2020 г. Все таблицы преобразования обновлены на страницах преобразователя.24 марта 2020 г. Содержимое Ascii Text To Binary Converter обновлено. Содержимое Ascii Text To Decimal Converter обновлено. Содержимое Ascii Text To Hexadecimal Converter обновлено. 28 октября 2019 Содержимое преобразователя десятичного числа в шестнадцатеричное обновлено. Содержимое преобразователя десятичного числа в восьмеричное обновлено. 17 октября 2019 г. Содержимое Hex To Binary Converter обновлено. 15 октября 2019 г. Содержимое конвертера двоичного текста в Ascii обновлено.14 октября 2019 Содержимое двоичного преобразователя в шестнадцатеричное обновлено. 12 октября 2019 г. Содержимое двоично-десятичного преобразователя обновлено. 12 октября 2019 г. Дизайн веб-сайта улучшен в лучшую сторону. Мы также обновили содержимое двоичной и десятичной системной информации. Также мы обновили двоично-десятичный преобразователь 14 мая 2019 Мы только что перешли на уровень защищенного соединения. Теперь вы можете использовать наш сайт в зашифрованном соединении.21 декабря 2017 Таблица преобразования двоичных файлов Ascii обновлена ​​для удобства чтения на мобильных устройствах. Оптимизация скорости для сокращения времени загрузки сайта. 4 октября 2016 г. В текстовых конвертерах Ascii обновлено и исправлено преобразование специальных символов. 23 сентября 2015 г. Исправлена ​​ошибка, когда между цифрами входного номера оставался пробел. 4 сентября 2015 г. Мы запустили наше простое приложение для Android, вы можете получить Android-приложение в магазине.30 июня 2015 г. Исправлена ​​проверка максимального шестнадцатеричного числа. Максимум. шестнадцатеричное значение — 7fffffffffffffff. 26 ноября 2014 г. Исправлена ​​проверка двоичных и шестнадцатеричных чисел. 22 сентября 2014 г. Теперь вы можете преобразовать до 32 шестнадцатеричных символов в десятичное число. 21 сентября 2014 г. Мы открыли наш официальный аккаунт в Твиттере, пожалуйста, Следуйте @BinHexConverter.16 сентября 2014 г. Фон сайта изменен для удобства чтения и расчета. 12 сентября 2014 г. Добавлен ascii в десятичный и шестнадцатеричный преобразователи. 2 августа 2014 г. Обновлена ​​информация в шестнадцатеричном формате, исправлена ​​информация о шестнадцатеричном формате html. 16 июля 2014 г. Исправлена ​​дополнительная битовая ошибка в преобразовании ascii в двоичное. 12 июля 2014 г. Информация о системе счисления обновлена.31 мая 2014 г. Цвета фона формы преобразования и стили ввода формы обновлены, чтобы упростить работу с калькулятором. 26 мая 2014 Дизайн binaryhexconverter.com был обновлен для облегчения чтения и навигации по сайту. Пожалуйста, свяжитесь со мной по любым вопросам или предложениям по дизайну и работе сайта. 24 мая 2014 Мы рекомендуем gbmb.org для преобразования единиц хранения данных. . Двоичный калькулятор Используйте следующие калькуляторы для сложения, вычитания, умножения или деления двух двоичных значений, а также для преобразования двоичных значений в десятичные значения и наоборот. Двоичное вычисление — сложение, вычитание, умножение или деление Преобразовать двоичное значение в десятичное Преобразовать десятичное значение в двоичное Калькулятор RelatedHex | Калькулятор IP-подсети Двоичная система счисления — это система счисления, которая функционирует практически идентично десятичной системе счисления, с которой люди, вероятно, более знакомы.В то время как в десятичной системе счисления используется число 10 в качестве основы, в двоичной системе используется 2. Кроме того, хотя в десятичной системе используются цифры от 0 до 9, в двоичной системе используются только 0 и 1, и каждая цифра называется битом. . Помимо этих различий, такие операции, как сложение, вычитание, умножение и деление, вычисляются по тем же правилам, что и десятичная система. Практически все современные технологии и компьютеры используют двоичную систему из-за простоты ее реализации в цифровых схемах с использованием логических вентилей.Намного проще разработать оборудование, которое должно определять только два состояния: включено и выключено (или истина / ложь, присутствует / отсутствует и т. Д.). Использование десятичной системы требует оборудования, которое может обнаруживать 10 состояний для цифр от 0 до 9, что является более сложным. Ниже приведены некоторые типичные преобразования между двоичными и десятичными значениями: Двоичное / десятичное преобразование Десятичное Двоичное 0 0 1 1 2 10 3 11 4 100 7 111 8 1000 10 1010 16 10000 20 10100 Работа с двоичным кодом поначалу может показаться запутанной, понимание того, что каждое двоичное разрядное значение представляет 2 n , так же, как каждое десятичное место представляет 10 n , должно помочь уточнить.Возьмем, к примеру, число 8. В десятичной системе счисления 8 находится в первом десятичном разряде слева от десятичной точки, что означает 10 0 место. По сути это означает: 8 × 10 0 = 8 × 1 = 8 Используя число 18 для сравнения: (1 × 10 1 ) + (8 × 10 0 ) = 10 + 8 = 18 В двоичном формате 8 представлено как 1000. При чтении справа налево первый 0 представляет 2 0 , второй 2 1 , третий 2 2 и четвертый 2 3 ; точно так же, как десятичная система, за исключением того, что с основанием 2, а не 10.Поскольку 2 3 = 8, в его позиции вводится 1, что дает 1000. Используя 18 или 10010 в качестве примера: 18 = 16 + 2 = 2 4 + 2 1 10010 = (1 × 2 4 ) + (0 × 2 3 ) + (0 × 2 2 ) + (1 × 2 1 ) + (0 × 2 0 ) = 18 Пошаговый процесс преобразования десятичной системы в двоичную: Найдите наибольшую степень двойки, лежащую в пределах данного числа Вычтите это значение из заданного числа Найдите наибольшую степень двойки в остатке, найденном на шаге 2 Повторять, пока не останется остаток Введите 1 для каждого найденного двоичного разряда и 0 для остальных Снова используя целевое значение 18 в качестве примера, ниже представлен другой способ визуализировать это: 2 n 2 4 2 3 2 2 2 1 2 0 Экземпляры в пределах 18 1 0 0 1 0 Цель: 18 18 — 16 = 2 → 2 — 2 = 0 Преобразование из двоичной системы в десятичную проще .Определите все значения разряда, в которых встречается 1, и найдите сумму значений. Пример: 10111 = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 ) = 23 Отсюда: 16 + 4 + 2 + 1 = 23. Сложение двоичных файлов Двоичное сложение следует тем же правилам, что и сложение в десятичной системе, за исключением того, что вместо переноса 1, когда добавленные значения равны 10, перенос происходит, когда результат сложения равен 2.Обратитесь к примеру ниже для пояснения. Обратите внимание, что в двоичной системе: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0, переносим 1, т.е. 10 EX: 1 0 1 1 1 1 1 0 1 + 1 0 1 1 1 = 1 0 0 1 0 0 Единственная реальная разница между двоичным и десятичным сложением состоит в том, что значение 2 в двоичная система эквивалентна 10 в десятичной системе.Обратите внимание, что единицы с надстрочным индексом представляют собой перенесенные цифры. Распространенная ошибка, на которую следует обратить внимание при выполнении двоичного сложения, — это случай, когда 1 + 1 = 0 также имеет 1, перенесенную из предыдущего столбца справа. Тогда значение внизу должно быть 1 из перенесенного на 1, а не 0. Это можно увидеть в третьем столбце справа в приведенном выше примере. Двоичное вычитание Подобно двоичному сложению, есть небольшая разница между двоичным и десятичным вычитанием, за исключением тех, которые возникают из-за использования только цифр 0 и 1.Заимствование происходит в любом случае, когда вычитаемое число больше, чем число, из которого оно вычитается. При бинарном вычитании заимствование необходимо только тогда, когда 1 вычитается из 0. Когда это происходит, 0 в столбце заимствования по существу становится «2» (изменение 0-1 на 2-1 = 1), в то время как уменьшение 1 в столбце, из которого заимствуется, на 1. Если следующий столбец также равен 0, заимствование должно происходить из каждого последующего столбца, пока столбец со значением 1 не может быть уменьшен до 0.Обратитесь к примеру ниже для пояснения. Обратите внимание, что в двоичной системе: 0 — 0 = 0 0-1 = 1, заимствовать 1, в результате чего -1 переносится на 1 — 0 = 1 1-1 = 0 EX1: -1 1 2 0 1 1 1 — 0 1 1 0 1 = 0 1 0 1 0 EX2: -1 1 2-1 0 0 — 0 1 1 = 0 0 1 Обратите внимание, что отображаемые верхние индексы — это изменения, которые происходят с каждым битом при заимствовании.Столбец заимствования по существу получает 2 от заимствования, а столбец, из которого заимствовано, уменьшается на 1. Двоичное умножение Двоичное умножение, возможно, проще, чем его десятичный аналог. Поскольку используются только значения 0 и 1, результаты, которые должны быть добавлены, либо те же, что и для первого члена, либо 0. Обратите внимание, что в каждой последующей строке необходимо добавить заполнитель 0, а значение сдвинуть влево, как в десятичном умножении. Сложность двоичного умножения возникает из-за утомительного двоичного сложения, зависящего от количества битов в каждом члене.Обратитесь к примеру ниже для пояснения. Обратите внимание, что в двоичной системе: 0 × 0 = 0 0 × 1 = 0 1 × 0 = 0 1 × 1 = 1 EX: 1 0 1 1 1 × 1 1 0 1 1 1 + 1 0 1 1 1 0 = 1 0 0 0 1 0 1 Как видно из приведенного выше примера, процесс двоичного умножения такой же, как и при десятичном умножении.Обратите внимание, что заполнитель 0 написан во второй строке. Обычно заполнитель 0 визуально не присутствует при десятичном умножении. Хотя то же самое можно сделать в этом примере (с предполагаемым заполнителем 0, а не явным), он включен в этот пример, потому что 0 актуален для любого двоичного калькулятора сложения / вычитания, подобного тому, который представлен на этой странице. Без отображения 0 можно было бы ошибиться, исключив 0 при добавлении двоичных значений, показанных выше.Еще раз обратите внимание, что в двоичной системе любой 0 справа от 1 имеет значение, а любой 0 слева от последней единицы в значении — нет. EX: 1 0 1 0 1 1 0 0 = 0 0 1 0 1 0 1 1 0 0 ≠ 1 0 1 0 1 1 0 0 0 0 Бинарный отдел Процесс двоичного деления аналогичен длинному делению в десятичной системе счисления. Дивиденд по-прежнему делится на делитель таким же образом, с единственной существенной разницей, заключающейся в использовании двоичного, а не десятичного вычитания.Обратите внимание, что хорошее понимание двоичного вычитания важно для проведения двоичного деления. Обратитесь к примеру ниже, а также к разделу двоичного вычитания для пояснения. . Похожие записи 21.11.2024 0 Особенности питания кормящей мамы: что можно и нельзя есть при грудном вскармливании 19.11.2024 0 Новорожденный какает слизью: причины появления слизи в кале грудничка 19.11.2024 0 Гемангиома у новорожденных: причины, виды, лечение и профилактика Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт