Эффект гаусса. Эффект Гаусса в полупроводниках и проводниках: принцип, применение и практическое значение

Что такое эффект Гаусса в полупроводниках и проводниках. Как он проявляется и от чего зависит. Где применяется эффект Гаусса на практике. Какое значение имеет для современной электроники и науки.

Что представляет собой эффект Гаусса

Эффект Гаусса (также называемый магниторезистивным эффектом) — это изменение электрического сопротивления проводника или полупроводника под действием внешнего магнитного поля. Был открыт немецким физиком Карлом Фридрихом Гауссом в 1851 году.

Суть эффекта заключается в том, что при помещении образца материала в магнитное поле, его удельное электрическое сопротивление увеличивается. Причем степень изменения сопротивления зависит от величины индукции магнитного поля.

Физический механизм возникновения эффекта Гаусса

Для понимания физической природы эффекта Гаусса необходимо рассмотреть поведение носителей заряда в проводнике или полупроводнике при наложении магнитного поля:

• В отсутствие магнитного поля носители заряда (электроны или дырки) движутся прямолинейно под действием электрического поля.
• При наложении магнитного поля на движущиеся заряды действует сила Лоренца, которая искривляет их траектории.
• Искривление траекторий приводит к увеличению длины пути носителей заряда и росту вероятности их рассеяния на дефектах кристаллической решетки.
• В результате подвижность носителей заряда уменьшается, а электрическое сопротивление материала возрастает.

Таким образом, магнитное поле как бы «тормозит» движение носителей заряда, что проявляется в увеличении удельного сопротивления материала.

От чего зависит величина эффекта Гаусса

Степень проявления магниторезистивного эффекта зависит от ряда факторов:

1. Индукция магнитного поля — чем сильнее поле, тем больше изменение сопротивления.
2. Подвижность носителей заряда — в материалах с высокой подвижностью эффект выражен сильнее.
3. Концентрация носителей заряда — при меньшей концентрации эффект проявляется сильнее.
4. Температура — с понижением температуры магниторезистивный эффект усиливается.
5. Геометрия образца — в тонких пленках и проволоках эффект выражен сильнее, чем в массивных образцах.

Кроме того, величина эффекта Гаусса зависит от ориентации магнитного поля относительно направления электрического тока в образце.

Математическое описание эффекта Гаусса

Количественно магниторезистивный эффект описывается относительным изменением удельного сопротивления материала:

Δρ/ρ = (ρ(B) — ρ(0)) / ρ(0)

где:

• Δρ/ρ — относительное изменение удельного сопротивления
• ρ(B) — удельное сопротивление в магнитном поле с индукцией B
• ρ(0) — удельное сопротивление в отсутствие магнитного поля

Для слабых магнитных полей зависимость имеет квадратичный характер:

Δρ/ρ ~ B²

В сильных магнитных полях наблюдается линейная зависимость:

Δρ/ρ ~ B

Точный вид зависимости определяется свойствами конкретного материала и геометрией образца.

Особенности проявления эффекта Гаусса в различных материалах

Магниторезистивный эффект наблюдается как в металлах, так и в полупроводниках, но имеет ряд особенностей:

В металлах:

• Эффект относительно слабый — изменение сопротивления составляет доли процента
• Наблюдается положительное магнитосопротивление (сопротивление растет с увеличением поля)
• Квадратичная зависимость от индукции магнитного поля

В полупроводниках:

• Эффект может быть очень большим — до сотен процентов
• Возможно как положительное, так и отрицательное магнитосопротивление
• Сложная нелинейная зависимость от индукции поля
• Сильная зависимость от температуры и концентрации примесей

Наиболее сильно эффект Гаусса проявляется в полупроводниках с высокой подвижностью носителей заряда, таких как InSb, InAs, GaAs.

Практическое применение эффекта Гаусса

Магниторезистивный эффект нашел широкое применение в различных областях науки и техники:

1. Магнитные датчики

На основе эффекта Гаусса создаются высокочувствительные датчики магнитного поля — магниторезисторы. Они используются для:

• Измерения слабых магнитных полей
• Бесконтактного измерения электрических токов
• Определения положения и перемещения объектов
• Создания электронных компасов

2. Магнитные головки

Эффект Гаусса применяется в считывающих головках жестких дисков и магнитных лент. Это позволяет считывать информацию с высокой плотностью записи.

3. Магниторезистивная память (MRAM)

Разработаны устройства энергонезависимой памяти на основе гигантского магниторезистивного эффекта. Такая память сочетает быстродействие, высокую плотность записи и энергонезависимость.

4. Магнитные сенсоры

Датчики на эффекте Гаусса используются в автомобильной электронике для контроля различных параметров:

• Положение педалей и рулевого колеса
• Скорость вращения колес
• Уровень жидкостей

5. Научные исследования

Измерение магнитосопротивления — мощный инструмент для изучения электронной структуры твердых тел, в частности:

• Определение концентрации и подвижности носителей заряда
• Исследование энергетического спектра электронов
• Изучение процессов рассеяния носителей заряда

Разновидности магниторезистивного эффекта

Помимо классического эффекта Гаусса, существуют и другие разновидности магниторезистивного эффекта:

1. Анизотропное магнитосопротивление

Наблюдается в ферромагнитных материалах. Сопротивление зависит от угла между направлением тока и намагниченностью образца.

2. Гигантское магнитосопротивление

Проявляется в многослойных структурах, состоящих из чередующихся ферромагнитных и немагнитных слоев. Изменение сопротивления может достигать сотен процентов.

3. Колоссальное магнитосопротивление

Наблюдается в некоторых магнитных полупроводниках. Характеризуется огромным изменением сопротивления (до миллионов процентов) в магнитном поле.

4. Туннельное магнитосопротивление

Возникает в структурах типа ферромагнетик-диэлектрик-ферромагнетик. Основано на спин-зависимом туннелировании электронов.

Эти эффекты также находят широкое применение в современной электронике и спинтронике.

Значение эффекта Гаусса для современной науки и технологий

Открытие и изучение магниторезистивного эффекта имело огромное значение для развития физики твердого тела и современных технологий:

• Позволило глубже понять процессы электропроводности в твердых телах
• Дало мощный инструмент для исследования электронной структуры материалов
• Привело к созданию новых типов электронных устройств и сенсоров
• Способствовало развитию спинтроники — электроники, использующей спин электрона
• Нашло применение в технологиях хранения и обработки информации

Исследование различных видов магниторезистивного эффекта остается актуальной задачей современной физики. Это открывает перспективы создания новых материалов и устройств с уникальными свойствами.

Заключение

Эффект Гаусса, открытый более 150 лет назад, до сих пор играет важную роль в физике твердого тела и современных технологиях. Его изучение позволило значительно продвинуться в понимании природы электропроводности и магнетизма.

Практическое применение магниторезистивного эффекта привело к созданию целого ряда устройств — от простых датчиков до сложных систем хранения информации. Дальнейшие исследования в этой области открывают перспективы развития новых направлений электроники и спинтроники.

Таким образом, эффект Гаусса наглядно демонстрирует, как фундаментальные исследования в физике могут приводить к революционным технологическим прорывам.

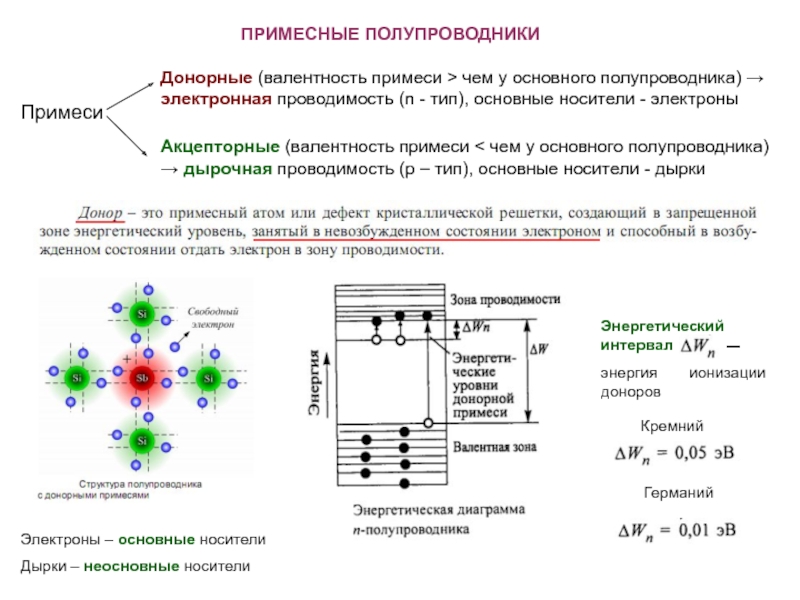
3.1.3. Магниторезистивный эффект (эффект Гаусса)

Магниторезистивный эффект (эффект Гаусса) – изменение удельного сопротивления проводниковых и полупроводниковых материалов в магнитном поле.

На рис. 3.4 показана структурная схема эффекта. При помещении образца прямоугольного сечения из проводникового или полупроводникового материала в магнитное поле и при пропускании по нему электрического тока, направление которого перпендикулярно вектору индукции магнитного поля, сопротивление образца будет возрастать (поперечный эффект Гаусса).Если магнитное поле направлено параллельно направлению тока, то наблюдаетсяпродольный эффект Гаусса. Следует отметить, что при продольном эффекте изменение магнитосопротивления незначительно, поэтому он не получил большого применения.

Рис. 3.4

Магниторезистивный эффект, как и эффект Холла, проявляется исключительно в полупроводниках [1]. Изменение удельного сопротивления вызвано тем, что носители заряда, перемещающиеся в полупроводнике под действием электрического поля, не имеют одинаковых скоростей. Скорости носителей заряда различны и подчиняются распределению, отвечающему статистике Ферми – Дирака [21]. В результате этого поперечное поле Холла компенсирует влияние силы Лоренца только на носители заряда, имеющие среднюю скорость V. Поэтому траектория носителей заряда со скоростью большей или меньшей скоростиVбудет искривлена, что приведет к увеличению числа столкновений (уменьшению длины свободного пробега) и тем самым – к повышению удельного сопротивления полупроводника.

Зависимость удельного сопротивления от магнитной индукции в большом диапазоне изменения индукции можно описать формулой

, (3.17)

где ρ₀ – удельное сопротивление приВ= 0;А– постоянная.

Из (3.17) следует, что при малых В(μ^. В << 1) удельное сопротивлениеρквадратично зависит от индукцииВ, а при больших значениях индукции удельное сопротивление достигает насыщения.

Изменение удельного сопротивления от магнитной индукции Вможет быть описано также приближенной формулой [19]

, (3.18)

где n= (1–2) – в зависимости от величины (μВ).

Магниторезистивный эффект зависит также от направления магнитного поля и размеров образца. Эффект наиболее ярко выражен у пластин, имеющих форму диска Корбино, а также у некоторых сложных конфигураций.

Эффект Гаусса широко используется при построении датчиков магнитного поля, магниторезистивных датчиков.

3.1.4. Эффект Зеебека Эффект Зеебека– возникновение эдс в цепи, состоящей из двух разных проводников (или полупроводников), соединенных концами при различной температуре мест их соединений.

С

Рис. 3.5

труктурная схема эффекта Зеебека показана на рис. 3.5. Если взять проводник, концы которого имеют разные температуры, то от теплого конца к холодному будет передаваться тепловая энергия. Градиент температур приводит к появлению в проводнике электрического поля, обусловленного эффектом Томсона, который заключается в поглощении или высвобождении тепла линейно пропорционально току, проходящего через однородный проводник, имеющий градиент температуры вдоль его длины. Индуцированное электрическое поле приводит к появлению разности потенциалов [21], которая для однородного материала может быть найдена как

, (3.19)

где α₁ – абсолютный коэффициент Зеебека;dT– градиент температур.

Уравнение (3.19) является основным математическим выражением для термоэлектрического эффекта.

Термоэлектрические свойства материалов исследуются с помощью контура (термоэлектрического контура), составленного из двух разных проводников или полупроводников, рис. 3.6а.

а б в

Рис. 3.6

В таком контуре индуцированная теплом разность потенциалов (термоЭДС) называется напряжением Зеебека и образуется тремя составляющими:

1) объемной, обусловленной возникновением разности потенциалов на концах проводника (полупроводника), имеющих разную температуру. Это объясняется тем, что носители зарядов на горячем конце приобретают более высокие энергии и скорости, и они диффундируют к холодному концу. В результате основные носители накапливаются на холодном конце проводника, а на горячем возникает потенциал противоположного знака;

2) контактной, обусловленной температурной зависимостью контактной разности потенциалов мест соединения проводников;

3) фононной, обусловленной увлечением электронов фононами, при превалирующем перемещении последних от горячего конца к холодному. Фононы сталкиваются с основными носителями заряда и увлекают их за собой. При низких температурах фононная составляющая может быть в десятки и сотни раз больше первых двух.

Напряжение Зеебека можно записать в виде степенного ряда от разности температур:

, (3.20)

где α₁,α₂,…, α_n – температурно-независимые коэффициенты;Т₀– некоторая заданная температура калибровки.

Для большинства материалов требуется примерно восемь коэффициентов α_i, чтобы получить погрешность определения термоЭДС не более ±1 % .

Для многих комбинаций материалов в узком интервале температур можно считать, что

, (3.21)

где α₁ – коэффициент Зеебека.

Законы термоэлектрического контура

1. Для получения термоЭДС контур должен состоять из разнородных материалов (проводников или полупроводников).

2. Алгебраическая сумма всех термоЭДС в контуре, состоящем из любого количества соединений разных материалов, будет всегда равна нулю, если все соединения находятся при одинаковых температурах.

Это значит, что при включении в любое плечо контура дополнительного материала С (рис. 3.6б) результирующая термоЭДС в контуре не изменится при условии, что оба новых соединения будут иметь одинаковую температуру. Отсюда следует, что термоэлектрический контур можно разомкнуть в любом месте и включить в него дополнительные материалы. Количество дополнительных материалов неограничено, необходимо поддерживать только одинаковую температуру в местах их соединений. Термоэлектрические соединения могут выполняться любым способом: сваркой, пайкой, скруткой, сплавлением и т. д.

Таким образом, если известны термоЭДС (Е₁ и Е₂) двух проводников А и В при их подсоединении к третьему проводнику С, то результирующее напряжение при непосредственном контакте проводников (А и В) будет равно алгебраической сумме термоЭДС Е₁ и Е₂:

. (3.22)

3. Если два соединения разных материалов, находящихся при температурах Т и Т₁, вырабатывают термоЭДС Е_Т1, а при температурах Т₁и Т₀(рис. 3.6в) результирующая темоЭДС равна Е_Т2, то при температурах Т и Т₀выходная ЭДС определяется суммой двух ЭДС Е_Т1и Е_Т2.

В табл. 3.3 приведены значения коэффициента термоЭДС некоторых материалов по отношению к платине (при 100 ⁰С) [6].

Таблица 3.3

Материал	Кремний	Железо	Константан	Молибденит
ТермоЭДС, мВ	+44	+1,8	-3,4	-69 … -104

В простейшем случае, когда цепь состоит из двух проводников или полупроводников, она называется термоэлектрическим преобразователем, или термопарой. Проводники или полупроводники, составляющие термопару, называются термоэлектродами, а места их соединения – спаями. Спай термопары, воспринимающий измеряемую температуру Т, называется рабочим (горячим) спаем. Второго спая обычно нет, а есть два так называемых «свободных» конца, с которых снимается термоЭДС.

Третий закон позволяет градуировать (калибровать) термопару в одном температурном диапазоне, а использовать в другом [20], и его называют законом промежуточных температур.

Эффект Зеебека нашел широкое применения в области измерения температуры, в частности в термоэлектрических преобразователях.

Эффект Гаусса. Диск Корбино — Мегаобучалка

Механизмы поглощения света в полупроводниках.

В полупроводниках имеются следующие четыре основных механизма поглощения света: 1. Поглощение на свободных носителях заряда. Для обозначения этого вида поглощения света иногда используется термин «друдевское» поглощение. Этот механизм поглощения связан с движением электронов в зоне проводимости и дырок в валентной зоне. Это движение из-за рассеяния носителей заряда приводит к ненулевой действительной части проводимости, которая и ответственна за поглощение. 2. Межзонное (фундаментальное) поглощение света. В этом случае при поглощении фотона электрон переходит из валентной зоны в зону проводимости.

3. Примесное поглощение света. При примесном поглощение начальное или конечное (или оба из них) состояние электрона в процессе поглощения света является связанным на примеси (доноре или акцепторе). 4. Решеточное поглощение света. В этом случае энергия света переходит в энергию колебаний решетки. Кроме того, свет может при определенных условиях поглощаться за счет взаимодействия с такими элементарными возбуждениями как плазмоны, магноны и др. Иногда в отдельный класс поглощения света выделяют процессы поглощения света в присутствии сильного магнитного поля (магнетопоглощение).

 

Люминесценция в полупроводниках при прямых фундаментальных переходах

 

Люминесценция является процессом, обратным поглоще­нию, т. е. случаем, когда полупроводник, находящийся в воз­бужденном состоянии, испускает электромагнитное излуче­ние.

Согласно принципу Франка—Кондона, спектр люминесцен­ции, как правило, смещен в сторону длинных волн по срав­нению с длиной волны возбуждения света.

Длительность спонтанного свечения определяется време­нем жизни носителей в возбужденном состоянии. В случае мономолекулярной релаксации возбужденных состояний I _Л ~ I ₀ e^{— t / τ . При большом уровне возбуждения интенсивность люминесценции описывается выражением}

I = I^{0 /(1+ βt )2}

где β — константа, зависящая от степени предварительного возбуждения. В случае такой зависимости считают, что лю­минесценция идет по бимолекулярному механизму. По анало­гии с процессом поглощения рассмотрим рекомбинационное излучение полупроводников при фундаментальных перехо­дах, которое возникает при непосредственной рекомби­нации свободных носителей, при аннигиляции экситонов, а также при излучательной рекомбинации носителей через рекомбинационные ловушки, которые выступают в качестве центров свечения.

Прямые переходы наиболее вероятны. С ростом темпера­туры в незаполненных зонах заполняются все более высоко­лежащие состояния и в спектре люминесценции появляется коротковолновый «хвост».

В примесных полупроводниках люминесценция идет пре­имущественно через локализованные центры рекомбинации. Отметим, кто при рекомбинации донор — акцептор последние необходимо рассматривать как неподвижную молекулу, по­мещенную в кристалл:

hυ=ΔE-E_A-E_D+e²/ε²

т. е. кулоново взаимодействие между донором и акцептором, находящихся в среде с диэлектрической проницаемостью ε , вызывает уменьшение их энергии связи на величину

ΔE _кул = e^{2 / ε2}

В зависимости от узлов кристаллической решетки, которые занимают доноры и акцепторы, существуют различные виды активных центров. Для получения стимулированного излуче­ния в полупроводниках система должна находиться в состоя­нии с инверсной заселенностью. При этом

F_n — F_p > hυ

F_n — F_p > ΔE

где F_n и F_p , — положения квазиуровня Ферми для электронов и дырок соответственно. В таком случае система прозрачна на длине волны излучения. Состояние с инверсной заселен­ностью в полупроводниках может быть создано инжекцией неосновных носителей через p — n переход за счет возбуж­дения материала электромагнитным излучением, облучением электронами высоких энергий, ударной ионизацией в силь­ном электрическом поле.

 

Эффект Гаусса. Диск Корбино

Эффект Гаусса – эффект зависимости удельного сопротивления полупроводника (металла), помещенного в магнитное поле, от значения индукции этого поля.

Такая зависимость объясняется тем, что носители заряда (фермионы), перемещающиеся в полупроводнике (металле) под действием электрического поля, обладают не одинаковыми значениями скорости перемещения, так как известно, что скорости носителей заряда подчиняются распределению, отвечающему статистике Ферми-Дирака:

 

где E_F – энергия Ферми; E_i – энергия i-го состояния фермиона; k – постоянная Больцмана; T – абсолютная температура.

В результате, наводимое поперечное поле Холла (4.1) компенсирует влияние силы Лоренца только на носители тока, имеющие некоторую скорость v (рис. 4.1). Траектория же носителей тока, скорость которых отлична от v, будет искривляться, приобретая дугообразную форму (рис. 1.1).

Такое искривление траекторий движения заряженных частиц приводит к увеличению числа их столкновений (сокращению длины свободного пробега), а, следовательно, – к понижению значения удельной проводимости и увеличению удельного сопротивления проводника или полупроводника (так называемый «физический эффект магнитосопротивления»).

где Δρ – приращение удельного сопротивления; ρ₀ – удельное сопротивление материала вне магнитного поля; σ₀ – удельная электрическая проводимость материала вне магнитного поля; σ_B – удельная электрическая проводимость в магнитном поле с индукцией B; μ_n – подвижность носителей заряда [12].

Естественно, что понятия слабого и сильного магнитных полей относительны, поскольку в условия μB<< 1 и μB>> 1 кроме магнитной индукции B, входит значение подвижности носителей заряда μ. Таким образом, сильное для полупроводников с высокой подвижностью электронов магнитное поле может являться слабым для полупроводников с меньшей подвижностью.

 

(4.9)

 

где A – коэффициент формы магниторезистора, при условии выражения подвижности носителей в единицах [см²·В^-1·см^-1], принимающий значение порядка ~10^-12.

Из выражения (4.9) следует, что при малых значениях магнитной индукции, величина ∆ρ/ρ₀ квадратично зависит от B, тогда как при больших значениях Bотношение ∆ρ/ρ₀ достигает насыщения.

 

В инженерной практике для оценки относительного изменения сопротивления полупроводника в магнитном поле также часто используется следующее выражение:

 

(4. 10)

где n – показатель степени, принимающий значения от 1 до 2, в зависимости от величины магнитной индукции.

Оптимальными геометрическими размерами, с точки зрения эффективности магниторезистивного эффекта, обладает так называемый диск Корбино – металлический или полупроводниковый диск, в котором один из электродов находится в центре диска, а другой расположен по длине его окружности (рис. 4.3). При такой конструкции магниторезистора, разность потенциалов Холла не возникает, так как отсутствуют грани, на которых могло бы происходить накопление заряда [13].

Здесь вне действия магнитного поля ток в образце направлен радиально. При помещении диска в магнитное поле B, вектор индукции которого перпендикулярен поверхности диска, носители тока будут отклоняться от изначальных радиальных прямых, вследствие чего траектория их движения будет удлиняться, но образование холловского поля, как было отмечено ранее – не происходит.

 

 

Рис. 4.3. Диск Корбино

 

В случае, когда проводимость диска Корбино обеспечивается зарядами одного знака, изменение его сопротивления рассчитывается как:

 

 

В другом случае, если в проводимости материала принимают участие и электроны и дырки, эффект изменения его удельного сопротивления будет определяться согласно выражению (4.12) [14].

 

(4.12)

 

где ε – отношение подвижности электронов к подвижности дырок; æ – отношение концентрации электронов к концентрации дырок.

В этом случае эффект Гаусса велик, так как электрическое поле Холла не противодействует силе Лоренца для носителей обоих типов.

 

 

Относительное изменение удельного сопротивления диска Корбино, изготовленного из полупроводника смешанной проводимости, определяется выражением (4.13) [12], [15].

 

(4.13)

 

Удельное сопротивление диска Корбино ρ никогда не бывает меньше удельного сопротивления образца ρ_B с a > b, но в некоторых случаях эти сопротивления могут быть равны.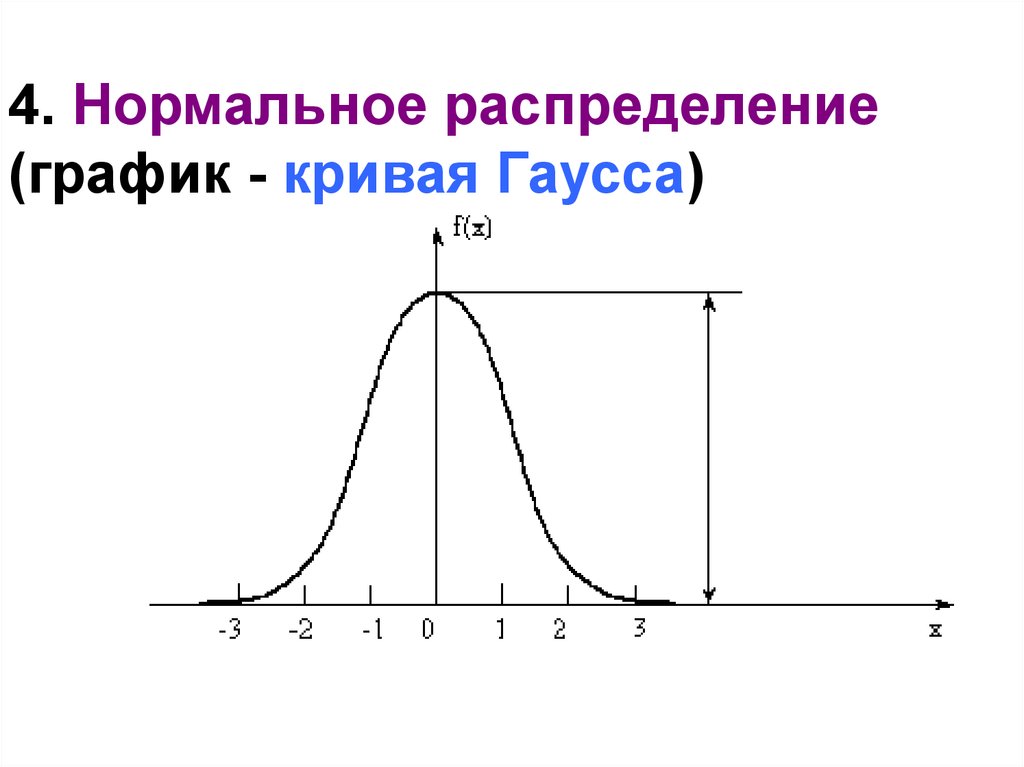 Выражение, связывающее их, имеет вид:

 

ρ = ρ_B(1+tan(θ)),

 

где θ – угол Холла (угол между направлением тока i и вектором суммарного поля E, т. е. угол отклонения носителей тока в результате эффекта Холла), рассчитываемый по формуле:

 

 

При θ=0 коэффициент Холла и поле Холла обращаются в ноль, и геометрические эффекты исчезают. Это возможно, при условии: ε=æ=1, тогда равенство соблюдается для всех значений B. Кроме этого, удельное сопротивление диска Корбино и магниторезистивное сопротивление образца прямоугольной формы совпадают при выполнении условия:

 

(4.14)

 

Выполнение условия (4.14) имеет место в полупроводниках с проводимостью p – типа, если ε > 1. В этом случае угол Холла меняет знак при увеличении магнитного поля и при некотором значении напряженности поля коэффициент Холла обращается в нуль.

 

Что такое размытие по Гауссу?

• по:
Левин Дэй

Размытие — это часто используемый визуальный эффект при цифровом редактировании фотографий и видео. Одним из наиболее распространенных размытий, используемых в этих областях, является размытие по Гауссу. Возможно, вы использовали этот инструмент тысячи раз, даже не задумываясь о нем. В конце концов, это делает хорошую работу и действительно делает вещи более размытыми.

Конечно, нам в Hackaday часто нравится копать глубже, поэтому вот наш краткий курс о том, что происходит, когда вы запускаете операцию размытия по Гауссу.

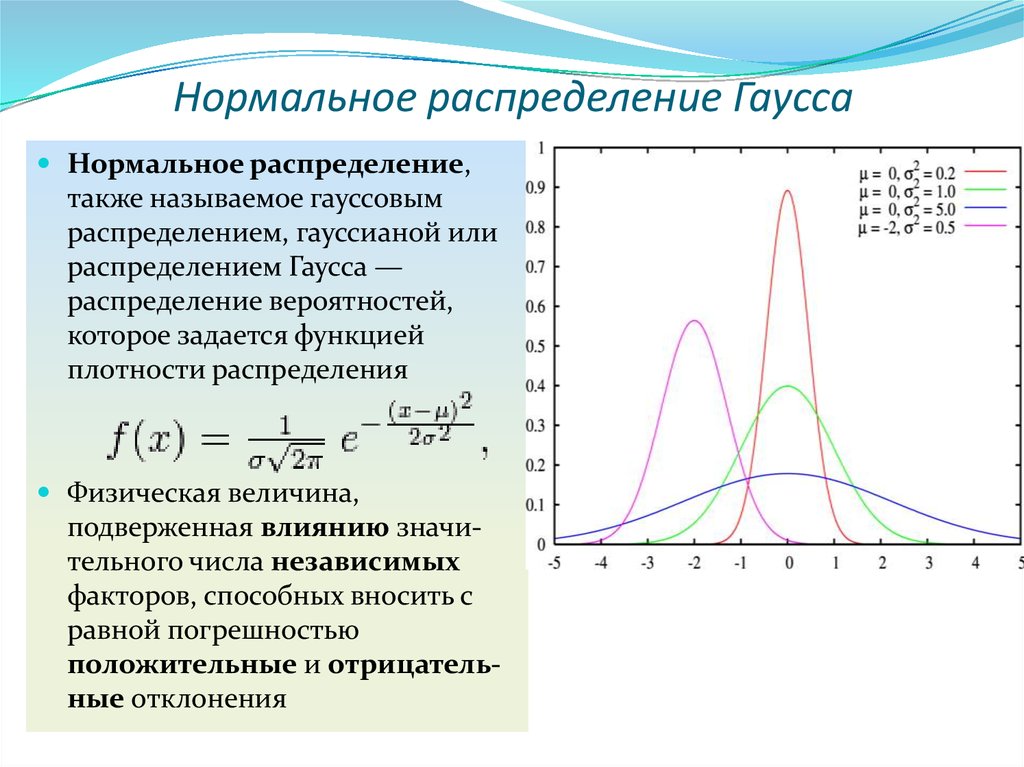
Двухмерное распределение Гаусса, показанное на трехмерном графике. Обратите внимание на более высокие значения по направлению к центру и уменьшающиеся по направлению к внешней стороне в форме колоколообразной кривой.

Цифровые изображения на самом деле представляют собой просто множество чисел, поэтому мы можем работать с ними математически. Каждый пиксель, из которого состоит типичное цифровое цветное изображение, имеет три значения: его интенсивность в красном, зеленом и синем цветах. Конечно, изображения в оттенках серого состоят только из одного значения на пиксель, представляющего его интенсивность по шкале от черного до белого с оттенками серого между ними.

Независимо от изображения, цветного или в оттенках серого, основной принцип размытия по Гауссу остается неизменным. Каждый пиксель в изображении, которое мы хотим размыть, рассматривается независимо, и его значение изменяется в зависимости от его собственного значения и значений его окружения на основе матрицы фильтра, называемой ядром .

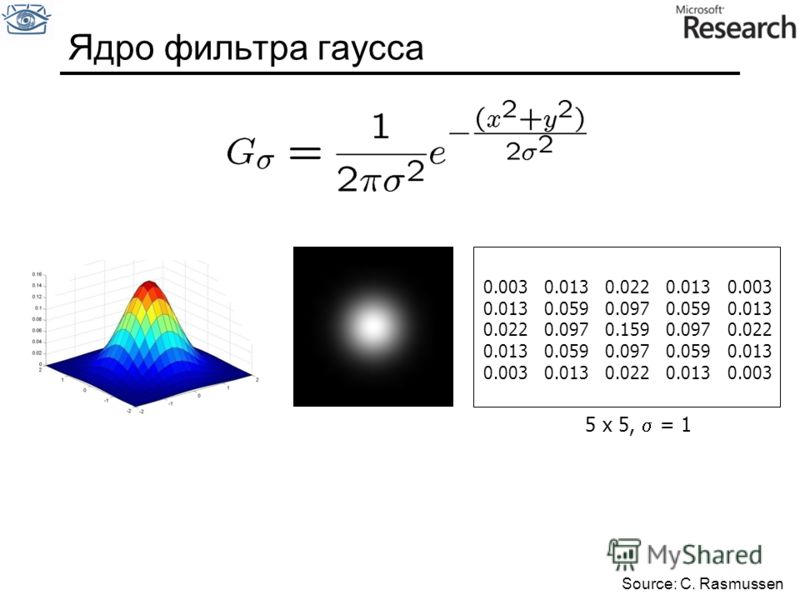
Ядро состоит из прямоугольного массива чисел, которые соответствуют распределению Гаусса, также известному как нормальное распределение или кривая нормального распределения.

На этой диаграмме показан способ обработки каждого пикселя. Для ядра 3×3 производится выборка интересующего пикселя и всех непосредственно окружающих пикселей. Затем ядро ​​используется для генерации нового значения выходного пикселя на основе средневзвешенного значения выбранных пикселей на основе распределения Гаусса.

Наше прямоугольное ядро ​​состоит из значений, которые выше в середине и уменьшаются к внешним краям квадратного массива, как высота колоколообразной кривой в двух измерениях. Ядро соответствует количеству пикселей, которое мы учитываем при размытии каждого отдельного пикселя. Ядра большего размера распространяют размытие на более широкую область, поскольку каждый пиксель модифицируется большим количеством окружающих его пикселей.

Для каждого пикселя, подлежащего операции размытия, вокруг интересующего пикселя берется прямоугольный участок, равный размеру ядра. Эти значения окружающих пикселей используются для вычисления средневзвешенного значения нового значения исходного пикселя на основе распределения Гаусса в самом ядре.

Ядро Гаусса 5×5. Обратите внимание на внешний фактор, который гарантирует, что сумма всех значений равна 1. Это позволяет избежать добавления какой-либо интенсивности к изображению, а только усредняет пиксели, не изменяя их интенсивность каким-либо иным образом.

Благодаря распределению исходное значение центрального пикселя имеет наибольший вес, поэтому оно не стирает изображение полностью. Непосредственно соседние пиксели оказывают следующее наибольшее влияние на новый пиксель и так далее. Это локальное усреднение сглаживает значения пикселей, и это размытие.

Пограничные случаи тоже просты. Когда производится выборка краевого пикселя, несуществующим в противном случае окружающим пикселям либо присваивается то же значение, что и у их ближайшего соседа, либо присваивается значение, совпадающее с их зеркальным противоположным пикселем в области выборки.

Такой же расчет выполняется для каждого пикселя в исходном изображении, которое необходимо размыть, при этом окончательное выходное изображение состоит из значений пикселей, вычисленных в процессе. Для изображений в градациях серого все просто. Цветные изображения можно сделать таким же образом, при этом размытие рассчитывается отдельно для красных, зеленых и синих значений каждого пикселя. Кроме того, вы можете указать значения пикселей в другом цветовом пространстве и сгладить их там.

Здесь мы видим исходное изображение и версию, отфильтрованную с помощью размытия по Гауссу с размером ядра три и размером ядра десять. Обратите внимание на усиление размытия по мере увеличения размера ядра. Больше пикселей, включенных в усреднение, приводит к большему сглаживанию.

Конечно, большие изображения требуют большего количества вычислений для работы с большим количеством пикселей, а большие размеры ядра выбирают больше окружающих пикселей для каждого интересующего пикселя, поэтому расчет может занять гораздо больше времени. Однако на современных компьютерах даже размытие изображений высокого разрешения с огромными размерами ядра можно выполнить в мгновение ока. Однако, как правило, редко используется размер ядра больше 50 или около того, поскольку к этому моменту все уже довольно размыто.

Размытие по Гауссу — отличный пример простой математики, которая эффективно используется при обработке изображений. Теперь вы знаете, как это работает на фундаментальном уровне!

 

Опубликовано в Избранные, Интерес, Оригинальное искусство, Слайдер, Взлом программного обеспеченияпомеченный размытие, цифровое фото, размытие по Гауссу, изображение, обработка изображений, изображения, фото

Понимание фильтров размытия по Гауссу | Medium

Давайте подробно рассмотрим реализацию размытия по Гауссу.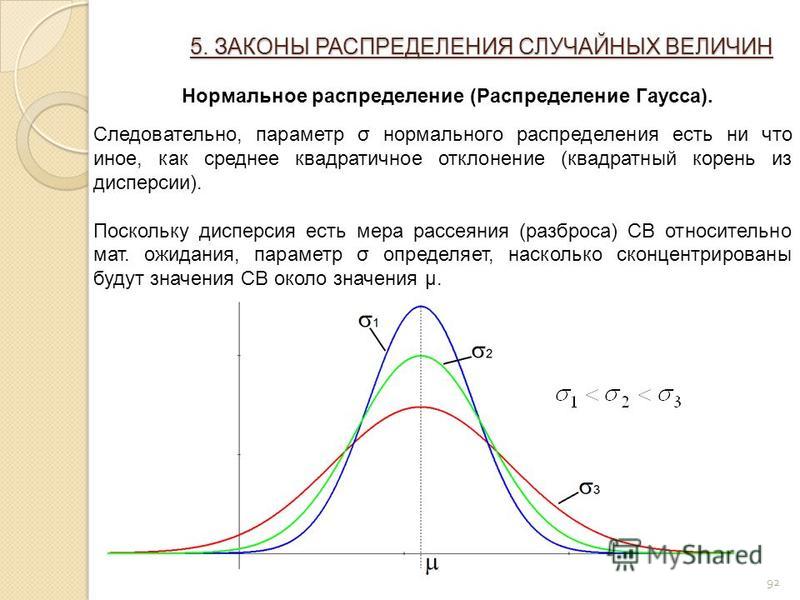 Это алгоритм обработки изображений, который позволяет манипулировать изображениями следующим образом:

Мы начнем с рассмотрения распределения Гаусса и свертки изображения — движущих сил размытия по Гауссу. Затем мы реализуем наш собственный алгоритм размытия по Гауссу с нуля с помощью Swift.

Если вы еще не читали мою статью о обнаружении границ в изображениях , я бы порекомендовал вам сначала прочитать ее. Это поможет заложить основу для свертки и основ обработки изображений.

Проще говоря, свертка — это просто процесс взятия небольшой матрицы, называемой ядром, и обработки ею всех пикселей изображения. Для каждого пикселя мы будем выполнять некоторую математическую операцию, включающую значения в матрице свертки и значения пикселя и его окружения, чтобы определить значение пикселя в выходном изображении.

Изменяя значения в ядре, мы можем изменить эффект на изображение — размытие, повышение резкости, обнаружение краев, уменьшение шума и т. д.

Теперь обратимся к гауссовой части размытия по Гауссу. Размытие по Гауссу — это просто метод размытия изображения с помощью функции Гаусса.

Возможно, вы уже слышали термин «гауссовский» по отношению к Распределение Гаусса (также известное как нормальное распределение) .

Ниже вы увидите двумерное распределение Гаусса. Обратите внимание, что в центре есть пик, а кривая сглаживается по мере продвижения к краям.

Представьте, что это распределение наложено на группу пикселей изображения. Глядя на этот график, должно быть очевидно, что если мы возьмем средневзвешенное значение значений пикселей и высоты кривой в этой точке, пиксели в центре группы внесут наибольший вклад в результирующее значение. По сути, так работает размытие по Гауссу.

TLDR: размытие по Гауссу применяется путем свертки изображения с помощью функции Гаусса.

На английском это означает, что мы возьмем функцию Гаусса и сгенерируем матрицу n x m . Используя эту матрицу и высоту распределения Гаусса в этом месте пикселя, мы вычислим новые значения RGB для размытого изображения.

Для начала нам понадобится функция Гаусса в двух измерениях:

Значения этой функции создадут матрицу/ядро свертки, которое мы применим к каждому пикселю исходного изображения. Ядро обычно довольно маленькое — чем оно больше, тем больше вычислений нам приходится выполнять для каждого пикселя.

x и y задают дельту от центрального пикселя (0, 0). Например, если для ядра выбран радиус 3, x и y будут варьироваться от -3 до 3 (включительно).

σ – стандартное отклонение – влияет на то, насколько сильно соседние пиксели центрального пикселя влияют на результат вычислений.

Технически, в функции Гаусса, поскольку она расширяется бесконечно, вы можете утверждать, что вам нужно учитывать каждый пиксель изображения, чтобы получить «правильный» эффект размытия, но на практике пиксели за пределами 3 σ очень мало влияют на результирующие значения.

Мы почти готовы начать внедрение.

Нам нужно создать отдельное выходное изображение. Мы не можем изменить исходное изображение напрямую, потому что изменение значений пикселей испортит математику для вычисления соседнего пикселя на следующей итерации.

Наконец, нам нужно подумать, как мы будем обрабатывать края. Если бы мы смотрели на самый первый пиксель изображения, ядро ​​вышло бы за пределы изображения. В результате реализации обычно игнорируют самый внешний набор пикселей, дублируют края или оборачивают изображение.

В нашем случае для простоты реализации мы будем игнорировать пиксели по краям.

Начнем с реализации функции Гаусса. Первая задача состоит в том, чтобы определить разумные значения для x , y и σ .

Хотя технически ядро ​​может быть произвольного размера, мы должны масштабировать σ пропорционально размеру ядра.