Как рассчитать эквивалентное сопротивление электрической цепи. Какие существуют методы для определения общего сопротивления цепи. Какие формулы применяются при последовательном и параллельном соединении резисторов. На каких примерах можно разобрать расчет эквивалентного сопротивления.
Понятие эквивалентного сопротивления электрической цепи
Эквивалентное сопротивление — это общее сопротивление участка электрической цепи, состоящего из нескольких резисторов. Его можно представить как один резистор, который оказывает такое же сопротивление току, как и вся рассматриваемая цепь.
Знание эквивалентного сопротивления позволяет:
- Упростить расчеты в сложных электрических схемах
- Определить общий ток и напряжение в цепи
- Рассчитать мощность, выделяемую на участке цепи
- Подобрать необходимые номиналы компонентов при проектировании схем
Методы расчета эквивалентного сопротивления
Существует несколько основных методов определения эквивалентного сопротивления электрической цепи:
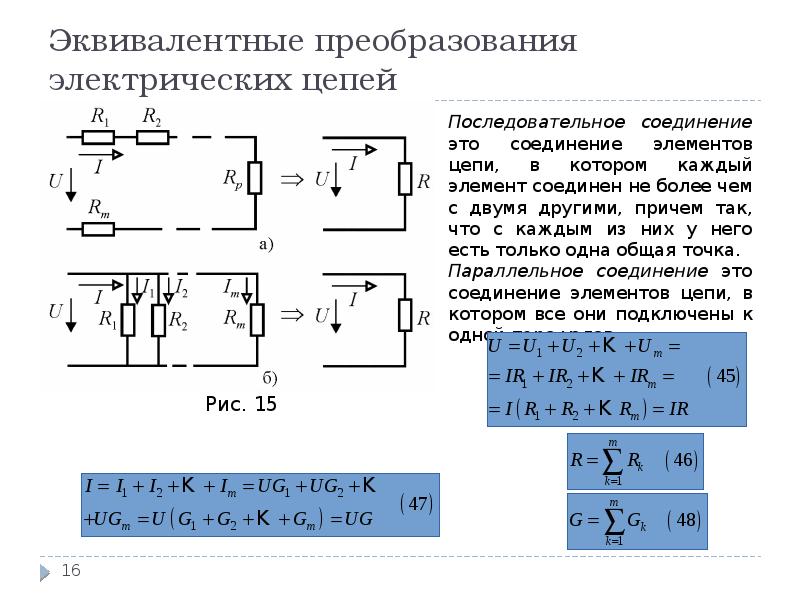
1. Метод эквивалентных преобразований
Заключается в последовательном упрощении схемы путем замены участков цепи их эквивалентами. Применяются формулы для последовательного и параллельного соединения резисторов.
2. Метод узловых потенциалов
Основан на составлении системы уравнений для узлов схемы с использованием законов Кирхгофа. Позволяет рассчитать потенциалы узлов и токи ветвей.
3. Метод контурных токов
Предполагает составление уравнений для независимых контуров схемы. Из полученной системы уравнений определяются контурные токи.
4. Метод наложения
Применяется в схемах с несколькими источниками ЭДС. Расчет ведется для каждого источника отдельно, а затем результаты суммируются.
Формулы для расчета эквивалентного сопротивления
При последовательном соединении резисторов общее сопротивление равно сумме сопротивлений отдельных резисторов:
Rэкв = R1 + R2 + R3 + … + Rn
При параллельном соединении используется формула:
1/Rэкв = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
Для двух параллельно соединенных резисторов часто применяется упрощенная формула:
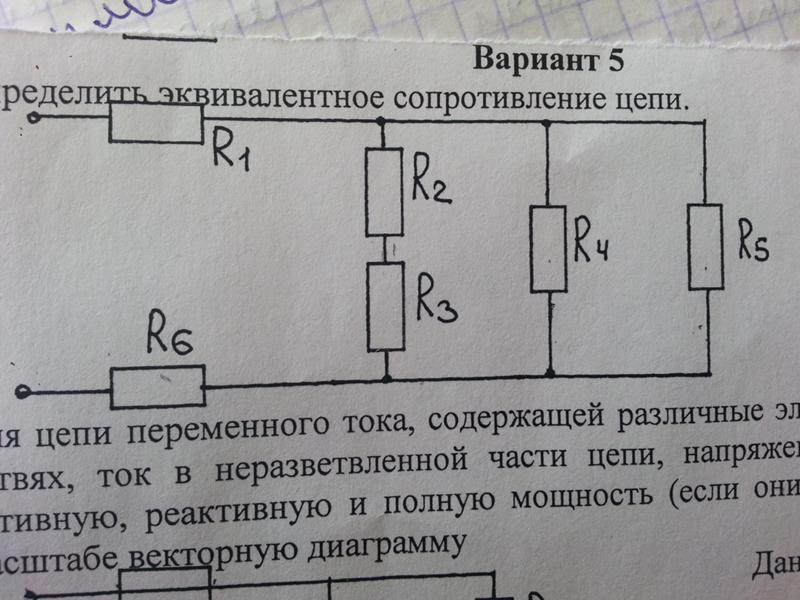
Rэкв = (R1 * R2) / (R1 + R2)
Примеры расчета эквивалентного сопротивления
Пример 1. Последовательное соединение
Дано: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом
Rэкв = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом
Пример 2. Параллельное соединение
Дано: R1 = 6 Ом, R2 = 3 Ом
Rэкв = (R1 * R2) / (R1 + R2) = (6 * 3) / (6 + 3) = 18 / 9 = 2 Ом
Пример 3. Смешанное соединение
Рассмотрим схему со смешанным соединением резисторов:
- R1 = 10 Ом и R2 = 20 Ом соединены последовательно
- R3 = 30 Ом подключен параллельно к R1 и R2
Решение:
- Находим эквивалентное сопротивление R1 и R2: R12 = R1 + R2 = 10 + 20 = 30 Ом
- Рассчитываем общее сопротивление параллельного участка R12 и R3:
Rэкв
Применение метода эквивалентных преобразований
Метод эквивалентных преобразований позволяет пошагово упростить сложную схему до одного эквивалентного резистора. Рассмотрим его применение на конкретном примере.
Пример расчета сложной цепи
Дана схема с 5 резисторами:
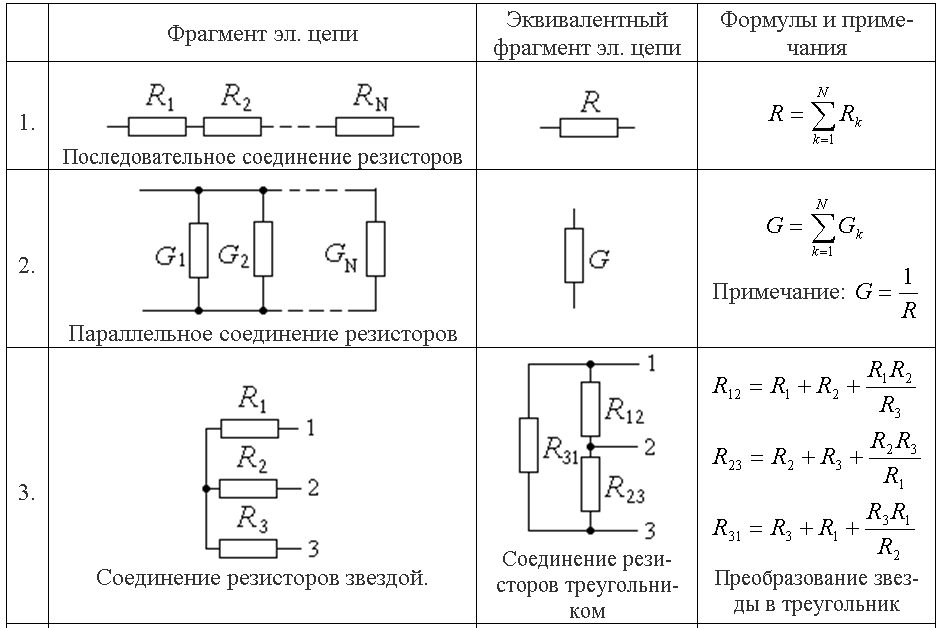
- R1 = 10 Ом и R2 = 20 Ом соединены последовательно
- R3 = 30 Ом и R4 = 40 Ом соединены параллельно
- R5 = 50 Ом подключен последовательно к параллельному участку R3-R4
Алгоритм решения:
- Находим эквивалентное сопротивление R1 и R2: R12 = R1 + R2 = 10 + 20 = 30 Ом
- Рассчитываем эквивалентное сопротивление параллельного участка R3-R4: R34 = (R3 * R4) / (R3 + R4) = (30 * 40) / (30 + 40) = 1200 / 70 ≈ 17,14 Ом
- Определяем сопротивление последовательного участка R34 и R5: R345 = R34 + R5 = 17,14 + 50 = 67,14 Ом
- Находим общее эквивалентное сопротивление цепи (R12 и R345 соединены параллельно): Rэкв = (R12 * R345) / (R12 + R345) = (30 * 67,14) / (30 + 67,14) ≈ 20,73 Ом
Особенности расчета сложных электрических схем
При анализе сложных электрических цепей следует учитывать ряд важных моментов:
- Необходимо правильно определять тип соединения резисторов (последовательное, параллельное, смешанное)
- Целесообразно начинать упрощение схемы с наиболее удаленных от источника питания участков
- Важно соблюдать порядок действий и не пропускать промежуточные вычисления
- При наличии нескольких источников ЭДС может потребоваться применение метода наложения
- Для проверки правильности расчетов полезно использовать законы Ома и Кирхгофа
Применение знаний об эквивалентном сопротивлении на практике
Умение рассчитывать эквивалентное сопротивление имеет широкое практическое применение:

- Проектирование электронных устройств
- Настройка и ремонт электрооборудования
- Оптимизация энергопотребления электрических систем
- Расчет параметров электрических сетей
- Разработка схем защиты электроцепей
Освоение методов определения эквивалентного сопротивления позволяет глубже понять принципы работы электрических цепей и эффективно решать практические задачи в области электротехники и электроники.
Онлайн определение эквивалентного сопротивления
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.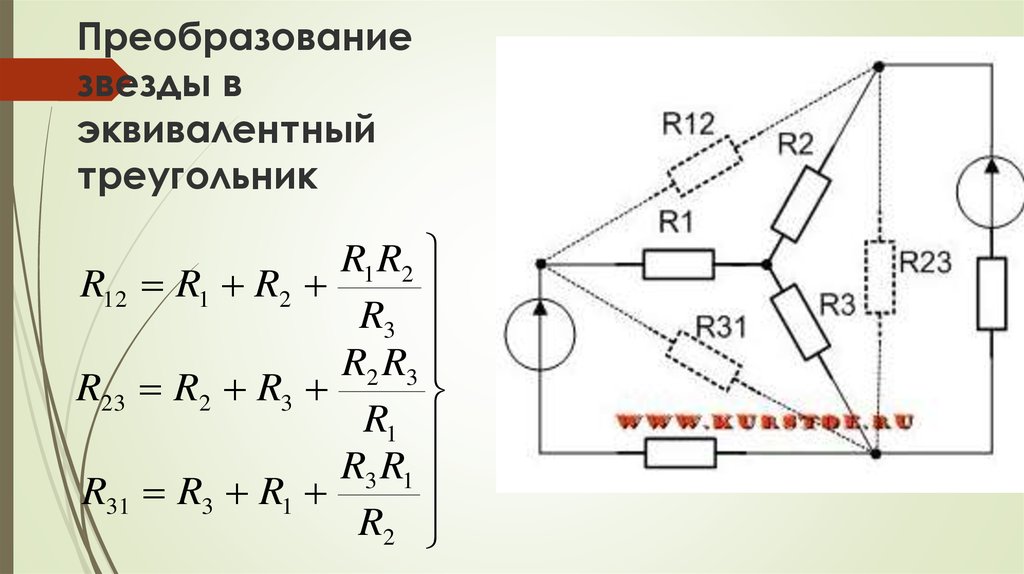
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.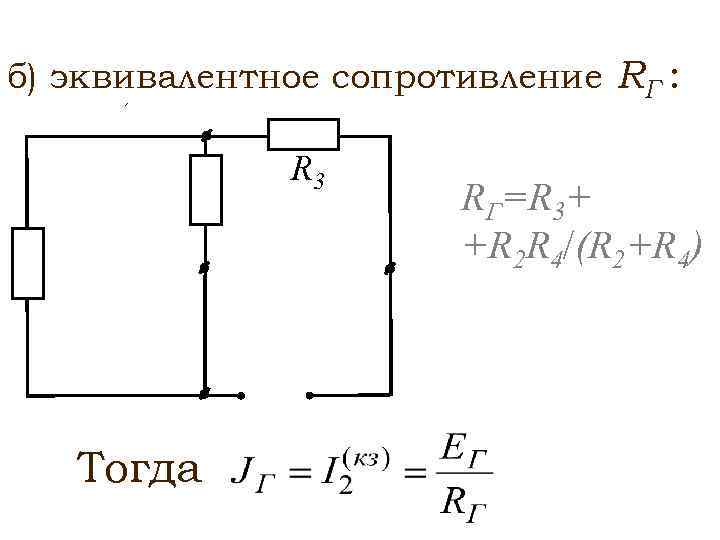
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.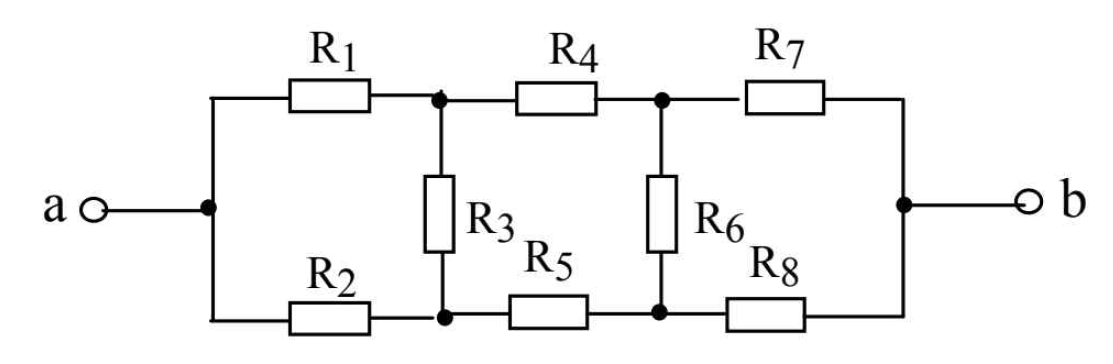
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
где R — величина сопротивления, Ом;
n — количество параллельно соединенных сопротивлений.
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
Задача 4.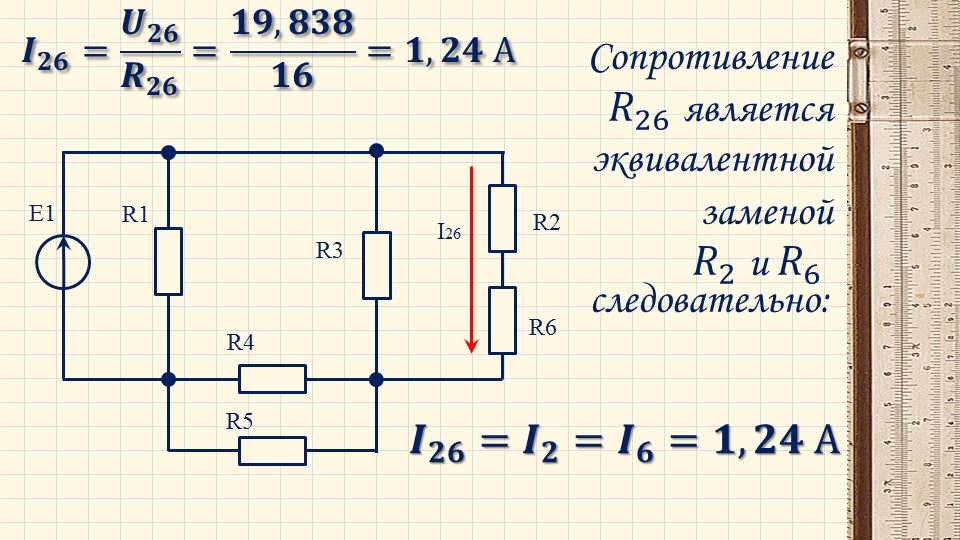 В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf.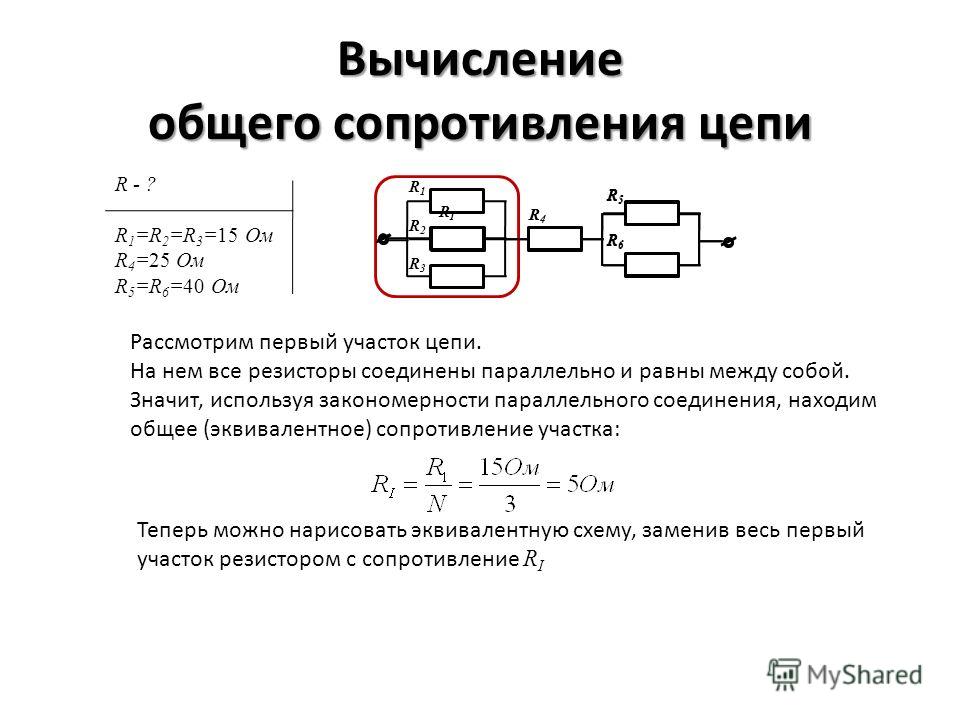 Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Красивые девушки в стиле ню.
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
Эквивалентное сопротивление — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
AP Physics 1 Справка » Электричество и волны » Электричество » Схемы » Эквивалентное сопротивление
Рассмотрим следующую цепь:
Каково общее эквивалентное сопротивление цепи?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала нам нужно уплотнить R3 и R4. Они расположены последовательно, поэтому мы можем просто сложить их, чтобы получить:
Они расположены последовательно, поэтому мы можем просто сложить их, чтобы получить:
Теперь мы можем уплотнить R2 и R34. Они параллельны, поэтому мы будем использовать следующее уравнение:
Следовательно:
Эквивалентная схема теперь выглядит так:
Так как все последовательно, мы можем просто сложить все:
Сообщить об ошибке точка от А до Б?
Возможные ответы:
Правильный ответ:
Пояснение:
В новой схеме параллельно подключены два резистора: R2 и новый. Чтобы найти эквивалентное сопротивление этих двух ветвей, воспользуемся следующим выражением:
В этой новой эквивалентной схеме все последовательно, поэтому мы можем просто сложить сопротивления:
Теперь мы можем использовать закон Ома для расчета полного тока в цепи:
Сообщить об ошибке
Рассмотрим данную цепь:
Какое сопротивление должно быть приложено между точками A и B, чтобы в цепи был общий ток 3А?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы будем работать над этой задачей в обратном порядке, используя ток для нахождения сопротивления. Мы знаем напряжение и требуемый ток, поэтому мы можем рассчитать общее необходимое сопротивление:
Мы знаем напряжение и требуемый ток, поэтому мы можем рассчитать общее необходимое сопротивление:
Затем мы можем рассчитать эквивалентное сопротивление двух резисторов, которые включены параллельно (R2 и наше неизвестное):
Теперь мы можем рассчитать, какое сопротивление между точкой A и B:
. Перестановка для желаемого сопротивления:
Отчет о ошибке
. Схема:
.
Если эквивалентное сопротивление цепи равно и каждый резистор одинаков, каково значение каждого резистора?
Возможные ответы:
Ни один из этих
Правильный ответ:
Объяснение:
Мы можем использовать уравнение для эквивалентного сопротивления параллельных резисторов, чтобы решить это уравнение:
Мы знаем эквивалентное сопротивление, и мы знаем, что сопротивление каждого из четырех резисторов равно:
Сообщить об ошибке
Рассмотрим схему:
Если мощность, рассеиваемая во всей цепи, равна , каково значение ?
Возможные ответы:
Правильный ответ:
Пояснение:
Зная мощность потерь и напряжение цепи, мы можем рассчитать эквивалентное сопротивление цепи, используя следующие уравнения:
Подставив закон Ома в уравнение для мощности, получим:0005
Переставляя сопротивления, получаем:
Это эквивалентное сопротивление всей цепи. Теперь мы можем рассчитать R4, используя выражение для параллельных резисторов:
Теперь мы можем рассчитать R4, используя выражение для параллельных резисторов:
Сообщить об ошибке
Рассмотрим цепь:
Если ток, протекающий через цепь, каково значение R1?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем использовать закон OHM’s для расчета эквивалентного сопротивления схемы:
Теперь мы можем использовать выражение для объединения параллельных резисторов для расчета R1:
9 9000 9000
9000 9000
Сообщить об ошибке
Рассмотрим схему:
Если эквивалентное сопротивление цепи равно , какая из следующих конфигураций значений сопротивления возможна?
Возможные ответы:
Ни один из этих ответов
Объяснение:
Нам нужно будет проверить значения каждого ответа, чтобы найти тот, который генерирует сопротивление, эквивалентное .
Мы знаем, что при соединении параллельных резисторов эквивалентное сопротивление никогда не будет больше наибольшего одиночного сопротивления и всегда будет меньше наименьшего сопротивления. Следовательно, два варианта ответа можно исключить сразу.
После того, как мы сузили наш выбор до других вариантов ответов, нам просто нужно проверить их по следующей формуле:
Сначала мы проверим неправильный ответ:
Теперь правильный ответ:
Сообщить об ошибке
Каково эквивалентное сопротивление от точки А до точки Б?
Возможные ответы:
Правильный ответ:
Пояснение:
Поскольку эта схема не является ни чисто последовательной, ни чисто параллельной, мы должны упростить ее, прежде чем решать. Замените правую ветвь, которая является чисто последовательной, ее эквивалентным сопротивлением:
Теперь у нас есть чисто параллельная цепь, каждая ветвь которой имеет сопротивление . Примените параллельную формулу и решите:
Примените параллельную формулу и решите:
Сообщить об ошибке
Каково эквивалентное сопротивление следующих резисторов, соединенных последовательно: ?
Возможные ответы:
Правильный ответ:
Пояснение:
Для последовательно соединенных резисторов эквивалентное сопротивление равно сумме сопротивлений.
Сообщить об ошибке
Каково эквивалентное сопротивление цепи, состоящей из группы резисторов (соединенных параллельно) со следующими сопротивлениями: ?
Возможные ответы:
Правильный ответ:
Объяснение:
Обратная величина эквивалентного сопротивления для параллельных резисторов равна сумме обратных величин сопротивлений:
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Учитесь по концепции
Эквивалентное сопротивление
Эквивалентное сопротивление
Используйте ряд, параллель и закон Ома, чтобы найти эквивалент Сопротивление
Учись!
Предварительные знания
Цель
Найти эквивалентное сопротивление.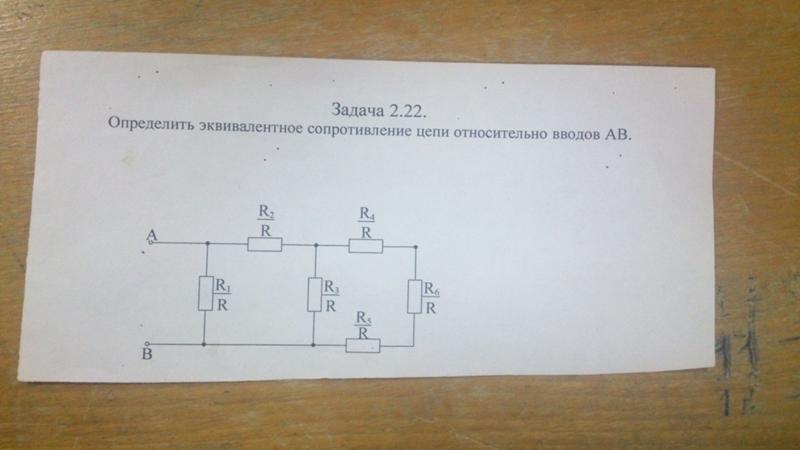
Эта группа резисторов действовать как один эквивалентный резистор. Каково его сопротивление?
Часть 1
Перерисовать схему
+
1A
Преобразование схемы
Принципиальные схемы являются абстракцией реальную схему, есть много способов их рисовать и перерисовывать. Этот пример показывает вам, как перерисовывать принципиальные схемы в соответствии с целями
Нам нужны вещи, которые выглядят так. Просто доверься мне. Все резисторы ориентированы вертикально. Терминалы, выходящие из середины сверху и дно.
В конечном итоге нам нужны только вертикальные резисторы. Наша первая задача
попробуйте разрешить эту диагональную часть с левой стороны. нам не нравится
диагонали.
нам не нравится
диагонали.
+
?
Растянуть и согнуть
Символ <-> означает, что вы можете другой свободно, в зависимости от того, что сделает вашу диаграмму более понятной и удобной. удобнее анализировать.
Растяжение и изгиб: Длина, ориентация и форма идеальных проводов в схемы не имеют значения. Длина и форма этих соединений не влияет напряжения и токи на элементах (для реальных цепей проволока длина имеет значение).
В качестве первого хода мы натяните немного проволоки, чтобы Т-образное соединение выглядело немного лучше.
+
?
Повернуть
Повернуть: Ориентация элемента схемы не имеет значения.
Давайте поверните их, чтобы они стали вертикальными. Мы сделаем их сразу узнаваемыми позже, после того, как мы поработаем над другими частями схемы.
+
?
Слайд
Слайд: Вы можете сдвинуть идеальный резистор вдоль куска идеального проводник.
Теперь немного почистим правую сторону. мы можем слайд \(4 \Омега\) резистор за углом, УРА!
Мы также можем Т-образно сдвинуть точки A и B так, чтобы они совпали с пересечением \(10 \Омега\) резистор
+
?
Т-образные направляющие
Т-образные направляющие также могут проходить повороты!
Теперь мы хотим получить этот \(8 \Омега\) резистор
в соответствии. Во-первых, давайте сделаем
Т-образный ползун , чтобы переместить этот угол к центру провода. Это дает нам
клеммы торчат сверху и снизу.
Во-первых, давайте сделаем
Т-образный ползун , чтобы переместить этот угол к центру провода. Это дает нам
клеммы торчат сверху и снизу.
Теперь сдвинем резистор 8 по проводу за угол на вертикаль сегмент.
★
Теперь наша схема преобразилась. Сделав это несколько раз, вы сможете сделать все это в своей голове. Просто нужно немного упражняться.
+
!
Являются ли допустимые ходы «настоящими»
Эти «разрешенные ходы» аналогичны операции на макетной плате тоже. Они не просто чистые абстракции для диаграммы.
Часть 2
Определение эквивалентного сопротивления
Использование формул параллельных и последовательных соединений для разложения цепей по частям
время.
+
2A
Уменьшите два последовательных резистора справа
Эта схема хороша. Обведенные сегменты выглядят так специальные шаблоны, упомянутые ранее в примере.
Эти конфигурации достаточно распространены и важны, чтобы иметь имена.
Тот, что справа, называется Серия
Два резистора соединены последовательно, если они совместно используют один узел, в отличие от других элемент подключен к.
Мы можем заменить ряд резисторов одним резистор с Эквивалентное сопротивление обозначается символом \(R_{eq} \)
\(R_{eq} =R_1+R_2\)
+
?
Как понять и запомнить эту формулу?
Помните о вычислениях
удельное сопротивление проводов? Поставить два одинаковых резистора последовательно, это как
удвоение длины провода и более длинные провода имеют пропорционально больше
сопротивление.
+
!
Доказательство
Если вы хотите увидеть доказательство того, как это было получено, кликните сюда. У вас есть все инструменты, чтобы следовать ему.
\[R_{eq1} = R_1 + R_2 = 4+2 = 6 \]
Теперь наша схема хорошо преобразована. Сделав это несколько раз, вы сможете сделать все это в своей голове. Просто нужно немного упражняться.
+
2B
Уменьшите два параллельных резистора слева
Перерисуйте схему с эквивалентным резистором.
Конфигурация в кружке также является специальной конфигурацией. это называется Параллельно
Резисторы включены параллельно, если они имеют одни и те же узлы, но идти по разным проводам
Имеет эквивалентное сопротивление
\(R_{eq} = \dfrac{1} {\dfrac{1}{R_1} + \dfrac{1}{R_2}} \)
Другим способом представления этого является Произведение по правилу сумм
\(R_{eq} = \dfrac {R_1 * R_2} {R_1 + R_2} \)
+
?
Как понять и запомнить эту формулу?
Запомнить
формула с удельным сопротивлением? Параллельное соединение двух одинаковых резисторов похоже на
удвоение площади куска проволоки. Это снижает сопротивление, обеспечивая более широкий
путь для тока.
Это снижает сопротивление, обеспечивая более широкий
путь для тока.
+
!
Доказательство
Хотите увидеть доказательство? Проверьте это здесь.
\[R_{eq2} = \dfrac{1}{\dfrac{1}{R_1} + {\dfrac{1}{R_2}}} = \dfrac {1} {\dfrac{1}{20} + \dfrac{1}{30}} = 12 \]
Примените формулу параллельного сопротивления! Обратите внимание, что наш ответ разумно: параллельная конфигурация снижает сопротивление.
+
2C
Уменьшите количество последовательных резисторов слева
Перерисуйте схему с заменой параллельных резисторов с их эквивалентным сопротивлением.
Поиск простых сокращений. Резистор \(8\Омега\) и
Req (\(12\Omega\) вместе) находятся в
серия .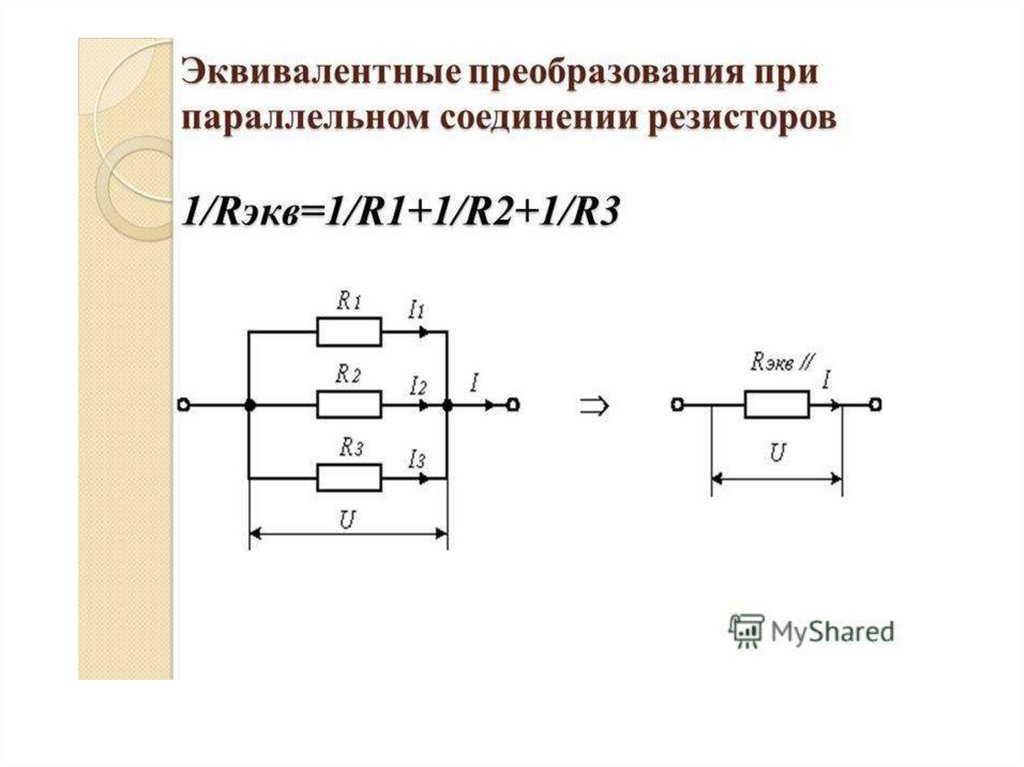
\[R_{eq3} = 8 +12 = 20 \]
Примените формулу последовательного эквивалентного сопротивления.
+
2D
Объединить три параллельных резистора
Перерисуем схему с третьим уменьшением вставлен.
Мы на финишной прямой. Выполнив несколько из них, вы сможете более одного шага за раз.
Параллельная формула работает для более чем двух резисторов как хорошо. Версия правила «произведение на сумму» с тремя или четырьмя резисторами уродлива. не используй это
В общем…
Для параллельных комбинаций резисторов
\(R_{eq}=\dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} +
\dfrac{1}{R_4} + .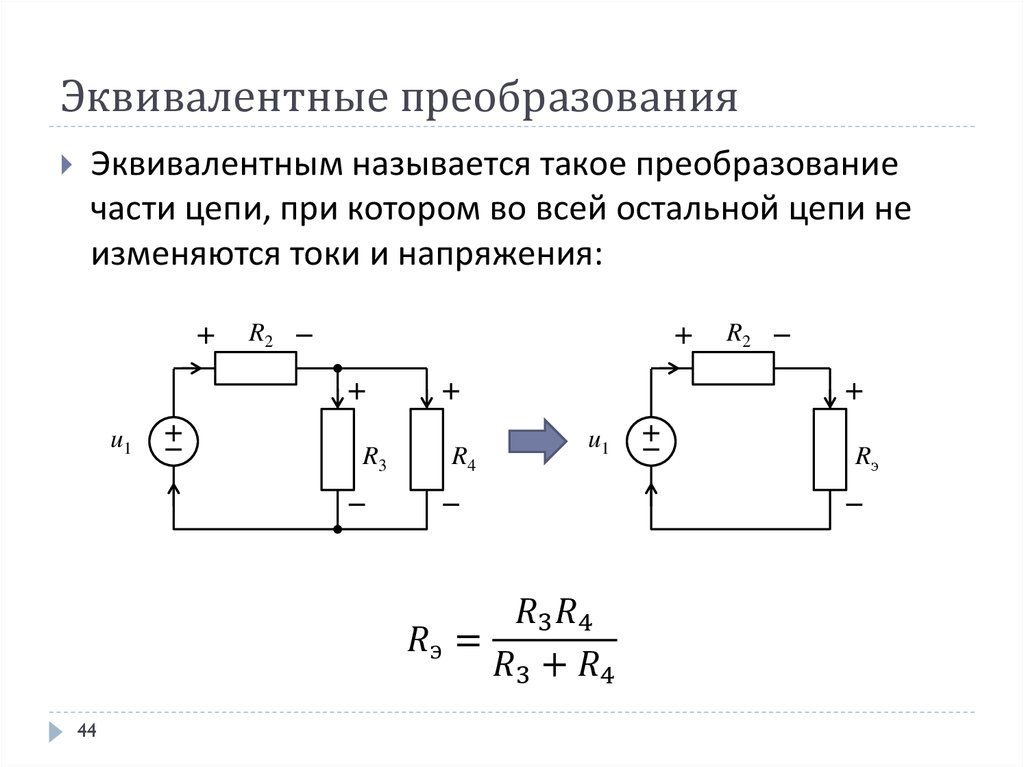


 Это вещь или объект которое по своим характеристикам повторяет оригинал. В электротехнике эквивалент сопротивления это замена части схемы состоящей из нескольких резисторов — одним элементом(эквивалентом)
Это вещь или объект которое по своим характеристикам повторяет оригинал. В электротехнике эквивалент сопротивления это замена части схемы состоящей из нескольких резисторов — одним элементом(эквивалентом)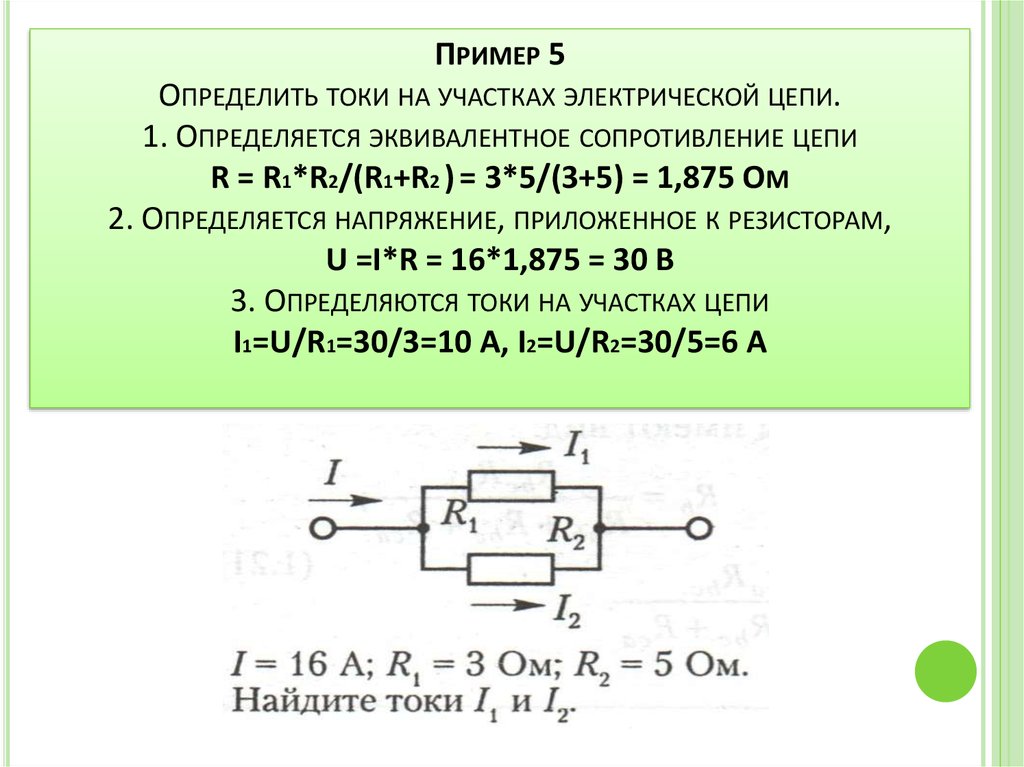
 >>
>>
 Настройка.
Настройка.
